1 Introduction

We welcome the opportunity to comment on Victor Truesdale’s paper, “Evidence and potential implications of exponential tails to concentration versus time plots for the batch dissolution of calcite” (Truesdale 2015). There are two major issues that warrant discussion here: (1) how rate “constants” are manipulated to describe overall reaction rates, and (2) the relationships of particle dissolution rate to surface area, defect distributions, and surface reaction mechanism. Before discussing these points, we provide a brief review of the paper’s major points. Truesdale introduces a dissolution model (the “shrinking object,” SO hereafter), which, he argues, is relevant to the dissolution of calcite under various conditions, as well as other minerals. In support of this model, he also presents the results of batch dissolution experiments (closed, stirred system) in which powdered calcite is added to solutions containing TRIS or NaOH buffer. Analytical results consist of dissolved calcium concentrations that are followed as a function of time (pH stability was also verified during solution sampling). He computes dissolution rates from the change in dissolved calcium concentration normalized to surface area (A) and assumes that there is no significant change in this term over the course of a given experiment (although A is given as “actual surface area of solid” in his Table 1, it is not clear from his text how this value was obtained).

According to the SO model, “ideal” reactions should proceed with simple, strict first-order dependencies, i.e., on surface area, in the case of the forward reaction step (dissolution), and on the product of surface area and a single concentration term in the case of the backward reaction (growth or precipitation). These assumptions, i.e., first-order growth rate dependence on concentrations of a single component, a surface reaction that proceeds mechanistically as written, with participation of the solid only as a fixed, unit surface area term, yield a solution of the resulting ODE, that is, to no great surprise, a simple exponential function of time:

$$\begin{aligned} c(t)&=c_{{\rm sat}}\left( 1-\exp \left( -k_{{\rm b}}\frac{A}{V}t\right) \right) \\&=c_{{\rm sat}}\left( 1-\exp \left( -k_{{\rm f}}\frac{1}{c_{{\rm sat}}} \frac{A}{V}t\right) \right) \end{aligned}$$

where \(\frac{A}{V}\) is the surface area per unit solution volume, \(k_{{\rm f}}\) and \(k_{{\rm b}}\) are the forward and backward reaction rate constants, respectively, and \(c_{{\rm sat}}\) is the equilibrium concentration of the single component (apparently determined separately as a function of pH). They also predict a simple linear dependency of the net rate on the concentration of the single component.

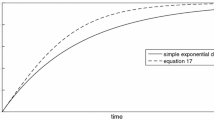
However, instead of this simple linear dependency, the observed concentration data show two apparent segments: an initial segment characterized by rapid dissolution \((t \sim O(N^{1}) \hbox {min})\), followed by a decaying, “long tail” \((t \sim O(N^{3}) \hbox {min})\), over which the rate \(({\frac{\hbox{d}[\hbox{Ca}^{2+}]}{\hbox{d}t}})\) approaches zero, and concentration converges on a fixed value. He computes initial rates using the slopes from the first segment, but argues that the long decay of rate over time is significant: if we understand his argument correctly, the departure of the observed rate from its expected congruence with this first-order SO model indicates a “complex” and “non-ideal” reaction. He further argues that despite the explicit first-order assumptions, “readers should avoid interpreting this as a first-order reaction, as it would have been had the kinetic system been a simple one.” Instead, he introduces another solution, a superposition of exponential terms parameterized by two other “rate constants,”

$$c=A(1-\exp ({-k_{1}t}))+B(1-\exp ({-k_{2}t}))$$
(1)

which are used to fit both the early and late reaction segments, accommodating the later rates as a straight line when these are plotted as a function of \(\ln (1-c/c_{{\rm sat}})\). Here, \(c_{{\rm eq}}=A+B\), and the new rate constants, as used here, presumably have subsumed the \(\frac{A}{V}\) terms as well.

2 Discussion

First, it has been understood for many years that the kinetics of calcite dissolution are complex, and that the value of “rate constants” depends on the origin and nature of the mineral, e.g., precipitated powder versus Iceland spar crystal rates (Rickard and Sjöberg 1983; Morse and Arvidson 2002). Although we are as yet unable to easily resolve the relationship between the distribution of the reaction rate over the mineral surface and measured changes in solution, there is new recognition of the sources of this problem and exploration of approach strategies (Fischer et al. 2012; Luttge et al. 2013; Fischer et al. 2014). The well-known, general problem of rate versus surface area is significantly enhanced in the case of particles. In addition to the interactions between solution composition and site and defect distributions, rate statistics in particle systems will be sensitive to contributions from crystal edges and similar features [grain and twin boundaries, corners, etc. (Schott et al. 1989; Arvidson et al. 2003; Fischer et al. 2012)], and thus a function of particle diameter. It thus seems likely that the assumption of constancy in the surface term is unwarranted, as the distribution of the surface reactivity changes as dissolution continues.

Fig. 1
figure 1

Schematic description of the dependence of rate on free energy, using the distinction between a near-equilibrium linear region and a far-from-equilibrium dissolution plateau (Lasaga and Luttge 2001). The former is controlled by the movement of extant steps, in which there is inadequate undersaturation \((|\Delta G_{{\rm r}}| < |G_{{\rm crit}}|)\) to initiate the development of hollow cores at screw dislocation centers; for the plateau \((|\Delta G_{{\rm r}}| > |G_{{\rm crit}}|)\), the continual generation of new steps at the margins of defect-generated etch pits ensures layer-by-layer removal. Data are from albite dissolution, figure adapted from Arvidson and Luttge (2010)

Full size image
Fig. 2
figure 2

Parabolic rate law for dissolution, \(r = Ak (1-\Omega )^{n}\). Top model rate versus \(\Delta G /\hbox {RT}\), with \(n=2\), showing far-from-equilibrium dissolution plateau (red line) and near-equilibrium linear region (magenta). It is possible that the intervening region may not reflect steady-state conditions (cf. Fig. 1), depending on the statistical distribution of reaction mechanism over the particle population. Rates are expressed in arbitrary units, see text for discussion. Bottom computed reaction path of above dataset in terms of \(\ln (1-\frac{c}{c_{{\rm eq}}})\) versus reaction time. Note that sluggish reaction progress in the near-equilibrium region requires increasing reaction times (per mole dissolved, arbitrary timescale), consistent with Truesdale’s observations (his fig. 4)

Full size image

Second, in discussing the canonical rate equation used for calcite dissolution (his eq. 1), Truesdale mentions that such an approach treats the reaction in a piecewise fashion, in which the resulting “reaction order(s)” assume purely empirical status. In the case of complex dissolution reactions, we agree that the attempt to unify rates under a global “rate law,” parameterized by empirical terms, although otherwise convenient from the standpoint of simple evaluation, may not otherwise yield much insight and in fact may conjoin rates that are quite distinct mechanistically. However, ignorance of reaction mechanism does not allow one to simply discard terms involved in its parameterization. To be sufficiently clear, we detour here slightly to review common rate equations used for calcite growth and dissolution in the context of detailed balancing and microscopic reversibility (Tolman 1925). As discussed elsewhere (Lasaga 1998), we can derive equations for dissolution and growth through detailed balancing, assuming for the sake of simplicity that concentrations are sufficiently small to warrant the approximation of single ion \(\gamma _{i}\sim 1\). We will also neglect, for now, the complex dependence of dissolution and growth reactions on surface area (A, hereafter assumed implicitly to be per unit volume solution). Similar to the treatment in Arvidson and Morse (2014), let us assume as a thought experiment that the concentration dependencies in the appearance of calcite during growth [r] versus its consumption [p] via dissolution for the reaction

$$\hbox {CaCO}_{3} \rightleftharpoons \hbox {Ca}^{2+}+\hbox {CO}_{3}^{2-}$$
(2)

can be represented as

$$\begin{aligned} {[}p]'&= {A}\,k_{+} \\ {[}r]'&= {A} \,k_{-} \,[\hbox {Ca}^{2+}]^n[\hbox {CO}_3^{2-}]^n \end{aligned}$$

where n is the reaction order that, although yet to be determined, is assumed to be the same with respect to both lattice species. At equilibrium, the net reaction must be zero,

$$\begin{aligned} {[}p]'-[r]'&= {A} \,\left( k_{+} - k_{-} \,[\hbox {Ca}^{2+}]^n [\hbox {CO}_3^{2-}]^n\right) = 0\\ k_{+}&= k_{-} K^{n} \end{aligned}$$

where K is the equilibrium constant for Eq. (2). For arbitrary, non-equilibrium conditions where the net rate \([p]'-[r]' \ne 0\), we can substitute \(\Omega ^n = \left( {[\hbox {Ca}^{2+}] [\hbox {CO}_3^{2-}]}/{K}\right) ^n\) to give expressions for dissolution and growth in terms of \(\Omega\) (as opposed to time, as in Eq. 1), respectively:

$$\begin{aligned} r_{{\rm d}}&= k_{-} \,{A} \,K^n \left( 1 - \Omega ^n\right) \\ r_{{\rm g}}&= k_{-} \,{A} \,K^n \left( \Omega ^n-1\right) \end{aligned}$$
(3)

Equations similar to Eq. (3) appear in previous treatments of calcite dissolution and growth kinetics with differences in the observed value of n (Reddy and Nancollas 1971; Sjöberg 1976). The difference between Eq. (3) and that most commonly used in geochemistry to describe the rate of carbonate mineral dissolution (Morse and Arvidson 2002),

$$r = k \,{A} \,\left( 1-\Omega \right) ^n$$
(4)

is in terms of the action of the reaction order, n. This critical point is discussed in Morse and Arvidson (2002), Arvidson and Morse (2014), and illustrated by expanding \(\Omega =e^{\Delta G/{{\rm RT}}}\) in a truncated Taylor series:

$$\exp (\Delta G / \hbox {RT}) = 1 + \frac{\Delta G}{\hbox {RT}} + \frac{1}{2!}\left( \frac{\Delta G}{\hbox {RT}}\right) ^2 + \cdots \approx 1 + \frac{\Delta G}{\hbox {RT}}$$

Close to equilibrium, the dissolution rate given by Eq. (3) is linear with respect to \(\Delta G\) (which is negative with respect to reaction 2):

$$r = A \,k \left( 1 - \Omega ^{n}\right) = - A \,k\, n \,\frac{\Delta G}{\hbox {RT}}$$

In contrast, the rate expressed by Eq.  (4) remains a nonlinear power function,

$$r = A \,k \left( 1 - \Omega \right) ^{n} = A \,k \, \left( \frac{|\Delta G|}{\hbox {RT}}\right) ^n$$

Thus, even close to equilibrium, the common expression for calcite dissolution (Eq. 4) remains nonlinear in \(\Delta G\), a distinction that should not be minimized. In the complementary expression for growth,

$$r = A \,k (\Omega - 1)^{n}$$

a similar nonlinear dependence was derived in the detailed treatment of crystal growth by Burton et al. (1951) and related to the fundamental role of screw dislocations (see also Nielsen 1981, 1984). The appearance of supersaturation raised to a power (typically \(n\sim 2\)) reflects the role of free energy as a driver for the diffusion of terrace ions toward step edges, as well as a control of the critical radius of curvature of the advancing spiral step (Arvidson and Morse 2014). A similar argument, in which screw dislocations cannot be regarded as equilibrium defects, can be made for crystal dissolution as well (see Lasaga 1998; Morse et al. 2007). Moreover, a detailed treatment of the relationship between \(\Delta G\) and dissolution rate for surface-limited reactions (Lasaga and Luttge 2001) demonstrates two regions to exist in terms of free energy dependence: a linear, near-equilibrium region in which dissolution is dependent on extant steps, and a far-from-equilibrium dissolution plateau (see, for example, albite dissolution in Fig. 1), whose boundary is a function of the value of \(\Delta G_{{\rm crit}}\), at which point there is sufficient free energy to permit hollow cores to form (Frank 1951). The bifurcation of rate with respect to these two distinct, surface reaction mechanisms is discussed in detail with respect to silicate reactions (see Luttge 2006; Beig and Luttge 2006).

Fig. 3
figure 3

Simulations of particle dissolution. Left kinetic Monte Carlo dissolution of a small, dissolving particle, assuming a simple cubic (Kossel–Stranski) crystal structure, in which reactive sites have been color-coded to reflect coordination and reactivity. Note that the corners and edges of the particle have suffered extensive material loss, with only minor pitting of terrace \(\{100\}\) faces. Crystal is free of defects. Right Details of inset region from left, clearly showing the high density of 3-bonded kink sites (yellow); 2-bonded sites are shown in red, step sites (4-bonded in tan and 5-bonded terrace sites) are in brown. In this kink-rich region, surface diffusion of adatoms (not shown) increases the probability that they will be accepted by a neighboring kink site prior to ultimate detachment and exit from the system

Full size image

With these thoughts in mind, we may consider the possibility that the persistence of the observed “long tails” described by Truesdale and the apparent transition between reactive regimes may be related to this \(\Delta G_{{\rm crit}}\) region. In calcite, the near-equilibrium region may be relatively small; nevertheless, as the system in these closed-system experiments traverses the overall reaction path described by Eq. (4), the solid will inevitably encounter a near-equilibrium region with time; depending on the volume distribution of defects among the particles and the previous consumption of extant step edges during the early dissolution “leg,” there may be inadequate driving force to continually nucleate new defect centers. These relationships are displayed in Fig. 2, constructed by computing the rate (Eq. 4) using \(n=2\). It is apparent that one can produce relationships using this “rate law” that are similar to those displayed in Truesdale’s dataset. Thus, we argue that rather than fit these data to piecewise expressions, a practice that, as has been argued previously (Beig and Luttge 2006; Arvidson and Luttge 2010), runs the risk of using a common expression to tie rates together that are otherwise mechanistically distinct: the slow, near-equilibrium “long tails” may simply reflect dissolution under conditions in which there is insufficient driving force to sustain new step generation beyond that already present.

Lastly, there is an additional important caveat here concerning the role of boundaries on particle surfaces (also as mentioned above). This can be illustrated with a simple Monte Carlo simulation involving an idealized, Kossel–Stranski crystal (see Fig. 3, left panel). This simulation illustrates a snapshot in time during the dissolution of a small particle, at which point substantial material has been lost from the original crystal corner and edge terminations. As the surface evolves, these areas become increasingly dominated by kink sites (shown in yellow). Atoms that are liberated from a given site on such high-index vicinal surfaces may thus not diffuse far before being trapped in an adjacent kink site, reducing the efficiency of the dissolution process and increasing the complexity in the relationship between surface area and net dissolution rate. We offer this as a simple example of the pitfalls of assuming a constant relationship between surface area, the extent of reaction, and the overall flux of material from the mineral particle.

3 Conclusions

Truesdale campaigns the significance of the observed stepwise change from fast initial to slow final decay of concentration over time, presenting these periods as “archetypes” with utility as reaction “templates” and emphasizing the fact that the concentration data fit exponential expressions. However, his statements that this work has revealed new aspects of the dissolution kinetics previously unrecognized appear to be at odds with the existing state-of-the-art understanding of calcite dissolution. Although he cites much of the voluminous work on calcite that has appeared over the last twenty years, much of the increased understanding in terms of site-specific reactivity (now a common observation in calcite AFM and related surface studies; see, e.g., Ruiz-Agudo et al. 2012) has not been fully incorporated in his paper. We do feel that the observations he has made are valuable, but our view diverges substantially from the approach he has taken in terms of integrating these into a larger heuristic framework.