Numerical Simulations of Short- and Long-Range Interaction Forces in Turbulent Particle-Laden Gas Flows

Abstract

The main objective of this work is to study the effects of distance-dependent interactions in turbulent gas-particle flows using an Euler–Lagrange simulation approach. The turbulent gas flow is accounted for via Direct Numerical Simulation to the Kolmogorov scale using a spectral method to solve the Navier–Stokes equations in a cubic computational domain with tri-periodic boundary conditions. This flow simulation is coupled (one-way) with a Lagrangian particle phase solver that performs particle trajectory tracking. Electrostatic forces can be calculated using two different approaches. Firstly, the direct method consists of a sum of all inter-particle interactions for all the particles of the computational domain and their periodic images. However, this purely Lagrangian approach is computationally costly for a large number of particles, therefore another approximative approach is considered. According to it, one can estimate the short-range interactions via a sum of inter-particle interactions within a cut-off distance and the long-range ones via a sum of particle interactions with clusters of particles that, from a distance greater than the cut-off, are “seen” as one pseudo-particle. This method is then adjusted in order to accommodate periodic boundary conditions, which are not trivial in the case of electrostatic interactions as periodicity entails an infinite number of periodic domain images that has to be truncated to a finite number. Simulations are then performed by varying the properties of the particles in terms of diameter, density (Stokes number) and charge (electrostatic Stokes number). Finally, a statistical analysis is performed in order to investigate how the dynamics of the turbulent gas-particle flow are affected by distance-dependent particle–particle interactions, namely electrostatic forces.

1 Introduction

Particulate flows are found in many practical applications from geophysical flows (pyroclastic flow, sediments transport, volcano ashes dispersion, ...) to industrial applications (pneumatic conveying, olefin polymerization, Fluid Catalytic Cracking of oil, silo discharge, ...). In these systems the inter-particle collisions or the particle-wall bouncing may lead the particles to accumulate electric charges which modify the dynamic behavior of the particles. As for example in fluidized beds (Rokkam et al. 2010; Kolehmainen et al. 2016), charges may lead the particles to form agglomerates (Ciborowski and Wlodarski 1962) that can change the fluidization regime or to adhere on the walls (Hendrickson 2006). In case of pneumatic conveying (Joseph and Klinzing 1983) or solid entrainment (Baron et al. 1987), charges may also alter granular flow dynamics. Effects of charges on particle dynamics have also been identified in geophysical flows especially for dust emission (Esposito et al. 2016) and for the saltating motion of grains (Schmidt et al. 1998; Zheng et al. 2006). Finally, electrostatic forces may be important in colloids, particularly regarding deposition (Li and Ahmadi 1993).

The present study is dedicated to the dispersion of inertial charged particles in turbulent flows. Several literature studies have been dedicated to charged particles transported by homogeneous isotropic turbulence (Lu et al. 2010; Lu and Shaw 2015; Karnik and Shrimpton 2012; Yao and Capecelatro 2018; Di Renzo and Urzay 2018) or by turbulent channel flow (Rambaud et al. 2002). These studies essentially focus on the modification of preferential concentration in the case of charged particles. Indeed, when solid non-charged particles are transported by a turbulent flow field, according to their inertia, they may accumulate in low-vorticity regions of the turbulence (Squires and Eaton 1991; Fessler et al. 1994). Such a mechanism leads to large local concentrations of particles that may modify the collision rate (Sundaram and Collins 1997; Reade and Collins 2000) or the coalescence rate if droplets are considered instead of solid particles (Wunsch et al. 2010). Furthermore, external forces may modify preferential concentration, as for example, Fede and Simonin (2010) showed that inter-particle collisions enhance preferential concentration. In addition, Dejoan and Monchaux (2013) investigated experimentally the effect of gravity on preferential concentration. Lu et al. (2010), Lu and Shaw (2015), Karnik and Shrimpton (2012), Yao and Capecelatro (2018) show that preferential concentration decreases when charges increase. However, they do not investigate how particle dispersion, in terms of agitation, is modified by electrostatic interactions. Basically, particles transported by stationary homogeneous isotropic turbulence follow the Tchen–Hinze theory (Hinze 1972) that entails that the particle kinetic energy is directly linked to the fluid agitation (see for example Zaichik et al. 2003; Fede and Simonin 2006) via fluid–particle velocity covariance. However, Laviéville et al. (1997) and later Fede et al. (2015) showed that when inter-particle collisions occur, particle agitation decreases even for elastic collisions. The way that electrostatic forces act on the particles is similar to collisions via the mechanism of Coulomb collisions typically found in cold plasma (Callen 2003).

In the present paper, DNS of stationary homogeneous isotropic turbulence are performed and coupled with Lagrangian tracking of the particles. Details of the physical problem are given in Sect. 2 and the numerical methods deployed are described in Sect. 3 with focus on the algorithm that accounts for electrostatic forces. The main material properties and statistics of the turbulence and particles are both given in Sect. 4. In this section, the case without charge is briefly analyzed. The main part of the paper is Sect. 5 where the effect of charges on the dispersion of inertial particles is analyzed. Conclusions are drawn in the last section of the paper.

2 Governing Equations for Charged Particles Transported by a Turbulent Fluid Flow

The studied configuration is a stationary homogeneous isotropic turbulent gas flow carrying mono-disperse inertial particles. The incompressible Navier–Stokes equations are solved by using a pseudo-spectral method. Periodic boundary conditions are applied on fluid and particle phase. Statistically steady flow is achieved by using the forcing scheme proposed by Eswaran and Pope (1988). The solid mass loading is sufficiently low for neglecting the turbulence modulation by the presence of particles.

The particles are considered as mono-disperse, with diameter $d_p$, and inertial, with density $\rho _p\gg \rho _f$. According to Maxey and Riley (1983) and Gatignol (1983), for the case of a large particle-to-fluid density ratio and for a particle diameter that is smaller than the Kolmogorov length scale, the force acting on the particles is only the drag force $\mathbf{F _d}$. In addition, if the particles are charged, then electrostatic force $\mathbf{F} _{e}$ may also be significant. Particle motion is governed by

$$\begin{aligned} \frac{d\mathbf{x} _p}{dt}= & {} \mathbf{u} _p \end{aligned}$$

(1)

$$\begin{aligned} m_p\frac{d\mathbf{u} _p}{dt}= & {} \mathbf{F} _{e}+\mathbf{F} _{d} \end{aligned}$$

(2)

where $\mathbf{x} _p$ is the particle position and $\mathbf{u} _p$ the particle velocity. In Eq. (2), the fluid–particle drag force is calculated by

$$\begin{aligned} \mathbf{F }_d = -\frac{\mathbf{u }_p - \mathbf{u }_{f@p}}{\tau _p}m_p \end{aligned}$$

(3)

where $\tau _p$ is the particle relaxation time given by Schiller and Naumann (1935)

$$\begin{aligned} \tau _p =\frac{\rho _p{d_p}^2}{18\rho _f\nu _f}\frac{1}{1+0.15{Re_p}^{0.687}} \end{aligned}$$

(4)

with $\nu _f$ the kinematic fluid viscosity, and $Re_p=d_p \Vert \mathbf{u} _p - \mathbf{u} _{f@p}\Vert /\nu _f$ the particle Reynolds number. In Eq. (3), $\mathbf{u} _{f@p}$ is the undisturbed fluid velocity at the particle position. The particle positions and velocities are time-advanced by a second order Adams-Bashforth scheme.

Coulomb’s law allows to calculate the electrostatic force $\mathbf{F} _{q\rightarrow p}$ acting on p due to q as following

$$\begin{aligned} \mathbf{F} _{q\rightarrow p} =\lambda \frac{Q_qQ_p}{\Vert \mathbf{r} _{qp}\Vert ^3}\mathbf{r} _{qp} \end{aligned}$$

(5)

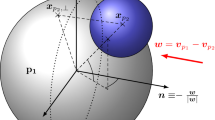
where $\lambda$ is Coulomb’s constant (with $\lambda = 1/\left(4\pi \epsilon _0\right)$ where $\epsilon _0$ is the vacuum permittivity), $Q_p$ is the electric charge of particle p and $\mathbf{r} _{qp} = \mathbf{x} _{p} - \mathbf{x} _{q}$ is the distance vector between particles p and q pointing to p as depicted in Fig. 1.

Fig. 1

Notations in electrostatic interaction of a dipole of iso-charged particles

In a system of $N_p$ charged particles, each particle p interacts with all $N_p-1$ particles in the computational domain, thus the total electrostatic force exerted on p is

$$\begin{aligned} \mathbf{F} _{e} = \sum \limits _{\begin{array}{c} q=1\\ q\ne p \end{array}}^{N_p} \mathbf{F} _{q\rightarrow p}\ . \end{aligned}$$

(6)

Next section is dedicated to the numerical methods for computing electrostatic force $\mathbf{F} _{e}.$

3 Numerical Methods for the Computation of Electrostatic Forces

3.1 Direct Dipole Summation

This method consists in calculating the total electrostatic force on a particle p by directly summing all the $N_p-1$ terms that correspond to the electrostatic interactions of the particle with all particles but itself as seen by Eq. (6). However, one could use Newton’s 3rd law for such a dipole that gives $\mathbf{F} _{p\rightarrow q} = -\mathbf{F} _{q\rightarrow p}$ in order to perform one operation per dipole thus divide the computational cost by two resulting in $N_p\left( N_p-1\right)/2 \sim {N_p}^2$ operations which is forbiddingly expensive.

3.1.1 Quasi-periodic Boundary Conditions

Periodic boundary conditions for the particle phase correspond to an infinite domain. Therefore, to compute the electrostatic forces it is necessary to take into account the contributions of all particles, including those not really represented/computed in the computational domain.

Let a cubic computational computational domain $\varOmega$ of length L (see Fig. 2). Consequently, consider a super-domain (due to periodic BCs) of (finite) length $\left( 2N_{per}+1\right) L$, where $N_{per}$ is the number of domain images per direction. If d is the number of (periodic) physical dimensions, then the number of periodic domain images including the original domain is $N_{im}=\left( 2N_{per}+1\right) ^d$. In theory, periodic boundary conditions are exactly represented for $N_{per}\rightarrow \infty$, however in practice $N_{per}$ will be considered finite based on a convergence criterion [see Eq. (8)] which entails an approximation error, thus these BCs are considered as quasi-periodic.

Fig. 2

The computational domain of interest is marked with bold contours and hatched in gray lines and its periodic images in white font. Two particles are put in the domain for simplicity and for each one, a spherical periodic volume of radius $\Vert \mathbf{r} _c\Vert = N_{per}L$ is centered at their respective positions

Therefore, each particle in $\varOmega$ has $N_{im}-1$ periodic images, and the electrostatic force acting on a particle p due to a particle q is the sum of all $N_{im}$ interactions due to q and its images. Hence, in the case of tri-periodic BCs, in order to calculate the total electrostatic force exerted on p, one should perform the sum of Eq. (6) over all $N_pN_{im}$ particles in the super-domain.

However, the computational domain (and its periodic images) is cubic, so a particle that is away from the domain center would be subjected to a force that always points outwards of the domain due to an anisotropic long-range electrostatic force distribution (see Fig. 2). In fact, this force would be proportional to the offset of the particle from the center of the computational domain. As a result, all particles would accelerate towards the domain borders and due to periodicity reenter from the opposite side, where they would re-accelerate outwards, which would eventually result in an oscillation of the particles around the borders. This behavior is not physical and in order to avoid it, each particle p interacts with the particles (images) that are located within a sphere $(\mathbf{x} _p,\mathbf{r} _c)$, where $\Vert \mathbf{r} _c\Vert = N_{per}L$, in order to ensure an isotropic long-range electrostatic force distribution.

In practice, if the positions of $N_p$ particles in the domain $\varOmega$ are known, then for the calculation of $\mathbf{F} _{e_p}$ only $N_p-1$ distance vectors $\mathbf{r} _{qp}$ are needed for $N_p-1$ particles q in $\varOmega$. Then, for each particle q, the $N_{im}$ distance vectors between p and the images of particle q (including itself) can be simply calculated as a translation of the original distance vector $\tilde{\mathbf{r }}_{qp} = \mathbf{r} _{qp} + m L_x\mathbf{i} + nL_y\mathbf{j} + lL_z\mathbf{k}$ with $m,n,l=-N_{per},N_{per}$. Apparently, for $m=n=l=0$ the distance vector is the original one. As more periodic images are taken into consideration, one particle that lies in the computational domain interacts with more particles $N_{im}\propto {N_{per}}^3$ that are placed in an increasingly greater distance $\Vert \tilde{\mathbf{r }}_{qp}\Vert \propto N_{per}$. One can deduce that

$$\begin{aligned} {U_e}_p = \lambda Q_p\sum \limits _{\begin{array}{c} q=1\\ q\ne p \end{array}}^{N_p} Q_q\sum \limits _{\begin{array}{c} m,n,l=-N_{per} \\ \Vert \tilde{\mathbf{r }}_{qp}\Vert \le N_{per}L \end{array}}^{N_{per}}\frac{1}{\Vert \tilde{\mathbf{r }}_{qp}\Vert }\propto {N_{per}}^2\ . \end{aligned}$$

(7)

which implies the particle electric potential energy diverges quadratically for tri-periodic boundary conditions as shown by Fig. 3.

Fig. 3

Average particle electric potential energy with respect to the number of periodic domain images. Quadratic divergence observed as $N_{per}\rightarrow \infty$

As far as the total electrostatic force on a particle is concerned, the same dynamics are in place due to periodicity, however it should be noted that $\mathbf{F} _e \propto 1/\Vert \mathbf{r} _{qp}\Vert ^2 \propto 1/{N_{per}}^2$. In addition, although the number of electrostatic interactions scales with ${N_{per}}^3$, the electrostatic force converges for $N_{per}\rightarrow \infty$ due to its vectorial nature and the symmetry of periodicity. In fact, Fig. 4 shows that electrostatic forces converge very quickly for $N_{per}\ge 2$, hence for the simulations carried out in this work, the domain is replicated two times towards each direction. Theoretically, from the point of view of a particle in the computational domain, as more particle images are taken into account around it, there is a cut-off distance after which the long-range electrostatic forces that are exerted on it tend to cancel out as $N_{per}\rightarrow \infty$. This is due to an isotropic long-range force distribution around it, resulting in the convergence of its total electrostatic force to a finite value. From Eq. (6), one can deduce that

$$\begin{aligned} \mathbf{F} _{e} = \lambda Q_p\sum \limits _{\begin{array}{c} q=1\\ q\ne p \end{array}}^{N_p} Q_q\sum \limits _{\begin{array}{c} m,n,l=-N_{per} \\ \Vert \tilde{\mathbf{r }}_{qp}\Vert \le N_{per}L \end{array}}^{N_{per}}\frac{\hat{\tilde{\mathbf{r }}}_{qp}}{\Vert \tilde{\mathbf{r }}_{qp}\Vert ^2}\propto \sum \limits _{\begin{array}{c} m = -N_{per} \\ \Vert \tilde{\mathbf{r }}_{qp}\Vert \le N_{per}L \end{array}}^{N_{per}}\mathbf{f _{e_p}}^{(m)}=\mathbf{f} _{e} . \end{aligned}$$

(8)

Fig. 4

Average norm of the electrostatic force with respect to the number of periodic domain images. Convergence is observed for $N_{per}\ge 2$

For periodic BCs, the computational cost of the direct method scales with the number of periodic images as $\underbrace{N_pN_{im}}_{\tiny {\text { particles + images}}}\left( N_p-1\right)/2 \sim N_{im}{N_p}^2$.

3.2 Pseudo-particle Method

Let the domain be discretized in $N_f$ cells per dimension (see Fig. 5). For each particle p, its neighborhood $V_p$ of size $\varDelta x_v=\left( 2N_v+1\right) \varDelta x$ is defined as the ensemble of $\left( 2N_v+1\right) ^3$ cells around it. The number of cells for which the neighborhood spans towards every direction x, y, z (excluding the cell that contains the particle) is $N_v$, as illustrated by Fig. 5. Each cell $\Omega_k$ contains $N_k \sim N_p/N_f^3$ particles and forms a pseudo-particle, which is a cluster of particles “viewed” from distance as one particle of equivalent charge $Q_{eq}^k$ and position $\mathbf{x} _{eq}^k$. The concept of pseudo-particles, inspired by Barnes and Hut (1986), is defined in Eqs. (9)–(11).

$$\begin{aligned} Q_{eq}^k= & {} \sum \limits _{p=1}^{N_k} \chi ^k_p Q_p \end{aligned}$$

(9)

$$\begin{aligned} \mathbf{x} _{eq}^k= & {} \frac{1}{Q_{eq}^k}\sum \limits _{p=1}^{N_k} \chi ^k_p Q_p \mathbf{x} _p \end{aligned}$$

(10)

with

$$\begin{aligned} \chi ^k_p = \left\{ \begin{array}{ll} 1 \quad &{}\quad \text {particle }p \text { is in cell } k \\ 0 \quad &{}\quad \text {otherwise} \end{array}\right. \end{aligned}$$

(11)

Fig. 5

Computational domain of length L is discretized in $N_f$ cells per dimension. For each particle p, its neighborhood $V_p$ (red) is defined as the ensemble of $\left( 2N_v+1\right) ^3$ cells around it. Pseudo-particles are represented as gray circles outside of $V_p$

Therefore, each particle interacts directly with all particles in neighborhood $V_p$ (short-range interaction), as well as with the pseudo-particles that are outside of $V_p$ (long-range interaction). The electrostatic force $\mathbf{F} _{k\rightarrow p}$ acting on particle p due to pseudo-particle k is calculated by treating k as another particle, meaning that in Eq. (5) $Q_q$ is replaced by $Q_{eq}^k$ and $\mathbf{x} _{q}$ by $\mathbf{x} _{eq}^k$.

Hence, the total electrostatic force on particle p is calculated by performing direct summations in $V_p$ and pseudo-particle summations outside of $V_p$.

$$\begin{aligned} \mathbf{F} _{e} = \underbrace{\sum \limits _{\begin{array}{c} k=1\\ k \in V_p \end{array}}^{N_f^3} \sum \limits _{\begin{array}{c} q=1\\ q\ne p \end{array}}^{N_k} \mathbf{F} _{q\rightarrow p}}_{\begin{array}{c} \text {short range} \\ \left( 2N_v+1\right) ^3 N_p/N_f^3-1 \ \text {terms} \end{array}} + \underbrace{\sum \limits _{\begin{array}{c} k=1\\ k \notin V_p \end{array}}^{N_f^3} \mathbf{F} _{k\rightarrow p}}_{\begin{array}{c} \text {long range} \\ {N_f}^3-\left( 2N_v+1\right) ^3 \ \text {terms} \end{array}} \end{aligned}$$

(12)

3.2.1 Quasi-periodic Boundary Conditions

Let the number of pseudo-particles plus their periodic images be $N_{im}{N_f}^3$. Apparently, $N_v$ must satisfy the inequality $N_v \le \left[ N_f\left( 2N_{per}+1\right) -1\right]/2$ in order to fit in $\left( 2N_{per}+1\right) L$, as shown by Fig. 6. As a result, the computational cost with periodic BCs becomes $N_p\left[ \underbrace{\left(2N_v+1\right)^3 N_p/N_f^3-1}_{\text {inside }V_p}+\underbrace{N_{im}{N_f}^3-\left(2N_v+1\right)^3}_{\text {outside }V_p}\right]$.

Fig. 6

Domain of interest $\varOmega$ (solid black), periodic domain images (dashed black) with $N_{per}=2$ and spherical periodic volume (dashed red) with radius $\Vert \mathbf{r} _c\Vert = 2L$. Neighborhood $V_p$ (solid red) with $N_v=1$ could span over several images of $\varOmega$

3.3 Error and Performance Analysis

An error and performance analysis of the proposed algorithm is presented in Fig. 7. As the error analysis is concerned, the direct method is considered to be of high fidelity as it allows for an exact calculation of the electrostatic forces and hence the results obtained with this method constitute a reference for simulations using other approximative methods such as the pseudo-particle method. Therefore, the relative error of total electrostatic force estimation for particle p at $t = 0$ is defined as $\epsilon _p^0 = \left(\Vert \left. \mathbf{F} _{e}^0\right| _\text {dir}-\left. \mathbf{F} _{e}^0\right| _\text {pseudo}\Vert\right) /\Vert \left. \mathbf{F} _{e}^0\right| _\text {dir}\Vert$.

Fig. 7

Error distribution (a) and performance (b) of periodic direct and pseudo-particle algorithm for $N_v=1$ and $N_{per}=2$

It is obvious that the latter is performing better than the former as it approximates the long-range interactions via pseudo-particles. It should also be noted that the calculated order of complexity $\sim {N_p}^{1.3}$ is considerably better than the expected theoretical one $\sim {N_p}^{1.5}$.

4 Numerical Simulation Setup and Flow Statistics

4.1 Numerical Schemes and Parameters

The numerical solver is fully parallelized for both the fluid and the particles. For the DNS the FFT are performed by the library P3DFFT (Pekurovsky 2012). In the present numerical simulations the number of grid points for the DNS is $N_x=N_y=N_z=256$ and the turbulent Reynolds number, based on the integral length scale $Re_{L_f}=\sqrt{2/3q_f^2}\,L_f/\nu _f$, is about 100. According to $\eta _K\kappa _{max}^F=2.92$ (where $\eta _K$ is the Kolmogorov length scale and $\kappa _{max}$ the highest solved wavenumber) the small turbulent scales are well resolved. As two-way coupling is neglected, the fluid velocity seen by the particles, $\mathbf{u} _{f@p}$, is computed by 3rd order polynomial interpolation of the fluid velocity field. According to the previous analysis and adjusting the parameters for optimal parallelization, the electrostatic forces have been computed with $N_f=8$, $N_v=1$ and $N_{per}=2$.

4.2 Fluid and Particle Material Properties

The fluid material properties and main turbulence statistics are gathered in Table 1. In this table, the fluid kinetic energy is defined by $q_f^2 = 1/2\langle {u}'_{f,i}{u}'_{f,i}\rangle _f$ where $\langle ~.~\rangle _f$ denotes an Eulerian average on the grid used for the fluid phase.

Table 1 Properties of the fluid and of the examined HIT

In this work, all particles are considered to bear equal positive charges. Practically, particles are charged via the phenomenon of triboelectrification (Grosshans and Papalexandris 2017) which occurs when particles collide with walls and other particles. In the simulated periodic particulate flow, it is assumed that particles have had sufficient time to redistribute their charges among them via collisions. However, collisions and triboelectrification are neglected in this study because of the small solid volume fraction.

In fact, numerical simulations have been performed with $N_p=10,000$ particles corresponding to a solid volume fraction $\alpha _p=2.64\times 10^{-6}$. In addition, all particles have been considered of the same diameter so that $\eta _K/d_p=4.56$ but they differ by density. Since particle diameter is smaller than the Kolmogorov scale, particles are numerically treated under the point-particle approximation. As such, the particle charge $Q_p$ is considered to be concentrated in one point (particle’s center of mass) defined as $Q_p=\pi {d_p}^2\times \rho _q$, where $\rho _q$ the particle surface charge density.

Several particle charges have been considered, all given in terms of a reference charge $Q_0=1\times 10^{-9}\,C$. It should be noted here, that according to Hamamoto et al. (1992) there is a saturation limit of surface charge density for small spheres, which can be translated (via $d_p$) to a corresponding limit for point-particle charges. For the configuration presented in this work, this value can be estimated to be approximately $4\times 10^{-9}$ C, which is of the same order of magnitude of the charges used in all simulations.

In Table 2, particle Stokes number based on the Stokes drag and the Kolmogorov time scale is given. However, as we consider non-linear drag force (see Eq. (3)), the particle relaxation time scale is introduced as $\tau _{fp}^F=\left[ \langle 1/\tau _p \rangle _p\right] ^{-1}$ where $\langle ~.~\rangle _p$ denotes a Lagrangian average on the particle distribution.

Therefore, the Stokes number is defined as $\tau _{fp}^F/\tau _{f@p}^t$ where $\tau _{f@p}^t$ is the Lagrangian integral time scale of the fluid seen by the inertial particles. Such a timescale is defined from the Lagrangian auto-correlation function of the fluid velocity seen:

$$\begin{aligned} R_{f@p}^{t}(\tau ) = \frac{\langle {u}_{f@p,i}'(t_0){u}_{f@p,i}'(t_0+\tau )\rangle _p}{2q_{f@p}^2(t_0)} \end{aligned}$$

(13)

where $q_{f@p}^2={1}/{2}\langle {u}'_{f@p,i}{u}'_{f@p,i}\rangle _p$ the kinetic energy of the fluid seen by the particles. The Lagrangian fluid integral time scale is defined by

$$\begin{aligned} \tau _{f@p}^t = \int _{0}^{\infty }R_{f@p}^{t}(\tau )d\tau \ . \end{aligned}$$

(14)

When motionless particles are considered, Eqs. (13) & (14) allow to compute the Eulerian time scale, $\tau _E$, and for fluid elements the Lagrangian fluid integral time scale, $\tau _f^t$. For the following statistical analysis we also define the particle kinetic energy, $q_p^2=1/2\langle {u}'_{p,i}{u}'_{p,i}\rangle _p$ and the fluid–particle velocity covariance as $q_{fp}=\langle {u}'_{f,i}{u}'_{p,i}\rangle _p$. Furthermore, statistical moments have been calculated over a sufficiently long duration $T_{stat}=10\times \max \{\tau _{f@p}^t, \tau _{fp}^F, \tau _{el}\}$ in order to achieve statistical convergence, which is calculated as a multiple of the maximum characteristic time scales of all the physical mechanisms involved.

Table 2 Material properties of particles with $\tau _p^{St}=\rho _pd_p^2/\left( 18\rho _f\nu _f\right)$ the Stokes particle time scale

Fig. 8

Schematic of a Coulomb collision of two iso-charged particles and notion of Coulomb diameter. Particle diameter $d_p$ is depicted with a solid black circle, while (fictitious) effective Coulomb diameter with a dashed black circle

4.3 Coulomb Collisions and Characteristic Time of Electrostatic Interactions

In order to analyze the effects of the charges one should define a characteristic time scale of electrostatic interactions. This time scale is the duration of particle velocity decorrelation under the sole presence of electrostatic interactions. The mechanism of this velocity decorrelation is the Coulomb collision, which is a binary elastic collision between two charged particles interacting through their own electric field. In order to understand a Coulomb collision of two particles, we can imagine that they undergo an elastic collision with an effective Coulomb diameter $d_{pq}^C$ as depicted by Fig. 8. These interactions are well resolved in the DNS carried out in this work and not modeled. The effective Coulomb diameter $d_{pq}^C$ is a notion typically found in cold plasma (Callen 2003) and in this case it is defined as

$$\begin{aligned} d_{pq}^C = \frac{1}{\pi \langle \Vert \mathbf{w} _{pq}\Vert \rangle _p}\sqrt{\frac{Q_pQ_q}{m_{pq}\epsilon _0}} \end{aligned}$$

(15)

where $\mathbf{w} _{pq}$ is the relative approach velocity of the particles defined as $\mathbf{w} _{pq} = \mathbf{u} _p-\mathbf{u} _q$ and the Lagrangian average of its norm is approximated by $\langle \Vert \mathbf{w} _{pq}\Vert \rangle _p = \sqrt{16/\pi \times 2/3 \times q_p^2}$. Additionally, $m_{pq}$ is the reduced mass of a pair of particles p and q calculated as $m_{pq} = m_pm_q/\left( m_p+m_q\right)$. If the kinetic energy of the particles is very large with respect to the electric potential energy, the deviation from the initial trajectories of the colliding particles is small. Therefore, $d_{pq}^C \le d_p$ and particles would undergo a hard sphere collision, however this is not treated in our simulations, as explained in Sect. 4.2. This length scale is also used to determine the size of the neighborhood $\varDelta x_v$ as it should be $\phi \gg 1$ times bigger than the effective Coulomb diameter $d_{pq}^C$. Therefore, one can deduce the number of cells $N_v$ in the neighborhood of short-range interactions as described in Sect. 3.

The Coulomb collision frequency is written as $\nu _c = n_pQ_c\langle \Vert \mathbf{w} _{pq}\Vert \rangle _p$, therefore the characteristic time scale of Coulomb collisions is $\tau _c = 1/\nu _c$. An estimation of this characteristic time scale can be obtained via a simple dimensional analysis using particle flow properties that yields

$$\begin{aligned} \tau _{el} \propto \frac{1}{Q_p}\sqrt{\frac{m_p}{\lambda n_p}}\ . \end{aligned}$$

In order for $\tau _{el}$ to be a good candidate for the characteristic time scale of electrostatic interactions, it should be of the same order of magnitude as $\tau _c$. This is confirmed in Table 3 that shows time and length scales for the case where $Q_p=8Q_0$.

Table 3 Characteristic scales of Coulomb interactions for $Q_p=8Q_0$

Having defined such a time scale, one could also define an electrostatic Stokes number as $\tau _{fp}^F/\tau _{el}$—in analogy with the particles Stokes number—that is directly proportional to the charge. It can be noticed that such a definition of the electrostatic Stokes number is substantially different from those found in literature. Indeed, on one hand Alipchenkov et al. (2004) uses the Coulomb number defined as the ratio of the potential energy of Coulomb inter-particle interaction to the kinetic energy at small scales of the turbulence. On the other hand, 0 defined an electric settling velocity representing the terminal velocity of a particle due to the influence of a given electric field.

Finally, one could attempt to link the two aforementioned Stokes numbers and describe their dependence on fluid–particle-electrostatics properties. In order to perform an elementary dimensional analysis one can make two crude hypotheses: $\tau _{fp}^F\simeq \tau _p^{St}$ and $\tau _{f@p}^t\simeq \tau _f^t$ that allow to rewrite the electrostatic Stokes number in terms of the particle Stokes number as

$$\begin{aligned} \frac{\tau _{fp}^F}{\tau _{el}} = \frac{2Q_p}{\pi {d_p}^2}\sqrt{\frac{\lambda \alpha _p\tau _f^t}{2\rho _f\nu _f}}\times \sqrt{\frac{\tau _{fp}^F}{\tau _{f@p}^t}}. \end{aligned}$$

(16)

Figure 9 shows that the relation between the two Stokes numbers is quadratic and that Eq. (16) fits well DNS data. It is evident that in order to perform simulations with adequate resolution of the Coulomb collisions, the time step of the simulation should be appropriate. In fact, the mean free path of the particles $\delta l = \langle \Vert \mathbf{w} _{pq}\Vert \rangle _p\varDelta t$ should be at least $\chi$ times smaller than the Coulomb effective diameter $d_{pq}^C$. That allows to calculate a maximum time step that ensures the resolution of electrostatic interactions as $\varDelta t \le \chi d_{pq}^C/\langle \Vert \mathbf{w} _{pq}\Vert \rangle _p$. Consequently, the time step should be kept below a given limit $\varDelta t_{max}= 3 \chi /32q_p^2\times \sqrt{Q_pQ_q/\epsilon _0m_{pq}}.$

Fig. 9

Electrostatic Stokes number with respect to the Stokes number. The symbols are the numerical simulation and the dashed lines the Eq. (16)

5 Analysis of Charged Particle-Laden Turbulent Gas Flows

Simulations of charged particle-laden turbulent gas flow have been performed using the pseudo-particle method described in Sect. 3 for particles of various inertia levels and different electric charges in order to investigate how electrostatic interactions affect particle dynamics.

Figure 10 shows the comparison between particle agitation and theoretical particle agitation as predicted by the Tchen–Hinze (Hinze 1972), and extended by Simonin et al. (1993). The theoretical relations of the extension of Tchen–Hinze theory are

$$\begin{aligned} 2q_p^2=q_{fp}=2q_{f@p}^2\frac{\tau _{f@p}^t}{\tau _{f@p}^t+\tau _{fp}^F}\ . \end{aligned}$$

(17)

Figure 10 shows the particle agitation and the fluid–particle velocity covariance with respect to the Stokes number in case without charge. Numerical simulations are in agreement with Eq. 17. As expected, small discrepancies are observed for particles with small relaxation time scale but this is due to from the assumption of an exponential auto-correlation function for the fluid velocity measured along the particle trajectory that is too crude. Work by Zaichik et al. (2003) showed that the Tchen–Hinze theory can be extended by using a two-exponential correlation proposed by Sawford (1991).

Fig. 10

Particle agitation with respect to the inverse of the Stokes number. The dashed line corresponds to the Tchen–Hinze theory given given by Eq. (17)

5.1 Effect of Electrostatic Interactions on Particle Agitation

In order to examine the effect of particle–particle electrostatic interactions on particle agitation, we shall reproduce Tchen–Hinze Eq. (17) for various electric charges. As seen by Fig. 11, the effect of electrostatic interactions on particle agitation is not straightforward. Particles with large inertia, are not particularly affected by electrostatic interactions, those with moderate inertia exhibit an increase in agitation, while on the contrary the lightest particles undergo a significant decrease in their levels of agitation.

Fig. 11

Effect of electric charges on particle agitation. The black dashed line corresponds to the Tchen–Hinze theory given by Eq. (17) and the red markers to the case without charge

In order to understand this behavior, one should consider the equation of particle agitation in the framework of the kinetic theory under the effect of electrostatic forces that yields

$$\begin{aligned} \frac{\partial }{\partial t}q_p^2 = \frac{q_{fp}}{\tau _{fp}^F}-\frac{2q_p^2}{\tau _{fp}^F} + \frac{\langle \mathbf{F} _{e}\mathbf{u} ^\prime _p\rangle _p}{m_p}\ . \end{aligned}$$

(18)

The four terms of Eq. (18) are shown by Fig. 12 and the balance of the equation is verified in the transient regime for $Q_p=8Q_0$ corresponding to an electrostatic Stokes number of $\tau _{fp}^F/\tau _{el}=1.63$. In case of stationary flow the Eq. (18) becomes

$$\begin{aligned} q_p^2 = \frac{1}{2}q_{fp} + \frac{1}{2}\tau _{fp}^F\frac{\langle \mathbf{F} _{e}\mathbf{u} _p^\prime \rangle _p}{m_p}\ . \end{aligned}$$

(19)

The additional term $\tau _{fp}^F\langle \mathbf{F} _{e}\mathbf{u} ^\prime _p\rangle _p/m_p$ represents the particle-induced electric potential energy which is equal to the time derivative of the work of electrostatic forces. This means that particle agitation depends on fluid–particle velocity covariance (i.e. the particle–turbulence interaction) and particle-induced electric potential energy. Physically, this implies that particle agitation is modified by both the drag and the electrostatic forces. As shown by Fig. 13, increasing particle charge, term $\tau _{fp}^F\langle \mathbf{F} _{e}\mathbf{u} _p^\prime \rangle /m_p$ becomes somewhat important especially for heavy particles. Furthermore, it is always positive so it acts as production of particle agitation. However, it only accounts for a $\sim [0,0.5]\%$ increase of particle agitation, hence it is responsible for a very small part of its increase $\sim [15,25]\%$ observed in Fig. 11 for particles of moderate inertia.

Fig. 12

Balance of Eq. (18) in transient regime for $\tau _{fp}^F/\tau _{el}=1.63$ ($Q_p=8Q_0$)

The physical meaning of this term could be better understood by considering Coulomb collisions. Table 3 shows that heavy particles exhibit minimum effective diameters and collision frequency. Therefore, their Coulomb collisions are more binary than those of light particles, which implies that the Coulomb collisions of the former have the tendency to modify the particles trajectories more abruptly. Finally, the small effect on particle agitation can be attributed to the elasticity of Coulomb collisions as electrostatic forces are conservative.

Fig. 13

Evolution of $\tau _{fp}^F\langle \mathbf{F} _{e}\mathbf{u} _p^\prime \rangle _p/m_p$ with respect to particle inertia and electric charges

Figure 14 shows that $q_{fp}$ is the most important term of Eq. (19), in that it accounts for most of the variation of particle agitation. Indeed, the observed variation of particle agitation to fluid–particle velocity covariance is of the order of magnitude $\sim 0.5\%$ of that of particle-induced electric potential energy to particle agitation seen by Fig. 13.

Fig. 14

Ratio between the particle kinetic energy and the fluid–particle velocity covariance with respect to particle inertia

5.2 Effect of Electrostatic Interactions on Fluid–Particle Velocity Covariance

It is shown in Sect. 5.1 that the key to understanding the behavior of particle agitation in such a flow, is to understand fluid–particle velocity covariance $q_{fp}$, which is a measure of fluid–particle correlation. Figure 11 shows that particles with large inertia, are not particularly affected by electrostatic interactions, those with moderate inertia exhibit an increase both in $q_{fp}\simeq 2q_p^2$ and in $\tau _{f@p}^t$, while on the contrary the lightest particles undergo a significant decrease in their levels of fluid–particle velocity covariance.

In the kinetic theory framework, under the effect of electrostatic forces, the transport equation of the fluid–particle velocity covariance may be derived from the joint-fluid-particle pdf equation (Simonin 1996) such as

$$\begin{aligned} \frac{\partial }{\partial t}q_{fp} =\langle \mathbf{a} ^\prime _{f@p} \mathbf{u} ^\prime _p\rangle _p-\frac{q_{fp}}{\tau _{fp}^F}+\frac{2q_{f@p}^2}{\tau _{fp}^F} + \frac{\langle \mathbf{F} _{e}\mathbf{u} ^\prime _{f@p}\rangle _p}{m_p}\ . \end{aligned}$$

(20)

The first term of the right hand side corresponds to the turbulent fluid dissipation and it is written in terms of the acceleration of the fluid seen by the particles $\mathbf{a} ^\prime _{f@p}$. In literature (Zaichik et al. 2003), it is usually modeled as $-q_{fp}/\tau _{f@p}^t$ which is not accurate in the case of light particles as shown by Fig. 15.

Fig. 15

Comparison between DNS results (black-filled symbols) and the standard model (open symbols) for term $\langle \mathbf{a} ^\prime _{f@p} \mathbf{u} ^\prime _p\rangle _p$ with respect to $\tau _{f}^t/\tau _{fp}^F$

Figure 16 depicts all five terms of Eq. (20) and the power equilibrium is verified in the transient regime for $\tau _{fp}^F/\tau _{el}=0.92$.

Fig. 16

Variation of fluid–particle velocity covariance and terms of Eq. (20) in transient regime for $\tau _{fp}^F/\tau _{el}=0.92$ ($Q_p=8Q_0$)

Furthermore, for stationary flows Eq. (20) becomes

$$\begin{aligned} q_{fp} = \tau _{fp}^F\langle \mathbf{a} ^\prime _{f@p} \mathbf{u} ^\prime _p\rangle _p + 2q_{f@p}^2 + \tau _{fp}^F\frac{\langle \mathbf{F} _{e_p}\mathbf{u} ^\prime _{f@p}\rangle _p}{m_p} \end{aligned}$$

(21)

where term $\tau _{fp}^F\langle \mathbf{F} _{e}\mathbf{u} ^\prime _{f@p}\rangle _p/m_p$ represents the turbulence-induced electric potential energy. In order to explain the behavior observed in Fig. 11 by $q_{fp}$, one needs to examine the three terms of the right hand side of Eq. (21).

Increasing particle charge, term $\tau _{fp}^F\langle \mathbf{F} _{e}\mathbf{u} ^\prime _{f@p}\rangle _p/m_p$ becomes very important, especially for light particles as shown by Fig. 17. More specifically, this term is most important for particles of moderate-to-low inertia, $\tau _{f}^t/\tau _{fp}^F\in [1,10]$. Therefore, in presence of electric charges the fluid–particle correlation competes with the repulsive electrostatic forces, which tend to constantly decorrelate the particle velocities from the fluid velocity field. This leads to a decorrelation of fluid–particle velocity, hence the negative sign of this term that serves as a destruction term of fluid–particle velocity covariance.

Fig. 17

Evolution of $\tau _{fp}^F\langle \mathbf{F} _{e}\mathbf{u} ^\prime _{f@p}\rangle _p/m_p$ with respect to particle inertia and charges

However, it does not account for the increase of fluid–particle velocity covariance in the case of moderate inertia particles, $\tau _{fp}^F/\tau _f^t\sim 1$ as shown by Fig. 11. This increase can be due to the first term of Eq. (21), thus due to a modification of $\tau _{fp}^F\langle \mathbf{a} ^\prime _{f@p} \mathbf{u} ^\prime _p\rangle _p$.

Indeed, Fig. 18 shows that term $\tau _{fp}^F\langle \mathbf{a} ^\prime _{f@p} \mathbf{u} ^\prime _p\rangle _p$ is modified by electrostatic forces. In particular, this term increases for an increasing electric charge that leads to an increase of fluid–particle velocity covariance especially for particles of moderate inertia, $\tau _{fp}^F/\tau _f^t\sim 1$.

Fig. 18

Effect of electric charges on acceleration term $\tau _{fp}^F\langle \mathbf{a} ^\prime _{f@p} \mathbf{u} ^\prime _p\rangle _p$ with respect to particle inertia. The red markers correspond to the case without charge

In order to better understand this, one could introduce a new characteristic time scale $\tau _{fp}^a=-q_{fp}/\langle \mathbf{a} ^\prime _{f@p} \mathbf{u} ^\prime _p\rangle _p$ that describes the dissipation rate of fluid–particle covariance by $\langle \mathbf{a} ^\prime _{f@p} \mathbf{u} ^\prime _p\rangle _p$. In Fig. 19, it is evident that this time scale increases for increasing electric charges, which essentially means that $q_{fp}$ dissipates in lower rates, resulting to its increase.

Fig. 19

Effect of electric charges on time scale $\tau _{fp}^a$ with respect to particle inertia. The red markers correspond to the case without charge

At this point, it would be interesting to examine the effect of electrostatic interactions on fluid acceleration seen at the position of particles $\langle \mathbf{a ^\prime _{f@p}}^2\rangle _p$. In Fig. 20, it is apparent that for increasing electrostatic forces there is a small decrease of $\langle \mathbf{a ^\prime _{f@p}}^2\rangle _p$ for particles of moderate inertia and a considerable increase for light particles, but for both cases the variance of fluid acceleration measured at the particles’ position tends to the value of the fluid acceleration variance measured along fluid elements. This implies that particles tend to be distributed more homogeneously. Lastly, it would be also interesting to examine the behavior of $q_{f@p}^2$.

Fig. 20

Effect of electric charges on fluid acceleration at the particles position $\langle \mathbf{a ^\prime _{f@p}}^2\rangle _p$ with respect to particle inertia

As far as the second term of Eq. (20) is concerned, in Fig. 21, it is shown that an increase in electric charge implies an increase in the fluid agitation from the point of view of the particles. More specifically, $q_{f@p}^2$ has the tendency to flatten to the value of $q_f^2$ for heavy particles, $\tau _{fp}^F\rightarrow \infty$ and to increase even further for moderate and light particles.

In order to explain this behavior, we first have to examine the levels of $q_{f@p}^2$ in the case of no electric charge. Indeed, inertial and light particles “see” the same fluid agitation, as the former are rather carried by large turbulent structures and the latter behave close to fluid elements. However, particles of moderate inertia get trapped in regions of low vorticity and therefore “see” slightly lower levels of fluid agitation.

Under the influence of electric charges, inertial particles are not as affected, while moderate particles are less prone to preferential concentration, thus they “see” a fluid agitation close to $q_f^2$. However, less inertial particles exhibit an increase in their “seen” fluid agitation, which needs to be further investigated.

Fig. 21

Effect of electric charges on fluid agitation seen by the particles with respect to particle inertia

Finally, Fig. 22 provides an overview of what has been discussed. It shows that for a given level of particle inertia, increasing particle charge leads to an increase of fluid–particle velocity covariance due to an increase of $\tau _{fp}^F\langle \mathbf{a} ^\prime _{f@p}\mathbf{u} ^\prime _p\rangle _p$ (see Fig. 18) and $q_{f@p}^2$ (see Fig. 21) which are the first two (production) terms of Eq. (21). This occurs up to a saturation limit where $q_{fp}$ starts to decrease as the third (destruction) term of Eq. (21), $\tau _{fp}^F\langle \mathbf{F} _{e}\mathbf{u} ^\prime _{f@p}\rangle _p/m_p$ becomes more important (see Fig. 17). Increasing particle inertia, actually moves that saturation limit to lower electrostatic response time scales $\tau _{el}\rightarrow 0$, thus higher electric charges.

Fig. 22

Fluid–particle covariance normalized by the value without charge with respect to the electrostatic Stokes number. Stokes numbers $\tau _{fp}^F/\tau _{f@p}^t$ correspond to the value without charge

5.3 Effect of Electrostatic Interactions on Preferential Concentration

In case of iso-charged particles, the effects of electrostatic forces on the preferential concentration are not extensively documented, however one could reflect on the nature of electrostatic interactions by observing snapshots of the particle flow in the stationary regime. In Fig. 23 it is observed that such electrostatic interactions tend to homogenize the particle distribution due to the repulsive nature of the electrostatic forces. This leads to a mitigation and eventually an elimination of preferential concentration especially for light particles as shown by Fig. 23i.

Fig. 23

Snapshots of a charged particle-laden turbulent gas flow for various levels of inertia and electric charges for $\varDelta x=L_f$

Electrostatic forces are conservative forces, thus a system of charged particles under their influence will start evolving with an initial electric potential energy, part of which will gradually transform to kinetic energy. However, in the presence of a turbulent fluid flow, the physics of the charged particle-laden turbulent gas flow are slightly more complex, so in order to gain some more insight we should consider three main mechanisms that govern it.

Firstly, according to the minimum potential energy principle, that is valid for conservative forces such as the electrostatic, the system of particles tends to an equilibrium of minimum electric potential energy which implies that the particles will try to separate themselves as much as possible. On the other hand, it has been mentioned in Sect. 2, that in turbulent particle-laden gas flows there are certain regions in the flow (high strain rate, low vorticity) that favor particle concentration resulting in a local increase of electric potential energy and thus in further production of kinetic energy. Lastly, the additional production by electrostatic effects tends to increase the average stationary level of $q_p^2$. This kinetic energy production is exactly compensated, in stationary flow, by an additional dissipation due to the drag force of the fluid which dissipates it in heat by viscous effect.

6 Conclusions and Perspectives

This study shows that the computational cost of the $N_p$-body problem is prohibitively high $\sim {N_p}^2$. However, separating the interactions in short- and long-range can be a viable solution. Such a method, is the pseudo-particle method that is more efficient $\sim {N_p}^{1.5}$ and with an acceptable error. Furthermore, in case of tri-periodic BCs, since electrostatic forces depend on the distance of particle images, electrostatic periodicity entails an additional cost which scales with the cube of the number of periodic images per direction. However, it is shown that in order to recreate accurately enough the periodic BCs, two periodic domain images per direction are enough so as to respect the isotropy of the system at large-scales. In order to ensure such periodic isotropy, every particle has to interact with particles within a sphere centered at its position.

Furthermore, a simulation of particle-laden turbulent gas flow without electric charges has been carried out. This requires the setup of a case of resolved stationary HIT and the calibration of the particle phase according to a desired range of Stokes number, which yields several particle classes based on different densities. This calibration occurs by performing a statistical analysis of the flow, by using velocity auto-correlation functions that allow to estimate characteristic time scales of the fluid and particle flow. This statistical analysis enables to recreate Tchen–Hinze theory concerning particle agitation which serves as verification of a successful particle-laden turbulent gas flow simulation.

In addition, we attempt to explain the particle–particle electrostatic interactions via the concept of Coulomb collisions borrowed from cold plasma theory. Hence, a time scale of electrostatic interactions is proposed, whose order of magnitude has been compared to the characteristic time of Coulomb collisions. This time scale allows to define an electrostatic Stokes number in analogy to the classic particle Stokes number. Then, we calibrate the electrostatics of the charged particle-laden turbulent gas flow simulation by selecting the electric charge according to a desired range of electrostatic Stokes numbers.

Following, several charged particle-laden turbulent gas flows have been simulated with different particle charges in order to investigate the effects of electrostatic interactions on particle agitation. A statistical analysis of these flows has been carried out so as to acquire an insight of the behavioral dynamics of these flows. This statistical analysis, along with a theoretical analysis enables to rewrite the transient equations of important statistical moments and effectively derive the modified Tchen–Hinze theory for the stationary regime in the presence of electrostatic forces.

Essentially, it is shown that particle agitation depends almost solely on fluid–particle velocity covariance which is a measure of fluid–particle velocity correlation. More specifically, particle–particle electrostatic forces lead to fluid–particle velocity decorrelation which is particularly prominent for very light particles. Furthermore, a qualitative analysis shows that electrostatic interactions of iso-charged particles mitigate preferential concentration.

Finally, these two last observations imply that particles, under the influence of electrostatic forces, “see” a slightly different flow which entails a change in the Lagrangian integral time scale $\tau _{f@p}^t$ as seen in Fig. 11. Therefore, in the future, more work needs to be carried out towards the investigation of the effect of electrostatic interactions on the auto-correlation functions of fluid velocity “seen” by inertial particles as well as auto-correlation functions of particle velocity. This study could allow us to further investigate particle dispersion, preferential concentration as well as modeling the electrostatic-related terms in the modified Tchen–Hinze equation.