1 Introduction

Correlations that predict the drag of flow over rough surfaces are important engineering tools. Identifying a single correlation that is valid for a range of roughness types in all roughness regimes has proven to be an extremely difficult challenge. Skin-friction predictions of surface roughness is generally characterized by ks, the equivalent sandgrain roughness height, the size of uniformly packed sandgrains tested by Nikuradse [19] that produces the same drag in the fully-rough regime. ks is a hydraulic scale, not a physical scale and this is what is listed on the Moody diagram [16] as ε, the equivalent roughness height. Ideally, robust engineering correlations should be based on information that can be obtained solely from the surface topography, thus excluding any information that requires hydrodynamic testing. While a significant number of studies have tackled this problem (see recent reviews by Flack and Schultz [8], Forooghi et al. [11]), correlations that are valid for a wide range of roughness types are still not available.

Previous experimental results [8], showed that the root-mean-square roughness height (krms) and the skewness (Sk) of the probability density function (pdf) are the roughness parameters that best predict drag in the fully-rough regime. A correlation was developed for roughness types ranging from commercial steel pipes to gravel-covered surfaces. These parameters also exhibited significant correlations for predicting ks for grit-blasted surfaces [10] and mathematically-generated surfaces with a power law distribution of surface elevations [2].

Predictive correlations for complex roughness have been investigated in several recent simulations. Yuan and Piomelli [31] used large eddy simulations (LES) for realistic roughness replicated from hydraulic turbine blades as well as sand-grain type roughness. Rough surface drag correlations were presented based on a slope/shape parameter [26, 30], the root-mean-square of the local surface slope [4], and the skewness of the pdf. The slope-based correlations yielded better collapse of the data since the surfaces generally had low effective slopes (ES), as defined by Napoli et al. [18]. Direct Numerical Simulation (DNS) was employed by Forooghi et al. [11] for randomly distributed roughness elements of random size and prescribed shape. The correlation that best predicted ks normalized with the maximum peak-to-trough roughness (kt) height was based on surface height skewness (Sk) and effective slope (ES). Thakkar et al. [28] used DNS to study a realistic irregular roughness for the entire range of roughness Reynolds numbers from hydraulically-smooth to fully-rough. Drag was best predicted by a correlation that included roughness solidity, skewness, the streamwise correlation length, and rms roughness height.

The present work focuses on random roughness that contains a range of roughness scales. This roughness represents naturally occurring and engineering surfaces with close-packed roughness elements having a wide distribution of roughness length scales. While a range of surface parameters have shown promise in predictive correlations of drag on rough surfaces, it is important to isolate the influence of each parameter. In the present study, both rms roughness height and skewness of the pdf are parametrically changed to investigate the shape and extent of the transitionally-rough regime and to determine if a two parameter model based on krms and skewness [8] is valid to predict the equivalent sandgrain roughness height.

2 Experimental methods

Experiments on rough surfaces were conducted in the high Reynolds number turbulent channel flow facility at the United States Naval Academy (Fig. 1). The test section is 25 mm in height (H), 200 mm in width (W), and 3.1 m in length (L). This gives an aspect ratio (W/H) of 8 which according to Monty [15] is sufficient to ensure two-dimensionality of the flow within the central part of the channel. The flow develops over smooth walls for a distance of 60H (1.5 m) in the upstream portion of the channel. The roughness covered plates form the top and bottom walls for the remainder of the test section. The channel flow facility has a reservoir tank containing 4000 L of water. The water temperature is held constant to within ±0.25∘ C using a thermostat-controlled chiller. The flow is driven by two 7.5 kW pumps operated in parallel. The flow rate is measured using a Yokogawa ADMAG AXF magnetic flow-meter that has an accuracy of 0.2% of the reading. The bulk mean velocity in the test section ranges from 0.4–11.0 m/s, resulting in a Reynolds number based on the channel height and bulk mean velocity (Rem) range from 10,000 - 300,000. Mean velocity profiles over rough surfaces show no difference within the experimental uncertainty of the measurement [24], indicating that the flow in the channel is fully-developed by a streamwise distance of 90H or 30H downstream of the onset of roughness. Nine static pressure taps are located in the test section of the channel. They are 0.75 mm holes and are placed along the centerline of the side wall of the channel and are spaced 6.8H apart. The streamwise pressure gradient (dp∕dx) is determined with a Honeywell FP2000 series differential pressure transducer with a 2 psi range and have an accuracy of ±0.1% of full scale. Pressure taps 5–8 are used to measure the pressure drop in the channel, located ~ 90H - 110H downstream of the trip at the inlet to the channel. A roughness fetch of 30H is present before the first tap used in the determination of dp/dx. The linearity in the measured pressure gradient using these four taps was quite good with a coefficient of determination (R2) of the regression generally greater than 0.995.

Fig. 1
figure 1

High Reynolds number flow channel

Full size image

The wall shear stress, τw, was determined via measurement of the streamwise pressure gradient, dp/dx, as detailed below:

$$ {\tau}_w=-\frac{H}{2}\frac{dp}{dx} $$
(1)

or as expressed as the skin-friction coefficient, Cf

$$ {C}_f=\frac{\tau_w}{\frac{1}{2}\rho {U}^2}=2{\left(\frac{u_{\tau }}{U}\right)}^2 $$
(2)

where H = channel height, p = static pressure, x = streamwise distance, ρ = fluid density, U = bulk mean velocity, and uτ = friction velocity. A similarity-law procedure of Granville [12] for fully-developed internal flows was employed to determine the roughness function, ΔU+. This procedure assumes mean flow similarity between rough and smooth walls outside of the roughness sublayer, as demonstrated with collapse of mean velocity profiles in velocity defect form. Collapse of the mean defect profiles for rough and smooth walls is consistent with the turbulence similarity hypotheses of Townsend [29]. Mean flow similarity has proven to be robust for a wide range of surface roughness (i.e. [5, 9]). Granville’s method states that the roughness function can be obtained by:

$$ \varDelta {U}^{+}={U}_S^{+}-{U}_R^{+}=\sqrt{\frac{2}{C_{fS}}}-\sqrt{\frac{2}{C_{fR}}} $$
(3)

where the subscripts S and R represent smooth and rough surfaces, respectively, evaluated at the same Rem(Cf)1/2 or Reτ.

The rough surfaces were generated mathematically so the surface statistics can be systematically altered to identify the roughness parameters that contribute the most to drag. The surfaces were generated in MATLAB using a circular Fast Fourier Transform (FFT) with a random set of independent phase angles, distributed between 0 and 2π, with a Gaussian power spectral density (PSD), in the form of \( E(k)=l{h}^2/\left(2\sqrt{\pi}\right)\ {e}^{-{k}^2{l}^2/4} \), where k is the wavenumber, and l and h are parameters that control the shape of the spectrum (l sets the length-scale of the roughness elements and h the roughness rms). The random phase was generated using the Pearson system random numbers [14], where both skewness (Sk) and flatness (Fl) can be set as input parameters. These values were adjusted until the desired Sk and Fl were achieved after the Gaussian power spectrum was imposed. The Gaussian-shape power spectrum was selected, as opposed to the power-law [2], because better control of the roughness parameters, down to the resolution of the printer, could be achieved. It should be noted that, even though a Gaussian power spectrum was chosen, the skewed surfaces possess a non-Gaussian probability density function.

The generated surfaces were reproduced using a high-resolution 3D printer (Objet 30 Pro) with lateral resolution 34 μm, elevation resolution 16 μm. A total of twenty plates for each roughness case were printed, each 216 mm × 165 mm, enough to cover the top and bottom of the rough section of the channel. The tiles were glued onto a piece of acrylic using an epoxy and vacuum bagging technique, and then machined to fit in the channel flow facility, as described in [2]. Four separate surfaces with different surface topographies but similar surface statistics were created and each was replicated five times. The tiles were randomly positioned along the streamwise length of the channel to avoid repeating features that have been shown to create secondary flows [1].

The surfaces were scanned to determine the statistics of the printed surfaces. The scanned region (50 mm by 15 mm, x and y direction, respectively), were obtained with an optical profilometer utilizing white light interferometry (Veeco Wyco NT9100), with sub-micron vertical resolution and 3.4 μm lateral resolution. The data acquired from the profilometer require careful post-processing in order to remove any anomalies and spurious data as well as filling any holes in the surface scans that result from angles that are too steep for the optical profilometer to measure accurately. The surface scans had tilt and curvature removed, and the holes were filled using a PDE-based interpolation method [3]. Spurious data from the interpolation step were removed by a median-test filter, followed by a second PDE-based interpolation. Further details of the post-processing can be found in Flack et al. [10].

Figure 2 shows both the mathematically generated and a scan of a printed surface, along with the corresponding pdf, indicating the ability of the printer to reproduce the desired surface. While the printer has limited spatial resolution, which filters the desired surface parameters, a systemic variation of parameters is achieved. Figure 3 shows representative surface topography profiles based on the surface scans, demonstrating the effect of varying krms and Sk.

Fig. 2
figure 2

Mathematically generated (a) and printed (b) surface roughness with corresponding pdf of surface elevation (c)

Full size image
Fig. 3
figure 3

Sample surface profiles - 1, 2, 3, and 6. The elevation color scale is mm. Comparison between 1 and 2 demonstrates the effect of krms (fix Sk ~ 0). Comparison between 2, 3 and 6 demonstrates the effect of skewness (fix krms)

Full size image

Table 1 lists the statistics of the surfaces as determined from the scans. These include the centerline average roughness height, \( {k}_a=\left(1/N\right){\sum}_{i=1}^N\left|{z}_i\right| \), the rms roughness height, \( {k}_{rms}=\sqrt{\left(1/N\right){\sum}_{i=1}^N{z}_i^2} \), the peak-to-trough roughness height, kt = zmax − zmin, skewness, \( Sk=\left(1/N\right){\sum}_{i=1}^N{z}_i^3/{\left[\left(1/N\right){\sum}_{i=1}^N{z}_i^2\right]}^{3/2} \), flatness, \( Fl=\left(1/N\right){\sum}_{i=1}^N{z}_i^4/{\left[\left(1/N\right){\sum}_{i=1}^N{z}_i^2\right]}^2 \), and the effective slope, \( ES=\frac{1}{L_s}\int \left|\frac{\partial z}{\partial \overline{x}}\right|d\overline{x} \), [18]. Surfaces 1, 2 and 7 have Gaussian distributions (Sk ≈ 0) with varying roughness heights (krms, ka, kt), while surfaces 2–6 have a range of skewness (both positive and negative) with the roughness heights approximately constant. The effective slope was also constant for surfaces 2–6 but varied for surfaces 1 and 7.

Table 1 Roughness statistics of tested surfaces
Full size table

Also listed in Table 1 is the equivalent sandgrain roughness height, ks, the roughness height that produces the same roughness function as the uniform sandgrain of Nikuradse in the fully rough regime. Using the roughness function, ΔU+ (eq. 3), ks can be determined from:

$$ {\varDelta U}^{+}=\frac{1}{\kappa}\ln {k}_s^{+}+A-B $$
(4)

where κ = 0.40 is the von Kármán constant, B = 5.0 is the log-law intercept for a smooth wall, and A = 8.5 is the intercept for a uniform sandgrain surface. The error in estimating ks is 7%.

3 Results and discussion

Sample skin-friction (Cf) results for all the tested surfaces are shown in fig. 4 as a function of the Reynolds number based on the channel height (H) and mean velocity (U), Rem = UH/ν. Also included are the smooth-wall results of Schultz and Flack [23]. At low Reynolds number, all the surfaces appear to be hydraulically smooth or nearly so. At higher Reynolds number the rough surfaces all exhibit fully-rough behaviour, where the skin-friction becomes independent of Reynolds number at sufficiently high Reynolds number. Skewness and rms roughness height are scales that impact the skin-friction coefficient. Focusing on surface 1 and 7 (red and green diamonds on fig. 4), as krms increases, the drag on the rough surfaces increases monotonically. Similarly, for sufaces from 2 to 6, as the skewness increases (and krms is remained constant) from negative to positive values, the drag on the rough surfaces increases. Negative skewness (pits) has a much smaller influence than positive skewness (peaks). There is a relatively small difference in the skin-friction coefficient for the negatively skewed surfaces compared to the surface with zero skewness, whereas, there is a dramatic difference in Cf as the skewness increases from Sk = 0 to +0.35 to +0.84. Comparing all cases, it is clear that positive skewness (peaks) has a stronger influence on increased drag than increased rms roughness height. Reduced drag for negatively skewed surfaces is likely a result of the flow filling in the surface depressions causing a skimming effect. For positively skewed surfaces, flow separation from the peaks and the resulting pressure drag contributes to increased losses. This is especially evident for the highly skewed surface (Sk = +0.84). The overall trend is in agreement with the numerical study of Jelly and Busse [13]. Their study investigated a Gaussian roughness height distribution with DNS performed for the original surface (zero skewness) and the Gaussian height map decomposed into ‘pits-only’ (negatively skewed) and ‘peaks-only’ components (positively skewed). The positive and zero skewness surfaces had similar roughness functions while the negatively skewed surface displayed significantly lower drag.

Fig. 4
figure 4

Skin-friction coefficient

Full size image

The roughness function (∆U+) is shown in Fig. 5. Most of the surfaces (2,3,4,5 and 7) collapse to a single roughness function that is similar to but offset slightly from the Nikuradse [19] roughness function for uniform sand grain. These surfaces depart from hydraulically-smooth at ks+ ≈ 4–6 and become fully-rough at ks+ ≈ 40–45. The two surfaces that do not collapse on the others are surface 1 (krms = 44 μm, Sk = −0.06), the surface with the smallest rms roughness height, and surface 6 (krms = 90 μm, Sk = +0.84), the most positively skewed. The shape of the roughness functions in the transitionally-rough regime for surfaces 1 and 6 are markedly different. High positive skewness leads to an abrupt departure from hydraulically-smooth to fully-rough. However, this surface also remains hydraulically-smooth and transitions to fully-rough at larger roughness Reynolds numbers (ks+) than the other surfaces. The transitionally-rough range for surface 6, the highly positive skewed surface, is 10 < ks+ < 70. On the other hand, surface 1 has a more gradual transition from hydraulically-smooth to fully-rough behaviour but the shape of the roughness function in the transitionally rough regime does not follow the Nikuradse roughness function or the Colebrook [6] roughness function that is used in the Moody diagram [16]. The transitionally-rough range for surface 1 (2 < ks+ < 15) is significantly less than the other surfaces. The abbreviated transitionally-rough regime extent was also observed for practical engineering surfaces such as honed pipe (Shockling et al. [25]) and commercial steel pipe (Langelandsvik et al. [17]). The difference in shape of ∆U+ for surface 1 is likely due to differences in effective slope (ES), also listed in Table 1, as noted by Barros et al. [2]. It has been shown [18, 22] that an effective slope less than 0.35 indicates that a surface is “wavy” or has undulating long wavelength scales that do not contribute significantly to the drag.

Fig. 5
figure 5

Roughness function (same symbols as 4)

Full size image

The present results can now be used to explore predictive correlations for the equivalent sandgrain roughness height ks, where ks = ks (krms, Sk). Figure 6 shows the results for the Gaussian-PSD surfaces along with other recent experimental results for grit-blasted roughness [10], random roughness with a power law distribution [2] as well as the surfaces used by Flack and Schultz [8] to develop the predictive correlation having the following form, with A = 4.43 and B = 1.37:

Fig. 6
figure 6

All data (Flack and Schultz [8])

Full size image
$$ {k}_s=A{k}_{rms}{\left(1+ Sk\right)}^B $$
(4)

The Gaussian-PSD surfaces do not all follow this correlation closely, as highlighted in the inset for smaller values of ks. This is not a surprising result since mostly positively-skewed surfaces were used to obtain the correlation shown in the figure and the Gaussian-PSD surfaces have skewness ranging from −0.70 to +0.84. Separate correlations for positive, negative and zero skewness are likely needed.

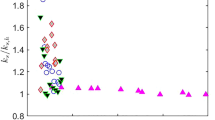
Figures 7, 8 and 9 show ks actual vs. ks predicted results for a compilation of surfaces with only positive, negative and zero skewness, respectively. Positive skewness (fig. 7) results in a correlation that is more strongly dependent on skewness as indicated by the increase in coefficient B and a decrease in A, as compared to the previously proposed correlation. While there is a high level of correlation, ks for the Gaussian-PSD surfaces are still under-predicted. This indicates that additional surface parameters such as effective slope or a shape-based scale may be needed.

Fig. 7
figure 7

Surfaces with positive skewness, Sk > 0

Full size image
Fig. 8
figure 8

Surfaces with negative skewness, Sk < 0

Full size image
Fig. 9
figure 9

Surfaces with zero skewness, Sk = 0

Full size image

Negative skewness (fig. 8) shows an opposite trend with a correlation that is more strongly dependent on the rms roughness height as indicated by the decrease in B and an increase in A. Coefficient B also changes sign as compared to the same coefficient for the positively skewed surfaces, indicating the need for separate predictive equations for positively and negatively skewed surfaces. The form of the equation was also slightly modified to allow for Sk < −1. The correlation shown in fig. 8 fits the data remarkably well (note change in scale) for a wide range of surface roughness.

Figure 9 shows predictive results for surfaces with zero skewness, a roughness that statistically has a similar distribution of pits and peaks. The form of the correlation for this type of surface roughness based solely on krms. For this sparse data set, results indicate that ks ≈ 2 krms for random roughness with Sk ≈ 0.

4 Conclusions

Experimental results are presented for systematically-varied random roughness. Positively-skewed surfaces (peaks) display significantly higher drag than negatively-skewed surfaces (pits). Results also indicate that high positive skewness has a stronger influence on increased drag than rms roughness height for the range of surfaces tested in this study. For similar rms roughness heights, negatively-skewed surfaces create less drag. The flow may be filling in the pits and skimming over these surface features.

The majority of the surfaces collapse to a single roughness function, following a Nikuradse-type roughness function throughout the transitionally-rough regime. Two surfaces displayed roughness functions with different shapes and extent of the transitionally-rough regime. The first exception is the most highly-skewed surface which has an abrupt transition from hydraulically-smooth to transitionally-rough along with a larger ks+ to reach fully-rough. The wavy surface displayed a more gradual transition from hydraulically-smooth to fully-rough behaviour with a lower range of the transitionally-rough regime. It is also important to note that none of the surfaces follow a Colebrook-type roughness function.

Results indicate that skewness and rms roughness height are important surface parameters however, a single correlation cannot adequately predict frictional effects of surface texture. Based on the present results, correlations should be separated by positive, negative and zero skewness of the pdf to capture the differences in near-wall flow interactions for peaked and pitted surfaces. Predictive correlations for wavy surfaces (ES < 0.35) and highly skewed surfaces require different or additional parameters. While the present results are promising, a single correlation is still elusive and may not be achievable. The effective slope (or similar slope parameter) appears to be necessary for wavy surfaces. Other candidates may include a planform or frontal shape parameter (or ES [27]) and correlation lengths of surface elevations. Additional studies are needed for a wider range of surfaces before definitive correlations can be obtained. Recent advancements in simulations of rough-wall flows may allow a larger range of the parameter space to be explored, eventually leading to better predictive correlations.