Outer layer similarity in fully rough turbulent boundary layers

Abstract

Turbulent boundary layer measurements were made on a flat plate covered with uniform spheres and also on the same surface with the addition of a finer-scale grit roughness. The measurements were carried out in a closed return water tunnel, over a momentum thickness Reynolds number (Re _θ ) range of 3,000–15,000, using a two-component, laser Doppler velocimeter (LDV). The results show that the mean profiles for all the surfaces collapse well in velocity defect form. Using the maximum peak to trough height (R_t) as the roughness length scale (k), the roughness functions (ΔU⁺) for both surfaces collapse, indicating that roughness texture has no effect on ΔU⁺. The Reynolds stresses for the two rough surfaces also show good agreement throughout the entire boundary layer and collapse with smooth wall results outside of the roughness sublayer. Quadrant analysis and the velocity triple products show changes in the rough wall boundary layers that are confined to y<8k_s, where k_s is the equivalent sand roughness height. The present results provide support for Townsend’s wall similarity hypothesis for uniform three-dimensional roughness. However, departures from wall similarity may be observed for rough surfaces where 5k_s is large compared to the thickness of the inner layer.

1 Introduction

Turbulent boundary layers over rough surfaces occur in a wide range of flows. These include boundary layers on ships (Grigson 1992; Schultz 2000), in turbomachinery (Acharya et al. 1986; Bons et al. 2001), in pipes (Moody 1944), and on air and spacecraft (Pimenta et al. 1979). Meteorologists also wish to understand and predict the effect that roughness, such as terrestrial topography and vegetation, has on the atmospheric boundary layer for weather prediction (Andreopoulos and Bradshaw 1981). For these reasons, a great deal of effort has been made to quantify the effect of surface roughness on boundary layer structure. Raupach et al. (1991) give a thorough review of this work and point out that, while rough wall flows are of great importance, they are much more poorly understood than flows over smooth walls. Their review also concludes that there is strong experimental support for Townsend’s wall similarity hypothesis (Townsend 1976). This hypothesis states that the turbulence outside of the roughness sublayer, a layer extending out approximately five roughness heights from the wall, is independent of the surface condition at sufficiently high Reynolds numbers. However, some recent research casts doubts on the wall similarity hypothesis, stating that roughness effects can be observed well into the outer layer. This is witnessed by studies that indicate that surface roughness alters the velocity defect profile (Krogstad et al. 1992; Acharya et al. 1986), leads to a higher degree of isotropy of the Reynolds normal stresses (Krogstadet al. 1992; Krogstad and Antonia 1999; Antonia and Krogstad 2001), and changes the Reynolds shear stress profiles in the outer region of the boundary layer (Krogstad et al. 1992; Krogstad and Antonia 1999; Antonia and Krogstad 2001). The implication of these results is that the interaction of the inner and outer regions of the boundary layer may be more important than previously thought. They also imply that classical mixing length approaches to modeling the Reynolds shear stress in the outer region of rough wall boundary layers may not be appropriate (Antonia and Krogstad 2001).

Some of the seminal studies of rough wall boundary layers were made by Clauser (1954) and Hama (1954). Both these authors showed that the effect of surface roughness on the mean flow was to cause a downward shift in the logarithmic region of the boundary layer. For k-type rough walls, this downward shift, ΔU⁺, the roughness function, correlates in some fashion with the roughness Reynolds number. The roughness Reynolds number, k⁺, is defined as the ratio of the roughness length scale, k, to the viscous length scale, ν/u _τ . The mean velocity profile in a rough wall boundary layer, therefore, can be expressed as:

$$ U^ + = \frac{1} {\kappa }\ln \left( {y^ + } \right) + B - \Delta U^ + + \left( {\omega (y/\delta )\frac{\Pi } {\kappa }} \right). $$

(1)

Hama (1954) found that, by evaluating Eq. 1 for both a rough and a smooth surface (ΔU⁺_s≡0) at y=δ, the roughness function is found by subtracting the rough wall log-law intercept from the smooth wall intercept, B, at the same value of Re _δ . The roughness function can, therefore, be expressed as:

$$ \Delta U^{ + } = {\left( {{\sqrt {\frac{2} {{C_{{\text{f}}} }}} }} \right)}_{{\text{S}}} - {\left( {{\sqrt {\frac{2} {{C_{{\text{f}}} }}} }} \right)}_{{\text{R}}} . $$

(2)

It should be noted that Eq. 2 is valid provided the mean velocity profiles collapse is in velocity defect form, given as (Clauser 1954):

$$ \frac{{U_e - U}} {{u_\tau }} = f\left( {\frac{y} {\delta }} \right). $$

(3)

A majority of the experimental evidence seems to support the universality of the defect law (Antonia and Krogstad 2001; Clauser 1954; Bandyopadhyay 1987). Collapse of the mean defect profiles for rough and smooth walls is also consistent with the wall similarity hypothesis of Townsend (1976).

The utility of the roughness function is that, once ΔU⁺=f(k⁺) for a given roughness is known, it can be used in a computational boundary layer code or a similarity law analysis to predict the drag of any body covered with that roughness (Townsin and Dey 1990). However, it is not presently clear how to specify k for a generic rough surface by a physical measurement of the surface roughness alone. Granville (1958) first pointed out that a single roughness length scale would not be suitable to collapse the roughness function for a range of roughness types, and multiple length scales were needed to account for the differences in texture. To this end, Townsin and Dey (1990) proposed that a height parameter based on the first three even moments of the surface profile power spectral density reasonably collapsed the roughness functions for a ship’s hull roughness. However, Grigson (1992) contends that, for arbitrary roughness, ΔU⁺ must be measured and cannot be predicted a priori based on correlation with measures of the surface topography. The collapse of the roughness functions for all types of surfaces also seems unlikely due to the inherent difference in the shape of the functions for uniform sand roughness (Nikuradse-type, Nikuradse 1933) and random engineering roughness (Colebrook-type) as noted by Colebrook and White (1937). Colebrook and White also showed that, in pipe flow, the inclusion of a few large scale roughness elements (covering ~5% of the surface area) in a uniform sand roughness greatly increased the friction factor in the fully rough regime. The ratio of the length scales of roughness used in their experiments was ~10. Interestingly, the friction factor with just the isolated large elements was much less than the large elements with the smaller background roughness. This indicates that small-scale roughness can have an effect on the mean flow in the presence of larger scale roughness. Ligrani and Moffat (1986) showed that the behavior of the roughness function in the transitionally rough regime for close-packed spheres is different to that for close-packed sand. This also seems to indicate that the roughness texture is important even for uniform roughness, but the question as how to best quantify it remains unanswered.

The purpose of the present study is to document and compare the mean velocity, Reynolds stress, and higher-order velocity moment profiles over two rough surfaces in the fully rough regime. One of the surfaces is covered with uniform diameter, close-packed spheres. The other is the close-packed spheres covered with a finer-scale grit roughness. The grit adds a secondary roughness length scale and effectively changes the roughness texture. The two surfaces, therefore, represent a uniform roughness and a roughness that is more random. From these results, it is hoped that the applicability of Townsend’s wall similarity hypothesis can be evaluated, and the existence of a suitable roughness scaling parameter related to the surface topography of both surfaces can be found. Both goals are important to properly model and predict turbulent flows over rough surfaces.

2 Experimental facilities and method

The present experiments were carried out in the closed circuit water tunnel facility at the United States Naval Academy Hydromechanics Laboratory. The test section is 40×40 cm in cross-section and 1.8 m in length, with a tunnel velocity range of 0–6.0 m/s. In the present investigation, the freestream velocity was varied between ~1.0 m/s and 3.5 m/s (Re _x =1.4×10⁶−4.9×10⁶). Flow management devices include turning vanes placed in the tunnel corners and a honeycomb flow straightener in the settling chamber. The honeycomb has 19-mm cells that are 150 mm in length. The area ratio between the settling chamber and the test section is 20:1. The resulting freestream turbulence intensity in the test section is ~0.5%.

The test specimens were inserted into a flat plate test fixture mounted horizontally in the tunnel. The test fixture is the same as that used by Schultz and Flack (2003) and is shown in Fig. 1. The fixture is 0.40 m in width, 1.68 m in length, and 25-mm-thick. The forward most 200 mm of the test fixture is covered with 36-grit sandpaper to trip the developing boundary layer. The use of a strip of roughness was shown by Klebanoff and Diehl (1951) to provide effective boundary layer thickening and a fairly rapid return to self-similarity. The test specimen mounts flush into the test fixture and its forward edge is located immediately downstream of the trip. The removable test specimens are fabricated from 12-mm-thick cast acrylic sheet 350 mm in width and 1.32 m in length. The boundary layer profiles presented here were taken 1.35 m downstream of the leading edge of the test fixture. The trailing 150 mm of the flat plate fixture is a movable tail flap. This was set with the trailing edge up at ~5° in the present experiments to prevent separation at the leading edge of the plate. The physical growth of the boundary layer and the inclined tail flap created a mildly favorable pressure gradient at the measurement location. The acceleration parameter (K) was <7.0×10⁻⁸ over the range of Reynolds numbers tested. The pressure gradient varied only slightly between the test specimens.

Fig. 1

Schematic of the flat plate test fixture for the velocity profile method

Three test surfaces were tested in the present study. One was a smooth, cast acrylic surface. Another surface consisted of uniform diameter, close-packed spheres. The last surface consisted of uniform diameter, close-packed spheres covered with a smaller-scale grit roughness. The surfaces with uniform spheres were constructed of no. 9 lead shot with a diameter of 2.12±0.04 mm (mean±95% confidence interval). The spheres were attached to the test specimen with polyamide epoxy sprayed over the surface. The uniform spheres with grit surface was the same as the uniform spheres surface but was also covered with a very thin layer of epoxy mixed with sand grit. The surface roughness profiles of the test plates were measured using a Cyber Optics laser diode point range sensor (model no. PRS 40) laser profilometer system mounted to a Parker Daedal two-axis traverse with a resolution of 5 μm. The resolution of the sensor is 1 μm, with a laser spot diameter of 10 μm. Data were taken over a sampling length of 50 mm and were digitized at a sampling interval of 25 μm. Ten linear profiles were taken on each of the test surfaces. No filtering of the profiles was conducted, except to remove any linear trend in the trace. Figure 2 shows typical roughness profiles for the two rough surfaces. Note that that the major influence of the grit on the surface was to increase the height and slope of the roughness peaks. The maximum peak to trough roughness heights (R_t) for the uniform spheres and uniform spheres with grit were 960±40 μm and 1130±60 μm, respectively. Roughness profiles were also taken on a smooth surface sprayed with the mixture of sand grit and epoxy in order to determine the secondary length scale that was added. R_t for this surface was 130±15 μm. The ratio of the sphere and sand grit length scales was ~7.5.

Fig. 2

Representative surface profiles for the rough specimens

Velocity measurements were made using a TSI IFA550 two-component, fiber-optic laser Doppler velocimeter (LDV) system. The LDV used a four-beam arrangement and was operated in backscatter mode. The probe volume diameter was 90 μm, and its length was 1.3 mm. The viscous length (ν/u _τ ) varied from a minimum of 5 μm for uniform spheres with grit at the highest Reynolds number to 24 μm for the smooth wall at the lowest Reynolds number. The diameter of the probe volume, therefore, ranged from 3.8 to 18 viscous lengths in the present study. The LDV probe was mounted on a Velmex three-axis traverse unit. The traverse allowed the position of the probe to be maintained to ±10 μm in all directions. In order to facilitate two-component, near-wall measurements, the probe was tilted downwards at an angle of 4° to the horizontal and was rotated 45° about its axis. Velocity measurements were conducted in coincidence mode with 20,000 random samples per location. Doppler bursts for the two channels were required to fall within a 50-μs coincidence window or the sample was rejected.

In this study, the skin-friction coefficient, C_f, for the smooth surface was found using the Clauser (1954) chart method with log-law constants κ=0.41 and B=5.0. For the rough walls, C_f was obtained using a procedure based on the modified Clauser chart method given by Perry and Li (1990). To accomplish this, the wall datum offset was first determined using an iterative procedure. This involved plotting U/U _e versus ln(yU _e /ν) for points in the log-law region (points between y⁺=60 and y/δ=0.2) based on an initial guess of u _τ obtained using the total stress method detailed below. Note that y=y_T+ɛ, where y_T is the location of the top of the roughness elements, and ɛ is the wall datum offset, which is initially taken to be zero. The wall datum offset was increased until the goodness of fit of a linear regression through the points was maximized. The following formula was then used to determine C_f based on the slope of the regression line (Lewthwaite et al. 1985):

$$ C_{\text{f}} = 2\kappa ^2 \left\{ {\frac{{{\text{d}}(U/U_e )}} {{{\text{d}}\left[ {\ln \left( {{{yU_e } \mathord{\left/ {\vphantom {{yU_e } \nu }} \right. \kern-\nulldelimiterspace} \nu }} \right)} \right]}}} \right\}^2 . $$

(4)

For all the test surfaces, the total stress method was also used to verify C_f. If the viscous and turbulent stress contributions are added together, C_f may be calculated using the following expression, evaluated in the inner layer or overlap region of the boundary layer:

$$ C_{\text{f}} = \frac{2} {{U_e^2 }}\left[ {\nu \frac{{\partial U}} {{\partial y}} - \overline {u'v'} } \right]. $$

(5)

On the smooth walls, the total stress was calculated at the plateau of the Reynolds shear stress profile in the overlap region of the boundary layer. For the rough walls, it was calculated outside of the roughness sublayer at the outer edge of the overlap region (y/δ=0.2). The results from the Clauser chart methods and the total stress method agreed to within their uncertainty for both the rough and smooth walls.

It should be noted that neither method used to determine the wall shear stress on the rough surfaces in the present study is ideal. The modified Clauser chart method assumes that the log law is valid for rough wall boundary layers and requires the solution of additional degrees of freedom (the wall offset, ɛ, and the roughness function, ΔU⁺). Krogstad et al. (1992) modified this procedure by including the wake region in the determination of the wall shear stress. Although this method allows for more points in the boundary layer to be used in determining the wall shear stress, it assumes both the existence of the log law and the functional form of the law of the wake for rough wall flows. The method also simultaneously determines C_f, ɛ, and ΔU⁺. It was noted by Acharya et al. (1986) that simultaneous selection of these parameters can yield an improved statistical fit of the data but may, in some cases, give increased an error in C_f. Using the total stress method on rough wall boundary layers has its own shortcomings. This method relies on a plateau in the Reynolds shear stress profile, which is often not clearly defined in the roughness sublayer, and has fairly high measurement uncertainty in this region.

Unfortunately, most wall shear stress determination methods employed on smooth wall boundary layers are either not feasible or have increased uncertainty on rough walls. For example, direct measurement methods, such as using a floating element force balance, can be fraught with difficulties. As discussed by Winter (1977), measurement uncertainties with force balances arise due to misalignment and gaps, as well as replicating the roughness exactly on the floating element. An accurate means of independently measuring the wall shear stress in rough wall boundary layers is obviously needed.

3 Uncertainty estimates

Precision uncertainty estimates for the velocity measurements were made through repeatability tests using the procedure given by Moffat (1988). Ten replicate velocity profiles were taken on both a smooth and a rough plate. The standard error for each of the measurement quantities was then calculated for both samples. In order to estimate the 95% confidence limits for a statistic calculated from a single profile, the standard deviation was multiplied by the two-tailed t value (t=2.262) for 9 degrees of freedom and α=0.05, as given by Coleman and Steele (1995). LDV measurements are also susceptible to a variety of bias errors, including angle bias, validation bias, velocity bias, and velocity gradient bias, as detailed by Edwards (1987). Angle or fringe bias is due to the fact that scattering particles passing through the measurement volume at large angles may not be measured since several fringe crossings are needed to validate a measurement. In this experiment, the fringe bias was considered insignificant, as the beams were shifted above a burst frequency representative of twice the freestream velocity (Edwards 1987). Validation bias results from filtering too close to the signal frequency and any processor biases. In general, these are difficult to estimate and vary from system to system. No corrections were made to account for validation bias. Velocity bias results from the greater likelihood of high-velocity particles moving through the measurement volume during a given sampling period. The present measurements were burst transit time weighted to correct for velocity bias, as given by Buchhave et al. (1979). Velocity gradient bias is due to variation in velocity across the measurement volume (Durst et al. 1998). The errors due to velocity gradient bias were negligible since all data in the present study were taken at y⁺≥35, therefore, no correction for this bias error were made. An additional bias error in the v′ measurements of ~2% was caused by introduction of the w′ component due to the inclination of the LDV probe. This error effects $\overline {u'v'}$ as well, but to lesser degree (<1%), since u′ and w′ are uncorrelated and u′ is much larger than v′ across the entire boundary layer.

These bias estimates were combined with the precision uncertainties to calculate the overall uncertainties for the measured quantities. The resulting overall uncertainty in the mean velocity is ±1%. For the turbulence quantities $\overline {{u'}^2 } ,\;\overline {{v'}^2 } ,$ and $\overline {u'v'} ,$ the overall uncertainties are ±2%, ±4%, and ±7%, respectively. The precision uncertainties in C_f were calculated using a series of repeatability tests, in a manner similar to that carried out for velocities. These were combined with bias estimates to calculate the overall uncertainty in C_f. The uncertainty in C_f for the smooth walls using the Clauser chart method is ±4%, and the uncertainty in C_f for the rough walls using the modified Clauser chart method was ±7%. The increased uncertainty for the rough walls resulted mainly from the extra two degrees of freedom in fitting the log law (ɛ and ΔU⁺). The uncertainty in C_f using the total stress method is ±10% for both the smooth and rough walls. The uncertainties in δ, δ^*, and θ are ±7%, ±4%, and ±5%, respectively.

4 Results and discussion

4.1 Experimental conditions

The experimental conditions for each test case are presented in Table 1. The results show significant increases in the boundary layer thickness (δ) on both of the rough surfaces compared to the smooth wall at the three highest values of Re _θ . While the integral length scales (δ^* and θ) were also increased on the rough walls, the change in δ^* was more pronounced. This is seen in the shape factor, H, which was higher on the rough walls. No significant changes were observed in these boundary layer parameters when comparing the packed sphere surfaces with and without grit. The wake parameter, Π, showed no definitive trend with change in the wall condition. The results of Krogstad et al. (1992) and Keirsbulck et al. (2002) showed that Π was increased on mesh-type and transverse-bar-type roughnesses, respectively. They attributed the increase to greater entrainment of irrotational fluid. The results of Schultz and Flack (2003) also showed a slight increase in Π over sandgrain roughness. It should be noted that the wake parameters for all of the present test cases are less than 0.55, the value given by Coles (1956) as the high Reynolds number asymptote for smooth walls. This may have been the result of slightly elevated freestream turbulence in the present study.

Table 1 Boundary layer parameters for the test cases

The skin-friction coefficient for the three test surfaces are shown in Fig. 3. Also shown for comparison are the smooth wall results of Coles (1962) and DeGraaff and Eaton (2000). The rough surfaces show a significant increase in C_f over the entire range of Re _θ , compared to the smooth wall. At the highest Re _θ , the uniform sphere surfaces exhibit a 120% and a 140% increase, with and without grit, respectively. The surface with the grit shows a modest increase (10%) over the surface without grit. While this increase is within the combined experimental uncertainty of the measurements, a consistent trend of higher C_f for this surface is observed throughout the range of Re _θ . It should be noted that the values of C_f presented in Fig. 3 and Table 1 were calculated based on the Clauser chart method for the smooth walls and the modified Clauser chart method for the rough walls. This was chosen because these methods have a lower experimental uncertainty than those obtained using the total stress method. The total stress method was used for verification, and in all cases, the results from the methods agreed to well within the experimental uncertainty.

Fig. 3

Skin-friction coefficient versus momentum thickness Reynolds number. (Overall uncertainty in C_f: smooth wall, ±4%; rough wall, ±7%)

4.2 Mean velocities

The mean velocity profiles in wall coordinates for all the test surfaces at Re _θ ~9,000 are presented in Fig. 4. The smooth wall results collapse well on a smooth log-law profile, while the rough wall results display a log region that is shifted by ΔU⁺ below the smooth profile. There is a slight increase in the roughness function for the surface with grit. The mean velocity profiles for the three surfaces at similar Re _θ are plotted in defect form in Fig. 5. Also shown for comparison is the smooth wall, direct numerical simulation (DNS) results of Spalart (1988) at Re _θ =1,410. The behavior of the mean profile for rough walls in the buffer layer depends strongly on ΔU⁺. If the roughness effect is weak (ΔU⁺ is small), the profile shape shows a departure of the mean profile below the log-law, as is seen for the smooth wall. If the roughness effect is large (ΔU⁺ is large), the profile in the buffer layer can lie above the log-law, as is seen for the present rough walls.

Fig. 4

Mean velocity profiles in wall coordinates for all surfaces at Re _θ ~9,000. (Overall uncertainty in U⁺: smooth wall, ±4%; rough wall, ±7%)

Fig. 5

Velocity defect profiles for all surfaces at Re _θ ~9,000. (Overall uncertainty in (U _e −U)/u _τ : smooth wall, ±5%; rough wall, ±7%)

As indicated by the velocity defect profiles, the surfaces collapse well in the overlap and outer regions of the boundary layer. A universal velocity defect profile for rough and smooth walls was proposed by both Clauser (1954) and Hama (1954). A collapse of the defect profiles also supports the wall similarity hypothesis of Townsend (1976) that states that turbulence outside of the roughness sublayer is independent of the surface condition at a sufficiently high Reynolds number. Numerous studies, including the works of Hama (1954), Antonia and Krogstad (2001), and Schultz and Flack (2003), have shown that the mean profiles for rough and smooth walls collapse in defect form for a range of roughness types.

The shift in the rough wall log-law profile as a function of the roughness height is called the roughness function, ΔU⁺=f(k⁺). The existence of a roughness function for a class of surface roughness facilitates the prediction of frictional drag based solely upon a physical measure of the roughness height. This was demonstrated for roughness on flat plates by Granville (1958), who used boundary layer similarity analysis to predict the frictional resistance coefficient, C_f=f(ΔU⁺), for plates of arbitrary length. The knowledge of the roughness function for a given surface roughness can also be extremely useful in turbulence modeling. If Townsend’s wall similarity hypothesis is valid, ΔU⁺ for a given surface could be used as an input for wall function and mixing length models to predict the drag of rough surfaces of engineering interest, as discussed by Patel (1998).

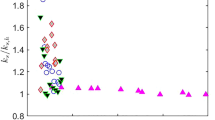
The roughness functions for the present surfaces are shown in Fig. 6. Also shown for comparison are the results of Ligrani and Moffat (1986) for a surface covered with close-packed uniform spheres. The results from both the present surfaces show good collapse to a Nikuradse-type roughness function (Schlichting 1979) using k=R_t, the maximum peak to trough height. In earlier work on sandpaper surfaces, Schultz and Flack (2003) observed a similar collapse using k=0.75R_t. It has been hypothesized by several researchers that, for random rough surfaces, a single length scale related to roughness height may not be sufficient to characterize roughness and that some means of quantifying the surface texture is also necessary (Townsin and Dey 1990; Musker 1980; Grigson 1992). Townsin and Dey (1990) have proposed a roughness length scale based on the first three even moments of the surface profile power spectral density in order to account for texture and have shown reasonable collapse of the roughness functions for a range of painted ship hull surfaces. In the present study, it was originally hypothesized that the addition of a secondary roughness length scale would make it necessary to employ a roughness parameter that accounts for surface texture. This proved not to be the case, as the roughness functions for the two surfaces collapsed well using simply R_t. Use of the Townsin and Dey (1990) roughness length scale yielded a much poorer collapse of the roughness functions. It should be noted that the present surfaces were operated in the fully rough regime, indicated by a linear roughness function. Both Ligrani and Moffat (1986) and Bandyopadhyay (1987) observed a greater degree of sensitivity of the roughness function to roughness geometry in the transitionally rough flow regime.

Fig. 6

Roughness functions (ΔU⁺ versus k⁺) for the rough specimens. (Overall uncertainty in ΔU⁺, ±10%)

4.3 Reynolds stresses and quadrant analysis

The Reynolds stresses for all the test surfaces are shown in Figs. 7, 8, and 9. Only the profiles at similar Reynolds number (Re _θ ~9,000) are presented. However, similar trends were observed for the entire range of Reynolds number tested. Also shown for comparison are the results of the smooth wall direct numerical simulation (DNS) of Spalart (1988) at Re _θ =1,410. The primary reason for the lack of agreement of the present smooth-wall data and the results of Spalart’s DNS is the difference in Reynolds number. The effects of the Reynolds number for the axial Reynolds stress are an increase in the peak and a shift in the peak towards the wall when plotted with the outer variables. The differences observed in the wall-normal Reynolds normal stress is a peak shifted closer to the wall for higher Reynolds numbers. These results were also documented by DeGraaff and Eaton (2000) for similar Reynolds numbers. Near the outer edge of the boundary layer, the present smooth-wall results lie above the DNS results. This is due to the fact that there was some freestream turbulence in the water tunnel (~0.5%), which was not present in the DNS.

Fig. 7

Normalized axial Reynolds normal stress profiles for all surfaces at Re _θ ~9,000. (Overall uncertainty in $\overline {{u'}^2 } /u_\tau ^2 :$ smooth wall, ±5%; rough wall, ±7%)

Fig. 8

Normalized wall-normal Reynolds normal stress profiles for all surfaces at Re _θ ~9,000. (Overall uncertainty in $\overline {{v'}^2 } /u_\tau ^2 :$ smooth wall, ±6%; rough wall, ±8%)

Fig. 9

Normalized Reynolds shear stress profiles for all surfaces at Re _θ ~9,000. (Overall uncertainty in $- \overline {u'v'} /u_\tau ^2 :$ smooth wall, ±8%; rough wall, ±10%)

The axial Reynolds normal stress $(\overline {{u'}^2 } /u_\tau ^2 )$ profiles are shown in Fig. 7. Some differences in $\overline {{u'}^2 } /u_\tau ^2$ are noted in the near-wall region (y/δ≤0.1) between the rough and smooth walls. For y/δ>0.1, collapse of the axial Reynolds normal stresses is observed for all of the surfaces. The results also show good agreement with the smooth wall DNS of Spalart (1988) for y/δ>0.1. It is of note that 5k, the approximate extent of the roughness sublayer given by Townsend (1976), corresponds to y/δ=0.16 and y/δ=0.18 for the uniform spheres and uniform spheres with grit surfaces, respectively. Excellent agreement in the axial Reynolds normal stress profiles is seen for both rough walls over the entire boundary layer. Agreement of rough and smooth wall axial Reynolds normal stresses outside the roughness sublayer has been observed previously by Krogstad et al. (1992), Perry and Li (1990), and Schultz and Flack (2003). The absence of a near-wall peak in the $\overline {{u'}^2 } /u_\tau ^2$ profiles over the rough walls as is seen in the smooth wall results is, according to Ligrani and Moffat (1986), indicative of a boundary layer in the fully rough regime.

The wall-normal Reynolds normal stress $(\overline {{v'}^2 } /u_\tau ^2 )$ profiles are presented in Fig. 8. Reasonably good agreement of the profiles is observed for all the surfaces throughout the boundary layer. Collapse of the wall-normal Reynolds normal stresses outside the roughness sublayer was also seen on mesh roughness by Perry and Li (1990) and on sandgrain and paint roughness by Schultz and Flack (2003). However, Krogstad et al. (1992) observed significant changes in $\overline {{v'}^2 } /u_\tau ^2$ well into the outer boundary layer for mesh roughness and, more recently (Krogstad and Antonia 1999), for transverse rod roughness. The differences seen in $\overline {{v'}^2 } /u_\tau ^2$ may result from a less severe boundary condition on the wall-normal velocity component for rough walls as compared to a smooth wall, as discussed by Krogstad et al. (1992). Between roughness elements, for example, y=0 is located at some distance above the wall itself, unlike the smooth wall case. However, the severity of the boundary condition depends largely on the roughness type. Some roughness types, including mesh, can provide a relatively large ΔU⁺ for their height, k.

A quantitative measure of the effect on the mean flow is the ratio of k_s/k, where the equivalent sand roughness height, k_s, is calculated as (Raupach, Antonia and Rajagopalan 1991):

$$ \Delta U^{ + } = \frac{1} {\kappa }\ln {\left( {k_{s} ^{ + } } \right)} - 3.2. $$

(6)

For the present rough walls, k_s/k~1, whereas k_s/k~3 for the mesh roughness of Krogstad et al. (1992) and k_s/k~6 for the transverse bar roughness of Krogstad and Antonia (1999). The present authors believe that, since k_s provides a “common currency” among roughness types for mean flow effects (Bradshaw 2000), it should be more effective than k itself in defining the extent of the roughness sublayer. Its main drawback is that it cannot be predicted a priori for a generic roughness from measurements of the roughness alone. Further research is needed to identify the physical length scale that best characterizes a generic rough surface.

If the extent of the roughness sublayer is taken to be 5k_s, the roughness sublayer corresponds to y/δ<0.33 for the mesh roughness of Krogstad et al. (1992), and to y/δ<0.66 for the transverse bar roughness of Krogstad and Antonia (1999), both of which are well into the outer layer. In the present rough wall cases, the sublayer defined in the aforementioned manner corresponds to y/δ<0.16 and y/δ<0.18 for the uniform spheres and uniform spheres with grit surfaces, respectively. The roughness sublayer in this study is, therefore, large compared with the thickness of the inner layer. Ligrani and Moffat (1986) noted good collapse of $\overline {{v'}^2 } /u_\tau ^2$ in the outer layer on uniform sphere roughness. In their study, the largest value of 5k_s/δ was ~0.1. This indicates that, if the extent of the roughness sublayer is larger than the inner layer itself (5k_s/δ>0.2), changes in the turbulence structure in the outer layer are to be expected. It is worth noting that the wall similarity hypothesis of Townsend (1976) takes the rough wall case to be a small perturbation to the smooth wall case, the assumption being that k<<δ. For many rough wall flows, both laboratory and real world, this simply is not the case and care should be made in the application of the wall similarity hypothesis. Further research is needed to better understand the differences in $\overline {{v'}^2 } /u_\tau ^2$ observed on roughness of different types.

The Reynolds shear stress $( - \overline {u'v'} /u_\tau ^2 )$ profiles are presented in Fig. 9. Outside the roughness sublayer (y/δ≥0.2), there is very good agreement among the Reynolds shear stresses for all of the surfaces and with Spalart’s DNS results (1988). These results are in agreement with the earlier studies of Ligrani and Moffat (1986) on uniform spheres and Schultz and Flack (2003) on sandgrain roughness. Krogstad et al. (1992) observed moderate increases in the Reynolds shear stress well into the outer layer on mesh roughness. They attributed this to a significant increase in both the strength and frequency of occurrence of the turbulent burst and sweep motions well into the outer layer. Again, a better understanding of how the type of the surface roughness affects the wall-normal momentum transport is needed. The Reynolds shear stress profiles for both of the rough surfaces in the present study agree throughout the entire boundary layer. The Reynolds shear stress correlation coefficient, R _uv , shown in Fig. 10, also indicates good agreement for y/δ>0.2. In the near-wall region, R _uv is larger for the rough walls than the smooth wall. This is mainly due to the near-wall peak in u′ for smooth walls, which is absent for rough walls.

Fig. 10

Reynolds shear stress correlation coefficient. (Overall uncertainty in R _uv ±8%)

In order to better quantify the possible differences between the rough and smooth wall boundary layers, the u′–v′ quadrant decomposition technique was used (Wallace et al. 1972). Using the hyperbolic hole size method of Lu and Willmarth (1973), calculations of the contributions of burst (Q2) and sweep (Q4) motions to the Reynolds shear stress were made. The contribution to $\overline {u'v'}$ from a given quadrant, Q, can be expressed as:

$$ {\left( {\overline{{{u}\ifmmode{'}\else$'$\fi{v}\ifmmode{'}\else$'$\fi}} } \right)}_{Q} = {\mathop {\lim }\limits_{T \to \infty } }\frac{1} {T}{\int\limits_0^T {u'v'(t)I_{Q} (t)\,{\text{d}}t} }{\text{,}} $$

(7)

where I _Q (t) is a trigger function defined as:

$$ I_Q = \left\{ {\begin{array}{*{20}l} 1 & {{\text{when}}\;\left| {u'v'} \right|_Q \geq h\sqrt {\overline {{u'}^2 } } \sqrt {\overline {{v'}^2 } } } \\ 0 & {{\text{otherwise}}.} \\ \end{array} } \right. $$

(8)

Figure 11 shows the normalized contribution from Q2 Reynolds shear stress for h=0. The results indicate that the Q2 contribution is significantly higher in the near-wall region (y/δ<0.15) for the rough walls than for the smooth wall. Outside of the roughness sublayer, the contributions for both the smooth and rough walls are very similar. The addition of a secondary roughness length scale had little effect on the Q2 contribution throughout the boundary layer. The results of Krogstad et al. (1992) for mesh roughness also showed an increase in the Q2 (h=0) contribution compared to a smooth wall, although the effect was observed throughout most of the boundary layer. The normalized contribution from Q4 Reynolds shear stress is presented in Fig. 12 for h=0. The results indicate that the magnitude of the Q4 events are also significantly higher in the near-wall region (y/δ<0.15) for the rough walls than for the smooth wall, but outside the roughness sublayer, the profiles collapse. Both rough walls show good agreement throughout the entire boundary layer. Krogstad et al. (1992) also showed an increase in the Q4 (h=0) contribution compared to a smooth wall, although the difference was observed to slowly decrease all the way out to the edge of the boundary layer, at which point, it was negligible.

Fig. 11

Normalized Reynolds shear stress contributions from Q2 with H=0 for all surfaces at Re _θ ~9,000. (Overall uncertainty in ${\left( {\overline{{{u}\ifmmode{'}\else$'$\fi{v}\ifmmode{'}\else$'$\fi}} } \right)}_{{Q2}} /u^{2}_{\tau } :$ ±10%)

Fig. 12

Normalized Reynolds shear stress contributions from Q4 with H=0 for all surfaces at Re _θ ~9,000. (Overall uncertainty in $- {\left( {\overline{{{u}\ifmmode{'}\else$'$\fi{v}\ifmmode{'}\else$'$\fi}} } \right)}_{{Q4}} /u^{2}_{\tau } :$ ±10%)

In order to investigate the contributions of the stronger Q2 and Q4 events, quadrant analyses were also made using h=2, which corresponds to instantaneous Reynolds shear stress producing events stronger than $5\,\overline {u'v'} .$ These results are shown in Figs. 13 and 14. The stronger Q2 events are observed to be enhanced for the rough wall over the range 0.1<y/δ<0.3. Further from the wall, the profiles show reasonable agreement. Very near the smooth wall, the contribution of strong Q2 events is more pronounced than on the rough wall. The upturn in the contribution from strong Q2 “ejection” events on smooth walls was also documented by Krogstad et al. (1992). This is due to the fact that strong Reynolds stress contributions from “ejection” events are more favored than from “sweep” events due to the wall boundary condition. On the rough wall, this is not the case.

Fig. 13

Normalized Reynolds shear stress contributions from Q2 with H=2 for all surfaces at Re _θ ~9,000. (Overall uncertainty in $- {\left( {\overline{{{u}\ifmmode{'}\else$'$\fi{v}\ifmmode{'}\else$'$\fi}} } \right)}_{{Q2}} /u^{2}_{\tau } :$ ±13%)

Fig. 14

Normalized Reynolds shear stress contributions from Q4 with H=2 for all surfaces at Re _θ ~9,000. (Overall uncertainty in $- {\left( {\overline{{{u}\ifmmode{'}\else$'$\fi{v}\ifmmode{'}\else$'$\fi}} } \right)}_{{Q4}} /u^{2}_{\tau } :$ ±13%)

In contrast (Fig. 14), the strong Q4 events were enhanced on the rough walls for y/δ<0.05. This was also observed by Krogstad et al. (1992), and is probably the result of the less strict boundary condition for wall-normal flow near the boundary. At y/δ>0.05, the results from both the smooth and rough walls show good agreement. The results for the two rough walls collapse for both Q2 and Q4 (h=2) over the entire boundary layer. To observe the relative importance of the Q2 and Q4 events in the boundary layer, their ratio is presented in Fig. 15 for h=0. The most significant difference is again noted for y/δ<0.05, where the strength of the Q2 events is higher than the Q4 for the smooth wall profiles, while the opposite is true for the rough wall. Although not presented here, the qualitative results for the h=2 case were quite similar to h=0.

Fig. 15

Ratio of Reynolds shear stress contributions from Q2 to Q4 with H=0 for all surfaces at Re _θ ~9,000. (Overall uncertainty in $- {\left( {\overline{{{u}\ifmmode{'}\else$'$\fi{v}\ifmmode{'}\else$'$\fi}} } \right)}_{{Q2}} /{\left( {\overline{{{u}\ifmmode{'}\else$'$\fi{v}\ifmmode{'}\else$'$\fi}} } \right)}_{{Q4}} :$ ±10%)

4.4 Triple products

The distributions of the normalized triple products, $\overline {{u'}^3 } /u_\tau ^3$ and $\overline {{v'}^3 } /u_\tau ^3 ,$ are presented in Figs. 16 and 17, respectively. The distributions of the normalized axial and wall-normal turbulent flux of Reynolds shear stress, $\overline {{u'}^2 v'} /u_\tau ^3$ and $\overline {u'{v'}^2 } /u_\tau ^3 ,$ are presented in Figs. 18 and 19, respectively. Also given for comparison are the smooth wall results of Murlis et al. (1982) at Re _θ =4,750 and the results over sandpaper roughness of Andreopoulos and Bradshaw (1981) at Re _δ =1.7×10⁵. There is good qualitative agreement between the present smooth wall results for $\overline {{u'}^3 } /u_\tau ^3$ and those of Murlis et al. (1982). However, there are significant differences in $\overline {{u'}^3 } /u_\tau ^3$ between the present rough walls and the smooth wall for 0.1<y/δ<0.3. The results indicate that there is increased turbulent flux of axial Reynolds normal stress in the streamwise direction for the rough walls. The region of influence is the same as that identified by quadrant analysis to be an area of enhanced strong Q2 events. It is of note that there is very good agreement between the uniform spheres and the uniform spheres with grit for $\overline {{u'}^3 } /u_\tau ^3 .$ Andreopoulos and Bradshaw (1981) also noted differences in the triple products for rough walls, compared to smooth walls, that extended out to y=10k. This is approximately the extent of influence noted in the present study (~8k). It should be noted, however, that there is considerable experimental uncertainty in all the triple products. It is most pronounced in $\overline {{v'}^3 } /u_\tau ^3$ and is an inherent limitation resulting from measuring velocities at an angle of ~45° to the mean flow. This was noted by Koskie and Tiederman (1991) for boundary layer data measured by LDV, but it is doubtlessly true for triple products measured with X-wire hot-wire probes as well. The fourth-order moments are effected to a lesser degree (Koskie and Tiederman 1991).

Fig. 16

Normalized triple product, $\overline {{u'}^3 } /u_\tau ^3 ,$ for all surfaces at Re _θ 9,000. (Overall uncertainty in $\overline{{{u}\ifmmode{'}\else$'$\fi^{3} }} /u^{3}_{\tau } :$ ±28%)

Fig. 17

Normalized triple product, $\overline {{v'}^3 } /u_\tau ^3 ,$ for all surfaces at Re _θ ~9,000. (Overall uncertainty in $\overline{{{v}\ifmmode{'}\else$'$\fi^{3} }} /u^{3}_{\tau } :$ ±38%)

Fig. 18

Normalized axial flux of Reynolds shear stress, $\overline {{u'}^2 v'} /u_\tau ^3 ,$ for all surfaces at Re _θ ~9,000. (Overall uncertainty in $\overline{{{u}\ifmmode{'}\else$'$\fi^{2} {v}\ifmmode{'}\else$'$\fi}} /u^{3}_{\tau } :$ ±22%)

Fig. 19

Normalized wall-normal flux of Reynolds shear stress, $\overline {{u'v'}^2 } /u_\tau ^3 ,$ for all surfaces at Re _θ ~9,000. (Overall uncertainty in $\overline{{{u}\ifmmode{'}\else$'$\fi{v}\ifmmode{'}\else$'$\fi^{2} }} /u^{3}_{\tau } :$ ±18%)

There is reasonable qualitative agreement between the present smooth wall results and those of Murlis et al. (1982) for $\overline {{v'}^3 } /u_\tau ^3$ (Fig. 17). While there is some increase in $\overline {{v'}^3 } /u_\tau ^3$ for the smooth wall compared to the rough wall, as also noted by Bandyopadhyay and Watson (1988), the difference is within the experimental uncertainty. Antonia and Krogstad (2001) noted differences in the sign of $\overline {{v'}^3 } /u_\tau ^3$ out to y/δ=0.3 on a wall covered with transverse rods compared to a smooth wall and a mesh roughness. There is quite good agreement between the uniform spheres and the uniform spheres with grit for $\overline {{v'}^3 } /u_\tau ^3$ over the entire boundary layer.

The axial turbulent flux of the Reynolds shear stress $(\overline {{u'}^2 v'} /u_\tau ^3 )$ results (Fig. 18) exhibit differences between the rough and smooth wall profiles. These are observed for 0.1<y/δ<0.3 as an increase in the turbulent flux of $- \overline {u'v'}$ in the upstream direction for the rough wall flows compared to the smooth wall. For y/δ>0.3, there is good agreement between all the surfaces. The agreement for the two rough walls is excellent throughout the entire boundary layer. Antonia and Krogstad (2001) also noted good agreement in $\overline {{u'}^2 v'} /u_\tau ^3$ for mesh roughness and a smooth wall, but observed significant differences over a large part of the boundary layer for transverse rod roughness. The wall-normal turbulent flux of the Reynolds shear stress $(\overline {u'{v'}^2 } /u_\tau ^3 )$ results (Fig. 19) show no significant differences for any of the surfaces tested.

5 Conclusion

In this work, the mean velocity and turbulence structure of two rough surfaces were compared to that for a smooth wall. Good collapse of the mean profiles for all the surfaces in velocity defect form was seen. The addition of a secondary roughness length scale had no effect on the Reynolds stresses or higher moment turbulence quantities throughout the entire boundary layer, indicating that the larger scale roughness has a dominant effect on the turbulence structure, even within the roughness sublayer. The roughness function increased slightly with the addition of the secondary length scale. However, if the change in the roughness height is accounted for, the roughness functions for both surfaces agree, indicating that this roughness texture had no effect on ΔU⁺. This is in contrast to the work of Colebrook and White (1937), who showed the inclusion of a smaller scale uniform roughness significantly increases the wall shear stress for surfaces with sparse larger scale roughness elements, even when the peak to trough roughness height is unchanged. It is believed that the reason for the difference is that the present rough surfaces were operated in the fully rough regime, while those of Colebrook and White were transitionally rough. The distinction being that viscous stresses are negligible in the near-wall region of fully rough boundary layers, whereas they may be appreciable in a transitionally rough boundary layer. The inclusion of a small scale roughness does not significantly alter the turbulent wake of the larger scale roughness elements in the fully rough regime.

The present results show good support for Townsend’s wall similarity hypothesis (1976). Excellent agreement among the smooth and rough surfaces was observed in the Reynolds stresses for y>5k. The higher-order turbulence statistics up to the fourth moment also showed good agreement for y>8k. The most salient change in the turbulence structure for the rough walls was an increase in the Reynolds shear stress contributions from the Q4 events in the near-wall region. This was also seen by Krogstad et al. (1992). It is presumably the result of the less severe boundary condition for the wall-normal velocity component on the rough wall. There were also differences in $\overline {{u'}^3 } /u_\tau ^3$ between the rough walls and the smooth wall for y<8k, indicating that there is increased turbulent flux of axial Reynolds normal stress in the streamwise direction for the rough walls. This is also thought to be related to the stronger Q4 events that occur near the rough wall.

Evaluation of this work and previous rough wall studies indicates that the equivalent sand roughness height, k_s, may be a more appropriate length scale for defining the extent of the roughness sublayer than the roughness height itself. The advantage of using k_s is that it provides a “common currency” (Bradshaw 2000) among disparate roughness types which reflects the roughness effect on the mean flow. Taking the roughness sublayer thickness to be equal to 5k_s also explains some of the departures from the wall similarity hypotheses that have been noted in the outer region of the boundary layer in previous rough wall studies. It should be stressed that Townsend’s hypothesis assumes that the rough wall flow case is a small perturbation to the smooth wall case (i.e., k«δ). For many laboratory and engineering flows, this underlying assumption is not satisfied. It is plausible, therefore, that if the roughness sublayer is large compared to the thickness of the inner layer (5k_s/δ>0.2), wall similarity should not be valid. A better understanding of the conditions that give rise to departures from wall similarity and the physical mechanisms responsible for the departures are needed.