An improved ID3 algorithm based on variable precision neighborhood rough sets

Abstract

The classical ID3 decision tree algorithm cannot directly handle continuous data and has a poor classification effect. Moreover, most of the existing approaches use a single mechanism for node measurement, which is unfavorable for the construction of decision trees. In order to solve the above problems, we propose an improved ID3 algorithm (called DIGGI) based on variable precision neighborhood rough sets. First, we introduce the notions of variable precision neighborhood (VPN) equivalence relation and VPN equivalence granule, and probe some basic properties of these notions. Second, we give the model of VPN rough sets and propose two extended measures: the VPN information gain and the VPN Gini index. Finally, we construct a hybrid measure by using the VPN dependence to combine the above two extended measures, and adopt the VPN equivalence granule as the splitting rule of DIGGI. Experimental results show that DIGGI is effective and its accuracy is greatly improved compared with three traditional decision tree algorithms, the neighborhood decision tree (NDT) and variable precision neighborhood decision tree (VPNDT) proposed in the latest literature.

1 Introduction

As an significant data analysis method, classification [1] plays significant roles in the task of data mining. In contrast to other classification algorithms [2, 3], the decision tree algorithms possess the advantages of fast classification, high accuracy, and good interpretability. Decision tree is one of the algorithms widely applied in inductive reasoning at present. It is built with the top-down recursive method, choosing the best feature as the current node, and branches down from the node according to the different values of the feature. Leaf nodes are classes to be divided. By now, scholars have proposed numbers of improvement decision tree algorithms. For instance, Breiman et al. [4] proposed the CART algorithm, which uses the Gini index to select splitting attributes. Moreover, Quinlan [5] proposed the well-known ID3 algorithm. ID3 is one of the classical decision tree algorithms at present and it adopts the information gain as the measure of nodes. However, this measure tends to select attributes with more values, which may generate a wide decision tree. To solve this problem, Quinlan [6] presented an improved algorithm (called C4.5) to induce decision trees, which uses the information gain ratio to select the optimal attribute division [7, 8].

Besides the above-mentioned shortcomings of ID3, there are also some other serious problems, e.g., ID3 can only deal with discrete data. When using this algorithm to deal with continuous data, we should first discretize the continuous data. Discretization will contribute to the loss of information, because the membership degree of numerical discretized values is not considered. In addition, when we face large-scale data sets, the log function will be called many times because we need to calculate the information entropy, and the computation amount will greatly increase. To solve the above problems, researchers have proposed many methods to improve decision tree. For instance, to overcome the problem of multivalued attribute bias, Liang et al. [9] presented a new attribute weighting method by using the simulation conditional probability to calculate the correlation between conditional and decision attributes. They linked information gain and attribute weights as new splitting criterion. Wang et al. [10] proposed a new decision tree optimization algorithm. Firstly, Gini index is used to improve the definition of boundary points and the calculation formula of information entropy in Fayyad theorem, so as to reduce the calculation times of information entropy in C4.5 algorithm. Then, CFS algorithm is introduced to optimize the calculation of information gain ratio, and the effectiveness of the algorithm is verified on Spark platform. Panhalkar et al. [11] proposed an African buffalo optimization algorithm suitable for solving complex problems to improve the decision tree and create a more efficient optimal decision tree.

The classical rough set model suggested by Pawlak [12] considered the whole research object as a universe. Information granules are obtained by dividing the universe of discourse into several proprietary equivalence classes using equivalence relations, which are used to describe arbitrary concepts in the universe. By now, the rough set theory has been widely used in classification, gene selection, attribute reduction and feature selection, etc. Some studies have shown that the decision method based on rough sets can flexibly deal with a variety of decision tables and is suitable for big data, but the output result is relatively complex. While decision tree generally deals with decision tables with multiple condition attributes and single decision attribute, the output result is relatively simple. Hence, by combining decision tree with rough sets, we can avoid the computational complexity caused by the logarithm operation and the bias problem of multivalued attributes. Wei et al. [13] discussed the combination of rough sets and decision tree. Wang et al. [14] proposed a concept of consistency based on rough sets and used it as a method of attribute selection. Moreover, they used this concept to solve the problems of multi-value bias of attribute values and huge amount of calculation in decision tree.

With the development of rough set theory, we gradually find that the classical rough set theory is no longer suitable for the application of the real world, and its limitations are more obvious. In order to solve this dilemma, scholars began to explore the generalization model of rough sets, and then the improved decision tree based on rough sets also turned to the use of more adaptable generalization models. Neighborhood rough set [15,16,17] is a generalization model of classical rough set. It replaces the strict equivalence relation with neighborhood relation, which greatly broadens its application scenario. At the same time, the problem that Pawlak rough set cannot deal with continuous data is also solved on this extended model, which reduces the problem of information loss caused by data discretization. Xie et al. [18] combined neighborhood rough setswith decision trees and designed an algorithm to solve the shortcoming of ID3 (i.e., it can only deal with discrete data) based on a neighborhood equivalence relation. In order to reduce the influence of noise on the construction of decision trees, the combination of variable precision rough sets [19,20,21] and decision trees were explored. Xie et al.considering the strict equivalence relation on the basis of the previous part, and then proposed an improved decision tree algorithm based on similarity relation, using similarity relation instead of equivalence relation, induced a variable precision decision tree algorithm, improved the classification accuracy. Liu et al. [23] found that the author of the previous literature ignored the geometric structure of the neighborhood system when considering the algebraic structure of the neighborhood system, resulting in unsatisfactory transitivity requirements, so they proposed solutions from a geometric perspective and combined with decision trees.

We observe that attribute dependence, information gain and Gini index are the most widely used splitting criteria in all literatures. Attribute dependency can best show the importance of conditional attributes to decision attributes. The information gain and gini index are two popular measures of nodes in decision trees, where the former has better classification ability for handling the chaotic data, while the latter is more effective in handling the pure data. Most of the existing decision tree algorithms use one of these metrics as a splitting criterion. If these metrics can be combined in a linear way to construct new metrics, can the classification accuracy of the decision tree be improved? There are few studies on the mixed metric, In [24], Xie et al. used the adaptive weighting of information gain and gini index to construct a hybrid measure and in [25], Jain et al. used constant weight to carry out linear combination integration. With the development of science and technology, uncertainty measurement is an important criterion in big data analysis. The emergence of hybrid measurement may provide people with new ideas. This paper attempts to combine these three metrics in a linear way to construct a new uncertainty measurement criterion to improve the classification performance of decision trees. On the basis of this idea, in this paper, we will propose two extended measures: the VPN Gini index, and the VPN information gain. Moreover, we will construct a hybrid measure by using the VPN dependence to combine the above two extended measures. This hybrid measure will be used to select nodes during the construction of decision trees. Experiments were confirmed on multiple UCI data sets, where the accuracy and the number of leaf nodes were used as the evaluation metrics. We verified the effectiveness of our algorithm by comparing it with the traditional CART algorithm, ID3 algorithm, C4.5 algorithm and the algorithms proposed in the latest literature[22, 23].

The main contributions of this work include: (1) The construction of neighborhood similarity by using Dice similarity can relax the strict equivalence relation between any two neighborhood granules. (2) Based on the neighborhood similarity and variable precision threshold, the equivalence relation of VPN is induced and a new VPN rough set model is proposed. The Gini index and information gain are extended to the variable precision neighborhood Gini index and variable precision neighborhood information gain by means of the VPN equivalence relation. (3) A new splitting criterion is defined by combining the variable precision dependence with the variable precision neighborhood Gini index and variable precision neighborhood information gain.

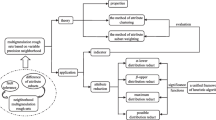
The remainder of this paper is structured as follows. Section 2 reviews the classical ID3 and CART algorithms, and introduces the model of neighborhood rough sets (NRSs). In Section 3, we propose the VPN equivalence relation and the VPN rough sets. Based on the VPN equivalence relation, the VPN information gain and the VPN Gini index are proposed. Moreover, a hybrid measure is constructed to improve the performance of the classical decision tree algorithms. In Section 4, we verify the effectiveness of our algorithm. Finally, we make a summary and some discussion in Section 5.

2 Preliminaries

This section reviews some basic definitions about ID3 algorithm, CART algorithm and neighborhood rough set model. Throughout the paper, U is called universe to represent a non-empty finite set.

2.1 Decision tree

We describe decision tree as a tree classifier, which is constructed from the top down and consists of nodes and directed edges. Nodes in a decision tree can be divided into internal nodes and leaf nodes, where each internal node represents a feature or attribute, and each leaf node represents a class. ID3, C4.5 and CART are three well-known decision tree algorithms, where C4.5 and CART are the improvements of ID3. The above three algorithms have been widely used in different fields because of their advantages such as good interpretability. This subsection mainly introduces ID3 and CART.

Definition 1

[5] Let $Dt = (U, C \cup D)$ be a decision table, where C is represented the set of conditional attributes and D is called the set of decision attributes. Let $U/D = \{ {D_1},{D_2},..., {D_n}\}$ be the decision classification, the information entropy H(D) of U/D is expressed as follows:

$$\begin{aligned} H(D) = - \sum \limits _{i = 1}^n {\frac{{|{D_i}|}}{{|U|}}} \log \frac{{|{D_i}|}}{{|U|}}. \end{aligned}$$

(1)

where for each $1\le i \le n$, ${{|{D_i}|} \over {|U|}}$ represents the probability of a sample falls into the decision class $D_i$.

For any $A \subseteq C$, let $U/A = \{ {A_1},{A_2},..., {A_m}\}$, the conditional entropy H(D|A) of decsion attribute D with respect to conditional attribute A is defined as follows:

$$\begin{aligned} H(D|A) = \sum \limits _{j = 1}^m {{{|{A_j}|} \over {|U|}}} H({A_j}). \end{aligned}$$

(2)

where for each $1\le j \le m$, $H({A_j}) = - \sum \limits _{i = 1}^n {{{|{A_j} \cap {D_i}|} \over {|{A_j}|}}} \log$ ${{|{A_j} \cap {D_i}|} \over {|{A_j}|}}$. Therefore, the information gain of attribute subset A is

$$\begin{aligned} Gain(A) = H(D) - H(D|A). \end{aligned}$$

(3)

ID3 algorithm needs to calculate the information entropy of each attribute, and selects the attribute with the largest information gain as the splitting attribute. The decision tree generated by ID3 is easy to understand for us and it shows the potential information behind the data clearly. Although the idea of ID3 is simple, it tends to prefer attributes with more values. There are many improved algorithms for ID3, and CART is one of them.

Definition 2

[4] Let $Dt = (U,C \cup D)$ be a decision table, and let $U/D = \{ {D_1},{D_2},..., {D_n}\}$ be the decision classification, the gini index Gini(D) of U/D is defined as follows:

$$\begin{aligned} {\begin{matrix} Gini(D) &{}= \sum \limits _{i = 1}^n {{{|{D_i}|} \over {|U|}}} \left( {1 - {{|{D_i}|} \over {|U|}}} \right) \\ \\ &{}= 1 - {\sum \limits _{i = 1}^n {\left( {{{|{D_i}|} \over {|U|}}} \right) } ^2}. \\ \end{matrix}} \end{aligned}$$

(4)

For any $A \subseteq C$, let $U/A = \{ {A_1},{A_2},..., {A_m}\}$, the gini index Gini(D, A) of D on A is defined as follows:

$$\begin{aligned} Gini(D,A) = \sum \limits _{j = 1}^m {{{|{A_j}|} \over {|U|}}Gini({A_j})}. \end{aligned}$$

(5)

where for each $1\le j \le m$, $Gini({A_j}) = 1 - {\sum \limits _{i = 1}^n {\left( {{{|{A_j} \cap {D_i}} \over {|{A_j}|}}} \right) } ^2}$.

CART selects the attribute with the smallest Gini index as the splitting attribute, and builds the corresponding regression tree or classification tree according to whether the value of category attribute is continuous or discrete.

2.2 Neighborhood rough set model

As we all know that the classical rough set model needs to use the step of discretization to preprocess the continuous data, which is easy to generate to information loss. To avoid this problem, the neighborhood rough set model is proposed and attracts much attention. In the following, we review some basic notions in neighborhood rough sets.

Definition 3

[16] Let $Dt = (U,C \cup D)$ be a decision table, where U is a non-empty finite set (called universe) with samples $\{ {ay_1},{ay_2},...,{ay_n}\}$, $C = \{ {c_1},{c_2},...,{c_m}\}$ is the set of condition attributes, and D represents the set of decision attributes. For any ${ay_i} \in U$ and $A \subseteq C$, the neighborhood ${\delta _A}({ay_i})$ of ${ay_i}$ on the attribute subspace A is defined as:

$$\begin{aligned} {\delta _A}({ay_i}) = \{ {ay_j} \in U | {\Delta ^A}({ay_i}, {ay_j}) \le \delta \}. \end{aligned}$$

(6)

where $\Delta$ is a distance function, and for any ${ay_1},{ay_2},{ay_3} \in U$, $\Delta$ satisfies that:

(1)$\Delta ({ay_1},{ay_2}) \ge 0$, $\Delta ({ay_1},{ay_2}) = 0$ only when ${ay_1} = {ay_2}$;

(2)$\Delta ({ay_1},{ay_2}) = \Delta ({ay_2},{ay_1})$;

(3)$\Delta ({ay_1},{ay_3}) \le \Delta ({ay_1},{ay_2}) + \Delta ({ay_2},{ay_3})$.

Assume that $A = \{ {c_1},{c_2},...{c_n}\}$ is an attribute subset of C, for any two samples ${ay_1},{ay_2} \in U$, the Minkowsky distance ${d_A}({ay_1},{ay_2})$ between ${ay_1}$ and ${ay_2}$ under A is defined as:

$$\begin{aligned} {d_A}({ay_1},{ay_2}) = {(\sum \limits _{i = 1}^m {|f({ay_1},{c_i}) - f({ay_2},{c_i}){|^p}} )^{1/p}}. \end{aligned}$$

(7)

where $f({ay_1},{c_i})$ is the value of sample $ay_1$ on attribute ${c_i}$, $1\le i \le m$.

When $p = 1$, the Minkowsky distance is called the Manhattan distance, it is called the Euclidean distance, and the Chebyshev distance when $p=2$ and $p = \infty$. The NRSs model usually uses the Manhattan distance. It can be seen that when $\delta = 0$, the NRSs model will degenerate into the classical rough set model.

Definition 4

[16] Given a decision table $Dt = (U,C \cup D)$ and attribute subset $B \subseteq C$. For any $AY \subseteq U$, the upper approximation and the lower approximation of set AY with respect to B are defined as follows:

$$\begin{aligned} \begin{aligned}&\overline{{N_B}} (AY) = \{ {ay_i} \in U | \delta ({ay_i}) \cap AY \ne \phi \},\\&\underline{{N_B}} (AY) = \{ {ay_i} \in U | \delta ({ay_i}) \subseteq AY \}. \end{aligned} \end{aligned}$$

(8)

Moreover, $B_N(AY) = \overline{{N_B}} (AY) - \underline{{N_B}} (AY)$ is called the boundary region of set AY with respect to B.

Definition 5

[16] Given a decision table $Dt = (U,C \cup D)$, let $U/D=\{D_1,D_2,...,D_n\}$ be the equivalence classes divided by decision attribute D on U. For any $B \subseteq C$, the upper approximation set $\overline{{N_B}} (D)$ and the lower approximation set $\underline{{N_B}} (D)$ of D with respect to A are defined as follows:

$$\begin{aligned} \begin{aligned}&\overline{{N_B}} (D) = \bigcup \limits _{i = 1}^n {\overline{{N_B}} ({D_i})} ,\\&\underline{{N_B}} (D) = \bigcup \limits _{i = 1}^n {\underline{{N_B}} ({D_i})}. \end{aligned} \end{aligned}$$

(9)

Then we can get the positive region as follows,

$$\begin{aligned} POS_{B}(D)=\underline{N}_{B} (D). \end{aligned}$$

(10)

Definition 6

[26] The Dice similarity between set ${Y_1}$ and set ${Y_2}$ is defined as:

$$\begin{aligned} D({Y_1},{Y_2}) = {{2*|{Y_1} \cap {Y_2}|} \over {|{Y_1}| + |{Y_2}|}}. \end{aligned}$$

(11)

Dice coefficient is a measure function used to describe the similarity of sets, which is mainly used to calculate the similarity of two given sets.

3 Variable precision neighborhood rough sets and measurement function

In this section, we first introduce the notions of VPN equivalence relation and VPN equivalence granule. Then we discuss the basic properties of them. At the same time, we propose a VPN rough set model and explore some of its digital characteristics. Based on the variable precision neighborhood equivalence relation, the Gini index is extended to the VPN Gini index, and the information gain is extended to the VPN information gain. Finally, a hybrid measure is established by using the VPN attribute dependence to combine the VPN Gini index and the VPN information gain.

3.1 Variable precision neighborhood rough sets

Definition 7

Let $NDS = (U,C \cup D,V,f,d,\delta )$ be a neighborhood decision system, and $\delta \in [0,1]$ be a neighborhood parameter. For any ${ay_1},{ay_2} \in U$ and $A \subseteq C$, the similarity of neighborhood granules ${\eta _A^\delta ({ay_1})}$ and ${\eta _A^\delta ({ay_2})}$ is expressed as follows:

$$\begin{aligned} NV_A^\delta ({ay_1},{ay_2}) = {{2*|\eta _A^\delta ({ay_1}) \cap \eta _A^\delta ({ay_2})|} \over {|\eta _A^\delta ({ay_1})| + |\eta _A^\delta ({ay_2})|}}. \end{aligned}$$

(12)

The above definition indicates a similarity relation between two neighborhood granules. Obviously, $NV_A^\delta ({ay_1},{ay_2}) \in [0,1]$.

Example 1

Let $U = \{ {bx_1},{bx_2},{bx_3},{bx_4},{bx_5},{bx_6}\}$ be a universe, and let ${\eta _A^\delta ({bx_1})} =\{ {bx_1},{bx_2},{bx_5},{bx_6}\}$ and ${\eta _A^\delta ({bx_2})}=\{ {bx_1},{bx_2},{bx_4},{bx_6}\}$ be two neighborhood granules. The granule similarity between ${\eta _A^\delta ({bx_1})}$ and ${\eta _A^\delta ({bx_2})}$ is $NV_A^\delta ({bx_1},{bx_2}) = {{2*|\eta _A^\delta ({bx_1}) \cap \eta _A^\delta ({bx_2})|} \over {|\eta _A^\delta ({bx_1})| + |\eta _A^\delta ({bx_2})|}} =$ ${{2*|\{ {bx_1},{bx_2},{bx_6}\} } \over {|\{ {bx_1},{bx_2},{bx_5},{bx_6}\} | + |\{ {bx_1},{bx_2},{bx_4},{bx_6}\} |}} = 0.75$.

Let $NDS = (U,C \cup D,V,f,d,\delta )$ be a neighborhood decision system, for any $ay \in U$ and $A \subseteq C$, let ${\eta _A^\delta (ay)}$ be the condition neighborhood granule of ay on A, and ${\eta _D^\delta (ay)}$ be the decision neighborhood granule of ay on D. The granule similarity between the condition neighborhood granule and the decision neighborhood granule is

$$\begin{aligned} NV(\eta _A^\delta (ay),\eta _D^\delta (ay)) = {{2*|\eta _A^\delta (ay) \cap \eta _D^\delta (ay)|} \over {|\eta _A^\delta (ay)| + |\eta _D^\delta (ay)|}}. \end{aligned}$$

(13)

Definition 8

Given a decision table $Dt = (U,C \cup D)$, for any $A \subseteq C$, the neighborhood equivalence relation on A is expressed as follows:

$$\begin{aligned} NER_A^\delta = \{ ({ay_1},{ay_2}) \in U \times U | \eta _A^\delta ({ay_1}) = \eta _A^\delta ({ay_2})\}. \end{aligned}$$

(14)

where $\delta \in [0,1]$ is a given neighborhood radius, and $\eta _A^\delta (*)$ represents the $\delta$-neighborhood of sample $*$ on A. The neighborhood equivalence partition induced by the neighborhood equivalence relation $ENR_A^\delta$ is defined as follows:

$$\begin{aligned} U/NER_A^\delta = \{ {[ay]_{NER_A^\delta }} | ay \in U \} = \{ Y_1^A,Y_2^A, ...,Y_n^A\}. \end{aligned}$$

(15)

where $Y_r^A = \{ {ay_i} \in U | \eta _A^\delta ({ay_i}) = \eta _A^\delta ({ay_j})\}, {ay_j} \in Y_r^A( r = 1,2, ...,n)$. ${[ay]_{NER_A^\delta }}$ represents equivalent granule and ${[ay]_{NER_A^\delta }} = \{ a{y_i} \in U|(ay,a{y_i}) \in NER_A^\delta \}$.

Example 2

Given a dataset listed in Table 1, according to the definition of neighborhood equivalence relation, we can divide the samples in the dataset into a set of equivalence classes (ECs) by a given attribute subset. For instance, the ECs induced by the attribute subset {$a_1$} are {$bx_1$,$bx_4$},{$bx_2$,$bx_3$},{$bx_5$}. The ECs induced by the attribute subset{$a_2$} are {$bx_1$,$bx_2$},{$bx_3$},{$bx_4$},{$bx_5$}. The ECs induced by the attribute subset {$a_3$} are {$bx_1$},{$bx_2$,$bx_3$},{$bx_4$},{$bx_5$}.

From the definition of neighborhood equivalence relation, we can easily see that only when the neighborhood of two samples is exactly equal, the two samples will be judged to be equivalent. The above definition is undoubtedly strict, hence we propose the variable precision neighborhood equivalence relation.

Table 1 A given dataset

Table 2 The sample neighborhoods of example decision table ($\delta =0.3$)

Definition 9

In $NDS = (U,C \cup D,V,f,d,\delta )$ , for any $({ay_1},{ay_2}) \in U \times U$ and $A \subseteq C$, if ${ay_1}$ and ${ay_2}$ satisfy the following equation

$$\begin{aligned} VNER_A^{(\delta , \alpha )} = \{ ({ay_1},{ay_2}) \in U \times U | NV_A^\delta ({ay_1},{ay_2}) \ge \alpha \}. \end{aligned}$$

(16)

then we consider that samples ${ay_1}$ and ${ay_2}$ are equivalent, where $\alpha \in [0.5,1)$ is the variable precision threshold.Here, we call it VPN equivalence relation.

In real-world applications, it is difficult for us to find exactly equal samples of two neighborhoods.If the above strict equivalence relationship is adopted, it will be greatly limited in the actual application scenario and produce unsatisfactory results. Especially when we apply this equivalence relation to the decision tree, it may lead to the generation of a large decision tree, which is an unfavorable classification effect, so we must improve this equivalence relation (Table 2).

Definition 10

Let $\delta \in [0,1]$ be the neighborhood radius, and $\alpha$ be the variable precision threshold, we obtain the VPN equivalence class based on the VPN equivalence relation as below.

$$\begin{aligned} U/VNER_A^{(\delta , \alpha )} \!=\! \{ {[ay]_{VNER_A^{(\delta , \alpha )}}}|ay \in U\} \!=\! \{ VX_1^A,VX_2^A, ...,\! VX_n^A\}. \end{aligned}$$

(17)

where $VX_r^A = \{ ay \in U|NV_A^\delta ({ay_i},ay) \ge \alpha \} ;{ay_i} \in VX_r^A; 1 \le r \le n$.

Example 3

Here we use neighborhood similarity to calculate the similarity of two tuples above the attribute subset {$a_1$} with the variable precision threshold $\alpha = 0.7$, the calculation results are shown in Tables 3, and 4 shows the results of equivalence classes.

Table 3 The results of neighborhood similarity between samples

Proposition 1

In $NDS = (U,C \cup D,V,f,d,\delta )$, $\alpha$ is the variable precision threshold,

• 1. If ${\delta _1} \le {\delta _2}$, then $U/VNER_A^{({\delta _1},\alpha )} \subseteq U/VNER_A^{({\delta _2},\alpha )}$;

• 2. If ${\alpha _1} \le {\alpha _2}$, then $U/VNER_A^{(\delta ,{\alpha _2})} \subseteq U/VNER_A^{(\delta ,{\alpha _1})}$.

Proof 1

• 1. If ${\delta _1} \le {\delta _2}$, for any ${ay_1},{ay_2} \in U$, obviously, we can obtain $\eta _A^{{\delta _1}}({ay_1}) \subseteq \eta _A^{{\delta _2}}({ay_1})$. Then we can get $NV_A^{{\delta _2}}({ay_1},{ay_2}) \ge NV_A^{{\delta _1}}({ay_1},{ay_2}) \ge \alpha$, therefore, $U/VNER_A^{({\delta _1},\alpha )} \subseteq U/VNER_A^{({\delta _2},\alpha )}$.

• 2. If ${\alpha _1} \le {\alpha _2}$, we can get $VNER_A^{(\delta , {\alpha _2})} \subseteq VNER_A^{(\delta ,{\alpha _1})}$, therefore, we have $U/VNER_A^{(\delta ,{\alpha _2})} \subseteq U/VNER_A^{(\delta ,{\alpha _1})}$.

Proposition 1 mainly reflects the sizes of neighborhood granule and variable precision equivalence granule. According to Proposition 1, we can see that the size of a neighborhood granule increases with the increase of the neighborhood radius, which means that the larger the neighborhood radius is, the more samples are contained in the neighborhood granule. Variable precision threshold $\alpha$ can control the thickness of the variable precision neighborhood equivalence granule. A lower threshold makes it easier to assume that two samples are similar, whereas the higher the degree of similarity between samples can be judged they are equal. A larger variable precision threshold means that a single VPN equivalence granule is rougher, while a smaller one is more accurate.

Definition 11

In $NDS = (U,C \cup D,V,f,d,\delta )$ , $\alpha$ is the variable precision threshold, for any $P \subseteq C$ and $ay \in U$, the VPN lower approximation and the VPN upper approximation are defined as follows:

$$\begin{aligned} \begin{aligned}&\underline{{R_P}} (D)_\delta ^\alpha \!=\! \{ ay \in U|NV(\eta _P^\delta (ay),\eta _D^\delta (ay)) \!\ge \! \alpha \}, 0.5 \!\le \! \alpha \!\!<\!\! 1,\\&\overline{{R_P}} (D)_\delta ^\alpha \!=\!\{ ay \in U|NV(\eta _P^\delta (ay),\eta _D^\delta (ay)) > 1 - \alpha \}. \end{aligned} \end{aligned}$$

(18)

The VPN lower approximation is also called the VPN positive region, which is denoted as:

$$\begin{aligned} PO{S_P}(D)_\delta ^\alpha = \underline{{R_P}} (D)_\delta ^\alpha . \end{aligned}$$

(19)

The VPN boundary region is defined as:

$$\begin{aligned} B{N_P}(D)_\delta ^\alpha = \overline{{R_P}} (D)_\delta ^\alpha - \underline{{R_P}} (D)_\delta ^\alpha . \end{aligned}$$

(20)

Obviously, for any $\alpha$, $\underline{{R_P}} (D)_\delta ^\alpha \subseteq \overline{{R_P}} (D)_\delta ^\alpha$.

Proposition 2

In $NDS = (U,C \cup D,V,f,d,\delta )$ , $\alpha$ is the variable precision threshold, if ${A_1} \subseteq {A_2} \subseteq C$, then $PO{S_{{A_1}}}(D)_\delta ^\alpha \subseteq PO{S_{{A_2}}}(D)_\delta ^\alpha$.

Proof 2

Given ${A_1} \subseteq {A_2}$, ay and metric $\Delta$, $\forall a{y_i} \in U$, $a{y_i} \in {\delta _{{A_1}}}(ay)$ if $a{y_i} \in {\delta _{{A_2}}}(ay)$ because ${\Delta _{{A_1}}}(a{y_i},ay) \le {\Delta _{{A_2}}}(a{y_i},ay)$. Therefore,we have ${\delta _{{A_1}}}(ay) \supseteq {\delta _{{A_2}}}(ay)$ if ${A_1} \subseteq {A_2}$. Assume ${\delta _{{A_1}}}(ay) \subseteq \underline{{R_{{A_1}}}} (D)_\delta ^\alpha$, where D represents one of the decision classes, then we have ${\delta _{{A_2}}}(ay) \subseteq \underline{{R_{{A_2}}}} (D)_\delta ^\alpha$. At the same time, it may exist $a{y_i}$, ${\delta _{{A_1}}}(a{y_i}) \not \subset \underline{{R_{{A_1}}}} (D)_\delta ^\alpha$ and ${\delta _{{A_2}}}(a{y_i}) \subseteq \underline{{R_{{A_2}}}} (D)_\delta ^\alpha$. Therefore, $\underline{{R_{{A_1}}}} (D)_\delta ^\alpha \subseteq \underline{{R_{{A_2}}}} (D)_\delta ^\alpha$. Assuming $D = \{ {D_1},{D_2},...,{D_m}\}$, we have $\underline{{R_{{A_1}}}} ({D_1})_\delta ^\alpha \subseteq \underline{{R_{{A_2}}}} ({D_1})_\delta ^\alpha ,...,\underline{{R_{{A_1}}}} ({D_m})_\delta ^\alpha \subseteq \underline{{R_{{A_2}}}} ({D_m})_\delta ^\alpha$. $PO{S_{{A_1}}}(D)_\delta ^\alpha = \bigcup \nolimits _{i = 1}^m {\underline{{R_{{A_1}}}} ({D_i})_\delta ^\alpha } ;PO{S_{{A_2}}}(D)_\delta ^\alpha = \bigcup \nolimits _{i = 1}^m$ ${\underline{{R_{{A_2}}}} ({D_i})_\delta ^\alpha }$, so we can obtain $PO{S_{{A_1}}}(D)_\delta ^\alpha \subseteq PO{S_{{A_2}}}(D)_\delta ^\alpha$.

Table 4 The results of ECs

Definition 12

In $NDS = (U,C \cup D,V,f,d,\delta )$, $\alpha$ is the variable precision threshold, for any $P \subseteq C$, the degree of dependence of D on P is defined as:

$$\begin{aligned} {\gamma _P}(D)_\delta ^\alpha = {{|PO{S_P}(D)_\delta ^\alpha |} \over {|U|}}. \end{aligned}$$

(21)

The degree of knowledge dependence indicates the degree of dependence of knowledge D on knowledge P.

Proposition 3

In $NDS = (U,C \cup D,V,f,d,\delta )$ , $\alpha$ is the variable precision threshold, for any $A \subseteq C$, $U/VENR_A^{(\delta ,\alpha )}$ is the VPN equivalence granule,

• 1. If $\alpha =1$, then ${\gamma _{U/VNER_A^{(\delta ,\alpha )}}}(D) = {\gamma _{_{U/NER_A^\delta }}}{(D) }$.

• 2. If $\alpha =1$ and $\delta =0$, then ${\gamma _{U/VENR_A^{(\delta ,\alpha )}}}(D) = {\gamma _{_{U/{R_A}}}}(D)$.

Proof 3

• 1. If $\alpha =1$, the VPN equivalence granule becomes the strict neighborhood equivalence granule and the VPN rough sets degenerates into the neighborhood rough sets. Therefore, the VPN dependence becomes the neighborhood attribute dependence.

• 2. If $\alpha =1$ and $\delta =0$, the VPN equivalence granule degenerates into the ordinary Pawlak’s equivalence granules and the VPN rough sets degenerates into the Pawlak’s rough sets. Therefore, the VPN dependence naturally becomes the classical Pawlak’s dependence.

Proposition 3 shows that the VPN rough sets are associated with classical rough sets and NRSs. When we set the neighborhood radius $\delta$ to 0 and the threshold $\alpha$ to 1, the VPN equivalence relation degenerates into the ordinary Pawlak’s equivalence relation, that is, the variable precision neighborhood rough set model becomes the classical rough set model. Therefore, the VPN attribute dependence becomes the Pawlak’s attribute dependence. When the threshold $\alpha$ is set to 1 and the neighborhood radius $\delta$ is retained, it degenerates into the NRSs model. So the VPN attribute dependence becomes the neighborhood attribute dependence.

Proposition 4

In $NDS = (U,C \cup D,V,f,d,\delta )$, $\alpha$ is the variable precision threshold, if ${A_1} \subseteq {A_2} \subseteq C$, then we have ${\gamma _{{A_1}}}(D)_\delta ^\alpha \le {\gamma _{{A_2}}}(D)_\delta ^\alpha$.

Proof 4

According to Proposition 2, we can obtain that $PO{S_{{A_1}}}(D)_\delta ^\alpha \subseteq PO{S_{{A_2}}}(D)_\delta ^\alpha$, so we have that ${\gamma _{{A_1}}}(D)_\delta ^\alpha \le {\gamma _{{A_2}}}(D)_\delta ^\alpha$.

Proposition 4 illustrates the monotonicity of variable precision neighborhood dependence. From Proposition 2, we can obtain that if we continue to add attributes to the condition attribute subset, then the positive domain will become larger. When U remains the same, the VPN dependence increases with the increase of the positive domain, showing a monotonically increasing trend.

3.2 Variable precision neighborhood Gini index and variable precision neighborhood information gain

In the classical CART algorithm, the gini index is used for measuring the nodes of the decision tree, and the attribute with the smallest Gini index is selected as the splitting attribute. In this subsection, the Gini index is extended to the variable precision neighborhood Gini index.

Definition 13

In $NDS = (U,C \cup D,V,f,d,\delta )$ , $\alpha$ is the variable precision threshold. Let $\{ VX_1^A,VX_2^A,...,VX_n^A\}$ be the VPN equivalence partition induced by $U/VENR_A^{(\delta , \alpha )}$, for any $A \subseteq C$, the VPN Gini index is defined as follows.

$$\begin{aligned} {\begin{matrix} VGini(U/VENR_A^{(\delta ,\alpha )}) &{}= \sum \limits _{i = 1}^n {{{|VX_i^A|} \over {|U|}}} \left( {1 - {{|VX_i^A|} \over {|U|}}} \right) \\ \\ &{}= \sum \limits _j^m {\sum \limits _i^n {{{|VX_i^A \cap {D_j}|} \over {|U|}}} } \left( {1 - {{|VX_i^A|} \over {|U|}}} \right) .\\ \end{matrix}} \end{aligned}$$

(22)

where $U/D = \{ {D_1},{D_2},...{D_m}\}$, and $VX_k^A \in U/VENR_A^{(\delta ,\alpha )}$ represents a granule in the equivalence granule of variable precision neighborhood. We can see that the above equation is the sum of information carried by each granule, so the neighborhood Gini index of a single granule can be constructed as follows:

$$\begin{aligned} VGini(VX_k^A) = {{|VX_k^A|} \over {|U|}}\left( {1 - {{|VX_k^A|} \over {|U|}}} \right) . \end{aligned}$$

(23)

Therefore, the neighborhood Gini index of D with respect to $VX_k^A \in U/VENR_A^{(\delta ,\alpha )}$ is expressed as follows:

$$\begin{aligned} VGini(D,VX_k^A) \!=\! \sum \limits _{j = 1}^m {{{|VX_k^A \cap {D_j}|} \over { |VX_k^A|}}} \left( \!{1 \!-\! {{|VX_i^A \cap {D_j}|} \over {|U|}}}\right) . \end{aligned}$$

(24)

The Gini index of variable precision neighborhood of D with respect to $A \subseteq C$ is defined as follows:

$$\begin{aligned} VGini(D,U/VENR_A^{(\delta ,\alpha )}) \!=\!\! \sum \limits _{i = 1}^n {{{|VX_i^A|} \over {|U|}}} VGini(D,VX_i^A). \end{aligned}$$

(25)

where ${{|VX_i^A|} \over {|U|}}$ represents the weight coefficient of D on the neighborhood Gini index of a single granule.

Proposition 5

Let $U/VENR_A^{(\delta ,\alpha )}$ be the VPN equivalence granule, when $\delta = 0$ and $\alpha = 1$,

• 1. $VGini(U/VENR_A^{(\delta ,\alpha )}) = Gini(A)$.

• 2. $VGini(D,U/VENR_A^{(\delta ,\alpha )}) = Gini(D,A)$.

Proof 5

When $\delta = 0$ and $\alpha = 1$, the VPN equivalence relation will degenerate into a general equivalence relation, and the VPN equivalence granule will degenerate into a general equivalence granule structure, therefore, the VPN Gini index will also become the general Gini index.

The VPN Gini index is a generalization of the Gini index, and their properties are basically the same. When the neighborhood radius $\delta$ and the variable precision threshold $\alpha$ are set to 0 and 1, the VPN Gini index degenerates into the familiar Gini index.

Definition 14

In $NDS = (U,C \cup D,V,f,d,\delta )$ , $\alpha$ is the variable precision threshold. Assume that the VPN equivalence partition is $U/VENR_A^{(\delta ,\alpha )} = \{ VX_1^A,VX_2^A,...,VX_n^A\}$, for any $A \subseteq C$, the VPN information entropy of A and the VPN information entropy of D are defined as follows:

$$\begin{aligned} {\begin{matrix} VH_\delta ^\alpha (A) &{}= - \sum \limits _{i = 1}^n {{{|VX_i^A|} \over {|U|}}} {\log _2}{{|VX_i^A|} \over {|U|}} \\ \\ &{}= - \sum \limits _j^m {\sum \limits _i^n {{{|VX_i^A \cap {D_j}|} \over {|U|}}} } {\log _2}{{|VX_i^A|} \over {|U|}}. \\ \end{matrix}} \end{aligned}$$

(26)

$$\begin{aligned} VH_\delta ^\alpha {(D)_{U/VENR_A^{(\delta ,\alpha )}}} = - \sum \limits _j^m {\sum \limits _i^n {{{|VX_i^A \cap {D_j}|} \over {|U|}}} } {\log _2}{{|{D_j}|} \over {|U|}}. \end{aligned}$$

(27)

Hence, we can obtain the VPN conditional entropy as follows:

$$\begin{aligned} VH_\delta ^\alpha (D|A) = - \sum \limits _j^m {\sum \limits _i^n {{{|VX_i^A \cap {D_j}|} \over {|U|}}} } {\log _2}{{|VX_i^A \cap {D_j}|} \over {|VX_i^A|}}. \end{aligned}$$

(28)

Therefore, the VPN information gain is defined as follows:

$$\begin{aligned} VGAIN_\delta ^\alpha (D,A) = VH_\delta ^\alpha {(D)_{U/VENR_A^{(\delta ,\alpha )}}} - VH_\delta ^\alpha (D|A). \end{aligned}$$

(29)

Proposition 6

When $\delta = 0$ and $\alpha = 1$, we have that $U/VENR_A^{(\delta ,\alpha )} = U/IND(A)$ and $VH_\delta ^\alpha (A) = H(A)$, then $VH_\delta ^\alpha (D|A) = H(D|A)$ and $VGAIN_\delta ^\alpha (D,A) = gain(D,A)$.

Proof 6

When $\delta = 0$ and $\alpha = 1$, the VPN equivalence relation will degenerate into the classical equivalence relation and the VPN information gain will also degenerate into the classical information gain.

Table 5 The DIGGI algorithm

3.3 The hybrid measure for selecting splitting attributes

As we all know, both information gain and gini index are two common measures used to select splitting attributes of decision trees. Information gain is derived from information entropy, which focuses on the representation of information. It is used to characterize the uncertainty in the data set and has a better ability to characterize the chaotic data. Normally, the attribute with the largest information gain will be selected as the current splitting attribute. Moreover, we select the attribute with the smallest gini index as the splitting attribute. Gini index mainly focuses on the algebraic representation and has better classification ability for the pure data. We can see that the above two measures are complementary, hence we can combine the advantages of the two measures and construct a hybrid measure for selecting splitting attributes.

In general, let $C = \{ {c_1},{c_2},...{c_{|C|}}\}$ be the set of condition attributes, for any $A \subseteq C$, the attribute increment chain ${A_1} = \{ {c_1}\} \subseteq {A_2} = \{ {c_1}, {c_2}\} \subseteq \cdots \subseteq {A_{|C|}} = \{ {c_1},{c_2},..., {c_{|C|}}\}$ is used to explore the rules of knowledge granularity, including the granulation monotonicity of uncertainty measure [27]. The information gain is characterized by granular monoadditivity, while the Gini index is characterized by granular non-monoadditivity [24], which are expressed as follows:

$${A_1} \subseteq {A_2} \subseteq C \Rightarrow gain({A_1}) \le gain({A_2}),$$

$${A_1} \subseteq {A_2} \subseteq C \nRightarrow gini({A_1}) \le gini({A_2}),$$

$${A_1} \subseteq {A_2} \subseteq C \nRightarrow gini({A_1}) \ge gini({A_2}).$$

According to the above monotonicity analysis, we can see that the extended variable precision neighborhood information gain and the variable precision neighborhood Gini index have the same granulation monotonicity, which are expressed as follows:

$${A_1} \subseteq {A_2} \subseteq C \Rightarrow VGain({A_1}) \le VGain({A_2}),$$

$${A_1} \subseteq {A_2} \subseteq C \nRightarrow VGini({A_1}) \le VGini({A_2}),$$

$${A_1} \subseteq {A_2} \subseteq C \nRightarrow VGini({A_1}) \ge VGini({A_2}).$$

Definition 15

By combining the variable precision neighborhood information gain and the variable precision neighborhood Gini index, we define a hybrid measure for selecting splitting attributes, which is given as follow:

$$\begin{aligned} VS(D,A)= & {} \varphi (A)*VGain(D,A) + (1 - \varphi (A))\nonumber \\{} & {} *VGini(D,A). \end{aligned}$$

(30)

where $\varphi (A) = {\gamma _A}(D)_\delta ^\alpha$. We elect an attribute with the largest VS(D, A) as the splitting attribute.

Proposition 7

The hybrid measure VS(D, A) has the property of granulation non-monoadditivity, which is described as follows:

$${A_1} \subseteq {A_2} \subseteq C \nRightarrow VS({A_1}) \ge VS({A_2}),$$

$${A_1} \subseteq {A_2} \subseteq C \nRightarrow VS({A_1}) \le VS({A_2}).$$

Attribute dependence can be used to measure the uncertainty of knowledge. From Definition 14, we can see that when $\varphi (A)$ increases, VGain(D, A) becomes larger and VGini(D, A) becomes smaller, hence VS(D, A) will be larger. When $\varphi (A)$ decreases, VGain(D, A) becomes smaller and VGini(D, A) becomes larger, hence VS(D, A) will be larger. According to the definition and the granulation monotonicity of the above two measures, from Proposition 6, we can obtain that the hybrid measure has the property of granulation non-monotonicity. Attribute dependence is used to weight the two measures, which can regulate the two measures and make them complement each other. The information gain tends to select attributes with more values, so calculating the dependence degree of the attribute and multiplying it can avoid the above problem to a certain extent. At the same time, the Gini index with more emphasis on algebraic representation is more reliable for data classification.

There are three states of attribute dependence: partial dependence, complete dependence and complete independence. When the attribute dependence equals 0, the hybrid measure depends on the Gini index, that is, $VS(D,A) = VGini(D,A)$. When the attribute dependence equals 1, the hybrid measure depends on the information gain and the attribute with the largest information gain is selected as the splitting attribute. This also solves the problem that the attribute dependence equals 0 when using a single measure, which will not occur when using the hybrid measure (Tab 5).

3.4 Algorithm design

The algorithm structure of DIGGI is similar to those of ID3 and CART, but there are still some differences between them. The differences are as follows: 1) DIGGI adopts a hybrid measure which combines information gain and Gini index in the way of attribute dependence weighting, while ID3 and CART adopt a single measure. The equivalence class is induced by the variable precision neighborhood equivalence relation. At the same time, the thickness of node branches can be adjusted by setting the variable precision threshold $\alpha$. When $\alpha =1$, it changes into the original strict neighborhood equivalence granule. To some extent, the hybrid measure overcomes the shortcomings of single measures. 2) ID3 needs to use the step of discretization to preprocess the continuous data, which may generate to the loss of information, and DIGGI could handle the continuous data directly.

The time complexity of the algorithm mainly comes from the calculation of uncertainty measure VS(D, a) in step 1. The generation of neighborhood granules involves the granulation operation of all samples in the domain, and its time complexity is $O(M*{N^2})$ . M represents the number of features, and N represents the number of samples in the domain. The time complexity of calculating the variable precision neighborhood information entropy and the variable precision neighborhood Gini index are $O(N*logN)$, and the granulation operation has been completed before the calculation of these two metrics. The calculation of each attribute dependency is relatively simple, and the time complexity is O(M). Then it is an equivalent partition of the decision tree, which needs to find the equivalence class involving all samples under each attribute, and its time complexity is $O(M*{N^2})$.Therefore, the time complexity of the DIGGI algorithm is $O(2*M*{N^2}*logN)$.

Table 6 The description of 14 datasets

Table 7 The accuracies of various algorithms

As for the ID3 algorithm, the time complexity of calculating information entropy is $O(N*logN)$, because each attribute value needs to be sorted. For the selection of the best partition attribute, the information gain corresponding to each attribute needs to be calculated, and the time complexity is $O(M*N*logN)$. For each non-leaf node, it is necessary to recursively select the best partition attribute and establish the number of words, and the time complexity is $O (M*N*logN)$. So the time complexity of the ID3 algorithm is $O(M*N*logN)$. The C4.5 algorithm is improved compared with the ID3 algorithm, and the continuous attributes are optimized. The time complexity is $O(M*N* logN)$, so the time complexity of the C4.5 algorithm is $O(M*N*logN)$. The pruning of CART algorithm is improved compared with ID3 algorithm, and the time complexity is $O(M*N*logN)$, so the time complexity of CART algorithm is $O (M*N*logN)$. Both the NDT algorithm and the VPNDT algorithm involve the granulation operation of all samples in the universe of domain. The time complexity of the operation is $O(M*{N^2})$, and the equivalent partitioning operation time is consistent with this article, that is $O(M*{N^2})$. NDT algorithm uses variable precision Gini index as the splitting node, and the time required to calculate the metric is $O(N*logN)$. The time complexity of NDT algorithm is $O(M*{N^2})$. The VPNDT algorithm uses the attribute dependency as the splitting node, and the time required to calculate the metric is O(M). Therefore, the time complexity of the VPNDT algorithm is $O(M*{N^2})$.

Table 8 The number of the leaves

Table 9 The running time of various algorithms

4 Experimental analysis

This section describes the comparative results of DIGGI and the existing algorithms. We used 14 public UCI datasets ( as shown in Table 6) to verify the effectiveness of DIGGI and most attributes in these datasets are continuous attributes, and MF is the abbreviation of messidor featureis dataset . DIGGI was compared with three traditional algorithms, the NDT algorithm and VPNDT algorithm in the latest literature. Considering that the traditional algorithms cannot deal with continuous data, we discretize the data by equi-distance discretization method. In order to evaluate the quality of decision tree, we usually consider the accuracy of the algorithm and the number of leaves. In this experiment, these two indexes are also selected as the evaluation criteria of DIGGI and the ten-fold cross-validation method is used to verify the data set. The experimental results are shown in Tables 7, 8 and 9. The experimental environment is Intel(R) Core(TM) I7-8700 CPU @ 3.20ghz 3.19ghz, RAM 16.0GB.

Fig. 1

The accuracy comparison of four algorithms with DIGGI

Fig. 2

Comparison of leaf numbers of four algorithms with DIGGI

The selection of neighborhood radius is closely related to the size of neighborhood granules, and its selection affects the whole neighborhood model. This paper mainly uses the adaptive radius constructed by standard deviation [23], which is expressed as ${\delta _{{C_1}}} = {{std({C_1})} \over w}$, where $std({C_1}) = \sqrt{{1 \over N}\sum \nolimits _{i = 1}^N {({x_i} - \overline{x} )} }$ represents standard deviation of the sample in the attribute $C_1$ and w represents adjustive parameter. In this paper, we set $w=2$. In this experiment, we select $90\%$ of the data in the data set as the training set, $10\%$ of the data as the test set, and the number of intervals used for equal distance divergence is 6. The neighborhood radius used by the NDT algorithm and the VPNDT algorithm is consistent with this paper. Their variable precision thresholds are set to 0.8, and the variable precision threshold $\alpha$ in this paper is set to 0.7.

We can see from the experimental results in Table 7 that DIGGI is effective and its accuracy has been greatly improved. Figure 1 specifically show the accuracy comparison of the five algorithms on different datasets. DIGGI not only can be directly applied to the classification and prediction of continuous data, but also has higher classification accuracy than the existing algorithms. From the statistical perspective of arithmetic average, the accuracy of DIGGI is 0.35 higher than ID3. Compared with all algorithms, it is improved by more than $10\%$. Among the 13 datasets, the results on Crayo, Seg, Glass and END2012 show the most obvious improvement, and the results on other datasets also show relatively large improvement, which indicate that DIGGI is effective.

We then observe the specific number of leaves of these algorithms on these 14 data sets from Table 8. Figure 2 shows them in a more intuitive form and shows the comparison of the number of leaves of the five algorithms on different datasets. We can see that DIGGI has fewer leaves than the existing algorithms on some datasets and has a higher number of leaves on the remaining datasets, but the number of leaves is still within the receivable range.In the high-dimensional data set SCADI, it can be clearly found that our proposed algorithm is still effective, while the CART algorithm and NDT algorithm obviously show the inapplicability in high-dimensional data.

Table 9 shows the time spent by each algorithm on 14 datasets. We can find that the running time of the three classical decision tree algorithms is very short, and the running time of the other three algorithms increases with the increase of the number of samples or attributes in the data set. Therefore, we can see that in the large data set, running the algorithm requires a computer with super computing power to run, so it is not suitable for using the algorithm in the large data set.

5 Conclusions

The strictness of neighborhood equivalence partition is difficult to achieve in real-world data. To overcome this problem, we propose the notion of neighborhood approximate equivalence, and thus propose a variable precision neighborhood equivalence relation and a new model of VPN rough sets. The VPN Gini index and the VPN information gain are constructed by the VPN equivalence relation. In the construction of decision tree, this paper proposes a new metric function for the measurement of splitting nodes. The experimental results show that DIGGI is effective, and its accuracy is also improved obviously. At the same time, DIGGI no longer needs to discretize the continuous data, so as to avoid the information loss.

As a summary of this work, we discuss the advantages and disadvantages of this work.

Now we first describe some of the contributions and advantages of the work done in this paper. (1)We propose a variable precision domain rough set based on similarity relation, and explore some related properties of the rough set, which enriches the rough set theory. (2)Based on the similarity relation, we extend the variable precision neighborhood information entropy and the variable precision neighborhood Gini index to omit the operation of data discretization and reduce the information loss caused by data discretization, which has certain reference significance for the improvement of decision tree. (3)The hybrid metric we constructed avoids the situation where the metric is 0 in a single metric to a certain extent, so the exploration of hybrid metrics is necessary, which also provides a new idea for the exploration and improvement of uncertain metrics. (4)From our experimental data, our improved algorithm is effective, which improves the classification accuracy of the decision tree within the acceptable range of leaf number, and is also effective in high-dimensional data (from the experimental results of the data set SCADI). Therefore, from the above summary, we can know that the work has certain significance and provides some new ideas for the improvement of decision tree.

Of course, at the same time, there are also some shortcomings in this work:(1)The improved decision tree algorithm in this paper is based on the neighborhood system. The generation of neighborhood granules involves the operation of neighborhood granulation. However, when the number of samples is large, the algorithm takes a long time and the time complexity is high, which cannot improve our work efficiency. (2)When our device configuration is low, it takes a lot of time to wait for a classification result, and we need to configure higher devices to run the algorithm. We also need to think about how to reduce the time complexity while maintaining good classification results, which will be a focus of future work.