1 Introduction

Co-clustering, also known as bi-clustering or two-way clustering, is a proposed clustering method for data with dual characteristics [1,2,3,4]. In contrast to conventional clustering, co-clustering can simultaneously cluster samples and features to investigate local patterns in a data matrix. Because of the duality of data, co-clustering has been applied in many fields. In document clustering, for instance, similar documents often correspond to similar topics. Co-clustering aims to explore similar documents on similar topics [1]. In movie recommendation, users with the same interests often provide the same scores for the same type of movies, and co-clustering aims to explore the user groups who like or dislike similar movies [5]. In recent decades, many co-clustering methods based on various theories have been proposed, such as the graph theory-based co-clustering method [1], a new clustering technique based on information theory [4], method for co-clustering based on matrix factorization [6], etc.

Nowadays, a growing number of datasets are collected from various sources or represented from various perspectives. For example, documents can be described in multiple languages [7]. Images can be described by the feature sets extracted by various feature extractors, including HOG, LBP, SIFT, GIST, etc [8]. A web page can be represented by the page’s content as well as by the content of a hyperlink leading to the page [9]. Each description is referred to as a ‘view’, and each view describes the same thing, but from a different perspective, with the information between views tending to be complementary. Mult-view learning is a significant area of research in machine learning, and it has been widely implemented in applications such as recommendation systems [10]. In recent years, researchers have successfully applied multi-view learning to other fields, including the discovery of the association between diseases and miRNAs [11].

Multi-view clustering [12] aims to use the complementary information between views to produce more precise and robust clustering results. In order to make full use of the complementarity of multiple views, some researchers have proposed methods such as co-regularization [13] and co-training [14]. Several multi-view weighted fusion methods have been proposed to account for the varying importance of the information in each view [15,16,17]. Compared with single-view clustering, the multi-view clustering algorithm achieves better clustering results. At the same time, multi-view clustering has also achieved many applications, such as image classification and text classification [7]. Recently, researchers have applied it to Alzheimer’s disease diagnosis [18].

Most existing multi-view clustering is based on the sample dimension, and ignores the duality of data, such as the co-occurrence between samples and features. Considering the benefits of co-clustering, researchers have developed a multi-view co-clustering algorithm in recent years [19,20,21]. Compared to conventional multi-view clustering, multi-view co-clustering simultaneously clusters the two dimensions (sample and feature) of multi-view data, further mines the latent information in the data, and achieves superior clustering results.

Although some multi-view co-clustering algorithms have been proposed to take advantage of the duality of data, most of them focus only on the co-occurrence characteristics between samples and features, and they do not account for sample-sample and feature-feature relationship information, which may limit their performance. For instance, the multi-view co-clustering algorithm based on a bipartite graph [19] uses the original data of each view to build a bipartite graph for each view, and then employs the spectral clustering algorithm to obtain clustering results. Obviously, it does not consider the similarity information between sample-sample and feature-feature. In fact, all information contributes to the clustering results [22, 23]. If only the information between samples and features is considered, the data’s potential information is not fully mined and utilized, thereby limiting the clustering performance. Therefore, all information between the data should be fully considered.

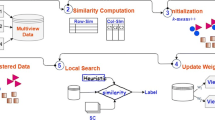
In this paper, we propose a multi-view co-clustering algorithm based on multi-similarity to maximize the use of similarity information between data and features. The main idea of our proposed algorithm is illustrated in Fig. 1. Firstly, considering the strong robustness of the ensemble algorithm, we use the ensemble method to calculate the sample-sample, feature-feature, and sample-feature three similarity matrices for each view data, and use them to build a graph. The objective is to fully exploit the data’s potential information for subsequent spectral clustering. Then, in order to distinguish the significance of each view, multi-view weighted fusion [17] and spectral clustering are performed on the graphs corresponding to the multiple views. The main contributions of this paper are as follows:

  • A multi-view co-clustering algorithm based on multi-similarity is proposed, which can fully mines the latent information contained in the data.

  • Based on spectral clustering, a method is proposed for constructing a data graph for multi-view co-clustering that is not restricted to the relevance between samples and features.

  • Experiments on several benchmark datasets demonstrate the superiority of the proposed method.

Fig. 1
figure 1

The proposed MVCCMS algorithm framework. First, the multiple co-clustering methods are applied to each view to obtain multiple co-clustering results, which include sample clustering results and feature clustering results. Then, based on the results of multiple co-clustering, multiple similarities are calculated, a hybrid graph is constructed according to it, and the hybrid graphs of multiple views are weighted and fused to form a comprehensive graph. Finally, the clustering results for the comprehensive graph are obtained via spectral clustering. At the same time, the results are used to update the weight of each view, and then update the clustering results. In this way, it is updated iteratively until convergence

Full size image

2 Related work

Co-clustering can simultaneously cluster data along two dimensions. BGSP [3] employs spectral clustering [24] to solve the clustering of word-documents. In this method, both the document and the word are considered graph nodes, and a bipartite graph is subsequently constructed. The word frequency information is regarded as the weight of the edge between the two corresponding nodes, and the document and the corresponding word are then clustered together.

Multi-view clustering is an important problem in the field of machine learning. The practice of weighted multi-view clustering is to assign a weight to each view to represent the importance of the view. The paper [25] proposes a kernel-based weighted multi-view clustering method, whereas [16] proposes a weighted strategy based on deep matrix factorization. In spectral clustering-based methods, [17] proposed a spectral clustering-based framework for weighted multi-view learning. The weight of each view depends on the objective function of its spectral clustering, and its main advantage is that it does not require any hyperparameter tuning.

To exploit the duality of data, [20] proposed a multi-view co-clustering method based on information theory, and it extended the information-theoretic based co-clustering method [4] to multi-view. However, certain prior knowledge is required. A weighted multi-view co-clustering algorithm for sparse data is proposed in [26]. However, it only calculates the similarity between samples-samples and features-features, ignoring the similarity between samples-features. Huang et al. [19] applied the multi-view weighted fusion framework proposed by [17] to multi-view co-clustering. Thus, a bipartite graph is constructed using the original data of each view, and the weight of each view is determined based on the spectral clustering objective function of each view before weighted multi-view fusion is performed. Finally, spectral clustering is performed on the fused graph. However, because it builds a bipartite graph, it only considers the relevant information between samples and features, ignoring the information between samples-samples and features-features.

Inspired by the above work, this paper proposes a multi-view co-clustering algorithm with multi-similarity (MVCCMS) that applies the ensemble method to multi-view learning and fully exploits the multiple similarity information of each view data.

3 Proposed method

This section starts by reviewing spectral co-clustering and multi-view co-clustering using bipartite graphs. Then, we describe how to use ensemble algorithms to compute similarity and construct hybrid graphs. Finally, we present the algorithm’s objective function.

3.1 Spectral co-clustering

Spectral clustering is a clustering method based on graph theory that is commonly employed to solve the co-clustering problem [2, 3, 27, 28]. It represents the data as nodes in a graph, with the weight of the edges between them representing their similarity. The higher the weight, the greater the likelihood that the data represented by the two nodes belong to the same category. Assume that the input data is X ∈ Rn×d, which means that there are n samples and each sample has d features. Graph G = (S,F,W) represents the bipartite graph between the constructed samples and features, S = {S1,S2,...,Sn} is the node set representing the sample, F = {F1,F2,...,Fd} is the node set representing the feature, and the value of W represents the weight of the edges between the nodes. Consider X as the weight matrix of the graph, Xij as the weight of the edge between node i(i-th sample) and node j(j-th feature), and consider X as the weight matrix of G and W as follows:

$$ W = \begin{bmatrix} 0 & X\\ X^{T} & 0 \end{bmatrix}. $$
(1)

The problem is then transformed into the graph G node partition problem. The objective of partitioning is to maximize the weight of edges within each subgraph while minimizing the weight of edges between subgraphs. The objective of spectral clustering is to identify the graph’s minimum standard tangent, and its objective function can be expressed as follows:

$$ \min\limits_{P} {\sum}_{i,j} W_{ij}\mid\mid P_{i} -- P_{j} \mid\mid^{2} $$
(2)

P is the indicator matrix:

$$ P=\begin{bmatrix} P_{r}\\ P_{c} \end{bmatrix} $$
(3)

where Pr ∈ Rn×k and Pc ∈ Rd×k represent the partitioning results of samples and features vertex set (k is the number of clusters), respectively. If the i-th node belongs to the j-th cluster, Pij = 1, otherwise, Pij = 0. Since solving the above problem is an NP-Hard problem, the constraint of P is generally relaxed to PTP = I. Then, the above problem will be converted to the optimal solution of the following formula:

$$ \min\limits_{P} Tr(P^{T} L P) \qquad s.t. P^{T} P = I, $$
(4)

where L represents the Laplace matrix of the graph, L = D − W,D is the degree matrix, and \(D_{ii}={\sum }_{j}W_{ij}\). According to [22] and [28], P can be obtained by calculating eigenvalues. Finally, traditional clustering methods, such as k-means, were applied to P to obtain clustering labels.

3.2 Multi-view co-clustering with bipartite graph

Given a multi-view data {X(1),X(2),...,X(v)}, where v represents the number of views. The multi-view co-clustering algorithm based on spectral clustering [19] constructs a bipartite graph for each view, and then, multiple graphs are fused into one graph, and the final result is obtained by spectral clustering. Its objective function can be expressed as follows:

$$ \min\limits_{P} {\sum}_{q=1}^{v}\alpha^{(q)} Tr(P^{T} L^{(q)} P) \qquad s.t. P^{T}P = I, $$
(5)

where

$$ \alpha^{(q)} = \frac{1}{2\sqrt{Tr(P^{T} L^{(q)} P)}}, $$
(6)

The indicator matrix P is enforced to be a unified one across all the views. The Laplace matrix of the bipartite graph corresponding to the q-th view is: L(q) = D(q) − W(q), where W(q) is the adjacency matrix of the bipartite graph corresponding to the q-th view, same as (1), W(q) can be expressed as:

$$ W^{(q)} = \begin{bmatrix} 0 & X^{(q)}\\ {X^{(q)}}^{T} & 0 \end{bmatrix}. $$
(7)

and \(D^{(q)}_{ii}={\sum }_{j}W^{(q)}_{ij}\) is its corresponding degree matrix.

Since P is public, the solution translates to:

$$ \min\limits_{P} Tr\left( P^{T} {\sum}_{q=1}^{v} \alpha^{(q)}L^{(q)} P\right) \qquad s.t. P^{T}P = I. $$
(8)

According to (6), we use the obtained P to update α, and update P according to (8). Then, iteratively update until convergence. To sum up, the process of the algorithm is: 1) initialize the weight α of each view and obtain the bipartite graph adjacency matrix of each view according to (7), 2) obtain P according to (8), 3) update α according to (6) , 4) repeat steps 2) and 3) until convergence. Concurrently, the author provides a convergence analysis.

Obviously, the weight matrix for the preceding method is the original data. At the same time, the weights between samples (sample-sample) and between features (feature-feature) are 0, that is, the similarity information between them is not considered. On the basis of this, we propose a multi-view co-clustering algorithm based on multi-similarity that takes into account all graph connections and converts a bipartite graph into a hybrid graph.

3.3 Similarity calculation

Co-clustering ensemble aims to produce more robust results by combining multiple base co-clustering methods. Let \(R^{(q)}_{1},R^{(q)}_{2},...,R^{(q)}_{l}(C^{(q)}_{1},C^{(q)}_{2},...,C^{(q)}_{l})\) represent the sample (feature) clustering indicator matrix of the q-th view produced by l base co-clustering methods. The purpose of the co-clustering ensemble is to combine l results to obtain a more robust result R(q)∗(C(q)∗). In this paper, we use the ensemble method to obtain the similarity information between the two dimensions of the data matrix, including the feature-feature, sample-sample, and sample-feature similarity matrices, and use this information as the weight matrix.

In order to better represent the samples-features similarity, we proposed a clustering ensemble method based on [29]. This method indicate that the clustering results of the sample depend on the local feature set (a subspace). According to the multiple clustering results, a basic probability matrix is constructed to represent the probability of each feature providing information for each sample. Finally, the final result is computed based on the matrix. The probability matrix of the q-th view data is calculated as follows:

$$ \left( S^{(q)}_{sf}\right)_{m^{\prime},n^{\prime}} = \frac{1}{l}{\sum}_{l^{\prime}=1}^{l} {\sum}_{d^{\prime}=1}^{d}\left( R^{(q)}_{l^{\prime}}\right)_{d^{\prime},m^{\prime}}^{T}\left( C^{(q)}_{l^{\prime}}\right)_{d^{\prime},n^{\prime}}^{T} $$
(9)

Since this matrix contains the relevant information between samples and features, we use it as the weight of the edge between samples and feature nodes in the spectral clustering, i.e., the degree of similarity between samples and features. At the same time, we introduce Mean Sum-squared Residue (MSR) [30] in the process of ensemble to evaluate the results obtained by the co-clustering method. Given a co-clustering block X, the MSR of X can be calculated as follows:

$$ MSR(X_{IJ})=\frac{1}{\mid I\mid}\frac{1}{\mid J\mid}{\sum}_{i\in I,j\in J}(x_{ij}-x_{iJ}-x_{Ij}+x_{IJ})^{2} $$
(10)

where xiJ represents the average value of row I, xIj represents the average value of column J, and xIJ represents the average value of the whole population. The smaller the MSR, the higher the relevance for the result obtained by the base co-clustering method. Conversely, the larger the MSR, the lower the relevance. Thus, a sample-feature correlation matrix Δ ∈ Rk×d is defined, where \({\Delta }_{k^{\prime },d^{\prime }}=\exp (-MSR_{k^{\prime },d^{\prime }})\), in this case, a larger value\({\Delta }_{k^{\prime },d^{\prime }}\) indicates a higher feature-sample relevance. By combining the information from all base co-cluster solutions, we can define the following sample-feature association matrix:

$$ (S^{(q)}_{sf})_{m^{\prime},n^{\prime}} = \frac{1}{l}{\sum}_{l^{\prime}=1}^{l}{\sum}_{k^{\prime}=1}^{k} {\sum}_{d^{\prime}=1}^{d}\left( R^{(q)}_{l^{\prime}}\right)_{d^{\prime},m^{\prime}}^{T}\left( {\Delta}^{(q)}_{l^{\prime}}\right)_{k^{\prime},d^{\prime}}\left( C^{(q)}_{l^{\prime}}\right)_{d^{\prime},n^{\prime}}^{T} $$
(11)

As the \(({\Delta }^{(q)}_{l^{\prime }})_{k^{\prime },d^{\prime }} \) represent the l′-th co-clustering method \((k^{\prime },d^{\prime })\) co-clustering block samples–feature relevance.

Most co-clustering algorithms only consider the similarity information between samples and features. According to [22], the mutual information between samples and between features also contributes to the results of co-clustering. Traditional clustering algorithms, such as k-means, only consider the similarity between samples, i.e., the similarity along the feature dimension. In contrast to conventional clustering, we take into account the similarity between features in addition to the similarity between samples. Inspiring by the calculation method of sample-feature similarity described in PCE [29] and the CSPA algorithm in [31], the similarity is defined as the clustering proportion of two objects in the same cluster, and the similarity calculation formula is obtained:

$$ S^{(q)}_{ss}=\frac{1}{l}{\sum}_{l^{\prime}=1}^{l}R^{(q)}_{l^{\prime}}*\left( R^{(q)}_{l^{\prime}}\right)^{T} $$
(12)
$$ S^{(q)}_{ff}=\frac{1}{l}{\sum}_{l^{\prime}=1}^{l}C^{(q)}_{l^{\prime}}*\left( C^{(q)}_{l^{\prime}}\right)^{T} $$
(13)

where Sss represents the similarity between samples, and Sff represents the similarity between features.

3.4 Objective function

After calculating the similarity matrix, the three matrices are combined to form the adjacency matrix of the mixed graph, and the data graph of the data matrix is constructed. That is:

$$ M^{(q)} = \begin{bmatrix} S^{(q)}_{ss} &S^{(q)}_{sf}\\ { S^{(q)}_{sf}}^{T} & S^{(q)}_{ff} \end{bmatrix} $$
(14)

In [19], \(S^{(q)}_{ss}=S^{(q)}_{ff}=0\), which indicates that it directly ignores this part of information. In contrast, we fully consider all relevant information between samples and features, resulting in an ideal clustering result. After constructing the data graph for each view, the spectral clustering objective function for each view can be obtained as follows:

$$ F^{(q)}=Tr(P^{T} L^{(q)} P) \quad s.t. P^{T}P=I, $$
(15)

where L(q) = D(q) − M(q). The objective function of multi- view clustering is as follows:

$$ {\sum}_{q=1}^{v} F^{(q)}={\sum}_{q=1}^{v}Tr(P^{T}L^{(q)}P) $$
(16)

where L(q) = D(q) − M(q).

According to (6), the weight of each view is obtained, and the final problem is converted into solving the optimal solution of the following objective function:

$$ \min\limits_{P} Tr(P^{T}\widetilde{L}P) $$
(17)

where,

$$ \widetilde{L}={\sum}_{q=1}^{v}\alpha^{(q)}L^{(q)} $$
(18)

The optimal solution is the eigenvector corresponding to the minimum k eigenvalues of \(\widetilde {L}\). According to [17], use the result to update the weights, which will eventually converge.

Figure 1 illustrates the overall MVCCMS framework and the flow of the whole algorithm is as Algorithm 1.

Algorithm 1
figure a

MVCCMS.

Full size image

3.5 Time and space complexity analysis

The time complexity of the MVCCMS algorithm is mainly divided into two parts. The first component is the time complexity of similarity calculation. For each view, the time complexity of this part is \({\sum }_{i} O(f_{i})\). The second component is the spectral clustering, and its time complexity is O((n + d)3). Assuming t is the number of iterations, the total time complexity is \(O(v\cdot {\sum }_{i} O(f_{i})+O(t\cdot (n+d)^{3}))\).

Similarity calculation is related to the selected integration algorithm. However, spectral clustering usually requires O(n3) time complexity to solve the eigenvector, which is a disadvantage of spectral clustering. The time and space complexity of some related algorithms based on spectral clustering is compared in Table 1. More specifically:

  • BiMVCC [19]: Compared with our algorithm, this algorithm does not use similarity calculation. But it directly uses the original data as the similarity, so the time complexity is O((n + d)3).

  • GBS [32]: The algorithm is divided into three parts: graph construction, graph fusion, and data clustering. The time complexity of graph construction and graph fusion is O(n2), and the time complexity of data clustering is O(t(vn2 + n3)). It makes the time complexity is O(t(vn2 + n3)).

  • GFSC [33], GMC [34], and MCLES [35]: The time complexity analysis of these algorithms can be found in their papers.

For space complexity:

  • GBS, GMC, and GFSC are all composed of three section: 1) The similarity matrix of each view is O(vn2). 2) The indicator matrix of spectral clustering is O(kn). 3) The weight of each view is O(v). So, the space complexity is O(vn2 + kn + v).

  • MCLES consists of four section: 1) Global similarity matrix, which is O(n2). 2) Mapping matrix of each view, which is \(O({{\sum }_{i}^{v}}d_{i}d)\). 3) Potential space representation, which is O(dn). 4) Indicator matrix of spectral clustering, which is O(kn). So, the space complexity is \(O(n^{2}+{{\sum }_{i}^{v}}d_{i}d+dn+kn)\).

  • BIMVCC and our method (MVCCMS) are composed of three section: 1) The similarity matrix or Laplace matrix of each view, which is O((n + d)2). 2) The spectral clustering indicator matrix, which is O(k(n + d)). 3) The weight of each view, which is O(v). So, the space complexity is O(v(n + d)2 + k(n + d) + v).

Table 1 Time and space complexity comparison of multi-view clustering algorithms based on spectral clustering
Full size table

It can be seen that all algorithms using spectral clustering have at least O(n3) time complexity and O(n2) space complexity. In our algorithm, we found through experiments (Section 4.5) that our algorithm has fewer iterations, which can reduce the number of using spectral clustering to reduce the computational complexity. Therefore, the scalability of this kind of algorithm, that is, the problem of high computational complexity, needs to be solved.

4 Experiment

In this section, extensive multi-view data experiments are conducted to demonstrate the effectiveness of our proposed MVCCMS.

4.1 Dataset

To evaluate the effectiveness of this method, we conducted experiments on three text datasets and one image dataset containing common multi-view data. The dataset is described below, and its size is displayed in Table 2.

  • Caltech101_20:Footnote 1 A dataset of images for object recognition is divided into 101 categories [36], with each image represented by six sets of features: Gabor, Wavelet Moments, Centrist, HOG, GIST, and LBP. In this experiment, a subset of 2386 images, including 20 classes, Face, Motorbike, DollaBill, Garfield, Snoopy, Leopards, Binocular, Brain, Camera, CarSide, Ferry, Hedgehog, Pagoda, Rhino, Stapler, Stop-Sign, WaterLilly, Windsor-Chair, Wrench and Yinyang is chosen. This subset is also known as Caltech101_20.

  • Cornell:Footnote 2 A subset of the WebKB dataset [37], widely used for multi-view learning. It contains 195 web pages collected from Cornell University. In the content view, each page is represented by 1703 words, and in the referenced links view, each page is represented by 195 referenced links. The 195 pages were divided into 5 categories: student, project, course, staff and faculty.

  • Reuters:Footnote 3 A text multi-view dataset consists of six categories, with each document translated into five languages and each language considered a view. In this experiment, text data in four languages and four views are selected.

  • Source3:Footnote 4 A multi-view text corpus contains 169 news reports, each with descriptions from three websites; thus, there are 169 samples and three views, of which two are chosen for this experiment.

Table 2 The dimension of each view
Full size table

Inspired by the weighted clustering strategy, we preprocessed the datasets and selected the data’s features using the classical unsupervised feature selection method [38]. The main purposes are as follows:

  • The most effective features are selected to improve the clustering effect and reduce the calculation time.

  • Unify the number of features of all view data, that is, select the same number of features for each view, so as to facilitate the smooth fusion of multiple views.

For convenience, we select the number of features d as the smallest number of features in all views, that is, \( d=\min \limits \{d^{(1)},d^{(2)},...,d^{(v)}\} \). At the same time, the processed datasets are also used as input to the comparison method for a fair comparison.

4.2 Methods and evaluation metrics

In order to evaluate the efficacy of the proposed method, it was compared to seven multi-view and single-view spectral clustering algorithms, including two older algorithms [13, 14] and five more recent algorithms. As the base co-clustering methods, we choose NetBC [39], LAC [40] and, SCC (Spectral Co-Clustering).

  • BiMVCC: BiMVCC is a multi-view co-clustering algorithm based on spectral clustering [19]. It applies the multi-view learning framework in [17] to multi-view co-clustering without setting parameters.

  • GMC: A multi-view clustering algorithm based on graph theory [34]. A parameter must be set, which can be automatically learned by the algorithm.

  • Co-reg: A multi-view clustering method based on spectral clustering [13]. It assumes that there are the same cluster members among views, and accomplishes this goal through co-regularized clustering.

  • Co-Training: A semi-supervised multi-view clustering method [14]. It assumes that regardless of the view, a point will be assigned to the same cluster by the actual underlying cluster.

  • GBS: A multi-view clustering method based on graph theory [32]. It extracts the data feature matrices of each view, constructs the graph matrices of all views, and combines the constructed graph matrices to produce a unified graph matrix, in order to achieve the final clustering. Parameters are set to the best parameters given in the original paper.

  • GFSC: A model for multi-view spectral clustering [33], that performs multi-view fusion and spectral clustering concurrently. The fusion graph approximates the original graph for each individual view, but maintains an explicit clustering structure. Its parameters are modified in accordance with the method described in the paper.

  • MCLES: A multi-view clustering method for learning global structure from a multi-view data that can effectively exploit potential embedded representations of complementary information from different views [35]. The parameters are set to the optimal values specified in the paper.

Each algorithm was executed ten times on each dataset with the best parameters, and the mean and standard deviation of its Accuracy (Acc), Normalized Mutual Information (NMI) and Adjusted Rand Index (ARI) values were recorded. The higher the value of each of the four evaluation indices, the better the clustering effect.

The formula for calculating Acc is as (19):

$$ ACC = \frac{1}{n}{\sum}_{i=1}^{n}y_{i} = map(\hat{y}_{i}) $$
(19)

where yi represents the predicted class label, \(\hat {y}_{i}\) is the true label, and map(⋅) represents the Hungarian matching algorithm [41].

The formula for calculating NMI is as (20):

$$ NMI = \frac{2\cdot{\sum}_{y\in Y,\hat{y}\in\hat{Y}}p(y,\hat{y})\log\left( \frac{ p(y,\hat{y})}{ p(y)p(\hat{y})}\right)}{H(Y)+H(\hat{Y})} $$
(20)

where y and \(\hat {y}\) denote two clusters labels, Y and \(\hat {Y}\) are their clusters sets, p(⋅) represents a marginal probability mass function, \(p(y, \hat {y})\) denotes a joint probability mass function of Y and \(\hat {Y}\), and H(⋅) represents an entropy.

The formula for calculating ARI is as (21):

$$ ARI = \frac{{\sum}_{ij}\begin{pmatrix}n_{ij}\\2 \end{pmatrix} - \left[{\sum}_{i}\begin{pmatrix}a_{i}\\2\end{pmatrix}{\sum}_{j}\begin{pmatrix}b_{j}\\2 \end{pmatrix}\right]/\begin{pmatrix}n\\2\end{pmatrix}}{\frac{1}{2}\left[{\sum}_{i}\begin{pmatrix}a_{i}\\2 \end{pmatrix} + {\sum}_{j}\begin{pmatrix}b_{j}\\2 \end{pmatrix}\right]-\left[{\sum}_{i}\begin{pmatrix}a_{i}\\2\end{pmatrix}{\sum}_{j}\begin{pmatrix}b_{j}\\2 \end{pmatrix}\right]/\begin{pmatrix}n\\2 \end{pmatrix}} $$
(21)

where n represents the total number of samples, nij denotes the number of samples which belongs to i-th cluster and j-th class in the true label, ai is the number of samples in i-th cluster, and bj is the number of samples in j-th class in true label. A larger ARI indicates a more satisfactory clustering solution.

4.3 Results

The experiment results of all methods on the four data sets are shown in Tables 3, 4, 5, and 6. The values in the table represent the mean and standard deviation of Acc,NMI and ARI derived from many simulations (the best results are boldface). The mean value and standard deviation reflect the algorithm’s precision and consistency, respectively. Note that the result of the MCLES algorithm in the Caltech101_20 dataset is null, because the running time is too long (more than 24 hours).

Table 3 Clustering result in terms of Acc, NMI, and ARI on the Caltech_20 dataset
Full size table
Table 4 Clustering result in terms of Acc, NMI, and ARI on the Cornell dataset
Full size table
Table 5 Clustering result in terms of Acc, NMI, and ARI on Reuters dataset
Full size table
Table 6 Clustering result in terms of Acc, NMI, and ARI on Source3 dataset
Full size table

The above table shows the clustering effect of the method in this paper is superior to most datasets. The proposed frameworks exceed other algorithms significantly on all datasets in terms of Acc and NMI. Our algorithm performs better than the BiMVCC [19] algorithm, which only considers the similarity of sample-feature, demonstrating that multiple similarity information is superior to single similarity information. Additionally, we can make the following observations. First, clustering with multiple views is better than clustering with a single view. This can be determined by comparing the results of spectral clustering for each view to the results of multi-view clustering. This is due to the fact that the information between multiple views is complementary, thereby enhancing the clustering performance. Then, we can observe that this method performs significantly better than other advanced methods on three text data sets: Cornell, Source3 and Reuters. In the Cornell dataset, for instance, the NMI value is 9% greater than the second. Finally, we can observe that the performance improvement on the image dataset is not so obvious, and the improvement is limited compared with other methods. One possible reason why the algorithm works better on text datasets than on image datasets is that text data has obvious co-occurrence characteristics, that is, matrix elements represent the frequency of each word in each document.

Consequently, the following experimental results can be drawn: 1) Clustering with multiple views is more effective than clustering with one view. 2) The algorithm’s performance depends on the dataset to some degree, but it is superior to other algorithms; 3) Integrating multiple similarity information is superior to using the original data directly as the graph’s adjacency matrix. To verify this further, we conducted ablation experiments in Section 4.4.

4.4 Component analysis

To further validate the effectiveness of the algorithm, we conducted ablation experiments, with sample-feature similarity for clustering, sample-sample and feature-feature similarity for clustering, and three similarities for clustering. The results are presented in Table 7.

Table 7 Ablation experiment for MvCCMS
Full size table

Through ablation experiments, we can observe that the clustering performance is not significantly improved when considering only one or two of these similarities (i.e., sample-feature, sample-sample, and feature-feature). When all components are considered, clustering performance on all datasets is enhanced. This demonstrates that using multiple similarities to clustering is superior to using a single similarity, which verifies the algorithm’s effectiveness and explains that one of the reasons our algorithm works so well is because it considers more similarity data than previous algorithms.

4.5 Weight change analysis

To verify that the algorithm can converge, we analyzed the changes in the weight of each view throughout the iteration process. The analysis results are shown in Fig. 2. Where the horizontal axis represents the number of iterations, and the vertical axis represents each weight’s value (The value of each view weight is normalized, that is, the weight of the i-th view is:\(\frac {w_{i}}{{{\sum }^{v}_{j}}{w_{j}}}\)).

Fig. 2
figure 2

The weight change curve of each view, the horizontal axis represents the number of iterations, and the vertical axis represents the weight value

Full size image

It can be seen that our algorithm can converge and the speed is relatively fast. On the Caltech101_20, Cornell, and Source3 datasets, convergence can be achieved in five iterations, whereas on the Reuters dataset, convergence can be achieved in only two iterations. The time required is correspondingly reduced due to fewer iterations. At the same time, during the iteration process, the weights of the more important views will gradually increase. One possible explanation is that we employ a the feature selection algorithm to select the most essential features of each view. Each view’s feature space is small, so convergence occurs relatively quickly. Therefore, the weight change analysis reveals that our algorithm possesses the characteristics of rapid convergence, proving the algorithm’s effectiveness.

5 Conclusion

This paper proposes an automatic weighted multi-view co-clustering method based on multi-similarity. The key idea is to use ensemble algorithms to mine the multi-similarity of data. Compared with the existing multi-view co-clustering algorithms, our method has the following advantages: 1) It considers multiple similarities in information between the two dimensions of samples and features. Previous multi-view clustering algorithms only considered the similarity between samples, which limits the performance of clustering. By contrast, we maximize the potential information in multi-view data. These similarities contribute to the computation of the co-clustering, which improves the clustering performance. 2) Our method calculates similarity using an ensemble algorithm, which improves the robustness of clustering. Meanwhile, MSR is introduced to reduce the impact of poor base co-clusterings and get a better similarity matrix. Experimental results on several benchmark datasets indicate that the proposed MVCCMS method is superior. At the same time, we also give ablation experiments to verify the effectiveness of multiple similarities. By analyzing the weight changes of each view, we have determined that the algorithm has a faster convergence speed, which reduces the amount of time spent to some degree.

However, our algorithm has several shortcomings, including: 1) While the ensemble method improves the robustness, it also increases time complexity. Moreover, the time complexity of spectral clustering is extremely high. 2) The algorithm’s performance on image datasets is subpar. In future work, we will attempt to resolve the aforementioned issues. In addition to the above plans, we still have the following ideas to try: 1) The neural network is adept at feature extraction and nonlinear fitting. Learning similarities between data based on neural networks might be an idea to try. 2) In addition to co-occurring data, different clustering techniques can be incorporated into multi-view clustering of other data types.