1 Introduction

In scientific research and engineering practice, many practical optimization problems ultimately boil down to solving constrained multi-objective optimization problems, such as WEB server placement problem [1], microgrid optimization scheduling problem [2], and near-space communication deployment problem [3], etc. This type of constrained multi-objective problems (CMOP) can be defined as the following form:

$$ \begin{array}{@{}rcl@{}} \begin{cases} \text { minimize } \mathbf{F}(\mathbf{x})&=\left( f_{1}(\mathbf{x}), \ldots, f_{m}(\mathbf{x})\right)^{T} \\ \text { subject to } g_{i}(\mathbf{x}) &\geq 0, i=1, \ldots, q \\ &h_{j}(\mathbf{x})=0, j=1, \ldots, p\\ &\mathbf{x} \in \mathbb{R}^{n} \end{cases} \end{array} $$
(1)

F(x) represents m objective functions that need to be optimized at the same time. fi(x) represents the i − th objective function, gi(x)and hj(x) represent inequality constraints and equality constraints, respectively, and q and p represent the number of inequality constraints and equality constraints, respectively. Due to the complexity of CMOP, traditional mathematical methods are difficult to obtain ideal results. The Evolutionary Algorithm (EA), as a type of optimization method developed by simulating biological evolution theory has many advantages in solving CMOP problems. Therefore, constrained multi-objective optimization algorithms have received widespread attention.

In the past two decades, multi-objective evolutionary algorithms (MOEAs) have achieved good results in solving various multi-objective problems [4]. When using MOEAs to solve CMOP, it is necessary to adopt appropriate constraint processing techniques to solve equality constraints and inequality constraints. Almost all constraint handling methods are to define an overall constraints violation function and minimize it [5]. Early MOEAs usually treated constraints and goals equally. For example: Penalty function method [6], which adds the constraint to the objective function by multiplying the constraint with a penalty factor, thereby transforming the constrained optimization problem into a special unconstrained problem; The dynamic penalty method [7] is to construct the penalty factor as a function that changes with the number of iterations or iteration time, so as to dynamically adjust the problem. If the penalty factor changes according to the feedback information during the search process, it is called an adaptive penalty method [8]. However, it is difficult to achieve a good balance between constraints and goals by adjusting the penalty factor [9]. In order to solve the deficiencies in the penalty function constraint processing method, T.P. Runarsson et al. proposed a random sorting constraint processing method [10], which use a process similar to bubble sorting to deal with constrained optimization problems. Based on the random parameter 𝜃, we can judge whether the current solution is based on the objective or the constraint. When 𝜃 is 0, the objective based sorting rule is used for random sorting; When 𝜃 is 1, constraint based sorting rules are used for random sorting. Decomposition based MOEA usually does not consider the Pareto domination, but it also uses a similar idea to solve the problem of judging infeasible solution in the aspect of constraint processing [11]. Specifically, when updating the solution of the weight vector, consider the degree of constraint violation of the solution, and prefer the solution with less constraint violation [12]. In the algorithm, when the angle between two feasible solutions is large, the relationship between the two solutions is considered as non-dominant, and the algorithm in [13] considers the minimization of objective values and the minimization of constraint violations as a two-objective optimization problem to be optimized.

However, there are two problems with the above methods: 1) There may be many non-zero local minima in the overall constraint violation function, which may lead to infeasible regions being searched. 2) The possible domains in the search space may be discontinuous, making it difficult to move from one area to another [14, 15]. In summary, existing multi-objective evolutionary algorithms (MOEAs) have encountered difficulties in solving CMOP. To solve these difficulties, many advanced constrained multiobjective optimization algorithms (CMOEAs) have been proposed. For example, the two archive coevolution algorithm (CTAEA) [16], which saves both convergence and diversity archives, improve the convergence of the population while maintaining the distribution of the population, and ultimately search for a non-dominant feasible region. PPS designs and uses a push-pull search method, which first pushes the population to the unconstrained Pareto front (PF), and then pulls the population into the feasible region. However, both the CTAEA’s diversity archive throughout the search process and the PPS locates the push phase of unconstrained PF has done a lot of useless work in the infeasible regions [17, 18].

In this regard, this paper proposes a staged coevolution algorithm to solve the above two dilemmas and improve search efficiency. The main contributions of this paper are as follows:

  1. 1.

    Aiming at the problem that the population is trapped in the local optimal feasible region, a new coevolution method is proposed. This method keeps the relative synchronization between the help population and the main population, makes the auxiliary population become more efficient auxiliary main population, and helps the population find the ideal non-dominated feasible region.

  2. 2.

    Aiming at the problem of waste of computing resources, a two-stage optimization strategy is designed. When the help population plays a positive guiding role, the coevolution stage is maintained; when the help population cannot play a role, the stage is changed in time so that the algorithm can search more efficiently.

  3. 3.

    A new algorithm, TSC-CMOEA, is obtained by combining these new coevolution methods with two-stage optimization strategies. Tests on multiple test sets show that TSC-CMOEA has great potential in solving CMOPs.

The main content of the rest of this paper is organized as follows: Section 2 is the basic knowledge of CMOPs, and introduces the shortcomings of algorithms such as CTAEA and CCMO in solving CMOP problems. In order to overcome the shortcomings of existing algorithms, an improved algorithm, TSC-CMOEA, is proposed in Section 3. The validity of TSC-CMOEA and its essential reasons is analysed in depth. Section 4 is the experimental part, which compares and analyses TSC-CMOEA with several CMOEAs which currently perform well, such as PPS, ToP and CTAEA. Section 5 is the conclusion of this article.

2 Related work

When solving most CMOPs, the feasibility of the solution is often considered before the convergence, so some MOEAs give priority to the feasibility of the solution in the dominance relationship. In NSGA-II, Deb et al. proposed a dominance-based constraint processing method called CDP [11]. This method embeds the feasibility criterion into Pareto dominance, in which feasible solutions dominate infeasible solutions, and solutions with lower constraint violations dominate solutions with higher constraint violations. Specifically, first, the overall constraint violation degree of each solution is obtained by calculating formula (2).

$$ \text{CV}(\mathrm{x})=\sum\limits_{\mathrm{i}=1}^{\mathrm{p}} \max \left\{\mathrm{g}_{\mathrm{i}}(\mathrm{x}), 0\right\}+\sum\limits_{\mathrm{j}=1}^{\mathrm{q}}\left\|\mathrm{h}_{\mathrm{j}}(\mathrm{x})\right\| $$
(2)

Where gi(x) and hj(x) are the i − th inequality constraint and the j − th equality constraint of CMOP. If any of the following conditions is met, the solution x is said to dominate another solution y: 1) If CV(x) = 0 and CV(y) = 0, any fi(x) ≤ fi(y), and there is at least one dimension fi(x) ≤ fi(y); 2) CV(x) ≤CV(y). CDP constraint processing technology can be used in other MOEAs based on the advantages of Pareto.

𝜖 Constraint processing technology [12] relaxes the definition of feasibility on the basis of CDP constraint processing technology, and sets the condition for judging feasible and infeasible solutions, that is, the overall constraint violation degree to a value can be dynamically adjusted 𝜖, When the overall constraint violation degree of a solution is less than 𝜖, the current solution is considered to be a feasible solution [12].

The most recent CMOEA can be divided into four categories according to the constraint processing technology:

The first type of CMOEA is derived from the rigor of constrained single-objective optimization, which mainly relies on penalty functions, such as MOSOS [19] and I𝜖+NSGA-II [8]. This idea is simple and easy to implement, but its performance is sensitive to the setting of the penalty factor with the corresponding penalty function. Too large a penalty factor can lead to indifference to an infeasible solution, while too small a penalty factor can lead to acceptance of an infeasible solution.

The second type of CMOEA, they mainly use feasibility information. For example, NSGA-II [11] proposes a constraint dominance principle (CDP) in NSGA-II. When comparing a pair of feasible solutions, this is exactly the same as the classical Pareto advantage, while infeasible solutions are compared according to their constraint conflicts. CDP is one of the most popular constraint processing technologies in EMO due to its simplicity and efficiency. In addition, Fan et al. proposed an angle-based CDP algorithm (MOEA/D-ACDP) [13], which utilizes classical Pareto advantage to compare infeasible solutions within a given Angle. However, the constraint information used by these methods is relatively simple, and they often need to be used together with other methods to achieve better results.

The third type of CMOEA, such as CM2M2 [20], is designed to increase selection pressure with useful infeasible solutions. CM2M2 proposed a CMOP evolutionary algorithm based on two groups of weight vectors. In particular, it maintains a set of “infeasible” weight directions to facilitate constrained multi-objective optimization.

The fourth class is based on 𝜖 functions, which use 𝜖 as a tolerance threshold for constraint conflicts containing infeasible solutions (e.g. 𝜖 de-HP [12]). However, the setting of 𝜖 can affect convergence to a large extent, where a large 𝜖 value exerts a large selection pressure on convergence, while a small 𝜖 value fine-tunes the local area.

Coevolution technology has achieved good results in solving many difficult optimization problems such as multi-objective optimization problems [21], dynamic optimization problems [22], and large-scale optimization problems [23]. But in terms of handling constraints, coevolution technology is still in its infancy. [17] In [24], the coevolutionary genetic algorithm and differential evolution algorithm for solving constrained optimization problems are respectively proposed [25]. These two algorithms evolve into multiple populations at the same time, and each population is assigned an independent penalty factor to balance constraints and objectives [26]. In [27], the algorithm decomposes the constraints and assigns a population to each constraint, where each population first tries to satisfy its assigned constraints, and then evolves another constraint from other populations.

Literature [28] proposed a multi-objective particle swarm optimization algorithm. The algorithm uses one population to store available particles and another population to store unavailable particles. Among them, available particles evolve into Pareto optimal, and unavailable particles evolve into available particles. In addition, once the infeasible solution becomes feasible, it can be transferred to the feasible solution group. In [17], the differential coevolution framework is used to solve constrained multi-objective problems. In this paper, the constrained multi-objective problem with m constraints is transformed into m constrained single-objective optimization problems, and m populations used to solve the constrained single-objective optimization problem are evolved to solve the original CMOP.

For more advanced coevolutionary algorithms, they put more emphasis on the coordination of multiple populations.Both CTAEA and CCMO are among the most advanced coevolutio algorithms.

CTAEA [28] is an evolutionary algorithm that evolves two populationes. In CTAEA, the convergence-oriented archiving (CA) evolves into optimization constraints and objectives, and the diversity-oriented archiving (DA) evolves into optimization objectives only. At the same time, the two populations cooperate with each other in mating selection and environmental selection. Usually CTAEA selects one parent from CA and another parent from DA to produce offspring. Therefore, most offsprings are located between CA and DA. The offsprings produced by this method not only have the diversity of DA, but also have the convergence of CA to a certain extent.

However, this method also has some problems as shown in Fig. 1: (1) From the distribution of the white dots Off1 population in Fig. 1, it can be seen that most individuals of Off1 are located in the infeasible area, and these offspring do not have good diversity or convergence. (2) Combining the black CA population and the white DA population in Fig. 1, it can be seen that Off1 is mainly distributed in the middle area between the CA and the DA, and cannot effectively update the CA to have better diversity. Therefore, CTAEA ultimately cannot find a sufficient number of feasible and well-convergent solutions [10].

Fig. 1
figure 1

Population distribution when problems occur in CTAEA

Full size image

CCMO [17] is a coevolutionary algorithm that simultaneously calculates two objectives problems-the original problem and the auxiliary problem. Usually, the original problem in CCMO is solved by Population 1. The auxiliary problem is defined as the original problem that removes the constraints and is solved by Population 2. The two populations have no other associations except for sharing offspring, which is called weak association. Specifically, Population 1 of CCMO generates its own offspring 1 through a predefined method, and Population 2 also generates its own offspring 2 through a predefined method. Two progeny populations are mixed with select individuals through their respective environments to finally solve the problem. This method is effective in the early stage of the algorithm, and the offspring produced by the auxiliary population can often help the population quickly cross the infeasible region [29].

But in the later stage of the algorithm, this method often has some problems, as showed in Fig. 2. (1) The offspring populations produced by Population 1 and Population 2 are near their respective populations. Offspring 1 and Offspring 2 seem to have nothing to do with each other and cannot cooperate well. (2) The calculation of Population 2 is not helpful to the main population, which is almost a waste of computing resources. As some recent studies have revealed, most existing MOEAs have encountered difficulties in obtaining a set of feasible solutions to a set of discrete and widely distributed CMOPs. In particular, the limitations of current coevolutionary algorithms are mainly due to the lack of interaction and waste of computing resources in the synergy between populations [18, 30, 31].

Fig. 2
figure 2

Population distribution when problems occur in CCMO

Full size image

3 The proposed algorithm

3.1 Algorithm framework

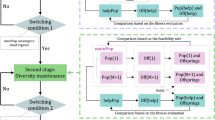
In order to alleviate the current CMOEA’s difficulty in effectively balancing convergence and diversity and waste of computing resources when processing complex CMOPs, this paper proposes a constrained multi-objective optimization algorithm (TSC-CMOEA) based on two-stage coevolution. As described in Algorithm 1, the TSC-CMOEA proposed in this paper is divided into two stages. Lines 6-21(marked by ‘\(\blacktriangle \)’) in Algorithm 1 are the first stage of TSC-CMOEA. In this stage, the coevolution constraint processing technology is used to make the population quickly approach the real PF. The main purpose of this stage is to quickly cross a large number of discontinuous infeasible regions with the help of help problems; When the help problem can no longer help the population evolution well, TSC-CMOEA switches to the second stage (as shown in lines 23-28 marked by ‘\(\blacksquare \)’ in Algorithm 1). This stage uses CDP constraint processing technology to better complete the search. This stage is mainly to increase the diversity of the population while reducing unnecessary function calculation requests.

figure g

3.2 The first stage

This section will specifically describe the evolutionary process of the first stage. It can be seen from Algorithm 1: In the first stage, the used dominance relationship and crowding distance are used as mating selection strategies, and two parent sets, Parent 1 and Parent 2, are selected from Population 1 and Population 2, respectively. Then, the two parent sets are generated by simulated binary crossover and polynomial mutation operators to generate offspring populations, Offspring 1 and Offspring 2. After that, Population 1 combined with the offspring population Offspring 1 used an environmental selection strategy based on fitness to select individuals. Population 2 is combined with Offspring 1 every 10 iterations, and with Offspring 2 in other iterations, and then individuals are selected using an environment selection strategy based on fitness.

Such a population combination strategy can make the main population and the auxiliary population relatively synchronized. It is worth noting that the individual selection strategy used in TSC-CMOEA is different from the commonly used selection strategy used in NSGA-II. Specifically, the environment selection strategy used in TSC-CMOEA is similar to that proposed in SPEA2. First, determine the solution set storing all the solutions dominated by x and the solution set Sx storing all the solutions dominated by x, and find the \(\lfloor \sqrt {2 n}\rfloor \) nearest neighbor of x in the population. Then calculate an fit(x) for each individual, fit(x) is defined as following

$$ \operatorname{fit}(\mathbf{x})=\sum\limits_{\mathbf{y} \in S_{\mathbf{x}}}\left\|R_{\mathbf{y}}\right\|+\frac{1}{\operatorname{dist}\left( \mathbf{x}, \mathbf{x}^{\prime}\right)+2} $$
(3)

Where the first component of fit(x) calculates the total number of solutions that dominate x, and the second component calculates the reciprocal of the Euclidean distance from x to its \(\lfloor \sqrt {2 n}\rfloor -th\) nearest neighbor. The smaller the value of fit(x), the better the quality of the solution. This individual selection strategy considers the distribution of the population more. Population 2 uses a special offspring population combination strategy to keep the original problem and the auxiliary problem as synchronous as possible. This operation can improve the utilization efficiency of the auxiliary problem. It should be noted that the solutions in Population 1 are all calculated from the raw problem fraw, and Population 1 is also the final output result of the first stage.

The solution in Population 2 is calculated from the help problem fhelp derived from the raw problem. Usually the help problem fhelp is selected as the original problem fraw without considering constraints.

3.3 The second stage

From the 23th line(marked by ‘\(\bigstar \)’) of Algorithm 1, we can see that the input of the second stage is the output of the first stage, Population 1. At this time, Population 1 is very close to the real PF, but due to the coevolution of some characteristics, the diversity is slightly insufficient. As can be seen from lines 23-28(marked by ‘\(\blacktriangle \)’) of the code in Algorithm 1, the processing of the entire problem in the second stage is similar to the processing of the main population in the first stage. Two Parent sets, Parent 1 and Parent 2, are selected from Population 1 by using dominant relationship and crowding distance as mating selection strategies. Then, the two parent sets are used to generate progeny populations, Offspring 1, through the simulated binary crossover and polynomial mutation operators, respectively. After that, Population 1 combined with the offspring population Offspring 1 uses the environmental selection strategy to generate a new Population 1. In the second stage, because the help problem can no longer support the main population well, we do not calculate Population 2 in the second stage to save the calculation.

The main steps of TSC-CMOEA include two stages, and it is particularly critical to completing the stage conversion at the right time. The strategy for the switching phase is as follows: rk < δ, where rk represents the rate of change of the lowest point in the population at the lowest l offspring, and δ is a minimum value set by the user (set δ = 1e − 3 in this article). Note that δ is an empirical value.rk is the change rate of the ideal point in the population. Through a large number of experiments, we found that when the δ value is set to a low value (1e − 3), the switching algorithm stage is effective, but the δ value does not tend to zero. We believe that when the population change rate is less than a certain threshold, is the best time to switch algorithm. If you let δ = 0, you don’t switch between the two phases, and the second phase doesn’t work.The rate of change of the lowest point in the last l generation is defined as follows:

$$ r_{k}=\frac{\left\|z^{k}-z^{k-l}\right\|}{\max \left\{\left\|z^{k-l}\right\|, 1 e-6\right\}} $$
(4)

Where zk is the ideal point of generation k and zk−l is the ideal point of generation (k − l). In (4) 1e − 6 is to ensure that the denominator is not zero, so its value can be closer to 0.

In general, the proposed TSC-CMOEA evolves Population 1 in the first stage to solve the raw problem, and at the same time evolves Population 2 to solve the help problem. The offspring produced by the two populations are shared conditionally. When the phase transition conditions are met, the proposed TSC-CMOEA enters the second phase. The second stage is based on Population 1 evolved in the first stage. CDP constraint processing technology cooperates with NSGA-II to evolve Population 1 to solve CMOPs.

It is worth noting that in the first stage, Population 1 may often fall into a narrow feasible area, and sharing the offspring of Population 2 can help it jump out of the local optimum. At the same time, because fhelp is usually simpler than fraw, the solution in Population 2 usually has better convergence than the solution in Population 1. Therefore, descendants generated by Population 2 are likely to improve the convergence of Population 1 after the sharing operation.

The coevolution of the two populations can greatly improve the speed and accuracy of the algorithm’s convergence, but it also comes with some minor problems. For example, because there is a mapping relationship between the PF of the help problem and the real PF, and this relationship can sometimes only lead the population to find a part of the PF, so that the diversity of the population is greatly lost. Therefore, when the coevolution constraint processing technology cannot complete the task well, it is very necessary to switch to an effective constraint processing technology in time. After Population 1 ends the first stage, the auxiliary problem cannot help the original problem in the second stage; by entering the second stage, the main population makes full use of some infeasible solutions to expand the diversity of the population.

3.4 Analysis of TSC-CMOEA

In the first stage, we deal with both populations simultaneously, strengthening the tie between the populations by mixing the two offspring populations. Population 1 is a constrained population, and feasible solutions are fully considered to ensure the feasibility of the algorithm. Population 2 is an unconstrained population, which usually approaches the unconstrained PF preferentially than population 1, and the offspring generated by population 2 has higher convergence. Therefore, the introduction of two-population strategy not only retains feasible solutions well, but also achieves higher convergence, making the performance of the two populations complementary.

In the second stage, the algorithm to the end, there is some distance between the unconstrained PF and the constrained PF, this time to maintain double population strategy is not cost-effective, because of the population are near the real PF for local search, population 2 unconstrained PF for population 1 help has been very small. So, in the second stage, we removed population 2 and maintained only one population, with the main purpose of conducting a more detailed local search on the results of the first stage. This operation directly reduces the evaluation times of the function and indirectly improves the performance of the algorithm.

Also, at the end of the algorithm, the population 1 with high convergence obtained in the first stage is used to conduct local search with a method similar to dominance, which directly improves the performance of the algorithm.Therefore, the performance of the algorithm is improved by the two strategies proposed by us.

In order to analyze the effectiveness and mechanism of TSC-CMOEA, we show the early, middle and last population distribution of TSC-CMOEA on the MW9 in Fig. 3, and compare the distribution results with CTAEA and CCMO.

Fig. 3
figure 3

The population distribution of CCMO, CTAEA and TSC-CMOEA in the early, middle and late stages on the MW9

Full size image

As showed in Fig. 3(a c), Population 1 of CCMO is responsible for the convergence of early populations relatively concentrated, and Population 2 auxiliary problems are widely distributed. Some individuals in the final population cannot skip the infeasible region ahead.

It can be seen from Fig. 3(d f) that for CTAEA, DA is a population that maintains diversity, and CA is a population that improves convergence. In the early stage, due to the influence of DA, the diversity of CA performed well, but the convergence was insufficient, and the performance of the offspring was also the same. In the middle stage, since the DA population only considers the objectives and ignores constraints, the DA population is distributed on the unconstrained PF. However, CTAEA usually selects a parent from CA, and then selects a parent from DA to produce offspring, so most offspring are located between CA and DA. Due to this offspring generation strategy, the offspring produced do not have good feasibility or good convergence, and the CA cannot be updated to achieve better diversity. Therefore, in the end, CTAEA cannot perfectly find a sufficient number of good enough solutions.

Figure 3(g i) shows that TSC-CMOEA and CCMO behave similarly in the early and middle stage, because TSC-CMOEA originated from CCMO. For the early days of TSC-CMOEA, Population 1 considers constraints, and Population 2 does not consider constraints. Thanks to Population 2, the distribution and convergence of the overall population are very good. It can be seen from the figure that the two populations are synchronized with each other, and the parents of TSC-CMOEA are selected from Population 1 and Population 2, which makes some offspring around Population 1 and Population 2, and the surrounding offspring can enhance the diversity of Population 1. When TSC-CMOEA enters the second stage, it pays more attention to convergence. Therefore, the final TSC-CMOEA results are relatively better than CTAEA and CCMO.

4 Experimental research

4.1 Test sets

In order to evaluate the performance of TSC-CMOEA, we selected five test sets of C-DLTZ, DC-DTLZ, MW, LIRCMOP and DOC as the test objects. C-DLTZ and DC-DTLZ are traditional constraint test problems, MW is a test problem based on constraint construction method and distance function design, LIRCMOP is a large-scale infeasible region test problem, and DOC is a test problem that includes decision constraints and objectives constraints. A detailed description of these test sets, including mathematical definitions and properties, can be found in their original papers [30,31,32,33].

4.2 Parameter setting

All the algorithms participating in the comparison have some common parameter settings. Table 1 shows the parameter settings of the proposed algorithm and the comparison algorithm. For the two-objective problem, the population size is set to 100, and for the three objective problem, the population size is set to 105. Termination conditions of all MOEAs participating in the comparison are set so that the total number of evaluations of all population functions reaches the specified number, and the setting is large enough to ensure that each MOEAs can converge. For constrained DTLZ and MW problems, the number of function evaluations is set to 100,000, while for LIR-CMOP and DOC problems, the number of function evaluations is set to 300,000. Since the DE operator has excellent performance in solving complex problems, for LIRCMOP and DOC problems, the DE operator and polynomial mutation are used to generate progeny, and for the remaining problems, the SBX operator and polynomial mutation are used to generate progeny. For the SBX operator, the crossover probability and distribution index are set to 0.9 and 20, respectively. For the DE operator, the crossover rate and scale factor are set to 1.0 and 0.5, respectively. For the polynomial mutation operator, the mutation probability and distribution index are set to Pm = 1/n (n is the number of decision variables) and 20, respectively. The parameters of all comparison algorithms are set according to the suggestions in the original paper [4, 9, 11, 17, 23, 30].

Table 1 Paramaters set of CCMO, NSGA-II, NSGA-III, C-MOEA/D, PPS, TOP, and TSC-CMOEA
Full size table

4.3 Performance indicators

The goal of CMOPS is to find a set of uniformly distributed feasible solution sets that are as close to the real PF as possible. In order to quantitatively compare the performance of each algorithm, we used two popular metrics in the experiment-Inverse Generation Distance (IGD). Their definitions are as following:

$$ \left\{\begin{array}{l} I G D\left( P^{*}, A\right)=\frac{y_{y^{*} \in P^{*}}^{\sum\left( y^{*}, A\right)}}{\left\|P^{*}\right\|} \\ d\left( y^{*}, A\right)=\min_{y \in A}\left\{\sqrt{{\sum}_{i=1}^{m}\left( y_{i}^{*}-y_{i}\right)^{2}}\right\} \end{array}\right. $$
(5)

Where P∗ represents a set of representative solutions in the real PF, and A is the approximate PF realized by CMOEA. m represents the number of objectives. y is a solution in A, yi is the i − th objective value of y, y∗ is the solution with the closest Euclidean distance to y in P∗, and \(y_{i}^{*}\) is the y − th objective function value.

HV reflects the proximity of the undominated solution set implemented by CMOEA to the true PF, a larger HV means that the corresponding undominated set is closer to the true PF.

$$ H V(S)=V O L\left( \underset{x \in S}\bigcup\left[f_{1}(x), {z_{1}^{r}}\right] \times \ldots\left[f_{m}(x), {z_{m}^{r}}\right]\right) $$
(6)

where V OL(−) is the Leberger measure, m denotes the number of objectives, and \(z^{r} = ({z_{1}^{r}}, ... , {z^{r}_{m}})^{T}\) is the user-defined reference point in the objective space. For each CMOP, the reference point is 1.2 times the distance from the lowest point of the true PF. It is worth noting that larger values of high pressure may indicate better performance in terms of diversity and/or convergence.

4.4 Effective test of algorithm improvement

In order to verify the effectiveness of TSC-CMOEA’s improvement strategy, we compared it with CTAEA and CCMO. Table 2 shows the average and standard deviation of the IGD for 30 independent runs of CTAEA, CCMO, TSC-CMOEA and TSC-CMOEA2 on the DTLZ, MW, LIRCMOP and DOC test problem sets. As can be seen from the table, TSC-CMOEA achieved the best results in 35 of the 47 test problems, followed by CTAEA which achieved 7 best results, and finally CCMO only achieved 5 best results. Table 2 also shows the statistical results of the Bonferroni-corrected Friedman test at the 0.05 significance level [34]. It can be seen that TSC-CMOEA is significantly better than CTAEA on 36 issues and significantly better than CCMO on 21 issues. TSC-CMOEA shows better convergence on these problems, which are caused by the two-stage design of the algorithm, and the increase in the second stage strengthens the convergence of the population.TSC-CMOEA2 is a variant of the TSC-CMOEA without two-phase strategy. As can be seen from IGD value data in Table 2, TSC-CMOEA2 has some advantages over CCMO, but it is not very obvious. However, by comparing TSC-CMOEA2 with TSC-CMOEA, it can be found that TSC-CMOEA has obvious advantages. This shows that the two stage strategy can improve the performance of the algorithm more greatly. At the same time, the two stage strategy mainly improves the local search performance of the algorithm, so the new coevolution method is also crucial for the population to reach the ideal region more efficiently.

Table 2 Mean and standard deviation of the IGD values obtained by NSGA-II, NSGA-III, C-MOEA/D, PPS, TOP, and TSC-CMOEA for 30 independent runs on the constrained DTLZ test suite and the MW test suite
Full size table

Combining Tables 2 and 3 and the above analysis, we can see that the new coevolution method and the phased strategy have good results.

Table 3 Mean and standard deviation of the IGD values obtained by NSGA-II, NSGA-III, C-MOEA/D, PPS, TOP, and TSC-CMOEA for 30 independent runs on the constrained DTLZ test suite and the MW test suite
Full size table

4.5 Experimental results of DTLZ and MW problems

In order to verify the performance of TSC-CMOEA, we select NSGA-II, NSGA-III, C-MOEA/D, PPS and ToP and other current algorithms that perform well in solving constrained multi-objective optimization problems as the comparison objects. All algorithms constrain the average and standard deviation of the IGD values obtained during 30 independent runs on the DTLZ test suite and the MW test suite. The IGD value of each question is calculated according to the method suggested in [35] for approximately 10,000 reference points sampled on the PF of the question. As showed in Table 3, the proposed TSC-CMOEA achieved the best results on 18 issues, and secondly, CMOEA/D achieved the best results on two issues.Then we computed the HV values of TSC-CMOEA and the comparison algorithm on the two test sets, DTLZ and MW. Table 4 shows the results of the HV values.The computed results are shown in Tables 3 and 4, and it can be seen that our proposed algorithm achieves the lead on most of the problems.

Table 4 Mean and standard deviation of the HV values obtained by NSGA-II, NSGA-III, C-MOEA/D, PPS, TOP, and TSC-CMOEA for 30 independent runs on DTLZ test suite and MW test suite
Full size table

Figures 4 and 5 plot NSGA-II, NSGA-III, C-MOEA/D, PPS, ToP, CTAEA, CCMO, and TSC-CMOEA of MW5 and C1_DTLZ3, and the feasible non-dominated solutions of the median IGD value in 30 runs. For MW5 and MW9 problems with discontinuous feasible regions, TSC-CMOEA shows better convergence and distribution than other MOEAs. This is because the help problem assists the raw problem. For Population1 which deals with the raw CMOP and Population2 which deal with help problems, the cooperative relationship between them effectively improves the convergence and diversity of Population1. It can be seen from Fig. 2 that the convergence of TSC-CMOEA is better than that of other MOEAs, and other MOEAs still have a large number of individuals in the feasible region far from the real PF. Rapid convergence rate of TSC-CMOEA is mainly attributed to the offspring produced by the help problem, which makes it easier for the raw CMOP to skip the infeasible region. In short, in the constrained DTLZ problem with multi-modal landscape and a wider infeasible region and the MW problem with a small and discontinuous feasible region, the offspring produced by Population 2 help Population 1 to skip the infeasible region and obtain better convergence and diversity.

Fig. 4
figure 4

The final populations of NSGA-II, NSGA-III, C-MOEA/D, PPS, ToP and TSC-CMOEA in C1_DTLZ3

Full size image
Fig. 5
figure 5

The final populations of NSGA-II, NSGA-III, C-MOEA/D, PPS, ToP and TSC-CMOEA in MW5

Full size image

4.6 Experimental results of LIR-CMOP and DOC problems

To further verify the performance of TSC-CMOEA, we used more difficult test suites (ie LIRCMOP and DOC) to perform supplementary tests. LIRCMOP contains 14 CMOPs with small feasible regions and complex relationships between position and distance variables. DOC contains 9 CMOPs with complex constraints in both decision space and target space. Table 5 shows the average and standard deviation of the IGD values obtained by NSGA-II, NSGA-III, C-MOEA/D, PPS, ToP, and TSC-CMOEA during 30 independent runs on the LIRCMOP test suite and the DOC test suite. TSC-CMOEA made on 15 test questions optimal, PPS is 5, ToP is 1. And we also computed HV values on these test sets and the results are shown in Table 6. The data in Table 6 shows that it performs similarly to the IGD values, and our proposed algorithm outperforms the comparison algorithm on most of the test problems, with only a few falling slightly back to the PPS. Therefore, it can be concluded that the proposed TSC-CMOEA has better overall performance than some of the most advanced MOEAs when solving the benchmark CMOP. This is precisely caused by the new coevolution method and the two-stage algorithm design.

Table 5 Mean and standard deviation of the IGD values obtained by NSGA-II, NSGA-III, C-MOEA/D, PPS, TOP, and TSC-CMOEA for 30 independent runs on LIRCMOP test suite and DOC test suite
Full size table
Table 6 Mean and standard deviation of the HV values obtained by NSGA-II, NSGA-III, C-MOEA/D, PPS, TOP, and TSC-CMOEA for 30 independent runs on LIRCMOP test suite and DOC test suite
Full size table

4.7 Experimental results of microgrid scheduling problem

Finally, we use the proposed TSC-CMOEA to optimize a microgrid dispatch model. The dispatch model of the microgrid is as follows.

$$ \begin{array}{@{}rcl@{}} &&\operatorname{minimize} \mathbf{f}(\mathbf{x})=\left\{\begin{array}{c} f_{1}=C_{\text{ex}}+C_{\text{DG}}+C_{\text{em}}+C_{\text{lc}} \\ f_{2}=\max P_{\text{ex}, t}-\min P_{\text{ex}, t}={\Delta} P_{\text{ex}} \end{array}\right. \\ &&~~~~~~~~~~~~~~~~~\text { subject to } g_{j}(\mathbf{x}) \leq 0, j=1,2,3 . \end{array} $$
(7)

Where Cex is the transaction cost of the external grid, CDG is the generation cost of DG, Cem is the operation and maintenance cost of EER and storage devices, Clc is the compensation cost of flexible load and Pex,t is the power exchanges value between hybrid microgrid and external grid. The objective function is to minimize the economic cost of the microgrid and minimize the peak-to-valley difference between power supply and demand. The decision variables include microgrid dispatchable units such as energy storage ESS charging and discharging power and levelizable load transfer. The model also has complex constraints such as the equal power constraint of shiftable load shift in and out, the ESS equipped capacity constraint and the battery hourly power variation constraint. We take the example of a microgrid system in a building of a university in Hunan Province. Table 7 lists the HV values obtained for five comparative MOEAs, where each MOEA is run for 1,000 generations with a population size of 100 . As can be seen from the Table 7, TSC-CMOEA shows better overall performance than the comparative MOEA in the optimization of the microgrid dispatch model, obtaining the best HV values. Therefore, it can be confirmed that the proposed TSC-CMOEA is also effective in solving CMOPs in applications.

Table 7 HV Value of NSGAII , NSGAIII , CMOEAD , PPS , ToP and SCCMO on microgrid dispatch model, where the best result on each test instance is highlight
Full size table

5 Conclusion

In this paper, we propose a new coevolution method and staged coevolutionary algorithm for constrained multi-objective algorithms which are difficult to converge or have poor distribution when dealing with complex constraints. It is designed to solve a difficult CMOP problem by adding a help problem and an additional processing stage. In the algorithm, the first stage uses the proposed new coevolution method to process CMOP, so that the population can quickly and efficiently cross the infeasible region. When the population change rate is too small during the evolution process, it will switch to the second stage; in the second stage, only the raw problem processing part is retained. Through further optimization of the raw problem, the expected solution set is finally obtained. The results of comparison with CTAEA and CCMO show that the coevolution and two-stage strategy in this paper are effective; comparative experiments with algorithms such as NSGA-II, NSGA-III, C-MOEA/D, PPS and ToP show that TSC-CMOEA can effectively avoid local optimization caused by constraints when solving multi-objective problem. The solution results of complex multi-objective optimization problems such as LIR-CMOP and DOC show that TSC-CMOEA has better convergence performance and distribution performance in solving complex CMOP problems. In addition, if the efficiency of the offspring generation strategy in this paper can be improved, it may improve the performance of the algorithm on large-scale problems.