Novel consistency and consensus of generalized intuitionistic fuzzy preference relations with application in group decision making

Abstract

Preference relations are an efficient technology to derive the priority vectors for the alternatives in group decision-making. In this paper, an analysis of the existing research on group decision-making with intuitionistic fuzzy preference relations (IFPRs) indicates that IFPRs have some desirable properties similar to those in fuzzy situation. Then, generalized intuitionistic fuzzy preference relations (GIFPRs) and their consistency are proposed to model all those desirable properties. The given consistent GIFPRs are completely characterized by intuitionistic fuzzy priority vectors (IFPVs). For inconsistent GIFPRs, the novel $\delta$-acceptable consistency and consensus are proposed to preserve the original preference information as much as possible and methods without thresholds seeking to reach the desirable requirements are provided and visualized. Some numerical examples are given to illustrate the proposed models work; and comparisons with the existing methods are also offered to demonstrate the validity, applicability and advantages of the proposed method.

1 Introduction

Group decision-making with preference relations has been extensively investigated over the past decades. By comparing alternatives from a set of feasible alternatives, decision-makers construct preference relations to model the decision processes and obtain a priority. In the procedure of group decision-making with preference relations, consistency and consensus are indispensable to avoid a misleading priority structure.

Among these preference relations, multiplicative preference relations [25] and fuzzy preference relations (FPRs) [24, 26] are basic preference relations that can be connected by a transformation function [5]. To well describe the complex information in real-world decision problems, various generalized preference relations based on these two basic preference relations have been developed [21,22,23, 35, 47, 48]. For example, to model decision-maker’s pairwise comparisons with hesitancy, Xu [35] introduced the concept of IFPRs, in which decision maker’s preferences are characterized by Atanassov’s intuitionistic fuzzy values [1], and the hesitation margin of a preference is determined by its intuitionistic fuzzy index.

The consistency of FPRs includes additive consistency and multiplicative consistency [26], which have been widely investigated [2, 6, 14, 15, 28, 37, 45, 46]. Particularly, it was proven that both consistencies could be characterized by priority vectors [26, 46]. For IFPRs, the situations seem to be complex. Different consistency conditions have been proposed to define consistent IFPRs, and several approaches have been developed to derive priority vectors from IFPRs [9, 12, 16, 29, 30, 32, 33, 36, 43, 44]. Liu et al. citeLiu2020 proposed another view on IFPR-based aggregation operators. Liu et al. [20] investigated the decision making problem based on IFPRs with additive approximate consistency. Xu et al. [36] introduced the multiplicative consistency of IFPRs that was modified to possess some desirable properties by several researchers. Liao and Xu [16] stated that the multiplicative consistency in Ref. [36] can not be reduced to the fuzzy case and provided a novel multiplicative consistency. Based on the isomorphism between multiplicatively consistent IFPRs and interval-valued FPRs, Wu and Chiclana [32, 33] strengthened Liao and Xu [16]’s consistency definition. Wang [29] put forward a novel geometric consistency to ensure that the consistency is robust for permutations of the intuitionistic fuzzy judgments given by the decision-makers. Wang [30] stated that none of the existing multiplicative consistencies [16, 29, 32, 36] is actual intuitionistic fuzzy extensions of the multiplicative consistency [26], and proposed a novel consistency using the cross ratio uninorm. To investigate the equivalence between consistent IFPRs and IFPVs similar to the fuzzy case, Yang et al. [43] modified the constraints on Xu et al. [36]’s consistency, further defined a novel consistency using a class of representable uninorms [44] and characterized them using IFPVs.

In practical applications, since the preference relations provided by decision-makers are not always individually consistent or consensus in a group, they should be modified to reach a given requirement. Xia et al. [39] proposed algorithms for improving the consistency or consensus of FPRs by a control parameter and threshold. Xu and Herrera [38] developed a graphical method to visualize and rectify different inconsistencies for FPRs. Liu et al. [18] developed a group decision making method based on DEA cross-efficiency with IFPRs. Liao [16] and Wan [27] provided a consistency index of IFPRs for reaching acceptable consistency by modifying the whole IFPR or a single element of IFPRs with a control parameter, respectively. Yang et al. [41] investigated the multiplicative consistency threshold of IFPRs that varies with the order of IFPRs. Xu et al. [40] developed a mathematical programming method to simultaneously modify the consistency and consensus in group decision-making with IFPRs. Yang et al. [42,43,44] proposed a novel method to simultaneously visualize and rectify the consistencies or consensus of IFPRs by local IFPVs.

Based on the review conducted above, some genuine challenges are identified which are presented below:

• 1. The existing multiplicative consistencies [16, 29, 30, 32, 36, 44] for IFPRs only partially have properties similar to those in the fuzzy case which inevitably leads to some shortcomings (see Section 3.2 and Table 1). Thus, it is a challenge to provide consistency for IFPRs with all desirable properties similar to those in fuzzy cases.

• 2. In some group decision-making problems, the optimal alternatives are expected to be derived, but the existing methods always reach the goal by providing a ranking of all the alternatives. By preserving the original preference information as much as possible when rectifying the IFPRs, the original IFPRs could be excessively modified.

Motivated by these challenges, there are three major contributions of this research:

• 1. Novel GIFPRs that can not only express more preference information of decision-makers than IFPRs but also demonstrate the relationships between the diagonal entries and consistency, which is necessary to equivalently describe an IFPV, are proposed.

• 2. Parameterized consistencies for GIFPRs that not only possesses properties similar to those in the fuzzy case, but also help to derive a more suitable IFPV than a constant consistency for a given GIFPR are defined.

• 3. The $\delta$-acceptable consistency and consensus are proposed to directly derive the optimal $\delta$ alternatives from n given alternatives for an individual decision-maker or those in a group. According to the existing method to derive a ranking of n given alternatives, the proposed method needs fewer modifications to the original preference information, and hence can preserve the original preference information as much as possible.

To accomplish this, the remainder of this paper is structured as follows. In Section 2, the FPRs and their multiplicative consistency are briefly reviewed. In Section 3, a comparative analysis of the existing multiplicative consistencies of the IFPRs is performed. Section 4 provides the notions of GIFPRs and their consistency and discusses some of their desirable properties. In particular, it has been proven that a consistent GIFPR could be completely characterized by an IFPV. In Sections 5 and 6, methods to check and repair the consistency and consensus of GIFPRs are investigated. Specifically, local IFPVs are defined by $n-1$ independent preference values, based on which the novel $\delta$-acceptable consistency and consensus are proposed to preserve the original preference information as much as possible. Then, methods to check and repair the $\delta$-acceptable consistency and consensus of the GIFPR are provided, and numerical examples are given to illustrate the effectiveness of our method. In Section 7, a discussion and comparison with other similar methods are provided. Section 8 gives the conclusions.

2 Preliminaries

In this section, we review some basic concepts of FPRs and their multiplicative consistency.

For a decision-making problem, let $X=\left\{{x}_1,{x}_2,\cdots \kern0.3em ,{x}_n\right\}$ be a finite set of alternatives. For convenience, suppose that $\omega ={\left({\omega}_1,{\omega}_2,\cdots \kern0.3em ,{\omega}_n\right)}^T$ is the normalized crisp vector of priority weights, where ${\omega}_i$ reflects the degree of importance of alternative ${x}_i$; ${\omega}_i\ge 0,i=1,2,\cdots \kern0.3em ,n$ and $\sum \limits_{j=1}^n{\omega}_i=1$. In the decision-making process, a decision-maker generally needs to provide preference information for each pair of alternatives, and then constructs an FPR.

Definition 1

[26] A fuzzy preference relation (FPR) R on X is a matrix $R={\left({r}_{ij}\right)}_{n\times n}$ with $0\le {r}_{ij}\le 1,{r}_{ij}+{r}_{ji}=1,{r}_{ii}=0.5,i,j=1,2,\cdots \kern0.3em ,n$, where ${r}_{ij}$ represents a fuzzy preference degree of the alternative ${x}_i$ over the alternative ${x}_j$.

If ${r}_{ij}=\frac{1}{2}$, then there is no difference between alternative ${x}_i$ and alternative ${x}_j$. If ${r}_{ij}>\frac{1}{2}$, then alternative ${x}_i$ is preferred to alternative ${x}_j$. The larger ${r}_{ij}$ is, the greater the degree of preference of alternative ${x}_i$ over ${x}_j$. If ${r}_{ij}=1$, then alternative ${x}_i$ is absolutely preferred to alternative ${x}_j$.

The multiplicative consistency of FPRs was proposed by Tanino [26] as follows:

Definition 2

[26] An FPR $R={\left({r}_{ij}\right)}_{n\times n}$ is said to be multiplicatively consistent, if it satisfies the following multiplicative transitivity:

$$ {r}_{ij}{r}_{jk}{r}_{ki}={r}_{ik}{r}_{kj}{r}_{ji}, $$

(1)

for $i,j,k=1,2,\cdots \kern0.3em ,n$ or equivalently, ${r}_{ij}={r}_{ik}{\otimes}_C{r}_{jk}$ where ${\otimes}_C$ is the cross ratio uninorm with the additive generator ${h}_C(t)=\ln \left(\frac{t}{1-t}\right)$ such that $x{\otimes}_Cy={h}_C^{-1}\left({h}_C(x)+{h}_C(y)\right)$.

The following theorem indicates that there exists a one to one correspondence between the set of the multiplicatively consistent FPRs and that of the normalized priority vectors as follows:

Theorem 1

[46]Let $R={\left({r}_{ij}\right)}_{n\times n}$ be an FPR. Then R is multiplicatively consistent if and only if there exists a normalized priority vector $\omega ={\left({\omega}_1,{\omega}_2,\cdots \kern0.3em ,{\omega}_n\right)}^T$ such that

$$ {r}_{ij}=\frac{\omega_i}{\omega_i+{\omega}_j}, $$

(2)

where ${w}_i,{w}_j\ge 0,i,j=1,2,\cdots \kern0.3em ,n$, $\sum \limits_{j=1}^n{w}_i=1$. In addition, it holds that

$$ {\omega}_i={\left(\sum \limits_{k=1}^n\frac{r_{ji}}{r_{ij}}\right)}^{-1} $$

(3)

Remark 1

In Theorem 1,

• 1. the condition ${r}_{ii}=\frac{1}{2}$ for $i=1,2,\cdots \kern0.3em ,n$ can be derived from (2) by taking $i=j$, for $i,j=1,2,\cdots \kern0.3em ,n$.

• 2. (3) indicates that the main diagonals always add a constant 1 comparing an alternative with themselves to produce a final ranking of alternatives. In Refs. [4, 10], the main diagonals are denoted as “-”.

3 Intuitionistic fuzzy sets and intuitionistic fuzzy preference relations

3.1 Intuitionistic fuzzy sets

Due to hesitancy and uncertainty, it may be difficult for decision-makers to quantify their preference values using crisp numbers in decision making problems, but they can be represented by intuitionistic fuzzy judgments in a pairwise comparison matrix. In what follows, the concepts of IFSs and IFPRs are introduced.

Definition 3

[1] Let X be a given universe. An intuitionistic fuzzy set (IFS) A in X is defined as

$$ A=\left\{x,{\mu}_A(x),{\nu}_A(x)|x\in X\right\} $$

${\mu}_A(x),{\nu}_A(x)\in \left[0,1\right]$ indicate the amounts of the guaranteed membership and non-membership of x in A, respectively and satisfy ${\mu}_A(x)+{\nu}_A(x)\le 1$.

We recall for an intuitionistic fuzzy set the membership grade of x in A which is represented as a pair $\left({\mu}_A(x),{\nu}_A(x)\right)$ is called an intuitionistic fuzzy number (IFN) [34]. Here, the expression ${\pi}_A(x)=1-{\mu}_A(x)-{\nu}_A(x)$ is called the hesitancy of x. The IFN $\alpha =\left({\mu}_{\alpha },{\nu}_{\alpha}\right)$ has a physical interpretation, for example, if $\alpha =\left(0.3,0.2\right)$, then it can be interpreted as “the vote for resolution is 3 in favor, 2 against, and 5 abstentions.” citeGau1993. For an IFN $\alpha$, a score function s [3], which is defined as the difference of membership and non-membership function, can be denoted as $s\left(\alpha \right)={\mu}_{\alpha }-{\nu}_{\alpha }$, where $s\left(\alpha \right)\in \left[-1,1\right]$. The larger the score $s\left(\alpha \right)$, the greater the IFN $\alpha$. To make the comparison method more discriminatory, an accuracy function h [11], which is defined as follows $h\left(\alpha \right)={\mu}_{\alpha }+{\nu}_{\alpha }$, where $h\left(\alpha \right)\in \left[0,1\right]$. When the scores are the same, the larger the accuracy $h\left(\alpha \right)$, the greater the IFN $\alpha$. However, it is obvious that $h\left(\alpha \right)+{\pi}_{\alpha }=1$. Furthermore, the methods for comparing and ranking IFNs are also a focus in the research of IFNs, and lots of ways have been proposed for solving the problem [8, 34, 35, 45]. At present, there is still not a perfect way for solving it completely. Because this paper doesn’t focus on the methods of comparing and ranking IFNs, we only use the common method introduced by Xu and Yager [34] as follows:

Definition 4

[34] Let $\alpha, \beta$ be two IFNs. Then, we have

• 1. If $s\left(\beta \right)>s\left(\alpha \right)$, then $\beta$ is bigger than $\alpha$ , i.e., $\beta \succ \alpha$.

• 2. If $s\left(\alpha \right)=s\left(\beta \right)$,

  • 1. if $h\left(\beta \right)>h\left(\alpha \right)$, then $\beta$ is bigger than $\alpha$ , i.e., $\beta \succ \alpha$;

  • 2. if $h\left(\alpha \right)=h\left(\beta \right)$, i.e., $\alpha =\beta$.

3.2 IFPRs and the existing consistencies based on representable uninorms

Definition 5

[35] An intuitionistic fuzzy preference relation (IFPR) P on X is characterized by an intuitionistic fuzzy judgment matrix $P={\left({p}_{ij}\right)}_{n\times n}$ with ${p}_{ij}=\left({\mu}_{ij},{\nu}_{ij}\right)$, where ${p}_{ij}$ is an IFN [34], and ${\mu}_{ij}$ is the certainty degree to which alternative ${x}_i$ is preferred to ${x}_j$, and ${\nu}_{ij}$ is the certainty degree to which alternative ${x}_i$ is non-preferred to ${x}_j$, and $0\le {\mu}_{ij}+{\nu}_{ij}\le 1,{\mu}_{ij}={\nu}_{ji},{\nu}_{ij}={\mu}_{ji},{\mu}_{ii}={\nu}_{ii}=0.5,i,j=1,2,\cdots \kern0.3em ,n$.

Yang et al. [43] stated that an IFPR can equivalently be described by its membership degree matrix ${P}_{\mu }={\left({\mu}_{ij}\right)}_{n\times n}$ with ${\mu}_{ij}+{\mu}_{ji}\le 1$ and ${\mu}_{ii}=0.5$ for all $i,j=1,2,\cdots \kern0.3em ,n$. Thus, in the following parts, we always denote IFPR P as ${P}_{\mu }$. Furthermore, Definition 5 indicates that to provide an IFPR, only $\frac{n\left(n-1\right)}{2}$ IFNs as preference values should be given on its upper triangle. Then, Xu et al. [36] used the cross ratio uninorm to define multiplicatively consistent IFPRs as follows:

Definition 6

[36] An IFPR ${P}_{\mu }$ is said to be multiplicatively consistent, if it satisfies the following multiplicative transitivity:

$$ {h}_C\left({\mu}_{ij}\right)=\left\{\begin{array}{cc}0,& i=j;\\ {}{h}_C\left({\mu}_{ik}\right)+{h}_C\left({\mu}_{kj}\right),& i<k<j\kern1em or\kern1em i>k>j,\end{array}\right. $$

(4)

where ${h}_C$ is the additive generator of the cross ratio uninorm ${\otimes}_C$ and $i,j,k=1,2,\cdots \kern0.3em ,n$.

Wang [29] stated that Xu et al. [36]’s consistency is not robust to permutations of the original intuitionistic fuzzy judgments provided by the decision-maker. In other words, this consistency is highly dependent on alternative labels. Yang et al. [43] overcome this consistency issue by modifying the constraints for i, j and k as follows:

Definition 7

[43] An IFPR ${P}_{\mu }$ is said to be multiplicatively consistent, if it satisfies the following multiplicative transitivity:

$$ {h}_C\left({\mu}_{ij}\right)=\left\{\begin{array}{cc}0,& i=j;\\ {}{h}_C\left({\mu}_{ik}\right)+{h}_C\left({\mu}_{kj}\right),& i\ne j\ne k,\end{array}\right. $$

(5)

where ${h}_C$ is the additive generator of the cross ratio uninorm ${\otimes}_C$ and $i,j,k=1,2,\cdots \kern0.3em ,n$.

They also characterized the nondiagonal entries of consistent IFPRs using IFPVs as follows:

Theorem 2

[43] Let ${P}_{\mu }$ be an IFPR. Then ${P}_{\mu }$ is multiplicatively consistent if and only if there exists an IFPV $\omega =\left({\omega}_1,{\omega}_2,\cdots \kern0.3em ,{\omega}_n\right)$ with the IFN ${\omega}_t=\left({\mu}_t,{\nu}_t\right)$ for $t=1,2,\cdots \kern0.3em ,n$ such that

$$ {h}_C\left({\mu}_{ij}\right)=\left\{\begin{array}{cc}0,& i=j;\\ {}{h}_C\left({\mu}_i\right)+{h}_C\left({\nu}_j\right),& i\ne j,\end{array}\right. $$

(6)

where ${h}_C\left({\mu}_t\right)={h}_C^{-1}\left(\sum \limits_{k=1}^n{\lambda}_k{h}_C\left({\mu}_{tk}\right)\right)$ and ${h}_C\left({\nu}_t\right)={h}_C^{-1}\left(\sum \limits_{k=1}^n{\lambda}_k{h}_C\left({\mu}_{kt}\right)\right)$, for $t=1,2,\cdots \kern0.3em ,n$, ${\lambda}_k\in \left[0,1\right]$ and $\sum \limits_{k=1}^n{\lambda}_k=1$.

Definition 8

[30] Let ${P}_{\mu }$ be an IFPR. Then ${P}_{\mu }$ is said to be of consistency, if there exists ${\theta}_k\in \left[0,1\right]$ such that

$$ {h}_C\left({\mu}_{ij}\right)=\left\{\begin{array}{cc}0,& otherwise;\\ {}{h}_C\left({\mu}_{ik}\right)+{h}_C\left({\mu}_{kj}\right)+{h}_C\left({\theta}_k\right),& i\ne j\ne k,\end{array}\right. $$

(7)

Theorem 3

[30] Let $\omega =\left({\omega}_1,{\omega}_2,\cdots \kern0.3em ,{\omega}_n\right)$ be an IFPV with the IFN ${\omega}_t=\left({\mu}_t,{\nu}_t\right)$ for $t=1,2,\cdots \kern0.3em ,n$. Then the IFPR determined by (6) is consistent.

Theorems 2 and 3 show that Yang et al. [43]’s consistency is always Wang [30]’s consistency. Furthermore, Wang [30]’s consistency could not be characterized by the provided IFPVs. In order to further demonstrate the relationship between consistent IFPRs and IFPVs, Yang et al. [44] proposed the following consistency definition:

Definition 9

[44] Let ${P}_{\mu }$ be an IFPR. Then ${P}_{\mu }$ is said to be of representable uninorm-based consistency if there exists a $\lambda \in \left(-1,+\infty \right)$ such that

$$ {h}_{\lambda}\left({\mu}_{ij}\right)={h}_{\lambda}\left({\mu}_{ik}\right)+{h}_{\lambda}\left({\mu}_{kj}\right), $$

(8)

for all $i,k,j=1,2,\cdots \kern0.3em ,n$, where ${h}_{\lambda }(t)=-\ln \left(-{\log}_{2+\lambda}\left(\frac{t}{1+\lambda -\lambda t}\right)\right),\lambda \in \left(-1,+\infty \right)$.

Taking $i=j$, we have ${\mu}_{ii}={h}_{\lambda}^{-1}(0)=0.5$ and ${\mu}_{ik}={h}_{\lambda}^{-1}\left(-{h}_{\lambda}\left({\mu}_{ki}\right)\right)$.

Theorem 4

[44] Let ${P}_{\mu }$ be an IFPR. Then ${P}_{\mu }$ is representable uninorm-based consistent if and only if there exists an IFPV $\omega =\left({\omega}_1,{\omega}_2,\cdots \kern0.3em ,{\omega}_n\right)$ such that

$$ {h}_{\lambda}\left({\mu}_{ij}\right)={h}_{\lambda}\left({\mu}_i\right)+{h}_{\lambda}\left({\nu}_j\right), $$

(9)

for some $\lambda \in \left(-1,+\infty \right),i,j=1,2,\cdots \kern0.3em ,n$, where ${\mu}_t={h}_{\lambda}^{-1}\left(\sum \limits_{k=1}^n{\lambda}_k{h}_{\lambda}\left({\mu}_{tk}\right)\right),{\nu}_t={h}_{\lambda}^{-1}\left(\sum \limits_{k=1}^n{\lambda}_k{h}_{\lambda}\left({\nu}_{tk}\right)\right)$ with ${\lambda}_k\in \left[0,1\right]$ and $\sum \limits_{k=1}^n{\lambda}_k=1$.

Although Yang et al. [44]’s consistency possesses more desirable properties similar to Tanino [26]’s consistency than the other consistencies [30, 36, 43](see Table 1), we find that if we define function $n(t)={h}_{\lambda}^{-1}\left(-{h}_{\lambda }(t)\right)$, then the degree of hesitancy of the IFNs in a consistent IFPR ${P}_{\mu }$ can be given as follows: ${\pi}_{ik}=1-n\left({\mu}_{ki}\right)-{\mu}_{ki}$. Figure 1 demonstrates the variation of ${\pi}_{ik}$ with parameter $\lambda$ from 0 to 50. That is, the degrees of hesitancy of any IFNs as preference values in a consistent IFPR ${P}_{\mu }$ are approximately no more than 0.12 ($\lambda \approx 4$ for all ${\mu}_{ki}\in \left[0,1\right]$) which limits the usage of the representable uninorm-based consistency in practice.

Fig. 1

The hesitancy degree varies $\pi$ with parameter $\lambda$

Table 1 Characteristics of the existing consistencies of preference relations

4 Generalized intuitionistic fuzzy preference relations and their consistencies

In this section, in order to overcome the shortcoming of the existing consistency [30, 36, 41, 44] and guarantee that consistent IFPRs possess many more properties similar to consistent FPRs, we introduce GIFPRs and their consistencies as follows:

Definition 10

A generalized intuitionistic fuzzy preference relation (GIFPR) P on X is characterized by an intuitionistic fuzzy judgment matrix $P={\left({p}_{ij}\right)}_{n\times n}$ with ${p}_{ij}=\left({\mu}_{ij},{\nu}_{ij}\right)$ such that $\left({\mu}_{ij},{\nu}_{ij}\right)=\left({\nu}_{ji},{\mu}_{ji}\right),i,j=1,2,\cdots \kern0.3em ,n$, where ${p}_{ij}$ is an IFN, and ${\mu}_{ij}$ is the certainty degree to which alternative ${x}_i$ is preferred to ${x}_j$, and ${\nu}_{ij}$ is the certainty degree to which alternative ${x}_i$ is non-preferred to ${x}_j$.

Note the following:

• 1. When all IFNs in GIFPR P reduced to a fuzzy case, the GIFPR reduces to an FPR.

• 2. Regarding the main diagonals of a preference matrix, first, they are not needed in practice as they do not add anything useful when comparing an alternative with itself to produce a final ranking of alternatives. Second, compared to the IFPRs in Ref. [35], GIFPRs are more logical, because ${p}_{ij}^c={p}_{ji}$ (${}^c$ is the natural negation in intuitionistic fuzzy case), which is similar to that in fuzzy case, i.e., ${r}_{ij}=1-{r}_{ji}$ for all $i,j=1,2,\cdots \kern0.3em ,n$.

• 3. Similar to that in Ref. [43], the GIFPRs can be equivalently described by their degree of membership matrix ${P}_{\mu }={\left({\mu}_{ij}\right)}_{n\times n}$ with ${\mu}_{ij}+{\mu}_{ji}\le 1$ for all $i,j=1,2,\cdots \kern0.3em ,n$. Thus, in the following parts, we always denote GIFPR P as ${P}_{\mu }$.

Using the additive generators of a class of logical operations similar to the cross ratio uninorm ${\otimes}_C$, we propose a novel consistency for the GIFPR as follows:

Definition 11

Let ${P}_{\mu }$ be a GIFPR. If there exists a $\lambda \in \left(0,1\right]$ such that

$$ {h}_{\lambda}\left({\mu}_{ij}\right)={h}_{\lambda}\left({\mu}_{ik}\right)+{h}_{\lambda}\left({\mu}_{kj}\right), $$

(10)

for $i,j,k=1,2,\cdots \kern0.3em ,n$, where ${h}_{\lambda }(t)=\ln \left(\frac{t^{\lambda }}{1-{t}^{\lambda }}\right)$, then ${P}_{\mu }$ is said to be consistent with respect to ${h}_{\lambda }$.

Different from the case of consistent IFPRs in Ref. [35], for a consistent GIFPR with respect to ${h}_{\lambda }$, the following results indicate that not only the nondiagonal entries but also the diagonal entries have close ties with the consistency. In spite of this, comparing an alternative with itself still does not provide anything useful for producing a final ranking of alternatives.

Theorem 5

Let ${P}_{\mu }$ be a consistent GIFPR with respect to ${h}_{\lambda }$. Then it holds that

• 1. ${h}_{\lambda}\left({\mu}_{ii}\right)=0$ for $i=1,2,\cdots \kern0.3em ,n$;

• 2. ${h}_{\lambda}\left({\mu}_{ij}\right)+{h}_{\lambda}\left({\mu}_{ji}\right)=0$ for $i,j=1,2,\cdots \kern0.3em ,n$;

Proof

It follows immediately from (10) by taking $i=j$ and $i=k$, respectively.

Although the main diagonals of a consistent GIFPR are not 0.5, in general, they are always the same and can be derived from ${h}_{\lambda}^{-1}(0)$. Thus, in order to simplify the computation, we always denote these main diagonals as “-, similar to those in Refs. [4, 10], in the following part.

Example 1

For a decision-making problem, there are four alternatives ${x}_i\left(i=1,2,3,4\right)$. The decision-maker provides his/her preferences over these four alternatives, and gives a GIFPR as follows:

$$ {P}_{\mu }=\left(\begin{array}{cccc}-& 0.25& 0.16& 0.16\\ {}0.25& -& 0.16& 0.16\\ {}0.36& 0.36& -& 0.25\\ {}0.36& 0.36& 0.25& -\end{array}\right). $$

Taking ${h}_{0.5}(t)=\ln \left(\frac{t^{0.5}}{1-{t}^{0.5}}\right)$, then we have

$$ {\displaystyle \begin{array}{ccc}\hfill {h}_{0.5}\left({\mu}_{ii}\right)=& 0,i=1,2,\cdots \kern0.3em ,n;\hfill & \hfill \\ {}\hfill {h}_{0.5}\left({\mu}_{ij}\right)+{h}_{0.5}\left({\mu}_{ji}\right)=& 0,i\ne j,i,j=1,2,\cdots \kern0.3em ,n;\hfill \\ {}\hfill {h}_{0.5}\left({\mu}_{ij}\right)={h}_{0.5}\left({\mu}_{ik}\right)+{h}_{0.5}\left({\mu}_{kj}\right)=& \ln \left(\frac{2}{3}\right),i\ne k\ne j,i,j,k=1,2,\cdots \kern0.3em ,n.\hfill \end{array}} $$

Thus, ${P}_{\mu }$ is a consistent GIFPR with respect to ${h}_{0.5}$. Furthermore, ${P}_{\mu }$ is obviously not an IFPR, because ${\mu}_{ii}=0.25\ne 0.5$ for all $i=1,2,\cdots n$.

We characterize the consistent GIFPR using an IFPV as follows:

Theorem 6

Let ${P}_{\mu }$ be a GIFPR. Then, for a given $\lambda \in \left(0,1\right]$, ${P}_{\mu }$ is consistent with respect to ${h}_{\lambda }$ if and only if there exists an IFPV $\omega ={\left({\omega}_1,{\omega}_2,\cdots \kern0.3em ,{\omega}_n\right)}^T$ such that

$$ {h}_{\lambda}\left({\mu}_{ij}\right)={h}_{\lambda}\left({\mu}_i\right)+{h}_{\lambda}\left({\nu}_j\right), $$

(11)

for all $i,j=1,2,\cdots \kern0.3em ,n$, where

$$ {\mu}_t={h}_{\lambda}^{-1}\left(\sum \limits_{k=1}^n{\lambda}_k{h}_{\lambda}\left({\mu}_{tk}\right)\right),{\nu}_t={h}_{\lambda}^{-1}\left(\sum \limits_{k=1}^n{\lambda}_k{h}_{\lambda}\left({\mu}_{kt}\right)\right), $$

(12)

$\Lambda =\left({\lambda}_1,{\lambda}_2,\cdots \kern0.3em ,{\lambda}_n\right)$ with ${\lambda}_k\in \left[0,1\right]$ and $\sum \limits_{k=1}^n{\lambda}_k=1$.

Proof

Since ${P}_{\mu }$ is consistent with respect to ${h}_{\lambda }$, we have ${h}_{\lambda}\left({\mu}_{ij}\right)={h}_{\lambda}\left({\mu}_{ik}\right)+{h}_{\lambda}\left({\mu}_{kj}\right)$, and hence $h\left({\mu}_{ij}\right)=\sum \limits_{k=1}^n{\lambda}_kh\left({\mu}_{ik}\right)+\sum \limits_{k=1}^n{\lambda}_kh\left({\mu}_{kj}\right)$. Thus, $h\left({\mu}_{ij}\right)=h\left({\mu}_i\right)+h\left({\nu}_j\right)$ where ${\mu}_t={h}^{-1}\left(\sum \limits_{k=1}^n{\lambda}_kh\left({\mu}_{tk}\right)\right),{\nu}_t={h}^{-1}\left(\sum \limits_{k=1}^n{\lambda}_kh\left({\mu}_{kt}\right)\right)$ with ${\lambda}_k\in \left[0,1\right]$ and $\sum \limits_{k=1}^n{\lambda}_k=1$.

Conversely, since ${h}_{\lambda}\left({\mu}_{ii}\right)=0$ and ${h}_{\lambda}\left({\mu}_{ii}\right)={h}_{\lambda}\left({\mu}_i\right)+{h}_{\lambda}\left({\nu}_i\right)$, we get ${h}_{\lambda}\left({\mu}_i\right)+{h}_{\lambda}\left({\nu}_i\right)=0$. Furthermore, we have ${h}_{\lambda}\left({\mu}_{ij}\right)={h}_{\lambda}\left({\mu}_i\right)+{h}_{\lambda}\left({\nu}_j\right),{h}_{\lambda}\left({\mu}_{ik}\right)={h}_{\lambda}\left({\mu}_i\right)+{h}_{\lambda}\left({\nu}_k\right)$ and ${h}_{\lambda}\left({\mu}_{kj}\right)={h}_{\lambda}\left({\mu}_k\right)+{h}_{\lambda}\left({\nu}_j\right)$, and hence ${h}_{\lambda}\left({\mu}_{ik}\right)+{h}_{\lambda}\left({\mu}_{kj}\right)={h}_{\lambda}\left({\mu}_i\right)+{h}_{\lambda}\left({\nu}_k\right)+{h}_{\lambda}\left({\mu}_k\right)+{h}_{\lambda}\left({\nu}_j\right)={h}_{\lambda}\left({\mu}_i\right)+{h}_{\lambda}\left({\nu}_j\right)={h}_{\lambda}\left({\mu}_{ij}\right)$. Thus, ${P}_{\mu }$ is consistent with respect to ${h}_{\lambda }$.

Next, we investigate the properties of the IFPVs derived from the consistent GIFPRs.

Theorem 7

Let ${P}_{\mu }$ be a consistent GIFPR with respect to ${h}_{\lambda }$. Then for the IFPV $\omega$ in Theorem 6, it holds that ${h}_{\lambda}\left({\mu}_i\right)+{h}_{\lambda}\left({\nu}_i\right)=0$ for $i=1,2,\cdots \kern0.3em ,n$.

Proof

It follows immediately from Theorems 5 and 6.

For convenience, for a consistent GIFPR ${P}_{\mu }$ with respect to ${h}_{\lambda }$, we set ${h}_{\lambda }(t)=\overset{\sim }{t}$, that is,

$$ \overset{\sim }{\omega }=\kern0.5em {\left({\overset{\sim }{\mu}}_1,{\overset{\sim }{\mu}}_2,\cdots \kern0.3em ,{\overset{\sim }{\mu}}_n,{\overset{\sim }{\nu}}_1,{\overset{\sim }{\nu}}_2,\cdots \kern0.3em ,{\overset{\sim }{\nu}}_n\right)}^T, $$

(13)

$$ B=\kern0.5em \left(\begin{array}{cccc}0& {\overset{\sim }{\mu}}_{12}& \cdots & {\overset{\sim }{\mu}}_{1,n}\\ {}-{\overset{\sim }{\mu}}_{12}& 0& \cdots & {\overset{\sim }{\mu}}_{2,n}\\ {}\vdots & \vdots & \vdots & \vdots \\ {}-{\overset{\sim }{\mu}}_{1,n}& -{\overset{\sim }{\mu}}_{2,n}& \cdots & 0\\ {}\end{array}\right), $$

(14)

$$ \overset{\sim }{b}=\kern0.5em {\left(0,{\overset{\sim }{\mu}}_{12},\cdots \kern0.3em ,{\overset{\sim }{\mu}}_{1n},{\overset{\sim }{\mu}}_{21},0,{\overset{\sim }{\mu}}_{23}\cdots \kern0.3em ,{\overset{\sim }{\mu}}_{2n},\cdots \kern0.3em ,{\overset{\sim }{\mu}}_{n,n-1},0\right)}^T $$

(15)

and T denotes transposition. Then (11) can further be rewritten as follows:

$$ A\overset{\sim }{\omega }=\overset{\sim }{b}, $$

(16)

where

(17)

and (12) can be rewritten as

$$ \overset{\sim }{\omega }=\left(\begin{array}{c}{B\Lambda}^T\\ {}{B}^T{\Lambda}^T\end{array}\right) $$

(18)

The following results are obvious but crucial.

Theorem 8

For the matrix A defined by (16), it holds that $\mathit{\operatorname{rank}}(A)=2n-1$.

Proof

It is trivial, so we omit it.

Theorem 9

Let ${P}_{\mu }$ be a GIFPR. Then, for a given $\lambda \in \left(0,1\right]$, ${P}_{\mu }$ is consistent with respective to ${h}_{\lambda }$ if and only if (16) is solvable with one free unknown.

Proof

It is trivial, so we omit it.

Example 2

We continue Example 1. Taking $\Lambda ={\left(\frac{1}{4},\frac{1}{4},\frac{1}{4},\frac{1}{4}\right)}^T$ and using (18), then $\overset{\sim }{\omega }=\left(\frac{1}{2}\ln \left(\frac{2}{3}\right),\frac{1}{2}\ln \left(\frac{2}{3}\right),-\frac{1}{2}\ln \left(\frac{2}{3}\right),-\frac{1}{2}\ln \left(\frac{2}{3}\right),-\frac{1}{2}\ln \left(\frac{2}{3}\right),-\frac{1}{2}\ln \left(\frac{2}{3}\right),\frac{1}{2}\ln \left(\frac{2}{3}\right),\frac{1}{2}\ln \left(\frac{2}{3}\right)\right)$ and $\omega \approx \left(\left(0.202,0.303\right),\left(0.202,0.303\right),\left(0.303,0.202\right),\left(0.303,0.202\right)\right)$. Thus $s\left({\omega}_1\right)=s\left({\omega}_2\right)=-0.101$ and $s\left({\omega}_3\right)=s\left({\omega}_4\right)=0.101$. By Definition 4, we get ${x}_3={x}_4\succ {x}_1={x}_2$.

Remark 2

• 1. Although IFPV $\omega$ varies with the weight vector $\Lambda$, the ranking is constant from Theorem 8.

• 2. The contribution of ${\overset{\sim }{\mu}}_{ii}$ to the transformed IFPV $\left({\overset{\sim }{\mu}}_i,{\overset{\sim }{\nu}}_i\right)$ for $i=1,2,\cdots \kern0.3em ,n$ is always equal to zero according to (18). That is, comparing an alternative with itself does not add anything.

5 Check and reach $\delta$-acceptable consistency for arbitrary GIFPRs

In some practical decision-making problems, GIFPRs are usually not consistent. That is, the equations in (10) do not hold. We provide the following model to determine parameter $\lambda$ and check the consistency for an arbitrary GIFPR ${P}_{\mu }$:

$$ d=\min \sum \limits_{\begin{array}{c}i,k,j=1\\ {}i\ne k\ne j\end{array}}^n{\left({\overset{\sim }{\mu}}_{ik}+{\overset{\sim }{\mu}}_{kj}-{\overset{\sim }{\mu}}_{ij}\right)}^2 $$

(19)

Obviously, $d=0$, which implies that GIFPR ${P}_{\mu }$ is consistent; otherwise, it is not consistent. We introduce the following acceptable consistency.

Definition 12

Let ${P}_{\mu }$ be a GIFPR and ${h}_{\lambda }$ be determined using (19).

• 1. For $n-1$ non-diagonal entries ${\mu}_{i_1,{j}_1},\cdots \kern0.3em ,{\mu}_{i_{n-1},{j}_{n-1}}$ in a GIFPR ${P}_{\mu }$, if the general solution of the following group of equations

  $$ \left\{\begin{array}{c}{\overset{\sim }{\mu}}_1+{\overset{\sim }{\nu}}_1={\overset{\sim }{\mu}}_{11}=0,\\ {}\vdots \\ {}{\overset{\sim }{\mu}}_n+{\overset{\sim }{\nu}}_n={\overset{\sim }{\mu}}_{nn}=0,\\ {}{\overset{\sim }{\mu}}_{i_1}+{\overset{\sim }{\nu}}_{j_1}={\overset{\sim }{\mu}}_{i_1,{j}_1},\\ {}\vdots \\ {}{\overset{\sim }{\mu}}_{i_{n-1}}+{\overset{\sim }{\nu}}_{j_{n-1}}={\overset{\sim }{\mu}}_{i_{n-1},{j}_{n-1}},\end{array}\right. $$

  (20)

  is of only one free unknown, then ${\mu}_{i_1,{j}_1},\cdots \kern0.3em ,{\mu}_{i_{n-1},{j}_{n-1}}$ is said to be independent;

• 2. The IFPV $\left(\left({h}_{\lambda}^{-1}\left({\overset{\sim }{\mu}}_1\right),{h}_{\lambda}^{-1}\left({\overset{\sim }{\nu}}_1\right)\right),\cdots \kern0.3em ,\left({h}_{\lambda}^{-1}\left({\overset{\sim }{\mu}}_n\right),{h}_{\lambda}^{-1}\left({\overset{\sim }{\nu}}_n\right)\right)\right)$ determined using $n-1$ independent preference values of ${P}_{\mu }$ with (20) is said to be local.

Theorem 10

Let ${P}_{\mu }$ be a GIFPR and ${h}_{\lambda }$ be determined using (19). Then ${P}_{\mu }$ is consistent with respect to ${h}_{\lambda }$ if and only all the local IFPVs are equal up to addition of a real constant.

Proof

It is trivial, so we omit it.

Obviously, all the local IFPVs are the same and naturally determine a single ranking for a consistent GIFPR. However, when a GIFPR is inconsistent, various rankings could be derived. In spite of this, the following case is acceptable.

Definition 13

Let ${P}_{\mu }$ be a GIFPR and $\delta$ be a positive integer with $\delta \le n$. If the rankings of the first $\delta$ alternatives are the same in the rankings determined by all the local IFPVs, then ${P}_{\mu }$ is said to be $\delta$-acceptable consistent.

Example 3

For a decision making problem, there are four alternatives ${x}_i\left(i=1,2,3,4\right)$. The decision maker provides his/her preferences over these four alternatives, and gives a GIFPR as follows:

$$ {P}_{\mu }=\left(\begin{array}{cccc}-& 0.6& 0.8& 0.9\\ {}0.3& -& 0.6& 0.8\\ {}0.1& 0.2& -& 0.6\\ {}0.1& 0.1& 0.2& -\end{array}\right). $$

Solving (19) by mathematical software Sagemath, we have $\lambda =0.827$. Furthermore, for ${\mu}_{12}=0.6,{\mu}_{13}=0.8$ and ${\mu}_{14}=0.9$ in ${P}_{\mu }$, using (20), we construct the following group of equations:

$$ \left\{\begin{array}{c}{\overset{\sim }{\mu}}_1+{\overset{\sim }{\nu}}_1={\overset{\sim }{\mu}}_{11}=0,\\ {}{\overset{\sim }{\mu}}_2+{\overset{\sim }{\nu}}_2={\overset{\sim }{\mu}}_{22}=0,\\ {}{\overset{\sim }{\mu}}_3+{\overset{\sim }{\nu}}_3={\overset{\sim }{\mu}}_{33}=0,\\ {}{\overset{\sim }{\mu}}_4+{\overset{\sim }{\nu}}_4={\overset{\sim }{\mu}}_{44}=0,\\ {}{\overset{\sim }{\mu}}_1+{\overset{\sim }{\nu}}_2={\overset{\sim }{\mu}}_{12}=0.643,\\ {}{\overset{\sim }{\mu}}_1+{\overset{\sim }{\nu}}_3={\overset{\sim }{\mu}}_{13}=1.596,\\ {}{\overset{\sim }{\mu}}_1+{\overset{\sim }{\nu}}_4={\overset{\sim }{\mu}}_{14}=\mathrm{2.396.}\end{array}\right. $$

It is trivial to verify that the rank of the coefficient matrix is $2n-1$, that is, ${\mu}_{12},{\mu}_{13}$ and ${\mu}_{14}$ are independent in ${P}_{\mu }$. Solving the above equations, we have a local IFPV ${\omega}_{local}=\left(\left(0.9,0.05\right),\left(0.824,0.099\right),\left(0.639,0.243\right),\left(0.433,0.433\right)\right)$. Using Definition 4, the ranking is ${x}_1\succ {x}_2\succ {x}_3\succ {x}_4$. Similarly, ${\mu}_{32}=0.2,{\mu}_{41}=0.1$ and ${\mu}_{43}=0.2$ are independent in ${P}_{\mu }$ and the corresponding local IFPV ${\omega}_{local}=\left(\left(0.823,0.1\right),\left(0.864,0.073\right),\left(0.69,0.2\right),\left(0.433,0.433\right)\right)$ with the ranking ${x}_2\succ {x}_1\succ {x}_3\succ {x}_4$. Thus, the GIFPR ${P}_{\mu }$ is not of 1-acceptable consistency.

An unacceptably consistent GIFPR is usually modified to satisfy the requirements of consistency in order to avoid an unreasonable result. We construct a model to derive the optimal IFPV for GIFPR ${P}_{\mu }$ as follows:

$$ {\displaystyle \begin{array}{ccc}\hfill & \min \sum \limits_{\begin{array}{c}i,j=1\\ {}i\ne j\end{array}}^n{\left({\overset{\sim }{\mu}}_i+{\overset{\sim }{\nu}}_j-{\overset{\sim }{\mu}}_{ij}\right)}^2\hfill & \hfill \\ {}\hfill & s.t.\kern1em {\overset{\sim }{\mu}}_i+{\overset{\sim }{\nu}}_i=0,i=1,2,\cdots \kern0.3em ,n.\hfill \end{array}} $$

(21)

Then, we provide a consistent GIFPR ${C}_{\mu }={\left({h}_{\lambda}^{-1}\left({h}_{\lambda}\left({\mu}_i\right)+{h}_{\lambda}\left({\nu}_j\right)\right)\right)}_{n\times n}$ using (11). Furthermore, in order to simplify the calculation process, we provide the approximate solution of (21) by solving the following model:

$$ \min \sum \limits_{\begin{array}{c}i,j=1\\ {}i\ne j\end{array}}^n{\left({\overset{\sim }{\mu}}_i+{\overset{\sim }{\nu}}_j-{\hat{\mu}}_{ij}\right)}^2 $$

(22)

where ${\hat{\mu}}_{ij}=\left\{\begin{array}{cc}0,& i=j,\\ {}{\overset{\sim }{\mu}}_{ij},& i\ne j.\end{array}\right.$ Thus, the approximate solution of (21) can be provided by the normal equation of (22) as follows:

$$ {A}^TA\overset{\sim }{\omega }={A}^T\overset{\sim }{b}. $$

(23)

Then, we establish a method to achieve $\delta$-acceptable consistency by the following steps:

Step 0:

Let ${P}_{\mu}^{(t)}={P}_{\mu }$ and the iteration $t=0$.

Step 1:

Determine parameter ${\lambda}^{(t)}$ for ${h}_{\lambda^{(t)}}$ by (19).

Step 2:

Solve all the local IFPVs $\left\{{\omega}_l^{(t)}\right\}$ of the GIFPR ${P}_{\mu }$ using (20) and record their positions in L. If ${P}_{\mu}^{(t)}$ is $\delta$-acceptable consistent, then go to Step 6; otherwise, go Step 3.

Step 3:

Compute the optimal IFPV ${\omega}^{(t)}$ using (23) and construct a GIFPR ${AC}_{\mu}^{(t)}={\left({h}_{\lambda}^{-1}\left({h}_{\lambda}\left({\mu}_i^{(t)}\right)+{h}_{\lambda}\left({\nu}_j^{(t)}\right)\right)\right)}_{n\times n}$ using (11).

Step 4:

Determine the positions where the preference values in ${P_{\mu}}^{(t)}$ should be modified using ${l}_0=\arg \underset{l\in L}{\max}\left\{ dis\left({\omega}^{(t)},{\omega}_l^{(t)}\right)\right\}$ (dis is the Chebyshev distance between two vectors).

Step 5:

According to ${l}_0$, replace the preference values in ${P_{\mu}}^{(t)}$ with those in GIFPR ${AC}_{\mu}^{(t)}$. The modified ${P_{\mu}}^{(t)}$ is denoted as ${P}_{\mu}^{\left(t+1\right)}$, and return to Step 1.

Step 6:

Output ${P}_{\mu}^{(t)}$.

Note the following:

• 1. The larger t is, the better the $\delta$-acceptable consistecy.

• 2. The above algorithm converges and can be used to derive a consistent GIFPR by adding iterations.

• 3. The process of checking and reaching $\delta$-acceptable consistency can be executed and visualized by the local IFPVs; hence, presetting a threshold is more convenient and intuitive than the existing methods.

• 4. The consistency of GIFPR ${AC}_{\mu}^{(t)}$ becomes improves as iteration increases.

• 5. The $\delta$-acceptable consistency is weaker than the n-acceptable consistency; hence, when a GIFPR has to be modified, $\delta$-acceptable consistency could be reached using less modification. Thus, the above algorithm with $\delta$-acceptable consistency could preserve the original preference values as much as possible.

To illustrate the proposed method, we provide the following numerical examples:

Example 4

We continue the GIFPR in Example 3 and have the following steps:

Step 1:

Using (19), the parameter ${\lambda}^{(0)}=0.827$ for ${h}_{\lambda^{(0)}}$.

Step 2:

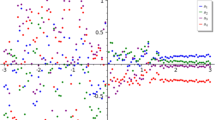
Using (20), all the local IFPVs $\left\{{\omega}_l^{(0)}|l=1,2,\cdots \kern0.3em ,128\right\}$ and the corresponding rankings are provided in Table 2 and Fig. 2 with $t=0$. ${P}_{\mu}^{(0)}$ is not 1-acceptable consistent, because all the IFPVs determine a ranking ${x}_1\succ {x}_2\succ {x}_3\succ {x}_4$ except the 126th IFPV, which provides a ranking ${x}_2\succ {x}_1\succ {x}_3\succ {x}_4$.

Step 3:

Using (23) and (11), we have the optimal IFPV ${\omega}^{(0)}=\left(0.894,0.801,0.601,0.446,0.064,0.106,0.232,0.433\right)$ and the GIFPR constructed using ${\omega}^{(0)}$ as follows:

$$ {AC}_{\mu}^{(0)}=\left(\begin{array}{cccc}-& 0.601& 0.78& 0.894\\ {}0.294& -& 0.626& 0.801\\ {}0.126& 0.197& -& 0.601\\ {}0.068& 0.112& 0.242& -\end{array}\right). $$

Step 4:

By computing, we have $104=\arg \underset{l}{\max}\left\{ dis\left({\omega}^{(t)},{\omega}_l^{(t)}\right)\right\}$, that is, ${\mu}_{23},{\mu}_{31}$ and ${\mu}_{41}$ should be modified.

Step 5:

${\mu}_{23},{\mu}_{31}$ and ${\mu}_{41}$ in ${P_{\mu}}^{(0)}$ are replaced with the corresponding entries in ${AC}_{\mu}^{(0)}$. Then, ${P_{\mu}}^{(0)}$ is modified as

$$ {P}_{\mu}^{(1)}=\left(\begin{array}{cccc}-& 0.6& 0.8& 0.9\\ {}0.3& -& 0.626& 0.8\\ {}0.126& 0.2& -& 0.6\\ {}0.068& 0.1& 0.2& -\end{array}\right). $$

Step 6:

Using (19), the parameter ${\lambda}^{(1)}=0.814$ for ${h}_{\lambda^{(1)}}$ is acquired.

Step 7:

Using (20), all the local IFPVs $\left\{{\omega}_l^{(1)}|l=1,2,\cdots \kern0.3em ,128\right\}$ and the corresponding rankings with $t=1$ are indicated in Fig. 2. It is obvious that ${P}_{\mu}^{(1)}$ is 4-acceptable consistent with the ranking ${x}_1\succ {x}_2\succ {x}_3\succ {x}_4$.

Table 2 Local IFPVs and Rankings in Example 4

Fig. 2

The rankings vary with iterations in Example 4

Example 5

For a decision-making problem, there are four alternatives ${x}_i\left(i=1,2,3,4\right)$. The decision-maker provides his/her preferences over these four alternatives, and gives a GIFPR as follows:

$$ {P}_{\mu }=\left(\begin{array}{cccc}-& 0.6& 0.7& 0.7\\ {}0.3& -& 0.6& 0.6\\ {}0.2& 0.3& -& 0.6\\ {}0.1& 0.2& 0.3& -\end{array}\right). $$

We investigate the acceptable consistency using the following steps:

Step 1:

Using (19), the parameter ${\lambda}^{(0)}=0.79$ for ${h}_{\lambda^{(0)}}$ is acquired.

Step 2:

Using (20), all the local IFPVs $\left\{{\omega}_l^{(0)}|l=1,2,\cdots \kern0.3em ,128\right\}$ and the corresponding rankings with $t=0$ are provided in Fig. 3, which indicates that ${P}_{\mu}^{(0)}$ is not of 1-acceptable consistent.

Step 3:

Using (23) and (11), we have the optimal IFPV ${\omega}^{(0)}=\left(0.749,0.639,0.534,0.38,0.13,0.226,0.341,0.416\right)$ and the GIFPR constructed using ${\omega}^{(0)}$ as follows:

$$ {AC}_{\mu}^{(0)}=\left(\begin{array}{cccc}-& 0.562& 0.688& 0.749\\ {}0.283& -& 0.566& 0.639\\ {}0.199& 0.324& -& 0.534\\ {}0.112& 0.199& 0.308& -\end{array}\right). $$

Step 4:

By computing, we have $12=\arg \underset{l}{\max}\left\{ dis\left({\omega}^{(t)},{\omega}_l^{(t)}\right)\right\}$, that is, ${\mu}_{12},{\mu}_{23}$ and ${\mu}_{34}$ should be modified.

Step 5:

${\mu}_{12},{\mu}_{23}$ and ${\mu}_{34}$ in ${P_{\mu}}^{(0)}$ are replaced with the corresponding entries in ${AC}_{\mu}^{(0)}$. Then, ${P_{\mu}}^{(0)}$ is modified as

$$ {P}_{\mu}^{(1)}=\left(\begin{array}{cccc}-& 0.562& 0.7& 0.7\\ {}0.3& -& 0.566& 0.6\\ {}0.2& 0.3& -& 0.534\\ {}0.1& 0.2& 0.3& -\end{array}\right). $$

Step 6:

Using (19), the parameter ${\lambda}^{(1)}=0.755$ for ${h}_{\lambda^{(1)}}$ is acquired.

Step 7:

Using (20), all the local IFPVs $\left\{{\omega}_l^{(1)}|l=1,2,\cdots \kern0.3em ,128\right\}$ and the corresponding rankings with $t=1$ are indicated in Fig. 3, which indicates that ${P}_{\mu}^{(1)}$ is 2-acceptable consistent, but is not 3-acceptable consistent.

Step 8:

Using (23) and (11), we have the optimal IFPV ${\omega}^{(1)}=\left(0.731,0.619,0.505,0.369,0.129,0.218,0.333,0.399\right)$ and the GIFPR constructed using ${\omega}^{(1)}$ as follows:

$$ {AC}_{\mu}^{(1)}=\left(\begin{array}{cccc}-& 0.548& 0.676& 0.731\\ {}0.28& -& 0.553& 0.619\\ {}0.191& 0.304& -& 0.505\\ {}0.114& 0.196& 0.305& -\end{array}\right). $$

Step 9:

By computing, we have $103=\arg \underset{l}{\max}\left\{ dis\left({\omega}^{(t)},{\omega}_l^{(t)}\right)\right\}$, that is, ${\mu}_{23},{\mu}_{31}$ and ${\mu}_{41}$ should be modified.

Step 10:

${\mu}_{23},{\mu}_{31}$ and ${\mu}_{41}$ in ${P_{\mu}}^{(1)}$ are replaced with the corresponding entries in ${AC}_{\mu}^{(1)}$. Then, ${P_{\mu}}^{(1)}$ is modified as

$$ {P}_{\mu}^{(2)}=\left(\begin{array}{cccc}-& 0.562& 0.7& 0.7\\ {}0.3& -& 0.553& 0.6\\ {}0.191& 0.3& -& 0.534\\ {}0.114& 0.2& 0.3& -\end{array}\right). $$

Step 11:

Using (19), the parameter ${\lambda}^{(2)}=0.771$ for ${h}_{\lambda^{(2)}}$ is acquired.

Step 12:

Using (20), all the local IFPVs $\left\{{\omega}_l^{(1)}|l=1,2,\cdots \kern0.3em ,128\right\}$ and the corresponding rankings with $t=2$ are indicated in Fig. 3, which indicates that ${P}_{\mu}^{(2)}$ is 4-acceptable consistent with the ranking ${x}_1\succ {x}_2\succ {x}_3\succ {x}_4$.

Fig. 3

The rankings in Example 3 vary with iterations

6 Group decision-making with GIFPRs

In this section, we propose a method to derive an IFPV from the GIFPRs in group decision-making problem which can be described as follows:

Let $X=\left\{{x}_1,{x}_2,\cdots \kern0.3em ,{x}_n\right\}$ and $E=\left\{{e}_1,{e}_2,\cdots \kern0.3em ,{e}_s\right\}$ be the set of alternatives under consideration and the set of s decision-makers who are invited to evaluate the alternatives, respectively. In many cases, since the problem is very complicated or the decision-makers are not familiar with the problem and thus they can not give explicit preferences over the alternatives, it is suitable to use the IFNs, which express the preference information from three aspects: “preferred”, “not preferred”, and “indeterminate”, to represent their opinions. Suppose that the decision maker ${e}_l$ provides his/her preference values for the alternative ${x}_i$ against the alternative ${x}_j$ as $\left({\mu}_{ijl}\right)$ in which ${\mu}_{ijl},i<j$ denotes the degree to which the object ${x}_i$ is preferred to the object ${x}_j$, ${\mu}_{ijl},i>j$ indicates the degree to which the object ${x}_i$ is not preferred to the object ${x}_j$ with ${\mu}_{ijl}+{\mu}_{jil}\le 1$, for $i,j=1,2,\cdots \kern0.3em ,n$ and $l=1,2,\cdots \kern0.3em ,s$. The GIFPR for the lth decision-maker can also be written as follows:

$$ {P}_{\mu l}={\left({\mu}_{ijl}\right)}_{n\times n}. $$

(24)

Before deriving the finial IFPV, consistency and consensus of these GIFPRs should be checked to avoid the unreasonable results.

Although it is perfect that all the GIFPRs ${P}_{\mu l}$ ($l=1,2,\cdots \kern0.3em ,s$) provided by a group of decision makers satisfy the following conditions:

(P${}_1$):

each ${P}_{\mu l}$ is consistent;

(P${}_2$):

all ${P}_{\mu l}$ reach consensus, that is, they derive a common IFPV,

that is, ${P}_{\mu 1}={P}_{\mu 2}=\cdots ={P}_{\mu s}$ and they are all consistent, in practical situations, these GIFPRs ${P}_{\mu l}$ ($l=1,2,\cdots \kern0.3em ,s$) can not determine a completely identical IFPV in general, that is, for an IFPV $\omega$, there exist ${\overset{\sim }{\mu}}_{ijl}\ne {\overset{\sim }{\mu}}_i+{\overset{\sim }{\nu}}_j$ for some $i\ne j$. Thus, we construct the following optimal model:

$$ {\displaystyle \begin{array}{ccc}\hfill & \min \sum \limits_{l=1}^s\sum \limits_{i\ne j,i,j=1}^n{\rho}_l{\left({\overset{\sim }{\mu}}_i+{\overset{\sim }{\nu}}_j-{\overset{\sim }{\mu}}_{ijl}\right)}^2\hfill & \hfill \\ {}\hfill & s.t.{\overset{\sim }{\mu}}_i+{\overset{\sim }{\nu}}_i=0,i=1,2,\cdots \kern0.3em ,n,\hfill \end{array}} $$

(25)

where $\rho =\left({\rho}_1,{\rho}_2,\cdots \kern0.3em ,{\rho}_s\right)$ is the weight vector of the decision makers determined as follows:

$$ {\rho}_i=\frac{T\left({P}_{\mu k}\right)}{\sum \limits_{k=1}^n\left(T\left({P}_{\mu k}\right)\right)} $$

(26)

$T\left({P}_{\mu k}\right)=\sum \limits_{l=1}^n Sup\left({P}_{\mu k},{P}_{\mu t}\right)$ and $Sup\left({P}_{\mu k},{P}_{\mu t}\right)$ are the supports for ${P}_{\mu k}$ from ${P}_{\mu t}$, with the conditions:

(1) $Sup\left({P}_{\mu k},{P}_{\mu t}\right)\in \left[0,1\right]$;

(2) $Sup\left({P}_{\mu k},{P}_{\mu t}\right)= Sup\left({P}_{\mu t},{P}_{\mu k}\right)$;

(3) $Sup\left({P}_{\mu k},{P}_{\mu t}\right)\ge Sup\left({P}_{\mu u},{P}_{\mu v}\right)$, if $d\left({P}_{\mu k},{P}_{\mu t}\right)<d\left({P}_{\mu u},{P}_{\mu v}\right)$, where d is the distance measure defined as follows:

$$ d\left({P}_{\mu k},{P}_{\mu t}\right)=\frac{1}{n\left(n-1\right)}\sum \limits_{\begin{array}{c}i,j=1\\ {}i\ne j\end{array}}^n\mid {\mu}_{ijk}-{\mu}_{ijt}\mid, $$

(27)

For convenience, we always assume that $Sup\left({P}_{\mu k},{P}_{\mu t}\right)=1-d\left({P}_{\mu k},{P}_{\mu t}\right)$. Furthermore, the parameter ${\lambda}_l$ for each GIFPR ${P}_l$, $l=1,2,\cdots \kern0.3em ,s$ is determined by (19).

In order to simplify the calculation process of (25), we provide the approximate solution of (25) by solving the following model:

$$ \kern0.5em \min \sum \limits_{l=1}^s\sum \limits_{i\ne j,i,j=1}^n{\rho}_l{\left({\overset{\sim }{\mu}}_i+{\overset{\sim }{\nu}}_j-{\hat{\mu}}_{ijl}\right)}^2 $$

(28)

where ${\hat{\mu}}_{ijl}=\left\{\begin{array}{cc}0,& i=j,\\ {}{\overset{\sim }{\mu}}_{ijl},& i\ne j.\end{array}\right.$ Then the optimal solution of (25) can be approximately obtained by the solution of the equation

$$ {A}^TA\overset{\sim }{\omega }={A}^T\sum_{l=1}^s{\rho}_l\tilde{b}_{l}. $$

(29)

We have the following result:

Theorem 11

The solution of (29) always exists with one free unknown.

Proof

It is trivial, so we omit it.

We also propose an acceptable consensus as follows:

Definition 14

Let ${P}_{\mu 1},{P}_{\mu 2},\cdots \kern0.3em ,{P}_{\mu s}$ be GIFPRs and $\delta$ be a positive integer such that $\delta \le n$. If the rankings of the first $\delta$ alternatives are the same in the rankings determined by all the local IFPVs of ${P}_{\mu 1},{P}_{\mu 2},\cdots \kern0.3em ,{P}_{\mu s}$, then ${P}_{\mu 1},{P}_{\mu 2},\cdots \kern0.3em ,{P}_{\mu s}$ are said to reach a $\delta$-acceptable consensus.

Theorem 12

Let ${P}_{\mu 1},{P}_{\mu 2},\cdots \kern0.3em ,{P}_{\mu s}$ be GIFPRs. If they are of $\delta$-acceptable consensus, then each of them is of $\delta$-acceptable consistency.

Proof

It follows immediately from Definitions 12 and 14.

While the $\delta$-acceptable consensus is being reached, the above theorem guarantees that each individual GIFPR is $\delta$-acceptable consistent. Then, a procedure for checking these given GIFPRs ${P}_1,{P}_2,\cdots \kern0.3em ,{P}_s$ to achieve a $\delta$-acceptable consensus can be established by the following steps:

Step 0:

Assume ${P}_{\mu l}^{(t)}={P}_{\mu l}^{(0)}$ for $l=1,2,\cdots \kern0.3em ,s$ and the iteration $t=0$.

Step 1:

Determine the parameter ${\lambda}_l$ of ${h}_{\lambda_l}$ using (19).

Step 2:

Solve all the local IFPVs ${\omega}_{l,k}^{(t)}$ for $l=1,2,\cdots \kern0.3em ,s$ and record their positions in K. If ${P}_l^{(t)}$ for $l=1,2,\cdots \kern0.3em ,s$ achieves a $\delta$-acceptable consensus by Definition 14, then go to Step 5; otherwise, record the set of the subscripts of these GIFPRs as M and go to the next step.

Step 3:

Using ${\overset{\sim }{\omega}}^{(t)}$ in (29), we construct a GIFPR ${AC}_{\mu l}^{(t)}={\left({h}_{\lambda_l}^{-1}\left({h}_{\lambda_l}\left({\mu}_i^{(t)}\right)+{h}_{\lambda_l}\left({\nu}_j^{(t)}\right)\right)\right)}_{n\times n}$ using (11) for each $l\in M$.

Step 4:

For each $l\in M$, compute ${k}_{l0}^{(t)}=\arg \underset{k\in K}{\max}\left\{d\left({\overset{\sim }{\omega}}^{(t)},{h}_{\lambda_l}\left({\omega}_{l,k}^{(t)}\right)\right)\right\}$ (d is the Chebyshev distance measure between two vectors), and replace the preference values in ${P}_{\mu l}^{(t)}$ with those in ${AC}_{\mu l}^{(t)}$ determined by ${k_{l0}}^{(t)}$. The modified ${P}_{\mu l}^{(t)}$ is denoted as ${P}_{\mu l}^{\left(t+1\right)}$ and return to Step 1.

Step 5:

Output the ranking.

Note the following

• 1. The above algorithm converges and can be used to derive consistent GIFPRs by adding iterations.

• 2. The process of checking and achieving a $\delta$-acceptable consensus can be executed and visualized by the local IFPVs; hence, presetting a threshold is more convenient and intuitive than the existing methods.

• 3. The $\delta$-acceptable consensus is weaker than the n-acceptable consensus; hence, when some GIFPRs have to be modified, $\delta$-acceptable consistency could be achieved using fewer modifications. Thus, the above algorithm with a $\delta$-acceptable consensus could preserve the original preference values as much as possible.

Example 6

Three decision-makers provide their GIFPRs ${P_{\mu}}_1,{P_{\mu}}_2$ and ${P_{\mu}}_3$ on a set of four alternatives $X=\left\{{x}_1,{x}_2,{x}_3,{x}_4\right\}$ as follows:

$$ {\displaystyle \begin{array}{ccc}\hfill {P_{\mu}}_1=& \left(\begin{array}{cccc}-& 0.6& 0.6& 0.8\\ {}0.2& -& 0.4& 0.7\\ {}0.2& 0.3& -& 0.7\\ {}0.1& 0.2& 0.1& -\\ {}\end{array}\right),\hfill & \hfill \\ {}\hfill {P_{\mu}}_2=& \left(\begin{array}{cccc}-& 0.6& 0.7& 0.8\\ {}0.2& -& 0.4& 0.7\\ {}0.2& 0.4& -& 0.7\\ {}0.1& 0.2& 0.2& -\\ {}\end{array}\right),\hfill \\ {}\hfill {P_{\mu}}_3=& \left(\begin{array}{cccc}-& 0.6& 0.6& 0.7\\ {}0.2& -& 0.4& 0.7\\ {}0.1& 0.3& -& 0.6\\ {}0.1& 0.2& 0.1& -\\ {}\end{array}\right).\hfill \end{array}} $$

To select the optimal alternative, we investigate the 1-acceptable consensus using the following procedure:

Step 0:

Assume ${P}_{\mu l}^{(t)}={P}_{\mu l}^{(0)}$ for $l=1,2,3$ and the iteration $t=0$.

Step 1:

The parameters ${\lambda}_1^{(0)}=0.653$, ${\lambda}_2^{(0)}=0.741$ and ${\lambda}_3^{(0)}=0.569$ are acquired according (19).

Step 2:

Solve all the local IFPVs ${\omega}_{l,k}^{(0)}$ for $l=1,2,3$ and record their positions in K. Figure 4 with $t=0$ indicates that ${P}_{\mu l}^{(0)}$ for $l=1,2,3$ do not achieve a 1-acceptable consensus according to Definition 14. Concretely, ${P}_{\mu 1}^{(0)}$ and ${P}_{\mu 3}^{(0)}$ are not 1-acceptable consistent and ${P}_{\mu 2}^{(0)}$ is 1-acceptable consistent.

Step 3:

Construct GIFPRs ${AC}_{\mu 1}^{(0)}$ and ${AC}_{\mu 3}^{(0)}$ using (29) and (11) as follows:

$$ {\displaystyle \begin{array}{ccc}\hfill {AC}_{\mu 1}^{(0)}=& \left(\begin{array}{cccc}-& 0.582& 0.581& 0.8\\ {}0.211& -& 0.39& 0.659\\ {}0.182& 0.353& -& 0.623\\ {}0.072& 0.169& 0.168& -\end{array}\right),\hfill & \hfill \\ {}\hfill {AC}_{\mu 3}^{(0)}=& \left(\begin{array}{cccc}-& 0.538& 0.536& 0.774\\ {}0.167& -& 0.34& 0.619\\ {}0.142& 0.302& -& 0.581\\ {}0.049& 0.13& 0.129& -\end{array}\right).\hfill \end{array}} $$

Step 4:

For each $l\in M=\left\{1,3\right\}$, compute ${k}_{l0}^{(0)}=\arg \underset{k\in K}{\max}\left\{d\left({\overset{\sim }{\omega}}^{(0)},{h}_{\lambda_l}\left({\omega}_{l,k}^{(0)}\right)\right)\right\}$. We have ${k}_{10}^{(0)}={k}_{30}^{(0)}=13$ (that is, ${\mu}_{12},{\mu}_{23}$ and ${\mu}_{41}$ in both ${P}_{\mu 1}^{(0)}$ and ${P}_{\mu 3}^{(0)}$ need to be modified). These preference values in ${P}_{\mu 1}^{(0)}$ and ${P}_{\mu 3}^{(0)}$are replaced by those in ${AC}_{\mu 1}^{(0)}$ and ${AC}_{\mu 3}^{(0)}$, respectively. The modified ${P}_{\mu 1}^{(0)}$ and ${P}_{\mu 3}^{(0)}$ are denoted as ${P}_{\mu 1}^{(1)}$ and ${P}_{\mu 3}^{(1)}$, respectively, as follows:

$$ {\displaystyle \begin{array}{ccc}\hfill {P_{\mu}}_1^{(1)}=& \left(\begin{array}{cccc}-& 0.582& 0.6& 0.8\\ {}0.2& -& 0.39& 0.7\\ {}0.2& 0.3& -& 0.7\\ {}0.072& 0.2& 0.1& -\end{array}\right),\hfill & \hfill \\ {}\hfill {P_{\mu}}_3^{(1)}=& \left(\begin{array}{cccc}-& 0.538& 0.6& 0.7\\ {}0.2& -& 0.34& 0.7\\ {}0.1& 0.3& -& 0.6\\ {}0.049& 0.2& 0.1& -\end{array}\right).\hfill \end{array}} $$

Step 5:

The parameters ${\lambda}_1^{(1)}=0.725$, ${\lambda}_2^{(1)}=0.813$ and ${\lambda}_3^{(1)}=0.63$ are determined using (19).

Step 6:

Solve all the local IFPVs ${\omega}_{l,k}^{(1)}$ for $l=1,2,3$ and record their positions in K. Figure 4 with $t=1$ indicates that ${P}_{\mu l}^{(1)}$ for $l=1,2,3$ still does not achieve a 1-acceptable consensus according to Definition 14. Concretely, ${P}_{\mu 1}^{(1)}$ and ${P}_{\mu 3}^{(1)}$ are not 1-acceptable consistent and ${P}_{\mu 2}^{(1)}$ is 1-acceptable consistent.

Step 7:

Construct GIFPRs ${AC}_{\mu 1}^{(1)}$ and ${AC}_{\mu 3}^{(1)}$ using (29) and (11) as follows:

$$ {\displaystyle \begin{array}{ccc}\hfill {AC}_{\mu 1}^{(1)}=& \left(\begin{array}{cccc}-& 0.588& 0.586& 0.809\\ {}0.207& -& 0.397& 0.67\\ {}0.183& 0.364& -& 0.64\\ {}0.068& 0.166& 0.165& -\end{array}\right),\hfill & \hfill \\ {}\hfill {AC}_{\mu 3}^{(1)}=& \left(\begin{array}{cccc}-& 0.542& 0.541& 0.783\\ {}0.163& -& 0.345& 0.631\\ {}0.141& 0.313& -& 0.598\\ {}0.045& 0.126& 0.126& -\end{array}\right).\hfill \end{array}} $$

Step 8:

For each $l\in M=\left\{1,3\right\}$, compute ${k}_{l0}^{(1)}=\arg \underset{k\in K}{\max}\left\{d\left({\overset{\sim }{\omega}}^{(1)},{h}_{\lambda_l}\left({\omega}_{l,k}^{(1)}\right)\right)\right\}$. We have ${k}_{10}^{(1)}=95,{k}_{30}^{(1)}=90$ (that is, ${\mu}_{21},{\mu}_{32}$ and ${\mu}_{43}$ in ${P}_{\mu 1}^{(1)}$ and ${\mu}_{21},{\mu}_{31}$ and ${\mu}_{42}$ in ${P}_{\mu 3}^{(1)}$ need to be modified). Then, these values in ${P}_{\mu 1}^{(1)}$ and ${P}_{\mu 3}^{(1)}$ are replaced by those in ${AC}_{\mu 1}^{(1)}$ and ${AC}_{\mu 3}^{(1)}$, respectively. The modified ${P}_{\mu 1}^{(1)}$ and ${P}_{\mu 3}^{(1)}$ are denoted as ${P}_{\mu 1}^{(2)}$ and ${P}_{\mu 3}^{(2)}$, respectively, as follows:

$$ {\displaystyle \begin{array}{ccc}\hfill {P_{\mu}}_1^{(2)}=& \left(\begin{array}{cccc}-& 0.582& 0.6& 0.8\\ {}0.207& -& 0.39& 0.7\\ {}0.2& 0.364& -& 0.7\\ {}0.072& 0.2& 0.165& -\end{array}\right),\hfill & \hfill \\ {}\hfill {P_{\mu}}_3^{(2)}=& \left(\begin{array}{cccc}-& 0.538& 0.6& 0.7\\ {}0.163& -& 0.34& 0.7\\ {}0.141& 0.3& -& 0.6\\ {}0.049& 0.126& 0.1& -\end{array}\right).\hfill \end{array}} $$

Step 9:

The parameters ${\lambda}_1^{(2)}=0.753$, ${\lambda}_2^{(2)}=0.79$ and ${\lambda}_3^{(2)}=0.611$ are calculated using (19).

Step 10:

Solve all the local IFPVs ${\omega}_{l,k}^{(2)}$ for $l=1,2,3$ and record their positions in K. Figure 4 with $t=2$ indicates that ${P}_{\mu l}^{(1)}$ for $l=1,2,3$ achieves a 1-acceptable consensus according to Definition 14 with the optimal alternative ${x}_1$.

Fig. 4

The local priority vectors in Example 6

7 Numerical example and comparative analysis

This section offers a numerical example to show the application of the new results. Furthermore, comparison analysis with Yang et al. [44]’s method is made.

7.1 A numerical example

Example 7

[17] The current globalized market trend identifies the necessity of the establishment of long term business relationship with competitive global suppliers spread around the world. This can lower the total cost of supply chain; lower the inventory of enterprises; enhance information sharing of enterprises; improve the interaction of enterprises and obtain more competitive advantages for enterprises. Thus, how to select different unfamiliar international suppliers according to the broad evaluation is very critical and has a direct impact on the performance of an organization. Suppose a company invites three experts ${e}_1$ , ${e}_2$ and ${e}_3$ from different field to evaluate four candidate suppliers ${x}_1$ , ${x}_2$, ${x}_3$ and ${x}_4$. Global supplier development is a complex problem which includes much qualitative information. In such a case, it is straightforward for the experts to compare the different suppliers in pairs and then construct some preference relations to express their preferences. Since the experts do not have precise information of the global suppliers, it is reasonable for them to use the IFSs to describe their assessments, and then three GIFPRs can be established:

$$ {\displaystyle \begin{array}{ccc}\hfill {P_{\mu}}_1=& \left(\begin{array}{cccc}-& 0.5& 0.7& 0.5\\ {}0.2& -& 0.6& 0.3\\ {}0.1& 0.2& -& 0.3\\ {}0.3& 0.6& 0.6& -\end{array}\right),\hfill & \hfill \\ {}\hfill {P_{\mu}}_2=& \left(\begin{array}{cccc}-& 0.6& 0.8& 0.6\\ {}0.1& -& 0.5& 0.3\\ {}0.2& 0.1& -& 0.4\\ {}0.3& 0.7& 0.6& -\end{array}\right),\hfill \\ {}\hfill {P_{\mu}}_3=& \left(\begin{array}{cccc}-& 0.6& 0.8& 0.7\\ {}0.2& -& 0.6& 0.2\\ {}0.1& 0.1& -& 0.2\\ {}0.2& 0.7& 0.3& -\end{array}\right).\hfill \end{array}} $$

To select the optimal supplier from these four candidates, it is reasonable to only investigate the 1-acceptable consensus by the following procedure:

Step 0:

Assume ${P}_{\mu l}^{(t)}={P}_{\mu l}^{(0)}$ for $l=1,2,3$ and the iteration $t=0$.

Step 1:

Using (19), we have ${\lambda}_1^{(0)}=0.653$, ${\lambda}_2^{(0)}=0.632$ and ${\lambda}_3^{(0)}=0.561$.

Step 2:

Solve all the local IFPVs ${\omega}_{l,k}^{(0)}$ for $l=1,2,3$ and record their positions in K. Figure 5 with $t=0$ indicates that ${P}_{\mu l}^{(0)}$ for $l=1,2,3$ do not achieve a 1-acceptable consensus according to Definition 14. Concretely, all of them are not 1-acceptable consistent according to Definition 13.

Step 3:

Construct GIFPRs ${AC}_{\mu 1}^{(0)}$, ${AC}_{\mu 2}^{(0)}$ and ${AC}_{\mu 3}^{(0)}$ by (11) and (29) as follows:

$$ {\displaystyle \begin{array}{ccc}\hfill {AC}_{\mu 1}^{(0)}=& \left(\begin{array}{cccc}-& 0.619& 0.738& 0.584\\ {}0.184& -& 0.509& 0.33\\ {}0.111& 0.249& 0.38& 0.22\\ {}0.281& 0.49& 0.628& -\end{array}\right),\hfill & \hfill \\ {}\hfill {AC}_{\mu 2}^{(0)}=& \left(\begin{array}{cccc}-& 0.609& 0.73& 0.574\\ {}0.174& -& 0.498& 0.319\\ {}0.103& 0.238& -& 0.209\\ {}0.27& 0.479& 0.619& -\end{array}\right),\hfill \\ {}\hfill {AC}_{\mu 3}^{(0)}=& \left(\begin{array}{cccc}0.351& 0.572& 0.702& 0.535\\ {}0.14& -& 0.455& 0.275\\ {}0.077& 0.198& -& 0.171\\ {}0.228& 0.436& 0.582& -\end{array}\right).\hfill \end{array}} $$

Step 4:

For each $l\in M=\left\{1,2,3\right\}$, compute ${k}_{l0}^{(0)}=\arg \underset{k\in K}{\max}\left\{d\left({\overset{\sim }{\omega}}^{(0)},{h}_{\lambda_l}\left({\omega}_{l,k}^{(0)}\right)\right)\right\}$. We have ${k}_{10}^{(0)}=104$, ${k}_{10}^{(0)}=118$ and ${k}_{10}^{(0)}=40$ (that is, ${\mu}_{231}^{(0)},{\mu}_{311}^{(0)}$ and ${\mu}_{421}^{(0)}$ in both ${P}_{\mu 1}^{(0)}$, ${\mu}_{312}^{(0)},{\mu}_{322}^{(0)}$ and ${\mu}_{422}^{(0)}$ in both ${P}_{\mu 2}^{(0)}$ and ${\mu}_{133}^{(0)},{\mu}_{213}^{(0)}$ and ${\mu}_{423}^{(0)}$ in both ${P}_{\mu 3}^{(0)}$ need to be modified). These preference values in ${P}_{\mu l}^{(0)}$ are replaced by those in ${AC}_{\mu l}^{(0)}$ for $l=1,2,3$, respectively. The modified ${P}_{\mu l}^{(0)}$ is denoted as ${P}_{\mu l}^{(1)}$ for $l=1,2,3$ as follows:

$$ {\displaystyle \begin{array}{ccc}\hfill {P_{\mu}}_1^{(1)}=& \left(\begin{array}{cccc}-& 0.5& 0.7& 0.5\\ {}0.2& -& 0.509& 0.3\\ {}0.111& 0.2& -& 0.3\\ {}0.3& 0.49& 0.6& -\\ {}\end{array}\right),\hfill & \hfill \\ {}\hfill {P_{\mu}}_2^{(1)}=& \left(\begin{array}{cccc}-& 0.6& 0.8& 0.6\\ {}0.1& -& 0.5& 0.3\\ {}0.103& 0.238& -& 0.4\\ {}0.3& 0.479& 0.6& -\end{array}\right),\hfill \\ {}\hfill {P_{\mu}}_3^{(1)}=& \left(\begin{array}{cccc}-& 0.6& 0.702& 0.7\\ {}0.14& -& 0.6& 0.2\\ {}0.1& 0.1& -& 0.2\\ {}0.2& 0.436& 0.3& -\end{array}\right).\hfill \end{array}} $$

Step 5:

Using (19), we have ${\lambda}_1^{(1)}=0.72$, ${\lambda}_2^{(1)}=0.758$ and ${\lambda}_3^{(1)}=0.606$, respectively.

Step 6:

Solve all the local IFPVs ${\omega}_{l,k}^{(1)}$ for $l=1,2,3$ and record their positions in K. Figure 5 with $t=1$ indicates that ${P}_{\mu l}^{(1)}$ for $l=1,2,3$ does not achieves a 1-acceptable consensus according to Definition 14. Concretely, all of them are not 1-acceptable consistent according to Definition 13 6.

Step 7:

Construct GIFPRs ${AC}_{\mu 1}^{(1)}$, ${AC}_{\mu 2}^{(1)}$ and ${AC}_{\mu 3}^{(1)}$ using (29) and (11) as follows:

$$ {\displaystyle \begin{array}{ccc}\hfill {AC}_{\mu 1}^{(1)}=& \left(\begin{array}{cccc}-& 0.599& 0.734& 0.595\\ {}0.174& -& 0.495& 0.335\\ {}0.114& 0.244& -& 0.241\\ {}0.238& 0.427& 0.584& -\end{array}\right),\hfill & \hfill \\ {}\hfill {AC}_{\mu 2}^{(1)}=& \left(\begin{array}{cccc}-& 0.615& 0.745& 0.61\\ {}0.189& -& 0.512& 0.353\\ {}0.127& 0.262& -& 0.259\\ {}0.256& 0.446& 0.6& -\end{array}\right),\hfill \\ {}\hfill {AC}_{\mu 3}^{(1)}=& \left(\begin{array}{cccc}-& 0.544& 0.692& 0.539\\ {}0.125& -& 0.433& 0.272\\ {}0.076& 0.187& -& 0.184\\ {}0.182& 0.364& 0.528& -\end{array}\right).\hfill \end{array}} $$

Step 8:

For each $l\in M=\left\{1,2,3\right\}$, compute ${k}_{l0}^{(1)}=\arg \underset{k\in K}{\max}\left\{d\left({\overset{\sim }{\omega}}^{(1)},{h}_{\lambda_l}\left({\omega}_{l,k}^{(1)}\right)\right)\right\}$. We have ${k}_{10}^{(1)}=20,{k}_{20}^{(1)}=92$ and ${k}_{30}^{(1)}=72$ (that is, ${\mu}_{121}^{(1)},{\mu}_{311}^{(1)}$ and ${\mu}_{341}^{(1)}$ in ${P}_{\mu 1}^{(1)}$, ${\mu}_{212}^{(1)},{\mu}_{322}^{(1)}$ and ${\mu}_{342}^{(1)}$ in ${P}_{\mu 2}^{(1)}$ and ${\mu}_{143}^{(1)},{\mu}_{313}^{(1)}$ and ${\mu}_{323}^{(1)}$ in ${P}_{\mu 3}^{(1)}$ need to be modified). Then, these values in ${P}_{\mu l}^{(1)}$ are replaced by those in ${AC}_{\mu l}^{(1)}$ for $l=1,2,3$. The modified ${P}_{\mu l}^{(1)}$ is denoted as ${P}_{\mu l}^{(2)}$ for $l=1,2,3$ as follows:

$$ {\displaystyle \begin{array}{ccc}\hfill {P_{\mu}}_1^{(2)}=& \left(\begin{array}{cccc}-& 0.599& 0.7& 0.5\\ {}0.2& -& 0.509& 0.3\\ {}0.114& 0.2& -& 0.241\\ {}0.3& 0.49& 0.6& -\end{array}\right),\hfill & \hfill \\ {}\hfill {P_{\mu}}_2^{(2)}=& \left(\begin{array}{cccc}-& 0.6& 0.8& 0.6\\ {}0.189& -& 0.5& 0.3\\ {}0.103& 0.262& -& 0.259\\ {}0.3& 0.479& 0.6& -\end{array}\right),\hfill \\ {}\hfill {P_{\mu}}_3^{(2)}=& \left(\begin{array}{cccc}-& 0.6& 0.702& 0.539\\ {}0.14& -& 0.6& 0.2\\ {}0.076& 0.187& -& 0.2\\ {}0.2& 0.436& 0.3& -\end{array}\right).\hfill \end{array}} $$

Step 9:

Using (19), we have ${\lambda}_1^{(2)}=0.714$, ${\lambda}_2^{(2)}=0.763$ and ${\lambda}_3^{(2)}=0.599$.

Step 10:

Solve all the local IFPVs ${\omega}_{l,k}^{(2)}$ for $l=1,2,3$ and record their positions in K. Figure 5 with $t=2$ indicates that ${P}_{\mu l}^{(2)}$ for $l=1,2,3$ do still not achieve a 1-acceptable consensus by Definition 14. Concretely, ${P_{\mu}}_1^{(2)}$ and ${P_{\mu}}_2^{(2)}$ achieve the 1-acceptable consistency, and ${P_{\mu}}_3^{(2)}$ does not achieve 1-acceptable consistency according to Definition 13.

Step 11:

Construct GIFPR ${AC}_{\mu 3}^{(2)}$ by (29) and (11) as follows:

$$ {AC}_{\mu 3}^{(2)}=\kern0.5em \left(\begin{array}{cccc}-& 0.559& 0.686& 0.497\\ {}0.137& -& 0.445& 0.253\\ {}0.075& 0.195& -& 0.153\\ {}0.186& 0.384& 0.525& -\end{array}\right). $$

Step 12:

For each $l=3$, compute ${k}_{l0}^{(2)}=\arg \underset{k\in K}{\max}\left\{d\left({\overset{\sim }{\omega}}^{(2)},{h}_{\lambda_l}\left({\omega}_{l,k}^{(2)}\right)\right)\right\}$. We have ${k}_{30}^{(1)}=15$ (that is, ${\mu}_{123}^{(2)},{\mu}_{233}^{(2)}$ and ${\mu}_{433}^{(2)}$ in ${P}_{\mu 3}^{(2)}$ need to be modified). Then, these values in ${P}_{\mu 3}^{(2)}$ are replaced by those in ${AC}_{\mu 3}^{(2)}$. The modified ${P}_{\mu 3}^{(2)}$ is denoted as ${P}_{\mu 3}^{(3)}$ as follows:

$$ {P_{\mu}}_3^{(3)}=\kern0.5em \left(\begin{array}{cccc}-& 0.559& 0.702& 0.539\\ {}0.14& -& 0.445& 0.2\\ {}0.076& 0.187& -& 0.2\\ {}0.2& 0.436& 0.525& -\end{array}\right). $$

Step 13:

Using (19), we have ${\lambda}_3^{(3)}=0.626$.

Step 14:

Solve all the local IFPVs ${\omega}_{l,k}^{(3)}$ for $l=1,2,3$ and record their positions in K. Figure 5 with $t=3$ indicates that ${P}_{\mu l}^{(3)}$ for $l=1,2,3$ achieves a 1-acceptable consensus with the optimal alternative ${x}_1$ according to Definitions 14.

Fig. 5

The local priority vectors in Example 6

7.2 Comparison with Yang et al. [44]’s method

Yang et al. investigated the consistency and consensus of IFPRs in group decision-making based on a class of representable uninorms. We make comparison with it from the following aspects:

• 1. As stated in Section 3, although some good properties can be derived from Yang et al. [44]’s consistency and the consensus of IFPRs, that method is stricter than the proposed method, because we could have to make many more modifications using Yang et al.’s consistency when some degrees of hesitancy of given preference values are larger than 0.12. However, this does not occur for the proposed consistency and consensus of GIFPRs. For example, for the GIFPR in Example 1, it is a consistent GIFPR with respect to ${h}_{0.5}$ with a ranking ${x}_3={x}_4\succ {x}_1={x}_2$ (see Example 2). Assume we modify the GIFPR as the following IFPR:

  $$ {P}_{\mu }=\left(\begin{array}{cccc}0.5& 0.25& 0.16& 0.16\\ {}0.25& 0.5& 0.16& 0.16\\ {}0.36& 0.36& 0.5& 0.25\\ {}0.36& 0.36& 0.25& 0.5\end{array}\right). $$

  Fig. 6

  

  The local priority vectors vary with iterations

  Using the method in Ref. [44], after 118 iterations, the iteration stops; then ${\lambda}^{118}=3.8996$, and the ranking is ${x}_4\succ {x}_3\succ {x}_1={x}_2$.

  $$ {P}_{\mu}^{(118)}=\left(\begin{array}{cccc}0.5& 0.5& 0.401& 0.16\\ {}0.5& 0.5& 0.401& 0.16\\ {}0.589& 0.589& 0.5& 0.25\\ {}0.753& 0.753& 0.696& 0.5\end{array}\right). $$

• 2. Yang et al. [44] also proposed acceptable consistency and consensus with local IFPVs, which can be considered n-acceptable consistency and consensus, respectively. First, as stated in Section 6, the proposed $\delta$-acceptable consistency and consensus are weaker than the n-acceptable consistency and consensus; hence, when some preference values have to be modified, the proposed values could be reached using fewer modifications. Thus, the original preference values could be preserved as much as possible. Second, $\delta$-acceptable consistency and consensus accord with some concrete practical situations. In some cases, we hope to derive the first $\delta$ ($\delta \le n$) optimal alternatives from n alternatives. At this time, $\delta$-acceptable consistency and consensus could be reached with fewer modifications to preference values than n-acceptable consistency and consensus. This also agrees with the modification principle, that is, the preference values should be preserved as much as possible. For example, we compare the results in Example 7 using the proposed method with those using Yang et al. [44]’s method with $\delta$-acceptable consistency and consensus. The results in Table 3 indicate that although both methods can obtain the same ranking, the proposed method could reach the goal with fewer iterations.

Table 3 Comparison with Yang et al. [44] method

8 Conclusions

The present paper proposed a novel decision framework for group decision-making with GIFPRs. Consistent GIFPRs are completely characterized by IFPVs. An inconsistent IFPR or those in the group are checked and repaired to achieve $\delta$-acceptable consistency or $\delta$-acceptable consensus. The advantages of the proposed method are realized by comparison with other methods under both theoretical and numerical perspectives as follows:

• 1. The proposed consistency for GIFPRs not only could be suitable for various GIFPRs with different parameters, but also possesses all the desirable properties similar to those of the multiplicative consistency for FPRs more than the existing method (see Table 1).

• 2. The process of achieving $\delta$-acceptable consistency and $\delta$-acceptable consensus could not only be visualized and without the aid of parameters, but also preserve the original preference information as much as possible.

The proposed methods are based on optimization models and could automatically achieve $\delta$-acceptable consistency and $\delta$-acceptable consensus. However, although the modified GIFPRs have high degree of consistency and consensus, they can not always agree with experts’ actual opinions. Inspired by Refs. [13, 31], we will establish an interactive model by integrating the revisions based on both the proposed optimization models and experts’ opinions in the future.