Abstract
In group decision making (GDM), to facilitate an acceptable consensus among the experts from different fields, time and resources are paid for persuading experts to modify their opinions. Thus, consensus costs are important for the GDM process. Notwithstanding, the unit costs in the common linear cost functions are always fixed, yet experts will generally express more resistance if they have to make more compromises. In this study, we use the quadratic cost functions, the marginal costs of which increase with the opinion changes. Aggregation operators are also considered to expand the applications of the consensus methods. Moreover, this paper further analyzes the minimum cost consensus models under the weighted average (WA) operator and the ordered weighted average (OWA) operators, respectively. Corresponding approaches are developed based on strictly convex quadratic programming and some desirable properties are also provided. Finally, some examples and comparative analyses are furnished to illustrate the validity of the proposed models.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Group decision making (GDM) requires the opinions provided by a group of experts (or individuals) to address unstructured problems, such as negotiations and conflict resolutions [1]. In GDM, experts often represent different interest groups, and their opinions may differ substantially even with the same interests and knowledge backgrounds [2,3,4,5]. However, in the real-life decision environments, the consent of all or most of experts to the collective option is very crucial [6,7,8,9,10,11,12,13,14].
Generally, solving GDM problems comprises two processes, the consensus process and the selection process. The former is dedicated to maximize the degree of consensus or agreement among experts [2, 3, 15,16,17,18,19,20]. Usually, the consensus process is coordinated by a moderator who has strong team leadership qualities and communication skills [21]. The selection process yields the final alternative according to the experts’ knowledge, which includes two different steps: aggregation of individual opinions and exploitation of group opinion [22, 23].
In general, the consensus process is complex and resource-consuming, during which moderator needs to convince experts to modify and change their opinions by spending time and resources [2]. Thus, cost is a significant issue in GDM [15, 24, 25]. For a moderator, what he/she concerns is not only the final consensus result, but also the cost in compensation for experts’ opinion change. To this end, this paper intends to develop a consensus approach, though which moderator can assist experts in reaching consensus at the minimum cost. The concept of minimum cost consensus was initiated by Ben-Arieh and Easton [24] and Ben-Arieh, Easton and Evans [15], based on which different minimum cost consensus models have been proposed for various GDM situations.
Although notable progress has been made in the research of minimum-cost consensus, there are some issues worth noting. (1) In real life, an expert generally expresses more resistance when the required opinion change rises, and the utility function of his/her opinion could be nonlinear [26, 27]. However, most existing methods are constructed under the linear cost functions, in which the unit adjustment cost of an expert is always fixed no matter how much the opinion is adjusted. Apparently, these studies did not consider the psychological changes of experts during the negotiation process. (2) Furthermore, in GDM problems, different aggregation operators are frequently used to aggregate individual opinions into a group collective opinion, according to their specific meanings and inherent relationships in a particular context. In order to expand the applications of minimum cost consensus theory, aggregation operators are necessary to be taken into account. (3) Finally, for the GDM problem, a unique optimal solution is more explicit and efficient than multiple solutions, which would lead to conflicts among experts once again. Therefore, another issue is how to design a minimum cost consensus approach that can obtain a unique optimal solution directly.
To the best of our knowledge, no study has addressed the above three issues simultaneously, thereby, this paper develops a kind of minimum quadratic-cost consensus models with aggregation operators. The proposed models have the following features: (1) Consensus costs are measured by quadratic cost functions, the unit costs of which are monotonically increasing with the magnitude of opinion change, showing the rising resistance of experts when more modifications are required. Compared with the linear costs, quadratic costs are closer to the real-life consensus costs of a moderator. Furthermore, under quadratic costs, the unique optimal solutions to the proposed consensus models are obtained by using strictly convex quadratic programming, avoiding the case of multiple solutions. (2) Aggregation operators are used to build the relationship between individual opinions and the group opinion. The importance of each expert’s opinion can also be intuitively reflected through the allocation of weights. (3) The order positions of the experts’ original opinions will not be changed by the proposed method, when the unit costs are uniform and the ordered weighted average (OWA) operators are used. This feature is called the property of order preservation in this paper.
The remainder of this paper is organized as follows. Section 2 introduces the related works and the basic knowledge with respect to the aggregation operators and the minimum cost consensus models. Section 3 constructs the minimum quadratic cost consensus model under aggregation operators, which will reduce to the model of Ben-Arieh, Easton and Evans [15], when the adjusted individual opinions are equal to each other. Further, this section focuses on the consensus models based on the weighted average (WA) operator and OWA operators. The corresponding properties of the proposed models under the different aggregation operators are explored in Sect. 4. In Sect. 5, three numerical examples are employed to manifest the validity of the proposed models, and a comparative analysis is also provided. Finally, concluding remarks are presented in Sect. 6.
2 Preliminaries and related works
This section introduces the basic knowledge of aggregation operators and related works on minimum cost consensus models.
2.1 Aggregation operators
To obtain a collective opinion from individual ones, aggregation operators are substantially used in the GDM process. They reveal the inherent relationships between individual opinions and the group collective opinion in specific GDM problems. Let {o1, o2, …, on} be a set of opinions to aggregate. An aggregation operator is a function that derives the collective opinion o grounded on the individuals’ one
Here we mainly introduce two typical aggregation operators: the WA operator and the OWA operator [28]. The WA operator is a simple additive weighting approach considering the importance degree of each expert’s opinion. Let {o1, o2, …, on} be as above. The WA operator is defined as
where w = (w1, w2, …, wn)T is an associated weight vector, such that wi ∈ [0, 1] and \( {\sum}_{i=1}^n{w}_i=1 \).
The OWA operator aggregates the individuals’ opinions by assigning appropriate weights to the reordered elements. Let {o1, o2, …, on} and w = (w1, w2, …, wn)T be as above. The OWA operator is defined as [28]
where {σ(1), σ(2), …, σ(n)} is a permutation of {1, 2,…, n} such that oσ(i − 1) ≥ oσ(i) for i = 2, 3, …, n. Since Yager [28] introduced the OWA operator in 1988, notable progress has been made in developing OWA operators, especially the corresponding weight generation methods (see reference [29]). Recently, Chen, Yu, Chin and Martinez [30] proposed an enhanced approach to OWA weight generation based on the interweaving method.
2.2 Minimum cost consensus models
Suppose that there are n experts E = {e1, e2, …, en} and oi ∈ R (i = 1, 2, …, n) denotes expert i’s initial opinion. Let \( {\overline{o}}_i \) and \( \overline{o} \) be the adjusted individual opinion and collective opinion, respectively. Besides, ci denotes the cost of moving expert i’s opinion one unit, then the linear cost paid to expert i is formulated as \( {c}_i\left|{\overline{o}}_i-{o}_i\right| \). Ben-Arieh and Easton [24] first proposed the minimum cost consensus model as follows
where \( O=\left\{\overline{o}\in R\left|\overline{o}>0\right.\right\} \) is a set of all possible consensus opinions. Particularly, when the adjusted opinion \( {\overline{o}}_i \) is identical to the collective opinion o, expert i is recognized as reaching consensus. This full and unanimous consensus is generally called as “hard” consensus.
Besides, Ben-Arieh and Easton [24] introduced the concept of ε consensus, which allows individuals’ opinions to approach the group opinion adequately. Compared with hard consensus, this kind of consensus is less strict and can be achieved in a more flexible way, which we call “soft” consensus [13]. The tolerated deviation threshold is denoted as ε. Thus, all adjusted opinions fitting into consensus should be within the interval \( \left[\overline{o}-\varepsilon, \overline{o}+\varepsilon \right] \). Obviously, only the opinions outside the interval need to be modified. Thus, the minimum cost consensus model with ε threshold is constructed as:
Under the nonlinear opinion elasticity, Ben-Arieh, Easton and Evans [15] formulated quadratic cost function \( {f}_i={c}_i{\left(\overline{o}-{o}_i\right)}^2 \), then the unanimous consensus at the minimum quadratic cost (CMQC) is obtained by the following model [15]:
A natural extension to CMQC is the ε consensus allowing all experts’ opinions within the given distance of group opinion (ε CMQC). The consensus model for ε CMQC is constructed as:
In addition, Ben-Arieh, Easton and Evans [15] also proposed the algorithm to yield the maximum number of experts that satisfy the consensus under a given budget B. The method to find the quadratic maximum expert consensus (QMEC) is presented as below:
where only when the opinion of an expert is the same as the group opinion (i.e., \( {\overline{o}}_i=\overline{o} \)), is the expert confirmed as a member of consensus group (zi=1).
It is worth noting that, although methods in references [15, 24] are groundbreaking and effective, but neither of them considered aggregation operators, and ignored the internal relationships between the individual opinions and the group one. Thus, only in some special cases are the above methods able to be used. Motivated by this, Zhang, Dong, Xu and Li [31] incorporated aggregation operators into the minimum-cost consensus methods and furnished corresponding linear-programming approaches. By using aggregation operator \( F\left({\overline{o}}_1,{\overline{o}}_2,\dots, {\overline{o}}_n\right) \) is derived from the adjusted experts’ opinions. The minimum cost consensus model under aggregation operators is constructed as:
where \( \left|{\overline{o}}_i-\overline{o}\right| \) measures the deviation of expert i’s opinion from the consensus opinion and ε ≥ is the consensus threshold. When ε (i.e., \( {\overline{o}}_1={\overline{o}}_2=\dots ={\overline{o}}_n=\overline{o} \)), model (M-6) reduces to (M-1). It should be noted that, (M-6) can be solved based on linear-programming models, so there may be multiple solutions in some cases (please see Example 2) and the uniqueness of optimal solutions can’t be guaranteed.
Besides, Cheng, Zhou, Cheng, Zhou and Xie [32] investigated the minimum cost consensus model with directional constraints in the asymmetric cost context. Gong, Zhang, Forrest, Li and Xu [2] and Gong, Xu, Zhang, Ozturk, Herrera-Viedma and Xu [33] constructed minimum cost consensus models and maximum return consensus models to balance the interests of both the moderator and the experts. Further, Zhang, Kou and Peng [23] proposed the soft minimum cost consensus models with a consensus level function and a generalized aggregation operator. Zhang, Liang, Gao and Zhang [34] developed a minimum cost consensus model with incomplete linguistic distribution assessments. Recently, Lu, Xu, Herrera-Viedma and Han [35] furnished a minimum cost consensus model based on robust optimization for the large-scale group decision making in social network. Wu, Dai, Chiclana, Fujita and Herrera-Viedma [36] proposed a minimum adjustment cost based feedback mechanism for network social GDM with distributed linguistic trust. Wu, Yang, Tu and Chen [37] devised multi-stage optimization models with interval additive preference relations. A comparison between the above related works in the existing literatures and the proposed method in this paper is presented in Table 1.
3 Minimum quadratic cost consensus models under aggregation operators
3.1 The proposed model
In various scenarios, different aggregation operators are employed to aggregate experts’ opinions into a collective one. Furthermore, utilizing different aggregation operators also impacts the consensus level. Thus, aggregation operators are pivotal to consensus methods.
For an expert, every number denoting his/her opinion has a specific utility value [27]. In the practical decision-making contexts, the utility functions do not just monotonically increase or decrease as experts’ opinions change. Instead, the utility functions generally show nonlinear trends, such as parabolic and S-shaped utility functions [26, 27]. In order to convince experts to adjust their original opinions, a moderator compensates experts for the utility they sacrifice by paying consensus costs. Generally, individuals are willing to cooperate with the moderator if the required opinion adjustments are relatively small, while they would show more resistance if the adjustments grow. Considering this psychological factor, this paper herein uses the quadratic cost functions [15], which embody the experts’ emotion changes. Although existing literatures mainly adopt the linear consensus cost functions, but they ignored the psychological changes of the experts, which leads to some limitations in practical application. Additionally, the quadratic cost function \( {f}_i={c}_i{\left({o}_i-{\overline{o}}_i\right)}^2 \) also results in distinct approaches and model properties. Thus, this paper proposes a generalized consensus model with aggregation operators which aims at minimizing the quadratic costs, i.e.,
At the same time, the group consensus is fulfilled under the constraint that each expert’s opinion is close enough to the collective opinion, that is\( \left|{\overline{o}}_i-\overline{o}\right|\le \varepsilon \), i = 1, 2, …, n where \( \overline{o} \) is the adjusted group opinion in (M-6).
In this way, a generalized consensus model for minimum quadratic cost is constructed as follows:
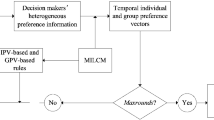
Obviously, model (M-7) reduces to (M-3) when \( {\overline{o}}_i=\overline{o} \) for i = 1,2,...,n. In addition, it’s proved that (M-7) can degrade into (M-4), when utilizing the OWA operator with weight vector (1/2, 0, ..., 0, 1/2)T [31]. Thus, model (M-7) is a generalized version of the consensus method of Ben-Arieh, Easton and Evans [15]. The flowchart of the proposed method is described in Fig. 1.
3.2 Minimum cost consensus models under some common operators
It’s clear that the proposed consensus model varies according to the aggregation operator. Since the WA operator and the OWA operators [28] are the most common and basic aggregation operators, this section further analyzes (M-7) under these two kinds of operators with quadratic programming models.
-
(1) WA operator
Using WAw operator to derive the collective opinion from individual opinions, model (M-7) can be described as:
Using WAw operator to derive the collective opinion from individual opinions,
Denote Ω8 as the feasible set to (M-8).
Theorem 1.
Let \( {x}_i={\overline{o}}_i \), then (M-8) can be described as the following strictly convex quadratic programming model:
Proof.
The constraints in (M-9) guarantee that \( \overline{o}={\sum}_{i=1}^n{w}_i{\overline{o}}_i \) and \( \left|{\overline{o}}_i-\overline{o}\right|\le \varepsilon \). Thus, (M-8) can be transformed into (M-9). Let \( f(x)=\underset{x_i}{\min }{\sum}_{i=1}^n{c}_i{\left({x}_i-{o}_i\right)}^2 \). Since f(x) is the sum of strictly convex functions, it is itself strictly convex. Moreover, the constraints of (M-9) are linear. Hence, (M-8) can be transformed into the strictly convex quadratic programming model. This completes the proof of Theorem 1.
-
(2) OWA operator
When OWAw operator is used to aggregate the individual opinions, (M-7) is presented as follows:
Let Ω10 be the feasible set to (M-10). Given the nonlinear constraint condition \( \overline{o}={OWA}_w\left({\overline{o}}_1,{\overline{o}}_2,\dots, {\overline{o}}_n\right) \), model (M-10) can’t be straightly transformed into a quadratic programming model. Thus, two specific cases of (M-10) are introduced below.
Case A: The unit adjustment costs of all expert are identical to each other, which means that c1 = c2= … = cn = c. In order to minimize the consensus cost, we hope the modifications to the individual opinions are as small as possible. The consensus model in this case is constructed as model (M-11).
Case B: In many competitions, a frequently used scoring rule is to remove the highest and lowest scores of participants first, and then calculate the average of the remaining scores to obtain the collective evaluation. It’s clear that this practice utilizes the \( {OWA}_{w_1} \) operator with weight vector w1 = (0, 1/(n − 2), …, 1/(n − 2), 0)T. Considering that some judges may deliberately express extreme opinions for their own or alliance benefits [38], this scoring format can prevent them from undermining the equity of the competition. The corresponding consensus models are shown below.
1) Case A: With the uniform unit cost of each expert, model (M-10) is equivalent to:
Denote Ω11 the feasible set corresponding to (M-11). Let \( {x}_i={\overline{o}}_i \) and σ(1), σ(2), …, σ(n) be a permutation of {1, 2, …, n} such that oσ(i − 1) ≥ oσ(i) for all i = 2, 3, …, n (i.e., oσ(i) is the ith largest value in {o1, o2, …, on}). Let {τ(1), τ(2), …, τ(n)} be another permutation of {1, 2, …, n} such that xτ(i − 1) ≥ xτ(i) for all i = 2, 3,...,n. (M-11) can be transformed into the following model:
Denote Ω12 as the feasible set to (M-12). Before presenting the approach to solve (M-12), we introduce a new model:
The constraint conditions xσ(i) − xσ(i − 1) ≤ 0 (i = 2, 3, …, n) guarantee that τ(i) = σ(i). Consequently,
Based on this, model (M-13) is equivalent to the following model:
Let \( {f}_1(x)=\underset{x_i}{\min }{\sum}_{i=1}^n{\left({x}_i-{o}_i\right)}^2. \) We prove that f1(x) is a strictly convex function. Besides, σ(i) is definite according to {o1, o2, …, on}, so the constraints in (M-14) are
Dong, Xu, Li and Feng [39] proposed an OWA-based consensus operator under the continuous linguistic model, finding that the initial opinions of experts can be optimally preserved by their consensus model. The optimal solution to Dong et al.’s [39] model is obtained by strictly convex quadratic programming. Based on the idea of Dong, Xu, Li and Feng [39], this paper introduces Lemma 1 and Lemma 2 to study the relationship between (M-12) and (M-14).
Lemma 1.
Let op, oq ∈ {o1, o2, …, on} and \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) be the optimal solution to (M-12). Then, \( {\overline{o}}_p^{\ast}\ge {\overline{o}}_q^{\ast } \) for op > oq
Proof.
Using reduction to absurdity, suppose that \( {\overline{o}}_q^{\ast }>{\overline{o}}_p^{\ast } \). Let a set of values be \( \left\{{\ddot{o}}_1,{\ddot{o}}_2,\dots, {\ddot{o}}_n,\ddot{o}\right\} \), where.
Since \( \ddot{o}={OWA}_w\left({\ddot{o}}_1,{\ddot{o}}_2,\dots, {\ddot{o}}_n\right)={OWA}_w\left({\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast}\right)={\overline{o}}^{\ast } \) we have that \( {\max}_i\left|{\ddot{o}}_i-\ddot{o}\right|={\max}_i\left|{\overline{o}}_i^{\ast }-{\overline{o}}^{\ast}\right|\le \varepsilon \) holds for all i = 1,2, ...,n, so \( \left\{{\ddot{o}}_1,{\ddot{o}}_2,\dots, {\ddot{o}}_n,\ddot{o}\right\}\in {\Omega}_{12} \). Furthermore,
which contradicts the fact that \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) is the optimal solution to (M-12). This completes the proof of Lemma 1.
Lemma 2.
Let op, oq ∈ {o1, o2, …, on} and op = oq. If \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) is the optimal solution to (M-12), then \( \left\{{\ddot{o}}_1,{\ddot{o}}_2,\dots, {\ddot{o}}_n,\ddot{o}\right\} \) is also the optimal solution to (M-12), where
Proof.
Based on the proof of Lemma 1, we get that \( \left\{{\ddot{o}}_1,{\ddot{o}}_2,\dots, {\ddot{o}}_n,\ddot{o}\right\}\in {\Omega}_{12} \) and \( {\sum}_{i=1}^n{\left({\ddot{o}}_i-{o}_i\right)}^2={\sum}_{i=1}^n{\left({\overline{o}}_i^{\ast }-{o}_i\right)}^2. \) Consequently, \( \left\{{\ddot{o}}_1,{\ddot{o}}_2,\dots, {\ddot{o}}_n,\ddot{o}\right\} \) is also the optimal solution to (M-12). This completes the proof of Lemma 2.
Remark 1.
Lemma 1 shows the property of order preservation, i.e., if a value is large in the original set, then its adjusted value is still large in the optimal solution. Lemma 2 shows that if a set of values is the solution of (M-12), when two values of the set are interchanged, the interchanged set is still the solution of (M-12).
Based on Lemmas 1 and 2, the following Theorem 2 is obtained.
Theorem 2.
If \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) is the optimal solution to (M-14), then \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) is the optimal solution to (M-12).
Proof.
Let \( \left\{{\overline{\overline{o}}}_1^{\ast },{\overline{\overline{o}}}_2^{\ast },\dots, {\overline{\overline{o}}}_n^{\ast },{\overline{\overline{o}}}^{\ast}\right\} \) be an optimal solution to (M-12) and Ω14 ⊆ Ω12 denotes the feasible set to (M-14). Since Ω14, \( {\sum}_{i=1}^n{\left({\overline{o}}_i^{\ast }-{o}_i\right)}^2\ge {\sum}_{i=1}^n{\left({\overline{\overline{o}}}_i^{\ast }-{o}_i\right)}^2 \) is obtained.
Here, we consider the following two cases:
-
a)
oi ≠ oj for any oi, oj ∈ {o1, o2, …, on}. Based on Lemma 1, we have that \( {\overline{\overline{o}}}_{\sigma \left(i-1\right)}^{\ast}\ge {\overline{\overline{o}}}_{\sigma (i)}^{\ast } \), so \( \left\{{\overline{\overline{o}}}_1^{\ast },{\overline{\overline{o}}}_2^{\ast },\dots, {\overline{\overline{o}}}_n^{\ast },{\overline{\overline{o}}}^{\ast}\right\}\in {\Omega}_{14} \). Consequently,
which means that \( {\sum}_{i=1}^n{\left({\overline{o}}_i^{\ast }-{o}_i\right)}^2={\sum}_{i=1}^n{\left({\overline{\overline{o}}}_i^{\ast }-{o}_i\right)}^2 \). Given that the optimal solution to (M-14) exists and is unique, \( \left\{{\overline{\overline{o}}}_1^{\ast },{\overline{\overline{o}}}_2^{\ast },\dots, {\overline{\overline{o}}}_n^{\ast },{\overline{\overline{o}}}^{\ast}\right\}=\left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \).
-
b)
Let op, oq ∈ {o1, o2, …, on} and op = oq. Without loss of generality, we suppose that oi ≠ oj for any oi, oj ∈ {o1, o2, …, on}/{op}. Lemma 2 guarantees that \( \left\{{\ddot{o}}_1^{\ast },{\ddot{o}}_2^{\ast },\dots, {\ddot{o}}_n^{\ast },{\ddot{o}}^{\ast}\right\} \) is also the optimal solution to (M-12), where
Based on Lemma 1, we can know that if oi ∈ {o1, o2, …, on}/{op, oq} is the kth largest variable in {o1, o2, …, on}, \( {\overline{\overline{o}}}_i^{\ast }/{\ddot{o}}_i^{\ast } \) is still the kth largest variable in \( \left\{{\overline{\overline{o}}}_1^{\ast },{\overline{\overline{o}}}_2^{\ast },\dots, {\overline{\overline{o}}}_n^{\ast}\right\}/\left\{{\ddot{o}}_1^{\ast },{\ddot{o}}_2^{\ast },\dots, {\ddot{o}}_n^{\ast}\right\} \). Therefore, either \( \left\{{\overline{\overline{o}}}_1^{\ast },{\overline{\overline{o}}}_2^{\ast },\dots, {\overline{\overline{o}}}_n^{\ast },{\overline{\overline{o}}}^{\ast}\right\} \) or \( \left\{{\ddot{o}}_1^{\ast },{\ddot{o}}_2^{\ast },\dots, {\ddot{o}}_n^{\ast },{\ddot{o}}^{\ast}\right\} \) is the feasible solution to (M-14). Without loss of generality, assume that \( \left\{{\ddot{o}}_1^{\ast },{\ddot{o}}_2^{\ast },\dots, {\ddot{o}}_n^{\ast },{\ddot{o}}^{\ast}\right\}\in {\Omega}_{14} \). Similar to case a), \( \left\{{\ddot{o}}_1^{\ast },{\ddot{o}}_2^{\ast },\dots, {\ddot{o}}_n^{\ast },{\ddot{o}}^{\ast}\right\}=\left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) can be obtained. This completes the proof of Theorem 2.
Theorem 2 guarantees the optimal solution to (M-12) can be obtained through a strictly convex quadratic programming model.
2) Case B: This case utilizes an OWA operator with weight vector w1 = (0, 1/(n − 2), …, 1/(n − 2), 0)T. The corresponding model under \( {OWA}_{w_1} \) is presented as follows:
Denote Ω15 as the feasible set corresponding to (M-15). Before solving (M-15), Lemma 3 is introduced.
Lemma 3.
If \( {\overline{o}}_m={\min}_i\left\{{\overline{o}}_i\right\} \) and \( {\overline{o}}_h={\max}_i\left\{{\overline{o}}_i\right\} \) (m, h ∈ {1, 2, …, n}), (M-15) can be described as:
Proof.
In model M(\( {\overline{o}}_m,{\overline{o}}_h \)), the constraints \( {\overline{o}}_m\le {\overline{o}}_i \) (i = 1, 2, …, n) and \( {\overline{o}}_h\ge {\overline{o}}_i \) (i = 1, 2, …, n) guarantee that \( {\overline{o}}_m={\min}_i\left\{{\overline{o}}_i\right\} \) and \( {\overline{o}}_h={\max}_i\left\{{\overline{o}}_i\right\} \), respectively. Hence, \( \overline{o}=\frac{1}{n-2}\left({\sum}_{i=1}^n{\overline{o}}_i-{\max}_i\left\{{\overline{o}}_i\right\}-{\min}_i\left\{{\overline{o}}_i\right\}\right) \) is identical to \( \overline{o}=\frac{1}{n-2}\left({\sum}_{i=1}^n{\overline{o}}_i-{\overline{o}}_h-{\overline{o}}_m\right) \). Consequently, (M-15) can be equivalently described as M(\( {\overline{o}}_m,{\overline{o}}_h \)), when \( {\overline{o}}_m={\mathit{\min}}_i\left\{{\overline{o}}_i\right\} \) and \( {\overline{o}}_h={\mathit{\max}}_i\left\{{\overline{o}}_i\right\} \). This completes the proof of Lemma 3.
Let \( {x}_i={\overline{o}}_i \), then M(\( {\overline{o}}_m,{\overline{o}}_h \)) (m = 1, 2, …, n and h = 1, 2, …, n) can be similarly transformed into the strictly convex quadratic programming models. The relationship between (M-15) and M(\( {\overline{o}}_m,{\overline{o}}_h \)) is embodied in Theorem 3. Let Ω15 and Ωmh be the feasible sets corresponding to (M-15) and M(\( {\overline{o}}_m,{\overline{o}}_h \)), respectively. Naturally, Ωmh ⊆ Ω15 holds for all m, h ∈ {1, 2, …, n}.
Theorem 3.
Let \( \left\{{\overline{o}}_1^{mh},{\overline{o}}_2^{mh},\dots, {\overline{o}}_n^{mh},{\overline{o}}^{mh}\right\} \) be the optimal solution to M(\( {\overline{o}}_m,{\overline{o}}_h \)) and\( {P}_{mh}={\sum}_{i=1}^n{c}_i{\left({o}_i-{\overline{o}}_i^{mh}\right)}^2 \). If Pjk = min {Pmh|m, h = 1, 2, …, n} (j, k ∈ {1, 2, …, n}), the corresponding optimal solution \( \left\{{\overline{o}}_1^{jk},{\overline{o}}_2^{jk},\dots, {\overline{o}}_n^{jk},{\overline{o}}^{jk}\right\} \) to M(\( {\overline{o}}_j,{\overline{o}}_k \)) is the optimal solution to (M-15).
Proof.
Let \( \left\{{\overline{\overline{o}}}_1^e,{\overline{\overline{o}}}_2^e,\dots, {\overline{\overline{o}}}_n^e,{\overline{\overline{o}}}^e\right\} \) be an optimal solution to (M-15). Since Ωmh ⊆ Ω15 holds for any m, h ∈ {1, 2, …, n}, we have that \( {\sum}_{i=1}^n{c}_i{\left({o}_i-{\overline{o}}_i^{jk}\right)}^2\ge {\sum}_{i=1}^n{c}_i{\left({o}_i-{\overline{\overline{o}}}_i^e\right)}^2 \).
Simultaneously, the minimum and maximum values (\( {\overline{o}}_m \) and \( {\overline{o}}_h \)) of \( \left\{{\overline{\overline{o}}}_1^e,{\overline{\overline{o}}}_2^e,\dots, {\overline{\overline{o}}}_n^e\right\} \) are known, so \( \left\{{\overline{\overline{o}}}_1^e,{\overline{\overline{o}}}_2^e,\dots, {\overline{\overline{o}}}_n^e,{\overline{\overline{o}}}^e\right\} \) is also a feasible solution to M(\( {\overline{o}}_m,{\overline{o}}_h \)). Thus, \( {\sum}_{i=1}^n{c}_i{\left({o}_i-{\overline{o}}_i^{jk}\right)}^2\le {\sum}_{i=1}^n{c}_i{\left({o}_i-{\overline{\overline{o}}}_i^e\right)}^2 \).
Consequently, \( {P}_{jk}={\sum}_{i=1}^n{c}_i{\left({o}_i-{\overline{o}}_i^{jk}\right)}^2={\sum}_{i=1}^n{c}_i{\left({o}_i-{\overline{\overline{o}}}_i^e\right)}^2 \).
Therefore, the corresponding optimal solution \( \left\{{\overline{o}}_1^{jk},{\overline{o}}_2^{jk},\dots, {\overline{o}}_n^{jk},{\overline{o}}^{jk}\right\} \) to M(\( {\overline{o}}_j,{\overline{o}}_k \)) is also an optimal solution to (M-15). This completes the proof of Theorem 3.
Remark 2.
Theorem 3 shows that (M-15) can be solved through n(n − 1)/2 quadratic programming models (i.e., M(\( {\overline{o}}_m,{\overline{o}}_h \)), where m, h ∈ {1, 2, …, n} and m ≠ h). Similarly, n(n − 1)/2 linear programming models can be employed to solve the linear cost version of (M-15) in Zhang, Dong, Xu and Li [31]. It should be noted that, when all ci (i = 1, 2, …, n) are equal, only one quadratic programming model needs to be solved. In this case, (M-15) is classified as Case A of (M-10) where the order preservation property mentioned in Remark 1 holds. Furthermore, we speculate that this property still holds for (M-15) when the differences among ci (i = 1, 2, …, n) are relatively small, yet this conjecture hasn’t been proved.
Remark 3.
As known to all, there are many classical methods such as Lemke algorithm to solve strictly convex quadratic programming. In this paper, we employ the function “quadprog” of software MATLAB to solve the proposed consensus models so that the optimal solutions can be efficiently obtained.
4 Properties of the models
Section 3 constructs the consensus models for minimum quadratic cost under the WA and OWA operators and reveals the property of order preservation in (M-12). More interesting and desired properties will be shown in this section, which embody the characteristics of the proposed models under the different aggregation operators.
Lemma 4.
Let {o1, o2, …, on} and \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast}\right\} \) be the original opinions and the modified opinions corresponding to (M-8) or (M-10), respectively. Then, we get that \(\min_{i} \{ \bar{o}_{i}^{*} \} \ge \min_{i} \{ o_{i} \}\) and \(\max_{i} \{ \bar{o}_{i}^{*} \} \le \max_{i} \{ o_{i} \}\).
Proof.
The statement \( {\min}_i\left\{{\overline{o}}_i^{\ast}\right\}\ge {\min}_i\left\{{o}_i\right\} \) is first proved through reduction to absurdity. Assuming that ∃Q ⊆ {1, 2, …, n} and \( Q=\left\{q|{\overline{o}}_q^{\ast }<\min \left\{{o}_i\right\}\right\} \). Let \( \left\{{\ddot{o}}_1,{\ddot{o}}_2,\dots, {\ddot{o}}_n,\ddot{o}\right\} \) be a set of values, where
and \( \ddot{o} \) represents the aggregated group opinion. Since \( \left|\ddot{o}-{\max}_i\left\{{\ddot{o}}_i\right\}\right|\le \varepsilon \) and \( \left|\ddot{o}-{\min}_i\left\{{\ddot{o}}_i\right\}\right|\le \varepsilon \), then \( \left\{{\ddot{o}}_1,{\ddot{o}}_2,\dots, {\ddot{o}}_n,\ddot{o}\right\}\in {\Omega}_8/{\Omega}_{10} \) holds. Moreover,
which contradicts the fact that \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) is the optimal solution to model (M-8) or (M-10). Thus, the statement \( {\min}_i\left\{{o}_i\right\}\le {\min}_i\left\{{{\overline{o}}_i}^{\ast}\right\} \) holds. Likewise, we have \( {\mathit{\max}}_i\left\{{{\overline{o}}_i}^{\ast}\right\}\le {\mathit{\max}}_i\left\{{o}_i\right\} \). This completes the proof of Lemma 4.
Remark 4.
Lemma 4 indicates that the adjusted optimal values are among the minimum and maximum values of the original values.
Corollary 1.
\( \left|{\max}_i\left\{{\overline{o}}_i^{\ast}\right\}-{\min}_i\left\{{\overline{o}}_i^{\ast}\right\}\right|\le \left|{\max}_i\left\{{o}_i\right\}-{\min}_i\left\{{o}_i\right\}\right| \).
Property 1.
Let \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) be the optimal solution to (M-8) or (M-10), then
Proof.
Since \( {\overline{o}}^{\ast }={WA}_w\left({\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast}\right) \) in model (M-8) and \( {\overline{o}}^{\ast }={OWA}_w\left({\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast}\right) \) in model (M-10), \( {\min}_i\left\{{\overline{o}}_i^{\ast}\right\}\le {\overline{o}}^{\ast}\le {\max}_i\left\{{\overline{o}}_i^{\ast}\right\} \) holds for both models. Based on Lemma 4, we can obtain that \( {\min}_i\left\{{o}_i\right\}\le {\overline{o}}^{\ast}\le {\max}_i\left\{{o}_i\right\} \). This completes the proof of of Property 1.
Property 2.
Let n = 2 and \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },{\overline{o}}^{\ast}\right\} \) be the optimal solution to (M-8) or (M-10). Then, \( {\overline{o}}_2^{\ast}\ge {\overline{o}}_1^{\ast } \) for o2 > o1.
Proof.
We first approve the property of (M-8). Using reduction to absurdity, we assume that o2 > o1 and \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },{\overline{o}}^{\ast}\right\} \) is the optimal solution to (M-8), where \( {\overline{o}}_1^{\ast }>{\overline{o}}_2^{\ast } \). Let \( {\ddot{o}}_1={\overline{o}}_2^{\ast } \) and \( {\ddot{o}}_2={\overline{o}}_1^{\ast } \), we find that\( \left|{\ddot{o}}_1-\ddot{o}\right|=\left|{w}_2\left({\overline{o}}_1^{\ast }-{\overline{o}}_2^{\ast}\right)\right|=\left|{\overline{o}}_1^{\ast }-{\overline{o}}^{\ast}\right|\le \varepsilon \) and \( \left|{\ddot{o}}_2-\ddot{o}\right|=\left|{w}_1\left({\overline{o}}_2^{\ast }-{\overline{o}}_1^{\ast}\right)\right|=\left|{\overline{o}}_2^{\ast }-{\overline{o}}^{\ast}\right|\le \varepsilon \).
Hence, \( \left\{{\ddot{o}}_1,{\ddot{o}}_2,\ddot{o}\right\}\in {\Omega}_8 \). By Lemma 4, we obtain that \( 2{o}_1-{\overline{o}}_2^{\ast }-{\overline{o}}_1^{\ast }<0 \) and \( 2{o}_2-{\overline{o}}_1^{\ast }-{\overline{o}}_2^{\ast }>0 \), therefore
which contradicts the assumption that \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },{\overline{o}}^{\ast}\right\} \) is the optimal solution to (M-8). Likewise, we validate Property 2 holds for (M-10). This completes the proof of Property 2.
Remark 5.
When n ≥ 3, the ranking of \( {\overline{o}}_i \) in \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast}\right\} \) may be different from that of oi in {o1, o2, …, on}. Thus, Property 2 is valid only when n = 2.
Property 3.
Let \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) be the optimal solution to (M-10), oh ∈ {o1, o2, …, on} such that oq =mini{oi} < oh < op = maxi{oi}, ch ≤ cp and ch ≤ cq. Then, \( {\overline{o}}_q^{\ast}\le {\overline{o}}_h^{\ast}\le {\overline{o}}_p^{\ast } \).
Proof.
We first approve that \( {\overline{o}}_h^{\ast}\le {\overline{o}}_p^{\ast } \). Using reduction to absurdity, we assume that \( {\overline{o}}_h^{\ast }>{\overline{o}}_p^{\ast } \). Let a feasible solution be \( \left\{{\ddot{o}}_1,{\ddot{o}}_2,\dots, {\ddot{o}}_n,\ddot{o}\right\} \), where
we find that
Let cp = ch + Δc and Δc ≥ 0, then we have.
which contradicts the fact that \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) is the optimal solution to (M-10).
Therefore, \( {\overline{o}}_h^{\ast}\le {\overline{o}}_p^{\ast } \). Likewise, we prove that \( {\overline{o}}_q^{\ast}\le {\overline{o}}_h^{\ast } \) holds. This completes the proof of Property 3.
Corollary 2.
Let {o1, o2, o3} be the original opinions such that o1 < o2 < o3 and c2 = mini{ci}. Then, \( {\overline{o}}_1^{\ast}\le {\overline{o}}_2^{\ast}\le {\overline{o}}_3^{\ast } \). In this case, (M-10) can be transform into a strictly convex programming model.
Property 4.
In (M-10), let op, oq ∈ {o1, o2, …, on} and \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) be the optimal solution to (M-10). Then, when cp = cq,
(1) if op > oq, \( {\overline{o}}_p^{\ast}\ge {\overline{o}}_q^{\ast } \);
(2) if op = oq, \( \left\{{\ddot{o}}_1,{\ddot{o}}_2,\dots, {\ddot{o}}_n,\ddot{o}\right\} \) is also the optimal solution to (M-10), where
Proof.
Using reduction to absurdity, we first prove part (1). Assuming \( {\overline{o}}_p^{\ast }<{\overline{o}}_q^{\ast } \) and \( \left\{{o}_1^{\prime },{o}_2^{\prime },\dots, {o}_n^{\prime },{o}^{\prime}\right\} \) is a feasible solution to (M-10), where
Then we have that \( {\sum}_{i-1}^n{c}_i{\left({o}_i-{o}_i^{\prime}\right)}^2-{\sum}_{i-1}^n{c}_i{\left({o}_i-{\overline{o}}_i^{\ast}\right)}^2=2{c}_p\left({\overline{o}}_p^{\ast }-{\overline{o}}_q^{\ast}\right)\left({o}_p-{o}_q\right)<0 \), which is contrary to the assumption that \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) is the optimal solution to (M-10). Therefore, part (1) is valid and it is straightforward to prove part (2). This completes the proof of Property 4.
Property 5.
Monotonicity. For model (M-8) and (M-10), let {o1, o2} be a set of original opinions and let {v1, v2} be a second set of original opinions, such that oi > vi, for i = 1, 2. Then, \( {\overline{o}}_i^{\ast}\ge {\overline{v}}_i^{\ast } \), for i = 1, 2.
Proof.
Without loss of generality, we assume that o2 > o1 and v2 > v1. Using reduction to absurdity, let \( {\overline{o}}_1^{\ast }<{\overline{v}}_1^{\ast } \) or \( {\overline{o}}_2^{\ast }<{\overline{v}}_2^{\ast } \). We consider the following three cases:
Case A: \( {\overline{o}}_1^{\ast }<{\overline{v}}_1^{\ast } \) and \( {\overline{o}}_2^{\ast }<{\overline{v}}_2^{\ast } \). In this case,
which contradicts the fact that \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },{\overline{o}}^{\ast}\right\} \) is the optimal adjusted opinions corresponding to {o1, o2}, when using (M-8) or (M-10).
Case B: \( {\overline{o}}_1^{\ast }<{\overline{v}}_1^{\ast } \) and \( {\overline{o}}_2^{\ast}\ge {\overline{v}}_2^{\ast } \). Under the circumstance, let \( {v}_1^{\prime }={\overline{o}}_1^{\ast } \) and \( {v}_2^{\prime }=\min \left\{{\overline{o}}_2^{\ast },{v}_2\right\} \). Then, \( \left\{{v}_1^{\prime },{v}_2^{\prime },{v}^{\prime}\right\}\in {\Omega}_8/{\Omega}_{10} \) and \( {\sum}_{i=1}^2{c}_i{\left({v}_i-{v}_i^{\prime}\right)}^2<{\sum}_{i=1}^2{c}_i{\left({v}_i-{\overline{v}}_i^{\ast}\right)}^2 \) hold, which is contrary to that \( \left\{{\overline{v}}_1^{\ast },{\overline{v}}_2^{\ast },\overline{v}\right\} \) is the optimal solution corresponding to {v1, v2}, when using (M-8) or (M-10).
Case C: \( {\overline{o}}_1^{\ast}\ge {\overline{v}}_1^{\ast } \) and \( {\overline{o}}_2^{\ast }<{\overline{v}}_2^{\ast } \). Let \( {o}_1^{\prime }=\max \left\{{o}_1,{\overline{v}}_1^{\ast}\right\} \) and \( {o}_2^{\prime }={\overline{v}}_2^{\ast } \). We prove that \( \left\{{o}_1^{\prime },{o}_2^{\prime },{o}^{\prime}\right\}\in {\Omega}_8/{\Omega}_{10} \) and \( {\sum}_{i=1}^2{c}_i{\left({o}_i-{o}_i^{\prime}\right)}^2<{\sum}_{i=1}^2{c}_i{\left({o}_i-{\overline{o}}_i^{\ast}\right)}^2 \), which contradicts the fact that \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },{\overline{o}}^{\ast}\right\} \) is the optimal solution corresponding to {o1, o2}, when using (M-8) or (M-10).
Based on the above three cases, we get that \( {\overline{o}}_1^{\ast}\ge {\overline{v}}_1^{\ast } \) and \( {\overline{o}}_2^{\ast}\ge {\overline{v}}_2^{\ast } \). This completes the proof of Property 5.
Remark 6.
This paper argues that Property 5 holds when n > 2, while it’s still an open problem when n ≥ 3.
Property 6.
Let{d1, d2, …, dn} and {o1, o2, …, on} be two sets of experts’ initial opinions, \( \left\{{\overline{d}}_1^{\ast },{\overline{d}}_2^{\ast },\dots, {\overline{d}}_n^{\ast },{\overline{d}}^{\ast}\right\} \) and \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) be the corresponding optimal solutions in model (M-10). If cp = cq, then \( {\sum}_{i=1}^n{c}_i{\left({o}_i-{\overline{o}}_i^{\ast}\right)}^2={\sum}_{i=1}^n{c}_i{\left({d}_i-{\overline{d}}_i^{\ast}\right)}^2 \), where
\( {d}_i=\left\{\begin{array}{c}{o}_q,i=p\kern1em \\ {}{o}_p,i=q\kern1em \\ {}{o}_i,i\ne p,q\end{array}\right. \) and \( {\overline{d}}_i^{\ast }=\left\{\begin{array}{c}{\overline{o}}_q^{\ast },i=p\kern1em \\ {}{\overline{o}}_p^{\ast },i=q\kern1em \\ {}{\overline{o}}_i^{\ast },i\ne p,q\end{array}\right. \).
Corollary 3.
Commutativity. Let {d1, d2, …, dn} be a permutation of {o1, o2, …, on} in (M-11). Then \( {\overline{d}}^{\ast }={\overline{o}}^{\ast } \).
Property 7.
Let {o1, o2, …, on} be a set of original opinions and {l1, l2, …, ln} be a second set of original opinions. Denote \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) and \( \left\{{\overline{l}}_1^{\ast },{\overline{l}}_2^{\ast },\dots, {\overline{l}}_n^{\ast },{\overline{l}}^{\ast}\right\} \) as the corresponding optimal solutions in (M-8). If oi + li = C (C is a constant) for all i = 1, 2, …, n, then \( {\overline{o}}^{\ast }+{\overline{l}}^{\ast }=C \) and \( {\overline{o}}_i^{\ast }+{\overline{l}}_i^{\ast }=C \) for all i = 1, 2, …, n.
Proof.
Denote the corresponding feasible sets of {o1, o2, …, on} and {l1, l2, …, ln} as Ω8o and Ω8l, respectively. Let \( {\ddot{l}}_i=C-{\overline{o}}_i^{\ast } \) for all i = 1, 2, …, n, then we can get that
Thus \( \left\{{\ddot{l}}_1,{\ddot{l}}_2,\dots, {\ddot{l}}_n,\ddot{l}\right\}\in {\Omega}_{8\mathrm{l}} \) and
Similarly, let \( {\ddot{o}}_i=C-{\overline{l}}_i^{\ast } \) for all i = 1, 2, …, n. Thus, \( \left\{{\ddot{o}}_1,{\ddot{o}}_2,\dots, {\ddot{o}}_n,\ddot{o}\right\}\in {\varOmega}_{8o} \) holds and
Consequently, \( {\sum}_{i=1}^n{c}_i{\left({l}_i-{\overline{l}}_i^{\ast}\right)}^2={\sum}_{i=1}^n{c}_i{\left({o}_i-{\overline{o}}_i^{\ast}\right)}^2 \). Thus, \( {\overline{o}}_i^{\ast }+{\overline{l}}_i^{\ast }=C \) for all i = 1, 2, …, n and \( {\overline{o}}^{\ast }+{\overline{l}}^{\ast }=C \). This completes the proof of Property 7.
Property 8.
Let {o1, o2, …, on} be a set of original opinions and {d1, d2, …, dn} be a second set of original opinions. Denote \( \left\{{\overline{o}}_1^{\ast },{\overline{o}}_2^{\ast },\dots, {\overline{o}}_n^{\ast },{\overline{o}}^{\ast}\right\} \) and \( \left\{{\overline{d}}_1^{\ast },{\overline{d}}_2^{\ast },\dots, {\overline{d}}_n^{\ast },{\overline{d}}^{\ast}\right\} \) as the as the corresponding optimal solutions in (M-14). If wi = wn + 1 − i and oi + di = C (C is a constant.) for all i = 1, 2, …, n, then \( {\overline{o}}^{\ast }+{\overline{d}}^{\ast }=C \) and \( {\overline{o}}_i^{\ast }+{\overline{d}}_i^{\ast }=C \) for all i = 1, 2, …, n.
Proof:
Denote the corresponding feasible sets of {o1, o2, …, on} and {d1, d2, …, dn} as Ω14o and Ω14d in (M-14). Let \( {\ddot{d}}_i=C-{\overline{o}}_i^{\ast } \) for all i = 1, 2, …, n, then we can derive that
Thus, \( \left\{{\ddot{d}}_1,{\ddot{d}}_2,\dots, {\ddot{d}}_n,\ddot{d}\right\}\in {\Omega}_{14d} \) and
Similarly, let \( {\ddot{o}}_i=C-{\overline{d}}_i^{\ast } \). We prove that \( \left\{{\ddot{o}}_1,{\ddot{o}}_2,\dots, {\ddot{o}}_n,\ddot{o}\right\}\in {\varOmega}_{14o} \) and
Then we get that \( {\sum}_{i=1}^n{c}_i{\left({d}_i-{\overline{d}}_i^{\ast}\right)}^2={\sum}_{i=1}^n{c}_i{\left({o}_i-{\overline{o}}_i^{\ast}\right)}^2 \). Therefore \( {\overline{o}}_i^{\ast }+{\overline{d}}_i^{\ast }=C \) for all i = 1, 2, …, n and \( {\overline{o}}^{\ast }+{\overline{d}}^{\ast }=C \). This completes the proof of Property 8. In the same way, we can prove that \( \left\{{\ddot{d}}_1,{\ddot{d}}_2,\dots, {\ddot{d}}_n,\ddot{d}\right\} \) is also the optimal solution to (M-15).
5 Illustrative examples and comparative analyses
In this section, we will offer three illustrative examples to demonstrate how the proposed models work in practice. In order to make a comparison with the methods in Ben-Arieh, Easton and Evans [15], Ben-Arieh and Easton [24], and Zhang, Dong, Xu and Li [31], this paper sets the same parameters and thresholds.
-
(1)
In Example 1, we apply the proposed methods to develop the government’s subsidy strategies for encouraging migrants to stay local during Spring Festival. Additionally, the results of CMQC, ε CMQC, and QMEC in Ben-Arieh, Easton and Evans [15] and the proposed methods are also numerically compared.
-
(2)
In Example 2, we mainly make a comparison with the existing linear cost consensus methods introduced by Ben-Arieh and Easton [24] and Zhang, Dong, Xu and Li [31].
-
(3)
The last example involves the GDM problem of house purchase, the data of which is from Zhang, Dong, Xu and Li [31].
5.1 Example 1
In January 2020, COVID-19 broke out in Wuhan, and then swept across the whole country with unprecedented hit to Chinese industries. Since April 29, 2020, the positive momentum in COVID-19 control has been locked in, and nationwide virus control in China is now being conducted on an ongoing basis.
Faced with the approaching Spring Festival in 2021, many places released rules for homecomings and persuaded employees to stay where they work during the holiday to reduce personnel flow and risks of epidemic prevention and control. In response to the call of the state, many people chose to stay put during Spring Festival. Yet they had to sacrifice the annual rights of family gathering. Thus, the subsidy policies introduced by the localities could be vital help in guaranteeing workers' welfare and enterprises’ production. Every migrant might expect different subsidy according to their own conditions, such as the affordability of tenancy in large cities, the willingness to work during the holiday and so forth. Thus, a government needs to negotiate with the workers in advance so as to provide reasonable subsidy strategies that satisfy the migrants’ expectation.
In the negotiation process, the local government plays the role of a moderator while employees who expect different levels of subsidies are the decision makers with divergent opinions. Suppose that the government could provide the basic allowance of at least 800 (Unit: RMB) to every migrant and there are mainly four different levels of expectations on the subsidy, denoted as e1, e2, e3, and e4. Compared with the basic allowance, the extra subsidies expected by the four types are: {o1, o2, o3, o4} = {0, 3, 6, 10} (Unit: %), and the corresponding weights are w1 = 0.3, w2 = 0.1, w3 = 0.4, and w4 = 0.2, respectively. Suppose the unit adjustment costs of e1, e2, e3, and e4 are c1 = 1, c2 = 2, c3 = 3, and c4 = 1 (Unit: 10RMB), respectively. To mitigate the difference among subsidy levels {o1, o2, o3, o4}, set the consensus threshold ε = 0.8 (Unit: %) Namely, the maximum deviation between any level of subsidy and the collective one is no more than 0.008 × 800 = 6.4 (RMB).
(1) Let the final collective opinion and individual opinions after adjustments be \(\bar{o}^{*}\) and \(\bar{o}_{i}^{*}\) (\(i = 1,2,3,4\)), respectively. If we use the WA operator to assemble the employees’ opinions, according to Theorem 1, (M-8) is equivalent to the following quadratic programming model:
The unique optimal solution to (M-16) is X∗ = (4.11, 4.11, 5.31, 5.71)T and the optimal value of the objective function is 39.19. Thus, for the government, the final subsidy policy provided to {e1, e2, e3, e4} is {833, 833, 842, 846} (Unit: RMB) and the minimum consensus cost is 391.9 RMB. Meanwhile, since the group consensus opinion is \( {\overline{o}}^{\ast }=\left(0.3,0.1,0.4,0.2\right){X}^{\ast }=4.91\% \), the collective subsidy standard is 839 RMB per person.
Let ε = 0.8. Under the different unit cost vectors (c1, c2, c3, c4), the final opinions of the employees and the minimum consensus costs in (M-8) are summarized in Table 2.
(2) If the OWA operator with weight vector w = (0.4, 0.3, 0.2, 0.1)T is used to aggregate the dispersive original opinions, (M-10) can be applied to achieve consensus. In (M-10), the group collective opinion is the ordered weighted average of the individual opinions sorted in descending order and assigned with importance weights of 0.4, 0.3, 0.2, and 0.1, respectively. If ε = 0.8, then grounded on, then grounded on (M-10), we have that
The constraint conditions xτ(i) − xτ(i − 1) ≤ 0, (i = 2, 3, 4) guarantee that xτ(i) is the ith largest value in the adjusted opinions {x1, x2, x3, x4} (i.e., \( \left\{{\overline{o}}_1,{\overline{o}}_2,{\overline{o}}_3,{\overline{o}}_4\right\} \)). Given that the real rankings of the opinions are unknown after being modified by (M-17), we need to consider all probable cases of order positions. Let \(P\) indicate the set of all the permutations on \(\{ 1,2,3,4\}\), then \(\left| P \right| = 24\). By inputting every possible permutation into (M-17) and comparing the corresponding optimal values, (M-17) is solved. We get that the unique optimal solution is \(X^{*} = (4.38,4.38,4.98,5.92)^{T}\) and the optimal value is \(f_{c} = 42.68\). Thus, during the whole consensus process, the subsidies paid by the government should increase by \(\bar{o}_{1}^{*} = 4.38\%\), \(\bar{o}_{2}^{*} = 4.38\%\), \(\bar{o}_{3}^{*} = 4.98\%\), and \(\bar{o}_{4}^{*} = 5.92\%\), respectively. Consequently, the optimal subsidies paid to e1, e2, e3, and e4 are 835, 835, 840, and 847 RMB, respectively. In addition, since the final group opinion is \(\bar{o}^{*} = (0.4,0.3,0.2,0.1)X^{*} = 5.18\%\), the collective subsidy for every employees equal to 841 RMB.
If we only transform the unit costs and preserve the remaining arguments, the unique optimal opinions provided by (M-10) can also be obtained, as shown in Table 3.
Results in Tables 1 and 2 validate Property 1 of (M-8) and (M-10). That is, the adjusted collective opinion is always within the scope of initial opinions. Based on Table 3, we observe that the order positions of the adjusted opinions are changed when \((c_{1} ,c_{2} ,c_{3} ,c_{4} ) = ({6},{3},{4},{1)}\). Thus, the property of order preservation is not valid for (M-10), when the unit costs are not uniform among experts. Besides, the result of (M-10) under \((c_{1} ,c_{2} ,c_{3} ,c_{4} ) = ({1},{2},{3},{1)}\) is consistent with Property 4 (1). To be specific, for any two experts with identical unit costs, if an initial opinion is larger, it will still be the larger one after being modified by (M-10).
(3) In this case, we use model (M-11), the first special case of (M-10), where the unit cost of each expert modifying his/her opinion is the same as each other. Let the associated weight vector of the OWA operator in (M-11) be w = (0.3, 0.1, 0.4, 0.2)T and the deviation threshold ε = 0.8. According to the property of order preservation, \( {\overline{o}}_4\ge {\overline{o}}_3\ge {\overline{o}}_2\ge {\overline{o}}_1 \) holds, thus \( \overline{o}=0.3{\overline{o}}_4+0.1{\overline{o}}_3+0.4{\overline{o}}_2+0.2{\overline{o}}_1 \). Then, based on Theorem 2, we get the following quadratic programming model:
The unique optimal solution to (M-18) is X∗ = (3.85, 4.25, 5.45, 5.45)T and the optimal value is fc = 37.97.. Therefore, the government could guide the employees to change their opinions into \( {\overline{o}}_1^{\ast }=3.85\% \), \( {\overline{o}}_2^{\ast }=4.25\% \), \( {\overline{o}}_3^{\ast }=5.45\% \), and \( {\overline{o}}_4^{\ast }=5.45\% \) {e1, e2, e3, e4} can receive are {831, 834, 844, 844} (Unit: RMB) and the collective level of allowance is 837 RMB based on \( {\overline{o}}^{\ast }=4.65\% \).
Table 4 lists the corresponding results obtained by (M-11) under the different consensus thresholds. Obviously, the lower the consensus degree is, the fewer opinion changes of experts are, which means less consensus cost has to be paid. Thus, the costs also have great impacts on the final individual consensus values.
(4) Here we utilize model (M-15), another special case of the consensus models under OWA operators, where the collective opinion is the arithmetic mean of the remaining values after deleting the maximum and minimum of individual opinions. Thus, the aggregation operator used by (M-15) in this case is the OWA operator with weight vector w = (0, 1/2, 1/2, 0)T. Suppose that x1 = maxi{xi}, and x2 = mini{xi}, then (M-15) can be transformed into the following model:
Based on Theorem 3, we need to solve another five models which assume the index tuples of maxi{oi} and mini{oi} to be (1, 3), (1, 4), (2, 3), (2, 4), and (3, 4), respectively. Through comparing the optimal values of the six models, we get that the optimal solution to (M-19) is X*= (3.94, 3.94, 4.54, 4.54)T and the optimal value is fc = 37.82. Thus, the local government would provide the allowances of {832, 832, 836, 836} (RMB) to {e1, e2, e3, e4} and pay the cost of 378.2 RMB to convince the employees. In addition, the collective subsidy obtained by (M-19) is 838 RMB under the adjusted group opinion o*= 4.74%.
Using (M-15) to aggregate individual opinions under the different unit costs ci (i = 1, 2, 3, 4), we get the corresponding results as shown in Table 5. It’s observed that under these four cost vectors, all the order positions of the adjusted opinions \( {\overline{o}}_i^{\ast } \) (i = 1, 2, 3, 4) in (M-15) coincide with the initial ones. However, it’s still an open problem to figure out the particular conditions under which the order preservation property holds for (M-15).
(5) If the relevant importance of the employees is assumed to be the same, then the group collective opinion is the arithmetic mean of the four kinds of opinions. Obviously, the aggregation operator used in this situation is the arithmetical mean operator with weight vector w = (0.25, 0.25, 0.25, 0.25)T. According to (M-8), we have the following quadratic programming model:
We get that the optimal solution to (M-20) is X* = (3.94, 3.94, 5.54, 5.54)T and the optimal value is fc = 37.82. Therefore, when the importance weight of each expert is uniform, e1, e2, e3, and e4 are suggested to change their opinions to \( {\overline{o}}_1^{\ast }=3.94\% \), \( {\overline{o}}_2^{\ast }=3.94\% \), \( {\overline{o}}_3^{\ast }=5.54\% \), \( {\overline{o}}_4^{\ast }=5.54\% \), and the final collective opinion \( {\overline{o}}^{\ast } \) is their arithmetical mean 4.74%. Under the collective allowance level of 838 RMB, the government would finally provide the subsidies of {832, 832, 844, 844} (RMB) to {e1, e2, e3, e4} and pay the consensus cost of 378.2 RMB.
Under the different unit adjustment costs, the unique optimal solutions and minimum consensus costs in (M-20) are summarized in Table 6.
Fig. 2 show the variation trends of optimal opinions of employees and optimal group opinion in every model as the deviation threshold grows, under the cost vector of (c1, c2, c3, c4) = (1, 2, 3, 1). Fig. 3 shows the changes of the consensus costs in the five models under the incremental deviation thresholds.
Figure 3 shows that the consensus costs in (M-10) under each value of ε are the highest, and the costs in models (M-15) and (M-20) are completely uniform. It’s observed that the distributions and variation trends of optimal opinions are influenced by the aggregation operators and deviation thresholds. In the consensus process, the costs paid by a moderator are closely related to the predefined consensus level. It’s no doubt that the higher consensus degree requires devoting more resources to be accomplished, yet the lower one can be easily achieved at a lower cost. Thus, the local government could select a proper deviation threshold to maximize the consensus degree under a given budget.
The above five cases match different types of scenes, respectively. In Case (1) (i.e., (M-8)), each expert is assigned with a settled importance weight according to his/her level of expertise (e.g., knowledge, confidence, the ability of making coherent assessments, etc.) with direct or indirect methods. Contrasted with Case (1), implicit in Case (2) (i.e., (M-10)) is the assumption that all experts are of equal importance. The OWA operators lie between the operators requiring all experts and at least one expert to be satisfied. Sometimes, the desired property of generalized commutativity also drives us to use OWA operators instead of the simple WA operators [28]. It should be noted that every importance weight assigned by OWA operators is associated with a particular ordered position rather than some decision maker. However, when the unit cost of each expert is equal (i.e., Case (3)), the weights of all experts are fixed. Case (4) aims at restraining deliberate manipulation in the decision making process by deleting the extreme values among individual opinions. In fact, Case (5) is also a special case of Case (2) that assigns the fixed weight of 1 / n to each expert.
Ben-Arieh, Easton and Evans [15] devised the methods of CMQC, ε CMQC, and QMEC. In the following, we compare the proposed methods with three existing quadratic cost consensus models using same indices.
We first compute the results of CMQC where adjusted individual opinions have to be uniform (i.e., ε = 0) and aggregation operators are not considered. Under the same cost vectors, the unanimous consensus results derived by CMQC are shown as Table 7.
Then we use the method of ε CMQC to assemble employees’ opinions. The optimal adjusted opinions under the different cost vectors are summarized in Table 8.
QMEC aims to maximize the number of experts fitting within consensus given a specified budget. Here we set the unit cost of each expert as c1 = 1, c2 = 2, c3 = 3, c4 = 1 and apply (M-5) to find the optimal adjustment alternatives under descending budgets B (Unit: 10RMB), as shown in Table 9. The consensus group is denoted as set \( {E}^{\prime } \). All members belonging to \( {E}^{\prime } \) share the same group opinion \( {\overline{o}}^{\ast } \), while the original opinions of other experts are preserved.
From the results in Tables 2, 3, 4, 5, 6, 7, 8, and 9, we make a comparative analysis of the proposed methods and CMQC, ε CMQC, and QMEC in Ben-Arieh, Easton and Evans [15]:
-
(1)
Compared with the results in other methods, the total costs of CMQC are always the highest. In CMQC, the adjusted opinions of all experts need to be completely uniform. Nevertheless, for the government, the unanimous consensus might be too expensive to be acomplished efficiently. Thus the consensus models acceptable for a proper deviation between individual opinions and group opinion are more feasible in operation.
-
(2)
In terms of the consensus costs, the method of ε CMQC is superior to the proposed methods considering aggregation operators. It seems that ε CMQC doesn’t consider the relationships between the individuals’ opinions and the group one. However, we observe that the optimal group collective opinions in ε CMQC are exactly equal to the averages of the maximum and minimum values of adjusted individuals’ opinions. In fact, Zhang, Dong, Xu and Li [31] revealed that the inherent aggregation operator of ε CMQC is the OWA operator with weight vector (1/2, 0, ..., 0, 1/2)T. That is, ε CMQC only considers the extreme opinions rather than the majority of decision makers’ opinions in pursurance of the minimum consensus cost. Apparently, the group opinion derived by ε CMQC is not representative enough as a result of overlooking the majority of views, especially when there are many decision makers involved. Therefore, compared with of ε CMQC, methods proposed in this paper have wider applications and can aggregate the group opinion from individual ones more resonably.
-
(3)
In Table 9, since the given budgets are lower than the minimum cost of CMQC (i.e., 608.6 RMB), the maximum number of experts that meet consensus is certainly no more than three. We find that in this caes, the method of QMEC can only earn the agreement among e1, e2, and e3 while e4 can never cross over into the consensus group, when the budget B are within the interval [30,60.86). Thus, every employee would receive the subsidy of 832 RMB even if e4 is not satisfied with this policy. This is mainly caused by the constraint of unanimous agreemnent. However, in the proposed methods, ε can be tuned to maximize the consensus levels among all employees under the specified budgets, as shown in Fig. 3. Therefore, utilizing the mehtods addressed in this paper, the opinion of every employee would be considered, and the government could also optimize its resource allocations during the consensus process.
5.2 Example 2
In this example, we use the data from Zhang, Dong, Xu and Li [31]. Assume that there are five experts, and their original opinions are: o1 = 0.5, o2 = 1.0, o3 = 2.5, o4 = 3.0, and o5 = 6.0. Let fc denote the minimum consensus cost and the deviation threshold ε be 0.8. In the following, we compare the results of the existing linear cost consensus methods (i.e., (M-1), (M-2), and (M-6)) and the proposed methods under WA and OWA operators.
-
(1)
We first use (M-8) to rectify individual expert’s opinions, where ε = 0.8 and the aggregation operator is the WA operator with weight vector w = (0.375, 0.1875, 0.25, 0.0625, 0.125)T. Table 10 displays the corresponding optimal individual and collective opinions and the minimum consensus costs obtained from (M-8) under the different values of unit costs ci (i = 1, 2, …, 5).
-
(2)
If the unit costs are uniform among experts, then (M-11) can be used to aggregate the individuals’ opinions. Set the associated weight vector of OWA operator be w = (0.375, 0.1875, 0.25, 0.0625, 0.125)T. The corresponding results are listed in Table 11, which shows that under the different consensus thresholds, the magnitude of experts’ opinion changes is different.
-
(3)
Utilize (M-15) to facilitate consensus among experts where ε = 0.8 and the OWA operator with weight vector w = (0, 1/3, 1/3, 1/3, 0)T is used. Table 12 presents the unique optimal solutions to (M-15) under varying cost vectors, which preserve the rankings of original opinions. However, the initial order positions were changed in Zhang, Dong, Xu and Li [31], when using the linear consensus cost model (M-6) with the same arguments and OWA operator.
This example was first investigated by Ben-Arieh and Easton [24], where they used the linear cost consensus models (M-1) and (M-2) to reach unanimous consensus and ε consensus, respectively. Let ε = 0. Table 13 shows the optimal solutions and the optimal values obtained by (M-1) under the varying cost vectors.
If we set ε = 0.8, the shifted individual opinions and collective opinion and the minimum consensus costs in (M-2) are shown in Table 14.
In Zhang, Dong, Xu and Li [31], (M-6) was also applied to examine this example, where {c1, c2, c3, c4, c5}={3, 4, 1, 6, 2}, ε = 0.8, and F is a WA operator with weight vector w = (0.375, 0.1875, 0.25, 0.0625, 0.125)T. It should be noted that (M-6) may have multiple optimal solutions. Table 15 shows three of the optimal solutions (\( \dot{o} \), \( \ddot{o} \) and \( \overset{\dddot{}}{o} \)) to (M-6).
Both Ben-Arieh and Easton [24] and Zhang, Dong, Xu and Li [31] constructed the consensus methods under the linear cost functions. From Tables 13 and 15, it is obvious that the consensus costs of (M-1) for the unanimous consensus are substantially higher than those of (M-6) that considers consensus degree. When complete agreement is not necessary, based on Tables 14 and 15, it’s observed that method (M-2) proposed by Ben-Arieh and Easton [24] has lower costs than (M-6) by Zhang, Dong, Xu and Li [31]. However, Zhang, Dong, Xu and Li [31] prove that when (M-6) uses the OWA operator with weight vector w = (1/2, 0, ..., 0, 1/2)T, (M-6) is equivalent to (M-2). Therefore, as we have pointed out in Sect. 2.2, method in Zhang, Dong, Xu and Li [31] is an extension of Ben-Arieh and Easton [24]’s work.
The main difference between the method in Zhang, Dong, Xu and Li [31] and the proposed method lies in the definition of consensus cost. The first derivative of the quadratic cost function increases as opinion adjustment rises, which reflects the psychological changes of experts. In general, an expert would show more resistance when he/she is required to make more compromises. However, the first derivative of the linear cost function is uniform no matter how much the individual opinion is changed. Thus, the quadratic cost functions could better characterize the consensus costs paid to the experts. Apart from the cost functions, the solving approaches are also distinct. The method in Zhang, Dong, Xu and Li [31] is based on linear programming to obtain the optimal solution, while the proposed methods are grounded on strictly convex quadratic programming. It is widely known that the optimal solution to the strictly convex quadratic programming exists and is unique. Thus, the proposed models are superior to Zhang, Dong, Xu and Li [31]’s models with respect to the uniqueness of optimal solution.
5.3 Example 3
Suppose there is a family consisting of four members ej (j = 1, 2, 3, 4) choosing an apartment from five alternatives Ai (i = 1, 2, …, 5). Denote oij the preference of ej on Ai. The stronger the preference of member ej for apartment Ai, the higher oij will be. The preference information of the four members is presented in Table 16.
We observe that e1, e2, e3, and e4 prefer A3, A2, A4, and A1, respectively. To this end, minimum cost consensus models are applied to reach consensus among the family members. Denote \( {\overline{o}}_{ij}^{\ast } \) as the optimal adjusted opinions of ej on Ai and \( {\overline{o}}_i^{\ast } \) the collective evaluation on Ai.
-
(1)
Model (M-8) is first applied to aggregate the original opinions, where {c1, c2, c3, c4} = {1, 2, 1, 1}, ε = 1, and the weight vector of WA operator is w = (0.2, 0.3, 0.25, 0.25)T. Table 17 lists the adjusted individual opinions \( {\overline{o}}_{ij}^{\ast } \) and collective opinions \( {\overline{o}}_i^{\ast } \) derived from (M-8).
-
(2)
Assume that the unit cost of each member is uniform, the weight vector of OWA operator is w = (0.2, 0.3, 0.25, 0.25)T and ε = 1, then (M-11) is employed to adjust the original individual opinions. Table 18 shows the corresponding results derived from (M-11).
-
(3)
Suppose {c1, c2, c3, c4} = {1, 2, 1, 1} and ε = 1, then under the OWA operator with weight vector w = (0, 1/3, 1/3, 1/3, 0)T, model (M-15) is used to facilitate consensus among the family members. The evaluations adjusted by (M-15) are presented in Table 19.
-
(4)
When ε = 0 and {c1, c2, c3, c4} = {1, 2, 1, 1}, the proposed method in this paper reduces to CMQC developed by Ben-Arieh, Easton and Evans [15]. CMQC is the quadratic cost consensus method to achieve completely unanimous agreement. The corresponding consensus results are shown in Table 20.
-
(5)
If we use the OWA operator with weight vector w = (1/2, 0, 0, 0, 1/2)T in (M-10), then the proposed model is equivalent to the model of ε CMQC. Table 21 shows the optimal solutions in ε CMQC.
-
(6)
When the quadratic cost function of CMQC is swapped for the linear one, (M-1) addressed by Ben-Arieh and Easton [24] can also be used to achieve complete agreement among family members. We still set {c1, c2, c3, c4} = {1, 2, 1, 1}, then the optimal solutions obtained by (M-1) are presented in Table 22.
-
(7)
In practice, it’s generally expensive and time-wasting to achieve the full and unanimous agreement. Thus, we set ε = 1 and {c1, c2, c3, c4} = {1, 2, 1, 1}. The linear cost model (M-2) is used to aggregate family members’ opinions and the adjusted opinions are shown in Table 23.
-
(8)
Furthermore, incorporating aggregation operators into (M-2), model (M-6) can be applied to attain consensus on the house purchase. Let the aggregation operator F in (M-6) be the WA operator with weight vector w = (0.2, 0.3, 0.25, 0.25)T, {c1, c2, c3, c4} = {1, 2, 1, 1}, and ε = 1. Table 24 lists the evaluations after being adjusted by (M-6).
According to the optimal collective opinions after modifying, we can obtain the ranking of Ai (i = 1, 2, …, 5). In Tables 17, 19, 20, 21 and 24, the ranking is: A2 ≻ A5 ≻ A4 ≻ A1 ≻ A3. In Table 18, the ranking is: A2 ≻ A4 ≻ A5 ≻ A1 ≻ A3. In Tables 22 and 23, the rankings are A1 ∼ A2 ∼ A4 ∼ A5 ≻ A3 and A2 ≻ A4 ∼ A5 ≻ A1 ∼ A3, respectively. Although the priorities of Ai are not exactly the same, each table shows that \( {\overline{o}}_2^{\ast }={\max}_i\left\{{\overline{o}}_i^{\ast}\right\} \). Hence, \(A_{2}\) is the optimal alternative for the family. Particularly, the prioritization between alternatives \(A_{4}\) and \(A_{5}\) is changed under the diverse aggregation operators, which shows the importance of aggregation operators in GDM.
The above numerical comparative analyses reveal the validity and usability of the proposed models. Compared with the consensus methods in Ben-Arieh, Easton and Evans [15], the consensus models proposed in this paper are not only more feasible and efficient in terms of practical applications, but are also more flexble when applied to different scenarios. Moreover, different form refrences [24, 31], this paper also employs quadratic cost functions to capture experts’ psychological changes in negotiation process and could provide unique optimal solutions for GDM problems.
6 Conclusions
In GDM, aggregation operators can be applied to reveal the inherent relationships between individuals’ opinions and the collective opinion. In the existing minimum cost consensus models, the objective functions are usually assumed to be linear cost functions and the optimal solutions are attained by linear programming. However, there may be infinite optimal solutions to a linear programming model, which may escalate the complexity of GDM problems. Additionally, the unit adjustment costs in the linear cost functions are constant, which ignores the impact on unit costs made by the opinion adjustments. In order to overcome the shortages, this paper develops an extended minimum cost consensus model with quadratic costs under aggregation operators. The proposed model reduces to the consensus model of Ben-Arieh, Easton and Evans [15] when the adjusted individual opinions are equal to the consensus opinion.
In addition, this paper closely examines the proposed models under the WA operator and OWA operators. Corresponding approaches are provided based on strictly convex quadratic programming, the optimal solution of which exists and is unique. Furthermore, these models are in line with some ideal properties.
Fuzzy information is often applied to denote the preference information of experts over a set of alternatives [33, 40,41,42] when experts’ opinions are vague. Both individual consistency and consensus level measures are essential for a rational GDM problem [40]. Thus, how to extend this model to a certain degree of individual consistency under reciprocal fuzzy preference relations is one of our future research topics. In addition, many other operators such as Bonferroni mean [43, 44], Maclaurin symmetric mean [45, 46], etc. are as effective as the WA and OWA operators in decision making problems. Hence, how to apply the proposed model to other aggregation operators will be also discussed in the future. With great prosperity in information technology, a large spectrum of decision makers could simultaneously participate in decision making processes, such as e-democracy and social networks. Recently, the large-scale group decision making (LSGDM) has become a hotspot among researchers [47,48,49]. Thus, how to employ the proposed method to practical LSGDM problems, like high-speed rail passenger requirement management [50, 51], systemic risk management of food supply chains [52] and so forth.
References
Palomares I, Liu J, Xu Y, Martínez L (2012) Modelling experts’ attitudes in group decision making. Soft Comput 16:1755–1766
Gong ZW, Zhang HH, Forrest J et al (2015) Two consensus models based on the minimum cost and maximum return regarding either all individuals or one individual. Eur J Oper Res 240:183–192
Dong QX, Cooper O (2016) A peer-to-peer dynamic adaptive consensus reaching model for the group AHP decision making. Eur J Oper Res 250:521–530
Li Y, Zhang HJ, Dong YC (2017) The interactive consensus reaching process with the minimum and uncertain cost in group decision making. Appl Soft Comput 60:202–212
Liu X, Xu YJ, Montes R et al (2019) Alternative ranking-based clustering and reliability index-based consensus reaching process for hesitant fuzzy large scale group decision making. IEEE Trans Fuzzy Syst 27:159–171
DeGroot MH (1974) Reaching a consensus. J Am Stat Assoc 69:118–121
Escobar MT, Aguarón J, Moreno-Jiménez JM (2015) Some extensions of the precise consistency consensus matrix. Decis Support Syst 74:67–77
Wu WS, Kou G (2016) A group consensus model for evaluating real estate investment alternatives. Financial Innov 2(1):8
Meng FY, An QX, Chen XH (2016) A consistency and consensus-based method to group decision making with interval linguistic preference relations. J Oper Res Soc 67:1419–1437
Palomares I, Estrella FJ, Martinez L, Herrera F (2014) Consensus under a fuzzy context: Taxonomy, analysis framework AFRYCA and experimental case of study. Inf Fusion 20:252–271
Sun BZ, Ma WM (2015) An approach to consensus measurement of linguistic preference relations in multi-attribute group decision making and application. Omega 51:83–92
Xu XH, Du ZJ, Chen XH (2015) Consensus model for multi-criteria large-group emergency decision making considering non-cooperative behaviors and minority opinions. Decis Support Syst 79:150–160
Zhang HJ, Zhao SH, Kou G et al (2020) An overview on feedback mechanisms with minimum adjustment or cost in consensus reaching in group decision making: Research paradigms and challenges. Inf Fusion 60:65–79
Xu YJ, Wen XW, Zhang WC (2018) A two-stage consensus method for large-scale multi-attribute group decision making with an application to earthquake shelter selection. Comput Ind Eng 116:113–129
Ben-Arieh D, Easton T, Evans B (2009) Minimum cost consensus with quadratic cost functions. IEEE Trans. Syst. Man Cybern. - Part A: Syst. Hum 39:210–217
Tapia Garcia JM, del Moral MJ, Martinez MA, Herrera-Viedma E (2012) A consensus model for group decision making problems with linguistic interval fuzzy preference relations. Expert Syst Appl 39:10022–10030
Dong YC, Zhang HJ, Herrera-Viedma E (2016) Consensus reaching model in the complex and dynamic MAGDM problem. Knowl Based Syst 106:206–219
Jose del Moral M, Chiclana F, Miguel Tapia J, Herrera-Viedma E (2018) A comparative study on consensus measures in group decision making. Int.J Intell Syst 33:1624–1638
Cao MS, Wu J, Chiclana F, Herrera-Viedma E (2021) A bidirectional feedback mechanism for balancing group consensus and individual harmony in group decision making. Inf Fusion 76:133–144
Wu J, Zhao ZW, Sun Q, Fujita H (2021) A maximum selft-esteem degree based feedback mechanism for group consensus reaching with the distributed linguistic trust propagation in social network. Inf Fusion 67:80–93
Herrera F, Herrera-Viedma E, Verdegay JL (1996) A model of consensus in group decision making under linguistic assessments. Fuzzy Sets Syst 78:73–87
Roubens M (1997) Fuzzy sets and decision analysis. Fuzzy Sets Syst 90:199–206
Zhang HH, Kou G, Peng Y (2019) Soft consensus cost models for group decision making and economic interpretations. Eur J Oper Res 277:964–980
Ben-Arieh D, Easton T (2007) Multi-criteria group consensus under linear cost opinion elasticity. Decis Support Syst 43:713–721
Kou G, Ergu DJ, Lin CS, Chen Y (2016) Pairwise comparison matrix in multiple criteria decision making. Technol Econ Dev Econ 22:738–765
Kahneman D, Tversky A (1979) Prospect theory: An analysis of decision under risk. Econometrica 47:263–291
Gong ZW, Xu XX, Li LS, Xu C (2015) Consensus modeling with nonlinear utility and cost constraints: A case study. Knowl Based Syst 88:210–222
Yager RR (1988) On ordered weighted averaging aggregation operators in multicriteria decision making. IEEE Trans Syst Man Cybern 18:183–190
Yager RR, Kacprzyk J, Beliakov G (2011) Recent developments in the ordered weighted averaging operators: Theory and practice. Springer-Verlag, Berlin Heidelberg
Chen ZS, Yu C, Chin KS, Martinez L (2019) An enhanced ordered weighted averaging operators generation algorithm with applications for multicriteria decision making. Appl Math Model 71:467–490
Zhang GQ, Dong YC, Xu YF, Li HY (2011) Minimum-cost consensus models under aggregation operators. IEEE Trans Syst Man Cybern - Part A: Syst Hum 41:1253–1261
Cheng D, Zhou ZL, Cheng FX et al (2018) Modeling the minimum cost consensus problem in an asymmetric costs context. Eur J Oper Res 270:1122–1137
Gong ZW, Xu XX, Zhang HH et al (2015) The consensus models with interval preference opinions and their economic interpretation. Omega 55:81–90
Zhang BW, Liang HM, Gao Y, Zhang GQ (2018) The optimization-based aggregation and consensus with minimum-cost in group decision making under incomplete linguistic distribution context. Knowl Based Syst 162:92–102
Lu YL, Xu YJ, Herrera-Viedma E, Han YF (2021) Consensus of large-scale group decision making in social network: the minimum cost model based on robust optimization. Inf Sci 547:910–930
Wu J, Dai LF, Chiclana F et al (2018) A minimum adjustment cost feedback mechanism based consensus model for group decision making under social network with distributed linguistic trust. Inf Fusion 41:232–242
Wu ZB, Yang XY, Tu JC, Chen X (2020) Optimal consistency and consensus models for interval additive preference relations: A discrete distribution perspective. J Oper Res Soc 71:1479–1497
Liu X, Xu YJ, Herrera F (2019) Consensus model for large-scale group decision making based on fuzzy preference relation with self-confidence: Detecting and managing overconfidence behaviors. Inf Fusion 52:245–256
Dong YC, Xu YF, Li HY, Feng B (2010) The OWA-based consensus operator under linguistic representation models using position indexes. Eur J Oper Res 203:455–463
Xu YJ, Wu NN (2019) A two-stage consensus reaching model for group decision making with reciprocal fuzzy preference relations. Soft Comput 23:8057–8073
Wan SP, Wang F, Dong JY (2017) Additive consistent interval-valued Atanassov intuitionistic fuzzy preference relation and likelihood comparison algorithm based group decision making. Eur J Oper Res 263:571–582
Liu J, Chan FTS, Li Y et al (2012) A new optimal consensus method with minimum cost in fuzzy group decision. Knowl Based Syst 35:357–360
Bonferroni C (1950) Sulle medie multiple di potenze. B Unione Mat Ital 5:267–270
Yager RR (2009) On generalized Bonferroni mean operators for multi-criteria aggregation. Int J Approx Reason 50:1279–1286
Qin JD, Liu XW (2014) An approach to intuitionistic fuzzy multiple attribute decision making based on Maclaurin symmetric mean operators. J Intell Fuzzy Syst 27:2177–2190
Maclaurin C (1729) A second letter to Martin Folkes, Esq.; concerning the roots of equations, with the demonstartion of other rules in algebra. Philos Trans R Soc A-Math Phys Eng Sci 36:59–96
Dong YC, Zhao SH, Zhang HJ et al (2018) A self-management mechanism for noncooperative behaviors in large-scale group consensus reaching processes. IEEE Trans Fuzzy Syst 26:3276–3288
Labella A, Liu Y, Rodriguez RM, Martinez L (2018) Analyzing the performance of classical consensus models in large scale group decision making: A comparative study. Appl Soft Comput 67:677–690
Zhang HJ, Dong YC, Herrera-Viedma E (2018) Consensus building for the heterogeneous large-scale GDM with the individual concerns and satisfactions. IEEE Trans Fuzzy Syst 26:884–898
Chen ZS, Liu XL, Chin KS et al (2021) Online-review analysis based large-scale group decision-making for determining passenger demands and evaluating passenger satisfaction: Case study of high-speed rail system in China. Inf Fusion 69:22–39
Chen ZS, Liu XL, Rodriguez RM et al (2020) Identifying and prioritizing factors affecting in-cabin passenger comfort on high-speed rail in China: A fuzzy-based linguistic approach. Appl Soft Comput 95:106558
Jin CY, Levi R, Liang Q et al (2021) Testing at the source: Analytics-enabled risk-based sampling of food supply chains in China. Manage Sci 67:2985-2996
Acknowledgements
This research was partly supported by National Natural Science Foundation of China (NSFC) under Grant 71871085, and also supported by the Spanish State Research Agency under Project PID2019-103880RB-I00/AEI/10.13039/501100011033.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zhang, R., Huang, J., Xu, Y. et al. Consensus models with aggregation operators for minimum quadratic cost in group decision making. Appl Intell 53, 1370–1390 (2023). https://doi.org/10.1007/s10489-021-02948-5
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-021-02948-5