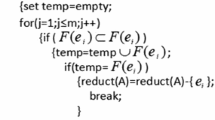A novel algorithm for all normal parameter reductions of a soft set based on object weighting and integer partition

Abstract

This paper aims to propose a novel algorithm for computing all normal parameter reductions of the soft set (# NPRS for short). Firstly, a weight vector is assigned to objects of the soft set domain. Then, a necessary condition for a normal parameter direction can be derived. A parameter subset is a solution only if the total value of the weighted sum of corresponding parameter approximations is a multiple of a constant number, which is equal to the sum of weights. Based on this necessary condition, we can figure out all potential solutions by using integer partition technique. It needs only to screen out the right ones at last. Experimental results are listed and compared when weight vectors are UNA, BIN, TER, OCT, DEC, DUO and HEX. Comparison results show that our method has a better performance for solving # NPRS.

1 Introduction

0-1 valued information systems are common in our daily life and research work. It is generally represented in a matrix or a table, where the rows correspond to the objects in the domain, and the columns are for the attributes or parameters. For instances, the black and white picture, the adjacency matrix for a graph [1], and the vote results in multi-attribute decision making when the parameters mean the experts, who are supposed to choose a subset of objects on their own opinions.

In 1999 Molodtsov brought in the concept of soft set [2], which provided a novel mathematical tool for dealing with uncertainties. A soft set can also be represented as a 0-1 valued information system [3]. Every column stands for a parameter approximation of the soft set. The decision making model is similar with that of multi-attribute decision making. The number of parameter approximations each object belongs to is defined as the choice value function of the soft set. An object is an optimal solution when it belongs to maximum number of parameter approximations. We refer to more details in Section 2.

Many works have been made by researchers on soft set theory and its potential applications [4,5,6,7,8,9,10,11,12]. Combined with different mathematical structures, soft set has been studied algebraically [13,14,15,16,17,18] and topologically [19,20,21]. Various types of vague concepts have been combined with soft set theory such as fuzzy soft sets [22,23,24,25,26, 33], soft rough sets [27,28,29,30].

Another important direction for soft set study is the parameter reduction problem of soft sets. Based on different conditions, several kinds of parameter reduction problems of soft sets or fuzzy soft sets [31, 32, 34,35,36,37,38,39,40,41,42,43,44] have been defined and discussed. The parameter reduction problems of soft sets actually deal with a kind of important structure for the parameter domain.

In this paper we will focus on a kind of parameter reduction problem, which is named as normal parameter reduction of soft sets. A normal parameter reduction is related with a parameter subset whose sum of rows are all equal. This means that once these parameters are deleted from the parameter domain, the same amount of choice values will be lost for every object, hence the same rank of the objects will be maintained.

Different algorithms have been proposed for computing the normal parameter reductions of a soft set in an efficient way. A kind of parameter subset whose sum of column values is an integral multiple of the number of rows (i.e., number of objects), was first given by [43]. This kind of parameter subset plays as a necessary condition in normal parameter reduction of soft set, i.e., the mentioned parameter subset is a candidate for normal parameter reduction of soft sets. Ma et al. [43] developed an algorithm for normal parameter reduction of soft set. Unnecessary repetition can be avoided because the sum of each column can be calculated in advance. In [45], a hierarchical algorithm for solving the minimal k|U| parameter subset is studied, and then based on the minimal candidate set, the normal parameter reduction problem of soft set can be solved by testing the disjoint combinations of these minimal k|U| parameter subsets.

Particle Swarm Optimization Algorithm was brought in to solve the normal parameter reductions in soft sets [36]. However, it can’t guarantee that an optimal solution will be found [37]. Then a 0-1 linear programming method for finding an optimal normal parameter reduction of a soft set has been investigated in [38]. But the problem of finding all normal parameter solutions has not been investigated in [38].

Recently [44] brought the integer partition technique into the normal parameter reduction problem of soft sets. It was based on the necessary condition pointed out in [43]. Its main contribution is that an explicit method for computing the candidates (i.e., k|U| parameter subsets) satisfying the necessary condition is proposed. However, there are two problems: (1) the number of candidates increases quickly when the size of soft sets grows; (2) the success rate of this method is quite low. Only a small proportion of the found candidates become the solutions.

The motivation of this paper is as follows: we should not be confined to the column sums. We notice that the column sum of a parameter approximation can be represented by each of the following expressions:

$$ \begin{array}{@{}rcl@{}} S_{F}(e)&=&\sum\limits_{i=1}^{n}F(u_{i},e), \end{array} $$

(1.1)

$$ \begin{array}{@{}rcl@{}} S_{F}(e)&=&\sum\limits_{i=1}^{n}(1\times F(u_{i},e)). \end{array} $$

(1.2)

From expression (1.2) we see that there exists a weight vector ω = (1, 1, ⋯ , 1) for objects of the soft domain. So our idea is: can we define different weight vector for objects and achieve a potential better efficiency? For example, every parameter approximation can be represented as a 0-1 valued vector. So we try to connect the weight vector with Binary system and some other systems.

It’s very interesting to investigate the efficiencies of different weight vectors. We find that the method of [44] can be improved.

The remainder of this paper is organized as follows. Section 2 introduces basic concepts such as soft set, and the problem of normal parameter reduction. The theoretical foundation of this paper is proposed in Section 3. Section 4 develops a novel algorithm for the mentioned problem. Experimental results showing the efficiency and success rate of our algorithm in normal parameter reduction problem are listed in Section 5. In Section 6 we make a short introduction to an APP, which is based on the algorithm and can be run as an application of our algorithm in MATLAB. Finally, we come to a conclusion of this article and outlook for potential future work.

2 Preliminaries

In this paper, suppose U = {u₁, u₂, ⋯ , u_n} is a finite set of objects, E is a set of parameters. For example, the attributes in information systems can be taken as parameters. ℘(U) means the power set of U, |A| means the cardinality of set A. By [2] and [38] we have basic concepts about soft sets shown in Definitions 2.1 and 2.2.

Definition 2.1 (Soft set)

A soft set on U is a pair S = (F, A), where

• (i) A is a subset of E;

• (ii) $F: A\rightarrow \wp (U)$, ∀e ∈ A, F(e) means the subset of U corresponding with parameter e, and F(e) is called e −approximation of S. We also use F(u, e) = 1 (F(u, e) = 0) to mean than u is (not) an element of F(e).

Definition 2.2 (Support set of parameters for objects)

Let S = (F, A) be a soft set over U. ∀u ∈ U, define the support set of parameters for u as the set {e ∈ A|F(u, e) = 1}, denoted by supp(u).

Definition 2.3 (Choice value function)

Let S = (F, A) be a soft set over U. The function $\sigma _{S}: U\rightarrow \mathbb {N}$ defined by $\sigma _{S}(u)=|supp(u)|={\sum }_{e\in A}F(u,e)$ is called the choice value function of S.

We write σ_S as σ for short if the underlying soft set S is explicit.

Definition 2.4

Let S = (F, A) be a soft set over U, $B\subseteq A$ define $S_{F}(e)={\sum }_{u\in U}F(u,e)$; $S_{F}(B)={\sum }_{e\in B}S_{F}(e)$.

Example 2.1

Table 1 represents a soft set S = (F, E) over objects domain U = {u₁, u₂, ⋯ , u₆} and parameters domain E = {e₁, e₂, ⋯ , e₇}, where F(e₁) = {u₁, u₄, u₅}, F(e₂) = {u₆}, F(e₃) = {u₁, u₂, u₄, u₅, u₆}, F(e₄) = {u₁, u₂, u₆}, F(e₅) = {u₁, u₂}, F(e₆) = {u₂, u₃, u₆}, F(e₇) = {u₂, u₃}, σ_S can be regarded as the choice value function of soft set S.

Table 1 Tabular representation of a soft set S = (F, A)

According to [38], we have the following concept about normal parameter reduction of soft sets.

Definition 2.5 (Normal parameter reduction)

For soft set S = (F, A) over U, $B\subseteq A$, B ≠ ∅, if the constraint

$$ \underset{e\in A-B}{\sum}F(u_{1},e)=\cdots=\underset{e\in A-B}{\sum}F(u_{n},e) $$

(2.1)

is satisfied, then B is called a normal parameter reduction of S.

Example 2.2

Take the soft set in Example 2.1 for instance. It’s easy to check that

$$\sum\limits_{e\in\{e_{1}, e_{2}, e_{7}\}}F(u_{1},e)=\cdots=\sum\limits_{e\in \{e_{1}, e_{2}, e_{7}\}}F(u_{6},e)=1,$$

thus A −{e₁, e₂, e₇} is a normal parameter reduction.

Note that we don’t require the minimality condition for normal parameter reductions as defined in [32].

Main Definition 2.1 (♯ NPRS)

For soft set S = (F, A) over U, compute the set of all normal parameter reductions of S, denoted by ♯ NPRS.

3 Theoretical foundations

3.1 Weighting operation for objects in U of a soft set

Definition 3.1

Suppose S = (F, A) is a soft set over U = {u₁, u₂,⋯, u_n}. |U| = n, |A| = m. ω = (ω₁, ω₂, ⋯ , ω_n) is a weight vector with non-negative component ω_i for u_i, i = 1, 2, ⋯ , n. ∀e_i ∈ A, define $S_{F}^{\omega }(e_{i})$ as follows:

$$ S_{F}^{\omega}(e_{i})=\sum\limits_{k=1}^{n}\omega_{k}F(u_{k}, e_{i}). $$

(3.1)

Definition 3.2

Suppose S = (F, A) is a soft set over U. |U| = n, |A| = m. A₁ ⊂ A. Define

$$ S_{F}^{\omega}(A_{1})=\underset{e\in A_{1}}{\sum} S_{F}^{\omega}(e). $$

(3.2)

Example 3.1

With respect to the soft set shown in Table 1, we define different weight vectors: (i) The weight vector ω in Table 2 is equal to (1, 1, ⋯ , 1). In this situation we denote $S_{F}^{\omega }(e)$ as $S_{F}^{UNA}(e)$, and we see that $S_{F}^{UNA}(e)$ is actually equal to S_F(e) defined in Definition 2.4.

• (ii) When a soft set is represented in a table as Example 2.1 does, every e −approximation F(e) can be regarded as a 0 − 1 vector. Inspired by Binary, we define a weight vector (2⁰, 2¹, ⋯ , 2⁵) for objects u_i, i = 6, 5, ⋯ , 1. Here we denote $S_{F}^{\omega }(e)$ by $S_{F}^{{{\mathscr{B}}\mathcal {I}\mathcal {N}}}(e)$.

• (iii) Similarly, if we make use of Ternary, Octal, Decimal, Duodecimal, and Hexadecimal, we can define weight vectors (3⁰, 3¹, ⋯ , 3⁵), (8⁰, 8¹, ⋯ , 8⁵), (10⁰, 10¹, ⋯ , 10⁵), (12⁰, 12¹, ⋯ , 12⁵), (16⁰, 16¹, ⋯ , 16⁵) to objects u_i, i = 6, 5, ⋯ , 1. See Table 3. We denote the function $S_{F}^{\omega }(e)$ by $S_{F}^{\mathcal {T}\mathcal {E}\mathcal {R}}(e_{i})$, $S_{F}^{\mathcal {O}\mathcal {C}\mathcal {T}}(e_{i})$, $S_{F}^{\mathcal {D}\mathcal {E}\mathcal {C}}(e_{i})$, $S_{F}^{\mathcal {D}\mathcal {U}\mathcal {O}}(e_{i})$ and $S_{F}^{{\mathscr{H}}\mathcal {E}\mathcal {X}}(e_{i})$, respectively. See Table 4 for more details.

Table 2 Function $S_{F}^{\mathcal {U}\mathcal {N}\mathcal {A}}(e_{i})$ for the soft set S = (F, A) in Table 1

Table 3 Different weighting vectors for the objects of soft set S = (F, A) in Table 1

Table 4 Function S_F(e_i) for the soft set S = (F, A) in Table 1

Proposition 3.1

Suppose S = (F, A) is a soft set over U. |U| = n, |A| = m. As to the function $S_{F}^{\omega }(e_{i})$, when ω = BIN, TER, OCT, DEC, DUO, HEX we have the following properties:

• (i) F(e_i) = F(e_j) if and only if $S_{F}^{\omega }(e_{i})=S_{F}^{\omega }(e_{j}).$

• (ii) If F(e_i) = ∅, then $S_{F}^{\omega }(e_{i})=0.$

• (iii) If F(e_i) = U, then $S_{F}^{\omega }(e_{i})={\sum }_{i=1}^{n}\omega _{i}.$

• (iv) ∀e ∈ A, we have $0<=S_{F}^{\omega }(e_{i})<={\sum }_{i=1}^{n}\omega _{i}.$

• (v) If $F(e_{i})\subsetneq F(e_{j})$, then $S_{F}^{\omega }(e_{i})<S_{F}^{\omega }(e_{j}).$

• (vi) If $S_{F}^{\omega }(e_{i})$ and n are both given, then we can retrieve F(e_i).

3.2 A new necessary condition for normal parameter reduction problems of soft set

Theorem 3.1

[43] (Necessary Condition I for normal parameter reduction of soft sets) Given a soft set S = (F, A) over U, $B\subseteq A$, B ≠ ∅, if B is a normal parameter reduction of S by Definition 3.1, then

i.e.,

Theorem 3.2 (Necessary Condition II for normal parameter reduction of soft sets)

Suppose S = (F, A) is a soft set over U = {u₁, u₂,⋯, u_n}. |U| = n, |A| = m. ω = (ω₁, ω₂, ⋯ , ω_n) is a real-valued weight vector with non-negative component ω_i for u_i, i = 1, 2, ⋯ , n. $B\subseteq A$, B≠∅. If B is a normal parameter reduction of S by Definition 3.1, then $\exists K\in \mathbb {Z}$ satisfying

i.e.,

Proof

$$\underset{e\in A-B}{\sum}S_{F}^{\omega}(e)=\underset{e\in A-B}{\sum}\left( \sum\limits_{i=1}^{n} F(u_{i}, e)\times \omega_{i}\right)$$

$$=\sum\limits_{i=1}^{n}\left( \underset{e\in A-B}{\sum}F(u_{i}, e)\times \omega_{i}\right)$$

$$=\sum\limits_{i=1}^{n}\left( \left( \underset{e\in A-B}{\sum}F(u_{i}, e)\right)\times \omega_{i}\right)$$

Since B is a normal parameter reduction, we have ∀i, $\underset {e\in A-B}{\sum }F(u_{i}, e)$ is constant. Denote $K={\sum }_{e\in A-B}F(u_{i}, e)$. Hence

$$\underset{e\in A-B}{\sum}S_{F}^{\omega}(e)=\sum\limits_{i=1}^{n}K\times \omega_{i}=K\times \sum\limits_{i=1}^{n}\omega_{i}. $$

□

According to Example 3.1 (i) we know that Theorem 3.1 is a special situation of Theorem 3.2 where ω = (1, 1, ⋯ , 1).

Corollary 3.1 (Necessary Condition II for normal parameter reduction of soft set under Binary weight vector)

Suppose S = (F, A) is a soft set over U = {u₁, u₂,⋯, u_n}. |U| = n, |A| = m. ω = (2^n− 1, 2^n− 2, ⋯ , 2⁰) is a weight vector. $B\subseteq A$, B ≠ ∅. If B is a normal parameter reduction of S by Definition 3.1, then $\exists K\in \mathbb {Z}$ satisfying

Example 3.2

Take the soft set in Example 2.1 where |U| = 6 for instance. By Example 2.2 A −{e₁, e₂, e₇} is a normal parameter reduction. With respect to the matrix representation in Table 1, by the third row which is green colored in Table 4 we have

$$\sum\limits_{e\in \{e_{1}, e_{2}, e_{7}\}}S_{F}^{\mathcal{B}\mathcal{I}\mathcal{N}}(e)=38+1+24=63=1\times (2^{|U|}-1).$$

It should be noticed that the order of objects doesn’t influence our result shown in expression N_ω. In Table 5, after we change the order of objects in the matrix representation of soft set in Table 1, we still have

$$\sum\limits_{e\in \{e_{1}, e_{2}, e_{7}\}}S_{F}^{\mathcal{B}\mathcal{I}\mathcal{N}}(e)=28+2+33=63=1\times (2^{|U|}-1).$$

Table 5 Function $S_{F}^{{\mathscr{B}}\mathcal {I}\mathcal {N}}(e_{i})$ for another representation of the soft set S = (F, A) in Table 1

Note 3.1 (An open problem on the relations among different weight vectors)

Suppose S = (F, A) is a soft set over U = {u₁, u₂,⋯, u_n}. |U| = n, |A| = m. $B\subseteq A$. Given two arbitrary weight vectors ω₁ and ω₂. It’s very interesting to consider the following question: is there any logical implication relation between the statements $\left ({\sum }_{e\in A-B}S_{F}^{\omega _{1}}(e)\right ) mod \left ({\sum }_{i=1}^{n}\omega _{1}\right ) =0$ and $\left ({\sum }_{e\in A-B}S_{F}^{\omega _{2}}(e)\right ) mod \left ({\sum }_{i=1}^{n}\omega _{2}\right ) =0$, and in which conditions? In this paper we will not investigate this problem thoroughly. However, we try to give some situations as follows:

• (i) Let ω₁ = (1, 1, ⋯ , 1), ω₂ = (2^n− 1, 2^n− 2, ⋯ , 1). Then we have:

$$N_{UNA}\not\Longrightarrow N_{BIN}.$$

Table 6 shows a soft set where A = {e₁, e₂, ⋯ , e₈}. The values $S_{F}^{UNA}(e)$ and $S_{F}^{BIN}(e)$ are listed. Note that ${\sum }_{i=1}^{5}\omega _{1}(i)=5$ and ${\sum }_{i=1}^{5}\omega _{2}(i)=2^{5}-1= 31$.

In Table 7 each 0-1 row-vector means the characteristic function of a subset A − B of A. For example, the fist row-vector is (1 1 0 0 0 0 0 0), then the related A − B is equal to {e₁, e₂}. For each yellow row-vector, the corresponding parameter subset A − B satisfies N_UNA but does not satisfy N_BIN. Notice that for any green row-vector, the corresponding A − B satisfies both N_UNA and N_BIN.

• (ii) Let ω₁ = (1, 1, ⋯ , 1), ω₂ = (2^n− 1, 2^n− 2, ⋯ , 1). Then we have:

$$N_{BIN}\not\Longrightarrow N_{UNA}$$

Similarly, in Table 8 for any yellow row-vector, the corresponding parameter subset A − B satisfies N_BIN but does not satisfy N_UNA. Notice that for any green row-vector, the corresponding A − B satisfies both N_UNA and N_BIN.

Table 6 Tabular representation of a soft set S = (F, A) for Note 3.1 (i) and (ii)

Table 7 Tabular representation for examples of Note 3.1 (i)

Table 8 Tabular representation for examples of Note 3.1 (ii)

3.3 Equivalent classes of parameters set of a soft set

Definition 3.3

Suppose S = (F, A) is a soft set over U = {u₁, u₂,⋯, u_n}. |U| = n, |A| = m. ω = (ω₁, ω₂, ⋯ , ω_n) is a real-valued weight vector with non-negative component ω_i for u_i, i = 1, 2, ⋯ , n. Define a relation $\mathcal {R}_{\omega }$ on parameters set A as follows: ∀e_i, e_j ∈ A,

$$ e_{i}\mathcal{R}_{\omega} e_{j} \ \ \ \ if \ \ and \ \ only \ \ \ if \ \ S_{F}^{\omega}(e_{i})=S_{F}^{\omega}(e_{j}). $$

(3.3)

It is easy to get that $\mathcal {R}_{\omega }$ is an equivalence relation. So the following proposition holds:

Proposition 3.2

Suppose S = (F, A) is a soft set over U = {u₁, u₂,⋯, u_n}. |U| = n, |A| = m. ω = (ω₁, ω₂, ⋯ , ω_n) is a non-negative weight vector. Then when ω ∈{BIN, TER, OCT, DEC, DUO, HEX}, we have

$$ e_{i}\mathcal{R}_{\omega} e_{j} \ \ \ \ if \ \ and \ \ only \ \ \ if \ \ F (e_{i})= F (e_{j}). $$

(3.4)

By using $\mathcal {R}$ we can divide A into different equivalent classes. We use $[e_{i}]_{\mathcal {R}_{\omega }}$ to denote the equivalent class containing e_i, i.e., $[e_{i}]_{\mathcal {R}_{\omega }} =\{e\in A|e{\mathcal {R}_{\omega }} e_{i}\}$.

By Proposition 3.2 we know that the number of equivalent classes induced by $\mathcal {R}_{\omega }$ depends on the number of the same parameter approximations. In other words, the equivalence relation becomes more practical especially when we have more parameter approximations.

Example 3.3

Consider the soft set S = (F, A) represented in Table 9, we can see $S_{F}^{{\mathscr{B}}\mathcal {I}\mathcal {N}}(e_{1})=38$, $S_{F}^{{\mathscr{B}}\mathcal {I}\mathcal {N}}(e_{2})=1$, $S_{F}^{{\mathscr{B}}\mathcal {I}\mathcal {N}}(e_{3})=39$, $S_{F}^{{\mathscr{B}}\mathcal {I}\mathcal {N}}(e_{4})=48$, $S_{F}^{{\mathscr{B}}\mathcal {I}\mathcal {N}}(e_{5})=48$, $S_{F}^{{\mathscr{B}}\mathcal {I}\mathcal {N}}(e_{6})=38$, $S_{F}^{{\mathscr{B}}\mathcal {I}\mathcal {N}}(e_{7})=1$. So we have $[e_{1}]_{\mathcal {R}_{BIN}}=[e_{6}]_{\mathcal {R}_{BIN}}=\{e_{1}, e_{6}\}$, $[e_{2}]_{\mathcal {R}_{BIN}}=[e_{7}]_{\mathcal {R}_{BIN}}=\{e_{2}, e_{7}\}$, $[e_{3}]_{\mathcal {R}_{BIN}}=\{e_{3}\}$, $[e_{4}]_{\mathcal {R}_{BIN}}=[e_{5}]_{\mathcal {R}_{BIN}}=\{e_{4}, e_{5}\}$.

Table 9 Tabular representation of a soft set S = (F, A)

We use $2^{\mathbb {U}}$ to denote the set {0, 1, 2, ⋯ , 2^|U|− 1}. For example if |U| = 5, then we have $2^{\mathbb {U}}=\{0, 1, 2, \cdots , 31\}$.

Definition 3.4

Suppose S = (F, A) is a soft set over U = {u₁, u₂, ⋯ , u_n}. |U| = n, |A| = m. ω = (ω₁, ω₂, ⋯ , ω_n) is a weight vector. Denote $W=\{0, 1, 2, \cdots , {\sum }_{i}\omega _{i}\}$. Define a function $\mathcal {F}_{\omega }: W\rightarrow \{[e_{i}]_{\mathcal {R}_{\omega }}|e_{i}\in A\}\cup \{\emptyset \}$ by

$$ \mathcal{F}_{\omega}(k)=[e_{i}]_{\mathcal{R}_{\omega}}\ \ if \ \ and \ \ only \ \ if \ \ S_{F}^{\omega}(e_{i})=k, $$

(3.5)

otherwise, $\mathcal {F}_{\omega }(k)=\emptyset$.

According to Example 3.3, we have

Example 3.4

Consider the soft set S = (F, A) represented in Table 9, we can see $\mathcal {F}_{{\mathscr{B}}\mathcal {I}\mathcal {N}}(1)=[e_{2}]_{\mathcal {R}_{BIN}}=\{e_{2}, e_{7}\}$, $\mathcal {F}_{{\mathscr{B}}\mathcal {I}\mathcal {N}}(38)=[e_{1}]_{\mathcal {R}_{BIN}}=\{e_{1}, e_{6}\}$, $\mathcal {F}_{{\mathscr{B}}\mathcal {I}\mathcal {N}}(39)=[e_{3}]_{\mathcal {R}_{BIN}}=\{e_{3}\}$$\mathcal {F}_{{\mathscr{B}}\mathcal {I}\mathcal {N}}(48)=[e_{4}]_{\mathcal {R}_{BIN}}=\{e_{4}, e_{5}\}$, $\mathcal {F}_{{\mathscr{B}}\mathcal {I}\mathcal {N}}(6)=\emptyset$.

4 A novel algorithm for all normal parameter reductions of a soft set based on the necessary condition N _ω (see Fig. 1 for its sketch map)

Now it’s time to show our algorithm for all normal parameter reductions of a soft set based on the necessary condition N_ω.

Fig. 1

A sketch map of Algorithm 1 for all normal parameter reductions

Notice that our weight vectors should not contain any negative coordinates. If the weight vector has negative coordinates, then it can’t be guaranteed that the sum of the values while searching along a branch is monotone increasing. Thus our pruning method would become theoretically wrong (Fig. 2).

Fig. 2

A sketch map of the integer partition technique in Algorithm 1

Example 4.1

Here we make an example with the soft set in Table 6.

Step 1.:

Input the soft set S = (F, A) represented in Table 6.

Step 2.:

Set up ω = (2⁴, 2³, 2², 2¹, 2⁰) by BIN, according to Table 6 we have $S_{F}^{\omega }(e_{1})=19, S_{F}^{\omega }(e_{2})=20, S_{F}^{\omega }(e_{3})=19, S_{F}^{\omega }(e_{4})=30, S_{F}^{\omega }(e_{5})=25, S_{F}^{\omega }(e_{6})=$ $12, S_{F}^{\omega }(e_{7})=23, S_{F}^{\omega }(e_{8})=3.$ $S_{F}^{\omega }(A)=151.$ $\mathcal {R}_{BIN}=\{\{e_{1}, e_{3}\},\{e_{2}\},\{e_{4}\},\{e_{5}\}, \{e_{6}\},\{e_{7}\},\{e_{8}\}\}$.

Step 3.:

${\sum }_{i}\omega _{i}=2^{5}-1= 31$, get the series of numbers to be partitioned: $k({\sum }_{i}\omega _{i})$, k = 1, 2, 3, 4 (0 can be deleted since $S_{F}^{\omega _{BIN}}(i)>0, \forall i,$ 1, 2, ⋯ , 4), and K = 4 since $K({\sum }_{i}\omega _{i})=4\times 31<=S_{F}^{\omega }(A)=151$, 5 × 31 > 151. So the series of numbers to be partitioned is 31, 62, 93, 124.

Step 4.:

With factors $\{S_{F}^{\omega }(i)\}=\{3, 12, 19, 20, 23, 25,$ 30}, it becomes a question to perform integer partition operation to integers 1 × 31, 2 × 31, 3 × 31 and 4 × 31. Pay attention to the constraint that the times of factor $S_{F}^{\omega }(e_{i})$ appears should not be bigger that |[e]_BIN|, where $S_{F}^{\omega }(e)=S_{F}^{\omega }(e_{i})$. In Fig. 2, we give a sketch map for the integer partition process when $k({\sum }_{i}\omega _{i})=93$. Then transform the integer partition results to tuples (p₁, p₂, ⋯ , p_m). See Table 10 where ω = (2⁴, 2³, 2², 2¹, 2⁰) for u_i, i = 1, 2, ⋯ , 5.

Step 5.:

Screen out all the normal parameter reductions B from the set of integer partitions (p₁, p₂, ⋯ , p_m) satisfying N_ω. See the tuples labeled with 1 in the last column of Table 10.

Table 10 The solutions of Example 4.1 when ω = BIN

As a comparison, we also set up other kinds of ω. Similar with Table 10, we list the solutions when ω ∈{TER, OCT, DEC, DUO, HEX} (See Table 11), ω = UNA (See Table 12).

Table 11 The solutions of Example 4.1 when ω = TER, OCT, DEC, DUO, HEX

Table 12 The solutions of Example 4.1 when ω = UNA

For each ω ∈{TER, OCT, DEC, DUO, HEX}, the corresponding set of all integer partitions is the same. What’s more, each of the three integer partitions relates to a normal parameter reduction B. That’s 100 percent accuracy. When ω = UNA, we have 45 integer partitions (See Table 12), and only three of them correspond to the normal parameter reduction solutions. The success rate is equal to 0.066. Hence as to this example, we can see that our new algorithm is much more efficient.

5 Experimental results for the proposed algorithm

In this section we introduce our experimental results of the proposed Algorithm 1. Particularly, when ω = UNA, it is actually the same with the method proposed in [43]. So we do give a comparison between the existing method by setting up ω = UNA and other kinds of weighting vectors.

Our experiments perform on a PC with an AMD Ryzen 5 3500U 2.10GHz CPU, 8GB RAM and the Win10 professional operating system. Our data is generated in the following way: first, we use the rand function of MATLAB to generate a uniformly distributed matrix of random numbers in the [0, 1] interval. Numbers less than or equal to N in the matrix are then changed to 1, and the rest of the numbers are changed to 0. We can thus obtain a matrix with a ratio of 1 as N.

The controlling parameters in our experiments are as follows:

• (i) The number of rows, i.e., the number of objects |U|.

• (ii) The number of columns, i.e., the number of parameters |A|.

• (iii) The ratio of value 1, i.e., the proportion of 1 values of the generated data.

For every combination of the above controlling parameters, the running times of our algorithm are set up as 100. In the following subsections we list our experimental results with respect to the time efficiency, success rate, the rate of variance of these corresponding rows in the initial soft set, the average number of total integer partitions and the average number of normal parameter reductions.

5.1 Experimental results of the time cost

• (i) Let |A| = 16, |U| = 8, 10, ⋯ , 16. The ratio of 1 is equal to 0.3. The results of the time cost are shown at the top-level of Fig. 3 (In Fig. 3, the subfigure on the right side of each level is the partial enlargement of the corresponding left one). With respect to ω = UNA, the time cost decreases when |U| increases. When ω = BIN, TER, OCT, DEC, DUO, HEX, the time cost is much lower when compared with ω = UNA.

• (ii) Let |U| = 8, |A| = 10, 12, ⋯ , 20. The ratio of 1 is equal to 0.3. The results of the time cost are shown at the middle-level of Fig. 3. With respect to |A|, the time cost increases when |A| increases. When ω = BIN, TER, OCT, DEC, DUO, HEX, the time cost is much lower than ω = UNA particularly when |A| is lager than 14.

• (iii) Let |U| = 8, |A| = 16. The ratio of 1 is from 0.1 to 0.5. The results of the time cost are shown at the bottom-level of Fig. 3. The time cost increases when the ratio of 1 increases. When ω = BIN, TER, OCT, DEC, DUO, HEX, the time cost is much lower than the situation when ω = UNA.

Fig. 3

The time efficiency of Algorithm 1

5.2 Experimental results of the success rate

• (i) Let |A| = 12, |U| = 8, 10, ⋯ , 14. The ratio of 1 is equal to 0.3. The results of success rate are shown at the left subfigure of the top-level of Fig. 4. As far as to our experiments, we see that the success rate increases when ω changes from UNA to HEX (in the order of BIN, TER, OCT, DEC, DUO, HEX). The success rate is equal to 1 when ω = OCT, DEC, DUO, HEX. When |A| = 18, we see that the success rate is not equal to 1 when ω = HEX.

• (ii) Let |U| = 10, |A| = 10, ⋯ , 16. The ratio of 1 is equal to 0.3. The results of success rate are shown at the left subfigure of the middle-level of Fig. 4. As far as to our experiments, we see that the success rate increases when ω changes from UNA to HEX (in the order of BIN, TER, OCT, DEC, DUO, HEX). The success rate is equal to 1 when ω = OCT, DEC, DUO, HEX. When |U| = 14, we have similar results (see the right subfigure of the middle-level of Fig. 4). Take TER for example, we see that when |A| increases, the rate of success deceases.

• (iii) Let |U| = 8, |A| = 16, the ratio of 1 is from 0.1 to 0.5. The results of success rate are shown at the left subfigure of the bottom-level of Fig. 4. As far as to our experiments, for each ratio of 1, we see that the success rate increases when ω changes from UNA to HEX (in the order of BIN, TER, OCT, DEC, DUO, HEX). The success rate is equal to 1 when ω = OCT, DEC, DUO, HEX. Let |U| = 14, |A| = 20, we see that the success rate is not equal to 1 when ω = HEX and the ratio of 1 is equal to 0.2 and 0.3 (see the right subfigure of the bottom-level of Fig. 4).

Fig. 4

Experimental results of the success rate for Algorithm 1

5.3 Experimental results: the rate of variance for these corresponding rows in initial soft set, the average number of total integer partitions and the average number of normal parameter reductions

• (i) For an input soft set S, we denote the number of all normal parameter reductions as N_NPRS, and we also use $N_{IPS}^{\omega }$ to mean the number of all integer partitions with weight vector ω. Then we define

  $$ success \ \ rate_{i} =\frac{N_{NPRS}}{N_{IPS}^{\omega} }. $$

  (5.1)

  According to the experimental results success rate_i, i = 1, 2, ⋯ , 100, we have the average rate of success as follows:

  $$ \sum\limits_{i=1}^{100} \frac{success \ \ rate_{i}}{100 }. $$

  (5.2)

  See the experimental results in the fifth column of both Tables 13 and 14.

  It should be noticed that when N_NPRS = 0 we always get success rate_i = 0. But it doesn’t mean our algorithm is inefficient. This is because there doesn’t exist any normal parameter reduction.

  As far as to our experiments, the rate of success becomes larger when weight vectors change from UNA to HEX in general. However, we couldn’t prove it theoretically. We also get a counterexample in the last row of Table 14.

• (ii) Although not all the integer partitions are the normal parameter reductions of the input soft set, we can use statistical method to describe the extent in which it can be taken as a normal parameter reduction. In other words, we choose analysis of variance to characterize how far an integer partition is from a normal parameter reduction.

  Suppose the j_th integer partition we get in the i_th experiment for the same size and the same weight vector is equal to (p₁, p₂, ⋯ , p_m). Denote $V_{IPS}^{\omega }(i,j)=var.({\sum }_{p_{j}=1}F(u_{1},e_{j}), \cdots ,{\sum }_{p_{j}=1}F(u_{n},e_{j}))$, here n = |U|.

  Assume the number of integer partition solutions we get in the i_th experiment for the same size and the same weight vector is equal to N(i), then define

  $$ V_{IPS}^{\omega}(i)=\frac{{\sum}_{j}V_{IPS}^{\omega}(i,j)}{N(i)}, $$

  (5.3)

  So we can compute the average degree of variance by

  $$ \frac{{\sum}_{i=1}^{100}V_{IPS}^{\omega}(i)}{100}. $$

  (5.4)

  See the experimental results in Tables 13 and 14. Generally, the larger the average rate of success is, the lower the average degree of variance is.

• (iii) The number of normal parameter reductions of a soft set is determined by its own data, and has nothing to do with our weight vectors. The last columns in Tables 13 and 14 give the experimental results in the average sense. Notice that the number of normal parameter reductions of a soft set is quite different when its size and the ratio of 1 are different.

Table 13 Experimental results for the proposed algorithm (to be continued)

Table 14 Experimental results for the proposed algorithm (the continuation of Table 13)

5.4 Experiments compared with other algorithms designed for # NPR

Firstly, we need to collect the algorithms right designed for the # NPRS. Before this we list and analysis the references which are closely related to normal parameter reduction problems. See Table 15 where the reference numbers for this paper, their excellent idea and the corresponding contribution are given.

Table 15 Diagram of references for # NPRS

Based on the above preparation, we decide to choose the recent published algorithms from references [38], [43] and [44] as comparative ones with our method. As mentioned in the Table 15, [38] didn’t propose an explicit algorithm for # NPRS, we need at first to revise the 0-1 linear method of optimal normal parameter reduction for suiting the # NPRS problems. For self-contained we cite an example in [38] here to show how we do this based on the work of [38].

Example 5.1

Table 16 represents a soft set S = (F, E) over objects domain U = {u₁, u₂, ⋯ , u₆} and parameters domain E = {e₁, e₂, ⋯ , e₈}. According to [38], we have the elements $D_{i\leftarrow i+1}$ and $D_{i+1\leftarrow i}$, i = 1, 2, ⋯ , 5 in the matrix of dominant support parameters as shown in Table 17.

Table 16 Tabular representation of a soft set S = (F, A)

Table 17 Dominant parameter subsets of adjacent objects for generating constraints in the linear programming models

Then by [38] we have the set of constraints for a normal parameter reduction:

$$ \left\{\begin{array}{ll} C_{1, 2}: e_{2}=e_{5}+e_{6}\\ C_{2, 3}: e_{3}+e_{7}+e_{8}=0\\ C_{3, 4}: e_{5}+e_{6}=e_{2}+e_{7}\\ C_{4, 5}: 0=0\\ C_{5, 6}: e_{2}=e_{1}+e_{3}+e_{5} \end{array}\right. $$

Based on these constraints, we can give the revised algorithm for # NPRS by using implicit enumeration. We choose to use the width-first searching method, with which we prune the searching branches once we find any contradiction with these constraints.

With Algorithm 2 we get all the normal parameter reductions B₄ = A −{e₄}, B₂ = A −{e₂, e₄, e₅}, B₃ = A −{e₁, e₂, e₄, e₆}, B₁ = A, B₅ = A −{e₁, e₂, e₆}, B₆ = A −{e₂, e₅} for Example 5.1.

Figures 5 and 6 are sketch maps for comparison results. It is clearly implied that the proposed method in this paper by integer partition and object weighting is better than the mentioned methods above as far as to the data simulated in the experiments.

Fig. 5

The time efficiency comparison results when |A| = 10 and 16

Fig. 6

The time efficiency comparison results when |U| = 12 and 16

6 Operational system based on MATLAB

In order to show the potential application of our algorithm, we integrate our Algorithm 1 into an APP, which can be installed in MATLAB 2019a or newer versions. Figure 7 is the interface after running an example. We would like to make a brief introduction to it as follows:

Fig. 7

The interface of our APP performing Algorithm 1 in MATLAB

As can be seen from Fig. 7, the interface of this APP is divided into several functional parts and marked with serial numbers.

Area i s where we input the data. The soft set data can be generated randomly. The controlling parameters for the size of soft set data and the ratio of 1 can be set up there. As far as to the example shown in Fig. 7, there are 5 objects in the soft set object domain and 7 parameters in the soft set parameter domain. And the ratio of 1 represents the proportion of 1 in the data, the number 0.5 in the figure means that 50% of the numbers in this soft set data matrix are equal to 1, which are randomly distributed in the matrix. The soft set data can be uploaded by the button marked with “ Open excel”. The generated or uploaded data is shown in area .

In area we can choose or enter the weight vectors. As instances, we list UNA, BIN, TER, OCT, DEC, DUO, HEX over there.

Since we want to make comparison among different weight vectors, we list the current results in area , while the best result is kept in area . In each of these two areas we can see the running results such as the time cost, weight vector, the factors involved in integer partition process, the number of all integer partitions satisfying the condition N_ω. The number “3” in the local area labeled with “ Success ” means there are 3 partitions which correspond to the normal parameter reductions of the input soft set. The number “6” in the local area labeled with “ All solutions ” means there are 6 partitions in total. That’s why we see the Success rate is equal to 0.5 there. Area contains all the integer partition results over there, and the solutions of the soft set are labeled with number 1 in the last column. All the maximal normal parameter reduction solutions can be easily got and are listed in area .

By button we can start the computation. The final results can be restored in an excel form and downloaded by button . If we click button , we can clear the data for the next round.

7 Conclusion and future work

7.1 Aims fulfilled and novelty

The main contributions of this paper are as follows:

• (i) We have solved # NPRS problem of a soft set (i.e., all of the normal parameter reductions of a soft set). Weight vectors for objects in the soft set domain are firstly brought in. As a result, we come up to a new necessary condition for a normal parameter reduction N_ω. That’s the principal theoretical foundation of our algorithm.

• (ii) Upon the derived necessary condition, the # NPRS problems can be solved by using integer partition technique. Different weight vectors result in different efficiency of the proposed algorithm. It is very interesting to investigate these differences among different weight vectors. Experimental results have been achieved with respect to the time cost, success rate and the mean variance of partitions.

• (iii) All maximal solutions or optimal ones can be filtered out in sequence right after ♯ NPRS.

7.2 Limitations of the proposed method

• (i) When |A| grows, the proposed algorithm has to confront with larger workload for the integer partition. This is determined by the nature of the problem.

• (ii) Although from our experimental results we do have 100 percent success rate under some situations, this paper doesn’t give the conditions under which N_ω becomes a sufficient condition for a normal parameter reduction theoretically.

7.3 A much more precise description for the idea of soft set and potential application of normal parameter reduction in data mining

7.3.1 Explanation of soft set as soft decision making scheme

Suppose U = {u₁, u₂, ⋯ , u_n} is a finite set of objects. In this paper we assume that a decision making on the set U of objects means to choose a subset of U. A soft set S = (F, A) over U defines a function from A to the power set of U, i.e., ∀e ∈ A, $F(e)\subseteq U$. Inspired by the assumption for what a decision making is, a soft set is actually a decision making strategy. That is “A decision making should be made upon different parameters or situations. Just like a soft material which is easy to deform, a decision making should be flexible to different situations.” As the saying goes, the benevolent see benevolence and the wise see the wisdom. Different people may have different opinions. So we can say that soft set is a kind of soft decision making scheme. Table 18 shows an example where different job hunters are searching for the same job. These hunters have to be judged by different interviewers or different criterions. It’s normal that there may exist different decisions for who should be hired by different experts. For instance, job hunter 4 and job hunter 5 would be hired according to interviewer 1, while job hunter 3 and job hunter 4 should be hired by the opinion of interviewer 2.

Table 18 An example of soft set taken as a soft decision making scheme

7.3.2 Potential application of normal parameter reduction in data mining

In big data era it becomes much more important to mine useful and valuable information from data generated in various ways. Our normal parameter reduction idea and skills can be applied as an useful model for data mining. To be more precise, here we take the 2016 US Presidential Election as an example. Table 19 shows basic information [46], where we can see which states TRUMP won or Hillary did. The numbers of electoral votes for each state are also listed. In this paper we make an assumption that once a candidate take an advantage in popular vote count of a state, he would win all the electoral votes. We make notations as follows: denote the set of objects as U = {TRUMP, Hillary}, parameter set E = {state₁, state₂, ⋯ , state₅₁} (i.e., E = {AK, AL, ⋯ , WY } ), the number of electoral votes for each state (the third row in Table 19) is modeled as the weight ω(e) for each parameter e. Now we get a weighted soft set S = (F, E), where for each parameter e in E, F(e) is equal to single-element set containing the candidate who won in state e. So now for a subset B of E, E − B is called a normal parameter reduction if and only if TRUMP and Hillary are completely evenly matched over B, i.e.,

$$\underset{e\in B}{\sum}\omega(e)F(TRUMP, e)= \underset{e\in B}{\sum}\omega(e)F(Hillary, e),$$

where F(TRUMP, e) = 1 means TRUMP won in the state e, similarly for F(Hillary, e) = 1. We figure out a normal parameter reduction E − B, where B is shown in Table 20 as follows. Table 20 tells us that the mainly reason for the lose of Hillary lies in the subset of states {1, 2, 3, 4, 10, 11, 13} (i.e., {AK, AL, AR, AZ, FL, GA, IA}). Because under our assumption the two candidates would get the same number of electoral votes which is equal to 229.

Table 19 Basic data for 2016 US presidential election

Table 20 Subset B of states that TRUMP and Hillary are completely evenly matched over E − B

7.4 Future work

• (i) A useful way for solving the problem mentioned in Section 7.2 (i) is to divide the parameter set into different parts. Then the proposed algorithm can be solved in an approximate way.

• (ii) What if we have weighted parameters, how can we extend our method for the normal parameter reduction problems in such a situation.

• (iii) It is very interesting to combine our theory of 0-1 valued information systems with other kinds of information systems, such as hypergraphs.

• (iv) There are some intelligent methods which could be useful for improving the efficiency of integer factorization. We will come into the potential combination with our algorithms.