Automatic feature scaling and selection for support vector machine classification with functional data

Abstract

FunctionalData Analysis (FDA) has become a very important field in recent years due to its wide range of applications. However, there are several real-life applications in which hybrid functional data appear, i.e., data with functional and static covariates. The classification of such hybrid functional data is a challenging problem that can be handled with the Support Vector Machine (SVM). Moreover, the selection of the most informative features may yield to drastic improvements in the classification rates. In this paper, an embedded feature selection approach for SVM classification is proposed, in which the isotropic Gaussian kernel is modified by associating a bandwidth to each feature. The bandwidths are jointly optimized with the SVM parameters, yielding an alternating optimization approach. The effectiveness of our methodology was tested on benchmark data sets. Indeed, the proposed method achieved the best average performance when compared to 17 other feature selection and SVM classification approaches. A comprehensive sensitivity analysis of the parameters related to our proposal was also included, confirming its robustness.

1 Introduction

Functional Data Analysis (FDA)has become an outstanding field in recent years [36, 71, 72]. Instead of assuming scalar covariates, FDA handles problems in which the data samples correspond to curves belonging to an infinite-dimensional space, and this evolution is modeled via functions. FDA is a fruitful line of research with applications in various domains, such as spectrometry, meteorology, physical and chemical processes, customer segmentation, or speech recognition [7, 8, 65, 67, 74]. Theoretically, functional data are assumed to be infinite-dimensional. In practice, such data are measured only on a (large) grid of points, which represents, for instance, the time instants. Because of their high dimensionality, functional data can be analyzed with the standard multivariate analysis techniques. Nevertheless, the direct use of such methodologies may have dramatic consequences, since the strong relationship between the measurements in two consecutive time instants is not taken into account, and limitations, such as the curse of dimensionality, may appear.

Consequently, many multivariate data analysis techniques have been developed in the FDA context, e.g. Principal Component Analysis (PCA) [12, 44], classification [56, 74], clustering [26, 57], or regression [17, 27].

Most studies on FDA have been focused on the univariate case, whereas the multivariate counterpart has received little attention. A multivariate functional datum is represented by a finite-dimensional vector where each covariate is defined by a different function. Moreover, the contributions on this topic are mainly devoted to PCA [4, 22, 46], and clustering [49, 52, 81], although we can also emphasize the recent work of [11] in the classification area. In this paper, we focus on a particular type of multivariate functional data, called hybrid functional data. They are finite-dimensional vectors that combine static and functional features. By static features, we mean real or scalar covariates, whereas a functional feature is simply a function. We can find a plethora of examples of hybrid functional data in real life. For instance, in the field of medicine, functional features of a patient as the temperature or the electrocardiogram can be recorded, but also static variables, as the gender or the age. Despite its obvious application in real-world problems, this type of data has not been studied deeply in the literature. In fact, to the best of our knowledge, hybrid functional data have been analyzed only in [35] to select the most informative variables in terms of prediction in a real data application coming from the Spanish Energy Market, and in Chapter 10 of [72] where this type of data is sketched in a PCA context.

In this article, we are interested in classifying the hybrid functional data into two predefined classes. Functional data classification has been deeply studied in the literature. Although the standard multivariate classification methods can be applied to the functional context, some differences, such as the non-inversion of the covariance operator, are to be mentioned. The authors of [50] explain different methodologies to overcome this issue. On the other hand, the near perfect classification phenomenon only takes place in the functional context, as is detailed in [28]. Different classification methods has been developed, e.g. Partial Least Squares [70] or logistic regression, [73]. A survey with different strategies for classification methods in functional data can be seen in [3], whereas [66] presents some representations of functional data in classification. In this paper, we use the well-known technique Support Vector Machine (SVM). It has gained popularity due to its numerous virtues: the ability to construct nonlinear functions thanks to the Kernel Trick, its superior predictive performance compared to traditional parametric techniques, such as logistic regression, and the flexibility that allows its quadratic programming (QP) formulation [2, 84]. It has been applied widely in finite-dimensional data, e.g. [19, 24, 25, 62, 64]. Functional data classification with SVM has been discussed in several works in the literature. The first contributions on this topic are done in [74, 75]. There are some articles which focus on their interpretability [65] or their representation [67]. To see recent works on the topic, the reader is referred to [9, 11]. The SVM extension to hybrid functional data is discussed in Section 2.1. Feature selection is a key preprocessing step in data mining. A large number of covariates are usually associated with a lower value of the classification rate, due to the redundant information that they introduce. Furthermore, we should emphasize that the model is more interpretable if the number of variables is reduced. Hence, it is crucial to design a methodology which selects the most important features in terms of classification performance.

One of the issues related to kernel-based SVM classification is that the method is unable to derive the relevance of the variables automatically, constructing models using all available information [42, 61, 62]. Several feature selection strategies have been proposed to overcome this problem. Specifically, filter methods aim to select the most relevant features by ranking the covariates according to a metric. These methods are usually very fast since they do not take into account the training model. For instance, Fisher Score [32], measures the existing relationship between a single explanatory variable and the label vector, through the associated features that are then ranked according to this measure. An alternative type of feature selection approaches are wrapper methods. They measure the relevance of the features based on the classifier performance. The Recursive Feature Elimination SVM (SVM-RFE) [31, 41] is one of the most used wrapper methods applied in static feature selection. It removes those features whose removal leads to the largest margin of class separation in a backward fashion. Finally, embedded methods aim at determining a subset of relevant attributes during the classifier construction, encouraging sparsity via feature regularization, as done for example with the Lasso approach [14] which seeks an adequate balance between sparsity and predictive performance by replacing the Euclidean norm in the SVM formulation with the ℓ₁-norm.

Variable selection has also been applied in the univariate functional data field in studies such as [5, 82]. Nevertheless, in these cases, the variables are represented by the time instants during which the functions are measured. We also highlight the work of [39] in which functions are summarized in a set of features containing the maximum possible information, and then the most relevant covariates are selected with multivariate data analysis techniques.

To sum up, the contributions and objectives achieved in this paper are:

• We propose a new embedded feature selection method with a modification of the standard SVM-classification to handle functional hybrid data sets, and as a byproduct, selects the most informative features.

• We empirically demonstrate that such hybrid data sets cannot be learned properly with the current methodologies for SVM classification, due to the few number of references regarding feature selection in multivariate functional data and, more specifically, in hybrid functional data is very scarce.

• The proposed method allows weighting the different natures of the data, functional and static, by means of the scaling factors of a modified Gaussian kernel. The idea of considering different bandwidth values for different features is not new. Indeed, it has been applied in [15, 21, 33, 76] for kernel density estimation purposes and in [63] for clustering problems.

The remainder of this paper is structured as follows: in Section 2 we formally describe the concepts used in our methodology and give the details of our approach. Section 3 is devoted to the computational experience. It includes the sensitivity analysis of our proposal given in Appendix A, as well as extra performance metrics, apart from the accuracy, namely the sensitivity, the specificity, and the Area Under Curve in Appendix B. Finally, the conclusions and possible future lines of research are described in Section 4.

2 The mathematical model

This section details the problem formulation of feature selection in SVM-classification with hybrid functional data. First, in Section 2.1 the main concepts of SVM for pure multivariate functional data are explained. Next, Section 2.2 is devoted to the extension of SVM to hybrid functional data, as well as to the problem formulation and the solving strategy.

2.1 Support vector machines for multivariate functional data classification

Let s be a sample of individuals with an associated pair (X_i,Y_i), i ∈ s. The datum $X_{i} \in \mathcal {F}^{p}$, is formed by a set of p functional features, i.e., $X_{i} = \left ({X_{i}^{1}}(t), \ldots , {X_{i}^{p}}(t)\right )$, where ${X_{i}^{v}}: [0, T]\rightarrow \mathbb {R}$, v = 1,…,p are functions belonging to the set $\mathcal {F}$ of Riemann integrable functions in the interval [0,T]. Moreover, Y_i ∈{− 1,+ 1} denotes the class label of the observation i.

The benchmark SVM methodology [25], builds a hyperplane yielding a classification rule. The dual formulation of the SVM problem is stated as follows:

$$ \left\{ \begin{array}{cl} \max\limits_{\alpha}& \sum\limits_{i\in s} \alpha_{i} -\frac{1}{2} \sum\limits_{i, j\in s} \alpha_{i}\alpha_{j} Y_{i} Y_{j} K(X_{i}, X_{j})\\ \text{s.t.} &\sum\limits_{i\in s} \alpha_{i}Y_{i}=0\\ &\alpha_{i}\in [0, C], i\in s, \end{array}\right. $$

(1)

where C > 0 is a regularization parameter, and $K: \mathcal {X}\times \mathcal {X}\rightarrow \mathbb {R}$ is the so-called kernel function. As the decision rule: a new observation $X\in \mathcal {X}$ is assigned to class + 1 if and only if $\hat {Y}(X)>\upbeta$, with β being a given threshold value. Here $\hat {Y}(X)$ is the score function, given by

$$ \hat{Y}(X)=\sum\limits_{i\in s} \alpha_{i}Y_{i} K(X, X_{i}), \quad X\in \mathcal{X}, $$

(2)

One of the most used kernel functions, as reported in the literature, is the Gaussian kernel. It has been applied widely when finite-dimensional data are considered [18, 25, 54]. The extension to the functional case has also been studied. Indeed, the functional isotropic Gaussian kernel is analyzed in studies where univariate data appear [51, 67, 74, 75] and also in references dealing with multivariate data [85]. The expression of the isotropic Gaussian kernel for multivariate functional data, i.e. $X\in \mathcal {F}^{p}$, can be seen in (3):

$$ K(X_{i}, X_{j}) = \exp\left( -\omega\sum\limits_{v = 1}^{p} {{\int}_{0}^{T}}\left( {X_{i}^{v}}(t)-{X_{j}^{v}}(t)\right)^{2} dt\right) $$

(3)

for a single bandwidth ω which weighs all the covariates equally. Section 2.2 formally defines the hybrid functional data, describes how the kernel in (3) is extended to such type of data, and explains the proposed formulation for SVM classification and feature selection with hybrid functional data.

2.2 Problem formulation

An hybrid functional datum $X_{i}\in \mathcal {X}$, with $\mathcal {X} = \mathcal {F}^{p}\times \mathbb {R}^{q}$, is defined as a vector of p functional features and q static features. In other words, $X_{i} = ({X_{i}^{1}}(t), \ldots , {X_{i}^{p}}(t), X_{i}^{p+1},$ $\ldots , X_{i}^{p+q})$, where ${X_{i}^{v}}: [0, T]\rightarrow \mathbb {R}$, v = 1,…,p are functions belonging to the set $\mathcal {F}$ of Riemann integrable functions in the interval [0,T], and ${X_{i}^{v}}\in \mathbb {R}$, v = p + 1,…,p + q.

The main objective of this paper is to design a model which obtains, via SVM, good classification rates in order to determine the class Y ∈{− 1,+ 1} of a new observation $X\in \mathcal {X}$, at the same time that it yields the most informative set of features $\mathcal {V}\subset \{1, \ldots , p+q\}$. To do this, we modify the standard Gaussian functional kernel in (3), in which a single bandwidth is considered, by associating a bandwidth with each feature, yielding the following expression:

$$ K(X_{i}, X_{j}, \boldsymbol{\omega}) = \exp\left( -\sum\limits_{v = 1}^{p} \omega_{v}{{\int}_{0}^{T}}\left( {X_{i}^{v}}(t)-{X_{j}^{v}}(t)\right)^{2} dt - \sum\limits_{v = p+1}^{p+q} \omega_{v}({X_{i}^{v}} - {X_{j}^{v}})^{2}\right), $$

(4)

for $X_{i}, X_{j} \in \mathcal {X}$. Notice that the dependency of the bandwidth ω = (ω₁,…,ω_p+q) on the kernel K is highlighted through the notation K(X_i,X_j,ω).

Our proposed kernel in (4) differs from the kernel in (3) in the role that the bandwidth plays. Whereas the bandwidth in (3) is just a single value, common to all the variables, the kernel in (4) has a bandwidth for each feature, which allows more flexibility in our model, weighting each covariate differently according to its contribution in the classification model, and allowing the link between variables of different nature, static and functional.

The feature selection problem implies the tuning of two parameters: the regularization parameter C of the SVM problem (1), and the bandwidths ω_v,v = 1,…,p + q associated with each feature of $X\in \mathcal {X}$ through the kernel (4).

In agreement with the methodologies of [9, 11], we propose combining a grid search to get the optimal value of C with a bilevel optimization problem which will yield the optimal bandwidth ω.

Multiple criteria can be used in the objective function of the bilevel optimization problem. Minimizing the misclassification rate is the usual approach utilized. Nevertheless, such a choice is a linear piecewise function which prevents the use of gradient-based optimization searches. We propose, instead, defining the objective function as the maximization of the Pearson correlation, ρ, between the class label Y_i and the score $\hat {Y}(X_{i}, \boldsymbol {\omega }, \alpha )$ in (2). The Pearson correlation coefficient has been used before in [9, 11] as surrogate of the number of misclassified with outstanding results. Although we are defining a linear relationship between vectors of different nature, since Y is a binary vector taking values in {− 1,+ 1} and $\hat {Y}$ is a real vector; the numerical experience in [9, 11] has shown that the usage of the Pearson correlation has two big advantages. On the one hand, this coefficient is very easy and fast to compute. On the other hand, the continuous behavior allows one to apply smooth optimization strategies. Parameter tuning usually leads to overfitting when the whole data set is considered. To avoid this issue, we divided the sample s into three independent parts, s₁, s₂ and s₃. Sample s₁ is utilized to solve the SVM problem (1), for fixed C and ω, yielding the variables α. The independent sample s₂ is used to measure the goodness of fit via the correlation $\rho ((Y_{i}, \hat {Y}(X_{i}, \boldsymbol {\omega }, \alpha ))_{i\in s_{2}})$ for α and C fixed. Finally, sample s₃ is employed to find the regularization parameter C, by computing the accuracy on s₃ for a given C in the grid, and keeping the one with the largest value. Therefore, for a fixed C, the bilevel optimization problem is stated as follows:

$$ \left\{ \begin{array}{cl} \max\limits_{\boldsymbol{\omega}, \alpha}& \rho((Y_{i}, \hat{Y}(X_{i}, \boldsymbol{\omega}, \alpha))_{i\in s_{2}})\\ \text{s.t.} &\alpha \text{ solves } (1) \text{ in } s_{1} \\ &\omega_{v}\geq 0, \quad \forall v, \end{array}\right. $$

(5)

Nonlinear bilevel optimization problems, such as (5), can be solved with the off-the-shelf methodologies described in [23]. Nevertheless, such strategies are computationally expensive. We propose using an alternating approach instead, as was done in [9, 11].

Our alternating approach consists of just a few iterations of two steps. First, Problem (1) is solved, for fixed ω in sample s₁, yielding the optimal variables α. Secondly, for fixed α, Problem (6) is solved in sample s₂, giving the optimal values of the parameter ω.

$$ \left\{ \begin{array}{cl} \max\limits_{\boldsymbol{\omega}}& \rho((Y_{i}, \hat{Y}(X_{i}, \boldsymbol{\omega}))_{i\in s_{2}})\\ \text{s.t.} &\omega_{v}\geq 0, \quad \forall v, \end{array}\right. $$

(6)

Problems (1) and (6) have different natures and, consequently, they should be solved with different strategies. Problem (1) is a quadratic maximization problem with linear constraints in which SMO-like algorithms can be applied to easily reach the global optimum of the problem. In contrast, Problem (6) is a continuous optimization problem whose optimal solution is obtained by combining classic local searches and a multi-start approach.

The alternating procedure is run, for a fixed C, until some stopping criterion is reached. Notice that, apart from obtaining good classification rates, our goal is to select the most informative features. To do this, once the alternating approach is finished, we eliminate those covariates v whose associated bandwidths ω_v are close enough to zero, and repeat the alternating algorithm with the remaining features. In other words, we keep those features satisfying ω_v > δ, where δ > 0 is a threshold value. This process is repeated until the selected features do not change in two consecutive iterations.

Once the alternating approach provides good values for α, ω, and therefore, the set $\mathcal {V}$ of selected features, the value of C is chosen by computing the accuracy on s₃ for all C values in the grid, and the one that leads to the largest accuracy is kept.

Finally, the effectiveness of our methodology is tested on an independent sample s₄, in which the classification accuracy is computed. A pseudocode of our approach is given in Algorithm 1.

Table 1 Data description summary (including number of individuals and records of each label)

Table 2 Data description summary (including number of features and their names)

3 Numerical Experiments

This section is devoted to the computational experience. In Section 3.1, the different databases are explained. Section 3.2 is devoted to the description of the experiments performed. Section 3.3 details the approaches utilized to compare our algorithm with. Finally, Section 3.4 gives the results of our proposal, including the sensitivity analysis explained in Appendix A.

3.1 Data Set Description

Two simulated examples, namely batch and trigonometric, and two real databases, denoted here as pen and retail, were studied. A summarized description of the data sets, including the number of individuals in the sample, the number of elements of each class, and the number of static and functional covariates as well as their names, can be seen in Tables 1 and 2.

Sections 3.1.1–3.1.4 detail how the different databases have been generated and Figs. 1, 2, 3 and 4 show respectively a subset of ten functions of the data sets batch, trigonometric, pen and retail. The functional features are depicted in a standard x − y plot, where the solid blue lines indicate the individuals with class 1 and the dashed red line mark the observations with class − 1. On the other hand, for the sake of visualization static covariates are shown in boxplots (or barplots in the case of categorical features), with the individuals with classes 1 and − 1 colored in blue and red respectively.

Fig. 1

Subset of batch data set

Fig. 2

Subset of trigonometric data set

Fig. 3

Subset of pen data set

Fig. 4

Subset of retail data set

3.1.1 Batch data set

The three functional covariates of the first data set, batch, come from Section 4.1 of Wang and Yao [85]. Although Wang and Yao [85] consider that the upper bound for the time interval in which the functions are measured follows an uniform distribution on [0.9,1.1], we assume, for the sake of simplicity, that $X^{v}:[0,1]\rightarrow \mathbb {R}$, v = 1,2,3. Formally:

$$ \begin{array}{@{}rcl@{}} {X_{i}^{1}}(t)& = & a_{i}\cdot t + {\varepsilon_{i}^{1}}(t)\\ {X_{i}^{2}}(t)& = & a_{i}\cdot t^{2} + {\varepsilon_{i}^{2}}(t)\\ {X_{i}^{3}}(t)& = & b_{i}\left( 4\sin(t) + 0.5\sin(\nu_{0}\cdot t)\right) \end{array} $$

for t ∈ [0,1], where (a_i,b_i) follows a bivariate Gaussian distribution with mean vector (2.5,2.5) and covariance matrix diag(2.5,2.5).

For each t ∈ [0,1], the measurements errors ${\varepsilon _{i}^{1}}(t)$ and ${\varepsilon _{i}^{2}}(t)$ are i.i.d. Gaussian noise with mean 0 and standard deviation 0.2. The individuals X_i with label Y_i = 1 have ν₀ = 10, whereas those with Y_i = − 1 are associated with ν₀ = 11.

Therefore, the third covariate is the only one that is relevant for classification, if just the functional component of the hybrid functional data is taken into account.

To complete the data set, we added two real variables, X⁴ and X⁵, in agreement with (7) and (8) for all i = 1,…,1000:

$$ {X^{4}_{i}} \sim \left\{ \begin{array}{ll} \mathcal{N}(\mu = 39, \sigma = 1), & \text{if } Y_{i} = 1\\ &\\ \mathcal{N}(\mu = 40, \sigma = 1), & \text{if } Y_{i} = -1 \end{array}\right. $$

(7)

$$ {X^{5}_{i}} \sim \left\{ \begin{array}{ll} \mathcal{N}(\mu = 2, \sigma = 1), & \text{if } Y_{i} = 1\\ &\\ \mathcal{N}(\mu = 3, \sigma = 1), & \text{if } Y_{i} = -1 \end{array}\right. $$

(8)

where $\mathcal {N}(\mu , \sigma )$ indicates a normal distribution of mean μ and standard deviation σ.

3.1.2 Trigonometric data set

The trigonometric database is formed by two functional features and two scalar covariates. Functional components ${X_{i}^{v}}:[1, 21] \longrightarrow \mathbb {R}$, v = 1,2 are based on the data generated in Section 5.2.2 of [49] and have the form:

$$ \begin{array}{@{}rcl@{}} {X_{i}^{1}}(t)& = & -\frac{21}{2} + t + \nu_{0}U_{1}\cos\left( \nu_{0} \frac{t}{10}\right) \\&&+ \nu_{0} U_{1} \sin \left( \nu_{0} + \frac{t}{10}\right) + {\varepsilon_{i}^{1}}(t)\\ {X_{i}^{2}}(t)& = & -\frac{21}{2} + t + \nu_{0}U_{1}\sin\left( \nu_{0} \frac{t}{10}\right)\\ &&+ \nu_{0} U_{2} \cos\left( \nu_{0} + \frac{t}{10}\right) \\ && +\nu_{0}U_{3}\left( \left( \frac{t}{10}\right)^{2} + \frac{t}{10} + 1\right) + {\varepsilon_{i}^{2}}(t) \end{array} $$

where t ∈ [1,21], $U_{1}, U_{2}, U_{3}\sim \mathcal {N}(1, 1)$ are independent Gaussian variables and ${\varepsilon _{i}^{1}}(t)$ and ${\varepsilon _{i}^{2}}(t)$ are white noise of unit standard deviation.

The value of ν₀ is dependent on the class label. More specifically, the individuals with label Y_i = 1 have ν₀ = 1, while the observations corresponding to Y_i = − 1 have ν₀ = 2.

The remaining static variables X³ and X⁴ have been created according to (9) and (10)

$$ {X^{3}_{i}} \sim \left\{ \begin{array}{ll} \mathcal{N}(\mu = 0, \sigma = 15), & \text{if } Y_{i} = 1\\ &\\ \mathcal{N}(\mu = 20, \sigma = 20), & \text{if } Y_{i} = -1 \end{array}\right. $$

(9)

$$ {X^{4}_{i}} \sim \mathcal{N}(\mu = 0, \sigma = 1), \quad \forall i $$

(10)

3.1.3 Pen data set

The pen data set comes from the Character Trajectories data set of the UCI Machine Learning repository [30] and has been used in papers such as [47, 48]. It contains the x and y trajectories, and the force with which multiple characters have been written. This data set is usually applied in multiclass classification frameworks, e.g., [77, 78, 80], where the labels of 20 characters are to be predicted. Since in this paper, we focus on a binary classification problem, we have adapted this data set to our setting. In particular, our aim is to classify between two randomly selected characters. In this case, we have chosen to distinguish between m and z, corresponding to the class labels 1 and − 1, respectively. The two functional features here considered are the x and y trajectories, while the pen tip force is the static covariate.

3.1.4 Retail data set

The second real-world application database retail is extracted from the Online Retail Data Set of the UCI Machine Learning Repository [30] and has been studied in [20]. It contains the monthly transactions of the customers of a UK-registered non-store, online retail during the first 10 months of the 13 months available. This database is originally used for clustering problems, where the customers are to be grouped according to their monthly transactions. In this paper, we focus on binary classification, and therefore the original database has been conveniently modified. Indeed, here the aim is to predict whether the customer will buy products in the last three months. Customers that only purchased items in the last three months were removed from the data set since no purchase history is available for constructing covariates, yielding an amount of 3,602 individuals instead of the original number of 3,630. The first functional feature is the amount of money spent by the customers. The second functional variable denotes the quantity of products bought. The last three functional covariates are the variables Recency, Frequency, and Monetary described in [20]. Finally, the scalar variable is a binary feature that indicates whether the customers come from the UK, coded by 1, or not, coded by 0.

3.2 Description of the experiments

This section explains the details of the computational experiments carried out to show the efficiency of our approach. Algorithm 1 has been run on the databases described in Section 3.1. Each data set is split into four parts, s₁ − s₄, whose roles are explained in Section 2.2. Since the features of the hybrid functional data may have different scales, we have normalized separately each feature before performing our approach, as explained in [85]. When selecting the most informative covariates, we remove those features such that ω_v ≤ 10^− 5, i.e. δ = 10^− 5. The stopping criterion is reached when the number of iterations is equal to five or when the values of the bandwidths, and therefore the selected features, do not change in two consecutive iterations. The parameter C moves in the set {2^− 7,…,2⁷} on a logarithmic scale. In order to have stable results, Algorithm 1 was run five times, and the average accuracy on the test sample s₄ is reported in Table 3. To compare our methodology with others, we consider the approaches detailed in Section 3.3 on the normalized data sets. The average accuracy of the comparative methods on the very same test sample is also given in Table 3.

In order to confirm our results, we perform the Friedman and Holm tests to evaluate the statistical significance, widely applied in the literature in papers such as [37, 59]. These tests were proposed in [29] to compare various machine learning strategies on multiple data sets. Firstly, the average rank is calculated for our approach and for all the alternative algorithms based on the accuracy of all data sets. Secondly, the Friedman test is applied for the hypothesis test which checks whether all the algorithms are equivalent or not in terms of performance. If the null hypothesis of similar performance is rejected, then the Holm post-hoc test is applied for pairwise comparisons between the algorithm with the highest rank and the rest of them. Each hypothesis test assesses whether the average accuracy of the algorithm with the highest rank and the comparative methodology is equal or not. The resulting p −values are sorted in increasing order, and the null hypothesis is rejected if the p −value is below a fixed significance threshold. In all these tests, we use α = 0.05 as significance level. Furthermore, we executed a sensitivity analysis in order to study the accuracy with respect to the parameters involved in the algorithm. The details of this analysis are explained in Appendix A. All the experiments were coded in R, [79], and carried out in a cluster with 2 terabytes of RAM memory at 6.2 TFlops, running CentOS Linux 7.3.

3.3 Comparative algorithms

Since, to the best of our knowledge, no methodology has been reported in the literature that deals with feature selection in hybrid functional data, we suggest some techniques with which to compare our proposal, even though not all of them are able to perform feature selection. Notice that the main objective of our approach is to obtain good classification rates at the same time that we select the most important features. The first algorithm gives the results of the classification of the hybrid functional data when no feature selection is made. The second comparative method treats the functional component of the hybrid functional data as static by summarizing the functions into a finite-dimensional vector. Such static extraction is done in two different ways. On the one hand, we summarize each functional component into a 4 −dimensional vector including the mean value, the standard deviation, the maximum and the minimum values. On the other hand, each functional covariate is considered as a finite-dimensional vector whose components are the evaluation of the functions in the discretization time points where they have been actually measured. We also compare our proposal with the eight regularized classification methods which can be found on the R library LiblineaR. Particularly, we have applied the eight classification regularization schemes they provided on the discretized hybrid functional data. Finally, we include the comparison of our approach with six filter methods included in the R library mlr on the discretized hybrid functional data. In all the above-explained algorithms the data set is divided into three parts, namely, training, validation, and test. For the sake of comparison with our proposed approach, the division is made in such a way that the test sample coincides exactly with the so-called sample s₄ described in Section 2.2. Furthermore, all the comparative algorithms were run five times for each data set, as stated in Section 3.2. The accuracy over all the runs, measured on the test sample, is used as the performance metric, and is given in Table 3. Sections 3.3.1–3.3.3 give details about all the comparative methods.

3.3.1 Functional SVM (FSVM)

The first alternative method corresponds to the SVM algorithm for functional data. In this case, the different types of features are not taken into account, and no variable selection is made. A grid search is performed to obtain the scalar parameters C and ω based on the following set of values: {2^− 7,…,2⁷} on a logarithmic scale. The SVM problem (1) is run with an isotropic Gaussian kernel in (11):

$$ K(X_{i}, X_{j}) = \exp\left( - \omega \left( \sum\limits_{v=1}^{p}{{\int}_{0}^{T}}\left( {X_{i}^{v}}(t)- {X_{j}^{v}}(t)\right)^{2} dt + \sum\limits_{v = p+1}^{q} \left( {X_{i}^{v}} - {X_{j}^{v}}\right)^{2}\right)\right) $$

(11)

for $X_{i}, X_{j} \in \mathcal {X}$. The parameters C and ω that lead to the best results in terms of the classification rate on the validation sample are kept. Finally, the accuracy of the selected parameters C and ω is computed as a measure of performance.

3.3.2 Standard (static) SVM (ℓ ₂ −SVM)

The second alternative approach corresponds to the soft-margin SVM model [24] when the functions of the hybrid functional data are summarized in scalar values. We solved the SVM problem (1) on the training set, for each of the values of C and ω belonging to the set {2^− 7,…,2⁷} in logarithmic scale.

In this case, the kernel function used in Problem (1) is the isotropic kernel in (12) for multivariate data, in which a transformation of X_i, namely Z_i, is used:

$$ K(Z_{i}, Z_{j}) = \exp\left( - \omega \|Z_{i} - Z_{j}\|^{2}\right), $$

(12)

where ∥⋅∥ denotes the ℓ₂ −norm.

Table 3 Result summary

The best values of C and ω are chosen by measuring the accuracy on the validation sample, and then, the final results are estimated with the optimal values for C and ω on the test sample.

Two different transformations Z_i are here suggested. In the first one, each functional component ${X_{i}^{v}}(t)$, v = 1,…,p is summarized in a 4 −dimensional vector which includes the mean value, the standard deviation, the minimum and the maximum values. Moreover, we add the values of the static covariates ${X_{i}^{v}}$, v = p + 1,…,p + q. Such transformation Z_i is given in (13):

$$ \begin{array}{@{}rcl@{}} {Z_{i}} &= &\Big(\text{mean}({X_{i}^{1}}(t)), \text{sd}({X_{i}^{1}}(t)), \min({X_{i}^{1}}(t)), \max({X_{i}^{1}}(t)), \ldots, \\ &&\text{mean}({X_{i}^{p}}(t)), \text{sd}({X_{i}^{p}}(t)), \min({X_{i}^{p}}(t)), \max({X_{i}^{p}}(t)),\\ && X_{i}^{p+1}, \ldots, X_{i}^{p+q}\Big) \end{array} $$

(13)

The second transformation here proposed consists of substituting each functional covariate by the H discretization points, t₁,…,t_H, where it has been recorded. We also add the values of the static covariates. In other words, the transformation Z_i turns out to be as in (14):

$$ \begin{array}{@{}rcl@{}} {Z_{i}} &= &\Big({X_{i}^{1}}(t_{1}), \ldots, {X_{i}^{1}}(t_{H}),\ldots,{X_{i}^{p}}(t_{1}), \ldots, {X_{i}^{p}}(t_{H}), X_{i}^{p+1}, \ldots, X_{i}^{p+q}\Big)\quad\\ \end{array} $$

(14)

3.3.3 Regularized classification methods

We also compare our proposal with eight regularized algorithms in order to assess the performance of various feature selection strategies that has been used with SVM classification in recent studies (see e.g. [1, 43, 58, 69, 86]). These eight methods stem from the well-known LiblineaR library [34]. The following strategies are studied:

• ℓ₂ −regularized logistic regression, primal implementation (ℓ₂ −LR_p).

• ℓ₂ −regularized SVM with ℓ₂ −norm loss function, dual implementation (ℓ₂ℓ₂ −SVM_d).

• ℓ₂ −regularized SVM with ℓ₂ −norm loss function, primal implementation (ℓ₂ℓ₂ −SVM_p).

• ℓ₂ −regularized SVM with ℓ₁ −norm loss function, dual implementation (ℓ₂ℓ₁ −SVM_d).

• The SVM implementation by Cramer and Singer (SVM_CS).

• ℓ₁ −regularized SVM with ℓ₂ −norm loss function (ℓ₁ℓ₂ −SVM).

• ℓ₁ −regularized logistic regression (ℓ₁ −LR).

• ℓ₂ −regularized logistic regression, dual implementation (ℓ₂ −LR_d).

For each regularized method, the functional covariates were transformed into static variables by using (14). The trade-off parameter C is sought in the set {2^− 7,…,2⁷} using a logarithmic scale, and the value yielding the best accuracy on the validation sample is saved. Finally, the accuracy of the best value of C is given as a result.

3.3.4 Filter methods

Finally, the proposed approach has been also compared with the following six filter methods provided by the recent R library mlr, [6, 13]:

• Chi-squared test ($\mathcal {X}^{2}$ test).

• Information gain entropy (information_gain).

• Kruskal-Wallis test (kruskal_test).

• Minimal depth variable selection (min_depth).

• Random forest variable importance (rf_importance).

• Low-variance method (variance).

These methodologies have been recently applied in works such as [16, 38, 40, 45, 53, 55, 60, 68, 83]. More precisely, the functional covariates have been transformed according to (14). Then, each of the above methods has been run on the transformed covariates and the 25% of the most relevant ones is selected. Such selected variables are used to train the SVM model (1) for a given C and applying different kernel functions. In particular, we have run the experiments using the standard multivariate Gaussian kernel with a fixed bandwidth, ω ∈{2^− 7,…,2⁷}, the polynomial kernel with degree parameter d ∈{1,…,5} and constant c in the set {− 2,…,2}, and the sigmoid kernel with offset parameter ranging also in the set {− 2,…,2}. The best values of C are found in the set {2^− 7,…,2⁷} in logarithmic scale, and the value with the largest accuracy and the best kernel choice on the validation sample is kept. The final results collect the accuracy on the test set for the best kernel hyperparameters and the regularization parameter C.

3.4 Experimental results

Algorithm 1 and all the comparative methods of Section 3.3 have been run five times. Table 3 shows the average accuracy values on the test sample. For each data set, we have highlighted in bold the best algorithm which is associated with the highest accuracy. Moreover, our approach is denoted as Alt. appr., and the FSVM strategy of Section 3.3.1 is designated with the very same name. The ℓ₂-SVM method for the finite-dimensional data in (13) and (14) are denoted as ℓ₂-SVM (4 dim) and ℓ₂-SVM (disc), respectively. Finally, the accuracy results of the eight classification methodologies of LiblineaR in Section 3.3.3 are indicated by ℓ₂-LR_p, ℓ₂ℓ₂-SVM_d, ℓ₂ℓ₂-SVM_p, ℓ₂ℓ₁-SVM_d, SVM_CS, ℓ₁ℓ₂-SVM, ℓ₁-LR, ℓ₂-LR_d, whereas the accuracy given by the six filter methods of mlr detailed in Section 3.3.4 are denoted by $\mathcal {X}^{2}$ test, information_gain, kruskal_test, min_depth, rf_importance and variance.

As a general conclusion from Table 3 we can state that our strategy is the best one in data sets batch and trigonometric. In the pen data set, we obtain comparable results with the existing methods, whereas the retail database is slightly better classified with the ℓ₂-LR_d strategy than with ours. More detailed information about the results is given in Sections 3.4.1–3.4.4.

The results obtained in Table 3 using accuracy as performance measure are complemented in Appendix B, in which we present the Area Under the Curve (AUC), sensitivity, and specificity metrics for all methods and data sets. These new metrics support the conclusions reported for Table 3, confirming that our proposal achieves the best predictive performance compared to the alternative classification techniques. In particular, our approach achieved the best sensitivity in all four data sets, the best specificity in two of the four data sets, and the best AUC in three of the four data sets. Furthermore, our proposal achieved competitive results in the data sets in which was not able to be the best-ranked method.

Table 4 Average rank and accuracy for all the methods

Apart from Table 3, we provide the average rank and the average accuracy of all the tested methods. For each methodology, the average rank is computed as the mean over all the ranks associated to the four databases. Such a rank is obtained by sorting in decreasing order the accuracy values. The average accuracy is simply obtained by computing the mean value over all the data sets of the accuracy results which appear in Table 3. It is clear that our approach is the best one when comparing with the remaining 17 methods. Indeed the average rank of the proposed methodology is 3.875 which is clearly far from the second and third best methods, ℓ₁ℓ₂SVM and ℓ₂ℓ₂SVM_p, both of them with an average rank of 6.125 (Table 4).

3.4.1 Batch data set

If we observe Table 3, it is quite apparent that the proposed methodology yields better results. Furthermore, we are able to identify the most informative features as a byproduct. In fact, the third variable was selected to be important by our algorithm in all the five runs. Remember that this feature is the only functional covariate that is correlated with the target variable. In the third run, for instance, we obtain the following optimal bandwidth: ω = (0,0,165.9076,0.0703,0), i.e. the third and the fourth variables are identified as relevant. Notice that our methodology is not influenced by the static or functional nature of the covariates. In fact, in this example, one variable of each type is selected.

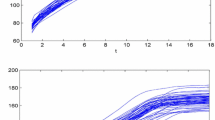
Regarding the sensitivity analysis of the parameters (see Appendix A), we observe that the value of C should be carefully chosen since, as can be seen in Fig. 5, the resulting accuracy depends on the value of C.

By contrast, our proposal is robust with respect to the elimination threshold δ and the number of iterations of the alternating approach, as shown by the stable behavior in Figs. 5b and c, respectively.

Finally, in Fig. 6 we see how the optimal values of the bandwidths evolve in the five runs. We observe that independent of the initial bandwidths selected, the bandwidth associated with the third variable tends toward a value greater than zero.

3.4.2 Trigonometric data set

Table 3 shows that our proposal improves the performance measure of the comparative algorithms. With respect to the feature selection output, features one and three are selected in the five runs, and variable two in three out of five. Indeed, the fourth run gives ω = (0.3758,0.1281,0.0929,0) as optimal solution. Focusing on the sensitivity analysis with respect to δ and the number of iterations, we state that stability in the results is obtained. Nevertheless, the value of C has an important role in the accuracy values. See Fig. 7 in Appendix A for more details. The evolution of the values of the bandwidths in all the five runs is depicted in Fig. 8.

3.4.3 Pen data set

Focusing on Table 3 we observe that our methodology is comparable with the rest of the strategies. As it was sketched in Section 3.1.3, this database is usually applied for multiclass classification purposes. Even though the results are not comparable, we want to remark that the best accuracy results obtained in this data set for multiclass classification in [77, 78, 80] are 94.50%, 88% and 84.5%, respectively. Regarding the number of relevant features, we should say that our approach selects just one variable out of three in two of the five runs. The evolution of the bandwidths values can be seen in Fig. 10 of Appendix A. In this example, the value of C is a critical point as can be observed in Fig. 9c, since the difference between the best and the worst case is around 40 points. However, our method is robust with respect to δ and the number of iterations, as shown in Figs. 9b and c.

3.4.4 Retail data set

We observe in Table 3 that our proposal yields better results than the strategies FSVM, ℓ₂-SVM (4 dim), ℓ₂-SVM (disc), ℓ₂ℓ₂-SVM_d, ℓ₂ℓ₁-SVM_d, $\mathcal {X}^{2}$ test, information_gain, kruskal_test, min_depth, rf_importance and variance, and slightly worse results than the remaining methodologies. Moreover, the selected variables are the third and sixth in four of five runs. As an illustration, the optimal bandwidth in one of these runs is ω = (0,0,1.5887,0,0,45.5919). Feature 3 and Feature 6 correspond to Recency (number of months since the last purchase) computed for each of the 10 months, and UK Customer (a dummy variable that indicates whether the customer comes from the UK). Since our objective is to predict whether a customer will buy products or not in the last three months, it seems that it is important to know the elapsed number of months since the last purchase. In addition, we observe that the customer origin plays an important role; customers in the UK tend to buy less than foreign customers. Finally, similar conclusions to the ones shown in the rest of the examples can be stated with respect to the sensitivity analysis.

In this example, it is even more clear that the choice of the parameter C is a crucial issue for obtaining good accuracy. See Fig. 11c in Appendix A for more details.

Figures 11b and c show again that the elimination threshold δ and the number of iterations do not affect the effectiveness of our approach. In Fig. 12 we can observe the evolution of the values of the different bandwidths which converge in a small number of iterations.

4 Conclusions and extensions

In this paper, we have shown how the well-known SVM technique can be embedded with a feature selection strategy to get the most informative covariates of hybrid functional data. In fact, we have compared our approach with 17 benchmark methodologies from the literature, and our proposal achieves the best average accuracy. In our proposed approach, we have modified the standard Gaussian kernel by associating a bandwidth with each variable. Such bandwidths and the rest of the SVM parameters are sought via a bilevel optimization problem solved with an alternating approach. Instead of minimizing the misclassification rate, we propose maximizing the Pearson correlation between the class label and the score. Other measures such as the correlation in [82] can also be applied. Our methodology can also be used if all the components of the data are functions, i.e. the pure multivariate functional data case. A sensitivity analysis of the setting parameters involved in our approach was made to show its robustness. We observe that the choice of the parameter C is critical to yielding good classification rates. Some standard cross-validation methods may be used to get a good value of C. In contrast, the elimination threshold and the maximum number of iterations allowed in the alternating approach do not affect the accuracy obtained. Moreover, the values of the bandwidths associated with the features converge in few iterations to their final value. We have restricted ourselves to the binary classification problem. The extension to other related fields, such as multiclass classification or regression, [10], deserves further study. In our proposal, we use standard optimization techniques solve Problems (1) and (6). As a future research line, we can develop more efficient optimization strategies compatible with the world of Big Data, e.g. methodologies applied to Problem (1) which do not need the computation of the whole kernel matrix, or the use of stochastic gradients to iterate in the bandwidth parameters of Problem (6). Finally, the application of our approach to other real-world contexts, such as the field of medicine, should be analyzed too.

Appendices

Appendix A: Sensitivity analysis

In order to study the robustness of our proposed algorithm with respect to the parameters involved, we ran a sensitivity analysis. We tested how sensitive our methodology is to the regularization parameter C, the threshold at which the features are removed δ, the maximum number of iterations of the alternating approach, and the bandwidths ω_v, v = 1,…,p + q. First, we ran five times the alternating approach of Algorithm 1 to test the sensitivity of the algorithm with respect to the parameter C, computing the average accuracy on s₃. Second, the sensitivity analysis for the elimination threshold δ is performed by running Algorithm 1 five times for the values given in the set {10^− 10,…, 10^− 5} in logarithmic scale. The average accuracy is estimated on s₃. Third, the maximum number of iterations of the alternating approach may affect the classification rates. In order to check the robustness of our proposal, Algorithm 1 is run five times with the maximum number of iterations belonging to the set {5,…, 10}. The average accuracy measured on the sample s₃ is then computed. Finally, we studied the convergence of the bandwidths. Note that in this paper, convergence does not mean that the bandwidths tend to the same value in all the runs, but that they are greater or less than δ, and yield the same features in most of the cases. For each of the five times that Algorithm 1 was run, the optimal values of the bandwidths after the alternating approach were obtained. The goal is to assess the importance of the variables visually. In all the sensitivity analysis studied, the remaining parameters which were not under study took the values given in Section 3.2. For instance, when the sensitivity with respect to C was analyzed, the elimination threshold was equal to 10^− 5, and the maximum number of iterations of the alternating approach was set to five. Plots of results of the sensitivity analysis for all the parameters above mentioned in the batch data set are depicted in Figs. 5 and 6. Figures 7 and 8 depict the results for trigonometric data set, whereas the results of the pen data set are shown in Figs. 9 and 10. Finally, Figs. 11 and 12 show the sensitivity analysis of the retail data set.

Fig. 5

Results of the sensitivity analysis for the batch data set

Fig. 6

Convergence of the bandwidths for the batch data set

Fig. 7

Results of the sensitivity analysis for the trigonometric data set

Fig. 8

Convergence of the bandwidths for the trigonometric data set

Fig. 9

Results of the sensitivity analysis for the pen data set

Fig. 10

Convergence of the bandwidths for the pen data set

Fig. 11

Results of the sensitivity analysis for the retail data set

Fig. 12

Convergence of the bandwidths for the retail data set

Appendix B: Analysis of sensitivity, specificity and area under the curve

This section provides three tables with new performance metrics, namely sensitivity (Table 5), specificity (Table 6) and Area under the Curve (Table 7). More details about the conclusions derived from these tables can be seen in Section 3.4.

Table 5 Result summary

Table 6 Result summary

Table 7 Result summary