Calibrating trajectory data for spatio-temporal similarity analysis

Abstract

Due to the prevalence of GPS-enabled devices and wireless communications technologies, spatial trajectories that describe the movement history of moving objects are being generated and accumulated at an unprecedented pace. Trajectory data in a database are intrinsically heterogeneous, as they represent discrete approximations of original continuous paths derived using different sampling strategies and different sampling rates. Such heterogeneity can have a negative impact on the effectiveness of trajectory similarity measures, which are the basis of many crucial trajectory processing tasks. In this paper, we pioneer a systematic approach to trajectory calibration that is a process to transform a heterogeneous trajectory dataset to one with (almost) unified sampling strategies. Specifically, we propose an anchor-based calibration system that aligns trajectories to a set of anchor points, which are fixed locations independent of trajectory data. After examining four different types of anchor points for the purpose of building a stable reference system, we propose a spatial-only geometry-based calibration approach that considers the spatial relationship between anchor points and trajectories. Then a more advanced spatial-only model-based calibration method is presented, which exploits the power of machine learning techniques to train inference models from historical trajectory data to improve calibration effectiveness. Afterward, since trajectory has temporal information, we extend these two spatial-only trajectory calibration algorithms to incorporate the temporal information, which can infer a proper time stamp to each anchor point of a calibrated trajectory. At last, we provide a solution to reduce cost, i.e., the number of trajectories that is necessary to be re-calibrated, of the updating of the reference system. Finally, we conduct extensive experiments using real trajectory datasets to demonstrate the effectiveness and efficiency of the proposed calibration system.

1 Introduction

Driven by major advances in sensor technology, GPS-enabled mobile devices and wireless communications, a large amount of data recording the motion history of moving objects, known as trajectories, are currently generated and managed in scores of application domains. This inspires a tremendous amount of research effort on analyzing large-scale trajectory data from a variety of aspects in the last decade. Representative work includes designing effective trajectory indexing structures [4, 6, 12, 34, 37], efficient trajectory query processing [9, 16, 46], and mining knowledge/patterns from trajectories [24, 25, 28, 30], to name a few.

In theory, a trajectory can be modeled by a continuous function mapping time to space; in practice, however, a trajectory can only be represented by a discrete sequence of locations sampled from the continuous movement of the moving object, due to limitations of location acquisition technologies. In other words, when a raw trajectory is reported to the server and stored in the database, it is just a sample of the original travel history. The sampling strategies used to generate trajectory data can vary significantly for several reasons. First of all, the sampling methods can be different, such as distance-based methods (e.g., report every 100 m), time-based methods (e.g., report every 30 s) and predication-based methods (e.g., report when the actual location exceeds a certain distance from the predicted location). Secondly, different parameters may be used even for the same sampling strategy. For example, based on the time-based sampling strategy, a geologist equipped with specialized GPS-devices can report her locations with high frequency (say every 5 s), while a casual mobile phone user may only provide one location record every couple of hours or even days (via, for example, a Web check-in service). Such variations can also be imposed by external factors (such as availability of on-device battery and wireless signal) and may change at owner’s discretion.

As such, trajectory data in real-world database applications are heterogeneous by nature. This, however, can be problematic when these heterogeneous trajectories are processed directly. For example, as we shall illustrate later, it does not make much sense to compare two trajectories obtained using different sampling strategies by directly applying existing trajectory similarity measures like Euclidean distance, DTW [27], LCSS [26] or EDR [8]. This is because these measures are all based on the spatial proximity between sampled locations and hence easily affected by the sampling strategies adopted. Consider in Fig. 1a that two moving objects follow highly similar routes in an urban area, but adopt different sampling strategies. As a result, the raw trajectory (denoted by the solid line) of object $A$ has fewer sample points than that of $B$ (denoted by the dashed line). Figure 1b illustrates the actual trajectory data stored in the database. It is easy to observe that the two trajectories may have a greater distance (than they are supposed to be) based on most trajectory similarity measures. A system relying on trajectory similarity search may produce misleading results to the users if these trajectories are processed without the awareness of this issue. Therefore, this issue of trajectory heterogeneity must be dealt with in order to make meaningful similarity-based trajectory processing.

Fig. 1

Motivation of calibration. a Original routes. b Raw trajectories. c After calibration

1.1 Problem analysis: a case study

Now let us examine the impact of sampling strategies on trajectory similarity analysis through a case study. We test with four commonly used trajectory distance measures: Euclidean Distance, DTW [27], LCSS [26] and EDR [8]. These distance measures perform reasonably well according to the reported results. However, whether it is explicitly mentioned or not, a prerequisite for these measures to be effective is that the sampling strategies of all trajectory data must be compatible (that is, very similar). In the sequel, we will demonstrate that the effectiveness of these distance measures are highly sensitive to how trajectory data are sampled.

In this experiment, we first select 500 densely sampled trajectories on a network as the original routes. For each of them, we adopt a time-based sampling method with variable sampling rates of 10, 20, 30, 60 and 100 s (denoted by $T_{10}, T_{20}, T_{30}, T_{60}$ and $T_{100}$, respectively). Then we choose $T_{30}$ as the baseline trajectory and calculate the distance between $T_{30}$ and other variants using these four trajectory distance measures. The average measured normalized distance values are reported in Table 1. One can see that, although all the trajectories re-sampled using different sampling rates refer to exactly the same original trajectory, the reported distance values vary widely no matter which distance measure is adopted. Consequently, all the data analysis tasks relying on such distance measures can be ineffective as similar trajectories may not be properly identified as such. The root cause of this phenomenon is that all these distance measures, as well as many other trajectory processing techniques, are merely sample based. In other words, all the distance evaluations are performed between sample points. These distance measures can work only based on some assumptions such as very dense point sampling. As we discussed earlier, these assumptions may no longer hold for many real-life trajectory datasets. This case study also illustrates the severity of the trajectory heterogeneity problem.

Table 1 Effect of sampling rates

1.2 Challenges and contributions

With the observation and awareness of this heterogeneity problem for trajectory data, a calibration process is necessary before raw trajectory data can be used for subsequent data analytics to transform a set of heterogeneous trajectories into one with more unified sampling strategies. The goal of this calibration processing is to reduce or even eliminate the negative impact of the sampling strategies on measuring trajectory similarity. In other words, all trajectories after calibration should better resemble their original continuous routes thus can be more accurately compared with each other regardless of the sampling strategies used in generating the raw trajectories. In order to achieve this goal, we need to construct a reference system that is trajectory independent and then rewrite raw trajectories based on the same reference system.

It is a non-trivial task to perform trajectory calibration. First, building a good reference set is the stepping stone for the entire system. Since our goal is to rewrite the trajectory data using the reference set, we expect a good reference set to be stable, independent of data sources, and have a strong association with the trajectory data. The first and second properties are essential for producing trajectories in a unified form, while the third property ensures that the calibration process will not introduce a large deviation from the original routes. Trajectory calibration may encounter three circumstances when rewriting a trajectory with the reference set: (1) a trajectory point may need to be shifted and aligned onto the reference; (2) some trajectory points may need to be removed or merged (when the sampling rate is higher than necessary); (3) some new trajectory points may need to be inserted (when the sampling rate is too low), all in the context of the chosen reference system. Further, the criteria to judge the goodness of the calibration results need to be established, for the system to enforce efficiently and effectively and for the users to understand to what extent the calibration can improve the data analysis results.

In this paper, we propose an anchor-based calibration system for heterogeneous trajectory data. It comprises two components: a reference system and a calibration method. For the first component, we present several reference systems by defining different types of anchor points (space-based, data-based, POI-based and feature-based), which are fixed small regions in the underlying space. A series of strategies are designed for the calibration component, including the methods to insert anchor points to trajectories in order to make them more complete without sacrificing geometric resemblance to the original routes. To this end, we first derive the transfer relationship among anchor points by learning from a historical trajectory dataset and then infer the most probable alignment sequence and complement points with high accuracy by exploiting the power of the Hidden Markov Model and Bayesian Network. We also perform an empirical study to examine the effect of calibration process, using the trajectories with a very high- sampling rate as the ground truth data (the original route) and generate raw trajectories using a different sampling rate in a controlled way. Then we measure the similarities between the raw trajectories, with a set of commonly used distance functions, before and after the calibration process. We will show in the experiment that while the similarities between the raw trajectories heavily depend on the sampling rates, with calibrated trajectories, their similarities always highly resemble those of the original routes for a wide range of sampling rates.

Continuing with the previous example in Fig. 1, one possible approach is to use the turning points $a_1,\ldots , a_{10}$ as the reference system as shown in Fig. 1c, and rewrite both trajectories with these points. Since trajectory $B$ has enough samples to describe its route, it is fairly simple to calibrate—just align each sample to its nearest turning point. However, there is so much information lost in trajectory $A$ that simply aligning each sample to its nearest turning point (i.e., $a_1, a_8, a_9$) still results in a low-quality trajectory. A good calibration system should help to infer that $a_7, a_3, a_4$ are very likely (indicated by a confidence value) to be passed by the routes from $a_1 \rightarrow a_8$, and $a_8 \rightarrow a_9$. After both trajectories have been calibrated, they can become similar again.

Our previous work [42] has demonstrated the effectiveness and efficiency of the proposed techniques for trajectory calibrating. However, the ignorance of temporal information causes the existing trajectory calibration to work for spatial-only trajectory similarity measures while leaving the spatial-temporal distance measures (e.g., Synchronous Euclidean distance [38] and Spatial-Temporal LCSS [46]) uninvestigated, which violates the ultimate goal to reduce or even eliminate the negative impact of the heterogeneous sampling strategies on the effectiveness of trajectory similarity measures. Therefore, it is critical to extend these two spatial-only trajectory calibration algorithms to incorporate the temporal information, which can infer a proper time stamp to each anchor point of a calibrated trajectory.

Besides, though overall the reference system is stable in a relatively long time, small updates, such as insertion or deletion of a few anchor points, can happen in practice. Obviously, it wastes a lot of time if we re-calibrated the whole trajectory set from scratch due to some local changes of the reference system. So a solution, which can reduce the number of trajectories that are necessary to be re-calibrated for both the geometry-based approach and the model-based approach, should be provided.

To sum up, we make the following major contributions.

• We make a key observation that widely existing heterogeneity in trajectory data caused by different sampling strategy can harm the effectiveness of trajectory data analysis, thus calls for a calibration system to reduce or eliminate the impact of the sampling heterogeneity.

• We design an anchor-based calibration system in two phases: building a reference system and performing calibration. As a comprehensive solution, we present four types of anchor points, which are suitable for building a stable reference system. On this basis, we propose two spatial-only approaches, geometry based and model based, to effectively align and complement trajectories using the anchor points.

• We extend the spatial-only calibration approaches to make them to incorporate temporal information. In extending geometry-based calibration, we introduce a time stamp inference mechanism, which does not affect the calibration results of the geometry-based alignment and complement in spatial dimension. In extending model-based calibration with temporal information, we use historical travel time to infer the real path that a low-sampled trajectory travelled by and thus estimate the corresponding time stamps for each anchor point more accurately.

• We control the update of reference system by providing a solution to reduce the number of trajectories that are necessary to be re-calibrated for both the geometry-based approach and the model-based approach.

• We conduct extensive experiments based on large-scale real trajectory dataset, which empirically demonstrates that the calibration system can significantly improve the effectiveness of most popular similarity measures for heterogeneous trajectories.

The remainder of this paper is organized as follows. Section 2 introduces the preliminary concepts and overviews the calibration system. We discuss the reference systems and calibration approaches in Sects. 3 and 4, respectively, followed by extending the calibration approaches to incorporate with temporal information in Sect. 5. The updates handling of reference system is presented in Sect. 6. Section 7 reports the experimental observations. We review the related work on several different research topics in Sect. 8. Section 9 concludes the paper and outlines some future work.

2 Problem statement

In this section, we present some preliminary concepts and give an overview of the proposed calibration system. Table 2 summarizes the major notations used in the rest of the paper.

Table 2 Summary of notations

2.1 Preliminary concepts

Definition 1

(Original route) An original route of a moving object is a continuous mapping from time domain to spatial coordinates (i.e., longitude and latitude), indicating the exact path travelled by the object.

The original route does not exist in a practical database since no positioning technique can acquire location records continuously. Instead, only a set of samples from the original route can be obtained and stored in the database.

Definition 2

(Raw trajectory) A raw trajectory $T$ is a finite sequence of locations sampled from the original route of a moving object, i.e., $T = [p_1,p_2,\ldots ,p_n]$.

Simply speaking, the raw trajectory of a moving object is only one possible sample from its original route by using a specific sampling strategy. A sampling strategy is the mechanism based on which the object decides to report its location. Time-based sampling, distance-based sampling, turning-based sampling and prediction-based sampling are among the most widely used sampling strategies. Besides, the object can also adopt different sampling rates, which is the frequency of reporting the location depending on the sampling strategy (e.g., every 500 m or 30 s). In the rest of the paper, we will use trajectory and raw trajectory interchangeably when the context is clear.

Definition 3

(Anchor point) An anchor point is a fixed spatial location in the space, which is stable and independent of the trajectory data source.

An anchor point can either refer to a geographical object that physically exists such as a point of interest (POI), or can be virtually defined such as the centroid of a grid. Actually, any kind of entities in space can serve as the anchor points as long as they are stable and not affected by the trajectory data input. Based on it, even a turning point extracted from historical trajectories can be an anchor point since a turning point is always stable in a network and is not affected by the input trajectory which needs to be processed.

Definition 4

(Reference system) A reference system is a set of anchor points in a certain region.

A reference system could comprise anchor points of different types. For example, a reference system of a city could consist of all the POIs and the road intersections. For the sake of simplicity, in the following discussion, we focus on reference systems whose anchor points are of the same type. However, our technique can easily generalize to reference systems of heterogeneous anchor points.

Definition 5

(Trajectory calibration) Given a reference system with anchor point set $\mathcal {A}$, trajectory calibration for $T=[p_1,p_2,\ldots ,p_n]$ is a process that transforms $T$ into another trajectory $\overline{T}=[a_1,a_2,\ldots ,a_m]$ where $a_i \in \mathcal {A}\,(1\le i\le m)$. $\overline{T}$ is called the calibrated trajectory of $T$.

We expect the new trajectory $\overline{T}$ after calibration to preserve the original route of $T$ as much as possible, which is critical to reduce the erroneous adjustments to the original route. Ideally, the trajectories that share the same original route will have the same calibrated trajectory no matter what sampling strategies they adopt. Therefore, an evaluation criterion is how well the calibrated trajectory resembles the original route.

2.2 System overview

Figure 2 shows the overview of the proposed calibration system, which comprises two parts: the reference system generation module and the trajectory calibration module (with or without temporal information). In this work, we study four types of anchor points for constructing a reference system, i.e., space-based, data-based, POI-based, and feature-based anchor points. The reference system is independent of the input data and thus can be built offline. We also provide efficient algorithms to further reduce the cost of updating the reference systems.

Fig. 2

System overview

The calibration process can be categorized into two approaches: geometry-based calibration and model-based calibration. Geometry-based calibration uses the spatial relationship between the trajectories and the anchor points, i.e., it aligns points to their nearest anchor points, and try to calibrate the trajectory by linear interpolation. Model-based calibration exploits the correlations between anchor points learned from historical trajectories, and uses a probabilistic approach to do calibration. We also extend both calibration approaches to incorporate temporal information. Regardless of the approaches, the calibration process can be divided into two phases: alignment and complement. Generally, the alignment phase maps existing sample points of a trajectory to the anchor points. The complement phase completes the trajectory by inserting additional anchor points, which is especially important for trajectories with low-sampling rates. The calibration process can be either online or offline depending on the application requirement (e.g., an on-the-fly process or a batch process). We will discuss each part in details in the next sections.

3 Reference systems

In this section, we will define several different types of anchor points for building a reference system. Although any fixed entity in the space can be an anchor point, not all of them are suitable for calibration. First, a reference system should have a sufficient number of anchor points in order to describe any given trajectory with high quality. For example, if we simply use all cinemas in a city as the reference system, a trajectory may have too few points after calibration. As such, most information in the raw trajectories will be lost. Second, a reference system should be stable and does not require substantial changes to calibrate new data. This property is crucial as it ensures that most new trajectories can be calibrated without refurbishing the reference system. Based on this guideline, we propose four types of anchor points that are expected to be suitable for building a reference system. We will study their effects on the calibration process with experiments later in this paper.

It is worth noting that road intersections and segments are natural choices for anchor points if a digital road map is available. But we will not adopt it in this work for two main reasons. First we attempt to make the proposed methods general enough to fit both constrained and unconstrained trajectories (e.g., traces of hiking, boating, walking, and many outdoor activities), and second, most digital maps actually have legal or technical restrictions on their use [22, 35], which hold back people from using them in creating new applications. Therefore, in this work, we will build reference systems based on resources that are easier to acquire.

3.1 Space-based anchors

The most straightforward idea is to divide the entire space into uniform grid cells and use the centroids of the cells as the anchor points. An obvious advantage of using grid centroids is that we can easily build a reference system for any trajectory dataset without extra resources or information. The idea of using grid to adjust trajectories is inspired by the Realm method [21], but their purpose is to represent spatial objects in a database with predefined precision.

3.2 Data-based anchors

A space-based reference system, despite its simplicity, may not capture the distribution of the trajectory data. In other words, the space partition may be too fine-grained for a set of sparsely distributed trajectories but too coarse for another with dense distribution. Another option is to select a large enough set of historical trajectories and use their sample points as the anchor points. Since these samples, called archived samples, represent the travel history of moving objects in the past, it is more reasonable to rewrite a given trajectory based on this type of anchor point. Besides, each anchor point is guaranteed to be a reachable location for a new trajectory. But using archived samples also has down sides. First, we must have a sufficient number of historical trajectories that locate in the same region with the input trajectories. Second, the calibrated trajectory may have a high degree of redundancy when the number of archived samples is large. For instance, in our experiments, we observe there can be more than 300 archived samples along a street one hundred meters long. Third, the effectiveness of the reference system may be affected by the noises residing in the archived data.

3.3 POI-based anchors

A point of interest (POI) refers to a semantic location such as a restaurant, hotel, shopping center. POIs are stable in terms of their locations since a business or facility can usually last for a long period. Besides, POIs have a consistent distribution with trajectories in the same area, since in most cases people travel from/to some POIs to perform certain activities. Due to this property, we can use a POI dataset to build a reference system for the same area (e.g., within a county/city). However, we observe that directly using the POIs can be problematic. Since POIs can be densely distributed in a small area, each trajectory point can be rewritten with many possible candidate anchor points within close proximity. As such, the trajectories after calibration may still have quite different sample strategies. In order to remedy this problem, we preprocess the POI dataset by applying a density-based clustering method (e.g., DBSCAN [15]) to generate a smaller number of clusters, which will be used as the anchor points. By this means, POIs in densely populated areas can be merged into clusters and a cluster becomes an anchor point. As such, trajectories with similar routes, but different samples, will have a better chance to be re-synchronized by mapping their sample points to POI clusters.

3.4 Feature-based anchors

The data-based reference system utilizes the historical archived trajectory points as the anchor points, which can have a high degree of redundancy. To remedy this issue, we can use only some important points in trajectory data, called features, as the anchor points. Moving objects usually travel in a constrained space such as road networks, tracks or waterways. Therefore, an important feature that can well characterize a trajectory is the turning points, at which a moving object changes its direction significantly. In other words, the main shape of a trajectory can be described by a few turning points regardless how many samples it has originally. So intuitively, if we can rewrite all the trajectories based on turning points, their shapes can be well preserved and the samples are also synchronized. We can adopt the algorithm in [10], which detects point clusters that satisfy both the density requirement and the direction change condition, to extract turning points.

4 Trajectory calibration

In this section, we discuss in detail about the calibration process based on a reference system built offline. Specifically, the calibration process can be divided into two phases: alignment and complement. The alignment phase maps a trajectory to some anchor points. The number of sample points in a trajectory may be kept unchanged or reduced since multiple samples in close proximity can be merged into the same anchor point. However, a low-sampling-rate trajectory cannot benefit from this phase alone since the calibrated trajectory will be still low sampled. The complement phase inserts some anchor points in between the trajectory points after alignment, by estimating those important but missing anchor points that the object may pass by.

4.1 Geometry-based calibration

In this part, we present a geometry-based calibration method, which simply explores the spatial relationship between trajectories and anchor points in space when choosing the anchor points for alignment and complement.

4.1.1 Alignment

The geometry-based alignment is based on the simple idea of finding the nearest anchor point for each sample point of a given trajectory and then mapping the original sample point to its nearest anchor point. More precisely, each sample point in a trajectory will be aligned to a nearest anchor point. In order to avoid the case that a sample point will be aligned to a faraway anchor point, we can map a sample point to some anchor points within a distance threshold $\eta _{ dist }$ and the sample points far away from any anchor point will be removed. Besides, if several consecutive sample points, i.e., $p_i, p_{i+1},\ldots ,p_j$, of trajectory $T$ are all close with each other thus can be aligned to the same anchor point $a$, we will only record one copy of $a$ in the aligned trajectory. By this means, we can reduce the unnecessary redundant samples and outliers in some trajectories. The alignment process involves a constrained nearest neighbor search against the anchor point set for each trajectory point, which has a logarithmic-scale complexity with respect to the number of anchor points ($O(\log |\mathcal {A}|)$) [33] when some space partition or tree-based index is used. Thus, the complexity of the alignment is $O(N_T\cdot \log |\mathcal {A}|)$, where $N_T$ is the size of the input trajectory.

4.1.2 Complement

The main idea of the geometry-based complement method is to add the anchor points around the line segment in between any two consecutive samples into the calibrated trajectory, based on the intuition that a moving object rarely changes its direction significantly between two consecutive sampled locations. The main difficulty of this method lies in that, after the anchor points nearby the line segments are selected, how to decide the right insertion order for these points. Algorithm 1 illustrates the main structure of our proposed method. Basically, given an aligned trajectory $\overline{T}$, the geometry-based method consists four steps. (1) Connect each two adjacent anchor points $a_i$ and $a_{i+1}$ by a line segment $l_i$ of $\overline{T}$ (line 1). (2) Build an anchor point set $C_i$ for each line segment that keeps all the anchored points $a$ whose distance to $l_i$ is less than a threshold $\eta _{dist}$ (lines 4–5). $C_i$ holds all the candidate anchor points that are potential to be used. (3) Then we iteratively find the next anchor point $a^*$ from $C_i$ to be inserted which has the minimum distance to the $a_i$ (line 8), and insert $a^*$ in between $a_i$ and $a_{i+1}$ if it does not change the moving trend of $l_i$ (lines 9–10). (4) Repeat step 2 and 3 until $C_i$ becomes empty.

The example in Fig. 3 demonstrates how the anchor points are selected and complemented into the trajectory segment in between $a_i$ and $a_{i+1}$ by using the geometry-based complement algorithm. First we find five candidate anchor points ($a_1, a_2, a_5, a_7$ and $a_8$) whose distances with the line segment $l_i$ are less than $\eta _{ dist }$. Then these points are sequentially connected in the order of their distances with $a_i$, and none of them conflicts with the major direction from $a_i$ to $a_{i+1}$.

Fig. 3

An example of the geometry-based complement

The complexity of the above algorithm is dependent on two factors: the length of aligned trajectory $\overline{T}$ (i.e., the sum of the lengths of the line segments) and the number of anchor points “close” to $\overline{T}$. Let $L$ denote the average length of a trajectory segment and $\rho$ the average density of anchor points in the given reference system. Then the average number of anchor points that are close to each line segment is $N_a = 2L\cdot \rho \cdot \eta _{ dist }$. Since these anchor points need to be sorted based on their distances with $a_i$, the overall complexity is $O(N_T \cdot N_a \log N_a)$, where $N_T$ is the average size of the aligned trajectory.

The geometry-based calibration has two major drawbacks. First, it takes a greedy strategy to align each trajectory point in an isolated manner, which ignores the relationship between anchor points. Second, the anchor points inserted in the complement step are all around the trajectory segments, which means it can only increase the sampling rate of the trajectory while keep the shape unchanged. But sometimes the shape of a trajectory has changed due to the loss of some descriptive samples (e.g., the one at turning points), in which case we need to complement the shape of the trajectory.

4.2 Model-based calibration

To further improve the calibration performance, we propose a more advanced model-based calibration approach, which explores the correlations between anchor points that are learned from a historical trajectory archive, and leverages the power of the Hidden Markov Model (HMM) and Bayesian inference to find the most probable alignment sequence and complement points, respectively. The model-based calibration consists of three steps: deriving anchor transition probability, global alignment and inferring complementary points. The first step learns from a historical trajectory dataset, the transition probability of an object moving from one anchor point to another. In the second step, we feed the anchor transition probability as well as the spatial relationship between sample points and anchor points into the HMM to derive the global optimal alignment. The third step also utilizes the anchor transition probability to infer the likelihood of one or multiple anchor points being passed through by the routes in between two aligned anchor points, and then complement the trajectory by inserting those anchor points whose likelihoods are more than a certain threshold.

4.2.1 Anchor transition probability

In this part, we will derive the transition probability between anchor points. First of all, a reference map, represented as a directed graph $G(V, E)$, is built to indicate the direct transition probability between two anchor points. Given a reference system and a historical trajectory dataset, we can construct the reference map in the following steps:

• 1. We add each anchor point in the reference system to the vertex set $V$ of the reference map.

• 2. We add a directed edge from $a_i$ to $a_j$, denoted by $e(a_i,a_j)$, if there exists a trajectory $T$ in the historical trajectory dataset traveling from $a_i$ to $a_j$ directly, i.e., two consecutive points $p_i, p_{i+1}$ of $T$ are in close vicinity of $a_i$ and $a_j$, respectively. We denote such a trajectory by $T(a_i \rightarrow a_j)$.

• 3. Each edge $e(a_i, a_j)$ is annotated with the number of $T(a_i \rightarrow a_j)$.

After the reference map has been constructed, we can immediately get the 1-step transition probability from $a_i$ to $a_j$ as follows, if $e(a_i,a_j)$ exists in the map:

$$\begin{aligned} {\Pr }_1 (a_i \rightarrow a_j) = \frac{|T(a_i \rightarrow a_j)|}{|T(a_i \rightarrow *)|} \end{aligned}$$

(1)

where $T(a_i \rightarrow *)$ represents the trajectories traveling from $a_i$ to any other anchor point. Figure 4 gives an example of the reference map, where the direction of arrow represents the transition relationship between two anchor points and the number around each arrow indicates how many trajectories travel through the two anchor points consecutively. Based on this reference map, we can derive the 1-step transition probability, e.g., $Pr_1(a_1 \rightarrow a_5) = \frac{5}{9}$.

Fig. 4

An example of the reference map

$\lambda$-step transition probability The first-order transition probability is not sufficient for inferring the relationship between anchor points without an edge. To address this issue, we leverage the first-order probability to get higher-order transition probabilities. First, a transition matrix $M$ with $m_{i,j}={\Pr }_1(a_i \rightarrow a_j)$ is defined. It is easy to get that $M^2$ contains all the second order transition probability, and entries $m_{i,j}$ (after normalization) in $M + M^2$ correspond to the $2$-step transition probability, which is the likelihood of transition from $a_i$ to $a_j$ within two steps. Analogously, we can get the $\lambda$-step transition probability by evaluating the matrix $M^{1:\lambda } = M + M^2 + \cdots + M^\lambda$. But it is not efficient to evaluate $M^{1:\lambda }$ during the calibration process since multiplication of large matrix is very expensive. In this paper, we pre-compute the transition matrix offline, by setting $\lambda$ to be sufficiently large to cover the most pairs of anchor points within the average distance of trajectory sample points.

Background transition probability Sometimes due to the sparsity of historical data, it cannot reflect all the transition relationships between two anchor points even though they are close to each other. To get a complete reference map, we define a background transition matrix $B$ by considering the spatial proximity between two anchor points. Each entry $b_{i,j}$ of $B$, which represents the background transition probability from $a_i$ to $a_j$, is defined as $e^{-d(a_i,a_j)}$.

Finally, we define the transition probability from $a_i$ to $a_j$, denoted by $\Pr (a_j|a_i)$, to be the normalized sum of the $\lambda$-step transition probability and the background transition probability, i.e.,

$$\begin{aligned} \Pr (a_j|a_i) = \frac{p_{i,j}}{p_{i,1}+p_{i,2}+\cdots +p_{i,|\mathcal {A}|}} \end{aligned}$$

(2)

where $p_{i,j} = m^{1:\lambda }_{i,j} + b_{i,j}$.

4.2.2 Global alignment

The geometry-based approach aligns each individual point in an isolated manner, which does not make use of the correlation between anchor points. Next, we propose an HMM-based approach to find the most probable alignment by utilizing the transition probability in the derived reference map. In particular, the candidate anchor points are sequentially generated and evaluated on the basis of their likelihoods. When a new trajectory sample point is to be aligned, past hypotheses of the solution are extended to account for the new observation. Among all candidates in the last stage, the surviving path of anchor points with the highest joint probability is then selected as the final solution. In contrast to local alignment results in the geometry-based approach, the HMM-based approach takes into account the anchor points in a collective manner when it generates the alignment.

Given a trajectory $T$, we treat each point $p_i \in T$ as an observed state and identify a set of candidate anchor points $A_i$, whose distance with $p_i$ is less than a certain threshold $\eta _{ dist }$. Each of these candidates is regarded as a hidden state in the HMM. Each hidden state $a_j \in A_i$ has an emission probability, $\Pr (p_i | a_j)$, which is the likelihood of observing the point $p_i$ conditioned on $a_j$ being the ground truth. Intuitively, we would assign a higher probability to an anchor point if it is closer to $p_i$. In this paper, we assume $p_i$ follows a normal distribution with $a_j$ as the mean and a constant $\sigma$ as the variance, i.e., $\Pr (p_i | a_j) = N(a_j, \sigma ^2)$. The transition probability between adjacent hidden states in the Markov chain, i.e., $\Pr (a_i | a_{i-1})$, can be obtained from the reference map that is derived earlier. Here we will adopt the first-order Markov chain based on the assumption of the 1-dependency, i.e., the probability of the current state is only dependent on the previous one, since the influence between two distant anchor points is usually very small.

Finally, we can compute the posterior probability of all hidden state variables given a sequence of observations, i.e., $\Pr (a_k|p_1,\ldots ,\,p_n)\,\forall a_k \in A_k$. It can be rewritten as

$$\begin{aligned}&\Pr (a_k| p_1, \ldots , p_k, p_{k+1}, \ldots , p_n) \end{aligned}$$

(3)

$$\begin{aligned}&\propto \Pr (a_k | p_1, \ldots , p_k) \Pr (a_k|p_{k+1}, \ldots , p_n) \end{aligned}$$

(4)

where $\Pr (a_k | p_1, \ldots , p_k)$ is the forward probability and $\Pr (a_k|\,p_{k+1}, \ldots , p_n)$ the backward probability. We can apply the forward-backward algorithm [7] to calculate the probability of each candidate anchor point and select the most probable alignment sequence.

Since the forward-backward algorithm has the time complexity of $O(T\cdot N^2)$, where $T$ is the length of sequence and $N$ is the number of symbols in the state alphabet, the time complexity of the global alignment algorithm is $O(N_T\cdot {|A|}^2)$, where $N_T$ is size of raw trajectory and $|A|$ is the total number of candidate anchor point sets (i.e., $|A_1\cup A_2 \cup \cdots \cup A_n|$). Theoretically $|A|$ can be arbitrarily big that may cause this algorithm inefficient. In this work, we consider a physical constraint that is the distance between possible hidden states (anchor points) and the observation (a sample point) should be within a threshold $\eta _{ dist }$. In other words, not all the sample points have hidden states. Moreover, since the distribution of some kind of anchor points, such as POIs and turning points, are not very dense, the amount of hidden states for a certain observation is not big.

4.2.3 Inferring complementary points

Next, we discuss how to infer the possible anchor points to be inserted in between two consecutive points $a_i$ and $a_{i+1}$ in an aligned trajectory $\overline{T}=[a_1,\ldots ,a_i,a_{i+1},\ldots ,a_n]$. The main idea is that if an anchor point participates in more possible paths, it is more likely to be a valid complementary point in the calibrated trajectory. Therefore, we accumulate the probabilities of the possible paths that contain the anchor point as the probability of it being a complementary point. However, this accumulation process is only for each consecutive pair $(a_i, a_{i+1})$. After proceeding to the next pair, the probabilities of all anchor points will be initialized to zero again. The Algorithm 2 illustrates the main structure of this approach.

We denote the probability of an anchor point $a^*$ being passed by the original route of $\overline{T}$ from $a_i$ to $a_{i+1}$ by $\Pr _i(a^*|\overline{T})$. The aim of this step is to find the anchor points $a^*$ such that $\Pr _i(a^*|\overline{T})$ is greater than a pre-defined confidence threshold $\eta _{ {confi} }$ (lines 13–14).

$\Pr _i(a^*|\overline{T})$ is defined as follows (lines 11–12):

$$\begin{aligned} {\Pr }_i(a^*|\overline{T}) = \sum _{P \in PP_\lambda (a_i,a_{i+1})} {{\Pr }_i (P|\overline{T}) \cdot exist(P,a^*)} \end{aligned}$$

(5)

where ${PP}_\lambda (a_i,a_{i+1})$ is the set of possible paths which are constructed by using anchor points and connect $a_i$ and $a_{i+1}$ within $\lambda$ intermediate steps. $exist(P, a^*)$ is an indicator, whose value is equal to one if $a^*$ lies in the path $P$, and zero otherwise. In the sequel, we will discuss how to obtain $PP_\lambda (a_i,a_{i+1})$ and compute $\Pr _i(P|\overline{T})$, respectively.

Generate the possible paths In order to obtain $PP_\lambda (a_i,a_{i+1})$, we need to enumerate all the possible paths from $a_i$ to $a_{i+1}$ within $\lambda$ hops. Let $N(a_i)$ denote the anchor points in the reference map that are directly reachable from $a_i$ in the reference map. We build a path tree from $a_i$ to $a_{i+1}$ to help us find possible paths from $a_i$ to $a_{i+1}$ (line 3-4). A path tree from $a_i$ to $a_{i+1}$ is built according to the following four rules: (1) the root of the tree is $a_i$; (2) the height of the tree is $\lambda +1$; (3) the child nodes of $a_j$ are $N(a_j)$; (4) $a_{i+1}$ must be the leaf node. An example of a path tree from $a_1$ to $a_6$ in illustrated by Fig. 5a. With the help of the path tree, finding all the paths $P$ of $PP_3(a_1,a_{6})$ is simplified to visiting the tree from root $a_1$ to all the leaf nodes.

Fig. 5

An original path tree and its optimized path tree

However, the above process can be very time consuming when $\lambda$ is large and/or each anchor point connects many other anchor points. In order to reduce the search space in the path tree, we can utilize the $\lambda$-step transition matrix $M^{1:\lambda }$ that is pre-computed with the reference map (line 2). Based on the $\lambda$-step transition matrix, it is easy to derive the set of destinations $S(a_i\rightarrow )$ that can be reached from $a_i$ within $\lambda$ steps. Similarly, we can also get the set of sources $S(\rightarrow a_{i+1})$ that can reach $a_{i+1}$ within $\lambda$ steps. The joint set $S(a_i\rightarrow a_{i+1})= S(a_i \rightarrow ) \cap S(\rightarrow a_{i+1})$ then contains all the anchor points on the paths from $a_i$ to $a_{i+1}$ within $\lambda$ steps. After that, we can delete the nodes that does not exist in $S(a_i\rightarrow a_{i+1})$ and their child nodes in the path tree, by which means many impossible paths can be filtered out and the search space gets reduced substantially. Notably, we do not actually remove the sub-paths from the path tree. Instead, we simply exclude the node that cannot be reached from either source and destination point within $\lambda$ steps (by probing the transition matrix) when building the path tree. Continuing with the previous example, from $M^{1:3}$ we know that $a_3$ can never reach $a_6$ within 3 steps, so $a_3$ and its child nodes can be deleted from the original path tree. The optimized path tree is shown in Fig. 5b.

Evaluate ${\Pr }_i(P|\overline{T})$ Now we need to evaluate the probability of a path $P$ that connects $a_i$ and $a_{i+1}$ within $\lambda$ steps, conditioned on the observed alignment $\overline{T}=[a_1,\ldots , a_i,\, a_{i+1},\ldots ,a_n]$ (line 6), i.e.,

$$\begin{aligned} {\Pr }_i(P|\overline{T}) = {\Pr }_i (a_1^*,a_2^*, \ldots ,a_k^*|a_1, \ldots , a_i, a_{i + 1}, \ldots , a_n) \end{aligned}$$

(6)

where $k \le \lambda$ and $a_1^*, a_2^*, \ldots , a_k^*$ are the points on path $P$. The resulting trajectory will be $[a_1,\ldots , a_i, a_1^*, \ldots ,\, a_k^*,\, a_{i+1}, \ldots , a_n]$.

However, the exact evaluation of Eq. (6) is too expensive to be feasible for calibration. To address this issue, we make the assumption that the probability of an anchor point is only affected by its precedent in a path. Then Eq. 6 can be simplified as follows:

$$\begin{aligned}&{\Pr }_i (a_1^*,a_2^*, \ldots ,a_k^*|a_1, \ldots , a_i, a_{i + 1}, \ldots , a_n) \nonumber \\&\quad = {\Pr }_i(a_1^*, \ldots ,a_k^*|a_{i}, a_{i+1}) \nonumber \\&\quad = \frac{\Pr (a_1^*|a_i) \Pr (a_2^*|a_1^*) \ldots \Pr (a_{i+1}|a_k^*)}{\Pr (a_{i+1}| a_{i})} \end{aligned}$$

(7)

The time complexity of Algorithm 2 is $O(N_T \cdot |{PP}|^2 )$, where $N_T$ is the size of the aligned trajectory and $|{PP}|$ is the average number of paths connecting two consecutive anchor points of $\overline{T}$ within $\lambda$ steps. Let $d_o$ denote the average out degree of an anchor point in the reference map, then $|{PP}|$ can be evaluated as $d_o^\lambda$. Usually the value of $\lambda$ is very small, which makes the practical time cost of Algorithm 2 reasonable. Besides, with the help of optimized path tree, only a small subset of the possible paths needs to be checked. The effect of this optimization will be verified in the experiment (Sect. 7.3.7).

5 Calibration using temporal information

We all know that trajectory has two dimensions of information, spatial information and temporal information. In the previous section, we introduce the calibration methods, geometry-based calibration and model-based calibration, which only use the spatial information. Therefore, with some modification, we can adopt these two calibration to use both spatial and temporal information to do calibration. The usage of both spatial and temporal information in calibration mainly has two extrusive advantages than the calibration methods only use spatial information. The first one is that with temporal information we can assign a time stamp to each anchor point of a calibrated trajectory, and with the time stamp the calibration technique can support trajectory distance measures which are sensitive to the temporal information, i.e., SED [13] and STLCSS [46]. The second advantages is that the accuracy of the complement phase of the model-based calibration can be improved since with temporal information we can better infer the original continuous trajectory from the aligned trajectory.

Adopting the temporal information of the two calibration methods can be also divided into two phases: (1) during alignment, we need to assign a proper time stamp to the aligned anchor point; (2) during complement, we need to infer a possible time stamp to the inserted anchor point.

5.1 Geometry-based calibration with temporal information

The geometry-based calibration with temporal information approach does not affect how a raw trajectory is aligned to the reference system or how to complement the aligned trajectory with some more anchor points. Based on unchanging geometry-based calibration, we assign proper time stamp to each anchor point of the calibrated trajectory in this the temporal version geometry-based calibration method.

5.1.1 Temporal sensitive alignment of geometry-based calibration

In the geometry-based alignment introduced in Sect. 4.1.1, a sample point $p$ is aligned to its nearest anchor point within distance $\eta _{ dist }$. Since several consecutive sample points $p_i, p_{i+1}, \ldots ,p_j$ of a trajectory $T$ may be aligned to a same anchor point $a$, we assign $p_i\cdot t$, the first time $T$ reaching $a$, to $a\cdot t$.

5.1.2 Temporal sensitive complementation of geometry-based calibration

The geometry-based complement (Sect. 4.1.2) assumes the trajectory $T=[a_1, \ldots , a_{i}, a_{i+1}, \ldots , a_n]$ was in linear uniform motion when moving from one aligned anchor point $a_i$ to its consecutive anchor point $a_{i+1}$ and interpolates anchor points along the straight line $[a_i,a_{i+1}]$. Based on the assumption, we can easily infer the time stamp of the interpolated anchor point $a_k^*$ in between $[a_i,a_{i+1}]$ by calculating the time interval moving from $a_i$ to $a_k^*$. So the time stamp assigned to $a_k^*$ is given by the following algorithm:

$$\begin{aligned} a_k^*\cdot t = {a_i}\cdot t + \frac{{({a_{i+1}}\cdot t - {a_i}\cdot t) \cdot d({a_i},{a_k^*}) \cdot \left| {\overrightarrow{{a_i}{a_k^*}} \cdot \overrightarrow{{a_i}{a_{i+1}}} } \right| }}{{d({a_i},{a_{i+1}}) \cdot \left| {\overrightarrow{{a_i}{a_k^*}} } \right| \cdot \left| {\overrightarrow{{a_i}{a_{i+1}}} } \right| }} \end{aligned}$$

5.2 Temporal-model-based calibration

Model-based calibration utilize the knowledge learned from historical trajectories to do statistical-based alignment and complement. Unlike the geometry-based calibration with temporal information, the model-based calibration with temporal information may affect the location of how to interpolate an aligned trajectory during complement phase. The new model-based calibration with temporal information is named temporal-model-based calibration.

5.2.1 Cost matrix

In Sect. 4.2.1, we have introduced the transition relationship between anchor points can be modeled by a graph, where the nodes of the graph are anchor points and the edges represent the transition direction and probability. Besides, it is observed that the time cost between two locations with low Euclidean distance are relatively stable. Thus, we can record the time cost $t(a_i\rightarrow a_j)$ for edge $a_i$ to $a_j$ by using the mean time for all trajectories $\mathbb {T}_{a_i\rightarrow a_{j}}$ moving from $a_i$ to $a_j$ directly spend on moving the edge, that is:

$$\begin{aligned} t(a_i\rightarrow a_j) =\frac{{\sum \nolimits _{{\overline{T}\in \mathbb {T}_{a_i\rightarrow a_{j}}}} {{a^{\overline{T}}_{j}\cdot t-a^{\overline{T}}_i\cdot t}} }}{|\mathbb {T}_{a_i\rightarrow a_{j}}|} \end{aligned}$$

where $a^{\overline{T}}_{m}\cdot t$ is the time stamp on $\overline{T}$’s anchor point $a_m$. Then a cost matrix $D$ indicating the average time cost between anchor points is defined with $d_{i,j}=t(a_i\rightarrow a_j)$.

5.2.2 Temporal sensitive alignment of model-based calibration

Like the alignment of geometry-based calibration, a sample point $p$ of a trajectory are assigned to an anchor point $a$ within the distance of $\eta _{ dist }$. So we can directly assign $p\cdot t$ to the time stamp of the aligned $a$. Similarly, if several consecutive sample points $p_i, p_{i+1},\ldots ,p_j$ are aligned to the same anchor point $a$, then we assign $p_i\cdot t$ to $a\cdot t$.

5.2.3 Temporal sensitive complement of model-based calibration

With temporal information, we can estimate the original path of the trajectory better. In other words, if the time duration between two consecutive aligned anchor points $a_i$ and $a_{i+1}$ is close to the average time cost of one certain path $P \in \mathrm{PP}_{\lambda }(a_i, a_{i+1})$, then $P$ has a high possibility to be the original path among others. So the probability $\Pr _i(P|\overline{T})$, which indicates the probability of a path $P$ that connects $a_i$ and $a_{i+1}$ within $\lambda$ steps, conditioned on the observed aligned trajectory $\overline{T}=[a_1,\ldots ,a_i, a_{i+1},\ldots ,a_n]$, is not only affected by the frequency of $P$ but also the time cost of $P$. Thus, the following equation is used to measure the $\Pr _i(P|\overline{T})$ instead of Eq. 6:

$$\begin{aligned} {\Pr }_i(P|\overline{T})=C\cdot {\Pr }_i^f(P|\overline{T}) \cdot \mathbb {S}_i^t(P|\overline{T}) \end{aligned}$$

(8)

where $C$ is a normalization parameter which satisfies

$$\begin{aligned} \sum \limits _{P\in {PP}_{\lambda }(a_i, a_{i+1})} {{\Pr }_i(P|\overline{T}) } =1 \end{aligned}$$

${\Pr }_i^f(P|\overline{T})$ indicates the frequency of $P$ to be the real path between $a_{i}$ and $a_{i+1}$; $\mathbb {S}_i^t(P|\overline{T})$ represents the similarity between the real-time cost and the time cost of $P$. Thus, ${\Pr }_i^f(P|\overline{T})$ can be easily evaluated by the following equation:

$$\begin{aligned}&{\Pr }_i^f(P|\overline{T})\nonumber \\&\quad = {\Pr }_i \left( a_1^*,a_2^*, \ldots ,a_k^*|a_1, \ldots , a_i, a_{i + 1}, \ldots , a_n\right) \nonumber \\&\quad = {\Pr }_i\left( a_1^*, \ldots ,a_k^*|a_{i}, a_{i+1}\right) \nonumber \\&\quad = \frac{\Pr \left( a_1^*|a_i\right) \Pr \left( a_2^*|a_1^*\right) \ldots \Pr \left( a_{i+1}|a_k^*\right) }{\Pr \left( a_{i+1}| a_{i}\right) } \end{aligned}$$

(9)

$\mathbb {S}_i^t(P|\overline{T})$ describes the intuition that the average historical time cost of a path $P$ should be close to the real-time cost. In other words, $P$ is unlikely the real path if the average historical time cost of $P$ is significantly larger or smaller than the real-time cost. Thus, the $\mathbb {S}_i^t(P|\overline{T})$ is defined as following:

$$\begin{aligned}&\mathbb {S}_i^t(P|\overline{T})\nonumber \\&\quad = \exp \left( -\left| \frac{{real~time~cost-time~cost~of~P}}{{time~cost~of~P}}\right| \right) \nonumber \\&\quad = \exp \left( -\left| \frac{{(a_{i+1}\cdot t-a_i\cdot t)-[t({a_i\rightarrow a_1^*})+t({a_1^*\rightarrow a_2^*})}}{{t({a_i\rightarrow a_1^*})+t({a_1^*\rightarrow a_2^*})+\cdots +t({a_k^*\rightarrow a_{i+1}})}}\right. \right. \nonumber \\&\qquad \left. \left. \frac{+\cdots +{t({a_k^*\rightarrow a_{i+1}})]}}{{t({a_i\rightarrow a_1^*})+t({a_1^*\rightarrow a_2^*})+\cdots +t({a_k^*\rightarrow a_{i+1}})}}\right| \right) \end{aligned}$$

(10)

where $a_i\cdot t$ is the time stamp assigned to $a_i$; $t{(a_i\rightarrow a_j)}$ is average time cost learned from historical trajectories, which is $d_{i,j}$ of the cost matrix. Here the time interval $a_{i+1}\cdot t$ and $a_{i}\cdot t$ are given in alignment phrase. $t_{(a_i \rightarrow a_1^*)},t_{(a_1^* \rightarrow a_2^*)}, \ldots , t_{(a_k^* \rightarrow a_{i+1})}$ can be directly obtained from the cost matrix, which means time complexity of the operation is O(1). So evaluating Eq. (10) can be efficient.

6 Handling reference system updates

Although the reference system is usually stable, in practice local updates that changes part of the reference system could happen, e.g., the opening of a new Walmart store, which could be an important new POI. Both triggering update every time an anchor point is added and running periodically when a new version of anchors is collected can be the option of handling the updating of reference system. In particular, we observed if the newly added anchor point $a^*$ locates in the area where the existing anchor points are sparsely distributed, then triggering update instantaneously can significantly improve the calibration effect for the trajectories nearby.

Thus, taking a naive approach, we would re-calibrate all the rewritten trajectories based on the updated reference system every time an anchor point changes, which incurs very high and unnecessary cost, especially when the model-based calibration methods are used (where all the transition probabilities need to be retrained). Actually, one can easily observe that a local update (addition or deletion) to an anchor point $a^*$ rarely affects places far away from $a^*$. For example, a new Walmart store opened in New York does not affect the calibration of the trajectories in Newark. Thus, if an anchor point is modified of one existing reference system, we do not need to re-calibrate all the trajectories already been calibrated by using the previous reference system. So in this section, we discuss how to use delta update methods to handle local updates to a reference system, including both addition and deletion of anchor points. In the following, we explain our update algorithms for geometry-based and model-based calibration, respectively. The update algorithms can be mainly divided into two phases: realignment and re-complement. For ease of exposition, we only discuss how to handle addition of an anchor point. The case of anchor points deletion is similar to the addition case and thus is omitted.

6.1 Handling updates for geometry-based calibration

The geometry-based calibration method only utilizes the geometric information of the reference system and the input trajectories. Therefore, when a new anchor point is added, one can simply repeat the alignment and complement algorithm introduced in Sect. 4 to rewrite a trajectory. More importantly, such rewriting can be limited to a few affected trajectories within certain distance from the newly added anchor points, or even segments of the affected trajectories. In this section, we discuss how to reduce the number of trajectories and the number of segments within a trajectory that need to be rewritten.

6.1.1 Realignment of geometry-based calibration

Let us denote the set of sample points from all the raw trajectories by $\mathbb {P}$. A sample point $p \in \mathbb {P}$ need to be realigned on the updated reference system, if and only if $a^*$ is $p$’s nearest neighbor on the updated reference system, and $a^*$ is within $\eta _{ dist }$ from $p$. Let us denote the nearest neighbor of $p$ by $\mathrm{NN}_1(p)$. We can formally define the set of sample points which need realignment as follows, denoted by

$$\begin{aligned} \mathbb {P}_{a^*} = \{p \in \mathbb {P}\mid dist(p, a^*) \le \eta _{dist} \wedge a^* \in NN_1(p)\} \end{aligned}$$

Thus, the anchor-based trajectories that need to be realigned, denoted by $\mathbb {T}_{a^*}$, is the set of trajectories which has at least one sample point from $\mathbb {P}_{a^*}$.

Given a newly inserted anchor point $a^*, \mathbb {P}_{a^*}$ can be quickly identified by three steps: (1) issue a reverse 1-nearest neighbor query on $a^*$, (2) issue a range query on $a^*$ which returns all the sample points within distance $\eta _{ dist }$ to $a^*$, and (3) take an intersection of the two result sets. Efficient index structures, such as MR$k$NNCoP-tree [1], can facilitate the reverse 1-nearest neighbor query. Furthermore, after getting $\mathbb {P}_{a^*}$, only those trajectories which have at least one sample point in $\mathbb {P}_{a^*}$ need to be realigned.

6.1.2 Re-complementation of geometry-based calibration

Let us denote the trajectories which need to be re-complemented by $\mathbb {T}_c$. $\mathbb {T}_c$ consists of two parts: (1) the realigned trajectories, i.e., $\mathbb {T}_a$, and (2) the trajectories whose line segments are within $\eta _{ dist }$ from the newly added anchor point $a^*$. We can formally define $\mathbb {T}_c$ as below:

$$\begin{aligned} \mathbb {T}_c&= \mathbb {T}_a \cup \{ \overline{T} \mid \exists ( p_i, p_{i+1}) \in \overline{T}, {dist}(a^*, (p_i, p_{i+1}))\\&\le \eta _{ dist } \} \end{aligned}$$

Part (2) can be identified by issuing a range query on $a^*$ which returns all the trajectory segments within $\eta _{ dist }$ to $a^*$. We can use spatial indices, such as R-Tree, to speed up the range query. Notably, within $\mathbb {T}_c$ only those segments within $\eta _{ dist }$ to $a^*$ need to be re-complemented.

6.2 Handling updates for model-based calibration

Unlike the geometry-based calibration method, the model-based calibration method utilizes statistical information learned from historical trajectories. Therefore, in order to handle reference map update, we first update the reference map with low cost, and then carry out the realignment and re-complement processes.

6.2.1 Updating the reference map and cost matrix

Let $G(V, E)$ denote the reference map learned from the existing reference system, and $G^*(V^*,E^*)$ denote the reference map learned from the updated reference system by adding a new sample point $a^*$. Clearly, according to the construction procedure of a reference map, we have $V^* = V \cup \{a^*\}$; while $E^*$ differs from $E$ by two parts: (1) some edges starting or ending at $a^*$ are added, i.e., $(a, a^*)$ and/or $(a^*, a)$ for some $a \ne a^*$ and (2) some previous edges connecting anchor points $(a, a')$ are deleted, where $a, a'$ are close to $a^*$ (within $\eta _{ dist }$ from $a^*$). We define the set of anchor points affected by the insertion of $a^*$ ($a, a'$ as above) as the impact set $\mathfrak {S}$ of $a^*$.

Now we are up to derive an updated $1$-step transition matrix $M^*$ from $G^*(V^*,E^*)$. It is easy to see that $M^*$ differs from the original $1$-step transition matrix $M$ only on the entries corresponding to anchor points in $\mathfrak {S}$. Adopting the calculation Eq. (1), $M^*$ can be easily generated by simply updating $M$ at $\mathfrak {S}$ and add a new row and a new column corresponding to $a^*$. What is more, in order to speed up the updating, we can store a matrix $R$ where $r_{ij}$ indicates how many trajectories directly moving from $a_i$ to $a_j$. Since the model-based alignment and complement is based on the $\lambda$-step transition probability, which is constructed from the $1$-step transition probability, in next paragraphs, we will introduce how to update the transition matrix in $\lambda$ steps.

Firstly, we introduce an important concept—the impact blanket of an anchor point $a$, denoted by $\mathbf {b}_{\lambda }{(a)}$. $\mathbf {b}_{\lambda }{(a)}$ is defined as the neighbors within $\lambda$ steps from point $a$, that is, all the nodes that can reach $a$ or be reached from $a$ in $\lambda$ steps. We abuse the notation a little by using $\mathbf {b}_{\lambda }{(\mathfrak {S})} = \bigcup _{a \in \mathfrak {S}}{\mathbf {b}_{\lambda }{(a)}}$. Clearly, in the updated $\lambda$-step transition matrix $M^{*1:\lambda }$, one entry $M^{*1:\lambda }_{i,j}$ is different from $M^{1:\lambda }_{i,j}$ if and only if anchor points $a_i,a_j \in \mathbf {b}_{\lambda }{(\mathfrak {S})}$. We have the following theorem:

Theorem 1

For anchor points $a_i \not \in \mathbf {b}_{\lambda }{(\mathfrak {S})}$,

$$\begin{aligned} M^{*1:\lambda }_{i,\cdot } = M^{1:\lambda }_{i,\cdot },\quad M^{*1:\lambda }_{\cdot ,i} = M^{1:\lambda }_{\cdot ,i} \end{aligned}$$

Proof

(Sketch) $M^{*1:\lambda }_{i,j} \ne M^{1:\lambda }_{i,j}$ if and only if there exists a path from $a_i$ to $a_j$ that pass through one edge which connects two points in $\mathfrak {S}$, say $a$ and $a'$. Therefore, $a_i$ must be in either $\mathbf {b}_{\lambda }{(a)}$ or $\mathbf {b}_{\lambda }{(a')}$. We reach a contradiction. We can prove $M^{*1:\lambda }_{\cdot ,i} = M^{1:\lambda }_{\cdot ,i}$ similarly. $\square$

$\mathbf {b}_{\lambda }{(\mathfrak {S})}$ can be easily computed by traversing the updated reference map $G^*(V^*, E^*)$. In order to compute $M^{*1:\lambda }$, we update $M^{1:\lambda }$ the entries corresponding to $\mathbf {b}_{\lambda }{(\mathfrak {S})}$, that is, the transition probability from some anchor point in $\mathbf {b}_{\lambda }{(\mathfrak {S})}$ to any anchor point in $\mathbf {b}_{\lambda }{(\mathfrak {S})}$. Let $M^{*1:\lambda }_{\mathbf {b}_{\lambda }{(\mathfrak {S})},\mathbf {b}_{\lambda }{(\mathfrak {S})}}$ denote these entries. We can compute $M^{*1:\lambda }_{\mathbf {b}_{\lambda }{(\mathfrak {S})},\mathbf {b}_{\lambda }{(\mathfrak {S})}}$ by the equation below.

$$\begin{aligned} M^{*1:\lambda }_{\mathbf {b}_{\lambda }{(\mathfrak {S})},\mathbf {b}_{\lambda }{(\mathfrak {S})}}&= M^*_{\mathbf {b}_{\lambda }{(\mathfrak {S})},\mathbf {b}_{\lambda }{(\mathfrak {S})}} + M^{*2}_{\mathbf {b}_{\lambda }{(\mathfrak {S})},\mathbf {b}_{\lambda }{(\mathfrak {S})}} \nonumber \\&+ \cdots + M^{*\lambda }_{\mathbf {b}_{\lambda }{(\mathfrak {S})},\mathbf {b}_{\lambda }{(\mathfrak {S})}} \end{aligned}$$

(11)

Importantly, to compute $M^{*k}_{\mathbf {b}_{\lambda }{(\mathfrak {S})},\mathbf {b}_{\lambda }{(\mathfrak {S})}}$, we do not need to multiply $M^*$ by $k$ times. Instead, we only need to multiply $M^*_{\mathbf {b}_{k-1}{(\mathbf {b}_{\lambda }{(\mathfrak {S})})},\mathbf {b}_{k-1}{(\mathbf {b}_{\lambda }{(\mathfrak {S})})}}$ by $k$ times, as only anchor points in $\mathbf {b}_{k-1}{(\mathbf {b}_{\lambda }{(\mathfrak {S})})}$ will affect the transition probabilities. We have the following result about the complexity of our update algorithm.

Theorem 2

Let the size of $\mathbf {b}_{\lambda }{(\mathbf {b}_{\lambda }{(\mathfrak {S})})}$ be $n$, then the time complexity of computing Eq. 11 is at most $O(\lambda n^{2.3729})$.

Proof

(Sketch) The complexity follows from the fact that we need to do $\lambda$ matrix multiplication and the state of the art matrix multiplication algorithm has a time complexity $O(n^{2.3729})$ [49]. Since matrices to be multiplied are always sparse, the time complexity of the equation is at most $O(\lambda \, n^{2.3729})$. $\square$

As for the updating of the cost matrix $D$, only the average time cost $d_{i,j}$ between anchor points $a_i$ and $a_j$, where $a_i,\, a_j\in \mathfrak {S}$, need to be changed. We can compute the new $d_{i,j}'$ by the following equation:

$$\begin{aligned} d_{i,j}'= \frac{{d_{ij}*(r_{ij}-n_{\mathrm{delete}}){+}\sum \nolimits _{\overline{T}\in \mathbb {T}(a_i\rightarrow a_j)_{\mathrm{new}}} {a^{\overline{T}}_j\cdot t{-}a^{\overline{T}}_i\cdot t} }}{{r_{ij}-n_{\mathrm{delete}}{+}| \mathbb {T}(a_i\rightarrow a_j)_{\mathrm{new}}|}} \end{aligned}$$

(12)

where $n_{\mathrm{delete}}$ denotes the number of deleted trajectories which passing $a_i$ to $a_j, \mathbb {T}(a_i\rightarrow a_j)_{new}$ is the added trajectories which passing $a_i$ to $a_j$.

6.2.2 Realignment of model-based calibration

Although the model-based alignment utilizes the power of the whole trajectory, it shares the same idea with the geometry-based calibration that sample points needs to be mapped to some local anchor point within the distance threshold $\eta _{ dist }$. However, differently, now any sample point which is within $\eta _{ dist }$ of $a^*$ could be mapped to $a^*$. Therefore, we can compute the set of trajectories which need to be realigned, i.e., $\mathbb {T}_a$ by issuing a range query on $a^*$ to return all the sample points within $\eta _{ dist }$ to $a^*$.

6.2.3 Re-complement of model-based calibration

Model-based complement tries to interpolate between any two consecutive anchor points of an aligned trajectory with high- confidence anchor points. Thus, the trajectories which need to be re-complemented are not simply those trajectories near the newly inserted anchor point $a^*$. As model-based complement utilizes the global information, some anchor point far away (at most $\lambda$ steps from the $a$ and $a'$) can be inserted into a consecutive segment $(a, a')$.

Interpolation of a segment $(a,a')$ may result in a different set of anchor points if and only if there exists a path with length less than $\lambda$ connecting $a$ and $a'$, which pass through some anchor points in $\mathbf {b}_{\lambda }{(\mathfrak {S})}$, due to the changes in the transition probability corresponding to $\mathbf {b}_{\lambda }{(\mathfrak {S})}$. We denote the set of trajectories which need to be re-complemented by $\mathbb {T}_c$. $\mathbb {T}_c$ is defined as follows

$$\begin{aligned} \mathbb {T}_c = \{\bar{T} \mid \exists (a,a')\in T, a \in \mathbf {b}_{\lambda }{(\mathfrak {S})} \vee a' \in \mathbf {b}_{\lambda }{(\mathfrak {S})} \} \end{aligned}$$

As $\mathbf {b}_{\lambda }{(\mathfrak {S})}$ is already computed when we update the reference map and transition matrix, $\mathbb {T}_c$ can be easily computed as a by-product. We can re-complement the trajectories in $\mathbb {T}_c$ by following the algorithm in Sect. 4.2.3.

7 Experiment

In this section, we conduct extensive experiments to validate the effectiveness of our proposed calibration system, which entail different combinations of reference systems and calibration methods. All the algorithms in our system are implemented in Java and run on a computer with Intel Core i7-2600 CPU (3.40 GHz) and 8 GB memory.

7.1 Experiment setup

7.1.1 Data preparation

Trajectory dataset We use a real trajectory dataset generated by 33,000+ taxis in a large city over 3 months. In total, this dataset has more than 100,000 trajectories. We define a trajectory as a high-sampling-rate trajectory if the average time interval between consecutive sample points is less than 10 seconds. According to this criterion, we select 11,028 high-sampling-rate trajectories from the dataset, and then divide them into two equal parts. One of them, called the training dataset, serves as an archived dataset which will be used for building a reference system, finding turning points and training the reference map. The other one, called the test dataset, is used for testing the effectiveness of calibration.

Manipulated trajectory dataset We re-sample each trajectory $T$ in the test dataset to obtain three counterparts with varied sampling rates, i.e., a sample per 50, 100, 150 s, denoted as $T_{50},T_{100}, T_{150}$. These trajectories refer to the same original route as the high sampled trajectory $T$ but have different sampling rates.

7.1.2 Anchor point

Grid centroids We divide the area of the large city into 1,570 by 1,358 cells, each with a side of 100 m, and get 2,132,060 grid centroids.

Archived samples We use the 1,485,284 sample points in the training dataset as the anchor points to build the data-based reference system.

POI clusters We purchase about 510,000 POI points of the same city from a reliable third-part company. Approximately 17,000 POI clusters are obtained using DBScan and the geometric center of each cluster is used as the anchor point.

Turning points We extract about 32,000 potential locations of turning points from the training dataset, and finally generate 2,400 turning points with the method described in Sect. 3.

7.2 Evaluation approach

7.2.1 Calibration methods

We propose four types of anchor points and three calibration methods (geometry-based calibration, model-based calibration and model-based calibration with temporal information), which lead to twelve combinations of calibration process. However, the only difference between geometry-based calibration and geometry-based calibration with temporal information is whether the anchor points of a rewritten trajectory are with time stamps or not. Thus, given a sample-based trajectory $T$, let $\overline{T_1}$ and $\overline{T_2}$ denote the calibrated anchor-based trajectory of $T$ applied by geometry-based calibration and geometry-based calibration with temporal information, respectively. The anchor point sequences of $\overline{T_1}$ and $\overline{T_2}$ are the same, but the anchor points of $\overline{T_2}$ have time stamps while anchor points of $\overline{T_1}$ have not. In the experiment, given any anchor-based trajectory $\overline{T}$, the distance $d(\overline{T_1}, \overline{T})$ and the distance $d(\overline{T_2}, \overline{T})$ measured by spatial-only distance measures (Euclidean distance, DTW, LCSS and EDR) are all the same. So the geometry-based calibration and geometry-based calibration with temporal information are not compared in the spatial-only distance measure experiments. We do not use the model-based calibration and model-based calibration with temporal information with the grid centroids and archived samples, since their cardinalities are very large that renders the inference process not efficient. Therefore, in the following experiments, we will apply the geometry-based approach to all types of anchor points, and the model-based and temporal-model-based calibration approaches on POI clusters and turning points only. All these calibration strategies and their abbreviations are listed in Table 3, in which SP stands for the method of using the raw trajectories without any calibration.

Table 3 Calibration methods

7.2.2 Parameters

Table 4 lists all the parameters we used throughout the experiments that all the parameters are assigned the default values unless specified explicitly.

Table 4 Parameter settings

7.3 Performance evaluation

7.3.1 Visualization of calibration effect

Before conducting the quantitative performance evaluation, we give an intuitive illustration for the calibration effect by visualizing the results. Figure 6a shows two trajectories with different sampling rates but referring to the same route. It can be imagined that conducting similarity analysis on them directly will result in a poor quality answer. Figure 6b illustrates their calibration result by using POI-based anchor points (represented by solid squares). For the high sampled trajectory, geometry-based and model-based approaches produce the same result (only POI $+$ M calibration result is shown for the sake of conciseness). But they make difference on how to choose the complementary anchor points for the low-sampled trajectory. Specifically, geometry-based approach can only complement the anchor points that are spatially “around” the trajectory segments (e.g., $a_6, a_8, a_{10}, a_{14}, a_{17}$), whereas the model-based method can choose more anchor points that are actually on the original route and thus gain better calibration result (i.e., the blue dashed line is more similar with the red solid line). Figure 6c demonstrates the calibration effects by using turning points as the reference system. We can see that turning points can give more precise and concise representation for both high sampled and low-sampled trajectories. Besides, the advantage of the model-based method is more obvious as we can see it fully recovers the original route for the low-sampled trajectory.

Fig. 6

Visualization of calibration effect

7.3.2 Effect on similarity measures: self-comparison

In the first set of experiments, we evaluate how the calibration methods can improve the effectiveness of trajectory similarity measures. For each trajectory $T$ of the test dataset, we use Euclidean distance (ED), DTW, LCSS, EDR, SED and STLCSS (ED, DTW, LCSS and EDR only consider the spatial information of trajectory, while SED and STLCSS consider both spatial and temporal information of trajectory) to calculate the distances between $T$ and its three low-sampling-rate counterparts, i.e., $d(T, \,T_{50}), d(T,\, T_{100})$ and $d(T,T_{150})$. Analogously, we use these six measures to calculate the distances between $\overline{T}$ and their calibrated low-sampling-rate counterparts, i.e., $d(\overline{T}, \overline{T}_{50}), d(\overline{T},\, \overline{T}_{100})$ and $d(\overline{T}, \overline{T}_{100})$. Since each pair of trajectories in comparison refers to the same original route, a smaller distance value means better effectiveness of the similarity measure. Figure 7 shows the results of the normalized distances (i.e., distance over the size of trajectory) based on the raw trajectories (denoted by SP) and trajectories with different calibration schemes. Not surprisingly, all distances gradually increase with the drop of sampling rate since more sample points characterizing the major shapes of trajectories are lost. However, raw trajectories have considerably greater distances than the calibrated trajectories do at all sampling rates, which demonstrates the ability of the proposed calibration methods to improve the accuracy of the common similarity measures. A general phenomenon from this figure is that, the POI and TP based methods achieve better effectiveness since the corresponding distance values are very close to the ground truth (zero), especially for ED and DTW distance. Besides, by learning the knowledge hidden in the historical data, model-based approach and model-based calibration with temporal information (i.e., POI $+$ M, POI $+$ TM, TP $+$ M, TP $+$ TM) lead to even better performance compared with the geometry-based approaches (i.e., POI $+$ G, TP $+$ G). What is more, the temporal-model-based approach (i.e., POI $+$ TM, TP $+$ TM) outperforms model-based approach (i.e., POI $+$ M, TP $+$ M) in most cases. Consequently, the combination of turning points as the reference system and model-based calibration with temporal information (i.e., TP $+$ TM) turns to be the most robust approach in terms of the capability of recognizing the trajectories of the same route, as we can see that the distance based on it is always the smallest among all the methods.

Fig. 7

Distance between the trajectories referring to the same original route.

7.3.3 Effect on similarity measures: cross-comparison

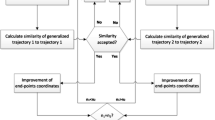
A good calibration method should not only improve the ability to recognize the trajectory variants of the same route, but can also preserve the distance between any trajectories regardless of their sampling strategies. In this experiment, we randomly select 5,000 trajectory pairs from the test dataset, and for each pair $(T_A, T_B)$ we use the six distance measures to calculate the distances between them, denoted as $d(T_{A}, T_{B})$. $d(T_{A}, T_{B})$ is regarded as the ground truth of the distance between the routes of $T_A$ and $T_B$. Then we calculate the distances between $T_A$ and different variants of $T_B$, i.e., $d(T_{A}, T_{B50}), d(T_{A}, T_{B100})$ and $d( T_{A}, T_{B150})$. Finally, we put $T_A, T_B$ and its variants through the calibration system, and re-calculate the distances between them, i.e., $d(\overline{T}_{A}, \overline{T}_{B50}), d(\overline{T}_{A},\overline{T}_{B100})$ and $d(\overline{T}_{A},\overline{T}_{B150})$. In order to illustrate how well these distances resemble their ground truth in a more intuitive way, we show in the results the distance deviation (dev) calculated by the following equation instead of the original distances:

$$\begin{aligned} dev(V(T_A), V(T_B)) = \frac{\left| d(V(T_A), V(T_B) - d({T_A},{T_B}) \right| }{{d({T_A},{T_B})}} \end{aligned}$$

where $V(T)$ denotes the variance of $T$ (e.g., with different sampling rates and/or calibration). The results are shown in Fig. 8, where smaller deviation means that the evaluated distance is closer to the ground truth. As we can see that most average deviations of the raw trajectories are over 50 %, and increase quickly with the drop of sampling rate. To the contrary, all the distance deviations between calibrated trajectories are smaller compared with the raw trajectories, which demonstrates the usefulness of our calibration methods in preserving the distances when the sampling strategies vary. Consistent with the previous experiment, POI and TP based approaches obtain much better performance as their $dev$ are all below 0.3, and even $<$0.1 for DTW distance. Again, the model-based approaches outperform the geometry-based approaches for all distance measures, and TP $+$ M and TP $+$ TM approaches achieve the best calibration results for most distance measures.

Fig. 8

Distance deviation of calibrated trajectories from the ground truth

7.3.4 Resynchronization capability

In this set of experiments, we evaluate the resynchronization capability of our calibration system. Intuitively, an effective calibration system should transform a specific trajectory into the one with similar sampling rate regardless of its original sampling rate. Thus, for each trajectory in the test dataset, we calibrate its low-sampling-rate counterparts and obtain the calibrated trajectories, i.e., $\overline{T}_{50}, \overline{T}_{100}, \overline{T}_{150}$, and then compare the size between $T$ ($\overline{T}$) and $T_{50} (\overline{T}_{50}), T_{100} (\overline{T}_{100}), T_{150} (\overline{T}_{150}$). Figure 9 shows how the average sizes of the raw trajectories and the calibrated trajectories change with the sampling rate (10, 50, 100 and 150 s). As we can see from this figure, the sizes of the raw trajectories decrease significantly with the drop of sampling rate. To the contrary, the average sizes of calibrated trajectories much more stable with the variation of sampling rates, which verifies our expectation that the reference systems are effective in resynchronizing all the trajectories with more unified sampling rates.

Fig. 9

Evaluation of resynchronization capability

7.3.5 Effect of confidence threshold

Next, we test how the confidence threshold $\eta _{ {confi} }$ used in the model-based and model-based calibration with temporal information (i.e., POI $+$ M, POI $+$ TM, TP $+$ M and TP $+$ TM) affect the calibration performance. Recall that a higher $\eta _{ {confi} }$ results in fewer but more accurate anchor points inserted into the calibrated trajectory. In order to work out a good trade-off between the completeness and correctness of the complementary points, we tune the confidence threshold $\eta _{ {confi} }$ from $0.5$ to $1$ with the step of $0.1$. Meanwhile, we calculate the edit distance between the calibrated trajectories and their low-sampling-rate counterparts using the POI $+$ M, POI $+$ TM, TP $+$ M and TP $+$ TM methods with different $\eta _{ {confi} }$. As shown in Fig. 10, generally all the distance values decrease when the confidence threshold rises, since a lot of incorrect insertions are avoided. However, when the threshold goes too high (${\ge }0.8$), the distances start to increase, which means the calibration effectiveness gets worse. The reason is that (almost) no anchor points can have high enough confidence to be complemented into the trajectories, thus leaving the low-sampling-rate trajectories largely incomplete. Based on the observations of this experiment, we recommend the threshold with the value between 0.8 and 0.9 to be appropriate.

Fig. 10

Edit distance of high rate trajectories and low rate trajectories with different confidence

7.3.6 Calibration time cost

We also evaluate the calibration time cost, which is especially important for online calibration systems. The average time cost for calibrating a single trajectory is shown in Fig. 11, from which we observe that all the methods can calibrate a trajectory within tens of milliseconds. GC turns out to be the most inefficient approach, because the cardinality of grid centroids is too large, which increases the search space in geometry-based alignment and complement. Besides, the order of time costs for GC, AS, POI $+$ G and TP $+$ G is consistent with the number of anchor points in respective reference systems. This implies that the efficiency of calibration is heavily dependent on the cardinality of anchor points. The geometry-based approach constantly runs faster than the model-based approach and temporal-model-based approach, since these two approach involves expensive global alignment and inference on the reference map. In geometry-based approaches, alignment costs longer times than complement, while complement costs longer in model-based approaches. The global alignment takes at least twice times longer than geometry-based alignment. As well, the model-based complementation takes more than twice times longer than geometry-based complement. Model-based approach is slightly faster than the temporal-model-based approach, since the temporal-model-based needs to infer the spare time matrix.

Fig. 11

Average time cost for calibrating one trajectory in millisecond

7.3.7 Effect of transition matrix optimization

Recall that we have used the pre-computed transition matrix $M^{1:\lambda }$ to accelerate the model-based calibration in both alignment and complement phases. In this experiment, we evaluate the effect of this optimization by comparing the running time of the POI $+$ M and TP $+$ M approaches with and without using the transition matrix. Figure 12a, b demonstrate the average time cost and the number of probed anchor points for calibrating a single trajectory. As expected, the pre-computation in the transition matrix brings significant speed-up to both approaches.

Fig. 12

Effect of transition matrix optimization

7.3.8 Effect on similarity queries

The ultimate purpose of calibration is to improve the robustness and effectiveness of similarity-based analysis for trajectories. The last set of experiments is conducted to verify if the K-nearest neighbor search—the most important type of similarity query—can benefit from our proposals. We first randomly choose 500 query trajectories from the test dataset and find their 20 NNs, which are considered as the ground truth of this kNN query. Then we keep the query trajectories unchanged and transform all the trajectories in the test dataset by dropping sampling rates and applying calibration methods. Finally, the same kNN queries are issued against the transformed datasets and the query precision is defined as the proportion of the correct results (the one existing in ground truth) in the new kNN result set. As shown in Fig. 13, though the precisions based on all distance measures reduce with the decrease of sampling rate, calibration methods can improve the accuracy of kNN search results. This benefit is especially obvious for turning point-based approaches as their precisions are constantly improved by around 20 % compared with the ones without any calibration.

Fig. 13

Effect of calibration methods on the accuracy of K-nearest neighbor search

7.3.9 Cost of updating of reference system

In these experiments, we evaluate the number of affected trajectories which need to be re-calibrated when a new anchor point is added to an existing reference system. Also, we evaluate both the time cost of re-calibrating the trajectories and the time cost of rebuilding the reference map of model-based calibration with temporal information approach. The average number of affected trajectories when adding a new anchor point to the existing reference system is shown in Fig. 14a, from which we can observe that the number of affected trajectories varies a lot due to the category of reference systems. The number of affected trajectories using SP and POI as reference system is about 1 and 3, respectively, while those number of TP reference system is more than 20. The time cost of each calibration method except GC $+$ G is shown in Fig. 14b. We can see that all the methods can calibrate a trajectory within hundreds of milliseconds. Model-based approach and temporal-model-based approach are less efficient than geometry-based approach. TP+TM costs the most time re-calibrating the calibrated trajectory set. In Fig. 14c, we demonstrate the power of our optimization method introduced in 6.2.1 in reducing the cost of adding an anchor point to the existing reference system. We can see that it takes about 28,000 and 700 ms to update the whole reference map of POI and TP, respectively, while it takes about 660 and 360 ms to updating the partial reference map of POI and TP, respectively. Updating the partial reference map can save at least 48 % to even 77 % time, and all the time cost of partial reference map updating can be controlled in 1 s.

Fig. 14

Time cost of handling the update of reference system

7.4 Experiments on other dataset

To further verify our observations, we use another trajectory dataset, and a POI set obtained from Sina Weibo. Since they show the similar results as in our paper, for the sake of presentation brevity, we do not include all the results of new experiments in this manuscript. Instead, we report the experiment results in a long-version technique report and put it on our website. You can reach the report through the following link: https://sites.google.com/site/technicalreportuq/.

8 Related work

To our knowledge, there is no existing work on trajectory calibration or trajectory rewriting. However, the assigning trajectory sample points to some semantical anchor points, i.e., POI, share the similar motivation of some research works of construction semantic trajectories, which we will firstly review. The building reference system process has the similar purpose with extracting road network from trajectory data. Also, although the trajectory calibrating is not restricted on road networks, the alignment phase shares similar idea of Map-matching technique. Thus, both extracting road network from trajectory data and Map-matching technique will be reviewed. In our model-based calibration approach, we leverage the historical trajectory data to find the best alignment and infer the possible intermediate anchor points to complement the trajectory, which share similar inspiration and techniques with the work on uncertainty management of trajectories and hot route discovery. Therefore, in this section, we will review these two lines of related work. As the goal of this work is to improve the effectiveness of similarity-based analysis, the distance measures studied in this paper are also reviewed at last.

8.1 Constructing semantic trajectories

Several works have studied the problem of assigning semantic information to raw trajectories. Spaccapietra et al. [41] proposes a trajectory conceptual model, which models trajectories as a set of stops and moves. Alvares et al. [2] extended [41] by proposing a method to extract stops and moves of trajectories, where the stops are represented by interesting spatial locations, such as hotels, airports and traffic lights, instead of sample points. Furletti et al. [17] focuses on inferring human activities by analyzing the categories of interesting spatial locations. All the three works focus on inferring the semantic meaning of the stops in trajectories, while our work simply uses semantic objects as reference points, and only focuses on the spatial relationship between semantics objects and trajectories.

8.2 Extracting road network from trajectory

Extracting road network from trajectories is one of the most important approaches. References [5, 14, 40] start with raw GPS traces and create road maps. The geometric aggregation of individual GPS tracks from passive mapping to generate attributed graph data structures as thus routable road information can be largely carried out in an automatic way [5]. References [14] and [40] not only generate reachable road network, but also infer lane structure. Heipke [23] adopts Crowdsourcing technique that it treats each GPS module as Crowdsourcer and proposes efficient algorithms to build real-time road network.

8.3 Map-matching techniques

Map-matching is the process of aligning a sequence of observed positions with the road network. There are two groups of map-matching algorithms: local/incremental method and global method. The local/incremental method [20, 47, 48] finds local best geometry match greedily, while the global method finds the global optimal match for the entire trajectory. The global method proposed in [3] uses Frechét distance to measure the distance between raw trajectory and the matching sequence. Lou et al. [31] proposes an algorithm that uses temporal information of trajectory to do map-matching and manages to get a high accuracy for low-sampling-rate GPS trajectories. Statistical methods are also widely used. Syed et al. [43] proposes a fuzzy logical based method that is able to handle noisy, imprecise input. Zheng et al. [54] proposes an algorithm which firstly extracts the reference trajectories, which are near the given trajectory, and then uses the information extracted from the reference trajectories to conduct map-matching.

There are three main differences between map-matching and calibration. First, the purposes are different. Map-matching tries to map sample-based trajectories to the road network, while calibration is to improve the effectiveness of trajectory distance measures. Second, the inputs are different. Road network is required in map-matching, and historical trajectories are also needed in recent map-matching techniques. However, calibration only requires historical trajectory as the input. Third, the outputs are different. The output of Map-matching is a continuous path, which is lack of temporal information. The output of calibration is a sequence of anchor points with or without time stamp. The most widely used distance measures (ED, DTW, LCSS and EDR) are measuring the distance on point-based trajectories; the spatial-temporal distance measure (SED and STLCSS) require the temporal information on the path. Besides in order to construct the continuous path, Map-matching may need to artificially add several low-confidence paths when the trajectory is low sampled. But calibration only adds the anchor point with high confidence to the aligned trajectory.

8.4 Managing uncertainty of trajectories

Several works have addressed the uncertainty issues of moving objects. Wolfson et al. [50, 51] proposed an information cost model, which captures uncertainty and deviation in the moving objects updating problem. Pfoser et al. [36] models moving objects with a concept of spatial zones that define an object’s whereabouts during two consecutive sampling positions as an ellipse under constraint maximum velocity. Trajcevski et al. [45] proposes a three-dimensional cylinder to measure a new concept of uncertain trajectory in order to limit errors that could occur while capturing the movement of an object. Based on the model, a set of spatiotemporal operators and algorithms are proposed for continuous range queries and nearest neighbor queries [44]. Cheng et al. [11] proposes a new model, which shows that the location uncertainties are updated at every time instant and range queries are issued at a current time point. Zhang et al. [52] designs an integrated indexing structure for inferring the future location of uncertainty moving objects. An intuitive model for an uncertain trajectory is proposed in Zheng et al. [53] to represent object movement along a road network, providing a unified probability distribution function (pdf) for the possible locations of a moving object at a given time instant. Zheng et al. [54] is the most relevant work in completing trajectories. The method of Zheng et al. [54] requires the input of road network, while calibration does not. Meanwhile, the process [54] of guessing which point is on the trajectory does not give a concrete existing probability of the point. The guessing process is not controlled by a confidence score.

8.5 Hot route discovery

Li et al. [29] extracts hot routes by using a density-based algorithm FlowScan based on a concept called “traffic density-reachable.” Sacharidis et al. [39] investigates efficient ways to find and monitor hot motion paths that are defined as those visited by a certain number of moving objects. Nevertheless these two works are limited to mine frequently visited paths only. The focus of [18, 19, 32, 55] is on mining trajectory patterns to help find the popular routes from a start location to a destination. Giannotti et al. [18] proposes to mine a sequence of temporally annotated points called T-pattern, in order to find all T-patterns with sufficiently high support. Similarly, in [19, 32, 55], frequent paths or sequences are explored by existing sequential pattern mining algorithms. However, not every pair of start and end locations is able to match patterns given by these works. Chen et al. [10] evaluates the probability from a start point to the destination, but they only consider the forward probability from one place to another without considering the backward probability.

8.6 Trajectory distance measures

There are a large number of trajectory distance measures, among which Euclidean distance, DTW, LCSS and EDR are the most representative. DTW [27] is originally introduced for signal processing, which allows time-shifting in comparison. LCSS [26] is proposed based on the concept of the longest common subsequence, which is robust to noise by allowing skip of some sample points. EDR [9], which is based on edit distance, is also robust to noise and addresses some deficiencies in LCSS. Dauria et al. [13] proposed a spatial-temporal Euclidean distance measure (SED). The distance of SED stands for the average distance between the comparing two trajectories at the same time. More precisely, it models two comparing trajectories as two continuous function mapping time to space and this distance measure restrict to consider only pairs of contemporary instantiations of objects, i.e., for each time instant, it compares the positions of the objects at that moment. Vlachos et al. [46] introduced a time sensitive LCSS (STLCSS) distance measure. This distance measure involves two threshold, distance threshold and time threshold, that two points of the comparing two trajectories, respectively, will be regarded the same if and only if both the distance and the time interval between the two points are no bigger than the distance threshold and time threshold, respectively.

Different distance measures have different capabilities. For example, LCSS, STLCSS and EDR are robust to noise. So recall the experiments in Sects. 7.3.2, 7.3.3 and 7.3.8, that SED has a better performance than other distance measures. This is because SED is robust to low trajectory sampling rate. Among all the mentioned distance measures, only SED treats trajectories as continuous paths by connecting every two consecutive points by lines. If a moving object moves along a straight line (a frequent pattern in networks), no matter what the sampling rate is the continuous path generated by SED has similar shape of the original trajectory. Thus, SED has a better tolerance in low-sampling-rate trajectories than others. Even though the better capacity in handling the reducing of trajectories sampling rate, SED has low efficiency and low tolerance to noise. Thus, SED is not widely as ED, DTW, LCSS and EDR in reality.

9 Conclusions

In this paper, we have taken an important step toward effective calibration of trajectories with different sampling strategies to make them compatible when using many existing trajectory similarity measures. After studying the impact of trajectory heterogeneity on similarity measures, we have proposed a framework of trajectory calibration. We have examined four different types of anchor points, which can be used to build stable reference systems. On top of that, four calibration approaches, the spatial-only geometry-based, spatial-temporal geometry-based approach, spatial-only model-based approach and the spatial-temporal-model-based approach, are designed to align and complement trajectory data using the anchor points in the reference system. Extensive experiments have been conducted using a real trajectory dataset and a range of commonly used trajectory similarity measures. We have demonstrated that the calibration process can significantly improve the effectiveness of most popular trajectory similarity measures. The temporal-model-based calibration approach, which is based on using turning points to build the reference system, is shown to be particularly effective. This calibration process and its algorithms can be easily integrated with most existing works on trajectory processing and mining, to reduce their reliance on high-quality (densely sampled) trajectory data and to improve their similarity measure effectiveness. The ideas from this work open a new direction for future research, such as novel indexing methods and query processing algorithms with calibrated trajectories based on the underlying reference system.