1 Introduction

The activated sludge process is one of the widely used technologies in the wastewater treatment processes (WWTPs) [1, 2]. In this method, activated sludge is formed after a certain reaction time as a result of the propagation of aerobic microorganisms via the continuous filling of air into wastewater. Under the action of bio condensation, adsorption and oxidation of the activated sludge organic pollutants are decomposed and then removed from the wastewater [3]. To meet the effluent discharge standards and reduce fines, wastewater treatment plants are typically operated at the full load status. In this case, the dissolved oxygen concentration (SO) in the aerobic zone and the nitrate nitrogen level (SNO) in the anaerobic zone are maintained at a high level through aeration and pumping [4]. However the operation of blowers and return sludge pumps requires a large amount of energy supply, resulting in higher operating costs. Besides, according to the biochemical reaction mechanism in the WWTPs, only the appropriate set-points of SO and SNO can ensure the smooth progress of nitrification and denitrification [5]. Therefore, the set-points of SO and SNO should be dynamically optimized based on the actual operating conditions so as to reduce energy consumption (EC) and effluent quality (EQ) as much as possible. Note that EQ is utilized to represent fines which are required to be paid due to the discharge of pollutants into the receiving water bodies in the benchmark simulation platform. To improve the treatment effect and reduce the running cost, it is imperative to develop an optimal control strategy in the WWTPs.

With the characteristics of nonlinearity, time variation and big lag, the control issues in the WWTPs have been extensively investigated. For example, Wahab et al. designed a multi-variable controller for SO and SNO by tuning the parameters of PID controller in [6]. Song et al. applied a robust PID controller to the tracking control of SO in [7] and the results showed that the controller could exhibit good robustness in the case of a model mismatch. Furthermore, Holenda et al. proposed a model predictive controller (MPC) for SO based on a third-order simplified model of the WWTP in [8] and the results indicated that MPC owns a remarkable performance under the conditions of constant and variable concentrations of SO. In [9], Belchior et al. investigated the application of the adaptive fuzzy control (AFC) for SO in which the consequent parameters of fuzzy rules are adaptively adjusted by Lyapunov comprehensive analysis approach. Qiao et al. introduced a self-organizing fuzzy neural network controller for SO in [10]. For these controllers [6,7,8,9,10], a group of fixed set-points which remains unchanged in the control process is preset. Therefore, the above control strategies could not meet the urgent need of wastewater treatment plants for efficiency promotion, energy saving and consumption reduction.

To effectively reduce EC in the WWTPs, the single-objective optimal control (SOOC) strategy considering EC as the only optimization objective and SO and SNO as the main decision variables has been proposed [11,12,13,14]. For example, Santin et al. presented a two-level hierarchical control structure in [13]. In this method, an upper controller was used to adjust the set-points of SO online and a lower controller was designed to track the set-points. The results showed that the proposed control strategy can effectively reduce the operating cost. In [14], a genetic algorithm was utilized to optimize EC so that EC can be reduced by dynamically optimizing the set-points of SO. However, these SOOC methods mainly focus on EC and might easily cause effluent parameters to exceed the standard, resulting in an increase of the total operating cost. Thus, weight factor scheme, which can convert the multiobjective optimization problem (MOP) into a single-objective optimization problem (SOP), is introduced to construct the loss function [15,16,17]. For example, a data-driven optimal controller (DDAOC) based on the adaptive dynamical programming was introduced to optimize the set-points of SO and SNO in [16]. The results showed that the proposed DDAOC can provide a reduction of 5.30% in EC. In [17], a Hopfield neural network optimal controller based on the Lagrange multiplier was designed to optimize the set-points of SO and SNO. In [18], a set-point optimization technique for WWTPs that is composed of dynamic real time optimization and nonlinear model predictive control (RTO-NMPC) was proposed. However, it is hard to obtain a balance between EC and EQ for these methods [16,17,18], since the determination of a suitable weight factor is difficult.

Fortunately, multiobjective optimization algorithm can overcome the shortcomings described above. Therefore, the design of multiobjective optimal controllers for the WWTPs has been extensively investigated [19,20,21,22,23,24,25]. In [20], an interactive software designed based on nondominated sorting genetic algorithm (NSGAII) called IND-NIMBUS, was utilized to construct an optimal operation model for the WWTP. In [21], NSGAII was adopted to establish a multiobjective optimization model for greenhouse emission, operating cost, and effluent contaminant concentration. The results revealed that the improvement of water quality and the decrease of operation cost can cause the increase of greenhouse emission. In [22], a dynamic multiobjective optimization algorithm was applied to establish an optimization model for running cost and wastewater treatment quality. The results demonstrated that these two objectives have conflicting characteristics. Furthermore, some other optimal controllers based on NSGAII for the WWTPs could be found in [23,24,25]. Recently, an optimal controller based on adaptive fuzzy neural network was developed to solve the problem of high EC in WWTPs, and a good energy-saving effect was achieved [26, 27]. From the analysis of the previous studies [20,21,22,23,24,25,26,27], it is easy to find that the multiobjective optimal controller can not only ensure that the effluent parameters satisfy the standard, but also reduce EC and operation cost effectively. However, there are still many challenges for developing a suitable optimal controller to tackle the multiple conflicting objectives. In addition, NSGAII has a high computational cost, and the convergence, diversity and coverage of the approximated optimal solutions should be enhanced.

The multiobjective evolutionary algorithm based on decomposition (MOEA/D) has been shown to be very efficient in solving MOPs. In MOEA/D, a MOP is decomposed into a number of scalar optimization subproblems and these subproblems are optimized simultaneously in a collaborative manner [28]. Decomposition mechanisms are utilized to push the population to approach the Pareto-optimal front (POF), while a set of uniformly distributed weight vectors are applied to maintain the population diversity [29, 30]. In addition, the concept of subproblem neighborhood, firstly presented in MOEA/D, can improve the balance between exploration and exploitation [31, 32]. However, recent research indicated that MOEA/D can only tackle MOPs with simple POFs, but cannot provide a good distribution for MOPs with irregular POFs. Due to the nonlinearity, big lag and strong interference, the MOPs in the WWTPs may have complex POFs, such as discontinuity, long tail and/or sharp peak, which could significantly degrade the performance of MOEA/D.

To improve the capability of MOEA/D in addressing MOPs with complex POFs, different approaches have been proposed in recent studies. In [33], Qi et al. proposed an adaptive weight adjustment (AWA) strategy for MOEA/D (MOEA/D-AWA). In MOEA/D-AWA, the AWA strategy is adopted to regularly adjust the distribution of the weight vectors. In [34], Yang et al. investigated the influence of the penalty factor θ in the penalty boundary intersection (PBI) decomposition method on the performance of MOEA/D, thus proposing an MOEA/D with an adaptive penalty scheme (MOEA/D-APS). In [35], Jiang and Yang introduced a kind of MOEA/D with a two-phase strategy and a new niche scheme (MOEA/D-TPN), aiming to find more boundary solutions for complex MOPs. In MOEA/D-TPN, the evolution process is divided into two phases. In the first phase, the ideal point is adopted as the reference point in Tchebycheff decomposition method. In the second phase, the nadir point is utilized as the reference point. When the generations reach a certain number, the algorithm can determine whether or not to execute the second phase based on the crowdedness. In [36], Wang et al. proposed a MOEA/D with multiple reference points (MOEA/D-MR), in which the ideal point and reference point are simultaneously utilized to optimize the subproblems. In [37], Ho-Huu et al. presented an improved MOEA/D (iMOEA/D), in which all the weight vectors are divided into odd and even weight vectors firstly, and then subproblems are optimized by using a two-phase strategy. Simulation results demonstrated the effectiveness of these methods on benchmark testing. However, it is still difficult to apply them to practical engineering. For example, the number of iterations for the first phase still needs to be set by experience in MOEA/D-TPN and tri-objective MOPs cannot be addressed by iMOEA/D

Furthermore, Li and Zhang pointed out that the simulated binary crossover (SBX) operator applied in MOEA/D often generates inferior solutions in [38]. Therefore, they proposed a well-known MOEA/D with a differential evolution (DE) operator, called MOEAD-DE. Considering the defects of a single DE operator, Li et al. applied four DE operators to form an operator pool and designed a bandit-based adaptive operator selection strategy which significantly improved the performance of the MOEA/D [39]. The DE operator pool strategy was also utilized in [40, 41] and [42]. These promising results encourage us to design a suitable operator selection strategy to enhance the proposed improved MOEA/D.

In this paper, to effectively address the MOPs in the WWTPs an adaptive MOEA/D algorithm (AMOEA/D) is proposed. In AMOEA/D, the advantages of multiple reference points and two-phase optimization in MOEA/D-TPN are still retained. To overcome the shortcomings of iteration setting for the first phase by experience, an auto-switching scheme which could automatically switch the algorithm to the second phase is designed based on the aggregation function enhancement (AFE). In addition, an adaptive operator selection (AOS) scheme, which can select appropriate DE operator online, is developed based on the solution replacement rate. Furthermore, a hybrid multiobjective optimal control (HMOOC) strategy is designed to reduce EC without violating effluent standards. First, a self-organizing fuzzy neural network approximator developed in the previous study [43, 44] is utilized to establish the objective functions of EC and EQ, according to the analysis of the control variables and optimization objectives. Second, the proposed AMOEA/D in this study is adopted to dynamically optimize the set-points of SO and SNO. Then, an intelligent decision-making system based on the fuzzy membership function method is applied to select the preferred solution as the optimized set-points of the current optimization cycle. Third, a self-organizing fuzzy neural network controller designed in the previous study [45] is used to track the optimal set-points. Finally, the international benchmark simulation model No.1 (BSM1) is introduced to validate the effectiveness of the proposed AMOEA/D-based HMOOC strategy.

The rest of this paper is organized as follows. Section 2 introduces the MOP in the WWTP. In Section 3, the proposed AMOEA/D is described in detail. Section 4 presents the HMOOC strategy for WWTP. Experimental studies for AMOEA/D on benchmark test instances and WWTP are presented in Sections 5 and 6, respectively. Finally, Section 7 concludes this paper.

2 MOP in the WWTP

2.1 BSM1

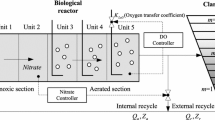
WWTP is a large nonlinear dynamic systems subject to large perturbations in influent flow rate and pollutant load, together with uncertainties concerning the composition of the incoming wastewater. To evaluate the possible control strategies, a benchmark was proposed by the Working Groups of COST Action 682 and 624-BSM1 [46]. The general overview of the BSM1 plant is depicted in Fig. 1, where the plant is composed of the biological reactor and the secondary settler. The biological reactor consists of five tanks connected in cascade. Tanks 1 and 2 are non-aerated but fully mixed with volume equal to 1000 m3 each. Tanks 3, 4 and 5 are aerated and their volumes are approximately equal to 1333 m3 each. The activated sludge model No.1 (ASM1) is selected to describe the biological phenomena taking place in the biological reactor. In BSM1, there are two control loops, namely the SO and SNO control loops. The first control loop tunes the dissolved oxygen concentration in the fifth tank SO,5 by manipulating the oxygen transfer coefficient KLa5, and the second one tunes the nitrate nitrogen level in the second tank SNO,2 by manipulating the internal recirculation flow rate Qa.

Fig. 1
figure 1

General overview of the BSM1 plant

Full size image

The general equations for mass balancing in BSM1 are as follows [46]:

For unit 1(k = 1):

$$ \frac{dZ_{1}} {dt}=\frac{1}{V_{1}} (Q_{a} Z_{a} +Q_{r} Z_{r} +Q_{0} Z_{0} +r_{1} V_{1} -Q_{1} Z_{1} ) $$
(1)
$$ Q_{1} = Q_{a} +Q_{r} +Q_{0} $$
(2)

where Qa, Qr, Q, and Q1 are, respectively, the internal recirculation flow rate, the external recirculation flow rate, the influent flow rate, and the flow rate in unit 1; Za, Zr, Z0, and Z1 are, respectively, the component concentration of the internal recirculation, the external recirculation, the influent, and unit 1; r1 is the component reaction rate in unit 1 and V1 is the volume of unit 1.

For unit 2-5 (k = 2-5):

$$ \frac{dZ_{k}} {dt}=\frac{1}{V_{k}} (Q_{k-1} Z_{k-1} +r_{k} V_{k} -Q_{k} Z_{k} ) $$
(3)
$$ Q_{k} = Q_{k-1} $$
(4)

where Qk, Zk, and rk are, respectively, the flow rate, the component concentration, and the component reaction rate in unit k. Vk is the volume of the k th unit.

In BSM1, three influent files, including dry weather, rain weather, and storm weather, are generated from a practical wastewater treatment plant. The data sampling interval is 15 min [46]. The plots of the influent flow rates and the influent SS, XBH and SNH concentrations under three different weather situations are presented in Fig. 2, which can indicate the characteristics of strong nonlinearity, severe uncertainty and strong coupling in the WWTP [46, 47].

Fig. 2
figure 2

The influent and SS, XB, H, SNH concentrations in three working conditions

Full size image

2.2 MOP in the WWTP

The aim of multiobjective optimal control is to achieve the best balance between EC and EQ by dynamically adjusting the set-points of SO,5 and SNO,2. In the WWTP, the set-points of SO,5 and SNO,2 not only affect EC but also show a close relationship with EQ. In this study, the proposed AMOEA/D is utilized to address these two conflicting objectives simultaneously.

Since the aeration energy consumption (AE) and the pump energy consumption (PE) account for more than 70% of the total energy consumption, the optimization objective EC is defined as the sum of AE and PE [24], as follows:

$$ EC=AE+PE $$
(5)

As defined in BSM1, AE and PE can be calculated as [46]

$$ AE=\frac{S_{O,sat}} {T\cdot 1.8\cdot 1000}{\int}_{kT}^{(k + 1)T} {\sum\limits_{i = 1}^{5} {V_{i} \cdot K_{Lai} (t)dt}} $$
(6)
$$ PE=\frac{1}{T\cdot 1000}{\int}_{kT}^{(k + 1)T} {(4Q_{a} (t)+ 8Q_{r} (t)+ 50Q_{w} (t))dt} $$
(7)

where Vi and KLai are the volume and oxygen transfer coefficient of the i th unit, respectively. SO, sat is the saturation concentration for oxygen. T is the optimal cycle. Qa, Qr, and Qw are, respectively, the internal recirculation flow rate, the external recirculation flow rate, and the sludge flow rate.

Moreover, EQ is defined as

$$ EQ=\frac{1}{T\cdot 1000}{\int}_{t_{0}}^{t_{f}} {\left( {\begin{array}{l} 2\cdot SS_{e} (t)+COD_{e} (t) \\ + 3\cdot S_{NKj,e} (t)+ 10\cdot S_{\mathit{NO},e} (t) \\ + 2\cdot BOD_{5,e} (t) \end{array}} \right)Q_{e} (t)dt} $$
(8)

where SSe, CODe, SNKj, e, SNO, e, and BOD5, e are, respectively, the effluent concentrations of suspended solid, chemical oxygen demand, Kjeldahl nitrogen, nitrate nitrogen, and biochemical oxygen demand of 5 days; Qe is the effluent flow rate.

The constraint condition of the MOP is the standard values of five kinds of effluent parameters given in BSM1, as follows [46]:

$$ \begin{array}{l} S_{\mathit{NH},e} \le 4{mg} / l,N_{tot,e} \le 18{mg} / l, \\ BOD_{5,e} \le 10{mg} / l,COD_{e} \le 100{mg} / l, \\ SS_{e} \le 30{mg} / l \end{array} $$
(9)

where Ntot, e is the effluent total nitrogen which is the sum of SNO, e and SNKj, e.

To sum up, the MOP is described as follows:

$$ \begin{array}{l} \text{minimize} \mathbf{F}(\mathbf{x})=(f_{EC} (\mathbf{x}),f_{EQ} (\mathbf{x}))^{T} \\ \text{subject to} g_{j} (\mathbf{x})=f_{j} (\mathbf{x})-c_{j} \le 0,j = 1, 2, ... , 5 \\ {x_{i}^{l}} \le x_{i} \le {x_{i}^{u}} ,i = 1, 2, ... , 5 \end{array} $$
(10)

where x = (x1, x2, x3, x4, x5)T = [Qw, KLa3, KLa4, SO,5, SNO,2]T is the decision vector, gj(x) ≤ 0 are inequality constraints, fj(x) represents the relationship between the j th effluent parameter and the decision vector, xui and xl i are the upper and lower limits of the i th decision variable.

3 The AMOEA/D algorithm

This section first provides some background knowledge, including the basic definition of constrained multiobjective optimization problem (CMOP) and the Tchebycheff decomposition method. Then, the advantages of multiple reference points and multiple DE operators are described. Furthermore, the AOS-based adaptive DE strategy and the auto-switching-based adaptive two-phase strategy are introduced. Finally, the procedure of the proposed AMOEA/D is given.

3.1 Background

3.1.1 Constrained multiobjective optimization problem

Without loss of generality, this paper considers the following CMOP [48]:

$$ \begin{array}{l} \text{minimize} \mathbf{F}(\mathbf{x})=(f_{1} (\mathbf{x}),f_{2} (\mathbf{x}), ... , f_{m} (\mathbf{x}))^{T} \\ \text{subject to} g_{j} (\mathbf{x})\le 0,j = 1, ... , J \\ h_{k} (\mathbf{x})= 0,k = 1, ... , K \end{array} $$
(11)

where x = (x1, ... , xn)T ∈ Ω is a decision variable vector, Ω is the feasible search region, F: Ω → Rm consists of m real-valued objective functions, Rm is the objective space, gj(x)≤0 are inequality constraints, and hk(x) = 0 are equality constraints.

3.1.2 The Tchebycheff decomposition method

The decomposition method used in the MOEA/D is the Tchebycheff method. In this method, the scalar objective optimization problem is in the form

$$ \begin{array}{l} \text{minimize} g^{te}(\mathbf{x}\left| {\mathbf{w}} \right.,\mathbf{z}^{\ast} )=\underset{1\le j\le m}{\max} \{w_{i} \vert f_{j} (\mathbf{x})-z_{j}^{\ast} \vert \} \\\text{ subject to} \mathbf{x}\in {\Omega} \end{array} $$
(12)

where w = (w1, ... , wm)T is a weight vector, i.e., λj ≥ 0 for all j = 1, ... , m and \(\sum \nolimits _{j = 1}^{m} {w_{j}} =  1\). z\(^{{\ast } }=(z_{1}^{{\ast } }\), ... , \(z_{m}^{{\ast } })\) is the ideal point in the objective space, i.e., \(z_{j}^{{\ast }}=\)min{fj(x)|x∈Ω} for each j = 1, ... , m. Since z∗ is generally unknown before searching, \(z_{j}^{{\ast } }\) can be replaced by fj(x) with the smallest value during the searching process [28].

3.2 Multiple reference points and multiple DE operators

3.2.1 Multiple reference points

Figure 3 shows the distribution of optimal solutions over a POF by using the ideal point z∗ and the nadir point znad. It is clear from Fig. 3 that, for a convex MOP, the optimal solutions would converge to the middle region of the POF, if z∗ is used as the reference point. On the contrary, in the case of using znad as the reference point, more boundary optimal solutions would be obtained. In addition, for a concave MOP, uniformly distributed optimal solutions can be obtained by using z∗ as the reference point. Otherwise, the optimal solutions would converge to the middle region of the POF, if znad is utilized as the reference point. Considering the complementarity of z∗ and znad, a two-phase strategy was proposed in [35], and a multiple reference points strategy was introduced in [36].

Fig. 3
figure 3

Pareto optimal solutions obtained by using z∗ and znad

Full size image

As demonstrated in [35] and [36], the scalar optimization problem using znad as reference point can be formed as

$$ \begin{array}{l} \text{maxmize} \!g^{te}(\mathbf{x}\left| {\mathbf{w}} \right.,\mathbf{z}^{nad}) = \underset{1\le j\le m}{\min} \{w_{j} \vert z_{j}^{nad} - f_{j} (\mathbf{x})\vert \} \\ \text{subject to} \mathbf{x}\in {\Omega} \end{array} $$
(13)

where z\(^{nad}=(z_{1}^{nad}\), ... , \(z_{m}^{nad})\) is the nadir point generated from the worst objective values of the obtained POF, i.e., \(z_{j}^{nad}=\)max{fj(x)|x∈Ωx} for each j = 1, ... , m.

3.2.2 Multiple DE operators

Due to different DE operators showing different search characteristics, the performance of MOEA/D could be improved through effective combination of them during the evolution process [39]. In this paper, three well-known DE operators (i.e., rand/1/bin, rand/2/bin and rand/1/bin˜, respectively named DE1, DE2, and DE3) with fixed parameters settings are utilized [41]. Their expressions are as follows:

$$ DE_{1} :{u_{j}^{i}} = \left\{ {\begin{array}{l} x_{j}^{r_{1}} +F\times (x_{j}^{r_{2}} -x_{j}^{r_{3}} )+F\times (x_{j}^{r_{4}} -x_{j}^{r_{5}} ) \text{if rand}<CR \\ {x_{j}^{i}} \text{otherwise} \end{array}} \right.,\text{with} CR= 0.9 \text{and} F = 0.7 $$
(14)
$$ DE_{2} :{u_{j}^{i}} = \left\{ {\begin{array}{l} x_{j}^{r_{1}} +F\times (x_{j}^{r_{2}} -x_{j}^{r_{3}} ) \text{if rand}<CR \\ {x_{j}^{i}} \text{otherwise} \end{array}} \right.,\text{with} CR= 0.5 \text{and} F = 0.5 $$
(15)
$$ DE_{3} :{u_{j}^{i}} = \left\{ {\begin{array}{l} {x_{j}^{i}} +F\times (x_{j}^{r_{1}} -x_{j}^{r_{2}} ) \text{if rand}<CR \\ {x_{j}^{i}} \text{otherwise} \end{array}} \right.,\text{with} CR= 0.1 \text{and} F = 0.5 $$
(16)

where \({u^{i}_{j}}\) is the j th dimension of the i th trial solution, \({x^{i}_{j}}\) is the j th dimension of the i th parent solution, rand is a random number generated from [0, 1], CR is the crossover rate, F is the scaling factor, and r1, r2, r3, r4, and r5 are five distinct individuals randomly selected from parent population.

For these three DE operators, the parent solutions of DE1 and DE2 are randomly selected from the population. Thus, they have a strong exploration ability and are suitable for the early evolution stage. Compared with DE2, DE1 with two random vectors, which could generate larger disturbances, has stronger capability to jump out of local POF, and is suitable for MOPs with complicated POFs. Furthermore, DE3 could improve local search ability since it can inherit much information from its parent.

In addition, the setting of control parameters CR and F also significantly influences the performance of DE. A large value of CR shows that the offspring solution could inherit a mutant gene from the parent with a large probability, improving the search ability around the target vector. Conversely, a small value of CR indicates that the offspring solution could inherit original gene from the parent with a high probability, increasing the exploitation ability around the target vector. For parameter F, a large value of F could increase the search step size, expand the search scope, and improve the population diversity. By contrast, a small value of F could enhance the exploitation ability around the target vector, and then improve the population convergence [41].

3.3 The AMOEA/D algorithm

The proposed AMOEA/D is developed based on MOEA/D-DE [38], which is a well-known improved version of MOEA/D. The flowchart of two-phase optimization with multiple adaptive strategies is first presented. Then, the initialization, AOS-based reproduction operation, constraint handling technique, replacement operation, and auto-switching scheme are briefly introduced. Finally, the pseudo-code of the proposed AMOEA/D is given.

Figure 4 shows the flowchart of two-phase optimization with multiple adaptive strategies. Since the concavity-convexity of an MOP is unknown in advance, z∗ is first utilized as the reference point in the first phase. At each iteration, a suitable DE operator selected by the AOS scheme is adopted to produce the offspring solutions. The algorithm runs until the auto-switching scheme detects that it is in a stagnation state, and then automatically switches to the second phase. At the end of the first phase, the obtained optimal solutions are saved to the external archive EA1. In the second phase, the reference point znad is derived from the maximum values of the objective functions at the end of the first phase. Once the preset maximum number of iteration is reached, the algorithm stops and the obtained optimal solutions in the second phase are saved to the external archive EA2. Finally, the nondominated solutions are identified from EA1 and EA2 by external archive maintenance algorithm.

Fig. 4
figure 4

The flowchart of two-phase optimization with multiple adaptive strategies

Full size image

3.3.1 Initialization

In MOEA/D, the initialization operation mainly includes the initialization of population and weight vectors. Since we have no prior knowledge about the position of the POS, the initial population is randomly generated from the decision space. During evolution, the optimization of each subproblem is completed by evolutionary operation between the subproblem and subproblems in its neighborhood. The relationship of adjacent subproblems is determined by the distance between weight vectors associated with subproblems. To a certain extent, the uniform distribution of weight vectors can improve the uniformity of the approximated POF obtained by the algorithm. MOEA/D adopts the simplex lattice design method, proposed by Scheff in 1958, to set weight vectors, as follows:

$$ {w_{j}^{i}} \in \left\{ {\frac{0}{H},\frac{1}{H},\frac{2}{H}, ... , \frac{H}{H}} \right\} $$
(17)
$$ \sum\nolimits_{j = 1}^{m} {{w_{j}^{i}} =  1} $$
(18)

where each subproblem i(i = 1, 2, ... , N) corresponds to a weight vector w\(^{i}=(w_{1}^{i}w_{2}^{i}\), ... , \({w_{m}^{i}})\), w\(_{j}^{i}\ge \)0, j = 1, 2, ... , m, the weight vector set is W = (w1, w2, ... , wN), where \(N=C_{H+m-1}^{m-1} \) is the total number of weight vectors [29]. In MOEA/D, a neighborhood of weight vector wi is defined as a set of its several closest weight vectors in {w1, w2, ... , wN}. The neighborhood of the i th subproblem consists of all the subproblems with the weight vectors from the neighborhood of wi. In initialization, we need to compute the Euclidean distances between any two weight vectors and then work out the T closet weight vectors to each weight vector [28]. For each i = 1, 2, ... , N, set B(i) = {i1, i2, ... , iT}, where i1, i2, ... , iT are the T closest weight vectors to wi. The pseudo-code of initialization is given in Algorithm 1. It is worth noting that the weight vectors need to be reinitialized at the beginning of the second phase, as described in [35].

figure c

3.3.2 AOS-based reproduction operation

In MOEA/D-DE, to maintain the population diversity, the maximum number of parent solutions replaced by an offspring solution is bounded by nr. In [38], the recommended setting of nr is 2. Let np be the maximum number of parent solutions replaced by an offspring solutions for all subproblems at each iteration, the parent solution updating rate at the t th iteration is defined as

$$ SRR(t)=\frac{n_{p}} {n_{p,\max} -n_{p,\min} } $$
(19)

where np,max is the maximum of np (np,max =  2 × N), and np,min is the minimum of np (np,min =  0 × N). A large value of np indicates that the algorithm is in diversity status, and it is advisable to select DE1 with large probability p1 to strengthen the global exploration ability. A small value of np shows that the algorithm is in convergence status, and DE3 operator should be applied with a large probability p3 to enhance the local exploitation capability. For median np, DE2 operator should be utilized to balance exploration and exploitation. Therefore, as the number of np decreases, p3 should decrease while p1 increase. In this paper, the expressions of p1 and p3 can be defined as follows:

$$ p_{1} (t)= 0.9\times \frac{1.0}{1+\exp (-20\times (SRR(t)-0.35))} $$
(20)
$$ p_{3} (t)= 0.9\times \frac{1.0}{1+\exp (20\times (SRR(t)-0.2))} $$
(21)

Figure 5a shows the relationship between p1, p3 and SRR. Figure 5b shows the dynamic trend of p1, p3 and SRR on F1 test instance. As seen from Fig. 5, in the initial evolution of the first phase np is large, and the DE1 operator is selected with a large probability to enhance the population diversity. With the operation of the first phase, np decreases, and the DE3 operator is selected with a large probability to improve the local search capability. The same phenomenon could be observed in the second phase. And the pseudo-code of the AOS scheme is presented in Algorithm 2.

figure d
Fig. 5
figure 5

The relationship and dynamic trend of p1, p3 and SRR on F1

Full size image

After the operation of the DE operator, AMOEA/D also needs to perform the mutation operator. For simplicity, the polynomial mutation operator [29, 38] is applied in AMOEA/D, as follows:

$$ {x}^{\prime i}_{j} = \left\{ {\begin{array}{l} {u_{j}^{i}} +\sigma_{j} \times (b_{j} -a_{j} ) \text{if rand}<p_{m} \\ {u_{j}^{i}} \text{otherwise} \end{array}} \right. $$
(22)
$$ \sigma_{j} = \left\{ {\begin{array}{l} (2\times rand)^{\frac{1}{{\eta + 1}}}-1 \text{if rand}<0.5 \\ 1-(2-2\times rand)^{\frac{1 }{ {\eta + 1}}} \text{otherwise} \end{array}} \right. $$
(23)

where j ∈ {1, 2, ... , n} , rand ∈ [0, 1], pm is the mutation probability, η is the distribution index, aj and bj are the lower and upper bounds of the j th decision variable, respectively. To maintain the population diversity in AMOEA/D, five parent solutions are selected from the whole population with a low probability 1-δ. In such a way, a very wide range of child solutions could be generated due to the dissimilarity among these parent solutions. Therefore, the exploration ability of the search could be enhanced. The pseudo-code of reproduction operation with the AOS scheme is given in Algorithm 3.

figure e

3.3.3 Replacement operation with constraint handling technique

When performing replacement operation, the processing of constraint conditions should be taken into consideration. In this paper, the constraint handing technique introduced in [48] is utilized. For infeasible solution x its constraint violation can be defined as

$$ cv(\mathbf{x})=\sum\limits_{j = 1}^{J} {\max (g_{j} (\mathbf{x}),0)} +\sum\limits_{j=J + 1}^{K} {\max (\left| {h_{j} (\mathbf{x})} \right|-\delta ,0)} $$
(24)

For parent solution x and offspring solution x′, x is substituted by x′ if one of the following conditions is met: (1) Both x′ and x are feasible solutions, and the aggregation function value of x′ is smaller than that of x; (2) x′ is a feasible solution, and x is in the infeasible region; (3) Both x′ and x are in the infeasible region, and the cv(x′) is smaller than cv(x). The pseudo-code of the replacement operation with constraint handling technique is presented in Algorithm 4. It should be noted that the condition of g(x′|wjz∗) ≤ g(xj|wjz∗) in the first phase should be changed as g(x′|wjznad) ≥ g(xj|wjznad) in the second phase.

figure f

3.3.4 Auto-switching scheme

In [35], a fixed number of iterations is needed to be set in advance for phase switching resulting in an unequal distribution of computing resources. In this paper, an auto-switching scheme is designed based on the aggregation function enhancement (AFE). According to (12), MOEA/D approaches POF by minimizing the aggregation function values of all the subproblems. If the value of the aggregation function of all subproblems could not be improved, it shows that the algorithm has found real POF or is in the stagnation status. At this point, the algorithm should be switched to the second phase from the first phase. The value of AFE for the i th subproblem at the t th iteration is calculated as below:

$$ AFE^{i}(t)=g^{te}(w^{i},t)-g^{te}(w^{i},t-1) $$
(25)

where gte(wi, t) and gte(wi, t − 1) are the aggregation function values of the i th subproblem at the t th and (t-1)th iterations, respectively. Let the maximum of AFE for all subproblems at the t th iteration be

$$ AFE_{\max} (t)=\underset{1\le i\le N}{\max} AFE^{i}(t) $$
(26)

Let varAFE be the variance of the vector of [AFEmax(t − γ + 1), AFEmax(t − γ + 2), ... , AFEmax(t)], if varAFE ≤ ε, the algorithm switches from the first phase to the second phase, where ε is a predefined stopping threshold. In the experiments, the value of ε is selected as ε =  10− 6 by trial-and-error.

3.3.5 The procedure of the AMOEA/D algorithm

The pseudo-code of the proposed AMOEA/D is provided in Algorithm 5. At the beginning of AMOEA/D some related parameters (i.e. N, maxIteration, p1, p3, r, and flag) are initialized in line 1. Then, in line 2, the weight vectors W and population P are generated according to Algorithm 1. From line 3 to line 34, the algorithm enters the major circle until the maximum number of iteration is reached and then the algorithm stops. From line 5 to line 20, the algorithm performs the first phase. From line 13 to line 19, the autos-witching scheme is run to determine whether to switch to the second phase. From line 21 to line 33, the algorithm executes the second phase. Besides, it is vital to note that the algorithm needs to store the nondominated solutions obtained in the first phase to the external archive EA1, reset the reference point with znad, reinitialize the weight vectors and recalculate the neighborhood relationship from line 21 to line 24. In line 35, the algorithm needs to save the non-dominated solutions acquired in the second phase to the external archive EA2 at the end of the second phase. Finally, in line 36, a certain number of non-dominated solutions with good diversity are identified from EA1 and EA2 by using the external archive maintenance algorithm with dynamic crowding distance method [49].

figure g

3.4 Computational cost of one generation of AMOEA/D

In this section, let us consider the computational cost of AMOEA/D in one generation. AMOEA/D has the same framework as MOEA/D-DE [38], thus the increased computation cost is attributed to its detection step for the auto-switching strategy and calculation of the parent solution updating rate for adaptive DE strategy. The calculation of the AFEmax value (line 13 in Algorithm 5) requires O(mN) computations. The calculation of the variance varAFE has a smaller computational cost. Therefore, the overall complexity of detection step is O(mN). Consider the adaptive operator selection presented in Algorithm 2, the calculation of the parent solution updating rate (line 2 in Algorithm 2) costs O(N) computations. At last, the reinitialization of the weight vectors and the recalculation of the neighborhood (line 24 in Algorithm 5) require O(mN) and O(mNT) computations, respectively. However, these two operations only need to be run once during the entire evolutionary process. In summary, the computational cost of AMOEA/D in each generation is O(mN).

4 Multiobjective optimal control based on AMOEA/D

By analyzing the (5)–(8), it can be found that EC and EQ have no explicit mathematical relationship with the five decision variables, particularly with SO,5 and SNO,2. Furthermore, the critical effluent quality parameters forming the constraint condition cannot be measured online. Therefore, the HMOOC strategy is proposed for the WWTP. First, a data-driven-based modeling approach is utilized to establish the accurate soft-computing models for EC, EQ and effluent quality parameters as optimization objectives and constraints. Second, the proposed AMOEA/D, utilizing multiple DE operators with AOS scheme and two-phase optimization with auto-switching scheme, is applied to dynamically optimize SO,5 and SNO,2 by minimizing the established objectives. Furthermore, an intelligent decision system is developed to select a preferred solution from the obtained POS as an optimized set-points. Finally, the multivariable controller, employing the self-organizing fuzzy neural network, is adopted to track the optimized set-points. And the overall structure of the HMOOC for the WWTP is shown in Fig. 6.

Fig. 6
figure 6

Architecture of HMOOC for the WWTP

Full size image

The overall process of the HMOOC for the WWTP is described as follows:

  • Step 1: The optimization objectives are established using the SOFNN-based prediction models with the process data in BSM1. The inputs of the models are the five decision variables and influent quality parameters. And the outputs of the models are the EC, EQ and effluent parameters.

    $$ f_{k}\textbf{(x)}=\sum\limits_{j = 1}^{u}w_{jk}\varphi_{j}=\frac{\sum\limits_{j = 1}^{u}\left[w_{jk}\exp\left( -\frac{\boldsymbol{\|}\mathbf{x-c}_{j}\boldsymbol{\|}^{2}}{\boldsymbol{\delta}_{j}^{2}}\right)\right]}{\sum\limits_{j = 1}^{u}\exp\left( -\frac{\|\mathbf{\boldsymbol{X}-c}_{j}\|^{2}}{\boldsymbol{\delta}_{j}^{2}}\right)} $$
    (27)

    where x=[x1x2, ... , xn]T is the input vector of SOFNN, n is the number of input variables, cj = [c1jc2j, ... , cnj] and δj = [δ1jδ2j, ... , δnj] are the center vector and width vector of the j th rule neuron, respectively φj is the normalized output of the j th rule neuron, wjk is the weight coefficient between the j th rule neuron and the k th output neuron j = 1, 2, ... , uu is the number of rule neurons, and k = 1, 2, ... , ss is the number of output variables. In SOFNN, the network structure is dynamically adjusted by a self-organizing mechanism designed based on the singular value decomposition method. Meanwhile, the network parameters are optimized by an adaptive learning algorithm developed based on the improved Levenberg-Marquardt (LM) optimization method [43, 44].

  • Step 2: The optimization objectives are minimized by using the proposed AMOEA/D to obtain a set of Pareto optimal solutions.

  • Step 3: The intelligent decision system designed by the fuzzy membership function approach is utilized to select a preferred solution from the Pareto solution set. Then, the optimal set-points of SO,5 and SNO,2 in the current optimal cycle could be determined. For the i th objective function fi, the satisfaction of nondominated solution f (xk) is defined as follows:

    $$ {\mu_{i}^{k}} \mathbf{=\!}\left\{ {\begin{array}{l} 1, f_{i} (\mathbf{x}_{k} )\le f_{i}^{\min} \\ \frac{f_{i}^{\max} -f_{i} (\mathbf{x}_{k} )}{f_{i}^{\max} -f_{i}^{\min}} , \!\!f_{i}^{\min} <f_{i} (\mathbf{x}_{k} )\!<f_{i}^{\max} \\ 0, f_{i} (\mathbf{x}_{k} )\ge f_{i}^{\max} \end{array}} \right. $$
    (28)

    where \(f_{i}^{\max }\) and \(f_{i}^{min}\) are the maximum and minimum of the i th objective function fi respectively. The normalized satisfaction of f (xk) is as follows:

    $$ \mu^{k}=\frac{\sum\nolimits_{i = 1}^{m} {{\mu_{i}^{k}}} } {\sum\nolimits_{k = 1}^{\left| S \right|} {\sum\nolimits_{i = 1}^{m} {\mu_{i}^{k}} } } $$
    (29)

    where m is the number of objectives and |S|is the number of elements in POS obtained. In this study, the solution with the maximum value of μk is selected by the intelligent decision system as the preferred solution.

  • Step 4: The optimal set-points of SO,5 and SNO,2 is tracked by the intelligent multivariable controller, which is designed using self-organizing fuzzy neural network [45]. The SOFNN controller displaying high steady-state accuracy and strong self-adaptability under complex conditions, can meet the needs of the bottom control loops. If the continuous 14-days data simulation is completed in BSM1, then stop. Otherwise, go to Step 1 for the next optimal cycle.

5 Benchmark problems testing

5.1 Test instances

To verify the validity of the proposed AMOEA/D algorithm, twelve unconstrained MOPs with complex POFs are used for testing. Table 1 gives the detailed description of the first six test instances (F1-F6) which were designed in [34] and Table 2 presents the detailed description of the remaining test instances (F7-F12) which were respectively adopted in [35] and [36].

Table 1 Test instances F1 - F6
Full size table
Table 2 Test instances F7 - F15
Full size table

5.2 Parameter settings

In this paper, the proposed AMOEA/D is compared with four state-of-the-art decomposition-based MOEAs, including MOEA/D-DE, MOEA/D-APS, MOEA/D-TPN, and iMOEA/D. In MOEA/D-DE, MOEA/D-TPN, and iMOEA/D, the Tchebycheff approach explained in (13) is adopted as the decomposition approach. MOEA/D-APS adopts the PBI-based decomposition method with adaptive penalty scheme. The parameters of MOEA/D-DE, MOEA/D-APS, MOEA/D-TPN, and iMOEA/D are set according to their corresponding references [34, 35, 37, 38], respectively. The detailed parameter settings of the proposed AMOEA/D are summarized as follows.

  1. 1)

    Control parameters in polynomial mutation:pm = 1/n and η = 20.

  2. 2)

    Neighborhood size:T = 20.

  3. 3)

    Probability to select in the neighborhood:δ = 0.9.

  4. 4)

    Control parameter in the replacement operator:nr = 2.

  5. 5)

    Population size:N = 100 for two-objective test instances, 300 for the three-objective ones.

  6. 6)

    Maximum number of iterations: maxIteration = 300 for F1-F5, 600 for F6-F12.

  7. 7)

    Number of runs: Each algorithm is run 30 times independently on each test instance.

5.3 Performance metric

In our empirical studies, we consider the following two widely used performance metrics [34].

  1. 1)

    Inverted Generational Distance (IGD)

Let S∗ be a set of points uniformly sampled from the true POF, and S be the set of approximated solutions obtained by an MOEA, the IGD indicator measures the gap between S∗ and S, which is calculated as follows:

$$ IGD(S^{\ast} ,S)=\frac{\sum\nolimits_{\mathbf{x}\in S^{\ast} } {d(\mathbf{x},S)}} {\left| {S^{\ast} } \right|} $$
(30)

where d(x, S) is the Euclidean distance between the solution x and its nearest neighbor in S, and |S∗| is the cardinality of S∗. If the number of points in S∗ is big enough, the IGD indicator can measure the convergence and diversity of the approximated POF obtained by an MOEA at the same time. The smaller the IGD value, the better the quality of the approximated POF. In the experimental studies, 500 uniformly distributed points are sampled from the true POF for bi-objective test instances, and 1000 for three-objective ones, respectively.

  1. 2)

    Hypervolume (HV)

Let z\(^{r}=(z_{1}^{r},z_{2}^{r}\), ... , \({z_{m}^{r}})^{T}\) be a reference point in the objective space that is dominated by all points on the true POF, and S be the set of approximated solutions obtained by an MOEA, the HV indicator measures the size of objective space dominated by the solution in S and bounded by zr

$$ HV(S)=VOL(\bigcup\limits_{\mathbf{x}\in S} {[f_{1} (\mathbf{x}),{z_{1}^{r}} ]} \times ...[f_{m} (\mathbf{x}),{z_{m}^{r}} ]) $$
(31)

where VOL represents the Lebesgue measure. The bigger the HV value, the better the quality of the approximated POF. In the experimental studies, zr is set to (1.1, 1.1)T for F1-F5 (1.1, 1.1, 1.1)T for F6, (1.1, 11)T for F7, (1.1, 1.1)T for F8-F9, (5.5, 5.5, 5.5)T for F10, and (1.1, 1.1, 1.1)T for F11-F12 when computing HV for the nondominated sets obtained by all the algorithms.

5.4 Experimental results

5.4.1 Comparisons on F1-F6

Tables 3 and 4 give the best, average, and worst values of IGD and HV for MOEA/D-DE, MOEA/D-APS MOEA/D-TPN, iMOEA/D, and AMOEA/D on F1-F6 test instances respectively, in which the bold means the corresponding algorithm achieves the best results on the test instance. The differences between the approximations are assessed by the Wilcoxon rank-sum test at the 0.05 significance level. Signs of a and b in the superscript form on mean values indicate the significance of the proposed algorithms. From Table 3, the proposed AMOEA/D can effectively tackle the complex MOPs. For F1, F3-F5, compared with MOEA/D-DE and MOEA/D-APS, the IGD values of AMOEA/D decrease significantly, indicating that the TP optimization with auto-switching scheme is more beneficial to find boundary solutions and to improve the population diversity. Compared with MOEA/D-TPN and iMOEA/D, the performance of AMOEA/D has a slight improvement since the adopted adaptive DE strategy and auto-switching scheme can enhance the quality of POS on F1-F4. For F2, it is easy for MOEA/D-DE and MOEA/D-APS to fall into a local POF, resulting in the high mean IGD values, while AMOEA/D has a stable performance and can approximate the whole POF in most cases. For the three-objective optimization problem F6, compared with MOEA/D-DE, the IGD values of MOEA/D-APS, MOEA/D-TPN, and AMOEA/D algorithms decrease to a certain extent. From Table 4, the similar conclusions can be drawn.

Table 3 IGD comparison results
Full size table
Table 4 HV comparison results
Full size table

Figure 7 shows the approximated POFs for MOEA/D-DE, MOEA/D-APS, and AMOEA/D when they obtain the lowest IGD values on F1 to F6. From Fig. 7, the solutions obtained by MOEA/D-DE and MOEA/D-APS might converge to the middle region of the POFs, resulting in the decrease of population diversity. The proposed AMOEA/D can obtain a better solution distribution along the actual POF, especially for F1, F3, and F4 test instances with convex POFs. It is worth noting that when the minimum IGD value is obtained, MOEA/D-DE, MOEA/D-APS, and AMOEA/D achieve the same performance on F2 with a concave POF.

Fig. 7
figure 7figure 7

The obtained approximated POF on F1-F6 when the minimum IGD is obtained during 30 times’ running

Full size image

In order to more clearly illustrate the proposed strategies, Fig. 8 plots the evolution curves of the IGD metric value versus the number of generations for each algorithm on F1 and F4 instances when the minimum IGD is obtained during the 30 times’ running. It can be observed that the proposed AMOEA/D can offer a significant improvement on the IGD metric when the TP optimization with auto-switching scheme is activated.

Fig. 8
figure 8

The IGD evolution curves of F1 and F4 when the minimum IGD value is obtained during the 30 times’ running

Full size image

Figure 9 presents the boxplots of the IGD metric obtained by the five algorithms from 30 independent runs on each instance. These results clearly indicate that the AMOEA/D is the best on F1-F5. And, more remarkably, for F2, the solutions obtained by MOEA/D-DE and MOEA/D-APS might converge to the peak point of the POF, while the solutions obtained by the proposed AMOEA/D can cover the entire POF in most cases. Thus, we can conclude that the proposed AMOEA/D has successfully improved the algorithm performance on MOPs with complicated POFs.

Fig. 9
figure 9

Boxplots for the comparison of AMOEA/D with MOEA/D-DE, MOEA/D-APS, MOEA/D-TPN, and iMOEA/D on IGD. DE, APS, TPN, i, and A in the horizontal axis stand for MOEA/D-DE, MOEA/D-APS, MOEA/D-TPN, iMOEA/D, and AMOEA/D, respectively

Full size image

5.4.2 Comparisons on F7-F12

To verify the robustness of AMOEA/D on MOPs with different shapes of POFs, AMOEA/D is compared with MOEA/D-DE, MOEA/D-APS, MOEA/D-TPN, and iMOEA/D on F7-F12 test instances in this section. Tables 5 and 6 show the performance of the five compared algorithms in terms of IGD and HV on F7-F12, in which the bold means the corresponding algorithm achieves the best results on the test instance. It can be observed that the proposed AMOEA/D performs significantly better than MOEA/D-DE and MOEA/D-APS on all test instances in terms of IGD. From Table 5, AMOEA/D has the best performance on F7, F8, and F11, and MOEA/D-TPN has the best performance on F12. The performance of AMOEA/D is very similar to that of MOEA/D-TPN on F9. Similar performance can be observed on the comparisons of five algorithms in terms of HV, where AMOEA/D performs better than the other compared algorithms on four out of six test instances. This further validates the efficiency of the proposed AMOEA/D algorithm in solving complex problems tested in this paper.

Table 5 IGD comparison results
Full size table
Table 6 HV comparison results
Full size table

Figure 10 shows the approximated POFs achieved by MOEA/D-DE, MOEA/D-APS, and AMOEA/D with the best IGD value on each test instance. It can be seen from Fig. 10 that F7, F8 and F9 have disparately scaled objectives, extremely convex POF and mixed POF, respectively. Furthermore, F10, F11 and F12 are three three-objective MOPs with complicated POFs, in which the boundary parts of their POFs are more difficult to approximate than other parts. Thus, it is desirable to obtain a more comprehensive evaluation on the performance of the compared algorithms by using these test problems with different characteristics. It can be observed that the solutions obtained by MOEA/D-DE and MOEA/D-APS might converge to the part region of the POFs on F7-F12 expect for F9, resulting in the decrease of population diversity. The proposed AMOEA/D can obtain a better solution distribution along the actual POF. It is worth noting that MOEA/D-APS with a smaller initial penalty factor is unable to find the actual POF on F12 due to the existence of many local POFs.

Fig. 10
figure 10figure 10

The obtained approximated POF on F7-F15 when the minimum IGD is obtained during 30 times’ running

Full size image

To compare the convergence speed of the compared algorithms, Fig. 11 plots the evolution curves of the IGD metric value versus the number of generations for MOEA/D-DE, MOEA/D-APS, and AMMOEA/D on F8 and F11 instances when the minimum IGD is obtained during the 30 times’ running. It can be observed that AMOEA/D converges faster than MOEA/D-DE and MOEA/D-APS, since they are easy to trap into local POFs. Meanwhile, a significant improvement of the IGD values can be observed when the second phase is automatically activated.

Fig. 11
figure 11

The IGD evolution curves of F10 and F12 when the minimum IGD value is obtained during the 30 times’ running

Full size image

Figure 12 shows the boxplots of the IGD metric obtained by the five algorithms from 30 independent runs on each instance. It can be observed that the performance of AMOEA/D is superior to MOEA/D-DE and MOEA/D-APS on all test problems. Besides, it can be seen from the boxplots of F7-F9 that the beards of MOEA/D-DE and MOEA/D-APS are longer than that of AMOEA/D. It means that MOEA/D-DE and MOEA/D-APS are still easy to trap into local POFs. Compared with MOEA/D-TPN, AMOEA/D obviously performs better on F7, F9, F10 and F11. Thus, we can conclude that the proposed AMOEA/D outperforms all the compared algorithms in most test instances. More remarkably, AMOEA/D is very robust with the shapes of POFs and can effectively solve MOPs with complicated POFs (e.g., discontinuous POFs or POFs with a sharp peak and long tail). It is interesting that MOEA/D-APS performs poorly on F7, F8 and F12 since it adopts PBI-based decomposition approach which is easily converged to the central region on MOPs with extremely convex POFs.

Fig. 12
figure 12

Boxplots for the comparison of AMOEA/D with MOEA/D-DE, MOEA/D-APS, MOEA/D-TPN, and iMOEA/D on IGD. DE, APS, TPN, i, and A in the horizontal axis stand for MOEA/D-DE, MOEA/D-APS, MOEA/D-TPN, iMOEA/D, and AMOEA/D, respectively

Full size image

6 Multiobjective optimal control in the WWTP

In this section, the proposed AMOEA/D is utilized to implement the multiobjective optimal control in the WWTP. The BSM1 is introduced to evaluate the effectiveness of the AMOEA/D-based HMOOC strategy. The sampling period of the SOFNN controller was set to 45 seconds and the optimal cycle was set to 2 hours. For AMOEA/D, the population size N was set to 100 and the maximum number of iteration was set to 300.

6.1 Modeling results

First, 500 data samples are generated with the usage of BSM1. Then, the SOFNN prediction models are adopted to establish the objective functions of EC, EQ and effluent parameters. The predicting results of EC and EQ with the usage of SOFNN and FNN are shown in Fig. 13. It can be observed that the prediction accuracy of SOFNN is higher than that of FNN. Obviously, the SOFNN-based approximator can provide more accurate objective functions for the HMOOC strategy. Specifically, for EC modeling, the testing RMSE of SOFNN and FNN are 5.49 and 7.87, respectively. For EQ modeling, the testing RMSE of SOFNN and FNN are 16.44 and 36.83, respectively.

Fig. 13
figure 13

The predicting results for EC and EQ

Full size image

6.2 Optimization results

The data file of dry weather is utilized to test the performance of different algorithms, and the approximated POFs obtained by MOEA/D-DE, MOEA/D-APS and AMOEA/D in some two optimal cycles are shown in Fig. 14. It can be seen that the convergence and diversity of solutions obtained by AMOEA/D is better than that of MOEA/D-DE and MOEA/D-APS. Especially, more boundary solutions can be found by AMOEA/D, which indicates that TP optimization with auto-switching scheme and adaptive DE strategy can enhance the search performance of MOEA/D. While using the intelligent decision system to select a preferred solution, the EC of AMOEA/D is lower than that of MOEA/D-DE and MOEA/D-APS.

Fig. 14
figure 14

Approximated POFs obtained by MOEA/D, MOEA/D-APS, and AMOEA/D

Full size image

6.3 Optimal control results

The variation of the optimized set-points and the tracking effect of the SOFNN controller in dry weather are presented in Fig. 15. It can be seen that SO,5 and SNO,2 can be dynamically adjusted with the change of influent condition and component concentration, achieving the dynamic balance between EC and EQ. Furthermore, the control effect of the SOFNN controller is better than that of the PID controller, achieving a fast and high-precision tracking control under complex conditions.

Fig. 15
figure 15

Optimized set-points and online tracking control performance of SO and SNO in dry weather

Full size image

In addition, the optimization effect of the AMOEA/D-based HMOOC strategy is compared with other optimal controllers: SOOC [25], DDAOC [16], Hopfield [17], RTO-NMPC [18], NSGA-II [25], MOPSO [27], MOEA/D-DE [38], MOEA/D-APS [34], MOEA/D-TPN [35], and iMOEA/D [37]. The results of AE, PE, EC, EQ and the average effluent parameters are given in Table 7, where influent represents the average influent parameters and PID denotes the constant control. From Table 7, in comparison with the PID constant control, the EC of AMOEA/D decreases by 6.88% in dry weather. Besides, the increase of EQ is smaller than that in SOOC and NSGAII. The experimental results indicate that AMOEA/D can not only ensure that the effluent parameters meet the standards, but also effectively reduce EC. In comparison with four MOEA/D variants, AMOEA/D presents an improved optimization effect, indicating that the proposed AMOEA/D with multiple adaptive strategies could obtain a set of high-quality optimal solutions. Compared with MOOC methods, the decrease of EC in SOOC is lower, and its energy-saving effect is less obvious. The increase of EQ in NSGAII is larger mainly due to the high effluent SNH.

Table 7 Comparison of EC and EQ with different optimal control strategies in dry weather
Full size table

To further verify the adaptability of AMOEA/D in the complex working conditions, the experiments were carried out with the usage of data files of rain weather. The optimal control results of SO,5 and SNO,2 under the rain weather are presented in Fig. 16. It can be seen that the set-points of SO,5 and SNO,2 can be dynamically optimized by the AMOEA/D in the case of the inflow rate and component concentration with large disturbance. In addition, the SOFNN controller has high tracking accuracy and sound anti-interference ability.

Fig. 16
figure 16

Optimized set-points and online tracking control performance of SO and SNO in rain weather

Full size image

Table 8 presents the comparative results of different optimal controllers in rain weather. Compared with the PID constant control, the EC of AMOEA/D decreases by 6.95% in rain weather. In addition, the EC of AMOEA/D is lower than that of NSGAII, MOPSO, and four MOEA/D variants, indicating that it can achieve a good energy-saving effect under complex conditions.

Table 8 Comparison of EC and EQ with different optimal control strategies in rain weather
Full size table

Figure 17 plots the optimized set-points of SO,5 and SNO,2 under the storm weather. The optimal results indicate that AMOEA/D can adjust the value of decision variables online regardless of the complex influent conditions. Table 9 presents the comparative results of different optimal controllers in storm weather. Compared with the PID constant control, the EC of AMOEA/D decreases by 7.44% in storm weather. In addition, the EC of AMOEA/D is lower than that of NSGAII, MOPSO, and four MOEA/D variants, indicating that it can achieve a good energy-saving effect under complex conditions.

Fig. 17
figure 17

Optimized set-points and online tracking control performance of SO and SNO in storm weather

Full size image
Table 9 Comparison of EC and EQ with different optimal control strategies in storm weather
Full size table

6.4 Discussion

Figure 18 shows the variation of the effluent SNH and Ntot in dry weather. In comparison with the PID constant control, the concentration of SNH in the optimal control exhibits a slight increase in some optimal periods, and the concentration of Ntot shows a downward trend in general. In addition, BOD5, COD and TSS remain unchanged, indicating that the HMOOC strategy can effectively reduce EC under the condition of ensuring the average effluent parameters to meet the standards. According to the analysis of the mechanism of the WWTP, SNH and Ntot are a pair of parameters with competitive relationship, and the optimal balance between them can be achieved with the usage of the proposed AMOEA/D.

Fig. 18
figure 18

Comparison of effluent parameters in dry weather

Full size image

According to the further analysis of Table 7, SNH slightly increases and Ntot decreases to a certain extent in AMOEA/D, whereas the other effluent parameters remain almost unchanged. These findings are consistent with the changes in the effluent parameters as shown in Fig. 18. It should be noted that all the comparison methods adopted in this study can ensure that the average effluent parameters satisfy the standard limits. According to the analysis of the removal rate of effluent contaminants, when compared with the influent parameters, the removal rates of the effluent SNH, Ntot, BOD5, COD and TSS can respectively reach 90.88%, 70.16%, 96.20%, 71.58%, and 93.66% by utilizing the AMOEA/D-based HMOOC strategy.

Furthermore, the average values of effluent SNH, Ntot, BOD5, COD and TSS in rain and storm weather are presented in Table 10. The results indicate that all the average value of effluent SNH, Ntot, BOD5, COD and TSS are remained within the limitations under complex weather conditions. The optimal control results shown in Figs. 15–18 and the performance indexes of different optimal controllers given in Tables 7–10 illustrate the effectiveness of the proposed AMOEA/D. The experimental results clearly indicate that the AMOEA/D-based HMOOC strategy can address the MOP in the WWTP under complex working conditions. In addition, the optimal results show that the objective functions constructed by the SOFNN approximator can meet the optimization needs of WWTP with high modeling accuracy. The multi-variable self-organizing controller can track the optimal set-points of SO,5 and SNO,2 with good stability and high control precision.

Table 10 Average effluent parameters of the proposed AMOEA/D in rain and storm weather
Full size table

7 Conclusion

In this paper, an HMOOC strategy based on the adaptive MOEA/D algorithm is proposed for the multiobjective optimization of EC and EQ in the WWTP. In fact, good optimal control performance mainly benefits from the following aspects. First, the HMOOC strategy, consisting of the SOFNN approximator, AMOEA/D algorithm and SOFNN controller, shows a good overall performance. The modeling accuracy of SOFNN approximator and the tracking precision of SOFNN controller could be enhanced by the self-organizing adjustment of the fuzzy rules and adaptive learning of network parameters, making them useful to the optimal control system. Second, for AMOEA/D, the AOS-based adaptive DE strategy could balance global exploration and local exploitation of the algorithm. The convergence and diversity of the Pareto solutions obtained by AMOEA/D could be improved. Third, based on the constraints handling mechanism, AMOEA/D can find more solutions with small violation values while performing the updating operation. Finally, by employing the two-phase optimization with auto-switching scheme, AMOEA/D can dig out more boundary solutions as well as effectively improve the quality of the candidate solutions, which is more suitable for the complicated MOPs in practical engineering. Future study is needed to fully explore the knowledge in the WWTP, and to construct an HMOOC strategy based on knowledge and processed data.