Mining constrained inter-sequence patterns: a novel approach to cope with item constraints

Abstract

Data mining has become increasingly important in the Internet era. The problem of mining inter-sequence pattern is a sub-task in data mining with several algorithms in the recent years. However, these algorithms only focus on the transitional problem of mining frequent inter-sequence patterns and most frequent inter-sequence patterns are either redundant or insignificant. As such, it can confuse end users during decision-making and can require too much system resources. This led to the problem of mining inter-sequence patterns with item constraints, which addressed the problem when end-users only concerned the patterns contained a number of specific items. In this paper, we propose two novel algorithms for it. First is the ISP-IC (Inter-Sequence Pattern with Item Constraint mining) algorithm based on a theorem that quickly determines whether an inter-sequence pattern satisfies the constraints. Then, we propose a way to improve the strategy of ISP-IC, which is then applied to the $i$ISP-IC algorithm to enhance the performance of the process. Finally, pi ISP-IC, a parallel version of $i$ISP-IC, will be presented. Experimental results show that pi ISP-IC algorithm outperforms the post-processing of the-state-of-the-art method for mining inter-sequence patterns (EISP-Miner), ISP-IC, and $i$ISP-IC algorithms in most of the cases.

1 Introduction

With the rapid growth of the Internet, the volume of data has become massive. Analyzing data to reveal knowledge that can be applied to intelligent systems constitutes a challenging problem [3]. Therefore, data mining, the crucial step for extracting knowledge, has been extensively studied. There are many types of systems with numerous types of data such as transaction databases, sequence databases, and streaming databases. Then, many problems have been proposed such as pattern mining Yun and Ryu [35]; Salehi et al. [21]; Saif-Ur-Rehman et al. [20]; Yun and Kim [37]; Ryang and Yun [38]; Kim and Yun [39]; Ryang et al. [40]; Kieu et al. [41]; Vo et al. [27] and its applications Liao and Chen [13]; Scalmato et al. [22]; Wright et al. [30]; Lin et al. [14], association rule mining, and classification. Mining frequent sequential patterns, the sub-sequential patterns in a sequence database that satisfy the given minimum support threshold (minsup), which are used in recommendation systems Salehi et al. [21], deep order-preserving sub-matrix problem solutions Xue et al. [31], biological sequence mining Liao and Chen [13] and smart health services Jung and Chung [9]. Recently, Jeyabharathi andShanthi [8] proposed a new technique for protein sequence database mining with hybrid frequent pattern mining algorithm. The proposed algorithm ensures the effective extraction of frequent patterns with the optimization of resource constraints. In the recent years, many algorithms for mining frequent sequential patterns Ayres et al. [1]; Gouda et al. [6]; Kaneiwa and Kudo [7]; Yen and Lee [32]; Lin et al. [43, 44]; Pei et al. [19], sequential closed patterns Tran, Le and Vo [23]; Zhang et al. [45], sequential rules Pham et al. [18], closed weighted sequential patterns Yun et al. [33], weighted approximate sequential pattern Yun et al. [34], important sequential patterns Yun and Ryu [35], and high utility-probability sequential patterns Zhang et al. [42] from sequence databases have been proposed.

Besides, the problem of mining inter-transaction (closed) patterns has been attracted a lot of attention with many algorithms such as EH-Apriori and EA-Apriori Lu et al. [16], FITI Tung et al. [24], ITP-Miner Lee andWang [12], and ICMiner Lee et al. [11]. Although sequential patterns and inter-transaction patterns include several itemsets across several transactions, the ordered relationships among items in a transaction are not considered. However, sequence database usually exhibits an ordered relationship among items (or itemsets) in a transaction. Therefore, inter-sequence pattern Wang and Lee [28]; Vo et al. [25] and closed inter-sequence pattern Wang et al. [29]; Le et al. [10] mining are then proposed which are more general models than those of sequential and inter-transaction pattern mining.

In essence, the end users usually consider a small number of patterns that contain at least one item from a set of given item constraints [2]. For example, when analyzing the sequence data-bases of supermarkets, there are a lot of inter-sequence patterns. However, at a time, managers only concerned the patterns contained a number of specific items. Therefore, the problem of mining inter-sequence patterns with item constraints requires thorough studies. However, this problem has not been previously considered. We propose two novel algorithms for fast mining inter-sequence patterns with item constraints. The main contributions of this article are as follows. First, the problem of mining inter-sequence patterns with item constraints is introduced. Second, we develop a theorem to reduce the time of determining whether a candidate sequence satisfies the constraints. The ISP-IC (Inter-Sequence Pattern with Item Constraint mining) algorithm based on the above theorem for mining inter-sequence patterns with item constraints is then proposed. Third, a lemma and the second algorithm, named $i$ISP-IC, are proposed. Then, we present a parallel version of $i$ISP-IC, named pi ISP-IC algorithm. Final, experiments are conducted to show the effectiveness of the pi ISP-IC in terms of mining time and memory usage compared to the post-processing of the-state-of-the-art method for mining inter-sequence patterns (EISP-Miner) which is called by POST-EISP-Miner, ISP-IC, and $i$ISP-IC algorithms.

The paper is organized as follows. Section 2 presents the related works. Then Section 3 summaries the basic concept of inter-sequence patterns, DBV structure, and the problem of patterns with constraints. Section 4 proposes three algorithms for mining inter-sequence patterns with item constraints attached with advanced examples. Section 5 presents the experimental results. The conclusions and future works are given in Section 6.

2 Related works

Inter-sequence patterns demonstrate the anti-monotone Apriori property (if any $k-$pattern is infrequent, then all its (k + 1)-super-patterns are infrequent) Wang and Lee [28]. Based on this property, Wang and Lee proposed the M-Apriori algorithm for mining inter-sequence patterns. However, the large numbers of candidates and database scans are the cause for decreasing the performance of this algorithm. The authors proposed a two-phase-algorithm named EISP-Miner (Enhanced Inter-Sequence Pattern Miner) for finding a complete set of frequent inter-sequence patterns. The first phase is to find 1-patterns and converts the original sequences into a structure for each 1-pattern, called a pattern-list which stores two pieces of information including a frequent pattern and a list of locations. The second phase uses an inter-sequence pattern tree (ISP-tree) to enumerate all frequent inter-sequence patterns by joining pattern-lists in a depth-first search manner. In 2012, Vo et al. proposed DBV-ISP algorithm, an enhanced version of EISP-Miner algorithm in which dynamic bit vector (DBV) is used instead of pattern-list to improve the performance. However, we cannot use these algorithms for mining inter-sequence patterns with item constraints because they have to find all the inter-sequence patterns and then filter these patterns to identify the patterns satisfying the item constraints. Therefore, it is necessary to study an approach for mining inter-sequence patterns with item constraints.

3 Basic concepts

3.1 Inter-sequence pattern mining

Consider the set of items $t=$ {u₁, $u_{2}$, $u_{3}$,…, $u_{m}$} , where $u_{i}$ is an item (1 $\le i \le m)$. A sequence $s = \langle t_{1}$, $t_{2}$, $t_{3}$,…, $t_{n}\rangle$ is the set of ordered itemsets, where $t_{i} \subseteq$$t$ (1 $\le i \le n)$ is an itemset. A sequence database $\Phi =$ {s₁, $s_{2}$, $s_{3}$,…, $s_{\mathrm {\vert \Phi \vert }}$} , where |$\Phi$| is the number of sequences in $D$ and $s_{i}$ (1 $\le i \le$ |$\Phi$|) is a tuple $\langle$DAT, Sequence〉 , where DAT is the property of s _i used to describe the contextual information. Table 1 shows an example sequence database (Φ_Ex). This database is used throughout the paper.

Table 1 Example sequence database (Φ_Ex)

Let $d_{1}$ and $d_{2}$ be two DAT values associated with sequences $s_{1}$ and $s_{2}$, respectively. Let d₁ be the reference point. [d₂ - $d_{1}$] is the span between $s_{2}$ and $s_{1}$. The sequence $s_{2}$ at domain attribute (DAT) $d_{2}$ with respect to $d_{1}$, denoted by $s_{2}$[d₂ - $d_{1}$], is called an $e$-sequence (extended sequence). For example, with $\Phi _{\text {Ex}}$ shown in Table 1, let the first sequence be the reference point. Then, the $e$-sequence of the second transaction is $\langle C$(ABC)A〉[1].

Let $s$[d] $= \langle t_{1}$, $t_{2}$, $t_{3}$,…, $t_{m}\rangle$[d] be a sequence where t _i is an itemset (1 $\le i \le m)$ and [d] is the span of $s$. The $t_{i}$ associated with [d] is defined as an extended itemset (e-itemset), denoted by $\langle t_{i}\rangle$[d]. If $t_{i} =$ (u₁, $u_{2}$, $u_{3}$,…, $u_{n})$, where each $u_{i}$ is the items (1 $\le i \le n)$, then the $u_{i}$ associated with [d] is defined as an extended item (e-item), denoted by (u _i )[d]. For example, $\langle C$(ABC)A〉 [1] has 3 e-itemsets (〈C〉 [1], 〈 (ABC)〉 [1], and A[1]) and 3 $e$-items ((C)[1], (A)[1], and (B)[1]).

Given the set of $k$ sequences $\langle d_{1}$, s₁〉 , 〈d₂, s₂〉 ,…, 〈d _k , s _k 〉 in Φ , Ψ = s₁[0] $\cup$s₂[d₂– $d_{1}$] ∪…$\cup s_{k}$[d _k – d₁] is called a mega-sequence with $k \ge$ 1. In a mega-sequence, the span between DAT of the first transaction and that of the last transaction have to be less than or equal to maxspan (i.e., $d_{k}$ – d₁ ≤maxspan in Ψ). For $\Phi _{\text {Ex}}$ shown in Table 1, with maxspan$=$ 1 and Dat$=$ 1 as the reference point, the list of mega-sequences is shown in Table 2.

Table 2 Megasequences of $\Phi _{\text {Ex}}$ with maxspan$=$ 1

Consider the pattern $\beta =$ (u₁)[v₁], (u₂)[v₂],…, (u _n )[v _n ], where (u _i )[v _i ] (1 $\le i \le n)$ is an $e$-item (extended item). The number of $e$-items in $\beta$ is called the length of $\beta$ and a sequence with length $k$ is denoted as a $k$-sequence. There are three types of relationship between two $e$-items (u _i )[v _i ] and (u_i+ 1)[v_i+ 1] in $\beta$ (1 $\le i$ <$n)$. (1)Itemset extension: if $v_{i} =$v_i+ 1and (u _i u_i+ 1) is an itemset, then (u_i+ 1)[v_i+ 1] is an itemset extension (+ _I ) of (u _i )[v _i ]. (2)Sequence extension: if $v_{i } = v_{i \mathrm {+ 1 } }$and 〈u _i u_i+ 1〉 is a sequence, then (u_i+ 1)[v_i+ 1] is a sequence extension (+ _S ) of (u _i )[v _i ]. (3)Inter extension: if v _i <$v_{i\mathrm {+ 1}}$, then (u_i+ 1)[v_i+ 1] is an inter extension (+ _T ) of (u _i )[v _i ].

For example, in $\Phi _{\text {Ex}}$, $\langle$BCD〉 [0] 〈(AB)C〉 [1] is a 6-sequence. (B)[0] is an itemset extension of (CD)[0]. (B)[0] is an inter extension of (C)[1] and AB[1] is a sequence extension of (C)[1]. In other words, (B)[0] $+_{I}$ (CD)[0] = 〈(BCD)〉 [0], (AB)[0] + _S (C)[0] $= \langle$(AB)C〉[0], and (B)[0] $+_{T}$ (C)[1] $= \langle B\rangle$[0]〈C〉[1].

Given two sequences, $s = \langle s_{1}$, s₂,…, $s_{n}\rangle$ and $s^{\prime } = \langle s^{\prime }_{1}$, $s^{\prime }_{2}$,…, $s^{\prime }_{m}\rangle$ with $n$≤ m, $s$ is the sub-sequence of $s^{\prime }$ if and only if $\exists n$, j₁, $j_{2}$,…, $j_{n}$ such that (1) 1 ≤ j₁<$j_{\mathrm {2 } }$<…<$j_{n}\le m$ and (2) $s_{\mathrm {1 } }\subseteq {s^{\prime }}_{j_{1}}$, $s_{\mathrm {2 } }\subseteq {s^{\prime }}_{j_{2}}$, …, $s_{n}\subseteq {s^{\prime }}_{j_{n}}$. For example, a sequence $\langle A$(BC)DF〉 is the subsequence of 〈A(ABC)(AC)D(CF)〉 , but it is not a subsequence of 〈(ABC)(AC)D(CF)〉 . Consider two patterns α = s₁[i₁], $s_{2}$[i₂], …, $s_{n}$[i _n ] and $\beta =$s1′[j₁], s2′[j₂],…., $s^{\prime }_{m}$[j _m ], with 1 ≤ n ≤ m. $\alpha$ is a subsequence of $\beta$ if and only if there exist $n$ e-sequences denoted by sk1′[j_k1], sk2′[j_k2],…, skn′[j _{k n} ] in $\beta$, such that $i_{\mathrm {1 } }=$j_k1 and $s_{1}$ is a subsequence of sk1′; $i_{2} = j_{k 2}$ and s₂ is a sub-sequence of $s^{\prime }_{k 2}$;….; i _n = j _{k n} and $s_{n}$ is a sub-sequence of $s^{\prime }_{kn}$. In this case, β is a super-pattern of α . For example, both 〈D〉 [0]〈BAC〉 [3] and 〈 (AD)〉 [0]〈(AC)C〉 [1] are sub-sequences of 〈D(AD)〉 [0] 〈B(AC)C〉 [1]〈BACC〉[3].

Definition 1

Let $a =$ (i _m )[x] and $b =$ (i _n )[y] be 2 e-items. $a = b$ if and only if (i _m = i _n )∧ (x = y) and $a$<$b$, if and only if $x$<$y$ or ((x = y)∧ (i _m <i _n )).

For example, (C)[1] $=$ (C)[1], (B)[1] <(A)[2], and (A)[1] <(C)[1].

Definition 2

Let $p$ be a pattern. Function sub _{i j} (p) is defined as (j-i + 1) subset $e$-items of $p$ from position $i$ to position $j$.

For example, sub_1,4(〈(AD)〉[0]〈(AC)C〉[1]) = 〈(AD)〉[0]〈(AC)〉[1] and sub_5,5(〈(AD)〉[0]〈(AC)C〉[1])= (C)[1].

Definition 3

Let $\alpha = \langle u\rangle$[0] and $\beta$= 〈v〉 [0] be two frequent 1-patterns. α is joinable to β in any instance. There are three types of join operation: (1) itemset extension: α∪ _I β ={〈 (uv)〉[0]}|{〈 (uv)〉 [0]} ; (2) sequence extension: α∪ _S β ={〈 uv〉 [0]} ; (3) inter extension: α∪ _T β ={〈u〉 [0]〈v〉 [x] |1 ≤ x ≤ maxspan} .

For example, let maxspan$=$ 2, $\langle A\rangle$[0] $\cup _{I} \langle B\rangle$[0] $= \langle$(AB)〉 [0]; 〈A〉 [0] ∪ _S 〈B〉 [0] = 〈AB〉 [0] and 〈A〉 [0] ∪ _T 〈B〉 [0] = {〈A〉 [0]〈B〉 [1], 〈A〉[0]〈B〉[2]} .

Definition 4

Let $\alpha$ and $\beta$ be 2 frequent $k$-patterns, where $k$>1, sub_k,k(α) = (u)[i], and sub_k,k(β) = (v)[j]. $\alpha$ is joinable to $\beta$ if sub_1,k− 1(α) = sub_1,k− 1(β) and $i \le j$, which generates three types of join operations: (1) itemset extension: $\alpha \cup _{I}\beta =${α+ _I (v)[j] |(i = j) ∧ (u<$v)$} ; (2) sequence extension: $\alpha \cup _{S}\beta =\{\alpha \cup +_{S}(v)$[j] |(i = j)} ; (3) inter extension: $\alpha \cup _{T}\beta =${α+ _T (v)[j] |(i<j)} .

For example, $\langle$AB〉 [0] ∪ _I 〈AC〉[0] = 〈A(BC)〉 [0], 〈AB〉 [0] ∪ _S 〈AC〉 [0] = 〈ABC〉 [0], and 〈AB〉 [0] ∪ _T 〈A〉 [0]〈C〉[2] = 〈AB〉 [0]〈C〉[2].

3.2 DBV-PatternList data structure

DBV structure is based on the BitTable structure including two elements. (1) Start position: the position of the first non-zero byte in the bit vector; (2) Bit-vector: the list of bytes after removing all zero bytes at the beginning. For example, give a BitTable “000011”, the DBV is { Start: 5, Bit-vector: “11”} .

Using DBV structure reduces the memory usage and computational operations in the intersection between two-bit vectors. Using a look-up table Vo et al. [26], the algorithm traverses the DBV once to determine the support of its pattern and therefore the complexity is $O(n)$ where $n$ is the number of elements in its Bit-vector.

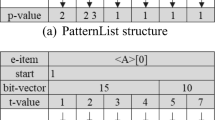
Based on the DBV concept, Vo et al. [26] proposed the DBV-PatternList structure that combines DBV and PatternList. The structure includes: (1) Sequence: storage information of the sequence; (2) Block sequence: one DBV and a list of transaction positions corresponding to each sequence. For example, in $\Phi _{\text {Ex}}$, consider the structure of sequence $\langle A\rangle$[0], where $A$ appears at sequences 1, 2, 3, 4, 5, and 7. DBV-PatternList of $\langle A\rangle$[0] is shown in Fig. 1.

Fig. 1

Structures of (a) PatternList and (b) DBV-PatternList of 〈A〉[0]

In Fig. 1b, the structure of a DBV-PatternList contains a number of block sequences. Each block sequence is placed in a cell containing information regarding the position of sequences that appear in the sequence database and the position of the sequence in each transaction. For detail, $A$ appears at sequences 1, 2, 3, 4, 5, and 7, so, bit vector of $A$ is 11111010 and therefore, DBV of A is {15, 10} (note that we use 4 bits for an integer). To find the appropriate extended sequence based on the sequence extension operation, the intersection operation has to be carried out on each block sequence. In Fig. 1, PatternList of $\langle A\rangle$[0] requires 26 bytes, whereas DBV-PatternList of $\langle A\rangle$[0] requires only 20 bytes.

3.3 Mining patterns with item constraints

Various strategies have been proposed for mining frequent pattern with itemset constraints. There are three main approaches including post-processing, pre-processing, and constrained patterns filtering. Post-processing approaches for mining patterns with item constraints firstly mine patterns and then check them against the constraints Ng et al. [17]; Lin et al. [15]. Pre-processing approaches firstly restrict the source dataset to records that contain the constraints and then find patterns in the filtered dataset Lin et al. [15]. Constrained patterns filtering approaches integrate the constraints into the actual mining process to generate only patterns that satisfy the constraints. CAP Ng et al. [17] and MFS_DoubleCons Duong et al. [4] algorithms use this strategy for mining frequent patterns with item constraints.

3.4 Problem statement

Given a sequence database $\Phi$, the minimum support (minsup), and a set of items $\chi =$ {u₁, $u_{2}$, …, $u_{k}$} , the problem of mining inter-sequence patterns with item constraints is to find all sequences $\alpha =$s₁[w₁], s₂[w₂],…, $s_{m}$[w _m ] such that ∃s _i [w _i ] $\in \alpha$, $\exists b_{j} \in$s _i [w _i ]: $b_{j} \in \chi$.

For example, let $\chi =$ {C} . Then, the sequence $\langle C$(AB)〉 [0] 〈C(ABC)A〉 [1] satisfies the constraints, whereas the sequence 〈AD〉 [0]〈A〉[1] does not.

4 Mining inter-sequence patterns with item constraints

4.1 ISP-IC algorithm

Theorem 1

If $a$ sequence $\alpha$ satisfies constraint $\chi$ , then the sequence $\gamma$ , generated from $\alpha$ , also satisfies constraint $\chi$ .

Proof

If $\alpha$ satisfies the constraint, it means that $\exists s_{i}$[w _i ] $\in \alpha$, $\exists b_{j} \in$s _i [w _i ]: $b_{j} \in \chi$. There are three cases to consider:

• 1. Itemset extension: There are two sub-cases. (i) If itemset extension $\notin$ itemset_i of $\alpha$, then $\exists$itemset_i in $\gamma$ that contains item $b_{j} \in \chi$. (ii) If itemset extension $\in$ itemset_i, then itemset_i(α) ⊂ itemset_i(γ), and thus $\exists b_{j} \in$ itemset_i(γ) such that $b_{j} \in \chi$.

• 2. Itemset extension: itemset_i is not changed. Therefore, $\exists$itemset_i ∈ γ includes item b _j such that $b_{j} \in \chi$.

• 3. Inter extension: Based on the inter extension definition, itemsets in the sequence just have their indices changed, and therefore $\exists$itemset_i contains item $b_{j} \in \chi$.

Based on Theorem 1, we propose the ISP-IC algorithm for mining inter-sequence patterns with item constraints. First, the ISP-IC algorithm finds all items (I₁) that satisfy the threshold. Then, the algorithm inserts $p \in I_{1}$ into the DBV-tree. ∀p ∈ I₁ such that $p \in \chi$, cs(p) = true. Next, the algorithm calls Join_1-PatternList to combine 1-PatternLists. Finally, for each $p \in$ DBV-Tree.root, the algorithm calls the Join_k-PatternList function to combine $p$ with other k-PatternLists that follow it. The details of the ISP-IC algorithm are presented in Alg. 1.

4.2 An illustrative example

Consider $\Phi _{\text {Ex}}$, which includes 7 sequences with items $I =${A,B,C,D} , maxpan$=$ 1, minsup$=$ 25%, and $\chi =$ {C} . DBV-PatternList of each item was shown in Table 3.

Table 3 Binary vectors of BitTable and their transformation into BitArray

Table 3a shows the bit arrays for the items in $\Phi _{\text {Ex}}$. In this example, assume that each block is encoded by 4 bits. In $\Phi _{\text {Ex}}$, bit array of $A$ is {1111, 1010} and bit vector of $A$ is {15, 10} . For each sequence, the position of each item in the sequence is stored as in Table 3b.

Once the sequences have been encoded into binary form and the positions in the sequence have become sequence blocks (with each sequence block containing 4 bits), the sequence database is transformed into a vertical format database and DBV-PatternList structures are created, as shown in Fig. 2. Note that index column the transaction position and come from Table 3b.

Fig. 2

DBV-PatternList of A[0], B[0] and C[0]

Then, the branch of $\langle A\rangle$[0] with two levels is obtained. The nodes on the second-level branch are then computed, followed by those on the third-level branch, and so on, until no extended sequences are found. Figure 3 shows a part of a DBV-tree extended on branch $\langle A\rangle$[0]. Note that the node $\langle C\rangle$[0] (red node) is the constraint and the nodes $\langle$AC〉 [0] and 〈A〉 [0]〈C〉 [1] (gray node) are inserted into the results without being checked whether they satisfy the constraint because their parent C[0] satisfies the constraint.

Fig. 3

DBV-tree extended on 〈A〉[0]

4.3 iISP-IC algorithm

Lemma 1

Let$\alpha$satisfy constraint$\chi$then$\forall \beta$,following sequencesγ _I = α∪ _I β,γ _S = α∪ _S β,and$\gamma _{T} = \alpha \cup _{T} \beta$also satisfy constraint$\chi$.

Based on Lemma 1, we propose the $i$ISP-IC algorithm. For each $p \in$childnodes(DBV-Tree), if $p$ satisfies $\chi , i$ISP-IC calls the Join_k-PatternList_NoChecking function to combine $p$ with other k-PatternLists that follow it. Otherwise, $i$ISP-IC calls the Join_k- PatternList_Plus function. The details of the $i$ISP-IC algorithm are presented in Alg.2.

In the example, suppose that $\chi =\{A\}$, the red node in Fig. 4. The $i$ISP-IC algorithm calls the Join_k-PatternList_NoChecking function to expand the node $\langle A\rangle$[0], as shown in Fig. 4. Based on Lemma 1, this function does not check all its child nodes.

Fig. 4

DBV-tree extended on 〈A〉[0] using i ISP-IC algorithm

4.4 The complexity discussion

The complexity of sequential pattern mining algorithms is based on the number of patterns in the search space, and the cost of the operations for generating and processing each itemset Fournier-Viger et al. [5].

Let $t =$ {u₁, $u_{2}$, $u_{3}$,…, $u_{\mathrm {m}}$} is the set of items, and let |$t$|denote its cardinality. We have to consider all possible permutations of the items as the possible frequent candidates. The subsequence search space is conceptually infinite since it comprises all sequences in $t$. The dataset $D$ consists of bounded length sequences in practice. Let $j$ be the length of the longest sequence in the dataset $D$, we will have to consider all candidate sequences of length up to $j$ in the worst case, which gives the following bound on the size of the search space |$t$|$^{1} +$ |$t$|$^{2} +$ |$t$|$^{3} +$…$+$ |$t$|^j (O(|$t$|$^{n}))$ since at level $k$ there are |t|$^{k}$ possible subsequences of length $k$.

However, the complexity of the proposed algorithms depends on the number of sequences, the number of itemsets in each sequence, and the constraints. Therefore, it is hard to compute the time complexity in the average case.

4.5 piISP-IC: a parallel version of iISP-IC algorithm

In the parallel mining of ISPs, each branch of the search tree can be regarded as a single task, which can be processed independently to generate ISPs. An example is given in Fig. 5 There are three tasks on level 1 of the task tree. Tasks 1 2, and 3 process branches $A B$and $C$ respectively.

Fig. 5

Example of task tree

The interaction between cores in multi-core CPU’s can be implemented by various mechanisms, affecting overall CPU performance due to shared workloads between cores. The most efficient way to allow on-chip interprocess communication (IPC) is through the use of shared memory. This is a very important feature for efficient hardware utilization of multi-core systems. Shared memory IPC is more efficient because data does not need to be copied from one process memory space to another. Instead, a memory space that is shared between the communicating processes is created. By this way, IPC that uses shared memory avoids many costly memory operations.

The task parallel formulation distributes the tasks among the processors in the following way. First, the tree is expanded using the data-parallel algorithm at level $k +$ 1, with $k$ > 0. Then, the different nodes at level $k$ are distributed among the processors. Once this initial distribution is done, each processor proceeds to generate the subtrees underneath the nodes to which they have been assigned.

pi ISP-IC algorithm is generally based on $i$ISP-IC algorithm and add a parallel implementation of tasks instead of threads. The advantage of pi ISP-IC is that each task is assigned for searching a branch of the tree and is processed independently. The advantages over using threads are as follows. First, tasks require less memory than do threads. Second, a thread runs on only one core, whereas a task can run on multiple cores. Finally, threads require more processing time than executing tasks because the operating system needs to allocate data structures for threads, such as initialization and destruction and must perform context switching between threads.

The time complexity of sequential pattern mining algorithms depends on the number of patterns in the search space, and the cost of the operations for generating and processing each itemset. In multi-core processors, a key factor is task scheduling. With the widespread use of multi-core processors, designing an effective task scheduling strategy has been a hot issue. Currently, the time complexity of task scheduling for multi-core processors is considered as an NP (Non-Deterministic Polynomial) problem and no optimal solutions exist. The existing scheduling algorithms can only get the suboptimal solutions based on solution approximated by heuristics. Heuristics are generally considered as the most suitable method to find the suboptimal solutions for NP problems.

5 Experimental studies

This section compares the mining time of POST-EISP-Miner, ISP-IC, $i$ISP-IC, and pi ISP-IC, to confirm the effectiveness of the proposed methods. All the experiments were performed on a PC with Intel Xeon Processor E5-2680 v2 (25M Cache, 2.80 GHz, 20 threads) CPUs installed with 768 GB of main memory and coded in C# in Visual Studio 2015. Synthetic databases were generated using the IBM synthetic data generator to mimic transactions in a retail environment. The synthetic data generation program used the following parameters: $C$ was the average number of itemsets per sequence, $T$ was the average number of items per itemset, S was the average number of itemsets in maximal sequences, $I$ was the average number of items in maximal sequences, $N$ was the number of distinct items, and $D$ was the number of sequences. Two synthetic datasets (C6T5S4I4N1KD10K and T10I4D100K) and BMSWebView2 which contains 77,512 sequences of click-stream data, were used in the experiments. These databases are available at http://1drv.ms/1EM0bqm.

5.1 Runtime

In Fig. 6, we compare the runtime of pi ISP-IC, $i$ISP-IC, ISP-IC and POST-EISP-Miner for C6T5S4I4N1KD10K dataset with various settings. Figure 6A fixes maxspan$=$ 1 and changes the threshold from 21 to 25 and we easily found that the runtime of $i$ISP-IC is less than that of ISP-IC and nearly twice as that of pi ISP-IC, while POST-EISP-Miner’s decreased a little. In a similar way, Fig. 6B fixes maxspan$=$ 2, Fig. 6C fixes maxspan$=$ 3, Fig. 6D fixes maxspan$=$ 4 and Fig. 6E fixes maxspan$=$ 5, pi ISP-IC is always the best algorithm for C6T5S4I4N1KD10K dataset. POST-EISP-Miner cannot perform with maxspan$=$ 5 with any threshold, takes a long time without results. Next, in Fig. 6F, we fix threshold$=$ 21, and change maxspan from 1 to 5. pi ISP-IC is still better than $i$ISP-IC, ISP-IC, and POST-EISP-Miner algorithms. Especially, when we decrease the threshold, the runtime of $i$ISP-IC, ISP-IC and POST-EISP-Miner significantly increase while that of pi ISP-IC gradually increase. In general, pi ISP-IC outperform i ISP-IC, ISP-IC, and POST-EISP-Miner for this dataset.

Fig. 6

Mining time of piISP-IC, iISP-IC, ISP-IC and POST-EISP-Miner for C6T5S4I4N1KD10K dataset with 15 random item constraints and A maxspan = 1; B maxspan = 2; C maxspan = 3; D maxspan = 4; E maxspan = 5; F threshold = 21%

Figure 7 performs the same for T10I4D100K dataset. We easy found that the runtimes of $i$ISP-IC and ISP-IC are nearly the same, POST-EISP-Miner is highest while the runtime of pi ISP-IC is much better than that of $i$ISP-IC, ISP-IC, and POST-EISP-Miner. POST-EISP-Miner cannot perform with minsup$=$ 4 and maxspan$=$ 5.

Fig. 7

Mining time of piISP-IC, iISP-IC, ISP-IC and POST-EISP-Miner for T10I4D100K dataset with 15 random item constraints and A maxspan $=$ 1; B maxspan $=$ 2; C maxspan $=$ 3; D maxspan $=$ 4; E maxspan $=$ 5; F threshold $=$ 4%

Figure 8 compares the runtime of pi ISP-IC, $i$ISP-IC, ISP-IC and POST-EISP-Miner for BMSWebView2 dataset with various settings. Figure 8A fixes maxspan$=$ 1, Fig. 8B fixes maxspan$=$ 2, Fig. 8C fixes maxspan$=$ 3, Fig. 8D fixes maxspan$=$ 4 and Fig. 8E fixes maxspan$=$ 5, pi ISP-IC is always the best algorithm for mining inter-sequence patterns with item constraints for BMSWebView2 dataset. Especially, with the smaller threshold, the time gaps between the runtime of pi ISP-IC and those of $i$ISP-IC, ISP-IC and POST-EISP-Miner are larger. In Fig. 8F, we fix threshold$=$ 1, and change maxspan from 1 to 5, the runtime of pi ISP-IC is less than those of $i$ISP-IC, ISP-IC, and POST-EISP-Miner. Therefore, pi ISP-IC outperform $i$ISP-IC, ISP-IC, and POST-EISP-Miner for this dataset. In short, through the above experiments, we can conclude that pi ISP-IC outperform $i$ISP-IC, ISP-IC, and POST-EISP-Miner for mining inter-sequence patterns with item constraints.

Fig. 8

Mining time of piISP-IC, iISP-IC, ISP-IC and POST-EISP-Miner for BMSWebView2 dataset with 15 random item constraints and A maxspan = 1; B maxspan = 2; C maxspan = 3; D maxspan = 4; E maxspan = 5; D threshold = 1%

5.2 Memory usage

Figure 9 reports the memory usage of pi ISP-IC, $i$ISP-IC, ISP-IC and POST-EISP-Miner for C6T5S4I4N1KD10K dataset with various settings. Figure 9A fixes maxspan$=$ 1, Fig. 9B fixes maxspan$=$ 2, Fig. 9C fixes maxspan$=$ 3, Fig. 9D fixes maxspan$=$ 4 and Fig. 9E fixes maxspan$=$ 5, we found that the memory usage of POST-EISP-Miner is the largest. However, the gap between the memory usage of pi ISP-IC and those of $i$ISP-IC and ISP-IC are insignificant for C6T5S4I4N1KD10K dataset. Then, Fig. 8F, which shows the memory usage of pi ISP-IC, $i$ISP-IC, ISP-IC and POST-EISP-Miner when we fix threshold$=$ 21 and change maxspan from 1 to 5, confirm that statement again. POST-EISP-Miner cannot perform with maxspan$=$5 and threshold$=$ 21, the memory value with maxspan$=$ 5 in Fig. 9F is an example.

Fig. 9

Memory usage of piISP-IC, iISP-IC, ISP-IC and POST-EISP-Miner for C6T5S4I4N1KD10K dataset with 15 random item constraints and A maxspan = 1; B maxspan = 2; C maxspan = 3; D maxspan = 4; E maxspan = 5; F threshold = 21%

Figures 10-11 reports the memory usage of pi ISP-IC, $i$ISP-IC, ISP-IC and POST-EISP-Miner for T10I4D100K and BMSWebView2. The results show that the memory usages of these algorithms are nearly the same. Summary, although the memory usage of pi ISP-IC is largest (compared to those of $i$ISP-IC, ISP-IC, and POST-EISP-Miner), the gap between the memory usage of pi ISP-IC and those of $i$ISP-IC, ISP-IC and POST-EISP-Miner are insignificant.

Fig. 10

Memory usage of piISP-IC, iISP-IC, ISP-IC and POST-EISP-Miner for T10I4D100K dataset with 15 random item constraints and A maxspan = 1; B maxspan = 2; C maxspan = 3; D maxspan = 4; E maxspan = 5; F threshold = 4%

Fig. 11

Memory usage of piISP-IC, iISP-IC, ISP-IC and POST-EISP-Miner for BMSWebView2 dataset with 15 random item constraints and A maxspan = 1; B maxspan = 2; C maxspan = 3; D maxspan = 4; E maxspan = 5; F threshold = 1%

6 Conclusions and future studies

This paper proposed three novel methods for mining inter-sequence patterns with item constraints. Firstly, the problem of mining inter-sequence patterns with item constraints was presented. Secondly, a theorem was developed to reduce mining time by fast determining whether an inter-sequence pattern satisfies item constraints. Based on this theorem, an efficient algorithm for mining inter-sequence patterns with constraints (ISP-IC algorithm) was proposed. Thirdly, a lemma was presented for improving the strategy of ISP-IC. Based on this lemma, the $i$ISP-IC algorithm was proposed. Fourthly, we presented a parallel version of $i$ISP-IC named pi ISP-IC to improve the performance. Finally, experiments were conducted to verify the proposed approaches. Experimental results show that the pi ISP-IC algorithm is better than the POST-EISP-Miner, ISP-IC and $i$ISP-IC algorithms.

This paper focused on item constraints. In the future, we will study mining inter-sequence patterns with both itemset and sequence constraints as well as the combination of many constraints and closed inter-sequence patterns with constraints (including item, itemset, and sequence constraints).