1 Introduction

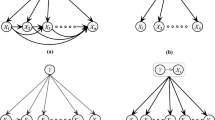
A Bayesian network (BN) is also called a belief network and is a directed acyclic graphical model that belongs to the family of probabilistic graphical models. BN can present probabilistic relations among variables [8] and can present causal structures induced from datasets of regular attributes, in practice. However, learning the optimal BN structure from an arbitrary BN search space of discrete variables is considered non-deterministic polynomial time-hard (NP-hard) [2]. In [2], the author suggested that research should be directed away from the search for a general, exactly presented algorithm and toward the design of efficient special-case, average-case, and approximate-case algorithms. Many researchers have followed these suggestions and have proposed some relatively reasonable algorithms that restrict the complexity of the structures of BNs, such as naïve Bayes tree (NBTree) [11], tree-augmented naïve Bayes (TAN) [6], hidden naïve Bayes (HNB) [10], and and averaged one-dependence estimators (AODE) [19]. Examples of the networks naïve Bayes, AODE, TAN, and HNB are shown in Fig. 1a, b, c, and d respectively. We will discuss the naïve Bayes learning algorithm at the beginning of this paper because it is efficient and has the simplest structure of a BN among the aforementioned learning algorithms based on BNs.

Fig. 1
figure 1

Bayesian net structures of naïve Bayes, AODE, TAN, and HNB

Full size image

A naïve Bayes learner is a supervised learning method based on the Bayes rule. It runs on labeled training examples and is driven by the strong assumption that all attributes in the training examples are independent of each other given the class: the so-called naïve Bayes conditional independence assumption. Naïve Bayes has demonstrated high performance and rapid classification speed in huge training instances with many attributes [14]. These benefits essentially originate from the naïve Bayes conditional independence assumption. In practice, classification accuracy could be affected by the conditional independence assumption, which is often violated in real-world applications. However, because of the attractive advantages of efficiency and simplicity, both originating from the class conditional independence assumption of attributes, many researchers have proposed effective methods to further improve the performance of naïve Bayes learners by weakening this strict attribute independence assumption without neglecting its advantages. From the perspective of BN, the methods used to weaken the attribute independence assumption for the naïve Bayes learner would prefer to learn a BN’s structure from a constrained BN search space rather than arbitrary BN search space.

Webb et al. [19] proposed a novel method called AODE. In AODE, the conditional probability of test instances given the class is tuned by a normal attribute (a super-parent of any other attribute). AODE has demonstrated significant improvement compared with naïve Bayes learners in two respects: The AODE classifier aggregates a set of weak classifiers and AODE relatively relaxes the independence assumption without learning the structure of a BN.

However, AODE does not consider the relationships between a super-parent node attribute, which is also called a one-dependence attribute in AODE, and other normal attributes. It is plausible that, for any pair of features A i and A j , the higher the dependence on each other, the more confidence there is in the probabilistic estimated values of P(A j |A i ) and P(A i |A j ). Hence, we propose weighted AODE (WAODE), which is an algorithm based on the AODE framework, and we expect it to improve the performance of AODE by considering the relation among features in real-world datasets. We expect that, based on our work, human experts can use their expertise to further tune the parameters that reflect the relationship among the pairs of attributes.

Zheng and Webb [21] proposed an improved AODE method called lazy elimination (LE) for AODE. LE is an interesting method that is simple, efficient, and can be applied to any Bayesian classifier. LE defines the specialization-generalization relationship between pairwise attributes and indicates that deleting all generalization attribute-values before training a classifier can relatively improve the performance of a Bayesian classifier. Zheng and Webb [21] proved that there is no information loss in the prediction after deleting the generalization attribute-values in the dataset. However, storing the generalization attribute-values (useless data) in the training datasets can cause prediction bias under the independence assumption because the independence assumption has the bias per se, which is violated in real-world problems.

Jiang and Zhang [9] proposed an algorithm called weightily averaged one-dependence estimators, which assigns weights to super-parent nodes according to the relationship between the super-parent node and class. The method proposed by [9] is different from our proposed method, WAODE, because the weight values in our paper indicate the relationships between the super-parent node and other normal attributes given the class.

Jiang et al. [10] proposed an algorithm called HNB, which is a structure extending method of naïve Bayes. In HNB, each feature in a dataset has one hidden parent that is a mixture of the weighted influences from all other attributes. HNB and our WAODE apply the same attribute weighting method to measure the relationship between a pair of attributes using the conditional mutual information metric. Additionally, both HNB and WAODE avoid direct learning of the BN structure. However, WAODE is different from HNB in two respects: first, in HNB, the probability estimator of an attribute relies on the hidden parent of that attribute, but in WAODE, the probability estimator of an attribute depends on the training data sampling. In fact, this difference originates from the BN’s structural difference between HNB and AODE. The second difference relates to the attribute weighing form: the weight is considered as a multiplier in the HNB learner, but as an exponent in WAODE.

Zaidi et al. [20] proposed a weighted naive Bayes algorithm called Weighting attributes to Alleviate Naive Bayes’ Independence Assumption (WANBIA), that optimizes weights to minimize either the negative conditional log likelihood or the mean squared error objective functions. WAODE and its variants use simple functions of conditional mutual information as weight multipliers.

There are two contributions of this paper:

  • We conduct a brief survey on improving AODE.

  • We propose a novel attribute weighting for AODE called WAODE. WAODE not only retains the advantages of AODE, but also considers the dependence among the attributes using conditional mutual information measure methods.

Our experimental results show that the WAODE learning algorithm provides an effective improvement when compared with standard AODE.

The remainder of this paper is organized as follows: we briefly discuss AODE and attribute weighting forms in Section 2. In Section 3, we explain WAODE. In Section 4, we describe the experiments and results in detail. Finally, we draw the conclusions of our study and describe future work in Section 5.

2 AODE and attribute weighting forms

In this section, we provide a brief overview of AODE. AODE is a supervised learning algorithm based on a naïve Bayes learner, which extends the learner by a limited relaxation of the conditional independence assumption. Averaged one-attribute-dependence is the main feature of AODE. Because AODE is extended from a naïve Bayes learner, we briefly introduce the naïve Bayes learner first. At the final part of this section, we discuss the forms of attribute weighting.

2.1 Naïve Bayes learner

In supervised learning, consider a training dataset \(\mathcal {D}=\left \{ \mathbf {x^{(1)}},\dots ,\mathbf {x^{(n)}} \right \}\) composed of n instances, where each instance \(\mathbf {x}=\left <x_{1},\dots ,x_{m}\right >\in \mathcal {D}\) (m-dimensional vector) is labeled with a class label y ∈ Y. For the posterior probability of y given by x,

$$ p(y|\mathbf{x})=\frac{p(\mathbf{x}|y)\cdot p(y)}{p(\mathbf{x})} \propto p(\mathbf{x}|y). $$
(1)

Note that it is usually difficult to estimate the likelihood p(x|y) directly from \(\mathcal {D}\) because there are insufficient data, in practice. Naïve Bayes uses the attribute independence assumption to alleviate this problem. From the assumption, p(x|y) can be estimated as follows:

$$ p(\mathbf{x}|y) = p(x_{1},\dots,x_{m}|y) \approx \prod\limits^{m}_{i=1}p(x_{i}|y). $$
(2)

Then, the classifier of naïve Bayes is

$$ \underset{y\in Y}{\arg\max} \hat{p}(y)\prod\limits^{m}_{i=1} \hat{p}(x_{i}|y). $$
(3)

2.2 AODE

AODE structurally extends naïve Bayes by applying an averaged one-attribute-dependence method. The details of AODE are described as follows:

Given a test instance x = <x 1,…,x i ,…,x m >, we have p(y,x) = p(y|x)p(x). Then

$$ p(y|\mathbf{x}) = \frac {p(y,\mathbf{x})}{p(\mathbf x)} = \frac {p(y)p(\mathbf x|y)}{p(\mathbf x)}. $$
(4)

Assuming that there exists a training dataset with sufficient data, a test instance x should be included in the training dataset. Because the attribute x i is in x,

$$ p(y,\mathbf{x}) = p(\mathbf{x}, x_{i}, y) = p(y, x_{i})p(\mathbf{x}|y, x_{i}). $$
(5)

By combining (4) and (5),

$$ p(y|\mathbf{x}) = \frac {p(y,x_{i})p(\mathbf{x}|y,x_{i})}{p(\mathbf{x})}. $$
(6)

Based on (6) and the attribute independence assumption, it follows that

$$ p(\mathbf{x}|y,x_{i}) \approx \prod\limits^{m}_{j=1}p(x_{j}|y, x_{i}), $$
(7)

where both x j and x i are the attribute-values in the test sample x. Hence, the classifier of AODE can be described as follows:

$$ \underset{y \in Y}{\arg\max} \left( \sum\limits_{i:1\leq i \leq m \wedge F(x_{i})\geq g} \hat {p}(y, x_{i}) \prod\limits^{m}_{j=1} \hat {p}(x_{j}|y, x_{i})\right), $$
(8)

where F(x i ) is the count of attribute-value x i in the training set and g is the minimum sample size for meaningful statistical inference. Following [19], we set g to 30, which is one of the widely used values.

2.3 Attribute weighting forms

Because AODE is an extended learning algorithm based on naïve Bayes, we discuss our forms of attribute weighting based on naïve Bayes as preliminary background information.

Essentially, there are several formulations of naïve Bayes attribute weighting schemes. First, the weight for each attribute is defined as follows:

$$ \hat{p}(c|\mathbf{x})=\hat{p}(c)\prod\limits^{m}_{i=1} \hat{p}(x_{i}|c)^{w_{i}}. $$
(9)

If the weight depends on an attribute and class, the corresponding formula is as follows:

$$ \hat{p}(c|\mathbf{x})=\hat{p}(c)\prod\limits^{m}_{i=1} \hat{p}(x_{i}|c)^{w_{ci}}. $$
(10)

The following formula is used for the case in which the weight depends on an attribute value:

$$ \hat{p}(c|\mathbf{x})=\hat{p}(c)\prod\limits^{m}_{i=1} \hat{p}(x_{i}|c)^{w_{i,x_{i}}}. $$
(11)

Referring back to (9), when ∀w i = w, the formula is as follows:

$$ \hat{p}(c|\mathbf{x})=\hat{p}(c)\prod\limits^{m}_{i=1} \hat{p}(x_{i}|c)^{w}. $$
(12)

Note that, in these weighting forms, if each weight is one, then each weighting form is simply naïve Bayes. For example, (12) is considered to be an extended version of the naïve Bayes classifier given that it will be the naïve Bayes classifier if each attribute A i has the same weight ∀w i = w = 1. Similarly, in (8), we can regard p(x j |y,x i ) of the AODE classifier to be analogous to p(x i |y) of naïve Bayes.

3 WAODE

In this section, we introduce our four forms of attribute weighting for AODE and then discuss the corresponding attribute-weight generating methods that can be used in AODE with our four proposed forms. Finally, we discuss our proposed WAODE algorithm.

3.1 Attribute weighting forms for AODE

In (8), we observe that the AODE learner does not consider the relation between attribute-j and attribute-i, which is also called the one-dependence attribute in AODE. Essentially, we propose using a set of parameters w i j to indicate the relatively suitable relation values between the pairs of attributes i and j under a particular attribute weighting form in AODE.

Thus, we propose four forms of attribute weighting for AODE:

$$ p(y,x_{i})\prod\limits^{m}_{j=1} \left( p(x_{j}|y,x_{i})\cdot w_{ij} \right), $$
(13)
$$ p(y,x_{i})\prod\limits^{m}_{j=1} p(x_{j}|y,x_{i})^{w_{ij}}, $$
(14)
$$ p(y,x_{i})\prod\limits^{m}_{j=1} p(x_{j}|y,x_{i})^{\sqrt {w_{ij}}}, $$
(15)

and

$$ p(y,x_{i})\prod\limits^{m}_{j=1} \left( p(x_{j}|y,x_{i}) \cdot \sqrt {w_{ij}} \right). $$
(16)

Note that each form of attribute weighting for AODE has a corresponding WAODE classifier shown as follows:

$$ \underset{y \in Y}{\arg\max} \left( \sum\limits_{i:1\leq i \leq m \wedge F(x_{i})\geq g} \hat {p}(y, x_{i}) \prod\limits^{m}_{j=1} \hat {p}(x_{j}|y, x_{i}) \cdot w_{ij} \right), $$
(17)
$$ \underset{y \in Y}{\arg\max} \left( \sum\limits_{i:1\leq i \leq m \wedge F(x_{i})\geq g} \hat {p}(y, x_{i}) \prod\limits^{m}_{j=1} \hat {p}(x_{j}|y, x_{i})^{w_{ij}} \right), $$
(18)
$$ \underset{y \in Y}{\arg\max} \left( \sum\limits_{i:1\leq i \leq m \wedge F(x_{i})\geq g} \hat {p}(y, x_{i}) \prod\limits^{m}_{j=1} \hat {p}(x_{j}|y, x_{i})^{\sqrt{w_{ij}}} \right), $$
(19)

and

$$ \underset{y \in Y}{\arg\max} \left( \sum\limits_{i:1\leq i \leq m \wedge F(x_{i})\geq g} \hat {p}(y, x_{i}) \!\prod\limits^{m}_{j=1} \hat\! {p}(x_{j}|y, x_{i}) \cdot \sqrt{w_{ij}} \right), $$
(20)

where w i j is the weight value that describes the relation between attribute-i and attribute-j. The details of w i j are discussed in Section 3.2. The definitions of the remaining parameters in (13)–(20) were discussed in Section 2.

3.2 WAODE

Some methods to generate attribute weights have been used in attribute weighting for the naïve Bayes classifier. Lee et al. [13] generated feature weights using the Kullback–Leibler measurement. Orhan et al. [16] used the least squares approach to weight attributes in naïve Bayes. Zaidi et al. [20] proposed a weighted naïve Bayes algorithm called weighting attributes to alleviate the naïve independence assumption (WANBIA), which selects weights to maximize the conditional log-likelihood or minimize the mean squared error for the corresponding objective functions.

For AODE, we expect that the attribute weight in AODE should indicate the relation between a pair of attributes: w i j should be assigned with a higher value when attribute-i, as a dependence attribute to attribute-j, provides more support to attribute-j and vice versa. Figure 2 shows the weighting form that our WAODE algorithm uses.

Fig. 2
figure 2

The weighting model and structure of WAODE: Y is the class attribute and w i j is a weight value of the pair of attributes A i and A j

Full size image

The conditional mutual information metric is used to generate this type of attribute weight. In our WAODE algorithm, weight w i j , which is the weight value of the i th attribute given the j th attribute, is formulated as follows:

$$ w_{ij} = \frac {I_{P}(A_{i};A_{j}|Y)}{{\sum}^{m}_{i=1}{\sum}^{m}_{j=2,j>i} I_{P}(A_{i};A_{j}|Y)} \cdot m, $$
(21)

where m is the number of attributes and I P (A i ;A j |Y) is the conditional mutual information among attribute-i and attribute-j given class Y. I P (A i ;A j |Y) is shown as follows:

$$ I_{P}(A_{i};A_{j}|Y) = \sum\limits_{i,j,y} p(x_{i},x_{j},y) \log {\frac {p(x_{i},x_{j}|y)}{p(x_{i}|y)p(x_{j}|y)}}, $$
(22)

where x i and x j are the attribute-values that correspond to the i th attribute and j th attribute, respectively. Note that w i j = w j i because I P (A i ;A j |Y) = I P (A j ;A i |Y). Furthermore, the likelihood in AODE, p(x j |y,x i ), equals one when i = j.

figure c

Hence, we only need to calculate w i j , such that i = 1…m and j > i. For example, consider a simple dataset with three attributes and (23) shows the matrix of attribute weights. In this case, we only need to calculate the upper (or lower) triangular part with the exception of the diagonal elements of the attribute matrix W. We choose the part of W in this paper, which is shown in (23).

Now, we propose WAODE, whose attribute weights are generated by (21). The classifier of WAODE is shown as follows:

$$\begin{array}{@{}rcl@{}} C_{WAODE}(\mathbf{t})&=& \underset{y \in Y}{\arg\max} \left(\sum\limits_{i:1\leq i \leq m \wedge F(x_{i})\geq g} \hat {p}(y, x_{i})\right.\\ &&\qquad\qquad\left.\prod\limits^{m}_{j=1} \left(\hat {p}(x_{j}|y, x_{i}) \cdot w_{ij} \right) \right). \end{array}$$
(24)

The learning algorithm of WAODE is shown in Fig. 3.

Fig. 3
figure 3

Weighted averaged one-dependence estimators (WAODE) algorithm

Full size image

According to (18)–(20), we obtain the following classifiers, C W A O D E1, C W A O D E2, and C W A O D E3, respectively, which are shown as follows:

$$\begin{array}{@{}rcl@{}} C_{WAODE1}(\mathbf{t})&=& \underset{y \in Y}{\arg\max} \left( \sum\limits_{i:1\leq i \leq m \wedge F(x_{i})\geq g} \hat {p}(y, x_{i})\right.\\ &&\qquad\qquad\left.\prod\limits^{m}_{j=1} \hat {p}(x_{j}|y, x_{i})^{w_{ij}} \right), \end{array} $$
(25)
$$\begin{array}{@{}rcl@{}} C_{WAODE2}(\mathbf{t})&=& \underset{y \in Y}{\arg\max} \left( \sum\limits_{i:1\leq i \leq m \wedge F(x_{i})\geq g} \hat {p}(y, x_{i})\right.\\ &&\qquad\qquad\left.\prod\limits^{m}_{j=1} \hat {p}(x_{j}|y, x_{i})^{\sqrt{w_{ij}}} \right), \end{array} $$
(26)

and

$$\begin{array}{@{}rcl@{}} C_{WAODE3}(\mathbf{t})&=& \underset{y \in Y}{\arg\max} \left( \sum\limits_{i:1\leq i \leq m \wedge F(x_{i})\geq g} \hat {p}(y, x_{i})\right.\\ &&\qquad\qquad\left.\prod\limits^{m}_{j=1} \hat {p}(x_{j}|y, x_{i}) \cdot \sqrt{w_{ij}} \right). \end{array} $$
(27)

During the training time, WAODE requires two cardinal time-consuming steps: first, to estimate p(y), p(x i ,y), and p(x i ,x j ,y), it requires time complexity O(t n 2). Additionally, compared with AODE, WAODE needs more time to calculate weights for all pairs of attributes, which requires time complexity O(k n 2 v 2). The classification of a single example requires the calculation of (24) and is of time complexity O(k n 2). Table 1 displays the time complexity of WAODE and the other algorithms discussed.

Table 1 Computational complexity, where k is the number of classes, n is the number of attributes, v is the average number of values for an attribute, and t is the number of training examples
Full size table

4 Evaluation

We conducted experiments on 25 datasets from the University of California, Irvine (UCI) Machine Learning Repository [1] to compare the performance of WAODE with that of naïve Bayes, AODE, NBTree, HNB, TAN, WANBIA CLL, and the variations of WAODE: WAODE1, WAODE2, and WAODE3. The UCI benchmark datasets that we used are shown in Table 2. We discretized all numeric attributes to each dataset.

Table 2 Description of datasets used in the experiments
Full size table

In the implementation of our algorithm, all the estimated probabilities, including \(\hat p(y)\), \(\hat p(x_{i},y)\), and \(\hat p(x_{i},x_{j},y)\) , were filtered using Laplacian smoothing estimations because of the zero count of the probabilistic calculation. The details are as follows:

$$ \hat p(y)=\frac{F(y)+1}{n+c(Y)}, $$
(28)
$$ \hat p(x_{i},y)=\frac{F(x_{i},y)+1}{n_{i}+c(attri\_i)\times c(Y)}, $$
(29)
$$ \hat p(x_{i},x_{j},y)=\frac{F(x_{i},x_{j},y)+1}{n_{ij}+c(attri\_i)\times c(attri\_j) \times c(Y)}, $$
(30)

where n is the number of training examples for which the class value is known; n i is the number of training examples for which both attribute i and the class are known; n i j is the number of training examples for which all the classes, and attributes i and j are known; c(∙) is the cardinality value of ∙; and F(∙) is the frequency of ∙.

We conducted experiments on the proposed algorithms, standard naïve Bayes, AODE [19], NBTree [11], HNB [10], and TAN [6]. To compare the performance of the algorithms, we used a t-test with 10-fold cross-validation. We applied all algorithms to the same training datasets and test datasets. We directly copied the experimental results of WANBIA CLL from [20].

Note that there are missing results for some datasets for HNB because the datasets have missing values. Additionally, there are missing results for WANBIA CLL that are not in [20].

Table 3 shows the accuracy results of WAODE, variations of WAODE, and previous developed algorithms on 25 UCI benchmark datasets. The average accuracies and 95 % confidence interval on all datasets are summarized at the bottom of the table. Conditional mutual information was used for WAODE, WAODE1, WAODE2, WAODE3, and HNB. Bayesian information criteria (BIC) were used for TAN. Conditional log-likelihood was used for WANBIA CLL. Some results are missing for the HNB algorithm because HNB cannot effectively manage datasets with missing values. Instead of using traditional methods to fill in the missing values or considering each missing value as a new attribute value, we simply omitted HNB from the experiments of datasets with missing values for a fair comparison. The results of dataset “breast-cancer,” “heart-c,” “heart-statlog,” “primary-tumor,” and “waveform-5000” are missing for WANBIA CLL because we did not locate the results in the paper. For a fair comparison, we omitted the results of the five datasets mentioned above for WANBIA CLL.

Table 3 Experimental results in terms of classifier accuracies; accuracies are estimated using 10-fold cross-validation with a 95 % confidence interval
Full size table

In Table 3, we observe that the classification performance of WAODE is better than all the other algorithms regarding the mean of the accuracy. Both WAODE1 and WAODE2, in which the weights are the exponential in the classifier, demonstrate worse results when compared with the other algorithms. WAODE3, which is same with WAODE, the weight as a multiplicator in its classifier, demonstrates relatively better performance than WAODE1 and WAODE2.

Win(w)/tie(t)/lose(l) are summarized in Table 4. We observe that WAODE provides comparable and sometimes better performance than naïve Bayes with a win/tie/lose record of 13/4/8. WAODE only demonstrates slightly better performance, with a win/tie/lose record of 8/10/7 when compared with AODE, and 11/0/9, when compared with WANBIA CLL.

Table 4 Win/tie/lose results of standard naïve Bayes, AODE, NBTree, HNB, TAN, and WANBIA CLL
Full size table

Despite the missing results for HNB and WANBIA CLL, WAODE did not outperform them for several datasets. We checked the results and found that the training accuracy of WAODE was usually higher than that of HNB. This implies that over-fitting degraded the performance of WAODE. However, WAODE can be used more broadly than HNB because WAODE can manage missing values more properly than HNB. Additionally, because we directly copied the experimental results of WANBIA CLL from [20], our comparison in this paper may not be fair and accurate.

Compared with NBTree and TAN, WAODE exhibits comparable and sometimes better performance, with win/tie/lose records of 13/2/9 and 16/0/9, respectively.

For the detailed analysis, we have performed bias-variance decomposition [12, 18] results to compare the performance of the classifiers with varying amount of data. Following [12], we calculated bias 2 and variance using 2-fold cross-validation and listed the results in Tables 5 and 6 respectively.

Table 5 Experimental results in terms of classifiers’ bias 2
Full size table
Table 6 Experimental results in terms of classifiers’ variance
Full size table

Bias 2 shows the quadratic loss which is calculated by squared difference between the average of actual output and the average of predicted output. Variance is a non-negative value that reflects the variability to measure how much the learner is sensitive to changes in the training set. Variance is zero if the learner makes consistent prediction regardless of the training set. The results of datasets “hepatitis”, “labor” and “lymph” are not included because they have too few instances (less than 200 instances) for statistically significant bias-variance decomposition.

It can be seen that NBTree shows the least bias and naïve Bayes shows the smallest variance among the learning algorithms. This indicates that NBTree might exhibit relatively low error for large data and naïve Bayes might produce relatively low error for small data. Note that we do not include the bias and variance results of WANBIA CLL from [20] because their paper has different experimental settings and datasets. WAODE(MI) algorithm and its variants do not show remarkable superiority or inferiority compared with other algorithms in terms of bias and variance. In Table 8, we will discuss these results in more detail with appropriate statistical tests.

The receiver operating characteristic (ROC) curve [5] is an effective tool to illustrate the behavior of binary classifiers. The ROC curve is widely used in binary classification because it does not degrade itself on imbalanced datasets. The area under the ROC curve (AUC) reflects the probability that the classifier ranks a random positive instance higher than a random negative instance. AUC can be formulated as a Gini index minus one divided by two [7]. AUC is usually an effective measure but is not always a more valued measure than accuracy because of several drawbacks [7, 15]. Despite those drawbacks, the ROC curve and its AUC are still widely used for measuring classifiers’ performance.

One main drawback of the ROC curve for measuring classifiers’ performance is that it is usually effective for binary classification. Because most benchmark datasets we have tested are multiclass datasets, it is difficult to measure performance with AUC for multiclass classifiers. In Table 7, we list the weighted averages of the AUCs of WAODE and the remaining algorithms. Because the ROC curve and AUC can be calculated for binary classification, we followed a one-vs-rest approach for the AUC calculations.

Table 7 Experimental results in terms of the weighted average of AUC: average AUCs are estimated using 10-fold cross-validation with a 95 % confidence interval
Full size table

From the results of Table 7, it can be seen that the overall results are somewhat mixed. WAODE(MI) shows much slightly lower or similar performance than AODE within the confidence interval. Again HNB shows slightly higher performance than AODE and WAODE(MI). As aforementioned, it is because over-fitting of WAODE and its variants reflected from its high training accuracy. Overall, we can see that AUC is generally too high for most classification results to effectively discriminate the classifiers’ performance, which complies the arguments of [7, 15].

For the statistical comparison of the classifiers, we employ binomial sign test and compare WAODE(MI) with other algorithms in Table 8. Following [19], we have calculated one-tailed p value for Naïve Bayes, and for other algorithms, we have reported two-tailed p values. Overall, WAODE(MI) shows higher performance than naïve Bayes. Compared with AODE, WAODE(MI) shows comparable performance with statistically approvable intervals. WAODE(MI) outperforms NBTree and TAN in accuracy, variance and AUC, but WAODE(MI) exhibits that it has high bias compared with them. As we noted before, overall, HNB shows higher performance than WAODE(MI). However, HNB does not always outperform WAODE(MI) and, considering the results with HNB in Table 8, reducing the bias error and avoiding over-fitting using proper regularization might lead WAODE(MI) to a promising direction.

Table 8 Win/Tie/Loss records of WAODE(MI) and other algorithms with binomial sign test
Full size table

5 Conclusion

In this paper, we proposed a novel Bayesian model called WAODE. Using our method, we considered the relationships between the super-parent attribute and other attributes. We conducted a systematic experiment to measure the classification accuracies of our WAODE algorithm, naïve Bayes, AODE, NBTree, HNB, TAN, WANBIA CLL, and three variations of WAODE (WAODE1, WAODE2, and WAODE3) on 25 UCI benchmark datasets. The experimental results showed that WAODE exhibited higher performance when compared with naïve Bayes, AODE, and the other algorithms. We observed that, in WAODE, the design of the weight was the core issue. The quality of the weight dominated the classification performance of WAODE. We used the conditional mutual information metric to generate weights in WAODE.

In our future work, we will explore more effective methods to estimate weights from data to improve our WAODE performance. Furthermore, note that we currently consider the relationship between the parent node and child node only to generate weights. It will be interesting if we may add other factors in generating weights. For example, a hybrid weighting scheme may possibly enhance the relationship between the child nodes. The experimental results indicate that WAODE has high bias value compared with NBTree and TAN. Finding an optimal trade-off point between bias and variance will be an essential problem of WAODE. Additionally, we will further compare the performance of our algorithms with ensemble learning methods [3, 4, 17].