Feature weighting and SVM parameters optimization based on genetic algorithms for classification problems

Abstract

Support Vector Machines (SVMs) are widely known as an efficient supervised learning model for classification problems. However, the success of an SVM classifier depends on the perfect choice of its parameters as well as the structure of the data. Thus, the aim of this research is to simultaneously optimize the parameters and feature weighting in order to increase the strength of SVMs. We propose a novel hybrid model, the combination of genetic algorithms (GAs) and SVMs, for feature weighting and parameter optimization to solve classification problems efficiently. We call it as the GA-SVM model. Our GA is designed with a special direction-based crossover operator. Experiments were conducted on several real-world datasets using the proposed model and Grid Search, a traditional method of searching optimal parameters. The results show that the GA-SVM model achieves significant improvement in the performance of classification on all the datasets in comparison with Grid Search. In terms of accuracy, out method is competitive with some state-of-the-art techniques for feature selection and feature weighting.

1 Introduction

The accuracy of a classifier depends on its parameters and the properties of the dataset. In non-separable cases, we can use kernel functions to map the data into higher dimensional spaces with the expectation that the data will be more easily separated or better structured. However, it is not a good choice due to the following reasons: first, it is difficult to find the most appropriate kernel function for a specific dataset. The choice of a kernel depends on the distribution of the data. For instance, a polynomial kernel is suitable for the data according to the multinomial distribution. Radial basis functions are used to separate data by hyper-spheres. In contrast, a linear kernel only allows us to select classifiers defined by hyperplanes. Second, the dimension of the new space can be very large in practice. Consequently, the computational time and required memory become very costly.

Thus, researchers try to explore the properties of datasets instead of mapping them into highly dimensional space. Two of the most efficient approaches are feature selection and feature weighting. Feature selection algorithms focus on selecting the best subset of the input feature set to reduce computational time and improve accuracy [1]. In feature weighting strategies, highly important features are emphasized and less informative ones are ignored [2]. Feature selection algorithms perform best when the features used to describe instances are either highly correlated with the class label or completely irrelevant [3]. Feature weighting is more appropriate for problems where the features vary in their relevance.

SVMs are widely applied for classification problems mainly due to its high accuracy and ability to deal with high-dimensional data. SVMs showed state-of-the-art performance in real-world applications such as text categorization, hand-written character recognition, image classification, biosequences analysis and so on [4–7]. However, like most machine learning algorithms, the classification accuracy depends on not only its settings but also the properties of the data. When using an SVM, two problems are confronted: how to rank the importance of features for input data, and how to set the best kernel parameters. Such problems have to be solved simultaneously because weighting features influences the appropriate kernel parameters and vice versa [8]. To design an SVM classifier, one must choose a kernel function, set the kernel parameters and determine a soft margin constant C (the penalty factor for miss-classified points). The Grid algorithm is an alternative to finding the best C and γ when using the RBF kernel function. However, this method is time-consuming and may not perform well [9, 10]. Moreover, the Grid algorithm cannot carry out the feature weighting task.

Genetic algorithms (GAs) are known as powerful tools for solving large-scale nonlinear optimization problems [11]. GAs find the optimal solution in parallel on multi-directions by maintaining a population of potential solutions from the search space. Unlike traditional multi-point searching algorithms, GAs can easily escape from local optima due to information exchange between solutions based on principles of natural evolution. GAs have been increasingly applied in conjunction with other techniques to tackle classification problems. Some researchers proposed GA-based approaches to selecting an optimal set of features, that is used to build the classifier models such as decision tree (DT), naive bayes (NB), k-nearest neighbor (k-NN) and SVMs [8, 12–14]. The other hybrid GA-SVM model was developed to generate both the optimal subset and the SVM parameters at the same time [1, 15]. Silva applied both single and multi-objective GA approaches to build sparse least square support vector machines (LSSVM) classifiers [16]. Wu used GA with real representation to optimize the parameters of SVM with the aim of predicting bankruptcy [17]. However, these papers only focused on feature selection and parameter optimization. In our research, we take advantages of GAs to optimize feature weighting and parameter setting simultaneously with the aim of increasing the robustness of SVM classifiers.

The main contribution of this paper is proposing a new method for finding an optimal set of feature weights and the classifier configuration using GAs with a special direction-based crossover operator. In feature weighting, finding optimal feature weights in a huge search space is a challenging task. In the paper, we designed a combination model of an efficient classifier and a powerful search strategy, in which the SVM classifier is used to guide the GA to the optimal solution. Unlike statistical methods, the GA-SVM model needs no information about the weights of features; it receives the feedback of the SVM classifier to determine the searching directions. The experiments were conducted with the RBF kernel. However, due to flexible design of GA, the proposed model can adapt to other kernel parameters as well as classifiers such as kNN and naive Bayes.

The remainder of the paper is organized as follows: a brief introduction to the SVMs is given in Section 3. Section 4 describes basic GA concepts. Section 5 describes the technique used to combine GA-SVM for feature weighting and parameter optimization. Section 6 discusses the experimental results from using the proposed method to classify several real-world datasets. Finally, general conclusions are given in Section 7.

2 Related work

Various algorithms have been proposed in the literature of feature weighting. These algorithms can be divided into two groups: one which searches a set of weights through an iterative algorithm and uses the performance of the classifier as feedback to select a new set of weights [12, 18, 19]; the other computes the weights using the pre-existing bias model, e.g. conditional probabilities, class projection, and mutual information [20–22].

For the iterative approaches, Wu employed an evolutionary computation based method, namely Artificial Immune System (AIS), to find optimal attribute weight values automatically for weighted NB classification (AISWNB) [23]. The performance of the proposed method was validated on 36 UCI datasets and six image classification datasets from Corel Image repository. The experimental results demonstrate that the AISWNB method can significantly outperform its peers in classification accuracy, class probability estimation, and class ranking performance.

Lee proposed a new paradigm of weighting method, which assigns a different weight to values of each feature [24]. The method is called value weighting and implemented in the context of naive Bayes using wrapper method (VWNB). They reported that the VWNB method improves the performance of naive Bayes significantly and can be competitive with other state-of-the-art supervised algorithms.

Regarding the pre-existing bias model, Sáez focused on imputation methods to improve k-NN classification [25]. Under the imputation methods, the weight for each feature is estimated based on the rest of data and the Kolmogorov–Smirnov nonparametric statistical test is utilized to measure the changes between the original and imputed distribution of values. Three used imputation methods are k-NN Imputation (kNNI) [26], using Support Vector Machine to fill in missing values (SVMI) [27], Concept Most Common (CMC) [28]. They showed that their method was an effective way of improving the performance of the Nearest Neighbor classifier.

Jiang used a deep feature weighting (DFW) approach, which estimates the conditional probabilities of naive Bayes by computing feature weighted frequencies from training data [29]. Firstly, they applied the correlation-based feature selection (CFS) to select relevant features, and then defined weights of selected features and non-selected features as 2 and 1, respectively. These values are used to estimate the conditional probabilities of naive Bayes. The experiments on 36 UCI datasets show that their method rarely degrades the quality of the model compared to standard naive Bayes and, in many cases, improves it dramatically.

Xiang proposed a novel attribute weighting framework called Attribute Weighting with Smooth Kernel Density Estimation (AW-SKDE) [30]. In the AW-SKDE framework, the attributes weights are generated by calculating the mutual information between the features and the class label. They made an assumption that if one attribute shares more mutual information with the class label, that attribute will provide more classification ability than other attributes, and should therefore be assigned a higher weight. The experimental results showed that the AW-SKDE algorithm achieves comparable and sometimes better performance than the classical naive Bayes as well as other algorithms using a relaxed conditional independence assumption. However, their algorithm suffers from over-fitting.

3 Introduction of support vector machines (SVMs)

This section will briefly describe an effective classification algorithm in supervised machine learning called Support Vector Machines (SVMs) [31]. Firstly, we introduce the algorithm for separable datasets, then present its general version designed for non-separable datasets, and finally provide a theoretical foundation for SVMs based on the notion of margin. We start with the description of binary (two-class) classification problems in the separable case.

3.1 The optimal hyperplane for separable data

Given a training set $S = {\{x_{i},y_{i}\}}^{m}_{i=1}$, with input vectors x _i ∈R ⁿ and target labels y _i ∈{−1,+1}, for the linearly separable case, the data points will be correctly classified by any hyperplanes w⋅x + b=0 satisfying

$$ y_{i}(x_{i} \cdot w + b) - 1 \ge 0 ,\ \forall i =1,.., m $$

(1)

Although many hyperplanes perfectly separate the training samples into two classes, SVMs find an optimal separating hyperplane with the maximum margin (distance to closest points) by solving the following optimization problem:

$$ \min\limits_{w,b}\frac{1}{2} {||w||}^{2} $$

(2)

subject to y _i (w⋅x _i + b)≥1,∀i∈[1,m]. This quadratic optimization problem can be solved by finding the saddle point of the Lagrange function:

$$ L\left( w,\ b,\ \alpha\right)=\ \frac{1}{2}{||w||}^{2}-\sum\limits^{m}_{i=1}{\alpha_{i}[y_{i}\left( w \cdot x_{i}+b\right)-1]} $$

(3)

where α _i denotes Lagrange variables, α _i ≥0 ∀ i=1,..m.

The Karush Kuhn -Tucker (KKT) conditions for a maximum of (3) are obtained by setting the gradient of the Lagrangian with respect to the primal variables w and b to zero and by writing the complementary conditions:

$$ {\nabla }_{w}L=w-\sum\limits^{m}_{i=1}{\alpha_{i}y_{i}x_{i}\ }=0\ \Rightarrow \ w=\sum\limits^{m}_{i=1}{\alpha_{i}y_{i}x_{i}\ } $$

(4)

$$ {\nabla }_{b}L=-\sum\limits^{m}_{i=1}{\alpha_{i}y_{i}\ }=0\ \Rightarrow \sum\limits^{m}_{i=1}{\alpha_{i}y_{i}\ }=0 $$

(5)

$$ {\forall i,\ \alpha}_{i}\left[y_{i}\left( w \cdot x_{i}+b\right)-1\right]=0\ \Rightarrow \alpha_{i}=0\ \vee\ y_{i}\left( w \cdot x_{i}+b\right)-1=0 $$

(6)

By (4), the weight vector w solution of the SVM problem is a linear combination of the training set vectors x ₁,...,x _m . According to complementary conditions (6), the value of w only depends on vectors x _i that correspond the α _i ≠0. Such vectors are called support vectors. They fully define the maximum-margin hyperplane or the SVM solution.

Substitute (4) and (5) into (3), the dual form Lagrangian L _D (α) of (2) is derived as follows:

$$ \underset{\alpha}{\max L_{D}(\alpha)}=\sum\limits^{m}_{i=1}{\alpha_{i}\ }-\frac{1}{2}\sum\limits^{m}_{i,j=1}{\alpha_{i}\alpha_{j}y_{i}y_{j}(x_{i} \cdot x_{j})\ } $$

(7)

subject to α _i ≥0 i=1,..,m and ${\sum }^{m}_{i=1}{\alpha _{i}y_{i}}=0$.

To find the optimal hyperplane, L _D (α) must be maximized with respect to non-negative α _i . The objective function is a standard quadratic optimization problem that can be solved by using several standard optimization methods. The solution α can be used directly to determine the parameters w ^∗ and b ^∗ of the optimal hyperplane returned by the SVM. Thus, we obtain an optimal decision hyperplane f(x) (8) and an indicator decision function s i g n[f(x)].

$$ f(x)=\sum\limits^{m}_{i=1}{\alpha^{*}_{i}y_{i}\ (x_{i} \cdot x)+b^{*}}=\sum\limits_{i\in SV}{\alpha^{*}_{i}y_{i}\ (x_{i} \cdot x)+b^{*}} $$

(8)

where b ^∗ is calculated based on rewriting condition (6) as follows:

$$ b^{*}=y_{i}-\ \sum\limits^{m}_{j=1}{\alpha_{j}y_{j}}(x_{j} \cdot x_{i}) $$

(9)

3.2 The optimal hyperplane for non-separable data

In most practical settings, data are often not linearly separable [31]. For any hyperplane w⋅x + b=0, there exists x _i such that

$$ y_{i}(x_{i} \cdot w + b) - 1 \ngeq 0 $$

(10)

In this case, an SVM selects a hyperplane that minimizes the training error. The constraints in Section 3.1 cannot all hold simultaneously, but the above concepts can be extended to the non-separable case. To get the formal setting of this problem, non-negative slack variables ξ _i are proposed such that:

$$ y_{i}(x_{i} \cdot w + b) \ge 1 - \xi_{i} ,\ \xi_{i } \geq 0 ,\ i =1,..,m $$

(11)

Here, a slack variable ξ _i measures the distance by which vector x _i violates the desired inequality, y _i (w⋅x _i + b)≥1. For a hyperplane w.x + b=0, a vector x _i with ξ _i >0 can be viewed as an outlier. An SVM finds the optimal hyperplane by minimizing the expression below:

$$ \min\limits_{w,b,}\frac{1}{2} {||w||}^{2}+\mathrm{C}\sum\limits^{m}_{i=1}{{\xi }_{i}} $$

(12)

subject to y _i (w⋅x _i + b)≥1−ξ _i ∧ξ _i ≥0, i∈[1,m].

Minimizing the expression (12) is an NP-hard problem. There are two conflicting objectives: seeking a hyperplane with larger margin and limiting the total amount of slack variables measured by ${\sum }^{m}_{i=1}{{\xi }_{i}}$. The parameter C≥0 is known as trade-off between two such objectives. Typically, C is determined via k-fold cross validation method.

The optimization model can be solved by maximizing the dual variables Lagrangian L _D (α) (13), which only differs from that of the separable case (7) by the constraints α _i ≤C:

$$ \underset{\alpha}{\max L_{D}(\alpha)}=\sum\limits^{m}_{i=1}{\alpha_{i}\ }-\frac{1}{2}\sum\limits^{m}_{i,j=1}{\alpha_{i}\alpha_{j}y_{i}y_{j}(x_{i} \cdot x_{j})\ }\ $$

(13)

subject to $0\ \le \alpha _{i}< C,\ i=1,..,m \wedge {\sum }^{m}_{i=1}{\alpha _{i}y_{i}}=0$.

Two parameters w and b of the optimal hyperplane can be determined directly via solution α similar to separable case (4) and (9). However, support vectors in non-separable case include outliers and vectors which lie on marginal hyperplanes.

3.3 Non-linear SVM

The main idea of creating non-linear kernel classifiers is mapping the data into a higher-dimensional feature space in the hope that in the higher-dimensional space the data could become more easily separated or better structured. This is performed by using a mapping function Φ and replacing the dot products in (13) by the kernel function (14):

$$ K(x_{i}, x_{j}) = ({\Phi}(x_{i}), {\Phi}(x_{j})) $$

(14)

$$ \underset{\alpha}{{\max L_{D}(\alpha)\ }}=\sum\limits^{m}_{i=1}{\alpha_{i}\ }-\frac{1}{2}\sum\limits^{m}_{i,j=1}{\alpha_{i}\alpha_{j}y_{i}y_{j}K(x_{i},x_{j})\ }\ $$

(15)

subject to $0\ \le \alpha _{i}<C,\ i=1,..,m \wedge {\sum }^{m}_{i=1}{\alpha _{i}y_{i}}=0$.

Some widely used kernel functions include polynomial, radial basis function (RBF) and sigmoid kernel, which are shown as functions (16), (17) and (18). Choosing the most appropriate kernel function and its parameters are completely based on the specific dataset. There are various methods to determine parameters in kernel functions. In this paper, we use the genetic algorithm to find the optimal values of parameters and weights of data attributes.

• Polynomial kernel:

  $$ K(x_{i},x_{j}) = (1+ x_{i} \cdot x_{j})^{d} $$

  (16)

• Radial basis function kernel (alternative form):

  $$ K(x_{i},x_{j}) = exp(-\gamma||x_{i} - x_{j}||^{2}) $$

  (17)

• Sigmoid kernel:

  $$ K(x_{i},x_{j}) = tanh(kx_{i} \cdot x_{j}-\delta) $$

  (18)

4 Genetic algorithms - GAs

Genetic algorithms have been used in science and engineering as adaptive algorithms for solving practical problems [32]. The exploitation of the principles of evolution as a heuristic method enables genetic algorithms to solve optimization problems effectively (with the acceptable solutions) without using the traditional conditions (continuity or differentiability of the objective function) as prerequisites.

One of the most important characteristics of GAs is the ability to work with a population of individuals, each representing a feasible solution to a given problem. The search is now performed in parallel on multi-points. However, this is not a simply multi-points searching algorithm because the points are interactive with each others based on principles of natural evolution [33]. The basic steps of GAs (Fig. 1) are described as follows [34]:

• Step 1: t=0 ; Initialize P(t)={x ₁,x ₂,...,x _n } , where n is the number of individuals.

• Step 2: Calculate the value of the objective functions for P(t).

• Step 3: Create a crossover pool M P = s e{P(t)} where se is selection operator.

• Step 4: Determine P ^′(t) = c r{M P}, with cr is the crossover operator.

• Step 5: Determine P ^″(t) = m u{P ^′(t)}, with mu is the mutation operator.

• Step 6: Calculate the value of the objective functions for P ^″(t)

• Step 7: Determine P(t+1) = P ^″(t) and set t = t+1

• Step 8: Return Step 3, if the stop condition is not satisfied.

Fig. 1

Basic steps of genetic algorithm

Solutions representation

This task plays a crucial role in designing genetic algorithms, deciding whether to apply the evolutionary operators. One of the traditional representations of GAs is the binary representation. In this way, a feasible solution to a problem is represented as a vector of bits called a chromosome. Each chromosome consists of many genes; a gene represents a parametric component of the solution. A different type of chromosome representation is using real numbers. With this representation, the evolution operators will perform directly on the real values(genes).

Selection

The goal of the selection stage is guiding the search towards better individuals and maintaining a high genotypic diversity in the population. The quality of each individual is evaluated by mean of the fitness function. This value is used to determine which individual will be selected for the next generation whereby the more greater quality the individual has the more chance it is chosen. Some commonly used selection methods include:

• Roulette wheel: Selecting individuals is based on probability (proportional to the value of the fitness function). Each is assigned a slice of a circular “roulette wheel”, the size of the slice being proportional to the individual’s fitness. The wheel is spun N times, where N is the number of individuals in the population. On each spin, the individual under the wheel’s marker is selected to be in the pool of parents for the next generation [32].

• Tournament selection: The selection process involves running several “tournaments” between two individuals chosen randomly from the population. The better individual (the winner) having the greater fitness value is selected for the next generation.

• Elitist selection: For this selection strategy, a limited number of individuals with the best fitness values are chosen for the next generation. Elitism avoids losing individuals with good genetics by crossover or mutation operators.

Crossover

Crossover operators are applied to generate new individuals from their parents. Crossover operators are inspired by the idea that offspring inherit the best characteristics from their parents. In terms of searching, crossover operators perform a search of the area around the solution represented by the parent individuals. There are some crossover techniques including single-point, two-point and uniform crossovers.

Mutation

Similar to crossover operators, mutation operators are also used to simulate mutation phenomena in biology. Mutations often generate new individuals different from their parents. In terms of searching, mutation operators aim to deploy the finding out of the local area. Figure 2 illustrates the genetic crossover and mutation operators.

Fig. 2

Illustration of the two-point crossover and mutation operators and their effects in the generation of the offspring

The evolutionary process is repeated until the stop criteria such as the pre-defined number of generations and an acceptable fitness value are satisfied [33, 35] (Fig. 1).

5 Hybrid model GA-SVM for feature weighting and parameter optimization

In this section, we present in detail how to combine GA and SVM for feature weighting and parameter optimization involving chromosome design, fitness function, and system architecture. Our implementation was carried out on C# language by extending LIBSVM, which is originally designed by Chang and Lin [36]. The source code is publicly available at http://www.mediafire.com/download/0movktlqv04c8qu/GA_SVM_Code.rar

5.1 Chromosome design

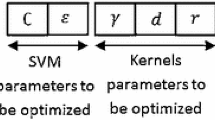
The proposed model searches kernel function parameters and the weights of features simultaneously. Hence, the chromosome must contain two such parts. In our experiments, we used the RBF kernel function for two reasons. Firstly, this kernel maps samples into a higher-dimensional space; hence, it can handle the case when the relation between class labels and attributes is nonlinear. The second reason is the number of hyperparameters, which influences the complexity of model selection. The RBF kernel only requires two parameters C and γ. Figure 3 shows the structure of a chromosome in this case.

Fig. 3

The structure of a chromosome for optimizing C, γ and weights of features

Real coding was used to represent the chromosome. All genes in the chromosome have value in the range [0, 1]. Two first genes c and g represent the values of C and γ respectively, while w ₁∼w _n represent the weights of features. Note that, we search values of C and γ in the ranges [ C1, C2] and [ γ ₁, γ ₂]. Thus, parameters C and γ of the SVM classifier are obtained by mapping c and g into corresponding ranges via the following formula:

$$ C = C_{1}+ c*(C_{2}-C_{1}) \ and\ \gamma = \gamma_{1} + g* (\gamma_{2} - \gamma_{1}) $$

(19)

In the implementation, we allow users to vary lower-bound and upper-bound values of C and γ as well as other parameters of the genetic algorithm.

5.2 Fitness function

The performance of SVM classifiers is used to design a single objective function for GAs. In the decoding process, both training and testing datasets are transformed by multiplying feature i ^th with the corresponding weight w _i , i=1,..,n. After that, the SVM model with the RBF kernel function is built based on C, γ (19) and the transformed training dataset. The accuracy of the classifier on the testing dataset is used to assesses the quality of the chromosome.

For multiple class datasets, we set the accuracy as the fitness value of the chromosome. Meanwhile, for two-class datasets, the fitness value can be constructed from other widely employed performance measures such as Accuracy, F-measure and Matthews correlation coefficient (MCC). These values are calculated according to the confusion matrix, which contains information about actual and predicted classifications done by a classification system (Table 1). In Table 1, we assume that the labels of data are 1 (positive) or -1 (negative). The meaning of values in the confusion matrix are as follows.

• TN is the number of correct predictions that an instance is negative.

• FN is the number of incorrect predictions that an instance is positive.

• FP is the number of incorrect of predictions that an instance negative.

• TP is the number of correct predictions that an instance is positive.

$$ Accuracy = \frac{TP+TN}{TP+FN+FP+TN} $$

(20)

$$ MCC = 2 \cdot\frac{TP \cdot TN-FP \cdot FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}} $$

(21)

$$ F-measure = 2\cdot\frac{Precision \cdot Recall}{Precision+Recall} $$

(22)

where p r e c i s i o n = T P/(T P + F P) and r e c a l l = T P/(T P + F N).

Table 1 The confusion matrix

In GAs, the objective functions are very important and they notably affect the rate of convergence and the quality of the best solutions [37]. We also conducted some experiments on several two-class datasets with different objective functions in (20 ∼22). Then, the output data are analyzed carefully to explore the effectiveness of each objective function according to two criteria: time efficiency and quality of the optimal solution measured by the accuracy of SVM classifiers.

5.3 System architecture

We suggest an architecture for the hybrid system GA-SVM as Fig. 4. In this model, the task of GA is to search optimal parameters of SVM and weight of features. Besides, the SVM plays a role as oriented search strategy for GA by evaluating the fitness of chromosomes. The details of the hybrid model are described as follows:

• 1. Data pre-processing (scaling). Scaling before applying SVM is very important. The main advantage of scaling is to prevent attributes in greater numeric ranges dominating those in smaller numeric ranges. Another advantage is to avoid numerical difficulties during the calculation process [9]. When using the Grid algorithm, according to our experimental results, feature value scaling can help to increase SVM accuracy. Normally, each feature is linearly scaled to the range [−1,+1] or [0,1] by formula (23).

  $$ v^{\prime} = \frac{v-min_{a}}{max_{a} - min_{a}} $$

  (23)

  where v ^′ is scaled value, v is original value, m i n _a , m a x _a are low bound and upper bound of the feature value, respectively.

  Typically, we have to use the same method to scale both training and testing data. For example, suppose that we scaled the first attribute of training data from [−10,+10] to [−1,+1]. If the first attribute of testing data lies in the range [−11,+8], we must scale the testing data to [−1.1,+0.8].

  For the task of finding the weights of features, scaling data may be unnecessary for GA-SVM model. However, in order to gain the best results for the Grid algorithm, we performed this process. Then all experiments of both the approaches were conducted on the scaled datasets.

• 2. Decoding(generating training data and parameters C, γ for SVM). This step converts the values of the chromosome into parameters C, γ of the SVM by (19) and the weights of features. In both the training and testing datasets, the feature values of instances are multiplied by the corresponding weights using following formula.

  $$ \bar{x}_{ij} = x_{ij}*w_{j} $$

  (24)

  where x _{i j} and $\bar {x}_{ij}$ are the value of the j ^th field of the i ^th instance before and after scaling. w _j is the weight of the j ^th field.

• 3. Fitness evaluation After decoding stage, C, γ and the scaled training dataset are used to build the SVM model. The scaled testing dataset is used to evaluate the performance of the classifier. When the predicted data is obtained, each chromosome is evaluated by the fitness functions described in Section 5.2.

• 4. Genetic operators. In this step, a new generation is produced by genetic operators including selection, crossover, mutation, and replacement.

• 5. Stopping criteria. The population is improved through many generations. The evolutionary process ends when stopping criteria are satisfied. Some typical criteria are used such as a number of iterations, acceptable results or a fixed number of last generations without changing the fitness value.

• 6. Elitism replacement. To maintain the good solutions of each generation that may be lost during the evolutionary process by crossover and mutation operators, we use the elitism replacement technique. For each generation, we store the best chromosome and replace worst chromosome in the next generation with such chromosome.

Fig. 4

The system architecture of the hybrid GA-SVM model for feature weighting and parameter optimization

6 Experiments

6.1 Experimental setup

The detailed settings for the genetic algorithm are as follows: population size 500, crossover rate 0.9, mutation rate 0.05, two-point crossover, elite selection and elitism replacement. In addition, we set the ranges of C [0.01 - 32000] and γ [ 10⁻⁶ - 8]. The aim of such ranges is to limit the searching bounds of two SVM parameters when using the RBF kernel (19). Corresponding to real-value coding, genetic operators are performed as follows:

• Crossover

  $$ X_{1}^{old} = \lbrace x_{11}, x_{12}, .., x_{1n}\rbrace,\ X_{2}^{old} = \lbrace x_{21}, x_{22}, .., x_{2n}\rbrace $$

  (25)
  $$ x_{1t}^{new} = x_{1t} + \sigma(x_{2t}- x_{1t}),\ t \in [p_{1}, p_{2}] $$

  (26)
  $$ x_{2t}^{new} = x_{2t} - \sigma(x_{2t}- x_{1t}),\ t \in [p_{1}, p_{2}] $$

  (27)
  $$ X_{1}^{new} = \lbrace x_{11}, .., x_{1 p_{1} - 1}, x_{1p_{1}}^{new}, .., x_{1p_{2}}^{new}, x_{1p_{2}+1},..., x_{1n}\rbrace $$

  (28)
  $$ X_{2}^{new} = \lbrace x_{21}, .., x_{2p_{1} - 1}, x_{2p_{1}}^{new}, .., x_{2p_{2}}^{new}, x_{2p_{2}+1},..., x_{2n}\rbrace $$

  (29)

  where p ₁ and p ₂ are two random values of cut points. $X_{1}^{old}$ and $X_{2}^{old}$ represent the pair of parents before crossover operation; $X_{1}^{new}$ and $X_{2}^{new}$ represent offspring. In addition, σ, which has the range of [-1,1], is a random micro number that controls the variance of each crossover operation. In other words, we partially perturb the parent in directions of the differential vector between two parents.

• Mutation

  $$ X^{old} = \lbrace x_{1}, x_{2}, .., x_{n}\rbrace $$

  (30)
  $$ x_{k}^{new} = LB_{k} + \sigma(UB_{k} - LB_{k}) $$

  (31)
  $$ X^{new} = \lbrace x_{1}, x_{2}, .., x_{k}^{new}, .., x_{n}\rbrace $$

  (32)

  where k is the position of the mutation. LB and UB are the lower and upper bounds on the parameters. L B _k and U B _k denote the lower and upper bounds at location k. X ^old and X ^new represent the individuals before and after the mutation operation.

The stopping criteria are that the number of generations reaches 600 or the best fitness value does not improve during the last 100 generations. The best chromosome of the final generation is selected as the solution of the problem.

To evaluate the effectiveness of the proposed system in different classification tasks, we conducted experiments on several real-world datasets from the UCI database (Hettich, Blake, and Merz, 1998) [38] and evaluated the results on various criteria. The criteria are detailed in Sections 6.2 and 6.3. The short description of the used datasets is mentioned in Table 2.

Table 2 The datasets from the UCI repository

We use k-fold cross validation technique to assess the results. In this method, the original data is randomly partitioned into k equal sized sub-parts. The cross-validation process is repeated k times (the folds). At step k, the k ^th part is used for testing by the trained model, which is built based on the remaining k−1 sub-parts. The k results from the folds can then be averaged (or otherwise combined) to produce a single estimation. The advantages of this technique are that all of the test sets are independent and the reliability of the the results could be improved. In our experiments, we choose k=10 and combine k results to estimate the performance of the classifiers (Fig. 4).

6.2 Evaluation criteria

Accuracy (overall hit rate) is considered the most important criterion to evaluate the effectiveness of a classification algorithm. However, the power of a classifier is demonstrated by not only the final results (the accuracy) but also other criteria, which are discussed in more detail in Section 6.3. One of these criteria is the ability of discrimination between classes. For binary classifiers, sensitivity and specificity are two metrics, which describe how well the classifiers discriminate between positive and negative classes. Where, sensitivity (or True Positive Rate - TPR) is the proportion of positive instances that are classified as positive. Specificity (or True Negative Rate - TNR) is the proportion of negative instances classified as negative.

The ability of a classifier to discriminate between positive cases and negative cases is evaluated using Receiver Operating Characteristic (ROC) curve analysis. This method is also used to compare the diagnostic performance of two or more diagnostic classifiers [39]. An ROC curve is a graph of sensitivity (y-axis) and 1 - specificity (x-axis). The curve contains all possible cut-off points, which are selected to discriminate between the two populations (with positive or negative class values). The ROC curve shows the trade-off between sensitivity and specificity. Based on the curve analysis method, the closer the curve follows the left-hand border and then the top border of the ROC space, the more accurate the classifier is. The area under the curve (AUC) is the evaluation criterion for the classifier. This criterion is less affected by sample balance than accuracy.

6.3 Experimental results and discussion

Table 3 shows the summary of classification results for the 11 UCI datasets using the two approaches. For this experiment, the accuracy is set as the fitness function of the GA. For multi-class datasets, TPR and TNR are marked N/A because they are not calculated. In the paper, we applied the optimal values of C, γ and the weights for entire instances of the dataset when doing k-fold cross validation (23). The results from k folds are combined to obtain the final output, which are used to calculate the performance metrics such as TPR, TNR and accuracy. This is different from the experiments of Cheng-Lung Huang and Chieh-Jen Wang [1]. They selected features and optimized the parameters for training and testing data in each step of cross-validation, separately. This may result in higher average of performance metrics; however, it does not indicate what a pair of (C, γ) and a set of features are useful for the dataset. Thus, the Grid algorithm is used as the baseline to compare with our model in the same experimental conditions.

Table 3 Experimental results of GA-SVM approach and Grid algorithm on the test sets (TPR - True Positive Rate, TNR - True Negative Rate)

The results in Table 3 indicate that the hybrid GA-SVM approach improves classifier performance significantly in comparison with the Grid algorithm; the bold values denote the improvement of the proposed model over the Grid algorithm. Based on measures of the TPR, TNR and accuracy, the proposed model always achieves higher values than the Grid algorithm for all the experimental datasets. Especially, there are improvement of 9.13 % and 8.71 % on accuracy of two datasets Sonar and Vowel. On the Sonar dataset, for the GA-SVM approach, its true positive rate is 98.20 %, its true negative rate is 94.85 % and its accuracy is 96.63 %. For the Grid algorithm, its true positive rate is 93.69 %, its true negative rate is 80.41 % and its accuracy is 87.5 %.

We also carried out the classifications by using different algorithms including C4.5, random forest, naive bayes and boosting to provide reference points for comparisons. We used the implementations of these algorithms in the WEKA workbench version 3-6-13¹ to conduct the tests. All the parameters in the algorithms were left as default values. Each dataset was classified by each classifier using 10-fold cross validation. The predicted results on 10 validation folds were combined to calculate the performance of the classifier. Table 4 summarizes the experimental results on 7 two-class datasets using various algorithms, where the values of our method and the highest values of other methods are marked in bold. The Table 4 shows that SVMs is not the most powerful algorithm but the hybrid GA-SVM model outperforms the other algorithms on all the datasets.

Table 4 Performance comparison of the proposed approach and other algorithms on two-class datasets

To verify the performance of the proposed method, we compared GA-SVM with several other state-of-the-art feature weighting approaches including AW-SKDE [30], AISWNB [23], DFWNB [29], FW-KNNI, FW-CMC and FW-SVMI [25]. The algorithms performance was evaluated in terms of the classification accuracy using 10-fold cross validation technique. As can be seen in Table 5, the GA-SVM significantly outperforms the other feature weighting methods on most of the datasets except the Breast cancer. The discrimination between the performance of the GA-SVM and the other feature weighting algorithms can be explained by two main reasons. Firstly, the pre-existing bias approaches (AW-SKDE, DFWNB, FW-KNNI, FW-CMC and FW-SVMI) use the attribute independence assumption when it is usually violated in real-world datasets. Secondly, SVM shows more efficient than the other algorithms on the experimental datasets (Table 4). Meanwhile, in our method, SVM classifiers are strengthened by using GA to automatically calculate feature weights and kernel parameters. As a result, the GA-SVM obtains the remarkable results in comparison with the state-of-the-art feature weighting methods.

Table 5 Performance comparison of the proposed approach and other feature weighting methods. The highest accuracy on each dataset is marked in bold

To assess the discrimination ability between classes of a classifier, we take German and Australian datasets to analyze ROC curves of GA-SVM approach and the Grid algorithm. In Fig. 5, the blue curves are closer the left-hand border and the top border of the ROC space than the red ones. AUC are 0.9236, 0.9189 (Australian) and 0.7853, 0.6809 (German). The AUC values reveal that the GA-SVM approach outperforms the Grid algorithm in terms of discrimination ability.

Fig. 5

ROC curves for two datasets using GA-SVM approach and Grid algorithm. Figure 5a and b show curves for Australian and German datasets, respectively

Analyzing the behavior of algorithms is not based on the final results, but also on results during the execution process. To assess the combination ability between GA and SVM, we recorded the fitness value (accuracy) of the best solution each 10 generations. As shown in Fig. 6, the performance of SVM classifiers are improved continuously and quickly converge to the optimal solutions. Specifically, it is after around 65 generations on most of the experimental datasets. For vehicle and heart dataset, the rates of convergence are slower than others. The optimal solutions are correspondingly obtained after near 150 and 250 generations.

Fig. 6

Running process of the hybrid system GA-SVM on 11 UCI datasets

For genetic algorithms, choosing a proper fitness function plays a very important role [37]. The fitness function orients searching strategy of GAs to obtain the best solutions within a large search space. Appropriate fitness functions will help GAs in exploring the search space more effectively and efficiently. In contrast, inappropriate fitness functions can easily lead GAs to get stuck in a local optimal solution and lose the discovery power. To illustrate, we take three datasets (Breast cancer, Ionosphere and Sonar) to conduct tests with different fitness functions including Accuracy, F-measure and Matthews correlation coefficient (MCC) (20 ∼22). For each dataset and objective function, we run the test 10 times using different random seeds.

In Table 6, the results are shown in the form of average ± standard deviation. As can be seen, for the three datasets, the Accuracy function achieves slightly higher average accuracy but the convergence velocity is slower in comparison with the MCC function. In particular, the Accuracy obtains the highest accuracies on the Ionosphere and Sonar datasets; the corresponding values are 97.95 % and 97.26 % after approximately 68 and 86 generations, respectively. For the MCC function, the accuracies reach 97.86 % and 97.12 % after around 57 and 59 generations. The MCC function obtains the highest accuracy, 97.61 %, on the Breast cancer dataset. The F-measure function is as slow as the Accuracy function in terms of computational time and the performance of the F-measure function does not outperform the other functions. It is worth noticing that the Accuracy function achieves the highest accuracies. The accuracies of the MCC function are not as high as that of the Accuracy function, but the MCC function converges faster. The F-measure function is weaker than the Accuracy and MCC functions regarding to time efficiency and optimal solution quality.

Table 6 The performance of the hybrid model GA-SVM by different objective functions. The bold values are the highest accuracy and the minimum number of generations on each dataset

When dealing with real-world applications, we often face a complicated problem called imbalanced datasets, which contain many more samples from one class than from the rest of the classes [40, 41]. For example, in medical diagnosis of a certain cancer, we assume that the cancer is the positive class and non-cancer (healthy) is the negative class. For diagnostic data, the number of negative instances is usually greater than positive ones. In this scenario, classifiers may bias the majority class due to the pursuit of error minimization. It results in great accuracy on the majority class, but very poor accuracy on the minority class. Meanwhile, detecting positive instances is more important than detecting negative ones. The imbalanced data problem can be seen in Tables 2 and 3. Taking the diabetes dataset, for example, the number of positive and negative instances are 268 and 500. For the GA-SVM approach, the true positive rate is 63.06 % and the true negative rate is 91.14 %. Similarly, for Grid algorithm, the true positive rate is 51.49 % and the true negative rate 90.2 %. Imbalanced datasets can be handled by sampling methods to re-balance them artificially or modifying SVMs [41]. Although our approach does not deal with imbalance problems, it is interesting that in the efforts of achieving the highest accuracy, the GA does not direct SVM classifiers to the majority classes. The hybrid model improves the accuracy rates on all classes and maintains the fairness between classes in comparison with the Grid algorithm (Table 3).

The average running time for the GA-SVM approach are slightly inferior to that of the Grid algorithm. However, the performance of classifiers are improved significantly according to various estimation. In addition, it is important to notice that the proposed model has abilities to find the general properties of the datasets that will be useful for further works.

7 Conclusions

In this paper, we presented a novel method that improves the performance of SVMs by using GAs based on directional information. The hybrid model GA-SVM is applied to optimize the parameters and feature weighting simultaneously for classification problems. It is essential because weighting feature influences the appropriate kernel parameters and vice versa. As far as we know, previous research did not use GAs to perform feature weighting and parameter optimization for support vector machines.

We conducted experiments to evaluate classification accuracy of the proposed GA-SVM approach with the RBF kernel and the Grid algorithm on the 11 real-world datasets from UCI database. According to different assessment criteria such as accuracy and AUC, the proposed GA-based approach always obtains better classifiers than some latest feature weighting approaches. This study showed experimental results with the RBF kernel. However, other kernel parameters can also be optimized using the same techniques due to the flexible design of GAs.

Currently, our approach is time-consuming because the training procedure of SVMs is repeated many times. Thus, to find the optimal parameters and attribute weights for big datasets using the proposed model, we need some modifications to reduce the computational time. In future work, we adapt the model for big datasets by concurrently applying following solutions:

• Speed up the training time of SVMs by using some methods to reduce the size of datasets.

• Split datasets into a ratio of 3:1:1 for training, validation, and testing instead of 10 folds for cross-validation.

• Adopt parallel computing to evaluation of individuals.