1 Introduction

Most of engineering and design problems include optimizing a number of objectives, simultaneously [1] known as Multi-Objective Optimization Problems (MOPs) which continue to gain increasing attention among researchers to find efficient methods of handling them. A Multi-Objective Optimization Problem (MOP) can be stated as follows:

$$ \begin{array}{cc} minimize\left\{\left(f_{\mathbf{1}}\left(\mathbf{x}\right).f_{\mathbf{2}}\left(\mathbf{x}\right).\mathellipsis.f_{k}\left(\mathbf{x}\right) \right) \right\}\\ {subject\,\, to \,\,x} \,\,\in \,\,{S} \end{array} $$
(1)

where \(\mathrm {f}\left ( \mathrm {x}\right )\) is a vector of k objective functions which are to be optimized and x is a vector of decision variables [2]. Here and in the rest of this paper, without loss of generality, we assume MOPs to be minimization problem. In such problems, there exists no single solution to optimize all objectives. Hence, it is desirable to find a set of incomparable solutions which would be considered as the optimal solutions to the MOP [1, 9]. Many researches have been conducted in solving MOPs ever since their introduction. Recently, a considerable number of studies have been devoted to applying Evolutionary Algorithms (EAs) for solving such problems. Evolutionary Algorithms are suitable for solving MOPs due to their parallel search capability and impressive performance in unknown environments [2–5]. Accordingly, one of the well-known problem solvers for MOP are Multi-Objective Evolutionary Algorithms (MOEAs). The main reason of their popularity is their ability to find multiple trade-off solutions in a single run. As it is said, finding a set of solutions as optimal is desirable in solving an MOP. These solutions are called non-dominant solutions and the set containing all these solutions is called Pareto front (non-dominated vectors are in the objective space). Converging to the true Pareto-front and maximizing the population diversity of non-dominated solutions in the objective space are the two main targets of all MOEA approaches. The formal definition of Pareto domination is: a vector u 2 Pareto dominates another vector u 1 if and only if for all objectives we have [1]:

$$ f_{i}\left(u_{1} \right)\ge f_{i}\left(u_{2}\right)i=12.\mathellipsis .m $$
(2)

and

$$ \exists i \epsilon \left\{1.2.\mathellipsis .m\right\}\Rightarrow f_{i}\left(u_{1}\right) \succ f_{i}\left(u_{2} \right) $$
(3)

Research in the field of Multi-Objective Evolutionary Algorithm(MOEAs) has been very active in the last 10 years and many potential algorithms with promising results have been proposed [6, 7], and [8]. Although the existing MOEAs show satisfying performance for MOPs with 2 or 3 objectives, their search ability for problems with more than three objectives often degrades. These problems are referred as Many-objective Optimization Problem (MaOP) [6]. This performance degeneration is due to the loss of selection pressure exerted by the Pareto dominance relation which will cause premature convergence of the algorithms [6–9]. Furthermore, approximating the Pareto front will become difficult, since we need more points to represent a larger space [2]. In high dimensional problems, Pareto dominance relation loses its discrimination capability. In other words, nearly all solutions in the population would become non-dominated and algorithms which use dominance relation directly would lose their selection pressure and accordingly would not converge.

The search effort in MOEAs can be divided into two main parts: converging to the Pareto Front and diversifying the population (representing all regions of the Pareto front). In many objective problems, the regular MOEAs would fail to discriminate between solutions according to their fitness so only the diversity part of their selection would work [6, 7]. Increasing selection pressure by modifying the dominance relation would cause the population to converge to a specific region while paying more attention to diversity would prevent the algorithm from convergence. In this way, convergence and diversity are two contradicting objectives of an MOEA.

In this regard, this paper attempts to adaptively control the population diversity among chromosomes to overcome this dilemma. In the proposed method, a diversity control mechanism is introduced along with a diversity measure which can be used in high dimensional spaces. In this approach, the selection of chromosomes is based on their participation in the preservation of diversity in addition to their fitness and we would adaptively change the importance of diversity in each generation. The proposed diversity metric is based on finding shortest Hamiltonian path. The experimental results confirmed that the proposed mechanism is capable of creating a set of well-distributed and optimal solutions which is competitive with the state-of-the-art methods.

Our contribution in this paper is two folded. First we have proposed a diversity control mechanism which is able to adaptively control the population diversity which consequently controls the amount of selection pressure and thus helps the algorithm to produce a diverse set of solutions close to real Pareto Front. Second, we designed a diversity measure to be used in high dimensional problems. In view of the fact that the proposed diversity control mechanism requires a diversity measure to assess the diversity of each generation and also other known diversity measures have some drawbacks in high dimensions, a new diversity measure is proposed. This diversity measure is based on finding a shortest Hamiltonian path in the complete distance graph of solutions in the objective space. Using this concept, we can capture a proper order in high dimensional spaces which do not have any intrinsic order.

In our experiments, we obtained contradictory results with respect to two well-known performance indicators: Hypervolume and IGD (Inverted Generational Distance); which was not odd according to similar experimental and theoretical studies [37]. In the next step, using known methodologies and arguments [20], we compared the two metrics and revealed that IGD can give a more accurate comparison between various methods. Since our method has obtained relatively smaller values of IGD we can conclude that the proposed framework along with the diversity measure have potential in optimizing many objective problems.

The rest of this paper is organized as follows: Section 2, explains the background and related work. Proposed method is described in Section 3. Section 4 shows the experimental results and analysis. Finally, Section 5 includes conclusion and future work in regard to the proposed method.

2 Related work

In this following section, we introduce the background and the concept of Multi and Many Objective Evolutionary Algorithms.

Many objective problems have been in the frontier of multi-objective optimization research for more than a decade. Since the main issue that hinders the evolution of algorithms is the loss of discrimination ability of the Pareto dominance operator, new algorithms are either using a modified version of this operator or using it in an indirect way [6]. Using modified versions of dominance operator can be useful for 4-6 objectives but it would fail in higher dimensional problems [6]. There are a variety of evolutionary meta-heuristic algorithms for handling many objective optimization problems. Many studies have been focused on improving the performance of these methods in solving problems [7–9, 16, 17]; here we will explore their offered approach.

By increasing the number of objective functions, in an optimization problem, the amount of non-dominated solutions will increase rapidly, leading to severe loss of pressure in the selection mechanism [6]. In order to address this problem, among many other methods, two classes of algorithms have shown great potential in solving many objective optimization problems: the decomposition based methods and indicator based methods. Decomposition based methods use a set of pre-specified uniformly distributed weight vectors, each of which constructs a single objective optimization problem that ideally would find a point of the true Pareto front. Collectively these sub-problems will find an acceptable representation of the Pareto front [11]. The pioneer method in this family is Multi-Objective Evolutionary Algorithm by Decomposition (MOEA/D) [11]. In order to search effectively, a neighborhood is assigned for each sub-problem which includes other problems that are near to it in the weight space. Mating is restricted within the neighborhoods so the variation operators would not be disruptive. In designing a decomposition based algorithm, one has to choose how to generate the weight vectors. If there is preference information available, it can be incorporated in the distribution of weight vectors. But, in most cases, the weights are generated uniformly using the procedure proposed by Das & Dennis [12]. Another design choice is the scalarization function which is used to combine the objective values and construct the sub-problems. Many different functions have been proposed in the literature [11], but in this paper we used the Tchebichev function.

Various attempts are provided to improve the performance of the MOEA/D. First the SBX was considered as its genetic operator but due to the poor performance of this operator for maintaining population diversity, Zhang et.al introduced MOEA/D-DE using DE operator to perform more efficient search [13]. In order to avoid the problem of high computational complexity, Zhang et al. introduced the idea of dynamic resource allocation in the form of MOEA/D-DRA [14]. This algorithm introduces a kind of MOEA/D that uses a utility function for assigning computational resources to each sub-problem and on the basis of this assignment, the computational load is distributed among all of them. In another work, Zhang et.al introduced MOEA/D-GM which presents two mechanisms to improve MOEA/D. First, in order to take full advantage of the neighborhood information of a sub-problem, it applies targeted mutation operator that uses both global and local information. Then, an update mechanism will apply to improve the algorithm, when there is no uniform distribution of sub problems. This update mechanism is implemented using a priority queue. In 2011, Gong et.al proposed iMOEA/D, this algorithm has an interaction with decision maker and guides the search in the direction of preferred regions in order to enhance the distribution of Pareto front and improve the search mechanism of MOEA/D especially in dealing with many objective optimization problems. Sato proposed a method named inverted PBI scalarization in which an effective scalarization function is used to produce approximation sets which are widely distributed in the objective space [15].

Another Many Objective algorithm that uses decomposition is NSGA-III [16]. NSGA-III is not technically a decomposition based MOEA but it borrows ideas from these algorithms. In order to overcome the loss of diversity in the population, NSGA-III uses a set of predefined points in the objective space which are spread on a hyper-plane and called reference points. All the solutions in the objective space are projected onto this hyper-plane and each one is assigned to the nearest reference point on the plane. For each solution the crowdedness of its corresponding reference point is an indicator of its contribution to the overall diversity. Yuan et al. proposed an improved NSGA-III named Θ-NSGA-III that inherits specific characteristics of NSGA-III including adaptive normalization and diversity maintenance which with the aid of reference points will lead to a well distributed Pareto front in the objective space [17]. However, Θ-NSGA-III differs from NSGA-III in various certain parts. It applies a new dominance relation, Θ-dominance, which assigns solutions to different clusters. These clusters are formed by reference points, which are well distributed throughout the space. Just the solutions that are found in similar clusters are participating in competitive relation. In this competitive relation a penalty based boundary intersection is described and the solutions will perform based on it. During environmental selection, the ?-dominance not only keeps the solutions with better fitness in each cluster but also ensures that the solutions are evenly distributed among all clusters [17].

Another class of algorithms for handling many objective optimization problems includes Indicator based methods. Indicator based algorithms are inspired by the idea of maximizing a performance indicator which would yield a good result in terms of that indicator. The main problem with these algorithms is the computational complexity of indicator measures. Hypervolume is the most popular indicator used in this context. In the following paragraphs we will describe two of the most popular indicator based algorithms briefly.

S-Metric Selection Evolutionary Multi-Objective Algorithm (SMS-EMOA) [18] is a steady-state evolutionary algorithm which uses hypervolume. S-Metric is another name for hypervolume which was more common in the early years of this metric’s introduction [18]. Since computing hypervolume is a computationally intense task, SMS-EMOA uses a steady-state population model to reduce the number of hypervolume computations. So in each generation, one new solution is created and added to the population and consequently one solution should be deleted. In each generation, in order to remove one solution, all the individuals in the first non-dominated front are sorted according to their hypervolume contribution. The hypervolume contribution of an individual is defined as the difference between the hypervolume of the population with and without that individual.

Since the main shortcoming of indicator based algorithms is their computational cost, Bader and Zitzler proposed a method that tries to estimate the value of the hypervolume. They designed Hypervolume Estimation algorithm (HypE), which uses Monte Carlo simulation for estimating the hypervolume contributions in an efficient way [19]. Monte Carlo simulation is a well-studied method for approximation of definite integrals and since hypervolume is a kind of integral, good estimations are expected from exploitation of this method.

3 Proposed method

As stated before, many objective optimization problems have introduced new challenges to MOEA community. In high dimensional problems, nearly all solutions in the population would become non-dominated which is caused by loss of selection pressure and accordingly the algorithm would not converge to Pareto front properly. Due to these challenges, finding reasonable approximation of diverse optimal Pareto-sets is so hard and requires a more delicate balance between convergence and diversity [17]. In this regard, common approaches in evolutionary multi-objective optimization either fails to provide enough selection pressure or the selection pressure is too much which causes concentration of the population to a specific region of space [6, 7], and [17]. In order to overcome this dilemma, one obvious direction for improving MOEAs is to add more effective diversity control mechanisms to algorithms with acceptable selection pressure. With the aim of preserving population diversity, this paper proposed a diversity control mechanism and also a new diversity measure which can be used in combination. In order to control the population diversity, we designed an adaptive framework which adjusts the selection operator according to diversity variation in the population. By an increase in the diversity of population the selection operator will change to increase the selection pressure and by a decrease in diversity the selection pressure will decline. Additionally, a new diversity measure which is based on shortest Hamiltonian path is proposed in order to monitor the variation of population diversity during each generation.

In the rest of this section, our contribution is presented in three parts. The first part introduces the diversity maintenance mechanism. After that, in the second part the novel diversity measure will be described and its details will be expounded and finally refinements needed for incorporation of diversity maintenance mechanism in MOEA/D will be explained.

3.1 Diversity maintenance mechanism

Here in this section, we aim to propose a diversity control mechanism to streamline the optimization process. As discussed in many other works, lack of discriminability in dominance relation propels optimizers to modify it so as to increase the selection pressure. Intensifying the selection pressure usually leads to loss of diversity in the population which is not desirable [10]. By using a diversity measure, we can detect any variation in the population diversity at each generation and make decisions based on that. After we identified that the population diversity is decreased we should regulate the selection mechanism in a way to compensate for this reduction. In order to incorporate diversity into the selection mechanism of algorithms in a more controlled way, this paper proposed a diversity maintenance framework. This framework is concisely illustrated in the Flowchart 1 where it uses the diversity measure that will describe in the next subsection. In most of common MOEAs, solutions are selected according to their fitness and diversity is used as a tie breaker [1]. We propose to alter this order adaptively. For instance, there may be situations where the population is converging toward a specific region of the Pareto Front or even a single point. In such a situation, the selection operator should pay more attention to the population diversity than fitness.

Flowchart 1
figure c

Flowchart of the proposed diversity maintenance mechanism

Full size image

There are two important issues in our proposed framework. First, we need to know when to switch the order of selection. Second, we need to determine which chromosome has the highest contribution in the diversity of the population so we give it an advantage in the selection mechanism. For the first concern, we measure the diversity of the population in each generation using accepted diversity measure, and by comparing to the one for the previous generation we can determine whether the population has got or lost diversity. Accordingly, we can set the order in the selection operator, i.e. “Fitness first” or “Diversity first”. For each chromosome we should be able to compute its contribution in the population’s overall diversity which can be done in different ways. This contribution in the diversity would be used as the second measure of selection for each solution. In the case of “Fitness first”, the selection mechanism will operate regularly, i.e. mainly based on the fitness of individuals and based on the diversity contribution in case of indifference. But for the “Diversity first”, we first select based on the solution’s diversity contribution and the fitness would be used breaking ties. You must note that by fitness we mean the scalar value assigned to each solution based on its objective values, like the domination rank or in NSGA2 or the scalarized value in MOEAD or distance to reference point in NSGAIII.

In the next sub sections, we introduce some popular diversity metrics and after exploring their inefficiencies we will propose a novel diversity measure.

3.2 Planning for diversity measure

In the previous sub section, we proposed an adaptive framework which adjusts the selection operator according to the diversity variation in the population. This diversity control mechanism requires to find the population diversity. As it can be seen, the main part of this framework is monitoring and computing the population diversity. In this section, first, we introduce some popular diversity metrics and review their features to find out whether they can be exploited in our framework or not.

Toward understanding the motivation of our proposed diversity metric, some quantitative metrics for multi and many objective optimization are examined. In particular, the quantitative metrics of multi-objective optimization realm are commonly categorized in to four groups [sweing]:

  1. 1.

    Capacity metrics: These metrics quantify the number (ratio) of non-dominated solutions in population that satisfies given predefined requirements. In general, a large number of non-dominated solutions in the population is preferred. (e.g. Error Ratio (ER) [21], Ratio of the Reference Points Found in [22, 23], non-dominated Points by Reference Set (C2R) [23], etc.)

  2. 2.

    Convergence metrics: These are metrics for measuring the degree of proximity of approximation set S based on the distance between the solutions in S to those in the Pareto Front. Convergence metrics measure proximity. (e.g. Generational Distance (GD) [24, 25], 𝜖-indicator [26], ...)

  3. 3.

    Diversity metrics: These metrics incorporate two notions: Distribution and spread. Distribution focuses on how evenly the solutions of the population are scattered in the objective space. The Spread quantifies how much of the extreme regions of the Pareto front are covered by the population

  4. 4.

    Convergence–Diversity metrics: These metrics are indicating both the convergence and the diversity of solution set S in a single value. (e.g. in [27, 28], Zitzler et al. proposed the popular performance metric Hypervolume (HV) which gives the volume of optimal solution set S in the objective space and the metric Inverted Generational Distance (IGD) in [29] which compute the average distance of the true Pareto front from the obtained optimal solution set S.)

In this paper we concentrate on diversity metrics and propose a new measure with the aim of preserving population diversity between generations. Since capacity metrics and convergence metrics are not related to our aim, the interested reader is referred to [20, 29] for further information. More specifically, we investigate three representative groups of diversity metrics including: distribution, spread and distribution-spread.

3.3 Diversity metrics

Most researchers have been trying to define a description that can characterize the concept of population diversity. In the literature, scientists mentioned that Diversity metrics should indicate the distribution and spread in the optimal solution set S [20]. Here, Fig. 1 is presented to convey the concept of distribution and spread.

Fig. 1
figure 1

Distribution and spread in a set

Full size image

In this figure a 2-dimentional PF is presented. The bounding solutions of the PF are (0,1) and (1,0) which are known as extreme points. The optimal solution set S with five non-dominated solutions in Fig. 1 a shows good distribution and poor spread since S does not contain bounding solutions. Conversely, the five non-dominated solution of optimal solution set S in figure (b) have good spread but poor distribution since the solutions in S are not scattered evenly.

To have a better comprehensive investigation, this part express three classes of diversity metrics. As mentioned before, diversity metrics are aimed to measure the distribution and spread of solutions in the optimal solution set S [20]. So researchers categorize diversity metrics in to three classes:

  1. 1-

    diversity metrics which focus on distribution

  2. 2-

    diversity metrics which focus on spread

  3. 3-

    diversity metrics which focus on both distribution and spread

3.4 Diversity metrics which focus on distribution

As mentioned before Distribution focuses on how evenly the solutions of an approximation set are scattered in the objective space [20]. Here we have investigated five representative diversity metrics which focus on distribution including: \({\Delta }^{\prime }\) [30], M\(_{3}^{\ast }\) [31], M\(_{2}^{\ast }\) [31], Uniform Distribution(UD) [32] and Spacing(SP) [33].

  1. 1)

    \({\Delta }^{\prime }:\) This metric is proposed by Deb et al. which compares all the consecutive distances of solutions’ with the average distance and is computed in the following way:

$$ {\Delta}^{\prime}\left(S \right)=\sum\limits_{i=1}^{\left| S \right|-1} \frac{(d_{i}-\bar{d})}{\left| S \right|-1} $$
(4)

where S is a solution set and d i is the Euclidean distance between consecutive solutions in S, and \(\bar {d}\) is the average of d i . The best distribution would produce a zero value when all the solutions have equal distance to their successor. The consecutive solutions are defined to be the next solution in the lexicographic ranking of the population [30]. As you can see \({\Delta }^{\prime }\) is a non-parametric metric with computational complexity of O(m|S|2).

  1. 2)

    \( M_{3}^{\ast } :\) it is a metric which is similar to \({\Delta }^{\prime }\) but instead of average distance, this metric considers the maximum distance instead [31]. So \(\mathrm {M}_{3}^{\ast }\) is also a non-parametric metric with computational complexity of O (m|S|2).

  2. 3)

    \(M_{2}^{\ast } \): The \(M_{2}^{\ast } \) metric is proposed by Ziztler and Deb et al. [31] which operates with niche radius( σ) parameter and its formulation is as follow:

$$ M_{2}^{\ast}\left(S \right)=\frac{{\sum}_{\vec{s}\in S} \vert \left\{ \vec{s}_{2} \in S \vert \vert \left| \vec{s}_{1}-\vec{s}_{2} \right|\vert < \sigma \right\}\vert} {\left| S \right|-1} $$
(5)

For each solution this metrics compute the average number of solutions in its local neighborhood defined by the niche radius parameter. As you see \(M_{2}^{\ast } \) is designed with user-specified parameter ( σ) and its computational complexity is O(m|S|2).

  1. 4)

    Uniform Distribution(UD): Uniform Distribution metric reveals the degree of uniformity on a given distribution. This measure computes the standard deviation of the number of neighbors for each solution. These neighbors are determined using a radius parameter. For a given population S the uniform distribution would be computed with the following formula [32]:

    $$ UD\left(S \right)= \frac{1}{1+D_{nc}} $$
    (6)

    ,

    $$ D_{nc}=\sqrt {\sum\limits_{\vec{s}_{i}\in S} {(nc\left(\vec{s}_{i} \right)- \bar{nc}(\vec{s})} )^{2} \left/ {(\left| S \right|-1)}\right.} $$
    (7)

    ,

    $$ nc\left(\vec{s}_{i} \right)=\left| \left\{ \vec{s}_{j}\in S \vert \vert \left| \vec{s}_{i}-\vec{s}_{j} \right|\vert < \sigma \right\} \right|-1 $$
    (8)

    In this equation \(\overline {nc}(\vec {s})\) is the average of \(nc\left (\vec {s}_{i}\right )\) This metric is designed with a user-specified parameter which determines the neighbors of a solution and its computational complexity is O(m|S|2).

  1. 4)

    Spacing (SP): In [33], the Spacing (SP) metric is defined as:

    $$ SP\left(S \right)=\sqrt{\frac{{\sum}_{i=1}^{\left| S \right|-1} {(d_{i}-\bar{d})}} {\left| s \right|-1}} $$
    (9)
    $$ d_{i}=\min\limits_{\vec{s}\in S\,\,\vec{s}_{i},\neq \vec{s}_{j}}{\left| \left| F\left(\vec{s}_{i} \right)-F\left(\vec{s}_{j} \right) \right| \right| and \,\,s_{i}\in S} $$
    (10)

    In order to compute mutual distances this metric finds closest distance instead of lexicographic order. SP is a non-parametric metric with computational complexity of O(m|S|2).

3.5 Diversity metrics which focus on spread

The spread property of a solution set S quantifies how much the solutions of S cover the PF completely or in other words how much the extreme points are explored. The Overall Pareto Spread (OS) is a famous metric for assessing the spread of a set which is proposed by J. Wu in [34] and expressed as:

$$ OS\left(S,P_{Good},P_{Bad} \right)=\prod\limits_{k=1}^{m} \frac{\left| \max\limits_{\vec{s} \in S}{f_{k}(\vec{s})}-\min\limits_{\vec{s} \in S}{f_{k}(\vec{s})} \right|}{\left| f_{k}\left(P_{Bad} \right)-f_{k}\left(P_{Good} \right) \right|} $$
(11)

where \(\max _{\vec {s} \in s}{f_{k}(\vec {s})}{f_{k}(\vec {s})}\) are the maximum and minimum values of the k th objective in S, respectively. The metric OS has a computational complexity of O(m|S|). In this metric we need to know to points in the objective space: a good point and a bad point. P B a d is a point in the objective space that is dominated by all the solutions of the Pareto front and P G o o d is a point that dominates all the point of the true Pareto front. Note that the good point would not be feasible at all but here it is used to find the bounds of Pareto front. In this paper we apply this measure for our comparison as a nominee of this group and the good and bad points are approximated using the offline archive of the algorithm.

3.6 Diversity metrics which focus on both distribution and spread

This group of metrics considers both the distribution and the spread of a solution set S simultaneously. Here we investigate five representative diversity metrics which focus on both distribution and spread of a set which are: Δ [35], Generalized Spread ( Δ∗) [20, 36], N D C μ and C L μ [20, 37], Metrics σ and \(\bar {\sigma } \) [20, 38] and The Entropy-based metric [39]

  1. 1)

    Δ: The metric Δ is introduced by Deb et al. [35], which is defined as follows:

    $$ {\Delta} \left(S,P \right)=\frac{d_{f}+d_{l}+{\sum}_{i=1}^{\left| S \right|-1} {\vert d_{i}-\bar{d}\vert}} {d_{f}+d_{l}+(\left| S \right|-1)\bar{d}} $$
    (12)

    where di is the Euclidean distance to the consecutive solution of i’th solution and \(\bar {d}\) is the average of di. The terms df and dl are the minimum Euclidean distances from solutions in S to the extreme (bounding) solutions of the PF (P).

  2. 2)

    The Generalized Spread ( Δ*): Requiring consecutive sorting in metric Δ restricts its application to 2-dimensional PFs only. Zhou et al. [36] introduced the Generalized Spread ( Δ*) as an extension of Δ, which takes the following form and can be exploited in high dimensional spaces.

    $$ {\Delta}^{\ast} \left(S,P \right)=\frac{{\sum}_{k=1}^{m} d\left(\vec{e}_{k},S \right)+{\sum}_{i=1}^{\left| S \right|} {\vert d_{i}-\bar{d}\vert}}{{\sum}_{k=1}^{m} {d\left(\vec{e}_{k},S \right)} +(\left| S \right|)\bar{d}} $$
    (13)

    ,

    $$ d\left(\vec{e}_{k},S \right)=\min\vert|\mathrm{F}(\underset{\vec{s}\in S}{\vec{e}_{k}} )-\mathrm{F}(\vec{s})\vert\vert $$
    (14)

    ,

    $$ d_{i}=\min\limits_{\vec{s}_{j} \in S, \vec{s}_{i}\neq \vec{s}_{j}}{\left| \left| F\left(\vec{s}_{i} \right)-F\left(\vec{s}_{j} \right) \right| \right| and \,\,s_{i}\in S} $$
    (15)

    Where \(\vec {e}_{\mathrm {k}}\in \mathrm {P}\) is the extreme solutions on the kth objective and di is to identify the closest pairwise solutions in S, and \(\bar {d}\) is the average of di.

These two measures ( Δ and Δ∗) require true PF for comparison set and both of them have the computational complexity of \(O((m{\vert S\vert }^{2})+m\left | S \right |\left | P \right |)\).

  1. 3)

    Metrics NDC μ and CL μ : The value of these metrics is obtained by partitioning the objective space in to \(\left ( \frac {1}{\upmu }\right )^{\mathrm {m}}\) grids where μ is a variable that can be varied between 0 and 1 [20, 37]. The number of grids that contains solution are take a part in these metrics. Since these metrics construct a grid structure their computational complexity exponentially increases with the dimension of space. These metrics also demand subtle parameter settings. (number of grids)

  2. 4)

    \(\sigma \,\,\text {and}\,\, \bar {\sigma }:\) Using a set of lines passing from the origin, the objective space would be divided into equal angels. The metric value is based on the number of reference lines. The computational complexity of these two metrics is also exponential and also the values of these metrics relay on the parameter settings (number of reference points, sub-regions or angles and etc.) [20, 38].

  3. 5)

    Entropy-based metrics: This metric also divides the objective space into some sub-regions and grids. By employing an influence function (Gaussian in this paper), it would compute a density value for each cell of the grid. Then the Entropy-based metric calculates the Shannon entropy of these density values [39].

As you see the main part of our proposed framework is monitoring and computing the population diversity. Here, we want to explore the possibility of these popular diversity metrics being incorporated in our mechanism. In this study we picked one candidate from each category, in order to compare with our proposed measure.

For the first category which is focused on the distribution of solutions we picked Spacing (SP). Note that \({\Delta }^{\prime }\) and \(M^{\ast }_{3}\). use consecutive distances and require the lexicography order of solutions in the population. Also \(M^{\ast }_{2}\) and Uniform Distribution (UD) are depended on user-specified parameters σ and the neighbors of a solution). For the second category, which is focused on spread, we selected Overall Pareto Spread (OS) and finally for the third category which considers both distribution and spread we chose Entropy-based metric. In this category Δ and Δ∗ require the True Pareto Front for comparison and it is not applicable for our purpose. The computational complexity of other Metrics of this group ( C L μ and σ , \(\overline {\sigma }\) and Entropy) are high but in this work we picked Entropy-based metrics as an example of this category.

All these metrics are either computationally expensive or are not able to capture the diversity of a solution set in high dimensions. Also many of these metrics relies on specific knowledge of the true Pareto front which is not available in practice and this would prevent their exploitation in the mechanism of evolutionary algorithms. We have designed a parameter free diversity measure which can be effectively incorporated in evolutionary algorithms and also has a polynomial computational complexity. The new diversity measure is based on shortest Hamiltonian path and supposed to effectively evaluate the diversity of populations in high dimensional spaces. A summary of all these classes of diversity measure is revealed in Table 1.

Table 1 A summary of different classes of diversity measure
Full size table

3.7 Proposed Diversity Measure

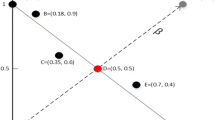
To explain our measure, let us assume that we are given two approximation sets or generally two sets of points in the objective space. For each set, we compose a complete weighted graph using the points in the set and their mutual distances. In such a graph, corresponding to each point we have a node which is connected to all other nodes. Then, we compute mutual distances between all the points and set them as a weight for the corresponding edge. We need to capture the distance between nearby points and the best tool for this purpose is a Hamiltonian path. A path is called Hamiltonian if it passes through all the points once and only once. Here, we need to find a Hamiltonian path with shortest length. It is worth noting that this effort is different from finding nearest point for each solution, which has been utilized in other measures like generalized spread [36]. Finding nearest point can be ineffective and there are usually situations that a distance would be missed while other distances might be considered multiple times, for more details see [1, 20].

The problem of finding shortest Hamiltonian path is NP-complete [40, 41], but there exist several heuristic approaches with polynomial complexity that yields an acceptable approximation to the optimal path. In this study, we used 2-opt algorithm which has a proven complexity of (n 1.2) [41]. This algorithm starts by a random Hamiltonian path in the graph and searches for a locally optimal solution. In each step a change involving two edges is applied to the path and any improvement would be applied in a greedy fashion. The algorithm continues until no change, involving two edges, would improve the path. These paths are identified in order to quantitatively compare the diversity of their corresponding sets of points. We propose to treat these paths as time series using which we can better compare any change in the density of the sets. In this regard, we need to define and find segments in each path.

Each edge in the optimal Hamiltonian path is called a segment. So, for a graph with n nodes we will have n-1 segments. We assume a natural order for the segments, the first segment is the edge between first and second nodes of the optimal path. The length of a segment is the weight of its corresponding edge and the length of a path is the total sum of the edge weights. As an example, we have constructed a graph from a sample set of points whose corresponding optimal path is illustrated in Fig. 2.

Fig. 2
figure 2

Graph of a sample solution set

Full size image

In order to compare the obtained paths, one can simply compare the sum of distances for each path but this can be ineffective in high dimensional spaces. Known metrics tend to lose their granularity in higher dimensions due to the infamous “curse of dimensionality” [20]. Beside, avoiding aforementioned problem, the main advantage of interpreting these paths as time series is that we can compare each set by their acquired time series and there exists a profound history of time series research that we can exploit.

After determining the segments, a time series is constructed using these segment lengths. We visualize this time series in a 2D graph where the x-axis shows the segments in their order and the y-axis shows their corresponding length. Figure 3 illustrates the time series corresponding to the example shown in Fig. 2. The median segment length is indicated by a horizontal line (red line in Fig. 3). In order to compare two time series, we borrow a concept from statistics, named run statistic. Each set of consecutive segments which all have a length below or above the median, is called a run [42]. In other words, if we travel on the time series’ plot, the set of all segments that we pass by, before crossing the median line, is called a run. After crossing the median line, we enter a new run. When a run is below the median it contains points that are close to each other which implies that the area represented by this run is dense; on the other hand, when it is above the median line, it contains points that are scattered. We can incorporate this knowledge obtained from time series into diversity measure.

Fig. 3
figure 3

Time series for the found path in Fig. 2

Full size image

By considering the number and the length of these runs we can compare the diversity of two sets without directly comparing the distances between points. In order to compare these time series precisely, a numerical value should be extracted for each of them. We propose to use the following equation in diversity comparison mechanisms:

$$ D=\frac{L_{max}}{n_{l}} $$
(16)

In this equation L m a x is the length of the largest run below the median and n l is the number of runs below the median. Here for more simplicity, the runs located below the median are called sub-median and the runs located above the median are called super-median. Since sub-median runs are indicator of how close the points are to each other, we decided to incorporate these runs into the proposed diversity measure. A set with a large sub-median run contains an area of dense points so it is not considered as a diverse set. In an ideal set, each point of the time series should constitute a single run and half of them would be sub-median. So, smaller values of this quantity is desired and lower values of D correspond to more diverse sets. Our proposed diversity method is suitable for high-dimensional problems since its complexity is polynomial in terms of number of objectives and also it uses a graph structure to find the order of solutions in the space which is more effective or efficient in higher dimensions than using direct techniques [41]. In the next sub-section utilization of this quality measure will be explained.

3.8 Diversity maintenance mechanism by means of proposed diversity measure

Here in this section, we aim to utilize the proposed metric into the evolution of algorithms and will propose a diversity control mechanism to streamline the optimization process. As stated in many other works, there is a dilemma between controlling diversity and converging to the Pareto front in MOEAs which is directly related to amount of selection pressure applied by the algorithm. In this framework we want to make a balance between these two contradicting objective by maintaining a steady selection pressure in the survival selection operator. In the previous sub section, we proposed a diversity metric which is supposed to effectively evaluate the diversity of populations in high dimensional spaces. Using this measure, we can detect any variation in the population diversity at each generation. After we identified that the population diversity is decreased we should regulate the selection mechanism in a way to compensate for this reduction. In order to incorporate diversity into the selection mechanism of algorithms, in a more controlled way, we proposed a diversity maintenance framework. This framework is concisely illustrated in the Flowchart 2 where it uses the diversity measure described in the previous subsection. In most of common MOEAs, solutions are selected according to their fitness and diversity is used as a tie breaker [1]. We propose to alter this order adaptively. For instance, there may be situations where the population is converging toward a specific region of the front or even a single point. In such a situation, the selection operator should pay more attention to the population diversity than fitness.

Flowchart 2
figure d

Flowchart of the teamwork of proposed diversity measure in proposed maintenance mechanism

Full size image

As stated before the two important issues in our proposed framework was finding a schedule for switching the order of selection and determining the chromosome which has the highest contribution in the diversity of the population to give it an advantage in the selection mechanism. For the former we compare the diversity of each generation to its predecessor and change the selection operator accordingly. Assume that, using the proposed diversity measure, we have acknowledged that diversity is decreased. So, we need to change the selection mechanism in favor of diversity control. In this situation solutions are selected according to their contribution to the diversity of the population rather than their fitness. While choosing between a child and its parent, the parent will be selected if it is located in a super-median run and the child resides in a sub-median run, since it is in a more scattered area of the space. And reversely the child will be chosen if it belongs to a super-median segment and the parent belongs to a sub-median one. If they both are in either above or below of the median line, the selection will be based on the run length. Different cases are illustrated in Table 2. Note that when they both are below the median we are selecting between two dense areas so the one with shorter run length is in a less crowded region, i.e. it contains fewer points. In the same way, when solutions are above the median, they are both in a sparse area and we select the one with larger run length which means less diverse.

Table 2 Different possible selection states
Full size table

The whole procedure of selection according to diversity can be integrated into the following formula:

$$ d(x)=\frac{(-1)^{[x is above the medium]}}{L(x)} $$
(17)

In this equation we used Iverson bracket, here it returns one if x is above the median and returns zero otherwise. Also note that L(x) is length of the run containing x. Points with smaller d values are in more sparse regions of the approximation set. By this equation we determine which chromosome has the highest contribution in the diversity of the population so we give it an advantage in the selection mechanism.

To better understand the selection, consider the plots in Fig. 4 that correspond a hypothetical offspring population and its parent population set. We are to select between parents or their offspring.

Fig. 4
figure 4

These plots represent the time series constructed from two hypothetical populations. The horizontal dashed line indicates the median length and two runs are highlighted in each plot

Full size image

First of all, note that the selection is according to diversity. When comparing either A and D or B and C the selection is based on their position relative to median line. So, for these comparison the solutions below the median line, namely A and C, will be selected. But when the solutions are on the same side of median line we must consider more information. For instance, when selecting between A or C since both are below median we select the one which resides in a shorter run, in this case C. Note that C is in a run with one segments while A is inside a run with three segments. When comparing B and B again we need to look at the run lengths since they both are above median. Here we select the one which is in the longer run. As highlighted in the figure, B is in a run with one segment while D is in a run with three segments so D will be selected.

3.9 Incorporation in MOEAD

So far, we proposed a measure to diagnose the reduction of population diversity along the generations in the high dimensional spaces and using this knowledge repaired and reformed the mechanism of selection based on chromosomes’ participation in either fitness or diversity. In this section, in order to investigate the capabilities of both the proposed diversity measure and the proposed framework we have made few modifications in the MOEA/D [10] algorithm. Actually the selection mechanism of MOEA/D is modified to use our method which is illustrated in Fig. 3. Despite the fact that MOEA/D is a well-known method in the MOEA community for sake of completeness, we have provided a pseudo-code of the modified version of it in Algorithm 1. In this algorithm the selection function (line 10) is the procedure described in Section 3.3, which adaptively changes the selection priority according to the difference in the computed diversity of current population in comparison to the previous one. Also, in line 5 for computing the diversity of current population we use our devised diversity metric which was described in details in Section 3.2.

figure e
figure f

4 The Experiments

This section describes the computational results of the evaluation of the proposed method that was introduced in the previous section. This section outlines three parts. The first part covers the experimental setup for the proposed method. The second part will explain our assessment methodology and two well-known evaluation metrics and finally the third part reports results of the application of the proposed method on a set of well-known artificial problems to test the performance of the proposed algorithm.

4.1 Experimental setup

To prove the potential of our method, we aim at comparing and demonstrating its behavior with known competing algorithms to well-known criteria in terms of diversity and convergence. For this target, we used MOEA/D as a baseline for comparison. Since the proposed mechanism is presumed to be an improvement over MOEA/D this comparison is acceptable. In order to expose the prospects of our method in solving many objective optimization problems, we have also included NSGA-III [16] in our comparisons.

Many test problems have been proposed in the literature where we decided to utilize the most comprehensive and fairly recent WFG problem family [43], since it covers various types of fronts and different form of hindering attributes. WFG Toolkit is designed in a systematic way that can introduce many different attributes to a test problem. Using this toolkit, they have created a set of 9 test problems. The essential properties of each problem in the WFG family are listed in Table 3. In a separable problem the Pareto front obtained from optimization using all variables would be equal to union of all Pareto fronts obtained from optimization using each single variable. The modality stated in Table 2 is for the function used for transforming the decision space to the objective space. For more information on these properties one can refer to [43].

Table 3 Main characteristics of WFG problems (NS: non-separable, S: separable, U: uni-modal, M: multimodal, D: deceptive, PD: parameter dependent bias)
Full size table

WFG problems are scalable in terms of number of objectives and we used problems with 2, 3, 4, 6 and 8 objectives. In our experiments, we used an open source Java library named jMetal, which is a well-known framework for implementing evolutionary algorithms [44, 45]. JMetal contains original implantations of WFG problem family as well as MOEA/D and NSGA-II algorithms.

There are a few parameters that must be set in both algorithms and problems, which are summarized in Table 4. These parameters are either selected empirically or chosen the same as the values proposed by the original authors. The invoked variation operators are polynomial mutation and simulated binary crossover with the same parameterization as mentioned in jMetal framework. Other necessary evolutionary parameters are also configured with the default setting of jMetal.

Table 4 Parameter settings
Full size table

4.2 Performance measures

There are various performance measures used for evaluation of MOEAs. Two of the most commonly used measures are Inverted Generational Distance (IGD) [29] and Hypervolume [27, 28]. These two measures are widely accepted among the researchers in this field and we have employed them in our study. Both measures are capable of evaluating diversity as well as convergence to the Pareto front [20]. These measures are described in the following paragraphs. Hypervolume computes the volume dominated by the points in the approximation set. In order to compute this value one needs a point or a set of points as a reference to limit the volume with it. It can be defined formally in the following way [27, 28].

$$ S(X,R)=\left(\int\bigcup\limits_{x\in X}\{x^{\prime}|x\preceq x^{\prime} \preceq R\}\right) $$
(18)

Here X is the approximation set we want to evaluate and R is the set of reference points. It is shown that hypervolume is the only unary indicator that is compliant with the Pareto operator [26].

A poor choice of reference point can significantly affect the performance of this metric [31]. We normalized all the values in the [0, 1] interval and chose 1 as the reference point for all the problems. Computation of hypervolume is exponential in number of objective and computing hypervolume for problems more than 6 objectives is impractical [19, 26, 31]. In this study we used a Monte Carlo simulation procedure to approximate the volumes for problems with more than 6 objectives [19]. In order to compute inverted generational distance, we need the true Pareto front or a representative subset of it. IGD is computed as the mean distance from each point in the true PF to the nearest point in the approximation set [29].

$$ IGD(P^{\ast}.P)=\frac{{\sum}_{vep^{\ast}}d(v.P)}{|P^{\ast}|} $$
(19)

Here, P is the approximation set we are evaluating and P ∗ is the true Pareto front. Also, d(v,P) is the distance between v and the nearest point in P.

4.3 Results

To have a satisfactory and comprehensive analysis, this paper has evaluated the proposed method using both performance metrics (Hypervolume and the IGD). In the following tables the values of HV and IGD are reported for the algorithms on the selected WFG problems.

Tables 5 and 6 illustrates the average of 30 independent outcomes for each algorithm for concave and convex WFG problems respectively. Here, several test problems with various numbers of objectives (2-8) are used to demonstrate the prospective performance of the proposed method. In these tables, the numbers in each cell is the average of both HV and IGD values of 30 runs.

Table 5 Obtained result for 2D-3D-4D-6D-8D convex problem
Full size table
Table 6 Obtained hypervolume values for 2,3,4,6, and 8 objective concave problems
Full size table

The evaluation of the proposed method on the benchmark test problems had shown a significant improvement in the solution space diversity. Since higher values for Hypervolume and lower values for IGD signify better approximation of Pareto front. These results show that the proposed method performs fine in high dimensional spaces. In order to determine the significance of these results we have used Kruskal-Wallis non-parametric statistical test [46]. The bolded numbers in each row are statistical different from others with 98 % confidence. For better comparison of the results, we have included box plot for all the problems which are depicted in the Figs. 5 and 6. These pictures show that the true median of the proposed method is higher (better) than its competitor.

Fig. 5
figure 5

Box plots comparing hypervolume of each algorithm for 30 independent runs

Full size image
Fig. 6
figure 6

Box plots comparing IGD values of each algorithm for 30 independent runs

Full size image

Results depicted in Tables 5 and 6 indicate that, generally our method has better values of IGD while MOEAD shows better performance in terms of HV. This distinction becomes more obvious as the number of objectives increases. The relative performance of the two algorithms is different for convex problems in comparison with concave problems. In concave problems the proposed method performs better in terms of both assessment measures while in convex problem it shows superiority only in terms of IGD. But the question is which of the two measures are the true indicator of algorithms’ performance. We answer this question in the next section.

4.4 Comparison with other classes of optimizers

In this section, we compare our algorithm with other prominent classes of multi-objective optimizers. As claimed in previous studies [49, 50] other types of population based optimizers can perform better than common multi-objective evolutionary algorithms in certain problem settings; in order to indicate the potential of our method in comparison with these methods we performed this experiment. Differential evolution and particle swarm optimization are two important population based optimization methods which have been generalized for solving multi-objective problems as well [47, 49].

There are many multi-objective particle swarm optimizers (MOPSO) in the literature which are reviewed in the survey by Durillo et al. [51]. One of the effective design choices of an MOPSO is the method of selecting global and personal best locations. Various methods for choosing these locations in each generation is reviewed in the work of Padhye et al. [48]. In order to compare the performance of our algorithm to this class we have selected Speed-constrained Multiobjective PSO (SMPSO) to be included in our experiments [50].

Differential evolution is a special class of evolutionary algorithms suited for real-valued optimization. There are various versions of these algorithms designed for solving multi-objective optimization problems among which Generalized Differential Evolution (GDE3) has shown promising results [49]. We included this algorithm in our experimental comparison to show the competitiveness of our method relative to this class.

Table 7 presents the Hypervolume and IGD values of these two methods along with the corresponding values for our proposed method in solving concave WFG problems. As it can be seen in the table the proposed method has shown superior results in most of the test problems.

Table 7 Comparing hypervolume and IGD values of Different classes of optimizers for concave WFG problems with 2,3,4,6, and 8 objectives
Full size table

Table 7 presents the average of 20 independent outcomes for three algorithms (the proposed method, SMPSO, and GDE3) on concave WFG problems. These test problems have dimensions in range of 2-8 to demonstrate the prospective performance of the proposed method. This evaluation confirms that as the number of objectives in each test function increased, the higher values for Hypervolume and lower values for IGD obtained, comparing to the other two methods, which signifies that the proposed method has better approximation of Pareto front. These results show that the proposed method performs fine in high dimensional spaces. In order to determine the significance of these results we have used Kruskal-Wallis non-parametric statistical test [46]. The bolded numbers in each row are statistical different from others with 98 % confidence.

5 Discussions

In this section we are going to discuss about the performance of our framework and compare the proposed diversity measure with other diversity metrics. In the first part the workflow of our algorithm is analyzed to find out whether it was able to maintain diversity beside convergence. In the second part we compared the obtained results and provided evidence for the superior performance of our algorithm. Finally, in the last part we considered using other diversity metrics in our framework and compared the results with the main approach.

5.1 Diversity Maintenance

It is widely accepted that the main aggravating factor in evolutionary many objective optimization is diversity reduction and here we will show that how our approach can handle this impediment. To better understand the effect of the proposed framework we have studied the behavior of the algorithm by plotting the populations diversity in all generations which is depicted in Fig. 7 for different test problems. The behavior of the algorithm is similar for different number of objectives so to make the paper brief we only presented the plots for 4 dimensional problems. This figure shows the values of the proposed diversity measure in different generations of the algorithm. As it is illustrated in the Fig. 7, whenever the diversity of a population was decreased, our approach detected this failure and the application of its framework had increased it in the next generation. So, over the course of the algorithm the diversity of the algorithm is maintained at a certain level while the population is being pushed toward Pareto front.

Fig. 7
figure 7figure 7

Diversity plot of generations for each problem, Horizontal axis is the number of generations and vertical axis is the diversity measure computed by (4)

Full size image

5.2 Outcome analyzing

Results depicted in Tables 5 and 6 indicate that our approach performs significantly better than their original counterparts in terms of IGD; but this is not true for hypervolume metric. So the main question is that how can we justify this contradiction? There have been many works on comparison between IGD and HV and their capabilities in the MOEA literature. All of them proved experimentally or theoretically that these measures show contradictory results in problems with concave Pareto front, especially in high dimensional objective spaces [20].

In order to evaluate the proposed method, in this study, we have applied our approach to both concave and convex methods. For convex problems, as you can see in the Table 4, our proposed method shows improvements with regard to both quality measures, IGD and hypervolume. But, in solving concave problems our method performed better only according to the IGD measure and there was no significant improvement in hypervolume values. In order to comprehend which method is showing the correct performance we refer to a comparative review of performance measures used in MEOA by Jiang et al. [20]. They proved that IGD and hypervolume measures act in contradiction to each other when dealing with concave problems. In the following, we will illustrate their point.

In their study they focused on problems with symmetric and continuous Pareto fronts which may have concave or convex shape. They define these types of fronts using the following equation:

$$ f^{p}_{1}+f^{p}_{2}+\cdots+f^{p}_{m}=1 $$
(20)

In this equation the objective values are normalized in [0.1] and p is a non-negative real number. The parameter p controls the geometry of the Pareto front. If p is smaller than 1, the Pareto front will be convex and if it is greater than 1 the Pareto front will be concave. According to the instructions given by Jiang et al. [20], we have created two sets of points, S1 and S2, on a Pareto front as they did which had different characteristics. In convex problems, the solutions in S2 are distributed around the extreme points of the front and are considered to be more diverse than the points in S1. This situation is illustrated in Fig. 7, where the sets are created for a 2-dimensional space.

On the contrary, S2 has better diversity than S1 in concave problems. For more details on generating S2 and S1 the interested readers may refer to [20].

As described in Section 4.2, smaller values of IGD and larger values of HV are desired. Figure 8 compares IGD and Hypervolume values for the previously defined sets. In this figure, the vertical axis indicates the difference of measures in a way that a positive value means S2 is better than S1 and a negative value means vice versa. The sets have been designed in a way that for convex problems, 0<p<1, S2 would be better than S1 and as we can see in Fig. 9, both measures acknowledge this fact. But in concave problems, \(1<p<\infty \), we know that S1 is better than S2. In this case, while IGD correctly prefers S1, hypervolume favors S2 which is not true. In conclusion, when we have contradiction between IGD and hypervolume in concave problems, IGD results are more reliable. In fact, this distinction is compatible with the definitions of these metrics. Since IGD is fed with a subset of the true Pareto front it have a knowledge of the extreme points of the true front but Hypervolume does not have this information, So IGD can exploit this extra details and yield more reliable comparison.

Fig. 8
figure 8

The optimal solution sets S1 and S2 for two dimensions. These figures are generated using the source code provided by the authors of [20]

Full size image
Fig. 9
figure 9

The figures in the section were generated using the source code provided by the authors of [20]

Full size image

5.3 Comparison with other diversity metrics

In order to experimentally compare our proposed diversity metric with other measures we have selected three diversity metrics to incorporate in the proposed framework (Section 3.3). These metrics are spacing, overall spread, and the entropy based method proposed in [20] (for more simplicity we call it the entropy metric). These metrics are briefly introduced in the Section 3.1 yet for further information we would refer readers to the original papers. To incorporate a diversity metric in our framework we need to assess the diversity of a population as well as computing the contribution of a single solution in diversity of a set. The former is straightforward since all the measures operate on a set of solutions. But for a solution we used a simple procedure and the desired contribution is computed as the difference between the population’s diversity with and without the considered solution. This method would have extra computations but one should note that this is only for analysis and assessment of our diversity measure.

Table 7 presents the IGD for the diversity control framework with different metrics applied to WFG problems. As you can see our proposed diversity measure performed better in most of the test problems. Since the only difference in the algorithms listed in the columns of this table is the exploited diversity measure, we can claim that our proposed diversity measure based on Hamiltonian path can better capture a population’s diversity Table 8.

Table 8 The performance results obtained for various WFG problems in different dimensions
Full size table

6 Conclusion

In this research, we tried to alleviate the sorts of difficulties that have been ailing multi-objective optimization of high-dimensional problems. Lack of selection pressure propels optimizers to modify selection operators accordingly. These modifications usually lead to loss of diversity in the population which is not desirable and considered as a low performance. Here we proposed a diversity measure and a diversity control mechanism which can be used in combination to remedy this problem.

To control the diversity of population, we used an adaptive framework which changes the selection operator according to changes in the diversity of the population. By an increase in the population diversity, the selection operator will change to increase the selection pressure and by a decrease in diversity the selection pressure will decline. In order to find the variation of diversity this paper proposed a diversity measure based on shortest Hamiltonian path to monitor the diversity variation in each generation.

With the intention of assessing the proposed method, we incorporated it into MOEA/D a well know multi-objective evolutionary algorithm. The only diversity control facility used in MOEA/D is the initial decomposition of the multi-objective optimization problem into a set of uniformly distributed sub-problems. In high dimensions, this decomposition is not coarse enough so it will not be as effective as expected. We exchanged the MOEA/D selection mechanism with our devised operator and used this new MOEA/D algorithm in the experiments. For experiments we used WFG problem family which are the most comprehensive and recent group of test problems in the literature. To evaluate and compare the obtained results two performance measures were used, IGD and hypervolume. Applying both methods to concave and convex problems revealed a contradiction between the two performance metrics. While the modified MOEA/D performed better in terms of IGD in convex problems, the original MOEA/D performed better in terms of Hypervolume. In order to ascertain which performance measure is right, we provided two types of solution sets with known diversity contrast and proved that IGD yields more accurate comparison. Consequently, our method is of a valuable potential and can be extended and refined to perform even better.