1 Introduction

Since the introduction of GP in 1992 [1], it has been successfully applied for problem solving in various domains such as circuits, controllers, image recognition, bioinformatics, robotics, reverse engineering and symbolic regression [2]. However, a relatively small number of theoretical results are available which explain why and how GP works. Furthermore, these theoretical results have been seldom used practically to improve GP and there is still a large gap between theory and practice [3, 4]. Schema theory is the oldest and the most well-known model of evolutionary algorithms. A schema is a subset of points in the search space that share some characteristics. The schema theory predicts the number of individuals that belong to the schema in the next generation in terms of information obtained from the current generation. The schema theory can provide a deeper understanding of the evolution process and population dynamics. Furthermore, the insight gained through schema theory investigations can result in advantageous practical feedbacks. A well-defined schema theory is a realistic model of evolutionary algorithm that is very useful in predicting the behavior of GP, for example detecting the convergence possibility in early stages of evolution. It can also be used for selecting the optimal configuration, including the combination of operators, parameter setting, fitness function, representation method and initialization strategy.

Schema theory was originally developed for explaining the power of GA [5]. Holland claimed that GA searches for optimal patterns called schemata, while searching for optimal chromosomes. His schema theory provides a lower bound on the expected number of chromosomes belonging to a given schema, in terms of some quantities measured in the current generation, e.g., the number and the average fitness of chromosomes matching the schema and the average fitness of the overall population. In the context of GA, a schema is usually represented by a string over the alphabet [6]. The character “#” refers to “don’t care” symbol that could be replaced by any arbitrary symbol of alphabets. Given a schema H and its information in generation t, the general form of schema theory (i.e., (1)) describes how the expected number of individuals sampling H varies in generation t+1,

$$ E[m(H,t+1)]=M\alpha (H,t), $$
(1)

where M is the size of the population, m(H, t+1) is the number of individuals belonging to H in generation t+1 and α (the transition probability) is the probability that a newly created individual belongs to schema H.

Schema theory was initially introduced for GA and later was extended for GP [1]. However, due to some GP search properties, principally the variability of individuals’ size and shape, obtaining the schema theory for GP is much more complicated than GA. After introducing the first schema theory for GP [1], it has been enhanced in various ways by extending the basic theorem for different operators, expressing the formulation in terms of different measures and improving the exactness of the theorem equation [3, 7–16]. However, there are still some fundamental issues concerning the GP schema theory which are not well addressed.

The most popular definition of a schema in GP literature is “a set of points in the search space that share some syntactic characteristics” [15–17]. Considering the principal objective of schema theory that is modeling the behavior of evolutionary algorithms, the schema must be a set of points of the search space which have common behavior. Therefore, the above definition of the schema can be valid just in the case that syntactically similar individuals have similar semantics and functionalities as well. Although this assumption is almost true for GA, it does not hold for GP because the representation of GP does not preserve the neighborhood in genotype-phenotype mapping [18, 19]. Nearly all schemata defined in the literature provide a partitioning over the genotype space. As a result, in spite of syntactic similarity, different instances of a syntactic schema may have extremely different phenotypes. There are several major issues with relying on these schema theories for predicting future populations and applying them in practice, principally:

  • The internal fitness variance in syntactic schemata is extremely high [13]. Therefore, the average fitness of schema instances is not an appropriate descriptor of samples’ fitness. The predicted schema status in the next generation based on the schema’s average fitness is far from the status of each of individuals sampling it. In other words, obtaining a unified model for describing the behavior of all schema samples is not promising, as individuals instantiating this kind of schema are mapped to different phenotypes.

  • The schema related quantities like fitness, change from one generation to another in an unexpected way because the schema is described based on syntactic features rather than semantic characteristics or fitnesses. Since the formulation of schema theorem is composed of these schema related factors, even in exact schema theories the prediction of the frequency of individuals sampling the schema in the next generation is not precise. Under these circumstances, estimating the propagation of a schema in further generations is not rational. Therefore, one cannot predict the results of evolution in early generations and schema theory remains just a theoretical formulation without any usages in practice.

  • As Majeed [20] noted, the fitness values of existing schemas follow independent trends in different runs. Thus, due to changes of schema frequency estimations from one run to another, it is not possible to find a single optimal configuration of GP for a specific problem based on schema theory predictions.

  • In syntactic schemata, there is a close relationship between schema theory and the underlying GP representation. Applying these schema theories to new variants of GP is difficult.

  • Most previous schema theorems provide the propagation of a given schema, without looking for schemata that are actually present in the population. They do not propose any extraction method for finding all or even important schemata of the population. The main reason possibly is the syntax-based definition of the schema, which causes the number of schemas to be greatly massive even in small populations. Thus, tracking and analyzing all schemata of the population is not practically possible and this makes the usage of schema theory difficult.

Consequently, syntactic schema theories are not reliable descriptors of GP dynamics. Schema definition based only on the genotype of individuals is inadequate [19]. Nearly all previous schema definitions are not beneficial enough in understanding and predicting the behavior of GP.

The main objective of this study is proposing a schema theory as a more realistic model of GP that can be potentially employed for improving GP in practice. To this end, the concept of semantic schema is introduced. The semantic schema partitions the search space according to semantics of trees, regardless of their shapes and structures. We interpret semantics of a tree in terms of the mutual information between its output and the target output. The semantic schema is characterized by a set of semantic building blocks together with their joint probability distribution. After defining the notion of semantic building blocks, we provide an extraction algorithm for finding these building blocks in a given population. A schema extraction method that looks for the most significant schema present in the population and an exact microscopic schema theorem are also proposed.

The rest of the paper is organized as follows. Section 2 aims to provide a comprehensive survey of GP schema theory and the proposed method is explained in Section 3. Experimental results are discussed in Section 4 and finally Section 5 concludes the paper.

2 Related work

The first schema theory for GP was developed by applying Holland’s schema theory to GP [1]. After presenting the earlier work in GP schema theory, the basic schema theorem was enhanced in many directions and several schema theories was introduced in the literature. Some researchers proposed a type of rooted (i.e., positioned) schema [7-10, 16, 21-23] and some others suggested non-rooted (i.e., position-less) variants [1, 13, 14, 20, 24]. In a rooted schema, the schema is forced to occur in the root of its instances. Hence, in addition to schema subtree or pattern, this kind of schema provides the information about the position of the subtree. In contrast, non-rooted schemata are subtrees that can occur at any point in a program tree and may repeat multiple times in the single individual.

The derived equation of schema theory is in terms of microscopic measures (i.e., the detail information of each individual) in some studies [9, 24] and macroscopic quantities (i.e., the overall information about sets of individuals) in others [1, 7, 7, 8, 10, 14, 16, 21, 23, 25].

The exactness of the schema equation was ignored in the earlier work [1, 9, 13, 14, 21] and undertaken in more recent ones [3, 7–14, 16, 23]. Inexact schema theories provide only lower bounds on the expected number of instances of a schema in the next generation.

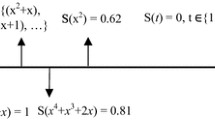
Koza [1] defined the schema to be a set of complete subtrees or S-expressions, for example H = {(- xy) (+ y(* xx))}. Each individual containing both specified subtrees, instantiates the H.

The GP specific schema theory was first presented by Altenberg [12] based on the probabilistic model of GP. He defined a schema as a subtree that must exist in each of the schema samples. Altenberg then obtained an equation that provides the frequency of a given program in the next generation. He expressed the equation in terms of quantities, such as the fitness and the frequency of each individual, the probability that inserting a given subtree in a given parent can result in a specified offspring and the probability that a given subtree is selected for crossover. The calculation was made under several assumptions, including: the population is very large, standard crossover and fitness proportionate selection are used and crossover produces just one offspring.

Koza’s work on schema theory was generalized later by O’Reilly and Oppacher [13] in order to include also incomplete subtrees called tree fragments. Tree fragment refers to a tree having at least one “don’t care” symbol as the leaf which can be matched by any valid subtree. In their study, a schema is then represented by a set of pairs. Each pair contains a complete or incomplete subtree along with an integer indicating the minimum required number of occurrences of the subtree in schema samples.

Whigham [14, 26] investigated the notion of schema for context-free grammar-based GP and suggested a partial derivation tree as a schema. Each program that can be obtained by completing the schema is considered its instance. He also provided the related schema theorem in the form of a simple equation for the probability of schema disruption under the presence of crossover and mutation.

Poli and Langdon [3, 22], defined a schema to be a tree composed of functions from the set F U {=} and terminals from the set T U {=}, respectivelyFootnote 1. Where F and T are problem specific function and terminal sets and “ =” is a “don’t care” symbol matched by a single terminal or function character. In contrast to previous research, this schema is rooted which force the schema to be instantiated at most once within a program. As a result, predicting the propagation of schema components in the population is equivalent to studying the number of schema samples. Furthermore, due to the special notion of the “don’t care” symbol in their schema, the shape and size of all samples are the same. Although this feature made the overall calculations easier, fixed shape and size schema faced with serious difficulties when investigating the effect of standard crossover because standard crossover changes the shape and size of trees. The resulting schema theorem was a worst-case scenario model, since the schema creations from non-instance parents were not calculated.

Rosca and Ballard [9, 27] also developed a rooted tree schema theory. In their definition, the “don’t care” symbol stands for any valid subtree. Rosca suggested a non-exact schema theorem for GP with standard crossover as a function of microscopic quantities such as the size and fitness of the programs matching the schema.

The difficulty with describing the effect of standard crossover in fixed size and shape schema [3] led authors to extend this schema in order to take the advantages of both single [3] and subtree [9] “don’t care” symbols, through the definition of hyperschema [10, 11]. As Poli defined, a GP hyperschema is a rooted tree composed of the function set of F U {=} and terminal set of T U {=, #}. The derived theorem corresponding to hyperschema was an exact formula for predicting the expected number of schema instances in terms of microscopic quantities, for GP with one-point crossover [11] which was then extended to macroscopic version [10]. Poli et al. continue to use this definition of schema in many studies on schema theory for GP with various operators like one-point crossover [15], standard crossover applicable to linear structures [28] and homologous crossover [29].

In order to obtain a valid schema theory for subtree-swapping crossovers, Poli [23] extended the notion of hyperschema to Variable Arity Hyperschema (or VA hyperschema for brevity). According to his definition, having all features of the hyperschema, a VA hyperschema can also include # symbol for internal nodes, which stands for exactly one function of arity not smaller than the number of linked subtrees. Poli proposed two exact schema theorems indicated by both microscopic and macroscopic measures respectively, for GP with subtree swapping crossover. This work was then extended also for headless chicken crossover and subtree mutation [30] and the general form with more details and results, appropriate for many types of crossovers was presented in [7, 8].

In 2004, Poli et al. [16] derived an exact macroscopic GP schema theory applicable to the class of homologous crossovers. This schema was based on the concepts of hyperschema and node reference system introduced in their previous work. The authors also tried to develop a Markov model for GP dynamics based on the suggested theory.

More recently, Majeed [20] defined a schema as a subtree with “don’t care” symbol in leaves and suggested a method to extract it from the final generation. In his opinion, a subtree with acceptable size must be present in at least half of the population in order to form a schema. After selecting a significant subtree, some nodes were probabilistically replaced by the # symbol. In similar work, Smart [25] defined schema as a subtree with “don’t care” symbol called tree fragment. None of them provided a mathematical formulation for predicting the schema instances in the next generation.

Li et al. [25, 31, 32] represented a GP schema with an instruction matrix. Each row of the matrix corresponds to a single node of the tree and contains multiple copies of primitive symbols. Each matrix element (i.e., instruction) stored the best and average fitness value based the fitness of individuals containing it at the specified location. This approach is considered to be more similar to Estimation of distribution algorithm (EDA) [33] rather than schema-based GP.

Table 1 summarizes the important previous work in the schema theory of GP. In this table, for each proposed schema theory, the schema definition, schema instantiation and an example are provided. The exactness of the schema theory, whether the schema is rooted or not, whether the theory is described in terms of macroscopic quantities or not and whether the “don’t care” symbol is used (in the form of single character (=) and/or subtree (#)) are reported in subsequent columns. Then, genetic operators under which the theory is developed are specified in the next column. Finally, in the last two columns, providing a schema extraction method and experimental results by the related study is determined.

Table 1 Summery of related work on schema theory
Full size table

As Table 1 demonstrates that in all studies the schema definition is based on a syntactic element, usually a subtree or a tree fragment. Thus, all of previously mentioned schema theories suffer from issues enumerated in Section 1. Except in very few researches [17, 20, 25], no extraction method is specified for finding the present schemata in a given population by studies of Table 1. Again, it is indicated in the table that researchers rarely provided experimental results for their schema theories. Some work analyzed and tracked the schema frequency or other schema theory terms in evolution [9, 17, 20, 21, 28]. Poli and Langdon [21] analyzed the empirical aspects of their schema [3] in a separate study. They tracked the number of all possible schemata in the population of Boolean programs with depth 2 and 3. The estimation of schema frequency by the schema theory was also compared with the observations under selection only. Rosca [9] analyzed the values of important terms in his schema theorem in actual populations. Poli and McPhee [28] studied the size bias of genetic operators both using schema theory and real runs in the case of linear representation. Majeed [20] extracted schemata as subtrees with acceptable sizes that occur in at least half of the population and present in the last generation. Smart and Zhang [17] also studied the number and size of fragments in population, the popularity of most frequent fragment and the number of “maximal fragments” over different generations. Some other researchers tried to employ schema theory for improving the GP performance [7, 8, 34]. Poli and McPhee [34] investigated the interaction of genetic operators in GP with linear structure and specified the optimum relative probability of different operators just theoretically. Again, Poli and McPhee proposed a selection strategy for controlling bloat based on the schema theory [7, 8].

3 Proposed approach

While a great deal of work has been done on developing the schema theory for GP, finding a reliable schema theory is still a critical issue. In addition to explaining theoretical aspects of the evolution process, a reliable schema theory can be applied for enhancing the performance of GP. Most of schema theories introduced in GP have been borrowed from GA. In fact, they tried to keep the concept of GP schema as close as possible to GA. However, the hierarchical representation utilized in GP causes difficulties that do not exist when dealing with linear chromosomes of GA. The representation of GP does not preserve the neighborhood in genotype-phenotype mapping [18, 19]. However, almost all existing GP schemata have been characterized based on syntactic features. Syntactic schemata perform a partitioning over the genotype space. In contrast to GA, different instances of a GP syntactic schema may have extremely different semantics and behavior. Since the main objective of schema theories is describing the behavior of evolutionary algorithms, to obtain a reliable schema theory, the schema must be matched by a set of points of the search space that share some semantic characteristics. The instances of this schema will have obviously common behavior.

Due to various issues of syntactic schemata listed in Section 1, we are interested in a semantic schema that partitions the semantic space rather than the syntactic space. For introducing the semantic schema, the notion of semantic space is first described in Section 3.1. The semantics of a tree is interpreted in terms of normalized mutual information of its output and the target output. The semantic space is then defined accordingly. The semantic schema is identified based on semantic building blocks instead of syntactic features. The concept of semantic building blocks is clarified in Section 3.2 and the related extraction approach is explained. Since the final solution found by evolution is a combination of building blocks, the co-occurrence of these blocks in individuals is also important in forming a semantic schema. Section 3.3 is devoted to describing the steps of the joint probability distribution estimation for a given population. In Section 3.4, the proposed schema is expressed in terms of the joint probability distribution of semantic building blocks. The extraction procedure of significant schema is also provided in this section. Significant schema refers to the most important schema of a given population that its samples have high semantic similarity to the target. Extracting the significant schema is performed initially by selecting a cluster of individuals which are semantically similar to the target, then discovering semantic building blocks contributing in the selected cluster and finally estimating their probability distribution.

3.1 Semantic space

In GP, the individual’s genotype is the actual representation of syntax in the tree and the individual’s phenotype or semantics refers to the behavior of the tree during the execution. The phenotype is often considered equal to fitness and fitness is typically calculated in terms of error-based quantities. Due to the weaknesses of error-based measures, we represent phenotype space using mutual information-based measures. This space is referred to as semantic space. As several genotypes may map to a same fitness, a phenotype space that is defined based on fitness, have less redundancy than genotype. Mutual information is even more abstract criterion for representing the phenotype and semantic spaces. A group of individuals with different fitness values may have the same semantic features. The semantics of each tree is interpreted as normalized mutual information between its output and the target output. Considering that the mutual information between the output of various trees (with different fitnesses) and the target may be equal, the semantic space has much less redundancy than the ordinary phenotype space.

Definition 1 (Semantic similarity)

let X be a random variable denoting the output value of tree t and Y be a random variable denoting the corresponding target output, the semantic similarity of tree t to the target is then defined to be the normalized mutual information of X and Y as shown in (2):

$$ SS(t)=\frac{I(X;Y)}{H(Y)}, $$
(2)

where I(X;Y) is the mutual information of X and Y and H(Y) is the entropy of Y, given in (3) and (4), respectively:

$$ I(X;Y)=\sum\limits_{y\in Y}\sum\limits_{x\in X}p(x, y)\log(\frac{p(x, y)}{p(x)p(y)}), $$
(3)
$$ H(Y)=-\sum\limits_{y\in Y}p(y)\log(p(y)). $$
(4)

In the above equations, x values are different samples of random variable X that denote output values of tree t when substituting the problem test cases for tree variables. Y values are samples of the random variable Y that refer to desired outputs obtained directly from the problem test cases. Extracting building blocks from semantic space is more efficient than syntactic or error-based phenotype spaces. Intuitively, mutual information measures the amount of information that subtree contains about the target. We interpret tree semantics in terms of mutual information rather than commonly used fitness measures, such as mean squared error, because arbitrary fitness indicators often fail to correctly reward potential building blocks contributing to the final solution [35]. It means that the components of the final solution do not necessarily have high fitness. Furthermore, mutual information is invariant under invertible transformation [36] and provides a general dependency measure [37] so it can be effective in identifying potential building blocks in early generations. In contrast to ordinary fitness measures, mutual information can safely ignore constant multiplication or addition in evaluating expressions of symbolic regression problems. Sensitivity of error-based fitness indicators to the details of expressions (e.g., constants) causes the search procedure to pay less attention to the principal components of the expressions and building blocks. Applying information theory to evolutionary computation has been already suggested in several studies [35, 38–40].

It should be noted that the relation of subtree-semantic similarity is not invertible, such that the mutual information between a group of subtrees and the target output may be the same. For example, all expressions of (x+y), (x+y+ 100), (2 x+2y) and (x+y+2x- 2 x) have the same semantics. If two subtrees are equal, their semantic similarities to the target are also equal, however, the inverse is not true. Hence, for detecting semantically equal subtrees the semantic similarity to the target is not adequate. The semantic equality of two subtrees is defined in Def. 2.

Definition 2 (Semantic equality)

let X and Y be random variables denoting the output values of two trees t 1 and t 2. Then, t 1 is semantically equal to t 2 if:

$$ \frac{I(X;Y)}{H(X,Y)}=1, $$
(5)

where I(X; Y) is the mutual information and H(X, Y) is the entropy of X and Y given in (6).

$$ H(X,Y)=-\sum\limits_{y\in Y}\sum\limits_{x\in X}p(x, y)\log(p(x,y)), $$
(6)

x and y values denote the different samples of random variables X and Y that are the output values of trees t 1 and t 2 respectively, when substituting the problem test cases for tree variables.

For referring to the set of semantically equal trees, a semantic representative treeis defined in Def. 3 as the smallest tree that is semantically equal to trees of that set.

Definition 3 (Semantic representative tree)

let A = {t 1, t 2...t n } be a set of semantically equal subtrees according to Def. 2. Then, t k ∈A is the semantic representative tree of set A if it is the smallest tree in A.

Take for example the set A = {(+xy),(+++xxyy),(++xy/xx),(++xy−+xx+xx)}, in which trees are represented in LISP language. According to Def. 3, the semantic representative tree of A is (+xy).

3.2 Semantic building block

Building block hypothesis was originally introduced by Goldberg for GA [41]. The hypothesis states that GA work by combining short, low order and highly fit schemata, named building blocks. These blocks combine with each other to construct larger schemata with potentially higher fitnesses and exponentially increasing instances in population. There are several studies on discovering the building blocks for GP. In the most of related work, the frequency of a syntactic structure such as a subtree [42–45], an expression [46] or an instruction sequence [47, 48] is measured. Likewise, Langdon and Banzhaf [49] considered the repetition of correlated outputs in best of run individual for detecting building blocks. For addressing the problems of syntactic structures, we defined building blocks in semantic space. The definition of a semantic building block is given in Def. 4.

Definition 4 (Semantic building block)

a semantic representative tree is a semantic building block if it satisfies three conditions: (1) it has high semantic similarity value (2) the occurrence frequency of subtrees that are semantically equal to it, is high and (3) its size is more than a threshold.

For a given cluster of population, the occurrence frequency and semantic similarity of all large enough subtrees to the target are investigated in order to identify building blocks. According to Holland’s theory [5], building blocks should have high fitness and occurrence frequency. However, due to definite advantages explained in Section 3.1, we looked for subtrees with high semantic similarity instead of fitness. Since introns distribute in high-fit individuals without any immediate positive impact on modeling the target, the semantic similarity is measured for all subtrees not just the whole trees. Enumerating all subtrees in one hand and selecting subtrees that have high semantic similarity to the target on the other hand, avoid detecting introns as building blocks. Similar to [49], for calculating the frequency of a semantics, we enumerate all subtrees that are semantically equal to its representative tree, regardless of their various shapes and structures. Clearly, after mapping the subtrees to semantic space, the frequency is measured in semantic space instead of genotype or fitness spaces. The pseudocode of Fig. 1 describes the details of related steps, in which three conditions of Def. 4 are checked with thresholds minSemanticSimilarity, maxFrequencyRankandminBlockSize. For each set of trees having semantic similarity value equal to ss, their semantic representative tree, referred by srt is identified.

Fig. 1
figure 1

Pseudocode of semantic building block detection

Full size image

Table 2 illustrates an example of extracted building blocks from generations 1, 10 and 20 of benchmark x 4+x 3+x 2+x (F1 in Section 4.1). For each building block, the value of semantic similarity and the corresponding frequency are also mentioned. The building blocks distribute and combine throughout the evolution process to form the final solution. As it is demonstrated in this table, two building blocks of generation 1 (i.e., x 2+x and x 2+2x) are also distinguished as building blocks in generation 10 with higher frequencies. The building blocks x 3and 2x 2+x from generation 1 are combined to form the building block x 3+2x 2+x in generation 10. In generation 20 the evolution converges to a single building block that is the final solution to the problem. Additionally, Table 2 illustrates the semantic similarities of building blocks to the target along with their corresponding fitnesses. It can be also inferred from the table that the average semantic similarities increase over evolution.

Table 2 An example of extracted semantic building blocks in different generations for x 4 + x 3 + x 2 + x (F 1 in Section 4.1)
Full size table

3.3 Estimating probability distribution

Due to the complex tree structure and node interactions, direct modeling of tree-based GP is very complicated [50]. Thus, we map the tree space to the new space of building blocks Ω, which is absolutely simpler and more effective in representation of the semantics behind the trees. Considering that the GP evolves the best solution by combining building blocks, describing trees in terms of building blocks simplifies evolution modeling. To this end, each tree t 𝜖 C is mapped to a point \(\hat {{t}}\epsilon \quad {\Omega } \) in building block space such that \(\hat {{t}}[i]\)denotes the number of subtrees in t, semantically equal to ith building block. As a result of this mapping, all trees are represented by fixed length vectors of integer values (i.e., building block frequencies) rather than variable shape-and-size tree structures. Considering k as the number of extracted building blocks, the mapping can be formally represented as,

$$\begin{array}{@{}rcl@{}} &&C\to {\Omega} \\ &&{\Omega} =\{\hat{{t}}\vert \hat{{t}}[i]=BB_{i} \,frequency\,in\,\,t\in C\,\,\,:\,\,i=1,...,k\}\\ \end{array} $$
(7)

Figure 2 illustrates the tree t in C and Ω spaces, assuming building blocks of generation 1 given in Table 2 as a required building block set.

Fig. 2
figure 2

An example of mapping a tree to building block space

Full size image

A tree may contain one or more occurrences of some extracted building blocks. When a tree does not include a building block, a zero value is inserted in the corresponding place of its mapped vector. In many problems the number of these zero values is relatively high, which results in sparse vectors that bias the modeling. This phenomenon is similar to what happens in natural language processing when documents are mapped to the vector space model [51]. By removing zero values, distribution estimation becomes simpler, however, points in k-dimensional space of Ω are converted to variable length vectors. Hence, vectors are partitioned based on their contributing building blocks to spaces \(\overset {[1]}{\Omega }\) containing the first building block, \(\overset {[2]}{\Omega }\) containing the second building block, \(\overset {[1,2]}{\Omega }\) containing both and so on:

$$ \overset{\left\{ {1,2,...,k+1} \right\}}{\Omega}=\bigcup\limits_{s\subset \left\{ {1,2,...,k+1} \right\}} {\overset{s}{\Omega} } \,\,\,\,\,\,\,\,,\,\,\,\overset{s}{\Omega}\! \,=\!\{\hat{{t}}\vert \forall j\in s,\hat{{t}}[j]\ne 0\}. $$
(8)

For estimation of the underlying distribution of Ω, we use a mixture of normal distributions such that each cluster \(\overset {s}{\Omega }\) is supposed to follow the multivariate normal distribution:

$$ \overset{s}{\Omega} \sim N_{\left| s \right|} (\mu_{s} ,{\Sigma}_{s} ), $$
(9)

the |s| refers to the size of s. The parameters μ s (mean) and Σ s (covariance matrix) are estimated using basic estimator biased to semantic similarity of \(\overset {s}{\Omega }\) members, as follows:

$$\begin{array}{@{}rcl@{}} \mu_{s}&=&\frac{1}{\sum\limits_{i=1}^{{\vert\overset{s}{\Omega}\vert }} {SS(\hat{{t}}_{i} )} }\sum\limits_{i=1}^{{\vert \overset{s}{\Omega} \vert}} {\hat{{t}}_{i} .SS(} \hat{{t}}_{i} )\,\,\,\,\,\,,\,\,\,\,\,{\Sigma}_{s} \,\\&=&\frac{1}{\sum\limits_{i=1}^{{\vert \overset{s}{\Omega}\vert }} {SS(\hat{{t}}_{i} )} }\sum\limits_{i=1}^{{\vert\overset{s}{\Omega}\vert }} {(\hat{{t}}_{i} -} \,\mu_{s} )(\hat{{t}}_{i} -\,\mu_{s} )^{T}.SS(\hat{{t}}_{i} ). \end{array} $$
(10)

Finally, the distribution of total set Ω will be the union of distributions of its partitions \(\overset {s}{\Omega }\). Like the Gaussian mixture model, a weight ϕ s is also assigned to each component \(\overset {s}{\Omega }\), taking into account the significance of each set:

$$\begin{array}{@{}rcl@{}} p(\hat{{t}}\left| \lambda \right.)=\sum\limits_{i=1}^{M} {\phi_{i} N_{\left| {s_{i} } \right|} (\mu_{s_{i} } ,{\Sigma}_{s_{i} } )} \\ \lambda =\left\{ {\lambda_{s} } \right\}_{s\subset \left\{ {1,2,...,k} \right\}} ,\,\,\,\,\lambda_{s} =\{\phi_{s} ,\mu_{s} ,{\Sigma}_{s} \}, \end{array} $$
(11)

where λ is the sequence of parameters λ s indexed in subset s. λ s is itself the set of μ s , Σ s and ϕ s parameters that characterizes the distributions of \(\overset {s}{\Omega }\). M is the number of subsets s⊂{1,2,..., k}with large enough members in \(\overset {s}{\Omega }\) and finally ϕ i is calculated as the average semantic similarity of set s i normalized by its maximum value as shown in the following equation:

$$ \phi_{s} =\frac{{\sum\limits_{\hat{{t}}\in \overset{s}{\Omega} }}{SS(\hat{{t}})} }{\underset{l=1:M}{Max} (\phi_{s_{l}} )}. $$
(12)

It should be noted that, in order to skip the bias of sparseness, the distribution of a mixture of non-sparse vectors is calculated and since the underlying distribution of each partition \(\overset {s}{\Omega }\) is unknown, normal distribution is employed. The pseudocode of probability distribution estimation is demonstrated in Fig. 3.

Fig. 3
figure 3

Pseudocode of probability distribution estimation

Full size image

3.4 Semantic schema

As discussed in previous sections, the schema is defined in GA and subsequently GP literature as a set of points in the search space that share some syntactic characteristics. Syntactic schemata are not reliable descriptor of GP behavior because they matched by semantically different individuals that behave differently under evolution. Our proposed schema called semantic schema appears as a partitioning over the semantic space. This schema is matched by a set of points of the search space that have common semantic features.

3.4.1 Definition

The semantic schema should be described so that reflects the semantic features of its samples. An ideal definition of the schema is a definition that is matched by semantically similar trees. In this study, the notion of semantic schema is defined in terms of semantic building blocks. According to the building block hypothesis, the final solution is constructed by combining building blocks during the evolution. Poli also claimed that schema theory is the result of representing the dynamics of GP in building block basis [52]. Consequently, we defined the semantic schema in terms of semantic building blocks. Since the final solution is a combination of building blocks, the co-occurrence of these blocks in a tree is a good representative of the degree of similarity of that tree to the final solution. As a result, a semantic schema should also specify the appropriate co-occurrence of building blocks in order to distinguish schema instances from other individuals. To the sum up, semantic schema is defined as given in Def. 5.

Definition 5 (Semantic schema)

given a cluster of trees, a semantic schema is composed of two components: (1) a set of semantic building blocks {B 1, B 2,..., B k }and (2) the joint probability distribution of building blocks in schema instances,\(p(\left . {\hat {{t}}} \right |\lambda )\):

$$ H=(\{B_{1} ,B_{2} ,...,B_{k} \}\sim p(\left. {\hat{{t}}} \right|\lambda )). $$
(13)

The definition of semantic building blocks in the semantic space enables the schema to keep high diversity in genotype space while it is restricted in semantic space. This feature vastly expands the expression power of schema because it can describe all subtrees with nearly similar meaning and many different shapes, structures and even functionalities. The definition of schema is actually responsible for describing the principal feature of the instances and leads them to have similar semantics. This feature is supposed to be the distribution of semantic building blocks in schema samples.

As discussed in Section 2, most researches in the literature provided the propagation of a given schema, without looking for real schemata that are present in the population. Lack of a practical definition and extraction method is one of the issues that caused criticizing the usefulness of schema theorems. In this paper, we intend to propose a schema theory that in addition to theoretical description of evolution process can be employed for improving GP in practice. Hence, the empirical aspects of schema theory, such as extraction method are also considered in the definition of the schema. According to practical considerations, the focus of this study is on a significant schema that its samples have high semantic similarity to the target. The definition of significant schema is given in Def. 6.

Definition 6 (Significant schema)

the significant schema is a semantic schema extracted from individuals with more than average semantic similarity.

3.4.2 Extraction approach

The significant schema is extracted through three steps. Inspired from the building block hypothesis [5], a cluster of trees, including individuals with more than average semantic similarity is first selected, the building blocks of this cluster are then detected as explained in Section 3.2 and the probability distribution of building blocks is finally estimated by the approach described in Section 3.3. Detecting the building blocks in schema instances and estimating their joint probability distribution characterize the underlying semantic schema.

3.4.3 Schema instances

In previously proposed schemata, instances are identified simply through matching a syntactic pattern. In the proposed method, a tree t instantiates the semantic schema H if its occurrence probability according to \(p(\hat {{t}}\left | \lambda \right .)\) is more than a specified threshold denoted by η:

$$ \,p(\hat{{t}}\left| \lambda \right.)>\eta \to t\in H. $$
(14)

Generating schema instances is also important for evaluation goals. Given the schema \(H=(\{B_{1} ,B_{2} ,...,B_{k} \}\sim p(\left . {\hat {{t}}} \right |\lambda ))\), a selection probability proportional to ϕ s is assigned to each set s ⊂ {1,2,..., k}. For generating a new schema instance, one set is first selected according to these probabilities. The contributing building blocks in the selected set are then added to GP terminal set and random tree t is regenerated until t∈H. This generation method guarantees that the trees will be generated in all clusters of \(\overset {s}{\Omega }\) proportional to the average semantic similarity of its members. Consequently, the diversity of generated trees is also preserved.

3.5 Schema theory

After defining the semantic schema, the effects of genetic operators are investigated. The total transmission probability of semantic schema H in generation t under selection and crossover operators can be expressed in (15):

$$ \alpha (H,t)=p(H,t)(1-p_{xo} )+p_{xo} \alpha_{xo} (H,t), $$
(15)

where p(H, t) is the probability of selecting schema samples, p xo is the probability of crossing over and α xo (H, t) is the transmission probability of H under crossover.

3.5.1 Effect of fitness proportionate selection

If fitness proportionate selection is used, the probability of selecting each schema instance is

$$ p(H,t)=\frac{m(H,t)f(H,t)}{M\bar{{f}}(t)}, $$
(16)

where f(H, t) and m(H, t) are the average fitness and the number of schema instances of H in generation \(t.\bar {{f}}(t)\) is the average fitness of the population in generation t.

3.5.2 Effect of standard crossover

In this section, the effect of standard crossover on schema samples is investigated under the assumption that crossover points are selected outside of subtrees semantically equal to building blocks. We restrict the selection of crossover points in order to protect building blocks from disrupting. This encapsulation preserves building blocks as problem specific subroutines and leads to more effective search. Inspired from [7, 8], the transmission probability of the semantic schema H due to the crossover in terms of microscopic quantities is given by (17).

$$\begin{array}{@{}rcl@{}} \alpha_{xo} (H,t)&=&\sum\limits_{h_{1} } {\sum\limits_{h_{2} } {p(h_{1} ,t)p(h_{2} ,t)} } \sum\limits_{i\in NB(h_{1} )} \sum\limits_{j\in NB(h_{2} )}\\ &&{\frac{\delta (p(\hat{{C}}(h_{1} ,i)+\hat{{S}}(h_{2} ,j)\vert \lambda_{s_{1} \cup s_{2} } )>\eta )}{\left| {NB(h_{1} )} \right|\left| {NB(h_{2} )} \right|}} ,\end{array} $$
(17)

where p(h, t) is the selection probability of tree h and NB(h) is the set of nodes of h not belonging to building blocks that can be selected as crossover points. C(h, i) is the context of h which is the remaining part of tree h after eliminating the subtree rooted at node i and S(h, i) is the subtree of h rooted at node i. \(\hat {{C}}(h,i)\) denotes the result of mapping C(h, i) to the building block space as discussed in Section 3.3 and δ(x) is a function returning 1 when x is true and 0 otherwise. The λ and η are defined as stated in (14). Finally, s 1 and s 2 are as follows:

$$ s_{1} =\{l\vert \hat{{C}}(h_{1} ,i)[l]\ne 0\}\,,\,\,s_{2} =\{l\vert \hat{{S}}(h_{2} ,j)[l]\ne 0\}. $$
(18)

The expression of right hand side of (17) iterates over all pairs of individuals enumerating the fraction of allowed crossover points under which the generated offspring is in schema H. The context and subtree parts of the parents are mapped to building block space, yielding, \(\hat {{C}}(h_{1} ,i)\) and \(\hat {{S}}(h_{2} ,j)\)vectors of the same size. The corresponding offspring in building block space is then obtained by the addition of these two vectors. It should be noted that the crossover operator in tree space is simply converted to the addition in building block space.

4 Experimental results

As indicated in Table 1, researchers rarely provided experimental results for evaluating their proposed schema theories. Most of the previous studies concentrated on theoretical definition and investigation of the schema. Thus, lack of practical and experimental evidences causes criticizing the usefulness of schema theory. In this section, we evaluate the proposed schema in representing semantic features and compare it with some existing GP schemata in literature. Furthermore, the estimation of schema theory under selection is verified by experimental results which show the agreement of theory and practice. The quality of extracted building blocks is also evaluated in terms of semantic similarity to the target.

4.1 Benchmarks

Table 3 shows the benchmarks used for evaluation. The first three functions are univariate. F 1 is a polynomial employed in [1, 53], F 2 is the square root function, suggested in [53, 54] and as a sample of logarithmic functions, F 3 is selected similar to [53]. F 4 is a bivariate trigonometric function used for testing numerous GP variants employed in [53, 55]. All functions are mentioned in [56] which enumerates many candidate benchmarks of GP literature.

Table 3 Benchmarks used for evaluation
Full size table

4.2 Settings

Giving any population of trees, the proposed method can extract the significant schema. For better investigation of the performance of the schema and building blocks, we extracted the schema from evolving population of different generations. To achieve this goal, a standard GP, based on a traditional fitness measure (MSE) is employed to produce different populations with different levels of diversity from the initial population up to 100 generations. The schema and building blocks are extracted every twenty generations from scratch, independent of what has been obtained in previous generations. The GP configuration and the parameter settings of schema extraction are given in Table 4. The terminal set consists of the input variables equal to the function dimensionality.

Table 4 Parameter settings
Full size table

4.3 Schema generalization

The main purpose of defining the semantic schema is to propose a descriptive model that is matched by semantically similar trees. This model should describe the semantics behind the schema instances. As discussed in Section 3, the schema is extracted from a cluster of semantically similar trees. If the schema explanation is specific and expressive enough, other trees matching it should also have similar semantics to initial cluster. Therefore, for evaluating the generalization of a schema, we generate a set of random sample matching the schema using the method explained in Section 3.4.3. The average semantic similarity of newly generated trees to the target is then compared with the average semantic similarity of initial cluster for different generations. Figure 4 reveals the initial and generated average semantic similarities over generations for different benchmarks.

Fig. 4
figure 4

The semantic schema generalization

Full size image

Figure 4 shows that the semantic similarity of generated instances to the target is changing close to initial cluster and schema is generalized well on newly created instances. Raising the average semantic similarity of generated instances shows that the schema is also evolved while its initial instances are evolving. Consequently, similar to Holland’s claim for GA [5], GP performs a far greater parallel search for good schemata, when searching for fit individuals.

Again, after generating new samples of the schema, the fraction of generated trees matching it is an evaluation criterion for studying the generalization ability of the schema. To do this, a generated tree is assumed to match the schema if its semantic similarity is higher than minSemanticSimilarity threshold. The percentage of generated individuals matching the schema (i.e., the schema generation rate) is illustrated in Fig. 5. As shown in this figure the schema generation rate is high for all generations of different benchmarks. The average of this measure is 0.91, 0.89, 0.90 and 0.89 for F 1, F 2, F 3 and F 4respectively. During the evolution process, minimum semantic similarities of initial clusters become higher and higher. Although generating individuals with semantic similarity more than this threshold is more difficult, the semantic schema definition is capable of modeling initial trees and generalizes well on generated instances.

Fig. 5
figure 5

The schema generation rate

Full size image

4.4 Building block evolution

Since the proposed schema is based on semantic building blocks, its efficiency is highly dependent on the quality of these blocks. Hence, in this section we analyze the number and semantics of different building blocks, extracted independently over generations. First, we investigate the number of extracted building blocks in different generations. As demonstrated in Fig. 6, the number of building blocks reduces over the generations until getting to a single building block with maximum semantic similarity. In earlier generations, the diversity of the population is high and individuals are distributed near several local optimums, so the number of building blocks is high. However, in further generations, by converging the population, the number of building blocks reduces gradually.

Fig. 6
figure 6

The number of extracted building blocks in different generations

Full size image

The quality of extracted building blocks is illustrated in Fig. 7 in terms of the average and standard deviation of their semantic similarity to the target. The average semantic similarity of each population is also depicted as a borderline. As shown in Fig. 7, the average semantic similarity of building blocks is more than the corresponding average of the population. This is due to the certain conditions of selecting building blocks enumerated in Def.4. By preceding the evolution, the extracted building blocks are also evolved until reaching to maximum semantic similarity of 1. Standard deviation, that is an indicator of the semantic diversity of building blocks, is high in initial populations and gradually tends to become zero in further generations.

Fig. 7
figure 7

The average semantic similarity of building blocks to the target in different generations

Full size image

4.5 Schema coverage

Since finding all possible schemata of the population is very complicated and time-consuming, in previous studies the schema extraction algorithm is seldom presented. In Section 3.4.2, we proposed a method to find and concentrate on the most significant schema of the population. Figure 8 reveals the proportion of population instantiating this schema in different generations. As you can see, the schema covers more individuals when evolution proceeds until it includes the whole population.

Fig. 8
figure 8

The schema coverage during the evolution

Full size image

It should be noted that, the most significant schema is extracted in generation 1, 10 and then every twenty generations, so it evolves implicitly in parallel with individuals’ evolution. Figures 8 and 4 together show increasing both quality and quantity of significant schema over evolution.

4.6 Comparison

As stated in Table 1, few studies have provided experimental results for evaluation of their suggested schemas. Among them only two work can be compared with the proposed approach. The first one is Majeed’s study [20] in which the fragment (exp #) is detected as a schema for benchmark F 1. Table 5 reveals that the standard deviation and entropy of schema instances (extracted from initial population) are lower in the semantic schema for both error-based fitness and semantic similarity measures. The average is higher for semantic schema in both domains. To sum up, Table 5 shows that the semantic schema can partition both semantic and fitness spaces better than syntactic schemas such as [20].

Table 5 Comparison of semantic schema with Majeed’s schema
Full size table

Again an experiment is conducted similar to [3] for validating the schema theory predictions. In this experiment, the number of estimated schema instances under selection only is compared with numerical results obtained from a real run. We investigate the exactness of schema estimations in two modes. In the first set of experiments, in every twenty generations a schema is extracted from the population and the number of individuals sampling it, is estimated for the next generation (Fig. 9). In the second set of experiments, a single schema is extracted from initial population and the number of its instances in further generations (i.e., generations 1, 10, 20, 40... 100) is estimated (Fig. 10).

Fig. 9
figure 9

The estimation error of schema theory under selection only for predicting one next generation

Full size image
Fig. 10
figure 10

The estimation error of schema theory under selection only, for predicting all generations

Full size image

These experiments suggest that there is a good agreement between predictions (E[ m(H, t+1)]) and observations (m(H, t+1)). Since predictions are very close to the observations, the absolute value of the estimation error is also depicted in logarithmic scale. This agreement is due to the powerful definition of semantic schema which describes trees with similar behavior not just similar syntaxes. The results of Figs. 9 and 10 demonstrate that the semantic schema theory can be employed for predicting the dynamics of evolution not only in the next generation but also in even 100 generations later. This capability makes the semantic schema reliable enough to be applied for improving GP in practice.

5 Conclusions

In this paper, the concept of schema was studied from a new point of view. Semanticschema, according to this view, was defined as a set of points in the search space that share some semantic characteristics. The mutual information between the output of a tree and the target output was considered as a metric for measuring the semantic similarity of that tree to the target. Semantic building blocks were introduced and an extraction approach was suggested to discover the building blocks of a given population. The main contribution of this study is proposing semantic schema which is identified by the joint probability distribution of semantic building blocks instead of syntactic features. An extraction procedure was presented to detect the most significant schema of a population, in contrast to previous work, in which a sample arbitrary schema was analyzed or all schemas of a population were tracked. For predicting the number of schema instances in the next generation, a semantic schema theory was provided. The theory describes the propagation of GP schema under selection and standard crossover through an exact microscopic formulation. For proving the performance of the semantic schema theory, a set of experiments was conducted. Results indicated that the semantic schema is more reliable to predict the dynamics of schema instances during the evolution. It was also demonstrated that the semantic schema can generalize the semantics to newly created instances.