Min–max relative regret for scheduling to minimize maximum lateness

Abstract

We study the single machine scheduling problem under uncertain parameters, with the aim of minimizing the maximum lateness. More precisely, the processing times, the release dates, and the delivery times of the jobs are uncertain, but an upper and a lower bound of these parameters are known in advance. Our objective is to find a robust solution, which minimizes the maximum relative regret. In other words, we search for a solution which, among all possible realizations of the parameters, minimizes the worst-case ratio of the deviation between its objective and the objective of an optimal solution over the latter one. Two variants of this problem are considered. In the first variant, the release date of each job is equal to 0. In the second one, all jobs are of unit processing time. Moreover, we also consider the min–max regret version of the second variant. In all cases, we are interested in the sub-problem of maximizing the (relative) regret of a given scheduling sequence. The studied problems are shown to be polynomially solvable.

1 Introduction

Uncertainty is a crucial factor to consider when dealing with combinatorial optimization problems, especially scheduling problems. Thus, it is not sufficient to limit the resolution of a given problem to its deterministic version for a single realisation of the uncertain parameters, i.e., a scenario. A widely-used method to handle uncertainty is the stochastic approach, which involves predicting the probabilistic distributions for uncertain problem parameters. However, this approach has its drawbacks. It requires extensive knowledge about the problem data for accurate predictions, a task that can be challenging in real-world situations, particularly in the context of scheduling problems. In our study, we investigate an alternative method of handling uncertainty that relies on a set of known possible values of the uncertain parameters without any need for a probabilistic description, namely the robustness approach or worst-case approach (Kouvelis & Yu, 1997). The aim of this approach is to generate solutions that will have a good performance under any possible scenario and particularly in the most unfavorable one, i.e, the worst case scenario.

The use of the robustness approach involves specifying two key components. The first component is the choice of the type of uncertainty set. Literature has proposed various techniques for describing the uncertainty set (Buchheim & Kurtz, 2018), with the discrete uncertainty and the interval uncertainty being the most well-examined. Indeed, the most suitable representation of uncertainty in scheduling problems is the interval uncertainty, where the value of each parameter is restricted within a specific closed interval defined by a lower and an upper bound. These bounds can be estimated through a data analysis on traces of previous problem executions.

The second component is the choice of the appropriate robustness criterion (Aissi et al., 2009; Tadayon & Smith, 2015). One such criterion is the absolute robustness or min–max criterion, which seeks to generate solutions that provide the optimal performance in the worst-case scenario, i.e, solutions that minimize the maximum of the objective function value over all scenarios. This conservative criterion is suitable for situations where anticipating adverse events is essential to prevent critical consequences. It is relevant in non-repeating decision-making contexts, such as unique items in financial analysis, and in situations where preventive measures are vital, like in public health. However, this criterion can be seen as overly pessimistic in situations where the worst-case scenario is unlikely, causing decision-makers to regret not embracing a moderate level of risk.

Two less conservative criteria are based on the definition of the “regret": First, the robust deviation or min–max regret criterion aims at minimizing the maximum absolute regret, which is the most unfavorable deviation from the optimal performance, i.e., the largest difference between the value of a solution and the optimal value, among all scenarios. Secondly, the relative robust deviation or min–max relative regret criterion seeks to minimize the maximum relative regret, which is the worst percentage deviation from the optimal performance, i.e., the greatest ratio of the absolute regret to the optimal value, among all possible scenarios. According to Kouvelis and Yu (1997), the min–max relative regret criterion is less conservative compared to the min–max regret criterion. Indeed, both criteria are particularly effective in applications where outcomes can be evaluated ex-post, especially in competitive environments. In such contexts, decision-makers aim to maximize their chances of success by minimizing missed opportunities that competitors could exploit. In a similar vein, Averbakh (2005) remarks that the relative regret objective is more appropriate compared to the absolute regret objective in situations where a percentage-based assessment, such as “10% more expensive", is more relevant than an absolute value comparison, like “costs $30 more". Indeed, using absolute regret, which is calculated by the difference, can obscure the scale of the solution, whereas relative regret effectively underscores the proportion between the solution and the optimal. However, despite its advantages and greater relevance compared to other criteria, the min–max relative regret criterion has a complicated structure and this may explain why limited knowledge exists about it.

Our contribution and organisation of the paper:

The focus of this paper is to investigate the min–max relative regret criterion for the fundamental single machine scheduling problem with the maximum lateness objective. The interval uncertainty can involve the processing times, the release dates or the delivery times of jobs.

In Sect. 2, we formally define our problem and the used criteria. In Sect. 3, we give a short review of the existing results for scheduling problems with and without uncertainty consideration. In Sect. 4, we introduce some initial observations that serve as foundational elements for our proofs. We next consider two variants of this problem.

In Sect. 5, we study the variant where all jobs are available at time 0 and the interval uncertainty is related to processing and delivery times. Kasperski (2005) has applied the min–max regret criterion to this problem and developed a polynomial time algorithm to solve it by characterizing the worst-case scenario based on a single guessed parameter through some dominance rules. We prove that this problem is also polynomial for the min–max relative regret criterion. An iterative procedure is used to prove some dominance rules based on three guessed parameters in order to construct a partial worst-case scenario. To complete this scenario, we propose a polynomial algorithm based on a linear fractional program, which is then transformed into a linear program. Subsequently, we develop an algorithm that replaces the linear program, omitting one constraint. The transition through the linear program is useful for excluding a difficult constraint while considering the entire procedure of the problem.

In Sect. 6, we study the maximum relative regret criterion for the variant of the maximum lateness problem where the processing times of all jobs are equal to 1 and interval uncertainty is related to release dates and delivery times. For a fixed scenario, Horn (1974) proposed an optimal algorithm for this problem. For the uncertainty version, we simulate the execution of Horn’s algorithm using a guess of five parameters, in order to create a worst-case scenario along with its optimal schedule. In Sect. 7, we give a much simpler analysis for the maximum regret criterion applied to a more general form of this variant of our scheduling problem, where the processing times of all jobs are uniformly constant. We conclude in Sect. 8.

2 Problem definition and notations

In this paper, we consider the problem of scheduling a set $\mathcal {J}$ of n non-preemptive jobs on a single machine. In the standard version of the problem, each job is characterized by a processing time, a release date and a delivery time. In general, the values of the input parameters are not known in advance. However, an estimation interval for each value is known. Specifically, given a job $j \in \mathcal {J}$, let $[p_{j}^{\min },p_{j}^{\max }]$, $[r_{j}^{\min },r_{j}^{\max }]$ and $[q_{j}^{\min },q_{j}^{\max }]$ be the uncertainty intervals for its characteristics.

A scenario $s=(p_{1}^{s},\ldots ,p_{n}^{s},r_{1}^{s},\ldots ,r_{n}^{s},q_{1}^{s},\ldots ,q_{n}^{s})$ is a possible realisation of all values of the instance, such that $p_{j}^{s} \in [p_{j}^{\min },p_{j}^{\max }]$, $r_{j}^{s} \in [r_{j}^{\min },r_{j}^{\max }]$ and $q_{j}^{s} \in [q_{j}^{\min },q_{j}^{\max }]$, for every $j \in \mathcal {J}$. The set of all scenarios is denoted by $\mathcal {S}$. A solution is represented by a sequence of jobs, $\pi =(\pi (1),\ldots ,\pi (n))$ where $\pi (j)$ is the jth job in the sequence $\pi$. The set of all sequences is denoted by $\varPi$.

Consider a schedule represented by its sequence $\pi \in \varPi$ and a scenario $s \in \mathcal {S}$. The lateness of a job $j \in \mathcal {J}$ is defined as $L_{j}^{s}(\pi ) = C_{j}^{s}(\pi ) + q_{j}^{s}$, where $C_j^s(\pi )$ denotes the completion time of j in the schedule represented by $\pi$ under the scenario s. The maximum lateness of the schedule is defined as $L(s,\pi ) = \max _{j \in J} L_{j}^{s}(\pi )$. The job $c \in \mathcal {J}$ of maximum lateness in $\pi$ under s is called critical, i.e., $L_{c}^{s}(\pi ) = L(s,\pi )$. The set of all critical jobs in $\pi$ under s is denoted by $Crit(s,\pi )$. We call first critical job, the critical job which is processed before all the other critical jobs. By considering a given scenario s, the optimal sequence is the one leading to a schedule that minimizes the maximum lateness, i.e., $L^{*}(s) = \min _{\pi \in \varPi } L(s,\pi )$. This is a classical scheduling problem, denoted by $1 \mid r_j \mid L_{max}$ using the standard three-field notation, and it is known to be NP-hard in the strong sense (Lenstra et al., 1977).

For this deterministic version of the studied problem, the lateness of a job j can be formulated as: (1) $L_j = C_j - d_j$ where $C_j$ is the completion time and $d_j$ is the due date of j or (2) $L_j = C_j + q_j$ where $q_j$ is the delivery time of j. These two formulations are equivalent in terms of sequence optimality since for each job j the due date $d_j$ can be replaced by a delivery time $q_j = K - d_j$ where K is a given constant. The reason we study the delivery time model instead of the due date model is due to the use of the min–max relative regret criterion, which requires calculating ratios from the lateness values of solutions. The use of due dates could lead to a negative maximum lateness, thus complicating the calculation process. Similarly, in approximation theory, the same observation can be done and the maximum lateness can be zero when we use the due date model, presenting analogous computational challenges.

In this paper, we are interested in the min–max regret and the min–max relative regret criteria whose definitions can be illustrated by a game between two agents, Alice and Bob. Alice selects a sequence $\pi$ of jobs. The problem of Bob has as input a sequence $\pi$ chosen by Alice, and it consists in selecting a scenario s such that the regret R of Alice $R(s,\pi ) = L(s,\pi ) - L^{*}(s)$ or respectively the relative regret RR of Alice

$$\begin{aligned} RR(s,\pi ) = \frac{L(s,\pi ) - L^*(s)}{L^{*}(s)} = \frac{L(s,\pi )}{L^{*}(s)} - 1 \end{aligned}$$

is maximized. The value of $Z(\pi ) = \max _{s \in S} R(s,\pi )$ (resp. $ZR(\pi ) = \max _{s \in S} RR(s,\pi )$) is called maximum regret (resp. maximum relative regret) for the sequence $\pi$. In what follows, we call the problem of maximizing the (relative) regret, given a sequence $\pi$, as the Bob’s problem. Henceforth, by slightly abusing the definition of the relative regret, we omit the constant $-1$ in $RR(s,\pi )$, since a scenario maximizing the fraction $\frac{L(s,\pi )}{L^{*}(s)}$ maximizes also the value of $\frac{L(s,\pi )}{L^{*}(s)}-1$. Then, Alice has to find a sequence $\pi$ which minimizes her maximum regret (resp. maximum relative regret), i.e., $\min _{\pi \in \varPi } Z(\pi )$ (resp. $\min _{\pi \in \varPi } ZR(\pi )$). This problem is known as the min–max (relative) regret problem and we call it as Alice’s problem.

Given a sequence $\pi$, the scenario that maximises the (relative) regret over all possible scenarios is called the worst-case scenario for $\pi$. A partial (worst-case) scenario is a scenario defined by a fixed subset of parameters and can be extended to a fully defined (worst-case) scenario by setting the remaining unknown parameters. For a fixed scenario s, any schedule may consist of several blocks, i.e., a maximal set of jobs, which are processed without any idle time between them.

Example: To illustrate the procedures of Alice and Bob, let us consider a concrete instance involving five jobs, as previously stated in the general problem. The parameters for each job, including processing time, release date, and delivery time intervals, are given in Table 1.

Table 1 Instance of five jobs

Let $\pi = (5,4,3,2,1)$ be the sequence chosen by Alice. The Bob’s strategy is to choose values within these intervals to create the worst-case scenario for the Alice’s sequence $\pi$, depending on the robustness criteria, i.e., the min–max regret or min–max relative regret criterion. Assume that Bob chooses the scenario presented in Table 2. Note that this scenario is given as an example and may not necessarily represent the worst-case scenario for the Alice’s sequence.

Table 2 The scenario chosen by Bob

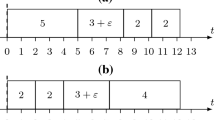
The sequence $\sigma = (4,5,1,3,2)$ is identified as optimal for this scenario s. Figure 1 illustrates the scheduling of sequences $\pi$ and $\sigma$ under scenario s. Here, the completion time of each job is noted below its end, while the lateness is indicated above it in the schedule.

Fig. 1

Scheduling of sequences $\pi$ and $\sigma$ under scenario s

In sequence $\pi$ under scenario s, job 1 is critical with the maximum lateness in this schedule being $L(s,\pi ) = L_{1}^{s}(\pi ) = 17$. In the optimal sequence $\sigma$ under s, jobs 1, 2, and 3 are critical, and the maximum lateness is $L^{*}(s) = L(s,\sigma ) = L_{2}^{s}(\sigma ) = 13$.

The absolute regret of Alice, $R(s,\pi )$, is calculated as $17 - 13 = 4$. The relative regret of Alice, $RR(s,\pi )$, is $\frac{17 - 13}{13} \approx 30.77\%$.

Aware of the Bob’s strategy, Alice focuses on selecting a sequence that minimizes her regret, whether absolute or relative, based on the desired robustness criterion.

3 Related work

In the deterministic version, the problem $1|r_j|L_{\max }$ has been proved to be strongly NP-hard (Lenstra et al., 1977). For the first variant where all release dates are equal, i.e, $1||L_{\max }$, the problem can be solved in $O(n \log n)$ time by applying Jackson’s rule (Jackson, 1955), i.e, sequencing the jobs in the order of non-decreasing due dates. In our specific context, we adapt Jackson’s rule by sequencing jobs based on non-increasing delivery times. For the second variant with unit processing time jobs, i.e, $1|r_j, p_j = 1|L_{\max }$, the rule of scheduling, at any time, an available job with the smallest due date, or for our context, the biggest delivery time, is shown to be optimal by Horn (1974). This method can be implemented in $O(n \log n)$ time. For the general version of the second variant with equal processing time jobs, i.e, $1|r_j, p_j = p|L_{\max }$, Lazarev et al. (2017) have proposed a polynomial algorithm to solve this problem in $O(Q \cdot n\log n)$ time, where $10^{-Q}$ is the accuracy of the input–output parameters.

For the discrete uncertainty case, the min–max criterion has been studied for several scheduling problems with different objectives. Kouvelis and Yu (1997) proved that the min–max resource allocation problem is NP-hard and admits a pseudo-polynomial algorithm. Aloulou and Della Croce (2008) showed that the min–max $1||\sum U_j$ problem of minimizing the number of late jobs with uncertain processing times and the min–max $1||\sum w_j C_j$ problem of minimizing the total weighted completion time with uncertain weights are NP-hard. In addition, they proved that the min–max problem of the single machine scheduling is polynomially solvable for many objectives like makespan, maximum lateness and maximum tardiness even in the presence of precedence constraints where processing times, due dates, or both are uncertain. Mastrolilli et al. (2013) proved that the min–max $1 \mid \mid w_jC_j$ problem with uncertain weights and processing times cannot be approximated within $O(\log ^{1 - \epsilon } n)$ unless NP has quasi-polynomial algorithms. For unweighted jobs, they developed a 2-approximation algorithm for this problem, with uncertain processing times, and demonstrated that it is NP-hard to approximate within a factor less than 6/5. The only single machine scheduling problem studied under discrete uncertainty for min–max (relative) regret is the $1||\sum C_j$. Daniels (1995) investigated this problem using both min–max regret and min–max relative regret criteria, proving that both are NP-hard. They developed a branch-and-bound algorithm and heuristic approaches. For the same problem, Yang and Yu (2002) presented a different NP-hardness proof for all the three robustness criteria. They also introduced a dynamic programming algorithm and two polynomial-time heuristics. Other scheduling problems have been also addressed in the literature. Kasperski et al. (2012) proved that both the min–max and min–max regret versions of the two-machine permutation flow shop problem, $F2 \mid \mid C_{\max }$, with uncertain processing times are strongly NP-hard, even with only two scenarios. The min–max (regret) parallel machine scheduling problem, $P \mid \mid C_{\max }$, with uncertain processing times, was studied in Kasperski et al. (2012); Kasperski and Zieliński (2014), where various NP-hardness and approximation results were presented.

For the interval uncertainty case, the min–max criterion has the same complexity as the deterministic problem since it is equivalent to solve it for an extreme well-known scenario. Considerable research has been dedicated to the min–max regret criterion for different scheduling problems. Many of these problems have been proved to be polynomially solvable. For instance, Averbakh (2000) considered the min–max regret $1||\max w_j T_j$ problem to minimize the maximum weighted tardiness, where weights are uncertain and proposed a $O(n^3)$ algorithm. He also presented a O(m) algorithm for the makespan minimization for a permutation flow-shop problem with 2 jobs and m machines with interval uncertainty related to processing times (Averbakh, 2006). The min–max regret version of the first variant of our problem has been considered by Kasperski (2005) under uncertain processing times and due dates. An $O(n^4)$ algorithm has been developed which works even in the presence of precedence constraints. As an extension of this earlier problem, Fridman et al. (2020) examined the general min–max regret problem of the cost scheduling problem. The cost function depends on the job completion time and a set of additional generalized numerical parameters, with both processing times and the additional parameters being uncertain. They developed polynomial algorithms that improved and generalized all previously known results. On the other hand, some problems have been classified as NP-hard. Lebedev and Averbakh (2006) showed that the min–max regret $1||\sum C_j$ problem with uncertain processing times is NP-hard. They also demonstrated that if all uncertainty intervals share the same center, the problem can be solved in $O(n \log n)$ time if the number of jobs is even, but it remains NP-hard if the number of jobs is odd. For the same problem, Montemanni (2007) presented the first mixed-integer linear programming formulation. For the min–max regret $1 \mid \mid w_jC_j$ problem with uncertain processing times, Pereira (2016) presented a branch-and-bound method. Kacem and Kellerer (2019) considered the single machine problem of scheduling jobs with a common due date with the objective of maximizing the number of early jobs and they proved that the problem is NP-hard and does not admit an FPTAS. The min–max regret criterion for minimizing the weighted number of late jobs was investigated: a polynomial algorithm for due-date uncertainty with uniform job weights (Drwal, 2018), and a branch-and-bound method for processing time uncertainty (Drwal & Józefczyk, 2020). Wang et al. (2020) tackled the min–max regret in single machine scheduling for total tardiness with interval processing times. They developed a mixed-integer linear programming model and demonstrated that an optimal schedule under the midpoint scenario provides a 2-approximation solution to the problem. Additionally, they proposed three methods to obtain robust schedules. The min–max regret criterion was also investigated in, Xiaoqing et al. (2013), Choi and Chung (2016), Liao and Fu (2020) and Wang and Cui (2021).

Finally, to the best of our knowledge, the only problem studied under the min–max relative regret criterion for scheduling with interval uncertainty is the total flow time problem $1||\sum C_j$ with uncertain processing times. Averbakh (2005) proved that this problem is NP-hard. Additionally, Kuo and Lin (2002) provided another NP-hardness proof, developed a fractional programming formulation, and introduced an algorithm using bisection searches based on parametric programming.

4 Preliminaries

In this section we present some preliminary observations that we use in our proofs.

Remark 1

(Monotonicity) Consider a set of jobs $\mathcal {J}$ and two scenarios $s_1$ and $s_2$ such that for each job $j \in \mathcal {J}$, we have $p_j^{s_1} \ge p_j^{s_2}$, $r_j^{s_1} \ge r_j^{s_2}$ and $q_j^{s_1} \ge q_j^{s_2}$. Then, the value of the maximum lateness in an optimal sequence for $s_1$ cannot be smaller than that for $s_2$, i.e., $L^*(s_1) \ge L^*(s_2)$.

Proof

Let us consider a set of jobs $\mathcal {J}$ and two scenarios, $s_1$ and $s_2$, such that for each job $j \in \mathcal {J}$, the conditions $p_j^{s_1} \ge p_j^{s_2}$, $r_j^{s_1} \ge r_j^{s_2}$, and $q_j^{s_1} \ge q_j^{s_2}$ hold. Suppose, contrary to our claim, that $L^*(s_1) < L^*(s_2)$. Let $\sigma$ be an optimal sequence for scenario $s_1$. Now, consider the schedules represented by the sequence $\sigma$ under scenarios $s_1$ and $s_2$, as illustrated in Fig. 2.

Given that the parameters of each job in scenario $s_2$ are smaller than or equal to those in scenario $s_1$, it logically follows that $L_{j}^{s_{2}}(\sigma ) \le L_{j}^{s_{1}}(\sigma )$ for each job $j \in \mathcal {J}$. Therefore, the maximum lateness in the sequence $\sigma$ under the scenario $s_2$ should not exceed that under the scenario $s_1$, i.e., $L(s_2, \sigma ) \le L(s_1, \sigma ) = L^*(s_1)$. This observation contradicts our supposition and thus validates our initial claim. $\square$

Fig. 2

Illustration of the schedules represented by $\sigma$ under $s_1$ and $s_2$

Remark 2

Let a and b be two real positive numbers. Consider the following functions:

• 1. For $f_1: \left[ 0, b\right) \rightarrow \mathbb {R}^{+}$ defined by $f_1(x) = \frac{a-x}{b-x}$, with $a \ge b$, the function $f_1$ is increasing on $\left[ 0, b\right)$.

• 2. For $f_2: \mathbb {R}^{+} \rightarrow \mathbb {R}^{+}$ defined by $f_2(x) = \frac{a+x}{b+x}$, the function $f_2$ is increasing if $a \le b$, and decreasing if $a > b$.

• 3. For $f_3: \mathbb {R}^{+} \rightarrow \mathbb {R}^{+}$ defined by $f_3(x) = \frac{a+2x}{b+x}$, the function $f_3$ is increasing if $a \le 2b$, and decreasing if $a > 2b$.

5 Min–max relative regret for $1 \mid \mid L_{max}$

In this section, we consider the min–max relative regret criterion for the maximum lateness minimization problem, under the assumption that each job is available at time 0, i.e., $r_{j}^{s} = 0$ for all jobs $j \in \mathcal {J}$ and all possible scenarios $s \in \mathcal {S}$. For a fixed scenario, this problem can be solved by applying the Jackson’s rule, i.e., sequencing the jobs in non-increasing order of delivery times. We denote by $B(\pi ,j)$ the set of all the jobs processed before job $j \in \mathcal {J}$, including j, in the sequence $\pi$ and by $A(\pi ,j)$ the set of all the jobs processed after job j in $\pi$.

5.1 The Bob’s problem

The following lemma presents some properties of a worst-case scenario for a given sequence of jobs.

Lemma 1

Let $\pi$ be a sequence of jobs. There exists (1) a worst-case scenario s for $\pi$, (2) a critical job $c_{\pi } \in Crit(s,\pi )$ in $\pi$ under s, and (3) a critical job $c_{\sigma } \in Crit(s,\sigma )$ in $\sigma$ under s, where $\sigma$ is the optimal sequence for s, such that:

• i For each job $j \in A(\pi ,c_{\pi })$, it holds that $p_j^s = p_j^{\min }$,

• ii For each job $j \in \mathcal {J} \setminus \{c_{\pi }\}$, it holds that $q_j^s = q_j^{\min }$,

• iii For each job $j \in B(\pi ,c_{\pi }) \cap B(\sigma ,c_{\sigma })$, it holds that $p_j^s = p_j^{\min }$, and

• iv $c_{\sigma }$ is the first critical job in $\sigma$ under s.

Proof

Consider a given worst-case scenario $s_1$. We will apply a series of transformations in order to obtain a worst-case scenario that fulfills the properties of the statement.

Let $c_{\pi } \in Crit(s_{1},\pi )$ be a critical job in $\pi$ under $s_{1}$. The first transformation (T1), from $s_{1}$ to $s_{2}$, consists in replacing:

• $p_{j}^{s_{1}}$ with $p_{j}^{\min }$ for each job $j \in A(\pi ,c_{\pi })$, i.e., $p_j^{s_2}=p_j^{\min }$,

• $q_{j}^{s_{1}}$ with $q_{j}^{\min }$ for each job $j \in \mathcal {J} {\setminus } \{c_{\pi }\}$, i.e., $q_j^{s_2}=q_j^{\min }$.

Note that the job $c_{\pi }$ remains critical in $\pi$ under $s_{2}$, since $L_{c_{\pi }}^{s_{1}}(\pi ) = L_{c_{\pi }}^{s_{2}}(\pi )$ and $L_{j}^{s_{1}}(\pi ) \ge L_{j}^{s_{2}}(\pi )$ for each other job $j \in \mathcal {J} {\setminus } \{c_\pi \}$. Moreover, by Remark 1, we have $L^{*}(s_{1}) \ge L^{*}(s_{2})$, since the value of several delivery times and processing times is only decreased according to transformation (T1). Thus, $s_{2}$ is also a worst-case scenario for $\pi$, i.e.,

$$\begin{aligned} RR(s_{1},\pi ) = \frac{L(s_{1},\pi )}{L^{*}(s_{1})} \le \frac{L(s_{2},\pi )}{L^{*}(s_{2})} = RR(s_{2},\pi ) \end{aligned}$$

Let $\sigma$ be an optimal sequence for $s_{2}$ and $c_{\sigma } \in Crit(s_{2},\sigma )$ be the first critical job in $\sigma$ under $s_{2}$. The second transformation (T2) consists in decreasing in an organized way the processing times of jobs in $B(\pi ,c_{\pi }) \cap B(\sigma ,c_{\sigma })$, leading to the scenario $s_{3}$. Note that, since the delivery times of jobs do not change in (T2), the optimal sequence for $s_3$ which is obtained by the Jackson’s rule remains also the same, i.e., $\sigma$.

Fig. 3

Illustration of the schedules represented by the sequences $\pi$ and $\sigma$ under the scenario $s_3$ obtained by Lemma 1

In order to implement the transformation (T2), we consider the jobs in $B(\pi ,c_{\pi }) \cap B(\sigma ,c_{\sigma })$ in the order that they appear in $\sigma$. Let $b_1,b_2,\dots ,b_\ell$ be these jobs according to this order and $\ell =|B(\pi ,c_{\pi }) \cap B(\sigma ,c_{\sigma })|$. Intuitively, we will decrease the processing time of each job in $B(\pi ,c_{\pi }) \cap B(\sigma ,c_{\sigma })$ using this order to its minimum value, until either the processing time of all jobs in $B(\pi ,c_{\pi }) \cap B(\sigma ,c_{\sigma })$ is reduced to their minimum value or some new jobs become critical in $\sigma$ or in $\pi$ (see Fig. 3). We denote by $N_\pi = Crit(s_{3},\pi ) {\setminus } Crit(s_{2},\pi )$ (resp. $N_\sigma = Crit(s_{3},\sigma ) {\setminus } Crit(s_{2},\sigma )$) the set of the new critical jobs that will appear in $\pi$ (resp. in $\sigma$) under $s_3$. Thus, we can consider one of the following three cases in the given order:

• Case 1: $N_\pi = N_\sigma = \emptyset$, that is no new critical job appears neither in $\sigma$ nor in $\pi$. Then, in the scenario $s_3$, we have:

  • $p_j^{s_3}=p_j^{\min }$ for each job $j \in B(\pi ,c_{\pi }) \cap B(\sigma ,c_{\sigma })$,

  • $c_{\pi }$ remains critical in $\pi$, and

  • $c_{\sigma }$ remains the first critical job in $\sigma$.

  Let $\varDelta = \sum _{j \in B(\pi ,c_{\pi }) \cap B(\sigma ,c_{\sigma })} (p_{j}^{s_{2}} - p_{j}^{min})$ be the total decrease of the processing times from $s_{2}$ to $s_{3}$. Note that $L(s_{3},\pi ) = L(s_{2},\pi ) - \varDelta$ and $L^{*}(s_{3}) = L^{*}(s_{2}) - \varDelta$. By setting $a=L(s_{2},\pi )$ and $b=L^{*}(s_{2})$ in Remark 2.1, we obtain:

  $$\begin{aligned} RR(s_{2},\pi ) = \frac{L(s_{2},\pi )}{L^{*}(s_{2})} \le \frac{L(s_{2},\pi ) - \varDelta }{L^{*}(s_{2}) - \varDelta } = \frac{L(s_{3},\pi )}{L^{*}(s_{3})}= RR(s_{3},\pi ) \end{aligned}$$

  where the inequality holds since $0 \le \varDelta \le L^{*}(s_{2})$ and $L^{*}(s_{2}) \le L(s_{2},\pi )$. Thus, $s_{3}$ is also a worst-case scenario for $\pi$ and, consequently, the triplet $(s_{3},c_{\pi },c_\sigma ) \in \mathcal {S} \times Crit(s_{3},\pi ) \times Crit(s_{3},\sigma )$ fulfills all the properties of the lemma.

• Case 2: $N_\sigma \ne \emptyset$, that is some new critical jobs appear in $\sigma$. In this case, $L^*(s_3)=L_{c_\sigma }^{s_3}(\sigma )= L_{j}^{s_3}(\sigma )$, for each job $j \in N_\sigma$. Let $b_p$, $1 \le p \le \ell$, be the job whose decrease in processing time results in the appearance of new critical jobs $N_\sigma$ in $\sigma$. Notice that $N_\sigma \subset B(\sigma ,b_p) \setminus \{b_p\}$, since the lateness of all jobs in $A(\sigma ,b_p) \cup \{b_p\}$ is decreased by the same amount as the processing time of $b_p$. Let $c'_\sigma \in N_\sigma$ be the first critical job in $\sigma$ under $s_3$ and let again $\varDelta = \sum _{j \in B(\pi ,c_{\pi }) \cap B(\sigma ,c_{\sigma })} (p_{j}^{s_{2}} - p_{j}^{s_{3}})$ be the total decrease of the processing times from $s_{2}$ to $s_{3}$. For the same reasons as before, we conclude that $RR(s_{2},\pi ) \le RR(s_{3},\pi )$. Therefore, $s_{3}$ is also a worst-case scenario for $\pi$. Consequently, since all the jobs in $B(\sigma ,c_\sigma ^{'})$ have their minimum processing times under $s_{3}$, the triplet $(s_{3},c_{\pi },c_\sigma ^{'}) \in \mathcal {S} \times Crit(s_{3},\pi ) \times Crit(s_{3},\sigma )$ fulfills all the properties of the lemma.

• Case 3: $N_\pi \ne \emptyset$, that is some critical jobs appear in $\pi$. In this case, $L(s_3,\pi )=L_{c_\pi }^{s_3}(\pi )= L_{j}^{s_3}(\pi )$, for each job $j \in N_\pi$. Let again $\varDelta = \sum _{j \in B(\pi ,c_{\pi }) \cap B(\sigma ,c_{\sigma })} (p_{j}^{s_{2}} - p_{j}^{s_{3}})$. For the same reasons as before, we conclude that $RR(s_{2},\pi ) \le RR(s_{3},\pi )$. Therefore, $s_{3}$ is also a worst-case scenario for $\pi$. However, the properties of the lemma are not yet fulfilled. In order to see this, let $b_p$, $1 \le p \le \ell$, be the job whose decrease in processing time results in the appearance of new critical jobs $N_\pi$ in $\pi$. Thus, there are still some jobs in $\big (B(\pi ,c_{\pi }) {\setminus } B(\sigma ,b_p)\big ) \cap B(\sigma ,c_{\sigma })$ whose processing time in $s_3$ does not have the minimum value. Then, we apply again transformation (T1) for scenario $s_{3}$ by considering a critical job $c_{\pi }^{'} \in N_\pi$ instead of $c_{\pi }$, as well as, transformation (T2), until we reach Case 1 or Case 2. This procedure will be repeated at most n times, since the sequence $\pi$ never changes and the new critical job $c_{\pi }^{'}$ appears always before the initial critical job $c_\pi$ in $\pi$. $\square$

Consider the sequence $\pi$ chosen by Alice. Bob can guess the critical job $c_\pi$ in $\pi$ and the first critical job $c_\sigma$ in $\sigma$. Then, by Lemma 1 (i)–(ii), he can give the minimum processing times to all jobs in $A(\pi ,c_\pi )$, and the minimum delivery times to all jobs except for $c_\pi$. Since the delivery times of all jobs except $c_\pi$ are determined and the optimal sequence $\sigma$ depends only on the delivery times according to the Jackson’s rule, Bob can obtain $\sigma$ by guessing the position $k \in \llbracket 1,n \rrbracket$ of $c_\pi$ in $\sigma$. Then, by Lemma 1 (iii), he can give the minimum processing times to all jobs in $B(\pi ,c_{\pi }) \cap B(\sigma ,c_{\sigma })$. We denote by the triplet $(c_\pi ,c_\sigma ,k)$ the guess made by Bob. Based on the previous assignments, Bob gets a partial scenario ${\bar{s}}_{c_\pi ,c_\sigma ,k}^\pi$. It remains to determine the exact value of $q_{c_\pi }$ and the processing times of jobs in $B(\pi ,c_{\pi }) \cap A(\sigma ,c_{\sigma })$ in order to extend ${\bar{s}}_{c_\pi ,c_\sigma ,k}^\pi$ to a fully defined scenario $s_{c_\pi ,c_\sigma ,k}^\pi$ that maximizes the relative regret for the guess $(c_\pi ,c_\sigma ,k)$. At the end, Bob will choose, among all the scenarios $s_{c_\pi ,c_\sigma ,k}^\pi$ created, the worst-case scenario $s_\pi$ for the sequence $\pi$, i.e.,

$$\begin{aligned} \displaystyle s_{\pi } = \mathop {\mathrm {arg\max }}\limits _{i,j,k} \left\{ \frac{L(s_{i,j,k}^\pi ,\pi )}{L^*(s_{i,j,k}^\pi )}\right\} \end{aligned}$$

In what follows, we propose a linear fractional program (P) in order to find a scenario $s_{c_\pi ,c_\sigma ,k}^\pi$ which extends ${\bar{s}}_{c_\pi ,c_\sigma ,k}^\pi$ and maximizes the relative regret for the given sequence $\pi$. Let $p_j$, the processing time of each job $j \in B(\pi ,c_{\pi }) \cap A(\sigma ,c_{\sigma })$, and $q_{c_\pi }$, the delivery time of job $c_\pi$, be the continuous decision variables in (P). All other processing and delivery times are constants and their values are defined by $\bar{s}_{c_\pi ,c_\sigma ,k}^\pi$. Recall that $\sigma (j)$ denotes the j-th job in the sequence $\sigma$. To simplify our program, we consider two fictive values $q_{\sigma (n+1)} = q_{c_\pi }^{\min }$ and $q_{\sigma (0)} = q_{c_\pi }^{\max }$.

$$\begin{aligned} \text {maximize } \frac{\sum _{i \in B(\pi ,c_\pi )} p_i + q_{c_\pi }}{\sum _{i \in B(\sigma ,c_\sigma )} p_i + q_{c_\sigma }}{} & {} (P) \nonumber \\ \text {subject to} \hspace{0.5cm} \sum _{i \in B(\pi ,j)} p_i + q_{j} \le \sum _{i \in B(\pi ,c_\pi )} p_i + q_{c_\pi }{} & {} \forall j \in \mathcal {J} \end{aligned}$$

(1)

$$\begin{aligned} \sum _{i \in B(\sigma ,j)} p_i + q_{j} \le \sum _{i \in B(\sigma ,c_\sigma )} p_i + q_{c_\sigma }{} & {} \forall j \in \mathcal {J} \end{aligned}$$

(2)

$$\begin{aligned} p_j \in [p_j^{\min }, p_j^{\max }]{} & {} \forall j \in B(\pi ,c_{\pi }) \cap A(\sigma ,c_{\sigma }) \end{aligned}$$

(3)

$$\begin{aligned} q_{c_\pi } \in [\max \{q_{c_\pi }^{\min },q_{\sigma (k+1)}\},\min \{q_{c_\pi }^{\max },q_{\sigma (k-1)}\}] \end{aligned}$$

(4)

The objective of (P) maximizes the relative regret for the sequence $\pi$ under the scenario $s_{c_\pi ,c_\sigma ,k}^\pi$ with respect to the hypothesis that $c_\pi$ and $c_\sigma$ are critical in $\pi$ and $\sigma$, respectively, i.e.,

$$\begin{aligned} ZR(\pi ) = \frac{L(s_{c_\pi ,c_\sigma ,k}^\pi ,\pi )}{L^{*}(s_{c_\pi ,c_\sigma ,k}^\pi )} =\frac{L_{c_\pi }^{s_{c_\pi ,c_\sigma ,k}^\pi }(\pi )}{L_{c_\sigma }^{s_{c_\pi ,c_\sigma ,k}^\pi }(\sigma )} \end{aligned}$$

Constraints (1) and (2) ensure this hypothesis. To preserve mathematical simplicity, Constraint (2) is formulated in its general form for all $j \in \mathcal {J}$. This is because in the case where $c_\pi \ne c_\sigma$ and $j \notin A(\sigma ,a) \cup \{a,c_\pi \}$, with a is the first job of the set $B(\pi ,c_{\pi }) \cap A(\sigma ,c_{\sigma })$ as ordered in $\sigma$, this constraint involves only fixed parameters and does not influence the optimization process. Constraints (3) and (4) define the domain of the continuous real variables $p_j$, $j \in B(\pi ,c_{\pi }) \cap A(\sigma ,c_{\sigma })$, and $q_{c_\pi }$. Note that, the latter one is based also on the guess of the position of $c_{\pi }$ in $\sigma$. The program (P) can be infeasible due to the Constraints (1) and (2) that impose jobs $c_\pi$ and $c_\sigma$ to be critical. In this case, Bob ignores the current guess of $(c_\pi ,c_\sigma ,k)$ in the final decision about the worst-case scenario $s_\pi$ that maximizes the relative regret.

Note that the Constraint (1) can be safely removed when considering the whole procedure of Bob for choosing the worst-case scenario $s_\pi$. Indeed, consider a guess (i, j, k) which is infeasible because the job i is not critical in $\pi$ due to the Constraint (1). Let s be the scenario extended from the partial scenario ${\bar{s}}_{i,j,k}^{\pi }$ by solving (P) without using the Constraint (1). Let $c_\pi$ be the critical job under the scenario s. Thus, $L_{c_\pi }^s(\pi ) > L_i^s(\pi )$. Consider now the scenario $s'$ of maximum relative regret in which $c_\pi$ is critical. Since $s_\pi$ is the worst-case scenario chosen by Bob for the sequence $\pi$ and by the definition of $s'$ we have

$$\begin{aligned} \frac{L(s_\pi ,\pi )}{L^*(s_\pi )} \ge \frac{L(s',\pi )}{L^*(s')} \ge \frac{L(s,\pi )}{L^*(s)} = \frac{L_{c_\pi }^s(\pi )}{L^*(s)} > \frac{L_i^s(\pi )}{L^*(s)} \end{aligned}$$

In other words, if we remove the Constraint (1), (P) becomes feasible while its objective value cannot be greater than the objective value of the worst-case scenario $s_\pi$ and then the decision of Bob with respect to the sequence $\pi$ is not affected. This observation is very useful in Alice’s algorithm. However, a similar observation cannot hold for Constraint (2) which imposes $c_\sigma$ to be critical in $\sigma$.

As mentioned before, the program (P) is a linear fractional program, in which all constraints are linear, while the objective function corresponds to a fraction of linear expressions of the variables. Moreover, the denominator of the objective function has always a positive value. Charnes and Cooper (1962) proposed a polynomial transformation of such a linear fractional program to a linear program by introducing a linear number of new variables and constraints. Hence, (P) can be solved in polynomial time.

Note also that, in the case where $c_\pi \ne c_\sigma$, the value of the maximum lateness in the optimal sequence ($\sum _{j \in B(\sigma ,c_{\sigma })} p_j^s + q_{c_{\sigma }}^s$) is fixed since the processing times of jobs processed before the job $c_\sigma$ in $\sigma$, as well as, the delivery time $q_{c_{\sigma }}^s$ of the job $c_\sigma$ are already determined in the partial scenario $\bar{s}_{c_\pi ,c_\sigma ,k}^\pi$. Therefore, if $c_\pi \ne c_\sigma$ then (P) is a linear program. Consequently, the Charnes-Cooper transformation is used only in the case where $c_{\pi } = c_{\sigma }$.

The procedure of Bob, given a sequence $\pi$, is summarized in Algorithm 1.

Algorithm 1

Bob’s algorithm for $1 \mid \mid L_{\max }$

Theorem 1

Given a sequence $\pi$, Algorithm 1 calculates the maximum relative regret by guessing $c_{\pi }$ the critical job in $\pi$, $c_\sigma$ the first critical job in $\sigma$, where $\sigma$ is the optimal sequence for the worst-case scenario s, and $k \in \llbracket 1,n \rrbracket$ the position of job $c_\pi$ in $\sigma$ and solving for each guess $(c_{\pi },c_\sigma ,k)$ a linear program with at most O(n) variables and O(n) constraints.

5.2 A better combinatorial algorithm for the Bob’s problem

In this subsection, we propose Algorithm 2, designed as a substitute for Line 5 in Algorithm 1. This line involves extending the partial scenario $\bar{s}^{\pi }_{i,j,k}$ generated by the guess (i, j, k), where i is the critical job in $\pi$ (the sequence chosen by Alice), j is the critical job in $\sigma$ (the optimal sequence for $\bar{s}^{\pi }_{i,j,k}$), and k is the position of the job i in $\sigma$. The goal of this extension is to form the fully defined scenario $s^{\pi }_{i,j,k}$ by solving the linear program (P) using the Constraints (2)–(4).

In addition to the inputs required by Algorithms 1, 2 takes as input the guess (i, j, k), the partial scenario $\bar{s}^{\pi }_{i,j,k}$ and the optimal sequence $\sigma$ for this scenario. Recall that $\sigma$ is obtained by applying the Jackson’s rule to the delivery times of all jobs and by guessing the position k of i in $\sigma$. Then, the algorithm determines the scenario $s^{\pi }_{i,j,k}$ that maximizes the relative regret by identifying the remaining parameters with respect to the Constraints (2)–(4). These parameters include $p_\ell$, the processing time of each job $\ell \in B(\pi ,i) \cap A(\sigma ,j)$, and $q_i$, the delivery time of the job i. Recall that the Constraint (2) ensures that i is critical in $\sigma$ and the Constraints (3) and (4) establish the domain of the remaining parameters. It is important to recall that Bob excludes the Constraint (1), which is typically used to ensure that the job i is critical in $\pi$. This exclusion is justified within the overall context of the Bob’s procedure, as was detailed earlier. We consider the jobs in the set $B(\pi ,i) \cap A(\sigma ,j)$, ordered as they occur in $\sigma$. Let this ordered set be denoted by ${a_1, a_2, \dots , a_m}$, where m is the number of jobs in $B(\pi ,i) \cap A(\sigma ,j)$.

Algorithm 2 describes this substitution for Line 5 in Algorithm 1. Initially, it starts with a basic scenario, setting all job parameters to their minimum values. It then addresses two main cases: the first, where the jobs i and j are distinct and the job j is critical in $\sigma$ under this basic scenario; and the second, where i equals j, referred to as c, with the potential for j to be critical in $\sigma$. Each case involves a series of modifications, transitioning from one scenario to another, or adjustments to the parameters of the scenario, with the aim of maximizing the relative regret. A third case arises as an exception to the main cases, considered when the guess (i, j, k) leads to an infeasible program (P).

Algorithm 2

Substitution of Line 5 in Algorithm 1

Theorem 2

Algorithm 2 replaces Line 5 in Algorithm 1 by extending ${\bar{s}}^{\pi }_{i,j,k}$ to the scenario $s^{\pi }_{i,j,k}$.

Proof

Let $s^*$ be the scenario extended from the partial scenario $\bar{s}^{\pi }_{i,j,k}$ and obtained by solving the program (P) using the Constraints (2)–(4), with $q_{i}^{s^{*}}, p_{a_1}^{s^{*}}, \dots , p_{a_m}^{s^{*}}$ as the values of the remaining parameters. Let $s_m$ be the scenario defined by the partial scenario ${\bar{s}}^{\pi }_{i,j,k}$ and by the values of the remaining parameters, specifically $q_{i}^{s_m}, p_{a_1}^{s_m}, \dots , p_{a_m}^{s_m}$, as constructed by the algorithm. We aim to demonstrate that $s^*$ can be transformed into $s_m$ while maintaining the objective value of (P) unchanged and adhering to the Constraints (2)–(4). This can be represented as:

$$\begin{aligned} \frac{L(s^*,\pi )}{L^{*}(s^*)} = \frac{L(s_m,\pi )}{L^{*}(s_m)} \end{aligned}$$

Fig. 4

Illustration of the increases in the remaining parameters from the initial scenario $s_{\min }$ to an extended scenario s

In Line 1, the algorithm extends the partial scenario $\bar{s}_{i,j,k}^{\pi }$ to the fully defined scenario $s_{\min }$ by initializing the remaining parameters to their respective lower bounds. For any scenario s, whether directly extending $\bar{s}_{i,j,k}^{\pi }$ or derived from such an extension, we define $\varDelta _q^s = q_i^s - q_i^{s_{\min }}$, and $\varDelta _{a_\ell }^s = p_{a_\ell }^s - p_{a_\ell }^{s_{\min }}$ for $\ell \in \llbracket 1, m \rrbracket$, as the increases in the respective remaining parameters with respect to $s_{\min }$ (see Fig. 4). Remark that any adjustment to the value of any increase directly corresponds to changing the value of its corresponding parameter for any given scenario. For a job $h \in A(\sigma ,a_1) \cup \{a_1\}$, b(h) is defined as the index of the job in the set $(a_\ell )_{\ell \in \llbracket 1,m \rrbracket }$, corresponding to h if included in this set, or to the job immediately preceding h in $\sigma$ otherwise. We assign a fictive value of $b(h) = 0$ for any job $h \in B(\sigma ,a_1) {\setminus } \{a_1\}$. It is observed that, for any scenario s, the completion time of a job $h \in \mathcal {J}$ can be expressed as: $C_h^{s}(\sigma ) = C_h^{s_{\min }}(\sigma ) + \sum _{\ell =1}^{b(h)} \varDelta _{a_\ell }^s$. This formulation is crucial for the subsequent reformulations of the objective of (P) and the Constraint (2), which will clarify the process of the exchange of charges during the scenario transformations in our proof. In what follows, we consider two cases.

• Case 1: When $i \ne j$, the lateness of j in the sequence $\sigma$ is fixed for any scenario extending $\bar{s}_{i,j,k}^\pi$, since both the processing times of the jobs in $B(\sigma ,j)$ and the delivery time of j are predetermined by ${\bar{s}}_{i,j,k}^\pi$. Consequently, if the second condition in Line 2 is not satisfied, specifically if the job j is not critical in $\sigma$ under $s_{\min }$, which is the scenario with the minimum possible lateness values for all jobs, then the guess (i, j, k) is ignored as indicated in Lines 2, 16, and 17. This is because such a guess results in an infeasible program (P). Suppose that this is not the case. To maximize the relative regret, the algorithm needs only to maximize the maximum lateness in $\pi$ since the maximum lateness in $\sigma$ is fixed. Let s be the scenario sought by the program (P). The objective of (P), considering the variables $\varDelta _q^s$ and $(\varDelta _{a_\ell }^s)_{\ell \in \llbracket 1,m \rrbracket }$, can be reformulated as follows:

  $$\begin{aligned} \text {maximize } L(s,\pi ) = L_i^{s_{\min }}(\pi ) + \sum _{\ell = 1}^m \varDelta _{a_\ell }^s + \varDelta _q^s \end{aligned}$$

  Furthermore, the Constraint (2) is restated as:

  $$\begin{aligned} L_j^{s_{\min }}(\sigma )&\ge L_i^{s_{\min }}(\sigma ) + \sum _{\ell =1}^{b(i)} \varDelta _{a_\ell }^s + \varDelta _{q}^s, \text { and}\\ L_j^{s_{\min }}(\sigma )&\ge L_h^{s_{\min }}(\sigma ) + \sum _{\ell =1}^{b(h)} \varDelta _{a_\ell }^s \qquad \forall h \in \big (A(\sigma ,a_1) \cup \{a_1\}\big ) \setminus \{i\}. \end{aligned}$$

  To effectively achieve this objective, Algorithm 2 starts with the scenario $s_{\min }$ and initially increases the delivery time of i to its maximum, thereby obtaining the scenario $s_0$. It then iteratively modifies each scenario $s_{\ell -1}$ to produce $s_{\ell }$, for $\ell = 1, \dots , m$, by increasing the processing time of the job $a_\ell$ to its maximum, with respect to the limits set by the Constraints (2)–(4) at each iteration. Let us first consider the value of the delivery time of i. According to Line 3, $q_{i}^{s_0}$ is increased from its previous value in the scenario $s_{\min }$ by the minimum of the following two quantities: (i) $L_{j}^{s_{\min }}(\sigma ) - L_{i}^{s_{\min }}(\sigma )$, which guarantees that the job j remains critical in $\sigma$ (the Constraint (2)), and (ii) $\min \{q_{i}^{\max }, q_{\sigma (k-1)} \} - q_{i}^{s_{\min }}$, which adheres to the upper bound for the delivery time of i (the Constraint (4)). Note that the resulting increase represents the maximum possible augmentation of the delivery time of i from the scenario $s_{\min }$ without violating the specified constraints. Consequently, given that $s_{\min }$ matches $s^*$ in all previously determined values by ${\bar{s}}_{i,j,k}^\pi$, and considering that $s_{\min }$ is characterized by the minimum values for the remaining parameters, it follows that the delivery time of i under $s^*$ cannot exceed that under $s_0$, i.e., $q^{s^*}_{i} \le q^{s_0}_{i}$. Subsequently, we transform $s^*$ to $s_0^*$ by increasing the delivery time of i to its maximum value, i.e., $q^{s_0^*}_{i} = q^{s_0}_{i}$. At the same time, we decrease the equivalent amount from the charges in the increases $\varDelta _{a_h}^{s^*}$, for $h \in \llbracket 1,m \rrbracket$, following the order in which their corresponding jobs appear in the sequence $\sigma$. This order is important to prevent the job i from becoming critical in $\sigma$, especially when $i \in A(\sigma ,a_1)$. Indeed, the exchange of charges initially involves decreasing the remaining processing times of the jobs in $B(\sigma ,i)$, during which the lateness of i in $\sigma$ remains unchanged. Once these processing times of the jobs in $B(\sigma ,i)$ reach their minimum values, $s_0^*$ will match $s_0$ in all processing times of the jobs in $B(\sigma ,i)$. Thus, it ensures that j remains critical in $\sigma$ under $s_0^*$, as our algorithm constructs $s_0$ under the same conditions. Moreover, since we decrease the completion time of i in $\pi$ by the same amount increased in its delivery time, we get $L(s^{*},\pi ) = L(s_0^{*},\pi )$. Therefore, the scenario $s_0^*$ matches $s_0$ in the delivery time of i, along with all values determined by $\bar{s}^{\pi }_{i,j,k}$, and maintains the same objective value of (P) as the scenario $s^*$, all while adhering to the Constraints (2)–(4). Now, we examine the processing time of the job $a_\ell$ for each iteration, where $\ell = 1, \dots , m$. As indicated in Lines 4 and 5, the processing time $p_{a_\ell }^{s_\ell }$ is increased from its previous value in $s_{\ell -1}$ by the minimum of the following two quantities: (i) $L_{j}^{s_{\ell -1}}(\sigma )- L_h^{s_{\ell -1}}(\sigma )$, where h is the job in $A(\sigma ,{a_\ell }) \cup \{{a_\ell }\}$ with the maximum lateness in $\sigma$, ensuring that the job j remains critical in $\sigma$ (the Constraint (2)), and (ii) $p_{a_\ell }^{\max } - p_{a_\ell }^{s_{\ell -1}}$, which adheres to the upper bound for the processing time of $a_\ell$ (the Constraint (3)). Recall that the maximum lateness in $\sigma$ is fixed, i.e., $L_j^{s_{\ell }}(\sigma ) = L_j^{s_{\min }}(\sigma )$ for all $\ell \in \llbracket 0,m \rrbracket$. Note also that this increase specifically applies to the processing time of the job $a_\ell$ at each iteration, while the remaining processing times of the subsequent jobs $a_h$, for $h \in \llbracket \ell + 1, m \rrbracket$, remain unchanged from their values in $s_{\min }$, i.e., $p_{a_h}^{s_\ell } = p_{a_h}^{s_{\min }}$ for $h \in \llbracket \ell +1,m \rrbracket$. The resulting increase represents the maximum possible augmentation of the processing time of $a_\ell$ from the scenario $s_{\ell -1}$ without violating the specified constraints. Consequently, since $s^{*}_{\ell -1}$ matches $s_{\ell -1}$ in all predetermined parameters and $s_{\ell -1}$ has the minimum values for the remaining undetermined parameters, it follows that the processing time of $a_\ell$ under $s^{*}_{\ell -1}$ cannot exceed that under $s_{\ell }$, i.e., $p_{a_\ell }^{s^{*}_{\ell -1}} \le p_{a_\ell }^{s_{\ell }}$. Subsequently, we transform $s^{*}_{\ell -1}$ to $s^{*}_{\ell }$ by increasing the processing time of $a_\ell$ to its maximum value, i.e., $p_{a_\ell }^{s^{*}_{\ell }}=p_{a_\ell }^{s_{\ell }}$. At the same time, we decrease the equivalent amount from the charges in the increases $\varDelta _{h}^{s^*_{\ell - 1}}$, for $h \in \llbracket \ell +1,m \rrbracket$, following the order in which their corresponding jobs appear in the sequence $\sigma$. For the same reasons as before, this order effectively ensures that no job within $A(\sigma ,a_\ell ) \cup \{a_\ell \}$ becomes critical in $\sigma$. Additionally, as the completion time of the job i remains constant in $\pi$ throughout this exchange of charges, we deduce that $L(s_{\ell -1}^{*},\pi )= L(s_{\ell }^{*},\pi )$. Moreover, the scenario $s_\ell ^*$ matches $s_\ell$ in the processing time of the job $a_\ell$ and in all values determined by $s_{\ell -1}$. By induction, we conclude that $s^*$ is transformed into $s_{m}^*$, which in turn matches $s_m$ in all parameter values, and they share the same objective value of (P), i.e., $L(s^{*},\pi )= L(s_{m},\pi )$, with respect to the Constraints (2)-(4).

• Case 2: When $i = j$, denoted as c, the completion time of the critical job c in the sequence $\sigma$ is fixed for any scenario extending $\bar{s}_{c,c,k}^\pi$, since the processing times of the jobs in $B(\sigma ,c)$ are predetermined by $\bar{s}_{c,c,k}^\pi$. However, the value of the maximum lateness of c in $\sigma$ is not fixed, since its delivery time is not determined yet. As outlined in Line 7, the algorithm forces c to become critical in $\sigma$ under $s_{\min }$ by increasing its delivery time by $L^{*}(s_{\min }) - L_{c}^{s_{\min }}(\sigma )$. If c cannot be made critical through this adjustment, i.e., the second condition of Line 6 is not satisfied, specifically when the required increase of the delivery time of c exceeds the allowable range for c, then the guess (c, c, k) is ignored. This is because such a guess results in an infeasible solution for the program (P). Assume that this is not the case. Let s be the scenario sought by the program (P). The objective of (P), considering the variables $\varDelta _q^s$ and $(\varDelta _{a_\ell }^s)_{\ell \in \llbracket 1,m \rrbracket }$, can be reformulated as follows:

  $$\begin{aligned} \text {maximize } \frac{L_c^{s_{\min }}(\pi ) + \sum _{\ell = 1}^m \varDelta _{a_\ell }^s + \varDelta _q^s}{L_c^{s_{\min }}(\sigma ) + \varDelta _q^s} \end{aligned}$$

  (5)

  The Constraint (2) is restated as:

  $$\begin{aligned} L_c^{s_{\min }}(\sigma ) + \varDelta _q^s&\ge L_h^{s_{\min }}(\sigma ) + \sum _{\ell =1}^{b(h)} \varDelta _{a_\ell }^s \qquad \forall h \in A(\sigma ,a_1) \cup \{a_1\} \end{aligned}$$

  Firstly, Algorithm 2 maintains the delivery time of c at its minimum possible value as determined in the scenario $s_{\min }$. This scenario is then used as the initial state, denoted $s_{0}$, for the following iterative process, as specified in Line 8. Throughout this procedure, for each $\ell = 1, \dots , m$, the algorithm modifies the scenario $s_{\ell -1}$ to produce the scenario $s_{\ell }$ by increasing the processing time of the job $a_\ell$ to its maximum, with respect to the Constraints (2)–(4). It is important to note that the algorithm maintains the delivery time of c constant during this procedure, i.e., $q_{c}^{s_{\min }} = q_{c}^{s_{\ell }}$ for $\ell = 1, \dots , m$. After completing this iterative process up to Line 10 and obtaining the scenario $s_m$, the scenario $s^*$ can be transformed into $s^*_m$, such that in this new scenario $s^*_m$, the processing times of all jobs in $(a_\ell )_{\ell \in \llbracket 1,m \rrbracket }$ are greater than or equal to those in the scenario $s_m$, i.e., $p_{a_\ell }^{s^*_m} \ge p_{a_\ell }^{s_m}$ for each $\ell = 1, \dots , m$. For convenience, we refer to $s^*$ as $s^*_0$. For each $\ell = 1, \dots , m$, we iteratively transform $s^*_{\ell - 1}$ into $s^*_\ell$ by adjusting the processing time of the job $a_\ell$. Specifically, whenever $p_{a_{\ell }}^{s^{*}_{\ell -1}} < p_{a_{\ell }}^{s_m}$, we increase the processing time of $a_\ell$ to match that in $s_m$, i.e, we set $p_{a_{\ell }}^{s^{*}_{\ell }} = p_{a_{\ell }}^{s_m}$. Simultaneously, we decrease the same amount from the increases $\varDelta _{h}^{s^*_{\ell -1}}$, for $h \in (B(\pi ,c) \cap A(\sigma ,c)) {\setminus } \{a_{\ell }\}$ where $p_{h}^{s^*_{\ell -1}} > p_{h}^{s_m}$, in order to align them with those in $s_m$, $\varDelta _{h}^{s_m}$. This transfer of charges follows the order in which the corresponding jobs are appear in $\sigma$. For the same reasons as before, this ordering ensures that c remains critical in $\sigma$, as effectively guaranteed by the scenario $s_\ell$. Consequently, this transformation preserves the objective value of (P), as it increases the lateness of c by the exact amount decreased and keeps its lateness in $\sigma$ constant. By applying inductive reasoning, we ultimately achieve the scenario $s^*_m$, which satisfies $p_{a_\ell }^{s^*_m} \ge p_{a_\ell }^{s_m}$ for each $\ell = 1, \dots , m$, while maintaining the objective value of (P) and adhering to the Constraints (2)–(4). Subsequently, if the delivery time of c has reached its maximum possible value under the initial scenario $s_{\min }$, it necessarily holds the same maximum value under the scenario $s_m$, i.e., $q_{c}^{s_{\min }} = q_{c}^{s_m} = \min \{q_{c}^{\max }, q_{\sigma (k-1)}\}$. For this case, we deduce that the scenarios $s_m$ and $s^*_m$ match in all parameter values. This is because: Firstly, if the delivery time of c in $s^*_m$ is less than that in $s_m$, then $s^*_m$ would not be a feasible scenario, as such a situation would necessarily violate the predefined constraints. Hence, this ensures that $q_{c}^{s^*_m} = q_{c}^{s_m}$. Secondly, the transformations from $s^*$ to $s^*_m$ in this specific case proceed in the same manner as in the previously proven case where $i \ne j$. Therefore, $p_{a_\ell }^{s^*_m} = p_{a_\ell }^{s_m}$ for each $\ell = 1, \dots , m$. Note that in this case, the algorithm does not apply any adjustments to the scenario $s_m$ as it is already optimized to maximize the relative regret. Otherwise, if $q_{c}^{s_m}$ does not achieve its maximum, i.e., $q_{c}^{s_m} < \min \{q_{c}^{\max }, q_{\sigma (k-1)}\}$, we examine two sub-cases:

  • (1) If $\sum _{\ell = 1}^m (p_{a_\ell }^{\max } - p_{a_\ell }^{s_m}) = 0$, this indicates that while the delivery time of c has the potential for further increase, all jobs in $(a_\ell )_{\ell \in \llbracket 1,m \rrbracket }$ have reached their maximum processing times under the scenario $s_m$. Consequently, these jobs have also reached their maximum processing times under the scenario $s^*_m$, since $p_{a_\ell }^{s^*_m} \ge p_{a_\ell }^{s_m} = p_{a_\ell }^{\max }$ for each $\ell = 1, \dots , m$. As a result, $s_m$ and $s^*_m$ match in terms of all processing times. To maximize the relative regret, the algorithm adjusts the scenario $s_m$ by setting $q_{c}^{s_m}$ to its maximum possible value, i.e., $\min \{q_{c}^{\max }, q_{\sigma (k-1)}\}$, under the condition that $L(s_m,\pi ) < L^{*}(s_m)$, as specified in Lines 14 and 15 (Adjustment of the scenario $s_m$: Step 2). This condition is crucial for increasing the relative regret. Indeed, in this specific case, increasing $q_{c}^{s_m}$ by $\epsilon > 0$ uniformly increases the maximum lateness in both $\pi$ and $\sigma$ by $\epsilon$. Thus, to ensure that the relative regret is an increasing function, it is necessary that the condition $L(s_m,\pi ) < L^{*}(s_m)$ is satisfied. This requirement is validated by the inequality $\frac{L(s_m,\pi )}{L^{*}(s_m)} < \frac{L(s_m,\pi ) + \epsilon }{L^{*}(s_m) + \epsilon }$, as shown in Remark 2.2, where a and b represent $L_c^{s_m}(\pi )$ and $L_c^{s_m}(\sigma )$, respectively. Therefore, since $s_m$ and $s^*_m$ matched in all processing times and the delivery time of c in $s_m$ is assigned the maximum possible value, we conclude that $s_m$ and $s^*_m$ match in all parameters.

  • (2) If $\sum _{\ell = 1}^m (p_{a_\ell }^{\max } - p_{a_\ell }^{s_m}) > 0$, this indicates that both the delivery time of c and the processing times of some jobs in $(a_\ell )_{\ell \in \llbracket 1,m \rrbracket }$ have the potential for further increase. According to the objective function 5, increasing the processing time of any job in the scenario $s_m$ by $\epsilon$ necessitates a corresponding increase in the delivery time of c by $\epsilon$ to ensure c remains critical in $\sigma$. Conversely, any increase in the delivery time of c by $\epsilon$ allows for the possibility to increase the total processing time of the remaining jobs by $\epsilon$ without violating the Constraints (2) and (3). Consequently, such adjustments lead to an increase in the maximum lateness in $\sigma$ by $\epsilon$, and in $\pi$ by $2\epsilon$. To maximize the relative regret, the algorithm proceeds through two steps to adjust the scenario $s_m$. In the first step, as detailed in Lines 11–13 (Adjustment of the scenario $s_m$: Step 1), the quantity $\varDelta = \min \left\{ \sum _{\ell = 1}^m (p_{a_\ell }^{\max } - p_{a_\ell }^{s_m}), \min \{q_{c}^{\max }, q_{\sigma (k-1)}\} - q_{c}^{s_m}\right\}$ is simultaneously added to the delivery time of c and the total processing time of the jobs $(a_\ell )_{\ell \in \llbracket 1,m \rrbracket }$ where $p_{a_\ell }^{s_m} < p_{a_\ell }^{\max }$, with respect to their maximum values. The order and the quantity of the increases applied to the total processing time of these jobs is not important. To ensure that this adjustment results in an increase in the relative regret, i.e., $\frac{L(s_m,\pi )}{L^*(s_m)} < \frac{L(s_m,\pi ) + 2 \epsilon }{L^*(s_m) + \epsilon }$, it is necessary that $L(s_m,\pi ) < 2 L^*(s_m)$. This requirement is derived from Remark 2.3, where we set $a = L(s_m,\pi )$ and $b = L^*(s_m)$. The second step is initiated when the processing times of all jobs have reached their maximum values, while the delivery time of c has not. Under these conditions, we return to the sub-case previously addressed. Consequently, given that all the remaining parameters in $s_m$ are less than or equal to those in $s^*_m$, and $s_m$ is adjusted to achieve the maximal possible increasing of the relative regret, it is deduced that $s^*_m$ can be transformed to match $s_m$.

In conclusion, we demonstrate that in all cases, $s^*$ can be transformed into $s_m$ while maintaining the objective value of (P) unchanged and adhering to Constraints (2)–(4). Consequently, $s_m$ extends ${\bar{s}}^{\pi }_{i,j,k}$ by maximizing the relative regret for the guess (i, j, k), thereby confirming the validity of the theorem. $\square$

Note that calculating the lateness of any job in a sequence under any scenario, as well as identifying the critical job in any sequence under any scenario, each requires O(n) time. Remark also that the most computationally intensive steps in Algorithm 2 occur in the iterative procedure, specifically during the operations in Lines 4 and 5, and Lines 9 and 10. These steps involve calculating the maximum lateness for jobs $h \in A(\sigma ,{a_\ell }) \cup \{{a_\ell }\}$ in the sequence $\sigma$ under the scenario $s_{\ell -1}$ for each $\ell = 1, \dots , m$. This calculation is performed in O(n) time and is repeated O(n) times.

However, it is important to note that this maximum lateness calculation can be performed once for the scenario $s_{\min }$ before initiating the iterative procedure. For $\ell = 1, \dots , m$ and for all jobs $h \in A(\sigma ,{a_\ell }) \cup \{{a_\ell }\}$, the lateness $L_h^{s_\ell }(\sigma ) = L_h^{s_{\min }}(\sigma ) + \sum _{\ell =1}^{b(h)} \varDelta _{a_\ell }^{s_\ell }$. Since $\sum _{\ell =1}^{b(h)} \varDelta _{a_\ell }^{s_\ell }$ increases for all such jobs h, the order of maximum lateness among the jobs remains consistent for any scenario $s_\ell$. Therefore, the computational complexity of Algorithm 2 is $O(n^2)$. Moreover, by substituting the direct solution of the program (P) in Line 5 with the application of Algorithm 2, the computational complexity of Algorithm 1 is effectively reduced to $O(n^5)$.

5.3 The Alice’s problem

In this section, we follow the ideas in Kasperski (2005) and we show how Alice constructs an optimal sequence $\pi$ minimizing the maximum relative regret, i.e., $\pi = \mathop {\mathrm {arg\min }}\limits _{\sigma \in \varPi } ZR(\sigma )$. Intuitively, by starting from the last position and going backwards, Alice searches for an unassigned job that, if placed at the current position and it happens to be critical in the final sequence $\pi$, will lead to the minimization of the maximum relative regret for $\pi$.

In order to formalize this procedure we need some additional definitions. Assume that Alice has already assigned a job in each position $n,n-1,\ldots ,r+1$ of $\pi$. Let $B_r$ be the set of unassigned jobs and consider any job $i \in B_r$. If i is assigned to the position r in $\pi$, then the sets $B(\pi ,i)$ and $A(\pi ,i)$ coincide with $B_r$ and $\mathcal {J}{\setminus } B_r$, respectively, and are already well defined, even though the sequence $\pi$ is not yet completed (recall that $B(\pi ,i)$ includes i). Indeed, $B(\pi ,i)$ and $A(\pi ,i)$ depend only on the position r, i.e., $B(\pi ,i)=B(\pi ,j)=B_r$ and $A(\pi ,i)=A(\pi ,j)$ for each couple of jobs $i,j \in B_r$. Hence, Alice can simulate the construction in Bob’s algorithm in order to decide which job to assign at position r. Specifically, for a given job $i \in B_r$, Alice considers all scenarios $s_{i,j,k}^{B_r}$, where $j \in \mathcal {J}$ is the first critical job in the optimal sequence $\sigma$ for this scenario and $k \in \llbracket 1,n \rrbracket$ is the position of i in $\sigma$, constructed as described in Bob’s algorithm. Note that, we slightly modified the notation of the scenario constructed by Bob for a guess (i, j, k) to $s_{i,j,k}^{B_r}$ instead of $s_{i,j,k}^{\pi }$, since a partial knowledge ($B_r=B(\pi ,i)$) of $\pi$ is sufficient to apply the Lines 4–5 of the algorithm. Moreover, the reason of omitting Constraint (1) in the program (P) is clarified here, since the job i is not imposed to be necessarily critical in $\pi$. For a job $i \in B_r$, let

$\displaystyle f_i(\pi ) = \max _{j \in \mathcal {J}, k \in \llbracket 1,n \rrbracket }\left\{ \frac{L(s_{i,j,k}^{B(\pi ,i)})}{L^*(s_{i,j,k}^{B(\pi ,i)})}\right\}$

Then, Alice assigns to position r the job i which minimizes $f_i(\pi )$. The procedure of Alice is summarized in Algorithm 3.

Algorithm 3

Alice’s algorithm for $1||L_{max}$

The following theorem proves that Algorithm 3 returns the optimal sequence.

Theorem 3

Algorithm 3 returns a sequence $\pi$ that minimizes the maximum relative regret for the problem $1 \mid \mid L_{\max }$ in $O( n \cdot T_{Bob} (n))$ time (i.e., $O(n^6)$ time), where $T_{Bob} (n)$ is the complexity of the Bob’s problem.

Proof

Recall that $B_r$ is the set of unassigned jobs at position r. For a sequence $\pi$, recall also that $s_{i,j,k}^{B_r}$ is the scenario constructed by Bob based on the guess (i, j, k) where $B(\pi ,i) = B_r$ and, for $i \in B_r$, the function $f_i(\pi )$ is defined by:

$\displaystyle f_i(\pi ) = \max _{j \in \mathcal {J}, k \in \llbracket 1,n \rrbracket }\left\{ \frac{L(s_{i,j,k}^{B(\pi ,i)})}{L^*(s_{i,j,k}^{B(\pi ,i)})}\right\}$

Let $\pi$ be the sequence constructed by Algorithm 3 and $\sigma$ be an optimal sequence for Alice’s problem. Consider r the last position in which $\sigma$ and $\pi$ are different, i.e., $\pi (r) \ne \sigma (r)$ and $\pi (i) = \sigma (i)$ for $r < i \le n$. We select $\sigma$ in way that minimizes r. If $r = 0$ then $\pi = \sigma$ and $\pi$ is optimal. Let $r > 0$. We form a new sequence $\sigma ^{'}$ by inserting job $\sigma (s)$ directly after job $\sigma (r)$ in the sequence $\sigma$. The illustration in Fig. 5 demonstrates the connections between the sequences $\pi$, $\sigma$, and $\sigma ^{'}$, and showcases the sets $A_r$, $B_r$, E, and D that result from it.

Fig. 5

The relationship between sequences $\pi$, $\sigma$ and $\sigma ^{'}$

Let $c \in \mathcal {J}$ be the critical job in $\sigma '$, i.e., $ZR(\sigma ') = f_c(\sigma ')$. We distinguish three cases:

• Case 1: $c \in A_r \cup D$, the set $B(\sigma , c)$ does not change from $\sigma$ to $\sigma '$, i.e., $B(\sigma , c) = B(\sigma ', c)$. Then, $\sigma '$ is also an optimal sequence for Alice since $ZR(\sigma ') = f_c(\sigma ) = f_c(\sigma ') \le ZR(\sigma )$.

• Case 2: $c \in E \cup \{\sigma (r)\}$, the set $B(\sigma , c)$ loses the job $\sigma (s)$ by moving from $\sigma$ to $\sigma '$, i.e., $B(\sigma ', c) = B(\sigma , c) \setminus \{\sigma (r)\}$. Let $j' \in \mathcal {J}$ and $k \in \llbracket 1,n \rrbracket$. We consider the worst-case scenarios $s_c(\sigma ')=s_{c,j',k}^{B(\sigma ', c)}$ and $s_c(\sigma )=s_{c,j',k}^{B(\sigma , c)}$ constructed by the Bob’s algorithm by the guesses (c, $j'$, k, $B(\sigma ',c)$) and (c, $j'$, k, $B(\sigma ,c)$) as seen previously. Notice that $s_c(\sigma ')$ and $s_c(\sigma )$ have the same Bob’s sequence $\sigma _{Bob}$ since it depends on the job c and its position k in $\sigma _{Bob}$. Moreover, we have $L^*(s_c(\sigma '))=L_{c'}^{s_c(\sigma ')}(\sigma _{Bob})=L_{c'}^{s_c(\sigma )}(\sigma _{Bob})=L^*(s_c(\sigma ))$ since $c'$ is the first critical job in $\sigma _{Bob}$ and $p_j^{s_c(\sigma ')}=p_j^{s_c(\sigma )}=p_j^{\min }$ for each $j \in B(\sigma _{Bob}, c')$ according to Lemma 1. Consequently, since $L(s_c(\sigma ')) \le L(s_c(\sigma ))$, we get $ZR(\sigma ') = \underset{j \in \mathcal {J}}{\textrm{max}} f_j(\sigma ') \le \underset{j \in \mathcal {J}}{\textrm{max}} f_j(\sigma ) \le ZR(\sigma )$. Thus, $\sigma '$ is also an optimal sequence for Alice.

• Case 3: $c = \sigma (s) = \pi (r)$, it is established that $B_r =B(\pi ,\pi (r))=B(\sigma ',\sigma (s))=B(\sigma ,\sigma (r))$. By equivalences, we get

  $$\begin{aligned} \begin{aligned} ZR(\sigma ') = f_{\sigma (s)}(\sigma ')&= \underset{(j',k) \in \mathcal {J}^2}{\textrm{max}}\{\frac{L(s_{\sigma (s),j',k}^{B(\sigma ',\sigma (s))})}{L^*(s_{\sigma (s),j',k}^{B(\sigma ',\sigma (s))})}\} \\&= \underset{(j',k) \in \mathcal {J}^2}{\textrm{max}}\{\frac{L(s_{\pi (r),j',k}^{B_r})}{L^*(s_{\pi (r),j',k}^{B_r})}\}\\&\overset{(*)}{\le }\ \underset{(j',k) \in \mathcal {J}^2}{\textrm{max}}\{\frac{L(s_{\sigma (r),j',k}^{B_r})}{L^*(s_{\sigma (r),j',k}^{B_r})}\}\\&= \underset{(j',k) \in \mathcal {J}^2}{\textrm{max}}\{\frac{L(s_{\sigma (r),j',k}^{B(\sigma ,\sigma (r))})}{L^*(s_{\sigma (r),j',k}^{B(\sigma ,\sigma (r))})}\} \\&= f_{\sigma (r)}(\sigma ) \le ZR(\sigma ) \\ \end{aligned} \end{aligned}$$

  The fact that $\pi$ is constructed by Algorithm 3, and $\pi (r) = \mathop {\mathrm {arg\min }}\limits _{i \in B_r}\{f_i(\pi )\}$ is the job selected by Algorithm 3 to be the job of minimum $f_i(\pi )$ among all jobs $i \in B_r$, implies the inequality $(*)$. Therefore, $\sigma '$ is also an optimal sequence for Alice.

The conclusion drawn from cases 1 to 3 is that $\sigma ^{'}$ is the optimal sequence, which contradicts the fact that r is minimal and therefore, concludes the proof. $\square$

6 Min–max relative regret for $1\mid r_j, p_j=1 \mid L_{\max }$

In this section, we consider the case of unit processing time jobs, i.e., $p_{j}^{s} = 1$ for all jobs $j \in \mathcal {J}$ and all possible scenarios $s \in \mathcal {S}$. In contrast to the previous section, the jobs are released on different dates whose values are also imposed to uncertainties. For a fixed scenario, Horn (1974) proposes an extension of the Jackson’s rule leading to an optimal schedule for this problem: at any time t, schedule the available job, if any, of the biggest delivery time, where a job j is called available at time t if $r_j \le t$ and j is not yet executed before t.

6.1 The Bob’s problem

Since all jobs are of unit the processing times, a scenario s is described by the values of the release dates and the delivery times of the jobs, i.e., by $r_{j}^{s} \in [r_{j}^{\min },r_{j}^{\max }]$ and $q_{j}^{s} \in [q_{j}^{\min },q_{j}^{\max }]$, for each $j \in \mathcal {J}$. In the presence of different release dates, the execution of the jobs is partitioned into blocks that do not contain any idle time. In a given schedule under a scenario s and a sequence $\pi$, a job $u_j$ is referred to as the first-block job for a job $j \in \mathcal {J}$ if it is the first job processed in the block containing j. The following lemma characterizes a worst-case scenario for a given sequence of jobs $\pi$.

Lemma 2

Let $\pi$ be a sequence of jobs. There exists a worst-case scenario s, a critical job $c \in Crit(s,\pi )$ and its first-block job $u_c$ in $\pi$ under s such that:

• i For each job $j \in \mathcal {J} \setminus \{c\}$, it holds that $q_j^s = q_j^{\min }$,

• ii For each job $j \in \mathcal {J} \setminus \{u_c\}$, it holds that $r_j^s = r_j^{\min }$.

Proof

Let $s_1$ be a worst-case scenario for a given sequence $\pi$, $c \in Crit(s_1,\pi )$ be a critical job in $\pi$ under $s_1$ and $u_c$ be its first-block job. We consider the following transformation, from $s_1$ to $s_2$, which consist in replacing:

• $q_{j}^{s_1}$ with $q_{j}^{\min }$ for all the jobs $j \in \mathcal {J} {\setminus } \{c\}$, i.e., $q_{j}^{s_2} = q_{j}^{\min }$,

• $r_{j}^{s_1}$ with $r_{j}^{\min }$ for all jobs $j \in \mathcal {J} {\setminus } \{u_{c}\}$, i.e., $r_{j}^{s_2} = r_{j}^{\min }$.

Note that the critical job c remains critical in $\pi$ under $s_{2}$, since $L_{c}^{s_{1}}(\pi ) = L_{c}^{s_{2}}(\pi )$ and $L_{j}^{s_{1}}(\pi ) \ge L_{j}^{s_{2}}(\pi )$ for each other job $j \in \mathcal {J} {\setminus } \{c\}$. Moreover, by Remark 1, $L^{*}(s_{1}) \ge L^{*}(s_{2})$, since the value of several delivery times and release dates is only decreased according to the transformation. Then, we get:

$$\begin{aligned} R(s_{1},\pi ) = \frac{L(s_{1},\pi )}{L^{*}(s_{1})} \le \frac{L(s_{2},\pi )}{L^{*}(s_{2})} = R(s_{2},\pi ) \end{aligned}$$

Therefore, $s_{2}$ is also a worst-case scenario for $\pi$ and the lemma holds. $\square$

Consider the sequence $\pi$ chosen by Alice. Bob can guess the critical job c in $\pi$ and its first-block job $u_c$. Using Lemma 2, we get a partial scenario ${\bar{s}}$ by fixing the delivery times of all jobs except for c as well as the release dates of all jobs except for $u_c$ to their minimum values. It remains to determine the values of $q_c$ and $r_{u_c}$ in order to extend the partial scenario ${\bar{s}}$ to a scenario s. At the end, Bob will choose, among all scenarios created, the worst-case one for the sequence $\pi$, i.e., the scenario with the maximum value of relative regret.

In what follows, we explain how to construct a sequence $\sigma$ which will correspond to an optimal schedule for the scenario s when the values of $q_c$ and $r_{u_c}$ will be fixed. The main idea of the proposed algorithm is that, once a couple of $\sigma$ and s is determined, then $\sigma$ corresponds to the sequence produced by applying Horn’s algorithm with the scenario s as an input. The sequence $\sigma$ is constructed from left to right along with an associated schedule which determines the starting time $B_j$ and the completion time $C_j=B_j+1$ of each job $j \in \mathcal {J}$. The assignment of a job j to a position of this schedule (time $B_j$) introduces additional constraints in order to respect the sequence produced by Horn’s algorithm:

• (C1) There is no idle time in $[r_j,B_j)$,

• (C2) At time $B_j$, the job j has the biggest delivery time among all available jobs at this time, and

• (C3) The delivery times of all jobs scheduled in $[r_j,B_j)$ should be bigger than $q_j^s$.

These constraints are mainly translated to a refinement of the limits of $q_c$ or of $r_{u_c}$, i.e., updates on $q_c^{\min }$, $q_c^{\max }$, $r_{u_c}^{\min }$ and $r_{u_c}^{\max }$. If at any point of our algorithm the above constraints are not satisfied, then we say that the assumptions/guesses made become infeasible, since they cannot lead to a couple $(\sigma ,s)$ respecting Horn’s algorithm. Whenever we detect an infeasible assumption/guess, we throw it and we continue with the next one.

Let $\ell [x]$ be the x-th job which is released after the time $r_{u_c}^{\min }$, that is, $r_{u_c}^{\min } \le r_{\ell [1]}^{{\bar{s}}} \le r_{\ell [2]}^{{\bar{s}}} \le \ldots \le r_{\ell [y]}^{{\bar{s}}}$. By convention, let $r_{\ell [0]}^{{\bar{s}}}=r_{u_c}^{\min }$ and $r_{\ell [y+1]}^{{\bar{s}}}=+\infty$. To begin our construction, we guess the positions $k_c$ and $k_{u_c}$ of the jobs c and $u_c$, respectively, in $\sigma$ as well as the interval $[r_{\ell [x]}^{{\bar{s}}},r_{\ell [x+1]}^{{\bar{s}}})$, $0 \le x \le y$, of $B_{u_c}$ in the optimal schedule s for $\sigma$. Let $k_{\min }=\min \{k_c,k_{u_c}\}$. We start constructing $\sigma$ and its corresponding schedule by applying Horn’s algorithm with input the set of jobs $\mathcal {J} \setminus \{c,u_c\}$ for which all data are already determined by the partial scenario ${\bar{s}}$, until $k_{\min }-1$ jobs are scheduled. Then, we set $\sigma (k_{\min }) = \mathop {\mathrm {arg\min }}\limits \{k_c,k_{u_c}\}$. We now need to define the starting time of $\sigma (k_{\min })$ and we consider two cases:

• Case 1: $k_c < k_{u_c}$. We set $B_c=\max \{C_{\sigma (k_{\min }-1)},r_c^{{\bar{s}}}\}$. If $B_c=r_c^{\bar{s}}$ and there is an idle time and an available job $j \in \mathcal {J} {\setminus } \{c,u_c\}$ in $[C_{\sigma (k_{\min }-1)},B_c)$, then we throw the guess $k_c$, $k_{u_c}$, $[r_{\ell [x]}^{\bar{s}},r_{\ell [x+1]}^{{\bar{s}}})$ since we cannot satisfy constraint (C1) for j, and hence our schedule cannot correspond to the one produced by Horn’s algorithm. Let $q_a^{{\bar{s}}}=\max \{q_j^{{\bar{s}}}:j \in \mathcal {J} {\setminus } \{c,u_c\} \text { is available at } B_c\}$. Then, in order to satisfy constraint (C2) we update $q_c^{\min }=\max \{q_c^{\min },q_a^{\bar{s}}\}$. Let $q_b^{{\bar{s}}}=\min \{q_j:j \in \mathcal {J} {\setminus } \{c,u_c\} \text { is executed in } [r_c,B_c)\}$. Then, in order to satisfy constraint (C3) we update $q_c^{\max }=\min \{q_c^{\max },q_b^{{\bar{s}}}\}$. If $q_c^{\max } < q_c^{\min }$, then we throw the guess $k_c$, $k_{u_c}$, $[r_{\ell [x]}^{{\bar{s}}},r_{\ell [x+1]}^{{\bar{s}}})$ since we cannot get a feasible value for $q_c^s$. It remains to check if there is any interaction between c and $u_c$. Since $k_c < k_{u_c}$, $u_c$ is not executed in $[r_c,B_c)$. However, $u_c$ may be available at $B_c$, but we cannot be sure for this because the value of $r_{u_c}^s$ is not yet completely determined. For this reason, we consider two opposite assumptions. Note that $B_c$ is already fixed by the partial scenario ${\bar{s}}$ in the following assumptions, while $r_{u_c}^{s}$ is the hypothetical release date of $u_c$ in the scenario s.

  • Assumption 1.1: $r_{u_c}^{s} \le B_c$. In order to impose this assumption, we update $r_{u_c}^{\max }=\min \{r_{u_c}^{\max },B_c\}$.

  • Assumption 1.2: $r_{u_c}^{s} > B_c$. In order to impose this assumption, we update $r_{u_c}^{\min }=\max \{r_{u_c}^{\min },B_c+1\}$.

  If in any of these cases we have that $r_{u_c}^{\max } < r_{u_c}^{\min }$, then we throw the corresponding assumption, since there is no feasible value for $r_{u_c}^s$. For each non-thrown assumption, we continue our algorithm separately, and we eventually get two different couples of sequence/scenario if both assumptions are maintained. More specifically, for each assumption, we continue applying Horn’s algorithm with input the set of jobs $\mathcal {J} {\setminus } \{\sigma (1),\sigma (2),\ldots ,\sigma (k_{\min }-1),c,u_c\}$ starting from time $C_c=B_c+1$, until $k_{u_c}-k_c-1$ additional jobs are scheduled. Then, we set $\sigma (k_{u_c}) = u_c$ and $B_{u_c}=\max \{C_{\sigma (k_{u_c}-1)},r_{u_c}^{\min },r_{\ell [x]}^{\bar{s}}\}$. Note that $B_{u_c}$ depends for the moment on the (updated) $r_{u_c}^{\min }$ and not on the final value of $r_{u_c}^s$ which has not been determined at this point of the algorithm. If $B_{u_c} \ge r_{\ell [x+1]}^{{\bar{s}}}$, then we throw the guess on $[r_{\ell [x]}^{{\bar{s}}},r_{\ell [x+1]}^{{\bar{s}}})$. We next check if the constraints (C1)-(C3) are satisfied for all jobs in $\mathcal {J} {\setminus } \{u_c\}$ with respect to the assignment of the job $u_c$ at the position $k_{u_c}$ of $\sigma$ with starting time $B_{u_c}$. If not, we throw the current assumption. Otherwise, Horn’s algorithm with input the jobs in $\mathcal {J} {\setminus } \{\sigma (1),\sigma (2),\ldots ,\sigma (k_{u_c})\}$ and starting from time $B_{u_c}+1$ is applied to complete $\sigma$.

• Case 2: $k_c > k_{u_c}$. We set $B_{u_c}=\max \{C_{\sigma (k_{\min }-1)},r_{u_c}^{\min },r_{\ell [x]}^{\bar{s}}\}$. As before, $B_{u_c}$ depends on $r_{u_c}^{\min }$ and not on the final value of $r_{u_c}^s$. If $B_{u_c} \ge r_{\ell [x+1]}^{\bar{s}}$ then we throw the current guess on $[r_{\ell [x]}^{\bar{s}},r_{\ell [x+1]}^{{\bar{s}}})$. We need also to check if the constraints (C1)-(C3) are satisfied for all jobs in $\mathcal {J} {\setminus } \{u_c\}$ with respect to the assignment of the job $u_c$ at the position $k_{u_c}$ of $\sigma$ with starting time $B_{u_c}$. If not, we throw the current guess $k_c$, $k_{u_c}$, $[r_{\ell (q)}^{{\bar{s}}},r_{\ell (q)+1}^{{\bar{s}}})$. Note that the last check is also applied for c and eventually leads to update $q_c^{\max }=\min \{q_c^{\max },q_{u_c}^{{\bar{s}}}\}$ if c is available at $B_{u_c}$. This can be easily verified because of the guess of the interval of $B_{u_c}$. Next, we continue applying Horn’s algorithm with input the set of jobs $\mathcal {J} {\setminus } \{\sigma (1),\sigma (2),\ldots ,\sigma (k_{\min }-1),c,u_c\}$ starting from time $B_{u_c}+1$, until $k_c-k_{u_c}-1$ additional jobs are scheduled. Then, we set $\sigma (k_c) = c$, $B_c=\max \{C_{\sigma (k_c-1)},r_c^{{\bar{s}}}\}$, and we check if the constraints (C1)-(C3) are satisfied for all jobs in $\mathcal {J} {\setminus } \{c\}$ with respect to the assignment of the job c at the position $k_c$ of $\sigma$ with starting time $B_c$. If not, we throw the current guess $k_c$, $k_{u_c}$, $[r_{\ell [x]}^{\bar{s}},r_{\ell [x+1]}^{{\bar{s}}})$. Moreover, an update on $q_c^{\min }$ and $q_c^{\max }$ is possible here, like the one in the begin of case 1. Finally, Horn’s algorithm with input the jobs in $\mathcal {J} {\setminus } \{\sigma (1),\sigma (2),\ldots ,\sigma (k_c)\}$ and starting from time $C_c=B_c+1$ is applied to complete $\sigma$. Note that after the execution of the above procedure for a given guess c, $u_c$, $k_c$, $k_{u_c}$, $[r_{\ell [x]}^{\bar{s}},r_{\ell [x+1]}^{{\bar{s}}})$, and eventually an assumption 1.1 or 1.2, we get a sequence $\sigma$ and its corresponding schedule, while the values of $q_c^s$ and $r_{u_c}^s$ are still not defined but their bounds are probably limited to fit with this guess. Then, we apply the following three steps in order to get the scenario s:

  • 1. Extend the partial scenario ${\bar{s}}$ to a scenario $s_{\min }$ by setting $q_c^{s_{\min }} = q_c^{\min }$ and $r_{u_c}^{s_{\min }} = r_{u_c}^{\min }$.

  • 2. Extend the scenario $s_{\min }$ to the scenario $s_1$ by increasing the delivery time of c to its maximum without increasing the maximum lateness and without exceeding $q_c^{\max }$, i.e., $q_{c}^{s_1} = q_{c}^{s_{\min }} + \min \{q_{c}^{\max }-q_{c}^{s_{\min }}, L^{*}(s_{\min })-L_{c}^{s_{\min }}(\sigma )\}$.

  • 3. Extend the scenario $s_1$ to the scenario s by increasing the release date of $u_c$ to its maximum without increasing the maximum lateness, without exceeding $r_{u_c}^{\max }$ and without violating the constraint (C1) and the current guess.

The following theorem holds since in an iteration of the above algorithm, the guess corresponding to an optimal sequence $\sigma$ for the worst-case scenario s will be considered, while Horn’s algorithm guarantees the optimality of $\sigma$. The algorithm iterates through all possible guesses of the critical job c, its first-block job $u_c$, their positions $k_c$ and $k_{u_c}$, and the interval $[r_{\ell [x]}^{{\bar{s}}}, r_{\ell [x+1]}^{{\bar{s}}}]$, resulting in $O(n^5)$ combinations. For each combination, the algorithm applies Horn’s algorithm with a complexity of $O(n \log n)$. Thus, the overall complexity is $O(n^6 \log n)$.

Theorem 4

There is a polynomial time algorithm which, given a sequence $\pi$, constructs a worst-case scenario $s_{\pi }$ of maximum relative regret for the problem $1|r_j, p_j=1|L_{\max }$. The complexity of the algorithm is $O(n^6 \log n)$.

6.2 The Alice’s problem

In this section, we describe Alice’s algorithm in order to construct an optimal sequence minimizing the maximum relative regret for $1|r_j,p_j=1|L_{\max }$. Since Alice knows how Bob proceeds, she can do a guess g of the five parameters c, $u_c$, $k_c$, $k_{u_c}$, $[r_{\ell [x]},r_{\ell [x+1]})$ in order to construct an optimal sequence $\sigma _g$ for a scenario $s_g$ corresponding to this guess. Then, she assumes that $\sigma _g$ is provided as input to Bob. Bob would try to maximize its relative regret with respect to $\sigma _g$ by eventually doing a different guess ${\hat{g}}$, obtaining a scenario $s_{{\hat{g}}}$, i.e.,

$$\begin{aligned} RR(s_{{\hat{g}}},\sigma _g)=\max _{g'}\frac{L(s_{g'},\sigma _g)}{L^*(s_{g'})} \end{aligned}$$

Note that, if $g = {\hat{g}}$, then $RR(s_{{\hat{g}}},\sigma _g)=1$ since by definition $\sigma _g$ is the optimal sequence for the scenario $s_g=s_{{\hat{g}}}$. Therefore, Alice can try all possible guesses in order to find the one that minimizes her maximum relative regret by applying Bob’s algorithm to the sequence obtained by each guess. Given the number of the possible guesses and the complexity of the Bob’s algorithm, the overall complexity of Alice’s algorithm is $O(n^{5} n^{6} \log n) = O(n^{11} \log n)$. Hence the following theorem holds.

Theorem 5

There is a polynomial time algorithm which constructs a sequence $\pi$ minimizing the maximum relative regret for the problem $1|r_j, p_j=1|L_{\max }$. The complexity of the algorithm is $O(n^{11} \log n)$.

Note that, Bob’s guess for this problem defines almost all parameters of a worst-case scenario, without really using the input sequence provided by Alice. This is not the case in Sect. 5 where, according to Lemma 1, the jobs that succeed the critical job in Alice’s sequence should be known. For this reason Alice’s algorithm is simpler here compared to the one in Sect. 5.3.

7 Min–max regret for $1 \mid r_j, p_j=p \mid L_{\max }$

In this section, we consider the min–max regret criterion for a general version of the problem studied in Sect. 6, which aims to minimize the maximum lateness subject to the constraint that the processing time for each job is fixed to a constant value, i.e., $1 | r_j,p_j=p | L_{max}$. For a given scenario, Lazarev et al. (2017) have proposed a polynomial algorithm to solve this problem in $O(Q \cdot n\log n)$ time, where $10^{-Q}$ is the accuracy of the input–output parameters.

7.1 The Bob’s problem

Bob characterizes the worst-case scenario for a given sequence $\pi$ based on the following Lemma.

Lemma 3

Let $\pi$ be a sequence of jobs. There exists (1) a worst-case scenario s, (2) a critical job $c \in Crit(s,\pi )$ and (3) its first-block job $u_c$ in $\pi$ under s such that:

• i For each job $j \in \mathcal {J} \setminus \{c\}$, it holds that $q_j^s = q_j^{\min }$,

• ii For each job $j \in \mathcal {J} \setminus \{u_c\}$, it holds that $r_j^s = r_j^{\min }$,

• iii $q_c^s = q_c^{\max }$,

• iv $r_{u_c}^s = r_{u_c}^{\max }$.

Proof

Let $s_1$ be a worst-case scenario for a given sequence $\pi$, $c \in Crit(s_1,\pi )$ be a critical job and $u_c$ be the first-block job for c in $\pi$ under $s_1$. We will show that this scenario can be transformed into another worst-case scenario that fulfills the properties of the statement. The first transformation (T1), from $s_1$ to $s_2$, consist in replacing:

• $q_{j}^{s_1}$ with $q_{j}^{\min }$ for all the jobs $j \in \mathcal {J} {\setminus } \{c\}$, i.e., $q_{j}^{s_2} = q_{j}^{\min }$,

• $r_{j}^{s_1}$ with $r_{j}^{\min }$ for all jobs $j \in \mathcal {J} {\setminus } \{u_{c}\}$, i.e., $r_{j}^{s_2} = r_{j}^{\min }$.

Note that the job c remains critical in $\pi$ under $s_{2}$, since $L_{c}^{s_{1}}(\pi ) = L_{c}^{s_{2}}(\pi )$ and $L_{j}^{s_{1}}(\pi ) \ge L_{j}^{s_{2}}(\pi )$ for each other job $j \in \mathcal {J} {\setminus } \{c\}$. Moreover, by Remark 1, $L^{*}(s_{1}) \ge L^{*}(s_{2})$, since the value of several delivery times and release dates is only decreased according to transformation (T1). Thus, $s_{2}$ is also a worst-case scenario for $\pi$, i.e.,

$$\begin{aligned} R(s_{1},\pi ) = L(s_{1},\pi ) - L^{*}(s_{1}) \le L(s_{2},\pi ) - L^{*}(s_{2}) = R(s_{2},\pi ) \end{aligned}$$

The second transformation (T2), from $s_2$ to s, consist in replacing:

• $q_{c}^{s_{2}}$ with $q_{c}^{\max }$, i.e., $q_{c}^{s} = q_{c}^{\max }$,

• $r_{u_{c}}^{s_{2}}$ with $r_{u_{c}}^{\max }$, i.e., $r_{u_{c}}^{s} = r_{u_{c}}^{\max }$.

The delivery time of c increases by $\varDelta ^{q} = q_{c}^{\max } - q_{c}^{s_{2}}$ and the release date of $u_{c}$ increases by $\varDelta ^{r} = r_{u_{c}}^{\max } - r_{u_{c}}^{s_{2}}$ from $s_2$ to s. As a result, the completion times of the jobs preceding $u_{c}$ in $\pi$ will increase by at most $\varDelta ^{r}$, i.e., $L_{j}^{s}(\pi ) \le L_{j}^{s_{2}}(\pi ) + \varDelta ^{r}$ for each job j preceding $u_c$ in $\pi$, while the completion time of job c will increase by $\varDelta ^{r} + \varDelta ^{q}$, i.e., $L_{c}^{s}(\pi ) = L_{c}^{s_{2}}(\pi ) + \varDelta ^{r} + \varDelta ^{q}$, since it belongs to the same block as $u_{c}$ in the schedule of $\pi$ under $s_2$. Thus, c remains critical in $\pi$ under s.

Let $\sigma$ be the optimal sequence for scenario $s_2$. Since the maximum lateness in $\sigma$ cannot increase by more than $\varDelta ^{r} + \varDelta ^{q}$ from $s_2$ to s, we get:

$$\begin{aligned}L^{*}(s) - L^{*}(s_2) \le L(s,\sigma ) - L(s_2,\sigma ) \le \varDelta ^{r} + \varDelta ^{q} = L(s,\pi ) - L(s_2,\pi ) \end{aligned}$$

Then $R(s_{2},\pi ) \le R(s,\pi )$, we conclude that s is also a worst-case scenario for $\pi$ and satisfies all the properties of the lemma. $\square$

Using Lemma 3, Bob can determine the worst-case scenario s for a given sequence $\pi$, chosen by Alice, by guessing the critical job c and its first-block job $u_c$ in $\pi$. The overall complexity of this process is $O(Q \cdot n^3 \log n)$, where $10^{-Q}$ is the accuracy of the input–output parameters.

Theorem 5

There is a polynomial time algorithm which, given a sequence $\pi$, constructs a worst-case scenario $s_{\pi }$ of maximum regret for the problem $1|r_j, p_j=p|L_{\max }$. The complexity of the algorithm is $O(Q \cdot n^3 \log n)$.

7.2 The Alice’s problem

The concept behind the Alice’s algorithm for minimizing the maximum regret for $1 \mid r_{j}, p_{j}=p \mid L_{\max }$ is similar to the one discussed in Sect. 6.2. The only difference is that in this case, Bob only needs to guess two parameters, c and $u_c$, which is a simpler task compared to the other problem. Therefore, Alice can minimize her maximum regret by testing all possible guesses using the Bob’s algorithm on the sequence generated by each guess. Thus, the overall complexity of the Alice’s algorithm is $O(Q \cdot n^5 \log n)$, arising from evaluating $O(n^2)$ combinations and applying Bob’s algorithm for each. As a result, the following theorem applies.

Theorem 6

There is a polynomial time algorithm which constructs a sequence $\pi$ minimizing the maximum regret for the problem $1|r_j, p_j=p|L_{\max }$. The complexity of the algorithm is $O(Q \cdot n^5 \log n)$.

8 Conclusions

We studied the min–max relative regret criterion for dealing with interval uncertain data for the single machine scheduling problem of minimizing the maximum lateness. We considered two variants and we proved that they can be solved optimally in polynomial time. Our main technical contribution concerns the sub-problem of maximizing the relative regret for these variants. The complexity of our results justifies in a sense the common feeling that the min–max relative relative criterion is more difficult than the min–max regret criterion.

Note that our result for the variant without release dates can be extended even in the case where the jobs are subject to precedence constraints. Indeed, Lawler (1973) proposed an extension of Jackson’s rule for the deterministic version of this problem, while the monotonicity property still holds. Thus, the corresponding lemma describing a worst-case scenario holds, and the determination of the optimal sequence depends only on the guess of the position of the critical job in this sequence which should be imposed to respect the precedence constraints.

In the future, it is interesting to clarify the complexity of the general maximum lateness problem with respect to min–max relative regret when all parameters are subject to uncertainty. We conjecture that this problem is NP-hard. If this is confirmed, the analysis of an approximation algorithm is a promising research direction.