Airline crew scheduling with sustainability enhancement by data analytics under circular economy

Abstract

As an energy-intensive industry, it is critical for airlines to enhance operation sustainability under the circular economy. Airline crew pairing problem is to construct job itineraries. Traditionally, crew pairings are developed based on pre-determined flight schedules. That is, flight departure times, arrival times, and flying times are considered to be fixed according to the schedule. However, analytics on historical data reveal that the actual flight duration often varies according to the actual departure time, which may lead to a deviation of the actual arrival time from the scheduled time point. Thus, propagated effects are generated as the departure time and flying time of the next flight are also affected. Aircraft energy research has revealed that the fuel consumptions and greenhouse gas emissions of aircraft are affected by the actual flying speed and flight duration. Therefore, it is crucial to consider sustainability cost factors (i.e., fuel consumptions and greenhouse gas emissions) when building crew pairings. In this work, in order to enhance operation sustainability and promote circular economy, we propose a novel crew pairing problem which aims to minimize the total basic operation cost, the total fuel consumptions and greenhouse gas emissions, and the robustness cost of the generated pairings. A column generation based solution algorithm is developed. Computational experiments show that the proposed model can bring a 7.98% decrease in the sustainability cost and an 1.81% decline in the robustness cost with only 0.55% increase in the basic operation cost when all the three cost factors are with equal weightings.

1 Introduction

The air transportation industry has played a crucial role for the current world (Choi et al., 2019; Wen et al., 2022a, 2022b). It is reported that more than one hundred thousand flights are operated each day during normal periods.¹ As forecasted, air traffic demand will double in the next twenty years,² which will certainly lead to a higher traffic volume. The aviation industry has long been well-known to be an energy-intensive industry. Thus, with the fast development of circular economy, how to enhance the operation sustainability has become a critical challenge for the aviation industry (Deveci et al., 2022; Pamucar et al., 2021; Sun et al., 2021). In the US, 18.27 billion gallons of fuel was consumed by airlines in 2019.³ The figure for the world is 96 billion gallons.⁴ The associated greenhouse gas emission is increasing rapidly. It is reported that the global aviation CO₂ emissions grow 70% faster than predicted from 2013 to 2018.⁵ Worldwide, the aviation industry produces 915 million tonnes of CO₂ in 2019, which occupies 2% of total human-generated carbon dioxide emissions. The air transport is responsible for 12% of the total emissions among all transport sectors.⁶ Among various sectors in commercial airlines, air passenger transport generates 81% of the total emissions. International Civil Aviation Organization (ICAO) expects that the aviation carbon emission will triple by the year of 2050, which will account for 25% of the total greenhouse gas emission all over the world (Graver et al., 2019). Therefore, it is obvious that the fuel consumption and greenhouse gas emissions are critical issues for the aviation industry. Authorities have proposed diverse schemes with the aim of enhancing the sustainability of the industry (Pamucar et al., 2022). For example, in 2005, the European Union (EU) launched the Emissions Trading System (EU ETS) which covers all flights within the EU and between EU ETS participating countries. Besides, ICAO proposes a basket of measures to help control the sustainability issue of the aviation industry. The measures include improving aircraft technologies with higher fuel efficiency, using sustainable fuels, market-based measures, and improving air operations.⁷ Focusing on improving airline operational strategies and promoting circular economy, this paper proposes a novel operational scheduling model with fuel consumption and greenhouse gas emission considerations from the perspective of crew pairing, in order to enhance the sustainability of the aviation transport industry.

Major airlines generally operate thousands of flights each week. Therefore, airline operational scheduling problem is generally divided into four sequential problems due to the large problem scale, including flight scheduling, fleet assignment, aircraft maintenance routing, and crew scheduling (Deveci and Demirel, 2018a, 2018b). Among them, crew scheduling assigns crews to serve the flights with a minimum cost. Due to the importance of air crews for passenger safety, authorities, airlines, and labor unions have regulated diverse rigorous working rules (like the feasible flight connection times, maximum duty period, and maximum number of flights allowed in a pairing), which further improves the complexity of the airline crew scheduling problem. Accordingly, the “unmanageable” airline crew scheduling problem is solved by sequentially dealing with a crew pairing problem and a crew rostering problem. The crew pairing problem aims to generate sufficient anonymous legal pairings by connecting flights to cover all flights. Next, in crew rostering problem, the pairings generated in the crew pairing problem are connected to form monthly rosters to be assigned to specific crew members. In some European airlines, crew preferences are considered during roster construction to better satisfy crew’s needs (e.g., leave and training), while in some American airlines, the bidding system is applied in which crew members bid for their preferred rosters published by airlines. In recent years, crew scheduling has attracted increasing attention as the crew-related cost becomes the second largest component of an airline’s total operation cost (just after fuel consumption). Therefore, a variety of research has been devoted to reducing the operation costs of air crews (Antunes et al., 2019; Deveci and Demirel, 2018a, 2018b). However, as will be discussed later, the sustainability cost is also critical for the crew pairing problem due to the flight duration variability led by different flight connections, which shall be integrated into the decision framework.

The crew pairing problem constructs crew pairings to ensure that each scheduled flight is covered by at least one legal pairing. A legal pairing is a sequence of flights to be served by the same crew member while the various working rules are satisfied, which starts from and ends at the crew’s home base. The objective of the traditional crew pairing problem is to minimize the total operation costs. Traditionally, flights are connected to form crew pairings according to the pre-determined flight schedules that are prepared several weeks or even months ago. Flight departure times, arrival times, and flying times are assumed as fixed. That is, flights are assumed to always depart and arrive on time, while flying times are deterministic for each flight segment. However, the aviation industry is highly volatile. Disruptions, like bad weathers, governmental traffic control, and airport congestions, always lead to deviations of flight schedules. By analyzing historical flight data, previous studies (Sun et al., 2020b; Wen et al., 2020) have identified that the actual flight duration is highly related to the actual flight departure time, and the departure time in the day greatly affects the flight on-time performance. According to Bureau of Transportation Statistics,⁸ the most appropriate departure time in the day is 6am-7am, during which flights are mostly possible to arrive at the destination on time. For every hour later, flight flying times are expected to grow up by minutes or even hours in some extreme cases. The variation in flying times inevitably lead to a deviation of the actual flight arrival time from the scheduled time point. Thus, propagated effects are generated as the departure time and flying time of the next flight are also affected. In other words, the actual departure time, flying time, and arrival time of each flight may vary when the flight is covered by different pairings with different preceding flights. Moreover, research on aviation energy consumption has found that the fuel consumptions and greenhouse gas emissions of aircraft are dependent on the actual flying time and flying speed (Aktürk et al., 2014). Therefore, constructing crew pairings just based on the pre-determined flight schedule without considering flight flying time variability may lead to poor sustainability performances, which is harmful for the environment and causes damages for airline’s image.

The main contributions of this study are as follows. First, we improve the sustainability level of airline crew schedules by proposing a novel crew pairing model which integrates the basic operation costs and the sustainability cost (i.e., fuel consumptions and greenhouse gas emissions) into the decision framework. Moreover, we also introduce the pairing robustness cost, i.e., the total deviations of flight departure/arrival times in the constructed pairings from the scheduled flight departure/arrival times, into the optimization objective. Second, when constructing pairings in this study, we calculated the departure-dependent flight flying times and the expected flight departure and arrival times based on the recursive relationship developed in our previous study (Sun et al., 2020b; Wen et al., 2020). Thus, we are able to compute the expected fuel consumption and carbon emissions for each flight in the generated pairings, as well as the total arrival/departure time deviations. Therefore, our proposed model can identify a trade-off among operation costs, sustainability costs, and robustness costs during pairing construction. With this new model, airlines are able to not only contribute to the environment through reduction in energy consumption and gas emission, but also develop their corporate social responsibility which is beneficial in image construction. Computational experiments based on real flight schedules show that the proposed model can bring a 7.98% decrease in the sustainability cost and an 1.81% decline in the robustness cost with only 0.55% increase in the basic operation cost when all the three cost factors are with equal weightings.

The rest of the paper is structured as follows. Section 2 reviews the related literature, while Sect. 3 introduces the problem definition. Then, the proposed novel crew pairing model is presented in Sect. 4, and Sect. 5 proposes the solution approach. Section 6 conducts computational experiments, and Sect. 7 concludes this work.

2 Literature review

We review the related literature from two aspects: (i) Airline crew pairing problems and (ii) airline scheduling with energy consumption considerations.

2.1 Airline crew pairing problems

The aviation industry has long performed an important role in worldwide economy (Choi, 2021; Feng et al., 2022; Li et al., 2021; Prakash et al., 2022). Among the airline scheduling problems, airline crew pairing problem has been long attracting great attention from both the industry and the academia (Haouari et al., 2019). After an airline has made the flight scheduling plan, fleet assignment plan, and aircraft routing plan, it is crucial to assign sufficient crew members to operate those scheduled flights on specific aircrafts (Quesnel et al., 2019). On one hand, modern airlines are operation thousands of flights per week. For a flight schedule with thousands of flights, there might be millions or even billions of possible pairings. Selecting a sub-set of pairings from the whole pairing pool with a minimum cost to cover all the scheduled flights is very difficult. On the other hand, the diverse rigorous working rules for crew members further complicate the crew pairing problem. If crew members are not arranged well, flight operations may be disrupted due to manpower problem (Wen et al., 2022a, 2022b).

As a standard optimization problem, the crew pairing problem has been studied extensively in the operations research society. Date back to 1970s, Marsten et al. (1979) reported a successful application of the integer programming approach for the crew planning problem. From then on, the airline crew pairing problem is generally modelled as a set-covering problem or a set-partitioning problem. As the number of possible pairings is enormous, researchers traditionally adopted a “once for all generation technique”. In this technique, a sufficiently large number of “good” pairings are generated by using heuristics. Then, a set-covering or set-partitioning problem is applied to identify a sub-set of pairings with a minimum cost through using integer programming techniques like branch-and-bound, cutting planes, and sub-gradient optimization. Later in 1980s, Lavoie et al. (1988) made a remarkable progress in the solution approach for the crew pairing problem by proposing a column generation based technique to deal with the large scale of the problem.

The objective of the crew pairing problem is to determine a set of legal pairings ($p \in P$) with a minimum cost, to ensure that each flight is covered by one pairing (set-partitioning problem) or at least one pairing (set-covering problem), as modelled below.

$$ \begin{gathered} min \mathop \sum \limits_{p \in P} c_{p} x_{p} , \hfill \\ s.t. \mathop \sum \limits_{p \in P} a_{pf} \cdot x_{p} = \left( \ge \right)1,\forall f \in F, \hfill \\ x_{p} \in \left\{ {0,1} \right\}, \forall p \in P. \hfill \\ \end{gathered} $$

$c_{p}$. represents the cost of Pairing $p$, while $a_{pj}$ means whether Pairing $p$ covers Flight f. When $a_{pf} = 1$, Flight f is involved in Pairing $p$; Otherwise, $a_{pf} = 0$. $x_{p}$, as the decision variable, equals 1 if Pairing $p$ is selected, and 0 otherwise.

In recent years, the research on the airline crew pairing problem is divided into two major directions. The first direction integrates the crew pairing problem with other stages of airline scheduling problems. For example, Cacchiani and Salazar-González (2017) deal with a fleet assignment, aircraft routing, and crew pairing integrated problem with the aim of minimizing the number of crew pairings, the number of aircraft, and the waiting time of crews between flights. Similarly, Shao et al. (2017) utilize the Benders decomposition approach to solve an integrated scheduling problem which involves the fleet assignment problem, aircraft maintenance routing problem, and crew pairing problem. The second direction tires to consider side constraints in the crew pairing framework in addition to the traditional flight coverage constraint. For instance, Quesnel et al. (2019) consider the language requirement in the pairing decisions and construct a new crew pairing problem variant. Wen et al., (2022a) integrate the manpower availability constraint into the stage of crew pairing problem to alleviate the shortcoming of the rigid separated airline crew scheduling approach to some extent.

In addition to the standard airline crew pairing problem, under the concept of disruption management, researchers also pay attention to enhancing the robustness of the pairings generated against potential disruptions or make recovery plans if disruptions occur. For example, Sun et al. (2020b) propose a bi-criteria robust crew pairing model. They first formulate the flying time variability and flight departure/arrival interdependency through data analytics on historical flight schedules. Then, a novel crew pairing model which minimizes not only the traditional financial costs, but also the robustness costs incurred by the differences between the scheduled flight departure/arrival times and the calculated expected values. Numerical analyses demonstrate that the proposed bi-criteria robust crew pairing approach can significantly improve the solution reliability without sacrificing too much financial costs. The research of Khan et al. (2021) also shows that flight flying time varies greatly depending on the actual flight departure time, which validates the importance of considering the uncertain flight duration in airline scheduling. To build airline crew recovery plans against maintenance problems or severe weather conditions, Lettovský et al. (2000) propose a new solution framework to reassign crew members to restore a disrupted schedule. Computational experiments based on real data collected from a major air carrier show the crew recovery efficiency of the proposed model (Lettovský et al., 2000).

2.2 Airline scheduling with energy consumption considerations

The carbon emissions released from human production activities have become increasingly serious (He et al., 2022). Especially, the fuel consumption is intensive in the aviation transportation industry (Justin et al., 2022), which not only incurs high costs, but also generates great burden to the environment due to the mass greenhouse gas emissions (Khan et al., 2019; Wang et al., 2020). As revealed by Base of Aircraft Data (BADA) project of the air traffic management organization of Europe (EUROCONTROL, 2012), the total fuel consumption during cruise stage is dependent on the actual flying time, flying speed, as well as other parameters like aircraft properties and air density. Previous research has found that, instead of being fixed as planned, the actual flying time always fluctuates according to the actual flight departure time. Accordingly, it is reasonable that airline scheduling decisions impose great impacts on the actual energy consumption for airlines, which further affects the sustainability level of the company. However, in the airline scheduling literature, sustainability issues (like fuel consumption and carbon emission) are studied rather less compared with the financial costs. Some studies considered the environmental factors from the perspective of cruise speed controllability which is utilized to optimize the scheduling problems for airlines. We review the related literature as follows.

Focusing on airline scheduling, Gürkan et al. (2016) take the cruise time control into account for a flight scheduling, fleet assignment, and aircraft routing integrated optimization problem, where a nonlinear mixed integer programming model is proposed for fuel consumption and CO₂ emissions. Interestingly, Gürkan et al. (2016) find that changing cruise time of flights can increase energy utilization and reduce the number of aircraft required.

In the domain of robust airline scheduling, cruise speed control is used to improve the robustness of solutions. For example, to improve the robustness of fleet assignment decisions, Şafak et al. (2017) control cruise speed to ensure passenger connections. In Şafak et al. (2017), the costs related to fuel consumption and gas emissions are considered, in addition to the traditional considerations like passenger demand and flight timing. A similar study can be found in Duran et al. (2015). However, only fuel consumption is considered, and the greenhouse gas emissions are ignored in Duran et al. (2015).

In terms of recovery operations, Aktürk et al. (2014) develop a flight re-scheduling model with cruise speed control on both disrupted and undisrupted flights. Aircraft Swapping is applied in Aktürk et al. (2014) to achieve recovery as quickly as possible (Aktürk et al., 2014). The fuel burn and gas emission functions further complicates the recovery model of Aktürk et al. (2014). Focusing on the recovery of aircraft and passengers, Arıkan et al. (2016) adopt the strategy of cruise speed control and several passenger recovery actions to achieve itineraries recovery under disruptions. The nonlinearity of fuel consumption is integrated into the recovery model of Arıkan et al. (2016). Their model is shown to be capable to identify the optimal tradeoff between passenger-related costs and operation costs in real time. A similar study is Arıkan et al. (2017). However, both Arıkan et al. (2016) and Arıkan et al. (2017) ignore the impact of carbon emissions.

2.3 Research gaps

From the above discussion, it is seen that despite the great importance, sustainability issues are considered rather less in the airline scheduling problems, compared with the traditional operation costs. However, the scheduling problems are crucial for the sustainability level of an airline, as the related decisions directly affect the actual flying times for each individual flight, which further influences the total fuel consumptions and greenhouse gas emissions. Existing research has integrated the fuel and gas considerations in flight scheduling, fleet assignment, aircraft routing and their related robust scheduling and recovery problems. However, none of the current studies have considered the fuel consumption and gas emission factors in the critical airline crew pairing problem. Due to the importance of crew pairing for the overall quality of airline scheduling, it is valuable to explore how the sustainability considerations affect the airline crew pairing solutions, and study how an airline can optimize their crew itinerates which can benefit both the airline and the environment. Our study thus fulfills this important research gap.

3 Problem description

In this section, we first introduce terminologies and definitions of the airline crew pairing problem. Then, the duty-based flight network is constructed for pairing generation. Last, the flight flying time variability and flight departure-arrival interdependency relationship are discussed. The major notations used in this work are summarized in Appendix.

3.1 Definitions

With a flight schedule containing flight departure/arrival airports, flight departure/arrival times, and flight flying times, the crew pairing problem identifies sufficient legal pairings to cover all scheduled flights, while satisfying all the working rules regulated by labor unions, civil aviation departments, and airlines (Wen et al., 2021). A duty is a sequence of flights connected by sits (or transits). A briefing at the start and a debriefing at the end are necessary for a duty. A duty period refers to the elapsed time from the start of to the end of the duty. Between two consecutive duties, a rest is required, during which crew members are free of any work. A pairing is a series of duties separated by rests which starts from and ends at the home base of the crew member. A pairing is operated by one crew member, while a pairing is legal (or feasible) if all the working rules are satisfied. A typical pairing generally lasts for two to five days. The total pairing elapse time is the time away from base (TAFB) (Wen et al., 2020).

3.2 Working rules

To ensure the safety level of passengers, airlines should comply with a variety of strict rules and regulations in scheduling crew members. In this work, we consider the following rules based on the practical operations of a major Hong Kong airline and The Avoidance of Fatigue in Aircrews (CAD 371) published by the Civil Aviation Department of the Government of the Hong Kong Special Administrative Region. First of all, two flights can be connected only when the arrival airport of the first flight is the departure airport of the second flight. The minimum and maximum sit time (or transit time) are 75 and 240 min, respectively. Second, the briefing (before a duty) and debriefing (after a duty) last for 60 and 30 min, respectively. Regarding the longest length of a duty, it varies based on the local starting time and the number of flights in the duty. For example, if a duty starts at 07:30 in local time with two flight sectors, the longest duty period is then 12.25 h. Third, two duties can be connected by a rest if the destination of the first duty is the origin of the second duty. A rest should last between 720 and 2160 min if the former duty lasts less than twelve hours. Otherwise, a minimum 840-min rest is compulsory. At last, maximum five duties, twelve flights, and 7200-min TAFB are allowed for a pairing.

3.3 Duty-based flight network

A duty-based flight network is developed for the crew pairing problem. F represents the set of flights (indexed by j). P stands for the set of feasible pairings in the duty-based flight network (indexed by p). Figure 1 shows an example of a duty-based flight network. The network is denoted by $G = \left( {N,A} \right)$. $N$ is the set of nodes (including a source node (s) representing home base, a sink node (k) representing home base, and duty nodes (d)), and $A$ represents the set of arcs. A duty ($d$) is composed of a sequence of flights connected by sit arcs. The set of sit arcs in duty d is denoted by $SA_{d}$, The set of flights covered by duty d is $F_{d}$, while the set of flights contained in Pairing p is $F_{p}$. Duties shall be constructed based on the diverse working rules. Duties are connected with each other by rests. All duties starting from the home base connect with s through a starting arc, and all duties ending at the home base link with k through an ending arc. The sets of starting and ending arcs are indexed by $A_{s}$ and $A_{e}$, respectively. For the duties that do not start from s, a deadhead starting arc is developed to connect s with the duty. Similarly, for the duties that do not end at k, a deadhead ending arc is utilized to link the duty with k. We use $A_{ds}$ and $A_{de}$. to represent the sets of deadhead starting arcs and deadhead ending arcs, respectively. A legal (or feasible) pairing refers to a resource-feasible s-k path in network. The set of arcs involved in Pairing p is denot by $A_{p}$.

Fig. 1

An example of the duty-based flight network

3.4 Flying time variability

Each flight has a scheduled departure time ($\vartheta_{f}^{s}$), a scheduled arrival time ($\theta_{f}^{s}$), and the associated scheduled flying time. However, from our preliminary analysis, we find that the actual flight departure/arrival time, as well as the actual flying times usually fluctuate significantly. For instance, if a flight departs late from its origin airport at a peak time (e.g., due to the traffic congestion at the origin airport), the aircraft can fly faster to meet its scheduled arrival time. If a flight arrives in peak times, the total flying time will increase accordingly due to the long landing queue. Other factors, like bad weather and governmental traffic control also affect the actual flying time. Researchers have paid attention to exploring the relationship among flying times, flight departure times, and arrival times to improve the decision making in the industry (Chung et al., 2017). Following previous studies (Sun et al., 2020a; Wen et al., 2020), the heteroscedastic regression model is used to characterize the uncertain flight duration which depends on the actual flight departure time, as shown in Eq. (1). $\zeta_{f} \left( K \right)$ represents the flight duration of Flight f if the flight departs at Time K. $\alpha_{f} \left( K \right)$ is the regression mean flight duration of Flight f if the flight departs at Time K, while $\beta_{f} \left( K \right)$ is the related regression standard deviation. $\partial$ is a random variable that follows the standard normal distribution. Then, two-year historical flight data provided by a local major airline are used to estimate the regression mean and variance of the duration of flights that depart in the same time slot at the same airport (Sun et al., 2020a; Wen et al., 2020). The ordinary least squares criterion and weighted least squares methods are applied for coefficient estimation and refinement.

$$ \zeta_{f} \left( K \right) = \alpha_{f} \left( K \right) + \beta_{f} \left( K \right)\partial $$

(1)

Denote the actual flight departure time for Flight f as $\vartheta_{f}$ and the actual arrival time as $\theta_{f}$. Please note that $\vartheta_{f}$ and $\theta_{f}$ are random variables, which are different from the scheduled times $\vartheta_{f}^{s}$ and $\theta_{f}^{s}$. $E\left[ {\left( \cdot \right)} \right]$ and $V\left[ {\left( \cdot \right)} \right]$ stand for mean and variance, respectively. Based on $\zeta_{f} \left( K \right)$, we can formulate the arrival time and departure time for each flight recursively. First of all, the flight arrival time $\theta_{f}$ is equal to the flight departure time plus the flight duration, as in Eq. (2). Taking expectation for $\theta_{f}$, we could obtain the expected flight arrival time for Flight f, as formulated in Eq. (3). Besides, the variance of flight arrival time for Flight f, can also be obtained as in Eq. (4).

$$ \theta_{f} = \vartheta_{f} + \zeta_{f} \left( {\vartheta_{f} } \right) $$

(2)

$$ E\left[ {\theta_{f} } \right] = E\left[ {\vartheta_{f} } \right] + \alpha_{f} \left( {E\left[ {\vartheta_{f} } \right]} \right) $$

(3)

$$ V\left[ {\theta_{f} } \right] = (1 + \alpha_{f} \left( {E\left[ {\vartheta_{f} } \right]} \right)^{2} V\left[ {\vartheta_{f} } \right] + \beta_{f}^{2} \left( {E\left[ {\vartheta_{f} } \right]} \right) $$

(4)

The above formulations are based on the knowledge of the mean and variance of the actual flight departure time. That is, $E\left[ {\vartheta_{f} } \right]$ and $V\left[ {\vartheta_{f} } \right]$, which can be further obtained by $\vartheta_{f} = Max\left\{ {\vartheta_{f}^{s} ,\theta_{{f^{ - } }} + M} \right\}$, where $M$ represents the minimum crew transit time between two flights. The reason that $\vartheta_{f}$ takes the maximum between $\vartheta_{f}^{s}$ and $\theta_{{f^{ - } }} + M$ can be explained as follows. First of all, if the arrival of the previous flight (i.e., $f^{ - }$) would not affect the on-time departure of the considered flight (i.e., Flight f), then Flight f will depart as scheduled (i.e., $\vartheta_{f}^{s}$). On the other hand, if the arrival delay of the previous flight makes it impossible for Flight f to depart on time, then this flight should depart with a legal miminum transit period after the arrival of the previous flight (i.e., $\theta_{{f^{ - } }} + M$). Consequently, the mean and variance of flight departure time can be obtained as in Eq. (5) and Eq. (6), respectively. Note that $\Phi$ and $\phi$ are the cumulative distribution function (cdf) and probability distribution function (pdf) of the standard normal distribution. For presentation simplicity, we use $\rho_{f}$ to represent the expected flight duration if the flight departs at $E\left[ {\vartheta_{f} } \right]$. That is, $\rho_{f} = E\left[ {\theta_{f} } \right] - E\left[ {\vartheta_{f} } \right] = \alpha_{f} \left( {E\left[ {\vartheta_{f} } \right]} \right)$. Besides, for traceability, all random variables are considered to follow the normal distribution in this study.

$$\begin{aligned}& E\left[ {\vartheta_{f} } \right] = \vartheta_{f}^{s} \phi \left( {\frac{{\vartheta_{f}^{s} - E\left[ {\theta_{{f^{ - } }} } \right] - M}}{{\sqrt {V\left[ {\theta_{{f^{ - } }} } \right]} }}} \right) + E\left[ {arr\left( {j^{ - } } \right)} \right]\phi\left( {\frac{{E\left[ {\theta_{{f^{ - } }} } \right] + M - \vartheta_{f}^{s} }}{{\sqrt {V\left[ {\theta_{{f^{ - } }} } \right]} }}} \right)\\ & + \sqrt {V\left[ {\theta_{{f^{ - } }} } \right]}\phi \left( {\frac{{\vartheta_{f}^{s} - E\left[ {\theta_{{f^{ - } }} } \right] - M}}{{\sqrt {V\left[ {\theta_{{f^{ - } }} } \right]} }}} \right)\end{aligned} $$

(5)

$$\begin{aligned} & V\left[ {\vartheta _{f} } \right] = E\left[ {\vartheta _{f}^{2} } \right] - E^{2} \left[ {\vartheta _{f} } \right]\left( E\left[ {\vartheta _{f}^{2} } \right] = E\left[ Max\left\{ {\vartheta _{f}^{s} ,\theta _{{f^{ - } }} + M} \right\}^{2} \right]\right.\\ &= \vartheta _{f}^{{s^{2} }} \Phi \left( {\frac{{\vartheta _{f}^{s} - E\left[ {\theta _{{f^{ - } }} } \right] - M}}{{\sqrt {V\left[ {\theta _{{f^{ - } }} } \right]} }}} \right) + \left( V\left[ {\theta _{{f^{ - } }} } \right] + E^{2} \left[ {\theta _{{f^{ - } }} } \right] + 2ME\left[ {\theta _{{f^{ - } }} } \right] + M^{2} \right)\\ &\left.\phi \left( {\frac{{E\left[ {\theta _{{f^{ - } }} } \right] + M - \vartheta _{f}^{s} }}{{\sqrt {V\left[ {\theta _{{f^{ - } }} } \right]} }}} \right) + \left( {E\left[ {\theta _{{f^{ - } }} } \right] + M + \vartheta _{f}^{s} } \right)\sqrt {V\left[ {\theta _{{f^{ - } }} } \right]} \phi \left( {\frac{{\vartheta _{f}^{s} - E\left[ {\theta _{{f^{ - } }} } \right] - M}}{{\sqrt {V\left[ {\theta _{{f^{ - } }} } \right]} }}} \right) \right) \end{aligned} $$

(6)

Thus, with $E\left[ {\theta_{f} } \right]$, $V\left[ {\theta_{f} } \right]$, $E\left[ {\vartheta_{f} } \right]$, $V\left[ {\vartheta_{f} } \right]$, and $\zeta_{f} \left( K \right)$, we could calculate the expected flight departure and arrival time for each flight contained in a crew pairing connected by transit periods. The first flight in the duty is assumed to have a zero mean and variance of v to initiate the computing, while the overnight rest between two duties are assumed to be able to absorb all disruptions encountered in daytime. Accordingly, we are able to compute the expected fuel consumption and the related carbon emission based on the expected flight durations. Therefore, a novel decision support system for crew pairing which can consider the fuel-related sustainability cost can thus be developed (see Sect. 4).

Note that the arrivals before the scheduled arrival time point are regarded as arrival on time. Figure 2 demonstrates an example of the recursive expected flight departure/arrival times. In this example, a duty involves F1, F2, and F3. The expected departure time for F1 is its scheduled departure time (i.e., $E\left[{\vartheta }_{1}\right]={\vartheta }_{1}^{s}$). Due to the flight duration variability, the expected arrival time for F1 is later than the scheduled point (i.e., $E\left[{\theta }_{1}\right]>{\theta }_{1}^{s}$). Accordingly, the expected departure time for F2 is also later than its scheduled time point (i.e., $E\left[{\vartheta }_{2}\right]>{\vartheta }_{2}^{s}$). The delay propagates to the following flight F3. As we can see from Fig. 2, if we only apply the scheduled departure/arrival times for the flights on the schedule without considering flight duration variability in the pairing generation process, crews can easily encounter disruptions. Moreover, flight durations deviate from the plan, which affects fuel consumptions and carbon emissions.

Fig. 2

An example of flight duration variability

Fig. 3

An illustration figure for Flight 26

4 Crew pairing with sustainability considerations

Based on the flight duration variability introduced in Sect. 3.4, in this section, we develop a novel decision support system for the airline crew pairing problem with sustainability considerations. To be specific, the novel crew pairing model can minimize the basic operation cost, the fuel consumption and greenhouse gas emission (named as sustainability cost in the following), and also the pairing robustness cost. The sustainability cost for Pairing p is denoted by ${c}_{p}^{s}$ (as explained in Sect. 4.1). The basic operation cost for Pairing p is denoted by ${c}_{p}^{o}$ (as described in Sect. 4.2). Section 4.3 introduces the robustness cost (${c}_{p}^{r}$). Then, Sect. 4.4 formulates the mathematical model.

4.1 Sustainability costs (fuel consumption & carbon emission)

The cost related to fuel usage is the largest composition of an airline’s total costs, while carbon emission control has become one of the most important topics for airlines in recent years along with the increasing awareness of the society for environmental sustainability. To formulate flight fuel consumptions and carbon emissions, we follow the cruise stage fuel consumption methodology proposed by the Base of Aircraft Data (BADA) project of the air traffic management organization of Europe (EUROCONTROL, 2012).

4.2 Fuel consumption

Fuel consumption in kg (i.e., $FU_{j} \left( {\rho_{f} } \right)$) for a flight duration ($\rho_{f}$) for Flight j is estimated in Eq. (7).

$$ FU_{j} \left( {\rho_{f} } \right) = \frac{{{\mathcal{R}}_{1}^{j} }}{{\rho_{f} }} + \frac{{{\mathcal{R}}_{2}^{j} }}{{\left( {\rho_{f} } \right)^{2} }} + {\mathcal{R}}_{3}^{j} \cdot \left( {\rho_{f} } \right)^{3} + {\mathcal{R}}_{4}^{j} \cdot \left( {\rho_{f} } \right)^{2} $$

(7)

In the function of $FU_{j} \left( {\rho_{f} } \right)$, ${\mathcal{R}}_{1}^{j}$, ${\mathcal{R}}_{2}^{j}$, ${\mathcal{R}}_{3}^{j}$, and ${\mathcal{R}}_{4}^{j}$ are coefficients related to aircraft properties and physical conditions. Referring to EUROCONTROL (2012), Şafak et al. (2017), and Gürkan et al. (2016), the detailed expressions of${\mathcal{R}}_{1}^{j}$,${\mathcal{R}}_{2}^{j}$,${\mathcal{R}}_{3}^{j}$, and ${\mathcal{R}}_{4}^{j}$ are shown in Eq. (8) to Eq. (11). To be specific,${C}_{1}$,${C}_{2}$,${C}_{3}$,${C}_{4}$, and ${C}_{5}$ are aircraft fuel consumption coefficients. ${S}_{j}$ is the surface area of the aircraft wing (${m}^{2}$), while ${w}_{j}$ is the mass of the aircraft (kg). Besides, ℊ is the air density at the given altitude (kg/m³), $g$ is the gravitational acceleration (m/s²), while $\varphi$ is bank angle. The distance of Flight j is ${d}_{j}$.

$${\mathcal{R}}_{1}^{j}=\frac{{C}_{1}\cdot {C}_{2}\cdot {C}_{4}\cdot \mathcalligra{g}\cdot {S}_{j}\cdot {d}_{j}^{2}}{2}$$

(8)

$${\mathcal{R}}_{2}^{j}=\frac{{C}_{1}\cdot {C}_{2}\cdot {C}_{4}\cdot \mathcalligra{g}\cdot {S}_{j}{\cdot d}_{j}^{3}}{2\cdot {C}_{3}}$$

(9)

$${\mathcal{R}}_{3}^{j}=\frac{2\cdot {C}_{1}\cdot {C}_{2}{\cdot C}_{5}\cdot {{w}_{j}}^{2}\cdot {g}^{2}}{\mathcalligra{g}{\cdot S}_{j}\cdot {cos(\varphi )}^{2}\cdot {d}_{j}^{2}}$$

(10)

$${\mathcal{R}}_{4}^{j}=\frac{2\cdot {C}_{1}\cdot {C}_{2}\cdot {C}_{5}\cdot {{w}_{j}}^{2}\cdot {g}^{2}}{{C}_{3}\cdot \mathcalligra{g}{\cdot S}_{j}{\cdot cos(\varphi )}^{2}\cdot {d}_{j}}$$

(11)

We denote the unit fuel price (per kg) by ${c}_{fuel}$. Therefore, the fuel cost for Flight j (${FC}_{j}\left({\rho }_{f}\right)$) is formulated as follows (i.e., Eq. (12)).

$${FC}_{j}\left({\rho }_{f}\right)={c}_{fuel}\cdot {FU}_{j}\left({\rho }_{f}\right)$$

(12)

4.2.1 Carbon emission

Regarding carbon emission, we apply the aircraft engine emission standard developed by International Civil Aviation Organization. It is stated that the carbon emission (i.e., CO₂) is around 3.15 times (i.e., b) the weight of fuel burnt. Accordingly, the cost related to carbon emission (${EC}_{j}\left({\rho }_{f}\right)$) is modeled as in Eq. (13), where ${c}_{emi}$ stands for the unit carbon emission cost, like carbon tax.

$${EC}_{j}\left({\rho }_{f}\right)={c}_{emi}\cdot b{\cdot FU}_{i}\left({\rho }_{f}\right)$$

(13)

Accordingly, the total fuel consumption and carbon emission cost (${FE}_{j}\left({\rho }_{f}\right)$ for a flight can be obtained as shown in Eq. (14).

$$\begin{aligned}& {FE}_{j}\left({\rho }_{f}\right)={FC}_{j}\left({\rho }_{f}\right)+{EC}_{j}\left({\rho }_{f}\right)\\ & =({c}_{fuel}+{c}_{emi}\cdot b)[\frac{{\mathcal{R}}_{1}^{j}}{{\rho }_{f}}+\frac{{\mathcal{R}}_{2}^{j}}{{({\rho }_{f})}^{2}}+{\mathcal{R}}_{3}^{j}{\cdot ({\rho }_{f})}^{3}+{\mathcal{R}}_{4}^{j}{\cdot ({\rho }_{f})}^{2}]\end{aligned} $$

(14)

Therefore, the flight duration based sustainability cost of a pairing can be formulated as ${c}_{p}^{s}=\sum_{j\in {F}_{p}}{FE}_{j}\left({\rho }_{f}\right)$. During the pairing construction process in our study, we apply the computed ${\rho }_{f}$ to calculated ${c}_{p}^{s}$. That is, the fuel consumption and carbon emissions are computed based on the expected flight durations considering flight duration variability.

4.3 Basic operation costs

Traditionally, only the basic operation costs are considered in the crew pairing problem. A crew pairing’s basic operation cost contains a fixed component (K) and arc-related costs. Arcs are categorized into duty arcs (${d}^{-},d$), (deadhead) starting arcs ($s,d$), and (deadhead) ending arcs ($d,k$). For (${d}^{-},d$), the arc-related cost (${t}_{{d}^{-},d}$, Eq. (15)) is made up of the waiting cost during flight connections (${c}_{{d}^{-},d}^{w}$, Eq. (18)), rest cost (${c}_{{d}^{-},d}^{r}$, Eq. (20)), and pairing minimum duty guaranteed (PMDG) cost (${c}_{{d}^{-},d}^{D}$, Eq. (21)). To be specific, the waiting cost is a function (${g}_{{j}^{-}}(\cdot )$) related to the flight connection time (${\delta }_{{f}^{-},f}$). Besides, the rest cost is a function (${l}_{{d}^{-}}(\cdot )$) related to the rest length between two duties (${\delta }_{{d}^{-},d}$). Readers are referred to Saddoune et al. (2013) and Chung et al. (2017) for the details of ${g}_{{j}^{-}}(\cdot )$ and ${l}_{{d}^{-}}(\cdot )$. The PMDG cost can force the algorithm to develop longer duties. If the credit flying time of a duty (${v}_{d}$) is shorter than a threshold (${V}_{min}$), a unit PMDG cost (v) will be generated. For ($s,d$), the arc-related cost (${t}_{s,d}$, Eq. (16)) is composed of waiting cost of flight connections (${c}_{s,d}^{w}$, Eq. (19)), pairing minimum duty guaranteed cost (PMDG) (${c}_{s,d}^{D}$, Eq. (22)), and deadhead cost (${c}_{s,d}^{h}$, Eq. (23) if this arc is deadhead and Eq. (24) otherwise). For ($d,k$), the arc-related cost (${t}_{d,k}$, Eq. (17)) only involves the deadhead cost (${c}_{d,k}^{h}$, Eq. (25) if this arc is deadhead and Eq. (26) otherwise). Note that the deadhead cost is $\aleph$ for each deadhead starting or ending arc.

Arc-related basic operation cost	${t}_{{d}^{-},d}={c}_{{d}^{-},d}^{w}+{c}_{{d}^{-},d}^{r}+{c}_{{d}^{-},d}^{D}$, $\forall \left({d}^{-},d\right)\in \left\{A-{A}_{e}-{A}_{de}-{A}_{s}-{A}_{ds}\right\},$	(15)
	${t}_{s,d}={c}_{s,d}^{w}+{c}_{s,d}^{D}+{c}_{s,d}^{h}$, $\forall \left(s,d\right)\in \left\{{A}_{s}+{A}_{ds}\right\}$,	(16)
	${t}_{d,k}={c}_{d,k}^{h}$, $\forall \left(d,k\right)\in \left\{{A}_{e}+{A}_{de}\right\}$,	(17)
Waiting cost	${c}_{{d}^{-},d}^{w}={\sum }_{\left({f}^{-},f\right)\in {SA}_{d} }{g}_{{f}^{-}}\left({\delta }_{{f}^{-},f}\right), \forall \left({d}^{-},d\right)\in \left\{A-{A}_{e}-{A}_{de}-{A}_{s}-{A}_{ds}\right\}$,	(18)
	${c}_{s,d}^{w}={\sum }_{\left({f}^{-},f\right)\in {SA}_{d} }{g}_{{f}^{-}}\left({\delta }_{{f}^{-},f}\right), \forall \left(s,d\right)\in \left\{{A}_{s}+{A}_{ds}\right\}$,	(19)
Rest cost	${c}_{{d}^{-},d}^{r}={l}_{{d}^{-}}\left({\delta }_{{d}^{-},d}\right),$ $\forall \left({d}^{-},d\right)\in \left\{A-{A}_{e}-{A}_{de}-{A}_{s}-{A}_{ds}\right\}$,	(20)
PMDG cost	${c}_{{d}^{-},d}^{D}=v*\mathrm{max}\left\{0, \left({V}_{min}-{v}_{d}\right)\right\}, \forall \left({d}^{-},d\right)\in \left\{A-{A}_{e}-{A}_{de}-{A}_{s}-{A}_{ds}\right\},$	(21)
	${c}_{s,d}^{D}=v*\mathrm{max}\left\{0, \left({V}_{min}-{v}_{d}\right)\right\}, \forall \left(s,d\right)\in \left\{{A}_{s}+{A}_{ds}\right\}$,	(22)
Deadhead cost	${c}_{s,d}^{h}=\aleph$, $\forall \left(s,d\right)\in {A}_{ds}$,	(23)
	${c}_{s,d}^{h}=0$, $\forall \left(s,d\right)\in {A}_{s}$,	(24)
	${c}_{d,k}^{h}=\aleph$, $\forall \left(d,k\right)\in {A}_{de},$	(25)
	${c}_{d,k}^{h}=0$, $\forall \left(d,k\right)\in {A}_{e}.$	(26)

Finally, the total basic operation cost for this pairing ${c}_{p}^{o}$ can be formulated as in Eq. (27), where ${A}_{p}$ represents all arcs contained in Pairing $p$ (including a (deadhead) starting arc, duty arcs, and a (deadhead) ending arc).

$${c}_{p}^{o}=K+\sum_{({n}_{p}^{-},{n}_{p})\in {A}_{p}}{t}_{{n}_{p}^{-},{n}_{p}}$$

(27)

4.4 Robustness cost

As discussed, a flight’s departure time and arrival time are dependent on those of the previous flight (see the details in Sect. 3.4). Thus, crew members usually face flight operations which are different from their schedules. For instance, they are supposed to arrive at an airport at 5 pm, while in operations, they land at 6 pm. Due to the recursive relationship of the flights in a duty, the effect of flight duration variability will propagate from flights to flights. Therefore, we would also like to minimize the total deviations of the computed expected flight departure/arrival times from the scheduled flight departure/arrival times. Besides, a pairing will also be penalized if the computed duty elapse time is larger than the maximum allowed duty duration. Therefore, ${c}_{p}^{r}$ is formulated as ${\sum }_{f\in {F}_{p}}{(E\left[{\vartheta }_{f}\right]-{\vartheta }_{f})}^{+}+{\sum }_{f\in {F}_{p}}{(E\left[{\theta }_{f}\right]-{\theta }_{f})}^{+}+{{\sum }_{p\in P}{\sum }_{d\in {D}_{p}}(E\left[{\theta }_{{f}_{d}^{last}}\right]-E\left[{\vartheta }_{{f}_{d}^{first}}\right]-MaxAllowedDutyElapse)}^{+}$. The first and second parts of ${c}_{p}^{r}$ stand for the total (positive) deviation of the expected arrival/departure time from the scheduled time points. In the third part, $E\left[{\theta }_{{f}_{d}^{last}}\right]-E\left[{\vartheta }_{{f}_{d}^{first}}\right]$ refers to the duty time length by computing the difference between the expected arrival time of the last flight in the duty with the expected departure time of the first flight in the duty. Thus, ${{\sum }_{p\in P}{\sum }_{d\in {D}_{p}}(E\left[{\theta }_{{f}_{d}^{last}}\right]-E\left[{\vartheta }_{{f}_{d}^{first}}\right]-MaxAllowedDutyElapse)}^{+}$ computes the time length of each duty exceeding the maximum allowed duty elapse time for all duties contained in the pairing.

4.5 The mathematical model for the sustainable crew pairing problem

With the sustainability cost, basic operation cost and robustness cost built above, we can build the novel decision support system for the crew pairing problem with sustainability considerations mathematically, which are presented in Eq. (28) to Eq. (30). To be specific, the objective is to minimize the weighted sum of the sustainability cost, basic operation cost, and robustness cost, where ${c}_{p}^{s}$ is determined by Eq. (7) to Eq. (14), ${c}_{p}^{o}$ is decided by Eq. (15) to Eq. (27), and ${c}_{p}^{r}$ is given in Sect. 4.3. ${w}_{1}$, ${w}_{2}$, and ${w}_{3}$ (${w}_{1}+{w}_{2}+{w}_{3}=1$) represent the weights for the basic operation cost, sustainability cost, and robustness cost respectively. With this proposed objective, airlines can optimize the environmental burdens their flights generate for the environment by limiting fuel consumption and greenhouse gas emissions. Constraint Eq. (29) is used to ensure that each flight is covered by at least one pairing, while Constraint Eq. (30) is to ensure that the decision variable is binary.

$$min \sum_{p\in P}({w}_{1}{c}_{p}^{o}+{w}_{2}{ c}_{p}^{s}+{w}_{3}{ c}_{p}^{r}){x}_{p,}$$

(28)

$$s.t. \sum_{p\in P}{a}_{pf}\cdot {x}_{p}\ge 1,\forall f\in F $$

(29)

$${x}_{p}\in \left\{\mathrm{0,1}\right\}, \forall p\in P$$

(30)

5 Solution approach

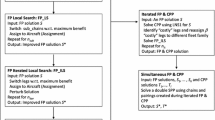
A column-generation based solution approach is developed to deal with the proposed crew pairing models. Column generation is a continuous optimization technology which can implicitly consider the whole pairing pool of the large-scale crew pairing problem without encountering the difficulty of explicitly dealing with all possible pairings. The crew pairing problem is thus separated into a restricted master problem and a sub-problem as explained in the following.

5.1 Restricted master problem

The restricted master problem is the linear relaxed version of the crew pairing problem with a restricted number of initial feasible pairings. In each iteration, the restricted master problem is solved to optimality by using linear programming technique. The dual prices associated with each constraint are transferred to sub-problem. Then, better pairings (i.e., those can further lower down the objective value) are identified to update the pairing pool of the restricted master problem. If no better pairings can be found, then the optimal solution for the restricted master problem is the optimal solution for the whole problem. Column generation procedure thus terminates. Last, mixed integer programming (MIP) technique is applied to obtain integer solutions.

5.2 Sub-problem

The sub-problem of the crew pairing problem is generally modelled as a shortest path problem with resource constraints. The aim of the sub-problem is to identify promising pairings with negative reduced costs from the whole solution pool, which is transferred to finding the shortest path in the flight network with resource constraints. Resources in the crew pairing problem refer to the diverse working rules, like the maximum number of flights and maximum time away from base allowed for a pairing. A pairing (path) is feasible (legal) only when all working rules are satisfied. The identified better pairing is added to the solution pool of the restricted master problem to start the next iteration. If no better pairings (paths) can be identified, the algorithm terminates, and the restricted master problem reaches optimality. Let ${\pi }_{f}$ stand for the dual price for the f _th row (Flight f) of the flight coverage constraint (i.e., Eq. (29)). The reduced cost of ${x}_{p}$ (i.e., $\overline{{c }_{p}}$) can be modelled as in Eq. (31).

$$\overline{{c }_{p}}={w}_{1}{c}_{p}^{o}+{w}_{2}{ c}_{p}^{s}+{w}_{3}{ c}_{p}^{r}-\sum_{f\in F}{a}_{pj}\cdot {\pi }_{f}$$

(31)

6 Computational experiments

In this section, we test the performances of our proposed sustainable crew pairing model based on real-world collected flight schedules. Section 6.1 introduces parameter setting and instance characteristics. Section 6.2 presents the model settings applied in the experiment. Then, Sect. 6.3 discusses the findings from the perspectives of the basic operation cost, sustainability cost, and robustness cost.

6.1 Parameter setting and instance characteristics

6.1.1 Parameters applied in the computational experiments

Following Şafak et al. (2017), we set the fuel price (per kg) (i.e.,${c}_{fuel}$) as 0.6 USD. Two types of aircraft are involved in our experiments. They are A320-111 and A320-212. For the parameters related to fuel consumption for each aircraft type, we apply those used in Şafak et al. (2017), as summarized in Table 1.

Table 1 Fuel consumption parameters by aircraft types

For air density coefficients, we follow the User Manual for the Base of Aircraft Data (EUROCONTROL, 2012). Below tropopause, air density (ℊ, kg/m³) is a function of temperature ($T$), and can be obtained by the following equation. In the equation, $-\frac{g}{{K}_{T}\cdot R}-1$ is approximated as 4.26. $R$ is the real gas constant for air, $g$ is the gravitational acceleration, ${K}_{T}$ is the International Standard Atmosphere temperature gradient with altitude below the tropopause. ${\mathcalligra{g}}_{0}$ is the air density at sea level. In our experiment, we apply the standard atmosphere air density at sea level (i.e., ${\mathcalligra{g}}_{0}$=1.225 kg/m³).

$$\mathcalligra{g}={\mathcalligra{g}}_{0}{\left[\frac{T(h)}{{T}_{0}}\right]}^{-\frac{g}{{K}_{T}\cdot R}-1}$$

(32)

In Eq. (32), ${T}_{0}$ is the temperature at sea level. We use the standard atmosphere seal level temperature (i.e., ${T}_{0}=288.15\mathrm{ K}$). For an altitude of $h$ (in meters), the temperature $T(h)$ is calculated as Eq. (33). For the altitude, as under standard atmosphere conditions, the tropopause is at 11,000 m altitude, we assume that flights fly at 11,000 m during cruise stage (i.e., $h=11000$ meters).

$$T(h)={T}_{0}-6.5*h/1000$$

(33)

Moreover, gravitational acceleration (g) is set as 9.81 m/s², and we apply the nominal bank angle for civil flights (i.e., $\varphi$=35 degree).

6.1.2 Instance characteristics

We test the proposed models by using the flight data applied in Wen et al. (2020). Specifically, 5 flight data sets are involved (with 36, 39, 56, 89 and 98 flights). Instances 1, 4, 5, and 6 contain airports of OKA, GUM, HKG, TPE, KIX, SIN, and ICN. Instances 2 and 3 involve airports of HKG, KIX, TPE, and ICN. By involving different types of aircraft, totally 10 instances are created.

6.2 Model setting

Recall that in the novel crew pairing model with sustainability considerations developed in Sect. 4.4, the objective function is to minimize $\sum_{p\in P}({w}_{1}{c}_{p}^{o}+{w}_{2}{ c}_{p}^{s}+{w}_{3}{ c}_{p}^{r}){x}_{p}$. Thus, based on the weights (i.e., ${w}_{1}$, ${w}_{2}$, ${w}_{3}$),⁹ we test 7 model settings. The details of the 7 settings are illustrated in Table 2. For example, Model 1 only considers the basic operation cost, while Model 4 considers all the three cost factors with equal weightings.

Table 2 Model settings

By running the model for each instance and for each model setting, we can obtain the corresponding operation costs, sustainability costs, and robustness costs. As they have different units, to ensure that the three cost factors are in a similar scale, a normalization process is carried out. The upper bound and the lower bound of each cost factors are first estimated, and the cost will then be converted into a normalized value between 0 to 1 in each iteration. The mean computation time for the ten instances is summarized in Table 3. It is seen that the computation time grows dramatically when the number of flights grows from 36 to 96. This is because that the complexity of the corresponding flight network rises greatly due to the sharp increase in the possible flight connections and duty combinations.

Table 3 Mean computation time

6.3 Analysis

In this section, we first use a simple example to demonstrate that the actual flight duration may deviate from the scheduled time length greatly, thus imposing great effects on the sustainability cost (i.e., fuel consumption and carbon emission). Then, we evaluate the model performances in terms of sustainability cost, operation cost, and robustness cost for the six settings.

6.3.1 An illustration example of flight flying time variability

We use Flight 26 in instance 1 in Model 1 to demonstrate flight duration variability and the importance of considering sustainability cost (see Figure 3). The scheduled departure time of Flight 26 is 6:05am. As Flight 26 is the first flight of this duty, its expected departure time is exactly the scheduled departure time. However, due to some reason (e.g., to avoid the possible traffic congestion at the destination airport), this flight may accelerate during the cruise stage and arrives earlier than scheduled (according to the calculation formula provided in Sect. 3.4 based on massive historical data). That is, the expected arrival time (7:46am) is earlier than the scheduled arrival time (8:09am), while the flight duration is reduced by 23 min. Thus, the fuel consumed and the carbon dioxide released by this flight can deviate from airline’s plan significantly.

6.3.2 Operation cost

The basic operation costs obtained for each instance under each model setting are summarized in Table 4 and depicted in Fig. 4. Besides, using Model 1 as the benchmark, the comparisons of the models in terms of operation costs are presented in Table 5. Recall that under Model 1, only the basic operation cost is considered (i.e., ${w}_{1}$=1, ${w}_{2}=0$, ${w}_{3}=0$). Thus, it is reasonable to see that Model 1 incurs the lowest cost among almost all model settings for each instance, as other model settings construct crew pairings with other considerations (like sustainability issues and robustness issues). On average, Model 2 to Model 7 generate 7.81% more operation costs than Model 1. Among these 6 model settings, we witness that for the settings where the operation cost is totally omitted (i.e., Model 3, Model 5 and Model 7), the operation cost incurred grows dramatically (19.70% for Model 3, 11.86% for Model 5 and 14.20% for Model 7). On the other hand, as long as the operation cost is considered in the optimization objective (e.g., Model 2, Model 4, and Model 6), considering other cost factors would not increase the operation cost significantly (0.54% for Model 2, 0.55% for Model 4, and only 0.01% for Model 6). One interesting finding is that for Model 6 (${w}_{1}$=0.5, ${w}_{2}=0$, ${w}_{3}=0.5$), considering solution robustness imposes very tiny influence on the operation cost. Specifically, under Model 6, the operation cost remains unchanged for instances 1–4, and 9–10.

Table 4 The operation cost obtained for each instance under each model setting

Fig. 4

Operation costs obtained by each instance under each model setting

Table 5 The operation cost compared with that obtained under Model setting 1

6.3.3 Sustainability cost

The sustainability costs generated under each model setting for each instance are given in Table 6 and depicted in Fig. 5. Moreover, using Model 1 as the benchmark, the comparisons of the models in terms of sustainability costs are presented in Table 7. Among all model settings, setting 3 places the highest emphasis on the sustainability cost (${w}_{1}$=0, ${w}_{2}=1$, ${w}_{3}=0$). Thus, it is reasonable to observe that Model 3 consumes the least fuel and release the least carbon emissions (reduced by 11.41% compared with Model 1 on average). On the contrary, Model 6 and Model 7 do not involve the sustainability cost factor, while we still witness a reduction in this cost factor by a mean of 1.14% and 1.17%. Therefore, we could conclude that maximizing pairing robustness could also help enhance energy efficiency slightly. This might be explained as follows. As improving solution robustness may adjust flight connections and affect flight durations strategically, the fuel consumption can thus be influenced. This can also be further validated by the analysis for Model 2, Model 4, and Model 5. Model 2 places equal emphasis on the operation cost and the sustainability cost. Model 4 places equal emphasis on all the three cost factors. Model 5 places equal emphasis on the sustainability cost and the robustness cost. We see that the sustainability cost reduction compared with Model 1 is 7.97%, 7.98%, and 8.62%, respectively. It is witnessed that by introducing the objective of minimizing the robustness cost and placing higher emphasis on it, the reduction in sustainability cost becomes more evident. Overall, the instances reduce the sustainability cost compared with the benchmark Model 1 by an average of 6.38%.

Table 6 The sustainability cost obtained for each instance under each model setting

Fig. 5

Sustainability costs obtained by each instance under each model setting

Table 7 The sustainability cost compared with that obtained under Model setting 1

6.3.4 Robustness cost

Recall that the robustness cost considered in this study refers to the total deviations of the expected flight departure/arrival times from the scheduled flight departure/arrival times. The robustness costs obtained for each instance under each model setting are summarized in Table 8, while the comparisons against model setting 1 are presented in Table 9. Model 7 places the highest emphasis on robustness cost (${w}_{1}$=0, ${w}_{2}=0$, ${w}_{3}=1$). Thus, it is expected that Model 7 achieves the least deviations from the scheduled flight departure/ arrival times (reduced by 2.86% compared with Model 1 on average). Moreover, we also see that all the other model settings (i.e., Model 2 to Model 6) achieves reduction in the robustness cost, even if the robustness cost factor is not considered in the objective function (like Model 2 and Model 3). This implies that considering sustainability cost generates a positive impact on solution robustness enhancement. This finding is consistent with the previous finding that considering solution robustness can help promote sustainability cost reduction. Thus, it is concluded that solution robustness enhancement and sustainability cost reduction are mutually supported. Therefore, it is reasonable to observe that Model 3 and Model 5 achieve more robustness cost reduction, in which the two models place more emphasis on the robustness cost and the sustainability cost (Fig. 6).

Table 8 The robustness cost obtained for each instance under each model setting

Table 9 The robustness cost compared with that obtained under Model setting 1

Fig. 6

Robustness costs obtained by each instance under each model setting

6.3.5 Discussions

Previous sections discuss the findings related to the operation cost, sustainability cost, and robustness cost, respectively. Here, based on these findings, we would like to extract some useful managerial insights regarding considering sustainability factors in airline crew pairing generation under the impact of operation costs and pairing robustness costs.

First of all, when considering the sustainability cost (and the robustness cost), if the operation cost is totally ignored from the optimization framework, the airline would suffer a lot due to the dramatical growth in the financial burden in terms of the basic operation cost. For instance, under Model setting 3, the airline will encounter a 19.7% increase in the basic operation cost, to obtain a 11.41% reduction in the sustainability cost and a 2.24% decrease in the robustness cost. On the other hand, it is interesting to find that simultaneously considering other cost factors (i.e., sustainability/robustness costs) with the operation cost can lead to a satisfactory reduction in the sustainability/robustness cost, while imposing little influence on the basic operation cost. For example, in Model setting 4 where the three cost factors are given equal weighting, a 0.55% increase in the basic operation cost can bring a 7.98% decrease in the sustainability cost and an 1.81% decline in the robustness cost. Moreover, it is revealed that the sustainability cost factor and the robustness cost factor are mutually supported, which is possibly because these two cost factors would lead to cruise speed adjustment in order to minimize the related cost value. Therefore, we observe that even if the sustainability cost is not involved in the optimization decision framework, but the robustness cost is minimized (i.e., Model 6), we still witness a reduction in the sustainability cost. Similarly, for Model 2 and Model 3 where the robustness cost is omitted while the sustainability cost is considered, we obtain an 1.81% and a 2.24% decrease in the robustness cost, respectively. It is also seen that by introducing the robustness cost into the objective function and placing higher emphasis on it, the reduction in sustainability cost becomes more evident.

7 Conclusion

As a crucial sector in transportation (Pamucar et al., 2020; Wen et al., 2019), airline scheduling problems have received massive attention from both the academia and the industry. In most of the existing studies, crew pairings are constructed according to the pre-determined flight schedules. However, existing research has shown that the actual flight flying time often varies according to the actual flight departure time, which may lead to a deviation of the actual flight arrival time from the schedule. Thus, propagated effects are generated as the departure time and flying time of the subsequent flight may also be affected. Aircraft energy research has revealed that the fuel consumptions and greenhouse gas emissions of aircraft are determined by the actual flying speed and flight duration. Therefore, it becomes crucial to consider sustainability cost factors when connecting flights to form crew pairings, as different flight connection may lead to different flight durations. In this study, we propose a novel crew pairing problem with sustainability considerations which aims to minimize the basic operation cost, the total fuel consumptions and greenhouse gas emissions, and the robustness cost of the generated pairings. By setting different weightings on the three cost factors, six model settings are examined. Computational experiments based on real-world collected flight schedules show that the proposed model can bring a 7.98% decrease in the sustainability cost and an 1.81% decline in the robustness cost with only 0.55% increase in the basic operation cost when all the three cost factors are with equal weightings. Besides, we identify that simultaneously considering other cost factors (i.e., sustainability/robustness costs) with the operation cost can lead to a satisfactory reduction in the sustainability/robustness cost, while imposing little influence on the basic operation cost. Moreover, it is revealed that the sustainability considerations and the robustness considerations can generate a synergy effect as they are mutually supported.

7.1 Policy implications

With the scarcity in resources and increasing awareness in environmental sustainability of consumers, circular economy has become prominent in many industries, including the aviation industry (Modarress et al., 2020; Rutkowski, 2021; Salesa et al., 2022). As an energy-intensive industry, aircraft consume massive amount of fuels and release a lot of carbon emissions per flight. In order to better fit the goal of circular economy, airlines and aircraft manufacturers have made many efforts, like designing fuel-efficient aircraft models (e.g., Airbus A320neo). In terms of airline scheduling, previous studies also investigate how to reduce fuel consumption when determining the cruise speed of aircraft (Aktürk et al., 2014). Airline crew scheduling, on the other hand, also imposes great effects on aircraft flying time by the flight connections implied in the crew schedules, which further affects fuel consumption and carbon emissions. However, although the airline crew scheduling problem has been extensively studied, the majority of research focus is on the reduction of operational costs and enhancement of schedule robustness, while little attention has been paid to the environmental impact of the schedules in terms of fuel consumption and carbon emission. As revealed from this study, ignoring the sustainability costs when constructing pairings may cause very high environmental burden, leading to high fuel costs and damages to airlines images, and harm the circular economy which airlines would like to achieve. Besides, we show that minimizing the sustainability costs together with traditional costs can significantly reduce environmental burden and promote circular economy. Although additional operation cost may be incurred with such environment and sustainability considerations, some recent surveys revealed that the travelers, nowadays, are more willing to pay for the reduction in their carbon footprints. Investors or other stakeholders for the aviation industry have also become increasingly interested in environmental, social and governance issues and weigh them more heavily. Thus, it is highly suggested that airlines can take the varying flight time, fuel consumption, and carbon emission into considerations when conducting scheduling for crew members.

Appendix

See Tables 10, 11.

Table 10 Major notations used in Sect. 3

Table 11 Major notations used in Sects. 4 and 5