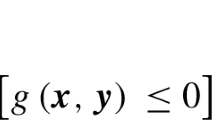Near-optimal solutions of convex semi-infinite programs via targeted sampling

Abstract

We propose an approach to find the optimal value of a convex semi-infinite program (SIP) that involves identifying a finite set of relevant constraints by solving a finite-dimensional global maximization problem. One of the major advantages of our approach is that it admits a plug-and-play module where any suitable global optimization algorithm can be employed to obtain the optimal value of the SIP. As an example, we propose a simulated annealing based algorithm which is useful especially when the constraint index set is high-dimensional. A proof of convergence of the algorithm is included, and the performance and accuracy of the algorithm itself are illustrated on several benchmark SIPs lifted from the literature.

1 Introduction

Consider the following convex semi-infinite program (SIP),

$$\begin{aligned} \begin{aligned}&\inf _{x}&f_0(x)\\&{{\,\mathrm{subject\;to}\,}}&{\left\{ \begin{array}{ll}f(x,u) \le 0 \,\, \text {for all } u \in \mathcal {U}, \\ x\in \mathcal {X}, \end{array}\right. } \end{aligned} \end{aligned}$$

(1.1)

with the following data:

• ((1.1)-a) The domain $\mathcal {X}\subset \mathbb {R}^n$ is a closed and convex set with non-empty interior.

• ((1.1)-b) The admissible set is defined by $\lbrace {x\in \mathcal {X}\vert f(x,u) \leqslant 0 \,\, \hbox { for all}\ u^{}_{} \in \mathcal {U}}\rbrace$ and is assumed to have non-empty interior, i.e., there exists a point $\overline{x} \in \mathcal {X}$ such that $f(\overline{x},u^{}_{})<0$ for every $u^{}_{} \in \mathcal {U}$.¹

• ((1.1)-c) The objective function $\mathcal {X}\ni x\mapsto f_0(x) \in \mathbb {R}$ is convex and continuous in $x$.

• ((1.1)-d) The constraint function $\mathcal {X}\times \mathcal {U}\ni (x,u) \mapsto f(x,u) \in \mathbb {R}$ is continuous in both the variables and is convex in x for each fixed u.

• ((1.1)-e) The set $\mathcal {U}$ is the constraint index set, and it is assumed to be a compact set $\mathcal {U}\subset \mathbb {R}^k$.

We denote the value of (1.1) by $y {^{*}}$. Further, we assume that $y{^{*}}$ can take the value $-\infty$. The family $\lbrace {f(x,u) \leqslant 0 \vert u \in \mathcal {U}}\rbrace$ of constraints is often classified as a semi-infinite constraint since it may contain infinitely many inequality constraints depending on the set $\mathcal {U}$. Consequently, the optimization problem (1.1) consists of a finite set of decision variables and (in general) infinitely many of constraints. A convex SIP is one in which the objective function and the constraint functions are convex in the decision variables, as in ((1.1)-a) and ((1.1)-d).

Towards the beginning of its history, SIPs emerged as a reformulation of the non-smooth Tchebyshev’s approximation problem (López & Still, 2007). Today its applications are not restricted to a particular domain, and have diversified into robust optimization (Ben-Tal et al., 2009; Bertsimas et al., 2010), mathematical physics, geometry (Hettich & Kortanek, 1993), and statistics (Dall’Aglio, 2001) to name a few. SIPs have also found applications in manufacturing engineering where the design of optimal layouts of the assembly lines under uncertainties is important (Weber, 2003; Li & Wang, 1997). In finance SIPs have found applications in various domains, particularly in risk-aware and portfolio optimization (Werner, 2010). In the control literature minimum time optimal control problems, and in robotics a vast collection of manoeuverability problems can also be recast in the language of SIPs (Quintero-Peña et al., 2021). For more applications, we refer the reader to the surveys (López & Still, 2007; Bertsimas et al., 2010; Goberna & López, 2018).

An SIP cannot, in general, be solved reasonably well by means of standard techniques and well-known algorithms (e.g., the interior point method and its many variants), even when the underlying problem is convex (see e.g., Ben-Tal and Nemirovski (2002), Ben-Tal et al. (2009)). This is because at optimality it is possible that an infinite number of constraints must be satisfied simultaneously, one for each $u \in \mathcal {U}$; this feature makes an SIP computationally intractable as stated in (1.1) in the absence of further structure. One of the important questions that arises in the context of a convex SIP is how and when can the SIP defined in (1.1) be recast into a tractable form so that it can be solved by the existing methods.

1.1 Background history

Several theoretical results and numerical schemes for solving SIPs have been proposed over the past few decades; readers are referred to López and Still (2007); Goberna and López (2018); Hettich and Kortanek (1993) for detailed surveys. In what follows, we focus on a few directions that are relevant in our setting. A discretization method was proposed in Still (2001), wherein a sequence of relaxed problems were considered; each of these relaxed problems has finitely many constraints, and is solved using grid generation schemes. One of the main disadvantages of discretization methods is that they become computationally expensive as the number of points in the grid increase. The exchange method (Laurent & Carasso, 1978) is another technique for solving SIPs in which a subprogram with a finite set of constraints is considered, and the finite set is updated in each iteration. As reported in Gribik (1979), the cutting plane algorithm is a popular technique but it is a special case of the exchange method. More recently, a new exchange method for solving convex SIP was proposed in Zhang et al. (2010), and randomized cutting plane algorithms were also reported in Calafiore and Campi (2005); Campi and Garatti (2008). A common randomized method is the scenario approach (Campi and Garatti, 2018) and in this technique the SIP is converted into a finite-dimensional approximate optimization program by drawing i.i.d samples from the constraint index set, followed by the assertion of a probabilistic guarantee concerning the closeness of the value of the original and sampled problems. More recently, the CoMirror algorithm with random constraint sampling was proposed in Wei et al. (2020a) to solve a convex SIP with low-dimensional constraint index set, and primal-dual algorithms and their approximations using the Monte-Carlo integration were advanced in Wei et al. (2020b) to solve more general SIP problems.

1.2 Our contributions

Against the preceding backdrop, the main contributions of this article are as follows:

• We propose an approach that ascertains the optimal value of a wide class of convex SIPs (1.1) as accurately as possible within the limitations of the resources at one’s disposal. Our chief observation is that the SIP (1.1) can be equivalently written as a finite-dimensional global maximization problem in the sense that the optimal value of the latter is identical to that of the former. One of the major advantages of our approach is that it admits a plug-and-play module, where one can use any global optimization algorithm to obtain the optimal value.

• To demonstrate the plug-and-play character of the approach, we include a simulated annealing based algorithm (requiring a quantum of memory bounded by a linear function of the dimension of the decision variable) to solve the convex SIP (1.1) via targeted sampling. We prove that the optimal value of the SIP, if solved using the simulated annealing based method, converges to the actual optimal value in probability, provided certain mild assumptions are satisfied.

• The introduction of global optimization algorithms such as simulated annealing, in the specific manner as demonstrated in this article, work well even when the dimension of the constraint index set is high. This is because such algorithms employ targeted (dependent) sampling, which attenuates the effects of the concentration of measure phenomenon.

At this point, we would like to highlight the importance of targeted sampling stated above, and emphasize that one of the main takeaways of this article is to employ targeted sampling in contrast to i.i.d. sampling, especially in high-dimensional problems. Targeted sampling originates in the observation that certain regions in the uncertainty space may be more important because, e.g., the uncertainty vectors therein may be dictating the value of the program (1.1) more strongly than elsewhere. If the samples are drawn from such regions, one can quickly draw a reasonably accurate estimate of the true value of (1.1). In particular, targeted sampling is a sampling strategy that draws samples based on the given task instead of being agnostic to it and hunting in the dark; the samples are biased towards the areas of the space that are more relevant to the problem at hand. The algorithm proposed in Sect. 3 is motivated by this idea.

1.3 Organization

The rest of the article is organised as follows: In Sect. 2 we provide the main result of this article. We demonstrate that the SIP problem (1.1) can be equivalently reformulated as a suitable finite-dimensional maximization problem, so that a global optimization scheme can be utilized to obtain the optimal value of (1.1). As an example, in Sect. 3 we propose a simulated annealing based algorithm to solve a convex SIP. It identifies a set of important constraints and recovers the optimal value of the original SIP. We report advantages of our method in more detail, especially in the high-dimensions through both qualitative and numerical observations. Finally, convergence of our algorithm is proved under mild assumptions, and we conclude in Sect. 5 after presenting several numerical experiments on convex SIPs in Sect. 4.

1.4 Notations

Standard notations are employed here. Given a parameter $\alpha > 0$ and a real value b we define the uniform distribution over the interval $[{b-\alpha ,b+\alpha }]$ as ${{\,\mathrm{Unif}\,}}(b,\alpha )$. An Euclidean open ball with radius $\epsilon >0$ centered at $\overline{u} \in \mathcal {U}$ is denoted by $\mathbb {B}(\overline{u},\epsilon ) {:=}\lbrace {u^{}_{} \in \mathbb {R}^k \vert \left\Vert u^{}_{} -\overline{u} \right\Vert < \epsilon }\rbrace$. For any set $S \subset \mathbb {R}^n$, the interior of the set $S$ is denoted by the symbol ${{\,\mathrm{int}\,}}{S}$. We write a selection Markov kernel for simulated annealing as $R(\cdot ,\cdot )$ over the set $\mathcal {V}\times \mathcal {B}$ and its density is $r(\cdot ,\cdot )$ defined over the set $\mathcal {V}\times \mathcal {V}$; i.e., for every $\zeta \in \mathcal {V}$, $R(\zeta ,\cdot )$ is a probability measure on $\mathcal {B}$, and for each $\mathcal {O}\in \mathcal {B}$, the function $R(\cdot ,\mathcal {O})$ is a measurable function.

2 Chief observation

We begin our technical sections by demonstrating that the SIP (1.1) can be recast as a suitable finite-dimensional maximization problem such that the optimal values of both the problems are identical. Recall from (1.1) and its associated data that n is the dimension of the decision variable. We define a function G on the Cartesian product $\mathcal {U}^{n}$ of the constraint index set by

$$\begin{aligned} \begin{aligned} \mathcal {U}^{n} \ni (u^{}_{1},u^{}_{2},\ldots ,u^{}_{n})&\mapsto G(u^{}_{1},u^{}_{2},\ldots ,u^{}_{n}) {:=}\\&\inf _{x\in \mathcal {X}} \lbrace {f_0(x) \vert f(x,u_i) \leqslant 0 \text { for }i=1,2,\dots ,n}\rbrace \in \mathbb {R}. \end{aligned} \end{aligned}$$

(2.1)

The values of this function $G$ are obtained by solving a finite-dimensional convex optimization problem, and fast and accurate algorithms are available for this purpose today. The function $G$ will play a central role in our investigation, and a structural property of $G$ will be examined in Sect. 3.

We fix some notations to be used throughout the manuscript. Let us define the set-valued map

$$\begin{aligned} \begin{aligned} \mathcal {U}^n \ni w\mapsto \varphi (w) = \lbrace {x\in \mathcal {X}\vert f(x,u^{}_{i}) \leqslant 0\,\, \text {for } i=1,\ldots ,n}\rbrace \subset \mathcal {X}, \end{aligned} \end{aligned}$$

(2.2)

where we abbreviate by $w$ a generic point $\bigl (u^{}_{1},u^{}_{2},\ldots , u^{}_{n} \bigr ) \in \mathcal {U}^n \subset \mathbb {R}^{kn}$. Observe that the set $\varphi (w)$ defined in (2.2) is a convex set for every $w\in \mathcal {U}^n$. Indeed, $\varphi (w) = \bigcap _{i=1, \ldots , n} f(\cdot , u^{}_{i})^{-1}\bigl (]{-\infty ,0}]\bigr )$ is an intersection of convex sets, and is therefore convex. The graph of $\varphi$ is defined by

$$\begin{aligned} {{\,\mathrm{graph}\,}}(\varphi ) {:=}\lbrace {(w,x) \in \mathcal {U}^n \times \mathcal {X}\vert x\in \varphi (w)}\rbrace . \end{aligned}$$

The function $G$ in (2.1) can therefore be written as

$$\begin{aligned} \mathcal {U}^n \ni w\mapsto G(w) = \inf _{x\in \varphi (w)} f_0(x). \end{aligned}$$

(2.3)

Remark 1

The function $G:\mathcal {U}^n \rightarrow \mathbb {R}$ is central to our approach and later we aim to maximize it suitably. Let us check if the function $G$ is concave in general. Consider an example in which the objective function and the constraint function are defined by $f_0(x)= (x-10)^2$ and $f(x,u^{}_{})=x+u^{}_{}+4$, respectively, and let the constraints be defined by $x\in [-30,30]$ and $u^{}_{}\in [-30,30]$. From (2.1) we note that the function $G:\mathcal {U}^n \rightarrow \mathbb {R}$ in this example is $G(u)=\inf _{x\in [-30,30]} \lbrace {(x-10)^2 \vert x+u^{}_{}+4 \leqslant 0}\rbrace$. Pick $u_1=5$, $u_2=10$, and $\alpha =0.4$, such that $u_0=\alpha u_1 +(1-\alpha )u_2 = 8$. For the preceding data we have $G(u_0)=\inf _{x\in [-30,30]} \lbrace {(x-10)^2 \vert x\leqslant -12}\rbrace$ = 484, $G(u_1)=\inf _{x\in [-30,30]} \lbrace {(x-10)^2 \vert x\leqslant -9}\rbrace =361$ and $G(u_2)=\inf _{x\in [-30,30]} \lbrace {(x-10)^2 \vert x\leqslant -14}\rbrace =576$. The preceding calculations demonstrate that there exist $u_1,u_2$ and $\alpha$ such that $G(u_0)<\alpha G(u_1) + (1-\alpha ) G(u_2)$; in other words, the function G defined above is not a concave function.

The above example illustrates that even in simple problems where the constraint function $f(\cdot ,\cdot )$ is affine in $u$ for every $x\in \mathcal {X}$, the function $G:\mathcal {U}^n \rightarrow \mathbb {R}$ may not be concave. However, if the constraint index set $\mathcal {U}$ happens to be convex, then we have the following result concerning convexity as opposed to concavity of G.

Proposition 1

Consider the convex SIP (1.1) along with its associated data ((1.1)-a)–((1.1)-e). Suppose the constraint index set $\mathcal {U}\subset \mathbb {R}^k$ is convex and the constraint function $f: \mathcal {X}\times \mathcal {U}\mapsto \mathbb {R}$ is jointly convex in both the variables. Then the function

$$\begin{aligned} \mathcal {U}^n \ni w \mapsto G(w) {:=}\inf _{x\in \varphi (w)} f_0(x) \end{aligned}$$

is convex.

Proof

The proof follows along the lines of Proposition 1.7, (Smirnov, 2002). We consider two points $w^1, w^2 \in \mathcal {U}^n$ and fix $\epsilon > 0$. Then there exist $x_1 \in \varphi \bigl (w^1\bigr )$ and $x_2 \in \varphi \bigl (w^2\bigr )$ such that $f_0(x_1) \leqslant G\bigl (w^1\bigr ) + \epsilon$ and $f_0(x_2) \leqslant G\bigl (w^2\bigr ) + \epsilon$. Pick $\alpha \in [0,1]$. Note that by convexity of $f$,

$$\begin{aligned} f\bigl (\alpha x_1 + (1- \alpha )x_2, \alpha u^{1}_{i} + (1- \alpha )u^{2}_{i} \bigr )&\leqslant \alpha f\bigl (x_1, u^{1}_{i}\bigr ) + (1-\alpha )f\bigl (x_2, u^{2}_{i}\bigr )\\&\leqslant 0 \quad \text {for every } i =1,2,\ldots ,n. \end{aligned}$$

It follows that the point $\alpha x_1 + (1- \alpha )x_2 \in \varphi \bigl (\alpha w^1 + (1- \alpha )w^2\bigr )$. By definition of $G$ we have

$$\begin{aligned} \begin{aligned} G\bigl (\alpha w^1 + (1- \alpha )w^2\bigr )&= \inf _{x\in \varphi \bigl (\alpha w^1 + (1- \alpha )w^2\bigr )} f_0(x)\\&\leqslant f_0\bigl (\alpha x_1 + (1- \alpha )x_2\bigr )\\&\leqslant \alpha f_0(x_1) + (1 - \alpha )f_0(x_2)\\&\leqslant \alpha G(w^1) + (1-\alpha )G(w^2) + \epsilon . \end{aligned} \end{aligned}$$

Since $\epsilon > 0$ was picked arbitrarily, it follows that $G$ is convex. $\square$

Despite the preceding observations, let us highlight the fact that the approach advanced in this article does not rely on concavity or convexity of the function $G:\mathcal {U}^n \rightarrow \mathbb {R}$. This feature will occupy the center stage in the next section.

Note that the constraint set $\lbrace {x\in \mathcal {X}\vert f(x,u^{}_{i}) \leqslant 0 \,\, \text {for each }i = 1,\ldots ,n}\rbrace$ is a relaxation of the admissible set $\lbrace {x\in \mathcal {X}\vert f(x,u^{}_{}) \leqslant 0 \,\, \text {for all } u^{}_{} \in \mathcal {U}}\rbrace$ in (1.1) and we will refer to the former as a relaxed admissible set. Then the SIP (1.1) with a relaxed admissible set is relaxed optimization problem associated with (1.1).

Fact 2.4

Under the preceding premise, there exists an $n\text{- }$tuple $\bigl (\overline{u}_1,\overline{u}_2,\ldots ,\overline{u}_n \bigr ) \in \mathcal {U}^n$ such that the optimal value of (1.1) is equal to $G\bigl (\overline{u}_1,\overline{u}_2,\ldots ,\overline{u}_n\bigr )$. This assertion follows from Theorem 3 in Appendix A, which we lift off the shelf.

We move to our main observation:

Theorem 1

Consider the SIP defined in (1.1) along with its associated data ((1.1)-a)-((1.1)-e). If $\bigl (u^{*}_{1},u^{*}_{2},\ldots ,u^{*}_{n}\bigr ) \in \mathcal {U}^n$ is an optimizer of the maximization problem

$$\begin{aligned} \sup _{(u^{}_{1},\ldots ,u^{}_{n}) \in {\mathcal {U}}^n} G(u^{}_{1},u^{}_{2},\ldots ,u^{}_{n}), \end{aligned}$$

(2.5)

then $G\bigl (u^{*}_{1},u^{*}_{2},\ldots ,u^{*}_{n}\bigr ) = y^*$.

Proof

Observe that the assumption ((1.1)-b) implies that the problem (1.1) is strictly feasible for every $u^{}_{} \in \mathcal {U}$. Consequently, there exists a point $\overline{x} \in \mathcal {X}$ such that for every $n\text{- }$tuple $\bigl (u^{}_{1},u^{}_{2},\ldots ,u^{}_{n} \bigr ) \subset \mathcal {U}$, the constraint function $f(x,u^{}_{i}) < 0$ for every $i=1,2,\ldots ,n$. This satisfies Slater’s condition in Theorem 3 in Appendix A. Then Fact 2.4 (via Theorem 3) asserts the existence of $\bigl (u^{\circ }_{1},u^{\circ }_{2}, \ldots , u^{\circ }_{n}\bigr ) \in \mathcal {U}^n$ such that

$$\begin{aligned} G\bigl (u^{\circ }_{1},u^{\circ }_{2}, \ldots , u^{\circ }_{n}\bigr ) = y {^{*}}. \end{aligned}$$

(2.6)

Since for any given $\overline{u} = \bigl (\overline{u}_1,\overline{u}_2,\ldots ,\overline{u}_n\bigr )$ we have the inclusion

$$\begin{aligned} \begin{aligned} \lbrace {x\in \mathcal {X}\vert f(x,u) \leqslant 0 \,\, \hbox { for all}\ u^{}_{} \in \mathcal {U}}\rbrace&\subset \\&\lbrace {x\in \mathcal {X}\vert f\bigl (x,\overline{u}_i \bigr ) \leqslant 0 \,\, \hbox { for all}\ i = 1,\ldots ,n}\rbrace , \end{aligned} \end{aligned}$$

(2.7)

it follows that $G\bigl (\overline{u}_1,\overline{u}_2,\dots ,\overline{u}_n\bigr ) \leqslant y{^{*}}$. In other words,

$$\begin{aligned} \sup _{(u^{}_{1},u^{}_{2},\ldots ,u^{}_{n}) \in \mathcal {U}^n} G(u^{}_{1},u^{}_{2},\ldots ,u^{}_{n}) \leqslant y {^{*}}. \end{aligned}$$

The above inequality along with (2.7) concludes the proof. $\square$

In view of Theorem 1, the optimal value of SIP (1.1) is equivalently written as

$$\begin{aligned} {\underline{y}} {^{*}} = \sup _{(u_1,\dots ,u_n) \in {\mathcal {U}}^n} G(u_1,u_2,\dots ,u_n), \end{aligned}$$

(2.8)

i.e., we have the relation ${\underline{y}}{^{*}} = y{^{*}}$. Moreover, it also asserts that the solution of the maximization problem (2.5) is attained for an $n\text{- }$ tuple $(u^{}_{1},u^{}_{2},\ldots ,u^{}_{n}) \in \mathcal {U}^n$. In the next section we shall focus on calculating the value of (1.1) as accurately as possible by treating (2.8) as its surrogate, and searching in a targeted fashion for the optimizers $\bigl ( u^{\circ }_{1}, u^{\circ }_{2}, \ldots , u^{\circ }_{n} \bigr )$ in (2.6).

Remark 2

The existence of the optimizers in the maximization problem (2.8) is guaranteed from Fact (2.4) and from the data of the problem (1.1). However it is difficult to assert uniqueness of the optimizers. In particular, it is important to stress that, in the notation of the Proof of Theorem 1, one cannot assert that $\bigl (u^{*}_{1},\ldots ,u^{*}_{n} \bigr ) = \bigl (u^{\circ }_{1},\ldots ,u^{\circ }_{n} \bigr )$. $\square$

Remark 3

In view of Fact 2.4 and Theorem 1, the optimal value in (2.8) is the same as the optimal value in (1.1). However, this result does not guarantee that we can recover the optimizers of (1.1). Let $\bigl (\overline{u}_1,\overline{u}_2,\ldots ,\overline{u}_n \bigr )$ be an optimizer for the finite-dimensional maximization problem (2.8). Then we obtain $\overline{x}$ such that $\overline{x} \in {{\,\mathrm{arg\,min}\,}}_{x\in \mathcal {X}}\lbrace f_0(x) \vert f\bigl (x,\overline{u}_i \bigr ) \leqslant 0 \text {for all } i = 1,\ldots ,n \rbrace$. While $f_0(\overline{x})$ is equal to the optimal value of (1.1), the point $\overline{x}$ may not be feasible for (1.1) since it is an element of the relaxed admissible set {$x\in \mathcal {X}\vert f\bigl (x,\overline{u}_i\bigr ) \leqslant 0 \text {for all } i = 1,\ldots ,n \}$ that contains the original admissible set. Hence, in general, it is difficult to guarantee that the optimizers of the original problem can be recovered. $\square$

However, it is still possible to recover the optimizers of the original convex SIP (1.1) under some additional conditions. To that end, we have following observations.

Proposition 2

Consider the convex SIP (1.1) along with its associated data $((1.1)-a)-((1.1)-e)$. Suppose that the optimal value of (1.1) is finite and it is attained. Denote by $u^{*}_{} = \bigl (u^{*}_{1}, \dots , u^{*}_{n}\bigr ) \in \mathcal {U}^n$ an optimizer of the maximization problem (2.5). Let $\mathcal {X}(u^{*}_{})$ be the set of optimal solutions of the relaxed problem (2.1), where $(u_1, \dots , u_n)$ is replaced with $u^{*}_{}$. Then, we have the following assertions:

• (2-a) If $\overline{x} \in \mathcal {X}(u^{*}_{})$ is a feasible solution of (1.1), then it is also an optimal solution of (1.1).

• (2-b) If the set $\mathcal {X}(u^{*}_{})$ contains only one element, then that point is an optimal solution of (1.1).

• (2-c) If $f_0$ is strictly convex, then $\mathcal {X}(u^{*}_{})$ contains only one element, and this element is also an optimal solution of (1.1).

Proof

For proving the first assertion, observe from (2.8) and the definition of G that ${\underline{y}}{^{*}} = G(u^{*}_{}) = f_0(\overline{x})$. From Theorem 1, ${\underline{y}}{^{*}} = y{^{*}}$. Thus, $f_0(\overline{x}) = y{^{*}}$ which proves the claim.

For the second assertion, we proceed by contradiction: assume that ${\overline{x}} \in {\mathcal {X}}(u^*)$ is not an optimal solution of (1.1). Note that an optimizer of (1.1) $x^* \not = {\overline{x}}$ exists as $y^*$ is finite. We have $x^{*} \in \lbrace {x\in \mathcal {X}\vert f(x,u) \leqslant 0 \,\, \text { for all } u \in \mathcal {U}}\rbrace \subset \lbrace {x\in \mathcal {X}\vert f(x,u^{*}_{i}) \leqslant 0\,\, \text {for every}~ i=1,\ldots ,n }\rbrace$. Further, from the reasoning given above, $f(x^*) = y^* = G(u^*) = f_0({\overline{x}})$. This implies that $x^* \in {\mathcal {X}}(u^*)$ which contradicts the fact that ${\mathcal {X}}(u^*)$ contains only one element.

The third assertion is a direct consequence of the second one using the fact that minimizing a strictly convex function yields a unique solution. $\square$

Remark 4

From Theorem 1 it can be concluded that a convex SIP is equivalent to a particular finite-dimensional global optimization problem if one is interested in only the optimal value of the SIP. The solution of this finite-dimensional problem can be obtained by means of any reasonable global optimization algorithms present in the literature. It is also important to note that the solutions of this finite-dimensional problem may be obtained by employing deterministic algorithms in sufficiently low-dimensional problems (however doing so would require the gradient/subgradient of $G$, which might be difficult to calculate analytically). This feature lends our approach a plug-and-play character, where a problem-specific method can be designed by a tailor-made selection of the global optimization algorithm, which is the primary highlight of Sect. 3. Moreover, it is also important to note that attributes like convexity of the constraint index set play no role in the selection of global optimization algorithms in Sect. 3.

3 Simulated annealing based algorithm for convex semi-infinite program

In this section we illustrate the plug-and-play nature of the approach established in Sect. 2. We propose a simulated annealing based Algorithm 1 to solve a convex SIP and demonstrate that the optimal value of (2.8) converges in probability to the optimal value of (1.1). A similar algorithm to solve a SIP model for tardiness production planning based on simulated annealing was introduced in Li and Wang (1997), where the authors modeled the constraint functions in the form of penalties to be added to the objective function in order to obtain an unconstrained SIP, following which the unconstrained optimization problem was solved in the decision variable by means of a simulated annealing algorithm.

Algorithm 1 is beneficial in applications where the SIP is an intermediate step and the decisions are taken based on the value of the SIP. Examples of such applications include portfolio optimization and intelligent investment decision making in businesses based on profit-loss margins (Weber, 2003; Werner, 2010).

3.1 Simulated annealing

Here we provide a brief description of the simulated annealing algorithm; interested readers are referred to Kirkpatrick (1984), C̆erný (1985) for a detailed exposition. The simulated annealing algorithm is an adaptation of the Metropolis-Hastings algorithm (Robert and Casella, 1999; Chib & Greenberg, 1995) to obtain the global optimum of a given function.

Suppose that we intend to obtain the minimum of a function $h:\mathcal {V}\longrightarrow [0,+\infty [$, where $\mathcal {V}\subset \mathbb {R}^k$. Let $\mathcal {V}\ni \zeta \mapsto \pi (\zeta ) {:=}\frac{1}{Z} \mathrm {e}^{- h(\zeta )/ \mathrm {T}} \in [0,+\infty [$ be a density on $\mathbb {R}^k$ where Z is a normalization constant. Here, the parameter $\mathrm {T}>0$ is the control parameter. It is analogous to temperature in annealing (metallurgy) and as the physical temperature behaves in annealing, the parameter $\mathrm {T}$ is reduced with the progress of the simulated annealing algorithm. To reduce $\mathrm {T}$, a cooling sequence denoted by $\bigl (T_N\bigr )_{N\geqslant 1}$ is used, where N denotes the current iteration number of the algorithm. Note that since $\pi (\zeta ) \propto \mathrm {e}^{- h(\zeta )/ \mathrm {T}}$, the density $\pi$ has its maximum value at the global minimum of h. Thus the samples drawn from $\pi$ are concentrated near the global minimum value of h. The simulated annealing algorithm utilizes this idea, along with a modification of the Metropolis-Hastings algorithm, to obtain the global minimum of h. The pseudo-code for the simulated annealing algorithm is given below:

Let $\zeta ^{N}_{}$ be the current state of the Markov chain generated by the simulated annealing algorithm with the selection Markov kernel $R(\cdot ,\cdot )$ and the cooling schedule $\bigl (T_N\bigr )_{N \geqslant 1}$. Then repeat the following steps until $\mathrm {T}\approx 0$:

• 1. Generate $Y_N \sim R\bigl (\zeta ^{N}_{},\cdot \bigr )$ for some transition kernel R.

• 2. Set $\zeta ^{N+1}_{}=Y_N$, if $h(Y_N)<h\bigl (\zeta ^{N}_{}\bigr )$. Otherwise set,

  $$\begin{aligned} \zeta ^{N+1}_{}={\left\{ \begin{array}{ll}Y_N\quad &{}\hbox { with probability}\ \min \left\{ \mathrm {e}^{-(h(Y_N)-h(\zeta ^{N}_{}))/T_N}, 1 \right\} , \\ \zeta ^{N}_{} \quad &{}\text {otherwise.} \end{array}\right. } \end{aligned}$$

A technical treatment of convergence of the above algorithm is provided in Appendix A.

Remark 5

In Sect. 3.2 we state our simulated annealing based algorithm in the context of $\mathcal {U}^n \subset \mathbb {R}^{nk}$ being a set with non-empty interior; cf. the data (1.1)-e and (3-a) . This premise may be viewed as a restriction since it does not include countable constraint index sets. However, various types of simulated annealing algorithms are available depending on the properties of the underlying set $\mathcal {U}$; in particular, simulated annealing would be a preferred option when the constraint index set is finite but so large that an enumeration of this index set is impossible to keep in memory. Our purpose here is partly illustrative, and to this end we restrict attention to the aforementioned premise and draw attention to the fact that the equivalence (2.8) obtained in Sect. 2 is not restricted by any such assumptions, and therefore, the optimal value of (1.1) can be obtained using any other global optimization method by solving (2.8) without imposing any additional restriction due to the reformulation. $\square$

3.2 Algorithm

Here are the assumptions to be cited in the main result of this section, following which we state our global maximization algorithm based on simulated annealing.

Assumption 1

In addition to the problem data ((1.1)-a)-((1.1)-e), we stipulate that

• (3-a) The constraint index set $\mathcal {U}$ has non-empty interior.

• (3-b) The selection Markov kernel $R:\mathcal {U}^n \times \mathcal {B}\bigl (\mathcal {U}^n \bigr ) \mapsto [0,1]$ used in the simulated annealing procedure is chosen such that it satisfies Assumption (B-a)-(B-c) (with $\mathcal {V}= \mathcal {U}^n$ there). Here the variable $\zeta ^{}_{}$ is the (current) state of the chain.

• (3-c) The cooling scheme (Hajek, 1988) used in Algorithm 1 for annealing is defined to be the sequence $(T_N)_{N \geqslant 1}$, where $T_N {:=}\frac{C}{\log (N+1)}$ for each N. Here $C > 0$ is a design parameter.

Remark 6

Observe that while one can explore the interior of the set $\mathcal {U}$, in practice the selection Markov kernel $R\Bigl (\bigl (u^{N-1}_{1},\ldots ,u^{N-1}_{n} \bigr ), \cdot \Bigr )$ is chosen such that at the $N^{\text {th}}$ instant of Algorithm 1 the proposal has an higher probability to lie in the neighborhood of the current state $\bigl (u^{N-1}_{1},u^{N-1}_{2},\ldots ,u^{N-1}_{n} \bigr )$. $\square$

3.2.1 Continuity of G

Now we proceed to identify conditions under which the function G defined in (2.1) is continuous over $\mathcal {U}^n$.

Lemma 1

Consider the SIP (1.1) along with its associated data and recall the definition of $\varphi$ given in (2.2). If for every $\overline{w} \in \mathcal {U}^n$,

• There exist $\alpha \in \mathbb {R}$ and a compact set $C \subset \mathcal {X}$ such that for every $w$ in some neighbourhood of $\overline{w}$, the level set

  $$\begin{aligned} \mathsf {lev}_{\alpha ,w} f_{0} {:=}\lbrace {x\in \varphi (w) \vert f_0(x) \leqslant \alpha }\rbrace \end{aligned}$$

  is nonempty and contained in C, and

• For any neighborhood $N_{\mathcal {X}}$ of the set $\varphi (\overline{w})$ there exists a neighborhood $N_{\mathcal {U}^n}$ of $\overline{w}$ such that $N_{\mathcal {X}} \cap \varphi (w) \ne \emptyset$ for all $w\in N_{\mathcal {U}^n}$,

then the function $G$ in (2.3) is continuous.

Proof

Consider the sequence $(w^{\nu }, x^{\nu })_{\nu } \subset {{\,\mathrm{graph}\,}}(\varphi )$ such that $w^{\nu } \rightarrow w^{\circ }$ and $x^{\nu } \rightarrow x^{\circ }$ as $\nu \rightarrow +\infty$. Observe that since $x^{\nu } \in \varphi (w^{\nu })$, we have $f\bigl (x^{\nu },u^{\nu }_{i}\bigr )\leqslant 0$ for every $i=1,2,\ldots ,n$. By continuity of the function f in both the variables, one has

$$\begin{aligned} \begin{aligned}&f\bigl (x^{\nu }, u^{\nu }_{i} \bigr ) \rightarrow f\bigl (x^{\circ }, u^{\circ }_{i} \bigr ) \,\, \text {for every }i=1,2,\ldots ,n, \\ \implies&f\bigl (x^{\circ },u^{\circ }_{i}\bigr ) \leqslant 0 \,\, \text {for every }i=1,2,\ldots ,n,\\ \implies&\bigl (w^{\circ },x^{\circ } \bigr ) \in {{\,\mathrm{graph}\,}}(\varphi ), \end{aligned} \end{aligned}$$

(3.1)

which in turn implies that ${{\,\mathrm{graph}\,}}(\varphi )$ is a closed subset of $\mathcal {U}^n\times \mathcal {X}$. Therefore, the set-valued map $\varphi (w)$ is closed everywhere. With the hypothesis and the fact that the set-valued map $\varphi (w)$ is closed, we assert the continuity of $G$ by invoking Proposition 4.4, (Bonnans & Shapiro, 2000). $\square$

Remark 7

Observe that the first bullet under the hypotheses of Lemma 1 is also satisfied when the set-valued map $w\mapsto \varphi (w)$ is compact-valued for every $w\in \mathcal {U}^n$. In general, assuring inner semi-continuity of the map $\varphi (w)$ is not straightforward. However we refer the readers to Hogan (1973) for a set of conditions under which the map $\varphi (w)$ is inner semi-continuous. $\square$

Convergence of Algorithm 1 to the optimal value of (1.1) concerns our next result:

Theorem 2

Consider the problem (1.1) along with its associated data ((1.1)-a–((1.1)-e)). Pick $C>0$ and the sequence $\bigl (T_N\bigr )_{N \geqslant 1}$ given by $T_N {:=}\frac{C}{\log {N+1}}$. Suppose that Assumption 1 and the hypotheses of  Lemma 1 hold. Let $\bigl (u^{N}_{1},u^{N}_{2}, \ldots , u^{N}_{n} \bigr )_{N \geqslant 1}$ be a Markov chain generated by Algorithm 1 with the selection Markov kernel $R(\cdot ,\cdot )$ and the cooling schedule $\bigl (T_N\bigr )_{N \geqslant 1}$. Then the sequence of function values $\Bigl (G\bigl (u^{N}_{1}, \ldots , u^{N}_{n}\bigr )\Bigr )_{N \geqslant 1}$ converges in probability to $y {^{*}}.$

Proof

Consider Algorithm 1. Let $\bigl (u^{N}_{1},u^{N}_{2},\ldots ,u^{N}_{n}\bigr )$ be the vector of states of the Markov chain at the instant N. The value of the objective function at this instant is given by $G\bigl (u^{N}_{1},u^{N}_{2},\ldots ,u^{N}_{n}\bigr )$. To prove that the sequence $\Bigl (G\bigl (u^{N}_{1},u^{N}_{2},\ldots ,u^{N}_{n}\bigr )\Bigr )_{N \geqslant 1}$ converges to the global maximum of G in probability, it suffices to show that Assumptions (B-a)–(B-d) of Theorem 4 in Appendix A are satisfied.² To that end, for the optimization problem (2.8) we observe that $G(\cdot )$ is continuous according to Lemma 1, which therefore verifies (B-a). The conditions (B-b) and (B-c) follow immediately from Assumption (3-b). Since the cooling temperature at the instant N is defined as in Assumption (3-c), we have $T_N\rightarrow 0$ as $N \rightarrow +\infty$, which verifies (B-d). Since all the assumptions required by Theorem 4 in Appendix A are satisfied, convergence of the sequence $\Bigl ( G \bigl (u^{N}_{1},u^{N}_{2},\ldots ,u^{N}_{n}\bigr ) \Bigr )_{N \geqslant 1}$ in probability to $y {^{*}}$ follows, and our proof is complete. $\square$

Remark 8

Algorithm 1 exploits the reformulation (2.8) to obtain an approximate global optimum for (1.1). It uses the well-known simulated annealing method for this task. Here is an informal description of Algorithm 1 to aid writing pseudocodes:

• We initialize the algorithm using an initial guess of n points $\bigl (u_i^0\bigr )_{i=1}^n \in \mathcal {U}^n$. These points correspond to the initial states of the Markov chain on $\mathcal {U}^n$. When propagated in accordance to the accept-reject rule for simulated annealing, the chain $\bigl (u^{N}_{1},u^{N}_{2}, \ldots , u^{N}_{n} \bigr )_{N \geqslant 1}$ converges in probability to a maximizer of G.

• For the initial guess, $G\bigl (u^{0}_{1},u^{0}_{2},\ldots , u^{0}_{n}\bigr )$ is calculated and stored in $y_{\max }$, i.e., the current value of $G(\cdot )$ and the global optimum is initialised as $y_{\max }$. At each iteration N, a candidate point $U^N = \bigl (u^{N}_{1},u^{N}_{2}, \ldots , u^{N}_{n} \bigr )\in \mathcal {U}^n$ is obtained where the components of $U^N$ are chosen according to $R\Bigl (\bigl (u^{N-1}_{1},u^{N-1}_{2}, \ldots , u^{N-1}_{n} \bigr ),\cdot \Bigr )$ (Step 2).

• Based on this candidate point $U^N$, the corresponding value $y^N=G\bigl (u^{N}_{1},\ldots ,u^{N}_{n}\bigr )$ is calculated (Step 3).

• To decide whether the candidate point should be accepted or not, for each iteration N we generate a random number $\eta$ and the annealing temperature $T_N$ (Step 4-5).

• Steps 6-9 in Algorithm 1 are performed using the random variable $\eta$ and the annealing temperature $T_N$ being generated in the preceding step. Accordingly the candidate point is accepted or rejected.

• Finally when the stopping condition is triggered, $y_{\max }$ gives the global optimum value of (1.1) in probability.

Here, the variable $y_{\max }$ is used to store the largest optimal value encountered by Algorithm 1 until the $N^{\text {th}}$ iteration, since we seek the largest optimal value possible irrespective of the current state of the Markov chains. $\square$

Remark 9

It is important to observe that the algorithm has constant memory requirement which is in contrast to some of the methods present in the literature that relies on progressively better approximations as the number of samples increase. $\square$

Remark 10

Since the cooling schedule picked in Algorithm 1 is deterministic and satisfies the condition $\sum _{N=0}^{+\infty } \exp {\frac{-1}{T_N}}= +\infty$, from Corollary of Theorem 2, (Bélisle, 1992) it can be concluded that the Algorithm 1 does not necessarily converge almost surely to its global maximum. $\square$

Remark 11

We highlight again that we do not advocate any one particular Monte-Carlo based technique to solve the convex SIP over the other available methods. While Theorem 2 asserts convergence in probability, almost sure convergence to the global maximum value is also guaranteed if some additional conditions on the selection Markov kernel and the cooling sequence are satisfied, as reported in Theorem 3, (Bélisle, 1992). Since this article aims to unveil a mechanism by which efficient frameworks can be designed for solving SIPs, especially in high dimension, we shall not focus on these variants and theoretical guarantees. $\square$

Remark 12

Optimization methods based on independent and identically distributed (i.i.d.) sampling such as the scenario approach (Campi and Garatti, 2018) are affected in high-dimensional spaces by the concentration phenomenon, due to which the i.i.d. samples drawn from the set $\mathcal {U}$ tend to congregate in specific regions of the space Sect. 1.5, (Mishal Assif et al., 2020). Consequently, the relative error between the approximate solution and the solution to the semi-infinite program tends to increase as the dimension of the constraint index set (space of uncertainties) increases for a given number of samples. Algorithm 1 is an attempt to attenuate the effects of concentration by means of targeted sampling. We illustrate this aspect with the help of an example borrowed from Mishal Assif et al. (2020) in the next section. $\square$

Remark 13

Since the convergence of simulated annealing is based on pure random search contained within the algorithm, its theoretical rate of convergence is very slow (Kushner & Huang, 1979; Spall et al., 2002; Zhigljavsky & Zilinskas, 2008). Consequently, an algorithm based on simulated annealing is typically sluggish since the accept-reject step starts witnessing a significant number of rejections in high dimensions. As a remedy, many problem-specific heuristics have been proposed, but the performances of these heuristics are comparable to the original simulated annealing algorithm. It had been reported in the literature that the estimated number of the objective function evaluations depending on the prescribed accuracy $\epsilon$ is of the order $\mathcal {O}(1/\epsilon ^k)$ (at best), where k is the dimension of the optimization space. However, this can be further improved by imposing restrictions on the objective; indeed, it was shown in Tikhomirov (2010) that a convergence rate of $\mathcal {O}(\log ^2 \epsilon )$ is possible. A faster convergence to the optimal value can be obtained if the algorithm is developed based on Hamiltonian Monte Carlo (HMC) (Betancourt, 2018), and it may have a better convergence rate than ordinary MCMC, especially in high dimensions. As a testament to this, in Mangoubi and Smith (2017) a dimension-free bound was obtained for the mixing time of an ideal HMC for a strongly log-concave target distribution. $\square$

4 Numerical experiments

In this section we employ Algorithm 1 to solve several convex SIPs. In Sect. 4.1 we illustrate that as the number of iterations in Algorithm 1 are increased, the optimal value of a convex SIP obtained by solving the problem using Algorithm 1 converges to the optimal value of the problem; we also present a comparative study of the performance of our algorithm evaluated against the conventional scenario method (Figs. 1, 2 and 3). In Sect. 4.2 we test the accuracy of Algorithm 1 by implementing it on several problems from the SIPAMPL problem database (Table 1). All the numerical experiments presented in this section were performed using Python 3.7 and Mathematica 12.3. Mention must be made about the fact that the simulated annealing technique employed in these numerical experiments has not been tuned/optimized for performance; in applications one typically gets significant scope to fine-tune the annealing algorithm in terms of both efficiency and speed.

Fig. 1

Histogram and time evolution of the optimal value of the SIP (4.2) over $N=5\times 10^3$ iterations with $k=15$

4.1 Example from Sect. 1.5 (Mishal Assif et al.2020)

Consider the optimization problem

$$\begin{aligned} \inf _{x\in \left[ 0,1\right] } \sup _{u^{}_{} \in \left[ -1,1\right] ^k} \Bigl (x\left\Vert u^{}_{} \right\Vert _{\infty } -\left\Vert u^{}_{} \right\Vert _{\infty }^2\Bigr ), \end{aligned}$$

(4.1)

where $x\in \mathcal {X}= \left[ 0,1\right]$ and $u^{}_{} \in \mathcal {U}= \left[ -1,1\right] ^k$. A careful scrutiny suggests that we can write

$$\begin{aligned} \begin{aligned} \inf _{x\in \left[ 0,1\right] }\sup _{u^{}_{} \in \left[ -1,1\right] ^k} \Bigl (x\left\Vert u^{}_{} \right\Vert _{\infty } - \left\Vert u^{}_{} \right\Vert _{\infty }^2 \Bigr )&=\inf _{x\in \left[ 0,1\right] }\sup _{\left\Vert u^{}_{} \right\Vert _{\infty } \in \left[ 0,1\right] } \Bigl (x\left\Vert u^{}_{} \right\Vert _{\infty } - \left\Vert u^{}_{} \right\Vert _{\infty }^2\Bigr )\\&= \inf _{x\in [0,1]}\frac{x^2}{4}\\&= 0. \end{aligned} \end{aligned}$$

This implies that the optimal value of (4.1) is 0. Now we will solve the optimization problem (4.1) using Algorithm 1. Note that (4.1) can be equivalently re-written as following convex SIP,

$$\begin{aligned} \begin{aligned}&\mathop {{{\,\mathrm{minimize}\,}}}_{x, y}&y\\&{{\,\mathrm{subject\;to}\,}}&{\left\{ \begin{array}{ll} x\left\Vert u^{}_{} \right\Vert _{\infty } -\left\Vert u^{}_{} \right\Vert _{\infty }^2 - y\leqslant 0 \,\, \text {for all } u^{}_{} \in \mathcal {U},\\ (x, y) \in \mathcal {X}\times \mathbb {R}. \end{array}\right. } \end{aligned} \end{aligned}$$

(4.2)

We claim that the optimal value obtained by solving the convex SIP (4.2) using Algorithm 1 is identical to the optimal value of (4.1), which is 0. For this example we picked $N=5 \times 10^3$, $C=1$ and the selection Markov kernel is assumed to be a truncated normal distribution over the set $\mathcal {U}^2$. Here $n = 2$ since this is the number of decision variables (4.2) and the dimension of constraint index set is $k=15$. We initialize each component of the Markov chain randomly according to ${{\,\mathrm{Unif}\,}}(0,1)^{k}$. Figure 1 shows the histogram plot as well as a time evolution plot of the optimal value obtained using Algorithm 1. Observe that at iteration $N=700$ approximately, the optimal value $y ^{*}= -2.71 \times 10^{-3}$ is approximately equal to the optimal value of (4.2), as shown in the Fig. 1b. This is also evident from the histogram Fig. 1a, which suggests that the concentration of Markov chains around zero is the highest and supports our claim. Of course, the error between the optimal value of (4.2) obtained using Algorithm 1 and the the true optimal value decreases to 0 as the number of iterations $N \rightarrow +\infty$.

Fig. 2

Plot of the absolute error between the computed optimal value of (4.2) and its true optimal value as a function of the dimension k of the constraint index set $\mathcal {U}$ and the number iterations N using Algorithm 1

Fig. 3

Plot of the absolute error between the computed optimal value of (4.2) and its true optimal value as a function of the dimension k of the constraint index set $\mathcal {U}$ and the number samples N, using scenario method

Next we show that our proposed method also works efficiently as the dimension $k$ of the set $\mathcal {U}$ increases. To that end we plot the absolute error $\left|{y^{*}}\right|$ between the approximate optimal value of the SIP (4.2) computed using our algorithm and its true value, as a function of the dimension $k$ and the number of iterations N, which is shown in Fig. 2. On the other hand, the plot obtained in Fig. 3 denotes the absolute error as a function of dimension $k$ and the number of samples $N$ when computed using the scenario method.

On comparing the Figs. 2 and 3, it can be clearly observed that in the high-dimension regime the absolute error obtained via scenario method is much high as compared to the absolute error obtained using Algorithm 1. This is because the scenario method is affected by the concentration of measure phenomenon whereas from Fig. 2, it can be inferred that the effect is attenuated because of targeted sampling.

4.2 Examples from the SIPAMPL test problem database

The test problem database for SIPAMPL has a collection of SIPs taken from various articles present in the literature.³ Table 1 shows a comparison of the optimal values obtained via Algorithm 1 with respect to the actual optimal values of some of the problems taken from the SIPAMPL database.

Table 1 Optimal value comparison for a few problems from SIPAMPL database

From Table 1 it is clear that Algorithm 1 performs very well for all the problems and the optimal values obtained are accurate, and this observation confirms the accuracy of Algorithm 1 when the constraint index set is low-dimensional.

5 Conclusion

In this article we presented a finite-dimensional reformulation of the convex SIP (1.1) to obtain its optimal value. As one of our chief observations, we demonstrated the equivalence of a certain finite-dimensional reformulation with the original SIP in the sense that the optimal values of both the problems are the same. The reformulation permits one to employ a plug-and play module where any global optimization algorithm can be used to ascertain the optimal value. It is important to note that the approach requires no particular structure on the constraint index set. However, as discussed in Remark 3, it may be difficult to recover the optimizers of the convex SIP by this approach.

As an example of our approach, we proposed a simulated annealing based algorithm (Algorithm 1) to solve the convex SIP. We proved the convergence in probability of the algorithm to the optimal value of the SIP (1.1). It can be seen from the numerical examples that the algorithm is accurate and performs reasonably well even when the dimension of the constraint index set is high, which is one of the important features of Algorithm 1 apart from the fact that the algorithm has constant memory requirement. Since the simulated annealing based approach is exploratory in nature, the rate of convergence of the algorithm is slow. However, there is plenty of scope to improve the rate of convergence in specific problems, and results in this direction will be reported subsequently.

Appendices

Appendix A

The following result from Borwein (1981) establishes the equivalence between a convex SIP and an optimization problem with a finite number of constraints. This result is central to the design of our algorithm.

Theorem 3

Theorem 4.1, (Borwein, 1981) Consider the SIP

$$\begin{aligned} \begin{aligned}&\inf&f_0(x), \\&{{\,\mathrm{subject\;to}\,}}&{\left\{ \begin{array}{ll}f(x, u^{}_{}) \leqslant 0 \,\, \text {for all } u^{}_{} \in \mathcal {U},\\ x\in \mathcal {X}, \end{array}\right. } \end{aligned} \end{aligned}$$

(A.1)

where the function f is convex in $x$ for every $u^{}_{} \in \mathcal {U}$, and continuous in both $x$ and $u^{}_{}$. The set $\mathcal {X}$ is assumed to be closed and convex and the objective function $f_0$ is convex and continuous. Moreover the constraint index set $\mathcal {U}$ is assumed to be compact. Let us denote by $y {^{*}}$ the optimal value of the SIP problem (A.1). Assume that ‘Slater’s condition’ is satisfied in the sense that given any $n+1$ points $\bigl (u^{}_{0},u^{}_{1},\dots , u^{}_{n}\bigr ) \in \mathcal {U}^{n+1}$, there exists $x\in \mathcal {X}$ with $f(x,u^{}_{i})<0$ for each $i=0,1,\ldots ,n$. Then, there exists an $n\text{- }$tuple $\bigl (u^{\circ }_{1},u^{\circ }_{2},\dots , u^{\circ }_{n}\bigr ) \in \mathcal {U}^n$ satisfying

$$\begin{aligned} y{^{*}} {:=}\left\{ \begin{aligned}&\inf&f_0(x) \\&{{\,\mathrm{subject\;to}\,}}&{\left\{ \begin{array}{ll} f(x, u^{\circ }_{i}) \leqslant 0 \,\, \text {for all } i=1,\ldots ,n, \\ x\in \mathcal {X}.\end{array}\right. } \end{aligned} \right. \end{aligned}$$

Moreover, if (A.1) admits a finite value, then there exist non-negative scalars $(\lambda )_{i=1}^n$ such that

$$\begin{aligned} y{^{*}} = \inf \left\{ f_0(x) + \sum _{i=1}^n \lambda _i f(x,u^{\circ }_{i}) \bigg \vert x\in \mathcal {X}\right\} \end{aligned}$$

Appendix B

In this appendix we present the theorem based on which the convergence of the proposed algorithm is proved. Consider a real valued continuous function h defined on a nonempty Borel set $\mathcal {V}\subset \mathbb {R}^{M}$. Let $\mathcal {B}$ be the trace of the Borel $\sigma \text{- }$algebra of $\mathbb {R}^{}$ on $\mathcal {V}$. Recall that a selection Markov kernel on $\mathcal {V}\times \mathcal {B}$ is a mapping $\mathcal {V}\times \mathcal {B}\ni (\zeta ^{}_{},S) \mapsto R(\zeta ^{}_{},S)\in [{0,1}]$ such that for every $S \in \mathcal {B}$, $\zeta ^{}_{} \mapsto R(\zeta ^{}_{},S)$ is measurable and for every $\zeta ^{}_{} \in \mathcal {V}$ the map $R(\zeta ^{}_{},\cdot )$ is a probability measure on $\mathcal {V}$. Let $\bigl (T_N \bigr )_{N \geqslant 1}$ denote a cooling sequence. Assume that:

• (B-a) The state space $\mathcal {V}\subset \mathbb {R}^{M}$ is compact and there exists $\zeta ^{*}_{} \in \mathcal {V}$ such that h achieves its minimum at $\zeta ^{*}_{}$. Moreover the set $\mathcal {V}\cap \mathbb {B}(\zeta ^{*}_{}, \epsilon )$ for every $\epsilon >0$ has positive Lebesgue measure.

• (B-b) The selection Markov kernel R is Lebesgue absolutely continuous on $\mathcal {V}$ and it has a density that is uniformly bounded away from 0. In other words, for every $\mathcal {O}\in \mathcal {B}$

  $$\begin{aligned} R(\cdot ,\mathcal {O})=\int _{\mathcal {O}} r(\cdot ,\xi )\, d\xi \,\,\,\, \text { and } \inf _{(\zeta ^{}_{},\xi ) \subset \mathcal {V}}r(\zeta ^{}_{},\xi )>0. \end{aligned}$$

• (B-c) For every open subset $\mathcal {O}\subset \mathcal {V}$, the mapping $\zeta ^{}_{} \mapsto R(\zeta ^{}_{},\mathcal {O})$ is continuous.

• (B-d) For every choice of initial state $\zeta ^{}_{0}$ and initial temperature $T_0$, the sequence of temperatures $\bigl (T_N \bigr )_{N\geqslant 1}$ converges in probability to 0.

Theorem 4

Theorem 1, (Bélisle, 1992) Consider the sequence $\bigl (\zeta ^{1}_{},\zeta ^{2}_{},\zeta ^{3}_{},\dots \bigr )$ produced by the simulated annealing algorithm in Sect. 3.1 with the selection Markov kernel R and the cooling sequence $\bigl (T_N \bigr )_{N\geqslant 1}$, and grant that the assumptions (B-a)–(B-d) are satisfied. Let $h {^{*}}$ denote the global minimum of h on $\mathcal {V}$. Then for every set of initial conditions $(\zeta ^{}_{0},T_0)$, the sequence $\bigl (h(\zeta ^{N}_{})\bigr )_{N\geqslant 0}$ converges in probability to $h {^{*}}$.