Scheduling problem in seru production system considering DeJong’s learning effect and job splitting

Abstract

Seru is a relatively new type of Japanese production mode originated from the electronic assembly industry. In practice, seru production has been proven to be efficient, flexible, response quickly, and can cope with the fluctuating production demands in a current volatile market. This paper focuses on scheduling problems in seru production system. Motivated by the realty of labor-intensive assembly industry, we consider learning effect of workers and job splitting with the objective of minimizing the total completion time. A nonlinear integer programming model for the seru scheduling problem is provided, and it is proved to be polynomial solvable. Therefore, a branch and bound algorithm is designed for small sized seru scheduling problems, while a local search-based hybrid genetic algorithm employing shortest processing time rule is provided for large sized problems. Finally, computational experiments are conducted, and the results demonstrate the practicability of the proposed seru scheduling model and the efficiency of our solution methods.

1 Introduction

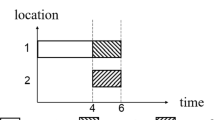
In Industrial Revolution 4.0, fast response is widely recognized as another dimension of demand in the manufacturing industry in addition to product volume and product variety (Yin et al. , 2018). Hence, more and more companies must reconfigure their production system since the traditional assembly line could not response to current volatile market quickly enough (Nikkei-Business , 2016; Wang et al. , 2019). In this situation, seru production system (SPS), which was first implemented at a factory producing video cameras for Sony company named Sony Minokamo in 1992 (Liu et al. , 2014a), is used to cope with the effect of fluctuating demand, and it could achieve efficiency, flexibility and fast response simultaneously. In fact, due to the autonomy in SPS, seru becomes a key factor in the smart manufacturing Industry 4.0 (Yin et al. , 2018). Roth et al. (2016) reviewed the research of operations management during the last 25 years and pointed out that seru production was one of eight promising future research directions because seru could response quickly to customer requirements with high efficiency and flexibility. Therefore, seru production has been regarded as a new “beyond lean” production mode for Industry 4.0 (Yin et al. , 2017). Seru is the Japanese pronunciation of cell, and the SPS is a work-cell-based assembly systems decomposed from the traditional assembly line (Lian et al. , 2018; Zhang et al. , 2021). Figure 1 is an example for an assembly line converting into SPS. The underlying philosophy of SPS is to benefit from both the high-efficiency advantage of the assembly line and the flexibility advantage of cellular manufacturing systems (CMSs) (Yu and Tang , 2019). In fact, according to references (Kimura and Yoshita , 2004; Kono , 2004; Noguchi , 2003), the benefits are not just efficiency and flexibility but also the reduction of throughput time, setup time, work-in-process (WIP) inventory, labor hours, shop floor space, and finished product inventory. For example, Sony Minokamo reduced 10,000 square meters of floor space and 170 workers by SPS just after one year (Yamada , 2009). Another example was in Canon company, the average working time of WIP was shortened from three days to six hours, and 720,000 square meters of workshop space in 54 factories were reduced after implementing SPS (Nikkei Mechanical , 2003; Hisashi , 2006). Some researchers also show that seru is more adaptive and competitive in an unpredictable environment with multiple product models, fluctuating volumes, and short product life cycles (Kaku , 2017; Zhang et al. , 2017). Hence, SPS has been considered as a potential production system for Industry 4.0 (Treville et al. , 2017; Yin et al. , 2018). Unfortunately, although so many remarkable benefits have been proven in production practice, the research on SPS is still minimal due to its short history. However, SPS still has recently attracted attention from some leading scholars and practitioners throughout the world (Roth et al. , 2016; Treville et al. , 2017; Yin et al. , 2018). In this paper, for the first time, we will focus on seru scheduling problems considering DeJong’s learning effect and job splitting, and hopefully it could improve the theory of seru scheduling problems, along with providing the professional guidance to practical seru production.

Fig. 1

An assembly line is decomposed into a seru production system

In practice, as an extension or upgrade to the Toyota’s traditional JIT material system (JIT-MS), the key to obtain the SPS’s high performance is JIT organization system (JIT-OS) (Stecke et al. , 2012). The difference between JIT-MS and JIT-OS is that JIT-MS focuses on materials while JIT-OS on organizations, i.e., serus. The mechanism of JIT-OS is the correct serus, in the right place, at the appropriate time, in the exact amount (Ayough et al. , 2020; Sun et al. , 2019; Yin et al. , 2018). It contains three-stage decisions in JIT-OS, i.e., seru formation, seru loading and seru scheduling (Sun et al. , 2020; Yu and Tang , 2019). First, a seru production system is configured with the appropriate serus amounts and types by seru formation. Then, by seru loading, the products ordered are allocated to each seru appropriately. Finally, considering the due date and schedule rule, the implement production plans are obtained by seru scheduling. Previous research mainly focused on seru formation and seru loading. Kaku et al. (2009) studied the insight of line-seru conversion problems by simulation experiments and pointed out the number of serus should be formatted in different cases. Liu et al. (2013) investigated the training and assignment problem of workers when a conveyor assembly line is entirely reconfigured into several serus and developed a bi-objective mathematical model to minimize the total training cost and to balance the total processing times among multi-skilled workers in each seru. To evaluate the performance of after converting the assembly line to SPS, Yu et al. (2012, 2013, 2014, 2017) constructed a series of mathematical models to investigate the line-seru conversion performances including the total throughput time and the total labor hours, and the mathematical characteristics such as solution space, combinatorial complexity and non-convex properties, were also analyzed. Shao et al. (2016) considered a line-seru conversion problem with stochastic orders based on queuing theory and developed a non-linear combination optimization model to confirm the seru formation. Luo et al. (2016) proposed a combinatorial optimization model for seru loading problem considering worker-operation assignment in single period and studied uncertain seru loading problems by a bi-objective model to minimize the makespan and the total tardiness penalty cost (Luo et al. 2017). Then, they designed a simulated annealing and genetic algorithm for a bi-level seru loading problem in SPS (Luo et al. , 2021). Lian et al. (2018) developed a mathematical model to improve the inter-seru and inter-worker workload balance to solve worker grouping, seru loading and task assignment concurrently, and a meta-heuristic algorithm based on NSGA-II was designed to solve the proposed model. Jiang et al. (2021) transformed the seru scheduling problem into the assignment problem and proved they could be solved in polynomial time. Yılmaz (2020a) provided workforce related operational strategies of SPS for the workforce scheduling and focused on a bi-objective seru workforce scheduling problem considering the inter worker transfer (Yılmaz , 2020b). Zhang et al. (2022) proposed a logic-based Benders decomposition method for the seru scheduling problem. However, the research on scheduling problem in SPS is still very rare due to its complexity even though it is one of the most important critical factors of JIT-OS. This paper will focus on the seru scheduling problems considering DeJong’s learning effect and job splitting and provide efficient solution methods for it.

Moreover, it can be noticed that the learning effect will occur and the processing time will be reduced when the job come from the same batch consecutively (Janiak et al. , 2013; Sun et al. , 2013). The later a given job is scheduled in the sequence repeatedly, the shorter its processing time (Mosheiov , 2001; Pei et al. , 2019). Taking camera assembly manufactory shown in Fig. 2 as an example, it is intuitive that learning effect for the same product style is significant, while insignificant for the different product styles. Many researchers concerned on the learning effect in production scheduling. Biskup (1999) analyzed learning effects in production scheduling problems and pointed out that the well-known learning effect had never been considered in connection with scheduling problems. (Mosheiov and Sidney , 2003) studied the scheduling problem of makespan and total flow-time minimization, a due-date assignment problem and total flow-time minimization with the job-dependent learning curves, where the learning in the production process of some jobs to be faster than that of others. Rostami et al. (2020) investigated an integrated scheduling of production and distribution activities considering deterioration and learning effect, and proved that the integrated decision can reduce costs significantly. Wang et al. (2020) constructed a joint decision model to solve cell formation and product scheduling problems together in cellular manufacturing systems considering the learning and forgetting effect, and designed an improved bacterial foraging algorithm to minimize the makespan. Biskup (2008) proposed state-of-the-art review on production scheduling problems with learning effect.

Fig. 2

Learning effects from jobs

In practice, an order is normally composed by several identical jobs, and a job batch can be split into several sub-jobs to improve the delivery time (Huang , 2010; Kim , 2018). Job spitting is always a hot issue in production scheduling. Nessah and Chu (2010) proposed a new lower bound of total weighted completion time for infinite split scheduling with job release dates and unavailability periods. Huang and Yu (2017) discussed the theoretical applications of subjects about multi-objective optimization, lot-splitting, and ant colony optimization. Liu et al. (2014b) proposed a lower bound of the production scheduling problem and a job-splitting algorithm corresponding to the lower bound, while a branch-and-bound algorithm and a hybrid differential evolution algorithm were also designed. Kim and Kim (2020) formulated the production scheduling problem with job splitting while the flexible idle time considering job splitting was inserted into initial schedule. To minimize both the makespan and electric power consumption, Chen et al. (2020) proposed a multi-objective mixed-integer programming for energy-efficient hybrid flow shop scheduling with job spitting. Figure 3 shows three different schedules for seru scheduling considering learning effect and job splitting, and it is interesting in production practice. For example, there are 10 jobs A, 9 jobs B, 5 jobs C, and 4 jobs D in a batch need to be scheduled in SPS. Schedule 1 is to finish the current job as soon as possible, thus, it just schedules the job to the current least heavily loaded seru one by one until all jobs are assigned in this SPS. In schedule 2, all jobs processed by one seru, i.e., jobs cannot be split. Total 10 jobs A are assigned to seru 1, 9 jobs B and 4 jobs D are assigned to seru 2, 5 jobs C are assigned to seru 3, respectively. The completion timed maybe longer due to the unbalanced job assignment. Schedule 3 splits the jobs in an appropriate way considering the learning effect at the same time, which is also the problem studied in this paper. As it can be seen, in Schedule 3, 10 jobs A are split into two parts and assigned to seru 1 (6 jobs A) and seru 3 (4 jobs A). For job B, C and D, they are allocated to one seru, i.e., seru 2, seru 3 and seru 1, respectively. Hence, comparing schedule 3 with schedule 1, the total processing time of schedule 3 is shorter than that of schedule 1 which is affected by the learning effect. Similarly, comparing schedule 3 with schedule 2, the total completion time of schedule 3 is shorter. By above comparisons, it can be seen that schedule 3 is the best schedule which considers both the total processing time and the total completion time. Therefore, this paper will also concentrate on seru scheduling problem considering job splitting and learning effect simultaneously to minimize the total completion time in SPS.

Fig. 3

A Gantt chart for a seru scheduling considering learning effect and job splitting

The remainder of this paper is organized as follows: Sect. 2 describes the seru scheduling problem and presents the analytical property. A non-linear integer programming model formulation is presented in Sect. 3, and the model analysis is also provided. Then, in Sect. 4, B&B algorithm, and a local search-based hybrid genetic algorithm (LS-hGA) employing shortest processing time (SPT) rule are designed for the small and large sized problems, respectively. Finally, Sect. 5 reports the computational results and conducts comparison analysis. Concluding remarks are made in Sect. 6, along with the discussion about further research.

2 Problem description

SPS has three types of seru, i.e., divisional seru, rotating seru and yatai (Liu et al. , 2014a), see Fig. 4. Yu and Tang (2019) provided a detailed description about three seru types according to the evolution of SPS. First, if the workers in an assembly line can handle more than one task, i.e., partially cross-trained workers, then, an assembly line could be decomposed several short lines and divisional serus are configured. In other words, a divisional seru is a short line staffed with partially cross-trained workers, where each worker will handle more tasks compared to the original assembly line (Yin et al. , 2018). In practice, the tasks in a divisional seru are divided into different sections in charge by the partially cross-trained workers (Stecke et al. , 2012). Subsequently, some workers are completely cross-trained along with the worker training on seru implementation. It means that these workers could assemble all tasks of a job from start to finish, thus, the rotating serus can be constructed (Stecke et al. , 2012). Now, the equipment is shared by completely cross-trained workers, and they move in rotating seru with one worker following another (Yin et al. , 2017). In addition, the worker returns to the first workstation and start a new round when a job is completed (Liu et al. , 2014a). In the end, some rotating serus could evolve into yatais when the waste of workers’ talents is eliminated (Stecke et al. , 2012). Yatai is an ideal production mode and only contains one completely cross-trained worker handles all tasks of a job, and it is a small single-person production unit with highly autonomous (Yu and Tang , 2019). Seru 1 in Fig. 1 is divisional seru, seru 2 is rotating seru and seru 3 is yatai, respectively. The seru type discussed in this paper is yatai because it is the most sensitive type for learning effect, and the divisional seru and rotating seru are left for the future research.

Fig. 4

Three types seru

Following the first study on the learning effect in aircraft industry manufacturing (Wright , 1936), many researchers proposed a large variety of position-based learning effect models. In Wright’s model, the learning effect is described as the cost: $C_x=C_1x^{b}$, where x is the cumulative production count, $C_x$ is the cumulative average cost for producing x units, $C_1$ is the cost for producing the first unit, and b is the learning curve exponent (i.e., learning index, $b\le 0$). Obviously, $C_x$ will decrease when x is increasing. Biskup (1999) constructed a production scheduling model with the learning effect: $p_{jr}={\bar{p}}_jr^{a}$, where ${\bar{p}}_j$ is the processing time for producing job j for the first time, $p_{jr}$ is the actual processing time of job j in position r of a schedule (i.e., the rth repetition), and $a\le 0$ is also the learning index. Mosheiov and Sidney (2003) proposed a job-dependent learning index $a_j$ and the learning effect is $p_{jr}={\bar{p}}_jr^{a_j}$, while Bachman and Janiak (2004) provided a linearized learning effect model as $p_{jr}={\bar{p}}_j-rv_j$, where $v_j$ is a given coefficient. Similarly, Cheng et al. (2013) applied $p_{jr}={\bar{p}}_j(1+\sum _{k=1}^{r-1} \beta _k ln {\bar{p}}_{[k]})^{a}r^{b}$ for production scheduling with a position-weighted learning effect. Unfortunately, all these models suffer a common drawback: if the job is processed late among many jobs, then $p_{jr}$ is close to zero, which is not going to occur in practice. In this situation, DeJong proposed a new learning effect model to cope with this defect as

$$\begin{aligned} T_s = T_1\left( M + \frac{(1-M)}{s^{m}}\right) \end{aligned}$$

(1)

where s stands for the sth cycle, $T_1$ is the processing time required for the first cycle of a batch, $T_s$ is the processing time required for the sth cycle of the batch, M is the factor of incompressibility in production practice ($0\le M\le 1$), and m is positive number and represents the exponent of reduction and is ($0< m< 1$). According to Eq. (1), the processing time for the sth cycle product will fall when s increases, but it will approach a certain limit $T_1M$. Thus, DeJong’s learning effect model overcomes the drawback. In addition, when $M=0$, Eq. (1) is $T_s = T_1\frac{1}{s^{m}}=T_1{s^{-m}}, 0< m< 1$, which means that Wright’s log-linear learning effect model is a special case of DeJong’s model. In this paper, we will use DeJong’ model to describe the learning effect in seru scheduling problems.

In the seru scheduling problem, there are $j\in J \equiv \{1,2,\ldots , n_J\}$ job need to be processed on $i\in I \equiv \{1,2,\ldots , n_I\}$ serus. For each job j, it has $N_j$ identical quantities which can be split into several sub-parts and assigned in parallel serus. Meanwhile, the processing time of job j is denoted as $p_j$. In the assembly process, learning effect will occur the same job is processed consecutively. Let $t(\tau ,p_j)$ be the processing time of job j in $\tau$th repetition, and $\tau$ a non-negative integer. $t(\tau ,p_j)$ satisfies

$$\begin{aligned} t(\tau ,p_j)\ge t(\tau +1,p_j) \end{aligned}$$

where $t(0,p_j)=0$ and $t(1,p_j)=p_j$. Define $f(\tau ,p_j)$ as the total processing time of consecutively processing $\tau$ items, and

$$\begin{aligned} f(\tau ,p_j)=\Sigma _{\upsilon =1}^{\tau }t(\upsilon ,p_j) \end{aligned}$$

Then, the following theorems hold.

Theorem 1

Assume that there are Q quantities in job j, and two sub-jobs are split with quantity $\tau _1$ and $\tau _2$ with $\tau _1+\tau _2=Q$. Without loss of generality, let $\tau _1 \ge \tau _2$, then:

(1) $f(\tau _1,p_j)+f(\tau _2,p_j) \ge f(\tau _1+1,p_j)+f(\tau _2-1,p_j)$;

(2) $\min \left( f(\tau _1,p_j)+f(\tau _2,p_j)\right) =f(Q,p_j)$.

Proof

(1) Following the property of function $t(\tau ,p_j)$, we know that $t(\tau _1,p_j)\ge t(\tau _1+1,p_j)$. Thus,

$$\begin{aligned} t(\tau _1+1,p_j) \le t(\tau _1,p_j)\le t(\tau _2,p_j) \end{aligned}$$

due to $\tau _1 \ge \tau _2$. Then,

$$\begin{aligned} t(\tau _1+1,p_j) \le t(\tau _2,p_j) \end{aligned}$$

i.e.,

$$\begin{aligned}&f(\tau _1+1,p_j)- f(\tau _1,p_j)\le f(\tau _2,p_j)-f(\tau _2-1,p_j)\\&\quad \Rightarrow f(\tau _1,p_j)+f(\tau _2,p_j) \ge f(\tau _1+1,p_j)+f(\tau _2-1,p_j). \end{aligned}$$

(2) Since $f(\tau _1,p_j)+f(\tau _2,p_j) \ge f(\tau _1+1,p_j)+f(\tau _2-1,p_j)$, then

$$\begin{aligned} \min \left( f(\tau _1,p_j)+f(\tau _2,p_j)\right) =f(\tau _1+1,p_j)+f(\tau _2-1,p_j) \end{aligned}$$

moreover,

$$\begin{aligned} f(\tau _1+1,p_j)+f(\tau _2-1,p_j)=f(\tau _1+\tau _2,p_j)=f(Q,p_j) \end{aligned}$$

hence,

$$\begin{aligned} \min \left( f(\tau _1,p_j)+f(\tau _2,p_j)\right) =f(Q,p_j) \end{aligned}$$

$\square$

From Theorem 1, we know that job splitting will increase the total processing time when considering learning effect.

Theorem 2

Let $\pi$ be an optimal schedule of SPS, then all sub-jobs coming from the same lot and scheduled on the same seru i should be processed as a single sub-job in $\pi$.

Proof

Assume that job j has sub-jobs 1 with $\tau _1$ quantities and sub-jobs 2 with $\tau _2$ assigned on the same seru i, and sub-jobs 1 is assigned before sub-jobs 2 while sub-jobs 1 and 2 are not allocated continuously. Now, let sub-jobs 1 move to the front of sub-jobs 2, and job j’s total processing time will decrease as $f(\tau _1+\tau _2,p_j)$.

According to Theorem 1 (2), we know that $f(\tau _1+\tau _2,p_j)\le f(\tau _1,p_j)+f(\tau _2,p_j)$. Therefore, all sub-jobs coming from the same lot and scheduled on the same seru i should be processed as a single sub-job in the optimal schedule $\pi$. $\square$

Theorem 3

For each single seru i in SPS, there exists an optimal schedule $\pi$ that assigns sub-jobs follow the same lot.

Proof

. Assume that $\pi$ is an optimal schedule, and the last completed sub-job of job j is completed in seru i. Subsequently, check other sub-jobs of job j assigned in other serus in SPS. If these sub-jobs are moved to the last position in its original seru, then job j’s completion time will remain the same. According to Theorem 2, the completion time of all other jobs will maintain stable or decrease. Hence, by removing job j, an optimal schedule which is no worse than the original one will be obtained. Therefore, all the assigned sub-jobs from job j could follow the same lot. $\square$

3 Model formulation

Based on Theorems 1–3, the non-linear integer programming model of seru scheduling problems considering DeJong’s learning effect and job splitting is constructed in this section.

3.1 Notation

i :

seru index, $i\in I \equiv \{1,2,\ldots , n_I\}$

j :

job index, $j\in J \equiv \{1,2,\ldots , n_J\}$

r :

position index, $r\in \{1,2,\ldots , n_J\}$

$p_j$ :

processing time of job j

$p_{rj}$ :

processing time of job j in the rth repetition

$N_j$ :

number of job j

a :

a constant, such that $a \ge \max _{j} N_j$

$q_{ij}$ :

quantities of job j assigned to seru i

$c_{ij}$ :

completion time of job j at seru i

$CT_{j}$ :

completion time of job j

M :

incompressible factor, $0\le M \le 1$

b :

learning index, $-1\le b\le 0$

T :

total completion time of all jobs

$x_{ijk}=$ :

$\left\{ \begin{array}{ll} 1,&{}\text {if}\; q_{ij}>k ;\\ 0,&{}\text {otherwise.} \end{array} \right.$

$y_{jr}=$ :

$\left\{ \begin{array}{ll} 1,&{}\text {if}\; j\; \text {is assigned in the position}\; r ;\\ 0,&{}\text {otherwise.} \end{array} \right.$

$z_{ij}=$ :

$\left\{ \begin{array}{ll} 1,&{}\text {if}\; q_{ij}>0 ;\\ 0,&{}\text {otherwise.} \end{array} \right.$

3.2 Modeling

The objective of seru scheduling problem considering learning effect and job splitting in this paper is to minimize the total completion time, thus:

$$\begin{aligned} \min T=\sum _{j=1}^{n_J} CT_{j} \end{aligned}$$

(2)

Since each job in SPS has one position in the sequence, so

$$\begin{aligned} \begin{array}{l} \sum _{j=1}^{n_J} y_{jr}\le 1,\quad r = 1,2,\ldots , n_J\\ \sum _{r=1}^{n_J} y_{jr}\le 1,\quad j = 1,2,\ldots , n_J\\ \end{array} \end{aligned}$$

(3)

Further, the sum of items quantity from job j assigned to seru i is equal to the total items number of jobs j, here

$$\begin{aligned} \sum _{i=1}^{n_I} q_{ij}=N_j, j = 1,2,\ldots , n_J \end{aligned}$$

(4)

Also, the items quantity of job j assigned to seru i can be interpreted by the binary variable $x_{ijk}$ as

$$\begin{aligned} q_{ij}= \sum _{k=1}^{N_j} x_{ijk}, i= 1,2,\ldots , n_I, j = 1,2,\ldots , n_J \end{aligned}$$

(5)

Moreover, if there are two quantity constants k and $k^{'}$, and $k^{'}> k$, then

$$\begin{aligned} x_{ijk}\ge x_{ijk^{'}}, \forall k^{'}> k \end{aligned}$$

(6)

Because the items quantity of job j assigned to seru i is non-negative integer, and $z_{ij}$ is a binary variable, hence

$$\begin{aligned} q_{ij}\ge z_{ij} \end{aligned}$$

(7)

Similarly,

$$\begin{aligned} az_{ij}\ge q_{ij} \end{aligned}$$

(8)

Considering the DeJong’s learning effect, the processing time of job j in the rth repetition is

$$\begin{aligned} p_{jr} = p_{j} (M+(1-M)r^{b}) \end{aligned}$$

(9)

where $-1\le b\le 0, 0\le M\le 1$. $M=0$ imply a completely manual operation as Wright’s model, and $M=1$ represents $p_{jr}=p_{j}$, respectively. Hence, the completion time of job j at seru i can be denoted as

$$\begin{aligned} \begin{array}{l} c_{ij}=z_{ij}\sum _{r=1}^{n_J} y_{jr}\left( \sum _{m=1}^{r}\sum _{n=1}^{n_J} y_{nm}p_{n} \sum _{k=1}^{N_n}x_{ink}(M+(1-M)r^{b})\right) \\ i= 1,2,\ldots , n_I; j = 1,2,\ldots , n_J \end{array} \end{aligned}$$

(10)

where Eq. (10) is a non-linear constraint which contains the multiplication of $x_{ijk}$, $y_{jr}$ and $z_{ij}$. In addition, the completion time job j at seru i should be less than or equal to the completion time of job j, thus

$$\begin{aligned} c_{ij} \le CT_{j} \end{aligned}$$

(11)

Finally, there are also have some logical constraints as

$$\begin{aligned} \begin{array}{l} x_{ijk}, y_{jr}, z_{ij} \in \{0,1\}, \forall i,j,k,r\\ n_I,n_J,N_j,q_{ij}\in Z\\ T,CT_j \in R, \forall i,j,k,r\\ -1\le b\le 0, 0\le M\le 1 \end{array} \end{aligned}$$

(12)

Hence, the non-linear integer programming model of seru scheduling problem considering DeJong’s learning effect and job splitting could be constructed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \min T=\sum _{j=1}^{n_J} CT_{j}\\ \begin{array}{ll} s.t.&{}\left\{ \begin{array}{l} \sum _{j=1}^{n_J} y_{jr}=1\\ \sum _{r=1}^{n_J} y_{jr}=1\\ c_{ij} \le CT_{j}\\ \sum _{i=1}^{n_I} q_{ij}=N_j\\ q_{ij}= \sum _{k=1}^{N_j} x_{ijk}\\ c_{ij}=z_{ij}\sum _{r=1}^{n_J} y_{jr}\left( \sum _{m=1}^{r}\sum _{n=1}^{n_J} y_{nm}p_{n} \sum _{k=1}^{N_n}x_{ink}(M+(1-M)r^{b})\right) \\ x_{ijk}\ge x_{ijk^{'}}, \forall k^{'}> k\\ q_{ij}\ge z_{ij}\\ az_{ij}\ge q_{ij}\\ x_{ijk}, y_{jr}, z_{ij} \in \{0,1\}, \forall i,j,k,r\\ n_I,n_J,N_j,q_{ij}\in Z\\ T,CT_j\in R, \forall i,j,k,r\\ -1\le b\le 0; 0\le M\le 1\\ r = 1,2,\ldots , n_J; i= 1,2,\ldots , n_I; j = 1,2,\ldots , n_J \end{array} \right. \end{array} \end{array} \right. \end{aligned}$$

(13)

3.3 Model analysis

Assume that now there are $n_I$ parallel serus in SPS, and the quantity of jobs assigned to seru i is $N_i=\sum _{j=1}^{n_J}q_{ij}, i= 1,2,\ldots , n_I$. Thus, the allocation of $n_J$ jobs to $n_I$ serus can be expressed as

$$\begin{aligned} A(n_J,n_I)=\left( \sum _{j=1}^{n_J}q_{1j}, \sum _{j=1}^{n_J}q_{2j}, \ldots , \sum _{j=1}^{n_J}q_{n_Ij}\right) \end{aligned}$$

(14)

with $\sum _{i=1}^{n_I}N_i=n_J$. Therefore, $\sum _{j=1}^{n_J} CT_{j}$ can be rewritten as

$$\begin{aligned} \sum _{j=1}^{n_J} CT_{j}=\sum _{i=1}^{n_I}\sum _{r=1}^{N_i}(N_i-r+1)[p_{j} (M+(1-M)r^{b})] \end{aligned}$$

(15)

Since each item of job can be only processed in one position of seru and each position of seru also can only process one item of job, so if the vector $A(n_J,n_I)$ is given, then the seru scheduling problem reduced to the matching problem with the objective:

$$\begin{aligned} \min T= \sum _{j=1}^{n_J}\sum _{r=1}^{N_i} p_{j}\theta _{jr} \end{aligned}$$

(16)

where $\theta _{jr}=(N_i-r+1)[(M+(1-M)r^{b})], i= 1,2,\ldots , n_I, r= 1,2,\ldots , N_i$. For provide the complexity result on seru scheduling problem, the following lemma should be stated first.

Lemma 1

Let $\alpha _n$ and $\beta _n$ be two sequences of non-negative numbers, and the sum of products $\sum _{n=1}^{N} \alpha _n\beta _n$ is the smallest if the sequences are monotonic in the opposite way, while the largest if the sequences are monotonic in the same way.

Proof

See Hardy et al. (1967) on Page 261. $\square$

According to Lemma 1, for Eq. (16), the largest processing time should be matched to the smallest $\theta _{jr}$, the second largest processing time with the second smallest $\theta _{jr}$, and so on. Hence, the minimum total completion time of seru scheduling problem is obtained.

Theorem 4

For the seru scheduling problem of SPS considered in this paper, it is polynomial solvable in $O(n_J^{n_I}\log ^{n_J})$ time given the number of serus $n_I$.

Proof

For the allocation of $n_J$ jobs to $n_I$ serus $A(n_J,n_I)$, $N_i=\sum _{j=1}^{n_J}q_{ij}$ may be $0,1,\ldots ,n_J$ for $i= 1,2,\ldots , n_I$. Thus, if the number of jobs on the first $n_I-1$ serus is known, the number of jobs processed on the last $n_I$ seru could be determined uniquely because $\sum _{i=1}^{n_I}N_i=n_J$. Therefore, an upper bound on the number of allocations $A(n_J,n_I)$ is $(n_J+1)^{(n_I-1)}$. Moreover, as a matching problem, $\min \sum _{j=1}^{n_J}p_{j}\theta _{j}$ requires $O(n\log ^{n})$ time to solve (Ji and Cheng , 2010). In this case, the seru scheduling problem of SPS in this paper $\min \sum _{i=1}^{n_I}\sum _{r=1}^{N_i} p_{j}\theta _{jr}$ is solvable in $O(n_J^{n_I}\log ^{n_J})$ time. $\square$

4 Solution methods

4.1 Branch and bound algorithm (B&B)

According to Theorem 4, the proposed seru scheduling problem model is polynomial solvable. Hence, branch and bound algorithm (B&B) is designed to solve the small-sized seru scheduling problem. In B&B, a node at the lth level in B&B tree represents a partial schedule where l jobs are scheduled. Let $\mathbf {\delta }_{j_{[l]}i}$ be the distributing array of job $j_{[l]}$, and

$$\begin{aligned} \begin{array}{l} \mathbf {\delta }_{j_{[l]}i}=\{\delta _{j_{[l]}1},\delta _{j_{[l]}2},\ldots , \delta _{j_{[l]}n_I} \}\\ \sum _{i=1}^{n_I}\delta _{j_{[l]}i}=N_{[j]} \end{array} \end{aligned}$$

(17)

where $j_{[l]}$ is lth assigned job index. Thus, the node at lth level $\xi _l$ can be defined as:

$$\begin{aligned} \xi _l=\left\{ (j_{[1]}, \mathbf {\delta }_{j_{[l]}i}),(j_{[2]}, \mathbf {\delta }_{j_{[2]}i}),\ldots , (j_{[l]}, \mathbf {\delta }_{j_{[l]}i})\right\} \end{aligned}$$

(18)

For example, assume that there is a SPS with two serus and three jobs need to be scheduled. Node $\{(1,(1,1)),(3,(2,2)),(2,(3,2))\}$ indicates that job 1 is split into two sub-jobs, and one is assigned to seru 1, while the other assigned to seru 2. Similarly, job 3 is also split into two sub-jobs, and two items are assigned to seru 1, while other two items are assigned to seru 2. Job 2 is split into two sub-jobs, and three items are assigned to seru 1, while other two items are assigned to seru 2. Further, the schedule sequence is job 1 $\rightarrow$ job 3 $\rightarrow$ job 2. For branching in B&B algorithm, the depth-first strategy with complete node enumeration is employed (Clausen and Perregaard , 1999), and the following dominance rule (DR) will be used in B&B algorithm: assume that there are two partial solutions $\pi _1$ and $\pi _2$ for the seru scheduling problem of SPS, and they are both assigned the same jobs to the serus. Without loss of generality if workloads of all serus in $\pi _1$ are no larger than that in $\pi _2$, and current $\pi _1$’s total completion time is no larger than $\pi _2$, then $\pi _1$ dominates $\pi _2$ , and the partial solution $\pi _2$ should be deleted from B&B process.

In addition, the lower bound (LB) of given node will be determined as follows. Let $\pi$ be a given node, and $J_A$ be the set of assigned jobs, while $J_{NA}$ be the set of unassigned jobs. Without splitting, the unassigned jobs in $J_{NA}$ are re-indexed according to the total processing time by the ascending order as $1,2,\ldots , |J_{NA}|$. Let $\mathbf {w}_{n_I}=(w_1,w_2,\ldots , w_{n_I}), w_i<w_{i+1}, i=1,2,\ldots , n_I-1$ be the vector of current serus workload for the node $\pi$, then LB of $\pi$ can be obtained by the following theorem.

Theorem 5

Define a function as

$$\begin{aligned} g_{\mathbf {w}}(x)=\sum _{i=1}^{n_I}\max \{x-w_i,0\},x \in (w_i, +\infty ) \end{aligned}$$

(19)

where $g_{\mathbf {w}}^{-1}$ is its inverse function. $c_j$ is the completion time of job j, and $AW_j$ is the possible additional workload from unassigned job. Then, the lower bound (LB) of the node $\pi$ is the completion time of assigned job j plus the additional workload from unassigned job, i.e.,

$$\begin{aligned} LB=\sum _{j\in {J_A}}c_j+\sum _{j=1}^{|J_{NA}|}g_{\mathbf {w}}^{-1}\left( \sum _{\iota =1}^{j}AW_\iota \right) \end{aligned}$$

(20)

Proof

If $x\in [w_i,w_{i+1}], w_i<w_{i+1}, i=1,2,\ldots , n_I-1$, then

$$\begin{aligned} g_{\mathbf {w}}(x)=\sum _{i=1}^{n_I}\max \{x-w_i,0\}=\sum _{\kappa =1}^{i} (x-w_\kappa ) \end{aligned}$$

(21)

Evidently, $g_{\mathbf {w}}(x)$ increases monotonously with x in interval $[w_i,w_{i+1}]$. If $x\ge w_{n_I}$, then

$$\begin{aligned} g_{\mathbf {w}}(x)=\sum _{i=1}^{n_I}\max \{x-w_i,0\}=\sum _{i=1}^{n_I} (x-w_i) \end{aligned}$$

(22)

and $g_{\mathbf {w}}(x)$ still increases monotonously with x in $[w_{n_I},+\infty ]$. Since the function $g_{\mathbf {w}}(x)$ is continuous, thus, in the whole definition domain, its monotonicity is preserved. In other words, $g_{\mathbf {w}}(x)$ increases monotonously with $x\in (w_1,+\infty )$.

Moreover, the optimal schedule assigns jobs in a fixed sequence according to Theorems 2 and 3. Assume that the unassigned jobs in $J_{NA}$ are allocated in the sequence $[1],[2],\ldots ,[|J_{NA}|]$ and the completion time is $c_j\le c_{j+1}$. Now, proving

$$\begin{aligned} g_{\mathbf {w}}^{-1}\left( \sum _{\iota =1}^{j}AW_\iota \right) \le c_{[j]} \end{aligned}$$

(23)

equals to

$$\begin{aligned} g_{\mathbf {w}}(c_{[j]})=\sum _{i=1}^{n_I}\max \{c_{[j]}-w_i,0\}\ge \sum _{\iota =1}^{j}AW_\iota \end{aligned}$$

(24)

according to $g_{\mathbf {w}}(x)$’s monotonically increasing. For the left side, $\sum _{i=1}^{n_I}\max \{c_{[j]}-w_i,0\}$ is greater than or equal the additional workload of $[1],[2],\ldots ,[j]$ jobs assigned to the seru, while for the right side, $\sum _{\iota =1}^{j}AW_\iota$ is the minimum additional workload of $[1],[2],\ldots ,[j]$. In addition, $\sum _{j\in {J_A}}c_j$ is a fixed value in node $\pi$, thus, LB for nodes $\pi$ in the B&B process is obtained and the Theorem 5 is proved. $\square$

Based on the discussion above, the detailed B&B algorithm procedure is shown as Algorithm 1.

4.2 Local search-based hybrid genetic algorithm (LS-hGA)

Although the B&B algorithm proposed in the last subsection is useful at solving small-sized seru scheduling problem, its computational time is still exponentially growing as the scheduling parameters. In this case, to solve the large-sized seru scheduling problem efficiently, a local search-based hybrid genetic algorithm (LS-hGA) employing shortest processing time (SPT) rule will be design in this subsection. In fact, hybrid genetic algorithm has been proved to be effective for the production scheduling problems already (Al-Hakim , 2001; Defersha and Rooyani , 2020; Li and Gao , 2016; Zhang et al. , 2009).

4.2.1 Individual representation

In this paper, the optimization seru scheduling problem concerns two points: one is determining job’s sequence in SPS, and the other is job’s splitting. According to the structure of proposed model and the analysis mentioned above, the encoding approach in this paper is based on two dimensions chromosome. Each chromosome in LS-hGA includes job’s index order

$$\begin{aligned} OI=\{j_{[1]},j_{[2]},\ldots ,j_{[n_J]}\} \end{aligned}$$

(25)

and job’s splitting ratio in $n_I$ serus

$$\begin{aligned} SR=\{sr_{ij}\}, i=1,2,\ldots ,n_I, j=1,2,\ldots ,n_J \end{aligned}$$

(26)

satisfying $\sum _{i=1}^{n_I}sr_{ij}=1, sr_{ij}\in [0,1]$. Therefore, the complete chromosome could be denoted as $Ch=\left\{ OI,\{sr_{ij}\}\right\}$.

In LS-hGA, the splitting ratio $sr_{ij}$ can be decoded by

$$\begin{aligned} \begin{array}{l} q_{ij}=\lfloor sr_{ij}\times N_j \rfloor , \forall i < n_I\\ q_{n_Ij}=N_j-\sum _{i=1}^{n_I-1}\lceil sr_{ij}\times N_j \rceil \end{array} \end{aligned}$$

(27)

Hence, chromosome’s total completion time can be gained if $q_{ij}$ and the scheduling sequence are obtained.

4.2.2 Procedure of genetic algorithm

Denote the hth individual of LS-hGA in the tth generation as

$$\begin{aligned} Ch^{h,t}=\left\{ OI^{h,t},SR^{h,t}\right\} =\left\{ \{j_{[1]}^{h,t},j_{[2]}^{h,t},\ldots ,j_{[n_J]}^{h,t}\}, \{sr_{ij}\}^{h,t}\right\} \end{aligned}$$

(28)

where $h\in H=1,2,\ldots ,n_{pop-size}$. For each generation t, the population will be evolved according until the maximum iteration number $t_{\max }$ is reached, and the best individual will be selected to perform the local search. The detailed procedure of LS-hGA is presented in Algorithm 2 and 3.

5 Computation results and analysis

To test the performance of B&B algorithm for the small sized seru scheduling problems and LS-hGA for the large sized ones, two sets of numerical experiments are conducted and performances are analyzed.

5.1 Experiments settings

The following procedure will be used to randomly generate two sets of numerical experiments:

• (1) Data setting for small sized seru scheduling problems: $n_I=\{2,3,4,5\}$, $n_J=\{6,7,8,9,10\}$, and items quantity of per job is an integer randomly generated from uniform distribution within [1, 10].

• (2) Data setting for large sized seru scheduling problems: $n_I=\{5,10,15,20\}$, $n_J=\{20,40,60,80,100\}$, and items quantity of per job is an integer randomly generated from uniform distribution within [1, 100].

In addition, the processing time of a single item for a job j is also an integer generated from the discrete uniform distribution within [10, 100]. For each combination of $n_I$ and $n_J$, 100 numerical examples are generated randomly. Further, set learning index $b=-0.8$, $M=0.5$, $n_{pop-size}=100$, $t_{\max }=500$, $P_{crossover}=0.7$ and $P_{mutation}=0.3$. All experiments are conducted on Windows 10 with an Intel 7, 8 GB RAM system, and the algorithms are developed with MATLAB R2019a.

5.2 Results and analysis

5.2.1 Computational results of the B&B algorithm

The computational results of the B&B algorithm for the small sized seru scheduling problems are shown in Table 1. From Table 1, we determine that the B&B algorithm can solve the small sized problems efficiently when $n_I\le 3$, $n_J\le 8$, and the item of per job is smaller than 10. However, its computational time will grow exponentially as the scheduling parameters increase, and uncompleted test times will also grow vigorously when $n_I\ge 4$, $n_J\ge 9$. In this situation, we can conclude that B&B algorithm cannot cope with the large sized seru scheduling problems considered in this paper, and the requirement of LS-hGA is justify manifestly.

Table 1 Computational results of B&B algorithm for small sized problems

5.2.2 Computational results of LS-hGA

Similarly, the computational results of the LS-hGA for small sized seru scheduling problems are presented in Table 2, where $RD^{1}$ is the relative deviation of the optimal schedule obtained by LS-hGA from the result of instance obtained by B&B algorithm, and $RD^{1}$ can be calculated by

$$ \begin{aligned} \begin{array}{l} RD^{1}=\frac{\sum _{\gamma =1}^{100}RD_{\gamma }^{1}}{100}\times 100\%\\ RD_{\gamma }^{1}=\frac{T_{LS-hGA}-T_{B \& B}}{T_{B \& B}}\times 100\% \end{array} \end{aligned}$$

(29)

After 50 runs of LS-hGA, $T_{LS-hGA}$ is the average total completion time, and $T_{B \& B}$ is the optimal solution of instance gained from by B&B algorithm. Table 2 shows that LS-hGA has a relatively steady calculation CPU time compared with B&B algorithm, and the average CPU time of LS-hGA is just 146.72 milliseconds. The larger of $n_I$ and $n_J$, the more obvious computational time advantage of LS-hGA. Moreover, when $n_I$ is fixed, $RD^{1}$ will increase following the $n_J$; while the $RD^{1}$ will increase following the $n_I$ even though $n_J/n_I$ decreases.

Table 2 Computational results of LS-hGA for small sized problems

Further, the computational results of the LS-hGA for large sized seru scheduling problems are provided in Table 3, where $RD^{2}$ is the relative deviation of the optimal schedule provided by LS-hGA from the best solution $T_{\min }$. Similarly, $RD^{2}$ is obtained by

$$\begin{aligned} \begin{array}{l} RD^{2}=\frac{\sum _{\gamma =1}^{100}RD_{\gamma }^{2}}{100}\times 100\%\\ RD_{\gamma }^{2}=\frac{T_{LS-hGA}-T_{\min }}{T_{\min }}\times 100\% \end{array} \end{aligned}$$

(30)

Similarly, $T_{LS-hGA}$ is the average total completion time, and $T_{\min }$ is the minimum total completion time of all 50 runs.

Table 3 Computational results of LS-hGA for large sized problems

From Table 3, we know that LS-hGA still effective for solving the large sized seru scheduling problems. On the hand, CPU time is more sensitive with the quantities of serus $n_I$, for example, the CPU time runs-up sharply from $n_I=15$ to $n_I=20$. On the other hand, if $n_I$ is fixed, the CPU time is almost steady. $RD^{2}$ is also sensitive with the quantities of serus $n_I$, and it also generally increases following the quantities of jobs $n_J$ increasing. Hence, in practice, the production manager must let the appropriate quantities of serus be a top priority in SPS to improve the efficiency of system.

5.2.3 Comparison analysis

To scrutinize the management insights for seru production practice, comparison analysis for both job splitting and Dejong’s learning effect are made.

For evaluating the effect of job splitting in seru scheduling problem, the comparison of $RD^{2}$ with un-splitting is performed by the large sized problems, and the results are shown in Table 4. It can be known that when $n_J/n_I$ is large, the performance of un-splitting type is better, and when $n_J/n_I$ is small, the job splitting performs well. That is because if $n_J/n_I$ is large, earlier job splitting may have significant indirect costs to unassigned jobs in production practice, such as the extended set-up time, insufficient learning effect, and so on. If $n_J/n_I$ is small, earlier job splitting will not have many additional costs to unassigned jobs because the balance between serus is one of the most important factors to minimize the total completion time for SPS.

Table 4 Comparison of $RD^{2}$ for job un-splitting and splitting

Further, for testing the Dejong’s learning effect on seru scheduling problems, the incompressibility factor $M=1$ is performed by the large sized problems (no learning effect). Detailed results for each case ($n_I = 5, 10, 15, 20$, $n_J = 20, 40, 60, 80, 100$) with different values of T are shown in Figs. 5, 6, 7 and 8.

Fig. 5

Total completion time T with $M=1$ ($n_I = 5$)

Fig. 6

Total completion time T with $M=1$ ($n_I = 10$)

Fig. 7

Total completion time T with $M=1$ ($n_I = 15$)

Fig. 8

Total completion time T with $M=1$ ($n_I = 20$)

Generally, for seru scheduling problems, the influence on the total completion time T from learning effect is significant. T usually reaches the maximum value (the worst one) in each case when $M=1$. We also find that the learning effect becomes more evident along with more $n_J$ jobs in the same amount of seru since increased range of the total completion time T is descending. For example, $T(n_I = 5, n_J = 20)-T(n_I = 5, n_J = 40)>T(n_I = 5, n_J = 40)-T(n_I = 5, n_J = 60)$. This phenomenon indicates that the learning effect should be considered in practice for seru production managers, especially when $n_J/n_I$ is large. Moreover, it is interesting to observe that the slope learning curve is decrease from $M=0\rightarrow M=0.5$ to $M=0.5\rightarrow M=1$, which indicates that the job’s processing time of decrease continuously and stabilize to a fixed value even $M=0$ (the strongest learning effect). Hence, the advantage of DeJong’s learning effect is validated. Therefore, to achieve high production efficiency, flexibility, and quick response, seru production managers of should also give attention of DeJong’s learning effect in SPS.

6 Conclusions

This paper concerns with the scheduling problem in seru production system considering DeJong’s learning effect and job splitting to minimize the total completion time. A non-linear integer programming model is developed, and B&B algorithm is designed for the small sized problem while LS-hGA is for the large one. Computational results of experiments demonstrate the effectiveness of proposed solution methods. Managerial insights are also provided to seru production managers.

Future research will focus on applying the proposed model and algorithm to other seru types including the divisional seru and rotating seru. Also, considering the conflicts of different decision goals in the practical decision-making process, the multi-objective model should be considered in seru scheduling problem. Additionally, the uncertain factors, such as stochastic product processing time, uncertain worker’s shortage, or redundancy, also should be concerned. Finally, software development for the practical application in SPS based on this paper is supposed to be considered in the future.