Data envelopment analysis model with decision makers’ preferences: a robust credibility approach

Abstract

Data envelopment analysis (DEA) is one of the widely used methods to measure the efficiency scores of decision making units (DMUs). Conventional DEA is unable to consider both uncertainty in data and decision makers’ (DMs) judgments in the evaluations. This study, to address the shortcomings of the conventional DEA, proposes a new best worst method (BWM)- robust credibility DEA (BWM-RCDEA) model to estimate the efficiency scores of DMUs considering DMs’ preferences and uncertain data, simultaneously. First, to handle uncertainty in input and output variables, fuzzy credibility model has been applied. Additionally, uncertainty in constructing fuzzy sets is modeled using robust optimization with fuzzy perturbation degree. In this paper, two new types of RCDEA models are proposed: RCDEA model with exact perturbation in fuzzy inputs and outputs and RCDEA model with fuzzy perturbation in fuzzy inputs and outputs. In addition, to deal with flexibility of weights and incorporating DMs’ judgement into the RCDEA model, a bi-objective BWM-RCDEA model is introduced. Finally, the proposed bi-objective model is solved using min–max approach. To illustrate the usefulness and capability of the proposed model, efficiency scores of 39 distribution companies in Iran is investigated and results are analyzed and discussed. Finally, based on the results, recommendations have been made for policy makers.

1 Introduction

Electricity industry plays a major role in economic development of the countries. Indeed, electricity industry as the mother industry, is the engine of economic growth in countries (Tavassoli et al., 2020). Electricity industry consists of three important sectors of power generation, transmission, and electricity distribution. Electricity distribution companies deliver final product to end customers and have direct relationship with customers. Therefore, electricity distribution companies’ performance evaluation has a great importance among decision makers, managers, and regulators. In other words, in most cases, the quality of the electricity delivered is directly related to the performance of the distribution companies. Hence, high performance of the distribution companies could improve the economic growth and customers satisfaction. For evaluating distribution companies’ performance various methods have been applied in the literature. Data envelopment analysis (DEA) is one of the widely used approach to estimate efficiency score of decision making units (DMUs). Data envelopment analysis (DEA) is a non-parametric method to measure the relative efficiency of a set of DMUs with homogenous inputs and outputs (Charnes et al., 1978). DEA is based on a series of optimizations to specify an efficient frontier curve using linear programming technique. While the numerous advantages of DEA in the field of efficiency evaluations have led researchers devote a considerable number of literatures to develop and apply DEA method in recent two decades (Chen et al., 2019; Emrouznejad & Yang, 2018; Hatami-Marbini et al., 2012), conventional DEA model suffers from some shortcomings such as weight flexibility and uncertainty in input and output data which have been addressed in this study.

One of the crucial assumptions in the conventional DEA is that input and output data are deterministic. In fact, DEA uses a deterministic amount of input to produce a deterministic amount of output. However, in real world applications, data are sometimes contaminated with uncertainty and vagueness. Since DEA is a linear programming model, hence, imprecise and uncertain data may lead to unreliable, incomplete and even infeasible results (Ben Tal and Nemirovski, 2000; Alizadeh & Omrani, 2019). Thereby, some researchers have addressed uncertainties in DEA data using various methods, such as fuzzy sets, robust optimization, stochastic programming, interval programming and etc. methods. This paper deals with uncertainty in input and output variables of DEA using mixed fuzzy sets and robust optimization approaches simultaneously. It is notable that in engineering and management practices it is difficult to collect data with knowing the probability distribution function of data which resulted to unavailability of probability models such as stochastic programming (Yin et al., 2018). In such cases, fuzzy sets and robust optimization are the most appropriate ways to handle uncertainties. So, a review of the literature on fuzzy sets and robust optimization is summarized in the next section.

In this paper, in order to incorporate DMs’ preferences and reducing flexibility in input and output weights, a fuzzy robust DEA model is combined to the latest multiple criteria decision making (MCDM) technique, namely best–worst method (BWM). BWM is a multi-criteria decision making (MCDM) method which was first introduced by Rezaei (2015). BWM applies reference comparisons in order to obtain the weights of criteria. The advantages of BWM in generating more consistent and reliable weights and also needing less pairwise comparison rather than other popular techniques such as AHP led to the application of this method in literatures (Vafadarnikjoo et al., 2020). Readers can refer to comprehensive review of application of BWM technique in decision making problems by Mi et al., (2019).

In summary, the main contributions of this study are as follows:

• Considering uncertainty in inputs and outputs using fuzzy credibility theory.

• Considering uncertainty in constructing fuzzy sets using robust optimization approach.

• Considering perturbation degree of data as a fuzzy number.

• Incorporating preferences into robust-credibility DEA (RCDEA) model using BWM.

The rest of the paper is as follows: Literature has been reviewed in Sect. 2. Section 3 presents the methodology (definitions, models and proofs) used in this study. In Sect. 4, the proposed model is applied to evaluate efficiency scores of Iranian electricity distribution companies. Section 5 analyzes the results of the model. Recommendations have been made for policy makers in Sect. 6 and finally, conclusion and summary is made in Sect. 7.

2 Literature review

In this paper, for considering uncertainty in input and output variables of DEA, fuzzy sets have been applied. Additionally, uncertainty in constructing fuzzy sets has been modeled using robust optimization. We proceed one more level in considering uncertainty and used fuzzy value for perturbation level in robust optimization. Finally, to incorporate DMs’ judgement and reduce weight flexibility in conventional DEA, BWM has been used. In this section literature of the used models have been reviewed. y

2.1 Fuzzy DEA

The first steps of incorporating fuzzy set theory into DEA (Emrouznejad & Tavana, 2014) models was taken by Sengupta (1992). Sengupta (1992) introduced a DEA model with fuzzy objective and constraints by defining a tolerance level on DEA constraint violations and analyzed the model using Zimmermann (1978) approach. Later, Triantis and Girod (1998) applied a novel three stage DEA model to measure the technical efficiency in a fuzzy environment. In the first stage, for input and output variables a membership function was defined, so that imprecise input and output variables are expressed in terms of their risk-free and impossible bounds. In the second stage, conventional DEA-VRS and DEA-CRS were formulated in terms of the risk-free and impossible bounds and the membership function for each of the fuzzy input and output variables. Finally, technical efficiencies were measured according to the different membership function values. Their proposed three stage DEA model is categorized in the most popular fuzzy α-level based approach. This method enables decision maker (DM) to observe the impact of modifying input and output values between risk-free and impossible bounds on the efficiency scores. In other words, the main purpose of the α-level based approach is to provide a pair of parametric programs which measures the upper and lower bounds of the α-level based membership function of efficiency scores (Emrouznejad et al., 2014). The α-level based approach was later extended and applied in many literatures. For instance, Liu (2008) in order to evaluate the upper and lower bound performance of flexible manufacturing systems (FMS) alternatives when the input and output data are represented as crisp and fuzzy data, transformed a two-level mathematical program into a one-level DEA assurance region model. Soltanzadeh and Omrani (2018) to deal with fluctuations in data which can be represented by fuzzy numbers, extended the dynamic network DEA model in a fuzzy framework. Their proposed method provided more information for management, since data was presented by membership function. Peykani et al. (2019) proposed an adjustable fuzzy DEA approach while Hatami- Marbini and Saati (2018) proposed a common-weight DEA method to evaluate system efficiency and the component process efficiencies in fuzzy environment.

Another approach to deal with fuzziness in DEA model is the fuzzy ranking which was first developed by Guo and Tanaka (2001). In the fuzzy ranking approach, DM defines a possibility level and the model converts to a linear programming model with crisp constraints and ranking occurs using the comparison rule for fuzzy numbers. Like α-level based approach, fuzzy ranking method has been widely applied in literatures. For instance, Guo (2009) proposed a fuzzy DEA for evaluating objects with fuzzy inputs and outputs and applied his method to analyze a case study involving a restaurant location problem in detail.

Finally, Lertworasirikul et al. (2003a, b) based on the Zadeh’s (1978) fundamental principles of possibility theory for fuzzy sets, proposed “possibility” and “credibility” approaches to overcome ranking problem in DEA-CRS model. Later, Lertworasirikul et al. (2003b) extended the possibility approach to fuzzy DEA-VRS model. Their model converted the fuzzy DEA model to a linear model which can be solved using linear programming solvers. Although “possibility” and “credibility” approaches are strong tool to deal with fuzzy and uncertain data, “credibility” mathematical programming is complex and difficult to solve (Amini et al., 2019). However, development of computer and appearance of algorithms have facilitated the use of these approaches in optimization problems (Liu & Liu, 2002). In the credibility approach, the fuzzy DEA model converted into a credibility programming DEA model and fuzzy variables were replaced by expected credits, which were obtained by applying credibility measure (Lertworasirikul et al., 2003b). Unlike possibility approach, in credibility approach, expected credits are replaced with fuzzy data to deal with fuzzy constraints and fuzzy objectives and there is no need to define any parameter to rank fuzzy efficiency by DM. Generally, credibility approach has been applied in a narrow of literatures. For example, Fasanghari et al., (2015) applied fuzzy credibility constrained programming and P-robust approaches simultaneously for analyzing enterprise architecture scenarios. The catered DEA model was linear, flexible, robust and successful in discrimination power improvement. Also, Amini et al., (2019) to estimate the road safety efficiency of provinces in Iran used a credibility DEA based on road safety (DEA-RS) model. In fact, the constraints of DEA-RS model are considered as credibility constraints and a counterpart credibility DEA-RS (CreDEA-RS) model was proposed. For a comprehensive review on literatures about fuzzy DEA readers can refer to Hatami-Marbini et al. (2011).

2.2 Robust optimization

As mentioned before, fuzzy sets constructed based on the DMs’ opinions. In real world applications, due to the dynamic and continuous change in preferences of stakeholders and DMs, considering certain values for DMs’ preferences may lead to the unrealistic and reliable evaluations (Omrani et al., 2018). Therefore, considering perturbation and noise, for DMs assigned values, in order to produce more realistic and precise results is inevitable. One of the most effective approaches to incorporate uncertainty and immunizes model against uncertainty in linear programming is robust optimization (RO) which proposed by Ben-Tal and Nemirovski (2000) and Bertsimas and Sim (2004). According to the Bertsimas and Sim (2004), it is almost implausible that all parameters get their worst case values, therefore, Bertsimas and Sim (2004) for each constraint i introduced a new parameter,$\Gamma_{i}$, to make a trade-off between the degree of conservatism of the solution and the protection level of the constraint i. Robust optimization has been used in diverse management and engineering practices such as supply chain management (Omrani et al., 2017), waste management (Saeidi-Mobarakeh et al., 2020), investment management (Kim et al., 2018), project selection (Lee et al., 2020), and portfolio optimization (Toloo & Mensah, 2019). Also, robust optimization has been applied on the conventional DEA as a well-known linear programming model widely. Robust DEA (RDEA) is first introduced by Sadjadi and Omrani (2008) and then developed in many researches (Sadjadi et al. (2011a, b), Omrani (2013), Salahi et al. (2016), Shabanpour et al. (2017) and Toloo and Mensah (2019)). In this paper, the robust optimization approach is used to handle uncertainties in both input and output data, simultaneously. In fact, since data are considered as fuzzy sets, a small perturbation in DMs’ preferences in specifying upper, medium and lower bounds may lead to unreal and imprecise results. In addition, in RO, perturbation degree (percentage of uncertainty) is considered as exact values which intensifies the impreciseness of the results. Therefore, in this study, perturbation level is handled using fuzzy sets.

2.3 Assurance region

The second issue addressed in the paper is weight flexibility in DEA. Each DMU in order to be on the efficient frontier is free to set its own weight (Omrani, 2013). This implies that a DMU can make a full benefit of the weighting system to maximize its own efficiency. This weights flexibility could be considered as a strength of DEA, because inefficient units interpreting is meaningful. In other words, these units cannot reach to the efficient frontier even in situation they can choose weights, freely. However, weight flexibility is the weakness of DEA models, too. Since, in some circumstances, some input and output variables take zero or extreme values (Liu, 2014). Therefore, it will be difficult to interpret the impact of these variables on the efficiency scores. Generally, in the literature, four approaches including common weights (Roll et al., 1991), weight restriction (Dyson & Thanassoulis, 1988), cone ratio (Charnes et al., 1990) and assurance region (AR) (Thompson et al., 1986) have been proposed to reduce weight flexibility. Among weight restriction approaches, AR is a well- known and appropriate approach to incorporate value judgment such as preference concepts, expert opinions and prior information in analysis (Liu, 2014). AR impose ratios between weights to be in a certain range of values (Khalili et al., 2010). AR is categorized to two ARI and ARII approaches. ARI determines bounds on using a priori information on marginal rates. ARII specifies bound for ratios of inputs/ outputs weights and mainly is applicable in profit efficiency analysis. Both ARI and ARII are sensitive to scaling of inputs and outputs (Allen et al., 1997).

Sarica and Or (2007) to evaluate performance of 65 electricity generation plants in Turkey applied DEA/AR model. Wang et al., (2008) presented a DEA model with AR for priority derivation in the analytic hierarchy process (AHP), which is referred as the DEA/AR model. Their proposed model overcame the shortcomings of the DEAHP such as illogical local weights, over insensitivity to some comparisons, information loss, and overestimation of some local weights, and provide better priority estimate and better decision conclusions than the DEAHP. Lai et al. (2015) applied AHP method to incorporate the weightings of input and output variables into DEA to evaluate 24 international airports. The results revealed that the discrimination power of their model has been increased in comparison with conventional DEA. Moreover, Degl’Innocenti et al. (2017) examined the efficiency of 116 banks for nine new EU members in Central and Eastern European (CEE) countries over the period 2004–2015 using weight assurance region in two-stage DEA model. They also extended their work by including a window-based approach to take into account the patterns of efficiency over time. Ebrahimi and Khalili (2018) proposed a mixed integer AR- imprecise DEA approach to find the best DMU and applied their model to solve a supplier selection problem. Recently, Omrani et al. (2020) integrated best–worst method (BWM) and DEA to measure the efficiency score of 39 electricity distribution companies in Iran. Also, they extended their proposed model to find common weights of input and output variables in DEA considering DMs’ judgement.

The main motivation of this study was to propose a novel model to handle uncertainty in data and DMs’ judgement comprehensively using the state- of- the- art techniques. As mentioned before, due to the complexity, few research studies have addressed uncertainty using credibility approach for evaluating the efficiency of DMUs. So, the gap of applying credibility DEA approach in the efficiency evaluation of DMUs was obvious. Although, mixed robust fuzzy DEA method has been applied in a few research studies, however, to the best of the authors knowledge, no study has investigated the robust credibility DEA approach with uncertain perturbation level and weight flexibility yet.

3 Methodology

In this section, the proposed BWM-RCDEA model has been illustrated. In summary, first a fuzzy credibility DEA model is introduced. Then, considering uncertainty in constructing fuzzy sets, a robust credibility DEA (RCDEA) model is used. Finally, DMs’ preferences is incorporated into the RCDEA model using BWM and a novel bi-objective BWM-CRDEA model is constructed. The proposed bi-objective BWM-RCDEA model is solved using a min–max approach. In the following, methods applied into the proposed model have been defined separately.

3.1 Preliminaries

First, a brief review of fuzzy sets definitions and terms have been explained in the following. For more details, the readers can refer to Dubois and Prade (1978), Zimmermann (2001), Liu and Liu (2002, 2003) and Li and Liu (2006). Moreover, the parameters used in models have been presented in Table 1.

Table 1 Parameters applied for the models in this study

Definition 1

Let $U$ be a universe set. A fuzzy set $\tilde{A}$ of $U$ is defined by a membership function $\mu_{{\tilde{A}}} (x) \to [0,1],{\kern 1pt} {\kern 1pt} \forall x \in U$.

Definition 2

The $\alpha - cut$ of fuzzy set $\tilde{A}$, $\tilde{A}_{\alpha }$, is the crisp set $\tilde{A}_{\alpha } = \{ x|\mu_{{\tilde{A}}} (x) \ge \alpha \}$.

Definition 3

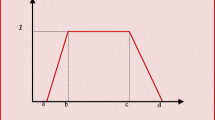
A fuzzy number L-R type is expressed as $\tilde{A} = (m,\alpha ,\beta )_{LR}$ with below membership function:

$$ \mu_{{\tilde{A}}} (r) = \left\{ {\begin{array}{*{20}c} {L(\frac{m - r}{\alpha })\quad {\kern 1pt} r \le m} \\ {R(\frac{r - m}{\beta })\quad r \ge m} \\ \end{array} } \right. $$

(1)

where L and R are the left and right functions, respectively, and $\alpha$ and $\beta$ are the (non-negative) left and right spreads, respectively.

Definition 4

An L-R fuzzy number, $\tilde{A} = (m,\alpha ,\beta )_{LR} = (m,\alpha ,\beta )$ is a triangular fuzzy number if.

$$ L(x) = R(x) = \left\{ {\begin{array}{*{20}l} {1 - x} \hfill & {0 \le x \le 1} \hfill \\ 0 \hfill & {otherwise} \hfill \\ \end{array} } \right. $$

(2)

Definition 5

Let $\tilde{A} = (m,\alpha ,\beta )_{LR}$ and $\tilde{B} = (\overline{m},\overline{\alpha },\overline{\beta })_{LR}$ be two positive triangular fuzzy numbers. The addition, subtraction and multiplication of $\tilde{A}$ and $\tilde{B}$ are as follows:

Addition:$\tilde{A} + \tilde{B} = (m,\alpha ,\beta )_{LR} + (\overline{m},\overline{\alpha },\overline{\beta })_{LR} = (m + \overline{m},\alpha + \overline{\alpha },\beta + \overline{\beta })_{LR}$.

Subtraction:$\tilde{A} - \tilde{B} = (m,\alpha ,\beta )_{LR} - (\overline{m},\overline{\alpha },\overline{\beta })_{LR} = (m - \overline{m},\alpha + \overline{\beta },\beta + \overline{\alpha })_{LR}$.

Multiplication (approximation):

$$ \tilde{A} \otimes \tilde{B} = (m,\alpha ,\beta )_{LR} \otimes (\overline{m},\overline{\alpha },\overline{\beta })_{LR} = (m\overline{m},m\overline{\alpha } + \overline{m}\alpha - \alpha \overline{\alpha },m\overline{\beta } + \overline{m}\beta + \beta \overline{\beta })_{LR} $$

Definition 6

A possibility space is defined as $(\Theta ,P(\Theta ),Pos)$ where $\Theta$ is nonempty set, $P(\Theta )$ is the power set of $\Theta$ and $Pos$ is the possibility measure. The possibility measure satisfies the below axioms:

• 1. $Pos(\emptyset ) = 0,{\kern 1pt} {\kern 1pt} Pos(X) = 1;$

• 2. $\forall {\kern 1pt} {\kern 1pt} A,B \in P(\Theta ){\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} if{\kern 1pt} {\kern 1pt} A \subseteq B \to Pos(A) \le Pos(B);$

• 3. $Pos(A_{1} \cup A_{2} ... \cup A_{k} ) = Sup{\kern 1pt} Pos_{j} (A_{j} )$.

where $X$ is the universe set.

Definition 7

The necessity measure is defined as $Nec(A) = 1 - Pos(A^{c} )$ where $A^{c}$ is the complementary set of $A$ set. The necessity measure satisfies the below axioms:

• 1. $Nec(\emptyset ) = 0,{\kern 1pt} {\kern 1pt} Nec(X) = 1;$

• 2. $\forall {\kern 1pt} {\kern 1pt} A,B \in P(\Theta ){\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} if{\kern 1pt} {\kern 1pt} A \subseteq B \to Nec(A) \le Nec(B);$

• 3. $Nec(A_{1} \cap A_{2} ... \cap A_{k} ) = Inf{\kern 1pt} {\kern 1pt} Nec_{j} (A_{j} )$.

Definition 8

The credibility measure is defined as $Cre(A) = \frac{1}{2}\{ Pos(A) + Nec(A)\}$. The credibility measure satisfies the below axioms:

• 1.$Cre(\emptyset ) = 0,{\kern 1pt} {\kern 1pt} Cre(X) = 1;$

• 2.$\forall {\kern 1pt} {\kern 1pt} A,B \in P(\Theta ){\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} if{\kern 1pt} {\kern 1pt} A \subseteq B \to Cre(A) \le Cre(B);$

• 3.$Cre(A) + Cre(A^{c} ) = 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} \forall A \subseteq P(X)$

Definition 9

Let $\lambda$ be a fuzzy variables. The possibility, necessity and credibility of the fuzzy event $(\lambda \ge r)$ are defined as:

$$ Pos(\lambda \ge r) = \mathop {Sup}\limits_{t \ge r} {\kern 1pt} {\kern 1pt} \mu_{\lambda } (t) $$

(3)

$$ Nec(\lambda \ge r) = 1 - Pos(\lambda < r) = 1 - \mathop {Sup{\kern 1pt} {\kern 1pt} \mu_{\lambda } (t)}\limits_{\lambda < r} $$

(4)

$$ Cre(\lambda \ge r) = \frac{1}{2}\{ Pos(\lambda \ge r) + Nec(\lambda \ge r)\} $$

(5)

3.2 Data envelopment analysis (DEA)

DEA is a nonparametric method that uses linear programming to measure the efficiency of DMUs with multiple inputs and multiple outputs. In DEA, efficiency is defined as a ratio of weighted sum of outputs to a weighted sum of inputs. The data form a frontier, DMUs which are on the frontier are evaluated as efficient. Output-oriented DEA models maximize output for a given quantity of input factors, contrariwise input-oriented models minimize input factors required for a given level of output. The input oriented DEA-CCR model is as follows (Charnes et al., 1978):

$$ \begin{gathered} \theta_{o}^{CCR} = \max \sum\limits_{i = t + 1}^{t + s} {w_{i} } y_{io} \hfill \\ st: \hfill \\ \sum\limits_{i = t + 1}^{t + s} {w_{i} } y_{ij} - \sum\limits_{i = 1}^{t} {w_{i} } x_{ij} \le 0,\quad j = 1,...,n \hfill \\ \sum\limits_{i = 1}^{t} {w_{i} } x_{io} = 1 \hfill \\ w_{i} \ge 0,{\kern 1pt} \quad i = 1,...,t + s \hfill \\ \end{gathered} $$

(6)

In model (6), jth DMU uses t inputs $x_{1j} ,...,x_{tj}$ for producing s outputs $y_{(t + 1)j} ,...,y_{(t + s)j}$. Also, the efficiency score of DMU under evaluation is $\theta_{o}^{CCR}$.

Multiplier form of DEA model (6) contains an equality constraint $\sum\nolimits_{i = 1}^{t} {w_{i} } x_{io} = 1$. Since, this paper assumes uncertainty in both inputs and outputs and the equality constraints have not the robust counterpart, hence, to handle uncertainty in inputs using robust optimization approach, the alternative DEA model (7) introduced by Zohrehbandian et al., (2010) is used instead of model (6).

$$ \begin{gathered} \max {\kern 1pt} {\kern 1pt} {\kern 1pt} z_{o} \hfill \\ s.t: \hfill \\ \sum\limits_{i = t + 1}^{t + s} {w_{i} } y_{io} - \theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} } x_{io} \ge z_{o} ; \hfill \\ \sum\limits_{i = t + 1}^{t + s} {w_{i} } y_{ij} - \theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} } x_{ij} \le 0,\quad j = 1,...,n \hfill \\ \sum\limits_{i = 1}^{t + s} {w_{i} } = 1 \hfill \\ w_{i} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,...,t + s \hfill \\ z_{o} \quad free \hfill \\ \end{gathered} $$

(7)

where $\theta_{j}^{CCR}$ is the efficiency score estimated for jth DMU in model (7). In model (7), the normalization constraint $\sum\nolimits_{i = 1}^{t} {w_{i} x_{io} } = 1$ has been replaced by $\sum\nolimits_{i = 1}^{t + s} {w_{i} } = 1$. Zohrehbandian et al. (2010) proved that the optimal solution of the models (6) and (7) are the same. In other words, the weights generated by the models (6) and (7) are same.

3.3 Credibility DEA (CDEA) model

In this section, the credibility DEA (CDEA) model is described. For developing DEA using fuzzy credibility theory, first following lemma is proven.

Lemma

Let $\widetilde{{\lambda_{1} }} = \left( {m_{1} } \right.,\alpha_{1} ,\left. {\beta_{1} } \right)_{LR}$ and $\widetilde{{\lambda_{2} }} = (m_{2} ,\alpha_{2} ,\beta_{2} )_{LR}$ be two L-R fuzzy numbers with continuous membership functions. For a given confidence level $\gamma \in [0,1]$ it is proven that (Tavana et al., 2012):

• I. If $\gamma \le 0.5$, then $Cr(\tilde{\lambda }_{1} \ge \tilde{\lambda }_{2} ) \ge \gamma {\kern 1pt} {\kern 1pt} {\kern 1pt} \Leftrightarrow m_{1} + \beta_{1} R^{ - 1} (2\gamma ) \ge m_{2} - \alpha_{2} R^{ - 1} (2\gamma )$.

• II. If $\gamma > 0.5$, then $Cr(\tilde{\lambda }_{1} \ge \tilde{\lambda }_{2} ) \ge \gamma {\kern 1pt} {\kern 1pt} {\kern 1pt} \Leftrightarrow m_{1} - \alpha_{1} L^{ - 1} (2(1 - \gamma )) \ge m_{2} + \beta_{2} L^{ - 1} (2(1 - \gamma ))$.

Proof

Suppose that.

$$ \begin{aligned} \lambda & = \lambda _{1} - \lambda _{2} = (m_{1} ,\alpha _{1} ,\beta _{1} )_{{LR}} \oplus ( - m_{2} ,\beta _{2} ,\alpha _{2} )_{{LR}} \\ & = (m_{1} - m_{2} ,\alpha _{1} + \beta _{2} ,\alpha _{2} + \beta _{1} )_{{LR}} = (\bar{m},\bar{\alpha },\bar{\beta })_{{LR}} \\ \end{aligned} $$

(8)

According to definition 9, we have:

$$ \begin{aligned} Cr(\widetilde{{\lambda_{1} }} \ge \widetilde{{\lambda_{2} }}) & = Cr(\widetilde{{\lambda_{1} }} - \widetilde{{\lambda_{2} }} \ge 0) = Cr(\widetilde{\lambda } \ge 0) = \frac{1}{2}\left[ {P_{0} ,(\widetilde{\lambda } \ge 0) + Nec(\widetilde{\lambda } \ge 0)} \right] \\ & = \frac{1}{2}\left[ {P_{0} ,(\widetilde{\lambda } \ge 0) + 1 - P_{0} ,(\widetilde{\lambda } \ge 0)} \right] = \frac{1}{2}\left[ {\sup_{t \ge 0} \mu (t) + 1 - \sup_{t < 0} \mu (t)} \right] \\ \end{aligned} $$

(9)

It is clear that the Eq. (9) can be expressed as follows:

$$ Cr(\widetilde{\lambda } \ge 0) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {0 \le \overline{m} - \overline{\alpha } } \hfill \\ {\frac{1}{2}\left[ {1 + 1 - L(\frac{{\overline{m} }}{{\overline{\alpha }}})} \right] = 1 - \frac{1}{2}L(\frac{{\overline{m}}}{{\overline{\alpha }}})} \hfill & {\overline{m} - \overline{\alpha } \le 0 \le \overline{m} } \hfill \\ {\frac{1}{2}\left[ {R( - \frac{{\overline{m} }}{{\overline{\beta } }}) + 1 - 1} \right] = \frac{1}{2}R(\frac{{\overline{m}}}{{\overline{\beta }}})} \hfill & {\overline{m} \le 0 \le \overline{m} + \overline{\beta } } \hfill \\ 0 \hfill & {\overline{m} + \overline{\beta } < 0} \hfill \\ \end{array} } \right. $$

(10)

If $\gamma \le 0.5$, then

$$ \begin{gathered} C_{r} (\widetilde{\lambda } \ge 0) \ge \gamma \Leftrightarrow \frac{1}{2}R(\frac{{ - \overline{m} }}{{\overline{\beta } }}) \ge \gamma \Leftrightarrow R(\frac{{ - \overline{m} }}{{\overline{\beta } }}) \ge 2\gamma \Leftrightarrow \frac{{ - \overline{m} }}{{\overline{\beta } }} \le R^{ - 1} (2\gamma ) \Leftrightarrow - \frac{{m_{1} - m_{2} }}{{\alpha_{2} + \beta_{1} }} \le R^{ - 1} (2\gamma ) \hfill \\ \Leftrightarrow m_{1} - m_{2} \le (\alpha_{2} + \beta_{1} )R^{ - 1} (2\gamma ) \Leftrightarrow m_{1} + \beta_{1} R^{ - 1} (2\gamma ) \ge m_{2} - \alpha_{2} R^{ - 1} (2\gamma ) \hfill \\ \end{gathered} $$

If $\gamma > 0.5$, then

$$ \begin{gathered} C_{r} (\widetilde{\lambda } \ge 0) \ge \gamma \Leftrightarrow 1 - \frac{1}{2}L\left(\frac{{\overline{m} }}{{\overline{\alpha } }}\right) \ge \gamma \Leftrightarrow \frac{1}{2}L\left(\frac{{\overline{m} }}{{\overline{\alpha } }}\right) \le 1 - \gamma \Leftrightarrow L\left(\frac{{\overline{m} }}{{\overline{\alpha } }}\right) \le 2(1 - \gamma ) \hfill \\ \Leftrightarrow \frac{{\overline{m} }}{{\overline{\alpha } }} \ge L^{ - 1} (2(1 - \gamma )) \Leftrightarrow \frac{{m_{1} - m_{2} }}{{\alpha_{1} + \beta_{2} }} \ge L^{ - 1} (2(1 - \gamma )) \Leftrightarrow m_{1} - m_{2} \ge (\alpha_{1} + \beta_{2} )L^{ - 1} (2(1 - \gamma )) \hfill \\ \Leftrightarrow m_{1} - \alpha_{1} L^{ - 1} (2(1 - \gamma )) \ge m_{2} + \beta_{2} L^{ - 1} (2(1 - \gamma )) \hfill \\ \end{gathered} $$

The credibility counterpart of dual of model (7) can be expressed as follows:

$$ \begin{gathered} \max {\kern 1pt} {\kern 1pt} {\kern 1pt} z_{o} \hfill \\ s.t: \hfill \\ Cr(\sum\limits_{i = t + 1}^{t + s} {w_{i} } \tilde{y}_{io} \ge \theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} } \tilde{x}_{io} + z_{o} ) \ge \gamma_{o} \hfill \\ Cr(\sum\limits_{i = t + 1}^{t + s} {w_{i} } \tilde{y}_{ij} \le \theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} } \tilde{x}_{ij} ) \ge \gamma_{j} ,{\kern 1pt} \quad j = 1,...,n \hfill \\ \sum\limits_{i = 1}^{t + s} {w_{i} } = 1 \hfill \\ w_{i} \ge 0,\quad {\kern 1pt} i = 1,...,t + s \hfill \\ z_{o} \quad free \hfill \\ \end{gathered} $$

(11)

where $\tilde{x}_{ij} = (x_{ij}^{m} ,x_{ij}^{\alpha } ,x_{ij}^{\beta } )_{LR} ,i = 1,...,t$ and $\tilde{y}_{ij} = (y_{ij}^{m} ,y_{ij}^{\alpha } ,y_{ij}^{\beta } )_{LR} ,i = t + 1,...,t + s$ are the L-R fuzzy numbers. The parameter $\gamma (\gamma_{o} ,\gamma_{i} )$ indicates the minimum level of confidence in feasibility of the constraints. Since the data and perturbations are considered as the L–R fuzzy numbers, hence, to protect the constraints against violation, the parameter $\gamma$ is used. As the parameter $\gamma$ increase, we lose more objective function to protect the constraints. The higher the value of the parameter $\gamma$, the higher the constraint confidence level. In other words, with increasing confidence level, the value of the objective function of the model (11) decreases. According to definition 3, the membership functions of inputs and outputs j = 1,…,n can be expressed as follows, respectively:

$$ \mu_{{\tilde{x}_{ij} }} (r) = \left\{ {\begin{array}{*{20}c} {L\left(\frac{{x_{ij}^{m} - r}}{{x_{ij}^{\alpha } }}\right)\quad r \le x_{ij}^{m} ,\quad i = 1,...,t} \\ {R\left(\frac{{r - x_{ij}^{m} }}{{x_{ij}^{\beta } }}\right)\quad r \ge x_{ij}^{m} ,\quad {\kern 1pt} i = 1,...,t} \\ \end{array} } \right. $$

(12)

$$ \mu_{{\tilde{y}_{ij} }} (r) = \left\{ {\begin{array}{*{20}l} {L\left( {\frac{{y_{ij}^{m} - r}}{{y_{ij}^{\alpha } }}} \right)\quad r \le y_{ij}^{m} ,\quad i = t + 1,...,t + s} \hfill \\ {R\left( {\frac{{r - y_{ij}^{m} }}{{y_{ij}^{\beta } }}} \right)\quad r \ge y_{ij}^{m} ,\quad i = t + 1,...,t + s} \hfill \\ \end{array} } \right. $$

(13)

According to Zadeh extension principle, the membership functions of the constraints of model (11) can be expressed as follows:

$$ \mu_{{\sum\limits_{i = 1}^{t} {w_{i} } \tilde{x}_{ij} }} (r) = \left\{ {\begin{array}{*{20}l} {L\left( {\frac{{\sum\limits_{i = 1}^{t} {w_{i} } x_{ij}^{m} - r}}{{\sum\limits_{i = 1}^{t} {w_{i} } x_{ij}^{\alpha } }}} \right){\kern 1pt} \quad r \le \sum\limits_{i = 1}^{t} {w_{i} } x_{ij}^{m} ,{\kern 1pt} {\kern 1pt} j = 1,...,n} \hfill \\ {R\left( {\frac{{r - \sum\limits_{i = 1}^{t} {w_{i} } x_{ij}^{m} }}{{\sum\limits_{i = 1}^{t} {w_{i} } x_{ij}^{\beta } }}} \right)\quad r \ge \sum\limits_{i = 1}^{t} {w_{i} } x_{ij}^{m} ,{\kern 1pt} {\kern 1pt} j = 1,...,n} \hfill \\ \end{array} } \right. $$

(14)

$$ \mu_{{\sum\limits_{i = t + 1}^{t + s} {w_{i} } \tilde{y}_{ij} }} (r) = \left\{ {\begin{array}{*{20}l} {L\left( {\frac{{\sum\limits_{i = t + 1}^{t + s} {w_{i} } y_{ij}^{m} - r}}{{\sum\limits_{i = t + 1}^{t + s} {w_{i} } y_{ij}^{\alpha } }}} \right){\kern 1pt} \quad r \le \sum\limits_{i = t + 1}^{t + s} {w_{i} } y_{ij}^{m} ,\quad j = 1,...,n} \hfill \\ {R\left( {\frac{{r - \sum\limits_{i = t + 1}^{t + s} {w_{i} } y_{ij}^{m} }}{{\sum\limits_{i = t + 1}^{t + s} {w_{i} } y_{ij}^{\beta } }}} \right)\quad r \ge \sum\limits_{i = t + 1}^{t + s} {w_{i} } y_{ij}^{m} ,\quad j = 1,...,n} \hfill \\ \end{array} } \right. $$

(15)

Based on the membership functions (14) to (15), the fuzzy numbers $\sum\nolimits_{i = t + 1}^{t + s} {w_{i} \tilde{y}_{io} }$,$\sum\nolimits_{i = t + 1}^{t + s} {w_{i} \tilde{y}_{ij} }$,$\theta_{j}^{CCR} \sum\nolimits_{i = 1}^{t} {w_{i} \tilde{x}_{ij} }$ and $\theta_{o}^{CCR} \sum\nolimits_{i = 1}^{t} {w_{i} \tilde{x}_{io} } + z_{o}$ are shown as below L-R fuzzy numbers:

$$ \sum\limits_{i = t + 1}^{t + s} {w_{i} \widetilde{y}_{io} } = \left( {\sum\limits_{i = t + 1}^{t + s} {w_{i} y_{io}^{m} } ,\sum\limits_{i = t + 1}^{t + s} {w_{i} y_{io}^{\alpha } } ,\sum\limits_{i = t + 1}^{t + s} {w_{i} y_{io}^{\beta } } } \right)_{LR} $$

(16)

$$ \sum\limits_{i = t + 1}^{t + s} {w_{i} \widetilde{y}_{ij} } = \left( {\sum\limits_{i = t + 1}^{t + s} {w_{i} y_{ij}^{m} } ,\sum\limits_{i = t + 1}^{t + s} {w_{i} y_{ij}^{\alpha } } ,\sum\limits_{i = t + 1}^{t + s} {w_{i} y_{ij}^{\beta } } } \right)_{LR} ,\quad j = 1,...,n $$

(17)

$$ \theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} \tilde{x}_{ij} } = \left( {\theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} x_{ij}^{m} } ,\theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} x_{ij}^{\alpha } } ,\theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} x_{ij}^{\beta } } } \right)_{LR} ,\quad j = 1,...,n $$

(18)

$$ \theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} \tilde{x}_{io} + z_{o} } = \left( {\theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} x_{io}^{m} + z_{o} } ,\theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} x_{io}^{\alpha } } ,\theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} x_{io}^{\beta } } } \right)_{LR} $$

(19)

In this study, the data are considered as triangular fuzzy numbers. Hence, according to definition 4, we have:

$$ L(x) = R(x) = L^{ - 1} (x) = R^{ - 1} (x) = 1 - x $$

(20)

According to above lemma, for $\gamma_{o} \le 0.5$, the first constraint of model (11) is expressed as follows:

$$ \begin{gathered} \sum\limits_{i = t + 1}^{t + s} {w_{i} y_{io}^{m} } + R^{ - 1} (2\gamma_{o} )\sum\limits_{i = t + 1}^{t + s} {w_{i} y_{io}^{\beta } } \ge \theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} x_{io}^{m} + z_{o} } - R^{ - 1} (2\gamma_{o} )\theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} x_{io}^{\alpha } } \hfill \\ \Rightarrow \sum\limits_{i = t + 1}^{t + s} {w_{i} (y_{io}^{m} } + R^{ - 1} (2\gamma_{o} )y_{io}^{\beta } ) \ge \theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{io}^{m} - R^{ - 1} (2\gamma_{o} )x_{io}^{\alpha } ) + z_{o} } \hfill \\ \Rightarrow \sum\limits_{i = t + 1}^{t + s} {w_{i} (y_{io}^{m} } + (1 - 2\gamma_{o} )y_{io}^{\beta } ) \ge \theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{io}^{m} - (1 - 2\gamma_{o} )x_{io}^{\alpha } ) + z_{o} } \hfill \\ \Rightarrow \sum\limits_{i = t + 1}^{t + s} {w_{i} (y_{io}^{m} } + (1 - 2\gamma_{o} )y_{io}^{\beta } ) - \theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{io}^{m} - (1 - 2\gamma_{o} )x_{io}^{\alpha } ) \ge z_{o} } \hfill \\ \end{gathered} $$

(21)

In addition, the second constraint of model (11) is converted to a linear constraint as follows:

$$ \begin{gathered} \sum\limits_{i = t + 1}^{t + s} {w_{i} y_{ij}^{m} } - R^{ - 1} (2\gamma_{j} )\sum\limits_{i = t + 1}^{t + s} {w_{i} y_{ij}^{\alpha } } \le \theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} x_{ij}^{m} } + R^{ - 1} (2\gamma_{j} )\theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} x_{ij}^{\beta } } \hfill \\ \Rightarrow \sum\limits_{i = t + 1}^{t + s} {w_{i} \left( {y_{ij}^{m} - R^{ - 1} (2\gamma_{j} )y_{ij}^{\alpha } } \right)} \le \theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{ij}^{m} + R^{ - 1} (2\gamma_{j} )x_{ij}^{\beta } )} \hfill \\ \Rightarrow \sum\limits_{i = t + 1}^{t + s} {w_{i} \left( {y_{ij}^{m} - (1 - 2\gamma_{j} )y_{ij}^{\alpha } } \right)} \le \theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{ij}^{m} + (1 - 2\gamma_{j} )x_{ij}^{\beta } )} \hfill \\ \Rightarrow \sum\limits_{i = t + 1}^{t + s} {w_{i} \left( {y_{ij}^{m} - (1 - 2\gamma_{j} )y_{ij}^{\alpha } } \right)} - \theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{ij}^{m} + (1 - 2\gamma_{j} )x_{ij}^{\beta } )} \le 0 \hfill \\ \end{gathered} $$

(22)

By considering the constraints (21) and (22), the final CDEA model for $\gamma_{o} ,\gamma_{j} \le 0.5$ is expressed follows:

$$ \begin{gathered} \max {\kern 1pt} {\kern 1pt} {\kern 1pt} z_{o} \hfill \\ s.t: \hfill \\ \sum\limits_{i = t + 1}^{t + s} {w_{i} \left( {y_{io}^{m} + (1 - 2\gamma_{o} )y_{io}^{\beta } } \right)} - \theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{io}^{m} - (1 - 2\gamma_{o} )x_{io}^{\alpha } ) \ge z_{o} } \hfill \\ \sum\limits_{i = t + 1}^{t + s} {w_{i} \left( {y_{ij}^{m} - (1 - 2\gamma_{j} )y_{ij}^{\alpha } } \right)} - \theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{ij}^{m} + (1 - 2\gamma_{j} )x_{ij}^{\beta } )} \le 0,\quad j = 1,...,n \hfill \\ \sum\limits_{i = 1}^{t + s} {w_{i} } = 1 \hfill \\ w_{i} \ge 0,\quad i = 1,...,t + s \hfill \\ z_{o} \quad free \hfill \\ \end{gathered} $$

(23)

Similar to above way and according to above lemma, the first constraint of model (11) for $\gamma_{o} > 0.5$ is expressed as follows:

$$ \begin{gathered} \sum\limits_{i = t + 1}^{t + s} {w_{i} y_{io}^{m} } - L^{ - 1} (2(1 - \gamma_{o} ))\sum\limits_{i = t + 1}^{t + s} {w_{i} y_{io}^{\alpha } } \ge \theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} x_{io}^{m} + z_{o} } + L^{ - 1} (2(1 - \gamma_{o} ))\theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} x_{io}^{\beta } } \hfill \\ \Rightarrow \sum\limits_{i = t + 1}^{t + s} {w_{i} (y_{io}^{m} } - L^{ - 1} (2(1 - \gamma_{o} ))y_{io}^{\alpha } ) \ge \theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{io}^{m} + L^{ - 1} (2(1 - \gamma_{o} ))x_{io}^{\beta } ) + z_{o} } \hfill \\ \Rightarrow \sum\limits_{i = t + 1}^{t + s} {w_{i} (y_{io}^{m} } - (2\gamma_{o} - 1)y_{io}^{\alpha } ) \ge \theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{io}^{m} + (2\gamma_{o} - 1)x_{io}^{\beta } ) + z_{o} } \hfill \\ \Rightarrow \sum\limits_{i = t + 1}^{t + s} {w_{i} (y_{io}^{m} } - (2\gamma_{o} - 1)y_{io}^{\alpha } ) - \theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{io}^{m} + (2\gamma_{o} - 1)x_{io}^{\beta } ) \ge z_{o} } \hfill \\ \end{gathered} $$

(24)

Also, the second constraint of model (11) is written as follows:

$$ \begin{gathered} \sum\limits_{i = t + 1}^{t + s} {w_{i} y_{ij}^{m} } + L^{ - 1} (2(1 - \gamma_{j} ))\sum\limits_{i = t + 1}^{t + s} {w_{i} y_{ij}^{\beta } } \le \theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} x_{ij}^{m} } - L^{ - 1} (2(1 - \gamma_{j} ))\theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} x_{ij}^{\alpha } } \hfill \\ \Rightarrow \sum\limits_{i = t + 1}^{t + s} {w_{i} (y_{ij}^{m} } + L^{ - 1} (2(1 - \gamma_{j} ))y_{ij}^{\beta } ) \le \theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{ij}^{m} - L^{ - 1} (2(1 - \gamma_{j} ))x_{ij}^{\alpha } )} \hfill \\ \Rightarrow \sum\limits_{i = t + 1}^{t + s} {w_{i} (y_{ij}^{m} } + (2\gamma_{j} - 1)y_{ij}^{\beta } ) \le \theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{ij}^{m} - (2\gamma_{j} - 1)x_{ij}^{\alpha } )} \hfill \\ \Rightarrow \sum\limits_{i = t + 1}^{t + s} {w_{i} (y_{ij}^{m} } + (2\gamma_{j} - 1)y_{ij}^{\beta } ) - \theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{ij}^{m} - (2\gamma_{j} - 1)x_{ij}^{\alpha } )} \le 0 \hfill \\ \end{gathered} $$

(25)

Finally, the CDEA model for $\gamma_{o} ,\gamma_{j} > 0.5$ is shown as model (26).

$$ \begin{gathered} \max {\kern 1pt} {\kern 1pt} {\kern 1pt} z_{o} \hfill \\ s.t: \hfill \\ \sum\limits_{i = t + 1}^{t + s} {w_{i} (y_{io}^{m} } - (2\gamma_{o} - 1)y_{io}^{\alpha } ) - \theta_{o}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{io}^{m} + (2\gamma_{o} - 1)x_{io}^{\beta } ) \ge z_{o} } \hfill \\ \sum\limits_{i = t + 1}^{t + s} {w_{i} (y_{ij}^{m} } + (2\gamma_{j} - 1)y_{ij}^{\beta } ) - \theta_{j}^{CCR} \sum\limits_{i = 1}^{t} {w_{i} (x_{ij}^{m} - (2\gamma_{j} - 1)x_{ij}^{\alpha } )} \le 0,\quad j = 1,...,n \hfill \\ \sum\limits_{i = 1}^{t + s} {w_{i} } = 1 \hfill \\ w_{i} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,...,t + s \hfill \\ z_{o} \quad free \hfill \\ \end{gathered} $$

(26)

3.4 Robust optimization

Robust optimization is a preeminent approach in dealing with uncertainty of data (Alem and Morabito, 2012) since robust optimization assumes no probability distribution for uncertain data as well as the capability in modeling problems with large number of uncertain parameters. In this study we have investigated the robust optimization model with data uncertainty of U (Bental and Nemirovski, 2000).

Although first steps of robust optimization with data uncertainty of U was taken by Soyester (1973) and then developed by Ben-Tal and Nemirovski (2000) and Bertsimas and Sim (2004), however, the advantages of Bertsimas and Sim (2004) in converting models into simple linear models and generating less conservatism solutions led to wide application of this approach in real world problems.

To illustrate the robust optimization model (Bertsimas & Sim, 2004), consider the following optimization model:

$$ \begin{gathered} \max \,c^{\prime } x \hfill \\ s.t: \hfill \\ \sum\limits_{j} {a_{ij}^{\prime } x_{j} } \le b_{i} ,{\kern 1pt} {\kern 1pt} \forall i \hfill \\ l_{j} \le x_{j} \le u_{j} ,{\kern 1pt} {\kern 1pt} \forall j \hfill \\ \end{gathered} $$

(27)

In the optimization model (27), $J_{i}$ is a set of uncertain coefficients in particular row i of matrix A. Each independent uncertain parameter $\tilde{a}_{ij}$ symmetrically distributed in a bounded interval $[a_{ij} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a}_{ij} ,a_{ij} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a}_{ij} ]$ which centered at point $a_{ij}$. Also $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a}_{ij} = e_{ij} \times a_{ij}$ where $e_{ij}$ indicates percentage of perturbation in the nominal value $a_{ij}$. Moreover, Bertsimas and Sim (2004) introduced a scaled deviation $z_{{ij}} = {\raise0.7ex\hbox{${\left( {\hat{a}_{{ij}} - a_{{ij}} } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {\hat{a}_{{ij}} - a_{{ij}} } \right)} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} _{{ij}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{a} _{{ij}} }$}}$ which take values in interval $[ - 1,1]$. Bertsimas and Sim (2004) believed that in real world problems, it is almost implausible that, all parameters take their worst case values simultaneously, which leads to the conservatism solution. Therefore, for each constraint i, Bertsimas and Sim (2004) introduced a new parameter of $\Gamma_{i}$, as a budget of uncertainty, which takes value in interval $[0,|J_{i} |]$. Indeed $\Gamma_{i}$ values make a trade-off between protection level of constraint and conservatism level of solutions. When $\Gamma_{i} = 0$, the constraints are vulnerable in dealing with uncertainty while in $\Gamma_{i} = |J_{i} |$ constraints are fully protected and solutions are too conservatism. Considering all aforementioned details, Bertsimas and Sim (2004) introduced the robust linear counterpart of model (27) as follows: (For more details, readers can refer to Bertsimas and sim (2004) and Alem and Morabito (2012))

$$ \begin{gathered} \max \,c^{\prime } x \hfill \\ s.t: \hfill \\ \sum\limits_{j} {a_{ij}^{\prime } x} + \Gamma_{i} P_{i} + \sum\limits_{{j \in J_{i} }} {q_{rj} } \le b_{i} ,\,\,\,\,\,\forall i \hfill \\ P_{j} + q_{rj} \ge \hat{a}_{ij} y_{j} ,\,\,\,\,\,\forall j \hfill \\ - y_{j} \le x_{j} \le y_{j} ,\,\,\,\,\,\forall j \hfill \\ I_{j} \le x_{j} \le u_{j} ,\,\,\,\,\,\forall j \hfill \\ q_{ij} \ge 0,\,\,\,\,\,\forall i,j \in J_{i} \hfill \\ y_{j} \ge 0,\,\,\,\,\,\forall j \hfill \\ p_{i} \ge 0,\,\,\,\,\,\forall i \hfill \\ \end{gathered} $$

(28)

3.5 Best worst method (BWM)

Best worst method was first introduced by Rezaei (2015) to weight criteria using pairwise comparison. Indeed, like AHP, BWM assign the weights based on the preferences of Decision makers. However, BWM has advantages in compared with AHP such ass less pairwise comparison and higher consistency ratio (Zhao et al., 2019). For example, for a set of n criteria, AHP needs $\frac{n * (n - 1)}{2}$ pairwise comparison while BWM applies $(2*n) - 3$, which is less than AHP technique.

The final BWM model is as model (29). It is important to note that the steps of the BWM are completely explained in Rezaei (2015, 2016) and readers for more details can refer to them.

$$ \begin{gathered} \min \,\xi_{r} \hfill \\ s.t: \hfill \\ \{ |w_{i} - a_{iW} w_{W} |\}_{r} \le \xi_{r} ,\quad i = 1,...,n \hfill \\ \{ |w_{B} - a_{Bi} w_{i} |\}_{r} \le \xi_{r} ,\quad i = 1,...,n \hfill \\ \sum\limits_{i = 1}^{n} {w_{i} } = 1 \hfill \\ w_{i} \ge 0,\quad j = 1,...,n \hfill \\ \end{gathered} $$

(29)

where the preference of the best criterion over ith criteria for rth DM is $a_{Bi}$ and preference of ith criteria on worst criterion for rth DM is $a_{iW}$. In this paper, linear BWM (29) is applied to estimate the indicators’ weights. Also readers can refer to comprehensive review of application of BWM technique in decision making problems by Mi et al., (2019).

3.6 Robust Credibility DEA (RCDEA)

In this section, the counterpart robust CDEA (RCDEA) models are proposed. The proposed RCDEA models are:

• RCDEA model with exact perturbation in fuzzy inputs and fuzzy outputs.

• RCDEA model with fuzzy perturbation in fuzzy inputs and fuzzy outputs.

Let $\tilde{x}_{ij} = (x_{ij}^{m} ,x_{ij}^{\alpha } ,x_{ij}^{\beta } )_{LR} ,i = 1,...,t$ and $\tilde{y}_{ij} = (y_{ij}^{m} ,y_{ij}^{\alpha } ,y_{ij}^{\beta } )_{LR} ,i = t + 1,...,t + s$ be the L-R fuzzy numbers. Let $x_{ij}^{m}$ and $y_{ij}^{m}$ are symmetrically distributed in intervals $[x_{ij}^{m} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{ij}^{m} ,x_{ij}^{m} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{ij}^{m} ]$ and $[y_{ij}^{m} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}_{ij}^{m} ,y_{ij}^{m} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}_{ij}^{m} ]$ where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}_{ij}^{m} = e_{ij} \times x_{ij}^{m}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}_{ij}^{m} = e_{ij} \times y_{ij}^{m}$. Since $x_{ij}^{m}$ and $y_{ij}^{m}$ are contaminated with perturbation, hence, $x_{ij}^{\alpha }$, $x_{ij}^{\beta }$, $y_{ij}^{\alpha }$ and $y_{ij}^{\beta }$ are symmetrically distributed in determined intervals, too.

3.6.1 RCDEA model with exact perturbation in fuzzy inputs and fuzzy outputs

To show the RCDEA model with exact perturbation in fuzzy inputs and fuzzy outputs, credibility DEA models (23) and (26) are converted to the counterpart robust CDEA models. According to approach proposed by Bertsimas and Sim (2004), the robust counterpart of CDEA models for $\gamma \le 0.5$ and $\gamma > 0.5$ are as (30) and (31) respectively:

$$ \begin{aligned} & \theta _{o}^{{RCDEA}} = \mathop {\max }\limits_{{\gamma _{o} ,\gamma _{i} \le 0.5}} \sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} (y_{{io}}^{m} } + (1 - 2\gamma _{o} )y_{{io}}^{\beta } ) - \theta _{o}^{{CCR}} \sum\limits_{{i = 1}}^{t} {w_{i} (x_{{io}}^{m} - (1 - 2\gamma _{o} )x_{{io}}^{\alpha } )} - \Gamma _{o} p_{o} - \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{io}} } - \sum\limits_{{i = 1}}^{t} {q_{{io}} } \\ & s.t: \\ & \sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} (y_{{ij}}^{m} } - (1 - 2\gamma _{j} )y_{{ij}}^{\alpha } ) - \theta _{j}^{{CCR}} \sum\limits_{{i = 1}}^{t} {w_{i} (x_{{ij}}^{m} + (1 - 2\gamma _{j} )x_{{ij}}^{\beta } )} + \Gamma _{j} p_{j} + \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{ij}} } + \sum\limits_{{i = 1}}^{t} {q_{{ij}} } \le 0,{\kern 1pt} j = 1,...,n \\ & \sum\limits_{{i = 1}}^{{m + s}} {w_{i} } = 1 \\ & p_{o} + q_{{io}} \ge e_{{io}} (y_{{io}}^{m} + (1 - 2\gamma _{o} )y_{{io}}^{\beta } )z_{i} ,\quad \forall i = t + 1,...t + s \\ & p_{o} + q_{{io}} \ge e_{{io}} (x_{{io}}^{m} - (1 - 2\gamma _{o} )x_{{io}}^{\alpha } )z_{i} ,\quad \forall i = 1,...t \\ & p_{j} + q_{{ij}} \ge e_{{ij}} (y_{{ij}}^{m} - (1 - 2\gamma _{j} )y_{{ij}}^{\alpha } )z_{i} ,\quad \forall i = t + 1,...t + s,\forall j = 1,...,n \\ & p_{j} + q_{{ij}} \ge e_{{ij}} (x_{{ij}}^{m} + (1 - 2\gamma _{j} )x_{{ij}}^{\beta } )z_{i} ,\quad \forall i = 1,...t,\forall j = 1,...,n \\ & - z_{i} \le w_{i} \le z_{i} ,\quad \forall i = 1,2,...,t + s \\ & p_{j} ,q_{{ij}} \ge 0,\quad \forall i,j \\ & w_{i} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,...,t + s \\ \end{aligned} $$

(30)

$$ \begin{aligned} & \theta _{o}^{{RCDEA}} = \mathop {\max }\limits_{{\gamma _{o} ,\gamma _{i} > 0.5}} \sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} (y_{{io}}^{m} } - (2\gamma _{o} - 1)y_{{io}}^{\alpha } ) - \theta _{o}^{{CCR}} \sum\limits_{{i = 1}}^{t} {w_{i} (x_{{io}}^{m} + (2\gamma _{o} - 1)x_{{io}}^{\beta } )} - \Gamma _{o} p_{o} - \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{io}} } - \sum\limits_{{i = 1}}^{t} {q_{{io}} } \\ & s.t: \\ & \sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} (y_{{ij}}^{m} } + (2\gamma _{j} - 1)y_{{ij}}^{\beta } ) - \theta _{j}^{{CCR}} \sum\limits_{{i = 1}}^{t} {w_{i} (x_{{ij}}^{m} - (2\gamma _{j} - 1)x_{{ij}}^{\alpha } )} + \Gamma _{j} p_{j} + \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{ij}} } - \sum\limits_{{i = 1}}^{t} {q_{{ij}} } \le 0,{\kern 1pt} {\kern 1pt} j = 1,...,n \\ & \sum\limits_{{i = 1}}^{{m + s}} {w_{i} } = 1 \\ & p_{o} + q_{{io}} \ge e_{{io}} (y_{{io}}^{m} - (2\gamma _{o} - 1)y_{{io}}^{\alpha } )z_{i} ,\quad \forall i = t + 1,...t + s \\ & p_{o} + q_{{io}} \ge e_{{io}} (x_{{io}}^{m} + (2\gamma _{o} - 1)x_{{io}}^{\beta } )z_{i} ,\quad \forall i = 1,...t \\ & p_{j} + q_{{ij}} \ge e_{{ij}} (y_{{ij}}^{m} + (2\gamma _{j} - 1)y_{{ij}}^{\beta } )z_{i} ,\quad \forall i = t + 1,...t + s,\forall j = 1,...,n \\ & p_{j} + q_{{ij}} \ge e_{{ij}} (x_{{ij}}^{m} - (2\gamma _{j} - 1)x_{{ij}}^{\alpha } )z_{i} ,\quad \forall i = 1,...t,\forall j = 1,...,n \\ & - z_{i} \le w_{i} \le z_{i} ,\quad \forall i = 1,2,...,t + s \\ & p_{j} ,q_{{ij}} \ge 0,\quad \forall i,j \\ & w_{i} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,...,t + s \\ \end{aligned} $$

(31)

where the free variable $z_{o}$ is removed and the first constraint of models (23) and (26) are moved to objective functions.

It is notable that the objective function and constraints of the models (30) and (32) are the same except the constraints related to robust optimization. In fact, the 3th to 6th constraints are different for these models. The constraints show that the feasible space of model (32) is greater than the feasible space of model (30). Consider the 3^th constraint for the models. For the model (30), the third constraint is as $p_{o} + q_{io} \ge e_{io} (y_{io}^{m} + (1 - 2\gamma_{o} )y_{io}^{\beta } )z_{i}$ and for the model (32), it express as $p_{o} + q_{io} \ge [e_{io}^{m} - (1 - 2\gamma_{io} )e_{io}^{\alpha } ](y_{io}^{m} + (1 - 2\gamma_{o} )y_{io}^{\beta } )z_{i}$. Since the value of $[e_{io}^{m} - (1 - 2\gamma_{io} )e_{io}^{\alpha } ]$ is a positive value, then the feasible space of model (32) is greater than the feasible space of model (30). Hence, the objective function of model (32) is equal or greater than the objective function model (30), namely, $\theta_{o}^{{RCDEA - Fuzzy{\kern 1pt} Perturbation}} \ge \theta_{o}^{RCDEA}$. Note that we set $e_{io}^{m} = e_{io}^{{}}$. In a similar way, for γ > 0.5, we can show that the objective function of model (33) is equal or smaller than the objective function model (31).

3.6.2 RCDEA model with fuzzy perturbation in fuzzy inputs and fuzzy outputs

In real world application, the level of uncertainty is unknown and considering certain values for uncertainty level of data (the value e) may be contributed to imprecise results. In this section, the percentage of perturbation is considered as L-R fuzzy number $\tilde{e}_{ij} = (e_{ij}^{m} ,e_{ij}^{\alpha } ,e_{ij}^{\beta } )_{LR}$. Consider the fifth constraint of RCDEA model (30). In fuzzy status, this constraint is written as $Cre(p_{j} + q_{ij} \ge \tilde{e}_{ij} (y_{ij}^{m} + (2\gamma_{j} - 1)y_{ij}^{\beta } )z_{i} ) \ge \gamma_{ij}$. According to above lemma, the later fuzzy constraint is converted to $p_{j} + q_{ij} \ge [e_{ij}^{m} - (1 - 2\gamma_{ij} )e_{ij}^{\alpha } ](y_{ij}^{m} + (2\gamma_{j} - 1)y_{ij}^{\beta } )z_{i}$. In fact, in order to obtain a RCDEA model with fuzzy perturbation, it is enough to replace $e_{ij}$ with $[e_{ij}^{m} - (1 - 2\gamma_{ij} )e_{ij}^{\alpha } ]$ for $\gamma_{ij} \le 0.5$ and $[e_{ij}^{m} + (2\gamma_{ij} - 1)e_{ij}^{\beta } ]$ $\gamma_{ij} > 0.5$. Therefore, models (30) and (31) are converted to (32) and (33), respectively:

$$ \begin{aligned} & \theta _{o}^{{RCDEA - Fuzzy{\kern 1pt} Perturbation}} = \mathop {\max }\limits_{{\gamma _{o} ,\gamma _{i} \le 0.5}} \sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} (y_{{io}}^{m} } + (1 - 2\gamma _{o} )y_{{io}}^{\beta } ) - \theta _{o}^{{CCR}}\\ &\qquad \sum\limits_{{i = 1}}^{t} {w_{i} (x_{{io}}^{m} - (1 - 2\gamma _{o} )x_{{io}}^{\alpha } )} - \Gamma _{o} p_{o} - \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{io}} } - \sum\limits_{{i = 1}}^{t} {q_{{io}} } \\ & s.t: \\ & \sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} (y_{{ij}}^{m} } - (1 - 2\gamma _{j} )y_{{ij}}^{\alpha } ) - \theta _{j}^{{CCR}} \sum\limits_{{i = 1}}^{t} {w_{i} (x_{{ij}}^{m} + (1 - 2\gamma _{j} )x_{{ij}}^{\beta } )} + \Gamma _{j} p_{j} + \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{ij}} } + \sum\limits_{{i = 1}}^{t} {q_{{ij}} } \le 0,{\kern 1pt} j = 1,...,n \\ & \sum\limits_{{i = 1}}^{{m + s}} {w_{i} } = 1 \\ & p_{o} + q_{{io}} \ge [e_{{io}}^{m} - (1 - 2\gamma _{{io}} )e_{{io}}^{\alpha } ](y_{{io}}^{m} + (1 - 2\gamma _{o} )y_{{io}}^{\beta } )z_{i} ,\quad \forall i = t + 1,...t + s \\ & p_{o} + q_{{io}} \ge [e_{{io}}^{m} - (1 - 2\gamma _{{io}} )e_{{io}}^{\alpha } ](x_{{io}}^{m} - (1 - 2\gamma _{o} )x_{{io}}^{\alpha } )z_{i} ,\quad \forall i = 1,...t \\ & p_{j} + q_{{ij}} \ge [e_{{ij}}^{m} - (1 - 2\gamma _{{ij}} )e_{{ij}}^{\alpha } ](y_{{ij}}^{m} - (1 - 2\gamma _{j} )y_{{ij}}^{\alpha } )z_{i} ,\quad \forall i = t + 1,...t + s,\forall j = 1,...,n \\ & p_{j} + q_{{ij}} \ge [e_{{ij}}^{m} - (1 - 2\gamma _{{ij}} )e_{{ij}}^{\alpha } ](x_{{ij}}^{m} + (1 - 2\gamma _{j} )x_{{ij}}^{\beta } )z_{i} ,\quad \forall i = 1,...t,\forall j = 1,...,n \\ & - z_{i} \le w_{i} \le z_{i} ,\quad \forall i = 1,2,...,t + s \\ & p_{j} ,q_{{ij}} \ge 0,\quad \forall i,j \\ & w_{i} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,...,t + s \\ \end{aligned} $$

(32)

$$ \begin{aligned} & \theta _{o}^{{RCDEA - Fuzzy{\kern 1pt} Perturbation}} = \mathop {\max }\limits_{{\gamma _{o} ,\gamma _{i} > 0.5}} \sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} (y_{{io}}^{m} } - (2\gamma _{o} - 1)y_{{io}}^{\alpha } ) - \theta _{o}^{{CCR}} \\ &\quad \sum\limits_{{i = 1}}^{t} {w_{i} (x_{{io}}^{m} + (2\gamma _{o} - 1)x_{{io}}^{\beta } )} - \Gamma _{o} p_{o} - \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{io}} } - \sum\limits_{{i = 1}}^{t} {q_{{io}} } \\ & s.t: \\ & \sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} (y_{{ij}}^{m} } + (2\gamma _{j} - 1)y_{{ij}}^{\beta } ) - \theta _{j}^{{CCR}} \sum\limits_{{i = 1}}^{t} {w_{i} (x_{{ij}}^{m} - (2\gamma _{j} - 1)x_{{ij}}^{\alpha } )} + \Gamma _{j} p_{j} + \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{ij}} } + \sum\limits_{{i = 1}}^{t} {q_{{ij}} } \le 0,\quad j = 1,...,n \\ & \sum\limits_{{i = 1}}^{{m + s}} {w_{i} } = 1 \\ & p_{o} + q_{{io}} \ge [e_{{io}}^{m} + (2\gamma _{{io}} - 1)e_{{io}}^{\beta } ](y_{{io}}^{m} - (2\gamma _{o} - 1)y_{{io}}^{\alpha } )z_{i} ,\quad \forall i = t + 1,...t + s \\ & p_{o} + q_{{io}} \ge [e_{{io}}^{m} + (2\gamma _{{io}} - 1)e_{{io}}^{\beta } ](x_{{io}}^{m} + (2\gamma _{o} - 1)x_{{io}}^{\beta } )z_{i} ,\quad \forall i = 1,...t \\ & p_{j} + q_{{ij}} \ge [e_{{ij}}^{m} + (2\gamma _{{ij}} - 1)e_{{ij}}^{\beta } ](y_{{ij}}^{m} + (2\gamma _{j} - 1)y_{{ij}}^{\beta } )z_{i} ,\quad \forall i = t + 1,...t + s,\forall j = 1,...,n \\ & p_{j} + q_{{ij}} \ge [e_{{ij}}^{m} + (2\gamma _{{ij}} - 1)e_{{ij}}^{\beta } ](x_{{ij}}^{m} - (2\gamma _{j} - 1)x_{{ij}}^{\alpha } )z_{i} ,\quad \forall i = 1,...t,\forall j = 1,...,n \\ & - z_{i} \le w_{i} \le z_{i} ,\quad \forall i = 1,2,...,t + s \\ & p_{j} ,q_{{ij}} \ge 0,\quad \forall i,j \\ & w_{i} \ge 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,...,t + s \\ \end{aligned} $$

(33)

3.7 BWM-RCDEA model with fuzzy perturbation in fuzzy inputs and fuzzy outputs

In this section, a novel BWM-RCDEA model is proposed. Existence of mutual normalization constraint of $\sum\nolimits_{i = 1}^{m + s} {w_{i} } = 1$ in both RCDEA and BWM made it possible to incorporate DMs’ preferences into the proposed BWM-RCDEA model. According to models (32) and (33), the proposed BWM- RCDEA model with fuzzy perturbation for $\gamma \le 0.5$ and $\gamma > 0.5$ can be expressed as models (34) and (35), respectively:

$$ \begin{gathered} \mathop {\max }\limits_{{\gamma _{o} ,\gamma _{i} \le 0.5}} f_{1} = \sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} (y_{{io}}^{m} } + (1 - 2\gamma _{o} )y_{{io}}^{\beta } ) - \theta _{o}^{{CCR}} \sum\limits_{{i = 1}}^{t} {w_{i} (x_{{io}}^{m} - (1 - 2\gamma _{o} )x_{{io}}^{\alpha } )} - \Gamma _{o} p_{o} - \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{io}} } - \sum\limits_{{i = 1}}^{t} {q_{{io}} } \hfill \\ \max \,f_{2} = - \xi \hfill \\ s.t: \hfill \\ \sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} (y_{{ij}}^{m} } - (1 - 2\gamma _{j} )y_{{ij}}^{\alpha } ) - \theta _{j}^{{CCR}} \sum\limits_{{i = 1}}^{t} {w_{i} (x_{{ij}}^{m} + (1 - 2\gamma _{j} )x_{{ij}}^{\beta } )} + \Gamma _{j} p_{j} + \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{ij}} } + \sum\limits_{{i = 1}}^{t} {q_{{ij}} } \le 0,j = 1,...,n \hfill \\ \sum\limits_{{i = 1}}^{{m + s}} {w_{i} } = 1 \hfill \\ p_{o} + q_{{io}} \ge [e_{{io}}^{m} - (1 - 2\gamma _{{io}} )e_{{io}}^{\alpha } ](y_{{io}}^{m} + (1 - 2\gamma _{o} )y_{{io}}^{\beta } )z_{i} ,\quad \forall i = t + 1,...t + s \hfill \\ p_{o} + q_{{io}} \ge [e_{{io}}^{m} - (1 - 2\gamma _{{io}} )e_{{io}}^{\alpha } ](x_{{io}}^{m} - (1 - 2\gamma _{o} )x_{{io}}^{\alpha } )z_{i} ,\quad \forall i = 1,...t \hfill \\ p_{j} + q_{{ij}} \ge [e_{{ij}}^{m} - (1 - 2\gamma _{{ij}} )e_{{ij}}^{\alpha } ](y_{{ij}}^{m} - (1 - 2\gamma _{j} )y_{{ij}}^{\alpha } )z_{i} ,\quad \forall i = t + 1,...t + s,\forall j = 1,...,n \hfill \\ p_{j} + q_{{ij}} \ge [e_{{ij}}^{m} - (1 - 2\gamma _{{ij}} )e_{{ij}}^{\alpha } ](x_{{ij}}^{m} + (1 - 2\gamma _{j} )x_{{ij}}^{\beta } )z_{i} ,\quad \forall i = 1,...t,\forall j = 1,...,n \hfill \\ - z_{i} \le w_{i} \le z_{i} ,\quad \forall i = 1,2,...,t + s \hfill \\ \left| {w_{B} } \right. - a_{{Bi}} \left. {w_{i} } \right| \le \xi {\kern 1pt} ,\quad i = 1,...,t + s \hfill \\ \left| {w_{i} } \right. - a_{{iW}} \left. {w_{W} } \right| \le \xi {\kern 1pt} ,\quad i = 1,...,t + s \hfill \\ p_{j} ,q_{{ij}} \ge 0,\quad \forall i,j \hfill \\ w_{i} \ge 0,\quad {\kern 1pt} i = 1,...,t + s \hfill \\ \end{gathered} $$

(34)

$$ \begin{gathered} \mathop {\max }\limits_{{\gamma _{o} ,\gamma _{i} > 0.5}} f_{1} = \sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} (y_{{io}}^{m} } - (2\gamma _{o} - 1)y_{{io}}^{\alpha } ) - \theta _{o}^{{CCR}} \sum\limits_{{i = 1}}^{t} {w_{i} (x_{{io}}^{m} + (2\gamma _{o} - 1)x_{{io}}^{\beta } )} - \Gamma _{o} p_{o} - \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{io}} } - \sum\limits_{{i = 1}}^{t} {q_{{io}} } \hfill \\ \max \,f_{2} = - \xi \hfill \\ s.t: \hfill \\ \sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} (y_{{ij}}^{m} } + (2\gamma _{j} - 1)y_{{ij}}^{\beta } ) - \theta _{j}^{{CCR}} \sum\limits_{{i = 1}}^{t} {w_{i} (x_{{ij}}^{m} - (2\gamma _{j} - 1)x_{{ij}}^{\alpha } )} + \Gamma _{j} p_{j} + \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{ij}} } + \sum\limits_{{i = 1}}^{t} {q_{{ij}} } \le 0,\quad j = 1,...,n \hfill \\ \sum\limits_{{i = 1}}^{{m + s}} {w_{i} } = 1 \hfill \\ p_{o} + q_{{io}} \ge [e_{{io}}^{m} + (2\gamma _{{io}} - 1)e_{{io}}^{\beta } ](y_{{io}}^{m} - (2\gamma _{o} - 1)y_{{io}}^{\alpha } )z_{i} ,\quad \forall i = t + 1,...t + s \hfill \\ p_{o} + q_{{io}} \ge [e_{{io}}^{m} + (2\gamma _{{io}} - 1)e_{{io}}^{\beta } ](x_{{io}}^{m} + (2\gamma _{o} - 1)x_{{io}}^{\beta } )z_{i} ,\quad \forall i = 1,...t \hfill \\ p_{j} + q_{{ij}} \ge [e_{{ij}}^{m} + (2\gamma _{{ij}} - 1)e_{{ij}}^{\beta } ](y_{{ij}}^{m} + (2\gamma _{j} - 1)y_{{ij}}^{\beta } )z_{i} ,\quad \forall i = t + 1,...t + s,\forall j = 1,...,n \hfill \\ p_{j} + q_{{ij}} \ge [e_{{ij}}^{m} + (2\gamma _{{ij}} - 1)e_{{ij}}^{\beta } ](x_{{ij}}^{m} - (2\gamma _{j} - 1)x_{{ij}}^{\alpha } )z_{i} ,\quad \forall i = 1,...t,\forall j = 1,...,n \hfill \\ - z_{i} \le w_{i} \le z_{i} ,\quad \forall i = 1,2,...,t + s \hfill \\ \left| {w_{B} } \right. - a_{{Bi}} \left. {w_{i} } \right| \le \xi ,\quad {\kern 1pt} i = 1,...,t + s \hfill \\ \left| {w_{i} } \right. - a_{{iW}} \left. {w_{W} } \right| \le \xi ,\quad i = 1,...,t + s \hfill \\ p_{j} ,q_{{ij}} \ge 0,\quad \forall i,j \hfill \\ w_{i} \ge 0,\quad i = 1,...,t + s \hfill \\ \end{gathered} $$

(35)

In models (34) and (35), the constraints belong to both BWM and RCDEA models. Also, the constraint $\left| {w_{B} } \right. - a_{Bi} \left. {w_{i} } \right| \le \xi$ is easily transformed to two linear constraints $w_{B} - a_{Bi} w_{i} \le \xi$ and $a_{Bi} w_{i} - w_{B} \ge \xi$.

Lemma

The models (34) and (35) are feasible.

Proof

Without loss of generality, it is assumed that the $w_{1} = z_{1} = 1$ and other variables are equal to zero except $q_{1j}$. If we find a feasible value for $q_{1j}$, then the model (34) is feasible. Since $w_{1} = z_{1} = 1$, the constraints of the model (34) is as follows:

The first constraint will be as $- \theta_{j}^{CCR} (x_{1j}^{m} + (1 - 2 \times (0.4))x_{1j}^{\beta } ) + q_{1j} \le 0,j = 1,...n$. It is assumed that the $x_{1j}^{\alpha }$ and $x_{1j}^{\beta }$ are 0.05 of the $x_{1j}^{m}$. Also, the $e_{1j}^{\alpha }$ and $e_{1j}^{\beta }$ are 0.05 of the $e_{1j}^{m}$. Hence, the first constraint can be written as $q_{1j} \le 1.01x_{1j}^{m} \times \theta_{j}^{CCR}$. In addition, the 4th and the 6th constraints will be $q_{1j} \ge 0.99e_{1j}^{m} \times 0.99x_{1j}^{m}$ and $q_{1j} \ge 0.99e_{1j}^{m} \times 1.01x_{1j}^{m}$. Therefore $0.99e_{1j}^{m} \times 1.01x_{1j}^{m} \le q_{1j} \le 1.01x_{1j}^{m} \times \theta_{j}^{CCR}$. Since $e_{1j}^{m}$ is the perturbation percentage (for instance $e_{1j}^{m} = 0.05$) and it is a small value, then, we can find a feasible value for $q_{1j} \ge 0.$ Other constraints including the constraints related to BWM are feasible. In a similar way, the model (35) is feasible, too.

The models (34) and (35) are bi-objective programming models which can be solved via some multiple objective programming models such as parametric method, constraint-$\varepsilon$, min–max approach, goal programming and etc. In this paper, the min–max approach has been used for solving models (34) and (35). The min–max approach for bi-objectives of model (34) is as follows:

$$ \begin{gathered} \min {\kern 1pt} {\kern 1pt} \max \left\{ {\left( {f_{1}^{*} - \left[ {\sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} \left( {y_{{io}}^{m} + \left( {1 - 2\gamma _{o} } \right)y_{{io}}^{\beta } } \right)} - \theta _{o}^{{CCR}} \sum\limits_{{i = 1}}^{t} {w_{i} \left( {x_{{io}}^{m} - \left( {1 - 2\gamma _{o} } \right)x_{{io}}^{\alpha } } \right)} } \right.} \right.} \right. \hfill \\ \left. {\left. { - \Gamma _{o} p_{o} - \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{io}} } - \sum\limits_{{i = 1}}^{t} {q_{{io}} } } \right]} \right),\left. {\left( {f_{2}^{*} - [ - \xi ]} \right)} \right\} \hfill \\ \end{gathered} $$

(36)

where $f_{1}^{*}$ and $f_{2}^{*}$ are the ideal values of first and second objective functions. For calculating $f_{1}^{*}$ and $f_{2}^{*}$, the objective functions $f_{1}$ and $f_{2}$ are optimized on the constraints of model (34), separately. In the other words, for obtaining the ideal value for $f_{1}$, the objective function $f_{2}$ is eliminated from the model (34) and the model is solved by using the objective function $f_{1}$. Also, the ideal value for $f_{2}$ is obtained by eliminating the objective function $f_{1}$ from the model (34). It is clear that the min–max (36) is easily converted to a linear model as follows:

$$ \begin{gathered} \min \kappa \hfill \\ s.t: \hfill \\ f_{1}^{*} - \left[\sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} (y_{{io}}^{m} } + (1 - 2\gamma _{o} )y_{{io}}^{\beta } ) - \theta _{o}^{{CCR}} \sum\limits_{{i = 1}}^{t} {w_{i} (x_{{io}}^{m} - (1 - 2\gamma _{o} )x_{{io}}^{\alpha } )} - \Gamma _{o} p_{o} - \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{io}} } - \sum\limits_{{i = 1}}^{t} {q_{{io}} } \right] \le \kappa \hfill \\ f_{2}^{*} - [ - \xi ] \le \kappa \hfill \\ \sum\limits_{{i = t + 1}}^{{t + s}} {w_{i} (y_{{ij}}^{m} } - (1 - 2\gamma _{j} )y_{{ij}}^{\alpha } ) - \theta _{j}^{{CCR}} \sum\limits_{{i = 1}}^{t} {w_{i} (x_{{ij}}^{m} + (1 - 2\gamma _{j} )x_{{ij}}^{\beta } )} + \Gamma _{j} p_{j} + \sum\limits_{{i = t + 1}}^{{t + s}} {q_{{ij}} } + \sum\limits_{{i = 1}}^{t} {q_{{ij}} } \le 0,\quad j = 1,...,n \hfill \\ \sum\limits_{{i = 1}}^{{m + s}} {w_{i} } = 1 \hfill \\ p_{o} + q_{{io}} \ge [e_{{io}}^{m} - (1 - 2\gamma _{{io}} )e_{{io}}^{\alpha } ](y_{{io}}^{m} + (1 - 2\gamma _{o} )y_{{io}}^{\beta } )z_{i} ,\quad \forall i = t + 1,...t + s\,\, \hfill \\ p_{o} + q_{{io}} \ge [e_{{io}}^{m} - (1 - 2\gamma _{{io}} )e_{{io}}^{\alpha } ](x_{{io}}^{m} - (1 - 2\gamma _{o} )x_{{io}}^{\alpha } )z_{i} ,\quad \forall i = 1,...t \hfill \\ p_{j} + q_{{ij}} \ge [e_{{ij}}^{m} - (1 - 2\gamma _{{ij}} )e_{{ij}}^{\alpha } ](y_{{ij}}^{m} - (1 - 2\gamma _{j} )y_{{ij}}^{\alpha } )z_{i} ,\quad \forall i = t + 1,...t + s,\forall j = 1,...,n \hfill \\ p_{j} + q_{{ij}} \ge [e_{{ij}}^{m} - (1 - 2\gamma _{{ij}} )e_{{ij}}^{\alpha } ](x_{{ij}}^{m} + (1 - 2\gamma _{j} )x_{{ij}}^{\beta } )z_{i} ,\quad \forall i = 1,...t,\forall j = 1,...,n \hfill \\ - z_{i} \le w_{i} \le z_{i} ,\quad \forall i = 1,2,...,t + s \hfill \\ \left| {w_{B} } \right. - a_{{Bi}} \left. {w_{i} } \right| \le \xi ,\quad i = 1,...,t + s \hfill \\ \left| {w_{i} } \right. - a_{{iW}} \left. {w_{W} } \right| \le \xi ,\quad i = 1,...,t + s \hfill \\ p_{j} ,q_{{ij}} \ge 0,\quad \forall i,j \hfill \\ w_{i} \ge 0,\quad i = 1,...,t + s \hfill \\ \end{gathered} $$

(37)

The linear BWM- RCDEA model (37) is solved and the optimal weights ($w_{1}^{*} ,...,w_{m}^{*} ,w_{m + 1}^{*} ,...,w_{m + s}^{*}$) are obtained for inputs and outputs. Then, the efficiency score of DMUo for $\gamma \le 0.5$ is calculated by Eq. (38).

$$ \theta_{{o,\gamma_{o} \le 0.5}}^{BWM - RCDEA} = \frac{{\sum\limits_{i = m + 1}^{m + s} {w_{{_{i} }}^{*} } [y_{io}^{m} + (1 - 2\gamma_{o} )y_{io}^{\beta } ]}}{{\sum\limits_{i = 1}^{m} {w_{{_{i} }}^{*} } [x_{io}^{m} - (1 - 2\gamma_{o} )x_{io}^{\alpha } ]}} $$

(38)

According to the above way, for $\gamma > 0.5$, the bi-objective model (35) can be transferred to linear models and the efficiency score of DMUo can be calculated as follows:

$$ \theta_{{o,\gamma_{o} > 0.5}}^{BWM - RCDEA} = \frac{{\sum\limits_{i = m + 1}^{m + s} {w_{{_{i} }}^{*} } [y_{io}^{m} - (2\gamma_{o} - 1)y_{io}^{\alpha } ]}}{{\sum\limits_{i = 1}^{m} {w_{{_{i} }}^{*} } [x_{io}^{m} + (2\gamma_{o} - 1)x_{io}^{\beta } ]}} $$

(39)

4 Illustrative application

In this section, data of 39 electricity distribution companies in Iran is collected and companies are evaluated through the proposed BWM-RCDEA model. Iranian distribution companies are run under supervision of TAVANIR Company (Iran Power Generation, Transmission and Distribution Management Company). TAVANIR was established in 1992 and is responsible for development of electricity power generation, transmission and distribution in Iran. Performance assessment of electricity distribution companies is very important from variety of aspects, especially service to customers and their satisfaction, selling electricity as an economic commodity at a lower cost, development of distribution network for covering the vast surface of the country and reduce electricity failure.

In order to evaluate efficiency of electricity distribution companies, first input and output variables must be selected. Since there is no firm consensus on which variables best describe the operation of distribution utilities, in literature, different variables have been selected. For instance, Petridis et al. (2019) evaluated 20 Turkish electric distribution companies using a network DEA model with criteria of number of staff, net consumption, length of cables, installed capacity as inputs, energy supply as intermediate and energy loses, annual faults and disruption, number of customers and number of towns/villages as desirable and undesirable output variables. Çelen and Aydin (2012) evaluated 21 electricity distribution companies in Turkey. They applied number of employees, length of the distribution line and transformers capacity as inputs and quality of service, number of customers and quantity delivered as outputs. Also, Çelen (2013) evaluated 21 distribution utilities in Turkey between years 2002–2009. Variables of number of employees, length of the distribution line, transformer capacity and quality of electricity considered as inputs and variables of electricity delivered and number of customers as outputs. Tavassoli et al. (2015) selected the number of employees, network length and transmission capacity as inputs and unit delivery and service area as outputs of their research. Moreover, Azadeh et al. (2015) evaluated Iranian distribution companies using network length, transport capacity and the number of employees as inputs while number of customers and total electricity sales are chosen as stochastic outputs. In other research for evaluating Iranian distribution units, Sadjadi and Omrani (2008) adopted number of employees, transformers capacity and network length as inputs and number of customers and total electricity sales as outputs. And finally, Omrani et al., (2020) for evaluating 39 electricity distribution companies in Iran, used four inputs of number of employees, service area network length, and, transformers capacity and three outputs of number of customers, energy delivery, and total electricity sales.

As it can be seen, different variables have been selected by different researchers. In this study, the most frequent variables in the literature are selected. For this purpose, four inputs including service area (km²), number of employees, transformers capacity (Mega Volt Amp) and network length (km) and three outputs including energy delivery (million KWh), number of customers (*1000) and total electricity sales (million KWh) are selected. Our data series involves annual data on 39 companies observed in 2017. These data are retrieved from Iran Ministry of Energy, TAVANIR Company (www.tavanir.org.ir) and presented in Table 2. It should be noted that since robust optimization is sensitive to normalization, data are normalized and presented in interval [0, 1].

Table 2 Data of electricity distribution companies for year 2017

5 Results and discussions

In this section the result of applying the proposed model has been presented. Indeed, electricity companies’ efficiency scores evaluated in three phases. In the first phase, a DEA model has been applied to estimate the efficiency scores of companies. Then considering data as fuzzy sets, and considering perturbation in constructing fuzzy sets, RCDEA model with and without fuzzy perturbation in fuzzy inputs and fuzzy outputs results are calculated. Finally, in the third phase, DMs’ preferences and judgments on input and output variables are incorporated into the RCDEA models and BWM-RCDEA models are generated. The results of implementing each phase of the proposed model are discussed below.

5.1 DEA results

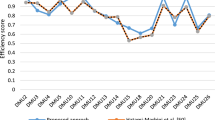
The results of conventional DEA model are presented in Table 3 and Fig. 1. According to the results, the efficiencies of 10 companies are equal to one. In other words, these 10 companies technically are efficient in converting inputs to outputs and form the efficient frontier. On the other hand, companies with efficiency scores less than 1 are inefficient and among inefficient units, Ilam has the worst performance with the score of 0.6351. Also, Gharb-e-Mazandaran with the score of 0.6685 and Golestan with the score of 0.6750 are the second and the third worst performance units respectively. As it can be observed from the Table 3, DEA is unable to rank all DMUs and low distinguish power of DEA is the weakness of this popular model to evaluate efficiency scores. Moreover, DEA uses only data to calculate efficiencies, and DMUs are free to find the best combination of input and output variables for reaching the efficient frontier. Finally, the mean of efficiency scores is 0.8681 which is more than both RCDEA and BWM-RCDEADEA results.

Table 3 Results of DEA and RCDEA with and without fuzzy perturbation in fuzzy inputs and outputs

Fig. 1

The scores generated by RCDEA model

5.2 RCDEA results

RCDEA results has been shown in the Table 3. Initially, in order to obtain RCDEA results, some parameters should be set. First, without losing any generality, it is assumed that $\gamma = \gamma_{i} = \gamma_{r}$. So, for different $\gamma$ ($\gamma \le 0.5$ and $\gamma > 0.5$) either model (23) or (26) can be applied. In this paper, proposed model is implemented for $\gamma = 0.4$ and $\gamma = 0.8$ respectively. The mean value of L-R fuzzy numbers (m) are considered as data reported in Table 2 after normalizing. In addition, the left and right spreads ($\alpha ,\beta$) are 0.05 of the mean value. It is assumed that in determining mean values, there is 0.03 perturbation, and this uncertainty degree is exact. Furthermore, to ensure full protection of model, budget of uncertainty parameter, $\Gamma$, is set equal 7 for all constraints. Indeed, model is immune if 100% of uncertain parameters take their worst-case value.

According to the results for $\gamma = 0.4$, although all scores get reduced than DEA model but ranking has not change tangibly and is almost the same with the DEA model. Since it is considered the same level of robustness and fuzziness for all data, hence, efficiency scores decreased by almost the same proportion. For example, units with the score of 1, in a new evaluation get the score of 0.9802 and like DEA model 10 companies have the best performance. On the other hand, on the bottom of the Table 3, Ilam, Gharb-e-Mazandaran and Golestan with the scores of 0.6115, 0.6452 and 0.6518 have the weakest performance, respectively. Moreover, the mean of all scores is 0.8425, which implies that model in order to keep constraints immune against uncertainty, releases the optimal solutions and scores get lower values to keep the model feasible.

Also, RCDEA model is implemented for $\gamma = 0.8$ and efficiencies are evaluated using model (31). According to the results, scores are lower than both DEA and RCDEA for $\gamma = 0.4$. However, units’ ranking has not changed significantly and is almost the same with previous two models. For example, top efficiency score is 0.8352 for 10 companies and the lowest score is 0.5210 which belongs to the Ilam. The mean of scores is 0.7173, which is lower than both DEA and RCDEA for $\gamma = 0.4$.

5.3 RCDEA with fuzzy perturbation results

To observe the impact of uncertainty on the perturbation level, the results of RCDEA model are recalculated considering fuzzy perturbation. The results are presented in the Table 3 and Fig. 1. According to the results, for $\gamma \le 0.5$ with fuzzy perturbation, efficiency scores show slight increase, and for $\gamma > 0.5$ with fuzzy perturbation scores indicate slight decrease in comparison with RCDEA models with exact perturbation. For instance, for $\gamma \le 0.5$ with fuzzy perturbation, best companies get the score of 0.9808 which is more than $\gamma \le 0.5$ with exact perturbation model results. Also, the mean of efficiency scores is 0.8467. The reason for increasing efficiency scores is that considering fuzzy data for perturbation values lead to decrease in value of perturbation and resulted in increase in efficiency scores. In the other words, when uncertainty level decreases, model keeps optimal solutions and is closer to conventional deterministic DEA model results.

In contrast, considering fuzzy sets for perturbation value for $\gamma > 0.5$, resulted in decreasing efficiency scores and consequently decrease in the mean of scores to 0.7158. Indeed, model to keep constraints against increase in uncertainty level releases optimal solutions. It should be noted that since uncertainty considered the same for all inputs, outputs and perturbation values, rankings remained almost unchanged in models.

5.4 BWM- RCDEA Results

In order to reduce input and output weights flexibility and to incorporate DMs’ judgement into the evaluations, a novel BWM- RCDEA model is applied and efficiency scores for electricity distribution companies are re-calculated. In this regard, a preference vector is designed according to the opinions of a team of experts consist of three members with sufficient experiences at the Azarbaijan Gharbi company. The values are outcome of the mentioned team closely working and are acceptable for all team members. Table 4 presents the best, the worst criteria and preference values of the best criterion over all criteria and preference of all criteria over the worst criterion.

Table 4 Preference values of best criterion over all criteria and all criteria over worst criterion

After determination of preferences’ vector, obtained BWM model is incorporated into the RCDEA model and a bi-objective BWM- RCDEA models (34) and (35) are obtained. Then the bi-objective models are solved with pre-defined parameters (Sect. 5.2, first paragraph) using min–max approach (37) and results are shown in the Table 5 and Fig. 2.

Table 5 Results of DEA and BWM- RCDEA models with and without fuzzy perturbation

Fig. 2

The score generated by BWM- RCDEA model

According to the results for $\gamma = 0.4$ with fuzzy perturbation, Tehran Bozorg and Ahwaz units with the score of 0.9802 have the best performance and are followed by Alborz and Mashhad with efficiency scores of 0.8371 and 0.7814 respectively. In contrary, Khorasan-e- Jonubi with the score of 0.1801 has the worst performance in converting inputs to outputs. Khorasan-e-Shomali with the score of 0.2260 is the second and Jonub-e-Kerman with the score of 0.2554 is the third worst performance among 39 companies. As it can be seen, the proposed model is able to rank DMUs almost fully and has improved the distinguish power of conventional DEA dramatically. Furthermore, the efficiency scores get reduced meaningfully, because we have added new constraints into the proposed BWM- RCDEA model and under such circumstance, results will not improve. Therefore, the mean of scores is 0.4510, which is less than RCDEA model results for $\gamma = 0.4$. Results imply that the preferences of DMs have a significant impact on the efficiencies, since data are normalized and higher weights for variables can subjectively modify the efficiencies.

According to the BWM- RCDEA results for $\gamma = 0.8$, again, Tehran Bozorg and Ahwaz with the efficiency score of 0.8352 has the best performance among 39 companies. Alborz unit with the score of 0.7161 is ranked second and is followed by Mashhad with the score of 0.6703. At the bottom of the ranking Khorasan-e- Jonubi with the score of 0.1539 has the weakest performance. Khorasan-e- Shomali with the score of 0.1923 has the second worst performance and Jonub-e-Kerman with the score of 0.2183 has the third weakest performance among 39 units. The other units’ performances get reduced than BWM- RCDEA results for $\gamma = 0.8$ with fuzzy perturbation, however, ranking has not changed dramatically in comparison with BWM-RCDEA model with $\gamma = 0.4$. In overall, distinguish power of DEA has been improved significantly and model is able to immune constraints and objective function against uncertainty obviously. Furthermore, using both data and DMs’ preferences in evaluations leads to a more precise and reliable ranking. Like RCDEA model, to observe the fuzziness impact on the perturbation degree results, we have implemented BWM-RCDEA with considering exact values for perturbation and reported results in the Table 5. Results approve that ignoring fuzziness of perturbation lead decrease in scores for $\gamma \le 0.5$ model in comparison with BWM- RCDEA model with fuzzy perturbation in fuzzy inputs and outputs. Also considering exact value for perturbation for $\gamma > 0.5$ resulted in increase in scores and the mean of scores in comparison with BWM- RCDEA model with fuzzy perturbation. To present the differences of scores generated by different models without and with fuzzy perturbation, the scores are depicted in Figs. 3 and 4, respectively.

Fig. 3

The scores generated by different models with exact perturbation value (e = 0.03)

Fig. 4

The scores generated by different models with fuzzy perturbation value

For investigating the relationship between the results of the DEA, RCDEA, RCDEA with fuzzy perturbation, BWM-RCDEA and BWM-RCDEA with fuzzy perturbation, we perform Pearson correlation test between efficiency scores and Spearman correlation test between ranks. The results for $\gamma = 0.4$ are presented in the Tables 6 and 7. As can be seen in Tables 6 and 7, the both correlations are significant at the 0.01 level.

Table 6 Pearson correlation test among different models

Table 7 Spearman correlation test among different models

5.5 Sensitivity analysis

Here, sensitivity analysis is performed on parameters such as $\gamma$, $\Gamma$ and $e$. For sensitivity analysis, we consider two scenarios for each parameter and compare the results. For example, for perturbation degree, $e$, we consider the perturbation equal to 0.05, solve the model and compare the results with our initial 0.03. Likewise, we run the model for different values of the,$\gamma$ and $\Gamma$. The results are presented in the Tables 8 and 9, respectively. The results indicate that by increasing perturbation degree ($e$), efficiency scores get lower. Also, by decreasing the budget of uncertain parameters in each constraints ($\Gamma$), efficiencies get higher scores and by increasing value for $\gamma$ in the model (37), scores take lower values. Moreover, by decreasing values for $\gamma$ in the case $\gamma > 0.5$, for example $\gamma = 0.6$, scores take higher values than RCDEA model for $\gamma = 0.8$.

Table 8 Sensitivity analysis for RCDEA with $\gamma \le 0.5$

Table 9 Sensitivity analysis for RCDEA with $\gamma > 0.5$

6 Recommendations for policy makers

In this section, according to the BWM- RCDEA results recommendations have been made for decision makers. In this regard, the average weight of criteria has been calculated after implementing BWM- RCDEA model and results are indicated in the Table 10.

Table 10 Weights of criteria

According to the Table 10, energy delivery has the least impact on the evaluations and in contrary, total electricity sale is the most important criterion. Units, in order to increase their efficiencies are better to put their attention to sale energy and generate energy from available and cheap resources such as renewable sources. For example, small sized power plants which are closer to customers, not only needs less network length, but also increases the outputs simultaneously. Also, renewing distribution infrastructures to improve energy delivery will lead to increase efficiencies of electricity distribution companies. Specifically, for Khorasan-e-Jonubi, Khorasan-e-Shomali and Jonub-e-Kerman that sale less electricity for customers because of small populations (located in desert areas with less population density), and it is almost impossible to increase their outputs substantially, decreasing the number of employers and network length by constructing small sized renewable resources may improve their efficiency.

7 Conclusion

In real competitive markets, performance evaluation is crucial for companies to know their strengths and weaknesses to set appropriate policies for improving their efficiencies. Distribution companies’ performance evaluation is considered crucial issue for regulators. In this study, we applied a novel approach of BWM- RCDEA model to investigate efficiency scores of 39 electricity distribution companies in Iran. Indeed, beside of considering uncertainty in data as fuzzy sets and uncertainty in constructing fuzzy sets as robust optimization with fuzzy perturbation, DMs’ preferences were incorporated into DEA model, too. The proposed bi-objective model was solved using min–max approach. As results, the proposed model improves the distinguish power of DEA and results are more reliable and precise than conventional DEA. Also, recommendations were proposed for decision makers to improve units’ efficiencies. In summary, due to the importance of total electricity sale criterion on the efficiency evaluations, generating energy from convenient and cheap resources may lead to increase in electricity sale and consequently improving performances. For future studies, the BWM model can be combined with other DEA models such as supper-efficiency DEA, additive models and etc. Also, researchers can consider DMs’ judgments as fuzzy numbers and fuzzy BWM model can be combined with the DEA models. Also, developing group BWM-DEA for considering the preferences of multiple DMs is very important in this field. Finally, for dealing with real worlds problem with integer variables, such as number of customers, the mixed integer model of BWM-RCDEA could be applied.