A Lagrangian relaxation algorithm for optimizing a bi-objective agro-supply chain model considering CO₂ emissions

Abstract

In this research, an agro-supply chain in the context of both economic and environmental issues has been investigated. To this end, a bi-objective model is formulated as a mixed-integer linear programming that aims to minimize the total costs and CO₂ emissions. It generates the integration between purchasing, transporting, and storing decisions, considering specific characteristics of agro-products such as seasonality, perishability, and uncertainty. This study provides a different set of temperature conditions for preserving products from spoilage. In addition, a robust optimization approach is used to tackle the uncertainty in this paper. Then, $\varepsilon$-constraint method is used to convert the bi-objective model to a single one. To solve the problem, Lagrangian relaxation algorithm is applied as an efficient approach giving lower bounds for the original problem and used for estimating upper bounds. At the end, a real case study is presented to give valuable insight via assessing the impacts of uncertainty in system costs.

1 Introduction

Agricultural products are introduced as a sub-class of fresh products with several particular attributes such as seasonality, perishability, long procurement time, and inherent uncertainty. Agro-products have a short lifetime and incur quality loss along the supply chain. According to Widodo et al. (2006), 20% through 60% of agro-products are losses across the supply chain in any country. These losses impose additional costs on the supply chain, which is about US$ 310 billion in developing countries (Dora et al. 2019). Generally, inefficient management is identified as a reason behind the increasing losses and costs of the agro-supply chain. In this respect, Jonkman et al. (2019) claimed 31% of agro-products in Europe are food losses due to inefficient management in the production process. Hence, recently, a need for good management of agro-supply chains has appeared to address both economic and environmental issues through designing and planning the supply chains.

Regarding good management of postharvest activities such as purchasing, transporting, and storing agro-products can significantly reduce quality and quantity losses (Yu and Nagurney 2013; Bourlakis and Weightman 2004). Indeed, dispersed suppliers and distributors with long-distance transportation, and excessive warehouses lead to an increase in food losses, that is what illustrates the pivot role of agro-supply chain management (Yu et al. 2020). On the other hand, food losses lead to the waste of million tonnes of resources and CO₂ emissions (Yakavenka et al. 2019). Therefore, one point of this paper is to incorporate supplier selection, and operational decisions in order to achieve profitability and sustainability in the supply chain. As a result, first, a decision should be made to select better suppliers in terms of quality grade and purchasing cost of products, and transportation distance. Besides, quality preservation during operations and activities becomes the most critical issue to eliminate food losses and decrease energy costs, and assure the desire quality level of agricultural products over unavailable harvesting seasons. To this end, different refrigerators with multi-temperature conditions in both transportation vehicles and storage rooms can constitute as important logistic activities for quality preservation or degradation. Furthermore, facility-location models can play an important role to aid operations and activities in agro-supply chains, among which rapid delivery of products may considerably affect mitigating quality degradation (Morganti and Gonzalez-Feliu 2015).

On the other hand, a review of the literature shows a lot of inherent uncertainties in the agro-supply chain, that naturally, it is impossible to accurately make forecast the values of them. Accordingly, efficient management of these uncertainties can play an important role to cope with enormous costs, lost sales, and quality decay along the supply chain. In this regard, a method should be utilized to deal with uncertainty with a lack of available information in agro-supply chain models. A Robust optimization method is proposed to cope with this uncertainty that is applied in existent studies in the field of agricultural products such as Paul and Wang (2015), Behzadi et al. (2017), Xu et al. (2020).

All above problems in the agro-supply chain including supplier selection, transportation decisions, storage room selection, facility location models, and robust optimization method have been addressed as hot topics due to specific characteristics of the agro-supply chain that some of which can be found in Costa et al. (2014), Accorsi et al. (2017), Atabaki and Aryanpur (2018), Sazvar et al. (2018), Roghanian and Cheraghalipour (2019), Naderi et al. (2020).

In this paper, a bi-objective mathematical model has been proposed under the uncertainty condition with the aim of minimizing the system costs and CO₂ emissions with respect to purchasing, facility location, inventory, and transportation decisions, and some operational constraints. A robust optimization approach is used due to unavailable probabilistic information. Then in order to evaluate the performance of the proposed model, first, $\varepsilon$-constraint is used to convert the bi-objective model to a single-objective one. Then, Lagrangian relaxation-based algorithm (LRA) is applied to solve the MILP problem. The results of the LRA are compared to the obtained solutions by CPLEX solver in terms of computational time and objective function values in order to validate the LRA. Finally, a real-life case study is applied and implemented to verify the applicability of the suggested model.

In the rest of the paper, Sect. 2 reviews papers related to agro-supply chain models. In Sect. 3, notations, assumptions, and the mathematical model are described. In Sect. 4, the solution approach is presented according to the mathematical model. In Sect. 5, results are summarized. Finally, Sect. 6 gives conclusions and some future directions.

2 Literature review

Although the recent trends in the concept of the abovementioned research type on the agro-supply chain have increased, it is still an interesting hot topic for further studies. Accordingly, the current study provides a global perspective by reviewing the literature in order to identify the necessity of this research and related gaps.

Over the last decades, Kusumastuti et al. (2016), Paam et al. (2016), Ganesh Kumar et al. (2017), have comprehensively reviewed details in the agro-supply chain. The related literature relies on the combination of economic and environmental issues in agro-supply chain models. Among these studies, Paul and Wang (2015) presented a robust agro-supply chain problem with multiple commodities supplied by different suppliers who offer the price of transporting the commodities based on freight terms. The motivation of their work was to address uncertainty in their optimization model. Ghezavati et al. (2017) investigated the quality degradation of agro-products in fridge facilities over their shelf life. The aim of their research was to maximize the total profit under the quality dependent price in the multi-period model. Banasik et al. (2017) investigated both economic and environmental impacts on a multi-level mushroom supply chain including factories and growers. Besides, losses due to diseases were taken into consideration in computing the total disposal and assessing its effects in their proposed model. Behzadi et al. (2017) studied risk-focused agro-supply chains in which robust and resilient strategies should be selected in a way to manage the risk of uncertainty and maximize the total profit. Then, managerial insights were provided in terms of evaluating the effects of strategies on harvest time and yield disruption, and benefits. Soto-Silva et al. (2017) formulated two optimization models which incorporated decisions on purchasing, transporting, and storing products considering three types of refrigerator technologies. Products were stored in each storage room to segregate their shelf lives accordingly. Then, they integrated both optimization models to compare the obtained results. Orjuela-Castro et al. (2017) proposed a multi-product MILP model for optimizing the transportation and distribution decisions that contributed to the temperature and humidity changes affecting losses in all levels of the agro-supply chain. Liu et al. (2018) considered a dynamic inventory problem for a seasonal agro-supply chain. In their model, a decision has been made on the amount of agro-product over harvesting seasons where the demand is dependent on the price of selling in the present and previous periods. Tsang et al. (2018) examined an intelligent food supply chain model in which the application of the Internet of Things was suggested for monitoring the food boxes. Their method has been added to the traditional refrigerated distribution which is not enough powerful in controlling the environmental condition to keep the agro-products. Besides they proposed a distribution mixed-integer non-linear programming (MINLP) model with the assumption of the cooling time of the window. Paam et al. (2018) proposed an agro-supply chain model with the aim of minimizing the total cost of systems where different refrigerator technologies were suggested for determining the shelf life of products under different scenarios. Thereafter, their model has been investigated by Paam et al. (2019) in a real case study. Li et al. (2020) considered perishability in a food supply chain for analyzing the effects of package selection in the shelf life of agro-products to make profits in storing the inventory, routing, and distribution planning. They used a hybrid metaheuristic algorithm for solving their proposed MILP model.

Another stream in reviewing the agro-supply chain models is to face environmental issues with respect to their specific characteristics. On this basis, Allaoui et al. (2018) proposed a two-stage food supply chain model considering economic, environmental, and social issues. In the first stage, a set of suppliers has been evaluated in terms of different types of indicators in order to select suppliers, which is used to solve the presented mathematical model in the second stage with the aim of optimizing two conflicting objective function values. Sazvar et al. (2018) presented an agricultural model regarding both economic and environmental impacts on adopting the optimal policies in minimizing the total system costs, CO₂ emissions, and maximizing social health. They also considered both conventional and organic agro-products. In their model, inventory of organic products can be used when conventional products face inventory shortages. Bortolini et al. (2018) investigated the effects of fresh food packaging in a closed-loop supply chain model in order to balance the disposable and reusable containers. They attempted to optimize a three-level mathematical model with two conflicting objectives dealing with both economic and environmental impacts on different network configurations. Jonkman et al. (2019) proposed an agro-supply chain considering both perishability and deterioration over the storage time of agro-materials with two conflicting objectives including profit maximization and CO₂ minimization. Moreover, their research has addressed pre-harvest and post-harvest activities to select the area of land, facilities location, inventory, and transportation decisions. Roghanian and Cheraghalipour (2019) developed a mathematical model which was presented by Cheraghalipour et al. (2018). They considered transportation and facility location decisions in a supply chain with the aim of minimizing the system costs and CO₂ emissions.

The current study has been classified in subsections with respect to perishability, economic, and environmental impacts of agricultural products in a supply chain that Table 1 illustrates the related gaps and the main contributions of this research.

Table 1 Literature review

The following contributions could be revealed through the current research.

• There are a small number of studies that have addressed both quality and quantity deterioration in the agro-supply chain problems. In this research, in order to adapt to real conditions, simultaneous quality and quantity deterioration are considered in the agro-supply chain model.

• The impact of temperature conditions on the shelf life of products is one of the key issues in this paper that has rarely been addressed in the literature review. Therefore, temperature conditions in refrigerators must be chosen somehow to maintain long-term agricultural products taking into consideration economic and environmental impacts.

• Although some researchers have dealt with supplier selection, inventory decisions, vehicle decisions, location-allocation models, separately; this paper incorporates all these issues in a mathematical model considering the special characteristics of agricultural products, such as seasonality and perishability.

• The studies in the field of agro-supply chain models reveal a lack of historical data to cope with the inherent uncertainty. Motivated by this concern, a robust approach is proposed to deal with uncertainty in demand rate and loss factors.

• In this paper, a Lagrangian relaxation-based algorithm is applied in order to obtain proper lower and upper bounds.

3 Problem description and analytic model

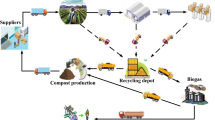
This paper presents a multi-period problem and indicates constraints and variables related to purchasing products, transportation decisions, facility location, and inventory planning after harvesting fresh products. Figure 1 depicts a schematic of the proposed agro-supply chain, in which different quality grades of agro-products are purchased from farmers to be sent to the warehouses. In this respect, decisions on the location of warehouses and operations and activities under different temperature conditions should be made.

Fig. 1

Schematic of the discussed problem

This paper deals with the economic and environmental aspects of losses generated by agro-products in post-harvest activities. Moreover, this problem relies on the uncertainty in the loss factors and demand of customers due to unavailability of enough information. In the following, model assumptions are provided in an agro-supply chain.

• Products with different quality grades are purchased from farmers that may have different shelf lives.

• Products are stored in different cold storage rooms under different temperature conditions. Therefore, products are segregated in terms of their shelf life.

• Each temperature condition in storage rooms generates different amount of CO₂.

• There are various quality degradation patterns. In this paper, a constant deterioration rate has been considered such as Parichehr Paam (2019) that can be seen in Fig. 2.

• Different types of vehicles can be used for transporting products from farmers to warehouses.

Fig. 2

Presentation of both quality and quantity degradation over the shelf life of products

3.1 Mathematical model

In this section, a MILP problem is proposed with the aim of optimizing two conflicting objective functions. The first objective function minimizes the total cost of the agro-supply chain and the second objective function minimizes the carbon emissions to the environment. All used notations throughout the mathematical model are introduced as follows:

3.1.1 Indices

$j$: Index of farmers, where $j = \left\{ {1, 2, \ldots , J} \right\}$.

$i, i^{\prime}$: Index of different quality grades of products, where $i = \left\{ {1, 2, 3} \right\}$.

$w$: Index of potential warehouses, where $w = \left\{ {1, 2, \ldots , W} \right\}$.

$v$: Index of number of storage rooms, where $v = \left\{ {1, 2, \ldots , V} \right\}$.

$c$: Index of different temperature conditions, where $c = \left\{ {1, 2, \ldots , C} \right\}$.

$k$: Index of vehicles, where $k = \left\{ {1, 2, \ldots , K} \right\}$.

$t$: Index of time periods, where $t = \left\{ {1, 2, \ldots , T} \right\}$.

$g$: Index of time periods, where $g = \left\{ {1, 2, \ldots ,TE_{iwvct} } \right\}$.

3.1.2 Parameters

$CT_{jw}$: Cost of transporting products from farmer $j$ to warehouse $w$.

$DS_{jw}$: Distance between farmer $j$ and warehouse $w$.

$O_{w}$: Operational cost in warehouse $w$.

$H_{c}$: Holding cost of products in warehouses controlled under the temperature condition $c$.

$CF_{k}$: Fixed cost of transporting products by vehicle type $k$.

$FW_{w}$: Fixed cost of establishing warehouse $w$.

$CW_{w}$: Capacity of each storage room in warehouse $w$.

$NW_{w}$: Available number of storage rooms in warehouse $w$.

$CV_{k}$: Capacity of loading vehicle type $k$.

$CQ_{ij}$: Purchasing cost of product with quality grade $i$ from farmer $j$.

$T_{ic}$: Shelf life of product with quality grade $i$ if it is stored in temperature condition $c$.

$\tilde{D}_{it }$: Demand for product $i$ in time period $t$.

$\widetilde{LF}_{ij}$: Loss factor of product $i$ purchased from farmer $j$.

$a_{t}$: Binary parameter indicating the harvesting periods.

$\delta_{i}$: The minimum acceptable quality level for product $i$ during the phase of deterioration.

$CK_{k}$: The CO₂ emission from vehicle type $k$ per km.

$CO_{i}$: The CO₂ emission from per tonne of product losses.

$EM_{c}$: The CO₂ generation by processing per tonne of stored crops under temperature condition $c$

$DE_{ic}$: Deterioration rate of product $i$ under temperature condition $c$

M: A large positive number.

3.1.3 Variables

$Q_{ijt}$: Quantity of product $i$ purchased from farmer $j$ in time period $t$.

$QF_{ijwvct}$: Quantity of product $i$ purchased from farmer $j$ to be stored in warehouse $w$ in storage room $v$ under temperature condition $c$ in time period $t$.

$QW_{iwvctg}$: Quantity of product $i$ stored in warehouse w in storage room $v$ under the temperature c in time period g to be used in time period $t$.

$I_{iwvctg}$: Inventory level of product $i$ stored in warehouse $w$ in storage room $v$ under the temperature $c$ in time period $g$ remaining until to time period $t$.

$LO_{iwvctg}$: Losses of product $i$ stored in warehouse $w$ in storage room $v$ under the temperature $c$ in time period $g$ remaining until to time period $t$.

$y_{kjwt}$: Number of vehicle type $k$ used for transporting products from farmer $j$ to warehouse $w$ in time period t.

$TE_{iwvct}$: Storage time for product $i$ in warehouse $w$ in storage room v under temperature condition $c$ in time period $t$.

$AC_{iwvct}$: Binary variable equals 1, if product $i$ is stored in warehouse $w$ in storage room $v$ under temperature condition $c$ in time period $t$.

$AW_{w}$: Binary variable equals 1, if a warehouse $w$ is established.

$Z_{iwvctg}$: Binary variable equals 1, if product $i$ is in warehouse $w$ in storage room v under temperature condition $c$ in time period $g$ and expires during time period $t$.

$TC$: Total costs of agro-supply chain.

$EQ$: Total carbon emissions throughout the supply chain

$$ \begin{aligned} Min\,TC & = \mathop \sum \limits_{i} \mathop \sum \limits_{j} \mathop \sum \limits_{t} a_{t} CQ_{ij} Q_{ijt} + \mathop \sum \limits_{i} \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{c} \mathop \sum \limits_{t} \mathop \sum \limits_{g} O_{w} QW_{iwvctg} + \mathop \sum \limits_{w} FW_{w} AW_{w} \\ & \quad + \mathop \sum \limits_{i} \mathop \sum \limits_{j} \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{c} \mathop \sum \limits_{t} CT_{jw} QF_{ijwvct} + \mathop \sum \limits_{k} \mathop \sum \limits_{j} \mathop \sum \limits_{w} \mathop \sum \limits_{t} CF_{k} y_{kjwt} + \mathop \sum \limits_{i} \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{c} \mathop \sum \limits_{t} \mathop \sum \limits_{g} H_{c} I_{iwvctg} \\ \end{aligned} $$

(1)

$$ \begin{aligned} Min\,EQ & = \mathop \sum \limits_{i} \mathop \sum \limits_{j} \mathop \sum \limits_{t} a_{t} CO_{i} \widetilde{LF}_{ij} Q_{ijt} \\ & \quad + \mathop \sum \limits_{i} \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{c} \mathop \sum \limits_{t} \mathop \sum \limits_{g} CO_{i} LO_{iwvctg} \\ & \quad + \mathop \sum \limits_{j} \mathop \sum \limits_{w} \mathop \sum \limits_{k} \mathop \sum \limits_{t} CK_{k} DS_{jw} y_{jwkt} \\ & \quad + \mathop \sum \limits_{i} \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{c} \mathop \sum \limits_{t} EM_{c} AC_{iwvct} \\ \end{aligned} $$

(2)

$$ \mathop \sum \limits_{i} \mathop \sum \limits_{c} AC_{iwvct} \le 1 \forall w \in W;v \in V;t \in T $$

(3)

$$ TE_{iwvct} \le T_{ic} AC_{iwvct} \forall i \in I;w \in W;v \in V; c \in C;t \in T; $$

(4)

$$ \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{c} QF_{ijwvct} \le a_{t} Q_{ijt} \left( {1 - \widetilde{LF}_{ij} } \right) \forall i \in I;j \in J;t \in T $$

(5)

$$ I_{iwvctg} = \mathop \sum \limits_{j} QF_{ijwvct} - QW_{iwvctg} \quad \forall i \in I;w \in W;v \in V;c \in C;t \in T; t = g $$

(6)

$$ LO_{iwvctg} = DE_{ic} I_{iwvctg } \forall i \in I;w \in W;v \in V;c \in C;t \in T;where g < t $$

(7)

$$ 1 - DE_{ic} TE_{iwvct} \ge \delta_{i} \forall i \in I;w \in W;v \in V;c \in C;t \in T $$

(8)

$$ \mathop \sum \limits_{j} QF_{ijwvct} + \mathop \sum \limits_{g} I_{iwvct - 1g} \ge \mathop \sum \limits_{g} QW_{iwvctg} \quad \forall i \in I;w \in W;v \in V;c \in C;t \in T; where t > 1 $$

(9)

$$ \mathop \sum \limits_{j} QF_{ijwvct} + \mathop \sum \limits_{g} I_{iwvcst - 1g} \le CW_{w} AC_{iwvct} \quad \forall i \in I;w \in W;v \in V;c \in C;t \in T; where t > 1 $$

(10)

$$ \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{c} \mathop \sum \limits_{g} QW_{iwvctg} \ge \tilde{D}_{it} \quad \forall i \in I; t \in T ;where g < t $$

(11)

$$ \mathop \sum \limits_{i} \mathop \sum \limits_{v} \mathop \sum \limits_{c} AC_{iwvct} \le NW_{w} AW_{w} \quad \forall w \in W;t \in T; $$

(12)

$$ \mathop \sum \limits_{i} \mathop \sum \limits_{v} \mathop \sum \limits_{c} QF_{ijwvct} \le \mathop \sum \limits_{k} CV_{k} y_{kjwt} \quad \forall j \in J;w \in W;t \in T $$

(13)

$$ t - g - TE_{iwvcg} \le M Z_{iwvctg} \quad \forall i \in I;w \in W;v \in V;c \in C;t \in T;g \in T;where g < t $$

(14)

$$ I_{iwvctg} \le M\left( {1 - Z_{iwvctg} } \right)\quad \forall i \in I;w \in W;v \in V;c \in C;t \in T;g \in T; ;where g < t $$

(15)

$$ QW_{iwvctg} \le M\left( {1 - Z_{iwvctg} } \right)\quad \forall i \in I;w \in W;v \in V;c \in C;t \in T;g \in T; where g < t $$

(16)

$$ I_{iwvctg} - \left( {I_{iwvct - 1g} - QW_{iwvctg} - LO_{iwvct - 1g} } \right) \le M\left( {1 - Z_{iwvctg} } \right)\quad \forall i \in I;w \in W;v \in V;c \in C;t \in T;where t > 1 \& g < t $$

(17)

$$ AC_{iwvct} \le Z_{{i^{\prime}wvctg}} \quad \forall i \ne i^{\prime};w \in W;v \in V;c \in C;t \in T;g \in T;t \ge g $$

(18)

$$ Q_{ijt} ,LO_{iwvctg} ,QF_{ijwvct} ,QW_{iwvctg} ,I_{iwvctg} \ge 0; Z_{iwvctg} , AW_{w} ,AC_{iwvct} \in \left\{ {0,1} \right\} ;y_{kjwt} ,TE_{iwvct} \in Integer^{ + } $$

(19)

.

The first objective function (1) minimizes total costs of the system, including purchasing costs, operational costs in warehouses, cost of establishing warehouses, transportation costs (transportation cost according to the number of trips and the amount of loading between farmers and warehouse), and inventory holding cost. CO₂ emissions from losses generated by fresh products after purchasing them, losses generated by deterioration of products over their storage life, transportation vehicles, and using different temperature conditions in storage rooms should be minimized in the second objective function (2).

Constraints (3) present that only one type of product can be stored in a storage room under temperature condition $c$. Constraints (4) indicate the effects of temperature condition on the shelf life of products with quality grade $i$. Constraints (5) ensure that the quantity of products in warehouses should be less than purchased products from farmers with considering losses generated by agro-products. Constraints (6) show the inventory level of products wherein demands are met with fresh products. Constraints (7) calculate the quantity of deteriorating products in each time period. Constraints (8) ensure the minimum acceptable quality level of products over their shelf life time. Constraints (9) show the balance between the input and output flows in warehouses. Constraints (10) describe the maximum capacity for storing products in each of storage room. Constraints (11) state that the demand of customers should be met. Constraints (12) restrict the number of storage rooms turned on in each time period. Constraints (13) restrict the capacity of vehicles. Constraints (14)–(16) depict the relation between time of entering and exiting products from warehouses according to their shelf lives in which inventory level of products is calculated based on constraints (17) when $t > g$. In constraints (14), $M$ is a large number such that $M \ge max\left\{ {T_{ic} } \right\}$. Similarly, in constraints (15)–(17), $M$ is a big number such that $M \ge max\left\{ {CW_{w} } \right\}$.

Constraints (18) ensure that only one type of products can be stored in a storage room considering the inventory of previous periods. Constraints (19) clarify the possible values for the decision variables.

3.2 Multi-objective optimization programming method

The proposed model is a MILP problem with two conflicting objectives leading to the use of a proper method to optimize both objective function values simultaneously. For this purpose, one approach is to use proper multi-objective decision making methods (MODM) for converting the multiple conflicting objectives into a single one (Hwang and Masud 2012). The $\varepsilon$-constraint method is known as an easy to implement and highly used MODM method for decision-makers to find appropriate feasible solutions in the trade-offs between objectives through optimizing the most important objective function considering others as constraints and assigning upper bounds for them (Dehghani et al. 2018). The $\varepsilon$-constraint method has been widely employed to solve the multi-objective problem in the literature due to its advantages, some of which are presented as follows:

• This method does not aggregate objective functions; however, decision-makers can choose the most important objective function and restrict other objective functions with specified values. As a result, this method gives a chance for assessing the information and decision-makers-preference ( Mohebalizadehgashti et al. 2020).

• A set of different $\varepsilon$ values can provide a set of Pareto solutions on trade-off objective functions leading to a proper choice of $\varepsilon$ value (Amin and Zhang 2013).

• The $\varepsilon$-constraint method can be easily implemented for both convex and non-convex multi-objective problems.

The general form of this method is presented as follows:

$$ \begin{aligned} & Minimize\, f_{i} \left( x \right) \\ & {\text{Subject to}}: \\ & f_{h} \left( x \right) \le UP_{h} h \in \left\{ {1,2, \ldots , H} \right\},h \ne i \\ & x \in S \\ \end{aligned} $$

(20)

where $f_{i} \left( x \right)$ represents the most important objective function from the decision maker’s point of view, $f_{h} \left( x \right)$ is $hth$ objective function held as a constraint and $UP_{h}$ is the upper bound for $hth$ objective function (obtained from the payoff table) and $S$ is the feasible space for the original proposed model.

In this paper, mean ideal distance (MID) metric is applied in order to select the best solution among the varied Pareto solutions for each instance. MID-metric finds the best trade-off solutions by selecting a Pareto solution with the least deviation from their ideal solutions (Coello et al. 2007). MID-metric is calculated as follows:

$$ MID_{j} = \mathop \sum \limits_{i}^{n} \frac{{f_{ij} \left( x \right) - f_{i,min} }}{{n(f_{i,max} \left( x \right) - f_{i,min} \left( x \right))}} \forall j $$

(21)

where $f_{i,min}$ and $f_{i,max} \left( x \right)$ represent the minimum and maximum values of the $ith$ objective function among the Pareto solutions. Besides, $f_{ij} \left( x \right)$ indicates the value of the $ith$ objective function for $jth$ Pareto solution, and $n$ is the number of objective functions.

3.3 Robust approach

In the real world, uncertainty in predicting the proportion of losses generated by agro-products in the postharvest activities, and demand rate is inevitable because of varying rainfall, climate change, and disasters like floods. Sometimes, estimating the probability distribution for these uncertain parameters is hard to obtain due to the lack of historical data; however, it is easy to determine an interval of uncertainty. Therefore, a method should be used to reasonably cope with the interval of uncertainty that occurs throughout the supply chain.

In this paper, uncertainties come from different sources to an agro-supply chain that could remain unknown due to the lack of historical data availability. These uncertainties lead to changes in demand and product losses which are realized during transporting, storing, and purchasing products. In these cases, it is necessary to deal with uncertain data in decision making that can profoundly affect operational processes, quality decay, shelf life of products, and meeting demands.

Clearly, a wide range of approaches can be employed to account for uncertainties, among which robust method can specifically adapt to those uncertainties derived from the lack of data for estimating the probability distributions. The robust method is known as a commonly used approach for handling the interval of uncertainty and has been proposed by Bertsimas and Sim (2004). The robust optimization approach is used in several published papers that can be seen in Zokaee et al. (2017), Jabbarzadeh et al. (2019), Yavari and Geraeli (2019), Xu et al. (2020).

This paper uses a robust approach due to its applicability to cope with the interval of uncertainty in demand and loss factor of products in the proposed multi-period MILP model. In this respect, first, a description of the robust counterpart problem is presented with a given uncertain parameter ${\text{a}}_{ij}$ in the following mathematical model.

$$ \begin{aligned} & Min \mathop \sum \limits_{i}^{I} \mathop \sum \limits_{j}^{J} C_{j} X_{ij} \\ & \mathop \sum \limits_{j} {\text{ a}}_{ij} X_{ij} \le b_{i} \quad \forall i \in I \\ & X_{ij} \in \left\{ {0,1} \right\} \\ \end{aligned} $$

(22)

Above, parameter ${\text{a}}_{ij}$ is randomized within the interval [$\overline{a}_{ij} - \hat{a}_{ij} , \overline{a}_{ij} + \hat{a}_{ij}$], where $\overline{a}_{ij}$ indicates the nominal value of uncertain parameter deviating $\hat{a}_{ij}$ value from this nominal value. Furthermore, the duality theory is utilized to take the deterministic values for uncertain parameters. Accordingly, the above formulation can be transformed by incorporating dual variables $\gamma_{i}$ and $q_{ij}$, and budget of uncertainty $\Gamma_{i}$, that is:

$$ \begin{aligned} & Min \mathop \sum \limits_{i}^{I} \mathop \sum \limits_{j}^{J} C_{j} X_{ij} \\ & \mathop \sum \limits_{j} \overline{a}_{ij} X_{ij} + \gamma_{i} \Gamma_{i} + \mathop \sum \limits_{j} q_{ij} \le b_{i} \quad \forall i \\ & \gamma_{i} + q_{ij} \ge \hat{a}_{ij} X_{ij} \quad \forall i,j \\ & \gamma_{i} \ge 0\quad \forall i \\ & q_{ij} \ge 0\quad \forall i.j \\ \end{aligned} $$

(23)

According to the above description, a robust optimization approach is implemented in the proposed model, while assuming uncertain parameters which are demand for product $i$ in time period $t(\tilde{D}_{it } )$, and loss factor of product $i$ purchased from farmer $j$ ($\widetilde{LF}_{ij}$).

3.3.1 Loss factor uncertainty

The proposed model is extended considering the uncertain parameter $\widetilde{LF}_{ij}$ in the second objective function (2) and constraints (5) that takes the value within a range of $\left[ {\overline{LF}_{ij} - \widehat{LF}_{ijt} ,\overline{LF}_{ij} + \widehat{LF}_{ijt} } \right]$. The parameter $\overline{LF}_{ij}$ denotes the nominal value of the loss factor and the parameter $\widehat{LF}_{ijt}$ represents the deviation of nominal value. By the use of $\varepsilon$-constraint method for solving the proposed bi-objective model, the second objective function with uncertain parameter $\widetilde{LF}_{ij}$ can be reformulated to the constraints (24)–(25) as follows:

$$ \begin{gathered} \mathop \sum \limits_{i} \mathop \sum \limits_{j} \mathop \sum \limits_{t} a_{t} CO_{i} \overline{LF}_{ij} Q_{ijt} + \mathop \sum \limits_{i} \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{c} \mathop \sum \limits_{t} \mathop \sum \limits_{g} CO_{i} LO_{iwvctg} + \mathop \sum \limits_{j} \mathop \sum \limits_{w} \mathop \sum \limits_{k} \mathop \sum \limits_{t} CK_{k} DS_{jw} y_{kjwt} \hfill \\ + \mathop \sum \limits_{i} \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{c} \mathop \sum \limits_{t} EM_{c} AC_{iwvct} + \gamma^{LF1} \Gamma^{LF1} + \mathop \sum \limits_{i} \mathop \sum \limits_{j} \mathop \sum \limits_{t} q_{ijt}^{LF1} \le \varepsilon \hfill \\ \end{gathered} $$

(24)

$$ \gamma^{LF1} \Gamma^{LF1} + q_{ijt}^{LF1} \ge a_{t} CO_{i} \widehat{LF}_{ijt} Q_{ijt} \quad \forall i \in I;j \in J;t \in T $$

(25)

where $\gamma^{LF1}$ and $q_{ijt}^{LF1}$ are dual variables, and $\Gamma^{LF1}$ is the budget of uncertainty that takes the value in the interval of $[0,I \times J \times T]$.

Besides, the robust approach is employed for transforming constraints (5) to constraints (26)–(27). For that, dual variables $\gamma_{ijt}^{LF}$ and $q_{ijt}^{LF}$ are defined, and budget of uncertainty $\Gamma^{LF}$ is a parameter in interval of $\left[ {0, 1} \right]$.

$$ \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{c} QF_{ijwvct} - a_{t} Q_{ijt} + a_{t} Q_{ijt} \overline{LF}_{ijt} + \gamma_{ijt}^{LF} \Gamma^{LF} + q_{ijt}^{LF} \le 0 \forall i \in I,j \in J,t \in T $$

(26)

$$ \gamma_{ijt}^{LF} + q_{ijt}^{LF} \ge a_{t} Q_{ijst} \widehat{LF}_{ijt} \quad \forall i \in I,j \in J,t \in T $$

(27)

3.3.2 Demand uncertainty

Similarly, the demand for product $i$ in time period $t$ is another uncertain parameter that can take a value in $\left[ {\overline{D}_{it} - \hat{D}_{it} ,\overline{D}_{it} + \hat{D}_{it} } \right]$. Where $\overline{D}_{it}$ and $\hat{D}_{it}$ indicate the nominal value and maximum deviation from the nominal value, respectively. In order to turn the uncertain constraints (11) into the deterministic, robust optimization approach can be used by replacing constraints (11) with constraints (28)–(29).

$$ \overline{D}_{it} + \gamma_{it}^{D} \Gamma^{D} + q_{it}^{D} - \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{c} \mathop \sum \limits_{g} QW_{iwvctg} \le 0\quad \forall i \in I; t \in T $$

(28)

$$ \gamma_{it}^{D} \Gamma^{D} + q_{it}^{D} \ge \hat{D}_{it} \quad \forall i \in I; t \in T $$

(29)

In the above constraints, $q_{it}^{D}$ and $\gamma_{it}^{D}$ are dual variables, and $\Gamma^{D}$ denotes the budget of uncertainty within a range of $\left[ {0, 1} \right].$

4 Solution procedure

The proposed model is a MILP problem whose complexity keeps on rising by increasing the size of the problem, accordingly, the computational time exceeds the reasonability. In these cases, Lagrangian relaxation algorithm (LRA) is known as a powerful algorithm that is able to provide efficient lower bounds to the original problem via relaxing a small set of hard constraints. Combining Lagrangian relaxation algorithm with a heuristic method has been developed in many NP-hard problems to obtain upper bounds. Lagrangian relaxation-based heuristic method is successfully used in many papers in the field of the supply chain that can be seen in the related works done by Zhang et al. (2014), Fahimnia et al. (2017), Heidari-Fathian and Pasandideh (2018), Rafie-Majd et al. (2018), Diabat et al. (2019), Rahmani (2019).

The LRA was proposed by Held and Karp (1970) and then comprehensively reviewed by Guignard (2003). The main idea of the LRA is to find the complicated constraints to be relaxed and move them to the objective function. This procedure accelerates the convergence via relaxing the complex constraints whereas the obtained solution may be infeasible for the original problem. Therefore, Lagrangian multipliers tend to penalize the violated constraints. Indeed, the LRA is an iterative algorithm to provide the lower bounds (LB) for the original problem. On the other hand, infeasible solutions can be converted to feasible solutions in each iteration and considered as upper bounds for the optimal value of the original problem. The LRA will continue until the relative gap between the LB and UB reaches near-zero or the relaxed problem derives to the feasible solution which is an optimal solution to the original problem.

Based on the above-mentioned content, it is necessary to find the complicated constraints in the proposed model. Thus, the number of constraints and computational times are compared in both original and transformed problems in order to select those constraints which are effective in simplifying the problem.

Numerical experiments are performed by relaxing some complex constraints and one of them is reported in this section in order to select the most effective in simplifying the problem. In this regard, results are summarized in Table 2 that show solving the original problem takes 200 s while relaxing the constraints (10) and (13) considerably affects reducing computational time. Moreover, Fig. 3 illustrates the convergence of the LRA when relaxing the constraints (10), (13), and (17). Obviously, relaxing the constraints (13) provide a better lower bound in comparison with other ones. Therefore, constraints (13) are selected to be relaxed.

Table 2 Impacts of the relaxed constraints in the number of constraints and computational time

Fig. 3

Comparison of different relaxed constraints in the LRA algorithm

4.1 Lower bound

It can be obtained from Table 2 relaxing constraints (13) is more effective in simplifying the mathematical model that makes the problem easier to solve. Therefore, the objective function should be reformulated to Eq. (30) by assigning non-negative Lagrangian multipliers ${\lambda }_{jwt}$ to vehicle capacity constraints with respect to constraints (3)–(4), (6)–(10), (12), (14)–(19), (24)–(29).

$$ \begin{aligned} LRA & = \mathop \sum \limits_{i} \mathop \sum \limits_{j} \mathop \sum \limits_{t} a_{t} CQ_{ij} Q_{ijt} + \mathop \sum \limits_{i} \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{c} \mathop \sum \limits_{t} \mathop \sum \limits_{g} O_{w} QW_{iwvctg} + \mathop \sum \limits_{w} FW_{w} AW_{w} \\ & \quad + \mathop \sum \limits_{i} \mathop \sum \limits_{j} \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{c} \mathop \sum \limits_{t} CT_{jw} QF_{ijwvct} + \mathop \sum \limits_{k} \mathop \sum \limits_{j} \mathop \sum \limits_{w} \mathop \sum \limits_{t} CF_{k} y_{kjwt} + \mathop \sum \limits_{i} \mathop \sum \limits_{w} \mathop \sum \limits_{v} \mathop \sum \limits_{c} \mathop \sum \limits_{t} \mathop \sum \limits_{g} H_{c} I_{iwvctg} \\ & \quad + \mathop \sum \limits_{j} \mathop \sum \limits_{w} \mathop \sum \limits_{t} \lambda_{jwt} \left( {\mathop \sum \limits_{i} \mathop \sum \limits_{v} \mathop \sum \limits_{c} QF_{ijwvct} - \mathop \sum \limits_{k} CV_{k} y_{kjwt} } \right) \\ \end{aligned} $$

(30)

$$ \begin{aligned} & Subject\,to\text{:} \\ & \quad Constraints \left( {3){-}(4} \right),\left( {6){-}(10} \right), \left( {12} \right), \left( {14){-}(19} \right), \left( {24} \right){-}\left( {29} \right) \\ \end{aligned} $$

In the following, a brief discussion on applying the LRA is provided based on the research done by Fisher (2004). First, the initial values of the Lagrangian multipliers, lower bound, and upper bound set to zero, $- \infty$, $\overline{Z}$, respectively. The relaxed problem is solved deriving a lower bound for the original problem. Then, the obtained lower bound is used as the main parameter for calculating the step size of the sub-gradient. Equation (31) denotes the step size of each sub-gradient.

$$ Step_{iter + 1} = \frac{{UB_{iter} - L\left( {U_{iter + 1} } \right)}}{{G_{iter}^{2} }} $$

(31)

where $UB_{iter}$ and $L\left( {U_{iter} } \right)$ are the upper and lower bounds obtained in the current iteration. Besides, $G_{iter}^{2}$ represents the Euclidean norm of the relaxed constraints corresponding to the optimal solution of the sub-gradient.

Lagrangian multipliers ($U_{iter + 1}$) update according to the Eq. (32) employing $Step_{iter}$ and Lagrangian multipliers of the previous iteration.

$$ U_{iter + 1} = U_{iter} + Step_{iter} \left( {G_{iter} } \right) $$

(32)

The value of the lower bound in each iteration ($L\left( {U_{iter + 1} } \right)$) should be compared with the maximum value of the lower bound found in previous iterations ($L\left( {U_{iter} } \right)$). If $L\left( {U_{iter + 1} } \right)$ is less than $L\left( {U_{iter} } \right)$, then, $L\left( {U_{iter + 1} } \right)$ should be equal to $L\left( {U_{iter} } \right)$.

4.2 Upper bound

As mentioned before, the solution of the relaxed problem does not guarantee feasibility. Therefore, a heuristic algorithm should be proposed to obtain a feasible solution in each iteration as an upper bound to the original problem. For this purpose, the upper bound is obtained from converting the infeasible solution (lower bound) to the feasible solution as follows:

Forasmuch as the violated values from relaxing the constraints (13) incorporate the variables $Q_{ijt}$, $QF_{ijwvct}$, and $y_{kjwt}$, they should be recalculated using a heuristic procedure, while the values of other variables set as parameters. In this regard, a change in variable $QF_{ijwvct}$ may affect the feasibility of constraints (24)–(27), (13). Therefore, equations should be provided to keep this variable constant through finding the upper bound. In this regard, Eqs. (33) are presented to keep the feasibility of the proposed model and demonstrate the equality of the purchased and stored products in both lower and upper bounds. Where $\overline{QF}_{ijwvct}$ is obtained from solving the relaxed problem and is fixed to generate a new amount of $QF_{ijwvct}$ in the feasible solutions.

$$ \mathop \sum \limits_{j} QF_{ijwvct} = \mathop \sum \limits_{j} \overline{QF}_{ijwvct} \quad \forall i \in I;w \in W;v \in V;c \in C;t \in T; $$

(33)

In order to find the upper bound, the objective function of the original problem is to minimize including the fixed amount of the variables $\overline{LO}_{iwvctg}$, $\overline{QW}_{iwvctg}$, $\overline{I}_{iwvctg}$, $\overline{AW}_{w}$, $\overline{AC}_{iwvct}$, $\overline{TE}_{iwvct}$ with respect to the Eqs. (13), (24)–(27), (33). The result is considered as the upper bound for the current iteration. After finding a feasible solution by the above heuristic algorithm, Lagrangian multipliers update considering the current obtained lower and upper bounds. This procedure continues until one of the criteria is satisfied.

In this respect, the assignment of the proposed procedure is summarized as follows:

• Step 0: Let iteration count $k$ equal to 1

• While stopping criteria is not satisfied

• Step 1: Solve the Lagrangian relaxation problem to find a Lower bound.

• Step 2: Input the obtained results from solving the LRA (Lower bound solutions) as follows:

  $$\overline{LO}_{iwvctg} ,\overline{QW}_{iwvctg} ,\overline{I}_{iwvctg} , \overline{AW}_{w} ,\overline{AC}_{iwvct} ,\overline{TE}_{iwvct} ,\overline{QF}_{ijwvct}$$

• Step 3: Solve the minimization problem (1) under constraints (13), (24)–(27), and (33) in which the obtained results from step 2 set as constants to find an upper bound. This procedure guarantees the feasibility of the main problem.

• Step 4: Update the values of $UB_{iter}$ (Upper bound from step 3), and $L\left( {U_{iter} } \right)$ (Lower bound from step 1), then recalculate Lagrangian multipliers according to the Eqs. (31)–(32).

• Step 5: If $(UB_{iter + 1} > UB_{iter} )$ then $UB_{iter + 1} = UB_{iter}$

• Step 6: Check the stopping criteria, while is not satisfied return to step 1, and update $k = k + 1$

• End While

As mentioned before, the initial value of the upper bound is set to $\overline{Z}$. The value of $\overline{Z}$ is obtained from the above heuristic algorithm in which the values of Lagrangian multipliers are assigned according to the decision maker’s preference.

4.3 Stopping criteria

The procedure will continue until it reaches one of the termination criteria, which are presented as follows:

• The solution of the LRA is feasible for the original problem.

• The maximum number of iteration is reached (200 iterations in this paper).

• The relative gap between the lower bound ($LB_{iter}$) and upper bound ($UB_{iter}$) is lower than a given threshold (5% in this paper) that is calculated as follows:

  $$ GAP\left( \% \right) = \left( {\frac{{UB_{iter} - LB_{iter} }}{{LB_{iter} }}} \right) \times 100 $$

  (34)

The flowchart of the Lagrangian relaxation-based algorithm is shown in Fig. 4 that demonstrates the used process in this paper.

Fig. 4

Flowchart of the proposed Lagrangian relaxation-based algorithm

5 Computational experiments

This section includes two subsections. First, numerical test problems have been executed to validate the performance of the mathematical model and the efficiency of the proposed LRA. Second, a case study has been investigated in the apple industry. Furthermore, this subsection provides insights into the uncertain parameters in the robust optimization model.

5.1 Performance evaluation

In this subsection, numerical test problems are randomly generated in a certain interval $\left[ {a, b} \right]$ with three classes including small, medium, and large sizes to evaluate the performance of the LRA in the proposed model. Tables 3 and 4 present the parameters which are randomly distributed in their corresponding intervals. Besides, the nominal values of the uncertain parameters and their related deviations in the robust optimization model are shown in Tables 3 and 4. These intervals have been suggested based on reviewing the related literature in the field of the agro-supply chain. Then, both the mathematical model and the LRA are coded in GAMS software (version 27.2.0) and implemented by the CPLEX solver using a computer with Intel^@ Core ™ i7-CPU 2.20 GHz and RAM 8.00.

Table 3 Input parameters

Table 4 Input parameters related to quality grade of products

The performance of the proposed model has been illustrated by implementing the numerical examples in GAMS software using CPLEX solver as an exact solution. Then, in order to validate the LRA and its suggested upper bounds, they are executed on different size instances presented in Table 5 and compared with the exact solutions obtained from CPLEX solver. To this end, percentage relative error (PRE) is used to calculate the relative deviation between upper bounds obtained from LRA and optimal values from CPLEX solver. The following equation is used to calculate the PRE value for each instance.

$$ PRE = \left( {\frac{UB - opt}{{opt}}} \right) \times 100 $$

(35)

Table 5 Numerical size examples

where $opt$ is the optimal value of objective function obtained from CPLEX solver, and $UB$ is the upper bound from LRA for each instance.

The LRA continues until the algorithm reaches one of the termination criteria. The results are presented in Table 6 depicting objective function values, lower bounds (LB), upper bounds (UB), and the computational time for both CPLEX solver and LRA. The results show CPLEX solver is able to obtain the optimal solutions in small and medium sizes with increasing computational time while the LRA gives proper upper and lower bounds in a reasonable time. Besides, the average of PRE values is about 0.41% meaning an insignificant difference between solvers. Hence, the LRA can be used as an efficient heuristic solution approach for large-scale test problems.

Table 6 Obtained results by both the LRA and CPLEX solver for solving numerical test problems

Figure 5 illustrates the comparison of the required CPU-time between CPLEX solver and the LRA, in which differences are being more obvious by increasing the size of the test problems. The relative gap between upper and lower bounds converges to nearly 5% less than one hour in LRA while CPLEX solver has run out of memory for large sizes.

Fig. 5

Comparison of required CPU-time between LRA and CPLEX solver

Figure 6 shows the gap between the objective function values obtained by CPLEX solver and lower and upper bounds by the LRA. As can be seen, there are no significant differences between them.

Fig. 6

Comparison between objective function values, lower bounds, and upper bounds obtained by CPLEX solver and the LRA

To make it clear how the $\varepsilon$-constraint method is applied to solve the proposed bi-objective model, Figs. 7, 8, 9, 10 and 11 demonstrate Pareto Frontiers obtained from different-sized test problems using CPLEX solver and the LRA. In all cases, a decrease in the value of $\varepsilon$ leads to an increase in total costs. Therefore, proper $\varepsilon$ values should be determined to simultaneously improve both objective functions. Green points tend to provide proper trade-offs among the Pareto-solutions from the point of view of the decision-makers using MID-metric.

Fig. 7

The trade-off curve for small-sized test problem (no. P1) using CPLEX solver

Fig. 8

The trade-off curve for small-sized test problem (no. P1) using the LRA

Fig. 9

The trade-off curve for medium-sized test problem (no. P6) using CPLEX solver

Fig. 10

The trade-off curve for medium-sized test problem (no. P6) using the LRA

Fig. 11

The trade-off curve for large-sized test problem (no. P11) using the LRA

5.2 Industrial application

Iran is a great apple producer which is known as an important fruit with a high annual demand rate. Apples with different quality grades are supplied by different farmers and stored in cold rooms during the harvesting seasons in order to meet customer demands for nearly a year. In fact, the quality grade of apples is one of the factors affecting their shelf lives. In addition, apple industries face a lot of uncertainties in loss factors and demand rates due to fluctuating conditions.

In this study, an apple industry has been examined in Iran to validate the proposed model. For this purpose, the necessary data has been collected from a known domestic distributor company with a face to face interview and a website link in relation to the justification cold storage construction project (www.damoon-co.com). In this respect, the company decides to open new warehouses owing to increasing lost sales. After seeking different places, four places in Tehran, Fars, Isfahan, and Razavi Khorasan were nominated to establish warehouses. It should be noted, apples are purchased from farmers in the main production areas which are Tehran, Alborz, Isfahan, West Azerbaijan, East Azerbaijan, and Semnan.

In this section, 11 months and 4 types of vehicles are considered. Input data is presented in Tables 7, 8, 9, 10 and 11. Besides, this study uses data sets in two published papers in relation to different temperature conditions in cold storage rooms, different types of vehicles, and product losses and their related CO₂ emissions (Sazvar et al. (2018), Boschiero et al. (2019)). Therefore, the CO₂ generated from transporting 1-tonne in 1-km by the vehicle types $k1$, $k2$, $k3$, and $k4$ is equal to1100, 1600, 2200, 2800 g, respectively. Different quality grades of products generate different CO₂ levels in 1-tonne of food losses that are 21,000, 16,000, 9300 g for product types $i1$, $i2$, and $i3$, respectively. Besides, refrigerator technology generates different CO₂ emissions according to their related temperature conditions. In this respect, CO₂ emissions in the storing process of 1-tonne of products under temperature conditions $c1$, $c2$, and $c3$ are equal to 12,200, 19,300, and 23,600 g, respectively. More information on temperature conditions is obtained by using the website (https://pdfsara.ir/container-storage-services-atmospheric-plan/), and purchasing costs of apples with different quality grades are available in fruit and vegetable organization in Iran. Also, the minimum acceptable quality levels during the phase of deterioration are equal to 0.11, 0.28, and 0.35 for the product with quality grades $i1$, $i2$, and $i3$, respectively.

Table 7 Nominal values for uncertain parameters and their related deviations

Table 8 Input parameters related to farmers and warehouses

Table 9 Inventory holding costs under different temperature conditions

Table 10 Input parameters related to warehouses

Table 11 Input parameters related to vehicles

5.3 Budget of uncertainty

Since the proposed model faces uncertainty in customer’s demand and loss factors, the budget of uncertainty should be determined for each of the restrictions. In this respect, the budget of uncertainty has been distributed in their possible interval values in order to take advantage of the model interpretation in multiple levels of uncertainty. The values of $\Gamma^{LF1} ,\Gamma^{LF} ,\Gamma^{D}$ can change in interval $[0,I \times J \times T]$, $\left[ {0, 1} \right]$, and $\left[ {0, 1} \right]$ respectively. Therefore, an experiment has been designed to illustrate the impact of reducing the budget of uncertainty on the system costs that can be seen in Table 12.

Table 12 Results of solving the model in simultaneous reduction of budget of uncertainty

To evaluate the performance of the mathematical model, the case study is solved according to the abovementioned multiple values of the budget of uncertainty. The results show the potential warehouses should be located in nodes Tehran and Fars at a cost of 2.160000E + 9 in all cases. In addition, reduction in the purchasing costs, operational costs, transportation costs, fixed transportation costs, and inventory holding costs are the results of reduction in the budget of uncertainty values. Figure 12 shows the decrease in different terms of the objective function value according to the reduction in the budget of uncertainty.

Fig. 12

Impacts of the budget of uncertainty on different terms of the objective function value

In consideration of the obtained results, purchasing costs, operational costs, transportation costs, fixed transportation costs, inventory holding costs, and cost of establishing warehouses are approximately 0.832, 0.0000126, 0.0438, 0.0511, 0.0479, and 0.0240 of the total cost of the agro-supply chain. Besides, the average of CO₂ emissions is equal to 8,861,044,000 g that 4.24% of which are generated from product losses, 95.65% from vehicles, and 0.11% from cold storages.

6 Conclusion and future directions

Agro-supply chain needs perpetual considerations due to the growing population, increasing human awareness, and their specific characteristics. By reviewing the related literature, some gaps were revealed as vital requirements for further studies. Therefore, this research has addressed some distinct features of agro-products such as perishability and seasonality. In this context, a bi-objective mathematical model was proposed supporting decisions on the shelf life of products which depend on the quality grade of products and temperature conditions in storage rooms. In consonance with this content, this research was done to make proper decisions in purchasing, transporting, and storing products in such a way that product losses to be controlled. For this purpose, two conflicting objective functions were recommended to be optimized. The first objective function aims to minimize the total costs without considering the harmful environmental effects of product losses, transportation vehicles, and storage temperature conditions, whereas, the second objective function minimizes the total CO₂ emissions throughout the supply chain.

On the other hand, as discussed in many papers, uncertainty is inevitable in the agro-supply chain. In this paper, uncertainties in the demand of customers and loss factors were considered, then, a robust optimization approach was used to tackle these uncertainties due to lack of information and fluctuations in some parameters.

Since the presented model is a bi-objective, first, $\varepsilon$-constraint method was applied to convert the model to a single objective. Then the model was coded in GAMS software and solved using CPLEX solver for small and medium sizes of instances. As the MILP model is complex, CPLEX solver is not capable of solving the large size instances. For this reason, Lagrangian relaxation-based algorithm was used to obtain the proper lower and upper bounds. Obtained results from both CPLEX solver and the LRA were compared in terms of required CPU-time and objective function value indicating the effectiveness of the suggested algorithm.

Also, the applicability of the proposed model was verified by implementing a real case study. The results have shown the best places for establishing warehouses, and suitable temperature conditions in storage rooms in each period considering both environmental and economic impacts. Noteworthy, the effects of changing the budget of uncertainty in different terms of the objective function have been analyzed.

Considering discounts on purchasing prices, some strict regulations in economic and environmental issues, and the possibility of shortages can be suggested as a few extensions of this paper.