A bi-level stochastic optimization model for multi-commodity rebalancing under uncertainty in disaster response

Abstract

In planning for a large-scale disaster, potential relief centers to accommodate evacuees need to be identified. The quantities of emergency commodities are prepared and stocked at relief centers in advance for possible disasters. In the event of a disaster, due to the different disaster severities and uncertain environment, some relief centers inevitably have surplus commodities, whereas some relief centers are still unmet. To use any surplus commodities effectively, a multi-commodity rebalancing process is necessary to rebalance the commodities among relief centers. However, various uncertainties make the multi-commodity rebalancing process extremely challenging, including uncertain demand and transportation-network availability. By recognizing those practical uncertainties, a bi-level stochastic mixed-integer nonlinear programming model is proposed to formulate this multi-commodity rebalancing problem. The upper-level objective is to minimize the total dissatisfaction level, which is measured by the expected total weighted unsatisfied demand, and the lower-level objective is to minimize the expected total transportation time. Finally, a case study on the Great Sichuan Earthquake in China is implemented; their results show that the proposed model facilitates effective decision-making in the practice of multi-commodity rebalancing.

1 Introduction

Whether natural or man-made, large-scale disasters such as earthquakes, floods, typhoons, and nuclear leaks occurred frequently in the last decade (Guha-Sapir et al. 2012; Ronke 2018), affecting a large number of people significantly and damaging a large number of assets severely (Gao et al. 2019; Besiou and Van Wassenhove 2019). In the event of such a disaster, rapid and effective disaster responses are required initially. Specifically, a number of relief centers to accommodate evacuees should be determined and a variety of critical commodities such as water, food, and medicine for supporting basic life should be distributed to those relief centers and stocked in advance. However, the deployment of an initial unsuitable stock of emergency commodities in the affected areas may lead to redundancy, the overconsumption of logistical resources, and even congestion in the system (Caunhye et al. 2012; Sheu and Pan 2015; Gao 2019).

In the event of a large-scale disaster, due to the unpredictable demand, some relief centers may have surplus commodities, whereas some relief centers are still lacking in commodities (Gao and Lee 2018a). To make full use of any surplus commodities effectively, those stored commodities need to be rebalanced among those relief centers. Besides, the commodities can be rebalanced and distributed quickly within the disaster area to reduce human sufferings. Although many research efforts have been dedicated to the commodity distribution in humanitarian logistics (Goldschmidt and Kumar 2017; Sabouhi et al. 2018; Cao et al. 2018; Dubey et al. 2019), none of them have addressed the multi-commodity rebalancing process, which is summarized as:

The multi-commodity rebalancing process in disaster response is to rebalance the commodities from the oversupplied nodes to unmet nodes over the transportation network to satisfy the potential demand at all nodes (relief centers).

In preparation for a possible disaster, various potential relief centers are identified and stocked with commodities in predetermined quantities (Goldschmidt and Kumar 2017; Ni et al. 2018; Balcik et al. 2019; Arnette and Zobel 2019). Besides, many studies (Wang et al. 2014; Rennemo et al. 2014; Rath et al. 2016; Nagurney et al. 2016; Zhou et al. 2017) have been dedicated to humanitarian logistics after disasters. However, none of the previous studies have addressed the multi-commodity rebalancing process right after disasters. Therefore, after the initial multi-commodity distribution, it is necessary to plan an appropriate and efficient multi-commodity rebalancing process to rebalance commodities among relief centers right after a large-scale disaster.

Due to the uncertain environment, demand is estimated and considered as uncertainty at relief centers. Another uncertain element is the transportation-network availability, due to factors such as (1) disaster damage, (2) debris removal, and (3) ongoing threats (e.g., rising floods and earthquake aftershocks) (Rath et al. 2016). Besides, for each commodity type, some relief centers are considered as demand nodes while some others are considered as supply nodes. Note that, some relief centers can be demand nodes and supply nodes at the same time because the multiple commodity types are involved. The aforementioned uncertainties and relief centers with mixed demand and supply make it difficult to rebalance the commodities among relief centers over the transportation network. Furthermore, the fair distribution of commodities is quite important in disaster response. Clark and Culkin (2013) summarized humanitarianism that comprises humanity, impartiality, and neutrality, based on the previous work (Tomasini and Van Wassenhove 2004; Van Wassenhove 2006). And many studies focused on this topic and addressed the significance of the fair distribution of emergency commodities (Huang et al. 2012; Rennemo et al. 2014; Starr and Van Wassenhove 2014; Huang et al. 2015; Yu et al. 2018; Gao and Lee 2018b; Li et al. 2019). Fair commodity distribution needs to be taken into account while distributing emergency commodities. In addition, many studies (Nagurney et al. 2015; Rath et al. 2016; Yilmaz and Kabak 2016; Tavana et al. 2018; Sabouhi et al. 2018) have emphasized the importance of minimizing the time in the relief operations. Hence, in this study, the multi-commodity rebalancing process should be able to address both fairness and timeliness since the goal is to deliver the commodities as quickly as possible to reduce the sufferings from evacuees.

Against this backdrop of uncertainties, this study focuses on developing a bi-level stochastic optimization model to plan an appropriate multi-commodity rebalancing process with uncertain elements. A bi-level stochastic mixed-integer nonlinear programming (SMINP) model is proposed that captures uncertainties in demand and transportation-network availability. The tasks are to identify the demand and supply relief centers and determine the incoming and outgoing shipments for each commodity type at relief centers first, and then the commodity flows and vehicle numbers of different types that transport mixed commodities are determined. To solve the proposed model, we proposed a linearization method to reformulate the proposed SMINP model so that it can be solved in CPLEX. Finally, their results show that the proposed model has the benefit to facilitate effective decision-making regarding the multi-commodity rebalancing in disaster response.

The remainder of this paper is organized as follows. In Sect. 2, the previous relevant studies in commodity distribution, rebalancing (also referred to as redistribution), and stochastic optimization models are reviewed, highlighting the novelty and contribution of this study. Section 3 describes the problem of interest in multi-commodity rebalancing with uncertainties and analyses three categories of relief centers. A bi-level SMINP model is proposed to formulate this problem in Sect. 4 and the solution method is developed in Sect. 5. In Sect. 6, a case study is conducted, including the result discussion and sensitive analysis on several key parameters. Finally, Sect. 7 concludes this study and outlines the possible directions for future work.

2 Literature review

As human suffering due to disasters increases, so does research into humanitarian logistics. The commodity distribution problem in disaster response has been extensively studied by many researchers. Here, some previous work is reviewed on the disaster management by discussing several studies of commodity distribution problems that consider various uncertainties and fairness commodity distribution, stochastic optimization models for commodity distribution. The research gap is discussed and then the novelty and contribution of this study are summarized.

2.1 Uncertainty and fairness in humanitarian logistics

To better reflect the realities of post-disaster relief efforts, various uncertainties in humanitarian logistics are widely considered to make the model close to reality. Jia et al. (2007) proposed a stochastic programming (SP) model to determine the facility locations of medical suppliers in response to a large-scale emergency disaster under the uncertainties of medical demand and supply. Sheu (2010) presented a dynamic relief demand management model under the considerations of disorder and uncertain relief demand information from affected areas. Rawls and Turnquist (2012) constructed a dynamic allocation model to optimize pre-event planning to meet short-term demand (the first 72 h after the disaster) for emergency supplies under the demand uncertainty. Murali et al. (2012) formulated a maximal covering location problem by applying (1) a loss function to obtain the distance-sensitive demand and (2) chance-constraints to handle the demand uncertainty. Rennemo et al. (2014) presented a three-stage stochastic mixed-integer programming model in disaster response where the available vehicles for transportation, the state of infrastructure, and the demand were considered as uncertainties. Haghi et al. (2017) developed a multi-objective programming model to determine distribution centers and health centers that were used to distribute commodities and transfer the casualties to health centers, under the uncertainties of demand, supply, and cost. Moreno et al. (2018) proposed a multi-trip location-transportation model to determine the facility location, transportation, and fleet-sizing decisions, regarding uncertainties of demand, supply, and road availability.

Many recent studies have emphasized that a suitable model for post-disaster humanitarian logistics should address fairness (also referred to as equity) (Rodríguez-Espíndola et al. 2018; Starr and Van Wassenhove 2014) and human suffering (Holguín-Veras et al. 2013), even though through a proxy measure, instead of focusing only on the monetary objective of commercial logistics. And many studies focused on this topic and addressed the significance of the fair distribution of emergency commodities (Huang et al. 2012, 2015; Yu et al. 2018; Li et al. 2019). Generally, fairness is measured as the penalty cost of unsatisfied demand at demand points (Lin et al. 2011; Rezaei-Malek and Tavakkoli-Moghaddam 2014; Bai 2016). Wang and Sun (2018) only used the unmet proportion of required resources to quantify fairness, whereas Rivera-Royero et al. (2016) measured the fairness and human suffering level by considering the proportion of unmet demand with priority score at each demand point. Hu et al. (2016) measured the utility satisfaction rate of all relief resources as fairness. Form the above literature, many previous studies care about the unsatisfied demand in humanitarian logistics without considering weighted values at demand points. However, minimization of weighted unsatisfied demand is more appropriate to measure the fairness because suffering needs be alleviated wherever it is found, and the most urgent need to be given priority without discrimination (Clark and Culkin 2013). In addition, minimization of transportation time is generally considered in the relief operations (Nagurney et al. 2015; Rath et al. 2016; Yilmaz and Kabak 2016; Tavana et al. 2018; Sabouhi et al. 2018). Hence, in this study, fairness and timeliness are considered as the objectives that we need to optimize.

2.2 Stochastic programming

In humanitarian logistics, various uncertainties make it more difficult to obtain optimal solutions. In previous studies, SP is one of the most popular modeling approaches to support the decision-making process in disaster operations under uncertainty (Falasca and Zobel 2011; Grass and Fischer 2016; Mahootchi and Golmohammadi 2018). In the last decade, various stochastic optimization models for commodity distribution have been developed in disaster response. Mete and Zabinsky (2010) presented a stochastic optimization approach to tackle the commodity storage and distribution problem under a wide variety of uncertain disaster types and magnitudes. Noyan (2012) considered a risk-averse two-stage SP model to determine the facility locations and the inventory levels at facilities subject to uncertain demand and disaster-network damage. Hong et al. (2015) introduced a risk-averse stochastic modeling approach to solve the problem of designing a pre-disaster relief network while considering uncertain demand and transportation capacities. Noyan et al. (2015) developed a two-stage SP model that applied a hybrid allocation policy to achieve high levels of accessibility and equity simultaneously while considering demand and transportation-network uncertainties. Bai (2016) proposed a two-stage SP model for an emergency supply allocation problem to minimize the expected proportion of unmet demand, the response time of emergency reliefs, and the total cost of the whole process, where the expected proportion of unmet demand was represented as fairness. Gao and Lee (2018a) proposed a stochastic mixed-integer programming model to facilitate the multi-commodity redistribution problem under uncertain demand, supply, and transportation-network availability. Elci and Noyan (2018) developed a chance-constrained mean-risk SP model for a humanitarian relief network design problem under uncertain demand and transportation-network availability. Paul and Zhang (2019) proposed a two-stage SP model to prepare the recourse actions for a hurricane disaster. The locations of distribution points, medical supply levels, and transportation capacity were determined in the first stage and the transportation decisions were determined in the second stage. The various previous studies illustrate that the SP model is the most appropriate approach to solve the humanitarian logistics problem under uncertainty.

2.3 Bi-level optimization

In humanitarian logistics, many real situations involve two levels of decision-making. Therefore, a bi-level optimization model enables to deal with decentralized and hierarchical two levels of decisions, where the decision variables in the subset are not under the control of the leader optimizer (also referred to as upper level) but is controlled by a follower (also referred to as lower level) who optimizes its own objective function with respect to the parameters set by the leader (Alizadeh et al. 2013). Once the leader chooses the value of its variables, the follower reacts by selecting the values of its own variables to optimize its objective function (Chen and Chen 2013; Safaei et al. 2018). Therefore, there are two kinds of variables in the bi-level optimization model, namely (1) upper-level decision variables and (2) lower-level decision variables. Mathematically, a bi-level programming model proposed by Bracken and McGill (1973) is generally expressed as

$$ \left( {\text{L}} \right)\mathop {\hbox{min} }\limits_{x \in X} F\left( {x,y} \right), $$

(1)

$$ \begin{aligned} & {\text{s}} . {\text{t}} .\\ & G\left( {x,y} \right) \le 0, \\ \end{aligned} $$

(2)

$$ \left( {\text{F}} \right)\mathop {\hbox{min} }\limits_{y \in Y} f\left( {x,y} \right), $$

(3)

$$ \begin{aligned} & {\text{s}} . {\text{t}} .\\ & g\left( {x,y} \right) \le 0, \\ \end{aligned} $$

(4)

$$ x,y \ge 0. $$

(5)

where $F\left( {x,y} \right)$ and $f\left( {x,y} \right)$ are the upper-level and lower-level objective functions, respectively.

For the humanitarian logistics problems with several objectives, the bi-level programming approach is a recently emerging way to separate the objectives into different levels and solve the problem hierarchically. After an extensive literature review, it is found that very few works modeling real-life situations as bi-level programming problems in the area of humanitarian logistics. Regarding the catastrophes caused by large-scale natural disasters, a few articles have been found. Kongsomsaksakul et al. (2005) formulated a bi-level programming model to determine the optimal shelter locations in the upper level and traveler behavior in the flood evacuation process in the lower level. Camacho-Vallejo et al. (2015) developed a bi-level programming model to optimize decisions related to the distribution of international aid after a catastrophic disaster; the upper-level objective was to minimize the total response time for delivering the aid and the lower-level objective was to minimize the cost. Gutjahr and Dzubur (2016) developed a bi-objective bi-level optimization model for the determination of relief distribution-center locations in humanitarian logistics, where the upper-level goal was to minimize total opening cost and total uncovered demand at distribution centers and the lower-level goal was to minimize the determination of the user equilibrium. Chen et al. (2017) proposed a bi-level programming model with two objectives; the upper-level objective was to minimize the weighted distribution time to deliver all relief materials and the lower-level objective was to maximize the minimum fulfillment rate at all affected sites required for every kind of relief material. Safaei et al. (2018) proposed a robust bi-level optimization model for a supply-distribution relief network under uncertain demand and supply. The upper-level objective minimized the total relief supply chain costs and the lower-level objective minimized the total supply risk over all suppliers. However, none of them analysed the situation of a multi-commodity rebalancing with multiple objectives in the disaster response. As a consequence, fairness is considered as the upper-level objective. And following the upper-level objective of fairness, lower-level objective cares about timeliness.

2.4 Summary

As discussed above, although many research efforts have been dedicated to the the pre-positioning network design and inventory strategy (Hong et al. 2015; Mohammadi et al. 2016; Ni et al. 2018; Arnette and Zobel 2019; Erbeyoğlu and Bilge 2020) and commodity distribution (Rath et al. 2016; Wang et al. 2014; Rennemo et al. 2014; Nagurney et al. 2016; Zhou et al. 2017) in humanitarian logistics, none of them have addressed the multi-commodity rebalancing process. However, multi-commodity rebalancing for disaster response is also an important issue in humanitarian logistics. Various uncertain elements make the multi-commodity rebalancing extremely challenging. Neither strategic approaches nor quantitative models to handle this multi-commodity rebalancing process with uncertain elements have been studied in the previous studies. Given these difficulties and different from previous studies, there is a critical need to fill this research gap by developing a bi-level stochastic optimization model to facilitate this multi-commodity rebalancing process with two objectives under uncertainty.

Different from the previous study (Gao and Lee 2018a), this study focuses on the multi-commodity rebalancing problem and combines various key decisions, including the identification of demand and supply relief centers, quantities of total incoming and outgoing shipments at relief centers, commodity flows between relief centers, and numbers of vehicles of different types transporting mixed commodities between relief centers, with uncertain demand and transportation-network availability. Under the uncertain elements, a bi-level SMINP model through a scenario-based approach is proposed for the multi-commodity rebalancing problem with the objectives of fairness and timeliness. In the upper level, the prior goal is to maximize fairness by minimizing the total dissatisfaction level to rebalance the commodities for all relief centers. In the lower level, the goal is to minimize the expected total transportation time of vehicles to achieve the fast delivery of commodities.

3 Problem description

In this section, the problem of multi-commodity rebalancing is described in a given transportation network after a disaster. The characteristics of this multi-commodity rebalancing problem are described in Sects. 3.1–3.3.

3.1 Network structure and facilities

In this context, a large-scale disaster is supposed to strike a wide area where a number of relief centers have been pre-identified for accommodating evacuees and various commodity types have been prepared to satisfy their great needs. Besides, a transportation network that comprises a number of roads connecting the relief centers is considered. However, once the disaster hits, the stored commodities are used to provide basic life support for evacuees. Inevitably, some relief centers have surplus commodities whereas others have not enough. To reduce the human sufferings and make full use of any surplus commodities effectively, it is necessary to plan an appropriate and efficient multi-commodity rebalancing process to rebalance the commodities among relief centers.

3.2 Uncertainties in demand and transportation network

The complex and dynamic nature of a large-scale disaster creates a highly uncertain environment for many reasons, such as the uneven distribution of damage, different populations, and evacuees with different needs at relief centers. It is difficult to determine how much of a particular commodity a relief center requires in the future, which makes the demand uncertain. In addition to the uncertainty of demand, the transportation-network availability is usually uncertain during a large-scale disaster relief effort, because the road recovery measures cannot be predicted precisely. The uncertain demand and transportation-network availability increase the complexity of multi-commodity rebalancing over the transportation network.

To account for these uncertain elements, the demand is divided into several independent scenarios. The uncertain demand is represented as a number of discrete stochastic quantities that constitute distinct scenarios. Here a specific realization of possible demand is considered as a scenario. For each commodity type, there is a set of scenarios $\varXi$. For a particular scenario $\xi \in \varXi$, there is a probability of occurrence π$\left( \xi \right)$ such that π$\left( \xi \right) \ge 0$ and $\sum\nolimits_{\xi \in \varXi } {\uppi\left( \xi \right) = 1}$. Similarly, several transportation-network availabilities with probabilities are also considered.

To better illustrate the problem, commodity-type $c$ is considered, for which the initial stock level is $S_{c}$ and the demand quantity is $D_{c}^{\xi }$ in scenario $\xi$. The relief centers are classified into three categories: namely (1) complete supply relief centers with surpluses, (2) complete demand relief centers with shortages and (3) potential demand or supply relief centers, based on their stock levels and uncertain demand. If $S_{c} > \hbox{max} \left\{ {D_{c}^{1} ,D_{c}^{2} , \ldots ,D_{c}^{\xi } , \ldots } \right\}$, this relief center is deemed a complete supply relief center with a surplus. If $S_{\text{c}} < \hbox{min} \left\{ {D_{c}^{1} ,D_{c}^{2} , \ldots ,D_{c}^{\xi } , \ldots } \right\}$, this relief center is deemed a complete demand relief center with a shortage. If $S_{c} \ge \hbox{min} \left\{ {D_{c}^{1} ,D_{c}^{2} , \ldots ,D_{c}^{\xi } , \ldots } \right\}$ and $S_{c} \le \hbox{max} \left\{ {D_{c}^{1} ,D_{c}^{2} , \ldots ,D_{c}^{\xi } , \ldots } \right\}$, then this relief center is deemed a potential demand or supply relief center. For a potential demand or supply relief center, this relief center needs to be identified as a supply relief center or a demand relief center in this study. Considering the stock level of commodity-type $c$ and the demand in scenario $\xi$ at this relief center, the surplus and shortage need to be calculated, which are denoted as $X_{c}^{\xi }$ and $Y_{c}^{\xi }$ and represented in the following two equations.

$$ X_{c}^{\xi } = \left\{ {\begin{array}{*{20}l} {S_{c} - D_{c}^{\xi } } \hfill & {{\text{if}}\;\; {\text{S}}_{c} > \hbox{max} \left\{ {D_{c}^{1} ,D_{c}^{2} , \ldots ,D_{c}^{\xi } , \ldots } \right\}} \hfill \\ {\hbox{max} \left\{ {S_{c} - D_{c}^{\xi } ,0} \right\}} \hfill & {{\text{if }}\;\;\hbox{min} \left\{ {D_{c}^{1} ,D_{c}^{2} , \ldots ,D_{c}^{\xi } , \ldots } \right\} \le {\text{S}}_{c} \le \hbox{max} \left\{ {D_{c}^{1} ,D_{c}^{2} , \ldots ,D_{c}^{\xi } , \ldots } \right\}} \hfill \\ \end{array} } \right. $$

(6)

$$ Y_{c}^{\xi } = \left\{ {\begin{array}{*{20}l} {D_{c}^{\xi } - S_{c} } \hfill & {{\text{if }} \;\;{\text{S}}_{c} < \hbox{min} \left\{ {D_{c}^{1} ,D_{c}^{2} , \ldots ,D_{c}^{\xi } , \ldots } \right\}} \hfill \\ {\hbox{max} \left\{ {D_{c}^{\xi } - S_{c} ,0} \right\}} \hfill & {{\text{if }}\;\;\hbox{min} \left\{ {D_{c}^{1} ,D_{c}^{2} , \ldots ,D_{c}^{\xi } , \ldots } \right\} \le {\text{S}}_{c} \le \hbox{max} \left\{ {D_{c}^{1} ,D_{c}^{2} , \ldots ,D_{c}^{\xi } , \ldots } \right\}} \hfill \\ \end{array} } \right. $$

(7)

After the surplus and shortage of the commodity are identified at relief centers, the relief center with a surplus is deemed an origin point and the one lacking in the commodity is deemed a destination point. Accordingly, any surplus at origin points needs to be redelivered to the destination points. This multi-commodity rebalancing from origin to destination points is implemented simultaneously. To better illustrate the problem, a network of six relief centers with two commodity types (c1 and c2) is depicted in Fig. 1. Note that a relief center can be an origin and destination point simultaneously as different commodities are involved. This is totally different from previous models in the multi-commodity distribution problems. As shown in Fig. 1, there are three possible relief-center categories, namely (1) a supply relief center with surpluses of both commodity types (relief center 2), (2) a demand relief center with shortages of both commodity types (relief center 5), (3) a demand and supply relief center with a surplus of one commodity type and a shortage of the other commodity type (relief centers 1, 3, 4 and 6). It is assumed that vehicles of different types are used to deliver mixed commodities between any pair of relief centers. Then, the main task is to rebalance the commodities among those relief centers by using vehicles of different types. Usually, for any relief centers with surpluses, they try to reduce their stock level by as little as possible because they may face a great demand in the near future. In contrast, for any relief centers with shortages, they hope to receive commodities as much as possible to meet their current highly pressing demand and procure more for possibly need in the future.

Fig. 1

A transportation network of six relief centers in multi-commodity rebalancing

3.3 Presumptions

Before the bi-level SMINP model for multi-commodity rebalancing is formulated, several certain assumptions are stated in advance. The relief-center locations are known. Each of the relief centers is a separate unit and the weighted values of relief centers are given. There are multiple vehicle types with different capacities and speeds. Each vehicle type is allowed to transport mixed commodities between relief centers. Each commodity type is allowed to be cut into portions during the transportation process.

4 Bi-level stochastic optimization model

4.1 Notations

The parameters and decision variables are collected and presented here for the proposed mathematical model:

Sets:

${\mathcal{S}}$:

Set of complete supply relief centers, indexed by $s \in {\mathcal{S}}$

${\mathcal{D}}$:

Set of complete demand relief centers, indexed by $d \in {\mathcal{D}}$

${\mathcal{R}}$:

Set of potential demand or supply relief centers, indexed by $r,t \in {\mathcal{R} }\;\& \; r \ne t$

${\mathcal{C}}$:

Set of commodity types, indexed by $c \in {\mathcal{C}}$

${\mathcal{Z}}$:

Set of vehicle types, indexed by $z \in {\mathcal{Z}}$

$\varXi$:

Set of scenarios of demand, indexed by $\xi \in \varXi$

$\varGamma$:

Set of scenarios of transportation-network availability, indexed by $\zeta \in \varGamma$

Deterministic parameters:

$S_{cs}$:

Stock level of commodity-type $c$ at relief center $s$

$S_{cd}$:

Stock level of commodity-type $c$ at relief center $d$

$S_{cr}$:

Stock level of commodity-type $c$ at relief center $r$

$N_{z}$:

Available number of vehicle-type $z$

$W^{c}$:

Weight of commodity-type $c$

$V^{c}$:

Volume of commodity-type $c$

$CW^{z}$:

Weight capacity of vehicle-type $z$

$CV^{z}$:

Volume capacity of vehicle-type $z$

$E^{cs}$:

Weighted value of relief centers $s$ for commodity-type $c$

$E^{cd}$:

Weighted value of relief centers $d$ for commodity-type $c$

$E^{cr}$:

Weighted value of relief centers $r$ for commodity-type $c$

$B_{sd}$:

Distance between relief centers $s$ and $d$

$B_{sr}$:

Distance between relief centers $s$ and $r$

$B_{rd}$:

Distance between relief centers $r$ and $d$

$B_{rt}$:

Distance between relief centers $r$ and $t$

$SP_{z}$:

Travel speed of vehicle-type $z$

$LT_{z}$:

Loading/unloading time of vehicle-type $z$

Stochastic parameters:

$D_{cs}^{\xi }$:

Demand of commodity-type $c$ at relief center $s$ in scenario $\xi$

$D_{cd}^{\xi }$:

Demand of commodity-type $c$ at relief center $d$ in scenario $\xi$

$D_{cr}^{\xi }$:

Demand of commodity-type $c$ at relief center $r$ in scenario $\xi$

$p^{\xi }$:

Probability of occurrence in scenario $\xi$

$A_{sd}^{\zeta }$:

Availability of road between relief centers $s$ and $d$ in scenario $\zeta$

$A_{sr}^{\zeta }$:

Availability of road between relief centers $s$ and $r$ in scenario $\zeta$

$A_{rd}^{\zeta }$:

Availability of road between relief centers $r$ and $d$ in scenario $\zeta$

$A_{rt}^{\zeta }$:

Availability of road between relief centers $r$ and $t$ in scenario $\zeta$

$p^{\zeta }$:

Probability of occurrence in scenario $\zeta$

Decision variables:

$o_{s}^{c}$:

Quantity of outgoing commodity-type $c$ at relief center $s$

$i_{d}^{c}$:

Quantity of incoming commodity-type $c$ at relief center $d$

$p_{r}^{c}$:

Quantity of outgoing commodity-type $c$ at relief center $r$

$q_{r}^{c}$:

Quantity of incoming commodity-type $c$ at relief center $r$

$w_{sd}^{c\zeta }$:

Flow of commodity-type $c$ from relief centers $s$ to $d$ in scenario $\zeta$

$w_{sr}^{c\zeta }$:

Flow of commodity-type $c$ from relief centers $s$ to $r$ in scenario $\zeta$

$w_{rd}^{c\zeta }$:

Flow of commodity-type $c$ from relief centers $r$ to $d$ in scenario $\zeta$

$w_{rt}^{c\zeta }$:

Flow of commodity-type $c$ from relief centers $r$ to $t$ in scenario $\zeta$

$m_{sd}^{\zeta z}$:

Number of vehicle-type $z$ used to deliver mixed commodities from relief centers $s$ to $d$ in scenario $\zeta$

$m_{sr}^{\zeta z}$:

Number of vehicle-type $z$ used to deliver mixed commodities from relief centers $s$ to $r$ in scenario $\zeta$

$m_{rd}^{\zeta z}$:

Number of vehicle-type $z$ used to deliver mixed commodities from relief centers $r$ to $d$ in scenario $\zeta$

$m_{rt}^{\zeta z}$:

Number of vehicle-type $z$ used to deliver mixed commodities from relief centers $r$ to $t$ in scenario $\zeta$

4.2 Objective functions

In this study, the goal is to achieve fairness in multi-commodity rebalancing at relief centers and timely delivery of commodities between relief centers, where the goal of fairness is prior to the timely delivery. Here, a bi-level stochastic optimization model is proposed for the multi-commodity rebalancing problem. The upper-level goal is to achieve fairness in multi-commodity rebalancing by minimizing the total dissatisfaction level at relief centers; the lower-level goal is to minimize the expected total transportation time of vehicles of different types that deliver mixed commodities. The upper-level objective with a higher priority focuses on fairness so that the relief center with the greatest need would receive the most attention. To measure the fairness, the dissatisfaction level is defined, which is the expected total weighted unsatisfied demand. The weighted value is used to prioritize the most urgent demand at each relief center. Each relief center has different weighted values for different commodity types. For commodity-type $c$, the weighted unsatisfied demand at those three groups of relief centers is represented as follows.

4.2.1 Weighted unsatisfied demand at complete supply relief centers

At complete supply relief center $s$, given the commodity-type $c$, weighted value $E^{cs}$, stock level $S_{cs}$, and demand $D_{cs}^{\xi }$ in scenario $\xi$, the outgoing shipment $o_{s}^{c}$ needs to be determined. If  $D_{cs}^{\xi } > \left( {S_{cs} - o_{s}^{c} } \right)$, the demand relief center will suffer a shortage (unsatisfied demand). By contrast, if $D_{cs}^{\xi } \le \left( {S_{cs} - o_{s}^{c} } \right)$, the delivery is satisfactory. The weighted unsatisfied demand $\varvec{S}\left( {S_{cs} , D_{cs}^{\xi } ,o_{s}^{c} ,\xi } \right)$ at complete supply relief center $s$ in scenario $\xi$ is defined as

$$ \varvec{S}\left( {S_{cs} , D_{cs}^{\xi } ,o_{s}^{c} ,\xi } \right) = E^{cs} \cdot \hbox{max} \left\{ {D_{cs}^{\xi } - \left( {S_{cs} - o_{s}^{c} } \right), 0} \right\} $$

(8)

4.2.2 Weighted unsatisfied demand at complete demand relief centers

At complete supply relief center $d$, given the commodity-type $c$, weighted value $E^{cd}$, stock level $S_{cd}$, and demand $D_{cd}^{\xi }$ in scenario $\xi$, the incoming shipment $i_{d}^{c}$ needs to be determined. If  $D_{cd}^{\xi } > \left( {S_{cd} + i_{d}^{c} } \right)$, the demand relief center will suffer a shortage (unsatisfied demand). By contrast, if $D_{cd}^{\xi } \le \left( {S_{cd} + i_{d}^{c} } \right)$, the delivery is satisfactory. The weighted unsatisfied demand $\varvec{D}\left( {S_{cd} , D_{cd}^{\xi } ,i_{d}^{c} ,\xi } \right)$ at complete demand relief center $d$ in scenario $\xi$ is defined as

$$ \varvec{D}\left( {S_{cd} , D_{cd}^{\xi } ,i_{d}^{c} ,\xi } \right) = E^{cd} \cdot \hbox{max} \left\{ {D_{cd}^{\xi } - \left( {S_{cd} + i_{d}^{c} } \right), 0} \right\} $$

(9)

4.2.3 Weighted unsatisfied demand at potential demand or supply relief centers

At potential demand or supply relief center $r$, given the commodity-type $c$, weighted value $E^{cr}$, stock level $S_{cr}$, and demand $D_{cr}^{\xi }$ in scenario $\xi$, both an outgoing shipment $p_{r}^{c}$ and an incoming shipment $q_{r}^{c}$ need to be determined. Note that at least one of them (i.e., $p_{r}^{c}$ and $q_{r}^{c}$) is 0. If $D_{cr}^{\xi } > \left( {S_{cr} - p_{r}^{c} + q_{r}^{c} } \right)$, the demand relief center will suffer a shortage (unsatisfied demand). By contrast, if $D_{cr}^{\xi } \le \left( {S_{cr} - p_{r}^{c} + q_{r}^{c} } \right)$, the delivery is satisfactory. The weighted unsatisfied demand $\varvec{R}\left( {S_{cr} , D_{cr}^{\xi } ,p_{r}^{c} ,q_{r}^{c} ,\xi } \right)$ at potential demand or supply relief center $r$ in scenario $\xi$ is defined as

$$ \varvec{R}\left( {S_{cr} , D_{cr}^{\xi } ,p_{r}^{c} ,q_{r}^{c} ,\xi } \right) = E^{cr} \cdot \hbox{max} \left\{ {D_{cr}^{\xi } - \left( {S_{cr} - p_{r}^{c} + q_{r}^{c} } \right), 0} \right\} $$

(10)

It is assumed that a set of possible quantities of demand at relief centers are given with probabilities. Then, the dissatisfaction level $\varPsi_{1}$ represented by the expected total weighted unsatisfied demand includes the weighted unsatisfied demand of ${\mathbb{E}}\left[ {\varvec{S}\left( {S_{cs} , D_{cs}^{\xi } ,o_{s}^{c} ,\xi } \right)} \right]$ at complete supply relief center $s$, ${\mathbb{E}}\left[ {\varvec{D}\left( {S_{cd} , D_{cd}^{\xi } ,i_{d}^{c} ,\xi } \right)} \right]$ at complete demand relief center $d$, and ${\mathbb{E}}\left[ {\varvec{R}\left( {S_{cr} , D_{cr}^{\xi } ,p_{r}^{c} ,q_{r}^{c} ,\xi } \right)} \right]$ at potential demand or supply relief center $r$. Then, the dissatisfaction level $\varPsi_{1}$ at all relief centers over all possible scenarios for all commodity types is given as

$$ \varPsi_{1} = \mathop \sum \limits_{{c \in {\mathcal{C}}}} \mathop \sum \limits_{{s \in {\mathcal{S}}}} {\mathbb{E}}\left[ {\varvec{S}\left( {S_{cs} , D_{cs}^{\xi } ,o_{s}^{c} ,\xi } \right)} \right] + \mathop \sum \limits_{{c \in {\mathcal{C}}}} \mathop \sum \limits_{{d \in {\mathcal{D}}}} {\mathbb{E}}\left[ {\varvec{D}\left( {S_{cd} , D_{cd}^{\xi } ,i_{d}^{c} ,\xi } \right)} \right] + \mathop \sum \limits_{{c \in {\mathcal{C}}}} \mathop \sum \limits_{{r \in {\mathcal{R}}}} {\mathbb{E}}\left[ {\varvec{R}\left( {S_{cr} , D_{cr}^{\xi } ,p_{r}^{c} ,q_{r}^{c} ,\xi } \right)} \right] $$

(11)

To minimize $\varPsi_{1}$, the unsatisfied demand at relief centers can be reduced by sharing commodities with demand relief centers that have larger weighted values and avoiding excessive shipments from supply relief centers with larger weighted values. The upper-level objective is to achieve maximum fairness in multi-commodity rebalancing by minimizing the dissatisfaction level $\varPsi_{1}$.

4.2.4 Transportation time

After the upper-level decision variables of incoming and outgoing shipments at relief centers are determined and therefore the potential demand or supply relief centers are also identified, the expected total transportation time needs to be minimized in the lower level. The transportation time $\varvec{T}\left( {m_{sd}^{\zeta z} ,\zeta } \right)$ on road connecting relief centers $s$ and $d$ with distance $B_{sd}$ in scenario $\zeta$ is formulated as

$$ \varvec{T}\left( {m_{sd}^{\zeta z} ,\zeta } \right) = \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sd}^{\zeta z} \cdot \left( {LT_{v} + \frac{{B_{sd} }}{{SP_{z} \cdot r_{sd}^{\zeta } }}} \right) $$

(12)

Similarly, the transportation time $T\left( {n_{sr}^{\zeta z} ,\zeta } \right)$ on road connecting relief centers $s$ and $r$ with distance $B_{sr}$, the transportation time $T\left( {n_{rd}^{\zeta z} ,\zeta } \right)$ on road connecting relief centers $r$ and $d$ with distance $B_{rd}$, and the transportation time $T\left( {n_{rt}^{\zeta z} ,\zeta } \right)$ on road connecting relief centers $r$ and $t$ with distance $B_{rt}$ in scenario $\zeta$ are formulated as

$$ \varvec{T}\left( {m_{sr}^{\zeta z} ,\zeta } \right) = \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sr}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{sr} }}{{SP_{z} \cdot r_{sr}^{\zeta } }}} \right) $$

(13)

$$ \varvec{T}\left( {m_{rd}^{\zeta z} ,\zeta } \right) = \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rd}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{rd} }}{{SP_{z} \cdot r_{rd}^{\zeta } }}} \right) $$

(14)

$$ \varvec{T}\left( {m_{rt}^{\zeta z} ,\zeta } \right) = \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rt}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{rt} }}{{SP_{z} \cdot r_{rt}^{\zeta } }}} \right) $$

(15)

The lower-level expected total transportation time $\varPsi_{2}$ can be represented as the sum of ${\mathbb{E}}\left[ {\varvec{T}\left( {m_{sd}^{\zeta z} ,\zeta } \right)} \right]$, ${\mathbb{E}}\left[ {\varvec{T}\left( {m_{sr}^{\zeta z} ,\zeta } \right)} \right]$, ${\mathbb{E}}\left[ {\varvec{T}\left( {m_{rd}^{\zeta z} ,\zeta } \right)} \right],$ and ${\mathbb{E}}\left[ {\varvec{T}\left( {m_{rt}^{\zeta z} ,\zeta } \right)} \right]$ over all possible scenarios.

$$ \varPsi_{2} = \mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{{d \in {\mathcal{D}}}} {\mathbb{E}}\left[ {\varvec{T}\left( {m_{sd}^{\zeta z} ,\zeta } \right)} \right] + \mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{{r \in {\mathcal{R}}}} {\mathbb{E}}\left[ {\varvec{T}\left( {m_{sr}^{\zeta z} ,\zeta } \right)} \right] + \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{d \in {\mathcal{D}}}} {\mathbb{E}}\left[ {\varvec{T}\left( {m_{rd}^{\zeta z} ,\zeta } \right)} \right] + \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{t \in {\mathcal{R}}}} {\mathbb{E}}\left[ {\varvec{T}\left( {m_{rt}^{\zeta z} ,\zeta } \right)} \right] $$

(16)

4.3 Model formulation

Under the previous considerations, the bi-level SMINP model is proposed through a scenario-based approach. The upper-level objective is to minimize the dissatisfaction level in the multi-commodity rebalancing process. The lower-level objective is to minimize the expected total transportation time. The bi-level SMINP model can be formulated as follows

$$ \begin{aligned} {\text{Min}}\,\varPsi_{1} & = \mathop \sum \limits_{{c \in {\mathcal{C}}}} \left\langle {\mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{\xi \in \varXi } E^{cs} \cdot p^{\xi } \cdot \hbox{max} \left\{ {D_{cs}^{\xi } - \left( {S_{cs} - o_{s}^{c} } \right), 0} \right\}} \right. \\ & \quad + \,\mathop \sum \limits_{{d \in {\mathcal{D}}}} \mathop \sum \limits_{\xi \in \varXi } E^{cd} \cdot p^{\xi } \cdot \hbox{max} \left\{ {D_{cd}^{\xi } - \left( {S_{cd} + i_{d}^{c} } \right), 0} \right\} \\ & \quad \left. { + \,\mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{\xi \in \varXi } E^{cr} \cdot p^{\xi } \cdot \hbox{max} \left\{ {D_{cr}^{\xi } - \left( {S_{cr} - p_{r}^{c} + q_{r}^{c} } \right), 0} \right\}} \right\rangle \\ \end{aligned} $$

(17)

$$ \begin{aligned} & {\text{s}} . {\text{t}} .\\ & \mathop \sum \limits_{{s \in {\mathcal{S}}}} o_{s}^{c} + \mathop \sum \limits_{{r \in {\mathcal{R}}}} p_{r}^{c} = \mathop \sum \limits_{{d \in {\mathcal{D}}}} i_{d}^{c} + \mathop \sum \limits_{{r \in {\mathcal{R}}}} q_{r}^{c} \quad \forall \;c \in {\mathcal{C}} \\ \end{aligned} $$

(18)

$$ \hbox{min} \left\{ {D_{cs}^{1} ,D_{cs}^{2} , \ldots ,D_{cs}^{\xi } , \ldots } \right\} \le S_{cs} - o_{s}^{c} \le \hbox{max} \left\{ {D_{cs}^{1} ,D_{cs}^{2} , \ldots ,D_{cs}^{\xi } , \ldots } \right\}\quad \forall \;s \in {\mathcal{S}},\;c \in {\mathcal{C}} $$

(19)

$$ \hbox{min} \left\{ {D_{cd}^{1} ,D_{cd}^{2} , \ldots ,D_{cd}^{\xi } , \ldots } \right\} \le S_{cd} + i_{d}^{c} \le \hbox{max} \left\{ {D_{cd}^{1} ,D_{cd}^{2} , \ldots ,D_{cd}^{\xi } , \ldots } \right\}\quad \forall \;d \in {\mathcal{D}},\;c \in {\mathcal{C}} $$

(20)

$$ \hbox{min} \left\{ {D_{cr}^{1} ,D_{cr}^{2} , \ldots ,D_{cr}^{\xi } , \ldots } \right\} \le S_{cd} - p_{r}^{c} + q_{r}^{c} \le \hbox{max} \left\{ {D_{cr}^{1} ,D_{cr}^{2} , \ldots ,D_{cr}^{\xi } , \ldots } \right\}\quad \forall \;r \in {\mathcal{R}},\;c \in {\mathcal{C}} $$

(21)

$$ o_{s}^{c} \; {\text{and}}\;i_{d}^{c} \;{\text{are}}\;{\text{positive}}\;{\text{integer}}\;{\text{variables}}\quad \forall \;s \in {\mathcal{S}},\;d \in {\mathcal{D}},\;c \in {\mathcal{C}} $$

(22)

$$ p_{r}^{c} \cdot q_{r}^{c} = 0\quad \forall \;r \in {\mathcal{R}},\;c \in {\mathcal{C}} $$

(23)

$$ p_{r}^{c} \;{\text{and}}\;q_{r}^{c} \;{\text{are}}\;{\text{nonnegative}}\;{\text{integer}}\;{\text{variables}}\quad \forall \,r \in {\mathcal{R}},\;c \in {\mathcal{C}} $$

(24)

$$ \begin{aligned} { \arg }\,{\text{Min}}\,\varPsi_{2} & = \mathop \sum \limits_{\zeta \in \varGamma } \left[ {\mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{{d \in {\mathcal{D}}}} \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sd}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{sd} }}{{SP_{z} \cdot r_{sd}^{\zeta } }}} \right) + \mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sr}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{sr} }}{{SP_{z} \cdot r_{sr}^{\zeta } }}} \right)} \right. \\ & \quad \left. { + \,\mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{d \in {\mathcal{D}}}} \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rd}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{rd} }}{{SP_{z} \cdot r_{rd}^{\zeta } }}} \right) + \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{t \in {\mathcal{R}}}} \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rt}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{rt} }}{{SP_{z} \cdot r_{rt}^{\zeta } }}} \right)} \right] \\ \end{aligned} $$

(25)

$$ \begin{aligned} & {\text{s}} . {\text{t}} .\\ & \mathop \sum \limits_{{d \in {\mathcal{D}}}} w_{sd}^{c\zeta } + \mathop \sum \limits_{{r \in {\mathcal{R}}}} w_{sr}^{c\zeta } \le o_{s}^{c} \quad \forall \;s \in {\mathcal{S}},\;c \in {\mathcal{C}},\;\zeta \in \varGamma \\ \end{aligned} $$

(26)

$$ \mathop \sum \limits_{{s \in {\mathcal{S}}}} w_{sd}^{c\zeta } + \mathop \sum \limits_{{r \in {\mathcal{R}}}} w_{rd}^{c\zeta } \ge i_{d}^{c} \quad \forall \;d \in {\mathcal{D}},\;c \in {\mathcal{C}},\;\zeta \in \varGamma $$

(27)

$$ \mathop \sum \limits_{{d \in {\mathcal{D}}}} w_{rd}^{c\zeta } + \mathop \sum \limits_{{t \in {\mathcal{R}}}} w_{rt}^{c\zeta } \le p_{r}^{c} \quad \forall \;r \in {\mathcal{R}},\;c \in {\mathcal{C}},\;\zeta \in \varGamma $$

(28)

$$ \mathop \sum \limits_{{s \in {\mathcal{S}}}} w_{st}^{c\zeta } + \mathop \sum \limits_{{r \in {\mathcal{R}}}} w_{rt}^{c\zeta } \ge q_{r}^{c} \quad \forall \;t \in {\mathcal{R}},\;c \in {\mathcal{C}},\;\zeta \in \varGamma $$

(29)

$$ \mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{{d \in {\mathcal{D}}}} w_{sd}^{c\zeta } + \mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{{r \in {\mathcal{R}}}} w_{sr}^{c\zeta } = \mathop \sum \limits_{{d \in {\mathcal{D}}}} \mathop \sum \limits_{{s \in {\mathcal{S}}}} w_{sd}^{c\zeta } + \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{s \in {\mathcal{S}}}} w_{sr}^{c\zeta } \quad \forall \;c \in {\mathcal{C}},\;\zeta \in \varGamma $$

(30)

$$ \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{sd}^{c\zeta } \cdot W^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sd}^{\zeta z} \cdot CW^{z} \quad \forall \;s \in {\mathcal{S}},\;d \in {\mathcal{D}},\;\zeta \in \varGamma $$

(31)

$$ \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{sd}^{c\zeta } \cdot V^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sd}^{\zeta z} \cdot CV^{z} \quad \forall \;s \in {\mathcal{S}},\;d \in {\mathcal{D}},\;\zeta \in \varGamma $$

(32)

$$ \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{sr}^{c\zeta } \cdot W^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sr}^{\zeta z} \cdot CW^{z} \quad \forall \;s \in {\mathcal{S}},\;r \in {\mathcal{R}},\;\zeta \in \varGamma $$

(33)

$$ \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{sr}^{c\zeta } \cdot V^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sr}^{\zeta z} \cdot CV^{z} \quad \forall \;s \in {\mathcal{S}},\;r \in {\mathcal{R}},\;\zeta \in \varGamma $$

(34)

$$ \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{rd}^{c\zeta } \cdot W^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rd}^{\zeta z} \cdot CW^{z} \quad \forall \;r \in {\mathcal{R}},\;d \in {\mathcal{D}},\;\zeta \in \varGamma $$

(35)

$$ \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{rd}^{c\zeta } \cdot V^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rd}^{\zeta z} \cdot CV^{z} \quad \forall \;r \in {\mathcal{R}},\;d \in {\mathcal{D}},\;\zeta \in \varGamma $$

(36)

$$ \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{rt}^{c\zeta } \cdot W^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rt}^{\zeta z} \cdot CW^{z} \quad \forall \;r,\;t \in {\mathcal{R}},\;\zeta \in \varGamma $$

(37)

$$ \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{rt}^{c\zeta } \cdot V^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rt}^{\zeta z} \cdot CV^{z} \quad \forall \;r,\;t \in {\mathcal{R}},\;\zeta \in \varGamma $$

(38)

$$ \mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{{d \in {\mathcal{D}}}} m_{sd}^{\zeta z} + \mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{{r \in {\mathcal{R}}}} m_{sr}^{\zeta z} + \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{d \in {\mathcal{D}}}} m_{rd}^{\zeta z} + \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{t \in {\mathcal{R}}}} m_{rt}^{\zeta z} \le N^{z} \quad \forall \;z \in {\mathcal{Z}},\;\zeta \in \varGamma $$

(39)

$$ w_{sd}^{c\zeta } , w_{sr}^{c\zeta } , w_{rd}^{c\zeta } ,\;{\text{and}}\;w_{rt}^{c\zeta } \;{\text{are}}\;{\text{nonnegative}}\;{\text{variables}}\quad \forall \;s \in {\mathcal{S}},\;d \in {\mathcal{D}},\; r,t \in {\mathcal{R}},\;\zeta \in \varGamma $$

(40)

$$ m_{sd}^{\zeta z} , m_{sr}^{\zeta z} , m_{rd}^{\zeta z} ,\;{\text{and}}\;m_{rt}^{\zeta z} \;{\text{are}}\;{\text{nonnegative}}\;{\text{integer}}\;{\text{variables}}\quad \forall \;s \in {\mathcal{S}},\;d \in {\mathcal{D}},\; r,t \in {\mathcal{R}},\;\zeta \in \varGamma $$

(41)

where Eq. (17) is the upper-level objective function which aims to minimize the dissatisfaction level for all commodity types at all relief centers. Constraint (18) guarantees the rebalancing balance between incoming and outgoing shipments for each commodity type. Constraints (19)–(22) define the decision variables. Constraints (23) and (24) guarantee that either outgoing or incoming shipment could happen. Equation (25) is the lower-level objective function that aims to minimize the expected total transportation time, which makes this problem a bi-level programming model. The optimal solution of the lower-level problem is defined by the Constraints (26)–(41). Constraint (26) ensures that the total outgoing shipment does not exceed the quantity of the commodity that needs to be delivered at relief center $s$. Constraint (27) ensures that the total incoming shipment is either greater than or equal to the quantity of the commodity that needs to be received at relief center $d$. Constraint (28) ensures that the total outgoing shipment does not exceed the quantity of the commodity that needs to be delivered at relief center $r$. Constraint (29) ensures that the total incoming shipment is either greater than or equal to the quantity of the commodity that needs to be received at relief center $t$. Constraint (30) guarantees the transportation balance of incoming and outgoing shipments for each commodity type. Constraints (31) and (32) ensure that the assigned vehicles can deliver mixed commodities between relief centers $s$ and $d$ by satisfying both weight and volume capacities. Constraints (33) and (34) ensure that the assigned vehicles can deliver mixed commodities between relief centers $s$ and $r$ by satisfying both weight and volume capacities. Constraints (35) and (36) ensure that the assigned vehicles can deliver mixed commodities between relief centers $r$ and $d$ by satisfying both weight and volume capacities. Constraints (37) and (38) ensure that the assigned vehicles can deliver mixed commodities between relief centers $r$ and $t$ by satisfying both weight and volume capacities. Constraint (39) ensures that the total number of used vehicles does not exceed the total available quantity. Constraints (40) and (41) define the decision variables.

5 Solution method

In this section, the previous bi-level SMINP model is reformulated so that it can be solved by using the IBM CPLEX Optimizer. In this study, because the upper-level objective has a higher priority than the lower-level objective, the upper-level problem needs to be solved under the Constraints (18)–(24) and (26)–(41). Then, the upper-level decision variables of $o_{s}^{c}$, $i_{d}^{c}$, $p_{r}^{c}$, and $q_{r}^{c}$ are fixed, then the lower-level problem becomes a multi-commodity transportation problem using different vehicle types. It is obvious that the previous bi-level SMINP model is nonlinear, due to the MAX function in the upper-level objective function (17) and Constraint (23). In the case of finite scenarios, it is necessary to reformulate the upper-level objective function and linearize the Constraint (23) by introducing a big positive number $M$ and five auxiliary binary variables (i.e.,$\fancyscript{a}_{cs}^{\xi }$,$\fancyscript{b}_{cd}^{\xi }$, $\fancyscript{g}_{cr}^{\xi }$, $\fancyscript{f}_{cr}$, and $\fancyscript{k}_{cr}$) into the model, which are presented as

$$ \fancyscript{a}_{cs}^{\xi } = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if }}\;\;D_{cs}^{\xi } > \left( {S_{cs} - o_{s}^{c} } \right)} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.\quad \forall \;s \in {\mathcal{S}},\;c \in {\mathcal{C}},\;\xi \in \varXi $$

(42)

$$ \fancyscript{b}_{cd}^{\xi } = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if }}\;\;D_{cd}^{\xi } > \left( {S_{cd} + i_{d}^{c} } \right)} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.\quad \forall \;d \in {\mathcal{D}},\;c \in {\mathcal{C}},\;\xi \in \varXi $$

(43)

$$ \fancyscript{g}_{cr}^{\xi } = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if }}\;\;D_{cr}^{\xi } > \left( {S_{cr} - p_{r}^{c} + q_{r}^{c} } \right)} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.\quad \forall \;r \in {\mathcal{R}},\;c \in {\mathcal{C}},\;\xi \in \varXi $$

(44)

$$ \fancyscript{k}_{cr} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\;\; p_{r}^{c} > 0} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.\quad \forall \;r \in {\mathcal{R}},\;c \in {\mathcal{C}} $$

(45)

$$ \fancyscript{k}_{cr} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if }}\;\;q_{r}^{c} > 0} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.\quad \forall \;r \in {\mathcal{R}},\;c \in {\mathcal{C}} $$

(46)

To realize the functions of the above binary variables, the previous bi-level SMINP model is reformulated, in which the corresponding constraints of binary variables are also formulated, which is represented as the following model ${\mathbf{O}}$.

$$ \begin{aligned} & {\mathbf{O}}: \\ & \quad {\text{Min}}\,\varPsi_{1} = \mathop \sum \limits_{{c \in {\mathcal{C}}}} \left\{ {\mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{\xi \in \varXi } E^{cs} \cdot p^{\xi } \cdot \left[ {D_{cs}^{\xi } - \left( {S_{cs} - o_{s}^{c} } \right)} \right] \cdot \fancyscript{a}_{cs}^{\xi } + \mathop \sum \limits_{{d \in {\mathcal{D}}}} \mathop \sum \limits_{\xi \in \varXi } E^{cd} \cdot p^{\xi } \cdot \left[ {D_{cd}^{\xi } - \left( {S_{cd} + i_{d}^{c} } \right)} \right] \cdot \fancyscript{b}_{cd}^{\xi } } \right. \\ & \quad \quad \left. { + \,\mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{\xi \in \varXi } E^{cr} \cdot p^{\xi } \cdot \left[ {D_{cr}^{\xi } - \left( {S_{cr} - p_{r}^{c} + q_{r}^{c} } \right)} \right] \cdot \fancyscript{g}_{cr}^{\xi } } \right\} \\ \end{aligned} $$

(47)

s.t.

Constraints (18)–(22), and (24)

$$ D_{cs}^{\xi } - \left( {S_{cs} - o_{s}^{c} } \right) \ge M \cdot \left( {\fancyscript{a}_{cs}^{\xi } - 1} \right)\quad \forall \;s \in {\mathcal{S}},\;c \in {\mathcal{C}},\;\xi \in \varXi $$

(48)

$$ D_{cs}^{\xi } - \left( {S_{cs} - o_{s}^{c} } \right) \le M \cdot \fancyscript{a}_{cs}^{\xi } \quad \forall \;s \in {\mathcal{S}},\;c \in {\mathcal{C}},\;\xi \in \varXi $$

(49)

$$ D_{cd}^{\xi } - \left( {S_{cd} + i_{d}^{c} } \right) \ge M \cdot \left( {\fancyscript{b}_{cd}^{\xi } - 1} \right)\quad \forall \;d \in {\mathcal{D}},\;c \in {\mathcal{C}},\;\xi \in \varXi $$

(50)

$$ D_{cd}^{\xi } - \left( {S_{cd} + i_{d}^{c} } \right) \le M \cdot \fancyscript{b}_{cd}^{\xi } \quad \forall \;d \in {\mathcal{D}},\;c \in {\mathcal{C}},\;\xi \in \varXi $$

(51)

$$ D_{cr}^{\xi } - \left( {S_{cr} - p_{r}^{c} + q_{r}^{c} } \right) \ge M \cdot \left( {\fancyscript{g}_{cr}^{\xi } - 1} \right)\quad \forall \;r \in {\mathcal{R}},\;c \in {\mathcal{C}},\;\xi \in \varXi $$

(52)

$$ D_{cr}^{\xi } - \left( {S_{cr} - p_{r}^{c} + q_{r}^{c} } \right) \le M \cdot \fancyscript{g}_{cr}^{\xi } \quad \forall \;r \in {\mathcal{R}},\;c \in {\mathcal{C}},\;\xi \in \varXi $$

(53)

$$ \fancyscript{f}_{cr} + \fancyscript{k}_{cr} \le 1\quad \forall \;r \in {\mathcal{R}},\;c \in {\mathcal{C}} $$

(54)

$$ p_{r}^{c} \le \fancyscript{f}_{cr} \cdot M\quad \forall \;r \in {\mathcal{R}},\;c \in {\mathcal{C}} $$

(55)

$$ q_{r}^{c} \le \fancyscript{k}_{cr} \cdot M\quad \forall \;r \in {\mathcal{R}},\;c \in {\mathcal{C}} $$

(56)

$$ \begin{aligned} { \arg }\,{\text{Min}}\,\varPsi_{2} & = \mathop \sum \limits_{\zeta \in \varGamma } \left[ {\mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{{d \in {\mathcal{D}}}} \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sd}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{sd} }}{{SP_{z} \cdot r_{sd}^{\zeta } }}} \right) + \mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sr}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{sr} }}{{SP_{z} \cdot r_{sr}^{\zeta } }}} \right)} \right. \\ & \quad \left. { + \,\mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{d \in {\mathcal{D}}}} \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rd}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{rd} }}{{SP_{z} \cdot r_{rd}^{\zeta } }}} \right) + \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{t \in {\mathcal{R}}}} \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rt}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{rt} }}{{SP_{z} \cdot r_{rt}^{\zeta } }}} \right)} \right] \\ \end{aligned} $$

s.t.

Constraints (26)–(41)

where the Eq. (47) is the upper-level objective function. Constraints (48) and (49) ensure that the unsatisfied demand at relief center $s$ is the larger of $\left[ {D_{cs}^{\xi } - \left( {S_{cs} - o_{s}^{c} } \right)} \right]$ and zero. Constraints (50) and (51) ensure that the unsatisfied demand at relief center $d$ is the larger of $\left[ {D_{cd}^{\xi } - \left( {S_{cd} + i_{d}^{c} } \right)} \right]$ and zero. Constraints (52) and (53) ensure that the unsatisfied demand at relief center $r$ is the larger of $\left[ {D_{cr}^{\xi } - \left( {S_{cr} - p_{r}^{c} + q_{r}^{c} } \right)} \right]$ and zero. Constraint (54) guarantees that either outgoing or incoming shipment could happen. Constraints (55) and (56) restrict the quantities of incoming and outgoing shipments, respectively.

However, after the auxiliary binary variables are applied and the upper-level decision variables are obtained, the lower-level problem is still difficult for the IBM CPLEX Optimizer to solve in a limited time because the delivery of mixed commodities by using different vehicle types is complicated to handle. The upper-bound objective function $\varPsi_{2}^{ *}$ can be used as the lower-level objective function before obtaining the optimal solution to the original lower-level problem. The idea is that each vehicle type carries only one commodity type, and the objective is to minimize the upper bound of the expected total transportation time using four temporary variables that are shown as follows.

$n_{sd}^{c\zeta z}$:

Number of vehicle-type $z$ used to deliver commodity-type $c$ from relief centers $s$ to $d$ in scenario $\zeta$

$n_{sr}^{c\zeta z}$:

Number of vehicle-type $z$ used to deliver commodity-type $c$ from relief centers $s$ to $r$ in scenario $\zeta$

$n_{rd}^{c\zeta z}$:

Number of vehicle-type $z$ used to deliver commodity-type $c$ from relief centers $r$ to $d$ in scenario $\zeta$

$n_{rt}^{c\zeta z}$:

Number of vehicle-type $z$ used to deliver commodity-type $c$ from relief centers $r$ to $t$ in scenario $\zeta$

Then, the previous bi-level SMINP model can be reformulated as the following model ${\mathbf{U}}$.

$$ \begin{aligned} & {\mathbf{U}}: \\ & \quad {\text{Min}}\,\varPsi_{1} = \mathop \sum \limits_{{c \in {\mathcal{C}}}} \left\{ {\mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{\xi \in \varXi } E^{cs} \cdot p^{\xi } \cdot \left[ {D_{cs}^{\xi } - \left( {S_{cs} - o_{s}^{c} } \right)} \right] \cdot \fancyscript{a}_{cs}^{\xi } + \mathop \sum \limits_{{d \in {\mathcal{D}}}} \mathop \sum \limits_{\xi \in \varXi } E^{cd} \cdot p^{\xi } \cdot \left[ {D_{cd}^{\xi } - \left( {S_{cd} + i_{d}^{c} } \right)} \right] \cdot \fancyscript{b}_{cd}^{\xi } } \right. \\ & \quad \quad \left. { + \,\mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{\xi \in \varXi } E^{cr} \cdot p^{\xi } \cdot \left[ {D_{cr}^{\xi } - \left( {S_{cr} - p_{r}^{c} + q_{r}^{c} } \right)} \right] \cdot \fancyscript{g}_{cr}^{\xi } } \right\} \\ \end{aligned} $$

s.t.

Constraints (18)–(22), (24), and (48)–(56)

$$ \begin{aligned} \arg \,{\text{Min}}\,\varPsi_{2}^{*} & = \sum\limits_{\zeta \in \varGamma } {\left[ {\mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{d \in {\mathcal{D}}} \mathop \sum \limits_{c \in {\mathcal{C}}} \mathop \sum \limits_{z \in {\mathcal{Z}}} } \right.n_{sd}^{c\zeta z} \cdot \left( {LT_{z} + \frac{{B_{sd} }}{{SP_{z} \cdot r_{sd}^{\zeta } }}} \right) + \mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{r \in {\mathcal{R}}} \mathop \sum \limits_{c \in {\mathcal{C}}} \mathop \sum \limits_{z \in {\mathcal{Z}}} n_{sr}^{c\zeta z} \cdot \left( {LT_{z} + \frac{{B_{sr} }}{{SP_{z} \cdot r_{sr}^{\zeta } }}} \right)} \\ & \quad \left. { + \mathop \sum \limits_{r \in {\mathcal{R}}} \mathop \sum \limits_{d \in {\mathcal{D}}} \mathop \sum \limits_{c \in {\mathcal{C}}} \mathop \sum \limits_{z \in {\mathcal{Z}}} n_{rd}^{c\zeta z} \cdot \left( {LT_{z} + \frac{{B_{rd} }}{{SP_{z} \cdot r_{rd}^{\zeta } }}} \right) + \mathop \sum \limits_{r \in {\mathcal{R}}} \mathop \sum \limits_{t \in {\mathcal{R}}} \mathop \sum \limits_{c \in {\mathcal{C}}} \mathop \sum \limits_{z \in {\mathcal{Z}}} n_{rt}^{c\zeta z} \cdot \left( {LT_{z} + \frac{{B_{rt} }}{{SP_{z} \cdot r_{rt}^{\zeta } }}} \right)} \right] \\ \end{aligned} $$

(57)

s.t.

Constraints (26)–(30), and (40)

$$ w_{sd}^{c\zeta } \cdot W^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} n_{sd}^{c\zeta z} \cdot CW^{z} , \quad w_{sd}^{c\zeta } \cdot V^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} n_{sd}^{c\zeta z} \cdot CV^{z} \quad \forall \;s \in {\mathcal{S}},\;d \in {\mathcal{D}},\;\zeta \in \varGamma $$

(58)

$$ w_{sr}^{c\zeta } \cdot W^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} n_{sr}^{c\zeta z} \cdot CW^{z} , \quad w_{sr}^{c\zeta } \cdot V^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} n_{sr}^{c\zeta z} \cdot CV^{z} \quad \forall \;s \in {\mathcal{S}},\;r \in {\mathcal{R}},\;\zeta \in \varGamma $$

(59)

$$ w_{rd}^{c\zeta } \cdot W^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} n_{rd}^{c\zeta z} \cdot CW^{z} , \quad w_{rd}^{c\zeta } \cdot V^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} n_{rd}^{c\zeta z} \cdot CV^{z} \quad \forall \;r \in {\mathcal{R}},\;d \in {\mathcal{D}},\;\zeta \in \varGamma $$

(60)

$$ w_{rt}^{c\zeta } \cdot W^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} n_{rt}^{c\zeta z} \cdot CW^{z} , \quad w_{rt}^{c\zeta } \cdot V^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} n_{rt}^{c\zeta z} \cdot CV^{z} \quad \forall \;r,\;t \in {\mathcal{R}},\;\zeta \in \varGamma $$

(61)

$$ \mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{{d \in {\mathcal{D}}}} \mathop \sum \limits_{{c \in {\mathcal{C}}}} n_{sd}^{c\zeta z} + \mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{c \in {\mathcal{C}}}} n_{sr}^{c\zeta z} + \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{d \in {\mathcal{D}}}} \mathop \sum \limits_{{c \in {\mathcal{C}}}} n_{rd}^{c\zeta z} + \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{t \in {\mathcal{R}}}} \mathop \sum \limits_{{c \in {\mathcal{C}}}} n_{rt}^{c\zeta z} \le N^{z} \quad \forall \;z \in {\mathcal{Z}},\;\zeta \in \varGamma $$

(62)

$$ n_{sd}^{c\zeta z} , n_{sr}^{c\zeta z} , n_{rd}^{c\zeta z} ,\;{\text{and}}\;n_{rt}^{c\zeta z} \;{\text{are}}\;{\text{nonnegative}}\;{\text{integer}}\;{\text{variables }}\quad \forall \;s \in {\mathcal{S}},\;d \in {\mathcal{D}},\; r,t \in {\mathcal{R}},\;\zeta \in \varGamma $$

(63)

where Eq. (57) is the lower-level objective function, which minimizes the upper bound of total expected transportation time of vehicles, and each vehicle type carries only one commodity type. Constraints (58)–(61) guarantee that the number of assigned vehicles can deliver commodity-type $c$ from relief centers $s$ to $d$, from relief centers $s$ to $r$, from relief centers $r$ to $d$, and from relief centers $r$ to $t$, respectively. Constraint (62) restricts the total number of available vehicles. Constraint (63) defines the nonnegative integer variables.

Then, the lower-level decision variables (i.e., $w_{sd}^{c\zeta *}$, $w_{sr}^{c\zeta *}$, $w_{rd}^{c\zeta *}$, and $w_{rt}^{c\zeta *}$) are obtained in model ${\mathbf{U}}$. However, in practice, each vehicle type is permitted to deliver mixed commodities. Thus, the number of assigned vehicles between any two relief centers can be reduced because each vehicle type is allowed to deliver mixed commodities. The lower-level model can be rewritten as the following model ${\mathbf{F}}$.

$$ \begin{aligned} & {\mathbf{F}}: \\ & \quad {\text{Min}}\,\varPsi_{1} = \mathop \sum \limits_{{c \in {\mathcal{C}}}} \left\{ {\mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{\xi \in \varXi } E^{cs} \cdot p^{\xi } \cdot \left[ {D_{cs}^{\xi } - \left( {S_{cs} - o_{s}^{c} } \right)} \right] \cdot \fancyscript{a}_{cs}^{\xi } + \mathop \sum \limits_{{d \in {\mathcal{D}}}} \mathop \sum \limits_{\xi \in \varXi } E^{cd} \cdot p^{\xi } \cdot \left[ {D_{cd}^{\xi } - \left( {S_{cd} + i_{d}^{c} } \right)} \right] \cdot \fancyscript{b}_{cd}^{\xi } } \right. \\ & \quad \quad \left. { + \,\mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{\xi \in \varXi } E^{cr} \cdot p^{\xi } \cdot \left[ {D_{cr}^{\xi } - \left( {S_{cr} - p_{r}^{c} + q_{r}^{c} } \right)} \right] \cdot \fancyscript{g}_{cr}^{\xi } } \right\} \\ \end{aligned} $$

s.t.

Constraints (18)–(22), (24), and (48)–(56)

$$ \begin{aligned} {\text{arg }}\,{\text{Min}}\,\varPsi_{2} & = \mathop \sum \limits_{\zeta \in \varGamma } \left[ {\mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{{d \in {\mathcal{D}}}} \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sd}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{sd} }}{{SP_{z} \cdot r_{sd}^{\zeta } }}} \right) + \mathop \sum \limits_{{s \in {\mathcal{S}}}} \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sr}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{sr} }}{{SP_{z} \cdot r_{sr}^{\zeta } }}} \right)} \right. \\ & \quad \left. { + \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{d \in {\mathcal{D}}}} \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rd}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{rd} }}{{SP_{z} \cdot r_{rd}^{\zeta } }}} \right) + \mathop \sum \limits_{{r \in {\mathcal{R}}}} \mathop \sum \limits_{{t \in {\mathcal{R}}}} \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rt}^{\zeta z} \cdot \left( {LT_{z} + \frac{{B_{rt} }}{{SP_{z} \cdot r_{rt}^{\zeta } }}} \right)} \right] \\ \end{aligned} $$

s.t.

Constraints (26)–(30), (39), and (41)

$$ \varPsi_{2} \le \varPsi_{2}^{ *} $$

(64)

$$ \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{sd}^{c\zeta *} \cdot W^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sd}^{\zeta z} \cdot CW^{z} , \quad \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{sd}^{c\zeta *} \cdot V^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sd}^{\zeta z} \cdot CV^{z} \quad \forall \;s \in {\mathcal{S}},\;d \in {\mathcal{D}},\;\zeta \in \varGamma $$

(65)

$$ \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{sr}^{c\zeta *} \cdot W^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sr}^{\zeta z} \cdot CW^{z} ,\quad \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{sr}^{c\zeta *} \cdot V^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{sr}^{\zeta z} \cdot CV^{z} \quad \forall \;s \in {\mathcal{S}},\;r \in {\mathcal{R}},\;\zeta \in \varGamma $$

(66)

$$ \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{rd}^{c\zeta *} \cdot W^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rd}^{\zeta z} \cdot CW^{z} , \quad \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{rd}^{c\zeta *} \cdot V^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rd}^{\zeta z} \cdot CV^{z} \quad \forall \;r \in {\mathcal{R}},\;d \in {\mathcal{D}},\;\zeta \in \varGamma $$

(67)

$$ \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{rt}^{c\zeta *} \cdot W^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rt}^{\zeta z} \cdot CW^{z} , \quad \mathop \sum \limits_{{c \in {\mathcal{C}}}} w_{rt}^{c\zeta *} \cdot V^{c} \le \mathop \sum \limits_{{z \in {\mathcal{Z}}}} m_{rt}^{\zeta z} \cdot CV^{z} \quad \forall \;r,\;t \in {\mathcal{R}},\;\zeta \in \varGamma $$

(68)

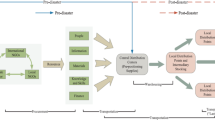
where Constraint (64) is the upper bound constraint. Constraints (65)–(68) restrict that assigned vehicle fleets are able to deliver the mixed commodities from relief centers $s$ to $d$, from relief centers $s$ to $r$, from relief centers $r$ to $d$, and from relief centers $r$ to $t$, respectively. Besides the description of the solution method, we also summarize the proposed method in the flowchart of Fig. 2.

Fig. 2

Flowchart of the solution method

6 Case study

6.1 Test instance

To illustrate the validity and effectiveness of the proposed method, a case study of the Great Sichuan Earthquake measured 8.0 on the Richter scale that occurred in 2008 in China is studied in this section. With the disaster-related information (e.g., relief-center locations, demand at relief centers, and routes), the proposed bi-level SMINP model and linearization method are employed to identify demand and supply relief centers and determine the total incoming and outgoing shipments at relief centers, commodity flows between relief centers, and numbers of vehicles of different types transporting mixed commodities between relief centers. This study considers 11 disaster areas (relief centers), 2 commodity types (i.e., water and food), and 3 vehicle types (i.e., small, medium, and large vehicles). Since the data are not yet released from the government, the partial data (e.g., demand and stock levels) are randomly generated and applied to test the model and approach, which will not lead to essentially different results.

In the impact area of the earthquake, for each commodity type, the relief centers are divided into three categories, namely complete supply relief centers, complete demand relief centers, and potential demand or supply relief centers. The possible quantities of demand and stock levels at relief centers are randomly selected from the specific intervals and presented in Table 1. Here, we consider five possible quantities (scenarios) of demand at each relief center. In the multi-commodity rebalancing process, those two commodity types need to be rebalanced simultaneously. The characteristics of commodities and vehicles are reported in Table 2. And each vehicle type is allowed to deliver mixed commodities under both weight and volume capacities.

Table 1 Demand and stock level at relief centers

Table 2 Characteristics of commodities and vehicles

During the multi-commodity rebalancing process, the state of the transportation network needs to be determined. In this study, the topology of the transportation network developed by Wang et al. (2014) is applied, where the first 11 nodes (disaster areas) are deemed relief centers after the earthquake. There are three relief-center categories, namely (1) complete demand relief centers (i.e., 1, 2, 3, and 5), (2) complete supply relief centers (i.e., 4, 9, and 11), (3) potential demand or supply relief centers (i.e., 6, 7, 8, and 10). The details about the transportation network with available links and distance are exhibited in Table 3. In the transportation process, there are three possible transportation-network availabilities that are 0.5, 0.8, and 1.0 with the corresponding probabilities of 0.5, 0.3, and 0.2, respectively.

Table 3 Distance between relief centers in the transportation network

Given the parameter values, the proposed models ${\mathbf{O}}$, ${\mathbf{U}}$, and ${\mathbf{F}}$ in Sect. 5 are implemented in the IBM ILOG CPLEX Optimization Studio (Version: 12.6). The maximum computation time for model ${\mathbf{O}}$ is 10 min. All the experiments are run on a computer with an Intel(R) Core(TM) i7-7700 CPU@3.6 GHz and 8 GB memory under the Windows 10 Pro system.

6.2 Computational results

The main results for the bi-level SMINP model are provided in this section. The results of the leader problem associated with two commodity types are shown in Fig. 3, involving the stock levels of commodities at 11 relief centers from left to right. Besides, the optimal upper-level decision variables of incoming and outgoing quantities of commodities at relief centers are also provided. As shown in Fig. 3, the incoming and outgoing quantities of commodities are closely related to the demand and stock levels at relief centers. Generally, for the complete demand relief centers, a demand relief center with a larger weighted value and less stock level receives more commodity to meet its high-pressure need, in the event that this demand relief center receives an inadequate delivery. For instance, in Fig. 3a the 5th relief center with weighted value 76 can receive more water than can the relief center 3 with weighted value 32 in the event that the former demand center receives an inadequate delivery. For the complete supply relief centers, a supply relief center with a larger weighted value and less stock level should deliver less commodity in the event of this supply relief center sharing an excessive quantity of the commodity of water to the demand relief centers. Figure 3b shows that the 11th relief center with weighted value 55 should maintain a higher food inventory level than the 4th relief center with weighted value 31. For the potential demand or supply relief centers, the relief centers with larger weighted values and smaller stock levels are usually identified as demand relief centers, whereas relief centers with smaller weighted values and higher stock levels are usually identified as supply relief centers. For example, in Fig. 3a, the 5th relief center is deemed a demand relief center and the 8th relief center is deemed a supply relief center.

Fig. 3

Multi-commodity rebalancing strategy at 11 relief centers

Having obtained the optimal upper-level decisions of incoming and outgoing quantities of commodities at relief centers, the optimal set of lower-level decisions can be constructed. The previous optimal multi-commodity rebalancing strategy is input into the models ${\mathbf{O}}$ and ${\mathbf{U}}$, the commodity flows between relief centers are presented in Table 4 without showing zero commodity-flow route. It is obvious that the commodity-flow routes are almost the same in models ${\mathbf{O}}$ and ${\mathbf{U}}$. However, the commodity flows are different in three scenarios, which indicates that the transportation-network availability also affects the commodity flows between relief centers. The above results indicate that the model ${\mathbf{U}}$ is acceptable to guide the multi-commodity rebalancing process.

Table 4 Commodity flows between relief centers in models $\varvec{O}$ and ${\mathbf{U}}$

The total required vehicles of different types are also obtained and reported in Table 5 for the models ${\mathbf{O}}$, ${\mathbf{U}}$, and ${\mathbf{F}}$. It is obvious that the total required vehicles of different types are also different in three scenarios because the different transportation-network availabilities affect the commodity flows and the number of vehicles between relief centers. As the vehicles have weight and volume capacities, it is better to satisfy both of them with the consideration of vehicle speed. In general, more medium vehicles are used because the lower-level objective emphasizes the significance of transportation time and medium vehicles can provide relatively quick delivery. Furthermore, compared with the model ${\mathbf{U}}$, Table 5 also reveals that a smaller number of vehicles are used by applying the model ${\mathbf{F}}$ because the utilization of vehicles is improved by allowing them to carry mixed commodities.

Table 5 Total required vehicles of different types in models $\varvec{O}$, $\varvec{U}$, and $\varvec{F}$

6.3 Sensitivity analysis

To analyze how relief-center weighted value affects the incoming and outgoing quantities of water at relief centers, three relief centers are tested, including a complete demand relief center (3rd) with weighted value 32, a complete supply relief center (9th) with weighted value 74, and a potential demand or supply relief center (10th) with weighted value 74. In Fig. 4, both the incoming and outgoing quantities of water change at those three relief centers as the weighted value goes from 20 to 80. As the relief-center weighted value grows [Fig. 4a], the complete demand relief center receives more water because a larger unmet relief center generally expects more water. By contrast, the complete supply relief center delivers less water as the weighted value increases [Fig. 4b] in case that this relief center faces an increased demand in the future. As shown in Fig. 4c, initially, this potential demand or supply relief center is identified as a supply relief center. However, with the increase of weighted value, this potential demand or supply relief center is deemed a demand relief center, to reduce the unmet risk at a relief center with a higher weighted value.

Fig. 4

Quantities of incoming and outgoing water given different weighted values at relief centers

The relief-center weighted value also has a great influence on the total shipment between demand and supply relief centers. In Fig. 5, with the increase of the weighted value at demand relief center 3, a growing total quantity of shipment (water) between demand and supply relief centers is required because the demand relief centers dominate the water rebalancing process and expect more incoming shipments. By contrast, as the increase of weighted value at supply relief center 9, there is a decreasing total quantity of shipment (water) between demand and supply relief centers because the supply relief centers dominate the water rebalancing process and expect less outgoing shipments. Compared with the demand relief center 3, the increase of weighted value at potential demand or supply relief center 10 only reduces the total quantity of shipment marginally.

Fig. 5

Total quantity of shipment (water) given different weighted values at relief centers

To investigate the effect of different stock levels at relief centers, the incoming and outgoing quantities of food are tested at three relief centers (i.e., relief centers 3, 10, and 11) from three groups, respectively. In Fig. 6, both the incoming and outgoing quantities of food change at those three relief centers when the stock level goes from 200 to 300. As the stock level grows [Fig. 6a], it is easy to observe that the complete demand relief center 3 receives less food due to its high stock level. By contrast, the complete supply relief center 11 delivers more food to other demand relief centers as the surplus quantity of food increases [Fig. 6b]. As shown in Fig. 6c, initially, this potential demand or supply relief center 10 is identified as a demand relief center. However, with the increase of stock level, this potential demand or supply relief center is deemed a supply relief center.

Fig. 6

Quantities of incoming and outgoing food given different stock levels at relief centers

To investigate the effect of different stock levels on the total quantity of shipment between demand and supply relief centers, three relief centers are evaluated under different stock levels, as shown in Fig. 7. Obviously, Fig. 7 shows similar decreasing trends in the total quantities of shipments at relief centers 3 and 10 because more food is stocked to meet their own demand at complete demand and potential demand or supply relief centers. On the contrary, at the complete supply relief center 11, the total quantity of shipment increases as the stock level grows, because more surplus food needs to be rebalanced and sent out. Thus, we clearly obtain the relationship between the total quantity of shipment and stock levels at different relief centers.

Fig. 7

Total quantity of shipment given different stock levels at relief centers

In addition to the relief-center weighted value and stock level, the probability of possible demand in each scenario also has a great influence on the multi-commodity rebalancing strategy. To validate the reliability of the proposed model and method, the solution performances are compared for three different demand shapes (i.e., shapes I, II, and III, as presented in Table 6) with different probability distributions.

Table 6 Three demand shapes with the probability distribution

The results of incoming and outgoing shipments at relief centers are presented in Table 7. As shown in Table 7, the proposed method determines the optimal incoming and outgoing quantities of commodities and successfully identifies the demand and supply relief centers. Specifically, relief centers 6 and 10 are deemed demand relief centers and relief centers 7 and 8 are deemed supply relief centers for the commodity of water, whereas relief centers 6, 7, and 8 are deemed demand relief centers and only relief center 10 is deemed a supply relief center for the commodity of food. And obviously, in multi-commodity rebalancing, relief centers 8 and 10 are demand and supply relief centers at the same time. According to the identification of relief centers with incoming and outgoing shipments, the next step is to use different vehicles to transport the mixed commodities among relief centers.

Table 7 Quantities of incoming and outgoing commodities given three different demand shapes

In order to validate the effectiveness and demonstrate the application of the proposed method, it is tested in terms of the solution performances based on the above three different demand shapes. The vehicle numbers of different types and Gaps in a required CPU time (600 s) are reported in Table 8. As illustrated in Table 8, both the models ${\mathbf{O}}$ and ${\mathbf{F}}$ outperform the model ${\mathbf{U}}$, because the vehicles of different types are allowed to deliver mixed commodities in the models ${\mathbf{O}}$ and ${\mathbf{F}}$. Interestingly, even though the small vehicle has the highest speed, the small weight and volume capacities limit the relatively quick delivery of mixed commodities between relief centers. By contrast, the medium vehicle can provide relatively quick delivery to reduce the total transportation time due to its higher weight and volume capacities. The lower-level objective-function values are presented in Fig. 8. In all demand shapes, even though the model ${\mathbf{O}}$ has the smallest lower-level objective function value, it has low effectiveness because the computational time is too long. And the model ${\mathbf{F}}$ obtains the optimal solution within a reasonable computational time without losing a big generosity.

Table 8 Results under three different demand shapes

Fig. 8

Lower-level objective function values in different models

7 Conclusions and future research

This study focused on the multi-commodity rebalancing problem that differs from previous studies and combines key decisions in the disaster response under uncertain demand and transportation-network availability. The strategic decisions of the model involve (1) incoming and outgoing shipments at relief centers; (2) identification of demand and supply relief centers; (3) commodity flows between relief centers; and (4) vehicle numbers of different types transporting mixed commodities between relief centers. To support those strategic decisions, a bi-level SMINP model using a scenario-based approach was proposed for the multi-commodity rebalancing problem with the objectives of fairness and timeliness. Two objectives were considered in the proposed model, namely (1) the upper-level objective is to maximize the fairness by minimizing the total dissatisfaction level (i.e., expected total weighted unsatisfied demand) at relief centers and (2) the lower-level objective is to minimize the expected total transportation time. In addition, a big positive number and five auxiliary binary variables were introduced to linearize the model so that the model could be solved in the CPLEX solver. Finally, a case study was conducted with result discussion and sensitivity analysis of several key parameters to illustrate the applicability and effectiveness of the proposed model.

Form the case study, we can obtain several managerial insights from the theory and practice in response to a disaster. First, an appropriate multi-commodity rebalancing strategy is determined, which is beneficial for the managers to decide the quantities of incoming and outgoing shipments at relief centers. Second, it is obvious that the upper-level decision variables are quite sensitive to the weighted values and stock levels at relief centers. From the sensitivity analysis, the area with high potential disaster severity needs more storage of the commodities to avoid the incoming shipments at relief centers. Third, we found that the medium vehicle can provide relatively quick delivery. As a consequence, more medium vehicles should be prepared in advance in the case of a large-scale natural disaster. However, there is a limitation that it is quite hard to find the lower-level optimal solution when the size of the problem is large.

Although this study addresses the notable gap between the previous studies and the current research in a real disaster situation, some directions are still meaningful to be extended in future studies. For example, this study has addressed a multi-commodity rebalancing process without considering traffic congestions. However, it is interesting to take the traffic congestions into account in the multi-commodity rebalancing. Another future consideration is to develop a more reliable multi-commodity rebalancing by considering a multi-period process in disaster response. An efficient algorithm also needs to be identified to address the computational issue for large-scale cases. Moreover, it is also an interesting research direction to consider various risks (i.e., facility and road disruption) so that a more reliable multi-commodity rebalancing process can be built.