Modeling single machine preemptive scheduling problems for computational efficiency

Abstract

We propose two modeling approaches to solve single machine preemptive scheduling problems with tardiness related objectives. Employing the conventional time-indexed formulation, we first build a model that explicitly identifies completion times of jobs with varying release times, due dates, and processing times. The second model adopts the aggregate planning view and eliminates binary constraints. Under this approach, each job is seen as a unit demand while its due date is mapped to a period where this unit is demanded. With this mapping, the periodic job allocation decisions are transformed into periodic production decisions that are measured by fraction of demand. Consequently, instead of explicit representation of the job completion times, this model tracks the amounts of production completed and backlogged via inventory and shortage variables and conservation of units constraints. We establish that the latter model provides tighter bounds and demonstrate that it provides a more efficient platform for optimization via computational analysis employing four commonly used tardiness related criteria and a case study from a real life application. Numerical computations reveal that aggregate planning view becomes more dominant in terms of computational performance as the problem size grows.

1 Introduction

In this paper, we introduce two alternative mathematical modeling approaches for the single machine preemptive scheduling problems with tardiness related criteria. In a schedule that allows preemption, a job can be temporarily interrupted for processing of another job with higher priority. The general structure of the problem involves a finite number of jobs with known release and due dates. The jobs have varying weights that represent the monetary penalties associated with the tardiness measures. In practice, these weights are typically determined based on tangible costs that are explicitly stipulated by contracts, intangible costs tied to loss of goodwill, or both. Using the notation due to Graham et al. (1979), we represent this general optimization problem as: $1 \text { } |\text { } pmtn, r_i, d_i, p_i \text { }|\text { } F$, where $r_{i}$, $d_{i}$, $p_i$, and F denote the release date, due date, workload requirement for job i, and the tardiness related objective respectively.

Our work is mainly motivated by our collaboration with a major aviation maintenance, repair and overhaul (MRO) company that services landing gear for aircraft. The MRO sector in general is very particular on timely turnaround times and on-time deliveries as the customers in this sector are burdened with large capital investments on equipment. For example, delays in landing gear service deliveries may result in an average cost of 50,000.00 USD per day for a commercial airline and thousands in tardiness penalties for the service provider—not to mention less quantifiable costs such as good-will losses. Therefore, finding optimal or near-optimal solutions are quite critical in such environments for profitability and sustenance of both the providers and their customers.

The first model introduced in our study adopts the conventional time-indexed formulation approach that builds on explicit representation of completion times of jobs using time indexed formulation. Thus, the tardiness of jobs can be directly measured by comparison of the completion times and the due dates. This approach necessitates the use of binary variables so as to identify the completion times. As such, we refer to this model as the Binary Preemptive Scheduling (BPS) Model. The second model that we propose in this paper is built on a quite different approach that employs the aggregate planning view and referred to as the Aggregate Preemptive Scheduling (APS) Model. In this approach, each job is seen as a unit demand while its due date is mapped to a period where this unit is demanded. With this mapping, the periodic job allocation decisions are transformed into periodic production decisions that are measured by fraction of demand. Consequently, instead of explicit representation of the job completion times, the proposed APS model tracks the amounts of production completed and backlogged via inventory and shortage variables and conservation of units constraints.

In our analysis we establish the equivalency of both models in terms of solving the same problem. Subsequently, we analytically show that the APS model provides better bounds compared to the BPS model, which suggests better computational performance for the former one. We carry out computational experiments using a variety of objectives to investigate and computationally compare the performances of both models. Specifically, we consider minimization of total weighted tardiness, total weighted completion times, total weighted tardiness and earliness, and total weighted number of tardy jobs. The computational results indicate a categorical dominance for the APS model over the BPS model in terms of computational times and quality of solutions obtained in limited time frames. The advantage of the APS model becomes more apparent as the number of jobs increases. To demonstrate the practicality of the APS model, we present a case study from the aviation MRO industry, where the dimension of the model is extended with the inclusion of overtime decisions. The overall analyses presented in this paper establish that APS model is a promising tool for generating optimal or near-optimal schedules reasonably quickly for real life applications.

1.1 Literature review

Most common tardiness related measures relate to total weighted tardiness (TWT), total weighted completion times (TWC), total weighted earliness and tardiness (TWET), and total weighted number of tardy jobs (TWNTJ). Majority of tardiness related objectives either directly use these objectives or their variations. Therefore, we employ these four measures as the base to investigate the performance of the proposed models in this paper. Of these criteria, TWT emerges as probably the most relevant and practical objective from which a diversity of tardiness related problems emerge. While the majority of reported work focus on non-preemptive scheduling, a few consider the preemptive case. A comprehensive survey of single-machine tardiness problems are provided by Sen et al. (2003), and  Koulamas (2010). It is established that the non-preemptive general TWT problem is NP-hard in the strong sense (Lenstra et al. 1977). Since every preemptive schedule can be transformed into a non-preemptive schedule with no larger objective value (McNaughton 1959), the complexity of the non preemptive case also applies to the general TWT problem with preemption (Yuan and Lin 2005; Bulbul et al. 2007). Recent research that focus on preemptive scheduling and tardiness either do not consider weights (Tian et al. 2009; Hendel et al. 2009) or assume identical processing times (Tian et al. 2006; Jaramillo and Erkoc 2017).

The TWC problem can be framed as a special case of the TWT problem, where the release date of each job is counted as its due date as well. The TWC problem with arbitrary release dates and no-preemption is identified as a NP-hard problem (Labetoulle et al. 1984). In earlier papers, Hariri and Potts (1983) and Belouadah et al. (1992) consider preemption for generating bounds for their branch and bound algorithms that they propose for the general TWC problem. More recently, Wang et al. (2005) provide a formal proof that shows that the preemptive TWC problem is also NP-hard in the strong sense. Heuristic solution approaches are proposed for various versions of this problem including identical processing times (Batsyn et al. 2013), rolling horizon (Sitters 2010; Schulz and Skutella 2002) and multiple uniform parallel machines (Leung et al. 2007).

With the advent of the “Just-in-time” paradigm, several researchers have integrated earliness penalties into the TWT problem. Branch and bound based heuristics (Li 1997; Liaw 1999; Vanhoucke et al. 2001) and metaheuristics (Liao and Cheng 2007; Yano and Kim 1991) are proposed for the the problem of minimizing total weighted earliness and tardiness (TWET).

Similar to the other tardiness related objectives, the majority of research on TWNTJ assume non-preemption (M’Hallah and Bulfin 2007; Adamu and Adewumi 2014). While the non-preemptive case is known to be NP-Hard (Karp 1972), the preemptive case is shown to be maximal pseudopolynomially solvable (Lawler 1990). The work reported on the preemptive version of this problem is limited by some early studies that consider polynomial algorithms for the special cases where the jobs have agreeable release and due dates (Lawler 1994; Baptiste 1999).

While the literature in the area of tardiness related problems is vast and very diverse, only a select minority of such work has a direct connection with the topics and problems discussed in this paper. Overall, due to the complexity of the scheduling problems with tardiness related objectives, the focus in research has been on development of heuristics and bounds. A few number of papers that consider efficient formulations and exact methods explicitly focus on the non-preemptive cases. These papers attempt to improve the exact solution methods by introducing valid inequalities (Sousa and Wolsey 1992; Berghman and Spieksma 2015), network based formulation (Pessoa et al. 2010), or bucket indexed formulation (Boland et al. 2016). Similar studies that tackle the preemptive case are virtually nonexistent or limited to instances of relatively small size. Our paper fills the existing gap in the relevant literature by introducing effective formulations for the preemptive scheduling problems that can be easily applied to a variety of tardiness related criteria.

The rest of the paper is organized as follows. Section 2 formally introduces the mathematical models. Analytical comparison of the models is discussed in Sect. 3. Section 4 presents the computational experiments using four different tardiness related objective functions and a case study from a real life application. Finally, Sect. 5 concludes the paper.

2 Mathematical models

Our focus is on the single machine preemptive scheduling problems with a variety of tardiness related objectives. In this context, processing of a job can be interrupted or temporarily suspended at any moment in order to allow for another job’s processing. It is assumed that there is no precedence relationship among jobs, and the objective is always subjected to known release and due dates across a finite number of jobs. The time horizon is constituted by a set of discrete periods of equal length, where the time index is represented by t, $t\in \{1,2,\dots ,T\}$. We represent this general optimization problem as: $1 \text { } |\text { } pmtn, r_i, d_i, p_i \text { }|\text { } F$, where $r_{i}$, $d_{i}$, $p_i$, F denote the release date, due date, workload requirement for job i, and the tardiness related objective respectively.

In our approach $p_i$ represents the amount of work to complete job i measured in terms of capacity such as labor hours. In that respect, our interpretation is slightly different than the conventional approach where $p_i$ represents the processing time. We map the maximum amount of work that can be performed on a job (i.e., capacity) in a given period to $\alpha$. To explain the relation between $p_i$ and $\alpha$, consider the example where $p_i = 1$ and $\alpha =0.4$. This indicates that only 0.4 work units of job i can be completed in a single period if all the available capacity is allocated to this job. As such, the processing time for the job is 2.5 periods, that is, this job can be completed in 2.5 periods with uninterrupted full capacity allocation. Clearly, any processing time can be easily transformed into the work units measured by $p_i$.

In this setting, unit tardiness (and earliness if applicable) costs may not be identical for all jobs due to varying value contribution of the jobs or the respective customers. They may also reflect the tangible contracted penalties. Therefore, jobs are typically weighed differently. These weights apply in a similar fashion if the problem involves earliness penalties and they are denoted by $w_i$.

In this section, we introduce two mathematical modeling approaches for this setting. The first one is based on the traditional time-indexed formulation that employs the sequencing view. It involves a mixed integer programming model with binary scheduling variables, which will be referred to as the Binary Preemptive Scheduling (BPS) Model in the rest of the paper. The second model adopts the principles of aggregate planning and eliminates the binary variables by employing the work-balance view. We refer to this model as the Aggregate Preemptive Scheduling (APS) Model.

2.1 The binary preemptive scheduling (BPS) formulation

The BPS model adopts the sequencing view of scheduling and depends on explicit representation of the job completion times, which requires use of binary variables. This model is basically built as a generalization of the mathematical model proposed by  Jaramillo and Erkoc (2017) specifically for the TWT problem, which considers only jobs with identical processing times. The BPS formulation in our context considers the more general case with nonidentical workload requirements, and employs binary, continuous, and discrete decision variables as listed in Table 1.

Table 1 Decision variables of the BPS model

The binary variable $y_{it}$ tracks the completion times of jobs for a finite set of jobs, N, over a planning horizon that consists of T periods; whereas, $u_i$ identifies whether or not job i is completed after its due date. While the continuous variables determine the amount of allocations of regular capacity $x_{it}$ that are necessary to complete the jobs, the discrete variables are needed to evaluate the finish dates $f_{i}$, the number of late periods $l_{i}$, and the number of early periods $e_i$. The tardiness of job i is captured by the positive lateness, i.e., $l_{i}=w_{i} \text { max}\{0,f_{i}-d_{i}\}$ and the earliness by $e_{i}=w_{i} \text { max}\{0,d_{i}-f_i\}$. Using this notation, we can write down the general BPS model as follows:

$$\begin{aligned} \text {minimize: }&\sum _{i \in N}w_iF_{i}(f_i) \nonumber \\&\text {subject to:} \end{aligned}$$

(1)

$$\begin{aligned}&\sum _{t=r_{i}}^{T}y_{it}=1, \qquad \qquad \forall i\in N \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{i \in N: r_i \ge t}x_{it}\le \alpha , \qquad \quad \forall t\in \{1, \dots ,T\} \end{aligned}$$

(3)

$$\begin{aligned}&\sum _{t=r_{i}}^{T} x_{it}= p_i,\qquad \qquad \forall i\in N \end{aligned}$$

(4)

$$\begin{aligned}&\sum _{t=r_{i}}^{\gamma } x_{it} \ge p_iy_{i\gamma }, \qquad \quad \forall i\in N,\ \forall \gamma \in \{r_{i},\dots ,T\} \end{aligned}$$

(5)

$$\begin{aligned}&f_{i}=\sum _{t=r_i}^{T}ty_{it}, \qquad \qquad \forall i\in N \end{aligned}$$

(6)

$$\begin{aligned}&l_{i}\ge f_{i}-d_{i}, \qquad \qquad \quad \forall i\in {N} \end{aligned}$$

(7)

$$\begin{aligned}&e_{i}\ge d_{i}-f_i, \qquad \qquad \quad \forall i\in N \end{aligned}$$

(8)

$$\begin{aligned}&T \cdot u_i \ge f_{i}-d_i, \qquad \quad \forall i\in N \end{aligned}$$

(9)

$$\begin{aligned}&x_{it} \ge 0;\text { } f_{i}, l_{i}, e_i, u_i \in {{\mathbb {Z}}^{+}};\text { }y_{it} \in \{0,1\} \qquad \forall i\in N, t\in \{r_i\dots ,T\} \end{aligned}$$

(10)

In the general representation, the objective given in (1) minimizes the sum of functions of the completion times denoted by $F_i(f_i)$. It is equivalent to $l_i$, $l_i+e_i$, and $u_i$, for the TWT, TWET, and TWNTJ problems respectively. We note that TWC is a special case of the TWT problem where the due dates of jobs are equal to their release dates. The first set of constraints (2) ensure that each job is completed by the end of the planning horizon. Constraint (3) enforces the regular capacity limit per period designated as $\alpha$. Constraint (4) ensures that all required work for each job can only begin after its release date and must be completed within the planning time horizon and (5) guarantees that no job is marked completed until all required work is carried out. The constraint set (6) captures the completion time for each job. Given completion times, constraint (7) tracks the number of tardy periods for the jobs. This constraint is relevant for the TWT, TWC, and TWET problems. Likewise, constraint (8) sets the earliness of the jobs, which is to be used in the TWET problem only. Constraint (9) is needed for the TWNTJ problem only and marks whether a job is tardy or not. We note that in this case, although $u_i$ must be binary, we define it as a positive integer in the model. Since the objective for the TWNTJ problem degrades with higher values of $u_i$, it is straightforward to observe that the model will never assign this variable a value greater than 1 at optimality. We refer to this attribute of the variable as the binary property.

It is also important to observe in the model that for integer values of due dates $d_i$ and t, variables $f_i$, $l_i$, and $e_i$ possess the integrality property. This follows from the fact that the right hand sides in constraints (6), (7), and (8) always produce integer values. As such, the integrality constraints for these variables can be relaxed in implementation of the model.

2.2 The aggregate preemptive scheduling (APS) formulation

The APS model employs the work-flow balance approach, where any partial work completed for a job is analogous to partial production of an order under the aggregate planning context. This view is enabled by preemption, which allows for partial allocation of workloads of jobs to the existing capacity across the planning horizon. In this context, any completed work of a job before its due date is akin to inventory carried over to the next period and any uncompleted work after the due date is analogous to backlogs. This way, the model maintains the workload balance for each job instead of explicitly representing the completion times. To enable this formulation, we introduce two new variables, namely $I_{it}$ and $B_{it}$, that capture the fraction of the completed work before the due date and the incomplete work past due for job i in period t, respectively. The APS model tracks the completion of jobs by means of these two key variables, which eliminate the need for job completion variables, $y_i$ and $f_i$, employed in the BPS model. In order to use these variables, we need to modify the work allocation variable, $X_{it}$, so that it measures the fraction of workload associated with job i assigned for processing in period t rather than a general workload unit as is the case in the BPS model. As such, $X_{it}$ can take values only in [0, 1].

While the BPS model employs a one-dimensional array to specify the due date for each job (i.e., $d_i$), the APS model requires a two-dimensional array (i.e., $D_{it}$) in order to assemble the workload balance constraints. In this model, $D_{it}$ is a binary input parameter and captures the due date of job i by taking the value of 1 if the due date for this job is period t and 0 otherwise. Under the aggregate planning view this representation implies that 1 unit (i.e, 100%) job i is demanded in period t if and only if $D_{it}=1$.

Since the completion time variables are eliminated in the new framework, the tardiness and earliness related variables are controlled via $B_{it}$ and $I_{it}$ respectively. As the backlog variable $B_{it}$ signifies tardiness, we need to map the tardiness measure to this variable. Similar to the due date parameter, we redefine the tardiness variable using the same two indices as $L_{it}$, which measures the tardiness of job i in period t. Likewise, the new earliness measure, $E_{it}$ will be linked to $I_{it}$. The decision variables for the general version of the APS model are listed in (Table 2).

Table 2 Decision variables of the APS model applied to the TWT problem

Using the new notation, we can write down the APS model as follows:

$$\begin{aligned} \text {minimize: }&\sum _{i \in N} \sum _{t=r_i}^T w_i {\overline{F}}_{it}(I_{it},B_{it}) \nonumber \\&\text {subject to:} \end{aligned}$$

(11)

$$\begin{aligned}&B_{i,r_i}-I_{i,r_i}=D_{i,r_i}-X_{i,r_i},\qquad \forall i\in N \end{aligned}$$

(12)

$$\begin{aligned}&B_{it}-I_{it}=D_{it}+B_{i,t-1}-X_{it}-I_{i,t-1}, \quad \forall i\in N,\forall t\in \{r_i+1,\dots ,T\} \end{aligned}$$

(13)

$$\begin{aligned}&\sum _{i\in N :r_i \ge t} p_iX_{it}\le \alpha , \qquad \qquad \text { } \text { } \forall t\in \{1,\dots ,T\} \end{aligned}$$

(14)

$$\begin{aligned}&\sum _{t=r_i}^{T} X_{it}= 1,\qquad \qquad \qquad \text { } \forall i \in N \end{aligned}$$

(15)

$$\begin{aligned}&L_{it}\ge B_{it}, \qquad \qquad \qquad \qquad \forall i \in N, \forall t\in \{d_i,\dots ,T\} \end{aligned}$$

(16)

$$\begin{aligned}&E_{it}\ge I_{it}-1+\epsilon , \qquad \qquad \text { } \forall i \in N, \forall t\in \{r_i,\dots ,d_i-1\} \end{aligned}$$

(17)

$$\begin{aligned}&U_i \ge B_{i,d_i}, \qquad \qquad \qquad \qquad \forall i\in N \end{aligned}$$

(18)

$$\begin{aligned}&X_{it},\ B_{it},\ I_{it}\in \left[ 0,1\right] , \qquad \text { } \text { } \forall i\in N, \forall t\in \{r_i,\dots ,T\} \end{aligned}$$

(19)

$$\begin{aligned}&L_{it},E_{it},U_i \in {{\mathbb {Z}}^{+},} \qquad \qquad \text { } \text { } \forall i\in N, \forall t\in \{r_i\dots ,T\} \end{aligned}$$

(20)

The objective given in (11) minimizes the sum of functions of the early and late work completions by ${\overline{F}}_{it}$, which is equivalent to $L_{it}$, $L_{it}+E_{it}$, and $U_i$, for the TWT, TWET, and TWNTJ problems respectively. As mentioned earlier, TWC is a special case of the TWT problem where all due dates are equal to their release dates, that is, $d_i=r_i$, $D_{i,r_i}=1$, and $D_{it}=0$ for all other periods. The first two constraints, namely, (12) and (13), are the work balance equations which capture the fraction of late work (backlog) for each job. With these constraints, the model tracks the fraction of work completed before and after the deadline of each job. Constraint (14) enforces the capacity limit. Constraint (15) ensures that all jobs must be completed by the end of the planning horizon.

While constraint (16) captures lateness of jobs at each period, constraint (17) determines the earliness. We note that due to the minimization objective, the model will attempt to assign the smallest possible values to $L_{it}$ and $E_{it}$. Since $B_{it} \le 1$, the lower bound for $L_{it}$ enforced by constraint (16) cannot be greater than 1. Consequently, it is not difficult to see that at any optimal solution, the value of $L_{it}$ must be either 0 or 1, although it is not designated as a binary variable in the model. As such, $L_{it}$ functions as a lateness indicator with $L_{it}=1$ indicating that the job is late in period t. Similar to $u_i$ of the BPS model, $L_{it}$ has the binary property. It is straightforward to observe from (11) and (17) that $E_{it}$ has the same property due to similar reasons. In (17), parameter $\epsilon$ represents any infinitesimal strictly positive value, which ensures that the right hand side is strictly positive if and only if $I_{it}=1$ indicating that the job is completed earlier than its due date. In this case, the constraint guarantees that the job will be regarded early in this period, that is, $E_{it}=1$. Consequently, the tardiness and earliness of a job can be measured by the sum of lateness and earliness indicators respectively over the time horizon as signified by the objective function. Finally, constraint (18) identifies whether a job is tardy or not by evaluating the backlog amount at its due date. As we show in the next section, similar to the BPS model, solution to the APS model provides a feasible optimal preemptive schedule for a given set of jobs with known release and due dates.

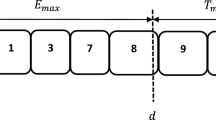
To illustrate how the APS framework functions consider the feasible schedule given in Fig. 1 as an example. Suppose that the release periods for jobs 1, 2, 3, and 4 be 1, 2, 4 and 7 respectively and the processing times are 2 periods for all jobs except job 3 which has a processing time of 1.5 periods. Moreover, let the due dates for the jobs be 4, 5, 5, and 9 respectively. The capacity per period is normalized to 1 ($\alpha = 1$) and as such, in each period at most half of the required work can be processed for jobs 1, 2, and 4 and at most two-thirds of the required work can be processed for job 3. Consequently, each block in the figure represents one-fourth of the required work for the first group of jobs and one-third of the required work for job 3.

Fig. 1

A sample feasible schedule

The corresponding values for the APS variables for jobs 1 and 2 obtained from constraints (12) and (13) are given in Table 3 for this example. We note that while job 1 is 2 periods tardy, job 2 is 2 periods early in this case. In the example, first period capacity is allocated for job 1 and thus, $X_{1,1}=0.5$. This job is completed with capacity allocations in periods 4 and 6 with $X_{1,4}=X_{1,6}=0.25$. Consequently, the completed work from period 1 is carried over as “inventory” until period 4, at which time the job is due (i.e., $D_{1,4}=1$). After this period one-fourth of job 1 will be unfinished until period 6, which is captured by $B_{1,4}=B_{1,5}=0.25$. Thus, in these periods $L_{1,4}=L_{1,5}=1$ due to constraint (16) and $U_1=1$ due to constraint (18). On the other hand, $B_{2,t}=0$ for job 2 across all periods since this job has no unfinished work after its due date. Since job 2 is completed in period 3, it has an inventory of 1 unit until its due date and as such the earliness values in this time interval must also be one because of constraint (17). It is straightforward from the BPS model that the corresponding values for its variables for these jobs are $y_{1,6}=1,f_1=6, l_1=2,y_{2,3}=1,f_2=3,e_2=2$.

Table 3 APS model variables for jobs 1 and 2

3 Analytical comparison of the models

Before moving on to computational analysis, we first discuss the analytic aspects of both modeling approaches. First, we establish the equivalence of the models indicating that they both provide the same optimal solution to the problem of single machine scheduling with preemption. Later, we examine the structures of both models in terms of their performances in generating lower bounds.

3.1 Model equivalency

In order to be able to establish that the BPS and the APS models can be employed to solve the same problem, we need to show that both models have equivalent objective functions that are subject to equivalent constraints resulting in matching optimal solutions. For both models, the core structure remains the same across all tardiness and earliness related objectives. It is straightforward to observe in the BPS and APS models, regardless of the objective of the schedule, the core constraint sets maintain that the entire required work for each job is assigned to the single resource across the planning period as per (4) and (15) and the limited capacity of the resource is enforced as per (3) and (14). Consequently, in both representations, these constraints are sufficient to build a feasible schedule. All other constraints are needed for optimization purposes and shaped by the objective of the problem. In order to measure tardiness or earliness, the models must be able to control the completion times. In the case of TWNTJ, they must track whether a job is tardy or not. Basically, the models differ from each other in regards to how they perform these functions.

The difference between the models in capturing completion times mainly stems from how they measure tardiness and earliness. From evaluating the components of the objective functions, we can observe that the measurement of tardiness ($l_i$ and $L_{it}$) and earliness ($e_i$ and $E_{it}$) variables do not map directly from one model to the other. While in the BPS model $l_i$ (resp.$e_i$) represents the actual number of tardy (resp. early) periods for job i, the variable $L_{it}$ (resp.$E_{it}$) in the APS model tracks the individual periods in which job i is actually tardy (resp. early). For both objective functions to match one-to-one at optimality, the tardiness expressions as defined in the BPS and the APS models must return the same value. To show that, we first make the following observation for any objective function that degrades with tardiness and/or earliness:

Theorem 1

Given any feasible schedule with completion times $f_i$ and due dates $d_i$, there exists a corresponding feasible solution in the APS model, where the following equations hold for any job i:

$$\begin{aligned} l_i= & {} (f_i - d_i)^+ = \sum _{t=r_i}^{T} L_{it} \end{aligned}$$

(21)

$$\begin{aligned} e_i= & {} (d_i - f_i)^+ = \sum _{t=r_i}^{T} E_{it} \end{aligned}$$

(22)

$$\begin{aligned} u_i= & {} U_i \end{aligned}$$

(23)

Moreover, the solution that satisfies the above equation provides the best possible objective value corresponding to this feasible schedule for the APS model.

Proof

Observe that in the APS model, the only constraint related to the non-negative integer variable $L_{it}$ is given by (eq. 16), which enforces a lower bound determined by $B_{it}$. In the same model, $B_{it}$ is constrained to satisfy the work balance equations given by (12) and (13). These constraints also involve the work assignment variables $X_{it}$. Note that the work assignment values in the BPS model ($x_{it}$) can be directly mapped to the APS model by $X_{it}=x_{it}/p_i$. Due to the constraints in the BPS model, we can easily verify that the mapped $X_{it}$ values satisfy constraints (14) and (15) in the APS model. As such, when $(f_i - d_i)^+ = 0$, job i is not tardy and with $X_{it}$ values mapped from the BPS model, we can easily construct a feasible solution for the APS model where $B_{it} = 0$ and $L_{it}=0$ for $t \ge d_i$. On the other hand, $(f_i - d_i)^+ > 0$ implies that there is unfinished work for job i in periods $d_i$ to $f_i$. In this case, it is straightforward to observe that due to (12) and (13), $B_{it}>0$ must be enforced for $t \in [d_i,f_i]$ implying that $L_{it}>0$ must also hold. Specifically, although $L_{it}$ can take any integer value in $[1,\infty )$ for $d_i < t \le f_i$ as $B_{it} \le 1$ by definition, it can be easily verified that equation (21) holds only if $L_{it}=1$ are selected. These scenarios correspond to the feasible solution where $L_{it}$ values take their lowest feasible values indicating that the best outcome for the objective function that degrades in tardiness can be achieved with this particular solution. The proof for the equations (22) and (23) follows from the relations between $I_{it}$ and $E_{it}$ and between $B_{d_it}$ and $U_i$ that are similar to that of $B_{it}$ and $L_{it}$ and as such, can be carried out in a similar way. $\square$

An important implication of the above result is that in the APS model, at optimality, the values that $L_{it}$ and $E_{it}$ can be either 0 or 1. As such, these variables have the binary property. From the practical perspective, they count tardy and early periods for job i respectively resulting in the measures of tardiness and earliness as defined in the BPS model. A key conclusion that we derive from the above observation is that any optimal solution to the BPS model can be mapped to a feasible solution in the APS model, where $L_{it}$ and $E_{it}$ take binary values. We know from (14) and (15) that any solution to the APS model is a feasible schedule. Since any feasible schedule can be represented by a feasible solution in the BPS model, the APS model cannot generate an optimal solution that is better than that of the BPS model. Hence, we have the following conclusion:

Corollary 1

The optimal schedule obtained by the BPS model must be also optimal for the APS model, and the reverse is also true.

3.2 Lower bounds

The difference in the performance between the models is primarily the result of each model’s ability to produce tight lower bounds. Tighter bounds typically help with the convergence performance of the solution process. In this section we investigate and compare the lower bounds that can be produced by the BPS and APS models. Particularly, we focus on the lower bounds obtained by linear relaxation where all integrality constrains are relaxed. We let $LB_{BPS}$ and $LB_{APS}$ denote the objective function values obtained by the lower bounds of the BPS and APS models respectively.

As explained in the previous section, the integrality constraints for $f_i$, $l_i$, and $e_i$ in the BPS model can be relaxed without any loss in optimality due to their integrality property. As such, it is sufficient to replace the integrality constraint for $y_{it}$ with $0 \le y_{it} \le 1$ for all jobs over the planning horizon so as to obtain the LP relaxation. The tardiness indicator $u_{i}$ must be relaxed the same way for the TWNTJ instances. The LP relaxation for the APS model is achieved by the removal of integrality constraints for variables $L_{it}$, $E_{it}$, and $U_{it}$. We first make the following conclusion regarding the LP relaxation of both models:

Theorem 2

Any feasible solution to the LP relaxation of the BPS model or the APS model corresponds to a feasible schedule.

The proof follows from the fact that the LP relaxation generates fractional values only for the variables that track the tardiness measures, not the feasibility of the schedules. The latter one is ensured by constraints (3) and (4) in the BPS model and constraints (12–15) in the APS model. None of these constraints involve any integer variables, and hence, they are not affected by the LP relaxation. Consequently, even though a feasible solution to the LP relaxation may be infeasible for either models, it still must correspond to a feasible schedule. For example, it is not difficult to see that in the relaxed BPS model, the schedule given in Fig. 1 is feasible and the minimum total tardiness measure that it can provide is zero, where completion times, $f_i$, are 1.5, 2.5, 4.67 respectively. Under the relaxed APS model, the minimum total tardiness measure for the same schedule is 0.5 ($L_{1,1}=0.25$ and $L_{1,2}=0.25$). Clearly these values are not feasible for the BPS and APS models. The feasible objective value for this schedule would be 2 in both the BPS (with completion times 6, 3, 5, and 8 respectively) and the APS (with $L_{1,1}=1$ and $L_{1,2}=1$) models.

For any feasible schedule obtained by the LP relaxation, we can easily derive the feasible completion-time and tardiness variables for the MIP models. In what follows, we represent the values of the variables in the relaxed models using the ${\widehat{\cdot }}$ notation. It is straightforward to deduce that the constraints regarding tardiness related measures will be binding when we solve the LP relaxations. Since the objective values are nondecreasing in tardiness and earliness measures, their comparisons can be based on these measures.

For any given feasible schedule, the objective function in the relaxed BPS model is captured by

$$\begin{aligned} {LB}_{BPS} = \sum _{i \in N}w_iF_{i}({\widehat{l}}_i, {\widehat{e}}_i, {\widehat{u}}_i) \end{aligned}$$

(24)

where $\widehat{f_{i}}, \widehat{l_{i}}, \widehat{e_{i}},$ and $\widehat{u_{i}}$ are obtained by the boundary equations in (6–9) respectively. Similarly, in the APS model we get

$$\begin{aligned} {LB}_{APS} = \sum _{i \in N} \sum _{t=1}^T w_i {\overline{F}}_{it}({\widehat{L}}_{it}, {\widehat{E}}_{it}, {\widehat{U}}_i) \end{aligned}$$

(25)

where $\widehat{L_{it}}, \widehat{E_{it}},$ and $\widehat{U_{i}}$ are obtained by the boundary equations in (16–18) respectively.

These boundary values enable us to compare the lower bounds of the objective values across both formulations. Since the objective values are nondecreasing in tardiness and earliness measures, their comparison can be based on these measures.

Theorem 3

For any given feasible schedule (i.e., any congruous $x_{it}$ and $X_{it}$ values), the tardiness and earliness values that can be generated by the LP relaxation of the BPS model are no greater than those generated by the LP relaxation of the APS model. Namely, the following inequalities always hold for a given feasible schedule:

$$\begin{aligned} \widehat{l_{i}}\le & {} \sum _{t=d_i}^{T} {\widehat{L}}_{it} \le l_i \qquad \qquad \forall i\in N \end{aligned}$$

(26)

$$\begin{aligned} \widehat{e_{i}}\le & {} \sum _{t=r_i}^{d_i} {\widehat{E}}_{it} \le e_i \qquad \qquad \forall i\in N \end{aligned}$$

(27)

$$\begin{aligned} \widehat{u_{i}}\le & {} {\widehat{U}}_{i} \le u_i \qquad \qquad \forall i\in N \end{aligned}$$

(28)

Proof

We first focus on the tardiness comparison. It is straightforward to observe that if a job is not tardy in a given schedule, both LP relaxations result in zero tardiness for that job and thus, (26) is satisfied. Next, we focus only on the tardy jobs. Inequality (26) implies that the following must hold for any tardy job i:

$$\begin{aligned} \sum _{t=r_i}^{T}t{\widehat{y}}_{it} - d_{i} \le \sum _{t=d_i}^{T} {\widehat{B}}_{it} \end{aligned}$$

(29)

Recall that ${\widehat{B}}_{it}$ variables represent the fraction of unfinished jobs in the APS model and they can be easily computed from (13) for given values of $X_{it}$. The computation of the best values for ${\widehat{y}}_{it}$ for a given feasible schedule is less straightforward. Observe that ${\widehat{f}}_{i}$ is a convex combination of all periods from $r_i$ to T and determined by ${\widehat{y}}_{it}$ values in this range. Since smaller completion time leads to lower tardiness, the relaxed BPS model will attempt to assign higher ${\widehat{y}}_{it}$ values to the earlier periods so as to reduce the completion time. However, constraint set (5) imposes upper bounds for this variable. We can easily deduce that at the release date the constraint must be binding and thus, we have:

$$\begin{aligned} {\widehat{y}}_{i,r_i}=\frac{x_{i,r_i}}{p_i}=X_{i,r_i} \end{aligned}$$

(30)

Accordingly, the best value for ${\widehat{y}}_{i,r_i+1}$ should be $X_{i,r_i}+X_{i,r_i+1}$ only if this summation is less than $1-{\widehat{y}}_{i,r_i}$ due to constraint (2). Otherwise, its value must be $1-{\widehat{y}}_{i,r_i}$. Generalizing this pattern, we can represent the ${\widehat{y}}_{it}$ values that minimize the relaxed BPS objective for a given feasible schedule with the following recursive function:

$$\begin{aligned} {\widehat{y}}_{it}=X_{i,r_i}+\min \left( 1-\sum _{\tau =r_i}^{t-1}{\widehat{y}}_{i\tau },{\widehat{y}}_{i,t-1}+X_{it}\right) \qquad \forall t \in [r_i+1,T] \end{aligned}$$

(31)

To prove that (29) always holds, it will be sufficient to show that it holds when the left hand side takes its largest feasible value. We can easily deduce that, for given $X_{it}$, the upper bound for the convex combination given in the left hand side can be attained when

$$\begin{aligned} {\widehat{y}}_{i,d_i}= 1-{\widehat{B}}_{i,d_i} \end{aligned}$$

(32)

where $1-{\widehat{B}}_{i,d_i}$ represents the fraction of work completed for a job by its due date. Observe that (31) implies that the ${\widehat{y}}_{it}$ values are determined cumulatively up to a period in which they are complemented to 1. Their values must be zero beyond this period. It is straightforward to deduce that this point is reached at or before the actual completion time in the relaxed model. Let $d_i+z$ be any arbitrary period, where $z \ge 0$ and

$$\begin{aligned} {\widehat{y}}_{i,d_i+z}= 1-\sum _{\tau =r_i}^{d_i+z-1}{\widehat{y}}_{i\tau } \end{aligned}$$

(33)

and as such, ${\widehat{y}}_{it}=0$ for $t>d_i+z$. Note that $z \le f_i-d_i$. In this representation we can calculate ${\widehat{y}}_{i,d_i+1}$ as follows:

$$\begin{aligned} {\widehat{y}}_{i,d_i+1}=1-{\widehat{B}}_{i,d_i}+X_{i,d_i+1}=1-{\widehat{B}}_{i,d_i+1} \end{aligned}$$

(34)

since $X_{i,d_i+1}={\widehat{B}}_{i,d_i} - {\widehat{B}}_{i,d_i+1}$. We can generalize this result to ${\widehat{y}}_{it}=1-{\widehat{B}}_{it}$ for $d_i \le t < z$. Consequently, we can rewrite (29) as follows:

$$\begin{aligned} \sum _{j=0}^{z-1} ((1-{\widehat{B}}_{i,d_i+j})(d_i+j))+\left( 1-\sum _{j=0}^{z-1} (1-{\widehat{B}}_{i,d_i+j})\right) (d_i+z)-d_i \le \sum _{t=d_i}^{T} {\widehat{B}}_{it} \end{aligned}$$

(35)

which reduces to

$$\begin{aligned} \sum _{j=0}^{z-1} ((1-{\widehat{B}}_{i,d_i+j})(j-z)) + z \le \sum _{t=d_i}^{T} {\widehat{B}}_{it} \end{aligned}$$

(36)

It is clear that the first term in the left hand side is nonpositive and $-\sum _{j=0}^{z-1} (1-{\widehat{B}}_{i,d_i+j})$ is an upper bound for it. Replacing this term, we get

$$\begin{aligned} -\sum _{j=0}^{z-1} (1-{\widehat{B}}_{i,d_i+j}) + z \le \sum _{t=d_i}^{T} {\widehat{B}}_{i,t} \end{aligned}$$

(37)

which reduces to

$$\begin{aligned} \sum _{j=0}^{z-1} {\widehat{B}}_{i,d_i+j} \le \sum _{t=d_i}^{T} {\widehat{B}}_{i,t} \end{aligned}$$

(38)

The above inequality clearly holds implying that (29) must also hold. As such, we conclude the proof for (26) indicating that LP relaxation of the APS model provides tighter bounds on tardiness compared to the LP relaxation of the BPS model.

Next, we consider the early jobs. In this case, the objective improves with larger completion times. It is straightforward to deduce from the BPS model that in the relaxed version zero earliness penalty is attained for $y_{i,d_i}=0$, which is not prevented by any constraint if job i is early. That is, LP relaxation of the BPS model always generates an earliness measure of zero for any given feasible schedule. On the other hand, the same measure in the APS model is provided by $\sum _{t={\widehat{f}}_i}^{d_i} \epsilon$. Consequently, (27) must always hold for any given feasible schedule.

Finally, the comparison of the count of number of tardy jobs in the relaxed models results in

$$\begin{aligned} \sum _{t=r_i}^T t {\widehat{y}}_{it} - d_i \le T {\widehat{B}}_{i,d_i} \end{aligned}$$

(39)

The proof of this inequality follows from the proof of (29) as $T {\widehat{B}}_{i,d_i} \ge \sum _{t=d_i}^{T} {\widehat{B}}_{it}$ due to the fact that ${\widehat{B}}_{it}$ values are nonincreasing in t. $\square$

The results obtained in this section so far establish that (i) LP relaxation of both models results with feasible schedules (but not feasible solutions for the original models), (ii) any feasible solution in one model can be mapped to a feasible solution in the other, and (iii) for any feasible schedule, LP relaxation of the APS model leads to higher tardiness and earliness measures in comparison to the LP relaxation of the BPS model. These observations lead us to the following induction:

Corollary 2

The optimal objective value for the LP relaxation of APS is always greater than or equal to the optimal objective value obtained by the LP relaxation of the BPS model. That is, $LB_{APS} \ge LB_{BPS}$ always holds.

This conclusion establishes the APS model’s dominance over the BPS model in producing tighter lower bounds. With tighter bounds it is plausible to expect better computational performance from the APS model. We infer from the proof of Theorem 3 that the performance of the APS model should especially be superior for the tardiness penalties in comparison to the earliness penalties since the gaps between the lower bounds are more significant in capturing tardiness and the number of tardy jobs. To put this expectation into test, we have carried out an extensive computational study which is discussed in the next section.

4 Computational experiments

We design and perform numerical analysis so as to evaluate the computational performance of the BPS and the APS models for the most commonly used tardiness objectives that include total weighted tardiness (TWT), total weighted completion time (TWC), total weighted tardiness and earliness (TWTE), and total weighted number of tardy jobs (TWNTJ). We aim to investigate the computational performance of both models specially with respect to the problem size (i.e. number of jobs). Our goal is to demonstrate that the proposed APS formulation significantly improves the computational performance. To this end, we perform numerical experiments that test both models under different conditions with respect to their convergence performances, computational times, and optimality gaps. We consider five problem sizes in all cases with $n=10$, 20, 40, 80, and 160 jobs. All problem instances are solved by both models in the experimentation.

We employ a set of expressions to generate all the parameters necessary to create the problem instances. To be consistent with the existing literature, we borrow the expressions from earlier research due to Yang et al. (2004) and Jaramillo and Erkoc (2017), and modify them to our context. Main random variables in the system are generated by a uniform distribution in order to enable diversity across all instances. Table 4 lists all the specific parameter generating expressions used in our analysis. For any given problem instance, the time horizon parameters T are derived by the makespan of the non-delay and non-preemptive schedule constructed via the earliest release date first (ERD) rule. Overall, 20 instances are generated for each problem size. Consequently, a total of 200 instances are obtained to test the performance of both models for each objective function under study. All instances generated for the BPS and APS models are solved using AMPL and CPLEX 12.6. All computations are performed on a PC with an I7-3770 Processor with 3.40 GHz and 16 GB of RAM.

Table 4 Parameter generating expressions

Due to computational complexity, not all the instances are solvable in reasonable amounts of time. Therefore, we set a fixed time limit for the execution of both models. Specifically, the computational runs are set to initiate a time-out sequence at 3600 s (1 hour) for the solution procedure. Although a time limit is present, we note that the total time typically exceeds this limit due to post-processing of the solver that finalizes the last iteration. In all the numerical experiments, the lower bound from the APS model is used as reference to assess the computational efficiency for both models; this is necessary for fair comparison since the BPS model generates smaller bounds in all cases. The disparity of optimality gaps across both models is also investigated in parallel so as to examine the convergence performances.

4.1 Total weighted tardiness (TWT)

We investigate the results of all 100 instances on each model (200 runs total) for the total weighted tardiness (TWT) problem represented by $1|pmtn, r_i, p_i |\sum _i w_i l_i$. Objective functions $\sum _{i \in N} w_i l_i$ and $\sum _{i \in N} \sum _{t=1}^T w_i L_{it}$ are employed in (1) and (11) respectively. In the BPS model, constraints (8) and (9) and variables $e_i$ and $u_i$ are redundant and therefore not used in the computations. Likewise, constraints (17) and (18) along with variables $E_i$ and $U_i$ are not employed in the APS model.

In our numerical analysis, we tracked the number of instances that were solved optimally by each model within the given time frame. It was observed that the BPS model was able to converge to the optimal solution in 18 of the 100 instances (18%); 14 of those in instances with 10 jobs and 4 with 20 jobs. In all other cases, the solution process was timed out. Moreover, the BPS model converged to a feasible solution in only 4 out of 20 instances with 160 jobs. In order to have sufficient number of solutions for comparison, we generated additional instances until we obtained 20 feasible solutions for this case. On the other hand, the APS model implementation resulted with optimal solutions in 40 instances (40%); all 20 instances with 10-job problems, 17 instances with 20 jobs, and 3 instances with 40 jobs. In contrast to the BPS model, the APS model was able to produce feasible solutions for all instances with 160 jobs. The results indicate a significant difference in convergence to optimality in favor of the APS model. As expected, in both cases, the number of optimally solved instances decreases as the problem size (i.e., the number of jobs) increases.

In order to further our investigation on convergence performance, we measure the optimality gaps generated by both models. In this respect, we measure the optimality gap as the percent deviation of the best solution from the lower bound obtained by the end of the given time frame. As depicted in Fig. 2, the APS model generates significantly lower optimality gaps suggesting better performance on convergence.

Fig. 2

Optimality gaps for the TWT problem

Next, we compare the computational time performances. Measures of computational time performance include the minimum, average, and maximum values reported for each problem size. In addition, in order to make a fair comparison of the quality of the solutions, we calculate their gaps relative to the lower bounds obtained by the APS model since this model provides tighter bounds consistently. We refer to this measure as the APSLB Gap and recorded the minimum, average, and maximum values for this measure. In both measures, the averages include instances that converged to optimal solutions or timed out with feasible solutions. Table 5 presents the results of the computational tests using the aforementioned measures. The “TO” column in the table lists the number of instances for which the timeout has been reached.

Table 5 Computational test results for the TWT objective (100 instances)

The results indicate a significant difference in computational time performance where the APS formulation dominates the BPS formulation in all instances as illustrated by Table 5 and Fig. 3. We observe that with relatively small size problems (i.e., 10 jobs), while it takes several minutes for the BPS model to reach at optimality, the APS achieves the same result within a matter of seconds on average. Specifically, while the average computational time for the 14 instances solved optimally by the BPS model for 10 jobs is 178.57 s, the APS model provides optimal solutions in all 20 instances with an average computational time of 9.95 s. For 20 jobs, the BPS model took 550.68 s on average to converge to the optimal solution in 4 instances, whereas the APS model achieved optimal solution in 17 instances with an average time of 146.27 s. As the problem size increases, the convergence performance degrades significantly for the BPS model. For more than 20 jobs the average optimality gap stays above 9.0%. By contrast, the average optimality gap with the APS stays under 6% upto 80 jobs and 28% for instances of 160 jobs. Overall, the APS model provided solutions with objective function values that are 0.06%, 1.59%, 6.40%, 22.97%, and 57.74% lower than the BPS model for 10, 20, 40, 80, and 160 jobs respectively. Clearly, the dominance of the APS model becomes more apparent and stronger as the problem size increases.

Fig. 3

APSLB gaps for the TWT problem

4.2 Total weighted completion time (TWC)

We investigate the total weighted completion times (TWC) problem using the same 100 instances on each model (200 runs total). This problem is denoted by $1|pmtn, r_i, p_i |\sum _i w_i C_i$, where $C_i$ represents the completion time (makespan) for job i. This problem can be modeled as a special case of the TWT model where due dates match the release dates of the jobs. This way, all jobs are essentially late and the minimization process is determined only by the completion times of each job. Therefore, $C_i$ variables can be directly mapped to and replaced by the tardiness variables $l_i$ and $L_{it}$ in both models respectively. Consequently, we use the same objective functions, constraints, and variables that we employ for the TWT problem discussed in the previous subsection.

In this case, the BPS model was able to find the optimal solution in 20 of the 100 instances while the APS model produced optimal solutions in 36 instances. While the BPS model was able to converge to the optimal solution in 16 instances of 10 jobs and 4 instances of 20 jobs, the APS model resulted with optimal solutions for all 20 instances of 10 jobs and 16 instances of 20 jobs. Both models fail to converge to optimality within the given time frame in all instances of 40 or more jobs. Similar to the TWT case, the BPS model converged to feasible solutions in only 4 out of 20 instances and again we employed additional instances to obtain a total of 20 feasible solutions. This approach was repeated for the TWET and TWNTJ problems in the case of 160 jobs.

Figure 4 compares the optimality gaps. Similar to the TWT case, the APS model generates significantly lower optimality gaps in comparison to the BPS model. Results pertaining to computational times and convergence are summarized in Table 6.

Fig. 4

Optimality gaps for the TWC problem

The results presented in Table 6 reveal that as the problem size increases, the convergence performance on the BPS model degrades significantly, and the average optimality gap stays above 16% for more than 40 jobs. On the other hand, the optimality gap with the APS model remains under 5% on instances of upto 80 jobs. In terms of the maximum values reported for the optimality gap with 160 jobs, the BPS model appears to produce slightly lower values than the APS model (81.25% vs. 96.61% respectively); this data artifact is the result of the lack of actual data from the BPS runs for 160 jobs which resulted in only 4 instances with feasible integer solutions and 16 instances for which the time limit was surpassed without the solver reaching an integer feasible solution.

Table 6 Computational test results for the TWC objective (100 instances)

Fig. 5

APSLB gaps for the TWC problem

Relative gaps for both models are depicted in Fig. 5. OF the optimally solved instances of 10 jobs, the BPS model required an average of 386.81 CPU seconds whereas the APS model converged to optimality within 24.51 CPU seconds on average. Objective function values are 0.01%, 0.57%, 3.00%, 12.68%, and 74.08% lower in the APS model results than in the BPS model results for 10, 20, 40, 80, and 160 jobs respectively. The pattern for the gap between the two models are similar to the TWT problem with a somewhat dampened scale, which can be explained by the induction that the TWC problem should not be more complex than its generalized TWT version.

4.3 Total weighted earliness and tardiness (TWET)

The total weighted earliness and tardiness problem aims to find an optimal schedule that minimizes the total cost of earliness and tardiness for a given set of jobs by determining work allocations that result with completion times as close as possible to their due dates. We consider equal penalties for earliness and tardiness for the same job as we intend to maintain a balanced influence of both penalty types on computational performances. The TWET problem can be represented by $1|pmtn, r_i, p_i |\sum _i w_i (e_i + l_i)$ in this context. As such, the objective functions are now $\sum _{i \in N} w_i (e_i+l_i)$ and $\sum _{i \in N} \sum _{t=1}^T w_i (E_{it} + L_{it})$ in (1) and (11) respectively. In the BPS model, constraint (9) and variable $u_i$ are not needed and thus, they are not used in the computations. In the APS model constraint (18) and variable $U_i$ are not needed and therefore not used in the computations.

Results from solving 100 instances show that the BPS model was able to find the optimal solution in 20 of the 100 instances while the APS model produced optimal solutions in 40 instances out of 100. The BPS model provided 16 and 4 optimal solutions for instances with 10 and 20 jobs respectively, and no optimal solutions for the instances of 40 jobs or larger. The APS model was able to reach optimality in all instances of 10 jobs, 17 instances of 20 jobs, and 3 instances of 40 jobs. We note that these are the same instances that were also optimally solved in the TWT case. This is not too surprising as the two problems differ only by the inclusion of the earliness penalties.

Figure 6 compares the optimality gaps between the two models. Comparing to the TWT cases, we observe that optimality gaps are wider for the TWET problem. This is expected as the TWET problem involves additional constraints and variables pertaining to earliness. However, interestingly, the growth in the optimality gap is more significant for the BPS model. This observation indicates that the increased complexity widens the performance gap between two models. This is more evident in Table 7 that summarizes the results related to computational times and APSLB gaps.

Fig. 6

Optimality gaps for the TWET problem

Table 7 Computational test results for the TWET objective (100 instances)

The average APSLB gap increases at an increasing pace in comparison to the TWT case for the BPS model. It quickly rises to 19.5% for 40 jobs and continues to increase with larger sizes. On the other hand, the gap stays well below 9% up to 80 jobs in the APS model. The comparison of the relative gaps are depicted in Fig.  7.

Fig. 7

APSLB gaps for the TWET problem

In terms of computational time performances we again observe that the convergence performance degrades significantly for the BPS model relative to the APS model. But this time at an increasing pace in comparison to the TWT problem. We observe that while the average computational time for the 14 instances solved optimally by the BPS model for 10 jobs is 207.85 s, the APS model provides optimal solutions in all 20 instances with an average computational time of 15.44 s.

4.4 Total weighted number of tardy jobs (TWNTJ)

The total weighted number of tardy jobs (TWNTJ) problem, denoted by $1|pmtn, r_i, p_i |\sum _i w_i u_i$, is only concerned about the jobs that are tardy regardless of how large the tardiness is. Therefore, constraints and variables related to earliness and tardiness are not needed in this problem. Specifically, in the BPS model, constraints (7) and (8) and variables $e_i$ and $l_i$ are omitted. In the APS model, constraints (16) and (17) and variables $L_{it}$ and $E_{it}$ are also dropped from the computations. For this problem, the objective functions are $\sum _{i \in N} w_i u_i$ and $\sum _{i \in N} w_i U_i$ in (1) and (11) respectively.

As in all previous cases, the number of instances that were solved optimally by each model was again significantly different. In this case, however, the total number of instances solved optimally was significantly higher than the number of optimal instances reported for the other problems. The BPS model was able to find the optimal solution in 50% of the instances (50 of the 100 instances) while the APS model produced optimal solutions in 88% (88 instances out of 100). The higher number of outcomes with optimal solutions may be explained by the fact that the TWNTJ is known to be maximal pseudo-polynomially solvable (Lawler 1990). The APS model optimally solved all problem instances up to 80 jobs and 8 out of 20 instances for 160 jobs.

As illustrated by Fig. 8, the difference in optimality gaps between two models continues to be significant as the problem size increases. As indicated in Table 8, the optimality gap for the APS stays quite low under 8%. Overall, the objective function values obtained by the APS model are 0.49% and 1.38% lower than by the BPS model for 40 and 80 jobs respectively. Clearly, the gap in this respect is much smaller between both models compared to the previous cases. However, as indicated in the table, there is still significant difference in computational time performance. We observe that the average computational times for the optimally solved instances in the BPS model are 0.96, 17.30, and 520.44 CPU seconds for 10, 20, and 40 jobs respectively. These values turned out to be much lower for the APS model at 0.12, 0.92, and 9.43 CPU seconds respectively.

Fig. 8

Optimality gaps for the TWNTJ problem

Table 8 Computational test results for the TWNTJ objective (100 instances)

4.5 Case study: early start penalties with overtime option

Numerical experiments presented so far show how the performance of the APS formulation is consistently and substantially better performing in comparison to the BPS formulation. In this section, we present an implementation of the APS model for a real industry case. As mentioned in the Introduction Section, our study is initially motivated by our earlier collaboration with a MRO service provider that is specialized on landing gear overhauls. The business of landing gear overhaul service operates within a very competitive market where failure to meet deadlines represents significant losses for airlines, and in turn loss of business for the overhaul service provider (OSP). The customers, who are most usually the airline companies, have strict expectations regarding the overhaul turnover times since any not-in-use (or grounded) equipment usually costs them tens of thousands of dollars daily.

The periodic overhauls are typically enforced by regulatory agencies such as the Federal Aviation Administration (FAA) in the U.S.A. Such agencies restrict the total flight hours for a landing gear set and therefore enforce overhaul deadlines on the commercial aircraft users. The airlines typically attempt to use their equipment to the fullest limit for revenue management purposes and require from the OSP to deliver their services just in time to minimize interruptions in equipment use. In a perfect world, the overhaul start and finish dates always stay within the airline’s scheduled time frame (e.g., 30 to 60 day turnaround time depending on the type of the equipment); however, this is not always possible due to capacity limitations of the OSP. Usually, the latest date an overhauled landing gear is delivered back to the airline is considered a hard constraint due to regulations. Since the OSP does not have much flexibility on late delivery, they may negotiate earlier starts (release dates) with the customers in return for discounts (or early start penalties) that aim to compensate the loss of the customer for grounding their equipment earlier. Consequently, the OSP faces the problem of minimizing the early start penalties.

In this case study, we focus on the scheduling problem for the so called “regional shop” of the OSP which services the landing gear only for narrow-body aircraft. The shop has orders for overhauling 82 landing gear sets from 4 major customers over a period that spans from the last quarter of 2017 to the first quarter of 2019. The jobs have known due dates and the desired release dates are set at 30 days before the due dates, which is typically a standard for narrow-body aircraft. All jobs have similar standard work requirements. We tackle the problem as a single processor preemptive scheduling problem as the majority of the overhaul processes can be interrupted in favor of higher priority work. We note that this is not an exact mapping of the real problem since in reality overhaul procedure involves multiple parallel and serial sub-processes and unexpected tasks that may emerge during the execution of these processes. The single machine scheduling solution basically serves as an approximation which is used as (i) a reference for business development (e.g., negotiating release dates and new contracts) and (ii) an initial benchmark for workload allocation and overtime planning at tactical level. Clearly, while this solution approach provides a useful reference for tactical planning for release dates and overtime capacity, adjustments are often necessary at the operational level, where detailed schedules are determined and executed.

Although the problem configuration in this case study is not strictly a tardiness problem, the early-start configuration of the OSP schedule in fact represents a mirror case of a tardiness problem. Using this property, we can transform the original release and due dates into their mirror equivalents to generate the equivalent tardiness problem and solve it using the APS model. Basically, we reverse the time line and obtain the mirror values for the release, and due dates, namely $r_m$ and $d_m$ from the actual release and due dates; $r_a$ and $d_a$. Figure 9 illustrates this process, where $r_{m} = T - d_{a} +1$ and $d_{m} = T - r_{a} +1$. With this transformation the start dates can be mapped by the mirrored finish dates, that is, $s_a = T - f_{m} + 1$.

Fig. 9

Schematic of the date correspondence between actual and mirror schedules

Since the shop has the option of working overtime, we need to incorporate the overtime decisions in to the APS model. For this reason, we introduce new parameters $\alpha _o$ and $C_o$ that represent the overtime capacity limit at each period and unit cost of using overtime capacity respectively. A new decision variable $V_t$ is defined to denote the amount of overtime capacity used in period t. Thus, we modify the objective function for the APS and constraint (14) as follows:

$$\begin{aligned}&\text {minimize: } \qquad \sum _{i \in N} \sum _{t=1}^T w_i L_{it} + \sum _{t=1}^T C_o V_{t} \end{aligned}$$

(40)

$$\begin{aligned}&\sum _{i\in N} p_iX_{it}\le \alpha + V_t, \qquad \text { } \text { } \forall t\in \{1,\dots ,T\} \end{aligned}$$

(41)

Finally, we need to add the following constraint to enforce the overtime capacity limit:

$$\begin{aligned} V_t \le \alpha _o, \qquad \text { } \text { } \forall t\in \{1,\dots ,T\} \end{aligned}$$

(42)

The earliness penalties are set based on the criticality of the customers for the OSP and as such, four distinct weights are considered. To protect the privacy of the OSP, we slightly modified all cost related data and significantly scaled them down for ease of representation. The actual due dates are depicted in Fig.  10 and all other input values used in the modified APS model are presented in Table 9. Processing time to finish each job is scaled to 120 hours (with full capacity allocation). The objective of the ensuing model is to produce an overhaul schedule that minimizes the cost of early start penalties and overtime incurred by the OSP.

Fig. 10

Actual due dates ($d_i^a$)

Table 9 Parameters and expressions of the case study

With a time limit of 3600 CPU seconds, the APS model was able to provide an objective function value with an optimality gap of 2.67%. The model produced an optimality gap of 6.5% within the first minute for this problem and converged to 2.67% after one hour. As expected, the convergence occurred with diminishing return. Likewise, the objective function value was convex decreasing in time. It produced an objective value of 1247 within the first minute, converged to 1207 at around 2400 CPU seconds and did not improve until the time limit is reached. This indicates only a 3.2% gain from the first minute, which supports our analytical and computational observations made earlier. When we increased the time limit to 12 CPU hours we observed that the optimality gap did not improve significantly with outcomes of 2.14% and 2.12% at 5 and 12 hours respectively. The objective function value remained to be 1207. Figure 11 depicts the convergence performance.

Fig. 11

Convergence of the APS model

5 Conclusions

We propose two modeling approaches that can be used to solve a variety of tardiness related problems on a single machine layout where preemption is allowed. Following the conventional time-indexed formulation, we first build a model using binary variables that explicitly identifies completion times of a finite set of jobs with varying release times, due dates, and processing times. We refer to this model as the Binary Preemptive Scheduling (BPS) model. The second model, which we call the Aggregate Preemptive Scheduling (APS) model, adopts the aggregate planning view and eliminates binary constraints resulting in significantly improved computational efficiency. Under this approach, each job is mapped to a unit demand and the due date of the job is represented by a period with a unit demand corresponding to the same job. Subsequently, the work units allocated to the processor are transformed into production decisions measured by fraction of demand. Consequently, instead of identifying the finish times of jobs, the proposed APS model tracks the amount of production completed and backlogged via the inventory and shortage variables and conservation of units constraints.

We compare the proposed models both analytically and computationally. First, we establish the equivalency of both models and show that APS formulation provides tighter lower bounds compared to the BPS formulation. Next, we carry out computational experiments for both models and test their computational performances under commonly used tardiness related objective functions including total weighted tardiness (TWT), total weighted completion time (TWC), total weighted earliness and tardiness (TWET), and total weighted number of tardy jobs (TWNTJ). The computational results reveal a considerable difference between the performances of the formulations, where the BPS model is outperformed with clear lead by the APS model in all tested tardiness objectives in terms of computational times and quality of solutions obtained in set time frames. The advantage of the APS model becomes more apparent as the problem size increases.

Finally, we demonstrate the performance of the proposed APS model on a problem adopted from a real life application in the aviation MRO industry. The case problem involved 82 jobs with release and due dates across a planning horizon of 630 days. The model in this case was modified by additional variables and constraints so as to incorporate overtime decisions. The computation resulted in a solution with a reasonably small optimality gap under an hour.

Our overall study establishes that the APS model is a promising tool for generating optimal or near-optimal schedules and capacity allocation plans reasonably quickly for real life applications. The proposed models can be generalized to and tailored for other scheduling settings where preemption is allowed. To name a few, flow shop and project scheduling problems are interesting extensions in this direction. Our results also indicate that with the tighter bounds it provides, the APS modeling is a promising optimization approach for other scheduling objectives such as minimizing the maximum lateness and minimizing the makespan.