1 Introduction

Since the first debates around sustainable development, it has been widely recognized the existence of a clear trade off between economic growth and environmental preservation (WCED 1987). Indeed, in order to allow for higher and higher output per capita to be reached, economic growth requires the level of production activities to consistently increase over time, generating thus rising pressure on the natural environment through the pollutant emissions generated as a side-product of production. However, the health of the natural environment plays also a vital role in economic activities by feeding back into production capabilities, since pollutant emissions tend to reduce the amount of output the economy can produce for a given level of production factors. Understanding the nature of such a mutual relation between economic growth and environmental outcomes has been the main focus of a large and growing economics literature (see Xepapadeas 2005; Brock and Taylor 2005; for some recent surveys). Several papers either analyze the extent to which it is possible to reconcile economic growth and environmental preservation by pursuing specific win-win policies (Porter and van der Linde 1995; Ansuategi and Marsiglio 2017; Marsiglio 2017), or discuss how the nature of the economy-environment relation is complicated further by the presence of uncertainty in environmental or economic dynamics (Soretz 2007; Athanassoglou and Xepapadeas 2012; La Torre et al. 2017) and transboundary externalities associated with pollution diffusion (Ansuategi and Perrings 2000; La Torre et al. 2015; de Frutos and Martín-Herran 2018), or argue why the economic growth and environment relation is nonmonotonic and specifically U-shaped (John and Pecchenino 1994; Stokey 1998; Marsiglio et al. 2016).

Several of these works, from different points of view, stress that the feedback effects between economic and environmental activities are particularly complicated and difficult to predict. Some even suggest that effectively resolving the economic and environmental trade off is unlike and thus it is imperative that economies start a process of degrowth to ensure the viability of the natural environment (Georgescu-Roegen 1971, 1977; Latouche 2009; Kallis et al. 2012). Such degrowth arguments emphasize that from an ecological perspective reducing the size of economic production and consumption activities is not only desirable but also to a large extent inevitable. Given the uncertainty in environmental and economic dynamics, understanding whether this is actually the case is not simple but still its possibility suggests that effectively planning sustainable development critically requires policymakers to consider not only economic goals but also environmental goals when determining their policy interventions. A natural method to do so consists of relying on a multicriteria approach in which economic and environmental factors can be simultaneously accounted for in the definition of the objective function that policymakers wish to optimize (see Roy and Vincke 1981, for a concise discussion of the basis of multicriteria analysis). Despite the popularity of multicriteria methods in environmental sciences and other disciplines (see Ballestero and Romero 1998; Greco et al. 2016, for some detailed surveys), only few attempts to introduce such an approach in economics have been made thus far (Colapinto et al. 2017a, b; Marsiglio and La Torre 2018). Specifically, Colapinto et al. (2017a, b) analyze numerically through both scalarization and goal programming approaches the intergenerational issues associated with sustainable development. Marsiglio and La Torre (2018) rely on a scalarization technique to analyze explicitly how uncertainty in environmental quality affects optimal policymaking. In this paper we wish to contribute to this scant literature by developing a simple multicriteria approach to analyze the mutual relation between economic growth and environmental outcomes. Specifically, we consider a bicriteria problem in which the social planner cares both for economic and environmental goals, quantified by the consumption level and the pollution stock, respectively.

The paper most closely related to ours is Marsiglio and La Torre’s (2018), which shows that a typical macroeconomic model can be interpreted as a multicriteria problem, in which the vectorial objective function is scalarized through some parameters representing the weight attached to the different goals in such an objective function. Such a link between traditional macroeconomic frameworks and multicriteria methods is very convenient since it allows to bridge the economics and operational research literature, showing how the two disciplines can borrow from each other in order to improve their approach to deal with real world problems. Different from Marsiglio and La Torre (2018) in which the relation between economy and environment is unidirectional (i.e., economic production determines the level of pollution deteriorating environmental quality), in our setup such a relation is bidirectional (i.e., economic activities determine pollution but also pollution affects economic production through an externality effect). We show that in such a framework, independently of the weight attached to the economic and environmental goals, optimality dictates (after an initial overshooting) economic degrowth accompanied by rising pollution. This introduces a novel scenario, not yet considered in the literature, which envisages decumulation of capital together with an increasing pollution stock, thus suggesting that, different from what discussed in the degrowth literature, economic degrowth is neither always optimal nor an obvious solution to environmental problems. Indeed, the economy will asymptotically reach the maximum pollution level that the environment can effectively bear. Such a paradoxical result is intuitively due to the fact that at the end of the planning horizon (i.e., asymptotically) the environment does not have any value left and as such it is convenient to exploit it as much as possible in order to boost finite-time consumption. This type of conclusion is somehow implicit in the definition of the objective function which, by being based on a discounted utilitarian approach, does not attach any value to asymptotic quantities, and this is the reason why several works argue that in order to deal with issues related to sustainability it would be best to review such a discounted utilitarian specification of the objective function (Ramsey 1928; von Weizcker 1967; Chinchilnisky et al. 1995; Chinchilnisky 1997).

The paper proceeds as follows. Section 2 introduces our model which consists of a bicriteria problem in which the social planner, who cares for both economic and environmental factors, needs to determine the level of consumption and the technology level to employ in production activities by accounting for the two-ways relation between economic and environmental outcomes. Section 3 analyzes the problem through a scalarization technique, by presenting a reduction of the model which allows to substantially simplify the analysis and derive closed-form solutions for the optimal policies and the optimal dynamic paths, along with the efficient frontier and social welfare. Our results show that, independently of the relative weight of economic and environmental goals, capital will initially overshoot its long run level in order to then decrease over time, while pollution will monotonically increase during the transition towards the long run equilibrium. This implies that it is optimal for the economy to asymptotically reach the maximum pollution level that the environment is able to bear. Section 4 analyzes the problem through a weighted goal programming approach, by employing the analytical results derived through scalarization in order to define the goals for the two objectives. We show that the results are qualitatively similar to those obtained under a scalarization technique, even if the goal programming solution favors the environmental goal and disadvantages the economic one with respect to the scalarized solution. Section 5 presents concluding remarks and proposes directions for future research. Technicalities are postponed to “Appendix A”.

2 The model

We consider a discrete-time Ramsey-type (1928) model of optimal growth where the social planner, by taking into account economic and environmental constraints, chooses the level of consumption, \(c_{t}\ge 0\), and a technology level, \(0\le z_{t}\le \bar{z}\) with \(\bar{z}\) measuring the maximal technology level available, in an attempt to simultaneously achieve two conflicting goals, related to economic and environmental performance respectively. The planner’s objective function is thus characterized by a bicriteria functional, in which each criterion is represented by the infinite discounted (\(0<\beta <1\) is the rate of time preference) sum of the instantaneous utilities associated with the respective goal, given by consumption and environmental quality, \(\bar{p}-p_{t}\), where \(p_{t}\ge 0\) denotes the level of pollution and \(\bar{p}>0\) the maximal pollution level that the environment can bear. The instantaneous utility functions associated with consumption and environmental quality are assumed to be logarithmic, \(u_{c}\left( c_{t}\right) =\ln c_{t}\) and \(u_{p}\left( p_{t}\right) =\ln \left( \bar{p}-p_{t}\right) \), respectively; note that the utility associated with the environmental quality decreases with pollution, which deteriorates the environment. Capital, \(k_{t}\ge 0\), accumulation is given by the difference between total net output (i.e., output adjusted for the technology level and net of depreciation), \(y_{t}>0\) and consumption: \(k_{t+1}=y_{t}+\left( 1-\delta \right) k_{t}-c_{t}\), where \(0<\delta <1\) is the depreciation rate. Total output is the product between output, \(q_{t}>0\), and the technology level given by \(z_{t}\). Output is produced through a Cobb–Douglas production function using capital as its only input, \(q_{t} =D_{t}k_{t}^{\alpha }\), where \(0<\alpha <1\) represents the capital share of  GDP, and \(D_{t}\) is the production externality associated with pollution. Pollution decreases the amount of output the economy through the following damage function \(D_{t}=\left( 1+p_{t}\right) ^{-\phi }\), where \(\phi >0\) denotes the elasticity of the damage function effectively reducing output. Pollution accumulation is given by the difference between flow emissions, \(e_{t}\), and the natural pollution absorption as follows: \(p_{t+1}=e_{t}+\left( 1-\eta \right) p_{t}\), where \(0<\eta <1\) represents the natural pollution decay rate. Emissions are proportional to total output according to \(e_{t}=\mu y_{t}\), where \(\mu >0\) measures the environmental inefficiency of economic production activities. As pollution negatively affects both utility—through the term \(u_{p}\left( p_{t}\right) =\ln \left( \bar{p}-p_{t}\right) \)—and production—through the term \(D_{t}=\left( 1+p_{t}\right) ^{-\phi }\)—the social planner chooses the technology level \(0\le z_{t}\le \bar{z}\) in order to contain the pollution level \(p_{t}\). Hence, total output turns out to be given by \(y_{t}=z_{t}\left( 1+p_{t}\right) ^{-\phi }k_{t}^{\alpha }\). The planner can choose between a continuum of technology levels \(0\le z_{t} \le \bar{z}\) determining thus, given the capital and pollution stocks, the level of total output. Note that total output reaches its maximum potential in a pristine environment, i.e., when there is no pollution, \(p_{t}=0\), in which case total output equals \(y_{t}=k_{t}^{\alpha }\) when there is full capacity in production and the technology level is equal to unity, that is \(z_{t}=1\). A higher (lower) technology level \(z_{t}>1\) (\(z_{t}<1)\) allows to increase (decrease) total output favoring (deteriorating) capital accumulation but also to increase (reduce) emissions increasing (decreasing) pollution accumulation and thus deteriorating (improving) environmental quality.

Note that our setting envisages only capital, \(k_{t}\), and pollution, \(p_{t}\), accumulation and thus rules out endogenous growth. Indeed there is a maximum capital level, \(\bar{k}>0\), that can be sustained in the long run; that is, if the initial capital level, \(k_{0}\), lies above \(\bar{k}\), then capital is doomed to decrease over time eventually converging to some steady value \(k^{s}\le \bar{k}\). Keeping this observation in mind, and noting that the environmental quality, measured by \(\bar{p}-p_{t}\), cannot improve beyond the level \(\bar{p}\), corresponding to zero pollution, without loss of generality we simplify notation by normalizing such level to one, that is, we set \(\bar{p}\equiv 1\). As when \(p_{t}=\bar{p}\equiv 1\) the utility associated with environmental quality \(u_{p}\left( p_{t}\right) =\ln \left( 1-p_{t}\right) \) tends to minus infinity, we consider such an extreme event as unsustainable for the economy from the quality of life perspective; on the other hand, when \(p_{t}=0\) the economy enjoys a pristine environment associated to zero utility, \(u_{p}\left( 0\right) =0\). In the following, thus, we shall consider only values of pollution stock between 0 and 1: \(0\le p_{t} \le 1\).

The social planner’s problem consists thus of choosing \(c_{t}\) and \(z_{t}\) in order to maximize the following concave bicriteria functional, given the capital and pollution dynamic constraints, and initial conditions, \(k_{0}>0\) and \(p_{0}\ge 0\):

$$\begin{aligned}&\max _{\left\{ c_{t},z_{t}\right\} _{t=0}^{\infty }} J=\left[ J_{1}, J_{2}\right] = \left[ \sum _{0}^{\infty }\beta ^{t}\ln c_{t},\sum _{0}^{\infty }\beta ^{t}\ln \left( 1-p_{t}\right) \right] \nonumber \\&\text {s.t.}\ \left\{ \begin{array}[c]{l} k_{t+1}=z_{t}\left( 1+p_{t}\right) ^{-\phi }k_{t}^{\alpha }+\left( 1-\delta \right) k_{t}-c_{t}\\ p_{t+1}=\mu z_{t}\left( 1+p_{t}\right) ^{-\phi }k_{t}^{\alpha }+\left( 1-\eta \right) p_{t}\\ k_{t},p_{t},c_{t},z_{t}\ge 0,\text { }p_{t}\le 1,\text { }z_{t}\le \bar{z};\text { }k_{0},p_{0}\text { given.} \end{array} \right. \end{aligned}$$
(1)

Note that the level of consumption, \(c_{t}\), and of the technology level, \(z_{t}\), impact on both the two (economic and environmental) criteria: a higher consumption level is directly beneficial for the economic goal \(J_{1}\) and, by determining the capital stock available in the future and therefore the level of pollution, indirectly impacts on the environmental goal \(J_{2}\) as well. A higher technology level allows to produce more and thus increases consumption possibilities but at the same time increases pollution, contributing thus indirectly to both the first and the second goals. The social planner by optimally choosing consumption and the technology level needs to balance their effects on the two goals determining the best compromise between them.

We now propose two alternative solution methods, based on a scalarization and a goal programming approach, respectively. We focus on the scalarization method first since, as it will become more clear later, it allows to derive an analytical solution which can be used to inform the goal programming method, whose solution is instead based on numerical analysis.

3 Scalarization

The bicriteria problem in (1) can be simplified by means of a linear scalarization technique as follows:

$$\begin{aligned}&\max _{\left\{ c_{t},z_{t}\right\} _{t=0}^{\infty }}\sum _{0}^{\infty } \beta ^{t}\left[ \nu _{c}\ln c_{t}+\nu _{p}\ln \left( 1-p_{t}\right) \right] \nonumber \\&\text {s.t.}\ \left\{ \begin{array}[c]{l} k_{t+1}=z_{t}\left( 1+p_{t}\right) ^{-\phi }k_{t}^{\alpha }+\left( 1-\delta \right) k_{t}-c_{t}\\ p_{t+1}=\mu z_{t}\left( 1+p_{t}\right) ^{-\phi }k_{t}^{\alpha }+\left( 1-\eta \right) p_{t}\\ k_{t},p_{t},c_{t},z_{t}\ge 0,\text { }p_{t}\le 1,\text { }z_{t}\le \bar{z};\text { }k_{0},p_{0}\text { given,} \end{array} \right. \end{aligned}$$
(2)

where \(\nu _{c}>0\) and \(\nu _{p}>0\) measure the weight of each goal in the planner’s problem. By defining \(\theta =\nu _{p}/\nu _{c}>0\), and using the linearity properties of the summation operators, the scalarized problem turns out to be completely equivalent to the following:

$$\begin{aligned}&\max _{\left\{ c_{t},z_{t}\right\} _{t=0}^{\infty }}W=\sum _{0}^{\infty }\beta ^{t}\left[ \ln c_{t}+\theta \ln \left( 1-p_{t}\right) \right] \end{aligned}$$
(3)
$$\begin{aligned}&\text {s.t.}\ \left\{ \begin{array} [c]{l} k_{t+1}=z_{t}\left( 1+p_{t}\right) ^{-\phi }k_{t}^{\alpha }+\left( 1-\delta \right) k_{t}-c_{t}\\ p_{t+1}=\mu z_{t}\left( 1+p_{t}\right) ^{-\phi }k_{t}^{\alpha }+\left( 1-\eta \right) p_{t}\\ k_{t},p_{t},c_{t},z_{t}\ge 0,\text { }p_{t}\le 1,\text { }z_{t}\le \bar{z};\text { }k_{0},p_{0}\text { given.} \end{array} \right. \end{aligned}$$
(4)

Similar to what discussed in Marsiglio and La Torre (2018), note that the scalarized objecting function represents social welfare, W, which is the typical objective function in traditional macroeconomic settings, in a context where the social planner’s instantaneous utility function depends additively on consumption and environmental quality: \(u\left( c_{t},p_{t}\right) =\ln c_{t}+\theta \ln \left( 1-p_{t}\right) \), with \(\theta \) representing the green preference parameter.

In order to find the closed-form solution for the above problem (3) we first reduce the model by eliminating the control variables \(c_{t}\) and \(z_{t}\). From the first dynamic constraint in (4) we get

$$\begin{aligned} c_{t}=z_{t}\left( 1+p_{t}\right) ^{-\phi }k_{t}^{\alpha }+\left( 1-\delta \right) k_{t}-k_{t+1}, \end{aligned}$$
(5)

which, as \(c_{t}\ge 0\), implies that capital must satisfy

$$\begin{aligned} 0\le k_{t+1}\le z_{t}\left( 1+p_{t}\right) ^{-\phi }k_{t}^{\alpha }+\left( 1-\delta \right) k_{t}. \end{aligned}$$
(6)

From the second dynamic constraint in (4) we get

$$\begin{aligned} \mu z_{t}\left( 1+p_{t}\right) ^{-\phi }k_{t}^{\alpha }=p_{t+1}-\left( 1-\eta \right) p_{t}\,\Longleftrightarrow \, z_{t}=\left( 1+p_{t} \right) ^{\phi }k_{t}^{-\alpha }\left( \frac{1}{\mu }p_{t+1}-\frac{1-\eta }{\mu }p_{t}\right) , \end{aligned}$$
(7)

which must satisfy \(0\le z_{t}\le \bar{z}\), that is:

$$\begin{aligned} z_{t}\ge 0\,\Longleftrightarrow \, p_{t+1}\ge \left( 1-\eta \right) p_{t}\quad \text {and}\quad z_{t}\le \bar{z}\,\Longleftrightarrow \, p_{t+1}\le \mu \bar{z}\left( 1+p_{t}\right) ^{-\phi }k_{t}^{\alpha }+\left( 1-\eta \right) p_{t}. \end{aligned}$$

On the other hand, recall that \(p_{t}\le 1\) must hold for all \(t\ge 0\), which will be the prevalent constraint in the reduced form of problem (3). Therefore, using the second constraint in (4),

$$\begin{aligned} p_{t+1}=\mu z_{t}\left( 1+p_{t}\right) ^{-\phi }k_{t}^{\alpha }+\left( 1-\eta \right) p_{t}\le 1\,\Longleftrightarrow \, z_{t}\le \frac{\left( 1+p_{t}\right) ^{\phi }k_{t}^{-\alpha }\left[ 1-\left( 1-\eta \right) p_{t}\right] }{\mu } \end{aligned}$$
(8)

must be satisfied. The last inequality in (8) suggests that the upper bound \(\bar{z}\) on the technology level should be sufficiently large in order to always allow the social planner to choose a control value \(z_{t}\) yielding a \(p_{t+1}\) value arbitrarily close to 1 from below. In Proposition 1 we shall assume that \(\bar{z}\) is large enough to guarantee the existence of an interior solution; more specifically, by adding some more restrictions on the initial stock values \(k_{0}\) and \(p_{0}\), \(p_{t}<1\) will hold for all \(t\ge 0\). For now, we can safely claim that the admissible range for \(p_{t+1}\) is

$$\begin{aligned} \left( 1-\eta \right) p_{t}\le p_{t+1}\le 1. \end{aligned}$$
(9)

Replacing \(z_{t}\) as in the second equation of (7) into (6) we obtain the admissible range for capital,

$$\begin{aligned} 0\le k_{t+1}\le \frac{1}{\mu }p_{t+1}-\frac{1-\eta }{\mu }p_{t}+\left( 1-\delta \right) k_{t}, \end{aligned}$$

while replacing the same \(z_{t}\) into (5) we obtain the expression of consumption in terms of the state variables,

$$\begin{aligned} c_{t}=\frac{1}{\mu }p_{t+1}-\frac{1-\eta }{\mu }p_{t}+\left( 1-\delta \right) k_{t}-k_{t+1}, \end{aligned}$$
(10)

so that we may state the reduced problem associated with (3):

$$\begin{aligned}&V\left( k_{0},p_{0}\right) =\max _{\left\{ k_{t},p_{t}\right\} _{t=0}^{\infty }}\sum _{0}^{\infty }\beta ^{t}\left\{ \ln \left[ \frac{1}{\mu }p_{t+1}-\frac{1-\eta }{\mu }p_{t}+\left( 1-\delta \right) k_{t}-k_{t+1} \right] +\theta \ln \left( 1-p_{t}\right) \right\} \end{aligned}$$
(11)
$$\begin{aligned}&\text {s.t.}\ \left\{ \begin{array}[c]{l} 0\le k_{t+1}\le \dfrac{1}{\mu }p_{t+1}-\dfrac{1-\eta }{\mu }p_{t}+\left( 1-\delta \right) k_{t}\\ 0\le \left( 1-\eta \right) p_{t}\le p_{t+1}\le 1\\ k_{0},p_{0}\text { given.} \end{array} \right. \end{aligned}$$
(12)

Note that under our assumptions problem (11) is characterized by a short-run utility in which both logarithms are linear in the state variables \(k_{t},p_{t},k_{t+1},p_{t+1}\); hence, the objective function is concave. Moreover, the range for both \(k_{t+1}\) and \(p_{t+1}\) in (12) turns out to be linear, which leads to the following lemma.

Lemma 1

The compact correspondence

$$\begin{aligned} \Gamma \left( k,p\right) =\left\{ \left( k^{\prime },p^{\prime }\right) \in \mathbb {R}_{+}^{2}:\left[ \left( 1-\eta \right) p\le p^{\prime } \le 1\right] \wedge \left[ k^{\prime }\le \frac{1}{\mu }p^{\prime } -\dfrac{1-\eta }{\mu }p+\left( 1-\delta \right) k\right] \right\} \nonumber \\ \end{aligned}$$
(13)

has a convex graph.

Hence, we can claim that problem (11) under the dynamic constraints (12) is concave. This ensures the sufficiency of the first order conditions that we will derive to characterize its optimal solution.

3.1 Equilibrium analysis

The Bellman equation associated with (11) is

$$\begin{aligned} V\left( k,p\right) =\max _{\left( k^{\prime },p^{\prime }\right) \in \Gamma \left( k,p\right) }\left\{ \ln \left[ \frac{1}{\mu }p^{\prime } -\frac{1-\eta }{\mu }p+\left( 1-\delta \right) k-k^{\prime }\right] +\theta \ln \left( 1-p\right) +\beta V\left( k^{\prime },p^{\prime }\right) \right\} , \end{aligned}$$
(14)

where \(\Gamma \left( k,p\right) \) is the correspondence describing the feasible values for \(\left( k^{\prime },p^{\prime }\right) \) defined in (13). Next proposition fully characterizes the solution of our optimization problem (the proofs of the proposition and other results, along with further technical details, are presented in “Appendix A”).

Proposition 1

Assume that the following conditions on parameters and on the arguments of the value function, \(\left( k,p\right) \), hold:

$$\begin{aligned} \bar{z}&=\frac{2^{\phi }}{\mu }\max \left\{ \frac{1}{k},\frac{\mu \delta }{\eta }\right\} \end{aligned}$$
(15)
$$\begin{aligned} \eta&>\frac{1-\beta }{2}+\delta ,\end{aligned}$$
(16)
$$\begin{aligned} k&>\frac{1-\eta }{\mu \left( 1-\delta \right) }p+\frac{\eta -\delta }{\mu \delta \left( 1-\delta \right) },\end{aligned}$$
(17)
$$\begin{aligned} k&<-{\frac{{\beta }\theta \left[ {\beta }\left( 1-{\delta }\right) -\left( 1-\eta \right) \right] +\eta -\delta }{\mu \beta \theta \left( 1-\beta \right) \left( 1-\delta \right) ^{2}}\left( 1-\eta \right) p}+{\frac{\left[ \beta \theta \left( 1-\beta \right) +{\delta }\left( 1+{\beta }^{2} \theta \right) \right] \left( \eta -\delta \right) }{\mu \beta \theta \delta \left( 1-\beta \right) \left( 1-\delta \right) ^{2}}}. \end{aligned}$$
(18)

Then,

  1. 1.

    the solution of the Bellman equation (14) is the function

    $$\begin{aligned} V\left( k,p\right) =\rho _{1}+\rho _{2}\ln \left( \rho _{3}k+\rho _{4}p+\rho _{5}\right) +\rho _{6}\ln (1-p) , \end{aligned}$$
    (19)

    where

    $$\begin{aligned} \rho _{1}&=-{\frac{\ln \mu }{1-\beta }-\frac{1+\beta \theta }{1-\beta }\ln }\left( {\frac{1+\beta \theta }{1-\beta }}\right) -\frac{\beta \theta }{1-\beta }\ln \left( \eta -\delta \right) +\frac{\beta +\beta \theta }{\left( 1-\beta \right) ^{2}}\ln \left[ \beta \left( 1-\delta \right) \right] \nonumber \\&\qquad +\frac{\beta \theta }{1-\beta }\ln \theta , \end{aligned}$$
    (20)
    $$\begin{aligned} \rho _{2}&=\frac{1+\beta \theta }{1-\beta },\quad \rho _{3}=\mu \left( 1-\delta \right) ,\quad \rho _{4}=-\left( 1-\eta \right) ,\quad \rho _{5} =-\frac{\eta -\delta }{\delta },\quad \rho _{6}=\theta ; \end{aligned}$$
    (21)
  2. 2.

    the optimal dynamics of capital and pollution are given by

    $$\begin{aligned} k_{t+1}&=\gamma _{1}k_{t}+\gamma _{2}p_{t}+\gamma _{3} \end{aligned}$$
    (22)
    $$\begin{aligned} p_{t+1}&=\gamma _{4}k_{t}+\gamma _{5}p_{t}+\gamma _{6}, \end{aligned}$$
    (23)

    where

    $$\begin{aligned} \gamma _{1}&={\frac{\theta \left[ {\beta }\left( 1-\delta \right) -\left( 1-\eta \right) \right] +\eta -{\delta }}{\left( \eta -\delta \right) \left( 1+\beta \theta \right) }}\beta ( 1-{\delta }) ,\\ \gamma _{2}&=-{\frac{\theta \left[ {\beta }\left( 1-\delta \right) -\left( 1-\eta \right) \right] +\eta -{\delta }}{\left( \eta -\delta \right) \left( 1+\beta \theta \right) }}\beta \left( \frac{1-\eta }{\mu }\right) , \\ \gamma _{3}&={\frac{\beta \left[ \delta \left( 2\eta -\theta -\delta \right) -\beta \theta \left( 1-\delta \right) \left( \eta -\delta \right) -\eta \left( \eta -\theta \right) \right] +\eta \left( \eta -\delta \right) }{\mu \delta \left( \eta -\delta \right) \left( 1+\beta \theta \right) },}\\ \gamma _{4}&=-{\frac{\mu \beta \theta \left( 1-\beta \right) \left( 1-{\delta }\right) ^{2}}{\left( \eta -\delta \right) \left( 1+\beta \theta \right) },}\qquad \gamma _{5}={\frac{\beta \theta \left( 1-\beta \right) \left( 1-\delta \right) \left( 1-\eta \right) }{\left( \eta -\delta \right) \left( 1+\beta \theta \right) },}\\ \gamma _{6}&={\frac{{\beta }^{2}\theta \left[ {\delta }\left( 1+\eta -{\delta }\right) -\eta \right] +\left( \beta \theta +{\delta }\right) \left( \eta -\delta \right) }{\delta \left( \eta -\delta \right) \left( 1+\beta \theta \right) };} \end{aligned}$$
  3. 3.

    the corresponding optimal policy for consumption and the technology level are given by

    $$\begin{aligned} c_{t}&=\gamma _{1}^{c}k_{t}+\gamma _{2}^{c}p_{t}+\gamma _{3}^{c} \end{aligned}$$
    (24)
    $$\begin{aligned} z_{t}&=\left( 1+p_{t}\right) ^{\phi }k_{t}^{-\alpha }\left( \gamma _{1}^{z}k_{t}+\gamma _{2}^{z}p_{t}+\gamma _{3}^{z}\right) , \end{aligned}$$
    (25)

    where

    $$\begin{aligned} \gamma _{1}^{c}&=\frac{\gamma _{4}}{\mu }-\gamma _{1}+1-\delta ={\frac{\left( 1-\beta \right) \left( 1-{\delta }\right) }{\left( 1+\beta \theta \right) } },\\ \gamma _{2}^{c}&=\frac{\gamma _{5}-\left( 1-\eta \right) }{\mu }-\gamma _{2}=-{\frac{\left( 1-\beta \right) \left( 1-\eta \right) }{\mu \left( 1+\beta \theta \right) }},\\ \gamma _{3}^{c}&=\frac{\gamma _{6}}{\mu }-\gamma _{3}=-{\frac{\left( 1-\beta \right) \left( \eta -\delta \right) }{\mu \delta \left( 1+\beta \theta \right) }},\qquad \gamma _{1}^{z}=\frac{\gamma _{4}}{\mu }=-{\frac{\beta \theta \left( 1-\beta \right) \left( 1-\delta \right) ^{2}}{\left( \eta -\delta \right) \left( 1+\beta \theta \right) }},\\ \gamma _{2}^{z}&=\frac{\gamma _{5}-\left( 1-\eta \right) }{\mu } ={\frac{\beta \theta \left[ 1{-}\eta -{\beta }\left( 1-\delta \right) \right] -\left( \eta -\delta \right) }{\mu \left( \eta -\delta \right) \left( 1+\beta \theta \right) }\left( 1-\eta \right) },\\ \gamma _{3}^{z}&=\frac{\gamma _{6}}{\mu }={\frac{\beta \theta \left[ 1-{\beta }\left( 1-\delta \right) \right] +\delta }{\mu \delta \left( 1+\beta \theta \right) }}; \end{aligned}$$
  4. 4.

    in the long run the economy will converge to its unique non-trivial (asymptotic) steady state \(\left( k^{s},p^{s},c^{s},z^{s}\right) \) with coordinates

    $$\begin{aligned} k^{s}=\frac{\eta }{\mu \delta },\qquad p^{s}=1,\qquad c^{s}=0,\qquad z^{s}=2^{\phi }\delta ^{\alpha }\left( \frac{\eta }{\mu }\right) ^{1-\alpha }. \end{aligned}$$
    (26)

The first condition (15) allows for inequality (8) to hold for the optimal dynamics defined by (22) and (23), that is, it guarantees a range for the technology level \(z_{t}\) sufficiently large so that \(p_{t+1}\le 1\) is always an admissible choice, for any \(p_{t+1}\) arbitrarily close to 1. The RHS in (20), in order to be defined, requires \(\eta >\delta \), which is implied by condition (16) as \(\left( 1-\beta \right) /2>0\); that is, in order to have a meaningful solution for problem (3) the pollution stock must decay faster than the pace at which capital depreciates. Note that coefficients \(\rho _{2}\), \(\rho _{3}\) and \(\rho _{6}\) in (21) are positive, while, under the condition \(\eta >\delta \), coefficients \(\rho _{4}\ \)and \(\rho _{5}\) are negative. The technical condition (17) has three purposes: (i) it guarantees that \(k_{t+1}\) in (22) is interior, i.e., it satisfies \(0<k_{t+1}<p_{t+1}/\mu -\left( 1-\eta \right) p_{t}/\mu +\left( 1-\delta \right) k_{t}\) for all \(t\ge 0\); (ii) together with condition (15), it guarantees that \(p_{t+1}\) in (23) is such that \(p_{t+1}<1\) for all \(t\ge 0\); and (iii) it guarantees that the first log in the RHS of (19) is well defined, that is, \(\rho _{3}k+\rho _{4} p+\rho _{5}>0\) holds. Condition (17) postulates that there must be a sufficient amount of initial capital to compensate the negative effects of the initial stock of pollution, both on production and utility. The last technical condition (18) ensures that \(p_{t+1}\) in (23) is such that \(p_{t+1}>\left( 1-\eta \right) p_{t}\); that is, under the assumption (15), conditions (17) and (18) together imply that the optimal plan for the pollution stock defined by (23) is interior as well.

Proposition 1 also states that optimal dynamics of both capital and pollution are linear in the stock of capital and pollution. The same applies to the optimal policy for consumption, while that for the technology level depends nonlinearly on both capital and pollution. The most interesting result in Proposition 1 is related to the steady state outcome: it is optimal for the economy to reach in the long run the maximum pollution level that the environment can effectively bear. Since pollution affects production via an externality effect captured by the damage function \(D_{t}=(1+p_{t})^{-\phi }\), in the long run capital will achieve a strictly positive level which depends both on economic (\(\delta \)) and environmental factors (\(\eta \) and \(\mu \)), which is clearly lower than its maximal level, that is \(k^{s}<\bar{k}\). This long run equilibrium represents what we can have referred to as an unsustainable outcome since the utility associated with environmental quality tends to minus infinity and as a result welfare tends to minus infinity as well. Such a paradoxical result suggesting that optimality implies unsustainability in the long run is intuitively due to the fact that at the end of the planning horizon (i.e., when the steady state is reached) the environment does not have any value left and as such it is convenient to exploit it as much as possible in order to boost finite-time consumption. It it interesting to observe that the scalarization parameter \(\theta \), which represents the green preference parameter, does not affect in any way the long run equilibrium: higher or lower concern levels for the environment are completely irrelevant in the long run. However, note that the steady state can only be reached asymptotically; indeed, the value function (19) is not defined on \(\left( k^{s},p^{s}\right) \) because the capital value \(k^{s}=\eta /\left( \mu \delta \right) \) does not satisfy condition (17).

The optimal trajectory generated by the dynamics (22) and (23) can be written in vector form as

$$\begin{aligned} \left[ \begin{array} [c]{c} k_{t+1}\\ p_{t+1} \end{array} \right] =\left[ \begin{array}[c]{cc} \gamma _{1} &{}\quad \gamma _{2}\\ \gamma _{4} &{}\quad \gamma _{5} \end{array} \right] \left[ \begin{array}[c]{c} k_{t}\\ p_{t} \end{array} \right] +\left[ \begin{array}[c]{c} \gamma _{3}\\ \gamma _{6} \end{array} \right] , \end{aligned}$$
(27)

which shows that the optimal dynamic for the capital and the pollution stock is an affine function. It turns out (see the proof of Proposition 1 in “Appendix A”) that the matrix

$$\begin{aligned} \left[ \begin{array}[c]{cc} \gamma _{1} &{}\quad \gamma _{2}\\ \gamma _{4} &{}\quad \gamma _{5} \end{array} \right] \end{aligned}$$
(28)

is singular; thus one eigenvalue is zero, \(\lambda _{1}=0\), while the other is \(\lambda _{2}=\beta \left( 1-{\delta }\right) \), so that it is positive and strictly less than 1, and the steady state in (26) is globally stable. Solving the general solution for the initial values \(\left( k_{0},p_{0}\right) \) satisfying (17) and (18), we find the following exact solution for the dynamical system (27):

$$\begin{aligned} \left\{ \begin{array}[c]{l} k_{t}=c_{2}\left[ \beta \left( 1-{\delta }\right) \right] ^{t}+\dfrac{\eta }{\mu \delta }\\ p_{t}=-c_{2}\dfrac{\mu \theta \left( 1-\beta \right) \left( 1-{\delta }\right) }{\theta \left[ {\beta }\left( 1-\delta \right) -\left( 1-\eta \right) \right] +\eta -{\delta }}\left[ \beta \left( 1-{\delta }\right) \right] ^{t}+1, \end{array} \right. \end{aligned}$$
(29)

where

$$\begin{aligned} c_{2}=\frac{\theta \left[ {\beta }\left( 1-\delta \right) -\left( 1-\eta \right) \right] +\eta -{\delta }}{1+\beta \theta }\left[ {\frac{k_{0} }{\eta -\delta }}-\frac{\left( 1-\eta \right) p_{0}}{\mu \left( 1-{\delta }\right) \left( \eta -\delta \right) }-\frac{1}{\mu \delta \left( 1-{\delta }\right) }\right] {.} \end{aligned}$$
(30)

In the proof of Proposition 1 in “Appendix A” we show that, under conditions (16) and (17), \(c_{2}\) defined in (30) is strictly positive; therefore, the optimal plan defined by (29) is characterized by a sequence of capital stocks, \(k_{t}\), that converges to the steady value \(k^{s}=\eta /\left( \mu \delta \right) \) defined in (26) from above; that is, starting from any initial state \(\left( k_{0},p_{0}\right) \) satisfying (17) and (18 ), all optimal sequences \(k_{t}\) generated by (22) contain capital levels which are all larger than the asymptotic value \(k^{s}=\eta /\left( \mu \delta \right) \). Note that this property holds also when the initial capital level lies below the steady value, \(k_{0}<k^{s}=\eta /\left( \mu \delta \right) \). This is due to the singularity of the matrix (28) which lets the optimal trajectory of capital jump on the line defined by the eigenvector associated with the positive eigenvalue, \(\lambda _{2}=\beta \left( 1-{\delta }\right) \), right after the first iteration of (27); as under condition (16) the slope of such line is negative, specifically, equal to

$$\begin{aligned} -\dfrac{\mu \theta \left( 1-\beta \right) \left( 1-{\delta }\right) }{\theta \left[ {\beta }\left( 1-\delta \right) -\left( 1-\eta \right) \right] +\eta -{\delta }}<0, \end{aligned}$$

all optimal paths approach the steady state \(\left( k^{s},p^{s}\right) =\left( \eta /( \mu \delta ) ,1\right) \) from south-east, that is, with values \(k_{t}>\eta /\left( \mu \delta \right) \) and \(p_{t}<1\). This suggests that the optimal dynamics imply that capital initially overshoots its long run value while pollution falls below its long run value, and along the transition to the steady state capital gradually decreases while pollution increases. This implies that asymptotically pollution achieves the maximal level the environment can effectively bear while capital achieves a strictly positive level determined by both economic and environmental factors.

Note that, after the initial overshooting, the optimal capital dynamic implies a situation of degrowth in which the size of economic activities tends to shrink over time, consistent with what discussed in the degrowth literature; however, the pollution dynamic implying increasing environmental deterioration is in net contrast with such degrowth arguments. Indeed, our model suggests that it is optimal at the beginning of the planning horizon to produce and consume a lot (more than in the long run) and at the same time devote many resources to environmental preservation (through the choice of the technology level), and then to gradually reduce production and technological control efforts in order to achieve asymptotically the maximal level of environmental degradation and a strictly positive capital level determined both by economic and environmental factors. This type of result clearly suggests that, different from what discussed in the degrowth literature, economic degrowth is not always optimal and even when it is (i.e., after the initial overshooting) degrowth goes hand-in-hand with environmental deterioration; therefore, economic degrowth does not represent an obvious solution to environmental problems. Note moreover that different from degrowth arguments, which are all qualitative in nature, our results are optimally derived from a social planner’s multicriteria optimization problem and such results hold true for every value of the scalarization parameter. Therefore, even if the relative weight of the environmental goal is infinitely larger than the economic goal (i.e., \(\theta \rightarrow \infty \)), which is somehow the implicit assumption underlying the degrowth point of view, a full asymptotic exploitation of the natural environment is the optimal course of action.

3.2 The efficient frontier and social welfare

The exact solution (29) allows to derive both the Pareto frontier and social welfare. In order to do so we need to determine the optimal value of the two criteria in problem 1, representing the economic goal \(J_{1}\left( k_{0},p_{0}\right) =\sum _{0}^{\infty }\beta ^{t}\ln c_{t}\) and the environmental goal \(J_{2}\left( k_{0},p_{0}\right) =\sum _{0} ^{\infty }\beta ^{t}\ln \left( 1-p_{t}\right) \), which are both function of the initial stocks \(k_{0}\) and \(p_{0}\) and for which the plans \(\left\{ c_{t}\right\} _{t=0}^{\infty }\) and \(\left\{ p_{t}\right\} _{t=0}^{\infty }\) are given by the optimal policies (24) and (23). To this purpose, let us first define

$$\begin{aligned} G_{0}=\mu \delta \left( 1-\delta \right) k_{0}-\delta \left( 1-\eta \right) p_{0}-( \eta -\delta ) , \end{aligned}$$

then (see the proof of Proposition 1 in “Appendix A”)

$$\begin{aligned} \overline{J}_{1}\equiv J_{1}\left( k_{0},p_{0}\right)&=\sum _{0}^{\infty }\beta ^{t}\ln c_{t}=\sum _{0}^{\infty }\beta ^{t}\ln \left[ \frac{1}{\mu } p_{t+1}-\frac{1-\eta }{\mu }p_{t}+\left( 1-\delta \right) k_{t}-k_{t+1}\right] \nonumber \\&=\sum _{0}^{\infty }\beta ^{t}\ln \left\{ \frac{\left( 1-\beta \right) G_{0} }{\mu \delta \left( 1+\beta \theta \right) }\left[ \beta \left( 1-{\delta }\right) \right] ^{t}\right\} \nonumber \\&=\ln \left[ \frac{\left( 1-\beta \right) G_{0}}{\mu \delta \left( 1+\beta \theta \right) }\right] \sum _{0}^{\infty }\beta ^{t}+\ln \left[ \beta \left( 1-{\delta }\right) \right] \sum _{0}^{\infty }t\beta ^{t}\nonumber \\&=\frac{1}{1-\beta }\ln \left[ \frac{\left( 1-\beta \right) G_{0}}{\mu \delta \left( 1+\beta \theta \right) }\right] +\frac{\beta }{\left( 1-\beta \right) ^{2}}\ln \left[ \beta \left( 1-{\delta }\right) \right] , \end{aligned}$$
(31)

and

$$\begin{aligned} \overline{J}_{2}\equiv J_{2}\left( k_{0},p_{0}\right)&=\sum _{0}^{\infty }\beta ^{t}\ln \left( 1-p_{t}\right) =\sum _{0}^{\infty }\beta ^{t}\ln \left[ {\frac{\theta \left( 1-\beta \right) G_{0}}{\delta \left( 1+\beta \theta \right) \left( \eta -\delta \right) }}\left[ \beta \left( 1-{\delta }\right) \right] ^{t}\right] \nonumber \\&=\ln \left[ {\frac{\theta \left( 1-\beta \right) G_{0}}{\delta \left( 1+\beta \theta \right) \left( \eta -\delta \right) }}\right] \sum _{0}^{\infty }\beta ^{t}+\ln \left[ \beta \left( 1-{\delta }\right) \right] \sum _{0}^{\infty }t\beta ^{t}\nonumber \\&=\frac{1}{1-\beta }\ln \left[ {\frac{\theta \left( 1-\beta \right) G_{0} }{\delta \left( 1+\beta \theta \right) \left( \eta -\delta \right) }}\right] +\frac{\beta }{\left( 1-\beta \right) ^{2}}\ln \left[ \beta \left( 1-{\delta }\right) \right] . \end{aligned}$$
(32)

The above two expressions imply that optimality implies that the economic goal decreases with the scalarization parameter \(\theta \), as

$$\begin{aligned} \frac{\partial \overline{J}_{1}}{\partial \theta }=-\frac{\beta }{\left( 1-\beta \right) \left( 1+\beta \theta \right) }<0, \end{aligned}$$

while the environmental goal increases with it, as

$$\begin{aligned} \frac{\partial \overline{J}_{2}}{\partial \theta }=\frac{1}{\theta \left( 1-\beta \right) \left( 1+\beta \theta \right) }>0. \end{aligned}$$

This suggests that the optimal choice of the two control variables \(c_{t}\) and \(z_{t}\) does not allow to solve the economic-environmental trade off, which persists also at the optimal solution and as such the Pareto frontier will bow outward. Indeed, by rearranging the expression \(\overline{J}_{1}\) in (31) and plugging it into that of \(\overline{J}_{2}\) in (32) we first obtain:

$$\begin{aligned} \overline{J}_{2}=\overline{J}_{1}+\frac{1}{1-\beta }\ln \left( \frac{\theta \mu }{\eta -\delta }\right) , \end{aligned}$$

and then, after solving the expression in (31) for \(\theta \) and plugging the result into the above equation, we get the explicit expression of the frontier:

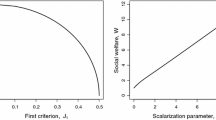
$$\begin{aligned} \overline{J}_{2}=\overline{J}_{1}+\frac{1}{1-\beta }\ln \left\{ \frac{(1-\beta )G_{0}}{\mu \delta }\left[ \beta \left( 1-{\delta }\right) \right] ^{\frac{\beta }{1-\beta }}e^{-(1-\beta )\overline{J}_{1}}-1\right\} +\frac{1}{1-\beta }\ln \left[ \frac{\mu }{\beta \left( \eta -\delta \right) }\right] , \end{aligned}$$

whose graphical representation is a nonlinear outward bowed curve, as shown in the left panel of Fig. 1.

Fig. 1
figure 1

Efficient frontier (left) and social welfare (right) under a scalarization approach

Full size image

It turns out that, even if the economic-environmental trade off still persists in the optimal solution of the bicriteria problem, its scalarization giving rise to a unicriterion problem makes such a trade off completely disappear. Indeed, using (31) and (32) we can explicitly derive social welfare as a function of the scalarization parameter \(\theta \) the follows:

$$\begin{aligned} {W}&{\equiv W(k_{0},p_{0})=\overline{J}_{1}+\theta \overline{J}_{2}}\\&=\frac{1}{1-\beta }\ln \left[ \frac{\left( 1-\beta \right) G_{0}}{\mu \delta \left( 1+\beta \theta \right) }\right] +\frac{\beta }{\left( 1-\beta \right) ^{2}}\ln \left[ \beta \left( 1-{\delta }\right) \right] \\&\qquad +\frac{\theta }{1-\beta }\ln \left[ {\frac{\theta \left( 1-\beta \right) G_{0}}{\delta \left( 1+\beta \theta \right) \left( \eta -\delta \right) }}\right] +\frac{\beta \theta }{\left( 1-\beta \right) ^{2} }\ln \left[ \beta \left( 1-{\delta }\right) \right] \\&=\frac{1+\theta }{1-\beta }\ln \left\{ {\frac{\left( 1-\beta \right) G_{0} }{\delta \left( 1+\beta \theta \right) }}\left[ \beta \left( 1-{\delta }\right) \right] ^{\frac{\beta }{1-\beta }}\right\} +\frac{1}{1-\beta } \ln \left[ \frac{1}{\mu }\left( {\frac{\theta }{\eta -\delta }}\right) ^{\theta }\right] {.} \end{aligned}$$

Numerical simulations show that social welfare monotonically decreases with the scalarization parameter, as shown in the right panel of Fig. 1. Hence, within the parameters’ range consistent with Proposition 1, if \(\theta \) increases, the effects of the decrease in (optimal) consumption always dominate those of the decrease in (optimal) pollution, which in turn improves environmental quality, thus neutralizing the trade off altogether. This means that putting more weight on the environmental goal has a negative effect on social welfare, as the negative effects associated with the economic goal more than offset the beneficial effects associated with the environmental goal, and thus social welfare turns out to be monotonically decreasing with the scalarization parameter.

A graphical representation of the efficient frontier and social welfare are given in Fig. 1, in which the parameter values are set in line with available empirical estimates (Barro and Sala-i-Martin 2004) and in order to verify the conditions in Proposition 1 as follows: \(\beta =0.96\), \(\delta =0.1\), \(\eta ={0}.2\), \(\alpha =0.33\), \(\phi =2\), \(\mu =0.5\), \(k_{0}=2.25\) and \(p_{0}=0\). Under these parameters’ values it turns out \(\bar{z}=3.56\), \(\bar{k}=\left( \delta /\bar{z}\right) ^{\frac{1}{\alpha -1} }=206.44\), the steady value for capital is \(k^{s}=\eta /\left( \mu \delta \right) =4\), and conditions (16)–(18) are satisfied as \(\eta =0.2>0.12=\left( 1-\beta \right) /2+\delta \), \(k_{0} =2.25>0.22=\left( \eta -\delta \right) /\left[ \mu \delta \left( 1-\delta \right) \right] \) and \(k_{0}=2.25<21.26=\left\{ \left[ \beta \theta \left( 1-\beta \right) +{\delta }\left( 1+{\beta }^{2}\theta \right) \right] \left( \eta -\delta \right) \right\} /\left[ \mu \beta \theta \delta \left( 1-\beta \right) \left( 1-\delta \right) ^{2}\right] \). Note that we have chosen a value for \(k_{0}\) very close to its lower bound in condition (17) for an initial pristine environment with \(p_{0}=0\) pollution. We can observe that the shapes of the frontier and of social welfare are consistent with our above discussion. The above results, showing that the economic-environmental trade off is present in the optimal solution of the bicriteria problem while it completely disappears in the solution of the scalarized problem, suggest that the traditional economics approach consisting of relying on a unicriterion objective function (i.e., social welfare) risks to oversimplify the complicated nature of the sustainability problem.

4 Goal programming

We now propose an alternative solution method, based on a weighted goal programming approach, to compare our previous results with. The bicriteria problem in (1) can be stated in terms of a weighted goal programming model as follows:

$$\begin{aligned}&\min \left( w_{1}\delta _{1}^{+}+w_{1}\delta _{1}^{-}+w_{2}\delta _{2} ^{+}+w_{2}\delta _{2}^{-}\right) \\&\text {s.t.}\ \left\{ \begin{array}[c]{l} J_{1}-\delta _{1}^{+}+\delta _{1}^{-}=G_{1}\\ J_{2}-\delta _{2}^{+}+\delta _{2}^{-}=G_{2}\\ \delta _{1}^{+},\delta _{1}^{-}\ge 0\\ \delta _{2}^{+},\delta _{2}^{-}\ge 0, \end{array} \right. \end{aligned}$$

and subject to the dynamic constraints and initial conditions in (4). In the above formulation we try to minimize the (weighted) positive and negative deviations from the aspiration level for each of the two criteria. Specifically, for criterion \(i=\{1,2\}\) where 1 represents the economic goal and 2 the environmental goal, \(G_{i}\) denotes the aspiration level, \(w_{i}\) the weight attached to it, \(\delta _{i}^{+}\) and \(\delta _{1}^{-}\) positive and negative deviations from the aspiration level, respectively. We rely on the analytical results derived earlier through the scalarization approach to determine the aspiration levels, which are set according to the optimal level of the two criteria (31) and (32) in which the scalarization parameter takes the extreme value associated with the presence of only the relevant criterion in the optimization problem. In particular, the aspiration levels are determined as follows:

$$\begin{aligned} G_{1}&\equiv \overline{J}_{1}(\theta =0)=\frac{1}{1-\beta }\ln \left[ \frac{\left( 1-\beta \right) G_{0}}{\mu \delta }\right] +\frac{\beta }{\left( 1-\beta \right) ^{2}}\ln \left[ \beta \left( 1-{\delta }\right) \right] \\ G_{2}&\equiv \overline{J}_{2}(\theta \rightarrow \infty )=\frac{1}{1-\beta } \ln \left[ {\frac{\left( 1-\beta \right) G_{0}}{\beta \delta \left( \eta -\delta \right) }}\right] +\frac{\beta }{\left( 1-\beta \right) ^{2}} \ln \left[ \beta \left( 1-{\delta }\right) \right] \end{aligned}$$

The results of our optimization problem, based on the same parametrization we employ in the previous section, are illustrated in the next figure which represents the efficient frontier. Figure 2 shows that from a qualitatively point of view the solutions under a scalarization and under a goal programming techniques are identical. Clearly, there exist some quantitative difference which is implicit in the different formulations of the two multicriteria approaches, but both solutions clearly point out the existence of a clear trade off between the economic and environmental goals. By comparing Fig. 2 with Fig. 1 we can note that, in our specific parametrization, the goal programming approach dictates less pollution and less consumption than the the scalarization method, as confirmed by the fact that the environmental (economic) goal takes higher (lower) values in the goal programming than in the scalarized solution. This implies that according to a goal programming approach the environmental goal needs to be favored at the cost of the economic goal with respect to what happens with the scalarization technique.

Fig. 2
figure 2

Efficient frontier under a weighted goal programming approach

Full size image

5 Conclusion

Discussing sustainability requires to critically account for both economic and environmental goals, which are to a large extent conflicting. In order to do so we rely on a multicriteria method based on both scalarization and goal programming techniques in order to analyze the trade off between economic growth and environmental outcomes in a framework in which the economy and environment relation is bidirectional. On the one hand, economic growth by stimulating production activities gives rise to emissions of pollutants which deteriorate the natural environment. On the other hand, the natural environment affects economic activities since pollution generates a production externality determining how much output the economy can effectively produce. In this setting we explicitly characterize the optimal solution showing that, independently of the relative importance of economic and environmental factors, after an initial overshooting capital decreases while pollution monotonically increases during the transitional path, implying that it is optimal for the economy to asymptotically reach the maximum pollution level that the natural environment can effectively bear. Such a paradoxical result is due to the fact that asymptotically the environment does not have any value left and as such it is convenient to exploit it as much as possible in order to boost finite-time consumption. To the best of our knowledge, despite the huge number of works on the economic growth and environment relation, none has thus far been able to explicitly characterize the optimal dynamics in a setting similar to ours in which the economy and the environment mutually affect each other.

Clearly the approach we adopt in this paper is a bit simplistic and the analysis could be extended along several directions in order to describe more realistically the economy-environment relation. In particular, we have assumed that capital is bounded in order to mimic a situation in which natural constraints limit the economy’s ability to accumulate assets. However, it may well be possible that technological progress allows the economy to continually expand such a bound, which could permit for sustained long run growth to occur. In such a setting it is no longer obvious that optimality requires full exploitation of natural assets, but it may be possible to find an asymptotic balance between economic and environmental goals. Extending the analysis in order to take this into account is left for future research.