Large-scale unit commitment under uncertainty: an updated literature survey

Abstract

The Unit Commitment problem in energy management aims at finding the optimal production schedule of a set of generation units, while meeting various system-wide constraints. It has always been a large-scale, non-convex, difficult problem, especially in view of the fact that, due to operational requirements, it has to be solved in an unreasonably small time for its size. Recently, growing renewable energy shares have strongly increased the level of uncertainty in the system, making the (ideal) Unit Commitment model a large-scale, non-convex and uncertain (stochastic, robust, chance-constrained) program. We provide a survey of the literature on methods for the Uncertain Unit Commitment problem, in all its variants. We start with a review of the main contributions on solution methods for the deterministic versions of the problem, focussing on those based on mathematical programming techniques that are more relevant for the uncertain versions of the problem. We then present and categorize the approaches to the latter, while providing entry points to the relevant literature on optimization under uncertainty. This is an updated version of the paper “Large-scale Unit Commitment under uncertainty: a literature survey” that appeared in 4OR 13(2):115–171 (2015); this version has over 170 more citations, most of which appeared in the last 3 years, proving how fast the literature on uncertain Unit Commitment evolves, and therefore the interest in this subject.

1 Introduction

In electrical energy production and distribution systems, an important problem deals with computing the production schedule of the available generating units, accordingly with their different technologies, in order to meet their technical and operational constraints and to satisfy several system-wide constraints, e.g., global equilibrium between energy production and energy demand or voltage profile bounds at each node of the grid. The constraints of the units are very complex; for instance, some units may require up to 24 h to start. Therefore, such a schedule must be computed (well) in advance of real time. The resulting family of mathematical models is usually referred to as the Unit Commitment problem (UC), and its practical importance is clearly proven by the enormous amount of scientific literature devoted to its solution in the last four decades and more. Besides the very substantial practical and economical impact of UC, this proliferation of research is motivated by at least two independent factors:

• 1. On the one hand, progress in optimization methods, which provides novel methodological approaches and improves the performances of existing ones, thereby allowing to tackle previously unsolvable problems;

• 2. On the other hand, the large variety of different versions of UC corresponding to the disparate characteristics of electrical systems worldwide (free market vs. centralized, vast range of production units due to hydro/thermal/nuclear sources,...).

Despite all of this research, UC still cannot be considered a “well-solved” problem. This is partly due to the need of continuously adapting to the ever-changing demands of practical operational environments, in turn caused by technological and regulatory changes which significantly alter the characteristics of the problem to be solved. Furthermore, UC is a large-scale, non-convex optimization problem that, due to operational requirements, has to be solved in an “unreasonably” small time. Finally, as methodological and technological advances make previous versions of UC more accessible, practitioners have a chance to challenge the (very significant) simplifications that have traditionally been made, for purely computational reasons, about the actual behaviour of generating units. This leads to the development of models incorporating considerably more detail than in the past, which can significantly stretch the capabilities of solution methods.

A particularly relevant trend in current electrical systems is the ever increasing use of intermittent (renewable) production sources such as wind and solar power. This has significantly increased the underlying uncertainty in the system, previously almost completely due to variation of users’ demand (which could however be forecast quite effectively) and occurrence of faults (which was taken into account by requiring some amount of spinning reserve). Ignoring such a substantial increase in uncertainty levels w.r.t. the common existing models incurs an unacceptable risk that the computed production schedules be significantly more costly than anticipated, or even infeasible (e.g., Keyhani et al. 2010). However, incorporating uncertainty in the models is very challenging, in particular in view of the difficulty of deterministic versions of UC.

Fortunately, optimization methods capable of dealing with uncertainty have been a very active area of research in the last decades, and several of these developments can be applied, and have been applied, to the UC problem. This paper aims at providing a survey of approaches for the Uncertain UC problem (UUC). The literature is rapidly growing: this is an update of our earlier survey Tahanan et al. (2015), that has also appeared as van Ackooij et al. (2018), and counts over 170 more citations, most of them being articles published in the last 3 years. This expansion of the literature is easily explained, besides by the practical significance of UUC, by the combination of two factors: on the one hand the diversity of operational environments that need to be considered, and on the other hand by the fact that the multitude of applicable solution techniques already available to the UC (here and in the following we mean the deterministic version when UUC is not explicitly mentioned) is further compounded by the need of deciding how uncertainty is modeled. Indeed, the literature offers at least three approaches that have substantially different practical and computational requirements: Stochastic Optimization (SO), Robust Optimization (RO), and Chance-Constrained Optimization (CCO). These choices are not even mutually orthogonal, yielding yet further modelling options. In any case, the modelling choice has vast implications on the actual form of UUC, its potential robustness in the face of uncertainty, the (expected) cost of the computed production schedules and the computational cost of determining them. Hence, UUC is even less “well-solved” than UC, and a thriving area of research. Therefore, a survey about it is both timely and appropriate.

We start with a review of the main contributions on solution methods for UC that have an impact on those for the uncertain version. This is necessary, as the last broad UC survey (Padhy 2004) dates back some 10 years, and is essentially an update of Sheble and Fahd (1994); neither of these consider UUC in a separate way as we do. The more recent survey Farhat and El-Hawary (2009) provides some complements to Padhy (2004) but it does not comprehensively cover methods based on mathematical programming techniques, besides not considering the uncertain variants. The very recent survey Saravanan et al. (2013) focusses mainly on nature-inspired or evolutionary computing approaches, most often applied to simple 10-units systems that can nowadays be solved optimally in split seconds with general-purpose techniques; furthermore these methods do not provide qualified bounds (e.g., optimality gap) that are most often required when applying SO, RO or CCO techniques to the solution of UUC. This, together with the significant improvement of solving capabilities of methods based on mathematical programming techniques (e.g., Lagrangian or Benders’ decomposition methods, MILP approaches,...), justifies why in the UC-part of our survey we mostly focus on the latter rather than on heuristic approaches. This version also significantly updates Tahanan et al. (2015), which appeared roughly simultaneously with Zheng et al. (2015), upon which we also significantly expand and update. Finally, the recent survey (Alqurashi et al. 2016) discusses uncertainty in energy problems in general; that is, besides UC, it also deals with market-clearing and long-term models. However, it does so by leaving out any methodological discussion of optimization algorithms; furthermore, it is somewhat light on certain approaches such as CCO ones. In our view, discussing solution approaches for a model is crucial since it closely ties in with the usefulness of its solutions; for instance, stochastic optimization models are only useful as long as they can be run with an appropriate number of scenarios, and the possibility of doing so depends on the employed solution methods. We therefore believe that limiting the presentation to the models leaves out too much important information that is crucial for properly choosing the right form of uncertainty modelling.

Because the paper surveys such a large variety of material, we provide two different reading maps:

• 1. The first is the standard reading order of the paper, synthesized in the Table of Contents above. In Sect. 2 we describe the varied technical and operational constraints in (U)UC models which give rise to many different variants of UC problems. In Sect. 3 we provide an overview of methods that deal with the deterministic UC, focusing in particular on methods dealing with large-scale systems and/or that can be naturally extended to UUC, at least as subproblems. In particular, in Sect. 3.1 we discuss Dynamic Programming approaches, in Sect. 3.2 we discuss Integer and Mixed Integer Linear Programming approaches, while in Sects. 3.3 and 3.4 we discuss decomposition approaches (Lagrangian, Benders and Augmented Lagrangian), and finally in Sect. 3.5 we (quickly) discuss (Meta-)Heuristics. UUC is then the subject of Sect. 4: in particular, Sect. 4.2 presents Stochastic Optimization (Scenario-Tree) approaches, Sect. 4.3 presents Robust Optimization approaches, and Sect. 4.4 presents Chance-Constrained Optimization approaches. We end the paper with some concluding remarks in Sect. 5, and with a list of the most used acronyms.

• 2. The second map is centred on the different algorithmic approaches that have been used to solve (U)UC. The main ones considered in this review are:

  • Dynamic programming approaches, that can be found in Sects. 3.1, 3.2.2, 3.3, 3.5.2, 4.1.1.1, 4.2.1, 4.2.3, 4.2.4, and 4.4;

  • Mixed-integer programming approaches, that can be found in Sects. 3.2, 3.3, 4.1.2.2, 4.2, 4.2.1, 4.2.3, 4.2.4, 4.3, and 4.4;

  • Lagrangian relaxation (decomposition) approaches, that can be found in Sects. 3.2.2, 3.3, 3.5.2, 4.2.1, 4.2.2, 4.2.3, 4.2.4, and 4.4;

  • Benders’ decomposition approaches, that can be found in Sects. 3.2.2, 3.3, 4.2, 4.2.1, 4.2.2, 4.2.3, 4.2.4, and 4.3;

  • Augmented Lagrangian approaches, that can be found in Sects. 3.3, 3.4, and 4.4;

  • Other forms of heuristic approaches, that can be found in Sects. 3.1, 3.2.2, 3.3, 3.5, 4.1.2.1, 4.2.2, and 4.2.3.

2 Ingredients of the unit commitment problem

We start our presentation with a very short description of the general structure of electrical systems, presenting the different decision-makers who may find themselves in the need of solving (U)UC problems and their interactions. This discussion will clarify which of the several possible views and needs we will cover; the reader with previous experience in this area can skip to Sect. 2.1 for a more detailed presentation of the various ingredients of the (U)UC model, or even to Sect. 3 for the start of the discussion about algorithmic approaches.

Fig. 1

Simplified electricity and balancing market structure

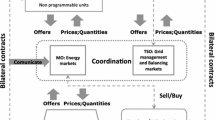
When the first UC models were formulated, the usual setting was that of a Monopolistic Producer (MP). The MP was in charge of the electrical production, transmission and distribution in one given area, often corresponding to a national state, comprised the regulation of exchanges with neighbouring regions. In the liberalized markets that are nowadays prevalent, the decision chain is instead decentralized and significantly more complex, as shown in the (still somewhat simplified) scheme of Fig. 1. In a typical setting, companies owning generation assets (GENCOs) have to bid their generation capacity over one (or more) Market Operator(s) (MO). Alternatively, or in addition, they can stipulate bilateral contracts (or contracts for differences, CfD) with final users or with wholesales/traders. Once received the bids/offers, the MO clears the (hourly) energy market and defines (equilibrium) clearing prices. A Transmission System Operator (TSO), in possession of the high voltage transmission infrastructure, then has the duty—acting in concert with the Power Exchange Manager (PEM)—to ensure safe delivery of the energy, which in turns means different duties such as real time frequency-power balancing, several types of reserve satisfaction, voltage profile stability, and enforcing real-time network capacity constraints. The TSO typically operates in a different way programmable and non programmable units, since for instance only the former can participate on balancing markets. However, very recently the growth of non programmable renewable sources required a greater integration also in the real time balancing market. As a consequence modifications of network codes and new regulation emerged. This is, e.g., the case of the resolution 300/2017/R/eel of the Italian Regulatory Authority for Energy, Networks and Environment (ARERA), which establishes the first guidelines for the active participation of the non programmable renewable sources, of the demand and of the storage in the balancing market. Notably the storage can be included within traditional production units giving birth to the concept of Integrated Production Units.

This basic setting, which can be considered sufficient for our discussion, is only a simplification of the actual systems, which also vary depending on their geographical position. For instance, transmission (and distribution) assets may actually be in possession of different companies that have to offer them under highly regulated fair and non-discriminative conditions, leaving the TSO only a coordination role. Also, the TSO and the MO may or may not be the same entity, the balancing market can actually follow a central dispatch paradigm (as alluded in Fig. 1) or a self dispatch one and so on. We leave aside these other factors, like how many and MOs there are and how exactly these are structured; we refer to Conejo and Prieto (2001), Harris (2011), Oren et al. (1997), Shahidehpour et al. (2002) and Conejo et al. (2010, Chapter 1) for a more detailed description. Because of this complexity, standard optimization models may not be entirely appropriate to deal with all the aspects of the problem, since the behaviour of different/competing decision makers need be taken into account. This may require the use of other methodologies, such as the computation of equilibria or agent-based simulation. We will not deal with any of these aspects, the interested reader being referred to Ventosa et al. (2005), Harris (2011), Oren et al. (1997), Shahidehpour et al. (2002), Leveque (2002), Gabriel et al. (2013), van Ackooij et al. (2018), van Ackooij and de Oliveira (2017), Dempe et al. (2015), Outrata (1990), Dempe and Dutta (2012), Adam et al. (2017) and Surowiec (2010) for further discussion.

2.1 A global view of UC

In broad terms, the (deterministic or uncertain) Unit Commitment problem (both UC in this section unless explicitly stated) requires to minimize the cost, or maximize the benefit, obtained by the production schedule for the available generating units over a given time horizon. As such, the fundamental ingredients of UC are its objective function and its constraints. Of course, another fundamental ingredient is the time horizon itself; UC being a short-term model this is most often a day or two of operations, and up to a week. In the following we will denote it by $\mathcal {T}$, which is typically considered to be a discrete set corresponding to a finite number of time instants $t \in \mathcal {T}$, usually hours or half-hours (down to 15 or 5 min). Thus, the typical size of $\mathcal {T}$ varies from 24 to a few hundred.

In mathematical terms, UC has the general structure

$$\begin{aligned} \min \big \{ \, f(x) \;:\; x \in X_1 \cap X_2 \, \big \}, \end{aligned}$$

(1)

where $x \in \mathbb {R}^n$ is the decision making vector. Usually (most) elements of x are indexed according to both the generating unit $i \in U$ and the time instant $t \in \mathcal {T}$ they refer to. Thus, one often speaks of the subvectors $x^t$ of all decisions pertaining to time t and/or $x_i$ of all decisions pertaining to unit i. Also, entries of x are typically split among:

• 1. Commitment decision discrete variables that determine if a particular unit is on or off at any given time (often denoted by $u^t_i$);

• 2. Production decision continuous variables that provide the amount of generated active power by a specific unit at a given time (often denoted by $p^t_i$). In this set other variables can be included, such as reactive power or reserve contribution by a specific unit at a given time (often denoted by $q^t_i$ and $r^t_i$ respectively);

• 3. Network decision such as these representing phase angle or voltage magnitudes at each node, describing the state of the transmission or distribution network.

A UC problem not having commitment decisions is often called Economic Dispatch (ED) (e.g. Zhu 2009) or Optimal Power Flow (OPF) when the network is considered, (e.g. Jabr 2008). It could be argued that commitment decisions can be easily derived from production decisions (each time a non-zero production output is present the unit has to be on), but for modeling purposes it is useful to deal with the two different concepts separately, cf. Sect. 3.2. Besides, the point is that in ED or OPF the commitment of units has already been fixed and cannot be changed. We remark that network decisions may also include binary variables that provide the open or close state of a particular branch, as entirely closing a branch is one of the few options that the physic of electrical networks allows for “routing” the electrical current (cf. Sect. 2.8). While ED can be expected to be simpler than UC, and in many cases it is a simple convex program that can nowadays be solved with off-the-shelf techniques, this is not always the case. ED was not only challenging in the past (e.g., Demartini et al. 1998 and the references therein), but can still be so today. Indeed, even when commitment decisions are fixed, the electrical system is highly nonlinear and nonconvex, e.g., due to hydro units efficiency curves (cf. Sect. 2.4) or the transmission network characteristics (cf. Sect. 2.7), so that ED can still be a nontrivial problem that may require ad-hoc approaches (e.g. Heredia and Nabona 1995; Oliveira et al. 2005; Jabr 2006, 2008; Lavaei and Low 2012; Molzahn et al. 2013).

In Eq. (1), $X_1$ is the set modeling all technical/operational constraints of the individual units and $X_2$ are the system-wide constraints. The first set is by definition structured as a Cartesian product of smaller sets, i.e., $X_1 = \prod _{i \in U} X^1_i$, with $X^1_i \subseteq \mathbb {R}^{n_i}$ and $\sum _{i \in U} n_i = n$. Moreover, the objective function f typically also allows for a decomposition along the sets $X^1_i$, i.e., $f(x) = \sum _{i \in U} f_i(x_i)$ and $x_i \in X^1_i$. Each of the sets $X_i^1$ roughly contains the feasible production schedules for one unit, that can differ very significantly between different units due to the specific aspects related to their technological and operational characteristics. In most models, $X_1$ is non-convex. However, units sharing the same fundamental operational principles often share a large part of their constraints as well. Because of this, these constraints are best described according to the type of the generating unit, i.e.,

• 1. Thermal units (cf. Sect. 2.3);

• 2. Hydro units (cf. Sect. 2.4);

• 3. Renewable generation units (cf. Sects. 2.3, 2.4, 2.5).

While hydro units are arguably a part of renewable generation, in the context of UC it is fundamental to distinguish between those units that are programmable and those that are not. That is, hydroelectric generation systems relying on a flow that can not be programmed are to be counted among renewable generation ones together with solar and wind-powered ones. This is unless these so-called run-of-river (ROR) units are part of a hydro valley, preceded by a programmable hydro one (cf. Sect. 2.4).

The set $X_2$, which usually models at least the offer-demand equilibrium constraints, is most often, but not always, convex and even polyhedral. This set may also incorporate other system-wide constraints, such as emission constraints, network transmission constraints (cf. Sect. 2.7) or optimal transmission switching constraints (cf. Sect. 2.8).

Solving (1) is difficult when n is large (which usually means that |U| is large) or $X_1$ is a complex set; the latter occurs e.g. when substantial modelling detail on the operations of units is integrated in the model. Finally, (1) contains no reference to uncertainty, but several sources of uncertainty are present in actual operational environments, as summarized in the following table:

Data	Uncertain for	Severity
Customer load	GENCOs, TSO	Low
Reservoirs inflows	GENCOs, TSO	Medium
Renewable generation	GENCOs, TSO	High
Prices/quantities	GENCOs, traders, loads users)	Medium/high
Units/network failure	GENCOs, TSO	Medium

Various ways to incorporate uncertainty in (1) are discussed in Sect. 4.1. Obviously, solving (1) becomes more difficult when uncertainty is present, even when n is small and $X_1$ relatively simple. Thus, properly exploiting the structure of the problem (the function f and the sets $X_1$ and $X_2$) is crucial to obtain efficient schemes for UC, and even more so for UUC. This is why we now provide some detail on different modeling features for each of these components.

2.2 The objective function

The objective function of UC is one of the main factors reflecting the different types of decision-makers described in the previous section. In fact, when the demand needs to be satisfied (as in the case of the MP, or of a TSO in the balancing market) the objective function fundamentally aims at minimizing energy production costs; this is not necessarily obvious (cf. the case of hydro units below), but the principle is clear. However, in the free-market regime the aim of a single GENCO is typically rather to maximize energy production profits. This again requires estimating the costs, so the same objective as in the MP case largely carries over, but it also requires estimating the revenues from energy selling, as it is the difference between the two that has to be maximized. In particular, if the GENCO is a price maker it may theoretically indulge in strategic bidding (David and Wen 2001), whereby the GENCO withdraws power from the market (by bidding it at high cost) in order to push up market prices, resulting in an overall diminished production from its units but higher profit due to the combined effect of decreased production cost and increased unitary revenue for the produced energy. Of course, the success of such a strategy depends on the (unknown) behavior from other participants in the market, which thereby introduces significant uncertainty in the problem. The electrical market is also highly regulated to rule out such behavior from market participants; in particular, larger GENCOs, being more easily price makers, are strictly observed by the regulator and bid all their available capacity on the market. Yet, the solution of strategic bidding problems is of interest at least to the regulators themselves, who need to identify the GENCOs who may in principle exercise market power and identify possible patterns of abuse. Even in the price taker case, i.e., a GENCO with limited assets and little or no capacity to influence market prices, uncertainty is added by the need of accurately predicting the selling price of energy for each unit and each $t \in \mathcal {T}$ (Gil et al. 2012). This uncertainty must then be managed, e.g. with techniques such as those of Robust Optimization (Baringo and Conejo 2011).

Energy production costs for fuel-burning units are typically modeled (in increasing order of complexity) as linear, piecewise-linear convex, quadratic convex, or nonconvex functions separable for each $t \in \mathcal {T}$. In fact, while the fuel-consumption-to-generated-power curve can usually be reasonably well approximated with a piece-wise linear function or a low-order polynomial one, other technical characteristics of generating systems introduce nonconvex elements. The simplest form is that of a fixed cost to be paid whenever the unit is producing at some $t \in \mathcal {T}$, irrespective of the actual amount of generated power. In alternative, or in addition, start-up costs (and, less frequently, shut-down ones) are incurred when a unit is brought online after a period of inactivity. In their simplest form start-up costs can be considered fixed, but most often they significantly depend on the time the unit has been off before having been restarted, and therefore are not separable for each time instant. The dependency of the start-up cost on time can be rather complex, as it actually depends on the choice between the unit being entirely de-powered (cooling) or being kept at an appropriate temperature, at the cost of burning some amount of fuel during the inactivity period, to make the start-up cheaper (banking). Technically speaking, in the latter case, one incurs a higher boiler cost to offset part of the turbine cost. The choice between these two alternatives can often be optimally made by simple formulae once the amount of idle time is known, but this is typically not true beforehand in UC since the schedule of the unit is precisely the output of the optimization problem. Fortunately, some of the solution methods allow inclusion of the start-up cost at a relatively minor increase of the computational complexity; this is the case e.g. of MILP formulations, cf. Sect. 3.2, exploiting the fact that the optimal start-up cost is nondecreasing as the length of the idle period increases (Nowak and Römisch 2000; Carrión and Arroyo 2006). In other cases start-up cost have basically no additional computational cost, such as in DP approaches, cf. Sect. 3.1. Other relevant sources of nonconvexity in the objective function are valve points (Wood and Wollemberg 1996), corresponding to small regions of the feasible production levels where the actual working of the unit is unstable (e.g., due to transitioning between two different configurations in a Combined Cycle Gas Turbine, CCGT, unit or other technical reasons) and that therefore should be avoided.

Nuclear units are generally considered thermal plants, although they significantly differ in particular for the objective function. Indeed, fuel cost has a different structure and depends on many factors, not only technical but also political (e.g., Cour des Comptes 2012). For convenience, formulae similar to that of conventional thermal plants are often used. However, these units incur additional significant modulation costs whenever variations of power output are required; this cost is therefore again not separable per time instant.

Hydro units are generally assumed to have zero energy production cost, although they may in principle have crew and manning costs. In the self-scheduling case, where profit has to be maximized, this would lead to units systematically depleting all the available water due to the fact that a short-term model such as UC has no “visibility” on what happens after the end of its time horizon $\mathcal {T}$ (the so-called “border effect”). Because of this, often a value of water coefficient is added to the objective function to represent the expected value of reserves left in the reservoirs at the end of $\mathcal {T}$. These values, as well as the required reservoir levels (cf. 2.4), are usually computed by means of specific mid-term optimization models. A very standard approach is to value the differential between the initial and end volume of a reservoir against a volume-dependent water value; we refer to van Ackooij et al. (2014) and Cerjan et al. (2011) for details on various other modelling choices. A particular difficulty appears when we wish to integrate the water head effect on turbining efficiency (e.g., Finardi and Silva 2006; Ramos et al. 2012), since this is typically a nonlinear and nonconvex relationship.

In general, the case of profit maximization requires knowledge of the selling and buying price of energy at each $t \in \mathcal {T}$. Because UC is solved ahead of actual operations, possibly precisely with the aim of computing the bids that will contribute to the setting of these prices (cf. e.g. Borghetti et al. 2003a; Bompard and Ma 2012; Kwon and Frances 2012; Rocha and Das 2012), this requires nontrivial forecast models in order to obtain reasonable estimates of the prices (e.g. Oudjane et al. 2006; Li et al. 2010; Zareipour 2012). Depending on the time horizon and specific application, different price models can be considered. These can be obtained from time series modeling (e.g. Diongue 2005; Muñoz et al. 2010; Pedregal et al. 2012), mathematical finance (e.g. Oudjane et al. 2006; Higgs and Worthington 2008; Benth et al. 2012; Nguyen-Huu 2012; Pepper et al. 2012) or can be based on electricity fundamentals (e.g. van Ackooij and Wirth 2007; Ea 2012). For the case where the producer is a price taker, that is, small enough so that its production can be deemed to have little or no effect on the realized prices, UC can typically be independently solved for each individual unit (thus being styled as the self-scheduling problem), and it is therefore much easier (Arroyo and Conejo 2000), although uncertainty in prices then becomes a critical factor and need be included in the models by appropriate techniques (Conejo et al. 2002; Nogales et al. 2002; Baringo and Conejo 2011; Jabr 2005). Things are significantly different in case the producer can exercise market power, that is, influence (increase) the prices by changing (withdrawing) the power it offers to the market; modeling this effect “ties” all the units back again into an unique UUC (Borghetti et al. 2003a; Conejo et al. 2002; de la Torre et al. 2002; Pereira et al. 2005). Uncertainty in this case is also very relevant, with the behavior of competitors being one obvious primary source (Anderson and Philpott 2002; Wen and David 2001; Vucetic et al. 2001; Pineau and Murto 2003; Wang et al. 2007). The matter is further complicated by the fact that the structure of the PE is usually complex, with more than one auction solved in cascade to account for different kinds of generation (energy, reserve, ancillary services, ...) (Baillo et al. 2004; Triki et al. 2005; Wang et al. 2005) and by the fact that tight transmission constraints may create zonal or even nodal prices, thereby allowing producers who may not have market power in the global context to be able to exercise it in a limited region (Li and Shahidehpour 2005; Peng and Tomsovic 2003; Pereira et al. 2005).

2.3 Thermal units

A thermal power station is a power plant in which the prime mover is steam driven. Technical/operational constraints can be classified as either static or dynamic: the former hold on each time step, whereas the latter link different (most often adjacent) time steps. Most typical static constraints are:

• 1. Offline when the unit is offline, the power output is less than or equal to zero (negative power output refers to the power used by auxiliary installations, e.g., for nuclear plants).

• 2. Online when the unit is online, the power output must be between Minimal Stable Generation (MSG) and maximal power output.

• 3. Starting the unit is ramping up to MSG. The ramping profile depends on the number of hours a unit has been offline (e.g. Le et al. 1990); see also the discussion on starting curves below in the section on dynamic constraints. A unit in this state can in principle still be disconnected, but at a cost.

• 4. Stopping the unit ramps down from MSG to the offline power output. As for starting, the ramping profile depends on the number of hours a unit has been online; see also the discussion on stopping curves below in the section on dynamic constraints.

• 5. Generation capacity the production capacity of each unit. For some units the production output has to be selected among a discrete set of values.

• 6. Spinning reserve the extra generating capacity that is available by increasing the power output of generators that are already connected to the power system. For most generators, this increase in power output is achieved by increasing the torque applied to the turbine’s rotor. Spinning reserves can be valued separately from actively generated power as they represent the main mechanism that electrical systems have to cope with real-time variations in demand levels.

• 7. Crew constraint number of operators available to perform the actions in a power plant.

Typical dynamic constraints instead are:

• 1. Minimum up/down time a unit has to remain online/offline for at least a specific amount of time.

• 2. Operating ramp rate (also known as ramp-down and ramp-up rate): the increment and decrement of the generation of a unit from a time step to another, excluding start-up and shut-down periods, must be bounded by a constant (possibly different for ramp-up and ramp-down).

• 3. Minimum stable state duration a unit that has attained a specific generation level has to produce at that level for a minimum duration of time.

• 4. Maximum numbers of starts the number of starts can be limited over a specific time horizon (such a constraint is also implicitly imposed by Minimum Up/Down Time ones, and in fact the two are somehow alternatives).

• 5. Modulation and stability these constraints are mainly applied to an online nuclear unit. A unit is in modulation if the output level changes in a time interval, whereas it is stable if the power level remains identical to that of the previous time step. The constraints ensure that the unit is “most often stable”, requiring that the number of modulations does not exceed a predefined limit over a given time span (say, 24 h).

• 6. Starting (stopping) curve (also referred to in literature as start-up/shut-down ramp rate): in order to start (stop) a unit and move it from the offline (online) state to the online (offline) state, the unit has to follow a specific starting (stopping) curve, which links offline power output (zero, or negative for nuclear plants) to MSG (or vice-versa) over the course of several time steps. Each starting (stopping) curve implies a specific cost, and the chosen curve depends on the number of hours the plant has been offline (online). Starting (stopping) may take anything from several minutes (and therefore be typically irrelevant) up to 24 h (and therefore be pivotal for the schedule).

• 7. Feasible state transition for CCGT These thermal units typically have at least two Gas Turbines and one Steam Turbine and have specific feasible state transition which are non trivial to formulate, e.g. (Fan et al. 2016).

2.4 Hydro units

Hydro units are in fact entire hydro valleys, i.e., a set of connected reservoirs, turbines and pumps that influence each other through flow constraints. When the hydro component is significant UC is often denoted as HUC; this may make the problem significantly more difficult, as the recent survey (Taktak and d’Ambrosio 2016) highlights. Turbines release water from uphill reservoirs to downhill ones generating energy, pumps do the opposite. Note that the power output of ROR units downstream to a reservoir (and up to the following reservoir, if any) must be counted together with that of the turbines at the same reservoir; usually it is possible to do this by manipulating the power-to-discharged-water curve of the unit at the reservoir, and thus ROR units in a hydro valley need not be explicitly modeled. We remark in passing that whether or not a unit is considered ROR depends on the time horizon of the problem: units with small reservoirs can be explicitly modeled in HUC because they do have a degree of modulation over the short term, but they may be considered ROR in longer-term problems since the modulation is irrelevant over long periods of time.

As for thermal units, we distinguish constraints as being either static or dynamic. The typical ones of the first kind are:

• 1. Reservoir level the level of water in each reservoir has to remain between a lower and upper bound. Frequently these bounds are used to reflect strategic decisions corresponding to optimal long-term use of water (cf. Sect. 2.2), and not necessarily reflect physical bounds. An alternative is to use a nonlinear cost of water that reflects the higher risk incurred in substantially depleting the reservoir level, as water in hydro reservoirs represents basically the only known way of efficiently storing energy on a large scale and therefore provides a crucial source of flexibility in the system. Yet, bounds on the level would ultimately be imposed anyway by physical constraints.

• 2. Bounds turbines and pumps can operate only within certain bounds on the flowing water. In particular, some turbines might have a minimal production level akin to the MSG of thermal units.

The most common dynamic constraints are:

• 1. Flow equations these equations involve the physical balance of the water level in each reservoir and connect the various reservoirs together. The reservoir levels get updated according to natural inflows, what is turbined downhill, what is spilled downhill (i.e., let go from the reservoir to the next without activating the turbines), and what is pumped from downhill to uphill. Spilling might not be allowed for all reservoirs, nor all have pumping equipment.

• 2. Flow delay the water flowing (uphill or downhill) from each unit to the next reservoir will reach it after a given delay, that can possibly be of several hours (and occasionally even more Belloni et al. 2003).

• 3. Ramp rate adjacent turbining levels have to remain sufficiently close to each other.

• 4. Smooth turbining over a a given time span (e.g., 1 h), turbining output should not be in a V-shape, i.e., first increase and immediately afterwards decrease (or vice-versa). This constraint is typically imposed to avoid excessive strain on the components, similarly to several constraints on thermal units such as Minimum up/down Time, Maximum Numbers of Starts, Modulation and Stability.

• 5. Turbining/pumping incompatibility some turbines are reversible and therefore pumping and turbining cannot be done simultaneously. Moreover, switching from turbining to pumping requires a certain delay (e.g., 30 min). Some of these constraints actually only refer to a single time instant and therefore they can be considered as static.

• 6. Forbidden zones in complex hydro units, effects like mechanical vibrations and cavitation strongly discourage using certain intervals of turbined water, as these would result in low efficiency and/or high output variation (similarly to valve points in thermal units, cf. Sect. 2.2). Therefore, constraints that impose that the turbined water lies outside of these forbidden zones might have to be imposed (Finardi and Scuzziato 2013).

2.5 Renewable generation units

Renewable generation in UC mostly refers to wind farms, solar generation, stand alone ROR hydro units, and geothermal production. The fundamental characteristic of all these sources, as far as UC is concerned, is the fact that they cannot be easily modulated: the produced energy, and even if energy is produced at all (in some wind farms energy is actually consumed to keep the blades in security when wind blows too strongly), is decided by external factors. Some of these sources, most notably solar and wind, are also characterized by their intermittency; that is, it is very difficult to provide accurate forecasts for renewable generation, even for short time horizons (say, day-ahead forecasts). Furthermore, in several cases renewable generation operates in a special regulatory regime implying that they cannot even be modulated by disconnecting them from the grid. This has (not frequently, but increasingly often) led to paradoxical situations where the spot price of energy is actually zero or, where allowed, even negative, i.e., one is paid to consume the energy that renewable sources have the right to produce (and sell at fixed prices) no matter what the demand actually is. All this has lead to significant changes in the operational landscape of energy production systems, that can be summarized by the following factors:

• 1. The total renewable production cannot be predicted accurately in advance;

• 2. Renewable generation has high variance;

• 3. The correlation between renewable generation and the load can be negative, which is particularly troublesome when load is already globally low, since significant strain is added to conventional generation assets which may have to quickly ramp down production levels, only to ramp them up (again rapidly) not much later. This goes squarely against most of the standard operational constraints in classical UC (cf. Sects. 2.3, 2.4).

In other words, in UC terms, renewable generation significantly complicates the problem; not so much because it makes its size or structure more difficult, but because it dramatically increases the level of uncertainty of net load (the load after the contribution of renewables is subtracted), forcing existing generation units to serve primarily (or at least much more often than they were designed to) as backup production in case of fluctuations, rather than as primary production systems. This increases the need of flexible (hydro-)thermal units ready to guarantee load satisfaction at a short notice, which however typically have a larger operational cost. We refer to Bouffard and Galiana (2008), Siahkali and Vakilian (2010), Moura and Almeida (2010) and Miranda et al. (2011).

2.6 Demand response and energy storage

With increasing awareness of the effect that electrical consumption may have on the “environment”, and as a result of economic incentives, users are increasingly willing to take an active part in altering their consumption pattern to accommodate for system needs. In view of testing such potential, experiments have carried out on a voluntary basis (e.g., NICEgrid in France and the pilot projects in Italy after the aforementioned ARERA resolution 300/2017/R/eel). These mechanisms can be seen as a particular type of Demand Response (DR). The novelty in itself is not so much the fact that some customers may be asked to not consume, or postpone their consumption, but rather the scale and size of the considered consumptions profiles. Indeed, traditionally only large industrial clients were addressed, but this has progressively moved to consider larger sets of households. From a modelling perspective, at least three kinds of phenomena can be looked at:

• A certain amount of load can be shedded, but a limited set of times over a given time horizon (Magnago et al. 2015).

• A certain amount of load can be shifted from one moment in time to another without implying any change in consumption (zero sum).

• A certain amount of load can be shifted from a moment in time to another while implying a global increase in consumption. Such is the case, for instance, of an heating system where, after some period of not warming a household, more energy is required to recover a given confort temperature.

In a similar way to Demand Response, energy storage allows to adapt electrical consumption (and generation), catering for flexibility needs. Energy storage gained popularity during the 1970’s, when power generation saw a significant shift from oil to nuclear power in North America and in Europe. Pumped hydro storage was used to complement base-load nuclear and coal plant by absorbing excess energy during periods of low demand and generating to meet peak consumption periods. In the subsequent decades, as generation portfolios diversified to include more flexible plant such as gas-fired units, and the power generation sector became deregulated, the economic and operational incentives justifying the installation of further electrical energy storage disappeared.

Energy storage technologies have regained popularity in recent years due to their capability to balance and facilitate the integration of wind and solar power. The flexibility inherent to most energy storage technologies can decrease wind and solar power curtailment and reduce the cycling burden on conventional generation units. Interest in energy storage is also due to its system service provision capability, including (primary) frequency control, secondary reserve and relieving network congestion. Moreover, synchronous storage technologies can address the inertia challenges that may arise due to the non-synchronous nature of wind and solar power, particularly in small or island power systems (Eyer and Corey 2010).

Although, in large part due to advances in the automotive industry, lithium-ion battery energy storage technologies for grid applications have gained the industry spotlight over the recent years, there exists a wide variety of energy storage technologies that may be employed for power system applications. These may be classified within: mechanical storage (i.e. compressed air energy storage and flywheels), electrochemical storage (including secondary and flow batteries), chemical storage (hydrogen and synthetic natural gas), electrical storage (i.e. double-layer capacitors), and thermal storage systems. As a result of the variety of technologies available, non-hydro energy storage models within UC vary widely depending on the technology implemented and its intended applications. The basic implementation of an energy storage unit performing energy arbitrage, which may apply to most storage assets in their simplest form, will contain the following elements:

• Maximum and minimum charging and discharging power constraints;

• Maximum and minimum state of charge constraints;

• Charge and discharge efficiency.

A generic deterministic and stochastic energy storage model is proposed in Pozo et al. (2014). Some battery UC models may also optimise the lifecycle of the asset by including charge and discharge penalties. Certain energy storage technologies may require additions to the basic model, e.g., compressed air energy storage operates in combination with a gas turbine, therefore, the interactions between both technologies must be modelled (Chen et al. 2016). An increasing number of publications addresses the issue of how the representation of uncertainty within UC formulations may impact the operation and the calculated value of energy storage from both system (Pozo et al. 2014; Suazo-Martinez et al. 2014; Kiran and Kumari 2016) and private investor perspectives (Muche 2014).

2.7 System-wide constraints

The most common form of system-wide constraints are the load constraints, guaranteeing that global energy demand is exactly satisfied for each $t \in \mathcal {T}$. This kind of constraint is not present in the self-scheduling version of UC, where each unit reacts independently to price signals, but global load satisfaction has to be taken into account, sooner or later, even in liberalized market regimes. For instance, in several countries, after the main energy market is cleared, GENCOs can swap demand between different units in order to better adjust the production schedules corresponding to the accepted bids to the operational constraints of their committed units, that are not completely represented in the auctions (Read 2010). Alternatively, or in addition, an adjustment market is ran where energy can be bought/sold to attain the same result (Palamarchuk 2012; Sauma et al. 2012) In both these cases the production schedules of all concerned units need be taken into account, basically leading back to global demand constraints. Also, in UC-based bidding systems the global impact of all the generation capacity of a GENCO on the energy prices need to be explicitly modeled, and this again leads to constraints linking the production levels of all units (at least, these of the given GENCO) that are very similar to standard demand constraints. Conversely, even demand constraints do not necessarily require the demand to be fully satisfied; often, slacks are added so that small amounts of deviation can be tolerated, albeit at a large cost (e.g., Dubost et al. 2005; Zaourar and Malick 2013).

Another important issue to be mentioned is that the demand constraints need, in general, to take into account the shape and characteristics of the transmission network. These are typically modeled at three different levels of approximation:

• The single bus model basically the network aspects are entirely disregarded and the demand is considered satisfied as soon as the total production is (approximately) equal to the total consumption, for each time instant, irrespectively of where these happen on the network. This corresponds to simple linear constraints and it is the most common choice in UC formulations.

• The DC model where the network structure is taken into account, including the capacity of the transmission links, but a simplified version of Kirchhoff laws is used so that the corresponding constraints are still linear, albeit more complex than in the bus model (Lee et al. 1994; Jabr 2010; Fonoberova 2010). In Ardakani and Bouffard (2013) the concept of umbrella constraints is introduced to define a subset of the network DC constraints that are active in order to significantly reduce the size of these constraints.

• The AC model where the full version of Kirchhoff laws is used, leading to highly nonlinear and nonconvex constraints, so that even the corresponding ED becomes difficult (Murillo-Sanchez and Thomas 1998; Momoh et al. 1999a, b; Sifuentes and Vargas 2007a, b). A recent interesting avenue of research concerns the fact that the non-convex AC constraints can be written as quadratic relations (Jabr 2006, 2008; Lavaei and Low 2012), which paves the way for convex relaxations using semidefinite programming approaches (Molzahn et al. 2013). In particular, in the recent Hijazi et al. (2013) a quadratic relaxation approach is proposed which builds upon the narrow bounds observed on decision variables (e.g. phase angle differences, voltage magnitudes) involved in power systems providing a formulation of the AC power flows equations that can be better incorporated into UC models with discrete variables, notably the ones of cf. Sect. 2.8. A recount of these recent developments can be found in Bienstock (2013).

Although market-based electrical systems have in some sense made network constraints less apparent to energy producers, they are nonetheless still very relevant nowadays; not only in the remaining vertically integrated electrical systems, but also for the TSO that handles network security and efficiency. This requires taking into account a fully detailed network model, even considering security issues such as $N - 1$ fault resilience, together with a reasonably detailed model of GENCOs’ units (comprising e.g. infra-hour power ramps, start-up costs, and start-up/shut-down ramp rate), when solving the Market Balancing problem. The latter is basically a residual demand, bidding-based UC. From a different perspective, network constraints might also be important for GENCOs that are able to exercise market power in case zonal or nodal pricing is induced by the network structure (Price 2007).

Finally, both for vertically integrated system and in the TSO perspective, other relevant system-wide constraints are spinning reserve ones: the committed units must be able to provide some fraction (at least 3% according to Takriti et al. 1996) of the total load in order to cope with unexpected surge of demand or failures of generating units and/or transmission equipment. Other global constraints linking all units, or some subsets of them, exist: for instance, all (or specific subsets of) fossil-fuel burning units may have a maximum cap on the generation of pollutants ($\hbox {CO}_2$, $\hbox {SO}_x$, $\hbox {NO}_x$, particles,...) within the time horizon (Hsu et al. 1991; Fu et al. 2005; Gjengedal 1996; Kuloor et al. 1992; Wang et al. 1995). Alternatively, a cluster of geographically near units (a plant) burning the same fuel (typically gas) may be served by a unique reservoir, and can therefore share a constraint regarding the maximum amount of fuel that can be withdrawn from the reservoir within the time horizon (Aoki et al. 1987, 1989; Tong and Shahidehpour 1989; Fu et al. 2005; Cohen and Wan 1987). Finally, there may be constraints on the minimum time between two consecutive start-ups in the same plant (Dubost et al. 2005), e.g., due to crew constraints. If a plant comprises a small enough number of units it could alternatively be considered as a single “large” unit, so that these constraints become technical ones of this aggregated generator. The downside is that the problem corresponding to such a meta-unit then becomes considerably more difficult to solve.

In systems with higher degrees of penetration of intermittent generation, such as islands, UC models are sometimes amended with further constraints to help control the frequency in case of a contingency. This is relevant since, generally, intermittent resources such as wind do not provide inertia to the system, although they might through power electronics. In order to evaluate the contribution of installing such additional equipment, the models must become more accurate. Two different ways have been proposed to account for frequency in UC. The first is through a set of indirect constraints that are neither a relaxation nor a restriction of the actually desired ones (e.g., Daly et al. 2015; Ahmadi and Ghasemi 2014; Ela et al. 2014a, b; Restrepo and Galiana 2005). Obvious downsides of such an approach is that one cannot ensure satisfaction of the original constraint, nor control sub-optimality. Directly accounting for frequency related constraints in UC models can be done through a very simplified version of the differential equation system governing the loss of frequency following a contingency (e.g., Teng et al. 2016); we refer to Arteaga (2016) and Cardozo et al. (2017) for a thorough account of different approaches and extensive tests. A more precise approach can also be designed, albeit under some theoretically hard to verify assumptions (Cardozo et al. 2018); the resulting UC models can be solved by Benders-like scheme (Cardozo et al. 2016) exploiting the convexifying effect of Lagrangian relaxations (Lemaréchal and Renaud 2001).

2.8 Optimal transmission switching

Traditionally, in UC models the transmission network has been regarded as a “passive” element, whose role was just to allow energy to flow from generating units to demand points. This is also justified by the fact that electrical networks, unlike most other networks (logistic, telecommunications, gas, water,...) are “not routable”: the current can only be influenced by changing nodal power injection, which is however partly fixed (at least as demand is concerned). Indeed, in traditional UC models there were no “network variables”, and the behavior of the transmission system was only modeled by constraints. However, as the previous paragraph has recalled, the transmission network is by far not a trivial element in the system, and separate network variables are required. Recently, the concept has been further extended to the case where the system behavior can be optimized by dynamically changing the topology of the network. This is a somewhat counterintuitive consequence of Kirchhoff laws: opening (interrupting) a line, maybe even a congested one, causes a global re-routing of electrical energy and may reduce the overall cost, e.g. by allowing to increase the power output of some cheaper (say, renewable) units (Fisher et al. 2008). This effect can be especially relevant in those parts of the network with a high fraction of renewables whose production is sometimes cut off because of network constraints.

Thus, a class of problems, called Optimal Transmission Switching (OTS) or System Topology Optimization (STO), has been defined whereby each line of the network has an associated binary decision (for each $t \in \mathcal {T}$) corresponding to the possibility of opening it. This makes the problem difficult to solve even with a very simple model of nodal injections and a simple network model such as the DC one (cf. Sect. 2.7); even more so with the AC model and a complete description of the generating units. The so-called UCOTS models (Fisher et al. 2008; Di Lullo 2013; Hedman et al. 2011a, b; Ruiz et al. 2012; Bienstock and Verma 2011; Villumsen and Philpott 2011; Papavasiliou et al. 2013; O’Neill et al. 2010; Ostrowski et al. 2012; Ostrowski and Wang 2012; Liu et al. 2012a, b; Korad and Hedman 2013; Hedman et al. 2009, 2010; Zhang and Wang 2014) extend UC: almost everything that can be said about UC is a fortiori valid for UCOTS, and therefore in the following we will not distinguish between the two unless strictly necessary.

3 Methods for the deterministic unit commitment

We now proceed with a survey of solution methods for (the deterministic) UC. Our choice to first focus on the case where the several forms of uncertainty arising in UC (cf. Sect. 2.1) are neglected is justified by the following facts:

• UC already being a rather difficult problem in practice, most work has been carried out in the deterministic setting;

• Uncertainty can be taken into account through various “engineering rules”: for instance, spinning reserves allow to account for uncertainty on load, tweaking reservoir volumes might allow to account for uncertainty on inflows, and so on;

• Methods for solving the deterministic UC are bound to provide essential knowledge when dealing with UUC.

As discussed in Sect. 2, UC is not one specific problem but rather a large family of problems exhibiting common features. Since the set of constraints dealt with in the UC literature varies from one source to another, we define what we will call a basic Unit Commitment problem (bUC) which roughly covers the most common problem type; through the use of tables we will then highlight which sources consider additional constraints. A bUC is a model containing the following constraints:

• 1. Offer-demand equilibrium;

• 2. Minimum up or down time;

• 3. Spinning and non spinning reserve;

• 4. Generation capacities.

The UC literature review (Sheble and Fahd 1994), of which (Padhy 2004) is essentially an update adding heuristic approaches, generally classify UC methodology in roughly eight classes. We will essentially keep this distinction, but regroup all heuristic approaches in “Meta-Heuristics”, thus leading us to a classification in:

• 1. Dynamic programming;

• 2. MILP approaches;

• 3. Decomposition approaches;

• 4. (Meta-)Heuristics approaches.

We will also add some of the early UC approaches in the Heuristic class such as priority listing. However, we will not delve much on that class of approaches, since the recent surveys (Farhat and El-Hawary 2009; Saravanan et al. 2013) mainly focus on these, while providing little (or no) details on approaches based on mathematical programming techniques, that are instead crucial for us in view of the extension to the UUC case.

3.1 Dynamic programming

Dynamic Programming (DP, see e.g. Bellman and Dreyfus 1962; Bertsekas 2005, 2012) is one of the classical approaches for UC. As discussed below, it is nowadays mostly used for solving subproblems of UC, often in relation with Lagrangian-based decomposition methods (cf. Sect. 3.3); however, attempts have been made to solve the problem as a whole. There have been several suggestions to overcome the curse of dimensionality that DP is known to suffer from; we can name combinations of DP and Priority Listing (DP-PL) (Snyder et al. 1987; Hobbs et al. 1988), Sequential Combination (DP-SC) (Pang et al. 1981), Truncated Combination (DP-TC) (Pang and Chen 1976), Sequential/Truncated Combination (DP-STC) (the integration of the two aforesaid methods) (Pang et al. 1981), variable window truncated DP (Ouyang and Shahidehpour 1991), approximated DP (de Farias and Van Roy 2003) or even some heuristics such as the use of neural network (Ouyang and Shahidehpour 1991) or artificial intelligence techniques (Wang and Shahidehpour 1993). The multi-pass DP approach (Yang and Chen 1989; Erkmen and Karatas 1994) consists of applying DP iteratively, wherein in each iteration the discretization of the state space, time space and controls are refined around the previously obtained coarse solution; usually, this is applied to ED, i.e., once commitment decisions have been fixed. In Pang et al. (1981) three of the aforesaid methods, DP-PL, DP-SC, and DP-STC are compared against a priority list method on a system with 96 thermal units, showing that the DP-related approaches are preferable to the latter in terms of time and performance. The recent Singhal and Sharma (2011) performs a similar study on a bUC with 10 thermal units, but only DP approaches are investigated.

Despite its limited success as a technique for solving UC, DP is important because of its role in dealing with sub-problems in decomposition schemes like Lagrangian relaxation. These typically relax the constraints linking different units together, so that one is left with single-Unit Commitment (1UC) problems, i.e., self-scheduling ones where the unit only reacts to price signals. In the “basic” case of time-independent startup costs 1UC can be solved in linear time on the size of $\mathcal {T}$. When dealing with time-dependent startup costs instead, this cost becomes quadratic (Bard 1988; Zhuang and Galiana 1988). However, this requires that the optimal production decisions $p^i_t$ can be independently set for each time instant if the corresponding commitment decision $u^i_t$ is fixed, which is true in bUC but not if ramp rate constraints are present. It is possible to discretize power variables and keep using DP (Bechert and Kwatny 1972), but the approach is far less efficient and the determined solution is not guaranteed to be feasible. An efficient DP approach for the case of ramp rate constraints and time-dependent startup costs has been developed in Fan et al. (2002) under the assumption that the power production cost is piecewise linear. This has been later extended in Frangioni and Gentile (2006b) for general convex cost functions; under mild conditions (satisfied e.g., in the standard quadratic case), this procedure has cubic cost in the size of $\mathcal {T}$. DP has also been used to address hydro valley subproblems in Siu et al. (2001) where a three stage procedure is used: first an expert system is used to select desirable solutions, then a DP approach is used on a plant by plant basis, and a final network optimization step resolves the links between the reservoirs. In Salam et al. (1991) expert systems and DP are also coupled in order to solve UC. We also mention the uses of expert systems in Mokhtari et al. (1988).

Most often DP approaches are applied to bUC, but other constraints have been considered such as multi-area, fuel constraint, ramp rates, emission constraints, and hydro-thermal systems. We refer to Table 1 for a complete list.

Table 1 Sources using dynamic programming

3.2 Integer and mixed integer linear programming

3.2.1 Early use: exhaustive enumeration

As its name implies, this approach focusses on a complete enumeration of the solution space in order to select the solution with the least cost. bUC is addressed in Kerr et al. (1966) and Hara et al. (1966), while in Hara et al. (1966) the cost function considers penalties for loss of load and over production. In Kerr et al. (1966) a set of 12 thermal units on a 2 h basis is scheduled. In Hara et al. (1966) a problem with two groups, each of which has 5 thermal units is analyzed. This traditional approach obviously lacks scalability to large-scale systems. However, some enumeration may find its way into hybrid approaches such as decomposition methods under specific circumstances, like in Finardi and Silva (2006) where enumeration is used in some of the subproblems in a decomposed hydro valley system.

3.2.2 Modern use of MILP techniques

With the rise of very efficient MILP solvers, MILP formulations of UC have become common. In general, their efficiency heavily depends on the amount of modelling detail that is integrated in the problem. Early applications of MILP can be found in Garver (1962), Muckstadt and Wilson (1968), Cohen and Yoshimura (1983), and in Cohen and Yoshimura (1983) it is stated that the model could be extended to allow for probabilistic reserve constraints. HUC is considered in Dillon et al. (1978), Pereira and Pinto (1983) and Shaw et al. (1985), where constraints regarding hydro units such as flow equations, storage level of reservoirs, pump storage and min/max outflow of each reservoir are incorporated in the model.

Some specific constraints such as the number of starts in a day or particular cost functions with integrated banking costs can be found in Turgeon (1978) and Lauer et al. (1982). In Lauer et al. (1982) the authors combine Lagrangian relaxation (e.g., Muckstadt and Koenig 1977) with a B&B procedure in order to derive valid bounds to improve the branching procedure. The upper bound is derived by setting up a dynamic priority list in order to derive feasible solutions of the UC and hence provide upper bounds. It is reported that a 250 unit UC was solved up to 1% of optimality in less than half an hour, a significant feat for the time. A similar approach is investigated in Parrilla and García-González (2006), where a heuristic approach using, among things, temporal aggregation is used to produce a good quality integer feasible solution to warm-start a B&B procedure.

While MILP is a powerful modelling tool, its main drawback is that it may scale poorly when the number of units increases or when additional modelling detail is integrated. To overcome this problem it has been combined with methods such as DP (Bond and Fox 1986), logic programming (Huang et al. 1998) and Quadratic Programming (QP) (Shafie-Khah and Parsa 2011). In Shafie-Khah and Parsa (2011) a HUC with various constraints is solved; a customized B&B procedure is developed wherein binary variables are branched upon according to their difference from bounds. The approach does not require any decomposition method, and it is reported to reduce solution time significantly in comparison to other methods. The paper builds upon (Fu and Shahidehpour 2007), where a six-step solution is proposed to solve large-scale UC; the algorithm is reported to be capable of solving security-constrained problems with 169, 676 and 2709 thermal units in 27 s, 82 s and 8 min, respectively. This so-called Fast-Security Constraint Unit Commitment problem (F-SCUC) method is based on an ad-hoc way of fixing binary variables and gradually unlock them if needed, using Benders-type cuts to this effect. However, in Frangioni et al. (2008) it is reported that MILP models, where the objective function is piecewise-linearly approximated, are much more effective than the direct use of MIQP models, at least for one specific choice and version of the general-purpose MIQP solver. In Frangioni et al. (2011) MILP and Lagrangian methods are combined, solving problems with up to 200 thermal units and 100 hydro units in a few minutes if the desired accuracy is set appropriately. In Sahraoui et al. (2017) the authors consider specific issues related to numerical errors in MILP in a HUC context and suggest some methods to deal with these errors.

Systems with a significant fraction of hydro generation require a specific mention due to a notable characteristic: the relationship between the power that can be generated and the level of the downstream reservoir (head-to-generated-power function), that can be highly nonlinear (Catalão et al. 2006), and, in particular, nonconvex. This can be tackled by either trying to find convex formulations for significant special cases (Yu et al. 2000), developing ad-hoc approximations that make the problem easier to solve (Catalão et al. 2010), or using the modelling power of MILP to represent this (and other nonconvex) feature(s) of the generating units (Piekutowki et al. 1994; Chang et al. 2001; Dal’Santo and Costa 2016; Chen et al. 2017). However, developing a good approximation of the true behaviour of the function is rather complex because it depends on both the head value of the reservoir and the water flow. MILP models for accurately representing this dependency have been presented in Jia and Guan (2011), and more advanced ones in Borghetti et al. (2008) and Alvarez et al. (2018) using ideas from (d’Ambrosio et al. 2010); while they are shown to significantly improve the quality of the generated schedules, this feature makes HUC markedly more complex to solve. Several solution approaches (MILP, MINLP and LR based decomposition) to represent hydro power generation are compared in Finardi et al. (2016). Through a 3-phase MILP strategy, accurate solutions are found for large-scale HUC instances in Marchand et al. (2018).

3.2.3 Recent trends in MILP techniques

Recently, MIP (and in particular MILP) models have attracted a renewed attention due to a number of factors. Perhaps the most relevant is the fact that MILP solvers have significantly increased their performance, so that more and more UC formulations can be solved by MILP models with reasonable accuracy in running times compatible with actual operational use (Carrión and Arroyo 2006). Furthermore, selected nonlinear features—in particular convex quadratic objective functions and their generalization, i.e., Second-Order Cone Constraints—are nowadays efficiently integrated in many solvers, allowing to better represent some of the features of the physical system. This is especially interesting because MIP models are much easier to modify than custom-made solution algorithms, which—in principle—allow to quickly adapt the model to the changing needs of the decision-makers. However, it has to be remarked that each modification to the model incurs a serious risk of making the problems much more difficult to solve. Two somewhat opposite trends have recently shown up. On one side, tighter formulations are developed that allow to more efficiently solve a given UC problem because the continuous relaxation of the model provides better lower bounds. On the other hand, more accurate models are developed which better reflect the real-world behavior of the generating units and all the operational flexibility they possess (cf. e.g. Hobbs et al. 2001; Lu and Shahidehpour 2005; Makkonen and Lahdelma 2006), thereby helping to produce better operational decisions in practice.

On the first stream, the research has focussed on finding better representations of significant fragments of UC formulations. Standard UC formulations either use three binary variables (3-bin: on/off, startup and shutdown) (Garver 1962) or one single binary variable (1-bin) (Carrión and Arroyo 2006). In recent years, development has gone into improving the tightness in particular of the 3-bin formulation. For instance, (Ostrowski et al. 2012; Morales-España et al. 2013a) develop better representations of the polyhedra describing minimum up- and down-time constraints and ramping constraints. A similar study is carried out in Morales-España et al. (2015), where specific investigations are made to account for generation while starting and stopping a unit (startup/shutdown curves). In a similar vein, Bendotti et al. (2018) provide an extension to many units of the analysis initiated in Rajan and Takriti (2005) as min-up/min-down constraints are concerned; in particular, a set of new valid inequalities is introduced. By extension, the computational complexity is looked at in Bendotti et al. (2017a); not surprisingly, UC is found to be NP-Hard even in simple situations. Further such investigations are related specifically to the consideration of start-up costs as in Brandenberg et al. (2017). In Yang et al. (2017) an alternative two binary variable (2-bin) formulation is proposed and widely tested, proving that it can be competitive with 1-bin and 3-bin ones. A different approach is proposed in Fattahi et al. (2017a), where a conic strengthened semidefinite program (SDP) is constructed for the convex relaxation of a classic UC formulation. The valid inequalities are based on the Reformulation-Linearization-Technique (RLT) (Sherali and Adams 1998) and the so-called triangle inequalities; incorporating them in the UC problem, several test cases—including the large-scale IEEE 300 bus one—can be solved to global optimality using the commercial-grade SDP solver Mosek. Recently, new formulations have been developed inspired by DP approaches (cf. Sect. 3.1), i.e., using state transition variables: these can be shown to represent the convex hull of integer solutions for the case of one single unit (Frangioni and Gentile 2015), even in presence of quadratic costs if perspective reformulation techniques are also employed (Frangioni and Gentile 2006a), and to improve performances in practice (Atakan et al. 2018). Conic programming techniques are also used in Frangioni et al. (2009), Wu (2011) and Jabr (2012), which focus on better piecewise-linear reformulations of the nonlinear (quadratic) power cost function of thermal units. Both approaches, that can be easily combined, have been shown to attain impressive speed-ups in cpu time for a fixed level of modelling detail, thus emphasizing (once more) the importance of carefully investigating the mathematical properties of the underlying optimization problem and its ingredients.

The second stream rather aims at improving the accuracy of the models in representing the real-world operating constraints of units, that are often rather crudely approximated in standard UC formulations. For hydro units this for instance concerns technical constraints (Chang et al. 2001) and the already discussed water-to-produced-energy function, with its dependency from the water head of the downstream reservoir (Piekutowki et al. 1994; Finardi and Silva 2006; Borghetti et al. 2008). For thermal units, improvements comprise the correct evaluation of the power contribution of the start-up and shut-down power trajectories (when a unit is producing but no modulation is possible) (Arroyo and Conejo 2004), which may make the model significantly more difficult unless appropriate techniques are used (Morales-España et al. 2013b), or a clearer distinction between the produced energy and the power trajectory of the units (García-González et al. 2007; Morales-España et al. 2014). Further, recent investigations involve the use of storage devices (Steber et al. 2018).

In the OTS context (cf. Sect. 2.8), special care must be given when modeling the Kirchhoff laws, as this leads to logic constraints that, in MILP models, are typically transformed into “big-M” (hence, weak) linear constraints. Moreover, severe symmetry issues (Ostrowski et al. 2010) must be faced (Di Lullo 2013; Ostrowski et al. 2012), as these can significantly degrade the performances of the B&B approach. Recent symmetry breaking techniques, known as orbital branching (a terminology pinned down in Ostrowski et al. (2011)) or orbitopal fixing (e.g., Kaibel et al. 2011) are applied to UC in Ostrowski et al. (2015) and Bendotti et al. (2017b). All these difficulties, not shared by UC with DC or AC network constraints, require a nontrivial extension of the “classic” MILP UC models. Many approaches use off-the-shelf B&B solvers, while possibly reducing the search space of the OTS binary variables (Ruiz et al. 2012; Ostrowski and Wang 2012; Liu et al. 2012b) and using tight formulations for the thermal units constraints. All these references use classic quadratic cost functions; one exception is (Di Lullo 2013), where a direct MILP approach is combined with a perspective cuts approximation (Frangioni et al. 2009) and a special perturbation of the cost function that successfully breaks (part of the) symmetries. Together with heuristic branching priorities that give precedence to the thermal UC status variables, this is shown to be much better than using a classic quadratic function, with or without perturbations, for solving the IEEE 118 test case. In Kocuk et al. (2016) cycle inequalities are proposed inspired by Kirchoff’s Voltage Law that are used to strengthen the MILP OTS formulation. Several types of valid inequalities are proposed in Kocuk et al. (2017) to strengthen a MISOCP formulation including a full AC model for the transmission constraints. In the very recent Fattahi et al. (2017b) it is proven that finding the “best” M for the disjunctive big-M constraints in the OTS problem is NP-hard in general, and this beyond the fact that problem itself is NP-hard. Yet, a procedure based on Dijkstra’s algorithm is proposed for OTS with a fixed connected spanning subgraph that finds non trivial upper bounds on the M constants, which significantly reduces the computational time in several test systems including the real Polish network. In Shi and Oren (2018) a UCOTS model for systems with high renewable production is shown to be capable of reducing total cost via transmission switching even in the absence of congestion; the proposed approach first decomposes the system into zones, and then solves the problem for each zone in parallel (Table 2).

Table 2 Sources using MILP approaches

3.3 Lagrangian and Benders decomposition

UC possesses several forms of structure that can be algorithmically exploited; the most obvious one is that (complex) units are usually coupled through demand and reserve requirements (the set $X_2$ in (1)). Since these constraints are usually in limited number and “simple”, Lagrangian Decomposition (or Relaxation, LR) (Lemaréchal 2001; Guignard 2003; Frangioni 2005) is an attractive approach and has been widely used. It is based on relaxing these coupling constraints by moving them in the objective function, weighted by appropriate Lagrangian multipliers, so that the relaxed problem then naturally decomposes into independent subproblems for each individual unit (1UC); for an arbitrary set of Lagrangian multipliers, the solution of all the 1UCs provides a lower bound on the optimal value of (1). Moreover the mapping (called the dual function, or Lagrangian function) assigning this optimal value to a given set of Lagrangian multipliers is concave; maximizing it, i.e., finding the best possible lower bound, is therefore a convex optimization problem for which efficient algorithms exists.

Two technical points are crucial when developing a LR approach:

• How the maximization of the Lagrangian function, i.e., the solution of the Lagrangian Dual (LD), is performed;

• Since (1) is in general nonconvex the approach cannot be expected to provide an optimal (or even feasible) solution, so methods to recover one have to be developed.

Regarding the first point, one can rely on the available well-developed theory concerning minimization of convex nondifferentiable functions. Standard approaches of this kind are subgradient methods (Polyak 1977; Nesterov 2009; d’Antonio and Frangioni 2009) and the cutting plane method (CP) (Kelley 1960), also known as the Dantzig–Wolfe decomposition method (Dantzig and Wolfe 1960). Early examples of the use of subgradient methods in UC are (Fisher 1973; Muckstadt and Koenig 1977; Bertsekas et al. 1983; Merlin and Sandrin 1983; Bard 1988; Zhuang and Galiana 1988), possibly with modifications such as successive approximation techniques (Cohen and Wan 1987) or variable metric approaches (Aoki et al. 1987). An early example of the use of CP is Aganagic and Mokhtari (1997). The two approaches are rather different: subgradient methods use very simple rules to compute the next dual iterate, whereas CP uses (possibly costly) Linear Programming (LP) problems for the same task, although hybrid versions have been devised (Tong and Shahidehpour 1989). This is necessary in practice because both approaches have convergence issues, for different reasons: subgradient methods lack an effective stopping criterion, whereas CP tends to be unstable and converge slowly. This is why variants of CP have been devised, e.g., using Interior Point ideas to provide some stabilizing effect (Merle et al. 1998); for an application to UC see Madrigal and Quintana (2000). In Ruzic and Rajakovic (1998) the KKT conditions of the Lagrange function are used in order to update the Lagrange multipliers and improve on subgradient approaches. In Redondo and Conejo (1999) CP is stabilized by a trust region. The latter turns out to be a special case of the most effective family of approaches capable of dealing with this kind of problems, that is, (generalized Frangioni 2002) Bundle methods (Lemaréchal 1975; Wolfe 1975). These can be seen as a hybrid between subgradient and CP (Bahiense et al. 2002) which inherits the best properties of both (Briant et al. 2008). Several variants of Bundle approaches exist, see e.g. (Lemaréchal and Sagastizábal 1994; Lemaréchal et al. 1995; Astorino et al. 2011). A recent development that is useful for UC is that of methods that allow the inexact solution of the Lagrangian relaxation (Kiwiel 2012; de Oliveira and Sagastizábal 2014; Oliveira et al. 2014; van Ackooij and Frangioni 2018); this feature is of particular interest if operational considerations impose strong restrictions on the solution times for the subproblems. For early application of Bundle methods to UC see e.g., (Lemaréchal and Sagastizábal 1995; Luh et al. 1998; Zhang et al. 1999; Gollmer et al. 1999; Feltenmark and Kiwiel 2000; Borghetti et al. 2001, 2003a).

Regarding the second point, one important property of LDs of non-convex programs is that, while they cannot be guaranteed to solve the original problem, they indeed solve a “convexified version” of it (Lemaréchal 2001; Frangioni 2005). In practice, this typically provides solution $\tilde{x} = (\tilde{p},\tilde{u})$ to (1) that is feasible for all constraints except the integrality ones. That is, rather than feasible commitment decisions $u^i_t \in \{0, 1\}$ one obtains pseudo-schedules $\tilde{u}^i_t \in [0, 1]$ that satisfy the constraints with the production decisions $\tilde{p}$. Such a solution can be obtained basically for free by (appropriately instrumented versions of) subgradient methods (Barahona and Anbil 2000; Anstreicher and Wolsey 2009) and all other algorithms, most notably Bundle ones (Feltenmark and Kiwiel 2000). The pseudo-schedule $\tilde{x}$ can for instance be heuristically interpreted as the probability that unit i be on at instant t, and then be used in this guise to devise primal recovery approaches to attain feasible solutions of (1), either by appropriately modifying the objective function (Dubost et al. 2005; Daniildis and Lemaréchal 2005) or by a heuristic search phase that exploits both $\tilde{x}$ and the integer solutions produced by the LR (Batut and Renaud 1992; Frangioni et al. 2008; Sagastizábal 2012).

Along with early papers which address the bUC (Muckstadt and Koenig 1977; Merlin and Sandrin 1983; Fisher 1973; Bertsekas et al. 1983), we mention papers which address large-scale UC (Merlin and Sandrin 1983; Bertsekas et al. 1983). The authors of Merlin and Sandrin (1983) are among the first who tried to use LR to obtain a solution, and not just to obtain lower bounds for B&B procedures, solving a problem of 172 units. In Lauer et al. (1982) the duality gap problem is tackled by approximating the dual problem with a twice-differentiable mapping which is then maximized by using a constrained Newton’s method, after which a heuristic is used to recover a nearly optimal primal solution; a 200 units UC is solved in about 10–12 min. In a subsequent work (Shaw et al. 1985), a three-stage approach is proposed to deal with a—for the time—large-scale hydro-thermal system (100 thermal units and 6 hydro ones). The first stage is based on LR, with the thermal 1UCs solved using DP, while the hydro subproblems are solved by using a penalty multipliers method (Kort and Bertsekas 1972) and a specially tailored Newton’s method. A “unit decommitment” method is suggested in Li et al. (1997) and Tseng et al. (2000) where all units are considered online over all $\mathcal {T}$ and then, using the results of the LR, units are decommitted one at a time. This method aims at providing feasible primal solutions first, whereas most LR approaches would aim at optimality first. Further references using LR are Ferreira (1994), Guan et al. (1994) and Salam et al. (1997, 1998), which consider specific dedicated approaches in order to tackle the subproblems, elementary ways of updating the dual and heuristics to recover a primal feasible solution. A particular interesting feature of LR (when compared to monolithic solution based methods such as MILP) is the possibility to solve the sub-problems in a parallel computing architecture. This potential is investigated and explored in Sher and Banerjee (2014), where the trade-off between the number of sub-problems and processors is examined. In Guan et al. (1995) the units cost functions are modified in order to reduce the oscillating behavior of subgradient approaches. In Gollmer et al. (1999) the authors compare a primal MIP based approach with a LR-based approach: Bundle methods are used in order to solve the LD and two Lagrangian heuristics are investigated for primal recovery. The first one searches for time steps where demand constraints are most violated and employs a strategy proposed in Zhuang and Galiana (1988) for changing the commitment variables, while the second one exploits nearly optimal Lagrange multipliers for fixing commitment decisions. In order to recover primal feasibility, both heuristics are followed by solving an ED, wherein the commitment variables are fixed; this LR-based method is shown to be capable of handling larger and more complex instances. In Takriti and Birge (2000) the Lagrangian heuristic consists of formulating a MIP that mixes solutions provided by the dual iterations, selecting the production schedule of a specific unit among the primal solutions generated by the LD phase in such a way as to minimize overall cost and satisfy (the dualized) demand constraints. The resulting MIP is then reformulated in order to allow for an efficient solution. A similar idea is exploited in Lucas and Triboulet (2012), where the MIP is solved by using Genetic Algorithms. In Feltenmark and Kiwiel (2000) the dual multipliers defining the pseudo-schedule are interpreted as probabilities for randomly selecting commitment decisions after a LD phase; four derived Lagrangian heuristics are investigated. In Belloni et al. (2003) a two step procedure is proposed, consisting of a LD phase followed by an Augmented Lagrangian (AL) phase for primal recovery. The AL term is linearized in an ad-hoc way and its penalty slowly sent to infinity. Bundle methods, CP and sub-gradient methods are compared for solving the LD phase; it is shown that bundle methods outperform alternative approaches. Finally, in Borghetti et al. (2001) Lagrangian approaches are compared with Tabu Search heuristics, and an improved primal phase is proposed in Borghetti et al. (2003a). The approach is later extended to the free-market regime (Borghetti et al. 2003b) and to the handling of ramping constraints (Frangioni et al. 2008) via the use of the specialized DP procedure of Frangioni and Gentile (2006b). An hybrid version also using MILP techniques is presented in Frangioni et al. (2011). A state-based formulation akin to that leading to the DP is proposed in Tumuluru et al. (2014), where all the (up to $2^{12}$) feasible sub-paths corresponding to half of the day are enumerated; the LD of the formulation is then solved by a subgradient algorithm and specific primal recovery techniques exploiting the generated sub-paths.

LR can be used to deal with ramp rate constraints, fuel related constraints and emission constraints (Cohen and Wan 1987; Aoki et al. 1987; Yan et al. 1993; Tong and Shahidehpour 1989; Zhuang and Galiana 1988) by simply relaxing them (in Lagrangian fashion). Similarly, LR can be employed to further decompose subproblems, in particular hydro ones; these ideas are explored in Guan et al. (1997), Ni et al. (1999), Finardi and Silva (2006), Takigawa et al. (2012, 2013) and Finardi and Scuzziato (2014). More specifically, the authors of Guan et al. (1997) consider the LD related to the bounds on the reservoir levels in the hydro subproblem, which effectively decomposes the problem in smaller MILPs that can then be readily dealt with, through the use of DP in this specific case. The LD is optimized using a subgradient approach, and heuristics are used to recover a primal feasible solution. A similar approach is used in Ni et al. (1999), where hydro units have discrete commitment decisions much like thermal ones. These constraints are then relaxed in a Lagrangian way, resulting in continuous network flow subproblems and a pure integer problem. In Finardi and Silva (2006), Lagrangian decomposition (Guignard and Kim 1987) is used to deal with forbidden zones in complex hydro units. The idea is to use LR to decompose hydro valley subproblems further into two parts: the first part deals with the flow constraints and basically leads to a simple LP, while the second part deals with the water-head effect and other combinatorial constraints and requires a specific NLP approach (an SQP-based method and partial exhaustive enumeration). Two dual formulations are considered which differ from each other in that in the second one the NLP problem is further decomposed through the use of auxiliary variables. The model is extended to consider network constraints in Takigawa et al. (2012), and different relaxation schemes are explored in Takigawa et al. (2013) and Finardi and Scuzziato (2014); in particular, the latter compares Lagrangian relaxation and Lagrangian decomposition. In Yan et al. (1993) a system with 70 thermal and 7 hydro units is addressed. Ramp rate constraints are also dualized, and the DP approach of Guan et al. (1991) is used to optimize the thermal units, while a merit order allocation is employed for the hydro subproblem. In Zhuang and Galiana (1988) a three stage approach is proposed based on first solving the LR, then finding a feasible solution for reserve requirements and finally solving an ED. In Nilsson and Sjelvgren (1996) a HUC with a fairly realistic model for hydro generation is considered that comprises forbidden zones (cf. Sect. 2.4) and the water head effect. The offer-demand equilibrium constraints and reservoir balance equations are dualized, and the LD is maximized with a subgradient approach, with a heuristic step fixing the discrete hydro variables to recover a primal feasible hydro solution. In Aganagic and Mokhtari (1997) some transmission constraints are considered. In Li and Shahidehpour (2003) an alternative to ramping rate constraints in the model for thermal units, a so-called stress effect, is proposed. Coupling offer-demand equilibrium and reserve requirement constraints are dualized; the corresponding LD is maximized using a subgradient approach, where the thermal subproblems are solved using Simulated Annealing techniques. In Fu et al. (2005) a ramp rate, fuel and emission constrained UC is solved (Table 3).

Table 3 Sources using Lagrangian relaxation

A different decomposition approach is the classic one due to Benders (Benders 1962; Bonnans et al. 2006, Chapter 11.1), which rather focuses on complicating variables that, once fixed, allow to separate the problem into independent (and, hopefully, easy) ones. Application of Benders’ decomposition to UC is fairly recent; in particular, it has been used for Transmission constraints, which decompose by hour once commitment and energy decisions are taken. In Wu and Shahidehpour (2010), Liu et al. (2010) and Wu (2013) techniques for improving the generated Benders’ cuts are described. In Fu et al. (2013) a conceptual and numerical comparison is made, in the context of the security constrained UC, between LR and MILP approaches (cf. Sect. 3.2) for the solution of master problem of Benders’ decomposition; for the subproblems, involving the network constraints, Benders’ cuts and linear sensitivity factor (LSF) approaches are compared. In Taverna (2017) Bender’s decomposition is also employed for a deterministic zonal UC problem and, as is popular in UUC, commitment variables are seen as complicating variables.

3.4 Augmented Lagrangian relaxation

One major downside of LR approaches is the difficulty in recovering a primal feasible solution. The use of the Augmented Lagrangian (AL) method, whereby a quadratic penalization of the relaxed constraints is added to the objective function alongside the linear penalization typical of standard LR, is known to be a potential solution to this issue. Yet, because (1) is nonconvex it should be expected that in general the AL approach leads to a local optimizer (Gill et al. 1982; Luenberger and Ye 2010). Furthermore, the AL relaxation is no longer separable into an independent subproblem for each unit, and therefore it is significantly more difficult to solve (in practice, as difficult as UC itself). This calls for some further approach to simplify the relaxation; in Batut and Renaud (1992) and Yan et al. (1994) the use of the auxiliary problem principle (Cohen 1980; Cohen and Zhu 1983) is suggested. The classic theory of the auxiliary problem principe requires restrictive assumptions such as convexity and regularity, which do not hold in practice; some recent advances have been made in the non-convex setting (Attouch et al. 2010; Razaviyayn et al. 2012; Tseng 2001). In Beltran and Heredia (2002) an alternative decomposition scheme based on block coordinate descent (e.g. Ruszczyński 1995; Bertsekas 1999) is proposed and it is found to be more efficient. The recent Mezger and Almeida (2007) includes in the UC formulation a DC network model and bilateral contracts defining the nodal injections. The AL of the coupling constraints is formed and then linearized in an ad-hoc way, while bundle methods are employed for updating the dual multipliers. Environmental constraints (Wang et al. 1995) and network transmission constraints (Beltran and Heredia 2002; Wang et al. 1995) have also been tackled with the AL approach. A common way to deal with additional constraints is variable duplication (Georges 1994), which is also used in Feizollahi et al. (2015) in the context of different variants of the Alternating Direction Method of Multipliers (ADMM), comprising some procedures for constructing feasible solutions (Table 4).

Table 4 Sources using augmented Lagrangian approaches

3.5 (Meta-)Heuristics

3.5.1 Operator rule based: priority listing

This method defines a list of units which should logically be scheduled prior to other units, with merit order scheduling being a special case. Priority listing was first employed on bUC in Baldwin et al. (1959), where units are listed according to their performance and the cost they yield (comprising maintenance costs). Must-on/must-off and crew constraint have been added in Lee (1988), and a limit on the number of starts is included in Lee (1991) through the use of a commitment utilization factor, which is claimed to provide a better list. While the former two papers and Amiri and Khanmohammadi (2013) address bUC, there has been an endeavour to integrate other factors such as multi-area constraints (Lee and Feng 1992) and hydro-thermal systems (Johnson et al. 1971) for large-scale UC. In the latter paper a two-step heuristic procedure is used to solve a UC with 100 units: the first step uses rules from real-world schedules (possibly enhanced by the use of UC software) to set up a priority list consisting of feasible production schedules, while the second step optimizes locally around the current solution. A very similar approach is investigated in Amiri and Khanmohammadi (2013). In Moradi et al. (2015), a methodology is developed to include minimum up and down times as well as ramping constraints through a non-iterative approach. The methodology is tested both on 10–100 unit systems (IEEE RTS 24 and 118-bus) and on the Korean power system (Table 5).

Table 5 Sources using priority listing

3.5.2 Guided random exploration

Since solving the UC (1) to optimality is quite difficult, many heuristic approaches such as Taboo search, Simulated Annealing, Augmented Lagrange Hopfield Networks, Nature Inspired (e.g., particle swarms, frog leaping,...) and Genetic Algorithms have also been employed. We refer to Farhat and El-Hawary (2009) and Saravanan et al. (2013) for a discussion of those approaches, and in this paper we by no means attempt to give a full overview of this subfield. This is because heuristic approaches like these are typically difficult to adapt to the Uncertain UC case, which is the main focus of this survey, unless they are at least partly based on mathematical programming techniques. We therefore concentrate mostly on hybrid approaches that use the latter at least to a certain degree. For instance, in Lucas and Triboulet (2012) genes are feasible schedules produced by a LR-based scheme: the genetic algorithm then mixes the solutions up to form new feasible schedules in order to hopefully produce a solution that better meets the demand constraints. In essence this simply means solving the recombination MIP of Takriti and Birge (2000) highly inaccurately. In Zhuang and Galiana (1990) a 100 thermal unit system is solved by using Simulated Annealing; this is reported to outperform a B&B procedure, but fails to outperform a LR approach (although in the later (Borghetti et al. 2001) Taboo search has been reported to be more competitive with LR). In Duo et al. (1999) and Juste et al. (1999) Evolutionary Programming is applied to adjust the solution provided by a LR approach. In Luh et al. (1999) a neural network approach is coupled to LR in order to optimize a system with up to 60 units: the thermal subproblems are optimized using a neuron-based DP algorithm.

In general, these approaches are not considered particularly competitive for UC; for instance, (Takriti et al. 2000) states that Simulated Annealing and Evolutionary Programming attempts have been unsuccessful. Also, usually these approaches deal with bUC, with only a few sources considering ramp rate, crew, maintenance or multi-area constraints, and hydro-thermal systems being very rarely dealt with. The likely reason is that purely combinatorial heuristics are best apt at problems that exhibit a predominant and relatively “simple” combinatorial structure to which the various elements of the heuristic (neighborhood(s) structure in Simulated Annealing, Taboo list and aspiration criteria in Taboo search, mutation and crossover operators in genetic algorithms,...) can be specifically tailored. UC is a fundamentally mixed combinatorial and continuous program, since both the commitment and the dispatch have to be provided. Furthermore, UC has several different combinatorial structures, especially when “complex” constraints have to be dealt with. Therefore, on the outset UC is best approached with mathematical programming techniques.

Table 6 provides a (very partial) overview of heuristic approaches.

Table 6 Sources using (meta-)heuristic approaches

4 Methods for the uncertain unit commitment

The complex nature of UC, due to its numerous technical constraints, forces the schedule to be determined quite ahead of time and consequently be given to the TSO one day in advance. This allows for uncertainty to have an important impact on the system. Furthermore, intra-daily optimization processes and communication between the TSO and the GENCOs allow for recourse decisions. Thus, dealing with uncertainty has always been necessary in UC. We now discuss the approaches that have been proposed (and sometimes compared van Ackooij 2017) in the literature. To the best of our knowledge, this has never been done before specifically for the UC. The chapter (Wallace and Fleten 2003) provides a general overview of the ways in which uncertainty arises in Energy Management, but it is mainly focussed on mid- and long-term problems, UC being only briefly addressed. Analogously, Conejo et al. (2010) offers a general survey on uncertainty issues in Energy Optimization, without a specific focus on UC. The chapter Römisch and Vigerske (2010) offers a general overview of properties of stochastic optimization problems and briefly provides some links to stochastic UC problems. The essential references used in these sources will be discussed below.

4.1 Dealing with uncertainty in UC

In most traditional approaches, load uncertainty is dealt with by computing the schedule corresponding to the worst scenario, i.e., typically that of peak demand in each period. This choice systematically overestimates demand and incurs the risk that significant ramp-down of the production is needed when the actual demand proves to be substantially smaller than the forecasted one, which can cause feasibility issues due to technical constraints like ramp-down ones (cf. Sect. 2.3). Another common approach has been to use spinning reserve constraints (cf. Sect. 2.7) (Wu et al. 2007; Anstine et al. 1963; Billinton and Karki 1999; Fotuhi-Firuzabad and Billinton 2000; Gooi et al. 1999; Morales et al. 2009); the advantage is that this protects against some degree of uncertainty while keeping the deterministic formulation. In general, the deterministic constraints can be “tweaked” heuristically in order to deal with uncertainty. For instance, in order to ensure that the solution can survive a certain degree of variability in the data we can underestimate the amount of water in a hydro reservoir and/or impose stricter ramp-rate constraints than justified by technical aspects. Obviously, this may result in a loss of optimality or control over feasibility. Worse, one may loose control over where the approximations have been made. Further simplifications may be related to relaxing integrality constraints or by considering certain uncertainties to be part of load (e.g., Ruiz et al. 2010)

In order to overcome these weaknesses, methods where uncertainty is directly modeled have been investigated. These comprise Stochastic Optimization (scenario tree), Robust Optimization, and Chance-Constrained Optimization.

4.1.1 Dealing with uncertainty in the model

4.1.1.1 Stochastic optimization Scenario tree based approaches (from now on denoted as SO, i.e., Stochastic Optimization) have been the subject of intense research in the last two decades; see e.g. (Prékopa 1995, Chapter 13; Birge and Louveaux 1997; Louveaux and Schultz 2003; Kall and Mayer 2005; Ruszczyński and Shapiro 2009a, b) among the many other general references. Their use in the UC context has been considered e.g. in Takriti et al. (1996), Carpentier et al. (1996), Ozturk et al. (2004), Wu et al. (2007) and Wong and Fuller (2007) and in HUC in e.g., (Séguin et al. 2017) (and references therein). The key advantage of using scenario trees is that uncertainty is assumed to be known in each node of the tree. Since uncertainty is now discretized on the tree, essentially this amounts to solving a deterministic UC of very large scale. The authors of Tuohy et al. (2009) demonstrate the interest of SO over deterministic optimization using such a direct reformulation. In Schulze and McKinnon (2016), two and multi-stage stochastic programming are compared against a deterministic rolling horizon approach, showing that stochastic models lead to cost savings, but only if the scenario tree well represents the underlying uncertainty. In view of this, Morales-España et al. (2017) considers the impact of uncertainty jointly with other approximations of reality (such as not considering stopping/starting curves), and proves that each feature has a non-negligeable effect on the expected costs. According to Bertsimas et al. (2013), SO methods have two major drawbacks. First, obtaining an accurate probability distribution can be difficult, i.e., setting up an accurate tree is hard. Indeed, while generating scenarios for each individual uncertainty factor may be relatively straightforward, combining these to form a tree structure is not easy. Second, these solutions provide only probabilistic guarantees. The first difficulty can be partially tackled by the approaches considered in Dupačová et al. (2003), Heitsch and Römisch (2003), Heitsch and Römisch (2009), Eichhorn et al. (2010) and Heitsch and Römisch (2011), that provide a systematic approach for generating manageable trees. Classical approaches (e.g. Takriti et al. 1996) to form a tree are those that start out with a set of scenarios and progressively regroup similar scenarios to form the nodes, in each of which a representing scenario is selected. The use of physical models for generating uncertainty (e.g. Constantinescu et al. 2011) could also help improve the realism of the underlying scenario tree. The recent work Feng and Ryan (2016) builds on classic scenario reduction (e.g., Heitsch and Römisch 2003) for a 2-stage UUC (with commitment/binary decisions restricted to the first stage) by regrouping scenarios according to some sensitivity index meaning to reflect important characteristics of the problem. In this view it is also worthwhile to mention that such scenario clusters can also be dynamically formed and managed by the algorithm (Song and Luedtke 2015; van Ackooij et al. 2018) without loosing any guarantee on the optimality with respect to the originally formulated problem. In Sari and Ryan (2017), building on and extending (Sari et al. 2016), a further criteria is developed for linking scenarios and estimating the cost of recourse. The second difficulty can be tackled by using a hybrid approach that also considers spinning reserve requirements on the scenario tree (Ruiz et al. 2009; Wu et al. 2007), which can be used to account for events not modeled in the tree. We mention in passing that similar techniques can also be applied to longer-term problems, such as the management of an hydro reservoirs, that although not strictly pertinent to this paper are clearly strongly related. For a recent instance, a specialized stochastic dual DP algorithm is proposed in Guigues (2013). In Dvorkin et al. (2015) there is one of the few attempts to mix the stochastic approach with an interval one, that in turn is similar to Robust Optimization, see also Sect. 4.1.1.2. The goal is to manage the complexity of the stochastic approach applying it only to the initial operating hours of the optimization horizon. The later hours use the interval approach (i.e., RO) since the uncertainty in net load is higher in these hours. In Aghaei et al. (2016) a classic stochastic approach is used for a full AC network constrained UC, while the solution approach is a Benders’ decomposition with one master and two sub-problems. The interesting modelling characteristic is the imposed relationship between the level of reserve and the (estimated) value of lost load (VOLL). In Zhang et al. (2016) a joint day-ahead scheduling of electric power systems with natural gas transmission constraints is considered together with a stochastic approach aimed at dealing with the uncertainty of the load and of random outages.

4.1.1.2 Robust optimization In order to be less demanding on the representation of uncertainty, Robust Optimization (RO) uses the notion of uncertainty set, which basically reunites the adverse events against which we wish to protect ourselves. For a comprehensive introduction to robust optimization we refer to Ben-Tal et al. (2009) and Bertsimas et al. (2011); other important references are Ben-Tal and Nemirovski (1998), Ben-Tal and Nemirovski (1999), Ben-Tal and Nemirovski (2000), Ghaoui and Lebret (2006), EI Ghaoui et al. (1998), Bertsimas and Sim (2003) and Bertsimas and Sim (2004). RO approaches might lead to a substantially higher costs of the proposed solution—a too high “price of robustness” (Bertsimas and Sim 2004)—w.r.t. SO ones when distributions of the uncertainty are sufficiently well characterized. This is mainly because RO protects against each event in the specified uncertainty set regardless of its probability, and therefore may have to account for extremely unlikely events. Several RO approaches have parameters (e.g., “budget of uncertainty”) that can be used to adjust the degree of protection offered by the model (Bertsimas and Sim 2003; Nemirovski and Shapiro 2006a; Chen et al. 2007); yet, in general tuning these parameters is far from trivial. To reduce the price of robustness associated with classical ellipsoidal and $\varGamma$-robustness uncertainty sets proposed in Ben-Tal and Nemirovski (1998), EI Ghaoui et al. (1998) and Bertsimas and Sim (2004), subsequent studies have investigated alternative soft and light robustness models (Ben-Tal et al. 2010; Fischetti and Monaci 2009). Recently, multiband robustness (Büsing and D’Andreagiovanni 2012, 2013), has been proposed as a generalization of $\varGamma$-robustness that can support an improved and stratified representation of uncertainty and a reduction in conservatism, while maintaining the computational tractability and accessibility of $\varGamma$-robustness.

4.1.1.3 Chance-constrained optimization Chance-Constrained Optimization provides an attractive way to select the trade-off between cost and robustness, using a notion—the probability of the selected solution to be feasible—that is easy for the decision-maker to understand and manage. We refer to Prékopa (1995), Prékopa (2003), Dentcheva (2009), Henrion (2004) and Henrion (2010) for a modern introduction to probabilistic programming. In van Ackooij et al. (2011) the potentials for energy management applications, such as UC, are discussed. However, a drawback of CCO is that probabilistic constraints can be nonconvex and hard to evaluate, thus making these approaches potentially computationally demanding.

4.1.1.4 The link between RO and CCO There actually is an important link between RO and CCO. Indeed, an intuitively appealing idea is to select the uncertainty set in such a way as to enforce a probabilistic constraint, so that the solutions produced by the RO approach are comparable with those produced by the CCO one. More generally, one may aim at replacing the probabilistic constraint with a convex, albeit possibly more restrictive, constraint. There are various ways of doing this (e.g. Nemirovski and Shapiro 2006a; Ben-Tal and Nemirovski 2009), often referred to as “safe-tractable approximation approaches” (a somewhat unfortunate terminology implicitly assuming that all CCO problems are intractable, which is not the case). Frequently, such convex outer approximations of the CCO-feasible set are derived by using individual probabilistic constraints, i.e., constraints that require that each individual inequality in the constraints system holds with high enough probability (e.g. Chen et al. 2007). Besides using a (not necessarily very tight) approximation, this approach gives little control over the joint violation of the constraints, although it does have the advantage that convexity makes the corresponding problems easier to solve. We refer to van Ackooij et al. (2010, 2014) for examples showing that individual probabilistic constraints may lead to an arbitrary number of violated constraints. We also refer to Bandi and Bertsimas (2012) and Guan and Wang (2014) for various other alternatives of building uncertainty sets. The scenario approximation approach (e.g. Calafiore and Campi 2005; Nemirovski and Shapiro 2004, 2006b) can be seen as a special case of RO with a discrete uncertainty set that arose by drawing random samples from the underlying distribution. For instance, a two stage UC model is proposed in Kalantari and Galiana (2015) wherein feasibility for the second stage offer-load balance is requested to hold for all scenarios belonging to a finite uncertainty set constructed by identifying specific extremal points of an ellipsoidal load set.

The link between CCO and RO can be concretely used. In Upahyay et al. (2016) a CCO problem is defined to compute the effective range of wind power output, that is then used in a RO UUC; a specific structure of the problem (discrete uncertainty) allows to formulate an equivalent MILP solvable with standard commercial solvers. A similar approach is used in Hreinsson et al. (2015), where a polyhedral uncertainty set is constructed by sampling the uncertain wind production in a large enough number of points as to have some guarantee on the probability of the events left out, and then standard RO techniques are used to formulate the UUC as a MILP. However, one can go further in combining CCO and RO. Indeed, in some applications not all sources of uncertainty are known equally well. Then, in order to best exploit available information on, say, the distribution of some components, while considering uncertainty on others in a broader sense, it is possible to consider a so-called “hybrid robust/chance constraint” (e.g., van Ackooij et al. 2016), or “probust” constraint (e.g., Gradón et al. 2017; Adelhütte et al. 2018). Both constraints capture the fact that the probability has to be taken over a system involving a worst-case situation over some uncertainty set, while also accounting for regular probabilistic information over other components. The other situation (easier since implied by the former, see, e.g., van Ackooij et al. 2016), which we could conveniently call “robility”, considers a parametric worst-case version of a standard probability constraint. This can be seen, at least at a high level, as analogous to distributionally robust chance constraints, wherein a worst case situation over an appropriate family of probability measures is taken (e.g., Calafiore and Ghaoui 2006; Hanasusanto et al. 2015; Zymler et al. 2013). Distributionally robust CCO is put into work in the two-stage stochastic UC model with first-stage integer variables of Xiong et al. (2017), where the expected recourse cost function is replaced by a worst-case expected cost over a specifically chosen ambiguity set. The latter set is special in so much that it allows for a specific reformulation of the full recourse cost function, when also exploiting linear decision rules. In Zhao and Guan (2016) the formulated two-stage UC accounts for ambiguity on the probabilities of the given set of scenarios, which are assumed to belong to either an $L_1$ or $L_{\infty }$ space thus allowing for a convenient reformulation of the second stage problem; a Benders decomposition algorithm is employed to solve the resulting problem.

4.1.2 Modelling and solution choices

4.1.2.1 The choice of recourse decisions A crucial decision in all two-stage (or multi-stage) models, be they SO, RO or CCO, is which variables represent “here and now decisions” (first stage), to be taken before the uncertainty is revealed, and which represent “recourse actions” (second or later stages) that can change when the uncertain parameters are revealed. In multi-stage models a whole chain of decisions and observation of uncertainty needs to be worked out properly, which ends with the observation of a last random realization offering no recourse actions (e.g., van Ackooij and Oudjane 2015). This could give rise to the need to consider multi-stage RO (CCO) approaches. When recourse is incomplete (i.e., can not guarantee feasibility of later stages regardless of the random realizations) such a need may also arise.

In general, recourse formulations aim at minimizing the total cost of the here and now decisions and the expected cost (or sometimes other utility functions Vieira et al. 2016) of the possible recourse actions. These problems are typically very challenging from both the computational and theoretical point of view, especially if recourse actions are integer-valued, or anyway belong to a non-convex set. In the integer setting, a general approach to deal with this formulation was introduced by Laporte and Louveaux (1993). In Løkketangen and Woodruff (1996) a progressive hedging algorithm and Taboo search are used to address multi-stage problems with mixed 0–1 variables. The approaches can become somewhat computationally less demanding if recourse variables are instead continuous, which is often the case in UC. In fact, here commitment variable are typically first-stage decisions, to be taken well in advance, while the actual energy production (usually continuous) is indeed managed in real time when the uncertain data (load, prices,...) is revealed. Such a choice is made in Bertsimas et al. (2013) where RO is applied to UC with a 2 stage approach. Restricting commitment choices to a first stage is a convenient simplification but it does not fully represent reality, where (a few) changes to the commitment of units are in general possible. The same 2 stage RO approach is considered in Lee et al. (2014) where a model with full transmission line constraints is proposed together with novel acceleration techniques comprising cutting plane for the master and column-generation methods for the sub-problems.

Accounting for recourse decisions, however, significantly increases the complexity of the problem, which justifies why restricting integer decisions to the first stage is the most common approach. The primal-dual approach explored in van Ackooij and Malick (2016) highlights how, by exploiting the LD in the second stage, an automatic convexifying effect is generated. The solved UC problem then actually “sees the recourse cost function through a convexified looking glass”, but the cost function does not necessarily coincide with the convex hull of the recourse cost function. Still, thanks to such an approach a highly efficient decomposition scheme can be designed.

A further choice, once say a 2-stage framework has been adopted, is that of the second stage criterium to optimize, e.g., expected costs, worst-case costs or some risk measure of the recourse costs. We refer to van Ackooij (2017) for a general comparison of some methods accounting for recourse decisions and other that do not, while also considering partially the choice of the criteria (expectation vs. worst case). The work Kazemzadeh et al. (2017) carefully compares optimization based on worst-case criteria versus risk (here CVaR) criteria. The authors conclude that even when low-tail probabilities are picked, the latter approach is quite less conservative.

4.1.2.2 Direct approaches versus decomposition Regardless of the simplifying assumptions on UUC, the resulting mathematical program is frequently a very-large-scale one, which means that decomposition approaches are especially attractive. In some special situations, direct use of MI(N)LP solvers remains possible. This is, for instance, the case of the self-scheduling of a single unit subject to uncertain prices, for which the deterministic problem has a low number of variables. Another example is the market based model of Laia et al. (2014), wherein all generators (including commitment decisions) can be adapted in a second decision stage. Often, however, the deterministic equivalent (if any) of the uncertain problem is usually so large that it cannot be directly solved by use of MILP solvers, and decomposition is required. This can be achieved by variable duplication, relaxing non-anticipativity constraints, system wide constraints or by using Benders’ decomposition. The resulting sub-problems are then CCO (e.g. van Ackooij 2014), RO, deterministic (e.g. Takriti et al. 1996) or stochastic programs (e.g. Carpentier et al. 1996).

Some authors develop ad-hoc “decomposition like” schemes such as in Lyon et al. (2016), where a 2-stage stochastic UC is considered, but with a Benders-like ad-hoc procedure to re-enforce constraints in the master problem dealing with the optimal commitment decisions. In particular, the effect of scenarios are approximated by means of capacity constraints on “slow” units whose RHS is the amount of power required in that scenario, thereby including the uncertainty; conversely, “fast” units are allowed to change their commitment when uncertainty is revealed, which implies having integer variables in the scenario subproblems. The coefficients in these constraints, i.e., the “qualified capacity” of a generator under a scenario, are ideally initialized as the maximum power of the generator, and then a deterministic UC is solved. The obtained schedule is evaluated in all scenarios by solving small-scale MILP akin to the scenario subproblems and evaluating if the cost of the scenario is too large than what anticipated; in this case the qualified capacities are reduced, and the deterministic UC is solved again (with a time limit of 4 min). Tests are performed on a modified version of the IEEE-73 bus test case.

We will now present more details on algorithms for Uncertain UC models using these three approaches.

4.2 Stochastic optimization (scenario-tree) approaches

In this section we will discuss four common solution approaches for solving scenario-tree based versions of UC: the direct MILP approach and three decomposition methods.

A SO program with scenario-tree structure can be decomposed in at least two ways. Perhaps the most natural one is to relax the so-called non-anticipativity constraints and solve as many deterministic UC problems as there are scenarios. This is called the Scenario Decomposition approach (Takriti et al. 1996) and includes well-known variants such as progressive hedging (Rockafellar and Roger 1991). The alternative is to dualize the demand and supply equilibrium constraints in each node to form a LD (Carpentier et al. 1996) and solve as many stochastic programming problems as there are units. This can be referred to as Space Decomposition, Unit Decomposition or Stochastic Decomposition, because one is basically optimizing a stochastic function, which in this case just happens to have an underlying discrete distribution. We will use Unit Decomposition, UD, to have a different shorthand from the Scenario Decomposition, SD. The discretization can be carried out after having formed the LD in an appropriate Banach space setting ($L^1$-type spaces); see for instance (Nürnberg and Römisch 2003). We refer to Ruszczyński (2003) for a thorough discussion on various alternatives. In general, it is hard to state beforehand which among UD and SD will perform better for a given instance; the recent Scuzziato et al. (2018) compares them using state-of-the-art Lagrangian techniques (in particular, the use of “easy components” (Frangioni and Gorgone 2012) is found to be quite significant) and tries to elaborate on some of the main trade-offs between the two approaches.

A different applicable approach is Benders’ decomposition, cf. Sect. 4.2.4. It exploits the L-shaped structure of the problem, whereby the second-stage (recourse) variables corresponding to each scenario are unrelated, and therefore the corresponding subproblems can be solved independently, once the first-stage variables are fixed (van Slyke and Wets 1969). This corresponds to seeing the second (or later) stage(s) as an aggregated expected cost function depending on first (or earlier) stage variables. Under appropriate hypotheses (e.g., no integer decisions in later stages) this expected cost function can be shown to be convex, and cutting planes based approximations can then be used to compute the solution of the master problem (e.g. de Oliveira et al. 2011). Recent and interesting trends in Bender’s decomposition are the consideration of inexact cuts and stabilisation techniques. We refer to Rahmaniani et al. (2017) for a general overview on Bender’s decomposition and to van Ackooij et al. (2016), Zaourar (2014) and Zaourar and Malick (2014) for more specific references concerning stabilization and energy related applications. Stabilized Bender’s decomposition has, in particular, been used in UC applications in van Ackooij et al. (2017) where the (simple) recourse cost function is a worst-case cost function over a very large uncertainty set; the numerical experiments show that stabilization results in impressive speed ups.

4.2.1 Mixed integer linear programming

In Valenzuela and Mazumdar (2003) the use of UC tools in a deregulated market is discussed. In particular, under the assumptions that prices are stochastic and there is no market power or transmission constraints, a GENCO can solve a self-scheduling UC for each of its units independently, which however, should be a SO model due to uncertainty on prices. A MILP formulation for (a basic) UC is proposed, along with three DP approaches to solve it. These approaches are used to produce a cost-based method to generate a distribution of energy prices, based on the assumption that in a competitive market the price should be equal to the marginal cost of the most costly committed unit. A different take on the same problem, i.e., generating offer curves for an energy market, is proposed in Li et al. (2007) based on a similar two-stage model where market prices are directly the uncertain quantity; the produced energy for each price scenario is used as a base to construct piecewise-linear offer curves.

In Philpott and Schultz (2006) a two-stage model is considered where the first stage decisions consist of commitment decisions and an offer curve, while in the second stage, the dispatch is computed. Single unit or identical unit systems are considered, although the model with several units can not cope with minimum up/down times. The focus is essentially on obtaining the offer-curve. A DP principle is presented, but no numerical experiments are provided. A very similar model is considered in Triki et al. (2011), wherein commitment decisions and offer curves are first-stage decisions and dispatch later stage decisions. The key focus of these papers is on the market mechanisms.

Hydro scheduling is looked at in a market-based setting in Fleten and Kristoffersen (2008). The problem integrates commitment decisions on the turbined output, which have minimum release rates. Expected gain from selling energy on the market is maximized, whereas volume-dependent water values are used in order to represent the cost of water as measured by the difference between the initial and final volume in the reservoir.

In Beraldi et al. (2008) a two-stage formulation is proposed wherein the first stage variables consist of bilateral contracts. Once these contracts have been selected, the market price is observed and a bUC is solved in order to meet the resulting load. The objective function consists of Markovitz mean-variance model related to expected profits. A specialized B&B method is used in order to solve the corresponding MILP problem; the numerical experiences cover a GENCO with 3 thermal units and up to 15 scenarios. A similar model is considered in Asensio and Contreras (2016) where the used risk measure is a CVaR and the usual linear reformulation of CVaR (Rockafellar and Uryas’ev 2000, 2002) is used to obtain a MILP formulation.

In Cerisola et al. (2009) a weekly UC model is studied wherein profit of a GENCO depends on bids made on the market. The GENCO is assumed to have a non-linear non-convex effect on market prices, modeled through the use of piece-wise linear functions and binary variables. The corresponding model is solved using a MILP solver, Lagrangian decomposition and two variants of Benders’ decomposition (taken from Cerisola 2004). The computed production schedule is a first stage decision, whereas all other stages and nodes in the scenario tree refer to different realizations of market settling. The Benders-based decomposition approaches are found to be the most interesting, despite the substantial implementation effort.

In Gazafroudi et al. (2017), a strategy to apportion expected reserve provision costs between the participants of electricity markets (GENCOs, TSOs, wind farm owners and customers) is employed using a two-stage stochastic program. The strategy is developed based on the concept that stakeholders should pay for the reserve that they generate the need for. As such, uncertainty from wind power generation, demand, transmission line outages and generator failure are considered in the model. A somewhat related work is that of Wang and Hobbs (2016), where a two-stage stochastic model is used as a yardstick to evaluate the impact of market instruments for buying ramp capacity (“flexiramp”). The stochastic model is based on a quite simple bUC on 15-min intervals, restricted to “fast” units, and it is compared with a deterministic variant with constraints representing the flexiramp instruments.

The 2-stage unit commitment model presented in Geng et al. (2018) adopts the usual framework of restricting integer variables to the first stage, but considers uncertainty on the total amount of emission of certain pollutants (since electrical generation is not alone to generate these pollutants). A 25 unit system is solved while considering 30 scenarios by using a “monolithic” MILP solver. DR is considered in Sahebi and Hosseini (2014), but only a 6-bus model is solved. Uncertainty on gas supply and prices and their effect on gas-power units are considered in a 2 stage stochastic UC framework in Zhao et al. (2017).

In Corchero et al. (2013) a two-stage model is considered where commitment decisions and bid prices are first-stage decisions, while total generation and energy matched in the day-ahead market are second-stage decisions (continuous variables). Uncertainty is mainly relative to the spot price, that enters in the generators objective function. The formulated MIQP has a quadratic second-stage cost function, which is linearized by means of perspective cuts (Frangioni and Gentile 2006a). The resulting problem with 10 scenarios and 9 thermal units is solved with a MIQP solver. In this vein we also cite Wang et al. (2008), where the second stage ED, involving wind generation, is used for adding feasibility cuts to the first stage master problem. The main focus here is on deriving “robust” commitment decisions. Further tricks to get complexity down in 2-stage stochastic UC is by playing with the discretization of time as in Bakirtzis and Biskas (2017); the authors then employ a rolling horizon strategy to test the 2-stage model against a deterministic model.

A somewhat different model is proposed in Kia et al. (2017). The peculiar aspects are the presence of Combined Heat and Power (CHP) units, which imply the presence of constraints about heat generation in addition to electricity generation and of energy storage devices, and the inclusion in the model of DR aspects, under the form of Load Commitment programs whereby users can submit hourly offers for decreasing their energy consumption. The considered number of scenarios is small and the solved instances contain only up a few tens of units, but $N - 1$ fault resilience is considered in the second stage; the corresponding monolithic MILP models are solved quite efficiently with off-the-shelf tools.

Since direct attempts to solve multi-stage (or even 2-stage) stochastic UC as a “monolithic” MILP are rare, it is worthwhile to mention (Jiang et al. 2016), where several valid inequalities are developed to improve the solution capabilities of a direct MILP approach. This allows to solve a 9-stage UUC on a binary tree and a 7-stage UUC on a ternary tree, each with 30 generators.

4.2.2 Scenario decomposition

In Takriti et al. (1996) progressive hedging is used to solve a large-scale bUC with 100 thermal units and 6 hydro ones. Recent dedicated progressive hedging methods are developed in Cheung et al. (2015). A SD scheme is presented in Carøe et al. (1997) and Carøe and Schultz (1998) for solving a two-stage bUC problem (with only a few thermal units), wherein integer variables are restricted to the first stage. The non-anticipativity constraints are dualized by using Lagrangian multipliers, and the overall scheme is inserted into a B&B procedure in order to ensure that an optimal solution is obtained. In Papavasiliou et al. (2011) SD is used, the focus being on reserve requirements in a system with high wind penetration. In Papavasiliou and Oren (2012) the uncertain renewable production is coupled with DR in a market environment. In Papavasiliou et al. (2013) SD is again used to solve a UUC where the uncertainty is caused by wind power generation, taking into account the network constraints. A decomposition approach mixing scenario and Benders’ decomposition is considered in van Ackooij and Malick (2016) which heavily relies on classical tools in deterministic UC (LR, Lagrangian-based primal recovery heuristics and Bundle methods) and needs no specific assumptions on the set of technically feasible schedules; a real-life problem with 136 thermal units, 22 hydro valleys, 96 times steps and 50 scenarios is solved. Relaxing the non-anticipativity constraints is also the approach of Schulze et al. (2017) for multi-stage UUC; the scheme uses a Dantzig–Wolfe master problem with (bundle-like/proximal) stabilization and efficient primal recovery heuristics that allow to obtain very good quality solutions. The non-anticipativity constraints can also be partially relaxed as suggested in Uçkun et al. (2016), where scenarios are regrouped into buckets, within which the constraints are enforced, while they are relaxed across buckets.

Starting from a 2-stage stochastic UC, also accounting for OPF, (Wang and Fu 2016) use variable duplication, augmented Lagrangians and the auxiliary problem principle to decompose the original problem into several sub-problems which can then be processed in parallel; large systems are considered, but with only 20 scenarios. A related approach is that of Papavasilou et al. (2015), where a two-stage stochastic UC (with OPF) is solved with high-performance computing employing a parallel LR algorithm. The modelled region is comprised of the California Independent System Operator operated system, as well as its interconnection with the Western Electricity Coordinating Council. The use of high-performance computing for the parallel implementation of the LR is found to reduce computational times of stochastic models to a level that may become acceptable from an operational perspective. Moreover, results indicate that reducing the duality gap of the Lagrangian Relaxation renders similar benefits to increasing the size of the scenario set.

4.2.3 Unit (stochastic) decomposition

The standard UD approach is proposed in Carpentier et al. (1996) for a bUC with 50 thermal units; the demand constraints are relaxed, resulting in stochastic sub-problems which are then solved by DP.

In Römisch and Schultz (1996) a multi-stage hydro-thermal UC problem is considered with random customer load. The load is observed after having chosen the commitment decisions, but the actual generation levels (including continuous hydro generation) are determined once that the load is known. The demand constraint is dualized in a general probabilistic space setting, then the probability measure is discretized; no numerical results are presented.

A multi-stage stochastic programming is proposed in Nowak and Römisch (2000) to deal with a hydro-thermal UC with 25 thermal units and 7 hydro units. Load uncertainty is addressed through the use of UD and DP for solving the stochastic sub-problems; Lagrangian heuristics are then used to recover a primal solution. Similar UD approaches are considered in Dentcheva and Römisch (1998), Nowak (2000) and Gröwe-Kuska et al. (2002).

In Takriti et al. (2000), three uncertainty factors are integrated in the UC problem: load, fuel and electricity prices. The fuel requirement problem basically becomes the second stage of the problem, the first one being a bUC formulation. A Benders’ decomposition approach is used to plug the second-stage cost function into the first stage, and a LR approach is used for the first stage. This method is tested on a UUC with 33 thermal units and about 729 demand scenarios.

In Bacaud et al. (2001) a weekly (10 days up to a month) stochastic UC problem is considered. A UD approach is employed, where the LD is solved by a disaggregate Bundle method. The approach associates a set of weights with each node that effectively precondition the LD; this preconditioning is reported to be crucial for performances. Problems having up to 2000 nodes are solved with the generating units of EDF.

A weekly two-stage UUC is also addressed in Schultz et al. (2003). Both stages have all time steps, and each is a bUC problem; load, price and cost uncertainty are revealed between the two. The problem is decomposed using a LR-based approach that yields a stochastic programming problem for each unit. Lagrangian heuristics based on Zhuang and Galiana (1988) and Gollmer et al. (1999) are employed to recover a primal feasible solution. A similar methodology is considered in Nowak et al. (2005), where a MILP for market price settling and bidding in a competitive environment is also presented: to incorporate both features into a single model, bid/offer decisions and first day commitment decisions are in a first stage, while all other variables are second-stage ones. Also Ni et al. (2004) has a focus on market mechanisms, wherein commitment decisions and offer curves are first-stage decisions and dispatch are later stage ones; the problem is solved by applying a global LR-based UD.

In Nürnberg and Römisch (2003) stochastic Lagrange multipliers are used in order to decompose uncertain demand constraints that have to hold almost surely. The resulting dual function is the expectation of this stochastic Lagrange function. Uncertainty is then discretized into a finite set of random drawings in order to approximate the expectation, and Bundle approaches are used to solve the dual. In this two-stage procedure, integer variables remain present in the second stage.

In Shiina and Birge (2004) the UD approach to the stochastic bUC with uncertain demand is revisited in terms of Dantzig–Wolfe decomposition (the equivalence between this and a LR approach solved by CP being well-known). This results in a column generation approach where the Lagrangian subproblem, solved by DP on the scenario tree, generates schedules for each unit that are added to the restricted master problem. The recent Shiina et al. (2016) considers a deterministic version of this problem solved through a Dantzig–Wolfe-like decomposition scheme; a 10 unit system and up to 72 time instants are considered.

4.2.4 Benders(-like) decomposition

The L-shaped method can be used to decompose UC problems with several stages. In its basic version a single cut is added to the first stage problem, whereas in advanced versions multiple cuts (e.g., one for each subproblem) can be added. This may increase convergence speed at an increased master problem cost; we refer to the discussion in Birge and Louveaux (1988) and Birge and Louveaux (1997) on this topic. The recent on-demand accuracy bundle methods (de Oliveira and Sagastizábal 2014; van Ackooij and Frangioni 2018) can be thought to provide a tradeoff between the multi-cut and mono-cut versions (Fábián 2013).

In Xiong and Jirutitijaroen (2011) another approach is proposed for finding such a trade-off. In this method, which is applied to a stochastic UC with load and generation uncertainty, scenarios are divided into (homogeneous) groups and cuts are derived for each group, as proposed in Trukhanova et al. (2010). Consequently, the dimension of the master problem is smaller in comparison with the classical multi-cut algorithm, while less information is lost compared to the single cut version. The authors also claim that heterogeneously grouping the scenarios may result in even better CPU time. Results are presented for a large-scale thermal UC with ramp rates and spinning reserves.

In Archibald et al. (1999) short-term cascaded reservoir management—as opposed to the more traditional approach where reservoir management is considered to be a mid-term problem—is considered wherein the gain function is explicitly given and depends on the water level and turbined quantity. Uncertainty is modeled as a Markov chain having 6 states per time step, which is expanded onto a scenario tree in order to allow for an LP formulation of the problem. This approach is compared with DP, nested Benders’ decomposition (closely related to SDDP) and a decomposed DP approach, which essentially efficiently samples the state space. Nested Benders’ decomposition is found to be computationally the most efficient approach.

Benders’ decomposition is compared with MILP approaches in Cerisola et al. (2009) (cf. Sect. 4.2.1) and proves to be in general preferable. In Wang et al. (2013), Benders’ decomposition is used to address UC problems under wind uncertainty. The authors use sub-hourly time steps (10, 15 or 30 min) to account for rapid variations in renewable generation. They also modify the standard approach by adding some of the second stage constraints to the master problem. A similar use of Bender’s decomposition for a 2-stage stochastic problem where wind uncertainty is revealed in the second stage can be found in Nasrolahpour and Ghasemi (2015).

In Zheng et al. (2013) a two-stage UC formulation is considered. Similarly to most approaches, load is revealed in between the first and second stage and power output is determined in the second stage, but the latter also contains integer commitment decisions related to quick-start units. The quadratic costs functions are linearized to obtain a MILP formulation. Then, because the second stage contains integer variables, the approach of Sherali and Fraticelli (2002)—essentially a RLT with Lift-and-Project cuts (Balas et al. 1993)—is employed to construct an approximation of the convex hull of the second-stage problem, so that a multi-cut Benders approach can be used to approximate the second stage recourse cost function. A problem with 5 units, up to 2000 scenarios and 16 time steps is solved.

In Papavasiliou and Oren (2013) both LR and Benders’ decomposition are used in a parallel high performance computing environment for solving a network constrained stochastic UC where uncertainty comes from different sources.

Bender’s like decomposition is used in Huang et al. (2014) for a 2-stage model, comprising storage devices and DR, wherein the second stage cost function is seen through a CVaR.

4.3 Robust optimization approaches

An early work using RO techniques is Sarić and Stankovic (2007), where a market clearing problem is considered under some UC-like constraints. The main idea is to use an adaptive RO approach which partitions the uncertainty set and allows decisions to be specific to each subset. The constraints are then weighed in the master problem. The results are compared with traditional RO and a worst-case fully anticipative approach.

In Wang et al. (2011), a RO approach is considered where the uncertainty set on the load is a simple interval, so that methods from interval LP (e.g., Chinneck and Ramadan 2000) can employed together with Benders’ decomposition to solve the model. The main focus of the work is on network security. In Wu et al. (2012), a similar interval uncertainty approach is compared with a scenario-based approach. The results show that the former is very sensitive to the choice of the interval but is quickly solved, whereas the latter yields more accurate solutions but it is more costly to solve. A two-stage model is formulated in Zhou et al. (2014), wherein the second stage is simplified by the use of an interval accounting for the uncertain generation of wind. Another interval-based model focussing on wind uncertainty is proposed in Soroudi et al. (2017), adding DR elements.

In Zhao and Zeng (2012), a 36 unit bUC with ramp rate constraints is considered, which includes wind energy supply and demand behaviour of the customers based on electricity prices. In this two-stage model, wind power enters under the guise of an uncertain budget constraint and the first stage is a day-ahead UC problem, while the second stage is performed once the wind supply is known. The problem is solved by applying Benders’ decomposing to the linearized problem along with a CP algorithm. It is claimed that this model significantly reduces the total cost and can fully exploit the available supply of wind energy. The same approach is employed in Jiang et al. (2014) to solve a 30 unit UC with ramp rates and transmission constraints where demand and supply are considered to be uncertain, and in Jiang et al. (2013) where the objective is to minimize the regret w.r.t. the best possible value obtained in each scenario, as opposed to just the cost of the scenario. In Li et al. (2015), the robust optimization concept of Bertsimas and Sim (2004) is employed in order to value carbon capture technology in the presence of uncertainty on wind generation. A direct MILP approach is used to solve a 2-stage robust model wherein the second stage is dedicated to capturing DR in Liu and Tomsovic (2015).

A two-stage robust aggregate model is proposed in Jin et al. (2017), modelling Energy Intensive Enterprises (EIE) as a generator unit, such that they may be included into unit commitment with little added modelling complexity and without violating EIE privacy issues. EIEs can provide valuable contributions to system operation by adjusting their load and, when on-site generation is available, their generation. The robust aggregate model of the EIEs ensures that any (uncertain) dispatch signal received from the system operator is feasible. The authors employ a column-and-constraint generation scheme, modified to fit the specificities of the robust aggregate model, to solve the problem.

In Bertsimas et al. (2013), the model proposed in Zhao and Zeng (2012) and Jiang et al. (2014) is extended to incorporate spinning reserve constraints, transmission limits and ramping constraints. The focus is on gauging the impact of robustness of the solutions on the efficiency and operational stability of the system. A two-stage adaptive RO model is used where the uncertainty set concerns the nodal net injection at each time period. In the first stage an optimal commitment decision is reached by using Benders’ decomposition algorithm, while in the second stage the associated worst case dispatch cost is calculated. Results from empirical studies with 312 generators have been compared to those of deterministic models with reserve adjustments under three aspects: the average dispatch and total cost, the cost volatility, and the sensitivity of the costs to different probability distributions. The sensitivity of the results to changes in the uncertainty set is not investigated. A very simplified two-stage RO model is investigated in Ben-Salem (2011), where sensitivity to the choice of the uncertainty set is instead explicitly addressed. The recourse cost function is the worst case cost over a specific uncertainty set involving uncertainty on load; a simple recourse assumption makes the second stage trivial. In Minoux (2009) and Minoux (2014) the model of Ben-Salem (2011) is expanded to take into account a huge uncertainty set which admits a representation as a Markov chain. A budget of uncertainty constraint restricts paths to be “not too extreme”; a comparison is made against stochastic programming approaches.

In Street et al. (2011), RO is used for uncertainty on contingency constraints; the resulting optimization problem is reformulated as an equivalent MILP and solved with standard solvers. This work is extended in Wang et al. (2013) by including transmission capacity constraints and by considering a two-stage RO setting. Commitment (and integer) variables are restricted to the first stage so that the second stage becomes a continuous optimization problem, further reduced to an LP by linearization techniques; Bender’s decomposition is used for solving the model. In Jiang et al. (2012) a similar model and solution approach can be found, integrating (interval) uncertainty on wind generation, with a budget of uncertainty limiting conservativeness of the model. Yet another model focussed on wind uncertainty is that of Yu et al. (2015); there, the interval uncertainty is combined with a Markov model for local winds, and the model is solved by a integrating Lagrangian techniques with a B&C. DR uncertainty is added in Zhao et al. (2013); commitment decisions are restricted to the first stage, the three stages of the model are brought down to two by a reformulation, and Bender’s decomposition is again used for solving the problem. By considering a two-stage RO with a specific uncertainty set (box or budget constrained), the authors of Zhai et al. (2017) manage to set up specific scenario reduction methods (envelope scenarios) without losing the guarantee that the solution remains feasible for the original unreduced problem. The main building stone is that each scenario is essentially a convex combination of a set of “extreme” scenario and the recourse problem is convex, thus conveying an appropriate structure. In Zhao and Guan (2013), a convex combination of expected second stage cost and worst-case robust cost is added to the objective function; uncertainty is restricted to load, and Bender’s decomposition is employed for solving the model. The latter model is further investigated in Morales-España et al. (2018), where an efficient reformulation is provided for when the uncertainty set is of box (or budget) type. The main innovation lies in identifying explicitly the worst case elements in the uncertainty set. A two-stage model wherein the objective function consists of a worst-case recourse cost and an expected value is also considered in Blanco and Morales (2017), where ad-hoc scenario reduction schemes and a column-and-constraint generation scheme are developed to solve the formulated problem. By considering a weighted sum of several worst case objective functions over different uncertainty sets, or by including specific targets for such worst case costs, the authors of An and Zeng (2015) provide further variants of two-stage robust optimization. Differently from most two-stage approaches, in Ye and Li (2016) dispatch decisions are first-stage ones, with the second stage variables then interpreted as variations w.r.t. the original dispatch decisions (this was already proposed in van Ackooij and Malick 2016); column-and-constraint generation is used to solve the resulting problem.

In Aïd et al. (2006), a RO approach to the management of electricity power generation is presented using concepts borrowed from classic risk management, i.e., Value-At-Risk. In Guigues (2009) a RO with the Affinely Adjustable Robust Counterpart (AARC) approach (Ben-Tal et al. 2003) is proposed to the longer term electricity production management. AARC is a restricted and more tractable version of the Adjustable Robust Counterpart (ARC), where recourse variables are allowed to depend on the values of uncertain parameters, but only in an affine way; the hypotheses are set up in such a way that the resulting problem has a MILP deterministic equivalent, which is then solved by a MILP solver. The same methods are looked at in Warrington et al. (2013) to define affine reserve policies which establish in advance how the power has to vary as a (simple, affine) function of the prediction error (typically due to uncertain renewable generation) w.r.t. the baseline scenario. Although not strictly a UC problem, we mention that AARC has been used for weekly hydro reservoir management under uncertainty on inflows in Apparigliato (2008) and Babonneau et al. (2010), where comparisons with sliding deterministic approaches are presented. Finally, in Jabr (2013) an adjustable robust OPF is suggested.

Interval Unit Commitment (IUC), a research branch highly related to RO, schedules units such that the cost of serving the most probable load is minimised, while guaranteeing that commitment schedules are robust to load realisations within an range of the central forecast. The work proposed in Pandžić et al. (2016) aims to limit the conservativeness of IUC schedules, given that they must be able to meet ramping requirements (of very low probability) arising from the transitions from the lower bound to the upper bound scenarios, and vice-versa. As such, the authors propose a new UC formulation by which maximum ramp trajectories from stochastically-generated scenarios are imposed as ramping limits within the IUC model. Tests conducted on the IEEE RTS-96 system (Reliability Test System Task Force 1999) indicate that the proposed methodology leads to more cost effective and less conservative schedules than in standard RO and IUC formulations.

4.4 Chance-constrained optimization approaches

In many optimization problems involving a final observation of uncertainty for which no recourse actions exist, feasibility for all constraints cannot be guaranteed. Rather, one has to provide solutions which are “reasonably feasible” under all except the most unlikely random outcomes. This is also the case in UC, where, for instance, one cannot actually guarantee that the demand constraints will never be violated. This is therefore an ideal setting for CCO, where the desired safety level can be specified under the form of a probability. Two approaches are possible: either the safety level is set for each constraint (e.g., time step) individually, giving an Individual CCO program, or for the system as a whole, resulting in a Joint CCO program. While the ICCO is obviously less robust than the JCCO (see the discussion in van Ackooij et al. 2014, 2018 in the context of UUC), the latter is in general significantly more difficult to solve, especially if one wishes to do this exactly (i.e., without artificially discretizing the underlying random vectors or approximating the probabilistic constraint). This explains why CCO (either Individual or Joint) models are the least employed in the literature on UC. However, it should be noted that these approaches have indeed been used in related problems such as power expansion and transmission ones (Sharaf and Berg 1982; Shiina 1999; Anders 1981), which need be formulated on a much longer time horizon than commonly considered in UC, and therefore crucially require taking uncertainty into account (Shiina 1999).

Individual CCO was applied for the first time in Ozturk et al. (2004) to solve a 100-units bUC where the uncertainty of load has to be met with a high probability. The problem is then decomposed by using LR, and the subproblems are solved by DP. The results show that solving the CCO UC produces better (less costly) solutions than a deterministic UC with spinning reserves requirements. Computing and scheduling reserve requirements is the topic of Ortega-Vazquez and Kirschen (2009) and Ahmadi-Khatir et al. (2013). In Pozo and Contreras (2013) a probability constraint is used for this purpose; the resulting model is solved by employing a sample-based approximation. A similar solution methodology is employed in Saravanan et al. (2014), where the authors consider an inner approximation (thus potentially very conservative) of a joint probability constraint by a set of individual probability constraint. They thus neglect in the process any temporal correlations in the load; furthermore, since uncertainty is assumed Gaussian, they fail to exploit the fact that the set defined by the joint probability constraint is actually convex. A similar methodology, based on ICCO to compute accurate endogenous reserve levels is used in Lujano-Rojas et al. (2016) and Bruninx and Delarue (2017).

In Ding et al. (2010), a ICCO UC model is formulated where different sources of randomness are considered: demand fluctuation, thermal units outage, uncertainty of wind generation and the schedule of flexible generating units. The authors claim that the proposed model could be extended to basically any stochastic factor. The individual chance constraints are converted into a deterministic model using the central limit theorem to recover a Gaussian model of uncertainty for outages; a standard MILP approach is then used to solve the problem. Again, the results are compared with those of a deterministic UC formulation. Uncertainty in wind generation is the main factor accounted for in Restrepo and Galiana (2011). The resulting ICCO model is reformulated linearly by assuming random wind generation to result from a discrete distribution (we also refer to Billinton et al. 2009 for more on modelling wind uncertainty in itself). In Wu et al. (2014) an ICCO UC model is also considered, but violated network constraints are added through the use of a separation oracle.

A stylized HUC model under joint probabilistic constraints has been considered first in Zorgati and van Ackooij (2011). The main focus there lies on dealing simultaneously with probabilistic constraints and binary variables. The suggested approach relies on the fact that some inequalities in the random system are more likely to be binding than others, which provides an ad-hoc way of reducing the difficulty for the JCCO (the experiments of van Ackooij et al. 2014 provide a rationale behind this approach). The reduced joint probabilistic constraint is then outer approximated by individual probabilistic constraints selecting appropriate weights. Finally, by using Hoeffding’s inequality outer and inner approximations of these individual probabilistic constraints can be obtained; the resulting binary conic programming problem can be solved with a standard solver.

Joint probabilistic constraints in HUC are dealt with exactly for the first time in van Ackooij (2014). Two sources of uncertainty are considered: randomness on load and on inflows for hydro reservoirs. In order to solve the JCCO UC problem, various decomposition approaches are investigated, among which LR and various forms of AL approaches.

In Bienstock et al. (2014) a DC OPF using an individual CCO approach is proposed considering the uncertainty of renewable generation. Under appropriate assumptions on the underlying uncertainty distribution, and by reformulating the bilateral individual probabilistic constraints as two unilateral ones, the resulting problem can be shown to be equivalent to a second order cone problem; the conic constraints are then linearized by using a cutting planes approach. A real life instance over the 2746 bus Polish network is solved. It is interesting to note that such a network application with joint probabilistic constraints would give rise to differentiability issues, essential for the application of first-order methods; we refer to Henrion and Möller (2012) for a thorough discussion of differentiability and an application to a stylized network problem.

In the recent van Ackooij et al. (2018), classic methods are developed and adapted from CCO to handle integer variables for a UC problem under uncertainty on wind generation, while accounting for a DC network. The method differs from the one considered in Arnold et al. (2014), where a cutting-plane based methodology (for the convex continuous part) is inserted in a Branch & Bound solver directly, i.e., in each node of the B&B tree a convex optimization problem has to be solved. In contrast, in van Ackooij et al. (2018) the approach is inverted: in each iteration of a cutting-plane-like method, two MILPs are solved, one of which defines the next iterate and a lower bound, while the other provides a feasible solution and thus an upper-bound. The methodology is shown to scale up to a 46-bus system in a HUC problem.

Recent investigations involving probability constraints focus in the combination of this concept and that of recourse. The more involved situation is the one wherein second stage information is handled through a probability constraint, for instance when second stage feasibility is only requested with a certain probability. These ideas date back at least to Prékopa (2003, Sect. 4), but have received a recent boost through advances in integer programming, e.g., (Liu et al. 2016). The “gained tractability” mostly stems from the discrete character of the underlying random vector. In the continuous case, the analytical properties of so-called dynamic chance constraints are not sufficiently clear yet and algorithms, to the best of our knowledge, are in their infancy. Far simpler combinations of chance constraints and recourse are problems wherein only first stage variables are further constrained in probability. Already, in Wang et al. (2012) a two-stage JCCO UC is considered with a joint probabilistic constraint for the use of wind power. The probabilistic constraint is not dealt with directly, but is discretized using a sample average approximation approach (e.g., Luedtke and Ahmed 2008; Luedtke 2014). A further example is given in Wu et al. (2016), where the authors consider a series of “individual” chance constraints with right-hand side uncertainty. The random data is assumed to follow a truncated Gaussian distribution (see also Diniz and Henrion 2017 for a deeper study of truncation on classic convexity and differentiability results). Through usual reformulations the probability constraints are recast into a deterministic equivalent. In Zhang et al. (2017), the authors instead consider the former concept of asking feasibility in the second stage offer-demand balance with a given probability. Rather than using a big-M formulation, the inequalities are multiplied with the associated binary variable; all resulting bilinear terms are linearized through the usual McCormick linearization techniques. A Bender’s like decomposition scheme is also proposed wherein violated inequalities are added progressively. In view of the above, we refer to Adam and Branda (2016) that carefully investigates the properties of the problem resulting when multiplying inequalities with binary variables rather than using usual big-M formulations to handle sample based chance constraints. A dedicated Benders’ like algorithm is even suggested in Adam et al. (2018). The work Zhao et al. (2014) considers using a chance constraint involving second stage variables, but also a constraint in expectation. By considering a finite set of scenarios, the former is handled through a big-M reformulation and the second is immediately reformulated. The authors consider a scheme of generating new scenarios to update the original set progressively.

Finally, it is worthwhile to note that stability theory for CCO is developed in Römisch and Schultz (1991); stability results provide an answer to the important question of how model results (cost or even solution sets) vary with respect to changes in the underlying distribution of the random vector. An application of stability results in the context of a simple recourse model is given as early as Römisch and Schultz (1993) and Gröwe et al. (1995); for more recent research we refer to Römisch (2003), Henrion and Römisch (1999), Henrion and Römisch (2004), Henrion et al. (2008, 2009) and references therein. In particular, the authors explicitly consider stability results for probabilistically constrained power dispatch models, showing that the models are stable for several underlying distributions of the load, such as discrete or multi-variate Gaussian. However, no computational results are presented.

We finish by pointing out two recent streams of theoretical investigations involving probability constraints that may in the future significantly extend the scope of its applicability in the exact form (that is, without approximations). These involve recent insights into differentiability, providing efficiently implementable formulae for gradients (van Ackooij and Henrion 2014, 2017; van Ackooij et al. 2017; Hantoute et al. 2018), and recent insights in convexity (Henrion and Strugarek 2008, 2011; van Ackooij 2015; van Ackooij and de Oliveira 2016; van Ackooij and Malick 2017; van Ackooij et al. 2018; Farshbaf-Shaker et al. 2017). The use of these methods has already proven succesful in the study of gas networks (Gotzes et al. 2016).

5 Concluding remarks

The Unit Commitment problem could be considered an archetypal example of what makes optimization techniques both relevant and challenging.

UC regards the optimal use of a highly valuable resource, energy, whose importance has possibly never been more strongly felt than in the present times. On the one hand, energy is a primary driver of, and a necessary requirement for, economic growth and improvement of peoples’ living conditions. On the other hand, fair and sustainable energy production and distribution raises enormous technical, economical, organizational, and even moral challenges. While optimization techniques (and in particular their strict subset regarding the UC problem) alone cannot clearly solve all these issues, they can indeed give a significant contribution to the improvement of the efficiency of the energy system, with a substantial positive economical and environmental impact.

From a technical perspective, UC arguably exhibits almost all possible characteristics that make an optimization problem extremely challenging. For a start it is not even a well-defined problem, but rather a large family of related problems that are as varied as the electrical systems worldwide. In almost all cases the problem is large- to very-large-scale, nonlinear, nonconvex and combinatorial. Thus, researchers continuously struggle between two contrasting needs: on the one hand providing more and more accurate models of the highly complex electrical systems, in order to allow better practical decisions, and on the other hand providing answers in the “unreasonably short” timeframe required by the actual operating environment. Furthermore, and perhaps more importantly for the present work, the operation of the electrical system requires a very articulate decision chain that spans from the decades (strategic decisions about the investments in new generation and transmission equipment, and even about funding of research capable of producing better ones) to the split-second range for on-line tracking of actual demand. This in turn means that uncertainty on the actual future status of the electrical system, and therefore on the consequences of the decisions that have to be taken here and now, is inherently present at all levels of the decision chain. This justifies the interest for techniques capable of dealing with uncertainty in energy optimization problems, and in particular in UC; hence the significance of this survey.

While UC cannot be presently considered a well-solved problem, and much less so UUC (which has arguably been tackled only relatively recently), research on such an extremely challenging problem will likely have positive side-effects. Indeed, the tools and techniques that will be developed will almost surely find applications in many different fields, other than the optimal management of the energy system. This has already happened for the methodological and algorithmic developments of Prékopa et al. (1978), Feltenmark and Kiwiel (2000), Daniildis and Lemaréchal (2005) and Frangioni and Gentile (2006a), that were motivated by the study of UC, but have since been applied to a much broader set of problems. We are confident that the study of UUC will lead, together with practical improvements on the efficiency and safety of electrical systems, to an analogous development of new ideas and techniques that will be beneficial for many other fields. Therefore, as a small stepping stone for researchers interested in broadening their knowledge in UUC, we hope that this survey may prove useful.