A branch-and-cut algorithm for the maximum covering cycle problem

Abstract

In many applications, such as telecommunications and routing, we seek for cost-effective infrastructure or operating layouts so that many nodes (e.g., customers) of a support network (typically modeled by a graph) are covered by, or at least are easily reachable from, such a layout. In this paper, we study the maximum covering cycle problem. In this problem we are given a non-complete graph, and the goal is to find a cycle, such that the number of nodes which are either on the cycle or are adjacent to the cycle is maximized. We design a branch-and-cut framework for solving the problem. The framework contains valid inequalities, lifted inequalities and a primal heuristic. In a computational study, we compare our framework to previous work available for this problem. The results reveal that our approach significantly outperforms the previous approach. In particular, all available instances from the literature could be solved to optimality with our approach, most of them within a few seconds.

1 Introduction

Covering and domination problems in graphs have attracted the interest of researchers since at least the 1970s. In such type of problems we are concerned with finding a subset of the nodes S of an input graph, such that a certain set of nodes are covered or dominated, i.e., either by belonging to S or by being adjacent to S. There exist many different versions of such problems, depending on topological constraints on S (e.g., it may need to form a tree or cycle), the nodes that are required to be covered, the objective function and, eventually, additional side constraints. While historically the focus has been on theoretical properties (see, e.g., Colbourn and Stewart (1991), Haynes et al. (1998), Kratochv et al. (1998)), recently, computational studies as well as the applications associated to these problems (ranging from telecommunication network design to facility location) have also been addressed (see, e.g., Aazami (2010), Bley et al. (2017), Jeong (2017)).

In this paper we look at the maximum covering cycle problem (MCCP), which was recently introduced by Grosso et al. (2016). The problems is defined as follows. Let $G=(V,E)$ be an undirected graph and $C \subseteq V$ be a cycle in G. The cycle C is said to cover a node $v \in V$, if either v is on the cycle C or it is adjacent to it. The goal of the MCCP is to find a cycle in G, which covers the maximum number of nodes. Let ${\mathcal {C}}$ be the set of all cycles of G and $f(V')=\{v \in V | v \in V' \vee \exists \{v,v'\} \in E: v' \in V' \}$. The problem, which was shown to be NP-hard in general graphs, can be formally stated as

$$\begin{aligned} \max |f(C)| \\ s.t., \quad C \in {\mathcal {C}}. \end{aligned}$$

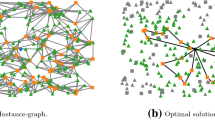
Note that the problem is trivial in complete graphs, as any single node covers all other nodes. It is also trivial if the graph is a star, as the center node of the star covers all nodes. Moreover, if the graph contains a Hamiltonian cycle, this Hamiltonian cycle is (one) optimal solution. Figure 1 shows an instance of the problem and a feasible solution.

Fig. 1

An exemplary instance and a feasible solution for the MCCP. The nodes covered in the solution are black, and the cycle constituting the solution is given by the black edges. a Instance of the MCCP. b Solution of the MCCP

To solve the MCCP, the authors of Grosso et al. (2016) propose a cutting plane approach based on Integer Linear Programming (ILP), which we briefly sketch in the following. Let binary variable $u_i\in \{0,1\}$ be a binary variable so that $u_i=1$ iff node $i \in V$ is covered by the cycle, and let $w_i\in \{0,1\}$ be a binary variable so that $w_i=1$, iff node $i \in V$ is on the cycle. Let A be the set of arcs obtained by bi-directing the edges E, i.e., $A=\{(i,j),(j,i): \{i,j\} \in E \}$. Thus, let $x_{ij}\in \{0,1\}$ be a binary variable, so that $x_{ij}=1$ iff arc (i, j) is on the cycle. The following formulation for the MCCP follows classic modeling techniques from, e.g., the asymmetric traveling salesman problem (ATSP, see, e.g., Balas (1989)), and the generalized TSP (see, e.g., Fischetti et al. (1997));

$$\begin{aligned} \max \quad \sum _{i \in V} u_i&\end{aligned}$$

(1)

$$\begin{aligned} s.t. \quad \quad x_{ij}+x_{ji}&\le 1 \quad \forall \{i,j\} \in E \end{aligned}$$

(2)

$$\begin{aligned} w_i +\sum _{j: \{i,j\} \in E} w_j&\ge u_i \quad \forall i \in V \end{aligned}$$

(3)

$$\begin{aligned} \sum _{(i,j) \in A} x_{ij}&=w_i \quad \forall i \in V \end{aligned}$$

(4)

$$\begin{aligned} \sum _{(j,i) \in A} x_{ji}&=w_i \quad \forall i \in V \end{aligned}$$

(5)

$$\begin{aligned} \sum _{i \in S} \sum _{j \in V \setminus S} x_{ij}+\sum _{j \in S} \sum _{j \in V \setminus S} x_{ij}&\ge 2 (w_k+w_l-1) \nonumber \\&\forall S \subset V, k \in S, l \in V \setminus S: 2 \le |S| \le |V|-2 \end{aligned}$$

(6)

$$\begin{aligned} u_i,w_i\in \{0,1\},\;\forall i \in V\;&\text{ and }\; x_{ij}\in \{0,1\},\;\forall (i,j) \in A \end{aligned}$$

(7)

Constraints (2) ensure that, for each edge, only one of the arc-variables $x_{ij}$ and $x_{ji}$ is taken. Constraints (3) make sure that either node i or at least one of its adjacent nodes is in the cycle, if i is chosen as covered. Constraints (4) and (5) ensure that every node on the cycle has exactly one ingoing and outgoing arc, respectively. Constraints (6) are cut constraints. These constraints are of exponential size. Finally, constraints (7) provide the variables nature. In the approach proposed in Grosso et al. (2016), the authors remove the subtour or cycle elimination constraints (6) to obtain a compact formulation. Integer solutions to this relaxed formulation give a set of disjoint cycles. Hence, their algorithm works by iteratively solving the relaxed formulation (to integer optimality). The cycle giving the largest coverage is stored as incumbent solution, and the constraints forbidding the cycles found in the previous iterations are added. The algorithm terminates when the objective of the relaxed formulation (with the added cycle elimination constraints) is larger then the objective of the incumbent. Note that this proves optimality of the incumbent and that the algorithm is finite. The authors enhance their approach by heuristically creating additional cycles, for which the corresponding cycle elimination constraints are also added.

Contribution and Paper Outline In this paper, we develop a solution framework for the MCCP based on ILP. The framework is based on an exponential-sized ILP formulation, which is solved by means of a branch-and-cut scheme. A computational study on instances from the literature and additional instances is carried out in order to assess the efficiency of our approach. The study shows that our algorithm outperforms the approach by Grosso et al. (2016). Moreover, most of the instances can be solved within a few seconds.

In the remainder of this section, we discuss related work. In Sect. 2 we present our ILP model along with additional valid inequalities. Section 3 contains the description of our algorithmic framework, including separation algorithms and a primal heuristic. The computational results are discussed in Sect. 4. Finally, concluding remarks are presented in Sect. 5.

Related Work As already mentioned in the introduction, connected covering and domination problems have been studied for a long time. Depending on the application, authors seek for different covering (resp. dominating) topologies and coverage (resp. domination) protocols.

Complementary, there are of course many problems in literature which are concerned with finding cycles in a graph, being the travelling salesman problem (TSP) the most famous of them (see, e.g., Dantzig et al. (1954), Hoffman et al. (2013)). In the TSP, we look for a minimum cost Hamiltonian cycle through all the nodes in the graph. A variant of the TSP, with covering aspects, is the covering salesman problem (CSP), in which the goal is to find a minimum cost cycle (a tour), such that every node in the graph is within a certain distance from the cycle. The problem has been introduced by Current and Schilling (1989), where a heuristic is presented. An approximation algorithm for the geometric version of the CSP is presented in Arkin and Hassin (1994), and multi-objective variants of the problem are considered in Current and Schilling (1994). Furthermore, generalized versions of the CSP have been proposed, for instance, in Golden et al. (2012), Ozbaygin et al. (2016) and Shaelaie et al. (2014). In Gendreau et al. (1997), the covering tour problem (CTP) is presented. In the CTP, we are concerned with finding a minimum cost tour, which must go through a given subset of nodes, while the remaining nodes may or may not be on the tour. A bi-objective variant of the CTP is studied by Jozefowiez et al. (2007).

We note that TSP-like problems are usually defined on a complete graph. The MCCP is of course trivial on such graphs, as any single node already covers all the nodes. From the algorithmic point-of-view, our approach also shares similarities with ILP approaches for the connected dominating set problem (see, e.g., Gendron et al. (2014)), the Steiner tree problem (see, e.g., Fischetti et al. (2017), Koch and Martin (1998)), or the connected facility location problem (see, e.g., Gollowitzer and Ljubić (2011), Leitner et al. (2017)).

2 ILP-Model and Valid Inequalities

Our approach is based on a slightly different ILP formulation compared to the one proposed in Grosso et al. (2016). In our formulation, we do not bi-direct the edges and, instead, work on the original graph. We redefine binary variables $x_{ij}\in \{0,1\}$, so that $x_{ij}=1$ iff edge $\{i,j\} \in E$ is in the cycle. Additionally, let $y_i\in \{0,1\}$ be binary variables such that $y_i=1$, if node i is on the cycle; and let $z_i\in \{0,1\}$ be binary variables so that $z_i=1$, if node i is not on the cycle, but covered by the cycle (i.e., it is covered by being adjacent to a node on the cycle). Finally, for $S \subset V$, let $\delta (S)= \{ \{i,j\} \in E: i \in S, j \in V \setminus S\}$. Considering all these elements, our formulation reads as follows:

The objective function (OBJ) is the sum of nodes directly on the cycle, and the additional nodes covered by the cycle. Constraints (YZ) ensure, that a node cannot be both on the cycle, and covered by adjacency to the cycle. Constraints (COV) ensure that if a node i is selected to be covered by adjacency to the cycle, at least one adjacent node of i is in the cycle. Constraints (DEG) ensure that every node on the cycle has two adjacent edges. The subtour-elimination constraints are encoded by (SEC); since there is an exponential number of them, we separate them on-the-fly. The separation procedure is described in Sect. 3.1.

The following so-called logic inequalities (see, e.g., Fischetti et al. (1997), Fischetti et al. (1999)) are valid for our formulation;

$$\begin{aligned} x_{ij} \le y_i, \quad \forall \{i,j\} \in E, i \in V. \end{aligned}$$

(LOG)

Moreover, the cut constraints (SEC) can be lifted in some cases, as detailed by the following proposition. For $V'\subset V$, let $K(V')=\{v \in V| v \in V' \cup v: \exists \{v,v'\} \in E: v' \in V'\}$, i.e., the set $V'$ and all nodes adjacent to it.

Proposition 1

Let $S \subset V, k \in S, l \in V \setminus S: 2 \le |S| \le |V|-2$. Suppose, $K(k) \subseteq S$. Then the following inequalities are valid

$$\begin{aligned} \sum _{ e \in \delta (S)} x_e \ge 2 (y_k+z_k+y_l-1). \end{aligned}$$

(L-SEC)

Proof

Due to constraints (YZ) only one of $y_k$ and $z_k$ can be one in a feasible solution. If $y_k$ is one, the inequalities reduce to inequalities (SEC). If $z_m=1$ for one $m \in K$, we must have $y_m=1$, due to (COV). As $m \in S$, any feasible solution must fulfill (SEC) defined by m, k and S, from which follows the validity of (L-SEC). $\square$

Let $L=\{v \in V| \{l,v\} \in E \}$. If $L \subseteq V \setminus S$, using the same arguments, (L-SEC) can be further lifted by additionally adding $z_l$ to the term in the parenthesis on right-hand-side. Moreover, if a feasible solution to the problem is available, an additional lifting is possible as shown in the following proposition.

Proposition 2

Let $S \subset V, k \in S, l \in V \setminus S: 2 \le |S| \le |V|-2$. Let ${\bar{Z}}$ be the objective value of a feasible solution. If $|{\bar{Z}}|>|K(V \setminus S)|$, then there exists one optimal solution which satisfies

$$\begin{aligned} \sum _{ e \in \delta (S)} x_e \ge 2 y_l. \end{aligned}$$

(L2-SEC)

Proof

Due to $|{\bar{Z}}|>{|K(V \setminus S)|}$, the optimal solution cannot be a cycle on the nodes in $V \setminus S$ (plus nodes adjacent to this cycle). Thus, at least one node in S must be in an optimal solution. $\square$

If $|{\bar{Z}}|>{|K(S)|}$, a similar lifting is possible. If both $|{\bar{Z}}|>{|K(V\setminus S)|}$ and $|{\bar{Z}}|>{|K(S)|}$, the right-hand-side in (L2-SEC) can be lifted to two; this means that a solution with objective value of at least ${\bar{Z}}$ cannot be a cycle contained only in S or $V\setminus S$, but must contain nodes from both S and $V\setminus S$. Finally, if it holds that $|{\bar{Z}}|>{|K(V\setminus S)|}$ and $|{\bar{Z}}|>{|K(S)|}$, then inequalities (L2-SEC) can also be lifted by using the arguments of (L-SEC) for node l; in this case, the term $2z_l$ can be added to the right-hand-side.

3 Algorithmic Framework

In this section, we give implementation details of our algorithmic framework. Namely, we give details of the separation procedure for inequalities (SEC) (and its lifted versions), and also the primal heuristic. In contrast to TSP-like problems, where inequalities (LOG) are usually separated by enumeration, we add them directly at the initialization, as the instances we are dealing with are sparse (while TSP-like problems normally consider complete graphs).

3.1 Separation Algorithms

Let $(\mathbf {x}^*,\mathbf {y}^*,\mathbf {z}^*)$ be the solution of the LP-relaxation at a branch-and-bound node. Depending on whether this solution is fractional or integer, different separation strategies are employed.

Separation of (SEC) for integer solutions. If the solution $(\mathbf {x}^*,\mathbf {y}^*,\mathbf {z}^*)$ is integer, it forms a set of disjoint cycles, say $C^1, \ldots {,} C^n$. For each cycle $C^i$, we add an inequality (SEC) with $S=C^i$. As node k, we randomly chose a node in $C^i$; as node l, we randomly chose a node in $C^{i+1}$ ($C^0$, if $i=n$).

Separation of (SEC) for fractional solutions. Inequalities (SEC) can be separated in polynomial time, $O(|V|^4)$, by maximum flow-computations (see, e.g., Fischetti et al. (1997)). As this turned out to be too time-consuming in preliminary computations, we used a heuristic separation instead. In particular, we used the heuristic from Gendreau et al. (1997): construct a maximum spanning tree on G (with edge weights given by the $\mathbf {x}^*$ values) using a greedy algorithm (in our implementation, we used Kruskal’s algorithm Kruskal (1956)). Whenever an edge e gets added to the partial tree during the algorithm, let S be the set where e gets added to. We take S as candidate for a violated inequality (SEC). As node k, we randomly chose a node in S among all nodes with maximum $y^*$ value in S, and for l, we randomly chose a node in $V \setminus S$ among all nodes with maximum $y^*$ value in $V \setminus S$. We do the separation throughout the branch-and-bound tree, and tried different settings for separation in our computational experiments (e.g., only separate for integer solutions of the LP-relaxation, or also for fractional solutions), for more details, see Sect. 4.

Separation of (L-SEC) and (L2-SEC). We do not separate (L-SEC) and (L2-SEC) explicitly, but whenever we detect a violated inequality (SEC), we check if a lifting is possible. This can be simply done by checking if any $v \in S$ or ${v} \in V\setminus S$ fulfills the condition for (L-SEC), and if S or $V \setminus S$ fulfills the condition for (L2-SEC).

3.2 Primal Heuristic

In order to find high-quality solutions during the branch-and-cut, we implemented a primal heuristic, which is driven by the values of the LP-relaxation in the branch-and-bound nodes. The heuristic works on the support graph $G^*$ induced by the LP-solution $(\mathbf {x}^*,\mathbf {y}^*,\mathbf {z}^*)$, i.e., the graph induced by $E^*=\{\{i,j\}\in E | x^*_{ij}>0\}$. Using $\mathbf {x}^*$ as weights, we compute a maximum spanning forest on $G^*$ using Kruskal’s algorithm. Whenever adding an edge during the course of the algorithm, would induce a cycle C, we check if C gives an improved primal solution; if yes, we take C as new incumbent.

In addition to the above primal heuristic, whenever we encounter an infeasible integer solution (which forms a disjoint set of cycles) during the branch-and-bound, we check if any cycle in this solution gives an improved primal solution. If such solution exists, we store it and we attempt adding it as incumbent the next time the CPLEX ILP-solver enters to the corresponding heuristic callback.

4 Computational Results

We implemented our framework in C++ and used CPLEX 12.7 for the branch-and-cut. All CPLEX parameters were left at their default values. The source-code is made available online at https://msinnl.github.io/pages/instancescodes.html. The experiments were done on a Xeon CPU with 2.5 GHz using a single-thread. For each run, we used a timelimit of 600 seconds and a memorylimit of 3GB. The study in Grosso et al. (2016) used the same timelimit, but unfortunately does not mention the specifications of the computer.

As benchmark instances, we used the instances from Grosso et al. (2016) and also considered additional instances. We obtained the instances from the authors of Grosso et al. (2016) and made them available online at https://msinnl.github.io/pages/instancescodes.html. Details of the instance sets are given next:

• Coloring: These are graph coloring instances from http://mat.gsia.cmu.edu/COLOR/instances.html. In Grosso et al. (2016), instances DSJ* and flat* were not used, thus this set has 57 instances.

• Scale-Free: These are instances generated in Grosso et al. (2016) based on scale-free graphs with up to 1000 nodes. According to the computational experience of Grosso et al. (2016), these instances turned out to be the most difficult ones. Note that for this set, we obtained 400 instances from the authors of Grosso et al. (2016), while in their paper, the set only has 336 instances (according to the authors, some instances of this set resulted in memory problems when using their solution approach, and thus were not reported in their final results).

• Random: These are randomly generated instances from Grosso et al. (2016). The graphs have up to 500 nodes and edge density (defined as $\frac{2|E|}{|V|(|V|-1)}$) up to 10%. The set contains 987 instances.

• Benchmark/Random-HC-DLV: These are instances containing a Hamiltonian cycle from http://wwwinfo.deis.unical.it/npdatalog/experiments/hamiltoniancycle.htm. Since they contain a Hamiltonian cycle, the value of the optimal solution is |V| for all of these instances, and the Hamiltonian cycle is an optimal solution (there can also be other optimal solutions). These instances were used in Grosso et al. (2016).

• Structured-3col-DLV: These are graph 3-coloring instances from http://wwwinfo.deis.unical.it/npdatalog/experiments/3-coloring.htm. As well as in Grosso et al. (2016), we consider three instances from there, the largest one being comprised by 900 nodes.

• ES250/500FST: As the results below will reveal, our approach can solve all instances from Grosso et al. (2016) within a few seconds. Thus, in order to push our approach to the limit, we looked at many different graph instances sets available online. In preliminary tests, the set ES250/500FST of SteinLIB Koch et al. (2001), a library of Steiner tree instances, available at http://steinlib.zib.de/showset.php?ES250FST and http://steinlib.zib.de/showset.php?ES500FST, proved to be the most challenging of sets containing graphs with a reasonable size (i.e., large enough for yielding difficult ILP problems, but for which solving the linear relaxation is still not burdensome). This set contains 30 instances.

4.1 Effects of the Framework Ingredients

To study the effects of the proposed enhancements in our framework, we tested the following settings:

• b: Basic setting, where we do not use the primal heuristic and only separate (SEC) for integer solutions.

• bh: b, but with the primal heuristic.

• bhf: Using the primal heuristic and separation of (SEC) also for fractional solution, but no lifting of (SEC).

• bhfl: bhf, where we also lift inequalities (SEC).

In Fig. 2, we show a performance profile plot of the runtime to optimality for all instances and all settings. Likewise, in Fig. 3, we show the performance profile of the optimality gap, which is calculated as $100 \cdot (z^{DB}-z^*)/z^*$, where $z^{DB}$ is the dual bound and $z^*$ is the best solution found.

From Fig. 2 we see that all settings except b manage to solve about 97% of the instances within ten seconds. In general, for most of the instances, there is not much difference in the runtime to optimality between the different settings, i.e., our branch-and-cut approach is already very effective in its most basic version. However, setting bhfl manages to solve a few more instances to optimality within the timelimit. Regarding the instances which cannot be solved within the given timelimit (they are all of the set ES250/500FST, as we will describe in the next section), we can see, from Fig. 3, more pronounced differences between the settings. Every additional ingredient added in our framework improves the performance. Therefore, we conclude that setting bhfl, which contains all enhancements, is the most effective one for the considered problem. Therefore, all the results reported in the remainder of the section are obtained with this setting.

Fig. 2

Runtime for different settings

Fig. 3

Optimality gap after 600s for different settings

4.2 Detailed Results

In Table 1 we give an overview of the results attained for each instance set. Column t[s] gives the runtime in seconds, $g [\%]$ gives the optimality gap, #BBn gives the number of branch-and-bound nodes, #(SEC) gives the number of separated cut constraints, while columns #(L-SEC) and #(L2-SEC) report how often each of the corresponding lifting was successful. Note that for one cut constraints constraint, both lifting strategies could be applied (both (L-SEC) and (L2-SEC) can be applied twice; for S and $V \setminus S$). The entries associated to each row in the table are averages over the corresponding whole instance set. From the results, we see that all instances from Grosso et al. (2016) could be solved to optimality. In Grosso et al. (2016), only 53 out of 57 instances of Coloring, two out of three from Structured-3col-DLV, 978 out of 987 from Random and 294 out of 336 instances from Scale-Free could be solved to optimality. The runtime and also the number of branch-and-bound nodes for all instance classes except ES250/500FST is very small. In particular, all instances from sets Benchmark/Random-HC-DLV and were solved in the rootnode, and also for Coloring, Scale-Free, Randomthe average runtime and number of branch-and-bound nodes is under one.

Table 1 Overview of results by instance class

In Table 2 we give a detailed overview on the results on the instances from set ES250/500FST, which is the only class where our algorithm did not find the optimal solution for all instances within the timelimit (these cases are indicated by TL in column t[s]). We manage to solve eight out of 30 instances of this set for optimality. For all except five instances, the gap is under ten percent. In particular, for most of the instances, the gap is under one percent.

Table 2 Detailed results for instance set ES250/500FST

5 Conclusion

In many applications, such as telecommunications and routing, we are concerned in finding layouts so that many nodes (e.g., customers) of the underlying graph are covered. In this paper, we study the maximum covering cycle problem (MCCP), which has been recently introduced by Grosso et al. (2016). In the MCCP we are given a (non-complete) graph, and the goal is to find a cycle such that the number of nodes which are either on the cycle or adjacent to this cycle is maximized. We design and implement a branch-and-cut framework for the problem. The framework contains valid inequalities, lifted inequalities and a primal heuristic. In a computational study, we compare our framework to the approach by Grosso et al. (2016). The results reveal that our approach significantly outperforms the previous approach. In particular, all instances from the literature could be solved to optimality with our approach, most of them within a second.

Regarding further work, the formulation can be easily extended to accommodate for a weighted coverage. Likewise, the coverage protocol can be extended to more general concepts. However, the primal heuristic may need non-trivial adaptations to satisfactory work in such cases, and additional valid inequalities could potentially be derived. It could also be interesting to investigate, if there are certain graphs, where the proposed formulation gives a complete description. Developing preprocessing tests to reduce the instance size could be useful. Furthermore, in a real-life setting, it is likely that both the set of nodes and links are subject to uncertainty; therefore, the study of a stochastic or robust version of the problem could be a worthwhile topic for research. For large-scale instances, solving the Integer Linear Programming formulation can become a bottleneck, thus the use of Lagrangian relaxation instead of Linear Programming may prove fruitful to quickly find reasonable dual bounds. The design of (meta)-heuristic approaches to tackle even larger instances could also be interesting for further work.