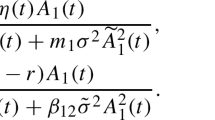Pareto-optimal reinsurance policies in the presence of individual risk constraints

Abstract

The notion of Pareto optimality is commonly employed to formulate decisions that reconcile the conflicting interests of multiple agents with possibly different risk preferences. In the context of a one-period reinsurance market comprising an insurer and a reinsurer, both of which perceive risk via distortion risk measures, also known as dual utilities, this article characterizes the set of Pareto-optimal reinsurance policies analytically and visualizes the insurer–reinsurer trade-off structure geometrically. The search of these policies is tackled by translating it mathematically into a functional minimization problem involving a weighted average of the insurer’s risk and the reinsurer’s risk. The resulting solutions not only cast light on the structure of the Pareto-optimal contracts, but also allow us to portray the resulting insurer–reinsurer Pareto frontier graphically. In addition to providing a pictorial manifestation of the compromise reached between the insurer and reinsurer, an enormous merit of developing the Pareto frontier is the considerable ease with which Pareto-optimal reinsurance policies can be constructed even in the presence of the insurer’s and reinsurer’s individual risk constraints. A strikingly simple graphical search of these constrained policies is performed in the special cases of Value-at-Risk and Tail Value-at-Risk.

1 Introduction

In various applied problems arising in engineering, finance, operations research, and the like, decisions are often made with the vexed aim of reconciling a host of conflicting criteria. In finance, for example, investors are struck with the desire to maximize the expected value of their portfolio returns while minimizing their risk, which is quantified by the standard deviation in the celebrated Markowitz mean–variance framework. In the statistics arena, reducing the probability of committing a Type I error of a hypothesis test for a given sample size generally leads to an increase in the Type II error probability. Typically, the decision-making process entails a compromise between several criteria that are at least partially at odds with one another, and the procedure is formally known as multi-criteria or multi-objective optimization. For recent accomplishments, applications (especially in finance), and anticipated future developments in this fertile field of research, readers are referred to Ehrgott (2005), Wallenius et al. (2008), Zopounidis and Pardalos (2010), Maggis and La Torre (2012), Aouni et al. (2014), Jayaraman et al. (2015), La Torre (2017), and Zarepisheh and Pardalos (2017) among others and the references therein.

Among the wide spectrum of multi-criteria optimization problems, this article centers on the design of optimal reinsurance policies in a one-period bilateral setting, which is a problem of considerable practical interest in actuarial science and risk management. Reinsurance, which is essentially insurance purchased by an insurance company (or insurer) from a reinsurance corporation (or reinsurer), is a commonly used liability management strategy that allows an insurer to reduce the amount of its risk exposure by transferring part of its business to reinsurers. This would in turn result in a more manageable portfolio of insured risks that dovetails with the risk-taking capability of the insurer. Technically, reinsurance can be viewed as a special form of risk sharing between an insurer and a reinsurer. Whereas optimal risk sharing consists in selecting a redistribution of risks to reach a certain level of optimality, the decision variable in optimal reinsurance problems is restricted to the indemnity function. In broader contexts in finance, risk management, and insurance, optimal risk sharing with various objective functionals has been an extensively studied research topic (see, e.g., Ludkovski and Young 2009; Grechuk and Zabarankin 2012; Asimit et al. 2013). Nevertheless, studies of optimal reinsurance policies are often not amenable to existing results in optimal risk sharing due to the comonotonicity of the shared risks inherent in optimal reinsurance problems and the presence of additional practical constraints. These technical complications have rendered optimal reinsurance a subtly unique optimal risk sharing problem deserving of separate investigation. Pioneered in Borch (1960) and Arrow (1963) in the context of variance minimization and expected utility maximization from the perspective of an insurer, and later extended to a risk-measure-based framework, as in Cai and Tan (2007), Cai et al. (2008), Chi and Tan (2011), Cui et al. (2013), Cong and Tan (2016) and Lo (2016, 2017b), just to name a few, the formulation of optimal reinsurance contracts has been examined with a diversity of objective functionals and premium principles of varying degrees of mathematical sophistication. Optimal solutions ranging from stop-loss, quota-share policies to general insurance layers have been found depending on the precise specification of the concerned optimization problem. Given the rising importance of reinsurance as a versatile risk optimization strategy in the current catastrophe-plagued age, the study of optimal reinsurance has gained substantial impetus and represented a burgeoning line of research.

Despite the vast literature on optimal reinsurance, most existing research is preoccupied with the mathematically feasible, but economically unrealistic study of reinsurance policies that are designed to be optimal to one and only one party, either the insurer or reinsurer. This overlooks the substantive fact that the insurer and reinsurer bear intrinsically conflicting interests as counterparties in a reinsurance contract. As noted in Borch (1969), a reinsurance arrangement which appears very attractive to one party may fail to be acceptable to the other. Due to the misalignment of the interests of the insurer and reinsurer, and consequently the general impossibility of a reinsurance policy being simultaneously optimal to both parties, reinsurers inevitably have to grapple with the problem of designing reinsurance contracts that ensure their long-run profitability and, at the same time, appeal to their customers, namely insurers. The construction of such bilaterally acceptable reinsurance policies that accommodate the joint interests of the insurer and reinsurer is therefore a technically challenging, but practically meaningful task. Along these lines of reasoning, recently Hürlimann (2011) obtained the optimal parameters of a partial stop-loss contract under various joint party criteria. Cai et al. (2013) determined the optimal reinsurance contract under the criteria of joint survival and profitability probabilities of an insurer and a reinsurer. Lo (2017a) derived the reinsurance policy which is optimal to one party while acceptable to the other from a Neyman–Pearson perspective. Cai et al. (2017) and Jiang et al. (2017) appealed to the celebrated notion of Pareto optimality and determined the collection of Pareto-optimal contracts in the Tail Value-at-Risk (TVaR) and Value-at-Risk (VaR) settings, respectively. By definition, a reinsurance policy is said to be Pareto-optimal if it is impossible to lower the risk of one party without deteriorating the other party. The concept of Pareto optimality is particularly useful in multi-criteria optimization as it helps decision makers eliminate decisions which do not deserve consideration and focus on those that represent good compromise between multiple parties.

Building upon the line of research of Cai et al. (2016, 2017), this article characterizes, algebraically and geometrically, the entire set of Pareto-optimal reinsurance policies when the insurer and reinsurer evaluate risk via distortion risk measures (DRMs), also known as dual utilities or Yaari’s functionals (Yaari 1987), and examines the implications of Pareto optimality for the insurer–reinsurer trade-off mechanism in the DRM-based-framework. The use of DRMs as the risk measurement vehicle strikes a due balance between modeling flexibility and analytic tractability. Not only do DRMs encompass a wide variety of contemporary risk measures, most notably VaR and TVaR, they also admit a convenient integral representation that sheds light on the perception of risk they reflect and lends itself readily to theoretical derivations. Under the general DRM framework, we associate the quest for Pareto-optimal reinsurance policies, which is inherently a two-criteria optimization problem, equivalently with a single-objective weighted sum functional minimization problem, which in turn provides a simple recipe for generating all Pareto-optimal solutions. This reduction procedure is commonly referred to as weighted sum scalarization (in contrast to the goal programming method employed in some of the contributions mentioned in the first paragraph; see also, e.g., Chapter 3 of Ehrgott 2005) in multi-criteria optimization. The weighted sum comprises the risks of the insurer and reinsurer measured by DRMs and captures the relative negotiation power of the insurer and reinsurer by means of a weight parameter. Applying the Marginal Indemnification Function approach developed in Assa (2015) and Zhuang et al. (2016), we manage to solve the weighted sum problem and derive all Pareto-optimal solutions analytically and expeditiously. In order to display the optimal solutions more concretely and gain further insights into their structure, we subsequently specialize our DRM-based analysis to VaR and TVaR, which are justifiably the most prominent risk measures in the insurance and banking industries, and obtain explicit expressions for the Pareto-optimal reinsurance contracts. Compared to Cai et al. (2016, 2017) and Jiang et al. (2017), the solutions in this paper are more clear-cut and the proofs more systematic and transparent due to the abstraction that DRMs offer. It is shown in the VaR case that the Pareto-optimal policy is equivalent to the one designed from the sole perspective of the insurer (resp. reinsurer) when the insurer receives more weight (resp. less weight) than the reinsurer in the weighted sum minimization problem. This phenomenon carries over to the TVaR case when the weight parameter is sufficiently large or sufficiently low, but for a range of intermediate values, there exists a compromise made between the insurer and reinsurer, meaning that the solution is neither optimal to the insurer nor to the reinsurer, but is the best on a collective basis.

As a side benefit, the explicitness of our optimal solutions enables us to represent our findings geometrically by portraying the insurer’s and reinsurer’s risk levels that the Pareto-optimal reinsurance arrangements give rise to. These pairs of points constitute, in the two-dimensional space, a convex curve known as the Pareto frontier, which proves to be a convenient visual aid for understanding the insurer–reinsurer trade-off structure. The geometry of the Pareto frontier depends critically on the choice of the DRMs. It is found that it is a downward sloping straight line in the VaR case, and typically comprises two downward sloping straight lines connected by a convex curve in the TVaR case. These salient geometric features, which we are among the first to study systematically, can be attributed to the properties of VaR and TVaR as particular members of the class of DRMs. Collectively, our analytic expressions for the Pareto-optimal reinsurance policies as well as our geometric descriptions in the form of the Pareto frontier shed valuable light on the insurer–reinsurer decision-making mechanism in the pursuit of Pareto efficiency.

It should be stressed that Pareto optimality is a minimal notion of efficiency. A Pareto-optimal reinsurance policy does not necessarily result in an equitable distribution of risk between the insurer and reinsurer, which tend to have constraints on their risk-taking capability. This casts doubt on the marketability of a Pareto-optimal reinsurance contract in practice for failing to be simultaneously acceptable to the insurer and reinsurer. This motivates us to embed, in the second part of this article, risk constraints on the part of the insurer and reinsurer, and study the resulting constrained collection of Pareto-optimal reinsurance arrangements. In multi-criteria optimization, this is sometimes known as the hybrid method (see, e.g., Section 4.2 of Ehrgott 2005). Our constraints include, as a special case, individual rationality constraints, which ensure that both the insurer and reinsurer are better off as a result of reinsurance. Technically, the presence of two constraints defies the direct application of Lo (2017a)’s Neyman–Pearson approach, which does not apply to the two-constraint TVaR setting. The Pareto frontier, apart from being interesting in its own right, is shown to be a useful device as it allows us to transform the constrained search of Pareto-optimal policies into a two-dimensional constrained optimization problem on the real plane, which can be solved graphically and easily. The search procedure is again illustrated in the VaR and TVaR cases.

The remainder of this article is organized as follows. Section 2 presents the DRM-based reinsurance model and formulates, in the language of multi-criteria optimization, the problem of identifying Pareto-optimal reinsurance policies, the central theme of the entire article. In Sect. 3, we solve the weighted sum functional minimization problem explicitly in the general framework of DRMs, followed by the VaR and TVaR settings. The Pareto frontier is developed and interpreted in the latter two cases. Section 4 revisits the weighted sum minimization problem with the insurer’s and reinsurer’s risk constraints added and provides graphical solutions in the VaR and TVaR cases. Finally, Sect. 5 concludes the article and summarizes its main contributions.

2 DRM-based optimal reinsurance model

In this section, we describe the key ingredients of the DRM-based reinsurance model and lay the mathematical groundwork of the problem of identifying Pareto-optimal reinsurance policies, paying special attention to the optimization criteria, reinsurance premium principle, and the class of feasible decisions.

2.1 Distortion risk measures

In this paper, the risk faced by an agent is evaluated via distortion risk measures (DRMs), whose definition requires the notion of a distortion function. A function $g:[0,1]\rightarrow [0,1]$ is said to be a distortion function if g is a non-decreasing function, not necessarily convex, concave or (left- or right-) continuous, such that $g(0_{+}):=\lim _{x\downarrow 0}g(x)=0$¹ and $g(1)=1$. The DRM of a non-negative random variable Y corresponding to a distortion function g is defined by the Lebesgue–Stieltjes integral

$$\begin{aligned} \rho _{g}(Y):=\int _{0}^{\infty }g(S_{Y}(y))\,\mathrm {d}y, \end{aligned}$$

(2.1)

where $S_{Y}(y):=\mathbb {P}(Y>y)$ is the survival function of Y. In order that (2.1) makes sense, throughout this article we tacitly assume that all random variables are sufficiently integrable in the sense of possessing finite DRMs.

Several remarks pertaining to the use of DRMs are in order. First, by Fubini’s theorem, one may write²

$$\begin{aligned} \rho _{g}(Y)=\int _{0}^{\infty }\int _{t}^{\infty }\mathrm {d}[-g(S_{Y}(y))]\,\mathrm {d}t=\int _{0}^{\infty }\int _{0}^{y}\mathrm {d}t\,\mathrm {d}[-g(S_{Y}(y))]=\int _{0}^{\infty }y\,\mathrm {d}[-g(S_{Y}(y))]. \end{aligned}$$

This representation reveals the fundamental differences between Yaari’s dual theory of choice and the classical expected utility theory in evaluating the riskiness of a loss random variable. Specifically, distortion risk measures seek to distort the survival function of a loss variable Y from $S_{Y}(\cdot )$ to $g(S_{Y}(\cdot ))$ while keeping the loss magnitude unchanged, in contrast to the use of utility functions which distort the size of losses without altering the loss distribution. Second, due to the translation invariance of distortion risk measures, i.e., $\rho _{g}(Y+c)=\rho _{g}(Y)+c$ for any constant c (see Equation (54) of Dhaene et al. 2006), non-random cash flows that are independent of the reinsurance arrangement, such as the premium that the insurer collects from its policyholders, do not affect the optimizers of our optimization problems and can be safely neglected in the analysis. Third, DRM as a risk quantification vehicle has proved to be a highly flexible modeling tool due to its inclusion of a wide class of common risk measures, such as VaR and TVaR, which are arguably the most popular DRMs in practice. Their definitions are recalled below. In the sequel, we denote by $1_{A}$ the indicator function of a given event A, i.e., $1_{A}=1$ if A is true, and $1_{A}=0$ otherwise, and write $x\wedge y=\min (x,y)$ and $x\vee y=\max (x,y)$ for any real x and y.

Definition 2.1

(Definitions of VaR and TVaR) Let Y be a random variable whose distribution function is $F_{Y}$.

• (a) The generalized left-continuous inverse and generalized right-continuous inverse of $F_{Y}$ are defined respectively by

  $$\begin{aligned} F_{Y}^{-1}(p):=\inf \{y\in \mathbb {R}\mid F_{Y}(y)\ge p\}\quad \text {and}\quad F_{Y}^{-1+}(p):=\inf \{y\in \mathbb {R}\mid F_{Y}(y)>p\}, \end{aligned}$$

  with the convention $\inf \emptyset =\infty$. The Value-at-Risk (VaR) of Y at the probability level of $p\in (0,1]$ is synonymous with the generalized left-continuous inverse of $F_{Y}$ at p, i.e., $\text {VaR}_{p}(Y):=F_{Y}^{-1}(p)$.

• (b) The Tail Value-at-Risk (TVaR)³ of Y at the probability level of $p\in [0,1)$ is defined by

  $$\begin{aligned} \text {TVaR}_{p}(Y):=\frac{1}{1-p}\int _{p}^{1}\text {VaR}_{q}(Y)\,\mathrm {d}q. \end{aligned}$$

The distortion functions that give rise to the p-level VaR and p-level TVaR are $g(x)=1_{\{x>1-p\}}$ and $g(x)=\frac{x}{1-p}\wedge 1$, respectively (see Equations (44) and (45) of Dhaene et al. 2006).

In this article, both $\text {VaR}_{p}(Y)$ and $F_{Y}^{-1}(p)$ will be used interchangeably. For later purposes, we point out the useful equivalence

$$\begin{aligned} F_{Y}^{-1}(p)\le y\quad \Leftrightarrow \quad p\le F_{Y}(y)\quad \text {for all }p\in (0,1). \end{aligned}$$

(2.2)

2.2 Model set-up

This article centers on a one-period reinsurance market comprising an insurer and a reinsurer, which interact as follows. The insurer is faced with a ground-up loss modeled by a general non-negative random variable X with a known distribution. To reduce its risk exposure quantified by the DRM, the insurer can decide to purchase a reinsurance policy I from the reinsurer. When x is the realized value of X, the reinsurer pays I(x) to the insurer, which in turn retains the residual loss $x-I(x)$. Terminology-wise, the function I is called the indemnityfunction (also known as the ceded loss function) and is the linchpin of a reinsurance policy. In this paper, the feasible class of reinsurance policies available for sale in the reinsurance market is confined to the set of non-decreasing and 1-Lipschitz functions null at zero, i.e.,

$$\begin{aligned} \mathcal {I}= & {} \left\{ I:[0,F_{X}^{-1}(1))\rightarrow \mathbb {R}^{+}\mid I(0)=0,\,0\le I(t_{2})-I(t_{1})\le t_{2}-t_{1}\text { for }0\le t_{1}\le t_{2}\right\} \\= & {} \left\{ I:[0,F_{X}^{-1}(1))\rightarrow \mathbb {R}^{+}\mid I(0)=0,\,0\le I^{\prime }(t)\le 1\text { for }t\ge 0\right\} . \end{aligned}$$

Practically, the conditions imposed on the feasible set $\mathcal {I}$ are intended to alleviate the issue of ex post moral hazard due to the manipulation of losses. As a matter of fact, for any reinsurance treaty selected from $\mathcal {I}$, both the insurer and reinsurer will be worse off as the ground-up loss becomes more severe, thereby having no incentive to manipulate claims. Mathematically, the 1-Lipschitzity condition does facilitate theoretical derivations, with I(X) and $X-I(X)$ being comonotonic, and with every $I\in \mathcal {I}$ being absolutely continuous with a derivative $I^{\prime }$ which exists almost everywhere and is bounded between 0 and 1. As in Assa (2015) and Zhuang et al. (2016), we term $I^{\prime }$ the marginal indemnity function, which measures the rate of increase in the ceded loss with respect to the ground-up loss. Moreover, because of the relationship $I(x)=\int _{0}^{x}I^{\prime }(t)\,\mathrm {d}t$, each indemnity function enjoys a one-to-one correspondence with its marginal counterpart. As will be shown later in this paper, it will be much more convenient to express our results equivalently but more compactly in terms of the marginal indemnity function.

In return for bearing the ceded loss, the reinsurer receives from the insurer the reinsurance premium $P_{I(X)}$, which is a function of the ceded loss I(X). The net risk exposure of the insurer is then changed from the ground-up loss X to $X-I(X)+P_{I(X)}$ and the reinsurer, as a result of the reinsurance contract, bears $I(X)-P_{I(X)}$. For a given indemnity function $I\in \mathcal {I}$, the reinsurer calibrates the reinsurance premium by the formula

$$\begin{aligned} P_{I(X)}:=\int _{0}^{\infty }h(S_{I(X)}(t))\,\mathrm {d}t, \end{aligned}$$

(2.3)

where $h:[0,1]\rightarrow \mathbb {R}^{+}$ is a non-decreasing function such that $h(0_{+})=0$. This premium principle has multi-fold desirable characteristics. First, this DRM-like premium principle does not require that h(1) be 1, and is flexible enough to encompass a wide variety of safety loading structures desired by the reinsurer. Second, analogous to the versatility of DRMs, a number of common premium principles, such as the well-known expected value premium principle and Wang’s premium principle, can be recovered from (2.3) by appropriate specifications of the function h (see Cui et al. 2013). Third, (2.3) is of the same structure as (2.1). Such symmetry, when put into perspective, will be highly conducive to our subsequent theoretical derivations.

In the later part of this paper, there will be numerous instances in which the DRM of a transformed random variable needs to be dealt with. To this end, the following transformation lemma, which can be found in Lemma 2.1 of Cheung and Lo (2017), will prove invaluable. It places the marginal indemnity function $I^{\prime }$ in the integrands of appropriate Lebesgue–Stieltjes integrals and is central to the optimal selection of $I^{\prime }$ (equivalently, I).

Lemma 2.1

(Integral representations of risk and premium functions) For any distortion function g and indemnity function I in $\mathcal {I}$,

$$\begin{aligned} \rho _{g}(X-I(X)+P_{I(X)})= & {} \rho _{g}(X)+\int _{0}^{\infty }[h(S_{X}(t))-g(S_{X}(t))]I^{\prime }(t)\,\mathrm {d}t,\\ \rho _{g}(I(X)-P_{I(X)})= & {} \int _{0}^{\infty }[g(S_{X}(t))-h(S_{X}(t))]I^{\prime }(t)\,\mathrm {d}t,\\ P_{I(X)}= & {} \int _{0}^{\infty }h(S_{X}(t))I^{\prime }(t)\,\mathrm {d}t. \end{aligned}$$

2.3 Pareto-optimal reinsurance policies

In this article, we take the possible tension between the insurer and reinsurer into account, factor in their joint interests, and study Pareto-optimal reinsurance policies within the set $\mathcal {I}$. In our DRM context, a reinsurance policy $I_{*}$ in $\mathcal {I}$ is said to be Pareto-optimal (or Pareto-efficient) if there is no $I\in \mathcal {I}$ such that

$$\begin{aligned} \rho _{g_{i}}(X-I(X)+P_{I(X)})\le \rho _{g_{i}}(X-I_{*}(X)+P_{I_{*}(X)}) \end{aligned}$$

and

$$\begin{aligned} \rho _{g_{r}}(I(X)-P_{I(X)})\le \rho _{g_{r}}(I_{*}(X)-P_{I_{*}(X)}), \end{aligned}$$

with at least one inequality being strict. Here, $g_{i}$ and $g_{r}$ are the distortion functions adopted by the insurer and reinsurer, respectively. In words, a Pareto-optimal policy is such that the risk borne by one party cannot be lowered without making the other party worse off. In the wider context of multi-criteria optimization, the search of Pareto-optimal policies is a two-criteria functional minimization problem, in which the two criteria (or objectives) are the insurer’s risk and the reinsurer’s risk quantified by DRMs and given respectively by

$$\begin{aligned} x(I):=\rho _{g_{i}}(X-I(X)+P_{I(X)})\quad \text {and}\quad y(I):=\rho _{g_{r}}(I(X)-P_{I(X)}), \end{aligned}$$

the decision variable is the indemnity function I, and the feasible set is $\mathcal {I}$. Informally, we may represent the identification of Pareto-optimal reinsurance policies as

$$\begin{aligned} \inf _{I\in \mathcal {I}}\left( x(I),y(I)\right) . \end{aligned}$$

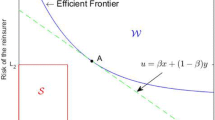
The images of all indemnity functions in $\mathcal {I}$ under the actions of $x(\cdot )$ and $y(\cdot )$ form the risk set (not to be confused with the feasible set) in the x–y plane consisting of all possible pairs of risk levels $\left( x(I),y(I)\right)$ achieved by some $I\in \mathcal {I}$. As will be shown in Sect. 3, the risk set in our DRM framework is convex. This allows us to apply tools in convex analysis to transform the search of Pareto-optimal solutions into a single-objective weighted sum functional minimization problem, which can be solved analytically and readily. In addition to identifying all Pareto-optimal policies algebraically, we will provide a geometric description of these solutions by portraying the Pareto frontier, which is loosely speaking the southwest border of the risk set. It is a graphical device that captures the set of risk levels all Pareto-optimal solutions give rise to and depicts the trade-off made between the insurer and reinsurer.

3 Characterization of Pareto-optimal reinsurance policies

In this section, we examine the collection of Pareto-optimal reinsurance policies in two stages, first in the general DRM framework, then specifically in the VaR and TVaR settings.

3.1 Pareto-optimal policies under general DRMs

The following proposition provides a recipe for constructing Pareto-optimal reinsurance policies by pointing out their connections to a weighted sum functional minimization problem.

Proposition 3.1

(Pareto optimality and weighted DRM minimization problem) A reinsurance policy $I_{*}\in \mathcal {I}$ is Pareto-optimal if and only if it solves the weighted sum functional minimization problem

$$\begin{aligned} \inf _{I\in \mathcal {I}}[\lambda x(I)+(1-\lambda )y(I)]\,\equiv \,\inf _{I\in \mathcal {I}}[\lambda \rho _{g_{i}}(X-I(X)+P_{I(X)})+(1-\lambda )\rho _{g_{r}}(I(X)-P_{I(X)})] \end{aligned}$$

(3.1)

for some $\lambda \in [0,1]$.

Proof

Let $I_{*}\in \mathcal {I}$ solve Problem (3.1) for some fixed $\lambda \in [0,1]$. Assume by way of contradiction that $I_{*}$ is not Pareto-optimal. Then there exists $\tilde{I}\in \mathcal {I}$ such that

$$\begin{aligned} x(\tilde{I})=\rho _{g_{i}}(X-\tilde{I}(X)+P_{\tilde{I}(X)})\le \rho _{g_{i}}(X-I_{*}(X)+P_{I_{*}(X)})=x(I_{*}) \end{aligned}$$

and

$$\begin{aligned} y(\tilde{I})=\rho _{g_{r}}(\tilde{I}(X)-P_{\tilde{I}(X)})\le \rho _{g_{r}}(I_{*}(X)-P_{I_{*}(X)})=y(I_{*}), \end{aligned}$$

where at least one of the inequalities is strict. It follows that

$$\begin{aligned} \lambda x(\tilde{I})+(1-\lambda )y(\tilde{I})<\lambda x(I_{*})+(1-\lambda )y(I_{*}), \end{aligned}$$

contradicting the minimality of $I_{*}$ for Problem (3.1) with the fixed $\lambda$.

To prove the reverse implication, we first show that the risk set is a convex set in the plane. Let $I_{1},I_{2}\in \mathcal {I}$. Define, for $\gamma \in [0,1]$, $I_{\gamma }:=\gamma I_{1}+(1-\gamma )I_{2}$, which also lies in $\mathcal {I}$ because of the non-decreasing monotonicity and 1-Lipschizity of $I_{1}$ and $I_{2}$. Appealing to the comonotonic additivity and positive homogeneity of DRMs as well as Lemma 2.1 yields

$$\begin{aligned} x(I_{\gamma })= & {} \rho _{g_{i}}(X-I_{\gamma }(X)+P_{I_{\gamma }(X)})\\= & {} \rho _{g_{i}}\left[ \gamma (X-I_{1}(X)+P_{I_{1}(X)})+(1-\gamma )(X-I_{2}(X)+P_{I_{2}(X)})\right] \\= & {} \rho _{g_{i}}\left[ \gamma (X-I_{1}(X)+P_{I_{1}(X)})\right] +\rho _{g_{i}}\left[ (1-\gamma )(X-I_{2}(X)+P_{I_{2}(X)})\right] \\= & {} \gamma \rho _{g_{i}}(X-I_{1}(X)+P_{I_{1}(X)})+(1-\gamma )\rho _{g_{i}}(X-I_{2}(X)+P_{I_{2}(X)})\\= & {} \gamma x(I_{1})+(1-\gamma )x(I_{2}). \end{aligned}$$

Similarly,

$$\begin{aligned} y(I_{\gamma })=\gamma y(I_{1})+(1-\gamma )y(I_{2}). \end{aligned}$$

In other words, the entire line segment connecting $(x(I_{1}),y(I_{1}))$ and $(x(I_{2}),y(I_{2}))$ belongs to the risk set, proving its convexity. Now let $I_{*}\in \mathcal {I}$ be a Pareto-optimal policy. By the definition of Pareto optimality, $I_{*}$ gives rise to a pair of points $(x_{*},y_{*}):=(x(I_{*}),y(I_{*}))$ on the southwest boundary of the risk set. Then by virtue of the convexity of the risk set and a version of the Hahn–Banach theorem (see, e.g., Lemma 7.7 on page 259 of Aliprantis and Border 2006), there exists a continuous linear functional $f:\mathbb {R}^{2}\rightarrow \mathbb {R}$ defined by $f(x,y):=a_{1}x+a_{2}y$, with $a_{1},a_{2}$ non-negative and not both zero, such that f supports the risk set at $(x_{*},y_{*})$, meaning that

$$\begin{aligned} a_{1}x_{*}+a_{2}y_{*}=f(x_{*},y_{*})\le f(x,y)=a_{1}x+a_{2}y \end{aligned}$$

for all (x, y) lying in the risk set. Equivalently, with $\alpha =f(x_{*},y_{*})$, the set $\{f=\alpha \}$ is a tangent at $(x_{*},y_{*})$ always lying below the risk set (see Fig. 1). Dividing both sides of the preceding inequality by $a_{1}+a_{2}$, which is non-zero, shows that $I_{*}$ solves Problem (3.1) with $\lambda =a_{1}/(a_{1}+a_{2})$. $\square$

Fig. 1

The function f used in the proof of Proposition 3.1

We remark that in the context of this article, the weighted sum scalarization illustrated in Proposition 3.1 is equivalent to the $\epsilon$-constraint method, which is another popular multi-criteria decision-making tool involving the minimization of the insurer’s risk (resp. reinsurer’s risk) subject to the constraint that the reinsurer’s risk (resp. insurer’s risk) is below any arbitrarily fixed level $\epsilon$ (see, e.g., Section 4.1 of Ehrgott 2005). The application of the $\epsilon$-constraint method is technically much more challenging than the weighted sum scalarization due to the presence of the additional constraint. Readers are referred to Lo (2017a) for a systematic approach based on the Neyman–Pearson Lemma to tackling such a kind of constrained minimization problem.

The proof of Proposition 3.1 relies on the geometry of the feasible set and risk set, both of which are convex, and is motivated from the ideas on page 90 of Gerber (1979). While a more general version of this proposition can be found in Theorem 2.1 of Cai et al. (2017), the proof above is self-contained and more elementary and germane to the context of this article. The significance of the proposition lies in transforming the two-criteria functional minimization problem into the single-objective Problem (3.1), which is amenable to contemporary techniques in the realm of optimal reinsurance and is solved analytically in the following theorem. Here, $\lambda$ is a parameter inherent in the problem. Intuitively, as $\lambda$ increases from 0 to 1, more and more weight is attached to the interests of the insurer, and the solution of Problem (3.1) shall approach the optimal contract designed from the sole perspective of the insurer. Unless otherwise specified, in the sequel $\gamma _{*}$ will denote a generic unit-valued function.

Theorem 3.1

(Solutions of Problem (3.1)) The solutions of Problem (3.1) are uniquely defined by

$$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} 1, &{} \text {if }r(S_{X}(t))<0,\\ \gamma _{*}(t), &{} \text {if }r(S_{X}(t))=0,\\ 0, &{} \text {if }r(S_{X}(t))>0, \end{array}\right. } \end{aligned}$$

(3.2)

where “a.e.” means “almost everywhere,” and

$$\begin{aligned} r(S_{X}(t)):=(2\lambda -1)h(S_{X}(t))-\lambda g_{i}(S_{X}(t))+(1-\lambda )g_{r}(S_{X}(t)). \end{aligned}$$

(3.3)

Proof

By Lemma 2.1, the objective function of Problem (3.1), in integral form, is

$$\begin{aligned}&\quad \rho _{g_{i}}(X)+\lambda \int _{0}^{\infty }[h(S_{X}(t))-g_{i}(S_{X}(t))]I^{\prime }(t)\,\mathrm {d}t\\&\quad +\,(1-\lambda )\int _{0}^{\infty }[g_{r}(S_{X}(t))-h(S_{X}(t))]I^{\prime }(t)\,\mathrm {d}t\\&= \rho _{g_{i}}(X)+\int _{0}^{\infty }[(2\lambda -1)h(S_{X}(t))-\lambda g_{i}(S_{X}(t))+(1-\lambda )g_{r}(S_{X}(t))]I^{\prime }(t)\,\mathrm {d}t\\&= \rho _{g_{i}}(X)+\int _{0}^{\infty }r(S_{X}(t))I^{\prime }(t)\,\mathrm {d}t, \end{aligned}$$

where $\rho _{g_{i}}(X)$ does not depend on the indemnity function. Because $I^{\prime }(t)\in [0,1]$ for all $t\ge 0$, the preceding integral, for any $I\in \mathcal {I}$, is in turn bounded from below by

$$\begin{aligned} \int _{0}^{\infty }r(S_{X}(t))I^{\prime }(t)\,\mathrm {d}t= & {} \int _{\{r\circ S_{X}<0\}}r(S_{X}(t))I^{\prime }(t)\,\mathrm {d}t+\int _{\{r\circ S_{X}=0\}}r(S_{X}(t))I^{\prime }(t)\,\mathrm {d}t\\&+\,\int _{\{r\circ S_{X}>0\}}r(S_{X}(t))I^{\prime }(t)\,\mathrm {d}t\\\ge & {} \int _{\{r\circ S_{X}<0\}}r(S_{X}(t))\,\mathrm {d}t\\= & {} \int r(S_{X}(t))I_{*}^{\prime }(t)\,\mathrm {d}t, \end{aligned}$$

where $I_{*}^{\prime }$ is given in (3.2). Moreover, equality prevails if and only if

$$\begin{aligned} \int _{\{r\circ S_{X}<0\}}r(S_{X}(t))I^{\prime }(t)\,\mathrm {d}t=\int _{\{r\circ S_{X}<0\}}r(S_{X}(t))\,\mathrm {d}t\quad \text {and}\quad \int _{\{r\circ S_{X}>0\}}r(S_{X}(t))I^{\prime }(t)\,\mathrm {d}t=0, \end{aligned}$$

which are in turn equivalent to $I^{\prime }=1$ almost everywhere on $\{r\circ S_{X}<0\}$ and $I^{\prime }=0$ almost everywhere on $\{r\circ S_{X}>0\}$ because $I^{\prime }$ is unit-valued. $\square$

Theorem 3.1 exhausts the solutions of Problem (3.1) analytically and demonstrates that the design of Pareto-optimal reinsurance policies hinges upon the sign of the composite function $r\circ S_{X}$, which depends on $\lambda$, defined in (3.3). The optimal policy is constructed by setting the marginal indemnity function $I^{\prime }$ to its maximum value of 1 (i.e., full coverage) when $r\circ S_{X}$ is strictly negative, to its minimum value of zero (i.e., no coverage) when $r\circ S_{X}$ is strictly positive, and to any value between 0 and 1 (i.e., arbitrary coverage) when $r\circ S_{X}$ is zero. In particular, when $\lambda =1$ (resp. $\lambda =0$), $r\circ S_{X}=h\circ S_{X}-g_{i}\circ S_{X}$ (resp. $r\circ S_{X}=g_{r}\circ S_{X}-h\circ S_{X}$), and Theorem 3.1 retrieves the solutions for the risk minimization problem from the sole perspective of the insurer (resp. reinsurer) considered in Cheung and Lo (2017) and Lo (2017a).

Parenthetically, Problem (3.1) bears some resemblance to the problem of minimizing a linear combination of Type I and Type II error probabilities of a statistical test in hypothesis testing theory. In that context, the unit-valued function $\gamma _{*}$ is referred to as the randomized part of the statistical test. For convenience, in the rest of this paper we shall refer to $\gamma _{*}$ generically as the randomization function.

The optimal solutions presented in Theorem 3.1 may appear abstract and esoteric. This is, in fact, a merit stemming from the generality of our problem framework, which applies to any distortion risk measure. To display a more concrete form of the solutions necessitates the prescriptions of the specific functions $g_{i},g_{r}$, and h. Only in this way can the three sets

$$\begin{aligned} \{r\circ S_{X}<0\},\quad \{r\circ S_{X}=0\},\quad \text {and}\quad \{r\circ S_{X}>0\} \end{aligned}$$

be determined explicitly. The next two subsections successively study the cases when the insurer and reinsurer are both VaR-adopters or TVaR-adopters together with the expected value premium principle. Our choices of the risk measures and premium principle are motivated by the explicitness of the resulting solutions, the prominence of VaR and TVaR in the insurance and banking industries, as well as the popularity of the expected value premium principle in reinsurance studies. We specialize Theorem 3.1 to these specific choices, describe the Pareto-optimal policies analytically, and illustrate our results geometrically by portraying the insurer–reinsurer Pareto frontier. Even for these simple choices of $g_{i},g_{r}$, and h, it turns out that the determination of Pareto-optimal solutions is a highly nontrivial task.

3.2 Pareto-optimal policies under VaR

When the insurer and reinsurer both adopt VaR as their risk measurement vehicles and the reinsurance premium is calibrated by the expected value premium principle with a safety loading of $\theta$ (i.e., $h(x)=(1+\theta )x$), Problem (3.1) becomes

$$\begin{aligned} \inf _{I\in \mathcal {I}}\left[ \lambda \text {VaR}_{\alpha }(X-I(X)+P_{I(X)})+(1-\lambda )\text {VaR}_{\beta }(I(X)-P_{I(X)})\right] , \end{aligned}$$

(3.4)

where $\alpha$ and $\beta$ are the probability levels of the insurer and reinsurer, respectively, and the function $r\circ S_{X}$ reduces to

$$\begin{aligned} r(S_{X}(t))=(2\lambda -1)(1+\theta )S_{X}(t)-\lambda 1_{\{S_{X}(t)>1-\alpha \}}+(1-\lambda )1_{\{S_{X}(t)>1-\beta \}}. \end{aligned}$$

3.2.1 Explicit solutions

The VaR-based Pareto-optimal reinsurance Problem (3.4) was considered in Jiang et al. (2017) and solved by distinguishing a series of cases involving the range of values of various model parameters (see Subsections 4.1 and 4.2 therein). With the aid of Theorem 3.1, we provide a much more systematic proof which dispenses with the lengthy derivations in Jiang et al. (2017) and, more importantly, provides full characterizations of the Pareto-optimal reinsurance policies. As noted earlier and will be shown in Sect. 3.2.3, the ability to exhaust the entire set of Pareto-optimal solutions is central to developing the Pareto frontier.

Theorem 3.2

(Solutions of Problem (3.4)) Assume that $\theta /(\theta +1)<\alpha \wedge \beta$.

• (a) If $0\le \lambda <1/2$, then Problem (3.4) is solved by

  $$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} 1, &{} \text {if }t<F_{X}^{-1}(\theta /(\theta +1))\text { or }t\ge F_{X}^{-1}(\beta ),\\ \gamma _{*}(t), &{} \text {if }F_{X}^{-1}(\theta /(\theta +1))\le t\le F_{X}^{-1+}(\theta /(\theta +1)),\\ 0, &{} \text {if }F_{X}^{-1+}(\theta /(\theta +1))<t<F_{X}^{-1}(\beta ). \end{array}\right. } \end{aligned}$$

• (b) If $\lambda =1/2$, then Problem (3.4) is solved by⁴

  $$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} 1, &{} \text {if }F_{X}^{-1}(\beta )\le t<F_{X}^{-1}(\alpha ),\\ \gamma _{*}(t), &{} \text {if }0\le t<F_{X}^{-1}(\alpha \wedge \beta )\text { or }t\ge F_{X}^{-1}(\alpha \vee \beta ),\\ 0, &{} \text {elsewhere}. \end{array}\right. } \end{aligned}$$

• (c) If $1/2<\lambda \le 1$, then Problem (3.4) is solved by

  $$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} 1, &{} \text {if }F_{X}^{-1+}(\theta /(\theta +1))\le t<F_{X}^{-1}(\alpha ),\\ \gamma _{*}(t), &{} \text {if }F_{X}^{-1}(\theta /(\theta +1))\le t<F_{X}^{-1+}(\theta /(\theta +1)),\\ 0, &{} \text {elsewhere}. \end{array}\right. } \end{aligned}$$

Proof

With a slight abuse of notation, we write “$\,{\displaystyle \begin{array}{c} <\\ \text {or}\\ \le \end{array} }\,$” and “$\,{\displaystyle \begin{array}{c} >\\ \text {or}\\ \ge \end{array} }\,$” while translating different inequalities into equivalent inequalities for t if both strict and weak inequalities are possible, depending on the nature (e.g. existence of jumps) of the distribution function $F_{X}$. Note that the choice of strict or weak inequalities does affect the definition of the optimal $I^{\prime }$, but has no effect on the optimal I at all because $I(x)=\int _{0}^{x}I^{\prime }(t)\,\mathrm {d}t$ and that functions which are almost everywhere equal share the same Lebesgue integral.

To apply Theorem 3.1, it suffices to determine the sets $\{t\in [0,F_{X}^{-1}(1))\mid r(S_{X}(t))<0\}$ and $\{t\in [0,F_{X}^{-1}(1))\mid r(S_{X}(t))=0\}$ for each $\lambda \in [0,1]$. To this end, consider the strict inequality

$$\begin{aligned} r(S_{X}(t))=(2\lambda -1)(1+\theta )S_{X}(t)-\lambda 1_{\{S_{X}(t)>1-\alpha \}}+(1-\lambda )1_{\{S_{X}(t)>1-\beta \}}<0 \end{aligned}$$

(3.5)

over $t\in [0,F_{X}^{-1}(1))$. Due to (2.2), we have

$$\begin{aligned} S_{X}(t)>1-\alpha \quad \Leftrightarrow \quad t<F_{X}^{-1}(\alpha )\quad \text {and}\quad S_{X}(t)>1-\beta \quad \Leftrightarrow \quad t<F_{X}^{-1}(\beta ). \end{aligned}$$

We consider four ranges of values of t.

Case 1.:

If $0\le t<F_{X}^{-1}(\alpha \wedge \beta )$, then (3.5) becomes

$$\begin{aligned} (2\lambda -1)(1+\theta )S_{X}(t)<2\lambda -1, \end{aligned}$$

which is equivalent to $t<F_{X}^{-1}(\theta /(\theta +1))$ for $0\le \lambda <1/2$, and to $t\,{\displaystyle \begin{array}{c} >\\ \text {or}\\ \ge \end{array} }\,F_{X}^{-1+}(\theta /(\theta +1))$ for $1/2<\lambda \le 1$. When $\lambda =1/2$, both sides of the inequality are zero and (3.5) does not hold.

Case 2.:

If $\beta \le \alpha$ and $F_{X}^{-1}(\beta )\le t<F_{X}^{-1}(\alpha )$, then (3.5) is identical to

$$\begin{aligned} (2\lambda -1)(1+\theta )S_{X}(t)<\lambda , \end{aligned}$$

which is always true regardless of the value of $\lambda$. This is because

$$\begin{aligned} (2\lambda -1)(1+\theta )S_{X}(t)\,{\left\{ \begin{array}{ll}<0\le \lambda , &{} \text {when }0\le \lambda<1/2,\\ =0<\lambda , &{} \text {when }\lambda =1/2,\\<2\lambda -1\le \lambda , &{} \text {when }1/2<\lambda \le 1. \end{array}\right. } \end{aligned}$$

Case 3.:

If $\alpha <\beta$ and $F_{X}^{-1}(\alpha )\le t<F_{X}^{-1}(\beta )$, then (3.5) reduces to

$$\begin{aligned} (2\lambda -1)(1+\theta )S_{X}(t)<\lambda -1, \end{aligned}$$

which is not satisfied by any value of $\lambda$. This is because

$$\begin{aligned} (2\lambda -1)(1+\theta )S_{X}(t)\,{\left\{ \begin{array}{ll}>2\lambda -1\ge \lambda -1, &{} \text {when }0\le \lambda<1/2,\\ =0>\lambda -1, &{} \text {when }\lambda =1/2,\\ >0\ge \lambda -1, &{} \text {when }1/2<\lambda \le 1. \end{array}\right. } \end{aligned}$$

Case 4.:

If $F_{X}^{-1}(\alpha \vee \beta )\le t<F_{X}^{-1}(1)$, then (3.5) becomes

$$\begin{aligned} (2\lambda -1)(1+\theta )S_{X}(t)<0, \end{aligned}$$

which is satisfied when and only when $0\le \lambda <1/2$.

Upon the combination of the four cases, we conclude that the solutions of inequality (3.5) and, analogously, the equality $r(S_{X}(t))=0$, in t classified according to different values of $\lambda$ are as given in Table 1. Inserting these results into (3.2) in Theorem 3.1 completes the proof of Theorem 3.2. $\square$

Table 1 The solutions of $r(S_{X}(t))<0$ and $r(S_{X}(t))=0$ over t for different values of $\lambda$

We remark that the assumption $\theta /(\theta +1)<\alpha \wedge \beta$ is an innocuous one and, for all intents and purposes, satisfied in practice, because the profit loading $\theta$ charged by the reinsurer usually takes a small positive value whereas the probability levels $\alpha$ and $\beta$ that define the VaR risk measure tend to approach one in practice.

3.2.2 Discussions

While the explicit expressions of the Pareto-optimal reinsurance policies $I_{*}$ are given in Theorem 3.2, more insights into their structure can be acquired via examining the qualitative behavior of the objective function in integral form. We begin by observing that the weight $\lambda$ plays its role in the design of $I_{*}$ only through classifying their construction into three cases, (a), (b), and (c); the precise value of $\lambda$ does not enter the expression of $I_{*}^{\prime }$ in any case. In other words, Problem (3.4) with $\lambda \in [0,1/2)$ (Case (a)) admits exactly the same set of solutions as Problem (3.4) when $\lambda =0$, which is the reinsurer’s risk minimization problem

$$\begin{aligned} \inf _{I\in \mathcal {I}}\text {VaR}_{\beta }(I(X)-P_{I(X)}). \end{aligned}$$

Likewise, Problem (3.4) for $\lambda \in (1/2,1]$ (Case (c)) is essentially equivalent to Problem (3.4) when $\lambda =1$, which is the risk minimization problem from the sole perspective of the insurer:

$$\begin{aligned} \inf _{I\in \mathcal {I}}\text {VaR}_{\alpha }(X-I(X)+P_{I(X)}). \end{aligned}$$

Theorem 3.2 therefore mathematically expresses the peculiarity that the Pareto-optimal reinsurance policies in the VaR setting are designed from the sole perspective of one party, depending on whether $\lambda <1/2$ (from the reinsurer’s point of view) or $\lambda >1/2$ (from the insurer’s point of view). This phenomenon may run counter to intuition given that Problem (3.4) is designed to accommodate the joint interests of the insurer and reinsurer in the first place, and that some compromise between the insurer and reinsurer should have been anticipated. When $\lambda =1/2$, meaning that equal weight is attached to the insurer and reinsurer, any reinsurance policy that entails full coverage on the set $[F_{X}^{-1}(\beta ),F_{X}^{-1}(\alpha ))$ is Pareto-optimal.

The anomalous reduction of Problem (3.4) to a one-party risk minimization problem can be heuristically understood taking into account the behavior of the integrands that constitute the insurer’s and reinsurer’s VaR. In integral form, we have

$$\begin{aligned} x(I)= & {} \text {VaR}_{\alpha }(X-I(X)+P_{I(X)})=\text {VaR}_{\alpha }(X)+\int _{0}^{\infty }f_{i}^{\text {VaR}}(t)I^{\prime }(t)\,\mathrm {d}t,\\ y(I)= & {} \text {VaR}_{\beta }(I(X)-P_{I(X)})=\int _{0}^{\infty }f_{r}^{\text {VaR}}(t)I^{\prime }(t)\,\mathrm {d}t, \end{aligned}$$

where

$$\begin{aligned} f_{i}^{\text {VaR}}(t):=(1+\theta )S_{X}(t)-1_{\{S_{X}(t)>1-\alpha \}}\quad \text {and}\quad f_{r}^{\text {VaR}}(t):=1_{\{S_{X}(t)>1-\beta \}}-(1+\theta )S_{X}(t). \end{aligned}$$

(3.6)

Note that $f_{i}^{\text {VaR}}$ and $f_{r}^{\text {VaR}}$ simultaneously take negative values on $[F_{X}^{-1}(\beta ),F_{X}^{-1}(\alpha ))$ and positive values on $[F_{X}^{-1}(\alpha ),F_{X}^{-1}(\beta ))$. This suggests that the optimal marginal indemnity function $I_{*}^{\prime }$, regardless of the value of $\lambda$, must be set to 1 on $[F_{X}^{-1}(\beta ),F_{X}^{-1}(\alpha ))$ and to 0 on $[F_{X}^{-1}(\alpha ),F_{X}^{-1}(\beta ))$ to achieve the greatest reduction in the objective function of Problem (3.4). Outside $[F_{X}^{-1}(\alpha \wedge \beta ),F_{X}^{-1}(\alpha \vee \beta ))$, $f_{i}^{\text {VaR}}$ and $f_{r}^{\text {VaR}}$ always differ in sign but share the same magnitude. It follows that ceding an additional unit of loss on $(F_{X}^{-1+}(\theta /(\theta +1)),F_{X}^{-1}(\alpha ))$, where $f_{i}^{\text {VaR}}$ is negative, generates a decrease in the insurer’s risk level x that is exactly offset by the increase in the reinsurer’s risk level y. If $\lambda >1/2$, this leads to an overall decrease in the objective function $\lambda x+(1-\lambda )y$. This explains why when $\lambda >1/2$, Problem (3.4) is solved by solely minimizing x(I) over $I\in \mathcal {I}$, which is Problem (3.4) with $\lambda =1$. Analogous explanations can be applied to justify the reduction of Problem (3.4) to the reinsurer’s risk minimization problem when $\lambda <1/2$ as well as the diversity of optimal policies when $\lambda =1/2$.

3.2.3 Pareto frontier

Armed with Theorem 3.2, we are in a position to give a pictorial description of the insurer–reinsurer Pareto frontier in the VaR framework. Geometrically, each Pareto-optimal reinsurance policy I in $\mathcal {I}$ gives rise to a pair of points capturing the insurer’s risk level and the reinsurer’s risk level. Collectively, these (x, y)’s constitute the Pareto frontier, which is traced out as the weight $\lambda$ ranges from 0 to 1 and when the randomization function $\gamma _{*}$ varies from the constant zero function to the constant one function. This is a continuous (because the risk set is convex) curve in the x–y plane that visualizes the insurer–reinsurer trade-off structure as far as Pareto optimality is concerned.

Exhibited in Fig. 2, the Pareto frontier in the VaR case is a downward tilting straight line with a slope of $-1$. The practical implication is that subject to Pareto optimality, the insurer and reinsurer trade risk linearly, in a one-to-one manner. To understand the geometry of the frontier, we first observe that when $0\le \lambda <1/2$ or $1/2<\lambda \le 1$, the specification of the randomization function $\gamma _{*}$ does not affect the risk levels of the insurer and reinsurer. This is because $\gamma _{*}$ is defined only on a subset on which $f_{i}^{\text {VaR}}$ and $f_{r}^{\text {VaR}}$ defined in (3.6) are zero. These two cases correspond respectively to points A and B in Fig. 2. When $\lambda =1/2$, the selection of $\gamma _{*}$ does affect the individual values of x and y. As $f_{i}^{\text {VaR}}$ and $f_{r}^{\text {VaR}}$ satisfy $f_{i}^{\text {VaR}}(t)=-f_{r}^{\text {VaR}}(t)$ for all $t\notin [F_{X}^{-1}(\alpha \wedge \beta ),F_{X}^{-1}(\alpha \vee \beta ))$, the change in x as a result of perturbing $\gamma _{*}$ coincides with the change in y of an opposite sign. As $\gamma _{*}$ varies from the constant zero function to the constant one function, a downward tilting straight line with a slope of $-1$ connecting points A and B is traced out. It should be noted that although different points on this straight line share different values of x and y, they all give rise to the same value of the objective function, which is $(x+y)/2$.

Fig. 2

The insurer–reinsurer Pareto frontier (in bold) in the VaR case. The shaded region represents the risk set

3.3 Pareto-optimal policies under TVaR

In the same spirit as the preceding subsection, we now investigate the TVaR-based Pareto-optimal reinsurance problem with the expected value premium principle:

$$\begin{aligned} \inf _{I\in \mathcal {I}}[\lambda \text {TVaR}_{\alpha }(X-I(X)+P_{I(X)})+(1-\lambda )\text {TVaR}_{\beta }(I(X)-P_{I(X)})] \end{aligned}$$

(3.7)

with

$$\begin{aligned} r(S_{X}(t))=(2\lambda -1)(1+\theta )S_{X}(t)-\lambda \left( \frac{S_{X}(t)}{1-\alpha }\wedge 1\right) +(1-\lambda )\left( \frac{S_{X}(t)}{1-\beta }\wedge 1\right) . \end{aligned}$$

3.3.1 Explicit solutions

Compared to their VaR counterparts, it turns out that the solutions of Problem (3.7) differ in structure depending on whether $\beta \le \alpha$ or $\alpha <\beta$ and are considerably more involved. The solutions for the case when $\beta \le \alpha$ are presented in Theorem 3.3 below, and those for the complementary case when $\alpha <\beta$ are collected in Theorem 3.4, followed by a unifying proof that covers both cases.

Theorem 3.3

(Solutions of Problem (3.7) with $\beta \le \alpha$) Assume that $\theta /(\theta +1)<\beta \le \alpha$, and let

$$\begin{aligned} c= & {} \frac{1/(1-\beta )-(1+\theta )}{1/(1-\beta )+1/(1-\alpha )-2(1+\theta )}\in (0,1/2],\\ d_{1}= & {} 1-\frac{\lambda }{[2(1+\theta )-1/(1-\beta )]\lambda +[1/(1-\beta )-(1+\theta )]}. \end{aligned}$$

• (a) If $0\le \lambda <c$, then Problem (3.7) is solved by

  $$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} 1, &{} \text {if }t<F_{X}^{-1}(\theta /(\theta +1)),\\ \gamma _{*}(t), &{} \text {if }F_{X}^{-1}(\theta /(\theta +1))\le t\le F_{X}^{-1+}(\theta /(\theta +1)),\\ 0, &{} \text {if }t>F_{X}^{-1+}(\theta /(\theta +1)). \end{array}\right. } \end{aligned}$$

• (b) If $\lambda =c$, then Problem (3.7) is solved by

  $$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} 1, &{} \text {if }t<F_{X}^{-1}(\theta /(\theta +1)),\\ \gamma _{*}(t), &{} \text {if }F_{X}^{-1}(\theta /(\theta +1))\le t\le F_{X}^{-1+}(\theta /(\theta +1))\text { or }t\ge F_{X}^{-1}(\alpha ),\\ 0, &{} \text {if }F_{X}^{-1+}(\theta /(\theta +1))<t<F_{X}^{-1}(\alpha ). \end{array}\right. } \end{aligned}$$

• (c) If $c<\lambda <1/2$, then Problem (3.7) is solved by

  $$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} 1, &{} \text {if }t<F_{X}^{-1}(\theta /(\theta +1))\text { or }t>F_{X}^{-1+}(d_{1}),\\ \gamma _{*}(t), &{} \text {if }F_{X}^{-1}(\theta /(\theta +1))\le t\le F_{X}^{-1+}(\theta /(\theta +1))\text { or }F_{X}^{-1}(d_{1})\le t\le F_{X}^{-1+}(d_{1}),\\ 0, &{} \text {if }F_{X}^{-1+}(\theta /(\theta +1))<t<F_{X}^{-1}(d_{1}). \end{array}\right. } \end{aligned}$$

• (d) If $\lambda =1/2$, then Problem (3.7) is solved by

  $$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} 1, &{} \text {if }t>F_{X}^{-1+}(\beta ),\\ \gamma _{*}(t), &{} \text {if }0\le t\le F_{X}^{-1+}(\beta ). \end{array}\right. } \end{aligned}$$

• (e) If $1/2<\lambda \le 1$, then Problem (3.7) is solved by

  $$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} 1, &{} \text {if }t>F_{X}^{-1+}(\theta /(\theta +1)),\\ \gamma _{*}(t), &{} \text {if }F_{X}^{-1}(\theta /(\theta +1))\le t\le F_{X}^{-1+}(\theta /(\theta +1)),\\ 0, &{} \text {if }t<F_{X}^{-1}(\theta /(\theta +1)). \end{array}\right. } \end{aligned}$$

Since a typical reinsurer is less risk-averse than a typical insurer because of a larger business capacity and greater geographical diversification, the case when $\beta \le \alpha$ is of higher practical interest than the complementary case when $\alpha <\beta$. For completeness, the next theorem deals with the solutions of Problem (3.7) in the latter case.

Theorem 3.4

(Solutions of Problem (3.7) with $\alpha <\beta$) Assume that $\theta /(\theta +1)<\alpha <\beta$, and let

$$\begin{aligned} c= & {} \frac{1/(1-\beta )-(1+\theta )}{1/(1-\beta )+1/(1-\alpha )-2(1+\theta )}\in (1/2,1),\\ d_{2}= & {} 1-\frac{1-\lambda }{(1+\theta )+[1/(1-\alpha )-2(1+\theta )]\lambda }. \end{aligned}$$

• (a) If $0\le \lambda <1/2$, then Problem (3.7) is solved by

  $$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} 1, &{} \text {if }t<F_{X}^{-1}(\theta /(\theta +1)),\\ \gamma _{*}(t), &{} \text {if }F_{X}^{-1}(\theta /(\theta +1))\le t\le F_{X}^{-1+}(\theta /(\theta +1)),\\ 0, &{} \text {if }t>F_{X}^{-1+}(\theta /(\theta +1)). \end{array}\right. } \end{aligned}$$

• (b) If $\lambda =1/2$, then Problem (3.7) is solved by

  $$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} \gamma _{*}(t), &{} \text {if }t\le F_{X}^{-1+}(\alpha ),\\ 0, &{} \text {if }t>F_{X}^{-1+}(\alpha ). \end{array}\right. } \end{aligned}$$

• (c) If $1/2<\lambda <c$, then Problem (3.7) is solved by

  $$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} 1, &{} \text {if }F_{X}^{-1+}(\theta /(\theta +1))<t<F_{X}^{-1}(d_{2}),\\ \gamma _{*}(t), &{} \text {if }F_{X}^{-1}(\theta /(\theta +1))\le t\le F_{X}^{-1+}(\theta /(\theta +1))\text { or }F_{X}^{-1}(d_{2})\le t\le F_{X}^{-1+}(d_{2}),\\ 0, &{} \text {elsewhere}. \end{array}\right. } \end{aligned}$$

• (d) If $\lambda =c$, then Problem (3.7) is solved by

  $$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} 1, &{} \text {if }F_{X}^{-1+}(\theta /(\theta +1))<t<F_{X}^{-1}(\beta ),\\ \gamma _{*}(t), &{} \text {if }F_{X}^{-1}(\theta /(\theta +1))\le t\le F_{X}^{-1+}(\theta /(\theta +1))\text { or }F_{X}^{-1}(\beta )\le t,\\ 0, &{} \text {if }t<F_{X}^{-1}(\theta /(\theta +1)). \end{array}\right. } \end{aligned}$$

• (e) If $c<\lambda \le 1$, then Problem (3.7) is solved by

  $$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} 1, &{} \text {if }F_{X}^{-1+}(\theta /(\theta +1))<t,\\ \gamma _{*}(t), &{} \text {if }F_{X}^{-1}(\theta /(\theta +1))\le t\le F_{X}^{-1+}(\theta /(\theta +1)),\\ 0, &{} \text {if }t<F_{X}^{-1}(\theta /(\theta +1)). \end{array}\right. } \end{aligned}$$

Proof

(For Theorems 3.3 and 3.4) The proof parallels that of Theorem 3.2. Again, we solve the strict inequality

$$\begin{aligned} r(S_{X}(t))=(2\lambda -1)(1+\theta )S_{X}(t)-\lambda \left[ \frac{S_{X}(t)}{1-\alpha }\wedge 1\right] +(1-\lambda )\left[ \frac{S_{X}(t)}{1-\beta }\wedge 1\right] <0 \end{aligned}$$

(3.8)

over four ranges of values of t.

Case 1.:

If $0\le t<F_{X}^{-1}(\alpha \wedge \beta )$, then (3.8) becomes

$$\begin{aligned} (2\lambda -1)(1+\theta )S_{X}(t)<2\lambda -1, \end{aligned}$$

which is the same as Case 1 in the proof of Theorem 3.2. Thus (3.8) is equivalent to $t<F_{X}^{-1}(\theta /(\theta +1))$ for $0\le \lambda <1/2$ and to $t\,{\displaystyle \begin{array}{c} >\\ \text {or}\\ \ge \end{array} }\,F_{X}^{-1+}(\theta /(\theta +1))$ for $1/2<\lambda \le 1$. The inequality does not hold when $\lambda =1/2$.

Case 2.:

If $\beta \le \alpha$ and $F_{X}^{-1}(\beta )\le t<F_{X}^{-1}(\alpha )$, then (3.8) is the same as

$$\begin{aligned}&\left[ (2\lambda -1)(1+\theta )+\frac{1-\lambda }{1-\beta }\right] S_{X}(t)\\&\quad =\left[ \left( 2(1+\theta )-\frac{1}{1-\beta }\right) \lambda +\left( \frac{1}{1-\beta }-(1+\theta )\right) \right] S_{X}(t)<\lambda . \end{aligned}$$

As

$$\begin{aligned}&\left[ 2(1+\theta )-\frac{1}{1-\beta }\right] \lambda +\left[ \frac{1}{1-\beta }-(1+\theta )\right] \\&\quad \ge {\left\{ \begin{array}{ll} \frac{1}{1-\beta }-(1+\theta )>0, &{} \text {if }2(1+\theta )-\frac{1}{1-\beta }\ge 0,\\ 1+\theta >0, &{} \text {if }2(1+\theta )-\frac{1}{1-\beta }<0, \end{array}\right. } \end{aligned}$$

it follows that (3.8) can be further written as

$$\begin{aligned} S_{X}(t)<\frac{\lambda }{[2(1+\theta )-1/(1-\beta )]\lambda +[1/(1-\beta )-(1+\theta )]}, \end{aligned}$$

which is equivalent to

$$\begin{aligned} t\,{\displaystyle \begin{array}{c} >\\ \text {or}\\ \ge \end{array} }\,F_{X}^{-1+}\left( 1-\frac{\lambda }{[2(1+\theta )-1/(1-\beta )]\lambda +[1/(1-\beta )-(1+\theta )]}\right) =F_{X}^{-1+}(d_{1}). \end{aligned}$$

Observe that $d_{1}$ is non-increasing in $\lambda$, equal to $\alpha$ when $\lambda =c$ and $\beta$ when $\lambda =1/2$.

Case 3.:

If $\alpha <\beta$ and $F_{X}^{-1}(\alpha )\le t<F_{X}^{-1}(\beta )$, then (3.8) reduces to

$$\begin{aligned}&\left[ (2\lambda -1)(1+\theta )-\frac{\lambda }{1-\alpha }\right] S_{X}(t)\\&\quad =\left[ \left( 2(1+\theta )-\frac{1}{1-\alpha }\right) \lambda -(1+\theta )\right] S_{X}(t)<\lambda -1. \end{aligned}$$

Since

$$\begin{aligned} \left[ 2(1+\theta )-\frac{1}{1-\alpha }\right] \lambda -(1+\theta )\le {\left\{ \begin{array}{ll} (1+\theta )-\frac{1}{1-\alpha }<0, &{} \text {if }2(1+\theta )-\frac{1}{1-\alpha }\ge 0,\\ -(1+\theta )<0, &{} \text {if }2(1+\theta )-\frac{1}{1-\alpha }<0, \end{array}\right. } \end{aligned}$$

it follows that (3.8) is equivalent to

$$\begin{aligned} S_{X}(t)>\frac{1-\lambda }{(1+\theta )+[1/(1-\alpha )-2(1+\theta )]\lambda }, \end{aligned}$$

or to

$$\begin{aligned} t<F_{X}^{-1}\left( 1-\frac{1-\lambda }{(1+\theta )+[1/(1-\alpha )-2(1+\theta )]\lambda }\right) =F_{X}^{-1}(d_{2}). \end{aligned}$$

Note that $d_{2}$ is strictly increasing in $\lambda$, equal to $\alpha$ when $\lambda =1/2$ and $\beta$ when $\lambda =c$.

Case 4.:

If $F_{X}^{-1}(\alpha \vee \beta )\le t<F_{X}^{-1}(1)$, then (3.8) is identical to

$$\begin{aligned} \left[ (2\lambda -1)(1+\theta )-\frac{\lambda }{1-\alpha }+\frac{1-\lambda }{1-\beta }\right] S_{X}(t)<0, \end{aligned}$$

which, because $S_{X}(t)$ is strictly positive on $[F_{X}^{-1}(\alpha \vee \beta ),F_{X}^{-1}(1))$ (if non-empty), is the same as

$$\begin{aligned}&(2\lambda -1)(1+\theta )-\frac{\lambda }{1-\alpha }+\frac{1-\lambda }{1-\beta }\\&\quad =\left[ 2(1+\theta )-\frac{1}{1-\alpha }-\frac{1}{1-\beta }\right] \lambda -(1+\theta )+\frac{1}{1-\beta }<0. \end{aligned}$$

Since $2(1+\theta )-1/(1-\alpha )-1/(1-\beta )<0$ by hypothesis, the preceding inequality is equivalent to

$$\begin{aligned} \lambda >\frac{1/(1-\beta )-(1+\theta )}{1/(1-\alpha )+1/(1-\beta )-2(1+\theta )}=c. \end{aligned}$$

Combining the four cases, we deduce that the solutions of (3.8) arranged according to the relative values of $\alpha$ and $\beta$ and various values of $\lambda$ are given in Tables 2 and 3. The use of Theorem 3.1 along with the results in the two tables proves Theorems 3.3 and 3.4. $\square$

It would be remiss not to point out that a version of Theorems 3.3 and 3.4 without assuming that $\theta /(\theta +1)<\alpha \wedge \beta$ has been independently and recently established in Cai et al. (2017) by means of some sophisticated algebraic arguments (see Theorems 3.1 and 3.2 therein). We remark that although Theorems 3.3 and 3.4 in this article presuppose that $\theta /(\theta +1)<\alpha \wedge \beta$, which is the scenario of predominant practical interest, the techniques used in our proofs can be easily modified to deal with the case of $\theta /(\theta +1)\ge \alpha \wedge \beta$; the solutions of inequality (3.8) will differ. Combining the two cases into a single theorem will substantially complicate the presentation of the results for a minimal gain in generality and applicability (note that Theorems 3.1 and 3.2 of Cai et al. (2017) are divided into 10 and 12 cases, respectively). Methodology-wise, it also merits mention that the proofs of Theorems 3.3 and 3.4, which are radically different from the algebraic proofs of Cai et al. (2017), not only are more systematic and transparent, but also allow us to formulate the optimal reinsurance policies as a ready by-product of solving the inequality $r(S_{X}(t))\le 0$. The need for a preconception about the shape of the solution and justifying its optimality a posteriori is obviated.

3.3.2 Discussions

In the remainder of this article, we will concentrate on the practically more important case when $\beta \le \alpha$.

A comparison of Theorems 3.2 and 3.3 reveals that the solutions of the TVaR-based Problem (3.7) with $\beta \le \alpha$ share some common features as those of the VaR-based Problem (3.4), yet possess some distinct and striking features. Again, the behavior of the integrands that constitute the insurer’s and reinsurer’s TVaR is highly conducive to understanding the structure of the optimal solutions. The integrands in the TVaR setting are

$$\begin{aligned} f_{i}^{\text {TVaR}}(t)=(1+\theta )S_{X}(t)-\frac{S_{X}(t)}{1-\alpha }\wedge 1\quad \text {and}\quad f_{r}^{\text {TVaR}}(t)=\frac{S_{X}(t)}{1-\beta }\wedge 1-(1+\theta )S_{X}(t). \end{aligned}$$

Table 2 The solutions of $r(S_{X}(t))<0$ and $r(S_{X}(t))=0$ over t for different values of $\lambda$ when $\beta \le \alpha$

Table 3 The solutions of $r(S_{X}(t))<0$ and $r(S_{X}(t))=0$ over t for different values of $\lambda$ when $\alpha <\beta$

First, Problem (3.7), in parallel with Problem (3.4), is essentially equivalent to the reinsurer’s TVaR minimization problem and the insurer’s TVaR minimization problem when $\lambda$ is small enough (Case (a) with $\lambda \in [0,c)$) and when $\lambda$ is large enough (Case (e) with $\lambda \in (1/2,1]$), respectively. It is interesting that the two cutoff values for $\lambda$, namely c and 1 / 2, are asymmetric about 1 / 2, the midpoint of 0 and 1. Moreover, in Cases (b) and (d), the randomization function $\gamma _{*}$ is again defined on subsets on which $f_{i}^{\text {TVaR}}$ is directly proportional to $f_{r}^{\text {TVaR}}$. In Case (b), we have

$$\begin{aligned} cf_{i}^{\text {TVaR}}(t)+(1-c)f_{r}^{\text {TVaR}}(t)= & {} \left[ \frac{1/(1-\beta )-(1+\theta )}{1/(1-\beta )+1/(1-\alpha )-2(1+\theta )}\right] \left[ (1+\theta )-\frac{1}{1-\alpha }\right] S_{X}(t)\\&+\,\left[ \frac{1/(1-\alpha )-(1+\theta )}{1/(1-\beta )+1/(1-\alpha )-2(1+\theta )}\right] \left[ \frac{1}{1-\beta }-(1+\theta )\right] S_{X}(t)\\= & {} 0 \end{aligned}$$

for all $t\ge F_{X}^{-1}(\alpha )$. Thus the design of $\gamma _{*}$ on $[F_{X}^{-1}(\alpha ), F_{X}^{-1}(1))$ does not affect the value of the objective function, although it does alter the individual values of x and y linearly. Explanations in the same vein apply to Case (d).

Among the five cases identified in Theorem 3.3, Case (c) is the most intriguing and of greatest theoretical and practical importance. It is a mathematical manifestation of the compromise between the insurer and reinsurer in their quest for Pareto optimality, as Problem (3.7) is designed to capture in the first place. For a range of intermediate values of $\lambda$, it is found that the solutions of Problem (3.7) are neither optimal to the insurer nor to the reinsurer, but are optimal to both of them on a conciliatory basis. In fact, the precise value of $\lambda$ enters the expression of $I_{*}^{\prime }$ through $d_{1}\in (\beta ,\alpha )$ when $\lambda \in (c,1/2)$. To understand the design of $I_{*}(t)$ over $t\in [F_{X}^{-1}(\beta ),F_{X}^{-1}(\alpha ))$ in this case, observe that when $t\in (F_{X}^{-1+}(d_{1}),F_{X}^{-1}(\alpha ))$, we have

$$\begin{aligned} \lambda f_{i}^{\text {TVaR}}(t)+(1-\lambda )f_{r}^{\text {TVaR}}(t)= & {} \lambda [(1+\theta )S_{X}(t)-1]+(1-\lambda )\left[ \frac{1}{1-\beta }-(1+\theta )\right] S_{X}(t)\\< & {} \lambda \left[ (1+\theta )(1-d_{1})-1\right] +\,(1-\lambda )\left[ \frac{1}{1-\beta }-(1+\theta )\right] (1-d_{1})\\= & {} 0, \end{aligned}$$

This suggests full reinsurance on the set $(F_{X}^{-1+}(d_{1}),F_{X}^{-1}(\alpha ))$. Furthermore, due to the absence of a proportional relationship between $f_{i}^{\text {TVaR}}$ and $f_{r}^{\text {TVaR}}$ on $[F_{X}^{-1}(\beta ),F_{X}^{-1}(\alpha ))$, the values of x and y evolve non-linearly as $\lambda$ varies from c to 1 / 2, as opposed to Cases (b) and (d).

3.3.3 Pareto frontier

Figure 3 exhibits the typical insurer–reinsurer Pareto frontier in the TVaR framework when the distribution function of the ground-up loss X is strictly increasing on its support, so that sets of the form $[F_{X}^{-1}(p),F_{X}^{-1+}(p))$ are always empty for any $p\in (0,1)$. It consists of two downward sloping straight lines corresponding to $\lambda \in [0,c]$ and $\lambda \in [1/2,1]$ connected by a convex curve indexed by $\lambda \in (c,1/2)$. Arguments analogous to those in the VaR setting presented in Sect. 3.2.3 can be readily applied to justify the construction of lines AB and CD, whose slopes are $c/(c-1)$ and $-1$, respectively. The distinguishing feature of the TVaR Pareto frontier as compared to the linear frontier in the VaR setting is the middle piece which is a convex curve emanating from point B to point C with a continuously changing slope as $\lambda$ varies from c to 1 / 2. This reflects the non-linear negotiation between the insurer and reinsurer over this intermediate range of values of $\lambda$. In general, for ground-up loss distributions that are not necessarily strictly increasing, the convex curve BC is replaced by an at most countable (because the set of flat parts of $F_{X}$ corresponds to the set where the non-decreasing function $F_{X}^{-1}$ is discontinuous, which in turn is at most countable) collection of downward sloping straight lines joined by convex curves. The straight lines arise from the selection of $\gamma _{*}$ on $[F_{X}^{-1}(d_{1}),F_{X}^{-1+}(d_{1})]$ (if non-empty), where $f_{i}^{\text {TVaR}}$ is negative while $f_{r}^{\text {TVaR}}$ is positive, the two functions are proportional to each other.

Fig. 3

The insurer–reinsurer Pareto frontier (in bold) in the TVaR case when the distribution function of X is strictly increasing

4 Pareto-optimal reinsurance policies subject to individual risk constraints

Building upon the development in Sect. 3, in this section we identify the set of Pareto-optimal reinsurance policies that satisfy the individual risk constraints, which include individual rationality constraints as special cases, prescribed by the insurer and reinsurer. Whereas the imposition of these constraints guarantees that the Pareto-optimal reinsurance contracts are simultaneously acceptable to both the insurer and reinsurer, their presence also raises the technical sophistication of the resulting optimization problem in the sense that only part of the Pareto frontier may become feasible, and that the specification of the randomization function $\gamma _{*}$ has to take into account the two additional risk constraints. Nevertheless, the Pareto frontier derived in the unconstrained setting of Sect. 3 remains as a valuable device that is highly conducive to the search of Pareto-optimal reinsurance policies even in the presence of individual risk constraints. Most strikingly, the Pareto frontier allows us to transform the constrained functional minimization problem into a two-variable constrained minimization problem on the real plane, which can be solved via a swift, geometric approach. As soon as the optimal point $(x_{*},y_{*})$ on the plane is identified, so can the optimal reinsurance policy $I_{*}$ by virtue of the correspondence between the Pareto frontier and the set of (unconstrained) Pareto-optimal solutions. As in Sect. 3, we illustrate our search procedure by means of the VaR and TVaR cases, where results can be made much more explicit, although the same techniques can carry over to the general DRM framework.

4.1 Constrained Pareto-optimal policies under VaR

The constrained counterpart to the VaR-based Pareto-optimal reinsurance problem takes the following form:

$$\begin{aligned} \left\{ \begin{aligned}\inf _{I\in \mathcal {I}}&\quad \lambda \text {VaR}_{\alpha }(X-I(X)+P_{I(X)})+(1-\lambda )\text {VaR}_{\beta }(I(X)-P_{I(X)})\\ \text {s.t.}&\quad \begin{aligned}\text {VaR}_{\alpha }(X-I(X)+P_{I(X)})&\le L_{i}\\ \text {VaR}_{\beta }(I(X)-P_{I(X)})&\le L_{r} \end{aligned} \end{aligned} \right. , \end{aligned}$$

(4.1)

where $L_{i}$ and $L_{r}$ are the maximum levels of risk the insurer and reinsurer are willing to bear, respectively. To ensure that the solution set of Problem (4.1) is nonempty, it is necessary and sufficient that $(L_{i},L_{r})$ lies in the risk set, or equivalently,

$$\begin{aligned} L_{i}\ge x_{B},\quad L_{r}\ge y_{A},\quad \text {and}\quad L_{i}+L_{r}\ge F_{X}^{-1}(\alpha \wedge \beta ), \end{aligned}$$

(4.2)

where $x_{j}$ and $y_{j}$ are respectively the x-coordinate and y-coordinate of point j for $j=A,B$ in Fig. 2. Note that setting $L_{i}=\text {VaR}_{\alpha }(X)$ and $L_{r}=0$, which satisfy (4.2), imposes the insurer’s and reinsurer’s individual rationality constraints into the Pareto-optimal policies search problem. Our solutions to be shown below, however, hold true for any $(L_{i},L_{r})$ fulfilling (4.2).

Problem (4.1) was first considered in Cai et al. (2016) via some convoluted algebraic arguments and later revisited in Lo (2017a) and solved more transparently from a Neyman–Pearson perspective. With the Pareto frontier developed in Sect. 3.2.3, Problem (4.1) now admits a geometric proof which not only renders the optimal solutions self-explanatory, but can also be applied to the much more intractable TVaR setting (see Sect. 4.2). The precise steps are as follows.

Step 1.:

We first observe that Problem (4.1) is equivalent to

$$\begin{aligned} \left\{ \begin{aligned}\inf _{I\in \mathcal {I}_{*}}&\quad \lambda \text {VaR}_{\alpha }(X-I(X)+P_{I(X)})+(1-\lambda )\text {VaR}_{\beta }(I(X)-P_{I(X)})\\ \text {s.t.}&\quad \begin{aligned}\text {VaR}_{\alpha }(X-I(X)+P_{I(X)})&\le L_{i}\\ \text {VaR}_{\beta }(I(X)-P_{I(X)})&\le L_{r} \end{aligned} \end{aligned} \right. , \end{aligned}$$

(4.3)

where $\mathcal {I}_{*}$ is the set of Pareto-optimal reinsurance policies. The restriction of the feasible set from $\mathcal {I}$ to $\mathcal {I}_{*}$ does not alter the minimization problem because the minimum point of Problem (4.1) must be attained at a Pareto-optimal policy by the very definition of Pareto optimality. Here the results in Theorem 3.2 derived in the unconstrained VaR setting will be instrumental in describing $\mathcal {I}_{*}$. Do note, however, that the value of $\lambda$ to which the solution(s) of Problem (4.3) correspond(s) in the Pareto frontier may or may not coincide with the value of $\lambda$ specified a priori in the objective function of Problem (4.3) due to the presence of the two risk constraints. We will elaborate on this towards the end of this section.

Step 2.:

On the basis of Problem (4.3), we label, for $I\in \mathcal {I}_{*}$,

$$\begin{aligned} x=x(I)=\text {VaR}_{\alpha }(X-I(X)+P_{I(X)})\text { and }y=y(I)=\text {VaR}_{\beta }(I(X)-P_{I(X)}) \end{aligned}$$

and perform the following two-variable constrained minimization on the plane:

$$\begin{aligned} \left\{ \begin{aligned}\inf _{(x,y)\in \text {Pareto frontier}}&\quad \lambda x+(1-\lambda )y\\ \text {s.t.}&\quad \begin{aligned}x&\le L_{i}\\ y&\le L_{r} \end{aligned} \end{aligned} \right. . \end{aligned}$$

(4.4)

Due to the simplicity of the objective and constraint functions coupled with the regular structure of the Pareto frontier developed in Sect. 3.2.3, Problem (4.4) can be solved graphically and almost effortlessly.

Step 3.:

Finally, it remains to translate the optimal solution(s) $(x_{*},y_{*})$ of Problem (4.4) on the Pareto frontier into the optimal solution(s) $I_{*}$ of Problem (4.1) via the correspondence between the Pareto frontier and the set of Pareto-optimal policies.

This three-step solution scheme for Problem (4.1) is accomplished in the following theorem.

Theorem 4.1

(Solutions of Problem (4.1)) Assume that $\theta /(\theta +1)<\alpha \wedge \beta$ and $(L_{i},L_{r})$ satisfies (4.2). Then Problem (4.1) is solved by

$$\begin{aligned} I_{*}^{\prime }(t)={\left\{ \begin{array}{ll} 1, &{} \text {if }F_{X}^{-1}(\beta )\le t<F_{X}^{-1}(\alpha ),\\ \gamma _{*}(t), &{} \text {if }0\le t<F_{X}^{-1}(\alpha \wedge \beta )\text { or }t\ge F_{X}^{-1}(\alpha \vee \beta ),\\ 0, &{} \text {elsewhere}, \end{array}\right. } \end{aligned}$$

for any unit-valued function $\gamma _{*}$ such that:

• (a) If $0\le \lambda <1/2$:

  $$\begin{aligned} x(I_{*})=L_{i}\wedge x_{A}. \end{aligned}$$

• (b) If $\lambda =1/2$:

  $$\begin{aligned} x(I_{*})\le L_{i}\wedge x_{A}\quad \text {and}\quad y(I_{*})\le L_{r}\wedge y_{B}. \end{aligned}$$

• (c) If $1/2<\lambda \le 1$:

  $$\begin{aligned} y(I_{*})=L_{r}\wedge y_{B}. \end{aligned}$$

Proof

Without loss of generality, we assume that $L_{i}\in [x_{B},x_{A}]$ and $L_{r}\in [y_{A},y_{B}]$, so that the two risk constraints restrict the Pareto frontier from line AB to line $A^{\prime }B^{\prime }$ (see Fig. 4). To solve Problem (4.4) graphically, we fix $\lambda \in [0,1]$ and introduce the level curves of the objective function $(x,y)\mapsto \lambda x+(1-\lambda )y$, namely $\{(x,y)\in \mathbb {R}^{2}\mid \lambda x+(1-\lambda )y=z\}$ for $z\in \mathbb {R}$. For each fixed $z\in \mathbb {R}$, the set $\{(x,y)\in \mathbb {R}^{2}\mid \lambda x+(1-\lambda )y=z\}$ corresponds to all $(x,y)\in \mathbb {R}^{2}$ giving rise to the same value of the objective function and is a straight line in the x–y plane with a slope of $\lambda /(\lambda -1)$. As z varies, a family of parallel lines is generated, and the optimal (x, y) is obtained by the level curve with the lowest value of z intersecting with the restricted Pareto frontier. For different values of $\lambda$, the point(s) of intersection also differ(s).

• Case 1: If $\lambda <1/2$, then $\lambda /(\lambda -1)>-1$, and the level curve with the lowest value of z touches the Pareto frontier at point $A^{\prime }$, at which the insurer’s risk constraint is binding.

• Case 2: If $\lambda =1/2$, then $\lambda /(\lambda -1)=-1$, and the level curve with the least value of z overlaps with the entire restricted Pareto frontier, namely line $A^{\prime }B^{\prime }$, which carries all (x, y) satisfying the insurer’s and reinsurer’s risk constraints.

• Case 3: If $\lambda >1/2$, then $\lambda /(\lambda -1)<-1$, and the level curve with the minimum value of z intersects the Pareto frontier at point $B^{\prime }$, at which the reinsurer’s risk constraint is binding.

Fig. 4

Illustration of the solution of Problem (4.1) when $\lambda >1/2$. The shaded region represents the constrained risk set and the four dashed lines are four level curves of the objective function

See Fig. 4 for an illustration of Case 3. By Theorem 3.2 (b), the solutions of Problem (4.1) are defined by

$$\begin{aligned} I_{*}^{\prime }(t){\mathop {=}\limits ^{\text {a.e.}}}{\left\{ \begin{array}{ll} 1, &{} \text {if }F_{X}^{-1}(\beta )\le t<F_{X}^{-1}(\alpha ),\\ \gamma _{*}(t), &{} \text {if }0\le t<F_{X}^{-1}(\alpha \wedge \beta )\text { or }t\ge F_{X}^{-1}(\alpha \vee \beta ),\\ 0, &{} \text {elsewhere}, \end{array}\right. } \end{aligned}$$

with the unit-valued function $\gamma _{*}$ selected to bind the insurer’s risk constraint (i.e., $x(I_{*})=L_{i}$) in Case 1, bind the reinsurer’s risk constraint (i.e., $y(I_{*})=L_{r}$) in Case 3, and to satisfy both the insurer’s risk constraint and reinsurer’s risk constraint in Case 2 (i.e., $x(I_{*})\le L_{i}$ and $y(I_{*})\le L_{r}$). $\square$

We note in passing that Theorem 4.1 (a) and (c) are indications of the equivalence between Problem (4.1) and the reinsurer’s VaR minimization problem subject to the insurer’s risk constraint:

$$\begin{aligned} \left\{ \begin{aligned}\inf _{I\in \mathcal {I}}&\quad \text {VaR}_{\beta }(I(X)-P_{I(X)})\\ \text {s.t.}&\quad \text {VaR}_{\alpha }(X-I(X)+P_{I(X)})\le L_{i} \end{aligned} \right. , \end{aligned}$$

when $0\le \lambda <1/2$, and the equivalence between Problem (4.1) and the insurer’s VaR minimization problem subject to the reinsurer’s risk constraint:

$$\begin{aligned} \left\{ \begin{aligned}\inf _{I\in \mathcal {I}}&\quad \text {VaR}_{\alpha }(X-I(X)+P_{I(X)})\\ \text {s.t.}&\quad \text {VaR}_{\beta }(I(X)-P_{I(X)})\le L_{r} \end{aligned} \right. , \end{aligned}$$

when $1/2<\lambda \le 1$. Arguments in Sect. 3.2.2 can be easily adapted to explain such a reduction of a two-constraint problem to a one-constraint problem. See also Remark 4.7 of Lo (2017a). When $\lambda =1/2$, any policy on the restricted Pareto frontier is a solution of Problem (4.1). The geometric proof of Theorem 4.1 above, based on the Pareto frontier in the VaR setting, has reduced the algebraic proof of Proposition 4.6 of Lo (2017a) to an almost self-explanatory graphical search process and made the solution of Problem (4.1) considerably more transparent. This speaks to the virtues of visualizing the insurer–reinsurer trade-off structure by fully developing the Pareto frontier.

4.2 Constrained Pareto-optimal policies under TVaR

We now turn our attention to the constrained TVaR-based Pareto-optimal reinsurance problem:

$$\begin{aligned} \left\{ \begin{aligned}\inf _{I\in \mathcal {I}}&\quad \lambda \text {TVaR}_{\alpha }(X-I(X)+P_{I(X)})+(1-\lambda )\text {TVaR}_{\beta }(I(X)-P_{I(X)})\\ \text {s.t.}&\quad \begin{aligned}\text {TVaR}_{\alpha }(X-I(X)+P_{I(X)})&\le L_{i}\\ \text {TVaR}_{\beta }(I(X)-P_{I(X)})&\le L_{r} \end{aligned} \end{aligned} \right. , \end{aligned}$$

(4.5)

where $(L_{i},L_{r})$ resides in the risk set depicted in Fig. 3. Due to the complexity of the geometry of the Pareto frontier in the TVaR framework relative to that in the VaR case, especially when $\lambda$ takes intermediate values, representing the solutions of Problem (4.5) for all possible pairs of $(L_{i},L_{r})$ can be unwieldy. Although our graphical search procedure works in all possible scenarios, to demonstrate the fundamental ideas we present a concrete numerical illustration in which the ground-up loss is exponentially distributed with a mean of 1000, $\alpha =0.95$, $\beta =0.9$, $\theta =0.1$, and $(L_{i},L_{r})=(3500,650)$. Then $F_{X}^{-1}(p)=F_{X}^{-1+}(p)=-1000\ln (1-p)$ for all $p\in [0,1)$, $c=0.3201$, and the horizontal line $y=L_{r}=650$ intersects the middle piece of the Pareto frontier at a unique point $C^{\prime }$ corresponding to $\lambda =0.4160$. The restricted Pareto frontier is exhibited in Fig. 5. Specializing Theorem 3.3 to these values and applying the graphical techniques illustrated in the proof of Theorem 4.1, we can formulate the solutions of Problem (4.5) for different values of $\lambda$ as follows:

Fig. 5

The insurer–reinsurer Pareto frontier in the TVaR case when the ground-up loss is exponentially distributed with a mean of 1000, $\alpha =0.95$, $\beta =0.9$, $\theta =0.1$, and $(L_{i},L_{r})=(3500,650)$

Case 1.:

If $0\le \lambda <0.3201$, then the optimal (x, y) is given by point $A^{\prime }$ in Fig. 5. The corresponding optimal I is defined by

$$\begin{aligned} I_{*}^{\prime }(t)={\left\{ \begin{array}{ll} 1, &{} \text {if }t<95.3102,\\ \gamma _{*}(t), &{} \text {if }t\ge 2995.7323,\\ 0, &{} \text {if }95.3102\le t<2995.7323, \end{array}\right. } \end{aligned}$$

for any unit-valued function $\gamma _{*}$ such that

$$\begin{aligned} \int _{2995.7323}^{\infty }f_{i}^{\text {TVaR}}(t)\gamma _{*}(t)\,\mathrm {d}t=-500.4221. \end{aligned}$$

Case 2.:

If $\lambda =0.3201$, then any (x, y) on line $A^{\prime }B$ gives rise to the same minimum objective value. The corresponding optimal I is defined by

$$\begin{aligned} I_{*}^{\prime }(t)={\left\{ \begin{array}{ll} 1, &{} \text {if }t<95.3102,\\ \gamma _{*}(t), &{} \text {if }t\ge 2995.7323,\\ 0, &{} \text {if }95.3102\le t<2995.7323, \end{array}\right. } \end{aligned}$$

for any unit-valued function $\gamma _{*}$ such that

$$\begin{aligned} \int _{2995.7323}^{\infty }f_{i}^{\text {TVaR}}(t)\gamma _{*}(t)\,\mathrm {d}t\le -500.4221. \end{aligned}$$

Case 3.:

If $0.3201<\lambda <0.4160$, then the optimal solution is

$$\begin{aligned} I_{*}^{\prime }(t)={\left\{ \begin{array}{ll} 1, &{} \text {if }t<95.3102\text { or }t>-1000\ln (1-d_{1}),\\ 0, &{} \text {if }95.3102\le t\le -1000\ln (1-d_{1}), \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} d_{1}=1-\frac{\lambda }{[2(1+\theta )-1/(1-\beta )]\lambda +[1/(1-\beta )-(1+\theta )]}=\frac{8.9-8.8\lambda }{8.9-7.8\lambda }. \end{aligned}$$

Case 4.:

If $0.4160\le \lambda \le 1$, then optimum is achieved at point $C^{\prime }$, with the optimal I given by

$$\begin{aligned} I_{*}^{\prime }(t)={\left\{ \begin{array}{ll} 1, &{} \text {if }t<95.3102\text { or }t>2609.6450,\\ 0, &{} \text {if }95.3102\le t\le 2609.6450. \end{array}\right. } \end{aligned}$$

The optimal solutions for other choices of $(L_{i},L_{r})$ and ground-up loss distributions can be deduced in a completely analogous fashion. We observe from the solutions of Problems (4.1) and (4.5) that the effect of the two individual risk constraints is to constrain the range of values of $\lambda$ indexing the Pareto frontier to a subset of [0, 1], say $[\lambda _{L},\lambda _{U}]$ with $0\le \lambda _{L}\le \lambda _{U}\le 1$. In the proof of Theorem 4.1 in Sect. 4.1, we have $\lambda _{L}=\lambda _{U}=1/2$, whereas $\lambda _{L}=0.3201$ and $\lambda _{U}=0.4160$ in the current TVaR-based subsection. In both cases, the Pareto frontier proves useful in finding $\lambda _{L}$ and $\lambda _{U}$. A general phenomenon is that when the value of $\lambda$ that enters the objective function $\lambda x+(1-\lambda )y$ is greater than $\lambda _{U}$ (resp. less than $\lambda _{L}$), the optimal (x, y) must be attained at the leftmost (resp. rightmost) end point of the constrained Pareto frontier.

5 Concluding remarks

In this paper, we undertake a comprehensive analysis of Pareto-optimal reinsurance policies in the general realm of DRMs and in the specific contexts of VaR and TVaR. Via translating the search problem into a weighted sum functional minimization problem, analytic solutions are derived, the insurer–reinsurer Pareto frontier is developed and the connections between its shape and the properties of the prescribed risk measures are elucidated. With the aid of the Pareto frontier, we also develop a simple geometric approach to determining the Pareto-optimal reinsurance arrangements that satisfy the risk constraints imposed by the insurer and reinsurer. All in all, our results not only generalize and clarify existing results in the literature of Pareto-optimal risk sharing, but also shed light on the economics of Pareto-optimal reinsurance through algebraic and geometric representations.

Because the emphasis of this article is laid on the trade-off of risk made between insurers and reinsurers in the sense of Pareto optimality, we have focused on a one-period two-party reinsurance market, which is mathematically tractable, geometrically simple, yet adequately rich in structure to showcase the theory of Pareto-optimal reinsurance. While extending our analysis to a multi-party setting is technically feasible, this will obscure the focus of our analysis and substantially complicate the presentation of our results for a minimal gain in insights. Moreover, the Pareto frontier will become a multi-dimensional surface, which does not lend itself to visual comprehension.