Computational study of valid inequalities for the maximum k-cut problem

Abstract

We consider the maximum k-cut problem that consists in partitioning the vertex set of a graph into k subsets such that the sum of the weights of edges joining vertices in different subsets is maximized. We focus on identifying effective classes of inequalities to tighten the semidefinite programming relaxation. We carry out an experimental study of four classes of inequalities from the literature: clique, general clique, wheel and bicycle wheel. We considered 10 combinations of these classes and tested them on both dense and sparse instances for $k \in \{3,4,5,7\}$. Our computational results suggest that the bicycle wheel and wheel are the strongest inequalities for $k=3$, and that for $k \in \{4,5,7\}$ the wheel inequalities are the strongest by far. Furthermore, we observe an improvement in the performance for all choices of k when both bicycle wheel and wheel are used, at the cost of 72% more CPU time on average when compared with using only one of them.

1 Introduction

Graph partitioning problems (GPPs) are an important class of combinatorial optimization. There are various types of GPP based on the number of partitions allowed, the objective function, the types of edge weights, and the possible presence of additional constraints such as restrictions on the number of vertices allowed in each partition. This work considers the GPP known as the maximum k-cut (max-k-cut) problem: given a connected graph $G = (V, E)$ with edge weights $w_{ij}$ for all $(i,j) \in E$, partition the vertex set V into at most k subsets so as to maximize the total weight of cut edges, i.e., the edges with end points in two different subsets. This problem is sometimes also called minimum k-partition problem (Ghaddar et al. 2011). The special case of max-k-cut with k = 2 is known as the max-cut problem and has received most attention in the literature, see e.g. Barahona et al. (1988), Deza and Laurent (1997), Goemans and Williamson (1995), Krislock et al. (2012), Palagi et al. (2011) and Rendl et al. (2010).

Graph partitioning and max-k-cut problems have myriad applications as VLSI layout design (Barahona et al. 1988), sports team scheduling (Mitchell 2003), statistical physics (Liers et al. 2005), placement of television commercials (Gaur et al. 2008), network planning (Eisenblätter 2002), and floorplanning (Wei-Ming and Kuh 1987).

The unweighted version of max-k-cut is known to be $\mathcal {NP}$-complete (Papadimitriou and Yannakakis 1991). Hence, researchers have proposed heuristics (Coja-Oghlan et al. 2006), (Ma and Hao 2017), approximation algorithms (Coja-Oghlan et al. 2006), (Frieze and Jerrum 1997), and exact methods (Anjos et al. 2013; Ghaddar et al. 2011) for solving the max-k-cut. In particular the approximation method proposed in Frieze and Jerrum (1997) extends the famous semidefinite programming (SDP) results for max-cut in Goemans and Williamson (1995) to max-k-cut. The authors of Klerk et al. (2004) subsequently improved the approximation guarantees for small values of k.

Ghaddar et al. (2011) propose the SBC algorithm. It is a branch-and-cut algorithm for the minimum k-partition problem based on the SDP relaxation of max-k-cut. They found experimentally that for $k>2$ the SDP relaxation yields much stronger bounds than the LP relaxation, for both sparse and dense instances. This algorithm was improved in Anjos et al. (2013) which introduced the bundleBC algorithm to solve max-k-cut for large instances by combining the approach of Ghaddar et al. (2011) with the design principles of Biq Mac  (Rendl et al. 2010). The results in Anjos et al. (2013) confirm that, computationally speaking, the SDP relaxations often yield stronger bounds than LP relaxations.

The matrix lifting SDP relaxation of the GPP, and the use the triangle and clique inequalities to strengthen it, were studied in Sotirov (2014) and van Dam and Sotirov (2015). In particular Sotirov (2014) shows that this relaxation is equivalent to the relaxation in Frieze and Jerrum (1997) and is as competitive as any other known SDP bound for the GPP. The results also show that the triangle inequalities are stronger than the clique (independent set) inequalities.

Using a similar approach as Sotirov (2014), the authors in Dam and Sotirov (2016) propose several new bounds for max-k-cut from the maximum eigenvalue of the Laplacian matrix of G. Moreover, Dam and Sotirov (2016) shows that certain perturbations in the diagonal of the Laplacian matrix can lead to stronger bounds. In Nikiforov (2016) the author proposes a more robust bound than the one proposed in Dam and Sotirov (2016) by using the smallest eigenvalue of the adjacency matrix of G.

In Fairbrother and Letchford (2016) the authors project the polytopes associated with the formulation with only edge variables into a suitable subspace to obtain the polytopes of the formulation that has both node and edge variables. They then derive new valid inequalities and a new semidefinite programming relaxation for the max-k-cut problem. The authors suggest that the new inequalities may be of practical use only in the case of large sparse graphs.

The objective of this work is to carry out a computational study of valid inequalities that strengthen the SDP relaxation for the max-k-cut problem, and to identify the strongest ones in practice. Valid and facet-inducing inequalities for k-partition were studied in Chopra and Rao (1993, 1995). We focus our analysis on the following inequalities: Triangle, Clique, General clique, Wheel and Bicycle wheel. To the best of our knowledge, no research has specifically focused on comparing the strength of the range of inequalities considered here.

This paper is organized as follows. Sections 1.1 and 1.2 review the SDP formulation and relaxation of the max-k-cut problem. Section 2 presents the classes of inequalities and discusses the separation methods used. Section 3 describes the cutting plane algorithm used, and Sect. 4 presents and discusses the test results. The conclusions from this study are provided in Sect. 5.

1.1 Problem formulation

We assume without loss of generality that the graph $G = (V,E)$ is a complete graph because missing edges can be added with a corresponding weight of zero. Let $k \ge 2$ and define the matrix variable $X = (X_{ij})$, $i,j \in V$, as:

$$\begin{aligned} X_{ij} = \left\{ \begin{array}{cl} \frac{-1}{k-1} &{}\quad \text {if vertices }i\text { and }j\text { are in different partitions of the }k-\text {cut of }G, \\ 1 &{}\quad \text{ otherwise. } \end{array} \right. \end{aligned}$$

The max-k-cut problem on G can be expressed as:

$$\begin{aligned} \max _{X}&\sum _{i,j \in V, i < j} w_{ ij}\frac{(k-1)(1-X_{ij})}{k} \end{aligned}$$

(1)

$$\begin{aligned} \text {s.t.}&X_{ii} = 1&\forall i \in V, \end{aligned}$$

(2)

$$\begin{aligned}&X_{ij} \in \biggl \{{\frac{-1}{k-1}, 1 \biggr \}}&\forall i,j \in V, i < j, \end{aligned}$$

(3)

$$\begin{aligned}&X \succeq 0. \end{aligned}$$

(4)

We refer to this formulation as ($\mathbf{M}k\mathbf{P}$). This formulation was first proposed by Frieze and Jerrum (1997). As mentioned in Frieze and Jerrum (1997, Lemma 4), the value $-1/(k -1)$ gives the best angle separation for k vectors.

1.2 Semidefinite relaxation

Replacing constraint (3) by $\frac{-1}{k-1} \le X_{ij} \le 1$ defines the SDP relaxation. However, the constraint $X_{ij} \le 1$ can be removed since it is enforced implicitly by the constraints $X_{ii} = 1$ and $X \succeq 0$. Therefore the SDP relaxation, denoted (RMkP), is:

$$\begin{aligned} \max _{X}&\sum _{i,j \in V, i < j} w_{ ij}\frac{(k-1)(1-X_{ij})}{k} \end{aligned}$$

(5)

$$\begin{aligned} \text {s.t.}&X_{ii} = 1&\forall i \in V, \end{aligned}$$

(6)

$$\begin{aligned}&X_{ij} \ge \frac{-1}{k-1}&\forall i,j \in V, i < j,\end{aligned}$$

(7)

$$\begin{aligned}&X \succeq 0. \end{aligned}$$

(8)

2 Formulation and separation of inequalities

The SDP relaxation (RMkP) can be tightened by adding valid inequalities, i.e., cutting planes that are satisfied for all positive semidefinite matrices that are feasible for problem (MkP) but are violated by solution $X^\prime$ of the (current) SDP relaxation. In this section we present the classes of inequalities from Chopra and Rao (1993, 1995) that we consider adding to tighten the SDP relaxation. For each class, we describe its properties, its formulation in terms of the SDP variable X, and the separation routine used.

The first two classes of inequalities (Triangle and Clique) were used in the SBC branch-and-cut method (Ghaddar et al. 2011) and in the matrix lifting approach (Sotirov 2014; van Dam and Sotirov 2015). We are unaware of the other classes having been computationally tested or used.

2.1 Triangle inequalities

Triangle inequalities are based on the observation that if vertices i and h are in the same partition, and vertices h and j in the same partition, then vertices i and j necessarily have to be in the same partition. The resulting $3{|V| \atopwithdelims ()3}$ triangle inequalities are:

$$\begin{aligned} X_{ih} + X_{hj} - X_{ij} \le 1&\quad \forall i,j,h \in V. \end{aligned}$$

(9)

2.1.1 Separation of triangle inequalities

As pointed out in Anjos et al. (2013), the enumeration of all triangle inequalities is computationally inexpensive, even for large instances. Therefore, a complete enumeration is done to find triangles in the graph G that violate (9). The tolerance used to detect a violation is $10^{-5}$.

2.2 Clique inequalities

The $\left( \begin{array}{c} |V| \\ k+1 \end{array} \right)$ clique inequalities ensure that for every subset of $k+1$ vertices, at least two of the vertices belong to the same partition. We express them as:

$$\begin{aligned} \sum _{i,j \in Q, i<j} X_{ij} \ge -\frac{k}{2}&\quad \forall Q \subseteq V \text { with } |Q| = k+1. \end{aligned}$$

(10)

2.2.1 Separation of clique inequalities

The exact separation of clique is ${\mathcal {NP}}$-hard in general, and the complete enumeration is intractable even for small values of k (Ghaddar et al. 2011). We use the heuristic described in Ghaddar et al. (2011) to find a violated clique inequality for a solution $X^\prime$ of the SDP relaxation. This heuristic is described here as Algorithm 1, and returns up to |V| clique inequalities. We use a tolerance $\upvarepsilon = 10^{-5}$.

2.3 General clique inequalities

The General clique inequalities in Chopra and Rao (1993) are a generalization of the Clique inequality (10).

Let $Q = (V(Q), E(Q))$ be a clique of size $p := tk+ q$ where $t \ge 1$ and $0 \le q < k$, i.e., t is the largest integer such that $tk \le p$. In terms of the SDP variable X, the general clique inequalities have the form:

$$\begin{aligned} \sum _{i,j \in Q} X_{ij} \ge \frac{k}{k-1} \left[ z +w\left( \frac{k-1}{k} - 1\right) \right]&\quad \forall Q \subseteq V, |Q| = p, \end{aligned}$$

(11)

where $z = \frac{1}{2}t(t-1)(k-q)+\frac{1}{2}t(t+1)q$ and $w = \frac{p(p-1)}{2}$. It is proved in Chopra and Rao (1993) that (11) is valid for the polytope of the max-k-cut problem if $p \ge k$, i.e., $t \ge 1$. Furthermore, it is facet-defining if and only if $1 \le q \le k - 1$, $t \ge 1$, i.e., p is not an integer multiple of k.

2.3.1 Separation of general clique inequalities

Because the clique inequalities are included in general clique, it is clear that enumeration is also impracticable for general clique. Thus, we propose a heuristic to find the most violated general clique inequalities for $X^\prime$.

Our heuristic is a small modification of the one used to separate the clique inequalities (Algorithm 1). Specifically:

• The argument in the WHILE condition becomes $|C| \le p-1$.

• The inequality in the IF condition is replaced by

  $$\begin{aligned} \left( \displaystyle w(j) < \frac{k}{k-1} \left[ z +w\left( \frac{k-1}{k} - 1\right) \right] - \upvarepsilon \right) . \end{aligned}$$

The parameter p may vary with the number of partitions k. After preliminary tests using $p \in \{5,7,8,10,11,13\}$ for $k=3$, $p \in \{6,7,9,11,13,14\}$ for $k=4$, $p \in \{7,9,11,13,16,18\}$ for $k=5$, and $p \in \{9,11,13,16,18,20\}$ for $k=7$, we settled on with the following choices: $p = 5$ for $k = 3$; $p = 6$ for $k = 4$; $p = 7$ for $k = 5$; and $p = 11$ for $k = 7$.

2.4 Wheel inequalities

In Chopra and Rao (1993), the q-wheel is defined as $W_q=(V_q, E_q)$, where

• $V_q=\{v, v_i | i = 1, 2, \ldots , q \}$

• $E_q= {\bar{E}} \cup {\hat{E}}$, where ${\bar{E}} =\{(v,v_i), i = 1, 2,\ldots ,q\}$ and ${\hat{E}} =\{(v_i, v_{i+1}), i = 1, 2,\ldots ,q\}$.

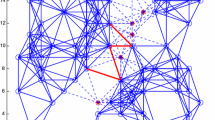
where $v \in V$, and all indices greater than q are modulo q. For $q=6$, $W_6$ is illustrated in Fig. 1.

Fig. 1

Example of wheel with $q = 6$

Let $W_q$ be a subgraph of G for $q \ge 3$. In terms of the SDP variable X, the wheel inequality is defined as:

$$\begin{aligned} \sum _{i = 1}^{ q}X_{v,v_i} -\sum _{i = 1}^{q}X_{v_i,v_{i+1}} \le \left\lfloor \frac{1}{2}q \right\rfloor \frac{k}{k-1}. \end{aligned}$$

(12)

The idea of this inequality is that vertex v can be in the same partition as vertices $v_i$ and $v_{i+1}$ if edge $e = (v_i,v_{i+1})$ is not cut. It is proved in Chopra and Rao (1993) that (12) is a valid inequality for max-k-cut, and that it defines a facet if q is odd and $k \ge 4$.

2.4.1 Separation of wheel inequalities

By inequality (12), a q-wheel is violated by $X^\prime$ if:

$$\begin{aligned} \sum _{i = 1}^{ q}X'_{v,v_i} -\sum _{i = 1}^{q}X'_{v_i,v_{i+1}} - \left( \left\lfloor \frac{1}{2}q \right\rfloor \frac{k}{k-1} \right) > 0. \end{aligned}$$

(13)

For each vertex $v \in V$, we wish to maximize the left-hand side of inequality (13) to find the most violated wheel inequality.

In Deza et al. (1992) it is shown that the odd wheel inequalities can be separated in polynomial-time. We also considered four heuristics, for a total of five methods tested:

• Exact algorithm (Deza et al. 1992).

• The GRASP meta-heuristic (Feo and Resende 1995).

• A genetic algorithm (GA) from Seyed et al. (2014).

• The K-step greedy lookahead (Scholvin 1999) with K=2.

• Our own greedy heuristic for multiple sizes of wheel (GMSW), described in Algorithm 2.

The GMSW heuristic achieved, on average, the best ratio between CPU time and performance for all tests. For instance, the performance ratio (see Sect. 4.2.1) was <0.03% higher than the exact method. In addition, its CPU time was in average 45% less. In GSMW, the parameter $NbIte \le |V| - 1$ is the maximum size allowed for the wheel. We obtained the best results using $NbIte = 2k$ when $2k \le |V|-1$.

2.5 Bicycle wheel inequalities

The fourth class of inequalities corresponds to a q-bicycle wheel $BW_q=(V_q, E_q)$ subgraph of G, where:

$$\begin{aligned} V_q&=\{u_1, u_2\}\cup \{v_i, i = 1, 2,\ldots ,q \}, \quad E_q= E_1 \cup E_2 \cup \{{\bar{e}}\},\\ E_1&= \{(u_i,v_j), i = 1,2, j = 1\ldots ,q \}, \quad E_2 = \{(v_j,v_{j+1}), j = 1\ldots ,q\},\\ {\bar{e}}&= \{(u_1, u_2)\}, \end{aligned}$$

where vertices $v , u \in V$. For $q = 5$, $BW_5$ is illustrated in Fig. 2.

Fig. 2

Example of bicycle wheel with $q = 5$

For $BW_q$ with $q \ge 3$, the corresponding bicycle wheel inequality is defined as:

$$\begin{aligned} \sum _{i = 1}^{2}\sum _{j=1}^{q}X_{u_i,v_j} -\sum _{j = 1}^{q}X_{v_j,v_{j+1}} - X_{u_1,u_2} \le \frac{k}{k-1}\left[ 2\lfloor \frac{1}{2}q \rfloor -q +1\right] +q -1, \end{aligned}$$

(14)

where $v \in V$ and all indices greater than q are modulo q . It is proved in Chopra and Rao (1993) that the bicycle wheel inequality is a valid inequality to (MSkP), and for $k \ge 4$ it induces a facet if q is odd and $BW_q$ is an induced subgraph of G.

The idea behind bicycle wheel inequalities is that at least one edge $e \in E_1$ must be cut for each edge from ē or $E_2$ that is cut.

2.5.1 Separation of bicycle wheel inequalities

In Deza et al. (1992) is pointed out that the separation for the odd bicycle wheel inequalities (14) can also be done in polynomial time, by adapting the approach in Gerards (1985).

As we did for wheel separation, we tested also some heuristic method to find violated inequalities of the form (14) for a given $X^\prime$.

The basic idea of those heuristics is:

• Search for a cycle that minimizes the sum $( \sum \nolimits _{j = 1}^{j \le q}X_{v_j,v_{j+1}})$.

• Find the best points $u_1$ and $u_2$ that maximize $( \sum \nolimits _{j,i = 1}^{i = 1,2, j \le q}X_{u_i,v_j})$ and $(- X_{u_1,u_2})$.

For finding good cycles in the first step of this heuristic, we tested the same four heuristics mentioned in Sect. 2.4.1. Our tests showed that the GA from Seyed et al. (2014) with $q=3$ obtained the best results in 95% of the cases. Moreover, this heuristic had the same performance as the exact method for all tests, and its CPU time was 95% lower.

The GA has the following features:

• Size of population is 100.

• Half of the initial population was constructed with the GRASP and other half was randomly selected.

• In crossover process the parents with higher fitness are favored.

• Offspring genes can accept some slight mutations.

We keep the best cycle $C_w$ found in the final population after 100 iterations of the GA. Using this cycle, the main heuristic then checks all the combinations of $u_1, u_2 \in V \backslash C_w$ to find the one that maximizes the right-hand side of (14).

3 Cutting plane algorithm

This section presents the cutting plane algorithm (CPA) used for our computational tests. This algorithm is similar to the one described in Ghaddar et al. (2011). The basic idea is to start by solving the SDP problem (RMkP), then check for violated inequalities, add them to the SDP problem, and resolve to obtain a better upper bound on the global optimal value of the max-k-cut instance.

The pseudo-code of the CPA is given in Algorithm 3. We use the following notation: i is the iterations counter, $F^i$ is the set of inequalities in iteration i, $X^i$ is the optimal solution of the SDP relaxation at iteration i, and $S(X^i)$ is the set of valid inequalities for (MkP) that are violated by $X^i$.

The set $S(X^i)$ of inequalities is obtained by the separation routines of triangle, clique, general clique, wheel and bicycle wheel inequalities described in Sect. 2. We say that a class of inequalities is active if its separation routine is applied to find violations in the relaxed solution at each iteration of the CPA.

The size of the set $S(X^i)$ is controlled by the parameter NbIneq: $|S(X^i)| \le NbIneq$ at each iteration of the CPA. After some tests with $NbIneq \in \{100, 300, 500, 1000, \infty \}$, the CPA with $NbIneq = 300$ was found to be the least expensive in terms of CPU time and CPA iterations for a variety of graphs and choices of k. This limitation in the CPA imposes that just the most violated inequalities of the set of activated families are added at each iteration.

4 Computational tests

The SDP relaxations of the max-k-cut were solved using the mosek solver (Mosek ApS 2015) on a linux PC with two Intel(R) Xeon(R) 3.07 GHz processors.

Tests were performed for each value of $k \in \{4,3,5,7\}$ on 147 test instances. Our instances were taken from the Biq Mac Library (Wiegele 2015) or generated using rudy  (https://www-user.tu-chemnitz.de/~helmberg/sdp_software.html).

Section 4.1 introduces the combinations of inequalities tested, and the instances used. Section 4.2 explains the benchmarking methodology used for analyzing the different algorithms, and Sect. 4.3 reports the computational results. Finally, a summary of our results is given in Sect. 4.4.

4.1 Combinations of inequalities and test instances

This section defines the ten combinations of active inequalities developed to analyze the performance of the four classes of inequalities, and the instances used in the tests.

4.1.1 Combinations of inequalities

This section presents ten combinations of classes of inequalities. Each combination differ from each other by the classes that are activated or deactivated when running the CPA described in Sect. 3.

The triangle inequalities have been extensively studied in the literature and their efficiency has been confirmed by various researchers (Sotirov 2014; Rendl et al. 2010; Anjos et al. 2013). For this reason, we activated them in all combinations.

From the sixteen possible combinations of the remaining four classes of inequalities (clique, wheel, bicycle wheel and general clique), we used the ten combinations defined in Table 1 that emphasize the impact of individual classes. The first column of Table 1 gives the name of each combination, and the other five columns indicate with an X which classes are activated in that combination.

Table 1 The ten combinations

The ten combinations can be summarized as: one that activates none of the four classes (Tri), another that activates them all (ALL), and for each class “inequality”, two additional combinations (Tri  $+$ inequality) and (ALL  − inequality).

Moreover, the ten combinations can be split into two groups: The first group, G1, is formed by the combinations that activate at most two classes of inequalities, and the second group, G2, corresponds to the combinations that deactivate at most one class.

4.1.2 Instances

Of a total of 147 instances, 76 are dense (edge density greater than or equal to 0.5), and the remaining 71 are sparse.

• Random Twelve complete graphs with the edge weights randomly selected and generated by rudy  (https://www-user.tu-chemnitz.de/~helmberg/sdp_software.html). The dimension varies from 50 to 100 and the density between 0.5 and 1.

• spinglass_2g(3g) Eleven instances (3g: four instances) of a toroidal 2D(3D) grid for a spin glass model with gaussian interactions. The grid has size $(n_{row}) \times (n_{columns})$. They are sparse with density between 0.05 and 0.3.

• spinglass_2pm (3pm) Two instances (3pm: six instances) of toroidal 2D(3D)-grid for a spin glass model with +/−J interactions. The grid has size $(n_{row}) \times (n_{columns}) \times (n_{layers})$. The percentage of negative weights is 50%, dimension n vary from 36 to 64 and density between 0.05 and 0.3.

• pm1s_n.i Ten weighted instances with edge weights drawn uniformly from $\{-1, 0, 1\}$, density 0.1 and dimension 80.

• pm1d_n.i Ten weighted graphs with edge weights drawn uniformly from $\{-1,0,1\}$ and density 0.99. For densities $n \in \{80,100\}$.

• gkai_a(b or c) For each type (a,b or c) five instances with dimensions from 30 to 100, densities from 0.0625 to 0.5 (b: density 1 and for c: densities from 0.1 to 0.8). Diagonal coefficients from [−100, 100] (b: [−63, 0] and c:[−100, 100]), off-diagonal coefficients from [−100, 100] (b: [0, 100] and c: [−50, 50]).

• bqp_n-i For each dimension n, ten weighted graphs with dimension $n \in \{50,100\}$ and density 0.1.

• g05_n.i Ten unweighted graphs with edge probability 0.5 and dimension $n \in \{60,80,100\}$.

• w01_100.i Ten graphs with integer edge weights chosen from [−10, 10], density 0.1 and dimension 100.

4.2 Comparison methodology

This section explains the tools used to analyze our results. First, we present the performance profiles proposed in Dolan and Moré (2002), then the data profiles as used in Moré and Wild (2009), followed by the performance versus time graphs, and the relevance histograms.

We define a comparison in terms of a set ${\mathcal {P}}$ of problems (the 147 instances) and a set $\mathcal {S}$ of optimization algorithms (the ten combinations).

4.2.1 Performance profiles

As in Dolan and Moré (2002) and Moré and Wild (2009), the performance profiles are defined in terms of final objective solution $z_{p,s} > 0$ obtained for each instance $p \in \mathcal {P}$ and combination $s \in \mathcal {S}$. In our case (relaxation of a maximization), larger values of $z_{p,s}$ indicate worse performance. For any pair (p, s) of problem p and combination s, the performance ratio is defined as:

$$\begin{aligned} r_{p,s} = 100\left( \frac{z_{p,s}-Best_{p}}{Best_{p}} \right) \end{aligned}$$

(15)

where $Best_{p} = min \{z_{p,s} \forall p \in {\mathcal {P}}: s \in {\mathcal {S}}\}$.

The performance profiles of a combination $s \in \mathcal {S}$ is defined as the fraction of problems for which the performance ratio is at most $\alpha$, that is,

$$\begin{aligned} \rho _s(\alpha ) = \frac{1}{|{\mathcal {P}}|} \text { size} \{ p \in {\mathcal {P}} : r_{p,s} \le \alpha \}. \end{aligned}$$

(16)

Thus, for a given $\alpha$ one knows the percentage of instances $p \in \mathcal {P}$ (y axis) that are solved for each combination $s \in \mathcal {S}$ ($\rho _s(\alpha )$ in the x axis).

4.2.2 Data profiles

As pointed out in Moré and Wild (2009), data profiles are useful to users with a specific computational time limit who need to choose a combination that is likely to reach a given performance. Hence, it shows the temporal evolution of combinations to a specific performance ratio ($r_{max}$).

The data profiles are defined in terms of CPU time $t_{p,s}$ obtained for each $p \in \mathcal {P}$ and $s \in \mathcal {S}$. So, for a given time $\beta$ we define the data profiles of a combination $s \in \mathcal {S}$ by:

$$\begin{aligned} d_s(\beta ) = \frac{1}{|{\mathcal {P}}|} \text { size} \{ p \in {\mathcal {P}}: t_{p,s}\le \beta \text { and } r_{p,s}\le r_{max} \}. \end{aligned}$$

(17)

Thus, for given $r_{max}$ and time $\beta$, one sees the percentage of instances that can be solved for each combination $s \in \mathcal {S}$.

Note that in the computational results we do not analyze the data profiles for dense and sparse graphs separately because the obtained results did not contribute additional insights.

4.2.3 Performance versus time graphs

This benchmark shows the average performance ratio ($\Delta r_{p,s} \forall p \in {\mathcal {P}} : s \in {\mathcal {S}}$) in the x-axis, and the average time of execution ($\Delta t_{p,s} \forall p \in {\mathcal {P}}: s \in {\mathcal {S}}$) in the y-axis.

A combination $\omega$ dominates $\sigma$ if $\Delta r_{p,\omega } < r_{p,\sigma }$ and $\Delta t_{p,\omega } < \Delta t_{p,\sigma }$. Thus, we can analyze domination between our combinations.

Fig. 3

Performance profiles for all instances. Ideal point is at (0.0, 100)

Fig. 4

Data profiles for all instances with $r_{max} = 0.0$. Ideal point is at (0.0, 100)

Fig. 5

Performance versus CPU time for all instances. Ideal point is at (0.0, 0.0)

Fig. 6

Relevance of the inequalities for all instances

4.2.4 Relevance histograms

We use relevance histograms to quantify the impact of each inequality on the quality of the SDP bound. Let ${\mathcal {I}} = \{Cl, Wh, BW, GC\}$ be the set of four classes of inequalities, and $\Delta r_{p,s}, \forall p \in {\mathcal {P}}$ be the average performance ratio of a combination $s \in {\mathcal {S}}$. We calculate the relevance $\mu _i$ of the inequality $i \in {\mathcal {I}}$ as:

$$\begin{aligned} \mu _i = \frac{(\Delta r_{p,Tri} - \Delta r_{p,T+i}) + (\Delta r_{p,A-i} -\Delta r_{p,ALL})}{2 \times (\Delta r_{p,Tri} -\Delta r_{p,ALL})} . \end{aligned}$$

(18)

Equation (18) is normalized by the largest gap, which is the gap between combinations Tri and ALL. Thus, if an inequality $i \in {\mathcal {I}}$ has relevance 1 it means that ALL $- i$ = Tri and Tri $+ i$ = ALL.

4.3 Computational results

This section presents and analyzes the results of our tests. Section 4.3.1 demonstrate the benchmarks of all types of graphs. Sections 4.3.2 and 4.3.3 show the benchmarks of sparse and dense instances, respectively.

4.3.1 Results on the full set of instances

In this part of the analysis we present and discuss the four benchmarks for all 147 instances (sparse and dense) together.

Performance profiles Figure 3 shows the performance profiles for the ten combinations. To facilitate the analysis, the performance ratio is limited to 0.8.

According to Fig. 3a (for $k=3$), the combinations with the best performance are ALL, A-GC and A-Cl, and the combinations of Group G2 almost always dominate the ones of Group G1. Moreover, results suggest that the bicycle wheel is an important inequality since T+BW dominates all the other combinations of G1 and A-BW has the worst performance of the G2. For the same reasons we can notice that wheel inequality is also very relevant to CPA for $k=3$.

The results presented in Fig. 3b–d (for $k= 4, 5$ and 7, respectively) are very similar. It can be noticed that all combinations that activate the wheel inequality dominate the others. Moreover, we observe that all the combinations that have wheel and general clique inequalities can solve more than 70% of the instances with performance ratio <0.05. We also observe that the plots of Tri and T+Cl are very similar for those partitions, suggesting that the clique inequalities are ineffective for $k \in \{4,5,7\}$.

Data profiles Figure 4 shows the data profiles for a maximum performance ratio ($r_{max}$) equal to 0.0. Each graph shows the results for one of $k \in \{3,4,5,7\}$. Moreover, the time in this analysis is limited to $5\,\times \,10^4$ s (approximately 14 h).

Fig. 7

Performance profiles for sparse instances. Ideal point is at (0.0, 100)

In Fig. 4a, it can be observed that ALL followed by A-GC are the best combinations, and we see that combinations of Group G2 perform better than those of G1.

The graphs in Fig. 4b–d can be separated in combinations with and without wheel inequality, and it can be noticed that all the algorithms that activate wheel inequalities have the better performance, e.g. T+Wh dominates A-Wh for $k \in \{4,5,7\}$.

Quality versus time Figure 5 presents the average performance versus CPU time for the ten combinations of the cutting plane algorithm.

In Fig. 5a it may be seen that A-Cl and T+GC are dominated by ALL and T+Cl, respectively. Moreover, for $k=3$, T+Cl, T+GC and Tri are the fastest combinations but they have the worst performance. It is also noticeable that combinations with bicycle wheel show better performance but require more CPU time.

It can be observed that the results for $k \in \{4,5,7\}$ (Fig. 5b–d) are very similar. In those graphs A-Wh is always dominated by T+Wh. We also notice that all combination that activate wheel have on average a performance ratio <0.2.

Finally, results in Fig. 5 suggest that the CPU time of all the combinations is increased with the number of partitions.

Relevance of inequalities Figure 6 presents the relevance histograms for partitions $k \in \{3,4,5,7\}$ of four inequalities: Clique, Wheel, Bicycle wheel (B. Wheel) and General clique (Gen. Clique). In Fig. 6a, we see that the bicycle wheel is the most relevant inequality followed by wheel. However, for $k \in \{4,5,7\}$ the wheel inequality is clearly the most significant. Figure 6 suggests that the relevance of the wheel inequality increases with k.

Fig. 8

Performance versus CPU time for sparse instances. Ideal point is at (0.0, 0.0)

Fig. 9

Relevance of the inequalities for sparse instances

Fig. 10

Performance profiles for dense instances. Ideal point is at (0.0, 100)

4.3.2 Results for sparse graphs

This section analyzes the results of the ten combinations on the sparse instances (density below 50%). We present the performance profiles, performance versus time and the relevance histograms for the ten combinations on these 70 instances.

Performance profiles Figure 7 shows the performance profiles of the combinations for sparse instances.

In Fig. 7a ($k=3$), it can be observed that the combinations with the best results are ALL, A-GC and A-Cl, followed by A-Wh. For $k=3$, it is also noticeable that bicycle wheel is the most important inequality, since all combinations that deactivate it have the worst performance. For the same reasons we can include wheel inequalities in second place of importance for $k=3$.

Figure 7b–d (for $k= 4, 5$ and 7, respectively) are very similar. It can be seen that all algorithms that the wheel inequality produce the best results. A closer look on those results reveals a strong relation between T+Wh (the best result for Group G1) and A-BW, suggesting that wheel is the most significant inequalities to the max-k-cut followed by bicycle wheel.

Quality versus time Figure 8 presents the average performance versus CPU time of the combinations for sparse instances.

Fig. 11

Performance versus CPU time for dense instances. Ideal point is at (0.0, 0.0)

Fig. 12

Relevance of the inequalities for dense instances

In Fig. 8a the combinations T+Cl, T+GC and Tri are the fastest, but they have the worst performance. The best performance can be credited to A-Wh or T+Wh since those results are the closest to the ideal point. It is apparent that combinations with the bicycle wheel have the best performance but the highest CPU time.

It can be noticed that the results for $k \in \{4,5,7\}$ (Fig. 8b–d) are very similar. Those graphs suggest that wheel is the most relevant class of inequalities because all the combinations where it is activated have the average performance ratio lower than 0.3. Moreover, the combinations that activate wheel and bicycle wheel inequalities at the same time (A-GC, A-Cl and ALL) have the best average performance, but the worst CPU time. They present an average time larger than $2\,\times \,10^5$ s.

Finally, we observe that the CPU time increases with the number of partitions. For example, for $k=7$ the combinations spend 70% more CPU time solving the cutting plane algorithm than for $k=4$.

Relevance of inequalities Figure 9 demonstrates the relevance of the four inequalities for sparse instances. For $k=3$, results shown in Fig. 9a, it can be seen that the bicycle wheel is the most relevant inequality followed by wheel.

For $k \in \{4,5,7\}$ it can be noticed that clique and general clique inequalities are ineffective, and that the wheel inequality is the strongest class by far.

4.3.3 Results for dense graphs

This section analyzes the results of the ten combinations on the dense instances (density greater than or equal to 50%).

Performance profiles Similarly to the previous performances profiles, it can be observed in Fig. 10a ($k=3$) that the combinations with the best results are ALL, A-GC and A-Cl, followed by A-Wh.

The results in Fig. 10a also suggest that bicycle wheel is the most significant inequality since combinations that activate it have the best performance of G1 and G2. A similar analysis reveals that wheel is also relevant for this partition.

Figure 10b–d (for $k= {4, 5, 7}$) suggest that wheel and general clique are, respectively, the most relevant, since the activation/deactivation of those inequalities have a huge impact in the results.

It is also apparent that for $k \in \{4,5,7\}$ the results of ALL, A-BW and A-Cl are similar and the same occurs to Tri, T+Cl and T+BW. It means that the activation or deactivation of clique and bicycle wheel does not change the performance of the CPA on these instances.

Quality versus time In Fig. 11a the combinations T+Cl, T+GC and Tri are the fastest. However, they have the worst average performance (higher than 0.8). It can be seen that A-Cl, A-BW, and T+GC are dominated by other combinations and it is also noticeable that algorithms with bicycle wheel have the best average performance.

The results for $k \in \{4,5,7\}$ (Fig. 11b–d) are very similar. In those graphs we notice the relevance of the wheel inequality, since all the algorithms using this inequality have average performance lower than 0.2. Furthermore, it can be concluded that T+Wh achieves the best results, because it is the closest to the ideal point.

Finally, we observe that all the combinations spend in average 25% more CPU time for $k=4$ than for the other partitions.

Relevance of inequalities Figure 12 presents the four relevance histograms for dense instances. In Fig. 12a it can be noticed that the bicycle wheel is the most relevant class of inequality followed by wheel and clique.

For $k \in \{4,5,7\}$ the results suggests that wheel inequalities are the most relevant. It is also notable that the clique and general clique inequalities are ineffective when the triangle inequalities are activated.

4.4 Summary of the computational tests

While it is normal that the combination ALL (activation of all the inequalities) has the best performance, it is also the combination that requires the most CPU time. On the other hand, Tri is the fastest combination but delivers the worst performance. The combination T+Wh achieves, on average, the best ratio between CPU time and performance for all values of k considered in this study.

Table 2 summarizes the results and shows the best inequalities for each benchmark [performance profile, performance vs. time (QvsT) and inequality relevance] for each value of $k \in \{3,4,5,7\}$, and for sparse/dense/all instances. We observe that the strongest inequalities for $k=3$ are bicycle wheel and wheel, and for $k \in \{4,5,7\}$ the wheel inequalities are the strongest.

Table 2 Summary of the best inequalities for each benchmark

It is also noticeable that the activation of wheel combined with bicycle wheel (or general clique for dense graphs) improves the performance for all types of partitions. However, it spends in average 72% (32%) more CPU time for the CPA to terminate. Generally, we see that an increase in k causes an increase in the CPU time, especially for the sparse instances.

From a practical point of view, wheel is the most attractive inequality because it shows good performances for all instances and for all types of partitions.

5 Discussion

In this paper we carried out an experimental study of several classes of valid inequalities to strengthen the SDP relaxation of the max-k-cut problem. Specifically we considered the following classes of cutting planes: Triangle, Clique, General clique, Wheel and Bicycle wheel. We developed a different separation algorithm for each class. For triangle inequalities we used complete enumeration, for clique, general clique, and wheel inequalities a greedy heuristics was developed, and for bicycle wheel a genetic algorithm was applied. The inequalities were then tested within a standard cutting plane algorithm for $k \in \{3,4,5,7\}$, using nearly 150 instances with varying properties.

To investigate the strength of each class of inequalities we created ten combinations by alternating the activation and deactivation of the inequalities. In order to guarantee a fair comparison of the combinations, we analyzed four different benchmarks: performance profiles, data profiles, quality versus time and relevance histograms.

The results are summarized in Table 2. We conclude that bicycle wheel is the strongest inequality for $k=3$ and wheel for $k \in \{4,5,7\}$. Moreover, the inclusion of wheel and bicycle wheel inequalities at the same time strengthens even more the SDP relaxation of the max-k-cut at the cost of 72% more CPU time, on average.

In future research we plan to study more efficient algorithms to solve the SDP relaxation with wheel and bicycle wheel inequalities, and to build a branch-and-cut algorithm to find the integer solution of the max-k-cut problem for both sparse and dense graphs for large instances.