A modified variables repetitive group sampling plan with the consideration of preceding lots information

Abstract

Various acceptance sampling plans have been developed for different objectives. A repetitive group sampling (RGS) plan has been shown to be an efficient and easy-to-implement scheme for lot sentencing. However, it does not consider the available information from preceding samples. As a result, it may reduce the sampling efficiency in terms of cost and time. In this study, a modified variables RGS plan is proposed based on the commonly used capability index $C_{pk}$ for normally distributed processes with two-sided specification limits and to consider the sample results from preceding lots. The plan parameters for various required quality levels and allowable risks are tabulated for practical applications, and the advantages of the proposed plan is compared with existing variables sampling plans in terms of operating characteristic curve and average sample size.

1 Introduction

Acceptance sampling is a widely used quality control tool, and it is used to determine whether a submitted lot should be accepted or rejected. Depending on different data types, i.e., attributes and variables data, two major categories of acceptance sampling plans are available. Attributes sampling plans are used for the quality characteristics that are determined on a pass/fail basis, while variables sampling plans are applied for the quality characteristics that are measured on numerical scales. Since variables sampling plans are based on the measurement data instead of simply labeling a product as good or bad, they can provide more information than the attributes sampling plans. Furthermore, while maintaining the same protection, variables sampling plans may require a smaller sample size than attributes sampling plans. Consequently, variables sampling plans have been adopted more and more frequently in practice these days. Nevertheless, neither traditional attributes nor variables sampling plans can tackle the lot sentencing problem very well in today’s manufacturing environment, especially when the fraction of defectives needs to be very low with two-sided specification limits. To encounter this problem, scholars have developed several variables sampling plans using process capability indices (PCIs). Some works include Pearn and Wu (2006), Wu and Pearn (2008), Negrin et al. (2009, 2011), Wu (2012), Aslam et al. (2013a, b, 2014), Wu et al. (2012, 2015a), Liu et al. (2014) and Wu and Liu (2014).

The concept of repetitive group sampling (RGS) was firstly introduced by Sherman (1965), who developed a RGS plan for attributes data. The operation of a RGS plan is very similar to a sequential sampling plan. The decision rule of the RGS is almost as simple as that of a single sampling plan (SSP), and the performance of the RGS plan is always more efficient than the SSP. Balamurali et al. (2005) and Balamurali and Jun (2006) extended the attributes RGS plan to variables inspection for a normally distributed quality characteristic with unilateral specification limit. The average sample number (ASN) required for the proposed variables RGS plan was calculated based on known and unknown standard deviation. However, a major disadvantage of the RGS plan is that the sampling results of preceding lots are not considered when making decision on the current lot. Such a sampling plan will reduce its efficiency in terms of time and cost for inspection.

Wortham and Baker (1976) proposed the concept of multiple dependent state (MDS) sampling for attributes inspection. The MDS plan belongs to the group of conditional procedures, and the decision rules are based on not only the information from the current lot but also the information obtained from preceding lots. Balamurali and Jun (2007) extended the attributes MDS sampling plan to the variables MDS sampling plan for the quality characteristic with unilateral specification limit (i.e, for the larger-the-better or smaller-the-better type quality characteristic). The variables MDS sampling plan was further investigated by Aslam et al. (2013a) based on the process capability index $C_{pk}$ by using normal approximation.

To overcome the drawbacks of the RGS plan, this research proposes a modified variables RGS plan (called Modified-VRGS plan) by considering preceding lots information based on the process capability index $C_{pk}$. The proposed Modified-VRGS plan is an extension of the conventional variables RGS plan by utilizing the concept of MDS. It can also be viewed as an extension of the variables MDS plan which considers the RGS concept. In addition, it can be applied when the quality characteristic follows a normal distribution with two-sided specification limits. The proposed plan overcomes the disadvantage of the conventional variables RGS plan and is more efficient than the conventional variables RGS plan. The design of the proposed sampling plan requires the determination of three plan parameters in order to meet the quality requirements and to provide protection to the producer and the consumer simultaneously. Thus, a minimization model is formulated to determine the plan parameters. The objective function is to minimize the ASN, and two constraints are set to the two-point condition on the operating characteristic (OC) curve of the proposed plan. Besides, the OC function, i.e. the probability of acceptance, of the proposed plan is developed based on the exact sampling distribution of the estimated $C_{pk}$.

The organization of this paper is as follows. Section 2 briefly reviews process capability indices. Section 3 proposes a modified variables RGS plan. The determination and the analysis of the plan parameters are presented here. A comparison of the proposed plan with several existing works is also performed in Sect. 4. An application example is presented in Sect. 5. Conclusion remarks are made in the last section.

2 Process capability indices

Process capability indices (PCIs) provide numerical measures to examine whether a process meets the capability requirement, and numerous kinds of PCIs have been developed and applied for evaluating process performance. The index $C_p$ was designed to measure the magnitude of the overall process variation relative to the manufacturing tolerance. The $C_{pk}$ index was further developed by considering both the magnitude of process variation and the process location. They are defined as (Kane 1986; Kotz and Lovelace 1998; Palmera and Tsui 1999):

$$\begin{aligned}&\displaystyle C_p =\frac{\hbox {USL}-\hbox {LSL}}{6\sigma }, \end{aligned}$$

(1)

$$\begin{aligned}&\displaystyle C_{pk} =\hbox {Min}\left\{ {\frac{\hbox {USL}-\mu }{3\sigma },\frac{\mu -\hbox {LSL}}{3\sigma }} \right\} =\frac{d-|\mu -M|}{3\sigma }, \end{aligned}$$

(2)

where $\mu$ is the process mean and $\sigma$ is the standard deviation of the quality characteristic, USL and LSL are the upper and lower specification limits, respectively, $d=(\hbox {USL}-\hbox {LSL})/2$ is half-length of the specification interval, and $M=(\hbox {USL}+\hbox {LSL})/2$ is the mid-point between the lower and the upper specification limits.

The index $C_{pk}$ has been treated as a yield-based index since it provides bounds on the process yield, $100[2\Phi (3C_{pk} )-1]\,\% \le Yield\,\% <100\Phi (3C_{pk} )\,\%$, for a normally distributed process (Boyles 1991), where $\Phi (\cdot )$ is the cumulative distribution function (CDF) of the standard normal distribution. Thus, a minimum $C_{pk}$ value is usually specified in a purchasing contract. The process is deemed incapable if the prescribed minimum $C_{pk}$ is not met. Montgomery (2009) suggested certain minimum capability requirements for processes under some designated quality conditions. In particular, $C_{pk} \ge 1.33$ for existing processes; $C_{pk} \ge 1.50$ for new processes; $C_{pk} \ge 1.50$ for existing processes on safety, strength, or critical parameter; and $C_{pk} \ge 1.67$ for new processes on safety, strength, or critical parameter.

The estimator of $C_{pk}$, i.e. $\hat{{C}}_{pk}$, can be calculated by replacing $\mu$ and $\sigma$ with their conventional estimators, sample average $\bar{{X}}=\sum _{i=1}^n {X_i } /n$ and sample standard deviation $S=\left[ \sum _{i=1}^n {(X_i -\bar{{X}})^{2}/(n-1)} \right] ^{1/2}$, which are usually obtained from a process that is demonstrably stable (under statistical control).

$$\begin{aligned} \hat{{C}}_{pk} =\hbox {Min}\left\{ {\frac{\hbox {USL}-\bar{{X}}}{3S},\frac{\bar{{X}}-\hbox {LSL}}{3S}} \right\} =\frac{d-|\bar{{X}}-M|}{3S}. \end{aligned}$$

(3)

The construction of confidence intervals for $C_{pk}$ has been investigated extensively. Some works include Franklin and Wasserman (1992), Kushler and Hurley (1992), Nagata and Nagahata (1994), Tang et al. (1997), Hoffman (2001), Mathew et al. (2007), and Wu et al. (2009a). Because the sampling distribution of the estimated $C_{pk}$ is rather complicated, all of the above methods are approximate or asymptotic.

Under the normality assumption, Pearn and Lin (2004) are the first to obtain an exact and explicit form of the cumulative distribution function (CDF) of the natural estimator $\hat{{C}}_{pk}$. The integration technique similar to that presented in Vännman (1997) is applied, and the CDF of $\hat{{C}}_{pk}$ is:

$$\begin{aligned} F_{\hat{{C}}_{pk} } (y)=1-\int _{0}^{b\sqrt{n}} {G\left( {\frac{(n-1)(b\sqrt{n}-t)^{2}}{9ny^{2}}} \right) } \left[ {\phi (t+\xi \sqrt{n})+\phi (t-\xi \sqrt{n})} \right] \hbox {d}t, \end{aligned}$$

(4)

for $y>0$, where $b=d/\sigma =3C_{pk} +|\xi |$, $\xi =(\mu -M)/\sigma$, $G(\cdot )$ is the CDF of the chi-squared distribution with degrees of freedom $n-1$, $\chi _{n-1}^2$, and $\phi (\cdot )$ is the probability density function of the standard normal distribution N(0, 1).

Details about PCIs and their statistical properties were presented by Kotz and Johnson (1993) and Kotz and Lovelace (1998). Kotz and Johnson (2002) and Wu et al. (2009b) provided an overview of theory and practice on PCIs and discussed the recent developments of process capability analysis. Yum and Kim (2011) provided an extensive bibliography of papers on PCIs.

3 The modified variables repetitive group sampling plan

3.1 Concept and procedure of the sampling plan

The operating procedures of the proposed Modified-VRGS plan is depicted in Fig. 1 and described as follows:

• 1. Select a random sample of size n from the submitted lot.

• 2. Calculate the estimator of $C_{pk}$, $\hat{{C}}_{pk} =(d-|\bar{{X}}-M|)/3S,$ based on the collected sample $\{X_1 ,X_2 ,\ldots ,X_n \}$.

• 3. If $\hat{{C}}_{pk} \ge k_a$ (critical value for acceptance), accept the lot. If $\hat{{C}}_{pk} \le k_r$ (critical value for rejection), reject the lot.

• 4. If $k_r <\hat{{C}}_{pk} <k_a$, consider the inspection result of the immediate preceding m lots. If the preceding m lots were all accepted ($m>0$), accept the lot. If any one of the preceding m lots was rejected, go back to Step 1 and make the judgment again.

Fig. 1

Operating procedures for the proposed Modified-VRGS plan

3.2 Probability of acceptance functions

Five probability functions for developing Modified-VRGS plan based on $C_{pk}$ are first defined here. The probability of directly accepting the lot after the first sampling, $P_a (C_{pk} )$, is described as follows:

$$\begin{aligned} P_a (C_{pk} )= & {} P(\hat{{C}}_{pk} \ge k_a )=1-P(\hat{{C}}_{pk} <k_a )=1-F_{\hat{{C}}_{pk} } (k_a ) \nonumber \\= & {} \int _0^{b\sqrt{n}} {G\left( {\frac{(n-1)(b\sqrt{n}-t)^{2}}{9\cdot n\cdot k_a ^{2}}} \right) } \times \left[ {\phi (t+\xi \sqrt{n})+\phi (t-\xi \sqrt{n})} \right] \hbox {d}t. \end{aligned}$$

(5)

Similarly, the probability of directly rejecting the lot after the first sampling, $P_r (C_{pk} )$, is:

$$\begin{aligned} P_r (C_{pk} )= & {} P(\hat{{C}}_{pk} <k_r )=F_{\hat{{C}}_{pk} } (k_r ) \nonumber \\= & {} 1-\int _0^{b\sqrt{n}} {G\left( {\frac{(n-1)(b\sqrt{n}-t)^{2}}{9\cdot n\cdot k_r ^{2}}} \right) } \times \left[ {\phi (t+\xi \sqrt{n})+\phi (t-\xi \sqrt{n})} \right] \hbox {d}t.\qquad \end{aligned}$$

(6)

Furthermore, the total probability of acceptance based on the first sampling, $P_1 (C_{pk} )$, can be calculated by summing the probability of directly accepting the lot after the first sampling and the probability of acceptance with the consideration of the inspection result of m preceding lots.

$$\begin{aligned} P_1 (C_{pk} )= & {} P(\hat{{C}}_{pk} \ge k_a )+P(k_r <\hat{{C}}_{pk} <k_a )\cdot P(\hat{{C}}_{pk} \ge k_a )^{m} \nonumber \\= & {} P_a (C_{pk} )+\left[ {1-P_a (C_{pk} )-P_r (C_{pk} )} \right] \cdot \left[ {P_a (C_{pk} )} \right] ^{m}. \end{aligned}$$

(7)

The probability of repetitive sampling, $P_2 (C_{pk} )$, is described as follows:

$$\begin{aligned} P_2 (C_{pk} )= & {} P(k_r <\hat{{C}}_{pk} <k_a )\cdot (1-P(\hat{{C}}_{pk} \ge k_a )^{m}) \nonumber \\= & {} \left[ {1-P_a (C_{pk} )-P_r (C_{pk} )} \right] \cdot \left[ {1-(P_a (C_{pk} ))^{m}} \right] . \end{aligned}$$

(8)

Thus, the probability of accepting the lot, i.e., the OC function, of the proposed Modified-VRGS plan, $\pi _A (C_{pk} )$, can be derived as:

$$\begin{aligned} \pi _A (C_{pk} )= & {} P_1 (C_{pk} )+P_2 (C_{pk} )P_1 (C_{pk} )+\left[ {P_2 (C_{pk} )} \right] ^{2}P_1 (C_{pk} )+... \nonumber \\= & {} \frac{P_1 (C_{pk} )}{1-P_2 (C_{pk} )}=\frac{P_a (C_{pk} )+\left[ {1-P_a (C_{pk} )-P_r (C_{pk} )} \right] \cdot \left[ {P_a (C_{pk} )} \right] ^{m}}{1-\left[ {1-P_a (C_{pk} )-P_r (C_{pk} )} \right] \cdot \left[ {1-(P_a (C_{pk} ))^{m}} \right] }. \end{aligned}$$

(9)

It is worth to note that (i) as m approaches to infinite, $\left[ {P_a (C_{pk} )} \right] ^{m}$ will approach to 0, then $P_1 (C_{pk} )=P_a (C_{pk} )$ and $P_2 (C_{pk} )=1-P_a (C_{pk} )-P_r (C_{pk} )$. The OC function of the proposed plan will reduce to the conventional variables RGS plan, i.e., $\pi _A (C_{pk} )=P_a (C_{pk} )/[P_a (C_{pk} )+P_r (C_{pk} )]$; (ii) if $k_a =k_r$, then $P_1 (C_{pk} )=P_a (C_{pk} )$, $P_2 (C_{pk} )=0$, and $\pi _A (C_{pk} )$ will be equal to $P_a (C_{pk} )$, which is the probability of accepting the lot using the variables SSP. To summarize, both the variables RGS plan and the proposed Modified-VRGS plan will reduce to the conventional variables SSP if $k_a =k_r$.

In general, both the producer and the consumer will specify their quality requirements and allowable risks in the contract. That is, the lot acceptance probability should be at least $1-\alpha$ if the submitted lot quality is at the acceptable quality level (AQL), and the lot acceptance probability should be no more than $\beta$ if the submitted lot quality is at the rejectable quality level (RQL). Based on the two-points condition on the OC curve, $(C_{\mathrm{AQL}} ,1-\alpha )$ and $(C_{\mathrm{RQL}} ,\beta )$, two required equations regarding the lot acceptance probability can be expressed as follows, where $C_{\mathrm{AQL}}$ and $C_{\mathrm{RQL}}$ denote the values of the AQL and RQL in terms of the $C_{pk}$ index, respectively.

$$\begin{aligned} \pi _A (C_{\mathrm{AQL}} )= & {} \frac{P_1 (C_{\mathrm{AQL}} )}{1-P_2 (C_{\mathrm{AQL}} )}\ge 1-\alpha , \end{aligned}$$

(10)

$$\begin{aligned} \pi _A (C_{\mathrm{RQL}} )= & {} \frac{P_1 (C_{\mathrm{RQL}} )}{1-P_2 (C_{\mathrm{RQL}} )}\le \beta . \end{aligned}$$

(11)

3.3 Mathematical models for the plan parameters

The proposed Modified-VRGS plan was characterized by four plan parameters, n, m, $k_r$ and $k_a$. As pointed by Balamurali and Jun (2007), the value of m can be considered as a fixed number depending on past data availability, and considering the cases of $m = 1, 2, 3$ may be sufficient in practice. However, multiple solutions may still be resulted if only Eqs. (10) and (11) are used to determine the other three parameters n, $k_r$ and $k_a$. It is desirable to design a sampling plan with minimum sample size required for inspection. Based on the findings from Balamurali et al. (2005), Balamurali and Jun (2009), Wu (2012) and Wu et al. (2015a), the problem can be solved by using the average sample number (ASN) of the sampling plan as the objective function and the two probability of acceptance functions as the constraint equations. The ASN is the expected number of sampled units per lot for making decisions. That is, an optimal mathematical model is constructed to find the minimum ASN while satisfying both the producer and the consumer’s risks. The ASN under the Modified-VRGS plan is:

$$\begin{aligned} \hbox {ASN}(C_{pk} )=n+nP_2 (C_{pk} )+n\left[ {P_2 (C_{pk} )} \right] ^{2}+\cdots =\frac{n}{1-P_2 (C_{pk} )}. \end{aligned}$$

(12)

It can be seen that the ASN is a function of the index value, and several options are available to set the objective function. The common option is to minimize the ASN at AQL or RQL, or to minimize the average value of ASNs at both AQL and RQL.

Table 1 $\hbox {ASN}_\mathrm{R}$, $\hbox {ASN}_\mathrm{A}$ and $\hbox {ASN}_{\mathrm{AR}}$ values for the proposed Modified-VRGS plan under $C_{\mathrm{AQL}} =1.33$ and $C_{\mathrm{RQL}} =1.00$

Table 2 $\hbox {ASN}_\mathrm{R}$, $\hbox {ASN}_\mathrm{A}$ and $\hbox {ASN}_{\mathrm{AR}}$ values for the proposed Modified-VRGS plan under $C_{\mathrm{AQL}} =1.50$ and $C_{\mathrm{RQL}} =1.33$

For example, if the objective function is set to minimize the average value of ASNs at the two quality levels, AQL and RQL, i.e., $\hbox {ASN}_\mathrm{AR} =[\hbox {ASN}(C_{\mathrm{AQL}} )+\hbox {ASN}(C_{\mathrm{RQL}} )]/2,$ the optimization problem below can be applied to determine the plan parameters $(n,k_r ,k_a )$:

(13)

If the objective function is to minimize the ASN at $C_{pk} =C_{\mathrm{AQL}}$ or $C_{pk} =C_{\mathrm{RQL}}$, then Eq. (13) can be changed to Eq. (14) or (15), respectively, in the optimization problem to solve the plan parameters $(n,k_r ,k_a )$.

$$\begin{aligned} \hbox {MIN ASN}_\mathrm{A} =\hbox {ASN}(C_{\mathrm{AQL}} )= & {} n+nP_2 (C_{\mathrm{AQL}} )+nP_2 (C_{\mathrm{AQL}} )^{2}\nonumber \\&+\cdots =\frac{n}{1-P_2 (C_{\mathrm{AQL}} )} \end{aligned}$$

(14)

$$\begin{aligned} \hbox {MIN ASN}_\mathrm{R} =\hbox {ASN}(C_{\mathrm{RQL}} )= & {} n+nP_2 (C_{\mathrm{RQL}} )+nP_2 (C_{\mathrm{RQL}} )^{2}\nonumber \\&+\cdots =\frac{n}{1-P_2 (C_{\mathrm{RQL}} )} \end{aligned}$$

(15)

The plan parameters of the proposed plan are determined under three different objective functions (i.e., $\hbox {ASN}_\mathrm{A}$, $\hbox {ASN}_\mathrm{R}$, and $\hbox {ASN}_{\mathrm{AR}}$) to illustrate and compare the performances. Tables 1, 2, 3 and 4 display the ASN values for these three different objective functions under various $\alpha$, $\beta$ and m with different combinations of $(C_{\mathrm{AQL}} ,C_{\mathrm{RQL}}$ = (1.33, 1.00), (1.50, 1.33), (1.67, 1.50) and (2.00, 1.67), respectively.

Table 3 $\hbox {ASN}_\mathrm{R}$, $\hbox {ASN}_\mathrm{A}$ and $\hbox {ASN}_{\mathrm{AR}}$ values for the proposed Modified-VRGS plan under $C_{\mathrm{AQL}} =1.67$ and $C_{\mathrm{RQL}} =1.33$

Table 4 $\hbox {ASN}_\mathrm{R}$, $\hbox {ASN}_\mathrm{A}$ and $\hbox {ASN}_{\mathrm{AR}}$ values for the proposed Modified-VRGS plan under $C_{\mathrm{AQL}} =2.00$ and $C_{\mathrm{RQL}} =1.67$

Based on Tables 1–4, we find that $\hbox {ASN}_\mathrm{R}$ is not always less than $\hbox {ASN}_\mathrm{A}$ under the proposed plan. For example, $\hbox {ASN}_\mathrm{A}$ is smaller than $\hbox {ASN}_\mathrm{R}$ when $(C_{\mathrm{AQL}} ,C_{\mathrm{RQL}} )=(1.33,1.00)$ and $(\alpha ,\beta )=(0.01,0.05)$, but $\hbox {ASN}_\mathrm{A}$ is larger than $\hbox {ASN}_\mathrm{R}$when $(C_{\mathrm{AQL}} ,C_{\mathrm{RQL}} )=(1.33,1.00)$ and $(\alpha ,\beta )=(0.05,0.01)$. Since $\hbox {ASN}_{\mathrm{AR}}$ is always between $\hbox {ASN}_\mathrm{A}$ and $\hbox {ASN}_\mathrm{R}$, this study adopts $\hbox {ASN}_{\mathrm{AR}}$ as the objective function for the proposed plan and uses it for further analysis.

3.4 Result analysis and application

This study applies Matlab 7.0 to solve the plan parameters $(n,k_r ,k_a )$ and calculate $ASN_{\mathrm{AR}}$ under different circumstances. Tables 5, 6 and 7 show the results of the three plan parameters $(n,k_r ,k_a )$ and the corresponding $ASN_{\mathrm{AR}}$ under various producer’s risk ($\alpha$), consumer’s risk ($\beta$) and quality levels $(C_{\mathrm{AQL}} ,C_{\mathrm{RQL}} )$ when $m=1, m=2$ and $m=3,$ respectively. For example, when $m=2, (C_{\mathrm{AQL}} ,C_{\mathrm{RQL}} )= (1.67,1.33)$ and $(\alpha ,\beta )=(0.05,0.05)$, we can check Table 6 to know that a sample of size 46 should be taken from the submitted lot, and two critical values are $k_r =1.3887$ and $k_a =1.6718$. This implies that the calculated $\hat{{C}}_{pk}$ based on the collected sample could then be compared with $k_a$ and $k_r$ for making decision on the submitted lot. The lot should be accepted if $\hat{{C}}_{pk} \ge 1.6718$, and rejected if $\hat{{C}}_{pk} \le 1.3887$. If $\hat{{C}}_{pk}$ is between 1.3887 and 1.6718, sentence the lot based on the results of the previous two lots.

Table 5 Plan parameters $(n,k_r ,k_a )$ and $\hbox {ASN}_{\mathrm{AR}}$ for the proposed Modified-VRGS plan when $m=1$

Table 6 Plan parameters $(n,k_r ,k_a )$ and $\hbox {ASN}_{\mathrm{AR}}$ for the proposed Modified-VRGS plan when $m=2$

Table 7 Plan parameters $(n,k_r ,k_a )$ and $\hbox {ASN}_{\mathrm{AR}}$ for the proposed Modified-VRGS plan when $m=3$

It can be found from Tables 5, 6 and 7 that when either $\alpha$ or $\beta$ increases, both n and $ASN_{\mathrm{AR}}$ decrease. This is because the producer or the consumer’s risk endurance level increases and it is not necessary to examine a large sample. When the difference between $C_{\mathrm{AQL}}$ and $C_{\mathrm{RQL}}$ becomes smaller, both n and $ASN_{\mathrm{AR}}$ will increase because more samples are demanded to better understand the quality information and to avoid judgment errors if acceptable and rejectable quality levels are similar. Moreover, it will require a larger sample size to extract the quality information of the submitted lot when the required quality level is higher.

4 Comparison analysis and discussion

4.1 Operating characteristic (OC) curve

The OC curve depicts the probability of acceptance under different quality levels, for instance, defect rate or the value of the capability index, and it shows the discriminatory power for a sampling plan. A sampling plan has a better discriminatory power when its OC curve approaches the ideal OC curve. That is, the larger the slope of the OC curve is, the higher the discriminatory power is.

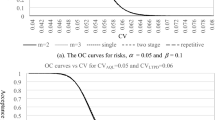
In order to investigate the behavior and the performance of the proposed Modified-VRGS plan, we examine the OC curve with several existing variables sampling plans based on the index $C_{pk}$, including variables SSP (Pearn and Wu 2007), variables resubmitted sampling plan (Wu et al. 2012), variables MDS plan (Wu et al. 2015b), and variables RGS plan (Wu et al. 2015a). Figure 2 shows the OC curves of the variables SSP, the variables resubmitted plan with $r=2$, the variables MDS plan with $m=1,2$, the variables RGS plan, and the proposed Modified-VGRS plan with $m=1,2$ under the same sample size $n=50$. The critical value $k=1.30$ is used for the variables SSP and the variables resubmitted plan, and two critical values $(k_a =1.30,k_r =1.10)$ are used for the variables MDS plan, the variables RGS plan and the proposed Modified-VGRS plan. It can be seen that the OC curves of the proposed plan are closer to the ideal curve than the OC curves of above-mentioned sampling plans. Thus, the proposed plan has a better discriminatory power for helping the producer and the consumer in lot sentencing.

Fig. 2

OC curves of the variables SSP, resubmitted plan, MDS plan, RGS plan and the proposed Modified-VGRS plan under $n=50$

4.2 Average sample number

In addition to the OC curve analysis, this research also examines the average sample number (ASN) required for inspection using existing variables sampling plans based on the index $C_{pk}$, including variables SSP, resubmitted sampling plan, MDS plan, RGS plan, and the Modified-VRGS plan proposed in this paper.

As noted before, we select $\hbox {ASN}_{\mathrm{AR}}$ as the objective function for the proposed plan. This study also calculates the ASN for these sampling plans under the same conditions. Note that the ASNs for the variables SSP and MDS are just the sample size n, the ASNs under the variables resubmitted sampling plan with $r=2,3$, the variables RGS plan and the proposed Modified-VRGS plan with $m=1,2,3$ are as shown in Tables 8, 9, 10 and 11. For instance, as can be seen in Table 10, when $(C_{\mathrm{AQL}} ,C_{\mathrm{RQL}} )=(1.67,1.33)$, $(\alpha ,\beta )=(0.05,0.05)$, the ASN under the variables SSP is 117, the ASNs under the variables resubmitted sampling plan are 139.10 and 167.89 for $r=2$ and 3, the ASNs under the variables MDS plan are 117, 119 and 128 for m = 1, 2 and 3, the ASN under the variables RGS plan is 77.93, and the ASNs under the Modified-VRGS plan are 64.14, 67.88 and 71.80 for m = 1, 2 and 3, respectively. It can be observed that under fixed quality requirements $(C_{\mathrm{AQL}} ,C_{\mathrm{RQL}} )$ and $(\alpha ,\beta )$, no matter m is 1, 2 or 3, the ASNs under the Modified-VRGS plan are all less than those under all the other sampling plans considered. It implies that the proposed Modified-VRGS plan requires smaller samples for inspection than all the other sampling plans under the same conditions while providing the same required protection to the producer and the consumer. The inspection cost and time can thus be reduced by applying the Modified-VRGS plan.

Table 8 Comparison of ASN under different sampling plans when $(C_{\mathrm{AQL}} ,C_{\mathrm{RQL}} )=(1.33,1.00)$

Table 9 Comparison of ASN under different sampling plans when $(C_{\mathrm{AQL}} ,C_{\mathrm{RQL}} )=(1.50,1.33)$

Table 10 Comparison of ASN under different sampling plans when $(C_{\mathrm{AQL}} ,C_{\mathrm{RQL}} )=(1.67,1.33)$

Table 11 Comparison of ASN under different sampling plans when $(C_{\mathrm{AQL}} ,C_{\mathrm{RQL}} )=(2.00,1.67)$

5 An application example

To demonstrate the practical applications of the proposed plan, an example of Printed Circuit Boards (PCBs) taken from Wu et al. (2008) is presented. Thickness of the PCB product is the key characteristic. For a particular model of PCBs, the lower and upper specification limits are $LSL=13.5\,\upmu \hbox {m}$ and $USL=28.5\,\upmu \hbox {m}$, respectively. Suppose the values of $(C_{\mathrm{AQL}} ,C_{\mathrm{RQL}} )$ based on the index $C_{pk}$ are set to (1.33, 1.00) and $(\alpha ,\beta )$ risks are set to (0.05, 0.05) in the contract. By checking Table 6, the plan parameters of the proposed plan with $m=2$ can be found to be $(n,k_r ,k_a )= (32, 1.0628, 1.3337)$. That implies that a sample size of 32 should be taken from the submitted lot, and two critical values for rejection and acceptance are $k_r =1.0628$ and $k_a =1.3337$, respectively.

The thickness data of the inspected 32 samples is displayed in Table 12, and the normal probability plot is depicted in Fig. 3. The data analysis results justify that the data is fairly close to the normal distribution with p-value $> 0.10$ based on the Anderson–Darling test. The sample mean and sample standard deviation are calculated as $\bar{{X}}=20.801$ and $S=2.360$, which yield the estimator of $C_{pk}$, $\hat{{C}}_{pk} =1.0312$. According to the decision rule, the submitted lot should be rejected in this case since $\hat{{C}}_{pk} <k_r =1.0628$.

In contrast, the lot should be accepted if $\hat{{C}}_{pk} \ge k_a =1.3337$. If $1.0628<\hat{{C}}_{pk} <1.3337$, the decision on the submitted lot must be made by considering the inspection results of the previous two lots. If the preceding two lots were all accepted, accept the submitted lot. If any one of the two preceding lots was rejected, take a new sample with the same size $n=32$ from the submitted lot and make the judgment again.

Table 12 Thickness data of the inspected 32 samples (Unit: $\upmu \hbox {m}$)

Fig. 3

Normal probability plot of the collected data

6 Conclusions

The RGS plans are available in the literature for judging the acceptability of a lot and have been shown to be superior to the single sampling plans. However, the previous RGS plans do not consider the sampling results of preceding lots, and as a result, reduce their sampling efficiency. In this research, a new plan (called Modified-VRGS plan) is developed for lot sentencing by considering the information of the current lot as well as the sample results from preceding lots. The proposed plan adopts the process capability index $C_{pk}$ to tackle normally distributed processes with two-sided specification limits. The performance of the proposed plan is also compared with existing variables sampling plans based on the $C_{pk}$ index, including the variables SSP, the variables resubmitted sampling plan, the variables MDS plan and the variables RGS plan, in terms of operating characteristic (OC) curve and average sample number (ASN). The results show that the OC curves of the proposed Modified-VRGS plan are closer to the ideal OC curve and the ASNs are less than those under all the other sampling plans considered. Therefore, the proposed Modified-VRGS plan has both the advantages of better discriminatory power and smaller sample size than those existing sampling plans. In other words, the proposed plan can help both the producer and the consumer to evaluate the quality of a lot using a smaller sample and providing the same protection.

The Modified-VRGS plan proposed in this research is based on the process capability index $C_{pk}$, which assumes that the quality characteristic is normally distributed. In practice, however, not all product quality characteristics follow normal distributions. Thus, variables RGS plans for non-normal distributions may be constructed in the future. Even though $C_{pk}$ is a very popular yield-based capability index, it does not consider quality loss due to the deviation of $\mu$ from the target value T. The quality loss issue can be incorporated in the future to develop a more comprehensive variables sampling plan.