1 Introduction

The financing for most hospitals in Germany is based on a fixed payment system which was introduced in the late 1990s. Payments are based on patients’ diagnosis related groups. A major change of that new system was that reimbursements for hospital treatments no longer depended on the patients’ length of stay but on the actual diagnosis. This forced hospitals to efficiently use their capacities and still challenges them to keep the process related variable costs low. The operating room, or more generally the operating theatre, is considered to be the largest cost and revenue centre within a hospital. Therefore, the utilisation of its capacity has a major influence on the hospital’s overall (financial) performance (cf. Lamiri et al. 2008).

In general, planning and decision making in health care and especially in hospitals affects multiple stakeholders’ interests and is often based on various criteria (cf. Kou and Wu 2014, Morton 2014 or Diaby et al. 2013). Particularly, when focusing on a hospital’s operating theatre, assigning elective and emergency patients for surgery to an operating room has an impact on patients’ waiting time as well as on staff’s workload and on the hospital’s throughput. In order to respect all interests simultaneously when constructing a compromise schedule, we apply a multi-criteria approach based on fuzzy sets. In addition to focusing on different objectives, we also include uncertain demand such as unknown surgery durations and additional demand caused by emergency patients into our model which have a strong impact on the quality in terms of the performance of an operating room schedule. From that perspective, attributes of a good schedule should be (1) high performance independent of a particular realisation of uncertain parameters and the (2) ability to balance different stakeholders’ interests. In order to evaluate the quality of such a schedule we investigate several aspects, e. g. the levels of satisfaction according to different goals, the performance in worst-case settings with very high demand and the impact of changes in assumptions regarding the uncertain model parameters.

1.1 Problem description

We consider the problem of scheduling elective patients into given surgical blocks that can be derived from a predetermined master surgical schedule (MSS). A MSS allocates time windows in the available operating rooms to medical specialities. This allocation is based on regular demand and can be executed repeatedly every week. Usually, there are time slots of 4 or 8 h available which are assigned to the surgical specialities. Revisions of this plan may become necessary due to significant changes in the demand (cf. Oostrum et al. 2008). Designing MSSs is a common tactical decision problem for hospitals and covers a medium-term planning horizon. The approach presented in this paper is intended to support short-term decision making which is based on an existing MSS.

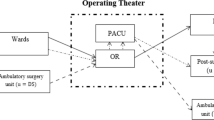
Available capacities of operating rooms and surgical blocks are reserved for the use of both elective and emergency patients. The respective durations for these surgeries are considered to be uncertain and influence the workload of a schedule. Scheduling elective patients and reserving emergency time is critical for the sum of surgery times not to exceed the maximum time limit for the planning period. Figure 1 shows the example of a day for a single operating room where two elective surgeries have been assigned for surgery and additional demand occurs while the schedule is executed. If the nominal level of planned utilisation (which is usually based on expected surgery times) is too high and if demand is also high then one of the elective surgeries has to be rescheduled to one of the following days, because the emergency surgery itself cannot be postponed and needs to be treated on the same day (see Fig. 1). We assume that it is beneficial if a schedule can be executed whatever values the uncertain parameters may take without changing the assignments of patients to days and rooms. Note that we focus on the allocation of surgeries only and no sequencing is considered, so our problem can be seen as a sub-problem of the one studied in Marques et al. (2014).

Fig. 1
figure 1

Visualisation of the decision setting depicting different demand settings and consequences on workload

Full size image

We suggest an optimisation approach which provides a robust schedule and simultaneously takes several stakeholders’ interests into account. The key feature of the approach is that the decision variables are split between those that are fixed in advance and those whose values depend directly on the uncertain outcome of the model parameters. Hence, the overall idea is to fix patients’ surgery dates before knowing the exact duration of the surgery and to provide additional variables which allow for re-actively adapting the schedule’s capacities. The planning should also account for reservation of additional capacity for emergency surgeries ahead of the execution of the schedule.

1.2 Literature review

The considered operation room scheduling problem is an offline operational problem according to a classification provided by Hans and Vanberkel (2012). At this offline planning level, sequences of surgeries may be taken into account, yet no emergency surgeries are considered. On the other hand, the main online planning task is to insert emergency surgeries into the existing schedule and to modify the schedule according to the performance of surgeries. The studies by M’Hallah and Al-Roomi (2014) and Zhao and Li (2014) simultaneously consider offline and online scheduling within combined approaches. Reviewing a lot of papers and covering various approaches Cardoen et al. (2010) and Guerriero and Guido (2011) provide well-structured overviews of publications and they analyse many relevant aspects. It is stated in both surveys that most, if not all, decisions in the field of operating room scheduling are considered from different stakeholders’ points of view which is the same with the allocation of hospital resources in general and many authors state that decision making in hospitals in general should be supported in order to meet these differing preferences (cf. Wachtel and Dexter 2008).

In a recent study, van Essen et al. (2012a) study the offline operational problem of emergency surgeries which need to be operated as soon as possible. They suggest to provide well structured Break-In-Moments in order to allow for as many points in time as possible to insert an emergency case into an existing schedule. Their approach supports structuring the sequence of elective surgeries before emergency surgeries arrive. Only a few studies focus explicitly on either multiple objectives or different stakeholders’ interests. van Essen et al. (2012b) focus on the actual offline operational planning problem in order to reschedule patients required by emergency demand. They discuss several stakeholders’ interests and evaluate scheduling policies regarding the impact on the stakeholder’s satisfaction. In their study, they focus on patients and staff as the most important stakeholders and re-organise an existing schedule which is necessary due to the arrival of an emergency patient. In contrast to the paper by van Essen et al. (2012b), Meskens et al. (2013) formulate a multiple-objective approach. However, both papers deal with a daily planning horizon and take into account the sequence of surgeries. Marques et al. (2014) present a bi-criteria approach focusing on the hospital management as the key stakeholder. Handling uncertainty aspects requires adequate modelling of elective and emergency patients. Studies by Min and Yih (2010), Lamiri et al. (2008), Bibi et al. (2007) or Zhang et al. (2009) examine only one out of the mentioned uncertainty aspects. To the best of our knowledge none of the discussed papers incorporate different stakeholders’ interests in terms of a multi-objective approach. Thus, we aim to fill this gap and especially investigate the benefits which can be attained considering several objectives simultaneously. In order to model the conflicting interests, we construct a compromising allocation and focus especially on its evaluation later on in a simulation study.

The remainder of this article is as follows: Sect. 2 presents an optimisation model which allocates surgeries to operating rooms and days with regard to three different objectives. Section 3 deals with an optimisation approach which is used to compute a robust compromise schedule. In Sect. 4 the implications regarding performance of a given schedule are derived in a simulation study and the proposed concept is evaluated. We analyse consequences of changes in several input parameters and point out possible effects on the quality of the schedule. A summary and an outlook to further research conclude the paper.

2 Multi-criteria optimisation approach

In this section, the optimisation approach is presented which considers the assignment of elective patients to operating rooms over a given period of time, yet without focusing on the intra-day sequence of surgeries. The approach also takes into account reservations for emergency surgeries. We discuss this optimisation approach particularly focusing on different stakeholders’ objectives.

On a superior planning level with a larger planning horizon, the approach to be presented is employed repeatedly and embedded into a rolling horizon approach. The approach consists of two interdependent stages which are executed consecutively in the real world setting and handled simultaneously within a single optimisation approach. The first stage assigns elective patients to rooms and days with consideration of given uncertainty restrictions and time reservations are made for emergency demand. Based on this assignment of appointments, the computed allocation can be adapted flexibly to various realisations of uncertain model parameters during the second stage which means that the allocation remains unchanged because the capacity levels can be adjusted. This includes particularly the reservation for emergency demand. First, we will describe sets, parameters and decision variables and discuss characteristics of the model and its parameters before presenting the optimisation model.

2.1 Sets, parameters and decision variables

We consider a planning horizon of T days and J parallel and identically equipped operating rooms (with \({\mathcal {J}}:= \{1,\ldots ,J\}\)) which provide time windows for either one or two of in total L medical specialities (\(\ell \in {\mathcal {L}}:= \{1,\ldots ,L\}\)). We refer to these time windows as (surgical) blocks in relation to the concept of a MSS (see previous section). Surgeries may be postponed to the following planning period which is indicated by an additionally introduced day \(T+1\). The overall planning period is denoted by \(\mathcal {T} := \{1,\ldots ,T,T+1\}\) in which postponements are explicitly included. The main task is to schedule a group of elective patients \(i \in I\) according to their diagnosis into the given blocks with respect to given constraints and objectives. Subsets of patients who require treatment from the same surgical speciality are introduced accordingly (\(I_{\ell } \subset I\), with \(I_{\ell } \cap I_{\ell '} = \emptyset \) and \(\ell \ne \ell '\)).

On each day available time for the individual specialities as well as the overall time of the operating rooms is denoted by \(\text {RC}_{\ell jt}\) (speciality blocks) and \(\text {C}_{jt}\) (rooms). Both times can be exceeded if necessary up a maximum level which is \(\text {MC}_{\ell jt}\) for specialities and \(\text {C}^{\text {max}}_{jt}\) for operating rooms. Besides, \(\text {r}^{\text {max}} < J\) limits the number of rooms to which capacity to be reserved for emergency treatments can be assigned. Assigning patients has to be done regarding stochastic surgery times \(\mathbf{dur }_{i}\)—these times can be approximated using an appropriate distribution, e. g. based on historical data. In addition, the stochastic parameter \(\mathbf E _{t}\) describes the overall time needed for emergency treatments on a day. Both parameters become relevant, when time for elective and emergency surgery has to be booked ahead of the execution of the schedule.

The binary decision variable \(x_{ijt}\in \left\{ 0; 1\right\} \) shows whether a patient is scheduled in a particular room on a certain day within the planning period (\(x_{ijt}= 1\)) or not (\(x_{ijt}= 0\)). If surgeries have to be postponed this is indicated by \(x_{ij (T+1)}=1\), in this case patients will be considered in the following planning period. The decision variable \(e_{jt}\ge 0\) indicates the amount of time (e. g. hours) which is blocked for emergency treatments in a particular room on a day within the planning period. The values of \(\text {e}_{jt}\) may be restricted to guarantee, for example, at least 1 h of time reserved for emergencies in order to avoid too short time slots. In terms of \(r_{jt} \in \left\{ 0; 1\right\} \) it is indicated whether capacity for emergency is reserved in a room (\(r_{jt}=1\)) or not (\(r_{jt}=0\)) which is required to limit the number of rooms which are considered for reservation. As deviations from the regular capacity level \(\text {C}_{jt}\) are tolerated, these are calculated in terms of continuous variables \(\eta ^{+}_{jt}, \eta ^{-}_{jt}\ge 0\) for overall room time. In order to assure that positive or negative deviations do not occur simultaneously \(\eta ^{+}_{jt}\cdot \eta ^{-}_{jt}= 0\) must hold which can easily be formulated as a linear term. Within each surgical block deviations from the regularly available amount of time are possible which are calculated accordingly using \(\delta ^{+}_{\ell jt}, \delta ^{-}_{\ell jt}\ge 0\). These require the same properties as \(\eta ^{+}_{jt},\eta ^{-}_{jt}\).

2.2 Constraints

There are three groups of constraints which cover the main aspects of the considered decision problem. These constraints focus on (1) the use of available capacities and the according limitations, (2) reservations for emergency surgery and (3) assignment conditions. In addition, there are a few technical formulations in order to guarantee feasibility of the schedule. First, the daily available level of overall room capacity is limited and can be used by elective patients and emergency reservations. Constraints have to ensure that for each day of the planning horizon the time allocated for elective and emergency surgery should utilise without excessively exceeding the regular capacity of a particular operating room. Deviations from that capacity are allowed because especially the capacity reservation for emergency surgeries depends on an unknown daily demand \(\mathbf E _{t}\).

Second, time windows for randomly arriving emergency patients are allocated. These high priority patients need to be treated on the day of their arrival. So sufficient slack needs to be provided. As mentioned above, in terms of \(\text {e}_{jt}\ge 0\) a part of the room time is reserved and dedicated to emergency surgeries. Wullink et al. (2007) showed that for the case of parallel operating rooms the dedication of single rooms to emergency surgeries should be avoided. We allow that reservations may be considered in a maximum number of \(\text {r}^{\text {max}}\) rooms. Providing capacity for emergencies in many rooms reduces the overall capacity, which is a common strategy (cf. Hans et al. 2012).

Third, we formulate constraints to schedule patients according to their date of hospitalisation. This means that a surgery cannot be planned on a day prior to a particular hospitalisation date \(\text {a}_i\). In addition, the model has to guarantee that patients will definitely be assigned—either within the planning period or referred to a waiting list. These constraints have an impact on the problem size, too, and affect the computational requirements as they significantly decrease the size of the solution space.

2.3 Stakeholder objectives

We capture patients, staff, and management as people or groups that are directly affected by a schedule. If these multiple interests need to be considered simultaneously, the problem is how to harmonise the existing interdependencies in order to provide a schedule which is finally acceptable for all stakeholders. All objectives can be met satisfactorily if the operating room scheduling problem is formulated as an (uncertain) multi-objective optimisation problem and three different objective functions \(z=(z_1, z_2, z_3)\) are used to represent the interests of the three stakeholder groups which are denoted by \(k \in {\mathcal {K}}= \left\{ 1,2,3\right\} \).

2.3.1 Patients

From a patient’s perspective, the quality of a schedule depends on the time between the first possible day for surgery—which is in fact the hospitalisation date—and the actual day of the surgery. We define this difference as waiting time in terms of (1). The day of hospitalisation depends on the hospital’s capacities and finally the pathway indicated by the diagnosis but may also be influenced by a patient’s preferences.

$$\begin{aligned} \sum _{i \in I}\left( \sum _{j \in {\mathcal {J}}}\sum _{t=\text {a}_i}^{T+1} t \cdot x_{ijt}- \text {a}_i\right) \rightarrow \min \end{aligned}$$
(1)

Focusing on the cumulative waiting time apparently is a fair aggregation of these time-dependent preferences because individual waiting times are weighted equally. Yet, there can be a large spread in the resulting waiting times. Focusing on minimising the maximum waiting time instead guarantees that a priori all patients are considered to be equal, too. In addition this ensures that all of them do not have to wait longer than a jointly minimised threshold. On the other hand there will be fewer short waits as the spread of results is likely to be smaller with a minmax approach. Implicitly assigned weights in this case are beneficial for those patients who would potentially wait longer. However, taking into account the cumulative waiting time will consider every patient’s waiting time to be of equal importance. Patients having their first possible day for surgery close to the end of the planning horizon are more likely to be deferred to the following planning period whatever approach is chosen (average waiting time vs. maximum waiting time). The resulting unfairness regarding postponements can be resolved using a multi-period or rolling-horizon approach taking into account multiple planning periods. However, this is beyond the scope of this publication. Note that we consider patients to be scheduled ahead of the planning period and that no elective appointments will be made for patients arriving within this period.

2.3.2 Staff

Once a schedule is fixed, the utilisation of the operating rooms depends on actual surgery times. To a certain extend, the available capacity can be adjusted to meet a demand at short notice. On the other hand, meeting the level of daily working time is also important. Hence, for each day and room the total deviation from available capacity has to be considered, too. This becomes necessary if a particular schedule is planned with adding a lot of slack to the uncertain surgery times to ensure there is enough capacity available. As a result, the performance lacks utilisation and throughput of patients which leads to a high amount of unused time. In fact, this unused time has to be considered being an opportunity loss. With objective (2) we aim to minimise the amount of overtime in order to meet the level of daily working time.

$$\begin{aligned} \sum _{j \in {\mathcal {J}}}\sum _{t=1}^{T} \eta ^{+}_{jt}\rightarrow \min \end{aligned}$$
(2)

In a simulation study later on, we will analyse how planning less overtime affects possible opportunity losses in terms of idle time in the operating theatre.

2.3.3 Management

With respect to a hospital’s financial situation, we formulate a third goal to maximise the number of patients treated within the planning period. Indirectly, we use the number of patients deferred to the next planning period and minimise the number of deferrals as a proxy for a maximal number of cases.

$$\begin{aligned} \sum _{i \in I}\sum _{j \in {\mathcal {J}}}x_{ij\,(T+1)} \rightarrow \min \end{aligned}$$
(3)

This objective function is reasonable especially for German hospitals due to the existing health care system. In general, hospitals and health insurance companies negotiate a certain amount of cases to be performed within a strategic planning horizon, e. g. 12 months or longer. In order to guarantee that a hospital is funded with the maximum payment possible for a particular period of time, the number of surgeries should be maximised.

2.3.4 Interdependencies

The different objective functions will not necessarily lead to the same optimal schedule because of the existing conflicts but to individual optimal solutions. The inherent interdependencies allow for good compromise solutions which will be approached using fuzzy sets for multi-criteria modelling later on in this paper. Minimising the waiting time of patients as within the first objective naturally leads to a high rate of utilisation on particular days depending on the patients’ hospitalisation dates. Focusing on this goal only, the risk of postponement increases if there are too many patients scheduled for surgery. In general, a large number of surgeries being scheduled increases the risk of overtime and has also a negative impact on staff’s satisfaction. The drawbacks of scheduling patients close to their date of hospitalisation can be approached by levelling the usage of the operating rooms as suggested in the second objective. This will in fact lead to a heterogeneous schedule according to the distances to the hospitalisation date. Besides, the management is also interested in an equally levelled utilisation of the hospital’s resources. In a way, this interest modelled in the third objective is partially incorporated in the first objective. A rapidly increasing number of requests for surgeries as it can be observed in Germany over the last years forces hospitals to control the number of surgeries performed. Therefore they do not focus on levelling the resource utilisation only but mainly work towards a high number of surgeries. Even though this might result in overtime, financial reimbursements for a high number of surgeries can be used to compensate for financial consequences.

2.4 Optimisation model

Following the previous section’s discussion the overall multi-objective optimisation model can be specified as follows—all parameters, variables and sets used for this and the following models are listed in the Appendix (see Tables 6, 7).

$$\begin{aligned}&\sum _{i \in I}\left( \sum _{j \in {\mathcal {J}}}\sum _{t=\text {a}_i}^{T+1} t \cdot x_{ijt}- \text {a}_i\right) \rightarrow \min&\,&\end{aligned}$$
(4)
$$\begin{aligned}&\sum _{j \in {\mathcal {J}}}\sum _{t \in {\mathcal {T}}}\eta ^{+}_{jt}\rightarrow \min&\,&\end{aligned}$$
(5)
$$\begin{aligned}&\sum _{i \in I}\sum _{j \in {\mathcal {J}}}x_{ij\,(T+1)} \rightarrow \min&\,&\end{aligned}$$
(6)
$$\begin{aligned} \nonumber&\text {subject to:}&\,&\qquad \quad \nonumber \\&\sum _{i \in I_{\ell }}\mathbf{dur }_{i}x_{ijt}+ \delta ^{-}_{\ell jt}- \delta ^{+}_{\ell jt,s}= \text {RC}_{\ell jt}&\,&\qquad \quad \forall \ell ,j,t \end{aligned}$$
(7)
$$\begin{aligned}&\delta ^{+}_{\ell jt}\le \text {MC}_{\ell jt}- \text {RC}_{\ell jt}&\,&\qquad \quad \forall \ell ,j,t \end{aligned}$$
(8)
$$\begin{aligned}&\sum _{j \in {\mathcal {J}}}\text {e}_{jt}- \mathbf E _{t}\ge 0&\,&\qquad \quad \forall t=1,2,\ldots ,T \end{aligned}$$
(9)
$$\begin{aligned}&\text {e}_{jt}\le M \cdot \text {r}_{jt}&\,&\qquad \quad \forall j,t \end{aligned}$$
(10)
$$\begin{aligned}&\sum _{j \in {\mathcal {J}}}\text {r}_{jt}\le \text {r}^{\text {max}}&\,&\qquad \quad \forall t \end{aligned}$$
(11)
$$\begin{aligned}&\sum _{\ell \in \mathcal {L}}\sum _{i \in I_{\ell }}\mathbf{dur }_{i}x_{ijt}+ \text {e}_{jt}+ \eta ^{-}_{jt}- \eta ^{+}_{jt}= \text {C}_{jt}&\,&\qquad \quad \forall j,t \end{aligned}$$
(12)
$$\begin{aligned}&\eta ^{+}_{jt}\le \text {C}^{\text {max}}_{jt}- \text {C}_{jt}&\,&\qquad \quad \forall j,t \end{aligned}$$
(13)
$$\begin{aligned}&\sum _{j \in {\mathcal {J}}}\sum _{t=\text {a}_i}^{T+1} x_{ijt}= 1&\,&\qquad \quad \forall i \end{aligned}$$
(14)
$$\begin{aligned}&\sum _{j \in {\mathcal {J}}}\sum _{t=1}^{\text {a}_i- 1} x_{ijt}= 0&\,&\qquad \quad \forall i \end{aligned}$$
(15)
$$\begin{aligned}&x_{ijt}\in \left\{ 0; 1\right\}&\,&\qquad \quad \forall i,j,t \end{aligned}$$
(16)
$$\begin{aligned}&\text {e}_{jt}\ge 0&\,&\qquad \quad \forall j,t \end{aligned}$$
(17)
$$\begin{aligned}&\text {r}_{jt}\in \left\{ 0; 1\right\}&\,&\qquad \quad \forall j,t \end{aligned}$$
(18)
$$\begin{aligned}&\eta ^{+}_{jt}, \eta ^{-}_{jt}\ge 0&\,&\qquad \quad \forall j,t \end{aligned}$$
(19)
$$\begin{aligned}&\delta ^{+}_{\ell jt}, \delta ^{-}_{\ell jt}\ge 0&\,&\qquad \quad \forall \ell ,j,t \end{aligned}$$
(20)

The objective functions minimise waiting time (4), staff overtime (5) and the number of deferrals (6) as discussed previously. The constraints (7) limits the regularly booked time for specialities and together with (8) exceeding the usually available time limit is possible up to a certain amount of time. In case of two surgical specialities sharing a room this enables to shift time from one discipline to the other if required. Constraint (9) assures that the time booked for emergency patients covers at least the uncertain amount of emergency demand – only during the actual planning period. In terms of (10) and (11) it is ensured that the booked time for the emergency surgeries is spread across a limited number of rooms. According to the first two constraints, restrictions (12) and (13) limit the time consumed by elective and emergency surgery reservations and allow for exceeding this limit up to a maximum time limitation. Through (14) an elective assignment can only be made for a day after a first possible day which is usually the day of admission or some day later. Correspondingly, no assignments are allowed before this mentioned date, which is ensured in terms of (15). Constraints (16)–(20) state the domain of the variables. The uncertain parameters \(\mathbf{dur }_{i}\) and \(\mathbf E _{t}\) are considered to be random variables and it requires assumptions on these before being able to solve the above presented model.

2.5 Scenario-based reformulation

We propose to apply a scenario-based optimisation approach using a set of S different scenarios (\(s \in \mathcal {S}:= \left\{ 1,2,\ldots ,S\right\} \)). A scenario is defined as a set of single-valued realisations of every stochastic parameter and it is assumed that every scenario can occur with identical probability. Consider that stochastic parameters are replaced by scenario-dependent parameters (e. g. \(\text {dur}_{i,s}\) and \(\text {E}_{t,s}\)) the resulting model can be solved for every \(k \in {\mathcal {K}}\) and \(s\in \mathcal {S}\) and a number of schedules (at most \(|{\mathcal {K}}|\cdot |{\mathcal {S}}|\)) can be obtained which are likely to differ due to changes in the model parameters. This would be a wait and see approach which is only applicable in case that one could wait until the realisation of a particular scenario can be observed and then choose a predetermined best solution. However, information about outcomes of stochastic model parameters is not available in advance and we propose to use a two-stage approach instead.

In order to avoid re-allocations of surgeries due to unexpected changes in surgery times we aim to fix patients’ dates of surgery and the respective operating rooms in advance. With this two-stage optimisation approach some of the variables are fixed before knowing which of the considered scenarios will occur (first stage) whereas the other variables are optimally adjusted for every of the considered scenarios (second stage). This means in particular that the variables \(x_{ijt}\), \(e_{jt}\), and \(\text {r}_{jt}\) do not change if a particular scenario happens. So the schedule and the included reservations of surgery times for emergency patients are fixed at the first stage. These allocations are done with respect to uncertainty and ensure that the amount of available capacity is sufficient for elective and emergency patients. At the second stage, necessary changes of block and room capacities are calculated for every of the considered scenarios with respect to the given maximum limitations. These changes indicate overtime or idle time and are calculated in terms of \(\eta ^{+}_{jt,s}\), \(\eta ^{-}_{jt,s}\), \(\delta ^{+}_{\ell jt,s}\) and \(\delta ^{-}_{\ell jt,s}\).

In relation to three different optimisation models we will refer to three different types of feasible solutions and respective sets which are listed in Table 1. For the basic model BM described in (4)–(20) we use \(\xi \in X\). Feasible solutions for the scenario-based model SBM 1 will be written as \(\xi _s \in X_s\). These solutions \(\xi _s\) consist of fixed values for \(x_{ijt}\), \(e_{jt}\) and \(r_{jt}\) and the according values for the adjustment variables \(\delta ^{+}_{\ell jt}, \delta ^{-}_{\ell jt}\) and \(\eta ^{+}_{jt}, \eta ^{-}_{jt}\). All of these variables are determined given a single scenario s. Finally, for the two-stage scenario-based model SBM 2 feasible solutions are denoted in terms of \(\xi ^{{\mathcal {S}}} \in X^{{\mathcal {S}}}\). Note that in terms of \(X_s\) we only consider a single scenario whereas with \(X^{{\mathcal {S}}}\) a set of scenarios \({\mathcal {S}}\) is taken into account. In particular, \(\xi ^{{\mathcal {S}}}\) includes optimal values for \(\delta ^{+}_{\ell jt,s}, \delta ^{-}_{\ell jt,s}\) and \(\eta ^{+}_{jt,s}, \eta ^{-}_{jt,s}\) in every of the chosen scenarios \(s \in {\mathcal {S}}\) and also values for \(x_{ijt}\), \(e_{jt}\), and \(r_{jt}\) which do not change if the outcomes of the uncertain model parameters change.

Table 1 Models and dependencies of variables
Full size table

An uncertain environment has major influence on the performance of an operating room schedule especially when the interests of multiple stakeholders are considered in terms of different objective functions. We assume that the decision-maker is risk-averse and hence we propose a robust optimisation concept in Sect. 3. This concept allows to generate a robust compromise schedule which is applicable even within some worst case settings. The suggested approach merges multi-criteria optimisation and a robustness concept in terms of a fuzzy sets approach which is being adapted to an uncertainty setting. Computational experiments in Sect. 4 will be based on the models presented in this and in the following chapter.

3 Robust multi-criteria approach

The overall goal of this approach is to provide schedules that are robust against variations in surgery times and meet the stakeholders’ individual goals as good as possible. These two aspects will be simultaneously covered in our approach. We consider robustness with respect to stochastic model parameters and multiple objectives. This means that a solution should be designed in a way such that flexible adjustments are possible in order to achieve objective function values close to scenario-dependent optimal values. The approach applied in this paper is explicitly described for on uncertainty setting in the following section. The reader is referred to Werners (1987a, b) and Werners (1988) for a presentation of the concept applied to a deterministic multi-criteria setting.

3.1 Evaluating achievement of stakeholder preferences

The main idea is to describe the quality of a schedule in terms of a linguistic expression such as an acceptable schedule regarding the first goal. We apply a fuzzy sets approach in order to describe whether a schedule is acceptable regarding a stakeholder’s individual interests within an uncertain environment. A piecewise linear function \(\mu _k\) describes for all feasible solutions whether a particular solution is part of a set of acceptable schedules regarding a certain goal k. We define a fuzzy set consisting of several tuples \((z_k(\xi ^{{\mathcal {S}}}), \mu (z_k(\xi ^{{\mathcal {S}}}))\) which indicate for possible schedules the relative distance to the best solution.

$$\begin{aligned} {\mathcal {F}}_k^{\,\text {acceptable}} := \left\{ \left( z_k(\xi ^{{\mathcal {S}}}), \mu _k(z_k(\xi ^{{\mathcal {S}}})) \right) \, | \, \xi ^{{\mathcal {S}}} \in X^{{\mathcal {S}}} \right\} \end{aligned}$$

The membership function \(\mu _k\,(\cdot )\) maps to what extent an objective function value and consequently a respective schedule belongs to the set of acceptable schedules with respect to the considered set of scenarios \(s \in {\mathcal {S}}\). Hence, the membership function allows to evaluate any given schedule regarding a stakeholder’s objective. The piecewise linear membership function takes the value 0 if the decision maker does not accept the solution and 1 if he is completely satisfied with the solution. For solution evaluations in between these values the membership function increases linearly. Therefore, objective functions values need to be identified or manually chosen by the decision maker which act as thresholds for full satisfaction (\(\mu _k (\cdot ) = 1\)) or disagreement (\(\mu _k (\cdot ) = 0\)). We consider these objective values being bounds which can also significantly reduce the size of the search space of schedules. Note that we will use scenario-dependent individually optimal solutions \(\xi _{k,s} \in X_{s}\) in order to determine these lower and upper bounds for acceptable objective function values. Later on, we will focus on \(\xi ^{{\mathcal {S}}} \in X^{{\mathcal {S}}}\) with regard to the membership functions to determine a robust compromise solution.

3.2 Normalisation of objective function values

As pointed out in Sect. 2.5 we consider that the unknown distributions for the model parameters can be approximated using a set of scenarios \({\mathcal {S}}\). We furthermore assume that each of the objectives can be solved optimally. Recall that there can be as many as \(|{\mathcal {K}}|\cdot |{\mathcal {S}}|\) diffferent scenario-dependent models. These models lead to the same number of scenario-dependent individually optimal schedules \(\xi _{k,s}\) which are likely to be non-identical. Given that the individually optimal solution is achieved, the stakeholder is naturally entirely satisfied because his goal is fully achieved. Regarding the proposed scenarios, a lower bound should be valid for all considered scenarios out of \({\mathcal {S}}\). Thus, in terms of (21) we set a lower bound for every objective.

$$\begin{aligned} \underline{z}_k := \min _{s \in {\mathcal {S}}} \{ z_k (\xi _{k,s}) \} \qquad k=1,2,3 \end{aligned}$$
(21)

For the given set of scenarios \({\mathcal {S}}\) this is a reasonable limitation and no solution will result in a lower objective function value. Depending on the chosen scenarios it may occur that the random variables take specific values which would lead to an even lower value for \(\underline{z}_k\). This might happen because the list of scenarios does not encompass all the actually possible situations. However, this is considered to happen occasionally and does not have a major impact.

Reasonable upper bounds can be formulated accordingly. It is supposed that with respect to conflicting goals a particular stakeholder is not entirely satisfied with a solution which does not reach his individually optimal schedule. For example, the level of satisfaction for the staff’s objective decreases with an increasing amount of (cumulative) overtime. This might be caused by shorter waiting times for patients. Hence, the last solution for a stakeholder to accept is a schedule \(\xi _{k', s}\) that minimises at least one of the other stakeholders’ objectives. In terms of (22) we set corresponding upper bounds for every objective function.

$$\begin{aligned} \overline{z}_k := \max \{z_k ( \xi _{k', s}) \mid k' \in {\mathcal {K}}, s\in {\mathcal {S}}\} \qquad k,k'=1,2,3 \end{aligned}$$
(22)

The quality of these limitations naturally depends on the chosen scenarios, especially if only a small number of characteristic scenarios is chosen. With respect to the existing individually optimal solutions, there are at least three Pareto-efficient schedules and thus a variation in one of the lower or upper bounds cannot influence the schedules’ efficiency.

On the basis of the identified limitations we assume that the stakeholders’ preferences can be described adequately in terms of a piecewise linear function. We focus on the increasing part of this function. For each objective function there exists a set of acceptable solutions \({\mathcal {F}}_k\) that is composed of schedules and the corresponding stakeholder’s levels of satisfaction. In terms of linear membership functions the objective function values are normalised and represent a particular level of acceptance. Note that we now consider solutions \(\xi ^{{\mathcal {S}}} \in X^{{\mathcal {S}}}\).

$$\begin{aligned} \mu _k ( \xi ^{{\mathcal {S}}} ) = \frac{\overline{z}_k - z_k (\xi ^{{\mathcal {S}}})}{\overline{z}_k - \underline{z}_k}, \quad \text { with }~ \underline{z}_k \le z_k(\xi ^{{\mathcal {S}}}) \le \overline{z}_k, ~\quad k=1,2,3 \end{aligned}$$
(23)

The membership function (23) takes its highest value 1 if a schedule \(\xi ^{{\mathcal {S}}}\) leads to an objective function value equal to the objective function value of the individually optimal solution. Recall that \(z_k(\xi ^{\mathcal {S}}) < \underline{z}_k\) is impossible because of the calculated lower bound. A stakeholder’s level of satisfaction decreases linearly with increasing objective functions values (for minimisation goals). Negative evaluation values might result if \(z_k(\xi ^{\mathcal {S}}) > \bar{z}_k\), yet those solutions are very unsatisfactory for the decision maker. Therefore, these solutions will be excluded from consideration in the model later on. Determining the membership functions for goals dependent on the other goals is a well-known approach in fuzzy multi-criteria optimisation and generally used (cf. Mehrbod et al. 2012).

In particular, the way how the various membership functions \(\mu _k\) are defined within this approach does depend on the degree of conflict between the goals of various decision makers. This is likely to impact the resulting number of schedules which are considered to be acceptable for all stakeholders. In addition, the difference between what the decision maker chooses to be best and worst case objective function values impacts the slope of the piecewise linear membership function. This can influence the implicit weights which are attached to the different goals. However, the presented approach enables to evaluate a particular solution, e. g. the robust compromise schedule, and its performance relative to the best possible and last acceptable solution. Moreover, it can also be seen as a way to obtain a first compromise solution which marks the starting point for negotiations among the stakeholders.

3.3 Aggregating preferences

In order to simultaneously meet the stakeholders’ interests with respect to the uncertain environment, we maximise their satisfaction levels which are modelled using membership functions. The aggregation of preferences is covered in terms of an a priori approach which combines the different objectives into one. This approach can be extended to an interactive procedure as described in Werners (1987a) if additional preference information is available. However, this extension is beyond the scope of this publication. Several approaches exist to combine multiple criteria into a single objective function. The weighted sum approach is well-know and is used in this context to combine the suggested membership functions if compensation is required. Due to the described normalisation of the objective functions, averaging of the membership functions equals a weighted sum approach with weights of equally normalised importance for the goals. Another well-known approach in multi-criteria decision making is the minimisation of the maximal distance to a predefined ideal. This approach does not allow compensation between different goals. An equivalent fuzzy sets approach is to maximise minimal membership of goal attainment where normalisation means an additional weighting of objectives. For multi-criteria models with partially compensating goals the fuzzy-and is suggested which is also a well-known approach (cf. Mehrbod et al. 2012; Werners 1988).

We extend the mentioned ways of aggregating objective functions to an uncertain environment in order to merge multi-criteria optimisation and handling of stochastic model parameters. In this case, the weighted sum approach can be seen as an expected value approach and the maxmin approach is, in fact, a robust approach. We apply the fuzzy-and-operator which is a convex combination of the weighted sum approach and the maxmin approach (cf. Werners 1988) and extend it to a new scenario-based planning approach. The idea of maximising the average level of goal achievement is similar to the idea of an expected value approach but new in terms of a fuzzy sets approach. In fact this means to assign implicit weights to the objective functions in terms of the normalisation as described above. The approach minimises the expected value of the weighted objectives because the model focuses on minimisation of objective functions. In terms of \(\alpha _{ks} \in [0,1]\) we measure the level of goal achievement for a goal in a particular scenario regarding a schedule \(\xi ^{\mathcal {S}}\). We aim to maximise this level by maximising \(\alpha _{ks}\).

Robustness with respect to the considered goals means to ensure a basic level of goal achievement over all scenarios. This is covered in terms of a maxmin approach which maximises the lowest level of membership \(\lambda ^{{\mathcal {S}}}\). It is well known that this type of approach does not guarantee Pareto-efficiency of an optimal solution. Hence, additional constraints ensure that the basic level of achievement which is valid for all goals and scenarios can be individually exceeded. We indicate this surplus using \(\lambda _{ks} \ge 0\). Finally, the term \(\lambda ^{{\mathcal {S}}} + \lambda _{ks} = \alpha _{ks}\) measures the relative distance to the individually optimal solution given a particular goal k and scenario s. In terms of \(\alpha _{ks}\) a stakeholder’s satisfaction with a given schedule \(\xi ^{{\mathcal {S}}}\) is represented. Maximising a basic level of goal achievement \(\lambda ^{\mathcal {S}}\) and considering positive values for \(\lambda _{ks}\) is, in fact, a robust optimisation approach. The following optimisation model allows to integrate both aggregation concepts (maxmin and weighted sum) in terms of the parameter \(\gamma \in [0,1]\) (see Tables 6, 7 for reference).

$$\begin{aligned} \begin{aligned}&\gamma \cdot \lambda ^{{\mathcal {S}}} + (1-\gamma )\frac{1}{|{\mathcal {K}}|\cdot |{\mathcal {S}}|}\sum _{s \in {\mathcal {S}}}\sum _{k \in {\mathcal {K}}}\alpha _{ks} \quad \rightarrow \quad \max&\, \qquad&\\&\text {subject to}&\,\qquad&\\&\alpha _{ks} = \mu _{k} (\xi ^{{\mathcal {S}}}) = \frac{\bar{z}_k - z_k(\xi ^{{\mathcal {S}}})}{\bar{z}_k - \underline{z}_k}&\qquad \,&\forall k,s\\&z_1 (\xi ^{{\mathcal {S}}}) = \sum _{i \in I}\left( \sum _{j \in {\mathcal {J}}}\sum _{t=\text {a}_i}^{T+1} t \cdot x_{ijt}- \text {a}_i\right)&\,\qquad&\\&z_2 (\xi ^{{\mathcal {S}}}) = \sum _{j \in {\mathcal {J}}}\sum _{t \in {\mathcal {T}}}\eta ^{+}_{jt,s}&\qquad \,&\forall s\\&z_3 (\xi ^{{\mathcal {S}}}) = \sum _{i \in I}\sum _{j \in {\mathcal {J}}}x_{ij\,(T+1)}&\,&\\&\lambda ^{{\mathcal {S}}} \le \alpha _{ks}&\qquad \,&\forall k,s\\&0 \le \lambda ^{{\mathcal {S}}}, \alpha _{ks} \le 1&\qquad \,&\forall k,s\\&\xi ^{{\mathcal {S}}} \in X^{{\mathcal {S}}} \end{aligned} \end{aligned}$$
(24)

For \(\gamma = 1 \) the approach (24) leads to the maxmin approach and \(\gamma = 0\) is a weighted sum approach. In order to ensure efficiency of the solution, we choose \(\gamma < 1\), yet close to 1. In this approach the maximum relative distance to a particular goal’s lower bound is considered as a regret. Robustness with respect to the given goals is achieved if the maximum regret is minimised. For a detailed description of the applied concept see Rachuba and Werners (2014). In fact, formulation (24) is a two-stage optimisation approach which allows to determine assignments for elective surgeries together with emergency reservations in advance. It also provides the best possible scenario-dependent adjustments of the capacities which are calculated depending on the considered scenarios \(s \in {\mathcal {S}}\) (cf. Sect. 2.5).

In addition, the concept offers supportive features for the considered application. First, the calculated lower and upper bounds for acceptable objective function values are based on scenarios which happen very seldom. It is not likely that all random variables simultaneously take values significantly lower (or higher) than their mean value. By using the suggested, partly extreme, scenarios the result is an admissible solution. The good quality of this solution will be shown in thorough simulation studies in Sect. 4. Even if real world data differs from the assumed scenarios, the proposed approach implicitly covers a large number of possible scenarios which can occur between the chosen limitations for high and low demand. The second important aspect is that stakeholders’ preferences can be adequately aggregated. This means that especially in uncertain situations at least a certain degree of satisfaction can be guaranteed for each stakeholder. Finally, our approach enables the decision maker to fix the assignments of elective patients and emergency reservations in advance for the planning period. It also allows for tolerated deviations from block and room time which might become necessary as a reaction to the outcomes of the stochastic model parameters. Fixing a subset of variables for all scenarios and allowing some variables to change following a scenario realisation is a typical robust approach (cf. Mulvey et al. 1995). It is to be noted that the presented concept in general is very conservative. Depending on the chosen scenarios, this can lead to significant opportunity losses in comparison to the optimal solution of a wait and see approach (cf. Bertsimas and Sim 2004 or Gülpinar et al. 2013 for a wider discussion of opportunity losses). Apart from the considered application in this paper, the approach is also suitable for other areas of application in which some decision variables need to be fixed in advance over a given period of time and where there are adjustments of capacities possible. The approach can also be extended to apply different techniques to derive lower and upper bounds or to interactively adjust them once they have been identified.

In the following chapter we demonstrate implications of this robust multi-objective approach on stakeholders’ preferences and other more general performance measures. We discuss the different approaches (\(\gamma \approx 1\) vs. \(\gamma = 0\)) and the balancing effects on the overall satisfaction levels. In particular, the configuration of a maxmin approach is very conservative and ensures feasibility for all chosen scenarios because it does not exceed the maximum tolerated workload. This is likely to come at a price of fewer scheduled surgeries. In addition to this, we illustrate consequences for patients waiting time, staff’s workload and the utilisation of the operating rooms if a robust approach is used.

4 Evaluation of robust schedules

In this chapter, the proposed fuzzy sets approach is evaluated using historical data records from a mid-size hospital in Germany. These data records are used to randomly generate surgery durations and emergency demand in order to simulate the performance of a computed schedule. Table 2 shows basic characteristics of the following analysis. We consider a planning horizon of 2 weeks (which equals 10 working days) and 4 equally equipped operating rooms. These rooms are available 8 h a day allowing not more than 3 h of planned overtime. Five surgical specialities share the available operating rooms and have either 4 or 8 h of operating room time allocated in a particular room on a particular day. The patient data set consists of 100 elective patients whose surgeries have expected durations between 0.5 and 6 h. The daily amount of time which is demanded for emergency surgeries varies between 0 and 4 h. Recall that all patients have to be scheduled at once for the entire planning period.

Table 2 Data setting for computational study
Full size table

Figure 2 summarises the steps described in the previous section and depicts the analysis within the following subsections. The set of elective patients is crucial for the following calculations. We randomly generate a first possible date for surgery and an expected value for the duration of their surgery. In general, surgery times for elective patients can be specified using either the surgeons knowledge or historical data records. Recall that the uncertain model parameters will be represented in terms of scenarios which is common practice with robust optimisation approaches (cf. Mulvey et al. 1995). However, an increasing number of scenarios causes long computation times in order to solve the respective models to optimality. In the interest of keeping the number of scenarios low, we focus on three scenarios. They represent the negative deviation from the expected duration (\(s=1\)), the expected duration itself (\(s=2\)) and positive deviations with regard to the expected times (\(s=3\)). Accordingly, we consider time required for emergency demand which is considered at an average level (\(s=2\)) as well as at a lower (\(s=1\)) and higher (\(s=3\)) level.

Fig. 2
figure 2

Determination and evaluation of a robust compromise schedule

Full size image

In a first step, computing a robust compromise schedule following the decision maker’s assumptions requires to solve every objective function for every scenario—which in fact means solving 9 different optimisation models. The resulting objective values are used to determine bounds as specified in (21) and (22) which are valid for all scenarios. These bounds allow to construct the membership functions which are required to solve model (24). Finally, the decision maker chooses the parameter \(\gamma \) according to his preferences regarding compensation which is required to solve the model (24).

The performance of the computed robust schedules will be evaluated using multiple randomly generated surgery times and emergency demands. Putting a single realisation of surgery times and emergency demand together, we refer to this being an evaluation scenario. These evaluation scenarios are used instead of the planning parameters in terms of a simulation study. Elective surgery times are simulated following a log-normal distribution (cf. Strum et al. 2000) and the demand for emergency surgeries is modelled in terms of a Poisson distribution (cf. Cayirli and Veral 2003). Besides, we will analyse levels of absolute and relative goal achievement. This requires to optimally solve all evaluation scenarios in order to determine what would be lower and upper limitations for the objectives in every of the scenarios given full information would be available (which is similar to a wait and see approach). This finally allows to determine relative and absolute distances of the objective functions to the scenario-dependent optimal objective function values regarding the computed robust schedule.

Three major aspects will be covered in our analysis. First, we compare the maxmin (\(\gamma \approx 1\)) and the weighted sum approach (\(\gamma = 0\)) and evaluate the overall performance of a robust compromise schedule (as obtained by solving (24)) in terms of absolute values. Second, the levels of goal achievements are compared for both approaches. Third, we conduct a sensitivity analysis to evaluate how the performance of the schedule changes if different assumptions are made regarding the stochastic model parameter. All optimisation models were implemented in Mosel and solved with FICO XPress 7.3. We generated the required distributions and evaluation scenarios to evaluate computed schedules using the Excel Add-In @RISK 5.5 which is part of the Palisade Decision Tools Suite. Both applications run on a standard desktop PC with IntelCore i5-2500 3.3 GHz processor with 8 GB RAM. All models were solved within reasonable time.

4.1 Simulation study to evaluate stakeholders’ goal achievements

In order to evaluate the performance of the robust schedules which are determined by the two-stage model SBM 2, 1000 realisations of every patient’s surgery time and additional 1000 realisations describing the demand for emergency surgery are simulated. These realisation are randomly combined to evaluation scenarios which represent surgery durations for both elective and emergency patients. We solve each of these simulated evaluation scenarios to optimality and calculate gaps between the maxmin or weighted sum approach’s solution and the optimal solution in terms of the three objectives.

First, we investigate the daily amount of overtime, because the absolute performance of this goal changes according to outcomes of the stochastic model parameters. The cumulative probability distribution of the average daily amount of overtime is compared for two schedules that have been computed using the weighted sum approach and the maxmin approach. The left graph in Fig. 3 indicates an increase of overtime of about 15 min per day for a less conservative planning approach (weighted sum). For both approaches, the maximum amount of overtime is below 1 h in all scenarios. In some particular settings the obtained robust compromise schedule might not be feasible which means that staff would be required to work more overtime then usually tolerated. However, for the data set used in this paper this occurred for less then 1 % of the scenarios which underlines the conservativeness of our approach. Further implications of this planning approach are shown in terms of resulting levels of goal achievement for the objective minimise overtime (see right graph in Fig. 3). The values for overtime in the scenarios are very close to the optimal solutions. Thus, both approaches provide acceptable schedules according to the stakeholders’ preferences. Relative levels of overtime for each of the computed evaluation scenarios regarding lower and upper bounds (right graph in Fig. 3) strengthen the good evaluation. We found that the resulting values for overtime are close to the optimal solutions applying the maxmin and the weighted sum approach. Using a maxmin approach, 40 % of the optimal solution value is achieved even for the worst case. Moreover, in half of the evaluated scenarios, the degree of satisfaction is at least 0.7. Because overtime is higher for the weighted sum approach, the resulting degree of satisfaction is lower for this approach, accordingly. Note that a level of goal achievement of 0 only indicates that the non-acceptance level is reached. There are solutions below these limitations, yet the corresponding schedules are not accepted.

Fig. 3
figure 3

Comparing weighted sum and maxmin approach with respect to cumulative probabilities for absolute and relative overtime

Full size image

Accordingly, within half of the scenarios, the average amount of idle time is at least 45 min and at most 60 min (weighted sum). For the maxmin approach, these values increase by approximately 15 min. Thus, the price for a slightly more conservative planning approach is a higher level of idle time per day compared to the weighted sum approach. Both approaches guarantee that the schedule can be executed without any postponements or cancellations even for evaluation scenarios with very high demand. In both cases, the amount of idle time implicitly indicates opportunity costs. On the other hand, the actual levels of average daily overtime indicate that a less conservative approach leads to an increase of daily overtime. It can be concluded that with the weighted sum approach the actual utilisation of the operating rooms is significantly higher than using the maxmin approach. Hence, the maxmin approach is slightly more conservative and leads to a lower amount of daily workload yet it can cause more idle time.

In a next step, we evaluate the average time between the day of hospitalisation and the actual day of surgery. This describes the patients’ satisfaction with a particular schedule. Again, we compare the same two schedules which have been evaluated above. A robust schedule in general leads to a low amount of patients scheduled and thus patients’ waiting time increases intuitively. There are different reasons for this. On the one hand this happens because surgery days are fixed in advance but on the other hand this is also affected by the scenario-dependent benchmark for waiting time itself. Examining the number of patients who do not wait longer than a given number of days, it becomes apparent that for both approaches 50 % of the patients can be treated within the first two admissible days (Fig. 4). The amount of waiting time for elective patients is correlated to the number of deferred patients. Table 4 indicates that the number of deferrals is slightly higher using the maxmin approach. Another price for a robust schedule is that quite a number of surgeries are postponed to the following planning period which results in idle time as discussed above. Again, the actual levels of satisfaction for the achievement of the goals waiting time and deferred patients are jointly analysed because their absolute values do not change in case of different scenario realisations. Table 3 shows that the two schedules are very close to the scenario-dependent optimal solutions. Thus, these schedules adequately incorporate the two goals.

Fig. 4
figure 4

Number of patients who do not have to wait longer than x days

Full size image
Table 3 Percentages of evaluation scenarios in which a robust schedules achieves a goal to a certain level and spreads of levels of goal achievement
Full size table

The weighted sum approach clearly tends to produce solutions closer to the scenario-dependent optima as the percentage for values within the interval 0.8–0.9 is always higher compared to the maxmin approach. In general, in 75 % of the evaluation scenarios the schedule using the weighted sum (maxmin) approach achieves at least 85 % (81 %) of the stakeholders’ individually optimal solution. Despite the very conservative planning approach this is a remarkable result. Finally, a comparison of the relative levels for overtime on the one hand and for waiting time and deferrals on the other hand points at a trade-off between the two approaches. A slight increase in the degree of satisfaction for the goals waiting time and deferrals due to the weighted sum or the maxmin approach causes a significantly larger decrease in the level of satisfaction for overtime (and vice versa).

4.2 Different variants and trade-offs

Using the maxmin approach, we now investigate how the performance of a robust schedule changes if different assumptions on patients’ surgery times and the demand for emergency surgeries have to be considered. This allows to further investigate consequences on the trade-offs between two goals if the assumptions regarding the stochastic parameters are changed. We allow that the decision maker wants to investigate different assumptions on the planned surgeries deviations with respect to the above mentioned sample sets of elective patients. Recall that the decision maker’s planning is based on scenarios for every patient’s surgery durations rather than considering the (unknown) probability distribution. We will denote these assumptions in terms of variants 1 through 4 which are specified below. Variants 1 and 2 assume that surgery times for elective patients vary symmetrically around an expected duration. In particular, we distinguish between very little (1) and larger or normal (2) deviations from expected durations. In addition we also investigate two sets of elective patients considering non-symmetrical deviations. In terms of variants 3 and 4 is is assumed that patients’ surgery durations tend to be shorter (3) or longer (4) than the expected surgery durations, e. g. with variant 3 it is assumed that there are more surgeries that take less time than expected and only few ones taking longer than expected (and vice versa). We consider respective settings for emergency demand according to the proposed variants 1 through 4. Beginning with an average amount of emergency demand for a regular day we assume that similar deviations as stated with elective surgeries are taken into account. Figure 5 depicts how the previous analysis is amended in order to account for the four different variants. Note, that the very first part planning information is not changed. The respective steps to compute a robust compromise solution and to evaluate this schedule and its emergency reservation are according to the previous studies in this chapter.

Fig. 5
figure 5

Analysing changes in decision maker’s assumptions in terms of different variants

Full size image

The number of patients being scheduled within the planning period and the average utilisation of the operating rooms alongside with the average waiting time are characteristic aspects of an operating room schedule. Note, that in terms of planned utilisation we consider the workload if every surgery takes its expected time to finish. These figures are shown in Table 4 and indicate the high level of overall quality of the schedules. For the compared approaches the results are very close within the different variants. The weighted sum approach systematically schedules at least the same number of patients and provides slight benefits regarding patient waiting times. This underlines that the maxmin approach in general incorporates a higher degree of conservatism which is especially indicated in terms of a lower amount of planned utilisation. The weighted sum approach provides a higher level of tolerance towards violations of the capacity limitations. The maxmin approach supports a lower risk of overtime and schedules fewer surgeries. However, the conservative way of planning covered by the maxmin approach provides a high degree of flexibility which is a major feature of this concept. This flexibility guarantees that a plan is executable with a very low risk of violating the capacity limitations. For the given application this allows to handle longer elective surgeries or a higher amount of emergencies. In general, focusing on maximising the minimum level of goal achievement rather than maximising the average leads to a smaller spread within the values of all objective functions.

Table 4 Number of patients scheduled and average level of planned utilisation compared in terms of variants 1 – 4 using the approaches weighted sum and maxmin
Full size table

First, the impact of these changes is demonstrated for the level of overtime. Applying variant 3 we assume that surgery durations are significantly longer, e. g. surgeries are more complicated and require more time than expected. In this case the amount of daily overtime in minutes significantly increases (Fig. 6). Connecting this result to the number of scheduled patients (see Table 4 for reference) we see that the planned nominal workload is higher and thus the risk of overtime increases with variant 3. Accordingly, the amount of idle time decreases significantly. Apparently, this shift is caused by a less conservative attitude towards realisations of the stochastic parameters. We observe similar changes if the weighted sum approach is applied and the absolute values differ accordingly. Similar results also occur if surgery durations are significantly shorter and the described shifts happen in opposite directions. It is interesting that for the case of different variants no major changes in waiting times can be concluded. The majority of patients has to wait not more than 2 days referring to the first possible date. Note that the hospitalisation date does not imply that the patient stays at the hospital.

Fig. 6
figure 6

Comparing two variants with respect to cumulative probabilities for overtime

Full size image

In a next step, we analyse trade-offs between two goals focusing on the maxmin approach. We compare both absolute levels of goals and subsequently their potential to achieve the optimal solution. First, the trade-off between the average waiting time of patients and the number of patients treated/deferred is investigated. Additionally, we indicate impacts if different variants are applied. Table 5 compares absolute values for average waiting time and the resulting changes if fewer surgeries are planned. The robust solutions focus on scenarios with high waiting times and low numbers of patients to be scheduled. For an exemplary robust schedule (maxmin, variant 1) it indicates that an average increase in waiting time of 0.5 days is tolerated which means that every second patient has to wait 1 day longer than expected. In more than 90 % of the evaluation scenarios, the robust approach additionally postpones between 4 and 8 patients according to the optimal number of deferrals. These deferrals lead to an increase of average waiting time which is in 20 % of all scenarios below 0.25 days and thus very small. According to the absolute values, the relative deviations and thus the stakeholder’s satisfaction with a solution are very close to the optimal solutions. This underlines the good results described in the table above, yet there are slight decreases with shorter surgery durations (maxmin, variant 4). In the latter case, the planning is too conservative because the number of patients scheduled is smaller than apparently necessary. Thus, waiting time increases significantly compared to the optimal amount of waiting time.

Table 5 Comparing number of additional waiting days (on average) and number of additionally deferred surgeries (maxmin, variant 1) – frequencies in %
Full size table

Investigating the impact of changes in waiting time or deferrals for the actual level of overtime strengthens our previous findings. The left graph in Fig. 7 indicates that in terms of absolute deviations an increase in waiting time is also combined with higher overtime (which is the same with relative deviations). An increasing amount of additional waiting time (compared to variant 1) occurs if the actual surgery durations are shorter and thus the workload increases only slightly. It can also be concluded that due to the fixed surgery dates there is a large spread especially within the achievement of the goal overtime minimisation. In general, shorter surgeries lead to a higher level of goal achievement for overtime. For longer surgeries the level of goal achievement decreases accordingly. The trade-off between overtime and the number of deferrals shows that the amount of overtime decreases with fewer patients being scheduled. In addition to this, the right graph in Fig. 7 shows that shorter surgery durations cause a higher number of patients being scheduled. Thus, the number of deferrals decreases compared to variant 1 but obviously the increase in overtime compared to variant 1 is lower. Finally, the acceptance for the management’s goal is high but the amount of overtime is also high. These effects become less intensive with surgeries being shorter as with variant 4.

Fig. 7
figure 7

Trade-Off between changes in average waiting time and overtime (left) and between changes in average number of deferrals and overtime (right)

Full size image

The presented approach incorporates robustness and fairness aspects and provides two major beneficial features. First, due to the normalisation of the objective function values, the final performance measured in absolute values is most acceptable. The results are close to the optimal solutions measured in terms of relative and absolute deviations regarding different stakeholders’ goals. Fixing surgery dates at the beginning of the planning period requires to plan a certain amount of slack time. The required amount of slack increases with a higher degree of conservatism. Subsequently, the resulting risk of idle time leads to opportunity losses. This approach enables the decision maker to balance the degree of conservatism according to his attitude towards risk. In general, the results of this computational study show that this approach is able to find solutions which are feasible for a large number of uncertainty settings given this particular area of application. High quality robust compromise solutions can be identified even if only a small number of scenarios is considered. Recall that the degree of conflict among the objectives as well as the width of the interval between best and worst accepted individual solutions influence the solutions. Besides, the chosen scenarios and their number also influence the quality of the robust compromise solution. However, given that the proposed concept is very conservative in terms of integrating both multiple preferences and uncertain planning parameters it is very well adaptable for other areas of application which face similar decision problems. Especially evaluating a robust compromise solution using scenarios different from those chosen to obtain the robust compromise solution makes this approach beneficial for risk-averse decision makers.

5 Conclusions

We presented an approach which simultaneously minimises relative distances to scenario-optimal solutions and individually optimal solutions. Decision making in hospitals affects multiple stakeholders’ interests which was discussed focussing on the operating room scheduling problem. At an intermediate level between tactical and offline operational planning, patients were allocated to a given block schedule in order to meet three conflicting goals. We demonstrated that only small changes in the absolute levels of the stakeholder’s goals are necessary in order to find an acceptable solution. The presented approach is able to balance the stakeholders’ interests at fair levels. Furthermore, we showed that the robust compromise solutions are very close to scenario-dependent individually optimal solutions measured in terms of relative deviations. Additional specifications of a stakeholder’s preferences can be integrated into the presented approach by interactive adjustments of the membership functions. The proposed robust compromise may also be used as a starting point for negotiations among the involved stakeholders. Finally, the presented approach is beneficial in order to reduce the risk of re-planning which is achieved by some opportunity losses due to the robustness of the solution. Integrating the proposed approach into a dynamic approach is considered a promising extension since it allows to develop additional scheduling policies in order to support the multiple stakeholder operating room scheduling problem.