1 Introduction

Cardiovascular disease is a prominent cause of death in the world today wreaking havoc on human life and health [1]. The ECG has become a common method for monitoring cardiac health due to its utility in both research and clinical use [2]. ECG is often the most cost-effective, least intrusive, and most efficient approach [3]. Because the atrium and ventricle comprise the majority of the heart’s cells, the strength of their signal is proportional to the total number of active heart cells [4]. As a result, changes in atrial and ventricular cell action potentials are the predominant cause of variation in a surface ECG waveform [5]. Figure 1 depicts the QRS bundle, P, and T waves in their entirety, as well as the whole ECG cycle. These waves, along with the derived QT, PR, and ST segments, are the most essential distinctive features of the ECG, indicating the conduction system of the heart and revealing whether the heart itself has abnormalities or not [6]. As a result, it is vital that the ECG not be disrupted by noise throughout the data collection process.

Fig. 1
figure 1

ECG trace: interval, wave, and bundle

Full size image

ECGs are distinguished by their quasi-periodicity, low frequency, and energy concentration. ECG sampling is frequently interrupted by a high level of noise, most notably Muscle Artefacts (MA), Baseline Wander (BW), and Electrode Motion (EM) artefacts [7] and it is given in Fig. 2. MA frequently occurs between 20 and 40 Hz (Hz), classifying them as high-frequency noise [8]. This background noise is caused by muscle tremors, which appears as an inconsistency between the portrayal of the muscles and the actual scene. Medical imaging professionals must apply effective ways to minimize the unfavourable effects of noise on image quality. EM artefacts are brief bursts of noise caused by insufficient skin contact with the electrodes. Electrode slippage and BW are both the result of low-frequency noise, such as that produced by breathing [9]. These abnormalities substantially impair clinical judgment, increasing the likelihood of making an inaccurate diagnosis. For this reason, de-noising sampled ECG data is critical. The hardware implementation of the ECG denoising technique using FPGA has gotten little attention [10, 11]. The FPGA is a reprogrammable integrated circuit that interacts with the DSP and the microcontroller unit (MCU) [12]. Implementing signal processing techniques on an FPGA presents significant challenges. Because all CPUs can do mathematical operations, nearly all of them can run DSP algorithms. An FPGA and a general-purpose DSP are functionally equivalent for this application. Designing digital systems with excellent efficiency and low consumption of energy is hard, especially for mobile devices. To lower the system’s overall power consumption, it is essential to have energy-efficient designs at the coarse-grained level. FPGAs are capable of handling a greater number of simultaneous operations than DSPs.

The goal of this study is to improve the quality of ECG data by eliminating noise, which results in a higher SNR and a lower RMSE. Specifically, we aim to improve healthcare outcomes by developing a noise reduction method that can effectively separate the relevant features of ECG data from the noise, thereby reducing the amount of distracting background noise, and increasing the reliability of the ECG data, allowing for a more precise diagnosis of heart disease. We use FPGA technology to achieve real-time deployment. To ensure efficient and long-lasting functioning, we will be picking an FPGA board that is well-suited for the task at hand and fine-tuning the model’s design to achieve low power consumption. The three main contributions of this study are as follows. First, we collected benchmark data and did an extensive study on the removal of three types of noise in ECG signals: MA, EM, and BW noise. Second, we developed a novel technique that considerably enhances the SNR during the denoising process, hence improving the quality of ECG data. Third, we have found an FPGA that is both suitable for real-time processing and well-known for its low power consumption; this ensures an effective and sustainable approach to implementing our model.

Fig. 2
figure 2

ECG and its noise

Full size image

The paper is properly divided into several sections that all have their purpose. Section 1 provides a thorough explanation of ECG, its importance in diagnosing disease, and the most frequent types of noise that can impact ECG readings. In Sect. 2, relevant prior literature on ECG denoising is offered for background on the current study. Section 3 describes the research methodology and provides a full explanation of the proposed method workflow. Section 4, explores an extensive analysis of the denoising algorithm’s performance and examines the resource utilization and power consumption of the FPGA. Finally, Sect. 6 concludes the research by underlining the excellence of the proposed technique and providing perspectives on future research.

2 Literature survey

Due to the growing relevance of precise and real-time ECG signal processing in healthcare and biomedical engineering, research on ECG denoising and its application in FPGA has seen a tremendous increase in recent years. Since ECG signals are frequently contaminated by a wide variety of noise sources, researchers have recognized the importance of identifying methods to improve their quality. This section describes some of the most recent works.

The paper [13] presents a unique approach for denoising ECG data affected by wideband noise. The proposed approach considers clean ECG data to be a composite of many elements. These components are distinct in the time domain, share some frequency-domain spectral coefficients, and operate over a wide range of frequencies. Based on this approach, this study presents a consecutive local filtering strategy for cleaning up ECG data by reducing wideband noise. A segmentation approach has been developed to divide the recorded ECG data into subsamples, each of which typically reflects a single dominating component, before trying to apply the proposed method to the data. By successively applying ideal filters to each segment, the denoised ECG signal can be built. The suggested approach automatically adjusts the BW for each ideal filter to match the BW of the dominant component in the studied subsegment. In simulations employing both synthetic and actual ECG data, the proposed technique was proven to be effective in denoising ECG data that had been contaminated by wideband noise. It is also demonstrated that the suggested approach significantly outperforms different existing algorithms. In research [14], the author describes a new denoising technique for ECG signals that improves performance and availability in a variety of noise settings. The solution builds on the conditional generative adversarial network (CGAN) paradigm for ECG denoising. An optimized convolutional auto-encoder (CAE) serves as the system’s generator, while a CAE serves as the discriminator. Comprehensive research findings from the MIT-BIH databases demonstrate that the denoised ECG signal achieves good SNR, outperforming state-of-the-art approaches for both single and mixed noises. The average accuracy of classifying four heart diseases using denoised data increases by roughly 32% when several noises are present at SNR = 0 dB. As a result, the proposed method may effectively remove noise while keeping the finer properties of ECG signals. In a paper [15], researchers disclose a DL-based ECG denoising system that exploits the natural periodicity of ECG signals. This technique stacks ECG cardiac cycles to form a 2D signal to train a convolutional neural network (CNN). As a result, by capitalizing on the correlation between cardiac cycles, ECG denoising can be made more effective and robust. The suggested CNN model incorporates a unique local/non-local cycle observation element is takes into consideration the cycles’ inherent association. The suggested approach will be tested on the MIT-BIH database. The concept’s performance has been evaluated in a variety of experimental configurations with varied degrees of background noise. In terms of RMSE and SNR improvement, the system outperforms prior art approaches.

The paper [16] shows the design and development of a low-cost, portable device that can clean up noisy ECG signals efficiently and discreetly. To begin, they employ a single-node reservoir Computing (SNRC) architecture to clean the damaged ECG signal in a very efficient manner. Second, by implementing the technique on a portable, low-cost FPGA chip, they obtain excellent speed and privacy. This text simulates regular EMG and PLI noises. To evaluate the efficacy of the technique, three performance metrics are used. The information comes from the MIT-BIH database. In the case of EMG and PLI noise, it achieves an excellent SNRimp and PRD with a 0 dB input SNR. The study [17] discusses a new approach for achieving the development of optimal IIR digital filters to eliminate interruptions in the ECG signal. Following synthesis and simulation, a summary of its power consumption, resource consumption, and timing is provided. To do this, the HDL command line interface is used to transform MATLAB code for various IIR filters designed for denoising ECG signals into Verilog code. The intended hardware was the Spartan-6 field-programmable gate array (XC6SLX75T in 3FGG676 package). The Xilinx Power software is utilized to calculate a digital design’s projected power consumption. The filter’s complex structure must be examined on the FPGA platform for it to be hardware efficient. According to the findings, the FPGA-based filter design looks to be ideal for ECG portable devices since it reduces complexity and expense by employing fewer multipliers and adders, which take up less space on the chip and use less power than MATLAB.

In the study [18], an FIR filter is employed to eliminate particular types of sounds. FIR filters for ECG noise have been created utilizing noise-specific coefficients. The filter’s performance attributes were prioritized during the design process. A Kaiser window has been included in the ECG to provide a happy medium between noise suppression and signal distortion. The period of the impulse response in an FIR filter is finite. The fundamental blocks of a multiplier, an adder, and a flip-flop can be used to create and execute FIR filters. The effectiveness of the FIR filter is greatly affected by the multiplier, the slowest component of the adder. It’s been proposed to use both the carry choose adder and the Booth Multiplier in tandem in a Finite Impulse Response Filter. Several of this filter’s properties have been contrasted to those of others. The proposed filter was created with the help of Verilog and Xilinx 14.7 Vivado. Time and space requirements were reduced. This FIR filter was utilized to build the filter for denoising ECG because its coefficients are well-suited for ECG denoising. The authors [19] suggest a hardware-efficient FPGA-based design for creating a noise-free ECG signal using lifting-based wavelet denoising and a universal threshold level-dependent function in tandem with soft thresholding. A simplified lifting-based DWT approach is also proposed in the article, which offers a single-step calculation for determining the DWT’s inverse and forward coefficients. Instead of using the comparators that are so difficult to build in VLSI, wavelet-based thresholding makes use of a median computation and soft thresholding block. The MIT-BIH database is the source for the ECG rhythm and noise data. When tested on MATLAB, the proposed denoising method improved the SNR of the ECG signal and reduced the mean squared error. The proposed wavelet-based denoising structure uses less hardware and operates at a higher frequency when compared with previous denoising solutions for ECGs. In the paper [20], researchers offer a novel FPGA architecture for noise reduction using variable step-size variable tap length delayed error normalized least mean square (VSS-VT-DENLMS) method. This strategy alters the DENLMS method’s weight update formula by adjusting the tap lengths and step sizes. At the same time to identify a better trade-off between error reduction and rapid convergence. To further enhance effectiveness in terms of area and speed, the suggested VSS-DENLMS adaptive filter structure integrates a systolic and folding structure with a compressor-based booth multiplier. The suggested filter design is tested on the MIT-BIH database, and the obtained filtrated results are evaluated. The simulation outcome shows that the suggested filter is superior to state-of-the-art filters while requiring less hardware complexity, proving the approach is viable for analysing ECG data in real-time.

3 Methodology

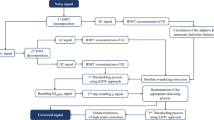
The ECG signal denoising methodology and its subsequent deployment in FPGA involve a series of crucial steps, as detailed in Table 1; Fig. 3.

Table 1 Details of the proposed method workflow
Full size table
Fig. 3
figure 3

Workflow of proposed ECG denoising

Full size image

3.1 Acquired ECG signal

The MIT-BIH Noise Stress Test Database and the Arrhythmia Database made up the main dataset [21]. The BIH arrhythmia laboratory recorded dual-channel dynamic ECGs on 47 individuals from 1975 to 1979, and the recordings are included in the MIT-BIH Arrhythmia Database. Across all of the records, there are 650,000 signal samples collected at 360 Hz. When slicing the ECGs, we used a slice size of 1024 signal samples per record, with a total of 30,240 slices used for the pure ECG data sample. The Noise Database was used to extract BW, EM, and MA noise, totalling 650,000 signal samples. We additionally selected 630 noise dataset slices, each comprising 1024 signal samples from the original noise signal. Using the following procedure on both the clean ECG dataset and the noisy dataset, the value of the ECG signal was normalized.

$$Normalized\left({x}_{i}\right)=\frac{{x}_{i}-{x}_{min}}{{x}_{max}-{x}_{min}}$$
(1)

The \({x}_{i}\) is the signal value in a given slice, \({x}_{max}\) is the biggest signal value in this particular slice, and \({x}_{min}\) is the least signal value in this particular slice. Then, we subjected the clean ECG to a variety of noises with SNR of -20 dB, -10 dB, 0 dB, 10 dB, and − 20 dB using Eq. 2. MA, EM, and BW noise were all included. To generate the noise, we utilized the following expressions:

$$Y=X+N,{N}_{i}={\eta }_{i}\sqrt{\frac{\sum {x}_{i}^{2}}{\left(\sum {\eta }_{i}^{2}\right)*{10}^{\frac{snr}{10}}}}$$
(2)

where \({x}_{i}\)denotes the pure ECG, \({\eta }_{i}\) denotes the noise signal, \(snr\) represents signal-to-noise ratio, and \(Y\) represents noisy ECG. The noise, represented by \({N}_{i}\), is the outcome of calculating the SNR. We segmented the ECG dataset with an 8:2 split between the training and validation/test sets. With this ratio in mind, we randomly divided each ECG record’s 630 data slices into 504 and 126 data slices, generating a total of 24,192 and 6048 data slices to be utilized in the ECG noise reduction train and test set, respectively.

3.2 Denoise ECG into series of IMF

The high-order synchrosqueezing transform (HSST) extends the standard short-time Fourier transform (STFT)-based SST (FSST) first established in the article [22] by using higher-order phase and amplitude approximations. The following is the definition of an AM-FM signal:

$$f\left(t\right)=A\left(t\right){e}^{i2\pi \varnothing \left(t\right)}$$
(3)

Where \(A \left(t\right)\) and \(\varnothing \left(t\right)\) represent the amplitude and phase functions. The STFT of the signal \(f\) is expressed as follows:

$${V}_{f}^{g}\left(t,n\right)=\int f\left(\tau \right){g}^{\text{*}}\left(\tau -t\right){e}^{-i2\pi n\left(\tau -t\right)}d\tau$$
(4)

The complex conjugate of the window function \(g\), denoted as \({g}^{*}\). Here is an expression for the traditional FSST:

$${T}_{f}^{g,\gamma }\left(t,\omega \right)=\frac{1}{{g}^{*}\left(0\right)}{\int }_{\left\{\eta ,\left|{V}_{f}^{g}\left(t,\eta \right)\right|>\gamma \right\}}{V}_{f}^{g}\left(t,\eta \right)\delta \left(\omega -{\omega }_{f}\left(t,\eta \right)\right)d\eta$$
(5)

Where \(\delta\) is the Dirac distribution and \(\gamma\) is the threshold. The instantaneous frequency estimation at frequency \(\eta\) and time \(t\) is denoted by \({\omega }_{f}(t,\eta )\) and is calculated as:

$${\omega }_{f}\left(t,\eta \right)=R\left\{\frac{{\partial }_{t}{V}_{f}^{g}(t,\eta )}{i2\pi {V}_{f}^{g}(t,\eta )}\right\}$$
(6)

Where \(R \left\{Z\right\}\) represents the real component of the \(Z\), and \({\partial }_{t}\)represents the temporal partial derivative.

The high-order SST calculates instantaneous frequency using Taylor expansions of phase and amplitude. For values near to 1, the signal’s Taylor expansion appears to be this.

$$f\left(t\right)=exp\left(\sum _{k=0}^{N}\frac{{\left[\text{log}\left(A\right)\right]}^{\left(k\right)}\left(t\right)+{i2\pi \varphi }^{\left(k\right)}\left(t\right)}{k!}{(\tau -t)}^{k}\right)$$
(7)

The kth derivative of \(Z\) at the time \(t\) is denoted by \({Z}^{\left(k\right)}\left(t\right)\). So, we can write this signal’s STFT at time \(t\) and frequency \(\eta\) as:

$${V}_{f}^{g}(t,\eta )=\int f(\tau +t){g}^{\text{*}}\left(\tau \right){e}^{-i2\pi \eta \tau }d\tau$$
(8)
$$=\int exp\left(\sum _{k=0}^{N}\frac{{\left[\text{log}\left(A\right)\right]}^{\left(k\right)}\left(t\right)+{i2\pi \varphi }^{\left(k\right)}\left(t\right)}{k!}{\left(\tau \right)}^{k}\right){g}^{\text{*}}\left(\tau \right){e}^{-i2\pi \eta \tau }d\tau$$
(9)

Using Eq. 4, we may estimate the instantaneous frequency \({\omega }_{f}\)\((t, \eta )\), at a given location.

$$\begin{array}{l} {\omega }_{f} (t, \eta )=\frac{{\left[\text{log}\left(A\right)\right]}^{{\prime }}\left(t\right)}{i2\pi }\\+{\varphi }^{{\prime }}\left(t\right)+\sum _{k=2}^{N}\frac{{\left[\text{log}\left(A\right)\right]}^{\left(k\right)}\left(t\right)+i2\pi {\varphi }^{\left(k\right)}\left(t\right)}{i2\pi \left(k-1\right)!}\frac{{V}_{f}^{{t}^{k-1}g}(t,\eta )}{{V}_{f}^{g}(t,\eta )}\end{array}$$
(10)

The frequency modulation operator \({q}_{\eta ,f}^{[k,N]}\) is introduced.

$${q}_{\eta ,f}^{[k,N]}=\frac{{\left[loglog \left(A\right) \right]}^{\left(k\right)}\left(t\right)+i2\pi {\varphi }^{\left(k\right)}\left(t\right)}{i2\pi \left(k-1\right)!}$$
(11)

The representation of the Nth-order local complex instantaneous frequency, \({\omega }_{n,f}^{\left[N\right]}\), at frequency \(\eta\) and time \(t\) is as follows:

$${\omega }_{n,f}^{\left[N\right]}(t,\eta )=\left\{\begin{array}{c}{\omega }_{f}\left(t,\eta \right)+\sum _{k=2}^{N}\left(\eta ,t\right)\left({-x}_{k},1\left(t,\eta \right)\right),\\ {V}_{f}^{g}\left(t,\eta \right)\ne 0,{\partial }_{\eta }{x}_{j.j-1}\left(t,\eta \right)\ne 0\left(j\ge 2\right),\\ {\omega }_{f}\left(t,\eta \right),\\ Otherwise.\end{array}\right.$$
(12)

Consequently, in Eq. 5, the high-order FSST can be expressed by substituting \({\omega }_{n,f}^{\left[N\right]}(t, \eta )\) for \({\omega }_{f}\)\((t, \eta )\):

$${T}_{N,f}^{g,\gamma }(t,\omega )=\frac{1}{{g}^{*}\left(0\right)}{\int }_{\left\{\eta ,\left|{V}_{f}^{g}\left(t,\eta \right)\right|>\gamma \right\}}{V}_{f}^{g}\left(t,\eta \right)\delta \left(\omega -{\omega }_{\eta ,f}^{\left[N\right]}\left(t,\eta \right)\right)d\eta$$
(13)

At last, the model will be approximately reconstructed by.

$$f\left(t\right)\approx {\int }_{\{\omega ,|\omega -\phi \left(t\right)|<d\}}{T}_{N,f}^{g,\gamma } \left(t,\omega \right)d\omega$$
(14)

Where \(d\) represents the compensation factor and \(\varphi \left(t\right)\) is an estimate for\({ \varphi }^{{\prime }}\left(t\right)\).

3.3 Eliminate noisy IMF

Detrended fluctuation analysis (DFA), as described in [23], is an effective method for obtaining a more trustworthy scaling exponent when the signal exhibits non-stationary characteristics. The DFA’s essential idea is to determine the link between the time scale n and the variance around the local trend in the box size. The first phase of the procedure is to calculate the integrated time series \(y\left(k\right)\) after eliminating the average, as seen below:

$$y\left(k\right)=\sum _{i=1}^{k}\left[x\left(i\right)-\stackrel{-}{x}\right], 1\le k\le N$$
(15)

Where \(N\) denotes the total samples and \(\underset{\_}{x}\) denotes the average throughout the range \([1,N\)]

Then, \(n\) compartments are created in \(y (k\)). The EMD residue is used to estimate the local trend \({y}_{n}\left(k\right)\) for each box. Definition of Root-Mean-Square Disturbance \(F\left(n\right)\)

After that, \(y (k\)) is split into n boxes. The EMD residue is used for determining the local trend \({y}_{n}\left(k\right)\) for each box. The root-mean-squared fluctuation, \(F \left(n\right)\), is described as

$$F\left(n\right)=\sqrt{\frac{1}{N}\sum _{k=1}^{N}{[y\left(k\right)-{y}_{n}\left(k\right)]}^{2}}$$
(16)

After \(n\) iterations, the scaling exponent, α, is expressed as the slope of the \(log \left[F\left(n\right)\right]/loglog \left(n\right)\)plot.

$$F\left(n\right)\propto {n}^{\alpha }$$
(17)

The scaling exponent can be employed to quantitatively describe the temporal correlation in the time series. A value of α = 0.5 represents the uncorrelated data. An anti-correlated signal has a value of α between 0 and 0.5. A value of α between 0 and 0.5 represents the long-range temporal correlations. When α > 1, power-law decay is not observed in the correlations. Additionally, the scaling exponent characterizes the volatility of the time series. Due to its capacity to detrend time series, DFA is commonly employed to detect scaling features and long-range correlations in non-stationary time series. We use DFA in the study to estimate the total number of IMFs and to separate the signal from the noise among the IMFs.

3.4 Denoise remaining IMF

The non-local-mean filter attempts to remove noise from the signal by restoring the original signal \(u\). If noise is denoted by \(n\), the noisy signal \(v\) is represented in the article [24]:

$$v=u+n$$
(18)

NLM will attempt to approximate the original signal utilizing Eq. 19.

$$\widehat{u}\left(s\right)=\frac{1}{Z\left(s\right)}\sum _{t\in N\left(s\right)}w\left(s,t\right)v\left(t\right)$$
(19)

\(u\left(s\right)\) represents the predicted signal given the \(s\) sample, and \(Z\left(s\right)\)is calculated by:

$$Z\left(s\right)=\sum _{t}w(s,t)$$
(20)

Where \(w\left(s,t\right)\) denotes the weights formalized by:

$$w\left(s,t\right)=exp\left(-\frac{{\varSigma }_{\delta ?\varDelta }{(v\left(s+\delta \right)-v\left(t+\delta \right))}^{2}}{2{L}_{\varDelta }{\lambda }^{2}}\right)$$
(21)
$$=exp\left(-\frac{{d}^{2}(s,t)}{2{L}_{\varDelta }{\lambda }^{2}}\right)$$
(22)

The bandwidth is specified by the \(\lambda\) value in the Eq. 21. In addition, \({L}_{\varDelta }\) samples are contained in the local patch denoted by \(\varDelta\), which surrounds \(s\). Since each patch has an average value of 1, the center patch is typically corrected to provide a more uniform outcome. Thus, the formalization of the weight is as follows:

$$w\left(s,s\right)={\text{max}}_{{t?N}\left(s\right),t\ne s} w\left(s,t\right)$$
(23)

PSO has been frequently utilized for algorithm optimization. PSO is well-known due to its ease of use and effectiveness in locating the best solution. Eberhart and Kennedy [25] suggested PSO, which was influenced by the patterns of behavior observed in schools of fish and flocks of birds. Each PSO particle represents a potential answer to a certain issue. Particles are dispersed at will throughout the search area. There are two aspects to every particle: its location (X) and its motion (V) [26]. Each iteration towards a global solution will involve updating these two parts. Equation 24 and Eq. 25 provide the current forms.

$${V}_{i}^{d}={V}_{i}^{d}+{c}_{1}*{rand1}_{i}^{d}\left({pbest}_{i}^{d}-{x}_{i}^{d}\right)+{c}_{2}*{rand2}_{i}^{d}({gbest}_{i}^{d}-{X}_{i}^{d})$$
(24)
$${X}_{i}^{d}={X}_{i}^{d}+{V}_{i}^{d}$$
(25)

If \(d\) = 1, 2, 3, … ,\(D\), then \(d\) is the particle’s dimension. Each particle is denoted by a different \(i\)from \(1\) to \(N\). Acceleration coefficients \({c}_{1}\) and \({c}_{2}\) are the constants in this equation. Both rand1 and rand2 are arbitrary numbers with values between zero and one. The \(pbest\) and \(gbest\) are the local best and global best particles accordingly [27]. Whenever a new, superior solution is discovered, it is added to both the global best and the local best.

The conventional NLM is optimized \(\lambda\) to maximize. Mean Squared Error (MSE) is employed as the fitness function. We begin by setting numerous parameters in the NLM, including \(p\) and \(M\). The number of particles and the iterations used to update their position and velocity were also determined. The input signal is then de-noised for each particle individually, and the MSE is calculated. Finally, we update the particles’ local and best positions and their positions. There will be \(t\) iterations of this procedure. The best possible value \(\lambda\) is determined.

The updated equations for the particle’s velocity and position are provided in Eq. 26 and Eq. 27, respectively, if the \({i}^{th}\) particle’s position and velocity are given as \({x}_{i}\)and \({v}_{i}\), correspondingly.

$${v}_{i}^{n+1}={v}_{i}^{n}+{c}_{1}.rand \left(\right). \left({p}_{i}^{n}-{x}_{i}^{n}\right)+{c}_{2}.rand \left(\right).({p}_{g}^{n}\left(t\right)-{x}_{i}^{n})$$
(26)
$${x}_{i}^{n+1}={x}_{i}^{n}+{v}_{i}^{n+1}$$
(27)

Where \({V}_{i}^{n+1}\) indicates the current particle’s velocity and \({x}_{i}^{n+1}\)indicates the current particle’s position at the \({(n+1)}^{th}\)iteration.

The local and the global best position are written as \({p}_{i}^{n}\)and \({p}_{g}^{n}\) correspondingly. Constants \({c}_{1}\) and \({c}_{2}\) stand for the individual and social dimensions, respectively.

3.5 Evaluate the suggested method

We used two benchmark measures for evaluating the designed denoising algorithms. These are RMSE and SNR [28]. The root of the squared error difference in the denoised and raw ECG readings is the RMSE. It is used to calculate the difference between the denoising model’s anticipated and the real signal. A lower RMSE number indicates that the model performed better. SNR is the difference in SNR values between the input and output. The evaluation measure is built around the RMSE and SNR, which are defined as follows:

$$RMSE=\sqrt{\frac{1}{i}\sum _{i=1}^{I}{({S}_{i}^{{\prime }}-{S}_{i})}^{2}}$$
(28)
$$SNR=10log\frac{\sum _{i}^{I}{\left({S}_{i}\right)}^{2}}{\sum _{i=1}^{I}{({S}_{i}^{{\prime }}-{S}_{i})}^{2}}$$
(29)

\({S}_{i}\) is the actual clean ECG signal, \({S}_{i}^{{\prime }}\) is the ECG signal followed by noise reduction, and \(i\) is the total amount of sample points. The RMSE measures the degree of similarity between two sets of data. The shorter the gaps between the two, the lower the RMSE score. The SNR is the ratio of the signal to the noise in the signal. The greater the SNR, the more effective the noise reduction mechanism.

3.6 Deploy in FPGA

In real-time deployment, the FPGA is a critical platform for hosting the proposed ECG denoising model [29]. Two different FPGA boards, Virtex [30] and Zedboard [31] were used for simulation and comparison to evaluate the performance and viability of the proposed architectures. FPGA-based applications place priority on the efficient use of resources and low on-chip power consumption, therefore these simulations were designed with those goals in mind. The effectiveness of the proposed model was thoroughly assessed by using two different FPGA boards (Virtex and Zedboard). For this investigation, we employed the widely-known FPGA design and analysis program VIVADO [32]. This study’s findings are useful for determining not only the viability and performance of the ECG denoising model but also the optimal FPGA board for its deployment in real-time in terms of resource utilization and power consumption. Through this approach, we ensure that the ECG denoising model can function efficiently in real-time environments.

4 Result and discussion

HSST-DFA-PSO-NLM is a unique ECG denoising model, and below we provide the results and analyse its performance in contrast to the non-optimized version. The model’s efficacy in denoising ECG signals was assessed in the presence of MA, EM, and BW noise.

Tables (2, 3, 4) summarises the SNR analysis of the proposed technique with and without optimization for denoising ECG signals impacted by MA, EM, and BW noise at various noise levels. It allows for a direct evaluation of the optimized and non-optimized models under various noise conditions. Our proposed HSST-DFA-PSO-NLM model performed exceptionally well for ECG signals contaminated with MA noise. SNR values were consistently higher compared to the unoptimized HSST-DFA-NLM model throughout a wide range of MA noise levels (-20 dB to 20 dB). Specifically, the SNR for the proposed model ranged from 29.05 dB to 30.57 dB, while the non-optimized model achieved SNR values between 26.41 dB and 27.57 dB. This demonstrates that the incorporation of PSO and NLM components enhances the denoising capabilities of our model, especially for ECG signals contaminated by MA noise. Similar to the results observed for MA noise, the proposed HSST-DFA-PSO-NLM model outperformed the non-optimized version when denoising ECG signals affected by EM noise. SNR values for the optimized model ranged from 29.33 dB to 30.55 dB, while the non-optimized model achieved SNR values between 26.29 dB and 27.58 dB at various EM noise levels. When addressing ECG signals corrupted by BW noise, the HSST-DFA-PSO-NLM model consistently exhibited better denoising performance compared to the non-optimized HSST-DFA-NLM model. The SNR values for the optimized model ranged from 28.91 dB to 29.35 dB for different BW noise levels (-20 dB to 20 dB). In contrast, the non-optimized model achieved SNR values between 26.34 dB and 27.18 dB. These results suggest that the incorporation of PSO and NLM techniques improves the denoising capabilities of our model for ECG signals affected by BW noise.

Table 2 SNR analysis of the proposed method’s denoising effects on MA-affected ECG signal
Full size table
Table 3 SNR analysis of the proposed method’s denoising effects on EM-affected ECG signal
Full size table
Table 4 SNR analysis of the proposed method’s denoising effects on BW-affected ECG signal
Full size table

Tables (5, 6, 7) provides a detailed summary of the RMSE analysis for the proposed HSST-DFA-PSO-NLM method with and without optimization for denoising ECG signals affected by MA, EM, and BW noise at different noise levels. It allows for a direct comparison of the performance of the optimized and non-optimized models for each type of noise and at various noise levels. For ECG signals affected by MA noise, the results demonstrated a significant improvement in denoising accuracy when using the HSST-DFA-PSO-NLM model. The RMSE values were notably lower across all noise levels. Specifically, for − 20 dB, -10 dB, 0 dB, 10 dB, and 20 dB of MA noise, the HSST-DFA-PSO-NLM model produced RMSE values of 0.0158, 0.015, 0.0144, 0.0141, and 0.0171, respectively. In contrast, the non-optimized HSST-DFA-NLM model yielded higher RMSE values, ranging from 0.0908 to 0.7701. Similar to the results for MA noise, the RMSE analysis for ECG signals corrupted by EM noise showed a marked improvement in denoising accuracy with the HSST-DFA-PSO-NLM model. The RMSE values for the optimized model ranged from 0.0181 to 0.0304 at different EM noise levels, spanning − 20 dB to 20 dB. In contrast, the non-optimized HSST-DFA-NLM model resulted in higher RMSE values, ranging from 0.0779 to 0.1843. When denoising ECG signals affected by BW noise, the HSST-DFA-PSO-NLM model consistently outperformed the non-optimized version in terms of accuracy. The RMSE values for the optimized model ranged from 0.0332 to 0.0485 for different BW noise levels (-20 dB to 20 dB). Conversely, the non-optimized model resulted in higher RMSE values, ranging from 0.1399 to 0.15488. These results emphasize the importance of employing optimization techniques to enhance the accuracy of the denoising process for ECG signals affected by BW noise.

Table 5 RMSE analysis of the proposed method’s denoising effects on MA-affected ECG signal
Full size table
Table 6 RMSE analysis of the proposed method’s denoising effects on EM-affected ECG signal
Full size table
Table 7 RMSE analysis of the proposed method’s denoising effects on BW affected ECG signal
Full size table

The comparison of our proposed ECG denoising method with previous research works, as detailed in Table 8, reveals the remarkable effectiveness of our approach. In contrast to existing studies, our method consistently attains superior results in terms of SNR and RMSE across various types of noise. Specifically, we achieved an average SNR of 29.56, 29.68, and 28.86 and RMSE values of 0.0153, 0.0249, and 0.04159 when denoising ECG signals affected by MA, EM, and BW noise. These results surpass the SNR and RMSE values reported in the referenced studies ( [33, 34], and [35]), demonstrating the substantial enhancements our proposed method brings to ECG signal denoising.

Table 8 Comparison of the proposed method with the existing methods
Full size table

From Table 9, a clear inference can be made regarding the power consumption of the two boards under consideration. The Virtex board utilizes 3% of LUTs, 6% of Flip Flops, and 11% of DSPs. The dynamic and static power consumed by the Virtex board is 32mW and 103mW, respectively. On the other hand, the Zedboard utilizes 9% of LUTs, 19% of Flip Flops, and 48% of DSPs. The Zedboard’s power consumption is notably lower, with dynamic and static power of 28mW and 96mW, making it a more power-efficient choice when compared to the Virtex board. The FPGA performance can be visualized in Fig. 4.

Table 9 Resource utilization and power consumption of FPGA
Full size table
Fig. 4
figure 4

FPGA performance evaluation

Full size image

5 Conclusion

The investigation of FPGA-based denoising techniques for improving signal quality in ECGs yielded promising results and insights. The accuracy of cardiac diagnosis and monitoring are directly related to the quality of the ECG data, making denoising the signal essential. In this research, we studied an iterative procedure that includes data acquisition, HSST-based decomposition, DFA-based noise reduction, NLM-based denoising with PSO optimization, and signal reconstruction. Our method was shown effective by a thorough analysis of the denoised signals utilising standard performance metrics like SNR and RMSE. The proposed method archives SNR values of 29.56 dB, 29.68 dB, and 28.86 dB and RMSE values of 0.0153, 0.0249, and 0.04159. The ECG denoising technique ran smoothly on an FPGA. We assessed the FPGA’s power consumption and resource utilization, as well as its signal quality increases, which are all critical for practical application. This study sheds light on the effectiveness of FPGA-based solutions as well as their potential for wider adoption in healthcare settings. The FPGA technology not only permits real-time processing but also enhances the portability of ECG monitoring devices, making them ideal for telemedicine and remote patient care.

Adding blockchain technology to our future work on FPGA-based ECG denoising systems will improve the privacy and security of patient data. This requires the use of stringent data encryption, the creation of immutable, tamper-proof records via blockchain, and the development of permissioned access mechanisms via smart contracts. Interoperable data standards and secure communication protocols are essential for protecting information during transmission. By combining FPGAs and blockchains, healthcare apps can more effectively empower patients, and protect their data.