1 Introduction

The prominent observed controlling features of the sinusoidal oscillators analysed so far are the Condition of Oscillation (CO), Frequency of Oscillation (FO) and the control of the amplitude of the sinusoid being generated. Thus, from fixed-frequency to variable-frequency, from multiple-element controlled to Single-Resistance Controlled Oscillator (SRCO) and single-phase to multiphase of the FO, the range of oscillator type has been pretty diverse. Research developments on oscillator circuit configurations from the past have been mostly employing active elements such as; Operational Amplifiers (OA), Operational Transconductance Amplifiers (OTA), Current Feedback Operational Amplifiers (CFOA), Current Conveyors (CC) for performance features suitable to different application situations. Since these integrated circuits are available off-the-shelf, the oscillator realizations from these are available in abundance in open literature. A book [1], recently published, presents a useful account on various facets of these oscillator developments involving variety of many other active elements too. To uncover better performances and new features from oscillators, new analog building blocks are being looked up to by motivated researchers. A comprehensive collection [2] of massive range of active elements was presented to assist circuit-designers recognize their proper choice of active element for their specific application requirement of analog signal processing and generation. Many of these analog building blocks are still in their symbolic infancy today and need bipolar and/or CMOS implementation for their utilization in linear/non-linear signal generation/processing circuit configurations and are yet to be used in advancing oscillator circuit configuration synthesis.

There has been lot of interest in evolving SRCO but to be able to control FO of the sinusoidal oscillator through voltage automatically makes it a preferred choice due to its programmable and flexible nature. As this manuscript is majorly concerned with the Current-Mode (CM), canonic (employing not more than three resistors and two capacitors only) Voltage Controlled Oscillators (VCOs) utilizing only one type of active device, hence, our focus of discussion in the following is in this light and on VCOs offering (or can be made capable of providing) current-mode outputs. A survey summary of features of some prominent selected VCOs is tabulated in Table 1 which provides, at a glance, comparison among them. It is obvious from Table 1, that all the voltage-mode sinusoidal VCO configurations (except [12]) have utilized two or more types of active devices to accomplish the voltage-control feature of FO and no additional FO control by any resistance. In the VCO of [12], however, only OTAs have been used for voltage control functionality but four matched grounded capacitors have been employed thereby making it non-canonic. The VCOs in [3,4,5, 9, 11] employ OA and FET and/or analog multiplier and are all Voltage-Mode (VM) type where possibility of achieving current output from a high impedance port is non-existent. However, in other voltage-mode VCOs such as [6,7,8, 10, 12,13,14,15,16,17,18] the second active device used are from Current Conveyor (CC) family where it can be said (in retrospect) that the voltage-mode VCOs realized, with CCs, CFOAs and/or other CC family device, could have yielded current output if additional current output ports (mostly Z-port) of these devices were tried to have been made available in these configurations.

Table 1 Comparative features of some selected prominent VCOs
Full size table

Now, in conclusion it can be said that VCOs [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18] have the following features and limitations.

  1. 1.

    All VCOs [3,4,5,6, 9,10,11,12,13,14,15,16,17,18] are voltage-mode VCOs and do not offer additional FO control by any resistance,

  2. 2.

    All employ two or more type of active devices except [12],

  3. 3.

    Except [6,7,8,9,10, 15,16,17,18] all are non-canonic, that is employ more than 3R and 2C passive components,

  4. 4.

    Except [5, 9, 11, 12, 15,16,17,18] all do not provide linear voltage control of FO and,

  5. 5.

    Current output availability is non-existent in all (except one circuit in [10]).

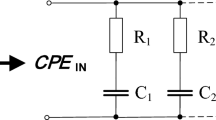
Currently traditional calculus is viewed as a mini breed from the huge fractional-order calculus which is a division of mathematics about non-integer-order differentiation and integration. Over the past few decades fractional-order calculus has obtained remarkable recognition from the investigators. Following innumerable fractional-order analysis the applications as therein [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37] have appeared for the situations of analog signal processing and generations. The Fractional-Order Element (FOE) or Constant Phase Element (CPE) is the generalized form of typical passive circuit component and has, mostly, been the core device utilized in these works. Phase angle of this CPE relies on the Order of the CPE and its impedance is called as fractional-order impedance. This fractional-order impedance is designated simply as fractance. Although CPE is not accessible commercially, several papers have proposed various techniques to realize CPE which incorporates rational approximations [20,21,22, 27], RC ladder network [30], and chemically realized CPE [24].

Due to extensive applications of sinusoidal oscillators [1], fractional-order synthesis of these has especially been given greater intentness. During the design and synthesis stage of oscillators, fractional-order calculus assists in the generalization of several oscillator characteristics specifically FO, CO and phase. Fractional-order calculus provides extra control over these parameters which make them useful in various application situations. Taking into account these noticeable features of fractional-order oscillators several oscillator design configurations can be found in open literature, for instance, see [19, 23, 32,33,34,35,36,37,38]. In all these oscillator configurations the conventional capacitance is replaced by fractance. The fractional-order oscillator configurations developed so far have mostly utilized active components such as OA, OTA, CFOA, Operational Trans Resistance Amplifiers (OTRA) and CCs. But till now none of the works talks about Fractional-Order Voltage-Controlled Oscillators (FO-VCO) except [19]. That becomes motivation of this communication to present to the readers a catalogue of a class of current-mode FO-VCOs systematically derived by invoking a well-known state-variable oscillator synthesis method [39]. As promised therein the work [19], this communication is, therefore, the extension of the same that uses the multiplication-mode current conveyor (MMCC). In [19] we have utilized only one \( Z^{ + } \) port of the MMCC but in this paper two output ports (\( Z^{ + } \) and \( Z^{ - } \)) of the MMCC device are being utilized, hence, a large number of VCO realizations are achievable.

The proposed MMCC-based oscillators are synthesized by utilizing state variable technique and employing FOE, hence these oscillators are termed as Fractional-Order Voltage Controlled Oscillators (FO-VCOs). The last row of Table 1 highlights deliverables of this work and the remainder of this manuscript is organized as follows. Section 2 introduces the MMCC and its ideal circuit equivalent. In Sect. 3, we present the state-variable methodology in the development of MMCC-based VCOs and the investigation of fractional-order oscillators. The non-ideal behaviour of MMCC and influence of their parasitics have been considered and analysed in Sect. 4. The simulations that justify the FO VCO performances have been included in Sect. 5 and in Sect. 6 some discussion about the proposed oscillators are carried out. Finally, in Sect. 7 the conclusions of this paper have been elaborated.

2 Multiplication-mode current conveyor (MMCC) and its applications so far

An interesting device of current conveyor category namely MMCC was initiated in 2009 [40]. A block description of MMCC is portrayed in Fig. 1 and its terminal relationship is specified in Eq. (1) where ideally \( m \) and \( n \) are unity and \( k \) is an MMCC constant. This constant relies on the parameters [40] of the transistors employed in MMCC.

$$ \left. {\begin{array}{*{20}c} {I_{y1} = I_{y2} = 0 } \\ {V_{X} = k m V_{y1} V_{y2} } \\ { \pm I_{Z} = \pm n I_{X} } \\ \end{array} } \right\} $$
(1)
Fig. 1
figure 1

The symbolic notation of an MMCC

Full size image

The MMCC [40] consists of CMOS Differential Voltage Current Conveyor (DVCC) preceded with a CMOS folded Gilbert multiplier. It has only one Z+ output port therein [40], which in light of [41], can easily be converted into multiple output ports with complementary (Z+ and Z−) current outputs with addition of few more numbers of PMOS and NMOS appropriately connected in the output part of the MMCC making it even more versatile. Thus, we can have one Z+ and one Z− port or n numbers of Z+ and Z− output ports. Some exemplary application configurations are reported in [14] to demonstrate utility of MMCC. Later, some more works involving MMCCs [29, 31] also appeared where [29] is on MMCC-based integrators and differentiators, and [31] is about realization of all pass filter using MMCC. Both of these [29, 31] works demonstrate voltage control feature to various possible tunable parameters of the realized circuit.

For the first time MMCC has been used to implement sinusoidal oscillator and/or VCO configurations in [19] and considers utilizing constrained output ports of the MMCCs, that is, making use of single \( Z^{ + } \) port of MMCC for the realization of the VCO configurations. Thus, two fractional-order VCOs have been explored in [19] that utilize three MMCCs along with canonic number of passive elements, that is less than or equal to three resistors and two capacitors. They provide explicit current output and facilitate linear voltage control of FO and additional FO control by single-resistance. In light of [41] when we do not constrain the output ports of MMCC [40] and allow them to offer more numbers of current-output ports (Z+ and Z−) then by using such MMCCs, indeed, the number of VCOs realized could be very large with possibly better features. Hence, by using MMCCs, with Z+ and Z− ports in this work, thirteen new fractional-order VCOs are uncovered.

An ideal controlled source equivalent circuit of this MMCC can be drawn as shown in Fig. 2. Using this, the ideal SPICE macro model for the MMCC was developed to test the ideal performances of MMCC-based VCOs of this work.

Fig. 2
figure 2

Controlled source equivalent of an ideal MMCC

Full size image

3 Derivation of fractional-order MMCC-based VCO

The oscillators are synthesised by using state variable approach [39] by employing MMCC as their active element. At first the oscillators are analysed for conventional case by make use of integer-order capacitors. Then by replacing integer-order capacitors by fractional-order capacitors, fractional-order investigation is carried out for all the oscillators.

3.1 State-variable approach of VCO synthesis using MMCC

By looking at voltage-product feature of Eq. (1) we intuitively consider utilizing MMCC for the realization of VCOs. Hence, we are employing MMCC of Fig. 1 with both \( Z^{ + } \) and \( Z^{ - } \) ports for the realization of single-resistance controlled oscillators (SRCO) following the state-variable synthesis approach [39]. Here, we briefly outline this state-variable SRCO synthesis methodology.

A canonic second order oscillator can be characterized by the following autonomous state equation

$$ \varvec{ }\left[ {\dot{\varvec{x}}} \right] = \varvec{ }\left[ \varvec{A} \right]\left[ \varvec{x} \right] $$
(2)

which can be expanded as-

$$ \left[ {\begin{array}{*{20}c} {\dot{x}_{1} } \\ {\dot{x}_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } \\ {a_{21} } & {a_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \right] $$
(3)

From Eq. (2) above, the Characteristic Equation (CE) can be extracted as

$$ s^{2} - \left( {a_{11} + a_{22} } \right)s + \left( {a_{11} a_{22} - a_{12} a_{21} } \right) = 0 $$
(4)

Which yields the CO and FO of the oscillator as

$$ {\text{CO}}:\;\left( {a_{11} + a_{22} } \right) = 0 \quad {\text{and}}\quad {\text{FO}}:\; \omega_{0} = \sqrt {\left( {a_{11} a_{22} - a_{12} a_{21} } \right)} $$
(5)

Now the methodology of SRCO synthesis involves selection of the parameters \( a_{11} , a_{12} , a_{21} \) and \( a_{22} \) in accordance with the required features; that is, choosing them for decoupled CO and FO, converting the resulting state equations into nodal equations and finally, arranging a physical circuit from these nodal equations. A large number of circuits are expected to be generated by making different choices of parameters \( a_{11} , a_{12} , a_{21} \) and \( a_{22} \). In [42] a total of 14 such \( \left[ A \right] \) matrices, that yield canonic SRCOs, have been spelled out that provided non-interacting CO and FO. In this work, we have followed the same approach to derive MMCC-based canonic SRCOs that eventually would turn out to be VCOs. For this we need to put \( R_{1} , R_{2} , R_{3} C_{1}^{\alpha } , C_{2}^{\beta } \) and \( V_{C} \) in \( a_{11} , a_{12} , a_{21} \) and \( a_{22} \) of \( \left[ A \right] \) in such way that \( \omega_{0} \) becomes a linear function of \( V_{C} \) and also CO and FO remain decoupled.

3.2 Fractional-order oscillator’s investigation

The fractional-order oscillators investigated in this segment comprises of two fractance devices with fractional orders α and β. In general, a linear fractional-order system described by the form

$$ \left( {\begin{array}{*{20}c} {D^{\alpha } v_{1} } \\ {D^{\beta } v_{2} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {a_{11} } & {a_{12} } \\ {a_{21} } & {a_{22} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {v_{1} } \\ {v_{2} } \\ \end{array} } \right) $$
(6)

can build oscillations only for a value of \( \omega \) that satisfies concurrently both the following two equations

$$ \omega^{\alpha + \beta } \cos \frac{{\left( {\alpha + \beta } \right)\pi }}{2} - a_{11} \omega^{\beta } \cos \frac{\beta \pi }{2} - a_{22} \omega^{\alpha } \cos \frac{\alpha \pi }{2} + \left| A \right| = 0 $$
(7a)
$$ \omega^{\alpha + \beta } \sin \frac{{\left( {\alpha + \beta } \right)\pi }}{2} - a_{11} \omega^{\beta } \sin \frac{\beta \pi }{2} - a_{22} \omega^{\alpha } \sin \frac{\alpha \pi }{2} = 0 $$
(7b)

where \( \left| A \right| = a_{11} a_{22} - a_{12} a_{21} \) is the determinant of the system coefficient matrix. The phase difference between the two states v1 and v2 is given as follows on the basis of [25] and [26]:

$$ \varphi = \left\{ {\begin{array}{ll} {\tan^{ - 1} \left( {\frac{{\omega^{\alpha } \sin \left( {\frac{\alpha \pi }{2}} \right)}}{{\omega^{\alpha } \cos \left( {\frac{\alpha \pi }{2}} \right) - a_{11} }}} \right),} &\quad {if\; the\; sign\; of\; a_{12} \; is\; positive} \\ {\tan^{ - 1} \left( {\frac{{\omega^{\alpha } \sin \left( {\frac{\alpha \pi }{2}} \right)}}{{\omega^{\alpha } \cos \left( {\frac{\alpha \pi }{2}} \right) - a_{11} }}} \right) - \pi } &\quad {if\; the\; sign \;of\; a_{12} \;is \;negative} \\ \end{array} } \right. $$
(8)

The characteristic equation of the system described by Eq. (2) is obtained by converting that into the \( s \)-domain as below

$$ s^{\alpha + \beta } - a_{11} s^{\beta } - a_{22} s^{\alpha } + \left| A \right| = 0 $$
(9)

3.3 Fractional-order MMCC-based VCOs

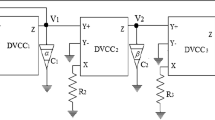
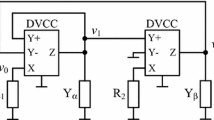
More number of single-resistance-controlled and voltage-controlled oscillators of extensive variety have been revealed by using the state-variable approach of [39] in concurrence with the terminal characteristic of the MMCC. By making use of one \( Z^{ + } \) port and one \( Z^{ - } \) port of the MMCC, thirteen VCOs are uncovered and presented in this paper. Each of the oscillators reported in this work is constructed by deploying three MMCCs, two fractional-order capacitors with fractional-orders \( \alpha \) and \( \beta \) and three resistors. The thirteen fractional-order voltage-controlled oscillator configurations and their corresponding state matrices are presented in Table 2. Out of these thirteen, six oscillators provide explicit current output from all the MMCC’s output ports, remaining oscillators provides explicit current output but not from all the output ports but only from some ports. Five oscillators are quadrature oscillators and eight are multiphase oscillators. It is evident from Table 3 that in all the FO-VCOs, CO is controlled by R1 and FO can be linearly controlled by controlling voltage Vc.

Table 2 The new uncovered fractional-order MMCC-based VCOs with their \( \left[ A \right] \) matrices
Full size table
Table 3 Four special cases for each of the oscillators
Full size table

3.3.1 Analysis of first circuit from Table 2 (FO VCO 2.1)

The FO VCO 2.1 given in Table 2 is described by the state matrix

$$ \left[ {\begin{array}{*{20}c} {D_{{v_{1} }}^{\alpha } } \\ {D_{{v_{2} }}^{\beta } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{{kV_{c} }}{{R_{3} C_{1} }}} & { - \frac{{kV_{c} }}{{C_{1} }}\left( {\frac{1}{{R_{1} }} + \frac{1}{{R_{2} }}} \right)} \\ {\frac{{kV_{C} }}{{R_{3} C_{2} }}} & {\frac{{kV_{c} }}{{C_{2} R_{1} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {v_{1} } \\ {v_{2} } \\ \end{array} } \right] $$
(10)

The characteristic equation extricated from (10) is given as

$$ s^{\alpha + \beta } - \frac{{kV_{c} }}{{C_{2} R_{1} }}s^{\alpha } + \frac{{kV_{c} }}{{C_{1} R_{3} }}s^{\beta } + \frac{{k^{2} V_{c}^{2} }}{{R_{2} R_{3} C_{1} C_{2} }} = 0 $$
(11)

Resolving individually, for the real and imaginary parts of Eq. (11) with the aid of Euler’s relations by putting \( s = j\omega \) in that, we obtain the succeeding two relationships:

$$ \omega^{\alpha + \beta } \cos \left( {\frac{{\left( {\alpha + \beta } \right)\pi }}{2}} \right) - \frac{{kV_{c} }}{{C_{2} R_{1} }}\omega^{\alpha } \cos \left( {\frac{\alpha \pi }{2}} \right) + \frac{{kV_{c} }}{{C_{1} R_{3} }}\omega^{\beta } \cos \left( {\frac{\beta \pi }{2}} \right) + \frac{{k^{2} V_{c}^{2} }}{{R_{2} R_{3} C_{1} C_{2} }} = 0 $$
(12)
$$ \omega^{\alpha + \beta } \sin \left( {\frac{{\left( {\alpha + \beta } \right)\pi }}{2}} \right) - \frac{{kV_{c} }}{{C_{2} R_{1} }}\omega^{\alpha } \sin \left( {\frac{\alpha \pi }{2}} \right) + \frac{{kV_{c} }}{{C_{1} R_{3} }}\omega^{\beta } \sin \left( {\frac{\beta \pi }{2}} \right) = 0 $$
(13)

If both (12) and (13) can be satisfied concurrently by some \( \omega \) then the circuit (FO VCO 2.1) can build sustained oscillations [25, 26]. Select R1 as the parameter to control the CO, R1 obtained from (12) and (13) is given as follows

$$ R_{1} = \frac{{kV_{c} R_{2} R_{3} C_{1} \omega^{\alpha } \cos \left( {\frac{\alpha \pi }{2}} \right)}}{{kV_{c} R_{2} C_{2} \omega^{\beta } \cos \left( {\frac{\beta \pi }{2}} \right) + R_{2} R_{3} C_{1} C_{2} \omega^{\alpha + \beta } \cos \left( {\frac{{\left( {\alpha + \beta } \right)\pi }}{2}} \right) + k^{2} V_{c}^{2} }} $$
(14)
$$ R_{1} = \frac{{kV_{c} R_{3} C_{1} \omega^{\alpha } \sin \left( {\frac{\alpha \pi }{2}} \right)}}{{kV_{c} C_{2} \omega^{\beta } \sin \left( {\frac{\beta \pi }{2}} \right) + R_{3} C_{1} C_{2} \omega^{\alpha + \beta } \sin \left( {\frac{{\left( {\alpha + \beta } \right)\pi }}{2}} \right)}} $$
(15)

Eliminating R1 from (14) and (15), the obtained FO can be given as

$$ \omega^{\alpha + \beta } \sin \left( {\frac{\beta \pi }{2}} \right) + \frac{{kV_{C} }}{{C_{1} R_{3} }}\omega^{\beta } \sin \left( {\frac{{\left( {\beta - \alpha } \right)\pi }}{2}} \right) - \sin \left( {\frac{\alpha \pi }{2}} \right)\frac{{k^{2} V_{c}^{2} }}{{R_{2} R_{3} C_{1} C_{2} }} = 0 $$
(16)

The phase difference between the two states \( v_{1} \) and \( v_{2} \) is given as

$$ \tan^{ - 1} \left( {\frac{{R_{3} C_{1} \omega^{\alpha } \sin \left( {\frac{\alpha \pi }{2}} \right)}}{{R_{3} C_{1} \omega^{\alpha } \cos \left( {\frac{\alpha \pi }{2}} \right) + kV_{C} }}} \right) - \pi $$
(17)

Oscillation parameters such as frequency of oscillation, condition of oscillation and phase are derived separately for each of the oscillators of Table 2. Furthermore, four cases are considered for each of the oscillator configurations. First case is the conventional case \( \left( {\alpha = \beta = 1} \right) \), second case is equal fractional-order case \( \left( {\alpha = \beta \ne 1} \right) \), third case is \( \left( {\alpha = 1} \right) \) and \( \left( {\beta \ne 1} \right) \) and the last one is \( \left( {\beta = 1} \right) \) and \( \left( {\alpha \ne 1} \right) \). For all the oscillators resistor R1 is chosen as the parameter for controlling the condition of oscillation. The FO-VCOs obtained parameters for each of the above described cases are organized in Table 3.

The plot showing the change of oscillator characteristics (FO, CO and phase) with respect to fractional-order parameters (α and β) for one of the oscillators (FO VCO 2.3) are displayed in Fig. 3. All these plots are generated with the help of MATLAB simulations by using the following values: C1= C2=10 μF, R2= 50 KΩ and R3=1 KΩ. Figure 3 also showcases the consequence of various values of VC on the FO, CO and phase for all the special cases (α = β\( \ne \) 1, 0 < α < 2; α =1, 0 < β < 2 and β =1, 0 < α < 2) in addition to the relationship between phase and frequency. By providing different values for Vc (0.5, 1 and 1.5), the consequence of oscillation parameters and fractional-order parameters can be deciphered from these MATLAB plots.

Fig. 3
figure 3

The parameters of oscillator FO VCO 2.3 with R2=50 kΩ and R3=1 kΩ when aα = β,bα = 1 and cβ = 1

Full size image

For identical fractional-order case (α = β\( \ne \) 1, 0 < α < 2) Fig. 3(a), high FO can be obtained when α is very small. When VC is greater than one, high FO in the range of GHz can be achieved with low values of α. With increase in α, FO decreases but R1 increases and phase increases first then decreases rapidly and again increases slowly. With respect to frequency, phase is decreasing then increasing suddenly and again decreasing gradually. From the phase versus α plot, it is evident that phase is independent of VC which is in contrast to the FO and CO. Surface plot of FO and CO are also shown in the figure. From the surface plot of FO, it is visible that high FO can be achieved when α reduces and VC rises.

For the first mixed case (α =1, 0 < β < 2) Fig. 3(b), FO is low compared to the identical fractional-order case and FO starts decreasing gradually when α increases. The CO initially increases and then reduces for high values of α. Phase for this case initially decreases and after some extent it increases rapidly and again decreases. The surface plot of FO versus β-VC plane and CO versus β-VC plane shows the values of frequency and R1 achieved by using the corresponding values of R2 and R3.

For the next mixed case (β = 1, 0 < α < 2) Fig. 3(c), FO initially reduces slowly and after some extent it rises slowly. When α increases, CO reduces for all the values of VC. From the phase versus frequency plot it is understandable that phase depends on VC. The surface plot of FO and CO shows how frequency and R1 varies with respect to the α-VC plane.

4 Non-ideal and sensitivity analyses on derived oscillators

The non-ideal analysis and sensitivity analysis are carried out for all the FO VCOs presented in Table 2. We have also considered non-ideal port transfer behaviour of the MMCC and also the port parasitics for investigating their effect on the VCOs performance

4.1 Non-ideal analysis

The non-ideal expressions of \( \omega_{0} \) and the sensitivity figures are presented in Table 4. Obviously, with m and n very close to unity, the port non-idealities are not affecting the \( \omega_{0} \) significantly.

Table 4 The worked out non-ideal expressions and sensitivity figures of \( \omega_{0} \)
Full size table

4.2 Consideration of port-parasitics on the derived oscillators

Now, considering the possible prominent port-parasitics of the MMCC as parallel RY-CY at y-terminals, parallel RZ-CZ at z-terminals and RX, the series resistance at port-x, as shown in Fig. 4, the FO-VCOs of Table 2 have been again analysed and their expressions for angular frequencies have been worked out. This self-explanatory parasitic analysis is tabulated in Table 5.

Fig. 4
figure 4

The possible prominent port-parasitics of the MMCC

Full size image
Table 5 The assumptions considered in parasitic analysis and expressions of affected angular frequency \( \left( {\omega_{0}^{'} } \right) \)
Full size table

It can be concluded that the port parasitics play some role in altering the CO and FO expressions of the FO-VCOs to some extent.

4.3 Monte-Carlo performance analysis results

The Monte-Carlo analysis was also performed for one of the oscillators of Table 2 (FO-VCO 2.8) and is presented here. This analysis generates histograms together with the summary of statistical data. The corresponding histogram plot is shown in Fig. 5. Tolerance of 10% is added to resistor R1 to generate various waveforms for different values of R1 and the simulation result is presented in Fig. 6.

Fig. 5
figure 5

Monte Carlo analysis: histogram plot

Full size image
Fig. 6
figure 6

Multiple simulation results during Monte Carlo simulation for different values of R1

Full size image

5 Verification of the workability of the derived MMCC-based VCOs

For validating workability of the synthesized FO-VCOs we have undertaken PSPICE simulation for all the oscillators shown in Table 2. The fractional-order capacitors Cα1 and Cβ2 of order 0.8 are simulated with the aid of RC ladder network [33] as shown in Fig 7 which is realized with a fifth-order Oustaloup Recursive Approximation [22, 43].

Fig. 7
figure 7

Realization of fractance

Full size image

MMCC is constructed by utilizing AD835 type analog multiplier and AD844 type current feedback operational amplifier (CFOA) taken from analog devices [44] as shown in Fig. 8. The implementation of MMCC requires a single analog multiplier and three CFOAs to generate two output ports (Z+ and Z−). The values of R1, R2, R3 and R4 are chosen to be 2.7 KΩ, 100Ω, 10Ω and 10Ω respectively. The MMCC constant k is ideally taken to be unity to meet out condition of Eq. (1).

Fig. 8
figure 8

MMCC created with one AD835 type multiplier and three AD844 type CFOA

Full size image

Under Table 6, PSPICE simulation of all the cases are presented to justify the theoretical findings. The component values chosen for all the cases are shown below the corresponding waveforms. All the thirteen oscillators presented in Table 2 are simulated separately for integer-order case, mixed case and pure fractional-order case. The maximum FO obtained for integer-order case is 157.6 kHz (FO-VCO 2.8), for mixed case is 65.3 kHz (FO-VCO 2.1) and for pure fractional-order case is 281.7 kHz (F0-VCO 2.2).

Table 6 Simulation results, Variation of FO with VC and FFT analysis for all the derived FO-VCOs
Full size table

The variation of FO with VC curve for pure fractional order case is also presented in Table 6 (fifth column). Slightly deviated level of simulated curve in contrast to the theoretical curve of FO variation against VC is a consequence of port-parasitics of MMCC. The theoretical value of ω0 cannot be calculated for some of the oscillators of mixed case due to the complex value of ω and hence it is not entered in Table 6. Fast Fourier Transform (FFT) analysis have been carried out for all the oscillators in pure fractional-order case and illustrated in Table 5. The Total Harmonic Distortion (THD) figures of the FO-VCOs of Fig. 2 found out through simulations are presented below each FFT analysis curve. All the simulation results demonstrate satisfactory operation of the synthesized FO-VCOs

6 Discussion

Of all the thirteen oscillators presented in Table 2, considering only the pure fractional-order case, the FO-VCOs 2.1, 2.2, 2.3, 2.8, 2.10, 2.11 and 2.12 provides explicit current output at all the output ports of MMCCs and the remaining five oscillators provides explicit current output at some output ports of the MMCCs. Compared to other oscillators, FO-VCOs 2.1 and 2.5 are having very low THD values. From the simulations it is observed that the FO-VCOs 2.3, 2.8, 2.9, 2.12 and 2.13 are quadrature oscillators and the rest of the seven oscillators are multiphase oscillators. The output waveforms of one of the quadrature oscillator (FO-VCO 2.13) and multiphase oscillator (FO-VCO 2.6) are depicted in Figs. 9 and 10 respectively. Amongst themselves FO-VCOs 2.1 and 2.3 are superior in terms of frequency of oscillation, quadrature phase, explicit current output and total harmonic distortion.

Fig. 9
figure 9

Quadrature oscillator FO-VCO 2.13 output waveform

Full size image
Fig. 10
figure 10

Multiphase oscillator FO-VCO 2.6 output waveform

Full size image

7 Conclusion

This work, for the first time, has demonstrated use of only one type of active element namely MMCC to synthesize current-mode sinusoidal FO-VCOs. Without constraining the output ports of MMCCs and following the well-established state-variable SRCO synthesis method [39], this work has revealed existence of thirteen new canonic FO-VCOs. All these FO-VCOs have employed three MMCCs, three resistors and two grounded capacitors. The oscillation parameters are derived for each of the oscillators by considering three special cases and are tabulated. The conventional case is also considered to compare with the fractional-order parameters. The FO of the generated FO-VCOs can be linearly controlled by the controlling voltage VC and all of which are also single-resistance-controlled. All the FO-VCOs of this work were checked for their functionality and validation of theoretical assertions using PSPICE. The commercial macro model of MMCC created with help of AD835 and AD844 integrated circuits from Analog Devices were considered to test the satisfactory operation of the synthesized VCOs. Finally, salient findings of this work are enumerated as below.

  1. (1)

    All thirteen FO-VCOs are also single resistance controlled VCOs

  2. (2)

    They are all canonic employing three resistors and two grounded capacitors only

  3. (3)

    All the oscillators have decoupled CO and FO

  4. (4)

    Seven oscillators provide explicit current output at all Z-ports

  5. (5)

    Five oscillators provide quadrature phase output

  6. (6)

    Five oscillators have very low THD values ranging from 0.001 to 0.008%

In conclusion, to the best knowledge of authors, this work for the first time presents the new set of voltage-controlled together with single-resistor controlled oscillators with fractional-order capacitor consideration and has successfully tabulated their significant features compared to other conventional oscillators by employing MMCCs.