1 Introduction

Power amplifiers (PAs) as essential components are commonly utilized in radio frequency transmitters. Power amplifiers are usually employed to amplify the communication signals [1]. Power amplifiers known as power hungry blocks consume a large amount of power in the transceivers [2]. Power amplifiers, which have superior linearity and good efficiency alike, are increasingly essential in the modern transmitters [3]. In addition, many of digitally modulated signals such as code division multiple access (CDMA) in the 3rd generation and frequency-division multiple access orthogonal (OFDMA) in the 4th generation were introduced to improve efficient spectrum and data transmission rate [4].

Moreover, transmission of these non-constant envelope signals using linear power amplifiers is not highly efficient since they have high peak to average power ratio (OFDM ~ 10 dB) and high back-off is required for linear transmission [5]. Consequently, the utilization of the back-off method reduces the power added efficiency (PAE) in the power amplifier circuits. In order to remove the compromise in the power amplifier design, linearization techniques can be employed to improve the linearity of power amplifiers without losing efficiency [6].

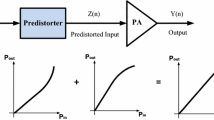
Linearization methods such as predistortion, feedback and feedforward have been proposed to ameliorate linearity without efficiency degradation [7]. Among the methods, the predistortion procedure has both high performance and low cost [8]. Fig 1 shows the conceptual diagram of the predistortion linearization process. In the predistortion linearization method, the input signal is predistorted before applying it to the input of a nonlinear power amplifier, so that the nonlinear response of the power amplifier can be compensated for making a linear response.

Fig. 1
figure 1

Simplified concept of a predistortion linearization technique

Full size image

The predistortion can be classified into two types in accordance with the frequency in which it is implemented: (1) analog predistortion (APD), (2) digital predistortion (DPD).

When the analog predistortion operates at a high frequency, the analog predistortion implementation is so straightforward, but it has a limited capability and low performance [9]. Many analog predistortion circuits that have cost-effective and simple structures have been entirely described in [10,11,12,13,14,15].

Although analog predistortion has several advantages compared to digital predistortion, such as simple structure and low cost, its capability of removing nonlinearity is less than that of digital predistortion. One of the linearization methods always utilized in modern communication systems is the digital predistortion method [6, 7, 16,17,18,19].

Owing to digital hardware implementation, digital predistortion is one of the most useful approaches of linearization, with high flexibility and low cost. The accuracy of the power amplifier linearization is substantially augmented by digital implementation [23].

A memoryless model was commonly employed in the primary linearization procedures based on digital predistortion so that the model compensated for the static nonlinear behavior of the power amplifier [20]. Yunsung Cho [19]  proposed a lookup table (LUT) instead of the memoryless model, but the LUT does not eliminate all distortions in modern wireless transmitters. Furthermore, when the bandwidth of the power amplifier is increased in most modern transmitters, the memory effects of the power amplifier are not trivial. The memory effects of the power amplifier must be investigated to get the best performance of digital predistortion [21]. The Volterra series expansion is the most appropriate model utilized to accurately model nonlinear dynamic systems [22]. Anyway, when the order of memory depth as well as nonlinearity growths, the number of utilized coefficients increases very rapidly; hence, the computational complexity of the model is augmented. Lei Guan [23] has recently proposed the Volterra series to model predistortion; however, the resource consumption as well as the complexity of the predistortion were increased. Therefore, many structures that originate from the Volterra model, such as Wiener model [24], Hammaerstion model [25], and memory polynomial model [26], are proposed in order to overcome the complexity of the Volterra series. The memory polynomial model is widely used to model the power amplifier. However, this model often results in an oversized model due to the use of a constant nonlinear degree in all branches [27].

Power amplifiers with memory effect can be modeled using the Wiener structure that includes a linear finite impulse response (FIR) filter and a memoryless nonlinear function. Actually, one of the main advantages of the power amplifier Wiener model is the proper choice for its predistorter. The best choice of the predistorter model for the Wiener model is the Hammerstein model that is a combination of a nonlinear memoryless function and a linear FIR filter.

There are a lot of metaheuristic algorithms to optimize complex systems. Three very famous methods among metaheuristics algorithms are named: genetic algorithm (GA), particle swarm optimization (PSO) and Ant colony optimization (ACO). The genetic algorithm is the population-based evolution algorithm that employs selection, combination and mutation operators in order to produce new samples in the search space. In order to optimize and find the parameters, the genetic algorithm is widely utilized in many applications [28, 29]. The accurate Wiener model can be obtained using the performance and effectiveness of the genetic algorithm which can find appropriate coefficients for the Wiener model. An accurate predistorter system is extracted by using the designed Wiener model. In this paper, the design of the novel digital predistorter according to the direct learning technique is proposed using the power amplifier modeling based on the Wiener model. The coefficients of the Wiener model are identified using the genetic algorithm (GA) [30]. The proposed digital predistorter using the Wiener model in conjunction with the genetic algorithm for identifying coefficients is the new approach to linearize the power amplifiers.

The structure of this paper is organized as follows. In Sect. 2, The Wiener power amplifier model with the memory effect is described. Next, in Sect. 3, the genetic algorithm is proposed to identify accurate coefficients of the Wiener model. The proposed digital predistorter is completely explained in Sect. 4. Also in this section, the implementation structure of the proposed predistorter is briefly explained in order to demonstrate easy hardware implementation of the Hammerstein model. The simulation results of the transmitter without protestation, genetic algorithm, implementation of the proposed predistorter and the transmitter with predistortion are presented in Sect. 5. Finally, a conclusion is presented in Sect. 6.

2 Power amplifier modeling with memory effect

A suitable model selection for the power amplifier is a principal part of the digital predistorter design. Many structures for behavioral modeling of the power amplifiers have been suggested that always complexity and precision trade-off exists among the models. An appropriate model of the power amplifier is the Wiener model which accurately considers both nonlinearity and memory effects [31]. The Wiener model includes the linear filter and the memoryless nonlinear function [i.e. G(A)]. The Wiener model has been employed in modeling the power amplifier for the proposed linearized power amplifier.

One of the main advantages the Wiener model is its appropriate structure so that the inverse of the Wiener model can be efficiently modeled using the Hammerstein structure. The Hammerstein model includes memoryless nonlinear function, i.e. G(A), and the linear filter. In Fig. 2, the use of the Wiener model as the power amplifier and the Hammerstein model as the digital predistorter is illustrated.

Fig. 2
figure 2

Power amplifier linearization by using the Wiener model as the power amplifier and the Hammerstein structure as the digital predistorter

Full size image

The memory effect of the Wiener model is indicated by the linear filter and its z-transfer function can be written as

$$H(z) = \sum\limits_{i = 0}^{n} {h_{i} \, } z^{ - i}$$
(1)

where the coefficients of the linear filter are defined by

$$h = [h_{0} \, h_{ 1} \, \ldots \, h_{n} ].$$
(2)

By applying the input signal w (n) to the linear filter, the linear filter output is determined as follows

$$z(n) = \sum\limits_{i = 0}^{n} {h_{i} {\text{ w}}(n - i)}$$
(3)

z(n) is the signal applied to the memoryless nonlinear part of the Wiener model. A Saleh model [32] has been employed in modeling the memoryless nonlinear part. The Saleh model applies four coefficients to fit the model to measured data. Actually, the Saleh model can emulate the AM/AM and AM/PM characteristics of the power amplifier.

The output signal of the linear filter can be written as

$$z(n) = \left| {z(n)} \right| \cdot \exp (j\angle x(n)) = b(n) \cdot \exp \left( {j\psi (n)} \right)$$
(4)

where \(b(n) = |z(n)|\) and \(\psi (n) = \angle z(n) \,\) indicate the amplitude and phase of z(n), respectively.

When passing through the linear filter, the input signal experiences memory effect. Then, the output signal of the linear filter is passed through the nonlinear memoryless block and amplitude and phase of the signal are changed according to AM/AM and AM/PM effects. Finally, the output signal y(n) considerably becomes distorted with respect to the amplitude of the input signal b(n). The output signal can be expressed as

$$\begin{aligned} y(n) = & |y(n)| \cdot \exp (j\angle y(n)) \\ { = } & \,Amp(b(n)) \cdot \exp (j(\psi (n) + \phi (b(n))) \\ \end{aligned}$$
(5)

The output amplitude Amp (b(n)) and phase of the power amplifier \(\phi (b(n)) = \angle y(n) - \psi (n)\) can be defined as follows, respectively [33].

$$Amp(b) = \frac{{\alpha_{a} b}}{{1 + \beta_{a} b^{2} }}$$
(6)
$$\phi (b) = \frac{{\alpha_{\phi } b^{2} }}{{1 + \beta_{\phi } b^{2} }}$$
(7)

The Amp(b) is changed proportional to 1/b and \(\phi (b)\) is approximately constant for very large input b. Finally, the output of the Wiener power amplifier model is completely specified by

$$y(n) = \frac{{\alpha_{a} b(n)}}{{1 + \beta_{a} b(n)^{2} }}\exp \left( {j\left( {\psi (n) + \frac{{\alpha_{\phi } b(n)^{2} }}{{1 + \beta_{\phi } b(n)^{2} }}} \right)} \right)$$
(8)

Nonlinear coefficients of the Saleh model are defined as

$$t = \left[ {\alpha_{a} \, \beta_{a} \, \alpha_{\phi } \, \beta_{\phi } } \right]$$
(9)

where the input amplitude that can saturate the power amplifier is defined as

$$b_{sat} = \frac{1}{{\sqrt {\beta_{a} } }}$$
(10)

and the saturation output amplitude is written as

$$A_{\hbox{max} } = \frac{{\alpha_{a} }}{{2\sqrt {\beta_{a} } }}$$
(11)

In order to assess the power amplifier modeling, consider the Wiener model with the following coefficients [34]

$$h = \left[ {0.7692 \, 0.1538 \, 0.0769} \right]$$
(12)
$$t = \left[ {2.1587 \, 1.1517 \, 4.0 \, 2.1} \right]$$
(13)

The vector h and t are named true matrixes for the Wiener model of the power amplifier. The input signals which are applied to the Wiener model are based on 64 QAM modulation (n = 10,000). A large number of the input data are generated and mapped onto the specified real and imaginary values as 64 QAM signals. Maximum and minimum values for the generated input data are limited to − 0.4 and 0.4. The input and output of the Wiener model have been depicted in Fig. 3. As depicted in Fig. 3(b), the output signal is totally distorted because of the linear filter, AM/AM and AM/PM functions. Although the input data are limited to the 0.4, the maximum of the output signals is considerably changed to the value of 0.8. For assessing model performance in the time domain, the most straightforward method is to evaluate the error in accordance with the difference between the input and desired output signal. A mean square error (MSE) criterion is always employed in the performance assessment of the behavioral model.

Fig. 3
figure 3

a Input signal of the Wiener model w(n) (n = 10,000), b the output signal of the Wiener model y(n)

Full size image

This criterion is often expressed in decibels and defined as follows:

$$MSE = 10\log_{10} \left( {\frac{1}{{N_{test} }}\sum\limits_{n = 1}^{{N_{test} }} {\left| {w(n) - y(n)} \right|} } \right)$$
(14)

where N test denotes the length of each time domain waveform, \(w(n)\) and \(y(n)\).\(w(n)\) and \(y(n)\) are the input and output of the Wiener model, respectively. It is obvious that a lower MSE indicates superior model accuracy. The criterion of MSE is − 4.2 dB for this model verification. This MSE value expresses the high bit error rate so that many data are not detectable.

3 Coefficients identification of the Wiener model using the genetic algorithm (GA)

In fact, we usually have a real measurement data of the power amplifier. Before the predistortion model had been designed, the power amplifier model should be designed and the coefficients of the model must be identified. In this paper, the true matrixes (12) and (13) have been employed in generating the output signal instead of the real output signal of the power amplifier.

The purpose of this section is an estimation and identification of a true vector for the Wiener model by using the input and output signals of the power amplifier. This vector is defined as

$$\rho = \left[ {h^{T} \, t^{\text{T}} } \right]^{T} = \left[ {\rho_{1} \, \rho_{ 2} \, \ldots \, \rho_{{{\text{N}}_{\rho } }} } \right]$$
(15)

where \(N_{\rho } = n + 5\). Three variables for estimation of the matrix h and four variables for the matrix t are considered. The Wiener model used matrix ρ can be rewritten as

$$y(n) = F_{\text{WPA}} \left( {{\text{w(n);}}\rho } \right),$$
(16)

where FWPA is the complex-valued nonlinear function specified by Eqs. (2)–(8). The output of the Wiener power amplifier model by using estimated coefficients \(\tilde{\rho }\) is given by

$$\tilde{y}(n) = F_{\text{WPA}} ( {\text{w(n);}}\tilde{\rho } ) ,$$
(17)

The error between the desired output y(n) and the output of the model \(\tilde{y}(n)\), which is employing matrix \(\tilde{\rho }\), is defined by

$$error(n) = y(n) - \tilde{y}(n)$$
(18)

Using the Eq. (18), a cost function is determined by

$$Cost{\text{ Function (}}\tilde{\rho }) = \frac{1}{N}\sum\limits_{n = 1}^{N} {|error(n)|^{2} }$$
(19)

The estimation of the true coefficient vector \(\tilde{\rho }\) is then specified as a solution to the following optimization:

$$\hat{\rho } = \arg {\text{ min Cost Function}}\; (\tilde{\rho }),$$
(20)

Calculation of the cost function is highly nonlinear and may trap into a local minimum. Thus, the conventional gradient-based methods require suitable initial parameters in order to avoid local minima [35]. When initial search space has been selected inappropriately, the conventional gradient methods may trap in the local minima and become failed to get the desired response.

There are a lot of metaheuristics algorithms to optimize systems. There are three useful famous methods among metaheuristics algorithms named: genetic algorithm (GA), particle swarm optimization (PSO) and Ant colony optimization (ACO). The ant colony optimization (ACO) method is a probabilistic technique and is usually utilized to find appropriate paths through graphs in networks. Another evolutionary technique named particle swarm optimization (PSO) was proposed by Kennedy and Eberhart [36]. The PSO algorithm was inspired by the sociological behavior associated with birds’ flocking. Because of its simple mechanism and high performance for global optimization, the PSO algorithm has been exploited for many optimization problems successfully [37]. Although the PSO algorithm has less computation time than GA algorithm, the cost function accuracy of GA is better than that of the PSO algorithm. Because this system is processed offline and then coefficients are placed in the predistortion model, the genetic algorithm has been selected.

In this paper, the continuous genetic algorithm is utilized to obtain the coefficients of the Wiener model. In the genetic algorithm, the initial population is generated and evolution of the population is conducted under a specific genetic process in order to minimize the cost function [38]. In this paper, the genetic algorithm is employed to minimize the cost function. A genetic algorithm flowchart is shown in Fig. 4.

Fig. 4
figure 4

Genetic algorithm flowchart

Full size image

In this algorithm, optimization or evolution of Wiener model coefficients is conducted through the genetic algorithm operators, such as elitism, sampling, composition, and mutation. At first, a biological term “chromosome” is used to generate the initial population. These chromosomes include seven genes or coefficients so that three of them are employed in emulating the memory effect of the power amplifier and the others are utilized to consider the phase and amplitude nonlinearity variations.

At the beginning of the genetic algorithm, random genes located in the chromosomes are generated. Maximum and minimum range of the generated random genes is determined as

$$S = \prod\limits_{i = 1}^{{N_{\rho } }} {\left[ {\rho_{i,\hbox{min} , \, } \rho_{i,\hbox{max} } } \right]}$$
(21)

Afterward, in order to specify the fitness of chromosomes, the generated chromosomes are separately processed. The fitness value of each chromosome is determined using the cost function Eq. (19).

In order to produce new generation and other population, a number of the generated chromosomes are picked out for production. Although elitism is the first solution for the generation of next population, the selection for reproduction is randomly carried out from the generated chromosomes in order to increase randomness property of the genetic algorithm. After the chromosomes are randomly selected as parents, they will be recombined in the fourth step. In this step, selected chromosomes, as a 2-by-2 block, are combined using a uniform crossover procedure, and consequently, the new chromosomes are generated. The used method to recombine chromosomes is depicted in Fig. 5.

Fig. 5
figure 5

Parent recombination presentation to generate new offspring using crossover method

Full size image

Each gene on each chromosome is selected using the genetic operator in order to generate the new offspring. In Fig. 5 as an example, the recombination has been shown for the first genes of two chromosomes. The first gene is multiplied by α and the second gene is multiplied by 1-α and then the sum of these two values as the first gene is placed in the first gene of the offspring. α is a random number between zero and one. Similarly, to generate the first gene of the second offspring, the first gene of a second parent and the first gene of the first parent are multiplied by α and 1 − α, respectively. Correspondingly, the sum of these two values is placed in the first gene of the second offspring. Similarly, this process continues for the rest of the genes in chromosomes and also other offsprings, in the same way, are generated through random chromosomes.

Currently, there are two categories of populations: (1) first population, (2) the offspring generated through reproduction.

In step 5, new population, which is different compared to the first population and offspring population generated through the crossover method, has been generated using a mutation mechanism in order to not trap in a local minimum.

In this mechanism, a random number is added to each gene. This number is the value between zero and one so that it is multiplied by the value which is proportional to the maximum and minimum of each generated gene in the first step. After applying the mutation mechanism on some of the initial population, three kinds of populations, which are named the first population, population generated by the crossover method and the mutation approach, are placed in a matrix and sorted proportional to their cost function.

In step 7, among the current population and the generated population through the crossover and mutation method, a selection operator has been carried out in order to substitute the best population for the low-cost function population. The selection operator has been conducted based on elitism in this paper such that the chromosomes that have a lower cost function are selected and the others are omitted. Finally, a stop condition is checked. Whenever the stop condition to be satisfied, genetic algorithm execution is ceased. Otherwise, algorithm execution continues with a new population. The details of the genetic algorithm are presented briefly as follows:

  1. (a)

    GA Initialization

    • Specify input data (data = 10,000),

    • Number of population (nPop = 50),

    • Min and max of chromosome(S),

    • Number of iteration (Maxit = 80)

    • Generating 64 QAM input data

    • Randomly initialize population \(\left\{ {\mathop \rho \limits^{ \sim } (m)} \right\}_{m = 1}^{nPop}\) in S boundary

    • Compute MSE cost function \(\left\{ {\cos t \, Function(\mathop \rho \limits^{ \sim } (m))} \right\}_{m = 1}^{nPop}\)

  2. (b)

    GA Main Loop

    for (i = 0; i < Maxit; i ++){

    • Calculate new offspring according to the crossover of the parents.

    • Calculate cost function of new offspring according to (19).

    • Calculate new offspring according to the mutation of the chromosomes.

    • Calculate cost function of new offspring according to (19).

    • Sort population according to their cost function.

    • Select best chromosomes and delete remain of them (truncation method).

    }

  3. (c)

    GA Termination

    The solution is a chromosome that has minimum cost function.

This algorithm can be applied to the each data set of the real power amplifier and exactly identifies the coefficients of the model. The evaluation of the GA is investigated in the simulation results section.

4 Digital predistorter design for the Wiener power amplifier model

According to the designed Wiener model for the power amplifier, the characteristic of the proposed predistorter must be totally the opposite of the behavior of the modeled power amplifier. The proposed predistorter model is the Hammerstein structure consisting of the memoryless nonlinear block and the linear filter (Fig. 2) [39].

The part of the linear filter in the predistorter model must be fully the reverse of the filter in the Wiener model. Also, memoryless nonlinearity (phase and amplitude variation) of the Hammerstein predistorter model must be exactly the inverse of the Wiener model in order to create the linear amplifier.

4.1 Algebraic equation for the predistorter Hammerstein

A transfer function of the linear filter in the Hammerstein model can be expressed as follows:

$$G(z) = \sum\limits_{i = 0}^{m} {g_{i} \, } z^{ - i}$$
(22)

Transfer function coefficients G(z), \(g = \left[ {g_{0} {\text{g}}_{1} \ldots {\text{g}}_{\text{M}} } \right]\), can be easily achieved with respect to the following equation:

$$G(z) \, . \, H(z) = 1$$
(23)

To guarantee the exact inverse modeling of the Wiener filter, the size of matrix g in the Hammerstein model should be doubled or tripled compared with the size of the matrix h in the Wiener filter. By solving the Eq. (23), the coefficients of the matrix g are extracted as follows:

$$\begin{aligned} g &= \left[ \begin{array}{lllll} {1.3001} & { - 0.2599} & { - 0.07805} & {0.0416} & { - 5.1678{\text{e}} {-} 3} \end{array} \right. \\ &\quad \left. \begin{array}{lll} { - 0.0041} & {8.6223{\text{e}} {-} 4} & {2.3288{\text{e}} {-} 4} \end{array} \right] \end{aligned}$$
(24)

The memoryless nonlinear part of the Hammerstein predistorter should create appropriate phase and amplitude functions which fully compensates the those of the Wiener model. The input signal amplitude x(n) is denoted by b(n) and have a magnitude of |x(n)|. The amplitude nonlinear function of the Hammerstein predistorter is denoted by P(b). Additionally, the predistorter amplitude function of memoryless nonlinear is equal to b.P(b) and the predistortion phase function is equal to Ω(b). According to Eq. (6), a required equation for the predistortion amplitude function can be expressed as follows

$$Amp(b \cdot P(b)) = b$$
(25)

connecting the Eq. (25) to the Eq. (6) leads to

$$b = \frac{{\alpha_{a} \, bP(b)}}{{1 + \beta_{a} b^{2} P^{2} (b)}}$$
(26)
$$\beta_{a} b^{2} \cdot \, P^{2} (b) - \alpha_{a} \cdot P(b) + 1 = 0$$
(27)

Two solutions are achieved by solving the Eq. (27) so that the smaller solution is selected according to the required amplitude function.

$$P(b) = \left\{ {\begin{array}{*{20}l} {\frac{{\alpha_{a} - \sqrt {\alpha_{a}^{2} - 4\beta_{a} b^{2} } }}{{2\beta_{a} b^{2} }}} \hfill & {{\text{b}} \le A_{\hbox{max} } } \hfill \\ 1 \hfill & {{\text{b}} \ge A_{\hbox{max} } } \hfill \\ \end{array} } \right\}$$
(28)

According to Eq. (7), required correction equation for the predistortion phase function can be considered as follows:

$$\phi (b.P(b)) + \varOmega (b) = 0$$
(29)

Based on Eq. (29) and (7), the solution of predistortion phase function Ω(b) is specified as

$$\varOmega (b) = - \phi (b \cdot P(b)) = - \frac{{\alpha_{\phi } (b \cdot P(b))^{2} }}{{1 + \beta_{\phi } (b \cdot P(b))^{2} }}$$
(30)

By using the nonlinear amplitude function of the power amplifier, Eq. (6), with variables αα = 2.1587 and βα = 1.15, Fig. 6 shows the amplitude function of the power amplifier Amp(b), the amplitude function of the digital predistorter b·P(b) and a combined amplitude function of the power amplifier and the predistorter Amp(b·P(b)). As shown in the Fig. 6, combined amplitude function of the power amplifier and predistorter Amp(b·P(b)) has linear characteristic so that it demonstrates the performance of the digital predistorter.

Fig. 6
figure 6

Amplitude function of the power amplifier Amp(b) amplitude function of the digital predistorter b·P(b) and combined amplitude function of the power amplifier and the predistorter Amp(b·P(b))

Full size image

The amplitude function of the predistorter, Eq. (28), consists of dividing by b2 and a square root calculation. When the signal b2 goes to near zero, division by b2 causes a less accurate solution. In order to simplify the hardware implementation, the calculation of P(b) without a square root calculation is very suitable. For this reason, Eq. (28) is expanded using the Taylor-series expansion method.

At first, the function is defined as follows:

$$w = \frac{{4\beta_{a} {\text{b}}^{ 2} }}{{\alpha_{a}^{2} }}$$
(31)

By expanding \((1 - w^{2} )^{1/2}\) around w = 0 and using the Taylor-series expansion, the amplitude function P(b) in the Eq. (28) can be expressed as follows:

$$P(b) = \frac{{\alpha_{a} - \alpha_{a} (1 - w)^{1/2} }}{{2\beta_{a} b^{2} }}$$
(32)
$$P(b) = \sum\limits_{i = 1}^{n} {\frac{{ 2\alpha_{\text{i}} (4\beta_{a} )^{i - 1} }}{{\alpha_{a}^{2i - 1} }}b^{2(i - 1)} + o(b^{2n} )}$$
(33)

where αI are constant coefficients with (1 ≤ i≤n) and the variable n is the order of Taylor series. So, the amplitude function P(r) for b2 ≤ A 2max can be approximated as follows

$$\hat{p}(b) = \sum\limits_{i = 1}^{n} {\frac{{2\alpha_{i} }}{{\alpha_{a} }}\left( {\frac{{4\beta_{a} }}{{\alpha_{a}^{2} }}} \right)^{i - 1} (b^{2} )^{i - 1} }$$
(34)

Increasing the order of Taylor series m can improve the performance of the proposed predistorter against the increased cost of calculation complexity. In Fig. 7, the behavior of the amplitude function P (b) and its Taylor estimation \(\hat{p}(b)\) have been shown with order equal to 8. As seen in Fig. 7, the approximation error of Taylor series \(\hat{p}(b)\) which is denoted by \(o(b^{2n} )\) is remarkable for inputs b > bsat. This approximation does not work as well for inputs close to the saturation point of the power amplifier. Therefore, the power amplifier should be operated at operating points that are below its saturation point.

Fig. 7
figure 7

Amplitude gain P(b) for predistorter and Taylor approximation \(\hat{p}(b)\) with order n = 8

Full size image

4.2 FPGA implementation of the proposed predistorter

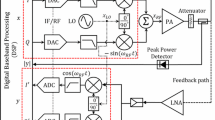
FPGAs are useful to design and implement a digital circuit in a short time because they can be reprogrammed. Recently, because of these advantages, implementation of digital systems on FPGAs has become very popular. In this article, the FPGA has been employed in implementing the proposed Hammerstein predistorter. Lately, high-level synthesis (HLS) tools such as Vivado HLS [40] have made it possible to program FPGAs using C code instead of VHDL/Verilog. HLS tools accept C syntax and generate a file format (typically VHDL/Verilog) that can be processed by the FPGA software. Based on the equations described in the previous section, the overall design of digital predistorter is depicted in Fig. 8. Part A accomplishes memory storage for the Taylor expansion coefficients and the implementation of the amplitude function. Equation (34) provides the effective structure to implement the memoryless nonlinear part of the Hammerstein structure. Using this equation, p(b) can be calculated in part A and proceed to the next stage. Implementation of the predistorter phase function Ω (b) using Eq. (30) is performed in part B.

Fig. 8
figure 8

The overall design of the digital predistorter

Full size image

The output of this part should be converted from the magnitude-phase format to real-imaginary format. This operation is performed by a CORDIC block. The CORDIC block implements a generalized coordinate rotational digital computer (CORDIC) algorithm, to iteratively solve trigonometric equations, including the hyperbolic and square root equations. Finally, the output of memoryless nonlinearity part is obtained according to Eq. (25).

At the end, the LTI filter implementation is conducted in the part C. The design is implemented using Vivado HLS. A summary of resources which is needed for implementing the proposed predistorter is presented in Table 1. DSP48E slices are the full-custom and low-power module, combining high speed with small size while retaining system design flexibility. The DSP slices enhance the speed and efficiency of many applications beyond digital signal processing, such as wide dynamic bus shifters, memory address generators, wide bus multiplexers, and memory-mapped I/O registers.

Table 1 Resource utilization of proposed predistorter implementation
Full size table

5 Simulation results

In this section, simulation results for the proposed digital predistortion are presented as follows:

  1. (A)

    Simulation results of the transmitter without predistortion.

  2. (B)

    Genetic algorithm results to obtain the coefficients of the Wiener model.

  3. (C)

    Implementation results of the proposed predistorter.

  4. (D)

    Simulation results of the transmitter with proposed predistortion.

In the following, simulation results for each section are fully presented.

5.1 Simulation of the transmitter without predistortion

The transmitter system depicted in Fig. 9 is designed and simulated for evaluating the modeled power amplifier and the proposed digital predistortion. In this part, the transmitter without the predistorter block is simulated and the transmitter with predistortion block is simulated in part D of this section. The operation of the designed transmitter is described as follows. First, the random bit generator module produces a random bit sequence such that the probability of a zero and one bit is 0.5. Then, the complex symbol mapper groups consecutive bits into the 64QAM structure. The QAM signal is applied to a complex to the real and imaginary converter. This module converts complex input values to real and imaginary output values. The real and imaginary signals are applied to a raised cosine filter module. In the raised cosine filter block, each symbol is multiplied by a sinc function. Also, this block implements a resampler that uses a raised cosine filter as the interpolating filter. Then, the output signals of the raised cosine filter are applied to the modulator, since we assume that there is no predistortion block in the transmitter system. The modulator module includes a mixer and combiner. This structure reads one sample from its inputs and writes the modulated sample in the frequency of the oscillator to its output.

Fig. 9
figure 9

Simulated transmitter system with and without predistortion

Full size image

The oscillator module has been employed in generating a signal with a frequency of 2.1 GHz. The power amplifier has an input and output matching network specified in Fig. 9 as input and output ports. The modulated signal, i.e. 10 MHz signals, is applied to the modeled power amplifier. The power amplifier operates at a 2.1 GHz center frequency and its bandwidth is as high as 10 MHz.

In order to assess the power amplifier model, the spectrum analyzer has been placed after the modulator and the power amplifier. The spectrum analyzer measures the spectrum of a complex envelope signal. The power spectrum density (PSD) curves of the input and output of the power amplifier have been depicted in Fig. 10 at the operating frequency of 2.1 GHz and bandwidth of 10 MHz. It is clear that the phenomenon of spectral regrowth has been happened due to the nonlinearity of the power amplifier. Because of the nonlinearity, the side lobes of the spectrum curves have grown. The adjacent channel power ratio (ACPR) is commonly used to quantify the nonlinearity that is generated by power amplifiers driven by modulated signals in the frequency domain. This is a significant linearity parameter since the power that is generated by the nonlinear distortions in the adjacent channels cannot be eliminated by filtering. Therefore, the power generated in the adjacent channels is considered as an unwanted emission that needs to be minimized and controlled.

Fig. 10
figure 10

Simulated power spectrum density of the Wiener power amplifier model

Full size image

5.2 Genetic algorithm simulation to obtain the coefficients of the Wiener model

The effectiveness of GA, which was presented in Section III, is demonstrated to obtain the coefficients of the Wiener model. The input 64QAM modulated signal is utilized to produce input data for the Wiener model. The number of the initial population and iterations equal to nPop = 50 and MaxIt = 80. The mean square error (MSE) of the cost function is shown in Fig. 11. As seen in Fig. 11, the MSE of the genetic algorithm is taken the value 0.1 after the twentieth iteration of the genetic algorithm. In other words, an extraordinary jump to obtain answer has been done from the first to the twentieth iteration. It is the main characteristic of the genetic algorithm that the solution at each step is better than the last step. After running the genetic algorithm, the amount of cost function or mean square error has reached the value of 9.16e-4. The matrix ρ with the minimum cost function is selected and given as follows

$$\hat{h} = \left[ {\begin{array}{*{20}c} {0.7773} & {0.1568} & {0.0813} \\ \end{array} } \right]$$
(35)
$$\hat{t} = \left[ {\begin{array}{*{20}c} {2.1346} & { 1. 1 1 7 0} & { 3. 9 4 0 1} & { 2. 0 6 5 4} \\ \end{array} } \right]$$
(36)
Fig. 11
figure 11

MSE of cost function versus the number of GA iteration

Full size image

The amplitude and phase response of the Wiener model using the true and estimated coefficients have been depicted in Fig. 12. The results show that the Wiener model coefficients with very high accuracy can be obtained using the genetic algorithm. Amplitude and phase responses of the Wiener model using approximated coefficients are quite accurate and the error between them is negligible.

Fig. 12
figure 12

A comparison of amplitude and phase response of the Wiener model using true and estimated coefficients

Full size image

5.3 Implementation results of the proposed predistorter

Constellation diagrams of output signals of proposed predistorter and combined proposed predistorter and the Wiener model have been depicted in Fig. 13. It is obvious that the proposed predistorter can completely compensate nonlinear distortion and memory effect of the power amplifier. As a result, constellation diagrams of input and output signals are identical using the proposed digital predistorter.

Fig. 13
figure 13

a Constellation diagram of output signals of proposed predistorter (input signal has 64 QAM modulation with n = 10,000, b constellation diagram of output signals of combined proposed predistorter and power amplifier Wiener model (input signal has 64 QAM modulation with n = 10,000)

Full size image

In order to validate the implementation of the proposed Hammerstein model, a test bench file is very well written in the Vivado HLS for evaluating the results of the synthesized HDL code. Since Vivado HLS employs C code to program the FPGA device, testing the implemented DPD model needs to be done by a C program. Therefore, the generated input data is transferred to the Vivado HLS. The output data of the implemented predistorter in FPGA has been illustrated in Fig. 14.

Fig. 14
figure 14

a Constellation diagram output for the implemented predistorter in FPGA (input signal has 64 QAM modulation with n = 10,000), b constellation diagram of system output using the implemented predistorter in FPGA (input signal has 64 QAM modulation with n = 10,000)

Full size image

It is obvious that the constellation diagrams of Figs. 13(b) and 14(b) are analogous to each other. However, the output of FPGA-based system includes minor errors in comparison with the output constellation of the digital predistortion and power amplifier model. By increasing the input magnitude of the system, the output constellation deviates slightly from the expected position.

5.4 Simulation of the transmitter with digital predistortion based on the Hammerstein model

The schematic of the simulated transmitter with digital predistortion has been depicted in Fig. 9. The digital predistortion based on the Hammerstein model are placed between the raised cosine filter and the modulator. In-phase and quadrature (I and Q) signals are applied to the predistortion block, and the signals are passed through the proposed predistorter model. When these signals are applied to the predistorter, they experience the static and dynamic nonlinearity of the model. Finally, the predistorted signals are applied to the modulator. The Hammerstein model, which was clearly described in Section III, has been employed for the predistorter block. The linear filter length of the predistorter is equal to 7 (n = 7). In order to create an appropriate trade-off between accuracy and simple implementation of the amplitude function, the order of seven (m = 7) is selected for Taylor series expansion. Fig 15 illustrates the input signal spectrum of the power amplifier X(n), the output signal spectrum of the nonlinear power amplifier and the output signal spectrum of the overall system (power amplifier + digital predistortion).

Fig. 15
figure 15

Power amplifier input spectrum, power amplifier output spectrum without digital predistortion and system output spectrum, which consists of the power amplifier and DPD

Full size image

It is very clear that the digital predistortion linearization method has compensated the distortion of the power amplifier, and the spectral regrowth of the power amplifier is totally removed. The measure of adjacent channel power ratio (ACPR) is presented in Table 2. It is very clear that the ACPR of the power amplifier with digital predistortion has been improved to about 16dBc at the offset frequency of 7.5 MHz from the center frequency. In addition, the value of MSE is − 35.49 dB for the linearized power amplifier using proposed digital predistorter. Due to utilizing the predistorter, the criterion of MSE has been improved approximately 30 dB.

Table 2 ACPR for power amplifier with and without digital predistortion
Full size table

In Table 3, the performance of the proposed predistortion model is compared with the performance of other methods in some papers. As presented in the table, the proposed predistorter model demonstrates a significant improvement in the removal of nonlinear memory effects and ACPR reduction. Obviously, the proposed Hammerstein model can eliminate some distortions generated by the power amplifier. In other words, the digital predistortion method in addition to improving linearity can enhance the efficiency of the power amplifier circuit. This proposed model (the predistorter model) was efficiently implemented in FPGA, because only standard structures, e.g., finite impulse response (FIR) filters, adder, and multipliers, are employed.

Table 3 Comparison of the performance of the proposed predistortion block with the performance of other methods
Full size table

6 Conclusion

This paper proposes the novel digital predistorter structure based on the Hammerstein structure for behavioral modeling and digital predistortion of nonlinear power amplifiers exhibiting memory effects. The genetic algorithm was utilized to extract coefficients of the Wiener model. Considering achieved coefficients for Wiener model, the predistorter based on the Hammerstein structure was designed. The proposed model was fully assessed through simulation of the transmitter excited by the 10 MHz 64QAM signal in advanced design system (ADS) software. The criterion of adjacent channel power ratio (ACPR) was reduced by about 16 dB according to the simulation results. Simulation results showed the ability of the proposed model to obtain better performance than the conventional predistortion method. The proposed Hammerstein model was implemented in Kintex FPGA using Vivado HLS. This proposed model enables a more accurate modeling of nonlinear distortion and memory effects compared to some of the previous linearization methods.