1 Introduction

The power amplifier (PA) is a fundamental component of wireless communication systems. Because a large amount of power is consumed by the radio frequency (RF) power amplifiers in transmitters, these circuits are known as power hungry blocks [27]. If the power amplifier circuits are driven at a saturation operating point, they generate the nonlinearities in an advanced communication system, causing not only out of band distortion, i.e., spectral regrowth, but also in-band distortions [29]. These distortions lead to severe interference of the adjacent channels and increase in the amount of error vector magnitude (EVM) [22]. Modern communication systems, such as worldwide interoperability for microwave access (WiMAX) and long-term evolution (LTE), exploit efficient modulation approaches in order to improve data transmission rate within a limited band [1].

The signals of the systems vary rapidly and have high peak to average power ratio [Orthogonal frequency-division multiplexing (OFDM) \(\sim 10\,\hbox {dB}\)]. Therefore, the power amplifier must be operated at a power level that is far from its saturation point. As a result, transmission of non-constant envelope signals employing power amplifiers at linear operation region has poor efficiency [6]. Thus, the efficiency of the power amplifier is dramatically reduced due to the large back-off from saturation operating point. Consequently, the trade-off between linearity and efficiency is emerging in RF power amplifier design. In order to improve linearity without losing efficiency, the use of power amplifier linearization methods is indispensable. For this reason, several linearization techniques, such as feedback, feedforward, and predistortion, have been proposed to improve the linearity of the transmitter and the power amplifier without sacrificing efficiency [26]. The predistortion method has suitable performance and low cost among the linearization techniques [2].

Figure 1 shows the conceptual diagram of the predistortion linearization process. In the predistortion linearization method, the input signal is predistorted before applying it to the input of a nonlinear power amplifier, so that the nonlinear response of the power amplifier can be compensated for, enabling the output of the amplifier to yield a linear response.

Fig. 1
figure 1

Simplified concept of a predistortion linearization technique

Full size image

It is clear from Fig. 1 that the response of the power amplifier is compressive, while the input/output characteristic of the predistortion has an expanding behavior. Theoretically, the expanding characteristic of the predistortion can compensate for the compressing behavior of the power amplifier. As a result, the relationship between the input and output of the system will be linear. The predistortion can be classified into two types in accordance with the techniques used: (1) analog predistortion (APD) (2) digital predistortion (DPD).

The analog predistortion (ADP) directly operates with the analog signal and is placed near the power amplifier. When the analog predistortion operates at a high frequency, the analog predistortion implementation is so straightforward, but it shows limited capability and low performance [21]. Many analog predistortion circuits that have cost-effective and simple structures are described [4, 14, 18, 24, 32, 34]. Although analog predistortion has several advantages compared to digital predistortion, such as simple structure and low cost, its capability to remove nonlinearity is less than that of digital predistortion. Indeed, while most analog predistortion circuits are employed in a narrow band application, the performance of analog predistortion is not comparable to digital predistortion. For example, Seo proposed an analog predistorter based on a Schottky diode, but the improvement in the adjacent channel power ratio is very small [30].

One of the linearization procedures commonly utilized in advanced communication systems is the digital predistortion method [2, 9, 12, 15, 26, 35].

Because of digital hardware implementation, digital predistortion is one of the most useful approaches of linearization, with high flexibility and low cost. The accuracy of linearization is substantially augmented by digital implementation [20]. A memoryless model was commonly employed in the primary linearization procedures based on digital predistortion such that the model compensated for the static nonlinear behavior of the power amplifier [23]. The static nonlinear behavior is fully characterized in terms of amplitude modulation/amplitude modulation (AM/AM) and amplitude modulation/phase modulation (AM/PM) effects [5]. Cho proposed a lookup table (LUT) instead of the memoryless model, but the LUT may not usefully eliminate distortions in modern wireless transmitters. Furthermore, when the bandwidth of the power amplifier is increased in most modern transmitters, the memory effects of the power amplifier are not trivial. The memory effects of the power amplifier must be investigated to achieve the best performance of digital predistortion [16]. The Volterra series is the most appropriate model used to accurately model nonlinear dynamic systems [28]. When the order of memory depth and nonlinearity increases, the number of utilized coefficients increases very rapidly; hence, the computational complexity of the model is augmented. Guan [11] has recently proposed the Volterra series to model predistortion; however, the resource consumption, as well as the complexity of the predistortion, has increased. Therefore, many structures that originate from the Volterra model, such as Wiener model [19], Hammaerstion model [20], and memory polynomial model [7], are proposed in order to overcome the complexity of the Volterra series. The models of Hammerstein and Wiener are commonly employed in low bandwidth applications. Moon [22] suggested an enhanced Hammerstein model, but the model and coefficients identification are very complex.

Fig. 2
figure 2

The schematic of the digital predistortion block and the power amplifier

Full size image

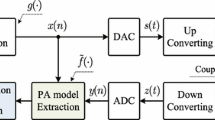
Nowadays, with the impressive growth in DSP techniques, most linearization methods based on digital predistortion are completely implemented in baseband domain. An overall system made of the power amplifier and digital predistortion-based linearization method has been depicted in Fig. 2. In this system, first, the generated baseband signal is distorted using the predistortion block, and then the distorted signal is passed through a digital to analog converter (DAC) in order to convert it to an analog signal. Similarly, the radio frequency signal is generated using a modulator composed of a mixer, local oscillator, and combiner, and then the RF signal is applied to the power amplifier in order to amplify the transmission signal.

In order to extract and update the coefficients of the digital predistortion model, as illustrated in Fig. 2, a small portion of the transmitted signal is taken by a coupler. The frequency of the return signal is down converted by the modulator, and the resultant signal is transformed to a digital signal using an analog to digital converter (ADC). The digital signal is then applied to the adaptation algorithm block, which takes a sample of input and output data and updates the coefficients of the predistortion block, in order to achieve an effective linearization method. The feedback path which is shown in Fig. 2 works only in the initial system setup or whenever the characteristics of the system have wide variations. Therefore, the design and implementation of a digital predistortion system include two parts: (1) The digital predistortion block: The input signals I and Q should be distorted by applying the digital predistortion block. (2) The adaptation algorithm block is utilized for updating the coefficients of the predistortion block.

This paper proposes a generalized parallel two-box (GPTB) model to model and carries out digital predistortion (DPD) of power amplifiers. The proposed predistortion scheme includes two separable boxes; the first is utilized to model the static behavior of the power amplifier, while the second is proposed in order to consider the memory effect and nonlinear distortion of the power amplifier.

This paper is organized as follows: In Sect. 2, the proposed generalized parallel two-box model is described and the methods of coefficients identification are accurately introduced. Next, the performance assessment of the proposed model is completely expressed in Sect. 3. In this section, power amplifier model extraction and verification are carried out first, after which coefficients identification of the proposed model is done using the indirect learning method. Simulation of the overall transmitter with and without predistortion is carried out at the end of this section. Finally, the conclusion is presented in Sect. 4.

2 Generalized Parallel Two-Box (GPTB) Behavioral Model Based on Hybrid Memory Polynomial

2.1 Model Architecture

In this section, the generalized parallel two-box structure is proposed for the modeling of the digital predistorter. The proposed model consists of hybrid memory polynomial and memoryless nonlinear function, as depicted in Fig. 3. The first memoryless box emulates the static behavior of the power amplifier, while the second box considers the linear and nonlinear memory effects of the power amplifier. The detailed operation of the proposed generalized parallel two-box structure is explained as follows:

2.1.1 Memoryless Nonlinear Function

The memoryless polynomial model is proposed in order to emulate the memoryless nonlinear function of the generalized parallel two-box predistorter. This function considers the static behavior of the power amplifier, which includes AM/AM and AM/PM characteristics.

Fig. 3
figure 3

The proposed generalized two-box predistorter

Full size image

The baseband complex output signal (\(y_{\mathrm{MLP}})\) of the memoryless polynomial function is defined as a function of its baseband complex input x(n) signal according to:

$$\begin{aligned} Y_\mathrm{{MLP}} (n)=\sum \limits _{k=1}^{K_{\text {MLP}} } {a_{k} \cdot x(n)\cdot \left| {x(n)} \right| }^{k-1} \end{aligned}$$
(1)

where \(a_{\mathrm{k}}\) indicates the coefficients of the memoryless polynomial and K represents the memoryless polynomial function nonlinearity order.

2.1.2 Hybrid Memory Polynomial

The hybrid memory polynomial has been suggested in order to consider the memory effect of the power amplifier in the proposed model. The hybrid memory polynomial model augments the memory polynomial model through the inclusion of cross-terms [13]. The parallel combination of the memory polynomial (MP) model and the envelope memory polynomial (EMP) model has been utilized to make the hybrid memory polynomial model, as illustrated in Fig. 4.

Therefore, the input/output signal of the hybrid memory polynomial model is defined as follows:

$$\begin{aligned} {y}_{{\text {HMP}}} (n)= & {} \sum _{m=0}^{M} {\sum \limits _{k=1}^{K} {a_{km} } \cdot x(n-m) \cdot \left| {x(n-m)} \right| ^{k-1}} \nonumber \\&+\sum \limits _{m=\hbox {1}}^{M_{\mathrm{e}} } {\sum _{K=1}^{K_{\mathrm{e}} } {b_{km} \cdot x(n)} } \cdot \left| {x(n-m)} \right| ^{k-1} \end{aligned}$$
(2)

where \(a_{{mk}}\) and \(b_{{mk}}\) are the coefficients of the memory polynomial and the envelope memory polynomial model, respectively. Also, K and M are the nonlinearity order and memory depth of the memory polynomial model, respectively. Similarly, \(K_{\mathrm{e}}\) and \(M_{\mathrm{e}}\) represent the nonlinearity order and memory depth of the envelope memory polynomial model, respectively. x(n) and \(y_{\mathrm{HMP}}(n)\) refer to the input and output baseband complex waveforms of the model, respectively. The hybrid memory polynomial consists of two basic functions; therefore, Eq. (2) can be rewritten as:

$$\begin{aligned} {y}_{\text {HMP}} (n)=\phi _{\mathrm{HMP}} {(n) }\cdot { A} \end{aligned}$$
(3)

where the input data vector \(\phi _{\mathrm{HMP}} {(n)}\) and the coefficients vector A are described as

$$\begin{aligned} A=\left[ {\begin{array}{l} A_{\text {MP}} \\ A_{\text {EnvMP}} \\ \end{array}} \right] \end{aligned}$$
(4)

with

$$\begin{aligned} A_{\text {MP}}= & {} \left[ {{a_{01}} \cdot \cdot \cdot {a_{0k}}\, \, {a_{11}} \cdot \cdot \cdot {a_{1K}} \cdot \cdot \cdot {a_{MK}} } \right] ^\mathrm{T}\end{aligned}$$
(5)
$$\begin{aligned} A_{\text {EnvMP}}= & {} \left[ {{b_{12}} \cdot \cdot \cdot {b_{{1k}_\mathrm{e}}}\, \, {b_{22}} \cdot \cdot \cdot {b_{2K_\mathrm{e} }} \cdot \cdot \cdot b_{M_\mathrm{e} {K_{e}} } } \right] ^\mathrm{T} \end{aligned}$$
(6)

where [.]\(^\mathrm{T }\) denotes the transpose operator and

$$\begin{aligned} {\varphi _{\text {HMP}}} (n)=\left[ {\phi _\mathrm{MP}} (n) {\phi _\mathrm{EnvMP}} (n) \right] \end{aligned}$$
(7)
Fig. 4
figure 4

Block diagram of the hybrid memory polynomial model

Full size image

with

$$\begin{aligned} \qquad \phi _\mathrm{MP} (n)= & {} \left[ {\begin{array}{l} \qquad x(n) \\ \quad \qquad \vdots \\ \qquad x(n) \cdot \left| {x(n)} \right| ^{{k-1}} \\ \qquad x(n-1) \\ \quad \qquad \vdots \\ \qquad x(n-1) \cdot \left| {x(n-1)} \right| ^{{k-1}} \\ \quad \qquad \vdots \\ \qquad x(n-M) \cdot \left| {x(n-M)} \right| ^{k-1} \\ \end{array}} \right] ^\mathrm{T} \end{aligned}$$
(8)
$$\begin{aligned} \qquad \phi _\mathrm{EnvMP} (n)= & {} \left[ {\begin{array}{l} \qquad x(n)\cdot \left| {x(n-1)} \right| \\ \quad \qquad \vdots \\ \qquad x(n) \cdot \left| {x(n-1)} \right| ^{{K}_\mathrm{e} {-1}} \\ \qquad x(n) \cdot \left| {x(n-2)} \right| \\ \quad \qquad \vdots \\ \qquad x(n) \cdot \left| {x(n-2)} \right| ^{{K}_\mathrm{e} {-1}} \\ \quad \qquad \vdots \\ \qquad x(n) \cdot \left| {x(n-M_\mathrm{e} )} \right| ^{{K}_\mathrm{e} {-1}} \\ \end{array}} \right] ^\mathrm{T} \end{aligned}$$
(9)

The hybrid memory polynomial model incorporates the memory polynomial model and the envelope memory polynomial model in order to construct a very high-performance model. This model is placed in the bottom box of the proposed model with the aim of generating a distortion that is complementary of the distortion of the power amplifier and eliminating the memory effect of the power amplifier.

2.2 Model Identification

In this paper, the memory polynomial model has been employed in order to model the highly nonlinear power amplifier. Kim and Konstantinou [17] proposed the memory polynomial model several years ago. Due to the trade-off possible between complexity and accuracy, this model is one of the most popular models for behavior modeling of the power amplifier and predistortion. However, the coefficients of this model increase quickly when the highly nonlinear memory effect appears in the power amplifier.

When the coefficients of Volterra series [11] change to diagonal terms (i.e., removing all cross-terms), the memory polynomial model is generated. The model is a two summation formula with two parameters: nonlinear order and memory depth. The baseband complex output signal \((y_{\mathrm{MP}}(n))\) of the memory polynomial model as a function of the baseband complex input signal (x(n)) can be described by the following equation:

$$\begin{aligned} {y}_{\text {MP}} (n)=\sum \limits _{m=0}^M {\sum \limits _{k=1}^K {\alpha _{mk}} \cdot x(n-m)\cdot \left| {x(n-m)} \right| ^{k-1}} \end{aligned}$$
(10)

where \(\alpha _{{mk}}\) indicates the coefficients of the model and K and M refer to the nonlinear order and memory depth, respectively. y(n) is the complex output sample of the model at instant n, and \(x(n-m) \) is the complex input sample at instant \(n-m\).

If we rewrite Eq. (10) as a generic formulation, the equation is rewritten in vector format as:

$$\begin{aligned} y_\mathrm{MP} (n)=\varphi _{\mathrm{MP}} {(n) }\cdot { A} \end{aligned}$$
(11)

where \(\varphi _{\text {MP}} (n)\) is a vector built using complex input signal samples \(x(n-m)\) and A is a vector containing the model coefficients. These vectors are given by:

$$\begin{aligned} \phi _{\text {MP}} (n)= & {} \left[ {\begin{array}{c} \qquad x(n) \\ \quad \qquad \vdots \\ \qquad x(n) \cdot \left| {x(n)} \right| ^{{k-1}} \\ \qquad x(n-1) \\ \quad \qquad \vdots \\ \qquad x(n-1) \cdot \left| {x(n-1)} \right| ^{{k-1}} \\ \quad \qquad \vdots \\ \qquad x(n-M) \cdot \left| {x(n-M)} \right| ^{k-1} \\ \end{array}} \right] ^\mathrm{T} \end{aligned}$$
(12)
$$\begin{aligned} A= & {} \left[ {\alpha _{01} \cdots \alpha _{{0k }}\,\, \alpha _{11} \cdots \alpha _{1k} \cdots \alpha _{{MK}} } \right] ^\mathrm{T} \end{aligned}$$
(13)

For a set of N samples, this vector representation can be rewritten in matrix format as follows:

$$\begin{aligned} y={X }\cdot { A} \end{aligned}$$
(14)

where y is the vector of N samples of the output signal and given by:

$$\begin{aligned} y=\left[ {\begin{array}{c} \quad y(n) \\ \quad y(n-1) \\ \qquad \ldots \\ \qquad \ldots \\ \qquad \ldots \\ \quad y(n-N+1) \\ \end{array}} \right] ^\mathrm{T} \end{aligned}$$
(15)

Also, X is a matrix whose rows are delayed versions of \(\varphi _{\mathrm{MP}} {(n)}\). It is defined as follows:

$$\begin{aligned} X= & {} \left[ { \varphi _{\text {MP}} (n)\quad \varphi _{\text {MP}} (n-1) \cdots \varphi _{\text {MP}} (n-N+1)} \right] ^\mathrm{T} \end{aligned}$$
(16)
$$\begin{aligned} X= & {} \left[ {\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} x(n)&{} \cdots &{}\quad x(n) \cdot \left| {x(n)} \right| ^{{K-1}}&{}\quad x(n-1) &{}\quad \cdots &{}\quad x(n-1) \cdot \left| {x(n-1)} \right| ^{{K-1}} \\ x(n-1)&{} \cdots &{}\quad x(n-1) \cdot \left| {x(n-1)} \right| ^{{K-1}}&{}\quad x(n-2)&{}\quad \cdots &{}\quad x(n-2) \cdot \left| {x(n-2)} \right| ^{{K-1}} \\ \vdots &{} \cdots &{}\qquad \qquad \vdots &{}\qquad \vdots &{}\quad \cdots &{}\qquad \qquad \vdots \\ x(n-N+1)&{} \cdots &{}\quad x(n-N+1) \cdot \left| {x(n-N+1)} \right| ^{{K-1}}&{}\quad x(n-N) &{}\quad \cdots &{}\quad x(n-N) \cdot \left| {x(n-N)} \right| ^{{K-1}} \\ \end{array}} \right. \nonumber \\&\quad \qquad \left. {\begin{array}{ll} \cdots &{}\quad x(n-M) \cdot \left| {x(n-M)} \right| ^{{K-1}} \\ \cdots &{}\quad x(n-M-1) \cdot \left| {x(n-M-1)} \right| ^{{K-1}} \\ &{}\qquad \qquad \vdots \\ \cdots &{}\quad x(n-M-N+1) \cdot \left| {x(n-M-N+1)} \right| ^{{K-1}} \\ \end{array}} \right] ^\mathrm{T} \end{aligned}$$
(17)

If the matrix X was invertible, the coefficients identification would be given by:

$$\begin{aligned} A={X}^{-1} \cdot { y } \end{aligned}$$
(18)

In order to perform coefficients extraction, an approximate solution can be achieved by minimizing the mean squared error, e, given by:

$$\begin{aligned} e=\left\| {{y - XA}} \right\| ^{2} \end{aligned}$$
(19)

To solve this problem, one method which is usually utilized is the method of computing the pseudo-inverse of the matrix X as follows [25, 31]:

$$\begin{aligned} \hbox {pinv}({X})=({X}^{\mathrm{T}}{X)}^{-1}{X}^{\mathrm{T}} \end{aligned}$$
(20)

Then, the coefficients are calculated using:

$$\begin{aligned} A=\hbox {pinv}({X})\cdot {y } \end{aligned}$$
(21)

By minimizing the error using least square criterion, this method allows for proper identification of the model coefficients.

3 Performance Assessment of the Generalized Parallel Two-Box Predistorter Model

The flow chart summarizing the evaluation steps of power amplifier linearization using the generalized parallel two-box model based digital predistortion and indirect learning structure is presented in Fig. 5.

The performance assessment steps are classified into four parts: First, one behavioral model is proposed for the power amplifier modeling, and the coefficients of the model are identified using the least square (LS) method. Next, coefficients identification of the digital predistorter based on the generalized parallel two-box model using the indirect learning structure is carried out. In step III, the overall system (PA \(+\) DPD) is simulated. Finally, the performance of the proposed predistortion model is compared with the performance of other methods in some papers. A detailed description of each stage is presented below.

Fig. 5
figure 5

Performance evaluation steps of the power amplifier and the proposed digital predistortion model

Full size image

3.1 Power Amplifier Model Extraction and Verification

Before the proposed predistorter model is verified, the power amplifier must be modeled and simulated. For this reason, the memory polynomial function, which was fully described in the last section, has been proposed to model the highly nonlinear power amplifier. The main device under test (DUT), which is utilized in this work for the performance assessment of the proposed predistorter model, is a high power and efficient Doherty power amplifier based on laterally diffused metal oxide semiconductor (LDMOS) technology. The DUT has a maximum output power of 300 W and operates at about 2.1 GHz. It is driven by a 20 MHz signal which was sampled at 120 MHz. The baseband input and output waveforms of the device under test were acquired using the experimental setup described above. The baseband complex input and output data have been gathered in order to identify the coefficients of the memory polynomial model. The nonlinearity order and memory depth of Eq. (10) were set to \(K=20\) and \(Q=10\), respectively, in order to accurately model the power amplifier. Because the power amplifier circuit will be utilized for real applications, the values of K and Q have been chosen to be very high in order to model the Doherty power amplifier accurately. The coefficients of the memory polynomial power amplifier model have been identified using the least square (LS) method described in the last section as well as the complex baseband input and data of the Doherty power amplifier.

For model performance evaluation in the time domain, the most straightforward method is to assess error in accordance with the difference between the desired and estimated output signal. The Normalized Mean Square Error (NMSE) is always employed for the performance assessment of behavioral model [10]. This criterion is often expressed in decibels and is defined as follows:

$$\begin{aligned} \hbox {NMSE}=10\log _{10} \left( {\frac{\sum _{n=1}^N {\left| {y_\mathrm{desired} (n)-y_\mathrm{estimated} (n)} \right| ^{2}} }{\sum _{n=1}^N {\left| {y_\mathrm{desired} (n)} \right| ^{2}} }} \right) \end{aligned}$$
(22)

where N denotes the number of samples, \(y_\mathrm{desired} (n)\) and \(y_\mathrm{estimated} (n).\) \(y_\mathrm{desired} (n)\) and \(y_\mathrm{estimated} (n)\) are the outputs of the power amplifier circuit and memory polynomial power amplifier model, respectively. It is obvious that a lower NMSE indicates superior model accuracy. In order to assess the identified coefficients of the memory polynomial model, the achieved coefficients are placed in the model. Then, the complex input signal is applied to the memory polynomial power amplifier model. The real and imaginary outputs, as well as the desired and estimated outputs of the Doherty power amplifier and memory polynomial model, are illustrated in Figs. 6 and 7, respectively.

Fig. 6
figure 6

The real output of the memory polynomial model and Doherty power amplifier

Full size image
Fig. 7
figure 7

The imaginary output of the memory polynomial model and Doherty power amplifier

Full size image

It can be seen that the real and imaginary outputs of the memory polynomial power amplifier model have been precisely matched with those of the Doherty power amplifier model. The criterion of NMSE is − 68.72 dB for this model verification. This NMSE means that the model extraction has been accurately carried out.

Another performance assessment metric is defined in the frequency domain. Since time domain signals are mainly dominated by the in-band components, a more accurate estimation of the model performance in the adjacent channels is required. For this reason and to further validate the accuracy of the memory polynomial model, the power spectrum density (PSD) of the Doherty power amplifier and memory polynomial power amplifier are plotted in Fig. 8.

It can also be concluded from Fig. 8 that the memory polynomial model accurately predicts the measured power spectrum density of the Doherty power amplifier. The output spectrum of the memory polynomial model is almost identical with that generated by the Doherty power amplifier. Therefore, the memory polynomial model accurately emulates both the linear and nonlinear memory effects of the Doherty power amplifier.

Fig. 8
figure 8

Measured power spectrum density of Doherty power amplifier and simulated power spectrum density of memory polynomial power amplifier

Full size image
Fig. 9
figure 9

Indirect learning structure

Full size image

3.2 Identifying Coefficients of the Proposed Generalized Parallel Two-Box Predistorter

In order to linearize the power amplifier and eliminate its nonlinearity, the predistortion block which is accurately modeled by the proposed generalized parallel two-box model is placed upstream of the power amplifier. Indeed, the behavior of the predistortion block is ideally the inverse characteristics of the power amplifier. The proposed generalized parallel two-box model shown in the previous section is employed as a digital predistorter and the memory polynomial model is utilized as a power amplifier model. The indirect learning structure employed for coefficients identification of the proposed predistortion is illustrated in Fig. 9. Actually, the indirect learning structure is a careful method in which a learning loop is closed around the power amplifier [3]. The input and output measurements of the Doherty power amplifier, which was described in the previous section, are utilized for extraction of the predistorter model. When the parameters of the predistortion in the learning loop are identified, this predistortion is then directly copied and employed as the predistortion block. The complex baseband input of the proposed predistorter is denoted by x(n); the output of the predistorter and input of the power amplifier are denoted by u(n), and the complex baseband output of the power amplifier is denoted by y(n). To identify the coefficients of the proposed model, the predistorter block located in the upstream of the power amplifier is disconnected and the indirect learning loop is closed. The indirect learning loop includes the power amplifier, predistorter block, and estimation of parameters block.

When the input of the power amplifier and the output of the predistorter block in the feedback path are equal (and consequently an error term, i.e., \(e(n)= u(n)-\mathop u\limits ^\wedge (n)\simeq 0\), is close to zero), the input and output of the system will be linear (i.e., \(y(n)=Gx(n)\)).

The coefficients of the proposed model have been identified by this structure. In this approach, when the error of energy \(\left\| {e(n)} \right\| ^{2}\) is minimum, the algorithm for finding the coefficients of the predistortion is fully converged. The identification method of the predistorter model is similar to the procedure that was clearly described in Sect. 2 by replacing the input of the predistorter with y(n) / G, where G is a small signal gain of the power amplifier and the output is \(\mathop u\limits ^\wedge (n)\).

3.3 Simulation of the Overall System (Power Amplifier \(+\) Digital Predistortion)

3.3.1 Simulation of the Transmitter Without Digital Predistortion

The transmitter system depicted in Fig. 10 is designed and simulated for evaluating the modeled power amplifier and digital predistortion. The operation of the designed transmitter is described as follows.

First, the random bit generator module produces a bit sequence such that the probability of a zero and one bit is 0.5. Then, the complex symbol mapper groups consecutive bits into a 64QAM structure. The QAM signal is applied to a complex to the real and imaginary converter. This module converts complex input values to real and imaginary output values. This block reads one sample from the input and writes it to each of the real (Re) and imaginary (Im) outputs. The real and imaginary signals are applied to a raised cosine filter module. In the raised cosine filter block, each symbol is multiplied by a sinc function. Also, this block implements a resampler that uses a raised cosine filter as the interpolating filter. Then, the output signals of the raised cosine filter are applied to the modulator. The modulator module includes a mixer and combiner. This structure reads one sample from its inputs and writes the modulated sample in the high frequency to its output. The oscillator module has been employed in order to generate a signal with a frequency of 2.1 GHz. The power amplifier has an input and output matching network specified in Fig. 10 as input and output ports. The modulated signal, i.e., 20 MHz signal, is applied to the modeled power amplifier. The power amplifier operates at a 2.1 GHz center frequency and its bandwidth is as high as 20 MHz.

In order to assess the power amplifier, the spectrum analyzer has been placed after the modulator and power amplifier. The spectrum analyzer measures the spectrum of a complex envelope signal. The power spectrum density (PSD) curves of the input and output of the power amplifier without using the digital predistortion are depicted in Fig. 11 at the operation frequency of 2.1 GHz and bandwidth of 20 MHz. It is clear that the sidelobe of the output spectrum of the power amplifier has been increased due to the nonlinearity of the power amplifier. The adjacent channel power ratio (ACPR) is commonly employed to quantify the nonlinearity that is generated by power amplifiers driven by modulated signals in the frequency domain. This is a significant linearity parameter since the power that is generated by the nonlinear distortions in the adjacent channels cannot be eliminated by filtering.

Fig. 10
figure 10

Simulated transmitter system with and without predistortion

Full size image
Fig. 11
figure 11

Simulated input and output spectrum of the power amplifier without using digital predistorter at the center frequency of 2.1 GHz with bandwidth of 20 MHz

Full size image

Therefore, the power generated in the adjacent channels is considered as an unwanted emission that needs to be minimized and controlled.

3.3.2 Simulation of the Transmitter with Digital Predistortion Based on the Generalized Parallel Two-Box Model

The schematic of the simulated transmitter with digital predistortion is depicted in Fig.10. The digital predistortion based on the generalized parallel two-box model is placed between the raised cosine filter block and modulator. In-phase and quadrature (I and Q) signals are applied to the predistortion block, and the signals are passed through the proposed predistorter model. When these signals are applied to the predistorter, they experience the static and dynamic nonlinearity of the model. Finally, the predistorted signals are applied to the modulator. The generalized parallel two-box model, which was clearly described in Sect. 2, has been employed for the predistorter block. The nonlinearity order, k, and memory depth, q, of the proposed model have been considered with normalized mean square error (NMSE) criterion. When the amounts of nonlinearity order and memory depth are \(K_{\mathrm{MLP}}=10\), \(M=12\), \(K=3\), \(M_{\mathrm{e}}=3\), and \(K_{\mathrm{e}}=3\), the NMSE will be as small as possible. If the proposed amounts are greater than these values, the complexity of the model grows and a higher accuracy is not achieved. Using indirect learning structure, the coefficients of the proposed model are accurately identified.

Figure 12 illustrates the input signal spectrum of the power amplifier X(n), the output signal spectrum of the nonlinear power amplifier and the output signal spectrum of the overall system (power amplifier \(+\) digital predistortion). It is very clear that the digital predistortion linearization method has compensated for the distortion of the power amplifier, and the spectral regrowth of the power amplifier is totally removed. The measure of adjacent channel power ratio (ACPR) is presented in Table 1. It is very clear that the ACPR of the power amplifier with digital predistortion has been improved to about 16 dB at the offset frequency of 15 MHz from the center frequency.

Fig. 12
figure 12

Power amplifier input spectrum, power amplifier output spectrum without digital predistortion and system output spectrum which consists of the power amplifier and DPD

Full size image
Table 1 ACPR for power amplifier with and without digital predistortion
Full size table

3.4 Performance Comparison with the Other Methods

In order to compare the proposed model, a memory polynomial model with nonlinearity order and memory depth of \(K=14\) and \(M=5\), respectively, has been chosen and placed in the predistorter model and simulated. The structure shown in Fig. 10 has been simulated twice with two models of the predistortion. First, the memory polynomial and then the proposed generalized parallel two-box model are accurately simulated. The values of the nonlinearity order and memory depth of the proposed model are chosen as \(K=12\), \(M=2\), \(M_{\mathrm{e}}=3\), \(K_{\mathrm{e}}=3\), and \(K_{\mathrm{ML}}=10\). The power spectrum density of the simulated transmitter with memory polynomial and the proposed model for digital predistortion is illustrated in Fig. 13. It is obvious that the memory polynomial model could not accurately remove the nonlinear distortion of the power amplifier.

Fig. 13
figure 13

Simulated power spectrum density of power amplifier input, power amplifier output without digital predistortion, power amplifier output with GPTB and MP digital predistortion spectrum which consists of the power amplifier and DPD

Full size image

However, the proposed model accurately reduces the spectral regrowth of the power amplifier compared to the memory polynomial model. Because of the separation of the static and dynamic parts in the proposed model, the generalized parallel two-box model can effectively diminish the nonlinearity and memory effect of the power amplifier. The features of the proposed model in terms of complexity and accuracy are better than the memory polynomial model. The measure of the adjacent channel power ratio (ACPR) and the employed coefficients are shown in Table 2. The ACPR of the proposed model was improved to about 7 dB compared to the memory polynomial model. Although the utilized coefficients of the proposed model diminished by about 22%, the accuracy of the model in removing spectral regrowth was boosted.

Table 2 The number of coefficients utilized in the proposed model and ACPR of the simulated power amplifier
Full size table
Table 3 Comparison of the performance of the proposed predistortion block with the performance of other methods
Full size table

In Table 3, the performance of the proposed predistortion model was compared with the performance of other methods in some papers. As presented in the table, the proposed predistorter model demonstrates a significant improvement in the removal of nonlinear memory effects and ACPR reduction. Obviously, the generalized parallel two-box model can eliminate some distortions generated by the power amplifier. As a result, the power amplifier can work near its saturation operation point. In other words, the digital predistortion method in addition to improving linearity can enhance the efficiency of the power amplifier circuit. This proposed model (the predistorter model) can be efficiently implemented in real digital circuits, e.g., digital signal processor (DSP) chips and field programmable gate array (FPGA), because only standard structures, e.g., finite impulse response (FIR) filters, adder and multipliers, are employed.

4 Conclusions

This paper proposes the generalized parallel two-box (GPTB) structure for behavioral modeling and digital predistortion of nonlinear power amplifiers exhibiting memory effects. The proposed model includes two boxes, so that the first box emulates the static behavior of the power amplifier, while the second considers the memory effect of the nonlinear power amplifier. The coefficients identification of the proposed model was carried out using the indirect learning structure and the least square method. The proposed model was fully assessed through simulation of the transmitter excited by the 20 MHz 64QAM signal in advanced design system (ADS) software. Simulation results showed that the ability of the proposed model to obtain better performance than the conventional memory polynomial model with complexity reduction was about 22%. Also, the proposed model showed superior performance in suppressing spectral regrowth than the other linearization methods.