Parametric estimation of spatial–temporal point processes using the Stoyan–Grabarnik statistic

Abstract

A novel estimator for the parameters governing spatial–temporal point processes is proposed. Unlike the maximum likelihood estimator, the proposed estimator is fast and easy to compute, and does not require the computation or approximation of a computationally expensive integral. This parametric estimator is based on the Stoyan–Grabarnik (sum of inverse intensity) statistic and is shown to be consistent, under quite general conditions. Simulations are presented demonstrating the performance of the estimator.

1 Introduction

A realization of a spatial–temporal point process is often characterized via its conditional intensity $\lambda$, the parameters of which are typically fit via maximum likelihood estimation (MLE) or Markov chain Monte Carlo (MCMC) methods. Specifically, for a realization $\{(t_i,x_i,y_i)\}_{i=1}^n=\{\tau _i\}_{i=1}^n$ of the point process N, one typically estimates the parameter vector $\theta$ by computing

$$\begin{aligned} \hat{\theta }_{\text {MLE}}=\arg \max _{\theta \in \Theta }\left( \sum _{i}\log \lambda (\tau _i;\theta )-\int _0^T \int \int \lambda (\tau ;\theta ) \textrm{d}t \textrm{d}x \textrm{d}y\right) . \end{aligned}$$

(1)

Such estimates are, under quite general conditions, consistent, asymptotically normal, asymptotically unbiased, and efficient, with standard errors readily constructed using the diagonal elements of the inverse of the Hessian (Krickeberg, 1982; Ogata, 1978). Unfortunately, for many point processes, the integral term on the right in Eq. (1) is often extremely difficult to compute (Harte, 2010; Ogata, 1998) especially when the conditional intensity $\lambda$ is highly volatile, as in this situation the user must approximate the integral of a highly variable and often high-dimensional stochastic process, which is not at all easy to do.

Approximation methods proposed for certain processes such as Hawkes processes suggest a computationally intensive numerical integration method (Ogata and Katsura, 1988; Schoenberg, 2013), but in general, the problem of computation or estimation of the integral term in the log-likelihood can be burdensome (Harte, 2010; Reinhart, 2018). Despite computational limitations, maximum likelihood remains the most common method for estimating the parameters of point process intensities (Reinhart, 2018).

We propose an alternative class of estimators based on the Stoyan–Grabarnik summed inverse intensity statistic introduced in Stoyan and Grabarnik (1991). The Stoyan–Grabarnik (“SG”) statistic

$$\begin{aligned} \bar{m}=\frac{1}{\lambda } \end{aligned}$$

(2)

was introduced as the exponential “mean mark” in the context of the Palm distribution of marked Gibbs processes (Stoyan and Grabarnik, 1991). As a primary property of Eq. (2), it is noted in Stoyan and Grabarnik (1991) that the expectation of the sum of the exponential marks corresponding to the points observed in some region is equal to the Lebesgue measure $\mu (\cdot )$ of that region. For the purposes of this paper, we define the SG statistic corresponding to a parameter vector $\theta$ and a realization $\{\tau _i\}_{i=1}^n$ of the point process N on spatial–temporal region $\mathcal {I}$ as

$$\begin{aligned} {\mathcal {S}}_{\mathcal {I}}(\theta )=\sum _{i: \tau _i \in \mathcal {I}} \frac{1}{\lambda (\tau _i;\theta )}. \end{aligned}$$

The SG statistic has been suggested as a goodness-of-fit model diagnostic for point processes (Baddeley et al., 2005) and, more recently, has been proposed for finding the optimum bandwidth for kernel smoothing to estimate the intensity of a spatial Poisson process (Cronie and Van Lieshout, 2018). Here, we consider a general spatial–temporal point process and suggest dividing the observation region into cells and estimating the parameters of the process by minimizing the sum of squared differences between the Stoyan–Grabarnik statistic and its expected value. We show that the resulting estimator is generally consistent and far easier to compute than the MLE.

We begin with notational definitions and basic characterizations of the properties of point processes in Sect. 2. Section 3 formally introduces the Stoyan–Grabarnik statistic and estimator, and in Sect. 4, we prove the consistency of two Stoyan–Grabarnik-type estimators. Section 5 provides some discussion and examples of the analytical properties and extensions of the estimator, and Sect. 6 contains a brief simulation study.

2 Preliminaries

A point process is a measurable mapping from a filtered probability space $(\Omega ,\mathcal {F},\mathcal {P})$ onto $\mathcal {N}$, the set of $\mathbb {Z}^+$-valued random measures (counting measures) on a complete separable metric space (CSMS) $\mathcal {X}$ (Daley and Jones, 2003), where $\mathbb {Z}^+$ denotes the set of positive integers. Following convention (e.g., Daley and Jones (2003)), we will restrict our attention to point processes that are boundedly finite, i.e., processes having only a finite number of points inside any bounded set. For a spatial–temporal point process, $\mathcal {X}$ is a portion of $\mathbb {R}^+ \times \mathbb {R}^2$ or $\mathbb {R}^+ \times \mathbb {R}^3$ where $\mathbb {R}^+$ and $\mathbb {R}^d$ represent the set of positive real numbers and d-dimensional Euclidean space, respectively. The point process is assumed to be adapted to the filtration $\{\mathcal {F}_t\}_{t\ge 0}$ containing all information on the process N at all locations and all times up to and including time t. In what follows we will assume the spatial domain of the point process $\mathcal {S}$ is a finite and bounded portion of the plane $\mathbb {R}^2$ and denote point i of the process as $\tau _i=(t_i,x_i,y_i)$, though the results here extend in obvious ways to the case where the spatial domain is a portion of $\mathbb {R}^3$.

A process is $\mathcal {F}$-predictable if it is adapted to the filtration generated by the left continuous processes $\mathcal {F}_{(-)}$. Intuitively, $\mathcal {F}_{(-)}$ represents the history of a process up to, but not including time t. A rigorous definition of $\mathcal {F}_{(-)}$ can be found in Daley and Vere-Jones (2007). Assuming it exists, the $\mathcal {F}$-conditional intensity $\lambda$ of N is an integrable, non-negative, $\mathcal {F}$-predictable process, such that

$$\begin{aligned} \lambda (\tau ) = \lim _{h, \delta \downarrow 0} \frac{\mathbb {E}[N\left( [t,t+h) \times \mathbb {B}_{(x,y),\delta }\right) | \mathcal {F}_{t-}]}{h \pi \delta ^2}. \end{aligned}$$

where $\mathbb {B}_{(x,y),\delta }$ is a ball centered at location (x, y) with radius $\delta$, and $\mathcal {F}_{t-}$ represents the history of the process N up to but not including time t.

A point process is simple if with probability one, all the points are distinct. Since the conditional intensity $\lambda$ uniquely determines the finite-dimensional distributions of any simple point process (Proposition 7.2.IV of Daley and Jones (2003)), one typically models a simple spatial–temporal point process by specifying a model for $\lambda$. A point process is stationary if the specified model has a structure which is invariant over shifts in space or time.

An important spatial–temporal point process result sometimes called the martingale formula states that, for any non-negative predictable process f,

$$\begin{aligned} \mathbb {E}\left[ \sum \limits _i f(\tau _i)\right] = \mathbb {E}\left[ \int _{\mathbb {R}^d} f(\tau ) \lambda (\tau ) \textrm{d}\mu \right] ; \end{aligned}$$

where the expectation is with respect to $\mathcal {P}$.

For a rigorous derivation of the martingale formula using Campbell measures, see Proposition 14.2.1 of Daley and Vere-Jones (2007). This result is the motivating impetus for exploring the Stoyan–Grabarnik estimator below. The martingale formula is a generalization of the Campbell formula which accommodates a non-negative deterministic function f (Cronie and Van Lieshout, 2018) and the Georgii–Nyugen–Zessin formula which accommodates an analogous equality using Papangelou intensities in a purely spatial context (Baddeley et al., 2005).

3 The Stoyan–Grabarnik estimator

Suppose the spatial–temporal domain ${{\mathcal {X}}}$ is partitioned into p cells $\{\mathcal {I}_j\}_{j=1}^p$. Define the estimator

$$\begin{aligned} \hat{\theta }=&\arg \min _{\theta \in \Theta }\sum _{j=1}^p\left( \sum _{i: (\tau _i)\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )} -\mathbb {E}\left[ \sum _{i:(\tau _i)\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )}\right] \right) ^2\nonumber \\ =&\arg \min _{\theta \in \Theta }\sum _{j=1}^p\left( {\mathcal {S}}_{\mathcal {I}_j}(\theta ) -\mathbb {E}\left[ {\mathcal {S}}_{\mathcal {I}_j}(\theta )\right] \right) ^2. \end{aligned}$$

(3)

Because $\lambda$ is non-negative and predictable, so is $1/\lambda$, and therefore, by the martingale formula, at the true value of the parameter vector $\theta ^*$,

$$\begin{aligned} \mathbb {E}\left[ \sum _{i:(\tau _i)\in {\mathcal {I}}_j}\frac{1}{\lambda (\tau _i;\theta ^*)}\right] =\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\tau ;\theta ^*)}{\lambda (\tau ;\theta ^*)}\textrm{d}\mu \right] =\mu (\mathcal {I}_j) \end{aligned}$$

where the expectation is with respect to $\mathcal {P}$. Thus, the computationally intensive integral term necessary to find the MLE is replaced with a term which is computationally trivial to compute, namely the volume of the cell ${{\mathcal {I}}}_j$. Therefore, in practice, it is convenient to plug in the volume of ${{\mathcal {I}}}_j$ for $\mathbb {E}\left[ {\mathcal {S}}_{\mathcal {I}_j}(\theta )\right]$ and thus define the SG estimator as

$$\begin{aligned} \tilde{\theta }=&\arg \min _{\theta \in \Theta }\sum _{j=1}^p\left( \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )} -\mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta ^*)}\right] \right) ^2\nonumber \\ =&\arg \min _{\theta \in \Theta }\sum _{j=1}^p\left( {\mathcal {S}}_{\mathcal {I}_j}(\theta ) -\mathbb {E}[{\mathcal {S}}_{\mathcal {I}_j}(\theta ^*)]\right) ^2\nonumber \\ =&\arg \min _{\theta \in \Theta }\sum _{j=1}^p\left( {\mathcal {S}}_{\mathcal {I}_j}(\theta ) -|\mathcal {I}_j|\right) ^2. \end{aligned}$$

(4)

The SG estimator is closely related to the scaled residual random field described in Baddeley et al. (2005). Specifically, for a fixed spatial–temporal kernel density $\mathcal {K}(\cdot )$ with fixed bandwidth b, let

$$\begin{aligned} Q(s)=\sum _{i=1}^n\frac{\mathcal {K}(s-\tau _i)}{\lambda (\tau _i;\theta )}-1, \end{aligned}$$

for s any location in space-time. Then if $\mathcal {X}$ is the observation window,

$$\begin{aligned} \mathbb {E}\left[ \int _\mathcal {X}Q(s)\textrm{d}\mu \right]&=\mathbb {E}\left[ \int _\mathcal {X} \sum _{i=1}^n\frac{\mathcal {K}(s-\tau _i)}{\lambda (\tau _i;\theta )}\textrm{d}\mu (s)\right] -|\mathcal {X}| \end{aligned}$$

(5)

$$\begin{aligned}&=\mathbb {E}\left[ \sum _{i=1}^n\frac{1}{\lambda (\tau _i;\theta )}\int _\mathcal {X}\mathcal {K}(s-\tau _i)\textrm{d}\mu (s) \right] -|\mathcal {X}|\nonumber \\&\approx \mathbb {E}\left[ \sum _{i=1}^n\frac{1}{\lambda (\tau _i;\theta )}\right] -|\mathcal {X}|\nonumber \\&=|\mathcal {X}|-|\mathcal {X}|=0, \end{aligned}$$

(6)

where the approximation in (6) stems from the fact that the integral over $\mathcal {X}$ of the kernel density will be close to unity provided the bandwidth is sufficiently small in relation to the size of the observation window $\mathcal {X}$. Ignoring such edge effects, the SG estimator minimizes the sum of squares of the integral of this residual field over cells in the partition, but one may alternatively find parameters $\theta$ minimizing some other criterion, such as for example the integral of $Q^2(s)$ over $\mathcal {X}$, or over cells of the partition. Given unbiased edge correction, (5) is exactly equal to zero.

4 Results

This section establishes the consistency of ${\hat{\theta }}$ and ${\tilde{\theta }}$, for a simple and stationary spatial–temporal point process N with conditional intensity $\lambda (\tau ; \theta )$, where $\tau =\{t,x,y\}$ is a location in space-time, and $\lambda$ depends on the parameter vector $\theta$ which is an element of some parameter space $\Theta$. Let $\theta ^*$ denote the true parameter vector, and suppose N is observed on the spatial–temporal domain $\mathcal {X}=[0,T) \times \mathcal {S}$, where $\mathcal {S}$ represents the spatial domain equipped with Borel measure $\mu$, and $\mathcal {X}$ is some CSMS. The following assumptions regarding N, $\Theta$ and $\mathcal {S}$ are useful in establishing consistency of the estimators.

4.1 Assumptions

Assumption A1

The spatial observation region $\mathcal {S}$ allows a partitioning scheme

$$\begin{aligned} \mathcal {S} = \bigcup _{j=1}^p \mathcal {S}_j \end{aligned}$$

such that $\mu (\mathcal {S}_j)>0$ $\forall j\in \{1,\ldots ,p\}$, for some fixed finite number p. We further assume that p is large enough that for any $\theta _1$ and $\theta _2$, if $\theta _1\ne \theta _2$, then

$$\begin{aligned} \mathbb {E}[{\mathcal {S}}_{\mathcal {I}_j}(\theta _1)]\ne \mathbb {E}[{\mathcal {S}}_{\mathcal {I}_j}(\theta _2)] \end{aligned}$$

(7)

or equivalently

$$\begin{aligned} \mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^*)}{\lambda (\theta _1)}\textrm{d}\mu \right] \ne \mathbb {E}\left[ \int _{\mathcal {I}_j} \frac{\lambda (\theta ^*)}{\lambda (\theta _2)}\textrm{d}\mu \right] \end{aligned}$$

(8)

$\forall j\in \{1,\ldots ,p\}$, where $\mathcal {I}_j = \mathcal {S}_j \times [0,T)$.

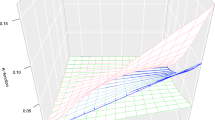
Note on Assumption A1: The assumption that p is sufficiently large that condition (7) or equivalently (8) holds is needed for the identifiability of ${\hat{\theta }}$ and ${\tilde{\theta }}$. The minimal value of p to satisfy this condition appears to depend on the underlying structure of the conditional intensity $\lambda$. In practice, a large value of p can be selected to ensure that condition (7) is met, although the computational expense of the estimator increases as p increases, and more importantly, the efficiency of the estimator appears to decrease as p grows (see Fig. 5). For finite datasets, p must not be chosen to be too small so as to ensure that $N(\mathcal {I}_j)>0$ $\forall j$. Note also that the cells $\mathcal {S}_j$ need not necessarily be connected, closed, or otherwise regular.

Assumption A2

$\Theta$ is a complete separable metric space and $\theta ^*\subset \Theta$. Further, $\Theta$ admits a finite partition of compact subsets $\{\Theta _T^1,\ldots ,\Theta _T^q\}$ such that $\lambda (\tau ;\theta )$ is a continuous function of $\theta$ within $\Theta _T^j$ $\forall j \in \{1,\ldots ,q\}$.

Note on Assumption A2: A2 ensures that ${\tilde{\theta }},{\hat{\theta \in \Theta }}$, i.e., that our estimator for $\theta ^*$ exists within the parameter space.

Assumption A3

Given an open neighborhood $\mathcal {U}(\theta ^*)$ around $\theta ^*$, $\lambda (\tau ;\theta ^*)-\lambda (\tau ;\theta )$ is uniformly bounded away from zero for $\theta \notin \mathcal {U}(\theta ^*)$.

Note on Assumption A3: A3 ensures that $\theta ^*$ is identifiable. In particular, this assumption excludes the case where $\lambda$ does not depend on $\theta$.

Assumption A4

$\lambda$ is finite and bounded away from zero across all cells $\mathcal {I}_j$, i.e., $\exists \zeta >0$ such that

$$\begin{aligned} \zeta<\int _{\mathcal {I}_j} \lambda (\theta )\textrm{d}\mu <\infty \end{aligned}$$

for j in $1,2,\ldots ,p$.

Note on Assumption A4: This assumption is needed for uniform integrability and precludes cases such as $\lambda (\tau ; \alpha )=\exp (-\alpha t)$ where only finitely many points occur as $T\rightarrow \infty$, and therefore, $\alpha$ is not consistently estimable via the SG estimator (or via MLE, for that matter). Similarly, because we restrict to stationary point processes, we similarly ensure that there are never finitely many points that occur as $T\rightarrow \infty$ which a parameter to be estimated is dependent on.

4.2 Results

Theorem 1

Under Assumptions A1–A4, the estimate ${\hat{\theta }}$ defined in (3) is a consistent estimator of $\theta ^*$.

Proof

For any $\epsilon > 0$ and any neighborhood $\mathcal {U}(\theta ^*)$ around $\theta ^*$, for all sufficiently large T,

$$\begin{aligned} \mathbb {P}(\hat{\theta }_T\notin \mathcal {U}(\theta ^*))<\epsilon . \end{aligned}$$

We begin with demonstrating that

$$\begin{aligned}&M(\theta ,T)=\sum _{j=1}^p\left( \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )}- \mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )}\right] \right) ^2\overset{\rightarrow }{\text {a.s.}}\quad E[M(\theta ,T)] \end{aligned}$$

for $\theta \in \Theta$ as $T\rightarrow \infty$. For a partition of $\mathcal {X}$ with index j, let

$$\begin{aligned} C_j(\theta ,T)=\sum _{i:\tau _i\in \mathcal {I}_j} \frac{1}{\lambda (\tau _i;\theta )} -\mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )}\right] . \end{aligned}$$

$C_j(\theta ,T)$ is a $\mathcal {F}$-martingale since $1 / \lambda$ is $\mathcal {F}-$predictable. By Jensen’s inequality, $C_j(\theta ,T)^2$ is a $\mathcal {F}-$sub-martingale as $g(x)=x^2$ is a convex function. Letting

$$\begin{aligned} M(\theta ,T)=\sum _{j=1}^p C_j(\theta ,T)^2, \end{aligned}$$

M is a $\mathcal {F}-$sub-martingale. It follows from martingale convergence, and the fact that $\lambda$ is absolutely continuous as a function of $\theta$ from Assumptions A2 and A4, that $M(\theta ,T)\rightarrow \mathbb {E}[M(\theta ,T)]$ uniformly.

We next demonstrate that

$$\begin{aligned} \theta ^*=\arg \min _{\theta \in \Theta }\mathbb {E}[M(\theta ,T)], \end{aligned}$$

(9)

concluding this result in lines (18) and (19). Note that for a given cell j in the partition,

$$\begin{aligned} \mathbb {E}[C_j(\theta ,T)]&=\mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )} -\mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )}\right] \right] = 0 \end{aligned}$$

for all $\theta \in \Theta$. One can find the second moment, as follows:

$$\begin{aligned} \mathbb {E}[C_j(\theta ,T)^2]&=\text {var}(C_j(\theta ,T))+\mathbb {E}[C_j(\theta ,T)]^2=\text {var}(C_j(\theta ,T)). \end{aligned}$$

If $\theta =\theta ^*$, then

$$\begin{aligned} \text {var}(C_j(\theta ,T))&=\text {var}\left( \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta ^*)} -\mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta ^*)}\right] \right) \nonumber \\&=\text {var}\left( \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta ^*)}-|\mathcal {I}_j|\right) \nonumber \\&=\text {var}\left( \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta ^*)}\right) \nonumber \\&=\mathbb {E}\left[ \left( \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta ^*)}\right) ^2\right] -\left[ \mathbb {E}\sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta ^*)}\right] ^2\nonumber \\&=\mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\left( \frac{1}{\lambda (\tau _i;\theta ^*)}\right) ^2+\sum _{i:\tau _i\in \mathcal {I}_j}\sum _{k:\tau _k\in \mathcal {I}_j,k\ne i}\frac{1}{\lambda (\tau _i;\theta ^*)\lambda (\tau _k;\theta ^*)}\right] \nonumber \\&\quad -\left[ \mathbb {E}\sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau ;\theta ^*)}\right] ^2 \end{aligned}$$

(10)

$$\begin{aligned}&=\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{1}{\lambda (\theta ^*)}\textrm{d}\mu \right] +\mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\sum _{k:\tau _k\in \mathcal {I}_j,k\ne i}\frac{1}{\lambda (\tau _i;\theta ^*)\lambda (\tau _k;\theta ^*)}\right] \nonumber \\&\quad -\left[ \mathbb {E}\int _{\mathcal {I}_j}\textrm{d}\mu \right] ^2, \end{aligned}$$

(11)

by applying the Martingale formula to both the first and last terms in (10). The middle cross-term can be evaluated as follows:

$$\begin{aligned}&\mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\sum _{k:\tau _k\in \mathcal {I}_j,k\ne i} \frac{1}{\lambda (\tau _i;\theta ^*)\lambda (\tau _k;\theta ^*)}\right] \nonumber \\&\quad =\mathbb {E}\left[ \int _{\mathcal {I}_j}\underbrace{\int _{\mathcal {I}_j:t<u}\frac{1}{\lambda (\theta ^*,t) \lambda (\theta ^*,u)}\textrm{d}N(t)}_{\hbox { Predictable w.r.t. filtration}\, \mathcal {F}_{t<u}} \textrm{d}N(u)\right] \end{aligned}$$

(12)

$$\begin{aligned}&=\mathbb {E}\left[ \int _{\mathcal {I}_j}\int _{\mathcal {I}_j:t<u}\frac{\lambda (\theta ^*,u)}{\lambda (\theta ^*,t)\lambda (\theta ^{*},u)}\textrm{d}N(t) \textrm{d}\mu (u)\right] \nonumber \\&\quad =\int _{\mathcal {I}_j}\mathbb {E}\left[ \int _{\mathcal {I}_j:t<u}\frac{1}{\lambda (\theta ^*,t)}\textrm{d}N(t)\right] \textrm{d}\mu (u)\nonumber \\&\quad =\int _{\mathcal {I}_j}\mathbb {E}\left[ \mu (\mathcal {S}_j)\cdot u\right] \textrm{d}\mu (u) \end{aligned}$$

(13)

$$\begin{aligned}&=\mu (\mathcal {S}_j)\mathbb {E}\left[ \int _{\mathcal {I}_j} u \textrm{d}\mu (u)\right] \nonumber \\&\quad ={\mu (\mathcal {S}_j)^2}\frac{T^2}{2}\nonumber \\&\quad =\frac{|\mathcal {I}_j|^2}{2}. \end{aligned}$$

(14)

Therefore, combining (11) and (14),

$$\begin{aligned} \mathbb {E}[C_j^2(\theta ,T)|\theta =\theta ^{*}]=&\mathbb {E}\left[ \int _{\mathcal {I}_j} \frac{1}{\lambda (\theta ^{*})}\textrm{d}\mu \right] -\frac{|\mathcal {I}_j|^2}{2}. \end{aligned}$$

Solving for the second moment of $C_j(\theta ,T)$ when $\theta \ne \theta ^*$, one similarly obtains

$$\begin{aligned} \mathbb {E}[C_j(\theta ,T)^2|\theta \ne \theta ^{*}]&=\text {var}\left( \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )} -\mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )}\right] \right) \nonumber \\&=\text {var}\left( \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )}\right) \nonumber \\&=\mathbb {E}\left[ \left( \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )}\right) ^2\right] -\left[ \mathbb {E}\sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )}\right] ^2\nonumber \\&=\mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\left( \frac{1}{\lambda (\tau _i;\theta )}\right) ^2\right] \nonumber \\&\quad +\mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\sum _{k:\tau _k\in \mathcal {I}_j,k\ne i}\frac{1}{\lambda (\tau _i;\theta )\lambda (\tau _k;\theta )}\right] \nonumber \\&\quad -\mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau ;\theta )}\right] ^2 \end{aligned}$$

(15)

$$\begin{aligned}&=\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^{*})}{\lambda (\theta )^2}\textrm{d}\mu \right] +\mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\sum _{k:\tau _k\in \mathcal {I}_j,k\ne i} \frac{1}{\lambda (\tau _i;\theta )\lambda (\tau _k;\theta )}\right] \nonumber \\&\quad -\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^{*})}{\lambda (\theta )}\textrm{d}\mu \right] ^2 \end{aligned}$$

(16)

$$\begin{aligned}&=\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^{*})}{\lambda (\theta )^2}\textrm{d}\mu \right] \nonumber \\&\quad +\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^*,u)}{\lambda (\theta ,u)} \int _{\mathcal {I}_j:t<u}\frac{\lambda (\theta ^*,t)}{\lambda (\theta ,t)}\textrm{d}\mu (t)\textrm{d}\mu (u)\right] \nonumber \\&\quad -\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^*)}{\lambda (\theta )}\textrm{d}\mu \right] ^2\equiv g(\theta ,\theta ^*, \mathcal {I}_j), \end{aligned}$$

(17)

again applying the Martingale formula to the first and third terms in (15). Equation (17) is obtained from (16) using the same logic as in lines 12-13.

Consider the division of $\mathcal {X}$ into two regions: the spatial–temporal locations where

$$\begin{aligned} 1<&\frac{\lambda (\theta ^{*},\tau )}{\lambda (\theta ,\tau )}&\quad{} & {} \text {Case C1} \end{aligned}$$

and

$$\begin{aligned} 0<\delta _1<&\frac{\lambda (\theta ^{*},\tau )}{\lambda (\theta ,\tau )}\le 1-\delta _2&\quad&\text {Case C2} \end{aligned}$$

for $\delta _1+\delta _2<1.$ That is, we can express $g(\theta ,\theta ^*, \mathcal {I}_j)$ as the sum of three integrals:

$$\begin{aligned} g(\theta ,\theta ^{*},\mathcal {I}_j)=&\sum _{h=1}^3 g(\theta ,\theta ^{*}, \mathcal {I}_j\cap \mathcal {A}_h)\\ =&\sum _{h=1}^2 g(\theta ,\theta ^{*}, \mathcal {I}_j\cap \mathcal {A}_h) \end{aligned}$$

where

$$\begin{aligned} \mathcal {A}_1=&\{\mathcal {X}\cap \{\lambda (\theta ,\tau )<\lambda (\theta ^{*},\tau )\}\}\\ \mathcal {A}_2=&\{\mathcal {X}\cap \{\lambda (\theta ,\tau )>\lambda (\theta ^{*},\tau )\}\}\\ \mathcal {A}_3=&\{\mathcal {X}\cap \{\lambda (\theta ,\tau )=\lambda (\theta ^{*},\tau )\}\}=\emptyset . \end{aligned}$$

We proceed by evaluating cases C1 and C2 separately for notational simplicity. In Case C1, we show that $\mathbb {E}[C_j(\theta ,T)^2|\theta =\theta ^{*}]<\mathbb {E}[C_j(\theta ,T)^2|\theta \ne \theta ^*]$ as follows:

$$\begin{aligned} \mathbb {E}[C_j(\theta ,T)^2|\theta \ne \theta ^{*}]&=\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^{*})}{\lambda (\theta )}\cdot \frac{1}{\lambda (\theta )} \textrm{d}\mu \right] \nonumber \\&\quad +\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^{*},u)}{\lambda (\theta ,u)} \int _{\mathcal {I}_j:t<u}\frac{\lambda (\theta ^{*},t)}{\lambda (\theta ,t)}\textrm{d}\mu (t)\textrm{d}\mu (u)\right] \nonumber \\&\quad -\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^{*})}{\lambda (\theta )}\textrm{d}\mu \right] ^2\nonumber \\&>\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{1}{\lambda (\theta )} \textrm{d}\mu \right] +\mathbb {E}\left[ \int _{\mathcal {I}_j}1\cdot \int _{\mathcal {I}_j:t<u}1\cdot \textrm{d}\mu (t)\textrm{d}\mu (u)\right] \nonumber \\&\quad -\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^{*})}{\lambda (\theta )}\textrm{d}\mu \right] ^2\nonumber \\&=\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{1}{\lambda (\theta )} \textrm{d}\mu \right] +\frac{|\mathcal {I}_j|^2}{2}-\mathbb {E}\left[ \int _{\mathcal {I}_j} \frac{\lambda (\theta ^{*})}{\lambda (\theta )}\textrm{d}\mu \right] ^2. \end{aligned}$$

(18)

Therefore, $\mathbb {E}[C_j(\theta ,T)^2|\theta =\theta ^*]<\mathbb {E}[C_j(\theta ,T)^2|\theta \ne \theta ^{*}]$, since given the assumptions of Case C1,

$$\begin{aligned}&\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{1}{\lambda (\theta )} \textrm{d}\mu \right] + \frac{|\mathcal {I}_j|^2}{2}-\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^{*})}{\lambda (\theta )}\textrm{d}\mu \right] ^2\\&>\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{1}{\lambda (\theta ^{*})} \textrm{d}\mu \right] +\frac{|\mathcal {I}_j|^2}{2}-\left( \int _{\mathcal {I}_j}\textrm{d}\mu \right) ^2. \end{aligned}$$

Equivalently,

$$\begin{aligned} \mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^{*})-\lambda (\theta )}{\lambda (\theta ^{*})\lambda (\theta )} \textrm{d}\mu \right] >&\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^{*})}{\lambda (\theta )}\textrm{d}\mu \right] ^2 -\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^{*})}{\lambda (\theta ^{*})}\textrm{d}\mu \right] ^2, \end{aligned}$$

and by the assumption of Case C1,

$$\begin{aligned} \mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^{*})}{\lambda (\theta )}\textrm{d}\mu \right] ^2 -\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^{*})}{\lambda (\theta ^{*})}\textrm{d}\mu \right] ^2>0. \end{aligned}$$

Assumption A3 guarantees that $\exists \delta _0>0$ such that $\lambda (\theta ^*)-\lambda (\theta )>\delta _0$ and therefore this condition is satisfied given Assumption A4.

In Case C2, as $T\rightarrow \infty$

$$\begin{aligned} \mathbb {E}[C_j(\theta ,T)^2|\theta \ne \theta ^{*}]&>\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\delta _1}{\lambda (\theta )} \textrm{d}\mu \right] + \frac{\left( \delta _1\cdot |\mathcal {I}_j|\right) ^2}{2} -\mathbb {E}\left[ \int _{\mathcal {I}_j}(1-\delta _2)\textrm{d}\mu \right] ^2 \end{aligned}$$

(19)

and therefore $\mathbb {E}[C_j(\theta ,T)^2|\theta =\theta ^{*}]<\mathbb {E}[C_j(\theta ,T)^2|\theta \ne \theta ^{*}]$, since

$$\begin{aligned} \mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\delta _1}{\lambda (\theta )}\textrm{d}\mu \right] + \frac{\left( \delta _1\cdot |\mathcal {I}_j|\right) ^2}{2}-2(1-\delta _2)^2\frac{|\mathcal {I}_j|^2}{2}&> \mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{1}{\lambda (\theta ^*)} \textrm{d}\mu \right] -\frac{|\mathcal {I}_j|^2}{2}\nonumber \\ |\mathcal {I}_j|^2\left( \frac{\delta _1^2+2\delta _2-1}{2}\right)&>\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta )-\delta _1\cdot \lambda (\theta ^{*})}{\lambda (\theta ^{*})\lambda (\theta )} \textrm{d}\mu \right] . \end{aligned}$$

(20)

Note that $\forall \delta _1\in (0,1)$, $\exists \delta _2\in \left( 2^{-1}\left( 1-\sqrt{2}\sqrt{\delta _1^2+1}\right) ,1\right)$, so the LHS of relation (20) is positive. The RHS is nonzero by the assumption of Case C2 and the fact that $\int \lambda (\theta )\textrm{d}\mu$ is nonzero as given by Assumption A4. As $M(\theta ,T)$ is the sum of $C_j(\theta ,T)^2$ for each partition $j\in \{1,\ldots ,p\}$, we can therefore conclude that for any ${{\check{\theta }}}\notin \mathcal {U}(\theta ^*)$, $\exists \delta >0$ such that

$$\begin{aligned} \inf _{\theta \in \Theta }\left\{ \mathbb {E}[M({\check{\theta }},T)-M(\theta ^*,T)]\right\} >\delta . \end{aligned}$$

Finally, by Assumption A2, and given that $M({\hat{\theta }},T)\rightarrow \mathbb {E}[M(\theta ^*,T)]$ uniformly, and $\inf _{\theta \in \Theta }\left\{ \mathbb {E}[M({\check{\theta }},T)-M(\theta ^*,T)]\right\} >\delta$ as proven above, we conclude that for sufficiently large T (or equivalently, sufficiently large space-time volume $|\mathcal {X}|$) and $\forall \alpha ,\epsilon >0$,

$$\begin{aligned} \mathbb {P}({\hat{\theta }}\notin \mathcal {U}(\theta ^*))&= \mathbb {P}\left( M({\hat{\theta }},T)\le \inf _{\theta \in \mathcal {U}(\theta ^*)}\{M(\theta ^*,T)\}\right) \\&<\mathbb {P}\left( M({\hat{\theta }},T)\le M(\theta ^*,T)-\alpha \right) \\&=\mathbb {P}\left( M(\theta ^*,T)-M({\hat{\theta }},T)\ge \alpha \right) \\&\le \mathbb {P}\left( M(\theta ^*,T)-\mathbb {E}[M(\theta ^*,T)]\ge \frac{\alpha }{3}\right) \\&\quad +\mathbb {P}\left( M({\hat{\theta }},T)-\mathbb {E}[M({\hat{\theta }},T)]\ge \frac{\alpha }{3}\right) \\&\quad +\mathbb {P}\left( \mathbb {E}[M(\theta ^*,T)-M({\hat{\theta }},T)]\ge \frac{\alpha }{3}\right) \\&=\frac{\epsilon }{2}+\frac{\epsilon }{2}+0. \end{aligned}$$

$\square$

Theorem 2

The estimator

$$\begin{aligned} {\tilde{\theta }}=\arg \min _{\theta \in \Theta }\sum _{j=1}^p\left( \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )} -|\mathcal {I}_j|\right) ^2 \end{aligned}$$

is a consistent estimator for $\theta ^*$. This estimator will be henceforth referred to as the SG estimator.

Proof

This results can be proven using the same method as in the proof of Theorem 1. A brief sketch of the proof is given below. When $\theta =\theta ^*$,

$$\begin{aligned} \mathbb {E}\left[ \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\lambda (\tau _i;\theta )}\right] =|\mathcal {I}_j|. \end{aligned}$$

Define

$$\begin{aligned} {\tilde{M}}(\theta ,T)=\sum _{j=1}^p\left( \sum _{i:\tau _i\in \mathcal {I}_j} \frac{1}{\lambda (\tau _i;\theta )}-|\mathcal {I}_j|\right) ^2, \end{aligned}$$

and note that although ${\tilde{M}}(\theta ,T)$ is not generally a sub-martingale, ${\tilde{M}}(\theta ^*,T)$ is. It follows as in the proof of Theorem 1 that $\tilde{M}(\theta ^*,T)\overset{\text {a.s.}}{\rightarrow }\mathbb {E}[\tilde{M}(\theta ^*,T)]$, and by absolute continuity of $\lambda$ with respect to $\theta$, this convergence is uniform. Similarly,

$$\begin{aligned} \arg \min _{\theta \in \Theta }\mathbb {E}[M(\theta ,T)]=\arg \min _{\theta \in \Theta }\mathbb {E}[\tilde{M}(\theta ,T)]=\theta ^* \end{aligned}$$

because

$$\begin{aligned} \mathbb {E}[\tilde{C}_j(\theta ,T)^2|\theta =\theta ^*]=\text {var}(\tilde{C}_j(\theta ,T)^2|\theta =\theta ^*) \end{aligned}$$

where ${\tilde{C}}_j$ is defined analogously to $C_j$ in Theorem 1, and

$$\begin{aligned} \mathbb {E}[{\tilde{C}}_j(\theta ,T)^2|\theta \ne \theta ^*] =&\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^*)}{\lambda (\theta )^2}\textrm{d}\mu \right] \nonumber \\&\quad +\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^*,u)}{\lambda (\theta ,u)}\int _{\mathcal {I}_j:t<u} \frac{\lambda (\theta ^*,t)}{\lambda (\theta ,t)}\textrm{d}\mu (t)\textrm{d}\mu (u)\right] \nonumber \\&\quad -2|\mathcal {I}_j|\mathbb {E}\left[ \int _{\mathcal {I}_j} \frac{\lambda (\theta ^*)}{\lambda (\theta )}\textrm{d}\mu \right] +|\mathcal {I}_j|^2\nonumber \\&\ge \mathbb {E}[ C_j(\theta ,T)^2|\theta \ne \theta ^*]. \end{aligned}$$

(21)

Relation (21) follows directly from the fact that

$$\begin{aligned} |\mathcal {I}_j|^2\ge 2|\mathcal {I}_j|\mathbb {E}\left[ \int _{\mathcal {I}_j} \frac{\lambda (\theta ^*)}{\lambda (\theta )}\textrm{d}\mu \right] -\mathbb {E}\left[ \int _{\mathcal {I}_j}\frac{\lambda (\theta ^*)}{\lambda (\theta )}\textrm{d}\mu \right] ^2. \end{aligned}$$

From this one concludes exactly as in Theorem 1 that for any $\epsilon >0$, for sufficiently large T, $\mathbb {P}({\tilde{\theta }}\notin \mathcal {U}(\theta ^*))<\epsilon$. $\square$

4.3 Discussion

In practice, a partitioning scheme and a set value of p must be decided upon before computing ${\tilde{\theta }}$ for realization N given a specified model $\lambda$. Analogous partitioning problems in the context of quadrature schemes needed for numerical approximation of likelihoods have been discussed, see Berman and Turner (1992); Baddeley and Turner (2005). A general solution or methodology for constructing a partitioning scheme which yields maximally accurate SG estimates is a difficult problem and future work.

Asymptotically, a very general class of partitioning schemes is sufficient to produce consistent SG-type estimates of the parameters of conditional intensity functions. As previously noted, cells are not assumed to be connected, closed, regular, or disjoint. The primary consideration for choosing a partitioning scheme in an asymptotic context is finding p large enough such that Assumption A1 is met and identifiability is ensured.

We therefore suggest that practitioners choose a simple partitioning scheme (e.g., a grid or Voronoï tessellation based on some subset of points in N) and some $p>2c$ where c is the cardinality of $\theta$. For relatively larger realizations of a process, $p>c^2$ may be an appropriate choice. This suggestion is only informed by trial and error via simulation of Hawkes, Cox and Poisson processes across various p for a given partitioning scheme. In the case of Poisson processes, it appears that for a Poisson intensity expressed as a polynomial, $p=c+1$ and any grid partitioning scheme is sufficient to produce consistent SG estimates, where c is the number of polynomial coefficients to be estimated. We note that in general, computational expense increases as p increases. Further, there appears to be a bias-variance trade-off wherein larger p results in less bias but more variance, see Fig. 5. Resultant bias and variance as a function of the number of parameters estimated, number of points realized, and selected p is the subject of future work.

5 Examples: Estimation of Poisson processes

5.1 Homogeneous Poisson process

Suppose N is a homogeneous Poisson process, i.e., $\lambda =\theta$ for some $\theta \in \mathbb {R}^+$. In this simple case, an analytical solution for the SG estimator $\theta$ can be derived.

$$\begin{aligned} \tilde{\theta }=&\arg \min _{\theta \in \mathbb {R}^+}\sum _{j=1}^p \left( \sum _{i:\tau _i\in \mathcal {I}_j}\frac{1}{\theta }-|\mathcal {I}_j|\right) ^2\\ =&\arg \min _{\theta \in \mathbb {R}^\infty }\sum _{j=1}^p\left( \frac{N(\mathcal {I}_j)}{\theta }-|\mathcal {I}_j|\right) ^2 \end{aligned}$$

and setting the derivative to zero:

$$\begin{aligned} 0\overset{!}{=}\ {}&\frac{\partial }{\partial \theta }\left( \sum _{j=1}^p\left( \frac{N(\mathcal {I}_j)}{\theta } -|\mathcal {I}_j|\right) ^2\right) = -2\sum _{j=1}^p\left( \frac{N(\mathcal {I}_j)}{\theta }-|\mathcal {I}_j|\right) \left( \frac{N(\mathcal {I}_j)}{\theta ^2}\right) \\ =&\sum _{j=1}^p\left( \frac{N(\mathcal {I}_j)^2 }{\theta ^3}-\frac{N(\mathcal {I}_j) \cdot |\mathcal {I}_j|}{\theta ^2}\right) . \end{aligned}$$

Thus, ${\tilde{\theta }}$ satisfies

$$\begin{aligned} \frac{\sum _{j=1}^p N(\mathcal {I}_j)^2 }{{\tilde{\theta }}^3}=&\frac{\sum _{j=1}^p N(\mathcal {I}_j) \cdot |\mathcal {I}_j| }{{\tilde{\theta }}^2} \nonumber \\ \frac{1}{{\tilde{\theta }}}\sum _{j=1}^p N(\mathcal {I}_j)^2 =&\sum _{j=1}^p N(\mathcal {I}_j) \cdot |\mathcal {I}_j| \nonumber \\ {\tilde{\theta }}=&\frac{\sum _{j=1}^p N(\mathcal {I}_j)^2}{\sum _{j=1}^p N(\mathcal {I}_j) \cdot |\mathcal {I}_j|}. \end{aligned}$$

(22)

Equation (22) has an interesting geometric interpretation. For the positive integer vector $\varvec{N}=N(\mathcal {I}_1),\ldots ,N(\mathcal {I}_p)$ and the positive real vector $\varvec{I}=|\mathcal {I}_1|,\ldots ,|\mathcal {I}_p|,$ we can express $\lambda ({\tilde{\theta }})$ as

$$\begin{aligned} \frac{\sum _{j=1}^p N(\mathcal {I}_j)^2}{\sum _{j=1}^p N(\mathcal {I}_j) \cdot |\mathcal {I}_j|}&=\frac{||\varvec{N}||_2^2}{\varvec{N}\varvec{\cdot }\varvec{I}}\nonumber \\&=\frac{||\varvec{N}||_2^2}{||\varvec{N}||_2 ||\varvec{I}||_2 \cos (\alpha )}\nonumber \\&=\frac{||\varvec{N}||_2}{||\varvec{I}||_2 \cos (\alpha )}. \end{aligned}$$

(23)

Note that $\cos (\alpha )$, the angle between $\varvec{N}$ and $\varvec{I}$, is constrained to $0\le \cos (\alpha )\le 1$ due to the signs of $\varvec{N}$ and $\varvec{I}$.

Equation (23) provides insight into the nature of the partitioning scheme chosen. As $\varvec{N}$ and $\varvec{I}$ become closer to orthogonal, $\cos (\alpha )$ approaches 0, forcing $\lambda ({\tilde{\theta }})$ to become arbitrarily large. Alternatively, if $\varvec{N}$ and $\varvec{I}$ are parallel, $\cos (\alpha )=1$ and in this case

$$\begin{aligned} \lambda ({\tilde{\theta }})=\frac{||\varvec{N}||_2}{||\varvec{I}||_2}=\sqrt{\frac{\sum _{j=1}^p N(\mathcal {I}_j)^2}{\sum _{j=1}^p |\mathcal {I}_j|^2}}. \end{aligned}$$

(24)

Equation (24) achieves the minimum value that $\lambda ({\tilde{\theta }})$ can attain over $\alpha \in [0,1]$ and is possible if there exists $\beta \in \mathbb {R}$ such that $N(\mathcal {I}_j)=\beta \cdot |\mathcal {I}_j|$ for all $j \in \{1,\ldots ,p\}$. It immediately follows that a partitioning scheme P minimizes Eq. (24) if it is chosen such that $N(\mathcal {I}_j)\propto |\mathcal {I}_j|$ for all j. This suggests that in the homogeneous Poisson case, ideally the partition will have roughly equal numbers of points per unit area in each cell.

Note a special case of Eq. (24). If $p=1$, then

$$\begin{aligned} \frac{\sum _{j=1}^p N(\mathcal {I}_j)^2}{\sum _{j=1}^p N(\mathcal {I}_j) \cdot |\mathcal {I}_j|} =\frac{N(\mathcal {X})}{|\mathcal {X}|}=\hat{\theta }_{\text {MLE}}. \end{aligned}$$

In this special case, the SG estimator is equivalent to the MLE and therefore inherits the desirable properties of the MLE such as consistency, asymptotic normality, asymptotic unbiasedness and efficiency (Ogata, 1978). For instance, if N has 100 points in an observed spatial–temporal region $\mathcal {X}$ such that $\mu (\mathcal {X})=20$, then $\hat{\theta }=100/20 = 5$, as expected.

5.1.1 Inhomogeneous Poisson with step function intensity

We now assume that N has conditional intensity

$$\begin{aligned} \lambda (\tau ; \theta )=\sum _{j=1}^p \gamma _j \mathbbm {1}\{\tau \in \mathcal {I}_j\} \end{aligned}$$

for $\gamma _j\in \mathbb {R}^+$ and $\theta = \{\gamma _1, \ldots , \gamma _p\}$. Thus, N is homogeneous Poisson within each cell, but with an intensity varying from cell to cell.

The properties of similar processes have been discussed in the context of Poisson Voronoi Tessellations (PVTs) (Błaszczyszyn and Schott, 2003, 2005). Total variation error bounds for approximation of an inhomogeneous Poisson process via a mixture of locally homogeneous Poisson processes are provided in Błaszczyszyn and Schott (2003), where the error is due to the “spill-over” or overlap of optimal cell partitioning. Further, the existence of an approximation for such a decomposition is described using a modulated PVT ((Błaszczyszyn and Schott, 2003), Proposition 4.1).

In this case, the SG estimator must satisfy

$$\begin{aligned} \tilde{\gamma }=&\arg \min _{\gamma \in \mathbb {R}^p_+}\sum _{j=1}^p\left( \sum _{i:\tau _i\in \mathcal {I}_j}\left( \sum _{j=1}^p \gamma _j \mathbbm {1}\{\tau_i \in \mathcal {I}_p\}\right) ^{-1}-|\mathcal {I}_j|\right) ^2. \end{aligned}$$

${\tilde{\gamma }}$ in this case is a vector of the p estimates $\tilde{\gamma _j}$. Each $\tilde{\gamma _j}$ is itself a SG estimator corresponding to a disjoint homogeneous Poisson process on the observation region $\mathcal {I}_j$. Following the same reasoning as in the homogeneous Poisson case, the resulting estimator reduces to when the partitioning scheme is such that $\mathcal {I}_j$ is the only cell, i.e., the observation region is equal to a single cell and $p=1$. We can therefore express the solution for the estimated coefficient within a single cell as

$$\begin{aligned} {\tilde{\gamma }}_j= \frac{N(\mathcal {I}_j)}{|\mathcal {I}_j|} \end{aligned}$$

and again is equivalent to the MLE and therefore in this case the SG estimator, like the MLE, is consistent, asymptotically normal, asymptotic unbiased and efficient (Ogata, 1978). As each estimator $\tilde{\gamma _j}$ is consistent, we can conclude that the sum ${\tilde{\gamma }}$ is also consistent by Slutsky’s Theorem.

6 Simulation study

As a proof of concept, we demonstrate that the SG estimates tend to be reasonably accurate and become increasingly accurate as T gets large for a variety of simple point processes. Figure 1 shows a simulated Cox process directed by intensity

$$\begin{aligned} \lambda (t,x,y) = e^{\alpha x} + \beta e^y + \gamma xy + \delta x^2 + \eta y^2 + W(x,y) \end{aligned}$$

on $[0,1] \times [0,1] \times [0,1]$, where $\theta = \{\alpha , \beta , \gamma , \delta , \eta \}$ and W(x, y) is a two-dimensional Brownian sheet. The estimated intensity using the SG estimator of $\theta$ closely resembles the true intensity even though T is only 1.

Figure 2 shows a simulated Hawkes process on the unit square and in time interval [0, 1000] with conditional intensity

$$\begin{aligned} \lambda (t,x,y) = \mu + \kappa \sum \limits _{i: t_i < t} g(t-t_i) h(x-x_i, y-y_i), \end{aligned}$$

where $g(t) = 1/ \alpha$ on $[0,\alpha ]$, $h(x,y) = 1/(\pi r^2)$ for $r \in [0, \beta ]$. Here, the parameters to be estimated are $\theta = \{\mu , \kappa , \alpha , \beta \}$ and the true values are $\{1,0.5,100,0.1\}$. As with the Cox process, the conditional intensity estimated using the SG estimator is a close approximation of the true conditional intensity for the Hawkes process.

Figure 3 shows a comparison of the root-mean-square error (RMSE) and R computation time for MLE and SG estimates of the process simulated in Fig. 2 observed on $[0,1]\times [0,1]\times [0,T]$ for various values of T. For this comparison, the integral approximation technique detailed in Schoenberg (2013) is used for MLE and $p=4^2$ is chosen for the SG estimator.

Figures 4 and 5 show the behavior of SG estimates as T increases for an inhomogenous Poisson process on $[0,T]\times [0,1]\times [0,1]$. We simulated six partitioning schemes ranging from $p=1^2$ to $p=32^2$, and various values of increasingly large T. We chose intensity

$$\begin{aligned} \lambda (t,x,y)= \alpha x^2 + \beta y^2 + \gamma x + \delta y + \epsilon , \end{aligned}$$

where the vector of parameters to be estimated is

$$\begin{aligned} \theta =\{\alpha , \beta , \gamma , \delta , \epsilon \} = \{1/3, 2/3, 1/2, 1/4, 1/5\}. \end{aligned}$$

The conditional intensity specified has t constant to avoid an explosive process or a process where too few points are observed as T gets larger. The estimates of $\theta$ are seen to converge to $\theta$ as $T \rightarrow \infty$.

7 Conclusion and future work

The SG estimator is very simple and efficient computationally and, like the MLE, is a consistent estimator for a wide class of point process models. We recommend its use as a complement to the MLE, in the many cases where the integral term in the log-likelihood is computationally burdensome to estimate accurately. This may be especially true for the rapidly emerging cases of big data where the observed number of points is very large and/or the spatial observation region is very large or complex. In situations where MLE is preferred but is sensitive to the choice of starting values in the optimization, a practical option may be to use the SG estimator as a starting value.

Future research should focus on how best to choose the nature and number of cells in the partition when implementing SG estimation. For example, in some cases, efficiency gains might be achieved via data-dependent partitioning schemes, such as Voronoi tessellations. Our preliminary investigations suggest, however, that any reasonable choice of partition will do, provided p is large enough to satisfy Assumption A1. Partitions for the case where the spatial dimension is 3 or higher are also important areas for future study.

As mentioned in Sect. 3, the SG estimator proposed here minimizes the sum of squares of the integral of the residual field over cells in a partition, but another area for future research would be to consider alternatively minimizing some other criterion, such as for example the integral of $Q^2(s)$. Such an alternative may avoid the need for choosing a rather arbitrary partition, but would replace this with the need to choose a bandwidth for the kernel smoother.

Another possibility for estimating point process parameters is via partial log-likelihood maximization (Diggle et al., 2010), and like the SG estimator, such estimators also do not require the computation or approximation of the integral term in the ordinary log-likelihood. As noted in the discussion in Diggle (2006), the partial log-likelihood estimate may be less efficient than the MLE but can be much easier and faster to compute. Future studies should investigate the advantages and disadvantages of such estimators relative to the SG estimator, both in terms of accuracy and computation speed.

Fig. 1

Clockwise from top left: a simulated Cox process with intensity dependent on a two-dimensional Brownian sheet. b The true intensity $\lambda (t,x,y) = e^{\alpha x} + \beta e^y + \gamma xy + \delta x^2 + \eta y^2 + W(x,y)$ on $[0,1] \times [0,1] \times [0,1]$, where W(x, y) is a two-dimensional Brownian sheet with zero drift and standard deviation $\sigma = 50$. The true parameter vector $\theta = \{\alpha , \beta , \gamma , \delta , \eta \} = \{-2,3,4,5,-6\}$. c The estimated intensity using the SG estimator of $\theta$

Fig. 2

Conditional intensity of a simulated Hawkes process with $\lambda (t,x,y) = \mu + \kappa \sum \limits _{i: t_i < t} g(t-t_i) h(x-x_i, y-y_i)$ where $g(t) = 1/ \alpha$ on $[0,\alpha ]$ and $h(x,y) = 1/(\pi r^2)$ for $r \in [0, \beta ]$ on $[0,1] \times [0,1] \times [0,T]$. $\theta = \{\mu , \kappa , \alpha , \beta \} = \{1,0.5,100,0.1\}$. Clockwise from top left: a true conditional intensity at time $T=100$. b Conditional intensity estimated via SG, at time $T=100$. c True conditional intensity at time $T=1000$. d Conditional intensity estimated via SG, at time $T=1000$

Fig. 3

Comparison of estimate accuracy and computational (time) expense for MLE and SG estimators. Conditional intensity of a simulated Hawkes process with $\lambda (t,x,y) = \mu + \kappa \sum \limits _{i: t_i < t} g(t-t_i) h(x-x_i, y-y_i)$ where $g(t) = 1/ \alpha$ on $[0,\alpha ]$ and $h(x,y) = 1/(\pi r^2)$ for $r \in [0, \beta ]$ observed on $[0,1]\times [0,1]\times [0,T]$. $\theta = \{\mu , \kappa , \alpha , \beta \} = \{1,0.5,100,0.1\}$. Left: root-mean-square error (RMSE) of parameter estimates for MLE and SG estimates across various T. Right: computational runtime in seconds for computing MLE and SG estimates

Fig. 4

Intensity $\lambda (t,x,y)= x^2/3 +(2y^2)/3+x/2+y/4+1/5$ estimated using $p=32^2$ partitions. Parameter estimates become increasingly accurate as $T\rightarrow \infty$. Horizontal dotted lines indicate true parameter values

Fig. 5

Estimates of a single parameter for a Poisson process with intensity $\lambda (t,x,y)= x^2/3 +(2y^2)/3+x/2+y/4+1/5.$ Note that if $p=1$ or $p=4$, estimates are not accurate as Assumption A1 is violated