Spline estimator for ultra-high dimensional partially linear varying coefficient models

Abstract

In this paper, we simultaneously study variable selection and estimation problems for sparse ultra-high dimensional partially linear varying coefficient models, where the number of variables in linear part can grow much faster than the sample size while many coefficients are zeros and the dimension of nonparametric part is fixed. We apply the B-spline basis to approximate each coefficient function. First, we demonstrate the convergence rates as well as asymptotic normality of the linear coefficients for the oracle estimator when the nonzero components are known in advance. Then, we propose a nonconvex penalized estimator and derive its oracle property under mild conditions. Furthermore, we address issues of numerical implementation and of data adaptive choice of the tuning parameters. Some Monte Carlo simulations and an application to a breast cancer data set are provided to corroborate our theoretical findings in finite samples.

1 Introduction

Due to recent rapid development in technology for data acquisition and storage, high dimensional data sets are especially commonplace in many scientific fields. Examples abound from signal processing (Lustig et al. 2008) to genomics (van’t Veer et al. 2002), collaborative filtering (Koren et al. 2009) and so on. A key feature is that the number of unknown parameters is comparable or even exceeds the sample size. Under the sparsity assumption of the high dimensional parameter vector, a widely used approach is to optimize a suitably penalized loss function (or negative log-likelihood). These regularized penalty functions include Lasso (Tibshirani 1996), SCAD (Fan and Li 2001), MCP (Zhang 2010) and among others. Such methods have been proved to possess high computational efficiency as well as desirable statistical properties in a variety of settings. Readers are referred to the review article in Fan and Lv (2010) and the monograph in Bühlmann and Van de Geer (2011) for a general survey.

To relax the linearity assumption in the classical linear model, many semiparametric models, which retain the flexibility of nonparametric models while avoiding the “curse of dimensionality,” have been proposed and studied (Bickel et al. 1998). A leading example of semiparametric models is the partially linear varying coefficient model:

$$\begin{aligned} Y_i=x_i^\top \beta _0+z_i^\top \alpha _0(u_i)+\varepsilon _i, \quad i=1,\ldots ,n, \end{aligned}$$

(1)

where $x_i=(x_{i1},\ldots ,x_{ip})^\top$ is a p-dimensional vector of covariates, $\beta _0$ is a p-dimensional vector of unknown regression parameters, $z_i=(z_{i1},\ldots ,z_{id})^\top$ is of dimension d and $\alpha _0(\cdot )=(\alpha _{01}(\cdot ),\ldots ,\alpha _{0d}(\cdot ))^\top$ is a d-dimensional vector of unknown regression functions, index variable $u_i\in [0,1]$ for simplicity, and error $\varepsilon _i$ is independent of $(x_i,z_i,u_i)$ with mean zero and finite variance $\sigma ^2<\infty$. Throughout the paper, we assume that $\{(Y_i, x_i, z_i, u_i), 1\le i\le n\}$ is an independent identically distributed random sample.

Model (1) includes many commonly used parametric, semiparametric and nonparametric models as its special cases. For instances, a constant vector of $\alpha _0(\cdot )$ corresponds to the classical linear model; $\beta _0=0$ leads to the varying coefficient model; when $d=1$, $z_i\equiv 1$, model (1) reduces to the partially linear model; and when $z_i$ is a vector of ones, $\beta _0=0$, this model becomes the well-known additive model. Model (1) has gained much attention in the recent literature. Fan and Huang (2005) and Ahmad et al. (2005) proposed the profile least squares method and nonparametric series estimation procedure, respectively. They established the asymptotic properties of the resulting estimators and showed that their estimators are efficient under some regularity conditions. You and Chen (2006a), Zhou and Liang (2009) and Feng and Xue (2014) extended the work in Fan and Huang (2005) to the case where all or some of the linear covariates $x_i$ are subject to error. Empirical likelihood method had been applied to construct the confidence regions of unknown parameter of interest for model (1), such as Huang and Zhang (2009) and You and Zhou (2006b). Li et al. (2011a) proposed a profile type smoothed score function to draw the statistical inference for the parameters of interest without using under-smoothing. Sun and Lin (2014) developed a robust estimation procedure via local rank technique. For variable selection, examples include but are not limited to Kai et al. (2011), Li and Liang (2008), Zhao and Xue (2009) and Zhao et al. (2014).

Obviously, the above studies merely focused on statistical procedures of the finite dimensional case of linear part. Important progress in the high dimensional semiparametric models has been recently made by Xie and Huang (2009) (still assumes $p<n$) for partially linear models, Huang et al. (2010) for additive models, Wei et al. (2011) for varying coefficient models, Wei (2012) for partially linear additive models. For model (1), Li et al. (2012) employed the empirical likelihood method to construct confidence regions of the unknown parameter. Li et al. (2011b) studied the properties of estimation based on B-spline technology. Although Li et al. (2017) studied variables screening problem for ultra-high dimensional setting, to the best of our knowledge, no work in the literature has been done on simultaneous variable selection and estimation. This might motivate us to consider the present work.

In this paper, we focus on sparse ultra-high dimensional partially linear varying coefficient models. We also allow $p\rightarrow \infty$ as $n\rightarrow \infty$ and denote it by $p_n$, but d is a fixed and finite integer. Our primary interest is to investigate the variable selection for linear part and estimation in ultra-high dimensional setting, i.e., $p_n\gg n$. In particular, $p_n$ can be chosen as an exponential order of the sample size n. Thus, this work fulfills an important gap in the existing literature on semiparametric models by developing variable selection methodology that allows ultra-high dimensional parameter vector.

We approximate the regression functions using B-spline basis, which is more computationally convenient and accurate than other bases. We first demonstrate the convergence rates as well as asymptotic normality of the linear coefficients for the oracle estimator, that is, the one obtained when the nonzero components are known in advance. Of course, it is infeasible in practice for unknown true active set. It is worth pointing out that our asymptotic framework allows the number of parameters grows with the sample size. This resonates with the perspective that a more complex statistical model can be fit when more data are collected. Next, we propose a nonconvex penalized estimator for simultaneous variable selection in the linear part and estimation when $p_n$ is of an exponential order of the sample size n and the model has a sparse structure. With a proper choice of the regularization parameters and the penalty function, such as the popular SCAD, we derive the oracle property of the proposed estimator under relaxed conditions. This indicates that the penalized estimators work as well as if the subset of true nonzero coefficients was already known. Lastly, we address issues of practical implementation of the proposed method.

The paper proceeds as follows. In Sect. 2, we first present the asymptotic properties of oracle estimators, then introduce a nonconvex penalized method for simultaneous variable selection and estimation, and provide its oracle property. Section 3 first discusses the numerical implementation. This is followed by the simulation experiments and a real data analysis which demonstrate the validity of the proposed procedure. Section 4 concludes the paper with a discussion of related issues. All technical proofs are provided in “Appendix.”

2 Methodology and asymptotic properties

For high dimensional statistical inference, it is often assumed that the true coefficient $\beta _0=(\beta _{01},\ldots ,\beta _{0p_n})^\top$ in model (1) is $q_n$-sparse vector. That is, let $A=\{1\le j\le p_n: \beta _{0j}\ne 0\}$ be the index set of nonzero coefficients, then its cardinality $|A|=q_n$. The set A is unknown and will be estimated. Our asymptotic framework also allows $q_n\rightarrow \infty$ as $n\rightarrow \infty$, which is of independent interests. Without loss of generality, we assume that the first $q_n$ components of $\beta _0$ are nonzero and the remaining $p_n-q_n$ components are zero. Hence, we can write $\beta _0=(\beta ^\top _{0I},0^\top _{p_n-q_n})^\top$, where $0_{p_n-q_n}$ denotes a $(p_n-q_n)$-vector of zeros. Let $X=(x_1,\ldots ,x_n)^\top$ be the $n \times p_n$ matrix of linear covariates and write $X_A$ to denote the submatrix consisting of the first $q_n$ columns of X corresponding to the active covariates. For technical simplicity, we assume that $x_i$ and $z_i$ are zero mean.

2.1 Oracle estimator

We use a linear combination of B-spline basis functions to approximate the unknown coefficient function $\alpha _{0l}(t)$ for $l=1,\ldots ,d$. First, one definition is provided to define the class of functions that can be estimated with B-splines. Define ${\mathcal {H}}_r$ as the collection of functions $h(\cdot )$ on [0, 1] whose $\lfloor r \rfloor$-th derivative $h^{(\lfloor r \rfloor )}(\cdot )$ satisfies the Hölder condition of order $r-\lfloor r \rfloor$, where $\lfloor r \rfloor$ denotes the largest integer strictly smaller than r. That is, for each $h(\cdot )\in {\mathcal {H}}_r$, there exists some positive constant c such that $|h^{(\lfloor r \rfloor )}(u_1)-h^{(\lfloor r \rfloor )}(u_2)|\le c|u_1-u_2|^{r-\lfloor r \rfloor }$, for any $0\le u_1, u_2\le 1$.

Let $\pi (u)=(b_1(u),\ldots , b_{k_n+\hbar }(u))^\top$ be a vector of normalized B-spline basis functions of order $\hbar$ with $k_n$ quasi-uniform internal knots on [0, 1]. Under Condition (C4) below, for $l=1,\ldots ,d$, $\alpha _{0l}(t)$ can be approximated using a linear combination of $\pi (u)$. Readers are referred to Boor (2001) for details of the B-spline construction, and the result that there exists $\gamma _{0l}\in {{\mathbb {R}}}^{K_n}$, where $K_n=k_n+\hbar$, such that $\sup _u|\pi (u)^\top \gamma _{0l}-\alpha _{0l}(u)|=O(K_n^{-r})$. For ease of notation and simplicity of proofs, we use the same number of basis functions for different coefficient functions in model (1). In practice, such restrictions are not necessary.

Now we consider oracle estimator with the oracle information that the index set A is known in advance, i.e., the last $(p_n-q_n)$ elements of $\beta _0$ are all zero. Let

$$\begin{aligned} ({\hat{\beta }}^o_I, {\hat{\gamma }}^o)=\mathop {{{\mathrm{argmin}}}}\limits _{\beta _I, \gamma } \sum _{i=1}^n(Y_i-x^\top _{A_i}\beta _I-\varPi _i^\top \gamma )^2, \end{aligned}$$

(2)

where $x^\top _{A_1}, \ldots , x^\top _{A_n}$ denote the row vectors of $X_A$, $\varPi _i=(z_{i1}\pi (u_i)^\top , \ldots , z_{id}\pi (u_i)^\top )^\top$ and $\gamma =(\gamma _1^\top ,\ldots ,\gamma _d^\top )^\top$. The oracle estimator for $\beta _0$ is ${\hat{\beta }}^o=({\hat{\beta }}^{o\top }_{I},0^\top _{p_n-q_n})^\top$. The oracle estimator for the coefficient function $\alpha _{0l}(u)$ is ${\hat{\alpha }}^o_l(u)=\pi (u)^\top {\hat{\gamma }}^o_l$ for $l=1,\ldots ,d$.

We next present the asymptotic properties of the oracle estimators as $q_n$ diverges. The following technical conditions are imposed for our theoretical analysis.

(C1):

The covariates $x_{ij}$ and $z_{il}$ are bounded random variables, and the eigenvalues of $\mathrm {E}\{(x^\top _{A_i}, z_i^\top )^\top (x^\top _{A_i}, z_i^\top )\}$ are bounded away from zero and infinity.

(C2):

The density function of $u_i$ is absolutely continuous and bounded away from zero and infinite on [0, 1].

(C3):

The noises $\varepsilon _1,\ldots , \varepsilon _n$ are iid with mean zero and finite variance $\sigma ^2$, and there exist some constants $c_1$ and $c_2$ such that $\mathrm {Pr}(|\varepsilon _1|>t)\le c_1 \exp \{-c_2t^2\}$ for any $t\ge 0$.

(C4):

For $l=1, \ldots , d$, $\alpha _{0l}(u)\in {\mathcal {H}}_r$ for some $r>1.5$. Furthermore, it is assumed that $K_n\asymp n^{1/(2r+1)}$. We use $a_n\asymp b_n$ to mean that $a_n$ and $b_n$ have the same order as $n\rightarrow \infty$.

(C5):

Assume that $q_n^3/n\rightarrow 0$ as $n\rightarrow \infty$.

The theorem below summarizes the convergence rates of the oracle estimators.

Theorem 1

Assume that regularity Conditions (C1)–(C5) hold, as $n\rightarrow \infty$, then

$$\begin{aligned} \Vert {\hat{\beta }}^o_I-\beta _{0I}\Vert= & {} O_P(\sqrt{q_n/n}),\\ \sum _{l=1}^{d}\Vert {\hat{\alpha }}^o_l(u)-\alpha _{0l}(u)\Vert ^2= & {} O_P((K_n+q_n)/n). \end{aligned}$$

An interesting observation is that since we allow $q_n$ to diverge with n, it affects the convergence rates for estimating both $\beta$ and $\alpha (\cdot )$. If $q_n$ is fixed, the convergence rates reduce to the classical $n^{-1/2}$ rate for estimating $\beta$ and $n^{-2r/(2r+1)}$ for estimating $\alpha (\cdot )$, the latter which is the optimal rate of convergence.

The parametric part can be shown to be asymptotically normal under slightly stronger conditions. Given $u\in [0,1]$ and $z\in {{\mathbb {R}}}^d$, let $\mathcal {G}$ denote the class of functions on ${{\mathbb {R}}}^{d}\times [0,1]$ as

$$\begin{aligned} \mathcal {G}=&\left\{ g(z,u): g(z,u)=\sum _{l=1}^dz_lh_l(u) \text { for some functions }h_l(u) \right. \\&\left. \text { such that } \mathrm {E}\left( \sum _{l=1}^d z_l^2h_l^2(u)\right) <\infty \right\} . \end{aligned}$$

For any random variable $\xi$ with $\mathrm {E}\xi ^2<\infty$, let $\mathrm {E}_\mathcal {G}(\xi )$ denote the projection of $\xi$ onto $\mathcal {G}$ in the sense that

$$\begin{aligned} \mathrm {E}[\{\xi -\mathrm {E}_\mathcal {G}(\xi )\} \{\xi -\mathrm {E}_\mathcal {G}(\xi )\}]=\inf _{g\in \mathcal {G}} \mathrm {E}[\{\xi -g(z,u)\}\{\xi -g(z,u)\}]. \end{aligned}$$

Definition of $\mathrm {E}_\mathcal {G}(\xi )$ trivially extends to the case when $\xi$ is a random vector by componentwise projection. Let $\varGamma (z,u)=(\varGamma _1(z,u),\ldots ,\varGamma _{q_n}(z,u))^\top =\mathrm {E}_\mathcal {G}(x_{A_1})$, then $\varGamma (z_i,u_i)$ is a projection of $\mathrm {E}[x_{A_1}|z_i,u_i]$ onto $\mathcal {G}$ and its j-th component $\varGamma _j(z_i,u_i)$ can be written as $\sum _{l=1}^dz_{il}h_{jl}(u_i)$. In addition to Conditions (C1)–(C5), we impose the following conditions.

(C6):

Assume that $h_{jl}(\cdot )\in {\mathcal {H}}_r$ for $j=1,\ldots ,q_n$ and $l=1,\ldots ,d$.

(C7):

Assume that $\varXi$ is a positive definite matrix, where $\varXi =\mathrm {E}[\{x_A-\varGamma (z,u)\}\{x_A-\varGamma (z,u)\}^{\top }]$.

As $q_n$ diverge, to investigate the asymptotic distribution of ${\hat{\beta }}^o_I$, we consider estimating an arbitrary linear combination of the components of $\beta _{0I}$.

Theorem 2

Let $Q_n$ be a deterministic $l\times q_n$ matrix with l an integer does not change with n, and $Q_nQ_n^\top \rightarrow \varPsi$, a positive definite matrix. Under regularity Conditions (C1)–(C7), we have

$$\begin{aligned} \sqrt{n} Q_n\varXi ^{1/2}({\hat{\beta }}^o_I-\beta _{0I}){\mathop {\longrightarrow }\limits ^{D}}N(0,\sigma ^2\varPsi ), \end{aligned}$$

where ${\mathop {\longrightarrow }\limits ^{D}}$ represents the convergence in distribution.

2.2 Variable selection

In real data analysis, we do not know which of the $p_n$ covariates in $x_i$ are important. To encourage sparse estimation, we minimize the following penalized least squares objective function for estimating $(\beta _0, \gamma _0)$,

$$\begin{aligned} l_n(\beta ,\gamma )=\sum _{i=1}^n\left( Y_i-x_i^\top \beta -\varPi _i^\top \gamma \right) ^2+n\sum _{j=1}^{p_n}p_\lambda (|\beta _j|), \end{aligned}$$

(3)

where $p_\lambda (\cdot )$ is a penalty function with tuning parameter $\lambda >0$ which controls the complexity of the selected model and goes to zero as $n\rightarrow \infty$. Although it is not necessarily that the tuning parameter $\lambda$ is the same for all $\beta _j$ in practice, we make the above choices for simplicity. Here, we focus on the popular nonconvex SCAD penalty given by

$$\begin{aligned} p'_\lambda (|t|)=\lambda \left\{ I(|t|\le \lambda ) +\frac{(a\lambda -|t|)_{+}}{(a-1)\lambda }I(|t|>\lambda ) \right\} ,\quad \mathrm {for~some}~a>2, \end{aligned}$$

where $x_+=\max (x,0)$, $I(\cdot )$ is the indicator function. Note that the SCAD penalty is continuously differentiable on $(-\infty ,0)\cup (0,\infty )$ but singular at 0 and its derivative vanishes outside $[-a\lambda ,a\lambda ]$. These features of SCAD penalty result in a solution with three desirable properties: unbiasedness, sparsity and continuity. Other choices of penalty, such as MCP, are expected to produce similar results in both theory and practice. In comparison, Lasso is known to over-penalize large coefficients, tends to be biased and requires strong conditions on the design matrix to achieve selection consistency. This is usually not a concern for prediction, but can be undesirable if the goal is to identify the underlying model.

The theorem below shows that the oracle estimator is a local minimizer of (3) using SCAD penalty with probability tending to one, provided the following additional Condition (C8), which is needed to identify the underlying model. (C8) (i) is how quickly a nonzero signal can decay which is not a concern when the dimension is fixed, and (C8) (ii) is concerning the divergence rate of $p_n$.

(C8):

(i) $\min _{1\le j\le q_n}|\beta _{0j}|\gg \lambda \gg \sqrt{(K_n+q_n)/n}$; (ii) $\max \{\sqrt{n}\log (p_n\vee n), nK_n^{-r}\}\ll n\lambda$.

Theorem 3

Consider the SCAD penalty with tuning parameter $\lambda$, let $\mathcal {S}_n(\lambda )$ be the set of local minimizers of (3), under regularity Conditions (C1)–(C8), we have

$$\begin{aligned} \mathrm {Pr}(({\hat{\beta }}^o, {\hat{\gamma }}^o)\in \mathcal {S}_n(\lambda ))\rightarrow 1,\quad \mathrm {as} ~ n\rightarrow \infty . \end{aligned}$$

As seen in Condition (C8), if $q_n$ is fixed, then $\lambda$ can be arbitrarily slow and the fastest rate of $p_n$ can be chosen as $o(\exp (n/2))$. Hence, we allow for the ultra-high dimensional setting. Theorem 3 is particularly attractive from a theoretical standpoint, because it follows that there exists a local minimizer of (3) inherit all the properties of the oracle estimators covered by previous subsection. In particular, the proposed variable selection procedure enjoys the oracle property, i.e., the following corollary holds.

Corollary 1

Suppose that regularity Conditions (C1)–(C8) hold, there exists a local minimizer $({\hat{\beta }},{\hat{\gamma }})$ of (3), with probability tending to 1 as $n\rightarrow \infty$, satisfies that: (i) ${\hat{\beta }}_j=0$ for $q_n+1\le j \le p_n$; (ii) $\Vert {\hat{\beta }}_I-\beta _{0I}\Vert =O_P(\sqrt{q_n/n})$ and $\sum _{l=1}^d\Vert {\hat{\alpha }}_l(u)-\alpha _{0l}(u)\Vert ^2=O_P((K_n+q_n)/n)$, where ${\hat{\alpha }}_l(u)=\pi (u)^\top {\hat{\gamma }}_l$; (iii) the asymptotic normality of the estimators for ${\hat{\beta }}_I$ holds as in Theorem 2.

3 Numerical studies

In this section, we conduct simulation experiments to evaluate the finite sample performance of the proposed procedures and illustrate the proposed methodology on a real data set. Firstly, we present a computational algorithm for obtaining the minimizers of (3) and selection methods for the tuning parameters.

3.1 Implementation

Algorithm For given the tuning parameters, finding the solution that minimizes (3) poses a number of interesting challenges because the SCAD penalty function is nondifferentiable at the origin and nonconvex. Following the idea in Fan and Li (2001), we apply iterative algorithm based on the local quadratic approximation (LQA) of the penalty function. More specifically, given the current estimator $\theta ^{(0)}=(\beta ^{(0)\top }, \gamma ^{(0)\top }/\sqrt{K_n})^\top$, if $|\beta _j^{(0)}|>0$, we have

$$\begin{aligned} p_{\lambda }(|\beta _j|)\approx p_{\lambda }(|\beta ^{(0)}_j|)+\frac{1}{2}\frac{p'_{\lambda }\left( |\beta ^{(0)}_j|\right) }{|\beta ^{(0)}_j|}\left\{ |\beta _j|^2-|\beta ^{(0)}_j|^2\right\} . \end{aligned}$$

Consequently, removing irrelevant terms, the penalized least squares objective function (3) can be locally approximated by

$$\begin{aligned} {\tilde{l}}_n(\beta ,\gamma )=(Y-W\theta )^\top (Y-W\theta )+\frac{n}{2}\theta ^\top \varOmega (\theta ^{(0)})\theta , \end{aligned}$$

(4)

where $\theta =(\beta ^{\top }, \gamma ^{\top }/\sqrt{K_n})^\top$, $Y=(Y_1,\ldots ,Y_n)^\top$, $W=(W_1,\ldots ,W_n)^\top$ with $W_i=(x_i^\top ,\sqrt{K_n}\varPi _i^\top )^\top$, and $\varOmega (\theta ^{(0)})=\mathrm {diag}\{ p'_{\lambda }(|\beta ^{(0)}_1|)/|\beta ^{(0)}_1|,\ldots ,p'_{\lambda }(|\beta ^{(0)}_{p_n}|)/|\beta ^{(0)}_{p_n}|, 0_{dK_n}^\top \}$. The quadratic minimization problem (4) yields the solution

$$\begin{aligned} \theta ^{(1)}=\{W^\top W+n\varOmega (\theta ^{(0)})\}^{-1}W^\top Y. \end{aligned}$$

During the iterations, set ${\hat{\beta }}_j=0$ if $|{\hat{\beta }}^{(1)}_j|<\epsilon$ ($\epsilon =10^{-4}$ in our implementation). To choose an appropriate initial value, we use a Lasso estimator with the penalty term $\lambda \sum _j|\beta _j|$.

Tuning parameters selection To implement the above estimation procedures and achieve good numerical performance, we also need to find a data-driven method to choose some extra parameters including the spline order $\hbar$, the number of basis $K_n$ as well as the regularization parameter $\lambda$. Due to the computational complexity, it is often impractical to automatically select all three components based on the observable data. As a commonly adopted strategy, we fix $\hbar =4$ (cubic splines). Note that $K_n$ should not be too large since the larger the $K_n$ is, the larger the estimation variance is, and the more difficult it is to distinguish important variables from unimportant ones. On the other hand, $K_n$ should not be too small to create probing biases. Here, we choose $K_n=\lfloor n^{1/5}\rfloor +\hbar$ for computation convenience. In our simulations, we also conduct a sensitivity analysis by setting $K_n$ to be different values. We observe similar numerical results if $K_n$ varies in a reasonable range.

Fixed $\hbar$ and $K_n$, finally we employ a data-driven method to choose $\lambda$, which is critical for the performance of the estimators. Cross validation is a common approach, but is known to often result in overfitting. In our high dimensional context, we employ the extended Bayesian information criterion (EBIC) in Chen and Chen (2008) that was developed for parametric models. More specifically, we can choose $\lambda$ by minimizing the following EBIC value

$$\begin{aligned} \mathrm {EBIC}(\lambda )=\log (Y-W{\hat{\theta }}_\lambda )^\top (Y-W{\hat{\theta }}_\lambda )+{\hat{q}}_{n\lambda }\frac{\log n}{n}+2\nu _n{\hat{q}}_{n\lambda }\frac{\log p_n}{n}, \end{aligned}$$

(5)

where ${\hat{\theta }}_\lambda$ is the minimizer of (3) for given $\lambda$, ${\hat{q}}_{n\lambda }$ is the number of nonzero values in ${\hat{\beta }}_\lambda$ and $\nu _n$ is a tuning parameter which is taken as $1-\log (n)/(3\log p)$ suggested by Chen and Chen (2008). Note that when $\nu _n=0$, the EBIC is the BIC. From our numerical studies, we find that the above data-driven procedure works well.

3.2 Simulation studies

Throughout our simulation studies, the dimensionality of parametric component is taken as $p_n=1000$, 2000 and the nonparametric component as $d=2$. We take $n=100$ and 200 to check the effect of sample size. As for the regression coefficient, we set $\beta _0=(1,1,1,1,1,0,\ldots ,0)^\top$, $\alpha _{01}(u)=2\sin (2\pi u)$ and $\alpha _{02}(u)=6u(1-u)$. Thus, there are $q_n=5$ nonzero constant coefficients. In addition, the index variable $u_i$’s are sampled uniformly on [0, 1]. The covariates $(x_i,z_i)$’s are independently drawn from multivariate normal distribution $N_{p_n+d}(0,\varSigma )$, where $\varSigma$ is chosen from the following two designs: (i) Independent (Inde): $\varSigma =I$; (ii) Autoregressive (AR(1)): $\varSigma _{jj'}=0.5^{|j-j'|}$ for $1\le j,j'\le p_n+d$. Then, the response $Y_i$’s are generated from the following sparse models:

$$\begin{aligned} Y_i=\sum _{j=1}^5x_{ij}\beta _{0j}+z_{i1}\alpha _{01}(u_i)+z_{i2}\alpha _{02}(u_i)+\varepsilon _i, \quad i=1,\ldots , n, \end{aligned}$$

where noise term $\varepsilon _i\sim N(0,\sigma ^2)$ with $\sigma =1, 1.5, 2$ for three signal-to-noise ratio settings. The number of replications is 500 for each configuration.

Table 1 Simulation results over 500 repetitions

We compare the SCAD penalized estimator with Lasso penalized estimator and oracle estimator. The oracle model, as the gold standard, is only available in simulation studies where the underlying model is known. The Lasso estimators are computed by the R package glmnet with $\lambda$ being selected by tenfold cross validation. The tuning parameter a in SCAD penalty function is 3.7 as recommended in Fan and Li (2001). As measures of their performance for model selection, we computed percentage of occasions (out of 500) on which the true model is correctly identified (CI). We also report the average numbers of false positive results (FP, the number of irrelevant variables incorrectly identified as relevant) and the average numbers of false negative results (FN, the number of relevant variables incorrectly identified as irrelevant). As measures of estimation accuracy, we report the average generalized mean square error (GMSE) for the parametric part, defined as

$$\begin{aligned} \mathrm {GMSE}=({\hat{\beta }}-\beta _0)^\top (\mathrm {E}x_ix_i^\top )({\hat{\beta }}-\beta _0), \end{aligned}$$

and the average square root of average errors (RASE) for nonparametric part, given by

$$\begin{aligned} \mathrm {RASE}=\left\{ n_{\mathrm {grid}}^{-1}\sum _{k=1}^{n_{\mathrm {grid}}}\Vert {\hat{\alpha }}(u_k)-\alpha (u_k)\Vert ^2\right\} ^{1/2}, \end{aligned}$$

over a fine grid $\{u_k\}_{k=1}^{n_{\mathrm {grid}}}$ consisting of $n_{\mathrm {grid}}=200$ points equally spaced on [0, 1].

Table 1 summarizes the simulation results. From this table, one may have the following observations. (i) At all settings, the SCAD penalized estimator tends to pick a smaller and more accurate model in terms of CI, FN and FP, which is comparable with oracle. This indicates that the proposed method is promising. In contrast, though Lasso penalized estimator is not significantly inferior in term of FN, but it tends to include more unnecessary zero coefficients with a lager FP. Therefore, the GMSE and RASE obtained from Lasso method are often the largest. (ii) For fixed n, the performance of the proposed method does not deteriorate rapidly when $p_n$ increases, while for fixed $p_n$ the performance improves substantially as the sample size increases. In turn, these results show that the sample size n is more important than the dimension of the covariates for high dimensional statistical inference. (iii) The signal-to-noise ratio has certain effect for the variable selection. As expected, the proposed method becomes worse as $\sigma$ increases. For example, the CI is only 7.4% for independent case if $(n,p_n,\sigma )=(100,2000,2)$, the reason may be that the signal-to-noise ratio is not large and the sample size is also not enough large to obtain a satisfactory CI. Note that CI will rise to 86.8, if increases sample size to $n=200$. (iv) It is easy to see that the proposed method is not sensitive to the different correlations between variables as long as the correlations are not particularly strong.

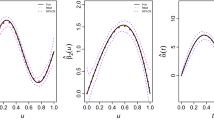
Figure 1 presents $\alpha _{01}(u)$ and its three estimators based on one random sample for AR(1) with $n=100$. It is clear that all estimators are biased, but they follow the shape of the true coefficient function $\alpha _{01}(u)$ quite well. Boxplots of three nonzero coefficients $\beta _1, \beta _3,\beta _5$ over 500 simulations for AR(1) are displayed in Fig. 2. The most striking result is that the SCAD method performs substantially better than Lasso and is comparable with oracle. Of course, the more difficult the configuration, e.g., the larger $p_n$ and/or $\sigma$, the worse the estimator is in terms of bias and variance. Both figures help us get an overall picture on the quality of the proposed estimators. To save space, the simulation results of other settings are not shown here. In sum, these simulation results corroborate our theoretical findings.

Fig. 1

Plots of $\alpha _{01}(u)$ and its three estimators in one run for AR(1) with $n=100$ and different $p_n$ and $\sigma$

Fig. 2

Boxplots shows for three nonzero coefficients estimation (top row: $\beta _1$, middle row: $\beta _3$, bottom row: $\beta _5$) for AR(1). Cases $(n, p_n, \sigma )=(100, 1000,1)$, (100, 2000, 1), (100, 1000, 2) and (200, 1000, 2) are demonstrated, respectively, from the left panel to the right panel

3.3 Real data analysis

As an illustration, we apply our method to a breast cancer data collected by van’t Veer et al. (2002). This data set includes $n=97$ lymph node-negative breast cancer patients 55 years old or younger. For each patient, expression levels for 24481 gene probes and 7 clinical risk factors (age, tumor size, histological grade, angioinvasion, lymphocytic infiltration, estrogen receptor and progesterone receptor status) are measured. Recently, Yu et al. (2012) proposed a receiver operating characteristic-based approach to rank the genes via adjusting for the clinical risk factors. They removed genes with severe missingness, leading to an effective number of $p=24188$ genes. The gene expression data are normalized such that they all have sample mean 0 and standard deviation 1.

Knight et al. (1977) found that the absence of estrogen receptor in primary breast tumors is associated with the early recurrence. So it is important to predict the metastatic behavior of breast cancer tumor jointly using clinical risk factors and gene expression profiles. Here, we are interested in selecting some useful genes whose expressions can be used to predict the values of estrogen receptor (ER). To set up the semiparametric partially linear varying coefficient regression model, we use the clinical risk factor age as the index variable to reveal potential nonlinear effect. The gene expression values (GE) are included as linear covariates, while tumor size (TS) as nonlinear covariates. The resulting model can now be expressed as

$$\begin{aligned} \mathrm {ER}_i=\alpha _0(\mathrm {age}_i) +\alpha _1(\mathrm {age}_i)\mathrm {TS}_i+\sum _{j=1}^{24188} \beta _j\mathrm {GE}_{ij}+\varepsilon _i, \quad i=1,\ldots ,97. \end{aligned}$$

It is expected that not all of the 24188 genes can have impact on the estrogen receptor. First, we apply the penalization method (3) with the SCAD and Lasso penalty functions to this data set. As in the simulations, the cubic B-spline with $\lfloor 97^{1/5}\rfloor =2$ internal knots is adopted to fit the coefficient functions. The regularization parameter is selected by EBIC for SCAD estimator and by tenfold cross validation for Lasso. As expected, the Lasso method selects a larger model than the SCAD penalty does. Lasso identified 9 genes: 1690, 6912, 7049,10177, 10478, 15141, 15835, 19230 and 20564, while SCAD identified 5 genes: 27, 3679, 5731, 6912 and 15835. The second column in the upper panel of Table 2 reports the number of nonzero elements (“O-NZ”).

Next, we compare different models on 100 random partitions of the data set. For each partition, we randomly select $n_1=90$ observations as a training data set to fit the model and to select the significant genes. The resulting models are used to predict the value of the $n-n_1=7$ observations in the test set. We observe that different models are often selected for different random partitions. The third column in the upper panel of Table 2 reports the average number of linear covariates included in each model (denoted “R-NZ”), while the 5 column on the left in the upper panel reports five order statistics of prediction error (PE) evaluated on the test data, defined as $7^{-1}\sum _{i=1}^7(Y_i-{\hat{Y}}_i)$. The lower panel of Table 2 summarizes the top 7 genes selected by our method and the frequency these genes are selected in the 100 random partitions. Note that gene 15835 is detected as important variable at each time among all random partitions. Obviously, the SCAD method results in a final model with smaller size and better prediction performances than Lasso method. In addition, we observed that gene 15835 was also identified in Cheng et al. (2016).

Table 2 Variable selection and prediction results of real data analysis

Fig. 3

Estimation, residual analysis and EBIC curve for real data example

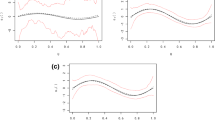
We refit the data with the five selected genes by SCAD penalty. The regression coefficients of genes 27, 3679, 5731, 6912 and 15835 are 0.242, 0.245, $-0.216$, $-0.219$, 0.858, respectively. The estimated coefficient functions are presented in the left panel of Fig. 3. The EBIC curve for variable selection and the residual analysis are presented in the right panel. It is seen that the proposed partially linear varying coefficient model fits the data reasonably well. Hence, from a practical point of view, we have demonstrated that our proposed method can be an efficient method for analyzing partially linear varying coefficient models.

4 Conclusion

This paper has investigated spline estimator for partially linear varying coefficient models with ultra-high dimensional linear covariates. Nonconvex penalty, e.g., SCAD, was used to perform simultaneous estimation and variable selection. The oracle theory was derived under mild conditions. We used EBIC as a criterion for automatically choosing the tuning parameters. It worked well in our numerical studies, although we are currently not able to provide any consistency proof for it, as has been done for parametric or nonparametric models in the case of fixed dimension. In addition, we developed the computation algorithm based on local quadratic approximation. Simulation studies and a real data example were provided to back up the theoretical results.

Some extensions provide interesting avenues for future study. First, a challenging problem, particularly for high dimensional data, is how to identify which covariates are parametric or nonparametric terms. Usually, we do not have such prior knowledge in real data analysis. Second, it would be interesting to take into account complex data in high dimensional semiparametric models, such as missing data, measurement error data, censored data. Another problem of practical interest is to construct prediction intervals based on the observed data. Given $(x^*,z^*,u^*)$, we can estimate $Y^*$ by $x^{*\top }{\hat{\beta }}+z^{*\top }{\hat{\alpha }}(u^*)$, where ${\hat{\beta }}$ and ${\hat{\alpha }}(\cdot )$ are obtained from penalized regression. We conjecture that the consistency of estimating the conditional function can be derived under somewhat weaker conditions in the current paper. Its uncertainty assessment will also be further investigated in the future. The last one is to identify conditions under which the proposed estimator achieves consistent variable selection and estimation even when $p_n\gg n$ and $d\gg n$.

Appendix: Some lemmas and proofs of main results

In this section, we outline the key idea of the proofs. Note that $c, c_1, c_2,\ldots$ denote generic positive constants. Their values may vary from expression to expression. In addition, $\varLambda _{\min }$ and $\varLambda _{\max }$ denote the smallest and largest eigenvalue of a matrix, respectively.

Lemma 1

Let $W^o_i=(x_{A_i}^\top ,\sqrt{K_n}\varPi _i^\top )^\top$, where the definitions for $x_{A_i}$ and $\varPi _i$ are the same as those in (2). Under regularity Conditions (C1) and (C2), we have

$$\begin{aligned} 0<c_1\le \varLambda _{\min }\left( \frac{1}{n}\sum _{i=1}^nW^o_iW_i^{o\top }\right) \le \varLambda _{\max }\left( \frac{1}{n}\sum _{i=1}^nW^o_iW_i^{o\top }\right) \le c_2<\infty . \end{aligned}$$

The proof of this lemma can be easily obtained by Lemma 6.2 in Zhou et al. (1998) and Lemma 3 in Stone (1985), so we omit the details.

Lemma 2

Let $Y_1,\ldots , Y_n$ be independent random variables with zero mean such that $\mathrm {E}|Y_i|^m\le m!M^{m-2}v_i/2$, for every $m\ge 2$ (and all i), some constants M and $v_i=EY_i^2$. Let $v=v_1+\cdots +v_n$, for $x>0$,

$$\begin{aligned} \mathrm {Pr}\left( \left| \sum _{i=1}^nY_i\right| >x\right) \le 2\exp \left\{ -\frac{x^2}{2(v+Mx)}\right\} . \end{aligned}$$

Lemma 3

If there exists $(\beta ,\gamma ) \in {\mathbb {R}}^{p_n+dK_n}$ such that (i) $\sum _i (Y_i-x_i^\top \beta -\varPi _i^\top \gamma )\varPi _{il}=0$ for $l=1,\ldots ,d$; (ii) $\sum _i (Y_i-x_i^\top \beta -\varPi _i^\top \gamma )x_{ij}=0$ and $|\beta _j|\ge a\lambda$ for $j=1,\ldots ,q_n$ and (iii) $|\sum _i (Y_i-x_i^\top \beta -\varPi _i^\top \gamma )x_{ij}|\le n\lambda$ and $|\beta _j|<\lambda$ for $j=q_n+1,\ldots ,p_n$, where $a=3.7$, $\varPi _{il}=z_{il}\pi (u_i)\in {\mathbb {R}}^{K_n}$, then $(\beta ,\gamma )$ is a local minimizer of (3).

This lemma is a direct extension of Theorem 1 in Fan and Lv (2011). Thus, we omit the proof.

Proof of Theorem 1

We will show that

$$\begin{aligned} \sum _{l=1}^d\left\| {\hat{\alpha }}^o_l(u)-\alpha _{0l}(u)\right\| ^2+\Vert {\hat{\beta }}^o_I-\beta _{0I}\Vert ^2=O_P((K_n+q_n)/n) \end{aligned}$$

(6)

and

$$\begin{aligned} \Vert {\hat{\beta }}^o_I-\beta _{0I}\Vert ^2=O_P(q_n/n), \end{aligned}$$

(7)

respectively. This will immediately imply the results stated in this theorem.

For $l=1,\ldots ,d$, recall that $\gamma _{0l}$ is the best approximating spline coefficient for $\alpha _{0l}(\cdot )$, such that $\Vert \alpha _{0l}(u)-\pi (u)^\top \gamma _{0l}\Vert =O(K_n^{-r})$. Let $W^o=(W^o_1,\ldots ,W^o_n)^\top$, $\theta _0=(\beta ^\top _{0I},\gamma ^{\top }_0/\sqrt{K_n})^\top$ and ${\hat{\theta }}=({\hat{\beta }}^o_I,{\hat{\gamma }}^o/\sqrt{K_n})$. It follows from (2) that $\sum _{i=1}^n(Y_i-W_i^{o\top }{\hat{\theta }})W^o_i=0$. Hence

$$\begin{aligned} \sum _{i=1}^n W^o_iW_i^{o\top }({\hat{\theta }}-\theta _0)= \sum _{i=1}^n (Y_i-W_i^{o\top }\theta _0)W^o_i=W^{o\top }(Y-W^o\theta _0). \end{aligned}$$

(8)

First, the eigenvalues of $\sum _{i=1}^n W^o_iW_i^{o\top }$ are of order n by Lemma 1. In the following, we will show that

$$\begin{aligned} \left\| W^{o\top }(Y-W^o\theta _0)\right\| ^2=O_P \left( nK_n+nq_n+n^2K_n^{-2r}\right) . \end{aligned}$$

(9)

Combining equations (8) and (9), and $K_n\asymp n^{1/(2r+1)}$ in Condition (C4), we have $\Vert {\hat{\theta }}-\theta _0\Vert ^2=O_P\{n^{-1}(K_n+q_n)\}$. This implies that (6), since

$$\begin{aligned}&\sum _{l=1}^d\Vert {\hat{\alpha }}^o_l(u)-\alpha _{0l}(u)\Vert ^2+\Vert {\hat{\beta }}^o_I-\beta _{0I}\Vert ^2\\&\quad \le \sum _{l=1}^d \left\{ 2\Vert \pi (u)^\top ({\hat{\gamma }}^o_l-\gamma _{0l})\Vert ^2+2\Vert \alpha _{0l}(t)-\pi (u)^\top \gamma _{0l}\Vert ^2\right\} +\Vert {\hat{\beta }}^o_I-\beta _{0I}\Vert ^2 \\&\quad =O_P(K_n^{-1}\Vert {\hat{\gamma }}^o-\gamma _0\Vert ^2)+O_P(K_n^{-2r})+\Vert {\hat{\beta }}^o_I-\beta _{0I}\Vert ^2=O_P(\Vert {\hat{\theta }}-\theta _0\Vert ^2). \end{aligned}$$

Now we consider (9). For any vector $v \in {\mathbb {R}}^{d K_n+q_n}$, we have $|(Y-W^o\theta _0)^\top W^ov|^2\le \Vert P_{W^o}(Y-W^o\theta _0)\Vert ^2\Vert W^ov\Vert ^2$, where $P_{W^o}=W^o(W^{o\top }W^o)^{-1}W^{o\top }$ is a projection matrix. Obviously $\Vert W^ov\Vert ^2=O_P(n\Vert v\Vert ^2)$. On the other hand, we have

$$\begin{aligned} \Vert P_{W^o}(Y-W^o\theta _0)\Vert ^2\le 2\Vert P_{W^o}\varepsilon \Vert ^2+2\Vert P_{W^o}( Y-W^o\theta _0 - \varepsilon )\Vert ^2{\mathop {=}\limits ^{\triangle }} \varDelta _1+\varDelta _2. \end{aligned}$$

The first term $\varDelta _1$ is of order $O_P(\mathrm {tr}(P_{W^o}))=O_P(K_n+q_n)$ since $\mathrm {E}(\varepsilon )=0$. The second term $\varDelta _2$ is obviously

$$\begin{aligned} \varDelta _2\le & {} 2\sum _{i=1}^n(Y_i-W_i^{o\top }\theta _0-\varepsilon _i)^2\\= & {} 2\sum _{i=1}^n\left\{ \sum _{l=1}^dz_{il}\left[ \alpha _{0l}(u_i)-\gamma ^\top _{0l}\pi (u_i)\right] \right\} ^2 =O_P\left( \frac{n}{K_n^{2r}}\right) . \end{aligned}$$

Then, (9) follows from the foregoing argument, if $v=W^{o\top }(Y-W^o\theta _0)$.

Let us check (7), define $\varsigma _n=\sqrt{q_n/n}$. Note that ${\hat{\beta }}^o_I$ can also be obtained by minimize

$$\begin{aligned} l_n^o(\beta _I)=\Vert (I-P_{\varPi })(Y-X_A\beta _I)\Vert ^2, \end{aligned}$$

where $P_\varPi =\varPi (\varPi ^\top \varPi )^{-1}\varPi ^\top$ with $\varPi =(\varPi _1,\ldots ,\varPi _n)^\top$. Our aim is to show that, for a given $\epsilon >0$,

$$\begin{aligned} \mathrm {Pr}\left\{ \inf _{\Vert v\Vert =C}l_n^o(\beta _{0I}+\varsigma _n v)>l_n^o(\beta _{0I})\right\} \ge 1-\epsilon . \end{aligned}$$

So that this implies that, with probability tending to one, there is a minimizer ${\hat{\beta }}^o_I$ in the ball $\{\beta _{0I}+\varsigma _n v: \Vert v\Vert \le C\}$ such that $\Vert {\hat{\beta }}^o_I-\beta _{0I}\Vert =O_P(\varsigma _n)$. By direct calculation, we get

$$\begin{aligned} l_n^o(\beta _{0I}+\varsigma _n v)-l_n^o(\beta _{0I})=-2(Y^*-X_A^*\beta _{0I})^\top \varsigma _n X_A^*v+\Vert \varsigma _nX_A^*v\Vert ^2{\mathop {=}\limits ^{\triangle }} D_1+D_2. \end{aligned}$$

Hereafter, for any matrix M with n rows, we define $M^*=(I-P_\varPi )M$. We can prove that

$$\begin{aligned} |D_1|\le 2 \varsigma _n \Vert (Y^*-X_A^*\beta _{0I})^\top X_A^*\Vert \Vert v\Vert =O_P(\varsigma _n\sqrt{nq_n}) \Vert v\Vert \end{aligned}$$

and

$$\begin{aligned} D_2=\varsigma _n^2 v^\top X_A^{*\top } X_A^* v= n \varsigma _n^2 v^\top \varXi v +o_P(1)n\varsigma _n^2 \Vert v\Vert ^2. \end{aligned}$$

It suffices to check $\mathrm {E}\Vert X_A^{*\top }(Y^*-X_A^*\beta _{0I})\Vert ^2\le C \mathrm {tr}( X_A^{*} X_A^{*\top })\le Cnq_n$ and $\Vert X^{*\top }_AX^*_A/n-\varXi \Vert =o_P(1)$, which follows similar lines to the proofs in Li et al. (2011b). Therefore, by allowing C to be large enough, $D_1$ are dominated by $D_2$, which is positive. This completes the proof. $\square$

Proof of Theorem 2

Let $m_{0i}=x_{A_i}^\top \beta _{0I}+z^\top _i\alpha _0(u_i)$, ${\hat{m}}_{0i}=x_{A_i}^\top \beta _{0I}+\varPi _i^\top {\hat{\gamma }}^o$ and ${\hat{m}}_i=x^\top _{A_i}{\hat{\beta }}^o_I+\varPi _i^\top {\hat{\gamma }}^o$. By Theorem 1, we have $|m_{0i}-{\hat{m}}_{0i}|=O_P(\zeta _n)$. Since the components $h_l(\cdot )$ of $\varGamma$ are in ${\mathcal {H}}_r$, it can be approximated by spline functions ${\tilde{h}}_l(\cdot )$ with the approximation error $O(K_n^{-r})$. Denote by ${\widetilde{\varGamma }}(z_i,u_i)$ the vector that approximates $\varGamma (z_i,u_i)$ by replacing $h_l(\cdot )$ with ${\tilde{h}}_l(\cdot )$. Note that, since ${\tilde{h}}_l(\cdot )$ is a spline function, the j-th component of ${\widetilde{\varGamma }}(z_i,u_i)$ can be expressed as $\varPi _i^\top v_j$ for some $v_j\in {\mathbb {R}}^{dK_n}$. We first show that

$$\begin{aligned} \left\| \sum _{i=1}^n\{x_{A_i}-{\widetilde{\varGamma }}(z_i,u_i)\} (Y_i-{\hat{m}}_{0i})-\sum _{i=1}^n\{x_{A_i}-\varGamma (z_i,u_i)\} \varepsilon _i\right\| =o_P(\sqrt{n}). \end{aligned}$$

(10)

In fact

$$\begin{aligned}&\left\| \sum _{i=1}^n\{x_{A_i}-{\widetilde{\varGamma }}(z_i,u_i)\}(Y_i-{\hat{m}}_{0i})-\sum _{i=1}^n\{x_{A_i}-\varGamma (z_i,u_i)\}\varepsilon _i\right\| \\&\quad \le \left\| \sum _{i=1}^n\{x_{A_i}-\varGamma (z_i,u_i)\}(m_{0i}-{\hat{m}}_{0i})\right\| \\&\qquad +\left\| \sum _{i=1}^n\{\varGamma (z_i,u_i)-{\widetilde{\varGamma }}(z_i,u_i)\}(m_{0i}-{\hat{m}}_{0i})\right\| \\&\qquad +\left\| \sum _{i=1}^n\{{\widetilde{\varGamma }}(z_i,u_i)-\varGamma (z_i,u_i)\}\varepsilon _i\right\| . \end{aligned}$$

From the definition of $\varGamma (z_i,u_i)$, the first term above is $O_P(n\sqrt{q_n/n}\zeta _n)$, the second term is $O_P(n\sqrt{q_n}K_n^{-r}\zeta _n)$ and the last term is $O_P(\sqrt{nq_n}K_n^{-r})=o_P(\sqrt{n})$ since $\Vert \varGamma (z_i,u_i)-{\widetilde{\varGamma }}(z_i,u_i)\Vert =O_P(\sqrt{q_n}K_n^{-r})$. Thus, (10) is shown.

In the other hand, Eq. (2) implies $\sum _{i=1}^n(x_{A_i}-{\widetilde{\varGamma }}(z_i,u_i))(Y_i-{\hat{m}}_i)=0$. By (10), we get

$$\begin{aligned} \frac{1}{\sqrt{n}}\sum _{i=1}^n\{x_{A_i}-\varGamma (z_i,u_i)\}\varepsilon _i= & {} \frac{1}{\sqrt{n}}\sum _{i=1}^n\{x_{A_i}-{\widetilde{\varGamma }}(z_i,u_i)\}\\&(Y_i-{\hat{m}}_{i}+{\hat{m}}_{i}-{\hat{m}}_{0i})+o_P(1)\\= & {} \frac{1}{\sqrt{n}}\sum _{i=1}^n\{x_{A_i}-{\widetilde{\varGamma }}(z_i,u_i)\}x_{A_i}^\top ({\hat{\beta }}^o_I-\beta _{0I})+o_P(1)\\= & {} \frac{1}{\sqrt{n}}{\mathcal {M}}({\hat{\beta }}^o_I-\beta _{0I})+o_P(1), \end{aligned}$$

where ${\mathcal {M}}=\sum _{i=1}^n\{x_{A_i}-{\widetilde{\varGamma }}(z_i,u_i)\}\{x_{A_i}-{\widetilde{\varGamma }}(z_i,u_i)\}^\top$. It is easy to show that ${\mathcal {M}}/n\rightarrow \varXi$ by the law of large numbers. Then, we can replace ${\mathcal {M}}/n$ by $\varXi$ which does not disturb the asymptotic distribution from Slutsky’s theorem. Based on above arguments, we only need to show that

$$\begin{aligned} n^{-1/2}Q_n\varXi ^{-1/2}\sum _{i=1}^n\{x_{A_i}-\varGamma (z_i,u_i)\}\varepsilon _i{\mathop {\longrightarrow }\limits ^{D}}N(0,\sigma ^2\varPsi ). \end{aligned}$$

Let $U_{ni}=n^{-1/2}Q_n\varXi ^{-1/2}\{x_{A_i}-\varGamma (z_i,u_i)\}\varepsilon _i$. Note that $\mathrm {E}(U_{ni})=0$ and $\sum _{i=1}^n\mathrm {E}(U_{ni}U_{ni}^\top )=\sigma ^2Q_nQ_n^\top \rightarrow \sigma ^2 \varPsi$. To establish the asymptotic normality, it suffices to check the Lindeberg-Feller condition. For any $\epsilon >0$, we have

$$\begin{aligned} \sum _{i=1}^n\mathrm {E}[\Vert U_{ni}\Vert ^2I\{\Vert U_{ni}\Vert>\epsilon \}] \le n[\mathrm {E}\Vert U_{ni}\Vert ^4]^{1/2} [\mathrm {Pr}(\Vert U_{ni}\Vert >\epsilon )]^{1/2}. \end{aligned}$$

Using Chebyshev’s inequality, we have

$$\begin{aligned} \mathrm {Pr}(\Vert U_{ni}\Vert >\epsilon )&\le n^{-1}\epsilon ^{-2}\mathrm {E}\Vert Q_n\varXi ^{-1/2}\{x_{A_i}-\varGamma (z_i,u_i)\}\varepsilon _i\Vert ^2 \\&\le C n^{-1}\epsilon ^{-2}\mathrm {E}\Vert \{x_{A_i}-\varGamma (z_i,u_i)\}\varepsilon _i\Vert ^2\\&=O(q_n n^{-1}). \end{aligned}$$

Also, we can show that

$$\begin{aligned} \mathrm {E}\Vert U_{ni}\Vert ^4\le n^{-2}\varLambda _{\min }(Q_nQ_n^\top )\varLambda _{\max }(\varXi )\mathrm {E}\Vert \{x_{A_i}-\varGamma (z_i,u_i)\}\varepsilon _i\Vert ^4=O(q_n^2 n^{-2}). \end{aligned}$$

Hence,

$$\begin{aligned} \sum _{i=1}^n\mathrm {E}[\Vert U_{ni}\Vert ^2I\{\Vert U_{ni}\Vert >\epsilon \}] =O\left( n q_n n^{-1} q_n^{1/2}n^{-1/2}\right) =o(1). \end{aligned}$$

Noting that $U_{ni}$ satisfies the conditions of the Lindeberg-Feller central limit theorem, then we complete the proof. $\square$

Proof of Theorem 3

Let $({\hat{\beta }}, {\hat{\gamma }})=({\hat{\beta }}^o, {\hat{\gamma }}^o)$, we will show that $({\hat{\beta }}, {\hat{\gamma }})$ satisfies equations (i)–(iii) of Lemma 3. This will immediately imply this theorem.

For $j=1,\ldots ,q_n$, note that $|{\hat{\beta }}_j|=|{\hat{\beta }}_j-\beta _{0j}+\beta _{0j}|\ge \min _{1\le j\le q_n}|\beta _{0j}|-|{\hat{\beta }}_j-\beta _{0j}|$, then $|{\hat{\beta }}_j|\ge a\lambda$ is implied by

$$\begin{aligned} \min _{1\le j\le q_n}|\beta _{0j}|\gg \lambda \quad \mathrm {and}\quad |{\hat{\beta }}_j-\beta _{0j}| \ll \lambda , \end{aligned}$$

and both equations above are implied by Condition (C8) as well as Theorem 1. Since $({\hat{\beta }}^o_I, {\hat{\gamma }}^o)$ is the solution of the optimization problem (2), we have

$$\begin{aligned}&\sum _i \left( Y_i-x_{A_i}^\top {\hat{\beta }}^o_{I}-\varPi _i^\top {\hat{\gamma }}^o\right) \varPi _{il} =0, \\&\sum _i \left( Y_i-x_{A_i}^\top {\hat{\beta }}^o_{I}-\varPi _i^\top {\hat{\gamma }}^o\right) x_{ij} = 0. \end{aligned}$$

It follows that (i) and (ii) trivially hold since $x_i^\top {\hat{\beta }}+\varPi _i^\top {\hat{\gamma }}=x_{A_i}^\top {\hat{\beta }}^o_I+\varPi _i^\top {\hat{\gamma }}^o$.

Now it remains to show (iii). For $j=q_n+1,\ldots ,p_n$, $|{\hat{\beta }}_j|<\lambda$ is trivial since ${\hat{\beta }}_j=0$. Furthermore,

$$\begin{aligned} \sum _{i=1}^n (Y_i-x_{A_i}^\top {\hat{\beta }}^o_{I}-\varPi _i^\top {\hat{\gamma }}^o)x_{ij}&=\sum _{i=1}^n (Y_i-W_i^\top \theta _0)x_{ij}-X_j^\top P_W(Y-W\theta _0) \nonumber \\&=X_j^\top (I-P_W)(\varepsilon +R), \end{aligned}$$

(11)

where $R=(R_1,\ldots ,R_n)^\top$ with $R_i=z_i^\top \alpha (u_i)- \varPi _i^\top \gamma _0$. It is easy to see that all the eigenvalues of the matrix $I-P_W$ are bound by 1 (in fact each eigenvalue is either 0 or 1), and thus $\Vert (I-P_W)X_j\Vert = c\sqrt{n}$ for some c, following Condition (C1). Write the vector $(I-P_W)X_j$ as $b_j=(b_{j1},\ldots ,b_{jn})^\top$, then $\max _i|b_{ji}|\le c\sqrt{n}$ and $X_j^\top (I-P_W)\varepsilon$ can be written as $\sum _i b_{ji}\varepsilon _i$. By Condition (C3), we have $\mathrm {E}|\varepsilon _i|^m\le \frac{m!}{2} S^2T^{m-2}$, $m=2, 3, \ldots$, for some constants S and T. Then, we have

$$\begin{aligned} \mathrm {E}|\varepsilon _ib_{ji}|^m \le \frac{m!}{2} (b_{ji} S)^2(b_{ji}T)^{m-2}\le \frac{m!}{2} (b_{ji} S)^2(c\sqrt{n}T)^{m-2} \end{aligned}$$

and

$$\begin{aligned} \sum _{i}\mathrm {E}|\varepsilon _ib_{ji}|^2\le \sum _{i}(b_{ji} S)^2\le S^2\sum _{i}b^2_{ji}\le S^2c^2 n. \end{aligned}$$

By Lemma 2 and a simple union bound, for $\epsilon >0$, we have

$$\begin{aligned} \mathrm {Pr}\left( \max _{q_n+1\le j\le p_n}\left| X_{(j)}^\top (I-P_W)\varepsilon \right|>\epsilon \right)&=\mathrm {Pr}\left( \max _j\left| \sum _{i=1}^nb_{ji}\varepsilon _i\right| >\varepsilon \right) \\&\le 2p_n\exp \left\{ -\frac{\epsilon ^2}{2nc^2S^2+2\sqrt{n}cT\epsilon }\right\} . \end{aligned}$$

Taking $\epsilon =c_1\sqrt{n}\log (p_n\vee n)$ for some $c_1>0$ large enough, the above probability tends to zero, thus we have

$$\begin{aligned} \max _{q_n+1\le j\le p_n}|X_j^\top (I-P_W)\varepsilon |=O_P(\sqrt{n}\log (p_n\vee n)). \end{aligned}$$

(12)

On the other hand

$$\begin{aligned} |X_j^\top (I-P_W)R|\le \Vert b_j\Vert \Vert R\Vert =O_P(\sqrt{n}\sqrt{n}K_n^{-r}). \end{aligned}$$

(13)

Combining equations (11)–(13) with Condition (C8), we prove (iii) in Lemma 3. This completes the proof. $\square$