1 Introduction

Single index model and its corresponding statistical inference methods have been extensively investigated over last three decades by many statisticians. For example, Powell et al. (1989) incorporated the average derivative method and kernel smoothing technique to estimate the single index coefficients. Ichimura (1993) gave a least squares estimate by virtue of kernel smoothing technique; Härdle et al. (1993) considered the optimal smoothness of the single index function; Li (1991) discussed the estimation of single index coefficients by sliced regression approach. Xia et al. (2002) studied several index vector estimation methods by a minimum average variance estimation method. Other estimation methods are included in Hall (1989), Klein and Spady (1993), Horowitz and Härdle (1996), Carroll et al. (1997), Xia and Li (1999), Hristache et al. (2001) etc.

Wang and Yang (2009) proposed a B spline-based estimation method for the following fully nonparametric heteroscedastic regression model

$$\begin{aligned} Y=m(X) + \sigma (X)\varepsilon ,\quad \ \ m(X)=E(Y|X) \end{aligned}$$
(1)

through the single index approximation

$$\begin{aligned} g(v)=E(Y|X^\prime \beta =v), \end{aligned}$$
(2)

where \(Y\in R\) is a response variable, \(X\in R^p\) is the corresponding covariate vector, \(g(\cdot )\) is a completely unspecified univariate function, termed by single index function, \(\beta =(\beta _1,\beta _2,\ldots ,\beta _p)'\in R^p\) is the regression parameter vector, termed by index parameter vector; \(X'\) represents the transpose of X; \(\varepsilon \) is the model random error and usually assumed to follow a distribution with \(E(\varepsilon |X)=0\) and \(Var(\varepsilon |X)=1\). For the model identification, it is also assumed that \(||\beta ||=1\) with last nonzero component positive. Hereafter \(||\cdot ||\) stands for the Euclid norm. There are mainly two advantages of the model (1) with the approximation (2). For one thing, it can avoid the model misspecification; For another one, it can also avoid the so-called “curse of dimensionality” in the nonparametric regression estimation.

In applications, we usually include as many covariates as possible into the working models to improve the modeling accuracy and then establish a high-dimensional statistical model. However, some of the included covariates may be unimportant, which, in turn, may increase estimate variance and so may lead to wrong statistical inference. Therefore variable selection is an important step before application of such models. In the context of linear regression models, many variable selection techniques were proposed and some of them have been extended into the context of semiparametric and nonparametric models. For example, LASSO (Tibshirani 1996, 1997; Knight and Fu 2000; Ciuperca 2014), SCAD (Fan 1997; Fan and Li 2001, Fan and Li 2002; Xu et al. 2014; Neykov et al. 2014), Hard thresholding (Fan 1997; Antoniadis 1997; Fan and Li 2002), Adaptive LASSO (ALASSO) penalty (Zou 2006; Zhang and Lu 2007; Lu and Zhang 2007; Zhang et al. 2010), Dantzig selector (Candes and Tao 2007; Antoniadis et al. 2010) etc. Fan and Lv (2010) overviewed the variable selection methods in details. Variable selection in the single index models also has been studied by some statisticians. Kong and Xia (2007) proposed a separated cross validation-based variable selection method; Zhu et al. (2011) considered the ALASSO approach for a general class of single index models; Zeng et al. (2012) studied the variable selection by a local linear smoothing approximation. Wang (2009) incorporated Bayesian method into the variable selection. Peng and Huang (2011) used a penalized least squares method and local linear approximation to select the important variables in single index model. In their methods, the bandwidth is a key for the convergence rate of resulting estimates and the implementation may suffer from intensive computation.

In this paper, by combining the B spline-based estimation approach in Wang and Yang (2009) and the nonconcave penalized least squares method in Fan and Li (2001), we consider the variable selection in model (1) with the single index approximation (2), which will be approximated by the B spline polynomial. One advantage of B spline approximation technique is that given the index regression vector \(\beta \), we can choose a B spline basis and then the unknown single index function can be characterized by the basis expansion coefficients. So we can obtain the approximated estimate of the unknown multivariate function \(m(\cdot )\) by estimating the base expansion coefficients of \(g(\cdot )\) using the commonly-used least squares method. Thus we can easily implement the proposed variable selection method in the current context. Under some regular conditions, we will show that the resulting estimates with the SCAD and HARD thresholding penalties enjoy the oracle and consistency properties. Using the proposed method, we not only can select the important single index variables but also can estimate the unknown single index functions and the regression parameters simultaneously. Some simulation studies and a real data application will be given to illustrate our proposed variable selection method.

The rest of this paper precedes as follows. In Sect. 2, we will introduce our proposed variable selection method for model (1) with the single index model approximation (2), including B spline approximation technique, penalized least squares method, the main theoretical results and an efficient implementation algorithm. Some numerical studies will be given in Sect. 3. Some conclusions will be made in Sect. 4. We will present the corresponding theoretical proofs in Appendix.

2 Method

2.1 Penalized B spline estimation

It is assumed that \(\{(Y_i,X_i)\}_{i=1}^n\) are the realizations of (Y, X) specified by the model (1). Without loss of generality, we assume \(||\beta ||=1\) with \(\beta _p>0\) and the true value \(\beta _0\) is in the upper unit hemisphere \(S_+^{p-1}=\{\beta :\ ||\beta ||=1, \beta _p>0\}\), otherwise, we can interchange the positions of the last covariate and the one with positive effect. Denote \( S_c^{p-1}=\left\{ \beta =(\beta _1,\beta _2,\cdots ,\beta _p)':\ ||\beta ||=1, \beta _p\ge \sqrt{1-c^2}\right\} \) with \(c\in (0,1)\) as a cap shape subset of \(S_+^{p-1}\). With a proper value of c, it is obvious that \(\beta _0\in S_c^{p-1}\). Since \(S_+^{p-1}\) is not a compact set, we assume \(\beta \in S_c^{p-1}\) in what follows. To define a B spline expansion of g(v), we also suppose that there exists a real positive number M such that \(P(||X||\le M)=1\). Consequently, \(X'\beta \) is bounded in some finite interval, say [a, b], with probability 1 for all \(\beta \in S_c^{p-1}\).

Following Wang and Yang (2009), we can estimate \(\beta \) by minimizing the following risk function

$$\begin{aligned} \mathcal {R}(\beta )=\text {E}[Y-m_\beta (X_\beta )]^2 \end{aligned}$$

or the corresponding empirical risk function,

$$\begin{aligned} R(\beta )=\frac{1}{n}\sum _{i=1}^n\left[ Y_i-m_\beta (X_{\beta ,i})\right] ^2, \end{aligned}$$

where \(X_\beta =X'\beta , X_{\beta ,i}=X_i'\beta , m_\beta (X_\beta )=E(Y|X_\beta )=E[m(X)|X_\beta ]\).

To stable the following B spline polynomial expansion of \(m_\beta (\cdot )\), Wang and Yang (2009) used the rescaled centered Beta cumulative density function to transform the covariate \(X_\beta \) such as

$$\begin{aligned} U_\beta =F_p(X_\beta ),\quad \ \ U_{\beta ,i}=F_p(X_{\beta ,i}),\quad \ \ i=1,2,\cdots ,n, \end{aligned}$$

where

$$\begin{aligned} F_p(v)=\int _{-1}^{v/a}\frac{\Gamma (p+1)}{\Gamma [(p+1)/2]^22^p}(1-t^2)^{\frac{p-1}{2}}dt,\quad \ \ v\in [-a,a]. \end{aligned}$$

Then, for fixed \(\beta \), \(U_\beta \) has a quasi-uniform[0, 1] distribution. So equally-spaced knots can be used to smooth the unknown function in the B spline approximation of \(m_\beta (\cdot )\). In terms of \(U_\beta \), the empirical risk function \(R(\beta )\) can be rewritten as

$$\begin{aligned} R(\beta )=\frac{1}{n}\sum _{i=1}^n\left[ Y_i-\gamma _\beta (U_{\beta ,i})\right] ^2, \end{aligned}$$
(3)

where \(\gamma _\beta (\cdot )=m_\beta (F_p^{-1}(\cdot ))\) and it is suggested to be approximated by B spline approximation.

Denote r as the order of B spline approximation. Let \(\xi _1=\xi _2=\cdots =\xi _r=a<\xi _{r+1}<\xi _{r+2}<\cdots <\xi _{r+N}<b=\xi _{r+N+1}=\xi _{r+N+2}=\cdots =\xi _{2r+N}\) be the knot points for the B spline approximation, where \(N=n^v\) with \(0<v<0.5\) such that \(\max _{1\le k\le N+1}\{|\xi _{r+k}-\xi _{r+k-1}|\}=O(n^{-v})\). Usually we call \(\{\xi _{r+i}\}_{i=1}^N\) as the inner knot points. The number of inner knots, N, can be chosen as a positive integer number between \(n^{1/6}\) and \(n^{1/5}\log ^{-2/5}(n)\). Denote \(\{B_j(x)\}_{j=1}^d\) as the B spline basis functions based on the knot set \(\{\xi _i\}_{i=1}^{2r+N}\), where \(d=r+N\) is the dimension of B spline basis. Following deBoor (1978), the B spline basis functions enjoy the following properties: (i) \(B_j(x)=0\) for \(x\notin [\xi _j,\xi _{j+r}]\); (ii) \(B_j(x)>0\) for \(x\in [\xi _j,\xi _{j+r}]\); (iii) \(\sum _{j=1}^dB_j(x)=1\) for any \(x\in [a,b]\) and 0 otherwise. Consequently, for any \(1\le j\le d\) and any \(x\in R\), we have \(B_j(x)\in [0,1]\).

Given the B spline basis \(\{B_j(x)\}_{j=1}^d\), \(\gamma _\beta (\cdot )\) can be approximated by

$$\begin{aligned} \tilde{\gamma }_\beta (v)=\theta _{\beta ,1}B_1(v)+\theta _{\beta ,2}B_2(v)+\cdots +\theta _{\beta ,d}B_d(v)=B(v)'\theta _\beta , \end{aligned}$$
(4)

where \(\theta _\beta =(\theta _{\beta ,1},\theta _{\beta ,2},\cdots ,\theta _{\beta ,d})'\) and \(B(x)=(B_1(x),B_2(x),\cdots ,B_d(x))'\). Hereafter the subscript \(\beta \) indicates that the corresponding quantity depends on the value of \(\beta \). Plugging (4) into (3), the empirical risk function (3) can be approximated by

$$\begin{aligned} \tilde{R}(\beta )=\frac{1}{n}\sum _{i=1}^n\left[ Y_i-B(U_{\beta ,i})'\theta _\beta \right] ^2. \end{aligned}$$
(5)

According to the least squares method, \(\theta _\beta \) can be estimated by \(\hat{\theta }_\beta =[\text {B}_\beta '\text {B}_\beta ]^{-1}\text {B}_\beta '\text {Y}\) for the fixed \(\beta \), where \(\text {B}_\beta =[B(U_{\beta ,1}),B(U_{\beta ,2}),\cdots ,B(U_{\beta ,n})]'\) and \(\text {Y}=(Y_1,Y_2,\) \(\cdots ,Y_n)'\). Then the empirical risk function (5) can be estimated by

$$\begin{aligned} \hat{R}(\beta )=\frac{1}{n}\sum _{i=1}^n\left[ Y_i-B(U_{\beta ,i})'\hat{\theta }_\beta \right] ^2. \end{aligned}$$
(6)

Let \(\hat{\beta }\) be the minimizer of \(\hat{R}(\beta )\). \(g(\cdot )\) can be estimated by

$$\begin{aligned} \hat{g}(v)=\tilde{\gamma }_{\hat{\beta }}(F_p^{-1}(v))=B(F_p^{-1}(v))'\hat{\theta }_{\hat{\beta }}. \end{aligned}$$
(7)

Considering the model restriction \(||\beta ||=1\) with \(\beta _p>0\), denote \(\beta ^{(1)}=(\beta _1,\beta _2,\cdots ,\beta _{p-1})\). Then the index regression parameter vector \(\beta \) can be rewritten as \(\beta =\left( \beta ^{(1)'},\sqrt{1-||\beta ^{(1)}||^2}\right) '\) with \(||\beta ^{(1)}||<1\), that is, the free index regression parameters in (2) are just \(\beta ^{(1)}\). Let \(R^*(\beta ^{(1)})=\hat{R}(\beta ^{(1)},\sqrt{1-||\beta ^{(1)}||^2})\). Adding the penalty term to the estimated risk function \(R^*(\beta ^{(1)})\), the penalized risk function is given by

$$\begin{aligned} Q(\beta ^{(1)})= R^*(\beta ^{(1)})+\sum _{j=1}^{p-1}p_\lambda (|\beta _j|), \end{aligned}$$
(8)

where \(\lambda >0\) is the tuning parameter and \(p_\lambda (\cdot )\) is a penalty function given \(\lambda \).

Given a proper penalty function \(p_\lambda (\cdot )\), we can obtain the penalized least squares estimate of \(\beta ^{(1)}\) by minimizing the function (8) with respect to \(\beta ^{(1)}\) . To achieve effective variable selection for model (1), the penalty function \(p_\lambda (\cdot )\) should be irregular at the origin, that is, \(p_\lambda (0+)>0\) (Fan and Li 2002). Let \(\hat{\beta }_n^{(1)}\) be the minimizer of (8) and then \(g(\cdot )\) can be estimated by (7) with \(\hat{\beta }_n=\left( \hat{\beta }_n^{(1)'},\sqrt{1-||\hat{\beta }_n^{(1)}||^2}\right) \). With a proper penalty function \(p_\lambda (\cdot )\) and a tuning parameter \(\lambda \), some components of \(\hat{\beta }_n^{(1)}\) are shrunk to 0 and so the corresponding covariates will disappear in model (1), which reaches the variable selection. In this paper, we consider three commonly-used penalty functions: SCAD, Hard threshoulding and Lasso. Their formula and the corresponding nice properties can be found in Fan and Li (2001).

In what follows, let \(\beta _0^{(1)}\) be the true value of \(\beta ^{(1)}\). Without loss of generality, we partition \(\beta _0^{(1)}=\left( \beta _{10}^{(1)'},\beta _{20}^{(1)'}\right) '\) such that \(\beta _{10}^{(1)}\) contains all the nonzero effects in \(\beta _0^{(1)}\) and \(\beta _{20}^{(1)}=\varvec{0}\) contains all the zero ones. We also assume that the length of \(\varvec{\beta }_{10}^{(1)}\) is s. Correspondingly, \(\beta ^{(1)}\) and \(\hat{\beta }_n^{(1)}\) also have the same partitions, namely, \(\beta ^{(1)}=\left( \beta _1^{(1)'},\beta _2^{(1)'}\right) '\), \(\hat{\beta }_n^{(1)}=\left( \hat{\beta }_{1n}^{(1)'},\hat{\beta }_{2n}^{(1)'}\right) '\), where \(\beta _1^{(1)'}\) and \(\hat{\beta }_{1n}^{(1)'}\) respectively consist of the first s components of \(\beta ^{(1)}\) and \(\hat{\beta }_n^{(1)}\).

Denote

$$\begin{aligned} a_n=\max \{\dot{p}_{\lambda _n}(|\beta _{j,10}^{(1)}|):\ \ \beta _{j,10}^{(1)}\ne 0\}\quad \text {and}\quad b_n=\max \{|\ddot{p}_{\lambda _n}(|\beta _{j,10}^{(1)}|)|:\ \ \beta _{j,10}^{(1)}\ne 0\}, \end{aligned}$$

where \(\beta _{j,10}^{(1)}\) is the jth component of \(\beta _{10}^{(1)}\), \(\dot{p}_{\lambda _n}\) and \(\ddot{p}_{\lambda _n}\) respectively are the first- and second-order derivatives of \(p_{\lambda _n}\). Then we have the following results.

Theorem 1

Under conditions (A1)-(A6) in Wang and Yang (2009), if \(b_n\rightarrow 0\), then there exists a minimizer \(\hat{\beta }_n^{(1)}\) of \(Q(\beta ^{(1)})\) such that \(||\hat{\beta }_n^{(1)}-\beta _0^{(1)}||=O_p(n^{-1/2}+a_n)\).

To present the oracle properties of \(\hat{\beta }_n^{(1)}\) denote

$$\begin{aligned} \tilde{\Sigma }_{\lambda _n}=\text {diag}\left\{ \ddot{p}_{\lambda _n}(|\beta _{1,10}^{(1)}|),\ddot{p}_{\lambda _n}(|\beta _{2,10}^{(1)})|,\cdots ,\ddot{p}_{\lambda _n}(|\beta _{s,10}^{(1)})|\right\} \end{aligned}$$

and

$$\begin{aligned} \tilde{\mathbf{b }}_{\lambda _n}\!=\!\left[ \!\dot{p}_{\lambda _n}(|\beta _{1,10}^{(1)}|)\text {sign}(\beta _{1,10}^{(1)}),\dot{p}_{\lambda _n}(|\beta _{2,10}^{(1)}|)\text {sign}(\beta _{2,10}^{(1)}),\cdots ,\dot{p}_{\lambda _n}(|\beta _{s,10}^{(1)}|)\text {sign}(\beta _{s,10}^{(1)})\!\right] '\!. \end{aligned}$$

Theorem 2

(Oracle properties) Assume that the penalty function \(p_{\lambda _n}(\cdot )\) satisfies that

$$\begin{aligned} \liminf _{n\rightarrow \infty }\liminf _{\theta \rightarrow 0+}\dot{p}_{\lambda _n}(\theta )/\lambda _n=c, \end{aligned}$$

where c is a positive constant. If \(\lambda _n\rightarrow 0\), \(\sqrt{n}\lambda _n\rightarrow \infty \) and \(a_n=O(n^{-1/2})\), then under the conditions of Theorem 1, the \(\sqrt{n}\)-consistent local minimizer \(\hat{\beta }_n^{(1)}=(\hat{\beta }_{1n}^{(1)'},\hat{\beta }_{2n}^{(1)'})'\) in Theorem 1 must satisfy:

  1. (i)

    (Sparsity) \(P(\hat{\beta }_{2n}^{(1)}=\varvec{0})\rightarrow 1\);

  2. (ii)

    (Asymptotic Normality)

    $$\begin{aligned} \sqrt{n}(V+\tilde{\Sigma }_{\lambda _n})\left[ \hat{\beta }_{1n}^{(1)}-\beta _{10}^{(1)}+(V+\tilde{\Sigma }_{\lambda _n})^{-1}\tilde{\mathbf{b }}_{\lambda _n}\right] \rightarrow N(\varvec{0}, A) \end{aligned}$$
    (9)

where V and A are the sth leading submatrix of \(E[H^*(\beta _0^{(1)})]\) and \(Cov[S^*(\beta _0^{(1)})]\), \(H^*(\beta ^{(1)})\) and \(S^*(\beta ^{(1)})\), the Hessian matrix and score function of \(R^*(\beta ^{(1)})\), are given in Sect. 2.2.

Remark 1

For SCAD and HARD thresholding penalties, when \(|\beta _i|\) is large enough, they are constant, which implies that \(\tilde{\mathbf{b }}_{\lambda _n}=\mathbf 0 \) and \(\tilde{\Sigma }_{\lambda _n}=\mathbf 0 \). So for the variable selection based on SCAD and HARD thresholding penalties, we have

$$\begin{aligned} \sqrt{n}\left( \hat{\beta }_{1n}^{(1)}-\beta _{10}^{(1)}\right) \rightarrow N\left( \varvec{0}, V^{-1'}AV^{-1}\right) . \end{aligned}$$

Remark 2

For LASSO penalty, \(a_n=\lambda _n\), which implies that there is a contradict between \(a_n=o(n^{-1/2})\) for estimation consistency in Theorem 1 and \(\sqrt{n}\lambda _n\rightarrow \infty \) for oracle properties in Theorem  2. Therefore the resulting consistent estimates based on LASSO penalty can not enjoy oracle properties.

2.2 Implementation

For the minimization of \(Q(\beta ^{(1)})\), we suggest to use the port optimization-based algorithm in Wang and Yang (2009) with the objective function \(Q(\beta ^{(1)})\) and the gradient vector

$$\begin{aligned} S(\beta ^{(1)})&=\frac{\partial Q(\beta ^{(1)})}{\partial \beta ^{(1)}}=\frac{\partial R^*(\beta ^{(1)})}{\partial \beta ^{(1)}}+\mathbf b _\lambda (\beta ^{(1)})=S^*(\beta ^{(1)})+\mathbf b _\lambda (\beta ^{(1)})\nonumber \\&=-\frac{2}{n}\sum _{i=1}^n\left[ Y_i-B(U_{\beta ,i})'\hat{\theta }_{\beta }\right] \dot{B}(U_{\beta ,i})'\hat{\theta }_{\beta }\dot{F}_p(X_i'\beta ) J_{\beta ^{(1)}}X_i+\mathbf b _\lambda (\beta ^{(1)}),\nonumber \\ \end{aligned}$$
(10)

where \(\mathbf b _\lambda (\beta ^{(1)})\!=[\dot{p}_\lambda (|\beta _1|)\text {sign}(\beta _1),\dot{p}_\lambda (|\beta _2|)\text {sign}(\beta _2),\cdots ,\dot{p}_\lambda (|\beta _{p-1}|)\text {sign}(\beta _{p-1})]'\), \(J_{\beta ^{(1)}}=\frac{\partial \beta }{\partial \beta ^{(1)}}=(\gamma _1,\gamma _2,\cdots ,\gamma _p)^T\), \(\gamma _i (i\le p-1)\) is a \((p-1)\)-dimensional zero column vector with ith element being 1, \(\gamma _p=-\beta ^{(1)}/\sqrt{1-||\beta ^{(1)}||^2}\), \(\dot{B}(v)=(\dot{B}_1(v),\dot{B}_2(v),\cdots ,\dot{B}_d(v))'\), \(\dot{B}_i(v),\) and \(\dot{F}_d(\cdot )\) are the first-order derivatives of the B spline basis function \(B_i(v)\), and the Beta cumulative density function \(F_d(\cdot )\).

In the view of Newton-Raphson iterative algorithm, \(\hat{\beta }_{n}^{(1)}\) can be seen as the values of \(\beta ^{(1)}\) at the convergence in the following iteration,

$$\begin{aligned} \beta ^{(1)}=\beta _0^{(1)}-\left[ H^*(\beta _0^{(1)})+\Sigma _\lambda (\beta _0^{(1)})\right] ^{-1}\left[ S^*(\beta _0^{(1)})+\mathbf b _\lambda (\beta _0^{(1)})\right] , \end{aligned}$$

where

$$\begin{aligned}&H^*(\beta ^{(1)})=\frac{\partial ^2R^*(\beta ^{(1)})}{\partial \beta ^{(1)}\partial \beta ^{(1)'}}=H_1(\beta ^{(1)})+H_2(\beta ^{(1)})+H_3(\beta ^{(1)}),\\&H_1(\beta ^{(1)})=\frac{2}{n}\sum \limits _{i=1}^n[\dot{B}(U_{\beta ,i})'\hat{\theta }_{\beta }\dot{F}_p(X_i'\beta )]^2 J_{\beta ^{(1)}}X_iX_i'J_{\beta ^{(1)}}',\\&H_2(\beta ^{(1)})=-\frac{2}{n}\sum \limits _{i=1}^n\left[ Y_i-B(U_{\beta ,i})'\hat{\theta }_{\beta }\right] \ddot{B}(U_{\beta ,i})'\hat{\theta }_{\beta }[\dot{F}_p(X_i'\beta )]^2 J_{\beta ^{(1)}}X_iX_i'J_{\beta ^{(1)}}',\\&H_2(\beta ^{(1)})=-\frac{2}{n}\sum \limits _{i=1}^n\left[ Y_i-B(U_{\beta ,i})'\hat{\theta }_{\beta }\right] \dot{B}(U_{\beta ,i})'\hat{\theta }_{\beta }\ddot{F}_p(X_i'\beta ) J_{\beta ^{(1)}}X_iX_i'J_{\beta ^{(1)}}',\\&\Sigma _\lambda (\beta ^{(1)})=\text {diag}\left\{ \dot{p}_\lambda (|\beta _1^{(1)}|)/|\beta _1^{(1)}|,\dot{p}_\lambda (|\beta _2^{(1)}|)/|\beta _2^{(1)}|,\cdots ,\dot{p}_\lambda (|\beta _{p-1}^{(1)}|)/|\beta _{p-1}^{(1)}|\right\} , \end{aligned}$$

\(\ddot{B}(v)=[\ddot{B}_1(v),\ddot{B}_2(v),\cdots ,\ddot{B}_d(v)]'\), \(\ddot{B}_i(v)\) and \(\ddot{F}_d(\cdot )\) are the second-order derivatives of the B spline basis function \(B_i(v)\) and the Beta cumulative density function \(F_d(\cdot )\). Thus the covariance of the estimate \(\hat{\beta }_{1n}^{(1)}\) can be estimated by

$$\begin{aligned} \text {Cov}(\hat{\beta }_{1n}^{(1)})=\left[ A(\hat{\beta }_{1n}^{(1)})+C_\lambda (\hat{\beta }_{1n}^{(1)})\right] ^{-1}\text {Cov}\left( D(\hat{\beta }_{1n}^{(1)})\right) \left[ A(\hat{\beta }_{1n}^{(1)})+C_\lambda (\hat{\beta }_{1n}^{(1)})\right] ^{-1}, \end{aligned}$$
(11)

where \(A(\beta _1^{(1)})\) and \(C_\lambda (\beta _1^{(1)})\) are the sth leading submatrix of \(H^*(\beta ^{(1)})\) and \(\Sigma _\lambda (\beta ^{(1)})\) with \(\beta _2^{(1)}=\mathbf 0\); \(D(\beta _1^{(1)})\) is a vector consisting of the first s components of \(S^*(\beta ^{(1)})\) with \(\beta _2^{(1)}=\mathbf 0\). This formula is consistent with the results of Theorem 2. Our numerical studies show that the formula performs very well for the finite sample size.

To sum up, the implementation of the proposed variable selection can be summarized as the following three steps.

Step 1 :

Given \(\beta \in S_c^{p-1}\), by use of Steps 1-2 in Wang and Yang (2009), we obtain the transformed single index variable \(U_\beta \) and the number of inner knots.

Step 2 :

Given the tuning parameter \(\lambda \), we obtain the penalized estimate of \(\beta ^{(1)}\) by minimizing \(R^*(\beta ^{1})\) through the port optimization with the linear model least squares estimate as the initial value of \(\beta ^{(1)}\) and the score function (10).

Step 3 :

With the penalized estimate of \(\beta ^{(1)}\) in Step 2, we can obtain the estimate of single index function through (7) and the covariance matrix of \(\hat{\beta }_{1n}^{(1)}\) can be estimated through the formula (11).

Another issue for the variable selection procedure is the selection of tuning parameter \(\lambda \). Following Wang et al. (2007), we use the following Bayesian information criteria (BIC) to select the tuning parameter \(\lambda \),

$$\begin{aligned} \text {BIC}(\lambda )=R^*(\hat{\beta }_{n}^{(1)})+df_n\frac{\log (n)}{n}, \end{aligned}$$

where \(df_n\) is the approximated degree of freedom for model (1) and it can be estimated by the number of nonzero element in \(\hat{\beta }_{n}^{(1)}\). The advantage of BIC is that it tends to identify the true model if the true model is included in the candidate model set.

3 Numerical studies

In this section, we present some simulation examples and an application to illustrate our proposed variable selection method. We use the median of model prediction error (MMPE), \(\text {E}[(\hat{\beta }_n-\beta _0)'\Sigma _X(\hat{\beta }_n-\beta _0)]\) with \(\Sigma _X=E(XX')\), over 500 runs to evaluate the efficiency of our proposed variable selection procedure. The code was complied using R. It’s available for any readers on requirement.

3.1 Simulation examples

We generate a sample \(\{(X_i,Y_i)\}_{i=1}^n\) of (X, Y) from the following model

$$\begin{aligned} Y=m(X)+\sigma (X)\varepsilon , \end{aligned}$$

where \(X=(X_1,X_2,\cdots ,X_5)'\mathop {\sim }\limits ^{i.i.d.}N(0,1)\), truncated by \([-2.5, 2.5]\), \(m(X)=X'\beta +4\exp \{-(X'\beta )^2\}+\delta ||X||\), \(\varepsilon \sim N(0,1)\) and \(\beta =(1,0,-1,0,1)'/\sqrt{3}\). When \(\delta =0\), this model is just the single index model. This model was ever used in Wang and Yang (2009) and Xia et al. (2004).

In this study, we consider four sample sizes: \(n=100,150,200,300\) and two cases of \(\sigma (x)\): \(\sigma (x)=1\), \(\sigma (x)=\frac{1-0.2\exp \{||x||/\sqrt{5}\}}{5+\exp \{||x||/\sqrt{5}\}}\). We run each case 500 times. The index function g(v) will be approximated by the cubic B spline technique. We choose tuning parameter \(\lambda \) in all the cases by BIC. We study all the three type of variable selection for the single index models (\(\delta =0, \sigma (x)=1\)). For the models away from single index model and heteroscedastic single index model, we only present the variable selection results based on SCAD penalty.

The summarized results are displayed in Tables 1, 2, 3 and 4. Table 1 shows the variable selection results in the single index model \((\delta =0, \sigma =1)\). Table 2 displays the variable selection results based on SCAD penalty in the models with \((\delta =1, \sigma (x)=1.0)\) and \(\left( \delta =0, \sigma (x)=\frac{1-0.2\exp \{||x||/\sqrt{5}\}}{5+\exp \{||x||/\sqrt{5}\}}\right) \). In the two tables, “MMPE”, “Corr.” and “ICorr.” respectively stand for the median of model prediction errors, the average number of nonzero effects correctly detected and the average number of zero effects incorrectly detected by our variable selection procedures. Tables 3 and 4 summarize the estimation results of nonzero effects \(\beta _1\) and \(\beta _3\) in the three model cases.

Table 1 Variable selection results (I)
Full size table
Table 2 Variable selection results (II)
Full size table

From Table 1, we can see that the variable selection procedure in all the cases can select the same number of important variables. Moreover, the average number of covariates incorrectly detected decreases as the increasing of sample size. In addition, we also find that the medians of model prediction errors decrease as the increasing of sample size and they are reasonably close to the oracle estimation results. Moreover, for all the sample sizes, the median of the model prediction error with Lasso penalty is most far away from the median with oracle estimation while the median with SCAD penalty is closest to the median with oracle estimation. Table 2 reveals that our proposed variable selection method also performs satisfactory for the true models away from single index model and heteroscedastic single index model.

Tables 3 and 4 summarize the estimation results of nonzero effects \(\beta _1\) and \(\beta _3\). In the table, “Bias”, “SSTD” and “MSTD” respectively represent the estimation bias, sample standard deviation and mean of estimated standard deviation based on the formula (11).

Table 3 Summarized estimation results (I)
Full size table
Table 4 Summarized estimation results (II)
Full size table

From Table 3, we can see that all the estimation biases are reasonably small and perform very similarly to the oracle estimation especially for the variable selection methods with SCAD and HARD penalties. In most cases, their absolute values decrease as the increasing of sample size. Ignoring the random error, “SSTD” can be seen as the true value of standard deviation. All “MSTD” and “SSTD” are reasonably as small as that based on the oracle estimation especially for large sample size cases. Moreover, their values are vary close in all cases. In addition, “MSTD” and “SSTD” based on the variable selection method with SCAD penalty perform most similarly to the oracle estimation method even for relative small sample size. Table 4 suggests that our proposed method also performs very well in estimation when the models are away from single index models.

In a word, the variable selection procedure with all the three penalties can perform very well and similarly to the oracle estimation according to the variable selection and estimation. Moreover, the variable selection procedure with SCAD outperforms the other two procedures. Therefore we suggest ones to use the variable selection with SCAD penalty in applications.

3.2 Application

In this section, we use our proposed variable selection procedures to analyze the body fat data set (Penrose et al. 1985). This data set involves 252 observations with 13 covariates (age,weight, height, neck, chest, abdomen, hip, thigh, knee, ankle, biceps, forearm and wrist). This data can be available from R package “mfp”. In this application, the response variable is Percent body fat (estimated by Brozek’s equation: 457/Density \(-\)414.2). In the original data set, we exclude the observations with the percentage body fat estimated as 0 and the density less than 1. Thus the data set used in this application involves 250 observations. Before application, we first standardize all the covaraites.

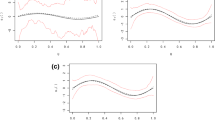
Under the restriction \(||\beta ||=1\) with \(\beta _d>0\), we use the model (1) with the single index function approximation (2) and our proposed cubic B spline variable selection procedure to select important variables. To compare the performance of our proposed procedures, we also apply the cubic B spline-based estimation method to the analysis of this data set. We summarize the variable selection results and estimates in Table 3, in which “Lasso”, “Scad”, “Hard” and “BE” respectively stand for the estimate results of variable selection procedures with Lasso, SCAD, Hard thresholding and B spline estimation approaches. The plots of estimated single index function \(\hat{g}(\cdot )\) are displayed in Fig. 1.

Fig. 1
figure 1

The plots of estimated single index function \(\hat{g}(\cdot )\)

Full size image
Table 5 Summarized estimation results for body fat data
Full size table

From the column labeled by “BE” in Table 3, we can see that the predictors Age, Abdomen, Thigh and Wrist contains most of information in interpreting the percent body fat while the other factors involves very little information. That is, the fat in a body mainly focuses on Thigh, Abdomen, Forearm and wrist. Moreover, the age also has something important with his percent body fat. From the first three columns in Table 5, all the three variable selection procedures can identify the same important factors. Therefore, we should take age and circumferences of abdomen, forearm, wrist, thigh as the important factors to measure the percent body fat. In addition, Fig. 1 displays the original data points and the B spline fitted lines. From upper-left to below-right, they are from variable selection based on Lasso, SCAD, HARD and the B spline estimation. This figure significantly indicates that \(X'\beta \) as a measurement has a nonlinear effect on the percent body fat, which flexibly shows the relationship between the percent body fat and the four main factors.

4 Conclusion

In this paper, we considered the variable selection for the model (1) with the single index model approximation (4) by incorporating B spline expansion technique. Under some regular conditions, we established the corresponding consistency and oracle properties of resulting penalized estimates. Some numerical studies illustrated that our proposed method performs very well for moderate sample size.

Our experiments shows that our proposed procedure performs very well when the dimension of covariates is less than sample size. For the dimensionality larger than n, some dimension reduction maybe needed such as SIS or ISIS methods. In many applications, some covariates can not be observed exactly and are prone to suffer from measurement error. It is also interesting to consider B spline variable selection with covariate measurement error. All the aspects will be investigated in our sequent research.