Abstract
Selecting an optimum technique for disposing of biomedical waste is a frequently observed obstacle in multi-attribute group decision-making (MAGDM) problems. The MAGDM is commonly applied to tackle decision-making states originated by obscurity and vagueness. The interval-valued q-rung orthopair fuzzy soft set is a novel variant of fuzzy sets. The main objective of this study is to introduce the interval-valued q-rung orthopair fuzzy soft Einstein-ordered weighted and Einstein hybrid weighted aggregation operators. Based on developed aggregation operators, a novel decision-making approach, the Evaluation based on the Distance from the Average Solution introduced to solve the MAGDM problem. The execution of the proposed approach demonstrates the significant impact of determining the most effective strategy to handle biomedical waste. Our proposed approach's practicality is confirmed by a case study focusing on selecting the most effective technique for Biomedical Waste (BMW) treatment. This study shows that autoclaving is the most effective method for the disposal of BMW. Comparative and sensitivity analysis confirms the consistency and effectiveness of our methodology. The comparative study indicates the effects of the proposed strategy are more feasible and realistic than the prevailing techniques.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The proper handling of medical waste is important in medical facilities and plays an integral part in protecting public safety. Biomedical waste management is the efficient administration, acquisition, transportation, production, and disposal of hazardous materials generated in healthcare facilities, research centres, and labs. The agreement between the National Health Insurance (NHI) and the World Health Organization (WHO) will evaluate the technologies implemented to manage medical waste in healthcare facilities and labs. The study attempts to carefully investigate the handling and disposal techniques for healthcare waste at these companies to preserve strict requirements in healthcare facilities. The worldwide COVID-19 pandemic has culminated in a substantial increase in Biomedical Waste (BMW)'s production. Waste products, mostly generated by medical facilities, represent a major threat because of their varying levels of harmful substances. The studies conducted by Rume and Islam (2020) and Padmanabhan and Barik (2019) highlighted the significance of properly managing this particular kind of waste to minimize its severe adverse effects on the community, the environment, and all living organisms.
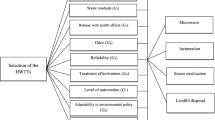
However, an important issue that has come up relates to the significance of categorizing different kinds of organizations that produce BMW. The obligation at hand implies designing a hierarchical structure that incorporates hospitals, public health organizations, polyclinics, and similar institutions to evaluate their level of competence in BMW management. The main objective of this assessment is to promote sustainable governance of cities, particularly in considering the managerial abilities of BMW within those organizations. The BMW management capacity-based assessment issue emerged as a significant focal point, encompassing several healthcare and environmental safety dimensions. In analyzing several healthcare organizations, experts must consider a wide variety of attributes to identify the most efficient organizational structure for their organization. This research examines the BMW management organization selection issue in a fuzzy context, including the inherent challenges and complications of this critical decision-making process.
Ordinary fuzzy sets were used in various kinds of scientific fields. Researchers have introduced several extensions to the original fuzzy sets over the years, including interval-valued fuzzy set (IVFS) (Turksen 1986), intuitionistic fuzzy set (IFS) and interval-valued IFS (IVIFS) (Atanassov 1986, 1999), Pythagorean fuzzy set (PFS) (Yager 2013), interval-valued PFS (IVPFS) (Peng and Yang 2016), q-rung orthopair fuzzy set (q-ROFS) (Yager 2016) and interval-valued q-ROFS (IVq-ROFS) (Joshi et al. 2018). The structures mentioned above are insufficient when dealing with the parametric description of possibilities. Molodtsov (Molodtsov 1999) developed the soft set (SS), an extensive conceptual tool, to solve and conquer this issue. Multiple studies have integrated fuzzy set extensions with SS, including fuzzy soft sets (FSS) (Maji et al. 2001a), intuitionistic fuzzy soft sets (IFSS) (Maji et al. 2001b), interval-valued IFSS (IVIFSS) (Jiang et al. 2010), Pythagorean fuzzy soft sets (PFSS) (Peng et al. 2015), interval-valued PFSS (IVPFSS) (Zulqarnain et al. 2022a), and q-rung orthopair fuzzy soft sets (q-ROFSS) (Hussain et al. 2020). Zulqarnain et al. (2023) developed the correlation-based Technique for Order of Preference by Similarity to the Ideal Solution (TOPSIS) technique in the IVPFSS structure to choose the appropriate extract, transform, and load technique. Recently, Ali et al. (2021) presented the idea of interval-valued q-ROFSS (IVq-ROFSS) as an extension of IVq-ROFS, IVPFSS, and q-ROFSS. The IVq-ROFSS notion is a constructive theory for reducing vagueness through the consideration of membership \(\left(\mathrm{\lambda }\right)\) and non-membership \(\left(\eta \right)\) grades between intervals defined as \({\left({\mathrm{\lambda }}^{\mho }\right)}^{q}+{\left({\eta }^{\mho }\right)}^{q}\le 1\), where \(q>2\). The IVq-ROFSS empowers executives to articulate their assessments within a broader scope. So IVq-ROFSS demonstrates more expertise in dealing with and replicating complicated problems with decision-making. Multiple studies endeavors were performed under the context of the IVq-ROFSS. Yang et al. (2022) presented aggregation operators (AOs) and interaction AOs for IVq-ROFSS using their developed algebraic operational rules. This approach was implemented to assess the most suitable automation organization for automation specialists, where they may effectively improve their abilities and areas of expertise. Hayat et al. (2023) extended the IVq-ROFSS to generalized IVq-ROFSS with its AOs and fundamental properties. Zulqarnain et al. (2024) developed the correlation-based TOPSIS method in the IVq-ROFSS structure and used their developed model in optimal cloud service provider selection.
Liao and Ho (2014) applied the failure mode and effects analysis methodology to examine the risk factors within BMW organizations. Rajan et al. (2019) reported an operational use of bio-remediation techniques in managing BMW. Nikolic et al. (2016) investigated the management of contagious healthcare waste by using the techniques of the Fault Tree Analysis approach in conjunction with risk estimation. In their study, Danner et al. (2011) assessed the integration of patients' perspectives into health technology, employing the analytic hierarchy process (AHP) methodology. Adunlin et al. (2015) examined a comprehensive literature review of medical care using multi-criteria decision analysis. Aung et al. (2019) are conducting the multi-criteria decision-making (MCDM) study, and eight hospitals in Myanmar have chosen to participate in the evaluation of BMW management approaches, both public and private. Liu et al. (2015a) introduced a new MCDM methodology that integrates the 2-tuple DEMATEL approach with the fuzzy Multi-Objective Optimisation based on the Ratio Analysis (MULTIMOORA) approach. Chauhan and Singh (Chauhan and Singh 2016) utilized the AHP and fuzzy TOPSIS method to tackle the issue of locating the disposal of medical waste sites. Hossain et al. (2011) investigated the impacts of healthcare waste disposal practices on people's health and the surroundings by employing group decision-making. Chou et al. (2008) designed a fuzzy MAGDM framework to address the site location allocation issue. Narayanamoorthy et al. (2020) proposed a simple ratio analysis strategy to estimate BMW disposal treatment techniques. Manupati et al. (2021) proposed a fuzzy VIsekriterijumsko KOmpromisno Rangiranje (VIKOR) technique to find the best BMW waste management methods before and after COVID-19 issues. Liu et al. (2021) proposed an integrated compromise approach to assess medical waste treatment techniques under the PF framework. Li et al. (2021) used the IVFS to explore the most significant factors affecting medical waste management's sustainability over the long term. Ozcelik and Nalkiran ( 2021) modified the Evaluation based on Distance from Average Solution (EDAS) technique in a trapezoidal bipolar fuzzy environment to boost healthcare management.
Dincer et al. (2023) developed the spherical fuzzy ranking technique using the geometric mean of similarity ratio to optimal solution determinants of the renewable energy transition. Nezhad et al. (2023) used the fuzzy DEMATEL and fuzzy AHP methods to rank and observe dimensions affecting the inclination of the execution of the Internet of Things. Al-Zibaree and Konur ( 2023) proposed a fuzzy analytic hierarchy process to solve MCDM complications. Ghoushchi and Sarvi (2023) discussed assessing and prioritizing risks in chemotherapy ordering and prescribing procedures. Barakati and Rani ( 2023) introduced a unique parametric divergence measure and proposed a double normalization-based multi-aggregation technique for IVIFS intending to solve MCDM obstacles. Chaurasiya and Jain (2022) established an entropy measure to assess the PFS. Also, they enlarged the use of complex proportional assessment methods to tackle the obstacles faced in MCDM issues. Rani et al. (2020) introduced an MCDM strategy for selecting and evaluating medical waste management approaches using Pythagorean fuzzy stepwise weight assessment ratio analysis. Limboo and Dutta (2022) proposed the q-rung orthopair basic probability assignment, which consists of a pair of belief degrees. Joshi and Gegov (2020) introduced the confidence levels of q‐rung orthopair fuzzy AOs and their applications to solve MCDM problems. Ranjan et al. (2023) developed the Archimedean AOs in probabilistic linguistic q-ROFS structure and established a group decision-making model to resolve real-life complications. Ahemad et al. (2023) established a novel distance measure for IVq-ROFNs and enlarged the implementation of the Complex Proportional Assessment approach to tackle MAGDM issues. Wan et al. (2023) developed the weighted fairly aggregation operator in the IVq-ROFS structure and developed a novel group decision-making model.
Wang and Liu (2012a, 2011) constructed the Einstein AOs for IFS as a solution to tackle the complicated nature of MAGDM issues, depicting inspirations from the remarkable nature of Einstein operations. Liu et al. (2015b) explored the use of Einstein averaging AOs for MAGDM challenges in the structure of IVIFS. Wang and Liu (2012b) prolonged the Einstein geometric AOs to incorporate IVIFS and designed a DM approach to deal with MAGDM challenges. Garg (2016, 2017) proposed the Einstein AOs and Einstein-ordered AOs for PFS. Rehman et al. (2018, 2020) extended a DM strategy to handle MAGDM problems and developed Einstein AOs for IVPFS. Xu (2023) developed Einstein's AOs in the IVq-ROFS structure to formulate an algorithm for locating recycling sources for bike sharing. Zulqarnain et al. (2021, 2022b) extended the Einstein operational laws for PFSS and presented the Einstein AOs for PFSS to account for difficult real-world situations. Furthermore, they proposed the DM strategies associated with their established Einstein AOs for q-ROFSS (Zulqarnain et al. 2022c, 2022d).
The EDAS methodology, initially proposed by Ghorabaee et al. (2015), gained prominence as a reliable method for the mathematical modeling of MAGDM issues that incorporate competing parameters. The EDAS methodology, as described by Ghorabaee et al. (2016), uses the average solution (AVS) to ascertain the significance of solutions by considering the disparity in AVS. Ilieva (Ilieva 2018) developed the EDAS method for IVFS to solve group decision-making problems. Mishra et al. (2020) extended the EDAS technique in the IF structure and explored hospital waste management practices. Li and Wang (2020) developed the EDAS method for IVIFS and used it to improve the quality of wireless sensor networks. The EDAS approach for PFS was extended by Liu et al. (2022). Yanmaz et al. (2020) extended the EDAS approach for IVPFS to solve the MCGDM problem. Güneri and Deveci (2023) used the EDAS technique to assess the selection criteria utilized by supplier businesses in the defense industry within a q-ROF context. Farrokhizadeh et al. (2020) extended the EDAS method in the structure of IVq-ROFS to resolve MAGDM problems in sustainable supplier selection.
After a detailed analysis of BMW’s management practices determined that no EDAS model had been developed within the IVq-ROFSS structure to choose the most suitable management structure for BMW effectively. This study aims to introduce an innovative EDAS technique to solve MAGDM problems within the framework of the IVq-ROFSS environment. The strategy establishes a reliable evaluation of BMW organizations using specified attribute weights. An outline of the justifications for why this study is necessary is provided below:
-
1.
The IVq-ROFSS model’s wide range of applicability allows it to reveal complicated data in a versatile and fact-encompassing mode; it is, after all, an environment-based DM strategy. Thus, the DM mechanism within the IVq-ROFSS structure deserves more attention.
-
2.
The Einstein operations are quite flexible because of the parameters. The literature shows that Einstein operations in IVq-ROFSS structure. We present a novel, Einstein-based operational laws for the IVq-ROFSS. We will develop the Einstein-ordered and Einstein hybrid AOs based on these operational laws with their fundamental properties.
-
3.
The EDAS method has become widely used since it is easy to use and produces excellent results in the DM process. The EDAS approach generates more robust and reliable decision outcomes than existing techniques.
-
4.
Numerous scholars have established several types of MAGDM approaches, including TOPSIS, VIKOR, and EDAS, in the existing collection of research. These approaches attempt to determine the most effective BMW disposal location or strategy in different fuzzy contexts. However, there has been a shortage of scientific studies on managing BMW in an IVq-ROFSS scenario using the EDAS technique. Moreover, selecting the optimal organization from a BMW management perspective has emerged as a big challenge for emerging economies in recent decades. Choosing the most suitable BMW management organization is not simple for the MAGDM procedure. The determined deficiencies in research will be addressed by applying the designed integrative model that exploits the IVq-ROFSS information to select the most significant BMW management bodies.
The suggested solution could resolve the following problems: How can the most optimal BMW management organization be effectively chosen amidst uncertain conditions? How can we accumulate information about the abilities of BMW's managerial team? How will the EDAS approach be used to develop the BMW management organization selection procedure?
Based on the above-described motivations, this research reveals multiple remarkable innovations explained as follows:
-
(1)
The formulation and demonstration of IVq-ROFSS Einstein AOs have been executed by integrating Einstein operations into the IVq-ROFSS paradigm. These operators are given as follows: interval-valued q-rung orthopair fuzzy soft Einstein ordered weighted average (IVq-ROFSEOWA), interval-valued q-rung orthopair fuzzy soft Einstein hybrid weighted average (IVq-ROFSEHWA), interval-valued q-rung orthopair fuzzy soft Einstein ordered weighted geometric (IVq-ROFSEOWG), and interval-valued q-rung orthopair fuzzy soft Einstein hybrid weighted geometric (IVq-ROFSEHWG) operators. Furthermore, we effectively defined and validated multiple fundamental aspects of these operators, particularly idempotency, boundedness, monotonicity, homogeneity, and shift-invariance.
-
(2)
A novel EDAS technique is developed using the proposed IVq-ROFSS Einstein AOs to solve MAGDM problems. The methodical process can be summarized into two main phases:
-
The starting point includes the compilation of data using the implementation of IVq-ROFSS Einstein AOs.
-
In the next phase, an EDAS algorithm is constructed in the IVq-ROFSS structure to find the most efficient alternative. This technique not only presents a viable reaction to complicated problems with decision-making but also includes the current decision-making theory by incorporating this unique approach.
-
-
(3)
The suggested approach is implemented to analyze and choose the BMW management structure. This investigation effectively tackles the current literature gaps in selecting a BMW management structure and provides an achievable solution. The method conducts comparative and sensitivity assessments, which are thoroughly investigated and analyzed. The research findings indicate the reliability and benefits of the advocated method.
The structure of this study is presented in the following way. Section 1 provides an introduction to the significance of incorporating the consideration of uncertainty and incomplete information within decision-making (DM) techniques. Section 2 presents a comprehensive discussion of the fundamental ideas and tenets that form the foundation of the subsequent research. This section builds the circumstances for the following proposals by presenting a foundation for appreciating the complexity of data management issues and the necessity for an improved, reliable, and precise methodology. Section 3 presents the operating laws proposed by Einstein for IVq-ROFSS and proceeds to establish the IVq-ROFSEOWA and IVq-ROFSEHWA operators, together with their significant qualities. Section 4 of the paper introduces the IVq-ROFSEOWG and IVq-ROFSEHWG operators and explains their respective features. Section 5 presents a novel MAGDM technique founded upon the principles of Einstein’s AOs. A numerical investigation illustrates the feasibility of the proposed model, as outlined in Sect. 6. The objective is to determine the most effective BMW management organization within the medical field. Section 7 of the study encompasses a comprehensive comparison analysis, determining the pragmatic nature of a model put forward in this research. In this analysis, we will assess the suggested methodology with reputable approaches, focusing on the metrics of reliability and precision. The benefits of this approach are concisely stated in the same section as well.
2 Preliminaries
The following section will look at basic ideas such as IVFS, SS, PFSS, IVIFSS, IVPFSS, q-ROFSS, and IVq-ROFSS to build a solid foundation for the subsequent discussion.
Definition 2.1 Turksen (1986)
An interval-valued fuzzy set \(\beta\) in a universe of discourse \(U\) is defined as:
where, \({\lambda }_{{\beta }_{j}}\left({u}_{i}\right)\) be the membership degree interval, such as \({\lambda }_{{\beta }_{j}}\left({u}_{i}\right)=\left[{\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\), also, \(\left[{\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\subseteq \left[0,1\right]\) and \({\lambda }_{{\mathcal{A}}_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\mathcal{A}}_{j}}^{\mho }\left({u}_{i}\right)\in \left[0,1\right]\).
The process of transforming interval-valued fuzzy sets into interval-valued intuitionistic fuzzy sets, and vice versa, will be performed easily.
Definition 2.2 Atanassov (1999)
An interval-valued intuitionistic fuzzy set \(\beta\) in a universe of discourse \(U\) is defined as:
where, \({\lambda }_{{\beta }_{j}}\left({u}_{i}\right)=\left[{\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\) and \({\eta }_{{\beta }_{j}}\left({u}_{i}\right)=\left[{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\) be the membership degree and non-membership degree intervals, respectively. Also, \(\left[{\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\subseteq \left[0,1\right]\) and \(\left[{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\subseteq \left[0,1\right]\), \(0\le {\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\le 1\), such as \(0\le {\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)+{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\le 1\).
Definition 2.3 Peng and Yang (2016)
An interval-valued Pythagorean fuzzy set \(\beta\) in a universe of discourse \(U\) is defined as:
where, \({\lambda }_{{\beta }_{j}}\left({u}_{i}\right)=\left[{\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\) and \({\eta }_{{\beta }_{j}}\left({u}_{i}\right)=\left[{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\) be the membership degree and non-membership degree intervals, respectively. Also, \(\left[{\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\subseteq \left[0,1\right]\) and \(\left[{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\subseteq \left[0,1\right]\), \(0\le {\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\le 1\), such as \(0\le {\left({\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right)}^{2}+{\left({\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right)}^{2}\le 1\).
This model was extended to the following concept:
Definition 2.4 Joshi et al. (2018)
An interval-valued q-rung orthopair fuzzy set \(\beta\) in a universe of discourse \(U\) is defined as:
where, \({\lambda }_{{\beta }_{j}}\left({u}_{i}\right)=\left[{\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\) and \({\eta }_{{\beta }_{j}}\left({u}_{i}\right)=\left[{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\) be the membership degree and non-membership degree intervals, respectively. Also, \(\left[{\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\subseteq \left[0,1\right]\) and \(\left[{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\subseteq \left[0,1\right]\), \(0\le {\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\le 1\), such as \(0\le {\left({\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right)}^{q}+{\left({\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right)}^{q}\le 1\); where \(q>2\).
A q-rung orthopair fuzzy set is a term ascribed to the corresponding model defined in Definition 2.4 if all intervals are reduced to single points. A previous study (Alcantud 2023) has effectively handled the challenge of choosing the most suitable value of q for describing a dataset that includes orthopairs (pairs of numbers within the interval [0,1]) as a q-ROFS, which also provides reasons for the logic of the predictive model.
Now, we intend to turn our interest to a distinct technique that contains uncertain facts:
Definition 2.5 Molodtsov (1999)
Let \(U\) be a universe of discourse, and \(\mathfrak{R}\) be the set of attributes, \(\mathcal{P}(U)\) be the power set over \(U\) and \(\beta \subseteq \mathfrak{R}\). Then, a pair \(\left(\mathcal{G},\beta \right)\) is called a soft set over \(U\), where \(\mathcal{G}\) is a mapping:
Moreover, it can be presented in the following way:
The intellectual study of the theoretical significance of soft sets is explored in Yang and Yao (2020) and (Alcantud 2022). Both studies concentrate on the premise of three-way decision-making.
Developing models that integrate the characteristics stated in Definition 2.5 with the previously articulated model is feasible. In this study, we will describe various fascinating scenarios.
Definition 2.6 Jiang et al. (2010)
Let \(U\) be a universe of discourse, and \(\mathfrak{R}\) be the set of attributes, \(\mathcal{P}(U)\) be the power set over \(U\) and \(\beta \subseteq \mathfrak{R}\). Then, a pair \(\left(\mathcal{G},\beta \right)\) is called an IVIFSS over \(U\), where \(\mathcal{G}\) is a mapping:
Moreover, it can be presented in the following way:
where, \({\lambda }_{{\beta }_{j}}\left({u}_{i}\right)=\left[{\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\) and \({\eta }_{{\beta }_{j}}\left({u}_{i}\right)=\left[{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\) be the membership degree and non-membership degree intervals, respectively. Also, \(\left[{\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\subseteq \left[0,1\right]\) and \(\left[{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\subseteq \left[0,1\right]\), \(0\le {\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\le 1\), such as \(0\le {\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)+{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\le 1\).
Definition 2.7 Zulqarnain et al. (2022a)
Let \(U\) be a universe of discourse, and \(\mathfrak{R}\) be the set of attributes, \(\mathcal{P}(U)\) be the power set over \(U\) and \(\beta \subseteq \mathfrak{R}\). Then, a pair \(\left(\mathcal{G}, \beta \right)\) is called an IVPFSS over \(U\), where \(\mathcal{G}\) is a mapping:
Moreover, it can be presented in the following way:
where, \({\lambda }_{{\beta }_{j}}\left({u}_{i}\right)=\left[{\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\) and \({\eta }_{{\beta }_{j}}\left({u}_{i}\right)=\left[{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\) be the membership degree and non-membership degree intervals, respectively. Also, \(\left[{\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\subseteq \left[0,1\right]\) and \(\left[{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\subseteq \left[0,1\right]\), \(0\le {\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\le 1\), such as \(0\le {\left({\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right)}^{2}+{\left({\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right)}^{2}\le 1\).
If \({\left({\lambda }_{ij}^{\mho }\right)}^{q}+{\left({\eta }_{ij}^{\mho }\right)}^{q}>1\), for \(q>2\), in such situations, the structures, such as IVIFSS (Jiang et al. 2010) and IVPFSS (Zulqarnain et al. 2022a), can't effectively replicate this information. In such cases, an IVq-ROFSS, which incorporates the distinctive features of IVq-ROFS and SS, can be considered a modified version of IVIFSS and IVPFSS, which appears to be an extraordinarily productive tool. IVq-ROFSS is an optimized, more powerful extension of IVq-ROFS with more capabilities. IVq-ROFSS provides accurate analysis of disruption and uncertainty, assisting in a comprehensive and reliable review of multifaceted information repositories. The IVq-ROFSS method demonstrates the practical implications of its use in decision-making and statistical evaluation.
Definition 2.8 Yang et al. (2022)
Let \(U\) be a universe of discourse, and \(\mathfrak{R}\) be the set of attributes, \(\mathcal{P}(U)\) be the power set over \(U\) and \(\beta \subseteq \mathfrak{R}\). Then, a pair \(\left(\mathcal{G},\beta \right)\) is called an IVq-ROFSS over \(U\), where \(\mathcal{G}\) is a mapping:
Furthermore, it can be presented in the following way:
where, \({\lambda }_{{\beta }_{j}}\left({u}_{i}\right)=\left[{\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\) and \({\eta }_{{\beta }_{j}}\left({u}_{i}\right)=\left[{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\) be the membership degree and non-membership degree intervals, respectively. Also, \(\left[{\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\subseteq \left[0,1\right]\) and \(\left[{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\subseteq \left[0,1\right]\), \(0\le {\lambda }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\le 1\), such as \(0\le {\left({\lambda }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right)}^{q}+{\left({\eta }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right)}^{q}\le 1\), for \(q>2\). Also, \({\pi }_{{\beta }_{j}}\left({u}_{i}\right)=\left[{\pi }_{{\beta }_{j}}^{l}\left({u}_{i}\right),{\pi }_{{\beta }_{j}}^{\mho }\left({u}_{i}\right)\right]\) be the indeterminacy of IVq-ROFSS. It can be calculated as:
In this context, we will proceed to deliver the operational laws, which are listed below:
Definition 2.9 Yang et al. (2022)
Let \({{\Delta }}_{a}=\left(\left[{\lambda }_{a}^{l},{\lambda }_{a}^{\mho }\right],\left[{\eta }_{a}^{l},{\eta }_{a}^{\mho }\right]\right)\), \({{\Delta }}_{{a}_{11}}=\left(\left[{\lambda }_{{a}_{11}}^{l},{\lambda }_{{a}_{11}}^{\mho }\right],\left[{\eta }_{{a}_{11}}^{l},{\eta }_{{a}_{11}}^{\mho }\right]\right)\), and \({{\Delta }}_{{a}_{12}}=\left(\left[{\lambda }_{{a}_{12}}^{l},{\lambda }_{{a}_{12}}^{\mho }\right],\left[{\eta }_{{a}_{12}}^{l},{\eta }_{{a}_{12}}^{\mho }\right]\right)\) be the interval-valued q-rung orthopair fuzzy soft numbers (IVq-ROFSNs) and \(\theta >0\). Then, the algebraic operational laws which were defined by Yang et al. (Yang et al. 2022) for IVq-ROFSNs are given as follows:
-
(1)
\({{\Delta }}_{{a}_{11}}\oplus {{\Delta }}_{{a}_{12}}=\left(\left[\sqrt[q]{{\left({\lambda }_{{a}_{11}}^{l}\right)}^{q}+{\left({\lambda }_{{a}_{12}}^{l}\right)}^{q}-{\left({\lambda }_{{a}_{11}}^{l}\right)}^{q}{\left({\lambda }_{{a}_{12}}^{l}\right)}^{q}},\sqrt[q]{{\left({\lambda }_{{a}_{11}}^{\mho }\right)}^{q}+{\left({\lambda }_{{a}_{12}}^{\mho }\right)}^{q}-{\left({\lambda }_{{a}_{11}}^{\mho }\right)}^{q}{\left({\lambda }_{{a}_{12}}^{\mho }\right)}^{q}}\right],\left[{\eta }_{{a}_{11}}^{l}{\eta }_{{a}_{12}}^{l},{\eta }_{{a}_{11}}^{\mho }{\eta }_{{a}_{12}}^{\mho }\right]\right)\)
-
(2)
\({{\Delta }}_{{a}_{11}}\otimes {{\Delta }}_{{a}_{12}}=\left(\left[{\lambda }_{{a}_{11}}^{l}{\lambda }_{{a}_{12}}^{l},{\lambda }_{{a}_{11}}^{\mho }{\lambda }_{{a}_{12}}^{\mho }\right],\left[\sqrt[q]{{\left({\eta }_{{a}_{11}}^{l}\right)}^{q}+{\left({\eta }_{{a}_{12}}^{l}\right)}^{q}-{\left({\eta }_{{a}_{11}}^{l}\right)}^{q}{\left({\eta }_{{a}_{12}}^{l}\right)}^{q}},\sqrt[q]{{\left({\eta }_{{a}_{11}}^{\mho }\right)}^{q}+{\left({\eta }_{{a}_{12}}^{\mho }\right)}^{q}-{\left({\eta }_{{a}_{11}}^{\mho }\right)}^{q}{\left({\eta }_{{a}_{12}}^{\mho }\right)}^{q}}\right]\right)\)
-
(3)
\(\theta {{\Delta }}_{a}=\left(\left[\sqrt[q]{1-{\left(1-{\left({\lambda }_{a}^{l}\right)}^{q}\right)}^{\theta }},\sqrt[q]{1-{\left(1-{\left({\lambda }_{a}^{\mho }\right)}^{q}\right)}^{\theta }}\right],\left[{\left({\eta }_{a}^{l}\right)}^{\theta },{\left({\eta }_{a}^{\mho }\right)}^{\theta }\right]\right)=\left(\sqrt[q]{1-{\left(1-{\left[{\lambda }_{a}^{l},{\lambda }_{a}^{\mho }\right]}^{q}\right)}^{\theta }},\left[{\left({\eta }_{a}^{l}\right)}^{\theta },{\left({\eta }_{a}^{\mho }\right)}^{\theta }\right]\right)\)
-
(4)
\({{\Delta }}_{a}^{\theta }=\left(\left[{\left({\lambda }_{a}^{l}\right)}^{\theta },{\left({\lambda }_{a}^{\mho }\right)}^{\theta }\right],\left[\sqrt[q]{1-{\left(1-{\left({\eta }_{a}^{l}\right)}^{q}\right)}^{\theta }},\sqrt[q]{1-{\left(1-{\left({\eta }_{a}^{\mho }\right)}^{q}\right)}^{\theta }}\right]\right)=\left(\left[{\left({\lambda }_{a}^{l}\right)}^{\theta },{\left({\lambda }_{a}^{\mho }\right)}^{\theta }\right],\sqrt[q]{1-{\left(1-{\left[{\eta }_{a}^{l},{\eta }_{a}^{\mho }\right]}^{q}\right)}^{\theta }}\right)\)
The aggregation operators for IVq-ROFSS are determined by the algebraic operational rules formulated by Yang et al. (Yang et al. 2022), which are interpreted as follows:
where \(q>2\).
It is important to note that the scoring function previously mentioned fails to determine the most beneficial alternative if the MD and NMD intervals are the same. To address this, we therefore present a more thorough score function for IVq-ROFSNs:
Definition 2.10 Hayat et al. (2023)
Let \({{\Delta }}_{a}=\left(\left[{\lambda }_{a}^{l},{\lambda }_{a}^{\mho }\right],\left[{\eta }_{a}^{l},{\eta }_{a}^{\mho }\right]\right)\) be an IVq-ROFSN. Then, its score can be defined as:
where \({\left[{\pi }_{a}^{l},{\pi }_{a}^{\mho }\right]}^{q}\), \(S\left({{\Delta }}_{a}\right)\in [-1,1]\) spectacles reluctance and \(q>2\). For the sake of the reader’s convenience, the IVq-ROFSN \({{\Delta }}_{{a}_{ij}}=\left\{\left({\lambda }_{{a}_{ij}}\left({u}_{i}\right),{\eta }_{{a}_{ij}}\left({u}_{i}\right)\right)|{u}_{i}\in U\right\}\) can be described as \({{\Delta }}_{{a}_{ij}}=\left({\lambda }_{{a}_{ij}},{\eta }_{{a}_{ij}}\right)\). Let \({{\Delta }}_{{a}_{11}}=\left({\lambda }_{{a}_{11}},{\eta }_{{a}_{11}}\right)\) and \({{\Delta }}_{{a}_{12}}=\left({\lambda }_{{a}_{12}},{\eta }_{{a}_{12}}\right)\) be two IVq-ROFSNs. Then, the established comparison laws are given as follows:
If \(S\left({{\Delta }}_{{a}_{11}}\right)>S\left({{\Delta }}_{{a}_{12}}\right)\), then we state \({{\Delta }}_{{a}_{11}}\succcurlyeq {{\Delta }}_{{a}_{12}}\)
If \(S\left({{\Delta }}_{{a}_{11}}\right)<S\left({{\Delta }}_{{a}_{12}}\right)\), then we state \({{\Delta }}_{{a}_{11}}\preccurlyeq {{\Delta }}_{{a}_{12}}\)
If \(S\left({{\Delta }}_{{a}_{11}}\right)=S\left({{\Delta }}_{{a}_{12}}\right)\), then \({{\Delta }}_{{a}_{11}}={{\Delta }}_{{a}_{12}}\)
If \({\pi }_{{a}_{11}}>{\pi }_{{a}_{12}}\), then we state \({{\Delta }}_{{a}_{11}}<{{\Delta }}_{{a}_{12}}\)
If \({\pi }_{{a}_{11}}<{\pi }_{{a}_{12}}\), then we state \({{\Delta }}_{{a}_{11}}>{{\Delta }}_{{a}_{12}}\).
3 Interval-valued q-rung orthopair fuzzy soft Einstein weighted average aggregation operators
In this section, we examine the subject of IVq-ROFSS to Einstein’s operational laws. These operational laws give us a framework for organizing the considerable quantity of IVq-ROFS data. Drawing inspiration from these fundamental ideas, we provide and validate Einstein averaging AOs for IVq-ROFSVs. These operators are the IVq-ROFSEOWA and IVq-ROFSEHWA, developed to facilitate the aggregation process more efficiently. We also investigate the fundamental properties of these operators, such as idempotency, boundedness, monotonicity, homogeneity, and shift-invariance.
Definition 3.1
Let \(\Delta _{{a\varsigma }} = \left( {\left[ {\lambda _{{a_{\varsigma } }}^{l} ,\lambda _{{a_{\varsigma } }}^{\mho } } \right],\left[ {\eta _{{a_{\varsigma } }}^{l} ,\eta _{{a_{\varsigma } }}^{\mho } } \right]} \right),\Delta _{{a_{{11}} }} = \left( {\left[ {\lambda _{{a_{{11}} }}^{l} ,\lambda _{{a_{{11}} }}^{\mho } } \right],\left[ {\eta _{{a_{{11}} }}^{l} ,\eta _{{a_{{11}} }}^{\mho } } \right]} \right)~and~\Delta _{{a_{{12}} }} = \left( {\left[ {\lambda _{{a_{{12}} }}^{l} ,\eta _{{a_{{12}} }}^{\mho } } \right],\left[ {\lambda _{{a_{{12}} }}^{l} ,\eta _{{a_{{12}} }}^{\mho } } \right]} \right)\) be three q-ROFSVs and \(\theta >0\) be any real number, then
-
(1)
$${\Delta }_{{a}_{11}}{\oplus }_{\varepsilon }{\Delta }_{{a}_{12}}=\left(\begin{array}{c}\left[\begin{array}{c}\frac{\sqrt[q]{{\left({\lambda }_{{a}_{11}}^{l}\right)}^{q}+{\left({\lambda }_{{a}_{12}}^{l}\right)}^{q}}}{\sqrt[q]{1+{\left({\lambda }_{{a}_{11}}^{l}\right)}^{q}{\left({\lambda }_{{a}_{12}}^{l}\right)}^{q}}},\frac{\sqrt[q]{{\left({\lambda }_{{a}_{11}}^{\mathrm{\mho }}\right)}^{q}+{\left({\lambda }_{{a}_{12}}^{\mathrm{\mho }}\right)}^{q}}}{\sqrt[q]{1+{\left({\lambda }_{{a}_{11}}^{\mathrm{\mho }}\right)}^{q}{\left({\lambda }_{{a}_{12}}^{\mathrm{\mho }}\right)}^{q}}}\end{array}\right],\left[\begin{array}{c}\frac{\left({\eta }_{{a}_{11}}^{l}\right)\left({\eta }_{{a}_{12}}^{l}\right)}{\sqrt[q]{1+\left(1-{\left({\eta }_{{a}_{11}}^{l}\right)}^{q}\right)\left(1-{\left({\eta }_{{a}_{12}}^{l}\right)}^{q}\right)}},\frac{\left({\eta }_{{a}_{11}}^{\mathrm{\mho }}\right)\left({\eta }_{{a}_{12}}^{\mathrm{\mho }}\right)}{\sqrt[q]{1+\left(1-{\left({\eta }_{{a}_{11}}^{\mathrm{\mho }}\right)}^{q}\right)\left(1-{\left({\eta }_{{a}_{12}}^{\mathrm{\mho }}\right)}^{q}\right)}}\end{array}\right]\end{array}\right)$$
-
(2)
$${\Delta }_{{a}_{11}}{\oplus}_{\varepsilon }{\Delta }_{{a}_{12}}=\left(\begin{array}{c}\left[\begin{array}{c}\frac{\left({\lambda }_{{a}_{11}}^{l}\right)\left({\lambda }_{{a}_{12}}^{l}\right)}{\sqrt[q]{1+\left(1-{\left({\lambda }_{{a}_{11}}^{l}\right)}^{q}\right)\left(1-{\left({\lambda }_{{a}_{12}}^{l}\right)}^{q}\right)}},\frac{\left({\lambda }_{{a}_{11}}^{\mathrm{\mho }}\right)\left({\lambda }_{{a}_{12}}^{\mathrm{\mho }}\right)}{\sqrt[q]{1+\left(1-{\left({\lambda }_{{a}_{11}}^{\mathrm{\mho }}\right)}^{q}\right)\left(1-{\left({\lambda }_{{a}_{12}}^{\mathrm{\mho }}\right)}^{q}\right)}}\end{array}\right],\left[\begin{array}{c}\frac{\sqrt[q]{{\left({\eta }_{{a}_{11}}^{l}\right)}^{q}+{\left({\eta }_{{a}_{12}}^{l}\right)}^{q}}}{\sqrt[q]{1+{\left({\eta }_{{a}_{11}}^{l}\right)}^{q}{\left({\eta }_{{a}_{12}}^{l}\right)}^{q}}},\frac{\sqrt[q]{{\left({\eta }_{{a}_{11}}^{\mathrm{\mho }}\right)}^{q}+{\left({\eta }_{{a}_{12}}^{\mathrm{\mho }}\right)}^{q}}}{\sqrt[q]{1+{\left({\eta }_{{a}_{11}}^{\mathrm{\mho }}\right)}^{q}{\left({\eta }_{{a}_{12}}^{\mathrm{\mho }}\right)}^{q}}}\end{array}\right]\end{array}\right)$$
-
(3)
$$\Delta _{{a_{\varsigma } }}^{\theta } \, = \,\left( {\begin{array}{*{20}c} {\left[ {\frac{{\sqrt[q]{{2\left( {\left( {\lambda _{{a_{\varsigma } }}^{l} } \right)^{q} } \right)^{\theta } }}}}{{\sqrt[q]{{\left( {2 - \left( {\lambda _{{a_{\varsigma } }}^{l} } \right)^{q} } \right)^{\theta } + \left( {\left( {\lambda _{{a_{\varsigma } }}^{l} } \right)^{q} } \right)^{\theta } }}}},\frac{{\sqrt[q]{{2\left( {\left( {\eta _{{a_{\varsigma } }}^{\mho } } \right)^{q} } \right)^{\theta } }}}}{{\sqrt[q]{{\left( {2 - \left( {\eta _{{a_{\varsigma } }}^{\mho } } \right)^{q} } \right)^{\theta } + \left( {\left( {\eta _{{a_{\varsigma } }}^{\mho } } \right)^{q} } \right)^{\theta } }}}}} \right],~~\left[ {\begin{array}{*{20}c} {\frac{{\sqrt[q]{{\left( {1 + \left( {\eta _{{a_{\varsigma } }}^{l} } \right)^{q} } \right)^{\theta } - \left( {1 - \left( {\eta _{{a_{\varsigma } }}^{l} } \right)^{q} } \right)^{\theta } }}}}{{\sqrt[q]{{\left( {1 + \left( {\eta _{{a_{\varsigma } }}^{l} } \right)^{q} } \right)^{\theta } + \left( {1 - \left( {\eta _{{a_{\varsigma } }}^{l} } \right)^{q} } \right)^{\theta } }}}},\frac{{\sqrt[q]{{\left( {1 + \left( {\eta _{{a_{\varsigma } }}^{\mho } } \right)^{q} } \right)^{\theta } - \left( {1 - \left( {\eta _{{a_{\varsigma } }}^{\mho } } \right)^{q} } \right)^{\theta } }}}}{{\sqrt[q]{{\left( {1 + \left( {\eta _{{a_{\varsigma } }}^{\mho } } \right)^{q} } \right)^{\theta } + \left( {1 - \left( {\eta _{{a_{\varsigma } }}^{\mho } } \right)^{q} } \right)^{\theta } }}}}} \\ \end{array} } \right]} \\ \end{array} } \right)$$
-
(4)
$$\theta \Delta _{{a_{\varsigma } }} \, = \,\left( {\left[ {\begin{array}{*{20}c} {\frac{{\sqrt[q]{{\left( {1 + \left( {\lambda _{{a_{\varsigma } }}^{l} } \right)^{q} } \right)^{\theta } - \left( {1 - \left( {\lambda _{{a_{\varsigma } }}^{l} } \right)^{q} } \right)^{\theta } }}}}{{\sqrt[q]{{\left( {1 + \left( {\lambda _{{a_{\varsigma } }}^{l} } \right)^{q} } \right)^{\theta } + \left( {1 - \left( {\lambda _{{a_{\varsigma } }}^{l} } \right)^{q} } \right)^{\theta } }}}},\frac{{\sqrt[q]{{\left( {1 + \left( {\lambda _{{a_{\varsigma } }}^{\mho } a_{\varsigma } } \right)^{q} } \right)^{\theta } - \left( {1 - \left( {\lambda _{{a_{\varsigma } }}^{\mho } } \right)^{q} } \right)^{\theta } }}}}{{\sqrt[q]{{\left( {1 + \left( {\lambda _{{a_{\varsigma } }}^{\mho } } \right)^{q} } \right)^{\theta } + \left( {1 - \left( {\lambda _{{a_{\varsigma } }}^{\mho } } \right)^{q} } \right)^{\theta } }}}}} \\ \end{array} } \right],\,\left[ {\begin{array}{*{20}c} {\frac{{\sqrt[q]{{\left( {\left( {\eta _{{a_{\varsigma } }}^{l} } \right)^{q} } \right)^{\theta } }}}}{{\sqrt[q]{{\left( {2 - \left( {\eta _{{a_{\varsigma } }}^{l} } \right)^{q} } \right)^{\theta } + \left( {\left( {\eta _{{a_{\varsigma } }}^{l} } \right)^{q} } \right)^{\theta } }}}},\frac{{\sqrt[q]{{\left( {\left( {\eta _{{a_{\varsigma } }}^{\mho } } \right)^{q} } \right)^{\theta } }}}}{{\sqrt[q]{{\left( {2 - \left( {\eta _{{a_{\varsigma } }}^{\mho } } \right)^{q} } \right)^{\theta } + \left( {\left( {\lambda _{{a_{\varsigma } }}^{\mho } } \right)^{q} } \right)^{\theta } }}}}} \\ \end{array} } \right]} \right)$$
Definition 3.2
Let \({{\Delta }}_{{a}_{ij}}=\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right],\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right),\) where \(\left(i=\mathrm{1,2},\dots \dots .n;j=\mathrm{1,2},\dots \dots .m\right)\) be a collection of IVq-ROFSVs. Then IVq-ROFSEOWA is defined as:
where \(\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)\) be the permutation of \(\left(i=\mathrm{2,3},\dots \dots .n;j=\mathrm{1,2},\dots \dots .m\right)\), such as \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}\le {{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i-1\right)\mathfrak{s}\left(j\right)}\right)}\) \(\forall\) \(i=\mathrm{2,3},\dots \dots .n;j=\mathrm{1,2},\dots \dots .m\) and \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}\le {{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j-1\right)}\right)}\) \(\forall\) \(i=\mathrm{2,3},\dots \dots .n;j=\mathrm{2,3},\dots \dots .m\). Also, \({v}_{i}\) and \({w}_{j}\) be the weights of experts and attributes such as \({v}_{i}>0,\sum _{i=1}^{n}{v}_{i}>0\) and \({w}_{j}>0,\sum _{j=1}^{m}{w}_{j}=1\).
Theorem 3.3
Let \({\Delta }_{{a}_{ij}}=\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right],\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right)\) be a collection of IVq-ROFSVs where \(\left(i=\mathrm{1,2},\dots \dots .n;j=\mathrm{1,2},\dots \dots .m\right)\). Then, the aggregation outcome of the IVq-ROFSEOWA operator is also an IVq-ROFSV and
where \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}\) be the largest element of \({i}^{th}\) row and \({j}^{th}\) column in \(\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots ,{{\Delta }}_{{a}_{nm}}\right)\), such as \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}\le {{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i-1\right)\mathfrak{s}\left(j\right)}\right)}\) and \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}\le {{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j-1\right)}\right)}\) \(\forall i,j\). Also, \({v}_{i}\) and \({w}_{j}\) be the weights of experts and attributes such as \({v}_{i}>0,\sum _{i=1}^{n}{v}_{i}>0\) and \({w}_{j}>0,\sum _{j=1}^{m}{w}_{j}=1\).
Proof:
See Appendix 1.
Proposition 3.4
If \({\Delta }{}_{{a}_{ij}}=\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right],\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right)\); \(\left(i=1,2,3,\dots ,n;j=1,2,3,\dots ,m\right)\) be a collection of IVq-ROFSVs. Also, \({v}_{i}\) and \({w}_{j}\) be the weights of experts and attributes such as \({v}_{i}>0,\sum _{i=1}^{n}{v}_{i}=1\) and \({w}_{j}>0,\sum _{j=1}^{m}{w}_{j}=1\).
3.4.1. Idempotency. Let \({\Delta }{}_{{a}_{ij}}={\Delta }{}_{{a}_{o}}=\left(\left[{{\lambda }_{{a}_{o}}}_{}^{l},{\lambda }_{{a}_{o}}^{\mathrm{\mho }}\right],\left[{\eta }_{{a}_{o}}^{l},{\eta }_{{a}_{o}}^{\mathrm{\mho }}\right]\right)\) holds for any \(i=1,2,3,\dots ,n;j=1,2,3,\dots ,m\). Then,
Proof:
See Appendix 2.
3.4.2. Boundedness. \({{\Delta }}_{{a}_{ij}}^{-}=\left(\left[min\left({\lambda }_{{a}_{ij}}^{l}\right),min\left({\lambda }_{{a}_{ij}}^{\mathrm{\mho }}\right)\right],\left[max\left({\eta }_{{a}_{ij}}^{l}\right),max\left({\eta }_{{a}_{ij}}^{\mathrm{\mho }}\right)\right]\right)\) and \({{\Delta }}_{{a}_{ij}}^{+}=\left(\left[max\left({\lambda }_{{a}_{ij}}^{l}\right),max\left({\lambda }_{{a}_{ij}}^{\mathrm{\mho }}\right)\right],\left[min\left({\eta }_{{a}_{ij}}^{l}\right),min\left({\eta }_{{a}_{ij}}^{\mathrm{\mho }}\right)\right]\right)\). Then
Proof:
See Appendix 2.
3.4.3. Monotonicity. Let \({\Delta }{}_{{a}_{ij}}=\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mathrm{\mho }}\right],\left[{\eta }_{{a}_{ij}}^{L},{\eta }_{{a}_{ij}}^{\mathrm{\mho }}\right]\right)and{{\Delta }}_{{a}_{ij}}^{\mathrm{*}}=\left(\left[{{\lambda }^{\mathrm{*}}}_{{a}_{ij}}^{l},{{\lambda }^{\mathrm{*}}}_{{a}_{ij}}^{\mathrm{\mho }}\right],\left[{{\eta }^{\mathrm{*}}}_{{a}_{ij}}^{l},{{\eta }^{\mathrm{*}}}_{{a}_{ij}}^{\mathrm{\mho }}\right]\right)\) be the families of IVq-ROFSVs. Then
\(IVq-ROFSEOWA\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right)\le IVq-ROFSEOWA\left({{\Delta }}_{{a}_{11}}^{\mathrm{*}},{{\Delta }}_{{a}_{12}}^{\mathrm{*}},\dots \dots \dots ,{{\Delta }}_{{a}_{nm}}^{\mathrm{*}}\right)\), if \({{\Delta }}_{{a}_{nm}}\le {{\Delta }}_{{a}_{nm}}^{\mathrm{*}}\) \(\forall i,j\).
Proof:
See Appendix 2.
3.4.4. Homogeneity. Let \({\Delta }{}_{{a}_{ij}}=\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mathrm{\mho }}\right],\left[{\eta }_{{a}_{ij}}^{L},{\eta }_{{a}_{ij}}^{\mathrm{\mho }}\right]\right)\) be a collection of IVq-ROFSVs, where, \(i=1,2,3,\dots ,m;j=1,2,3,\dots ,n\). Then
\(IVq-ROFSEOWA\left(\theta {{\Delta }}_{{a}_{11}},\theta {{\Delta }}_{{a}_{12}},\dots \dots \theta {{\Delta }}_{{a}_{nm}}\right)=\theta IVq-ROFSEOWA\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right)\) For \(\theta >0.\)
Proof:
See Appendix 2.
3.4.5. Shift Invariance. Let \({\Delta }{}_{{a}_{ij}}=\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mathrm{\mho }}\right],\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mathrm{\mho }}\right]\right)\) be a collection of IVq-ROFSVs and \({\Delta }{}_{a}=\left(\left[{\lambda }_{a}^{l},{\lambda }_{a}^{\mathrm{\mho }}\right],\left[{\eta }_{a}^{l},{\eta }_{a}^{\mathrm{\mho }}\right]\right)\) be an IVq-ROFSV. Then
Proof:
See Appendix 2.
Remark 3.1
Concerning the relations between different ideas, it is necessary to consider the subsequent aspects:
If \(q=2\) and \({\left({\lambda }_{ij}^{\mho }\right)}^{q}+{\left({\eta }_{ij}^{\mho }\right)}^{q}\le 1\), then the IVq-ROFSS reduces to an IVPFSS (Zulqarnain et al. 2022a).
If \(q=1\) and \({\left({\lambda }_{ij}^{\mho }\right)}^{q}+{\left({\eta }_{ij}^{\mho }\right)}^{q}\le 1\), then the IVq-ROFSS reduces to an IVIFSS (Jiang et al. 2010).
The IVq-ROFSS, when a single attribute exists, simplifies to an IVq-ROFS (Joshi et al. 2018).
Hybrid operators deliver a way to seamlessly include multiple aspects, particularly opinions of experts, and attribute importance weights. The Einstein-ordered aggregation operators mainly concentrate on the ordered placement of variables. This feature retains particular significance in practical scenarios while decision inputs originate from multiple sources and opinions. Using Einstein hybrid aggregation operators enables an improved and versatile strategy for aggregation, enabling cases when integrating both factors is necessary. However, it is necessary to recall that all these operators solely focus on a particular subset of these factors. In the following, we will look at the IVq-ROFSEHWA operator as a potential solution for this limitation.
Definition 3.5
Let \({{\Delta }}_{{a}_{ij}}^{\text{'}}=\left(\left[{{\lambda }^{\text{'}}}_{{a}_{ij}}^{l},{{\lambda }^{\text{'}}}_{{a}_{ij}}^{\mho }\right],\left[{{\eta }^{\text{'}}}_{{a}_{ij}}^{l},{{\eta }^{\text{'}}}_{{a}_{ij}}^{\mho }\right]\right),\) where \(\left(i=\mathrm{1,2},\dots \dots .n;j=\mathrm{1,2},\dots \dots .m\right)\) be a collection of IVq-ROFSVs. Then IVq-ROFSEHWA is defined as:
where \({v}_{i}={\left\{{v}_{1},{v}_{2},\dots \dots ,{v}_{n}\right\}}^{T}\) and \({v}_{i}={\left\{{w}_{1},{w}_{2},\dots \dots ,{w}_{j}\right\}}^{T}\) be the weight vectors for experts and parameters such as \({v}_{i}>0,\sum _{i=1}^{n}{v}_{i}=1\) and \({w}_{j}>0,\sum _{j=1}^{m}{w}_{j}=1\) and \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\text{'}}\) be the largest element interval-valued q-rung orthopair fuzzy soft arguments \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\text{'}}=m{w}_{j}\left(n{v}_{i}\left({a}_{ij}\right)\right)\), and \(m\), \(n\) are the balancing coefficients. If the \({v}_{i}={\left\{{v}_{1},{v}_{2},\dots \dots ,{v}_{n}\right\}}^{T}\to {\left\{\frac{1}{n},\frac{1}{n},\dots \dots ,\frac{1}{n}\right\}}^{T}\) and \({v}_{i}={\left\{{w}_{1},{w}_{2},\dots \dots ,{w}_{j}\right\}}^{T}\to {\left\{\frac{1}{m},\frac{1}{m},\dots \dots ,\frac{1}{m}\right\}}^{T}\), then \({\left(m{w}_{1}\left(n{v}_{1}\left({a}_{11}\right)\right),m{w}_{1}\left(n{v}_{2}\left({a}_{21}\right)\right),\dots \dots ,m{w}_{m}\left(n{v}_{n}\left({a}_{nm}\right)\right)\right)}^{T}\to {\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right)}^{T}\).
Theorem 3.6
Let \({{\Delta }}_{{a}_{ij}}^{\text{'}}=\left(\left[{{\lambda }^{\text{'}}}_{{a}_{ij}}^{l},{{\lambda }^{\text{'}}}_{{a}_{ij}}^{\mho }\right],\left[{{\eta }^{\text{'}}}_{{a}_{ij}}^{l},{{\eta }^{\text{'}}}_{{a}_{ij}}^{\mho }\right]\right)\) be a collection of IVq-ROFSVs where \(\left(i=\mathrm{1,2},\dots \dots .n;j=\mathrm{1,2},\dots \dots .m\right)\). Then, the aggregation outcome of the IVq-ROFSEHWA operator is also an IVq-ROFSVs and,
where \({v}_{i}={\left\{{v}_{1},{v}_{2},\dots \dots ,{v}_{n}\right\}}^{T}\) and \({v}_{i}={\left\{{w}_{1},{w}_{2},\dots \dots ,{w}_{j}\right\}}^{T}\) be the weight vectors for experts and parameters such as \({v}_{i}>0,\sum _{i=1}^{n}{v}_{i}=1\) and \({w}_{j}>0,\sum _{j=1}^{m}{w}_{j}=1\) and \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\text{'}}\) be the most considerable element interval-valued q-rung orthopair fuzzy soft arguments \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\text{'}}=m{w}_{j}\left(n{v}_{i}\left({a}_{ij}\right)\right)\), and \(m\), \(n\) are the balancing coefficients. If the \({v}_{i}={\left\{{v}_{1},{v}_{2},\dots \dots ,{v}_{n}\right\}}^{T}\to {\left\{\frac{1}{n},\frac{1}{n},\dots \dots ,\frac{1}{n}\right\}}^{T}\) and \({v}_{i}={\left\{{w}_{1},{w}_{2},\dots \dots ,{w}_{j}\right\}}^{T}\to {\left\{\frac{1}{m},\frac{1}{m},\dots \dots ,\frac{1}{m}\right\}}^{T}\), then \({\left(m{w}_{1}\left(n{v}_{1}\left({a}_{11}\right)\right),m{w}_{1}\left(n{v}_{2}\left({a}_{21}\right)\right),\dots \dots ,m{w}_{m}\left(n{v}_{n}\left({a}_{nm}\right)\right)\right)}^{T}\to {\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right)}^{T}\).
Proof:
Proof is similar to Theorem 3.3.
Moreover, the IVq-ROFSEHWA operator demonstrates some significant characteristics, just like the IVq-ROFSEOWA operator. These properties comprise idempotency, boundedness, homogeneity, monotonicity, and shift-invariance. These properties will be further explained as follows:
Proposition 3.6
If \({{\Delta }}_{{a}_{ij}}^{\text{'}}=\left(\left[{{\lambda }^{\text{'}}}_{{a}_{ij}}^{l},{{\lambda }^{\text{'}}}_{{a}_{ij}}^{\mho }\right],\left[{{\eta }^{\text{'}}}_{{a}_{ij}}^{l},{{\eta }^{\text{'}}}_{{a}_{ij}}^{\mho }\right]\right)\); \(\left(i=1,2,3,\dots ,n;j=1,2,3,\dots ,m\right)\) be a collection of IVq-ROFSVs. Also, \({v}_{i}\) and \({w}_{j}\) be the weights of experts and attributes such as \({v}_{i}>0,\sum _{i=1}^{n}{v}_{i}=1\) and \({w}_{j}>0,\sum _{j=1}^{m}{w}_{j}=1\).
3.6.1. Idempotency. Let \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mathrm{\text{'}}}={{\Delta }}^{\mathrm{\text{'}}}=\left(\left[{\lambda }^{\mathrm{\text{'}}l},{\lambda }^{\mathrm{\text{'}}\mathrm{\mho }}\right],\left[{\eta }^{\mathrm{\text{'}}l},{\eta }^{\mathrm{\text{'}}\mathrm{\mho }}\right]\right)\) \(\forall\) \(i=1,2,3,\dots ,n;j=1,2,3,\dots ,m\), then
3.6.2. Boundedness. Let \({{\Delta }}_{{a}_{ij}}^{-\mathrm{\text{'}}}=\left(\left[min\left({\lambda }_{{a}_{ij}}^{\mathrm{\text{'}}l}\right),min\left({\lambda }_{{a}_{ij}}^{\mathrm{\text{'}}\mathrm{\mho }}\right)\right],\left[max\left({\eta }_{{a}_{ij}}^{\mathrm{\text{'}}l}\right),max\left({\eta }_{{a}_{ij}}^{\mathrm{\text{'}}\mathrm{\mho }}\right)\right]\right)\) and \({{\Delta }}_{{a}_{ij}}^{+\mathrm{\text{'}}}=\left(\left[max\left({\lambda }_{{a}_{ij}}^{\mathrm{\text{'}}l}\right),max\left({\lambda }_{{a}_{ij}}^{\mathrm{\text{'}}\mathrm{\mho }}\right)\right],\left[min\left({\eta }_{{a}_{ij}}^{\mathrm{\text{'}}l}\right),min\left({\eta }_{{a}_{ij}}^{\mathrm{\text{'}}\mathrm{\mho }}\right)\right]\right)\). Then
3.6.3. Monotonicity. Let \({{\Delta }}_{{a}_{ij}}^{\mathrm{\text{'}}}=\left(\left[{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l},{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }}\right],\left[{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l},{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }}\right]\right)and{{\Delta }}_{{a}_{ij}}^{\mathrm{\text{'}}\mathrm{*}}=\left(\left[{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l\mathrm{*}},{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }\mathrm{*}}\right],\left[{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l\mathrm{*}},{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }\mathrm{*}}\right]\right)\) be the families of IVq-ROFSVs. Then
\(IVq-ROFSEHWA\left({{\Delta }}_{{a}_{11}}^{\text{'}},{{\Delta }}_{{a}_{12}}^{\mathrm{\text{'}}},\dots \dots ,{{\Delta }}_{{a}_{nm}}^{\text{'}}\right)\le IVq-ROFSEHWA\left({{\Delta }}_{{a}_{11}}^{\text{'}*},{{\Delta }}_{{a}_{12}}^{\mathrm{\text{'}}\mathrm{*}},\dots \dots ,{{\Delta }}_{{a}_{nm}}^{\text{'}*}\right)\), if \({{\Delta }}_{{a}_{nm}}^{\text{'}}\le {{\Delta }}_{{a}_{nm}}^{\text{'}*}\) \(\forall i,j\).
3.6.4 Homogeneity. Let \({{\Delta }}_{{a}_{ij}}^{\mathrm{\text{'}}}=\left(\left[{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l},{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }}\right],\left[{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l},{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }}\right]\right)\) be a collection of IVq-ROFSVs, where, \(i=1,2,3,\dots ,m;j=1,2,3,\dots ,n\). Then \(IVq-ROFSEHWA\left(\theta {{\Delta }}_{{a}_{11}}^{\text{'}},\theta {{\Delta }}_{{a}_{12}}^{\mathrm{\text{'}}},\dots \dots ,\theta {{\Delta }}_{{a}_{nm}}^{\text{'}}\right)=\theta IVq-ROFSEHWA\left({{\Delta }}_{{a}_{11}}^{\text{'}},{{\Delta }}_{{a}_{12}}^{\mathrm{\text{'}}},\dots \dots ,{{\Delta }}_{{a}_{nm}}^{\text{'}}\right)\) For \(\theta >0.\)
3.6.5 Shift Invariance. Let \({{\Delta }}_{{a}_{ij}}^{\mathrm{\text{'}}}=\left(\left[{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l},{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }}\right],\left[{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l},{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }}\right]\right)\) be a collection of IVq-ROFSVs and \({{\Delta }}^{\mathrm{\text{'}}}=\left(\left[{\lambda }^{\mathrm{\text{'}}l},{\lambda }^{\mathrm{\text{'}}\mathrm{\mho }}\right],\left[{\eta }^{\mathrm{\text{'}}l},{\eta }^{\mathrm{\text{'}}\mathrm{\mho }}\right]\right)\) be an IVq-ROFSV. Then \(IVq-ROFSEHWA\left({{\Delta }}_{{a}_{11}}^{\mathrm{\text{'}}}{\oplus }_{\varepsilon }{{\Delta }}^{\mathrm{\text{'}}},{{\Delta }}_{{a}_{12}}^{\mathrm{\text{'}}}{\oplus }_{\varepsilon }{{\Delta }}^{\mathrm{\text{'}}},\dots ,{{\Delta }}_{{a}_{nm}}^{\mathrm{\text{'}}}{\oplus }_{\varepsilon }{{\Delta }}^{\mathrm{\text{'}}}\right)=IVq-ROFSEHWA\left({{\Delta }}_{{a}_{11}}^{\mathrm{\text{'}}},{{\Delta }}_{{a}_{12}}^{\mathrm{\text{'}}},\dots \dots ,{{\Delta }}_{{a}_{nm}}^{\mathrm{\text{'}}}\right){\oplus }_{\varepsilon }{{\Delta }}^{\mathrm{\text{'}}}\).
Proof:
The proof of proposition 3.6 is similar to proposition 3.4 (see Appendix 1).
4 Interval-valued q-rung orthopair fuzzy soft Einstein weighted geometric aggregation operators
In this section, we examine the IVq-ROFSEOWG and IVq-ROFSEHWG operators and investigate the fundamental properties of these operators, such as idempotency, boundedness, monotonicity, homogeneity, and shift-invariance.
Definition 4.1
Let \({{\Delta }}_{{a}_{ij}}=\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right],\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right),\) where \(\left(i=\mathrm{1,2},\dots \dots .n;j=\mathrm{1,2},\dots \dots .m\right)\) be a collection of IVq-ROFSVs. Then IVq-ROFSEOWG is defined as:
where \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}\) be the largest element of \({i}^{th}\) row and \({j}^{th}\) column in \(\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots ,{{\Delta }}_{{a}_{nm}}\right)\), such as \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}\le {{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i-1\right)\mathfrak{s}\left(j\right)}\right)}\) and \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}\le {{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j-1\right)}\right)}\) \(\forall i,j\). Also, \({v}_{i}\) and \({w}_{j}\) be the weights of experts and attributes such as \({v}_{i}>0,\sum _{i=1}^{n}{v}_{i}=1\) and \({w}_{j}>0,\sum _{j=1}^{m}{w}_{j}=1\).
Theorem 4.2
Let \({\Delta }{}_{{a}_{ij}}=\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right],\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right)\) be a collection of IVq-ROFSVs where \(\left(i=\mathrm{1,2},\dots \dots .n;j=\mathrm{1,2},\dots \dots .m\right)\). Then, the aggregation outcome of the IVq-ROFSEOWG operator is also an IVq-ROFSV and,
where \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}\) be the largest element of \({i}^{th}\) row and \({j}^{th}\) column in \(\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots ,{{\Delta }}_{{a}_{nm}}\right)\), such as \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}\le {{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i-1\right)\mathfrak{s}\left(j\right)}\right)}\) and \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}\le {{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j-1\right)}\right)}\) \(\forall i,j\). Also, \({v}_{i}\) and \({w}_{j}\) be the weights of experts and attributes such as \({v}_{i}>0,\sum _{i=1}^{n}{v}_{i}>0\) and \({w}_{j}>0,\sum _{j=1}^{m}{w}_{j}=1\).
Proof:
Similar to Theorem 3.3.
Proposition 4.3
If \({\Delta }{}_{{a}_{ij}}=\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right],\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right)\); \(\left(i=1,2,3,\dots ,n;j=1,2,3,\dots ,m\right)\) be a collection of IVq-ROFSVs. Also, \({v}_{i}\) and \({w}_{j}\) be the weights of experts and attributes such as \({v}_{i}>0,\sum _{i=1}^{n}{v}_{i}=1\) and \({w}_{j}>0,\sum _{j=1}^{m}{w}_{j}=1\).
4.3.1. Idempotency. Let \({\Delta }{}_{{a}_{ij}}={\Delta }{}_{{a}_{o}}=\left(\left[{\lambda }_{{a}_{o}}^{l},{\lambda }_{{a}_{o}}^{\mathrm{\mho }}\right],\left[{\eta }_{{a}_{o}}^{l},{\eta }_{{a}_{o}}^{\mathrm{\mho }}\right]\right)\) holds for any \(i=1,2,3,\dots ,n;j=1,2,3,\dots ,m\). Then,
4.3.2. Boundedness. Let \({{\Delta }}_{{a}_{ij}}^{-}=\left(\left[min\left({\lambda }_{{a}_{ij}}^{l}\right),min\left({\lambda }_{{a}_{ij}}^{\mathrm{\mho }}\right)\right],\left[max\left({\eta }_{{a}_{ij}}^{l}\right),max\left({\eta }_{{a}_{ij}}^{\mathrm{\mho }}\right)\right]\right)\) and \({{\Delta }}_{{a}_{ij}}^{+}=\left(\left[max\left({\lambda }_{{a}_{ij}}^{l}\right),max\left({\lambda }_{{a}_{ij}}^{\mathrm{\mho }}\right)\right],\left[min\left({\eta }_{{a}_{ij}}^{l}\right),min\left({\eta }_{{a}_{ij}}^{\mathrm{\mho }}\right)\right]\right)\). Then
4.3.3. Monotonicity. Let \({\Delta }{}_{{a}_{ij}}=\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mathrm{\mho }}\right],\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mathrm{\mho }}\right]\right)and{{\Delta }}_{{a}_{ij}}^{\mathrm{*}}=\left(\left[{{\lambda }^{\mathrm{*}}}_{{a}_{ij}}^{l},{{\lambda }^{\mathrm{*}}}_{{a}_{ij}}^{\mathrm{\mho }}\right],\left[{{\eta }^{\mathrm{*}}}_{{a}_{ij}}^{l},{{\eta }^{\mathrm{*}}}_{{a}_{ij}}^{\mathrm{\mho }}\right]\right)\) be the families of IVq-ROFSVs. Then \(IVq-ROFSEOWG\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right)\le IVq-ROFSEOWG\left({{\Delta }}_{{a}_{11}}^{*},{{\Delta }}_{{a}_{12}}^{*},\dots \dots \dots ,{{\Delta }}_{{a}_{nm}}^{*}\right)\), if \({{\Delta }}_{{a}_{nm}}\le {{\Delta }}_{{a}_{nm}}^{*}\) \(\forall i,j\).
4.3.4. Homogeneity. Let \({\Delta }{}_{{a}_{ij}}=\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mathrm{\mho }}\right],\left[{\eta }_{{a}_{ij}}^{L},{\eta }_{{a}_{ij}}^{\mathrm{\mho }}\right]\right)\) be a collection of IVq-ROFSVs, where, \(i=1,2,3,\dots ,m;j=1,2,3,\dots ,n\). Then \(IVq-ROFSEOWG\left(\theta {{\Delta }}_{{a}_{11}},\theta {{\Delta }}_{{a}_{12}},\dots \dots \theta {{\Delta }}_{{a}_{nm}}\right)=\theta IVq-ROFSEOWG\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right)\) For \(\theta >0.\)
4.4.5. Shift Invariance. Let \({\Delta }{}_{{a}_{ij}}=\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mathrm{\mho }}\right],\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mathrm{\mho }}\right]\right)\) be a collection of IVq-ROFSVs and \({\Delta }{}_{a}=\left(\left[{\lambda }_{a}^{l},{\lambda }_{a}^{\mathrm{\mho }}\right],\left[{\eta }_{a}^{l},{\eta }_{a}^{\mathrm{\mho }}\right]\right)\) be an IVq-ROFSV. Then \(IVq-ROFSEOWG\left({\Delta }{}_{{a}_{11}}{\oplus}_{\varepsilon }{\Delta }{}_{a},{\Delta }{}_{{a}_{12}}{\oplus}_{\varepsilon }{\Delta }{}_{a},\dots ,{\Delta }{}_{{a}_{nm}}{\oplus}_{\varepsilon }{\Delta }{}_{a}\right)=IVq-ROFSEOWG\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right){\oplus}_{\varepsilon }{\Delta }{}_{a}\).
Definition 4.4
Let \({{\Delta }}_{{a}_{ij}}^{\text{'}}=\left(\left[{{\lambda }^{\text{'}}}_{{a}_{ij}}^{l},{{\lambda }^{\text{'}}}_{{a}_{ij}}^{\mho }\right],\left[{{\eta }^{\text{'}}}_{{a}_{ij}}^{l},{{\eta }^{\text{'}}}_{{a}_{ij}}^{\mho }\right]\right),\) where \(\left(i=\mathrm{1,2},\dots \dots .n;j=\mathrm{1,2},\dots \dots .m\right)\) be a collection of IVq-ROFSVs. Then, the IVq-ROFSEHWG operator is defined as:
where \({v}_{i}={\left\{{v}_{1},{v}_{2},\dots \dots ,{v}_{n}\right\}}^{T}\) and \({v}_{i}={\left\{{w}_{1},{w}_{2},\dots \dots ,{w}_{j}\right\}}^{T}\) be the weight vectors for experts and parameters such as \({v}_{i}>0,\sum _{i=1}^{n}{v}_{i}=1\) and \({w}_{j}>0,\sum _{j=1}^{m}{w}_{j}=1\) and \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\text{'}}\) be the largest element interval-valued q-rung orthopair fuzzy soft arguments \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\text{'}}=m{w}_{j}\left(n{v}_{i}\left({a}_{ij}\right)\right)\), and \(m\), \(n\) are the balancing coefficients. If the \({v}_{i}={\left\{{v}_{1},{v}_{2},\dots \dots ,{v}_{n}\right\}}^{T}\to {\left\{\frac{1}{n},\frac{1}{n},\dots \dots ,\frac{1}{n}\right\}}^{T}\) and \({v}_{i}={\left\{{w}_{1},{w}_{2},\dots \dots ,{w}_{j}\right\}}^{T}\to {\left\{\frac{1}{m},\frac{1}{m},\dots \dots ,\frac{1}{m}\right\}}^{T}\), then \({\left(m{w}_{1}\left(n{v}_{1}\left({a}_{11}\right)\right),m{w}_{1}\left(n{v}_{2}\left({a}_{21}\right)\right),\dots \dots ,m{w}_{m}\left(n{v}_{n}\left({a}_{nm}\right)\right)\right)}^{T}\to {\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right)}^{T}\).
Theorem 4.5
Let \({{\Delta }}_{{a}_{ij}}^{\text{'}}=\left(\left[{{\lambda }^{\text{'}}}_{{a}_{ij}}^{l},{{\lambda }^{\text{'}}}_{{a}_{ij}}^{\mho }\right],\left[{{\eta }^{\text{'}}}_{{a}_{ij}}^{l},{{\eta }^{\text{'}}}_{{a}_{ij}}^{\mho }\right]\right)\) be a collection of IVq-ROFSVs where \(\left(i=\mathrm{1,2},\dots \dots .n;j=\mathrm{1,2},\dots \dots .m\right)\). Then, the aggregation outcome of the IVq-ROFSEHWG operator is also an IVq-ROFSVs and.
where \({v}_{i}={\left\{{v}_{1},{v}_{2},\dots \dots ,{v}_{n}\right\}}^{T}\) and \({v}_{i}={\left\{{w}_{1},{w}_{2},\dots \dots ,{w}_{j}\right\}}^{T}\) be the weight vectors for experts and parameters such as \({v}_{i}>0,\sum _{i=1}^{n}{v}_{i}=1\) and \({w}_{j}>0,\sum _{j=1}^{m}{w}_{j}=1\) and \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\text{'}}\) be the largest element interval-valued q-rung orthopair fuzzy soft arguments \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\text{'}}=m{w}_{j}\left(n{v}_{i}\left({a}_{ij}\right)\right)\), and \(m\), \(n\) are the balancing coefficients. If the \({v}_{i}={\left\{{v}_{1},{v}_{2},\dots \dots ,{v}_{n}\right\}}^{T}\to {\left\{\frac{1}{n},\frac{1}{n},\dots \dots ,\frac{1}{n}\right\}}^{T}\) and \({v}_{i}={\left\{{w}_{1},{w}_{2},\dots \dots ,{w}_{j}\right\}}^{T}\to {\left\{\frac{1}{m},\frac{1}{m},\dots \dots ,\frac{1}{m}\right\}}^{T}\), then \({\left(m{w}_{1}\left(n{v}_{1}\left({a}_{11}\right)\right),m{w}_{1}\left(n{v}_{2}\left({a}_{21}\right)\right),\dots \dots ,m{w}_{m}\left(n{v}_{n}\left({a}_{nm}\right)\right)\right)}^{T}\to {\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right)}^{T}\).
Proof:
Proof is similar to Theorem 3.3.
Proposition 4.6
If \({{\Delta }}_{{a}_{ij}}^{\text{'}}=\left(\left[{{\lambda }^{\text{'}}}_{{a}_{ij}}^{l},{{\lambda }^{\text{'}}}_{{a}_{ij}}^{\mho }\right],\left[{{\eta }^{\text{'}}}_{{a}_{ij}}^{l},{{\eta }^{\text{'}}}_{{a}_{ij}}^{\mho }\right]\right)\); \(\left(i=1,2,3,\dots ,n;j=1,2,3,\dots ,m\right)\) be a collection of IVq-ROFSVs. Also, \({v}_{i}\) and \({w}_{j}\) be the weights of experts and attributes such as \({v}_{i}>0,\sum _{i=1}^{n}{v}_{i}=1\) and \({w}_{j}>0,\sum _{j=1}^{m}{w}_{j}=1\).
4.6.1. Idempotency. Let \({{\Delta }}_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mathrm{\text{'}}}={{\Delta }}^{\mathrm{\text{'}}}=\left(\left[{\lambda }^{\mathrm{\text{'}}l},{\lambda }^{\mathrm{\text{'}}\mathrm{\mho }}\right],\left[{\eta }^{\mathrm{\text{'}}l},{\eta }^{\mathrm{\text{'}}\mathrm{\mho }}\right]\right)\) \(\forall\) \(i=1,2,3,\dots ,n;j=1,2,3,\dots ,m\), then
4.6.2. Boundedness. Let \({{\Delta }}_{{a}_{ij}}^{-\mathrm{\text{'}}}=\left(\left[min\left({\lambda }_{{a}_{ij}}^{\mathrm{\text{'}}l}\right),min\left({\lambda }_{{a}_{ij}}^{\mathrm{\text{'}}\mathrm{\mho }}\right)\right],\left[max\left({\eta }_{{a}_{ij}}^{\mathrm{\text{'}}l}\right),max\left({\eta }_{{a}_{ij}}^{\mathrm{\text{'}}\mathrm{\mho }}\right)\right]\right)\) and \({{\Delta }}_{{a}_{ij}}^{+\mathrm{\text{'}}}=\left(\left[max\left({\lambda }_{{a}_{ij} }^{\mathrm{\text{'}}l}\right), max\left({\lambda }_{{a}_{ij}}^{\mathrm{\text{'}}\mathrm{\mho }}\right)\right], \left[min\left({\eta }_{{a}_{ij}}^{\mathrm{\text{'}}l}\right), min\left({\eta }_{{a}_{ij}}^{\mathrm{\text{'}}\mathrm{\mho }}\right)\right]\right)\). Then
4.6.3. Monotonicity. Let \({{\Delta }}_{{a}_{ij}}^{\mathrm{\text{'}}} =\left(\left[{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l},{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }}\right],\left[{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l},{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }}\right]\right) and {{\Delta }}_{{a}_{ij}}^{\mathrm{\text{'}}\mathrm{*}} =\left(\left[{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l\mathrm{*}},{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }\mathrm{*}}\right],\left[{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l\mathrm{*}},{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }\mathrm{*}}\right]\right)\) be the families of IVq-ROFSVs. Then
\(IVq-ROFSEHWG\left({{\Delta }}_{{a}_{11}}^{\text{'}},{{\Delta }}_{{a}_{12}}^{\mathrm{\text{'}}},\dots \dots ,{{\Delta }}_{{a}_{nm}}^{\text{'}}\right)\le IVq-ROFSEHWG\left({{\Delta }}_{{a}_{11}}^{\text{'}*},{{\Delta }}_{{a}_{12}}^{\mathrm{\text{'}}\mathrm{*}},\dots \dots ,{{\Delta }}_{{a}_{nm}}^{\text{'}*}\right)\), if \({{\Delta }}_{{a}_{nm}}^{\text{'}}\le {{\Delta }}_{{a}_{nm}}^{\text{'}*}\) \(\forall i,j\).
4.6.4. Homogeneity. Let \({{\Delta }}_{{a}_{ij}}^{\mathrm{\text{'}}} =\left(\left[{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l},{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }}\right],\left[{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l},{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }}\right]\right)\) be a collection of IVq-ROFSVs, where, \(i=1, 2, 3, \dots , m;j=1, 2, 3, \dots ,n\). Then \(IVq-ROFSEHWG\left(\theta {{\Delta }}_{{a}_{11}}^{\text{'}},\theta {{\Delta }}_{{a}_{12}}^{\mathrm{\text{'}}},\dots \dots ,\theta {{\Delta }}_{{a}_{nm}}^{\text{'}}\right)=\theta IVq-ROFSEHWG\left({{\Delta }}_{{a}_{11}}^{\text{'}},{{\Delta }}_{{a}_{12}}^{\mathrm{\text{'}}},\dots \dots ,{{\Delta }}_{{a}_{nm}}^{\text{'}}\right)\) For \(\theta >0.\)
4.6.5. Shift Invariance. Let \({{\Delta }}_{{a}_{ij}}^{\mathrm{\text{'}}} =\left(\left[{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l},{{\lambda }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }}\right],\left[{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{l},{{\eta }^{\mathrm{\text{'}}}}_{{a}_{ij}}^{\mathrm{\mho }}\right]\right)\) be a collection of IVq-ROFSVs and \({{\Delta }}^{\mathrm{\text{'}}}=\left(\left[{\lambda }^{\mathrm{\text{'}}l},{\lambda }^{\mathrm{\text{'}}\mathrm{\mho }}\right],\left[{\eta }^{\mathrm{\text{'}}l},{\eta }^{\mathrm{\text{'}}\mathrm{\mho }}\right]\right)\) be an IVq-ROFSV. Then \(IVq-ROFSEHWG\left({{\Delta }}_{{a}_{11}}^{\mathrm{\text{'}}}{\oplus}_{\varepsilon }{{\Delta }}^{\mathrm{\text{'}}}, {{\Delta }}_{{a}_{12}}^{\mathrm{\text{'}}}{\oplus}_{\varepsilon }{{\Delta }}^{\mathrm{\text{'}}},\dots ,{{\Delta }}_{{a}_{nm}}^{\mathrm{\text{'}}}{\oplus}_{\varepsilon }{{\Delta }}^{\mathrm{\text{'}}}\right)= IVq-ROFSEHWG\left({{\Delta }}_{{a}_{11}}^{\mathrm{\text{'}}},{{\Delta }}_{{a}_{12}}^{\mathrm{\text{'}}},\dots \dots ,{{\Delta }}_{{a}_{nm}}^{\mathrm{\text{'}}}\right){\oplus}_{\varepsilon }{{\Delta }}^{\mathrm{\text{'}}}\).
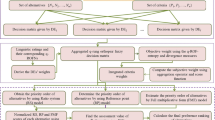
5 Extended EDAS technique based on einstein ordered and hybrid aggregation operators
Experts in different fields with distinct perspectives and perceptions of the world around them frequently have different opinions on the most effective course of action. Interval-valued q-rung orthopair fuzzy values are usually used between experts to describe unclear and confusing scenarios and indicate their opinions. This research proposes the “Interval-valued q-rung orthopair fuzzy soft Einstein ordered and hybrid AOs based EDAS method” to address MAGDM problems using interval-valued q-rung orthopair fuzzy values. The ideal solution of the EDAS approach is associated with two specific measures, positive distance matrix (PDA) and negative distance matrix (NDA), which efficiently measure the differences between various solutions. The EDAS technique is suitable for dealing with MAGDM issues without formally evaluating ideal and non-ideal solutions. The section that follows provides specifics on the established strategy’s computational framework.
Let \(\mathfrak{H}=\left\{{\mathfrak{H}}_{1},{\mathfrak{H}}_{2},\dots \dots {\mathfrak{H}}_{k}\right\}\) be a collection of \(k\) alternatives and \(\mathcal{H}=\left\{{\mathcal{H}}_{1},{\mathcal{H}}_{2},\dots \dots {\mathcal{H}}_{s}\right\}\) be a team of experts with weight vector \(v={\left({v}_{1}, {v}_{2},\dots , {v}_{n}\right)}^{T}\), such as \({v}_{i}>0\) and \(\sum _{i=1}^{n}{v}_{i}=1.\) Let \(\mathfrak{R}=\left\{{\mathfrak{R}}_{1},{\mathfrak{R}}_{2},\dots \dots {\mathfrak{R}}_{z}\right\}\) be a collection of attributes whose weight vector is given as \(w={\left({w}_{1}, {w}_{2},\dots , {w}_{n}\right)}^{T}\) such as \({w}_{j}>0\) and \(\sum _{j=1}^{m}{w}_{j}=1\). For each possibility, the group of experts \(\left\{{\mathcal{H}}_{i}: i=1, 2,\dots , s\right\}\) expresses their thoughts using IVq-ROFSNs after considering the specified set of attributes \(\left\{{\mathfrak{R}}_{z}:z=1, 2, 3, \cdots , n\right\}\). The experts’ opinion for each alternative in the form of IVq-ROFSNs is denoted as \({\mathrm{\Xi }}_{{\mathrm{a}}_{\mathrm{i}\mathrm{j}}}^{p}=\left({\lambda }_{{a}_{ij}}^{(p)}, {\eta }_{{a}_{ij}}^{(p)}\right)\), where \({\lambda }_{{a}_{ij}}^{(p)}=\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right]\), \({\eta }_{{a}_{ij}}^{(p)}=\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\), and \(0\le {\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho },{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\le 1\) and \({\left({\lambda }_{{a}_{ij}}^{\mho }\right)}^{q}+{\left({\eta }_{{a}_{ij}}^{\mho }\right)}^{q}\le 1\), \(\forall i,j\), and \(q>2\).
The following steps for implementing the stated approach are given:
-
Step 1: Build decision matrices for each alternative \(\left\{{\mathfrak{H}}_{j}: z = 1, 2, \dots , k\right\}\) in IVq-ROFSNs form under considered attributes.
$${\left[{\mathrm{\Xi }}_{{a}_{ij}}^{p}\right]}_{n\times m}=\begin{array}{c}{\mathcal{H}}_{1}\\ {\mathcal{H}}_{2}\\ \vdots \\ {\mathcal{H}}_{n}\end{array}\left(\begin{array}{cccc}\left(\left[{\lambda }_{{a}_{11}}^{l},{\lambda }_{{a}_{11}}^{\mho }\right],\left[{\eta }_{{a}_{11}}^{l},{\eta }_{{a}_{11}}^{\mho }\right]\right)& \left(\left[{\lambda }_{{a}_{12}}^{l},{\lambda }_{{a}_{12}}^{\mho }\right],\left[{\eta }_{{a}_{12}}^{l},{\eta }_{{a}_{12}}^{\mho }\right]\right)& \cdots & \left(\left[{\lambda }_{{a}_{1m}}^{l},{\lambda }_{{a}_{1m}}^{\mho }\right],\left[{\eta }_{{a}_{1m}}^{l},{\eta }_{{a}_{1m}}^{\mho }\right]\right)\\ \left(\left[{\lambda }_{{a}_{21}}^{l},{\lambda }_{{a}_{21}}^{\mho }\right],\left[{\eta }_{{a}_{21}}^{l},{\eta }_{{a}_{21}}^{\mho }\right]\right)& \left(\left[{\lambda }_{{a}_{22}}^{l},{\lambda }_{{a}_{22}}^{\mho }\right],\left[{\eta }_{{a}_{22}}^{l},{\eta }_{{a}_{22}}^{\mho }\right]\right)& \cdots & \left(\left[{\lambda }_{{a}_{2m}}^{l},{\lambda }_{{a}_{2m}}^{\mho }\right],\left[{\eta }_{{a}_{2m}}^{l},{\eta }_{{a}_{2m}}^{\mho }\right]\right)\\ \vdots & \vdots & \vdots & \vdots \\ \left(\left[{\lambda }_{{a}_{n1}}^{l},{\lambda }_{{a}_{n1}}^{\mho }\right],\left[{\eta }_{{a}_{n1}}^{l},{\eta }_{{a}_{n1}}^{\mho }\right]\right)& \left(\left[{\lambda }_{{a}_{n1}}^{l},{\lambda }_{{a}_{n1}}^{\mho }\right],\left[{\eta }_{{a}_{n1}}^{l},{\eta }_{{a}_{n1}}^{\mho }\right]\right)& \cdots & \left(\left[{\lambda }_{{a}_{nm}}^{l},{\lambda }_{{a}_{nm}}^{\mho }\right],\left[{\eta }_{{a}_{nm}}^{l},{\eta }_{{a}_{nm}}^{\mho }\right]\right)\end{array}\right)$$ -
Step 2: Therefore, the matrix \({\left[{\mathrm{\Xi }}_{{a}_{ij}}^{p}\right]}_{n\times m}\) is analyzed by classifying the parameters into two groups: attributes connected with costs and attributes related to benefits. In the case of identical parameters, normalization is not necessary. If the decision matrices show different kinds of attributes, then the normalization technique should be used to make them uniform, given as follows:
$${R}_{ij}^{(z)}=\left\{\begin{array}{c}{\left({\mathrm{\Xi }}_{{a}_{ij}}^{p}\right)}^{c}=\left(\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right],\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right]\right)\\ {\mathrm{\Xi }}_{{a}_{ij}}^{p}=\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right],\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right)\end{array}\right.$$(6) -
Step 3: Evaluate the ordered matrices for each alternative.
-
Step 4: The cognitive decision data is used for integrating the expert opinion evaluations, considering the weight of each expert, using the IVq-ROFSEOWA, IVq-ROFSEOWG, IVq-ROFSEHWA, or IVq-ROFSEHWG operators. Considering the stated criteria, the preceding technique determines the comprehensive preference values for alternates.
$${\left[{\mathrm{\Xi }}_{{a}_{ij}}\right]}_{n\times m}={\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right],\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right)}_{n\times m},i=\mathrm{1,2},\dots n,j=\mathrm{1,2},\dots m$$ -
Step 5: Determine the average solution matrix
$$= \left[ {{\text{\AA}}S_{h} } \right]_{{1 \times m}} = \frac{1}{n}\mathop {\mathop \oplus \limits_{{i = 1}} }\limits^{n} \left( {\Xi _{{a_{{ij}} }} } \right)$$(7) -
Step 6: Compute the PDA and NDA matrices; for this, let \({D}_{b}\) and \({D}_{c}\) be the set of beneficial criteria and non-beneficial criteria, respectively. Then, \(PD{{\text{\AA}}}S\) and \(ND{\text{\AA}}S\) matrices can be determined as: \(PDA={\left[{\rho }_{{a}_{ij}}\right]}_{n\times m}\) , \(NDA={\left[{\partial }_{{a}_{ij}}\right]}_{n\times m}\), where
$$\rho _{{a_{{ij}} }} = \left\{ {\begin{array}{*{20}c} {\frac{{\max \left( {0,\left( {\Xi _{{a_{{ij}} }} - {{{\text{\AA}}}}S_{h} } \right)} \right)}}{{S\left( {~{{{\text{\AA}}}}S_{h} } \right)}}~for~i = 1\left( 1 \right)n,~j = 1\left( 1 \right)m~and~\Re _{z} \in D_{b} ~} \\ {\begin{array}{*{20}c} {\frac{{\max \left( {0,\left( {{{{\text{\AA}}}}S_{h} - \Xi _{{a_{{ij}} }} } \right)} \right)}}{{S\left( {~{{{\text{\AA}}}}S_{h} } \right)}}} \\ \end{array} ,~for~i = 1\left( 1 \right)n,~j = 1\left( 1 \right)m~and~\Re _{z} \in D_{c} } \\ \end{array} } \right.$$(8)and
$$\partial_{{a_{{ij}} }} = \left\{ {\begin{array}{*{20}c} {\frac{{\max \left( {0,\left( {{\text{\AA}}S_{h} - \Xi _{{a_{{ij}} }} } \right)} \right)}}{{S\left( {{\text{\AA}}S_{h} } \right)}}\;for\;i = 1\left(1 \right)n,\;j = 1\left( 1 \right)m\;and\;{\Re _{z}} \in D_{b}} \\ {\begin{array}{*{20}c} {\frac{{\max \left( {0,\left( {\Xi _{{a_{{ij}} }} - {\text{\AA}}S_{h} } \right)} \right)}}{{S\left( {{\text{\AA}}S_{h} } \right)}}} \\ \end{array} \;for\;i = 1\left( 1 \right)n,\;j = 1\left( 1 \right)m\;and\;{\Re _{z}} \in D_{c} } \\ \end{array} } \right.$$(9) -
Step 7: Calculate the positive weighted distance \({{\rm P}}_{\tau }\) and negative weighted distance \({Q}_{\tau }\) for IVq-ROFSEOWA and IVq-ROFSEHWA operators.
$${P}_{\tau }=\mathop \oplus \limits_{{j = 1}}^{m}{w}_{j}\left(\mathop \oplus \limits_{{i = 1}}^{n}{v}_{i}{\rho }_{{a}_{ij}}\right)$$(10)$${Q}_{\tau }=\mathop \oplus \limits_{{j = 1}}^{m}{w}_{j}\left(\mathop \oplus \limits_{{i = 1}}^{n}{v}_{i}{\partial }_{{a}_{ij}}\right)$$(11)Or using IVq-ROFSEOWG and IVq-ROFSEHWG operators given as:
$${P}_{\tau} = \mathop \otimes \limits_{{j = 1}}^{m} w_{j} \left( {\mathop \otimes \limits_{{i = 1}}^{n} v_{i} \rho _{{a_{{ij}} }} } \right)$$(12)$${Q}_{\tau} = \mathop \otimes \limits_{{j = 1}}^{m} w_{j} \left( {\mathop \otimes \limits_{{i = 1}}^{n} v_{i} \partial_{{a_{{ij}} }} } \right)$$(13)where \({w}_{j}>0,{v}_{i}>0\), such as \(\sum _{j=1}^{m}{w}_{j}=1\) and \(\sum _{i=1}^{n}{v}_{i}>0.\)
-
Step 8: Normalize the values of \({{\rm P}}_{\tau }\) and \({Q}_{\tau }\), \(\tau =\mathrm{1,2},\dots \dots m.\)
$$N{{\rm P}}_{\tau }=\frac{{{\rm P}}_{\tau }}{max\left({{\rm P}}_{1},{{\rm P}}_{2},\dots \dots {{\rm P}}_{m}\right)}$$(14)$$N{Q}_{\tau }=1-\frac{{Q}_{\tau }}{max\left({Q}_{1},{Q}_{2},\dots \dots {Q}_{m}\right)}$$(15)where \(max\left({{\rm P}}_{1},{{\rm P}}_{2},\dots \dots {{\rm P}}_{m}\right)\) and \(max\left({Q}_{1},{Q}_{2},\dots \dots {Q}_{m}\right)\) be the maximum distances.
-
Step 9: Derive the integrative appraisal score \(I\)
$$I=\frac{1}{2}\left(N{{\rm P}}_{\tau }\oplus N{Q}_{\tau }\right)$$(16)where \(I\in \left[\mathrm{0,1}\right].\)
-
Step 10: Based on their appraisal scores, each alternative is eventually ordered in descending order. The alternative with the highest score is considered the most beneficial, and the one with the lowest score is referred to as the least favourable.
A flowchart of the proposed approach can be presented in the following Fig. 1.
6 Application of the proposed EDAS method in biomedical waste management
This section will analyze the implementation of the abovementioned model to identify the most effective BMW management technique.
6.1 Description of BMW management techniques
Biomedical waste management is crucial to laboratory, healthcare, and research operations. It entails the safe and effective disposal of waste products from labs, healthcare facilities, and research institutions. Medical waste must be disposed of appropriately to prevent the spread of illness, preserve the environment, and secure the comfort of healthcare workers and disposal workers. A few significant techniques and strategies used in the field of biomedical waste management are as follows:
6.1.1 Autoclaving
For the secure and efficient handling of potentially transmissible and harmful materials produced in hospitals, research centers, and other similar locations, autoclaving is an essential technique used in BMW management. The autoclaving procedure is crucial for ensuring that BMW is secure for disposal later. It’s a sterilizing procedure that exposes microorganisms, including viruses, bacteria, and fungi, to extreme temperatures and pressures using pressurized steam. As water heats up in a sealed container under higher pressure, its boiling point rises above 100 °C, based on the pressure exerted. At ordinary atmospheric pressure, water boils at 100 °C. We refer to this sterilizing process as autoclaving. Blood and blood products, body fluids, and microbial particles are sterilized for 30 min at 121 °C, after which they are dumped or disposed of properly. This approach is particularly efficient at deactivating microorganisms, substantially reducing the probability of spreading illnesses.
Waste Segregation: The procedure of separating waste at the point of generation is a component of the initial stage in BMW management. Sharp objects, lab supplies, and other kinds of debris that pose a higher risk of infection can be disposed of using specialized containers.
Loading the autoclave: The management of biomedical waste requires the utilization of containers that are compatible with autoclaves, which are then installed into the sterilization chamber of the autoclave.
Steam exposure: Steam is compelled in the autoclave when it is sealed. The temperature in the chamber is too warm and agitated for microbes to survive.
Sterilization phase: The waste is kept within this pressurized, high-temperature atmosphere for a specific time, enabling effective disinfection.
Cooling phase: Throughout the sterilization procedure, the autoclave steadily decreases pressure and temperature, thus facilitating the steady cooling of the waste materials.
Post-treatment handling: When the autoclave operation is completed, the waste goes through sterilization and no longer causes a health risk.
Benefits of autoclave technique in BMW management: Autoclaving is a highly prevalent procedure utilized in the field of BMW management, which has numerous noteworthy advantages. Primarily, it exhibits a high level of efficacy in eradicating detrimental bacteria and ensuring the safe disposal of medical waste. The execution of this method significantly mitigates the risk of disease spread among medical professionals, waste management workers, and the general public. Also, autoclaving has been demonstrated to efficiently minimize the overall volume of waste, contributing to considerable reductions in transportation and final disposal expenses. The utilization of this technology can be regarded as ecologically conscientious due to its capacity to generate minimal levels of detrimental emissions compared to alternative treatments such as incineration. Autoclaves can be conveniently implemented at the location, so they are a versatile and scalable alternative suitable for both diminutive healthcare establishments and expansive treatment plants for waste.
Limitations of the autoclave technique: Whereas autoclaving has multiple advantages, it also carries a few limitations. The task needs significant power, particularly during prolonged execution, which may impact operating expenditure. Moreover, the process of autoclaving may necessitate the allocation of specific areas inside hospitals or waste disposal facilities. The tools and equipment used must comply with recognized safety standards and regulations. It is essential to realize that particular kinds of biological waste can’t get enough processing just by an autoclave, mandating the execution of several types of treatments. Autoclaving is generally considered a remarkably effective and ecologically sensitive approach to managing biomedical waste. However, it needs to consider the use of energy and structural issues related to implementing this strategy.
6.1.2 Chemical treatment
Chemical treatment plays an integral part in managing biomedical waste, as it assists in disinfecting and rendering infectious and hazardous waste safer for its final destination. This approach focuses on adopting chemical compounds that make microorganisms harmless and reduce any risks connected with biomedical debris. Chemical sterilization, frequently called chemical sterilization, involves using specified chemicals to eliminate or mitigate microorganisms, such as viruses, bacteria, and fungal infections, that are ineffective in medical waste. Materials such as acupuncture needles, sharp-edged items, recyclable plastic, pathogenic beverages, blood, and body fluids are generally exposed to appropriate sanitation using an adequate disinfectant, such as a 2–5% solution consisting of Lysol, followed by autoclaving. The chemical waste is neutralized and disposed of, contingent upon its inherent characteristics. As mentioned above, the technique is recognized for its significant efficacy when handling pathogenic materials, making it a valuable addition to other treatment modalities such as autoclave and cremation.
Waste segregation: Waste segregation is the initial phase in any BMW management procedure. There are designated bins for each type of waste.
Chemical selection: Selecting an appropriate chemical for cleaning or sterilization is essential. Sodium hypochlorite, hydrogen peroxide, and chlorine dioxide are commonly employed chemicals for cleaning. Selection relies on the kind of waste and legislative restrictions.
Contact time: The waste material is treated with disinfectant for a long time to ensure all of the microbes are removed.
Dilution and neutralization: Under specific circumstances, destroying or diluting chemicals before their removal is important to minimize all possible adverse environmental effects.
Final disposal: Waste materials will be adequately disposed of in compliance with the defined waste disposal rules after completing proper processing.
Benefits of chemical treatment in BMW management: Chemical processing is a beneficial procedure with several benefits to manage biological contaminants. It is highly efficient in reducing infections, such as fungi, viruses, and bacteria, facilitating secure removal of harmful material. Due to its resilience, this technique may efficiently manage several kinds of biological trash, such as liquids, pharmaceuticals, and lab wastes. Chemical reaction treatments are more beneficial to our environment than alternative procedures. It will be handled directly at healthcare facilities, offering a flexible solution suitable for multiple waste disposal circumstances.
Limitations of chemical treatment technique: Whereas chemical treatments possess several advantages, they carry limitations. To prevent mishaps or improper management, handling and preserving disinfecting substances with extreme caution using safety protocols is necessary. The development of disinfection resistance in certain microbes highlights the significance of appropriate chemical selection and contact durations. Furthermore, not all biomedical waste can be treated chemically; some waste types might need to be disposed of using different techniques. As a result, it's critical to thoroughly assess the waste type and select the best treatment option in line with that assessment.
6.1.3 Microwaving
The Microwave sterilization technology is a smart and sustainable technique applied for the treatment in BMW management. The main purpose of this methodology is to completely reduce toxic materials frequently found within healthcare organizations, research labs, and analogous places. Through microwave technology, BMW management implements a process that includes the controlled release of heat to sterilize waste materials effectively, thus ensuring their safety for subsequent disposal. Microwaves, conventionally recognized for their role in food heating, have been recently employed in BMW management, ensuring security and supporting a sustainable environment.
Waste segregation: The adequate segregation of waste at its generation location is the beginning of any approach addressing BMW's management. There are different types of waste, and each one needs a different way to be treated.
Containerization: The BMW dumped into containers designed to be microwave-safe. The vessels carry the capacity needed to deal with the thermal energy produced throughout heating with a microwave.
Microwave exposure: The waste vessels are placed into a microwave chamber and then processed using microwaves to boost the internal temperatures of the garbage cans up to a higher level.
Cooling phase: The waste needs a cooling procedure after treatment to attain the proper temperature for dumping.
Post-treatment handling: The waste is disinfected after microwaving, facilitating its final disposal.
Benefits of microwaving in BMW management: The implementation of microwaves in BMW management is a novel and revolutionary method with several advantages. Committing harmful objects to intense temperatures is an efficient way of sanitation, which causes the removal of pathogens such as bacteria, viruses, and fungi. The sanitizing operation makes waste appropriate for its proper elimination. This method often results in a reduction in waste size, increasing efficiency in transportation and disposal. The use of microwaves is known because of their excellent energy efficiency, as they utilize less energy than other treatments. Moreover, it is necessary to remember that these treatment techniques can decrease their negative effect on the environment by generating minimal greenhouse gases, promoting sustainable growth.
Limitations of the microwaving technique: Still, microwaves face some disadvantages. Implementing microwaves effectively in healthcare facilities may require reserving particular infrastructure and securing specific tools, limiting their usefulness in particular circumstances. Also, implementing microwaves may require a higher initial investment, but it may result in fewer maintenance expenses than other alternatives. Strict compliance with protection regulations and laws is necessary to reduce the potential of fatalities or improper waste handling. A few kinds of waste can't be suitable for microwave treatment, necessitating different disposal methods. A thorough evaluation of the attributes of the biological waste and its suitability for using microwaves is necessary to handle this kind of waste efficiently.
6.1.4 Deep burial
Deep burial is a BMW management approach in which potential toxic waste generated in medical centres, labs, and research organizations is concealed. Executing this method properly produces a suitable and extracted environment to contain BMW. The method involves excavating committed burial sites or tunnels to dump BMW underground. This method is implemented when alternative disposal procedures, such as microwaving or autoclaving, are not feasible or waste management laws permit deeper graves.
Benefits of Deep Burial in BMW management: Deep burial, as a technique for processing biological matter, delivers a distinct approach with advantages and drawbacks. The main benefit of the method is its ability to deliver an adequate level of isolation. Deep burial of biological materials properly excludes the waste from its surroundings, decreasing the potential challenges of disease spread and contaminants. This method is characterized by its ecologically sensitive aspect, as it significantly prevents the dispersal of possibly dangerous chemicals into the surroundings. The deep burial approach is highly versatile as it can be used efficiently for multiple kinds of biological waste, such as clinical waste, laboratory components, and medication waste.
Limitations of the Deep burial technique: While deep burial presents some benefits, it also has drawbacks. This method is liable to severe compliance with regulations, including strict surveillance and certification procedures, due to its possible effect on groundwater quality and other environmental concerns. Determining proper ground for deep burial may pose challenges, particularly in populated towns lacking land availability. It is important to properly monitor and preserve burial cavities to prevent inappropriate access and mitigate possible environmental effects. Implementing a deep burial includes supplementary expenditures related to the construction process, persistent site maintenance, and continual monitoring operations. When exploring using that approach to control biological waste, it is necessary to assess these factors in connection to the corresponding advantages thoroughly.
6.1.5 Incineration
Incineration is a well-established and critical method of regulating potentially dangerous substances generated from healthcare facilities, medical labs, and other associated fields to dispose of them efficiently and properly. Incineration is a process that transforms BMW into ash using controlled combustion, rendering it pure and harmful. The waste is burned in a specially developed dual-chamber burner, attaining a temperature between 900 and 1200 degrees Celsius, causing its transformation into ashes. This method is highly effective for sterilizing and disposing of hazardous products, pharmaceutical waste, and other potentially harmful substances.
Benefits of incineration in BMW management: Incineration is a very effective approach to reducing BMW, delivering several benefits. Initially, it regularly reduces undesirable organisms, generating healthcare waste free of infection and secures removal. This method significantly reduces the potential of spreading disease to the general public, waste handlers, and health care workers. Incineration minimizes costs for disposal and transportation by reducing the volume of solid waste produced. Moreover, to reduce their negative effects on the surroundings, burning facilities are provided with pollution mitigation devices that collect and eradicate contaminants. In certain situations, the environmental impact can be further reduced by extracting energy from the heat produced during combustion.
Limitations of the Incineration technique: It presents benefits; however, it also has certain drawbacks. Emissions need to be controlled and scrutinized regularly to remain within legal parameters. Also, incineration facilities might need substantial inception expenditures, and maintenance costs vary according to the equipment adopted and the level to which it is required to adhere to the applicable laws and regulations. In crowded towns, there can sometimes not be enough space in hospitals or waste disposal centers for this procedure. Some forms of BMW can't be suitable for burning and must be managed with other techniques. Sustaining performance while decreasing the impact on the environment while conducting incineration needs exact compliance with safety rules and regulations.
A flow chart of the working process of all considered BMW management techniques is given in the following Fig. 2.
6.2 Selection of BMW disposal technique
The task of determining the most appropriate treatment technique for BMW disposal is of paramount importance. We concentrate on a case study within this section, presented in the research by Liu et al. (2015a). It was executed in Shanghai, China, demonstrating how BMW currently selects its waste disposal treatment strategy. We examine all aspects of this particular case study in the subsection (6.1). In this study, we concentrate on five distinct suggested BMW methods for treatment. This issue will address the following objectives: determining the best method and developing an organizational structure for the selected treatment strategies. A justification for the different BMW disposal treatment techniques is given as follows: \(\mathfrak{H}=\left\{{\mathfrak{H}}_{1}=\mathrm{C}\mathrm{h}\mathrm{e}\mathrm{m}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l} \mathrm{t}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}, {\mathfrak{H}}_{2}=\mathrm{I}\mathrm{n}\mathrm{c}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}, {\mathfrak{H}}_{3}=\mathrm{M}\mathrm{i}\mathrm{c}\mathrm{r}\mathrm{o}\mathrm{w}\mathrm{a}\mathrm{v}\mathrm{i}\mathrm{n}\mathrm{g}, {\mathfrak{H}}_{4}=\mathrm{D}\mathrm{e}\mathrm{e}\mathrm{p} \mathrm{B}\mathrm{r}\mathrm{u}\mathrm{i}\mathrm{a}\mathrm{l}, {\mathfrak{H}}_{5}=\mathrm{A}\mathrm{u}\mathrm{t}\mathrm{o}\mathrm{c}\mathrm{l}\mathrm{a}\mathrm{v}\mathrm{i}\mathrm{n}\mathrm{g}\right\}\). The variables’ weights are significant in determining BMW disposal alternatives to treatment, enabling experts to evaluate their decisions between five potential alternatives. We consider the subsequent five parameters in this into perspective: \(\mathfrak{R}=\{{\mathfrak{R}}_{1}=\mathrm{S}\mathrm{o}\mathrm{c}\mathrm{i}\mathrm{a}\mathrm{l} \mathrm{A}\mathrm{c}\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\) (benefit), \({\mathfrak{R}}_{2}=\mathrm{E}\mathrm{n}\mathrm{v}\mathrm{i}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{l} \mathrm{p}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\) (benefit), \({\mathfrak{R}}_{3}=\mathrm{N}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}\) (cost), \({\mathfrak{R}}_{4}=\mathrm{H}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{h} \mathrm{R}\mathrm{i}\mathrm{s}\mathrm{k}\) (cost), and \({\mathfrak{R}}_{5}=\mathrm{T}\mathrm{e}\mathrm{c}\mathrm{h}\mathrm{n}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l} \mathrm{c}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}\) (benefit)} are used to the selection criteria with weights \(w=(0.18,\mathrm{0.15,0.25,0.21,0.21}),\) respectively. of BMW disposal treatment methods. Let \(\mathcal{H}=\left\{{\mathcal{H}}_{1}, {\mathcal{H}}_{2}, {\mathcal{H}}_{3}, {\mathcal{H}}_{4},{\mathcal{H}}_{5}\right\}\) be a team of five experts with weights \(v=(\mathrm{0.22,0.23,0.25},0.11,0.19).\) Where \({\mathfrak{R}}_{3}=\mathrm{N}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}\) and \({\mathfrak{R}}_{4}=\mathrm{H}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{h} \mathrm{R}\mathrm{i}\mathrm{s}\mathrm{k}\) are cost-type parameters, and other parameters are of benefit type. The classified structure of criteria for selecting the BWM technique is given in the following Fig. 3.
Considering the abovementioned criteria, our present technique delivers recommendations for determining the most significantly ideal solution. The selection process builds significant interest in protecting environmental stability and the health of humans and plants. The main priority of modern BMW systems is economic and social sustainability. Nevertheless, this study evaluates the potential dangers to human health, declaring its essential relevance to establishing an environment of satisfaction within a society. Through rigorous investigation and careful contemplation of these variables, experts can recommend the most proper and effective method for BMW's disposal. Experts expressed their evaluations in the form of IVq-ROFSNs for each BMW alternative mentioned in Table 1. These are eventually incorporated into the EDAS technique, which employs the Einstein-ordered and Einstein hybrid AOs elaborated above in Sect. 5 to establish the most effective BMW disposal technique. The selection process of most appropriate BMW disposal technique using the proposed EDAS method is presented in the following:
Step 1: The group of experts carefully assessed all of the stated BMW disposal methodologies and presented their opinions. Table 1 presents a summary of expert's preferences in the form of IVq-ROFSNs for each alternative.
Step 2: As we know that, the matrix \({\left[{\mathrm{\Xi }}_{{a}_{ij}}^{p}\right]}_{n\times m}\) is analyzed by classifying the parameters into two groups: attributes connected with costs and attributes related to benefits. If the parameters are the same type, then no need to normalize. But, the parameters \({\mathfrak{R}}_{3}=\mathrm{N}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}\) and \({\mathfrak{R}}_{4}=\mathrm{H}\mathrm{e}\mathrm{a}\mathrm{l}\mathrm{t}\mathrm{h} \mathrm{r}\mathrm{i}\mathrm{s}\mathrm{k}\mathrm{s}\) are of cost type parameters, and other considered parameters are of benefit type. Thus, it is necessary to normalize the experts' evaluations using Eq. 10, given in Table 2.
Step 3: The overall normalized decision matrices are ordered in Table3.
Step 4: The process of constructing the aggregated decision matrix involves decision experts’ involvement and assigning attribute weights using the IVq-ROFSEOWA operator or IVq-ROFSEOWG operator (Eq.2 or Eq.8), as revealed in Tables 4 and 5.
Step 5: Apply the Eq.11 to determine the average solution matrix given as follows: \(\left[ {{\text{\AA}}S_{h} } \right]_{{1 \times 5}}\) \(=\left[\begin{array}{ccccc}\left(\begin{array}{c}\left[0.38950,0.51012\right],\\ \left[0.82559,0.89267\right]\end{array}\right)& \left(\begin{array}{c}\left[0.312842,0.58448\right],\\ \left[0.85315,0.91051\right]\end{array}\right)& \left(\begin{array}{c}\left[0.29976,0.41225\right],\\ \left[0.86236,0.92746\right]\end{array}\right)& \left(\begin{array}{c}\left[0.24565,0.35052\right],\\ \left[0.88103,0.93444\right]\end{array}\right)& \left(\begin{array}{c}\left[0.25202,0.37716\right],\\ \left[0.91471,0.96874\right]\end{array}\right)\end{array}\right]\)
Step 6: Table6 presents the outcomes of Eqs.12 and 13, which govern the required form and the mathematical computation of the PDA and NDA matrices,respectively.
Step 7: Calculate the positive weighted distance \({{\rm P}}_{\tau }\) and negative weighted distance \({Q}_{\tau }\) using Eqs. 14 and 15 given as follows:
\({{\rm P}}_{1}=\left(\left[0.25415, 0.41961\right], \left[0.21702, 0.50256\right]\right)\), \({{\rm P}}_{2}=\left(\left[0.30071, 0.41637\right], \left[0, 0.37563\right]\right)\), \({{\rm P}}_{3}=\left(\left[0.18631, 0.38822\right], \left[0, 0.469\right]\right)\), \({{\rm P}}_{4}=\left(\left[0.44343, 0.63025\right], \left[0, 0.65831\right]\right)\), \({{\rm P}}_{5}=\left(\left[0.35359, 0.51131\right], \left[0, 0.37659\right]\right)\), \({Q}_{1}=\left(\left[0.16911, 0.23591\right], \left[0.46501, 0.59011\right]\right)\), \({Q}_{2}=\left(\left[0, 0.24237\right], \left[0.39924, 0.59369\right]\right)\), \({Q}_{3}=\left(\left[0.21291, 0.29517\right], \left[0.25283, 0.57353\right]\right)\), \({Q}_{4}=\left(\left[0.48115, 0.56494\right], \left[0.68239, 0.76919\right]\right)\), and \({Q}_{5}=\left(\left[0, 0\right], \left[0.51774, 0.64505\right]\right)\).
Moreover, we use Eqs. 16 and 17 to find a positive weighted distance \({{\rm P}}_{\tau }\) and negative weighted distance \({Q}_{\tau }\) in the case of the IVq-ROFSEOWG operator.
Step 8: Normalized the values of positive weighted distance \({{\rm P}}_{\tau }\) and negative weighted distance \({Q}_{\tau }\) by using Eqs. 18, 19 respectively, which are given as follows:
\(N{{\rm P}}_{1}=\left(\left[0.12487, 0.20798\right], \left[0.10653, 0.25121\right]\right)\), \(N{{\rm P}}_{2}=\left(\left[0.14799, 0.20632\right], \left[0, 0.18558\right]\right)\), \(N{{\rm P}}_{3}=\left(\left[0.09141, 0.19196\right], \left[0, 0.23291\right]\right)\), \(N{{\rm P}}_{4}=\left(\left[0.22024, 0.32189\right], \left[0, 0.33845\right]\right)\), \(N{{\rm P}}_{5}=\left(\left[0.17446, 0.25587\right], \left[0, 0.18607\right]\right)\), \({NQ}_{1}=\left(\left[0.87826, 0.91283\right], \left[0.68607, 0.75686\right]\right)\), \({NQ}_{2}=\left(\left[ 0.87491, 1\right], \left[0.68396, 0.79243\right]\right)\), \({NQ}_{3}=\left(\left[0.10981, 0.89018\right], \left[0.69577, 0.86947\right]\right)\), \({NQ}_{4}=\left(\left[0.70075, 0.74799\right], \left[0.56984, 0.62941\right]\right)\), and \({NQ}_{5}=\left(\left[1, 1\right], \left[0.65296, 0.72764\right]\right)\).
Step 9: Derive the integrative appraisal score \(I\) using Eq. 20 such as follows:
\({I}_{1}=0.51114\), \({I}_{2}=0.51227\), \({I}_{3}=0.48880\), \({I}_{4}=0.50598\), and \({I}_{5}=0.52549\).
Step 10: Finally, the alternatives are ranked in descending order of appraisal score. The first-ranked alternative is the best, while the last one is the worst \({\mathfrak{H}}_{5}>{\mathfrak{H}}_{2}>{\mathfrak{H}}_{1}>{\mathfrak{H}}_{4}>{\mathfrak{H}}_{3}\).
The proposed approach delivers significant enhancements compared to the prevailing EDAS approach. The prevailing EDAS method communicates the MD and NMD of the evaluated data employing real numbers, although the proposed method reflects these via interval values. So, the suggested model enables specialists to express their perspectives more flexibly.
7 Comparative and sensitivity analysis
This section will analyze the sensitivity of our model along with a comparison analysis with prior studies.
7.1 Comparative analysis
In the following subsection, we will analyze our suggested model from three different perspectives. First, we compare this new EDAS technique to existing EDAS methods with distinct fuzzy frameworks. After that, we will compare the proposed EDAS approach with existing aggregation operators within the IVq-ROFS framework. Finally, we will compare our proposed approach to the TOPSIS method in the IVq-ROFSS structure.
7.1.1 Comparison with EDAS approaches in different structures
Notably, prevalent approaches, like the fuzzy EDAS (Ghorabaee et al. 2016) and IVFS EDAS (Ilieva 2018), only consider the MD and MD interval, respectively, for each alternative. Comparatively, certain models, such as the IFS EDAS (Mishra et al. 2020) and IVIFS EDAS (Li and Wang 2020), consider the MD and NMD when evaluating alternatives. Liu et al. (2022) designed the EDAS approach for PFS. Yanmaz et al. (2020) developed the EDAS model for IVPFS. Güneri and Deveci (2023) and Farrokhizadeh et al. (2020) extended the EDAS approach in the q-rung orthopair fuzzy and interval-valued q-rung orthopair fuzzy structures. Still, these methods have drawbacks regarding addressing the parameterization of alternatives. The theoretical analysis of our proposed EDAS technique, as compared with existing EDAS techniques under different structures of fuzzy sets, is presented in Table 7.
The developed EDAS approach effectively conquers the inherent challenges imposed by traditional EDAS methods, such as resolving the problem of managing the parameterization of alternatives. The feasibility of the developed EDAS model is shown by its ability to determine the most productive BMW disposal technique. The findings in Table 7 abundantly demonstrate that the proposed approach is superior to the other methods when choosing the most optimal decision among the available alternatives.
7.1.2 Comparison with different aggregation operators
Comparisons are carried out from the perspectives of aggregation operators to confirm and clarify the upsides of the proposed strategy. Compared the proposed method with different operators such as the IVq-ROFSWA (Yang et al. 2022), IVq-ROFSWG (Yang et al. 2022), IVq-ROFSIWA (Yang et al. 2022), IVq-ROFSIWG (Yang et al. 2022), GGIVq-ROFSWA (Hayat et al. 2023) operator, and GGIVq-ROFSWG operator (Hayat et al. 2023) is one aspect of the comparison. To be more accurate, the IVq-ROFSEOWA operator applied in Step 2 is replaced, in turn, by the operators stated earlier in the numerical example in Sect. 6.2, retaining the rest of the information. Table 8 and Fig. 4 illustrate the classification outcomes obtained using different operators. The ranking levels for the BMW disposal technique vary when methodologies of different operators are used to synthesize evaluation information, as Table 8 shows. Still, the BMW technique's rankings remain stable, with \({\mathfrak{H}}_{5}\) being continuously deemed the most effective disposal technique.
The finding reveals that our research has the identical optimized selection as prior research, confirming the reliability and practicality of the proposed technique for choosing a disposal technique in BMWs. This explicitly shows the potential and ability of the presented technique. Furthermore, there is some discrepancy among rankings. This variation is most likely caused by the described Einstein operations, which can collect complicated and confusing data on interactions while eliminating exaggeration and data degradation. Still, the operators in place neglected the integration of precise and frequently changing information at the time.
7.1.3 Comparison with TOPSIS method
We analyze the similarities and differences between the proposed methodology and the TOPSIS technique (Zulqarnain et al. 2024). Where \({\mathfrak{H}}_{5}\) is identified to be the most suitable alternative when scrutinizing the BMW disposal process in the TOPSIS technique. The disparity is in the order in which alternatives are displayed, resulting from the method used to determine positive and negative ideal solutions. This factor is more detailed by evaluating the differences between these possible outcomes. On the other hand, our presented method depends on the average solution principle, compromising the implementation of optimum techniques and requiring computational analysis of similar distances. While assessing the consequences demonstrated in Table 9, it will be observed that the proposed EDAS technique now in use and integrates IVq-ROFSNs determines the most efficient alternative with more accuracy for BMW disposal processes.
Figure 5 shows the graphical comparisons between the proposed technique and the TOPSIS (Zulqarnain et al. 2024) method.
7.2 Sensitivity analysis
To demonstrate the reliability and efficacy of the proposed approach, a sensitivity analysis is carried out on parameter \(q\). The organization's standards indicate that selections \({\mathfrak{H}}_{5}\) and \({\mathfrak{H}}_{3}\) are the most detrimental and poorest choices, respectively. Table 10 demonstrates that if “\(q\)” varies between 1 and 15, the alternatives are in a particular ascending order: \({\mathfrak{H}}_{5}>{\mathfrak{H}}_{2}>{\mathfrak{H}}_{1}>{\mathfrak{H}}_{4}>{\mathfrak{H}}_{3}\). The most stimulating aspect of this ranking is that there is no effect on the best and worst alternatives. Furthermore, the appraisal score of the alternatives demonstrates decreasing trends as the numeric value of the parameter “\(q\)” increases, indicating the reliance of assessing computations on the value of the stated parameter. It can be seen in Table 10 and Fig. 6. Also, in a scenario where the expression \({\left({MD}^{\mho }\right)}^{q}+ {\left({NMD}^{\mho }\right)}^{q}>1\), where \(q>2\), it must be determined which both IVIFSS (Jiang et al. 2010) and IVPFSS (Zulqarnain et al. 2022a) have been unable to present a sign that disputes this outcome. Still, the parameter “\(q\)” reflects the degree of ability to adapt to this particular information-extracting strategy. This research explored the prospective significance of parameters of the location in assisting expert evaluation.
The stated methodology aims to boost the compilation of facts by using multiple aspects, which facilitates the visualization of inadequate knowledge. Implementing the parameter “\(q\)” enables experts to evaluate every given assignment more thoroughly, advising experts to exercise caution in selecting an appropriate value for “\(q\)” to locate an appropriate behavior.
Based upon our detailed study and thorough analysis, the findings derived from the proposed method are superior to those attained by multiple other techniques. Figure 6 presents an animated illustration of the impact of the parameter “\(q\)” on the results.
7.3 Results and discussion
The effective use of the extended EDAS technique is transparent in its superior outcomes relative to preceding studies and the comparability of its findings with those gained through preexisting techniques. The leading advantage of this approach is the capability to comprise more details describing the confines that constitute the alternatives, efficiently addressing the unpredictability inherent in the data. So, integrating attribute-related data has been significantly streamlined, leading to a more comprehensive and precise description of facts. This enhancement has bestowed upon it a significant usefulness in facilitating informed decision-making.
Moreover, the comparison study determines the distinctive characteristics of the decision-making procedure of the presented technique compared to preceding strategies. This can be because of the ability to manage a higher level of uncertain data effectively. It reduces the apparent threat of data corruption that may arise while assigning score values to specific parameters without seriously considering their influence on the rest of the variables. By properly articulating the extent of perception and resemblance between clarifications while preventing drawing inferences using inadequate data, the EDAS approach presents substantial benefits over traditional approaches.
From our particular analysis, it is necessary to note that the proposed strategy evaluates every possible option while executing the disposal technique in BMW. The prevailing EDAS approaches under different frameworks, such as Ghorabaee (2016), Ilieva (2018), Mishra et al. (2020), Liu et al. (2022), and Güneri and Deveci (2023), can not handle alternative parametric modeling and particular scenarios such as MD and NMD intervals. The decision-making approaches, which were proposed by Peng and Yang (2016), Ahemad et al. (2023), Wan et al. (2023), Liu et al. (2015b), Rahman et al. (2018, 2020), Xu (2023) can deal with the MD and NMD intervals. However, these decision-making models cannot handle the parametric values and fail to find the optimal alternative using the average solution matrix. The EDAS techniques developed by Li and Wang (2020), Yanmaz et al. (2020), and Farrokhizadeh et al. (2020) compute the optimal alternative using the average solution matrix and MD and NMD intervals.
Still, these models are unable to handle the parametrized evaluation for alternatives. Jiang et al. (2010) and Zulqarnain et al. (2022a) introduced the decision-making techniques in IVIFSS and IVPFSS structures to overcome the above-stated drawbacks. If \({\left({MD}^{\mho }\right)}^{2}+{\left({NMD}^{\mho }\right)}^{2}>1\), then the IVIFSS and IVPFSS failed to solve the problem. Yang et al. (2022) and Hayat et al. (2023) extended the IVPFSS to IVq-ROFSS and the generalized IVq-ROFSS to solve the abovementioned concern. They developed several AOs with their basic properties and decision-making techniques. Both of these research studies effectively addressed the concerns stated above. The effect of parameter \(q\) on alternatives ranking using the Hayat et al. (2023) method is given in Fig. 7.
Hayat et al. (2023) method
Another finding derived from the evaluation of Figs. 6 and 7 indicates the proposed approach presents a more progressive development of categorical parameters as \(q\) increases, compared to its results Hayat et al. (2023) method. The ranking of the alternatives is not consistent by varying the value of parameter \(q\). This indicates that the proposed method presents less sensitivity to the variable \(q\), providing enhanced versatility and resilience. So, the approach proposed in this research reveals a higher level of impact and durability than the previous works (Yang et al. 2022; Hayat et al. 2023).
7.4 Advantages and theoretical executions of the extended EDAS method
Selecting the organization that appears to have the most potential to maintain BMW in this scenario is challenging. We developed an extensive structure that integrates facts obtained from numerous BMW executives and the features they indicate to deal with this diversity. The integrity and applicability of our evaluation findings by using this technique.
The EDAS technique that we presented produced an outcome in order of priority among all alternatives. Between them, \({\mathfrak{H}}_{5}\) has been determined to be the most beneficial, followed by \({\mathfrak{H}}_{2}\), \({\mathfrak{H}}_{1}\), \({\mathfrak{H}}_{4}\), and \({\mathfrak{H}}_{3}\) as shown by the preferred relation \({\mathfrak{H}}_{5}>{\mathfrak{H}}_{2}>{\mathfrak{H}}_{1}>{\mathfrak{H}}_{4}>{\mathfrak{H}}_{3}\). Acknowledging that various sets of attribute weights might influence the ranking results is crucial. But it is interesting to note that the most effective option that consistently delivers the best findings is \({\mathfrak{H}}_{5}\). Due to this capability, a city administrator can modify the attribute weights to fit real-life scenarios, generating a dynamic ranking compatible with particular requirements.
Optimizing the handling of BMW in metropolitan areas considerably impacts environmental sustainability. Evaluating BMW managerial effectiveness compared to other organizations helps city administrators with beneficial data to analyze decisions and develop further programs for the community's prosperity. Lower-ranked organizations could need more funding and regulation than their higher-ranked peers.
Our suggested strategy is simple to implement and performs well when combined with additional tools for decision-making. We ensure the accuracy of the assessments and generate criteria and objectives leading to their essential contribution by engaging various experts. Our EDAS approach helps identify the best organization to manage BMW efficiently and deal with the practical issues about MAGDM in uncertain real-world circumstances.
Furthermore, this method's versatility extends beyond BMW management and applies to various facets of city management. Employing decision support tools and familiarizing decision-makers with the method can significantly enhance the assessment’s quality while reducing managerial workloads. Developing a computer software program is advisable to streamline the decision-making process, minimizing the time and effort required to solve such problems and potentially reallocating surplus funds to advance BMW management initiatives.
7.5 Limitations of the extended EDAS method
Implementing the EDAS approach into the IVq-ROFSS framework delivers numerous advantages, optimizing the overall impact of the proposed strategy. This fusion promotes more efficient decision-making procedures, improving system reliability and stability. Still, it is important to note the multiple intrinsic drawbacks of the stated method. It is essential to thoroughly investigate the limitations described below to understand the feasibility of the model properly and to determine aspects that require improvements.
-
1.
The outcomes and the approach reported in this research may be influenced by context and can lack broad implications across varied scenarios, geographic regions, or societal contexts. The particular characteristics of the case study might affect the ability to use the suggested technique in various circumstances.
-
2.
The practicality of the extended EDAS method depends on the general availability and quality of the information at issue. The validity of its findings can be impacted by inconsistencies or shortcomings in the information provided, particularly regarding BMW's managerial processes and expert opinions.
-
3.
The order of preference and assignment significance to attributes depend upon expert assessments, so applying a component of bias. The existence of multiple points of view among experts and the prospect of biased opinions can influence the credibility and integrity of the process of making decisions.
-
4.
This approach implies that other factors do not affect attributes that benefit the decision-making process. In real-life scenarios, characteristics can demonstrate interdependencies, and omitting to weigh these interactions can affect the decision strategy.
8 Conclusion
Disposing of waste generated in healthcare facilities mostly entails the safe disposal of human organs, infectious diseases such as fungi, bacteria, and viruses, and the proper disposition of instruments used to clean blood vessels. In this paper, we introduce the Einstein operational laws for IVq-ROFSS. Moreover, based on these operational laws, some AOs, such as IVq-ROFSEOWA, IVq-ROFSEHWA, IVq-ROFSEOWG, and IVq-ROFSEHWG operators are developed to aggregate IVq-ROFS data. Moreover, we discussed the most important properties of these operators, such as idempotency, boundedness, monotonicity, homogeneity, and shift-invariance. An EDAS method is proposed to deal with the MAGDM challenges in the IVq-ROFSS framework, integrating the developed Einstein AOs. To validate the constructive characteristics of the proposed EDAS approach, we considered a case study that concerns the most applicable treatment technique in BMW management. The comparative analysis also shows the productivity and reliability of the method, validating its significant stability and applicability in assisting decision-makers during the DM process.
Future studies will explore interactive Einstein-ordered and Einstein hybrid AOs with their important properties. Moreover, the methodology presented in this article will be extended to interval-valued q-rung orthopair fuzzy hypersoft sets. Also, we will investigate the integration of IVq-ROFSNs with other MAGDM techniques to examine their implications in medical diagnosis, material selection, pattern recognition, and municipal solid waste management. Several topological, algebraic, and ordered structures can be developed with their decision-making methodologies under the IVq-ROFSS structure.
Data availability
All the data used and analyzed is available in the manuscript.
References
Adunlin G, Diaby V, Xiao H (2015) Application of multicriteria decision analysis in health care: a systematic review and bibliometric analysis. Health Expect 18(6):1894–1905
Ahemad F, Khan AZ, Mehlawat MK, Gupta P, Roy SK (2023) Multi-attribute group decision-making for solid waste management using interval-valued q-rung orthopair fuzzy COPRAS. RAIRO Op Res 57(3):1239–1265
Al-Barakati A, Rani P (2023) Assessment of healthcare waste treatment methods using an interval-valued intuitionistic fuzzy double normalization-based multiple aggregation approach. Environ Develop Sustain. https://doi.org/10.1007/s10668-023-03154-8
Alcantud JCR (2022) The semantics of N-soft sets, their applications, and a coda about three-way decision. Inf Sci 606:837–852
Alcantud JCR (2023) Complemental fuzzy sets: a semantic justification of q-rung orthopair fuzzy sets. IEEE Trans Fuzzy Syst 31(12):4262–4270
Ali G, Afzal M, Asif M, Shazad A (2021) Attribute reduction approaches under interval-valued q-rung orthopair fuzzy soft framework. Appl Intell 52:8975–9000
Al-Zibaree HKY, Konur M (2023) Fuzzy analytic hierarchal process for sustainable public transport system. J Op Intell 1(1):1–10
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96
Atanassov KT (1999) Interval valued intuitionistic fuzzy sets. Intuitionistic fuzzy sets. Studies in fuzziness and soft computing, vol 35. Physica, Heidelberg
Aung TS, Luan S, Xu Q (2019) Application of multi-criteria-decision approach for the analysis of medical waste management systems in Myanmar. J Clean Prod 222:733–745
Chauhan A, Singh A (2016) A hybrid multi-criteria decision making method approach for selecting a sustainable location of healthcare waste disposal facility. J Clean Prod 139:1001–1010
Chaurasiya R, Jain D (2022) Pythagorean fuzzy entropy measure-based complex proportional assessment technique for solving multi-criteria healthcare waste treatment problem. Granul Comput 7(4):917–930
Chou SY, Chang YH, Shen CY (2008) A fuzzy simple additive weighting system under group decision-making for facility location selection with objective/subjective attributes. Eur J Oper Res 189(1):132–145
Danner M, Hummel JM, Volz F, Van Manen JG, Wiegard B, DintsiosIJzerman CMMJ (2011) Integrating patients’ views into health technology assessment: Analytic hierarchy process (AHP) as a method to elicit patient preferences. Int J Technol Assess Health Care 27(4):369–375
Dinçer H, Yüksel S, Eti S (2023) Identifying the right policies for increasing the efficiency of the renewable energy transition with a novel fuzzy decision-making model. J Soft Comput Decis Anal 1(1):50–62
Farrokhizadeh E, Seyfi Shishavan SA, Donyatalab Y, Seifi SH (2020) Interval valued q-Rung orthopair fuzzy EDAS method and its application to supplier selection. In International conference on intelligent and fuzzy systems (pp. 457–465). Springer International Publishing, Cham. https://doi.org/10.1007/978-3-030-51156-2_53
Garg H (2016) A new generalized Pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. Int J Intell Syst 31(9):886–920
Garg H (2017) Generalized Pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multicriteria decision-making process. Int J Intell Syst 32(6):597–630
Ghorabaee MK, Zavadskas EK, Olfat L, Turskis Z (2015) Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica 26(3):435–451
Ghorabaee MK, Zavadskas EK, Amiri M, Turskis Z (2016) Extended EDAS method for fuzzy multi-criteria decision-making: an application to supplier selection. Int J Comput Commun Control 11(3):358–371
Ghoushchi SJ, Sarvi S (2023) Prioritizing and evaluating risks of ordering and prescribing in the chemotherapy process using an extended SWARA and MOORA under fuzzy Z-numbers. J Op Intell 1(1):44–66
Güneri B, Deveci M (2023) Evaluation of supplier selection in the defense industry using q-rung orthopair fuzzy set based EDAS approach. Expert Syst Appl 222:119846
Hayat K, Raja MS, Lughofer E, Yaqoob N (2023) New group-based generalized interval-valued q-rung orthopair fuzzy soft aggregation operators and their applications in sports decision-making problems. Comput Appl Math. https://doi.org/10.1007/s40314-022-02130-8
Hossain MS, Santhanam A, Norulaini NN, Omar AM (2011) Clinical solid waste management practices and its impact on human health and environment–a review. Waste Manage 31(4):754–766
Hussain A, Ali MI, Mahmood T, Munir M (2020) q-Rung orthopair fuzzy soft average aggregation operators and their application in multicriteria decision-making. Int J Intell Syst 35(4):571–599
Ilieva G (2018) Group decision analysis algorithms with EDAS for interval fuzzy sets. Cybern Inf Technol 18(2):51–64
Jiang Y, Tang Y, Chen Q, Liu H, Tang J (2010) Interval-valued intuitionistic fuzzy soft sets and their properties. Comput Math Appl 60(3):906–918
Joshi BP, Gegov A (2020) Confidence levels q-rung orthopair fuzzy aggregation operators and its applications to MCDM problems. Int J Intell Syst 35(1):125–149
Joshi BP, Singh A, Bhatt PK, Vaisla KS (2018) Interval valued q-rung orthopair fuzzy sets and their properties. J Intell Fuzzy Syst 35(5):5225–5230
Li S, Wang B (2020) Research on evaluating algorithms for the service quality of wireless sensor networks based on interval-valued intuitionistic fuzzy EDAS and CRITIC methods. Math Probl Eng 2020:1–12. https://doi.org/10.1155/2020/5391940
Li H, Dietl H, Li J (2021) Identifying key factors influencing sustainable element in healthcare waste management using the interval-valued fuzzy DEMATEL method. J Mater Cycles Waste Manage 23:1777–1790
Liao CJ, Ho CC (2014) Risk management for outsourcing biomedical waste disposal–using the failure mode and effects analysis. Waste Manage 34(7):1324–1329
Limboo B, Dutta P (2022) A q-rung orthopair basic probability assignment and its application in medical diagnosis. Decis Mak Appl Manag Eng 5(1):290–308
Liu HC, You JX, Lu C, Chen YZ (2015) Evaluating health-care waste treatment technologies using a hybrid multi-criteria decision making model. Renew Sustain Energy Rev 41:932–942
Liu P, Li Y, Chen Y (2015) Some generalized Einstein aggregation operators based on the interval-valued intuitionistic fuzzy numbers and their application to group decision making. Scientia Iranica 22(6):2684–2701
Liu P, Rani P, Mishra AR (2021) A novel Pythagorean fuzzy combined compromise solution framework for the assessment of medical waste treatment technology. J Clean Prod 292:126047
Liu C, Rani P, Pachori K (2022) Sustainable circular supplier selection and evaluation in the manufacturing sector using Pythagorean fuzzy EDAS approach. J Enterp Inf Manag 35(4/5):1040–1066
Maji PK, Biswas R, Roy AR (2001) Fuzzy soft sets. J Fuzzy Math 9:589–602
Maji PK, Biswas R, Roy AR (2001) Intuitionistic fuzzy soft sets. J Fuzzy Math 9:677–692
Manupati VK, Ramkumar M, Baba V, Agarwal A (2021) Selection of the best healthcare waste disposal techniques during and post COVID-19 pandemic era. J Clean Prod 281:125175
Mishra AR, Mardani A, Rani P, Zavadskas EK (2020) A novel EDAS approach on intuitionistic fuzzy set for assessment of health-care waste disposal technology using new parametric divergence measures. J Clean Prod 272:122807
Molodtsov D (1999) Soft set theory—first results. Comput Math Appl 37(4–5):19–31
Narayanamoorthy S, Annapoorani V, Kang D, Baleanu D, Jeon J, Kureethara JV, Ramya L (2020) A novel assessment of bio-medical waste disposal methods using integrating weighting approach and hesitant fuzzy MOOSRA. J Clean Prod 275:122587
Nezhad MZ, Nazarian-Jashnabadi J, Rezazadeh J, Mehraeen M, Bagheri R (2023) Assessing dimensions influencing IoT implementation readiness in industries: a fuzzy DEMATEL and fuzzy AHP analysis. J Soft Comput Decis Anal 1(1):102–123
Nikolic MD, Petrovic N, Belic A, Rokvic M, Radakovic JA, Tubic V (2016) The fault tree analysis of infectious medical waste management. J Clean Prod 113:365–373
Özçelik G, Nalkıran M (2021) An extension of EDAS method equipped with trapezoidal bipolar fuzzy information: an application from healthcare system. Int J Fuzzy Syst 23(7):2348–2366
Padmanabhan KK, Barik D (2019) Health hazards of medical waste and its disposal. Energy from toxic organic waste for heat and power generation. Elsevier, Amsterdam
Peng X, Yang Y (2016) Fundamental properties of interval-valued Pythagorean fuzzy aggregation operators. Int J Intell Syst 31(5):444–487
Peng X, Yang Y, Song J (2015) Pythagoren fuzzy soft set and its application. Comput Eng 41(7):224–229
Rahman K, Abdullah S, Khan MSA (2018) Some interval-valued Pythagorean fuzzy Einstein weighted averaging aggregation operators and their application to group decision making. J Intell Syst 29(1):393–408
Rahman K, Ali A, Abdullah S (2020) Multiattribute group decision making based on interval-valued Pythagorean fuzzy Einstein geometric aggregation operators. Granul Comput 5:361–372
Rajan R, Robin DT, Vandanarani M (2019) Biomedical waste management in Ayurveda hospitals–current practices and future prospectives. J Ayurveda Integr Med 10(3):214–221
Rani P, Mishra AR, Krishankumar R, Ravichandran KS, Gandomi AH (2020) A new Pythagorean fuzzy based decision framework for assessing healthcare waste treatment. IEEE Trans Eng Manage 69(6):2915–2929
Ranjan MJ, Kumar BP, Bhavani TD, Padmavathi AV, Bakka V (2023) Probabilistic linguistic q-rung orthopair fuzzy Archimedean aggregation operators for group decision-making. Decis Mak Appl Manag Eng 6(2):639–667
Rume T, Islam SMDU (2020) Environmental effects of COVID-19 pandemic and potential strategies of sustainability. Heliyon. https://doi.org/10.1016/j.heliyon.2020.e04965
Turksen IB (1986) Interval valued fuzzy sets based on normal forms. Fuzzy Sets Syst 20(2):191–210
Wan B, Hu Z, Garg H, Cheng Y, Han M (2023) An integrated group decision-making method for the evaluation of hypertension follow-up systems using interval-valued q-rung orthopair fuzzy sets. Complex Intell Syst 9:4521–4554
Wang W, Liu X (2011) Intuitionistic fuzzy geometric aggregation operators based on Einstein operations. Int J Intell Syst 26(11):1049–1075
Wang W, Liu X (2012) Intuitionistic fuzzy information aggregation using Einstein operations. IEEE Trans Fuzzy Syst 20(5):923–938
Wang W, Liu X (2012) Some interval-valued intuitionistic fuzzy geometric aggregation operators based on einstein operations. In 2012 9th international conference on fuzzy systems and knowledge discovery (pp. 604–608). IEEE. https://doi.org/10.1109/FS2012.6234364
Xu Y (2023) A two-stage multi-criteria decision-making method with interval-valued q-Rung Orthopair fuzzy technology for selecting bike-sharing recycling supplier. Eng Appl Artif Intell 119:105827
Yager RR (2013) Pythagorean membership grades in multi-criteria decision making. IEEE Trans Fuzzy Syst 22(4):958–965
Yager RR (2016) Generalized orthopair fuzzy sets. IEEE Trans Fuzzy Syst 25(5):1222–1230
Yang J, Yao Y (2020) Semantics of soft sets and three-way decision with soft sets. Knowl-Based Syst 194:105538
Yang X, Hayat K, Raja MS, Yaqoob N, Jana C (2022) Aggregation and interaction aggregation soft operators on interval-valued q-rung orthopair fuzzy soft environment and application in automation company evaluation. IEEE Access 10:91424–91444
Yanmaz O, Turgut Y, Can EN, Kahraman C (2020) Interval-valued Pythagorean fuzzy EDAS method: an application to car selection problem. J Intell Fuzzy Syst 38:4061–4077
Zulqarnain RM, Siddique I, Ahmad S, Iampan A, Jovanov G, Vranješ Đ, Vasiljević J (2021) Pythagorean fuzzy soft Einstein ordered weighted average operator in sustainable supplier selection problem. Math Probl Eng 2021:1–16. https://doi.org/10.1155/2021/2559979
Zulqarnain RM, Siddique I, Iampan A, Baleanu D (2022) Aggregation operators for interval valued Pythagorean fuzzy soft set with their application to solve multi-attribute group decision making problem. Comput Model Eng Sci 131(3):1717–1750
Zulqarnain RM, Siddique I, EI-Morsy S (2022) Einstein-ordered weighted geometric operator for Pythagorean fuzzy soft set with its application to solve MAGDM problem. Math Probl Eng 2022:1–14.https://doi.org/10.1155/2022/5199427
Zulqarnain RM, Rehman HKU, Awrejcewicz J, Ali R, Siddique I, Jarad F, Iampan A (2022) Extension of Einstein average aggregation operators to medical diagnostic approach under Q-rung orthopair fuzzy soft set. IEEE Access 10:87923–87949
Zulqarnain RM, Ali R, Awrejcewicz J, Siddique I, Jarad F, Iampan A (2022) Some Einstein geometric aggregation operators for Q-rung orthopair fuzzy soft set with their application in MCDM. IEEE Access 10:88469–88494
Zulqarnain RM, Siddique I, Asif M, Ahmad H, Askar S, Gurmani SH (2023) Extension of correlation coefficient based TOPSIS technique for interval-valued Pythagorean fuzzy soft set: a case study in extract, transform, and load techniques. PLoS ONE 18(10):e0287032
Zulqarnain RM, Garg H, Ma WX, Siddique I (2024) Optimal cloud service provider selection: An MADM framework on correlation-based TOPSIS with interval-valued q-rung orthopair fuzzy soft set. Eng Appl Artif Intell 129:107578
Acknowledgements
Research Supporting Project number (RSP2024R167), King Saud University, Riyadh, Saudi Arabia.
Funding
This project is funded by King Saud University, Riyadh, Saudi Arabia.
Author information
Authors and Affiliations
Contributions
R. M. Z. wrote the main manuscript text. All authors reviewed the manuscript. M. D and O. C. are supervision.
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
We can use mathematical induction to prove the above-stated Theorem.
For \(n=1\), we get \({v}_{i}=1\). So,
For \(m=1\), we get \({w}_{j}=1\). So,
Equation (2) is satisfied for \(n=1\) and \(m=1\).
For \(n=2\) and \(m=1\)
For simplicity, Let \({\rho }_{1}={\left({\left(1+{\left({\lambda }_{{a}_{11}}^{l}\right)}^{q}\right)}^{{v}_{1}}\right)}^{{w}_{1}}\); \({\varrho }_{1}={\left({\left(1-{\left({\lambda }_{{a}_{11}}^{l}\right)}^{q}\right)}^{{v}_{1}}\right)}^{{w}_{1}}\); \({\mathrm{\Gamma }}_{1}={\left({\left(1+{\left({\lambda }_{{a}_{11}}^{\mho }\right)}^{q}\right)}^{{v}_{1}}\right)}^{{w}_{1}}\); \({\xi }_{1}={\left({\left(1-{\left({\lambda }_{{a}_{11}}^{\mho }\right)}^{q}\right)}^{{v}_{1}}\right)}^{{w}_{1}}\); \({\rho }_{2}={\left({\left(1+{\left({\lambda }_{{a}_{21}}^{l}\right)}^{q}\right)}^{{v}_{2}}\right)}^{{w}_{1}}\); \({\varrho }_{2}={\left({\left(1-{\left({\lambda }_{{a}_{21}}^{l}\right)}^{q}\right)}^{{v}_{2}}\right)}^{{w}_{1}}\); \({\mathrm{\Gamma }}_{2}={\left({\left(1+{\left({\lambda }_{{a}_{21}}^{\mho }\right)}^{q}\right)}^{{v}_{2}}\right)}^{{w}_{1}}\); \({\xi }_{2}={\left({\left(1-{\left({\lambda }_{{a}_{21}}^{\mho }\right)}^{q}\right)}^{{v}_{2}}\right)}^{{w}_{1}}\); \(\widehat{{\rho }_{1}}={\left({\left({\left({\eta }_{{a}_{11}}^{l}\right)}^{q}\right)}^{{v}_{1}}\right)}^{{w}_{1}}\); \(\widehat{{\varrho }_{1}}={\left({\left(2-{\left({\eta }_{{a}_{11}}^{l}\right)}^{q}\right)}^{{v}_{1}}\right)}^{{w}_{1}}\); \(\widehat{{\mathrm{\Gamma }}_{1}}={\left({\left({\left({\eta }_{{a}_{11}}^{\mho }\right)}^{q}\right)}^{{v}_{1}}\right)}^{{w}_{1}}\); \(\widehat{{\xi }_{1}}={\left({\left(2-{\left({\eta }_{{a}_{11}}^{\mho }\right)}^{q}\right)}^{{v}_{1}}\right)}^{{w}_{1}}\); \(\widehat{{\rho }_{2}}={\left({\left({\left({\eta }_{{a}_{21}}^{l}\right)}^{q}\right)}^{{v}_{2}}\right)}^{{w}_{1}}\); \(\widehat{{\varrho }_{2}}={\left({\left(2-{\left({\eta }_{{a}_{21}}^{l}\right)}^{q}\right)}^{{v}_{2}}\right)}^{{w}_{1}}\); \(\widehat{{\mathrm{\Gamma }}_{2}}={\left({\left({\left({\eta }_{{a}_{21}}^{\mho }\right)}^{q}\right)}^{{v}_{2}}\right)}^{{w}_{1}}\); and \(\widehat{{\xi }_{2}}={\left({\left(2-{\left({\eta }_{{a}_{21}}^{\mho }\right)}^{q}\right)}^{{v}_{2}}\right)}^{{w}_{1}}\). Then,
\({w}_{1}\left({v}_{1}{{\Delta }}_{{a}_{11}}\right)=\left(\left[\begin{array}{c}\frac{\sqrt[q]{{\rho }_{1}-{\varrho }_{1}}}{\sqrt[q]{{\rho }_{1}+{\varrho }_{1}}},\frac{\sqrt[q]{\widehat{{\mathrm{\Gamma }}_{1}}-\widehat{{\xi }_{1}}}}{\sqrt[q]{\widehat{{\mathrm{\Gamma }}_{1}}+\widehat{{\xi }_{1}}}}\end{array}\right], \left[\begin{array}{c}\frac{\sqrt[q]{2\widehat{{\rho }_{1}}}}{\sqrt[q]{\widehat{{\rho }_{1}}+\widehat{{\varrho }_{1}}}},\frac{\sqrt[q]{2\widehat{{\varrho }_{1}}}}{\sqrt[q]{\widehat{{\rho }_{1}}+\widehat{{\varrho }_{1}}}}\end{array}\right]\right)\) and \({w}_{1}\left({v}_{2}{{\Delta }}_{{a}_{21}}\right)=\left(\left[\begin{array}{c}\frac{\sqrt[q]{{\rho }_{2}-{\varrho }_{2}}}{\sqrt[q]{{\rho }_{2}+{\varrho }_{2}}},\frac{\sqrt[q]{\widehat{{\mathrm{\Gamma }}_{2}}-\widehat{{\xi }_{2}}}}{\sqrt[q]{\widehat{{\mathrm{\Gamma }}_{2}}+\widehat{{\xi }_{2}}}}\end{array}\right], \left[\begin{array}{c}\frac{\sqrt[q]{2\widehat{{\rho }_{2}}}}{\sqrt[q]{\widehat{{\rho }_{2}}+\widehat{{\varrho }_{2}}}},\frac{\sqrt[q]{2\widehat{{\varrho }_{2}}}}{\sqrt[q]{\widehat{{\rho }_{2}}+\widehat{{\varrho }_{2}}}}\end{array}\right]\right)\)
So,
Equation 2 satisfied for \(n=2\) and \(m=1\). Suppose Eq. 2 is true for \(n=k\) and \(m=\mathcal{l}\).
for \(n=k+1\) and \(m=\mathcal{l}+1\).
For Simplicity \({\rho }_{1}=\prod _{j=1}^{\mathcal{l}}{\left(\prod _{i=1}^{k}{\left(1+{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}\); \({\varrho }_{1}=\prod _{j=1}^{\mathcal{l}}{\left(\prod _{i=1}^{k}{\left(1-{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}\); \({\mathrm{\Gamma }}_{1}=\prod _{j=1}^{\mathcal{l}}{\left(\prod _{i=1}^{k}{\left(1+{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}\); \({\xi }_{1}=\prod _{j=1}^{\mathcal{l}}{\left(\prod _{i=1}^{k}{\left(1-{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}\); \({\rho }_{2}={\left({\left(1+{\left({\lambda }_{{a}_{\left(k+1\right)\left(\mathcal{l}+1\right)}}^{l}\right)}^{q}\right)}^{{v}_{k+1}}\right)}^{{w}_{\mathcal{l}+1}}\); \({\varrho }_{2}={\left({\left(1-{\left({\lambda }_{{a}_{\left(k+1\right)\left(\mathcal{l}+1\right)}}^{l}\right)}^{q}\right)}^{{v}_{k+1}}\right)}^{{w}_{\mathcal{l}+1}}\); \({\mathrm{\Gamma }}_{2}={\left(\left({\left(1+{\left({\lambda }_{{a}_{\left(k+1\right)\left(\mathcal{l}+1\right)}}^{\mho }\right)}^{q}\right)}^{{v}_{k+1}}\right)\right)}^{{w}_{\mathcal{l}+1}}\); \({\xi }_{2}={\left(\left({\left(1-{\left({\lambda }_{{a}_{\left(k+1\right)\left(\mathcal{l}+1\right)}}^{\mho }\right)}^{q}\right)}^{{v}_{k+1}}\right)\right)}^{{w}_{\mathcal{l}+1}}\); \(\widehat{{\rho }_{1}}=\prod _{j=1}^{\mathcal{l}}{\left(\prod _{i=1}^{k}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}\); \(\widehat{{\varrho }_{1}}=\prod _{j=1}^{\mathcal{l}}{\left(\prod _{i=1}^{k}{\left(2-{\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}\); \(\widehat{{\mathrm{\Gamma }}_{1}}=\prod _{j=1}^{\mathcal{l}}{\left(\prod _{i=1}^{k}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}\); \(\widehat{{\xi }_{1}}=\prod _{j=1}^{\mathcal{l}}{\left(\prod _{i=1}^{k}{\left(2-{\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}\); \(\widehat{{\rho }_{2}}={\left({\left({\left({\eta }_{{a}_{\left(k+1\right)\left(\mathcal{l}+1\right)}}^{l}\right)}^{q}\right)}^{{v}_{k+1}}\right)}^{{w}_{\mathcal{l}+1}}\); \(\widehat{{\varrho }_{2}}={\left({\left(2-{\left({\eta }_{{a}_{\left(k+1\right)\left(\mathcal{l}+1\right)}}^{l}\right)}^{q}\right)}^{{v}_{k+1}}\right)}^{{w}_{\mathcal{l}+1}}\); \(\widehat{{\mathrm{\Gamma }}_{2}}={\left(\left({\left({\left({\eta }_{{a}_{\left(k+1\right)\left(\mathcal{l}+1\right)}}^{\mho }\right)}^{q}\right)}^{{v}_{k+1}}\right)\right)}^{{w}_{\mathcal{l}+1}}\); and \(\widehat{{\xi }_{2}}={\left({\left(2-{\left({\eta }_{{a}_{\left(k+1\right)\left(\mathcal{l}+1\right)}}^{\mho }\right)}^{q}\right)}^{{v}_{k+1}}\right)}^{{w}_{\mathcal{l}+1}}\). So,
\(IVq-ROFSEOWA\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{\left(k+1\right)\left(\mathcal{l}+1\right)}}\right)= \left(\left[\begin{array}{c}\frac{\sqrt[q]{{\rho }_{1}-{\varrho }_{1}}}{\sqrt[q]{{\rho }_{1}+{\varrho }_{1}}},\frac{\sqrt[q]{\widehat{{\mathrm{\Gamma }}_{1}}-\widehat{{\xi }_{1}}}}{\sqrt[q]{\widehat{{\mathrm{\Gamma }}_{1}}-\widehat{{\xi }_{1}}}}\end{array}\right], \left[\begin{array}{c}\frac{\sqrt[q]{2\widehat{{\rho }_{1}}}}{\sqrt[q]{\widehat{{\rho }_{1}}+\widehat{{\varrho }_{1}}}},\frac{\sqrt[q]{2\widehat{{\varrho }_{1}}}}{\sqrt[q]{\widehat{{\rho }_{1}}+\widehat{{\varrho }_{1}}}}\end{array}\right]\right)\), and
Thus,
Equation (2) is true for \(n=k+1\), \(m=l+1\). As a result, Eq. (2) is valid for all positive values of \(n\) and \(m\).
Theorem 3.3 states that the outcome derived from using IVq-ROFSEOWA operators also serves as an IVq-ROFSN. This claim may be confirmed through the following proof:
\({\Delta }{ }_{{a}_{ij}}=\left(\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right],\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right)\) is an IVq-ROFSVs, so \(0\le {\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho },{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\le 1 and {\left({\lambda }_{{a}_{ij}}^{\mho }\right)}^{q}+{\left({\eta }_{{a}_{ij}}^{\mho }\right)}^{q}\le 1\).
\(0\le \frac{\sqrt[q]{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1+{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}-\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1-{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}}{\sqrt[q]{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1+{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}+\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1-{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}},\begin{array}{c}\frac{\sqrt[q]{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1+{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}-\prod _{j=1}^{m}{\left(\left(\prod _{i=1}^{n}{\left(1-{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)\right)}^{{w}_{j}}}}{\sqrt[q]{\prod _{j=1}^{m}{\left(\left(\prod _{i=1}^{n}{\left(1-{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)\right)}^{{w}_{j}}+\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1-{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}}\end{array}\le 1\). Since,
\(0\le {\eta }_{{a}_{ij}}^{l}\le 1\), \(0\le {\left({\eta }_{{a}_{ij}}^{l}\right)}^{q}\le 1\), \(1\le 2-{\left({\eta }_{{a}_{ij}}^{l}\right)}^{q}\le 2\), so, \(0\le {\left({\eta }_{{a}_{ij}}^{l}\right)}^{q}\le 2-{\left({\eta }_{{a}_{ij}}^{l}\right)}^{q}\le 2\). So,
\(0\le \frac{\sqrt[q]{2\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}}{\sqrt[q]{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(2-{\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}+\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}}\le \begin{array}{c}\frac{\sqrt[q]{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(2-{\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}+\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}}{\sqrt[q]{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(2-{\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}+\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{l}\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}}\end{array}=1\).
Similarly,
\(0\le \frac{\sqrt[q]{2\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}}{\sqrt[q]{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(2-{\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}+\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}}\le \begin{array}{c}\frac{\sqrt[q]{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(2-{\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}+\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}}{\sqrt[q]{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(2-{\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}+\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}}\end{array}=1\).
Since \({\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}+{\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\le 1\), so, \(\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}\le \prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1-{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}\), \(\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1+{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}\le \prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({2-\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}\). Then \({\left(\frac{\sqrt[q]{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1+{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}-\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1-{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}}{\sqrt[q]{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1+{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}+\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1-{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}}\right)}^{q}+{\left(\frac{\sqrt[q]{2\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}}{\sqrt[q]{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({2-\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}+\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}}\right)}^{q}.\)
\(\le \frac{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1+{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}-\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1+{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}+\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}+\frac{2\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}{\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left(1+{\left({\lambda }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}+\prod _{j=1}^{m}{\left(\prod _{i=1}^{n}{\left({\left({\eta }_{\sigma \left({a}_{\mathfrak{r}\left(i\right)\mathfrak{s}\left(j\right)}\right)}^{\mho }\right)}^{q}\right)}^{{v}_{i}}\right)}^{{w}_{j}}}=1.\)
It is verified that the aggregation outcome in Eq. (2) is still an IVq-ROFSV.
Appendix 2
Proof 3.4.1
As \({{\Delta }}_{{a}_{ij}}={{\Delta }}_{{a}_{o}}=\left(\left[{\lambda }_{o }^{l},{\lambda }_{o}^{\mho }\right],\left[{\eta }_{o}^{l},{\eta }_{o}^{\mho }\right]\right)\), for any \(i=1, 2, 3, \dots , n;j=1, 2, 3, \dots ,m\). Then
As \(\sum _{i=1}^{n}{v}_{i}=1\) and \(\sum _{j=1}^{m}{w}_{j}=1.\) So,
Proof 3.4.2
Let \(f\left(x\right)=\frac{1-x}{1+x}\) \(x\in \left[\mathrm{0,1}\right]\), then \(f^{\prime}\left( x \right) = - \frac{2}{{\left( {1 + x} \right)^{2} }}\, \Rightarrow \,f\left( x \right) \ge f^{\prime}\left( x \right)\). So, \(f\left(x\right)\) is a decreasing function. Let \(min\left({\lambda }_{{a}_{ij} }^{l}\right)={\lambda }_{min }^{l}\), \(max\left({\lambda }_{{a}_{ij} }^{l}\right)={\lambda }_{max }^{l}\), thus, \({\left({\lambda }_{min }^{l}\right)}^{q}\le {\left({\lambda }_{{a}_{ij} }^{l}\right)}^{q}\le {\left({\lambda }_{max }^{l}\right)}^{q}\), then \(f\left({\left({\lambda }_{max }^{l}\right)}^{q}\right)\le f\left({\left({\lambda }_{{a}_{ij} }^{l}\right)}^{q}\right)\le f\left({\left({\lambda }_{min }^{l}\right)}^{q}\right)\) for any \(i\), \(j\).
Similarly,
Let \(g\left( u \right) = \frac{{2 - u}}{u}\), where \(u \in \left[ {0,~1} \right]\), then \(g^{\prime}\left( u \right)\, = \, - \,\frac{2}{{u^{2} }}\). So, \(g\left(u\right)\) be a decreasing function. Let \(min\left({\eta }_{{a}_{ij} }^{l}\right)={\eta }_{min}^{l}\), \(max\left({\eta }_{{a}_{ij} }^{l}\right)={\eta }_{max}^{l}\), so, \({\left({\eta }_{min }^{l}\right)}^{q}\le {\left({\eta }_{{a}_{ij} }^{l}\right)}^{q}\le {\left({\eta }_{max }^{l}\right)}^{q}\Rightarrow g{\left({\eta }_{max }^{l}\right)}^{q}\le g{\left({\eta }_{{a}_{ij} }^{l}\right)}^{q}\le g{\left({\eta }_{min }^{l}\right)}^{q},\frac{2-{\left({\eta }_{max }^{l}\right)}^{q}}{{\left({\eta }_{max }^{l}\right)}^{q}}\le \frac{2-{\left({\eta }_{{a}_{ij} }^{l}\right)}^{q}}{{\left({\eta }_{{a}_{ij} }^{l}\right)}^{q}}\le \frac{2-{\left({\lambda }_{min }^{l}\right)}^{q}}{{\left({\eta }_{min }^{l}\right)}^{q}}.\) Therefore,
Similarly,
Let \(IVq-ROFSEOWA\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right)={{\Delta }}_{a}=\left(\left[{\lambda }_{a}^{l}, {\lambda }_{a}^{\mho }\right], \left[{\eta }_{a}^{l}, {\eta }_{a}^{\mho }\right]\right)\). Then, from Eqs. (3) to (6), we get \({\lambda }_{min}^{l}\le {\lambda }_{{a}_{ij} }^{l}\le {\lambda }_{max}^{l}\), \({\lambda }_{min}^{\mho }\le {\lambda }_{{a}_{ij} }^{\mho }\le {\lambda }_{max}^{\mho }\), \({\eta }_{min}^{l}\le {\eta }_{{a}_{ij}}^{l}\le {\eta }_{max}^{l}\), \({\eta }_{min}^{\mho }\le {\eta }_{{XXXXXXXXX}_{ij}}^{\mho }\le {\eta }_{max}^{\mho }\). Thus
\(\Rightarrow S\left( {\Delta _{a} } \right) \le ~S\left( {\Delta _{{a_{{ij}} }}^{ + } } \right)\) and
\(\Rightarrow S\left( {{\mathcal{F}}_{\varsigma } } \right) \ge ~S\left( {{\mathcal{F}}_{{\varsigma _{{ij}} }}^{ - } } \right)\). So, there are two possibilities.
If \(S\left({{\Delta }}_{a}\right)< S\left({{\Delta }}_{{a}_{ij}}^{+}\right) \mathrm{a}\mathrm{n}\mathrm{d} S\left({{\Delta }}_{a}\right)> S\left({{\Delta }}_{{a}_{ij}}^{-}\right)\), then \({{\Delta }}_{{a}_{ij}}^{-}<IVq-ROFSEOWA\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right)<{{\Delta }}_{{a}_{ij}}^{+}\).
If \(S\left({{\Delta }}_{a}\right)=S\left({{\Delta }}_{{a}_{ij}}^{+}\right),\) then \(S\left({{\Delta }}_{a}\right)={\left(\left[{\lambda }_{a}^{l}, {\lambda }_{a}^{\mho }\right]\right)}^{q}-{\left(\left[{\eta }_{a}^{l}, {\eta }_{a}^{\mho }\right]\right)}^{q}+\left(\frac{{e}^{{\left(\left[{\lambda }_{a}^{l}, {\lambda }_{a}^{\mho }\right]\right)}^{q}-{\left(\left[{\eta }_{a}^{l}, {\eta }_{a}^{\mho }\right]\right)}^{q}}}{{e}^{{\left(\left[{\lambda }_{a}^{l}, {\lambda }_{a}^{\mho }\right]\right)}^{q}-{\left(\left[{\eta }_{a}^{l}, {\eta }_{a}^{\mho }\right]\right)}^{q}}+1}-\frac{1}{2}\right){\left(\left[{\pi }_{a}^{l}, {\pi }_{a}^{\mho }\right]\right)}^{q}={\left(\frac{}{}{0pt}{}{max}{j}\frac{}{}{0pt}{}{max}{i}\left[{\lambda }_{a}^{l}, {\lambda }_{a}^{\mho }\right]\right)}^{q}-{\left(\frac{}{}{0pt}{}{min}{j}\frac{}{}{0pt}{}{min}{i}\left[{\eta }_{a}^{l}, {\eta }_{a}^{\mho }\right]\right)}^{q}+\left(\frac{{e}^{{\left(\frac{}{}{0pt}{}{max}{j}\frac{}{}{0pt}{}{max}{i}\left[{\lambda }_{a}^{l}, {\lambda }_{a}^{\mho }\right]\right)}^{q}-{\left(\frac{}{}{0pt}{}{min}{j}\frac{}{}{0pt}{}{min}{i}\left[{\eta }_{a}^{l}, {\eta }_{a}^{\mho }\right]\right)}^{q}}}{{e}^{{\left(\frac{}{}{0pt}{}{max}{j}\frac{}{}{0pt}{}{max}{i}\left[{\lambda }_{a}^{l}, {\lambda }_{a}^{\mho }\right]\right)}^{q}-{\left(\frac{}{}{0pt}{}{min}{j}\frac{}{}{0pt}{}{min}{i}\left[{\eta }_{a}^{l}, {\eta }_{a}^{\mho }\right]\right)}^{q}}+1}- \frac{1}{2}\right){\left(\left[{\pi }_{{a}_{ij}}^{l}, {\pi }_{{a}_{ij}}^{\mho }\right]\right)}^{q},\) we get \(\left[{\lambda }_{a}^{l}, {\lambda }_{a}^{\mho }\right]= \frac{}{}{0pt}{}{max}{j}\frac{}{}{0pt}{}{max}{i}\left\{\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right]\right\}\), and \(\left[{\eta }_{a}^{l}, {\eta }_{a}^{\mho }\right]= \frac{}{}{0pt}{}{min}{j}\frac{}{}{0pt}{}{min}{i}\left\{\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right\}\). Hence, \({\left(\left[{\pi }_{a}^{l}, {\pi }_{a}^{\mho }\right]\right)}^{q}={\left(\left[{\pi }_{{a}_{ij}}^{l}, {\pi }_{{a}_{ij}}^{\mho }\right]\right)}^{q}\). Then \(IVq-ROFSEOWA\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right)={{\Delta }}_{{a}_{ij}}^{+}\) .
If \(S\left({{\Delta }}_{a}\right)=S\left({{\Delta }}_{{a}_{ij}}^{-}\right),\) then \({\left(\left[{\lambda }_{a}^{l}, {\lambda }_{a}^{\mho }\right]\right)}^{q}-{\left(\left[{\eta }_{a}^{l}, {\eta }_{a}^{\mho }\right]\right)}^{q}+\left(\frac{{e}^{{\left(\left[{\lambda }_{a}^{l}, {\lambda }_{a}^{\mho }\right]\right)}^{q}-{\left(\left[{\eta }_{a}^{l}, {\eta }_{a}^{\mho }\right]\right)}^{q}}}{{e}^{{\left(\left[{\lambda }_{a}^{l}, {\lambda }_{a}^{\mho }\right]\right)}^{q}-{\left(\left[{\eta }_{a}^{l}, {\eta }_{a}^{\mho }\right]\right)}^{q}}+1}-\frac{1}{2}\right){\left(\left[{\pi }_{a}^{l}, {\pi }_{a}^{\mho }\right]\right)}^{q}={\left(\frac{}{}{0pt}{}{min}{j}\frac{}{}{0pt}{}{min}{i}\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right]\right)}^{q}-{\left(\frac{}{}{0pt}{}{max}{j}\frac{}{}{0pt}{}{max}{i}\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right)}^{q}+\left(\frac{{e}^{{\left(\frac{}{}{0pt}{}{min}{j}\frac{}{}{0pt}{}{min}{i}\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right]\right)}^{q}-{\left(\frac{}{}{0pt}{}{max}{j}\frac{}{}{0pt}{}{max}{i}\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right)}^{q}}}{{e}^{{\left(\frac{}{}{0pt}{}{min}{j}\frac{}{}{0pt}{}{min}{i}\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right]\right)}^{q}-{\left(\frac{}{}{0pt}{}{max}{j}\frac{}{}{0pt}{}{max}{i}\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right)}^{q}}+1}- \frac{1}{2}\right){\left(\left[{\pi }_{{a}_{ij}}^{l}, {\pi }_{{a}_{ij}}^{\mho }\right]\right)}^{q}.\) Then \(\left[{\lambda }_{a}^{l}, {\lambda }_{a}^{\mho }\right]= \frac{}{}{0pt}{}{min}{j}\frac{}{}{0pt}{}{min}{i}\left\{\left[{\lambda }_{{a}_{ij}}^{l},{\lambda }_{{a}_{ij}}^{\mho }\right]\right\}\), and \(\left[{\eta }_{a}^{l}, {\eta }_{a}^{\mho }\right]= \frac{}{}{0pt}{}{max}{j}\frac{}{}{0pt}{}{max}{i}\left\{\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right\}\). Hence, \({\left(\left[{\pi }_{a}^{l}, {\pi }_{a}^{\mho }\right]\right)}^{q}={\left(\left[{\pi }_{{a}_{ij}}^{l}, {\pi }_{{a}_{ij}}^{\mho }\right]\right)}^{q}\). Then \(IVq-ROFSEOWA\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right)={{\Delta }}_{{a}_{ij}}^{-}\) .
So, it is proved that.
\({{\Delta }}_{{a}_{ij}}^{-}\le IVq-ROFSEOWA\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right)\le {{\Delta }}_{{a}_{ij}}^{+}\).
Proof 3.4.3.
Let \(f\left(t\right)=\sqrt[q]{\frac{1-{t}^{2}}{1+{t}^{2}}}\), \(t\in \left[0,1\right]\), then \(\frac{d}{d\left(t\right)}\left(f\left(t\right)\right)=-\frac{1}{q}{\left(\frac{1-{t}^{q}}{1+{t}^{q}}\right)}^{\frac{1}{q}-1}\left\{\frac{q{t}^{2q-1}+q{t}^{2q-1}}{{\left(1+{t}^{q}\right)}^{2}}\right\}< 0\), so \(f\left(t\right)\) is decreasing function on \(\left[0,1\right]\). If \({{\Delta }}_{{a}_{nm}}\le {{\Delta }}_{{a}_{nm}}^{*}\), then \(f\left({{\Delta }}_{{a}_{nm}}\right)\le f\left({{\Delta }}_{{a}_{nm}}^{*}\right)\) \(\forall i, j\).
\({v}_{i}\) and \({w}_{j}\) be the weights of experts and parameters such as \({v}_{i}>0\), \({\sum }_{i=1}^{n}{v}_{i}=1\) and \({w}_{j}>0,\) \({\sum }_{j=1}^{m}{w}_{j}=1\). So,
Similarly,
So,
Let \(g\left(v\right)=\sqrt[q]{\frac{2-{v}^{q}}{{v}^{q}}}\), \(v\in \left[0,1\right]\), then \(\frac{d}{dv}\left(g(v)\right)=-\frac{1}{q}{\left(\frac{2-{v}^{q}}{{v}^{q}}\right)}^{\frac{1}{q}-1}\left(\frac{2}{{\left({v}^{q}\right)}^{2}}\right)<0\). So, \(g(v)\) is decreasing on \(\left[0,1\right]\). If \({{\Delta }}_{{a}_{nm}}\le {{\Delta }}_{{a}_{nm}}^{*}\), then \(g\left({{\Delta }}_{{a}_{nm}}\right)\le g\left({{\Delta }}_{{a}_{nm}}^{*}\right)\forall i, j\).
Now \({\eta }_{{a}_{ij}}^{l}\le {{\eta }^{*}}_{{a}_{ij} }^{l}\Rightarrow {\left({\eta }_{{a}_{ij}}^{l}\right)}^{q}\le {\left({{\eta }^{*}}_{{a}_{ij} }^{l}\right)}^{q}\) \({v}_{i}\) and \({w}_{j}\) be the weights of experts and parameters such as \({v}_{i}>0\), \({\sum }_{i=1}^{n}{v}_{i}=1\) and \({w}_{j}>0,\) \({\sum }_{j=1}^{m}{w}_{j}=1\). So, \({\left({\left({\left({\eta }_{{a}_{ij}}^{l}\right)}^{q}\right)}^{{\sum }_{i=1}^{n}{v}_{i}}\right)}^{{\sum }_{j=1}^{m}{w}_{j}}\le {\left({\left({\left({{\eta }^{*}}_{{a}_{ij} }^{l}\right)}^{q}\right)}^{{\sum }_{i=1}^{n}{v}_{i}}\right)}^{{\sum }_{j=1}^{m}{w}_{j}}\)
As \({{\eta }^{*}}_{{a}_{ij} }^{l}\le {\eta }_{{a}_{ij}}^{l}\)
Similarly,
So,
Hence,
Proof 3.4.4
As \({\Delta }{ }_{{a}_{ij}}=\left(\left[{\lambda }_{{a}_{ij} }^{l},{\lambda }_{{a}_{ij}}^{\mho }\right],\left[{\eta }_{{a}_{ij}}^{l},{\eta }_{{a}_{ij}}^{\mho }\right]\right)\) be a collection of IVq-ROFSVs and \(\theta >0\), then.
So we have,
\(\theta IVq-ROFSEOWA\left({{\Delta }}_{{a}_{11}},{{\Delta }}_{{a}_{12}},\dots \dots {{\Delta }}_{{a}_{nm}}\right)\).
Proof 3.4.5
As we know
From Eq. (2),
Appendix 3
See Table
11.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zulqarnain, R.M., Naveed, H., Askar, S. et al. Assessment of bio-medical waste disposal techniques using interval-valued q-rung orthopair fuzzy soft set based EDAS method. Artif Intell Rev 57, 210 (2024). https://doi.org/10.1007/s10462-024-10750-1
Accepted:
Published:
DOI: https://doi.org/10.1007/s10462-024-10750-1