1 Introduction

Intelligent techniques are being achieved tremendous attentions nowadays, because of the spectacular promotions that artificial intelligence brings to all walks of life (Silver et al. 2016). Within the plentiful applications related to artificial intelligence, an obvious feature is the possession of intelligent optimization. As an important foundation of several disciplines, such as cybernetics, computer science, and applied mathematics, the optimization methods are commonly used in many research fields and engineering practice. Note that optimization problems may be proposed with respect to minimum fuel, minimum energy, minimum penalty, maximum reward, and so on. Actually, most organisms in the nature desire to act in optimal fashions for conserving limited resources and meanwhile achieving their goals. Without exception, the idea of optimization also plays a key role in artificial-intelligence-based advanced control design and constructing intelligent systems. However, with the wide popularity of networked techniques and the extension of computer control scales, more and more dynamical systems are encountered with increasing communication burdens, the difficulty of building accurately mathematical models, and the existence of various uncertain factors. As a result, it is always not an easy task to achieve optimization design for these systems and the related control efficiencies are often low. Hence, it is extremely necessary to establish novel, advanced, and effective optimal control strategies, especially for, complex discrete-time nonlinear systems.

Unlike solving the Riccati equation for linear systems, the optimal control design of nonlinear dynamics often contains the difficulty of addressing the Hamilton-Jacobi-Bellman (HJB) equation. Though dynamic programming provides an effective pathway to deal with the problems, it is often computationally untenable to run this method to obtain optimal solutions due to curse of dimensionality (Bellman 1957). Moreover, the backward searching direction obviously precludes the use of dynamic programming in real-time control. Therefore, considering the usualness of encountering with nonlinear optimal control problems, some numerical methods have been proposed to overcome the difficulty of solving HJB equations, particularly under the dynamic programming formulation. Among them, the adaptive-critic-related framework is an important avenue and artificial neural networks are often taken as a kind of supplementary approximation tools (Werbos 1974, 1977, 1992, 2008). Although other computational intelligence methods, such as fuzzy logic and evolutionary computation, also can be adopted, neural networks are employed more frequently to serve as the function approximator. In fact, there are several synonyms are included within the framework, including adaptive dynamic programming, approximate dynamic programming, neural dynamic programming, and neuro-dynamic programming (Bertsekas 2017; Bertsekas and Tsitsiklis 1996; He et al. 2012; He and Zhong 2018; Liu et al. 2012; Prokhorov and Wunsch 1997; Si et al. 2004; Si and Wang 2001). These methods have been used to solve optimal control problems for both continuous-time and discrete-time systems. Remarkably, the well-known reinforcement learning is also closely related to such methods, which provides the important property of reinforcement.

Actually, classical dynamic programming is deemed to have limited utilities in the field of reinforcement learning due to the common assumption of exact models and the vast computational expense, but it is still significant to boost the development of reinforcement learning in the sense of theory (Sutton and Barto 2018). Most of the strategies of reinforcement learning can be regarded as active attempts to accomplish much the same performances as dynamic programming, without directly relying on perfect models of the environment and making use of superabundant computational resources. At the same time, an essential and pivotal foundation can be provided by traditional dynamic programming to better understand various reinforcement learning techniques. In other words, they are highly related with each other and both of them are useful to address optimization problems by employing the principle of optimality.

In this paper, we name the effective integration of learning approximators and the reinforcement formulation as critic intelligence. Within this new component, dynamic programming is taken to provide the theoretical foundation of optimization, reinforcement learning is regarded as the key learning mechanism, and neural networks are adopted to serve as an implementation tool. Then, considering complex nonlinearities and unknown dynamics, the so-called critic intelligence methodology is deeply discussed and comprehensively applied to optimal control design within discrete-time domain. Hence, by involving critic intelligence, a learning-based intelligent critic control framework is constructed for complex nonlinear systems under unknown environment. Specifically, combining with artificial intelligence techniques, such as neural networks and reinforcement learning, the novel intelligent critic control theory as well as a series of advanced optimal regulation and trajectory tracking strategies are established for discrete-time nonlinear systems (Dong et al. 2017; Ha et al. 2020a, 2021b, c, 2022; Li et al. 2021; Liang et al. 2020a, b; Lincoln and Rantzer 2006; Liu et al. 2015; Luo et al. 2021; Liu et al. 2012, 2018; Luo et al. 2020; Mu et al. 2018; Na et al. 2021; Song et al. 2021; Wang et al. 2022, 2020, 2021a, 2020, 2012, 2021c, d, 2011; Wei et al. 2015, 2020, 2021; Zhang et al. 2014; Yan et al. 2017; Zhao et al. 2015; Zhong et al. 2018, 2016; Zhu and Zhao 2021; Zhu et al. 2019), followed by application verifications to complex wastewater treatment processes (Wang et al. 2021a, 2020, 2021c). That is, the advanced optimal regulation and trajectory tracking of discrete-time affine nonlinear systems and general nonaffine plants are addressed with applications, respectively.

It’s worth mentioning that, in this paper, we put emphasis on discrete-time nonlinear optimal control. Here, we incidentally point out that the adaptive-critic-based optimal control design for continuous-time dynamics has also achieved great progresses, in terms of normal regulation, trajectory tracking, disturbance attenuation, and other aspects (Abu-Khalaf and Lewis 2005; Beard et al. 1997; Bian and Jiang 2016; Fan et al. 2021; Fan and Yang 2016; Gao and Jiang 2016, 2019; Han et al. 2021; Jiang and Jiang 2015; Luo et al. 2020; Modares and Lewis 2014a, b; Mu and Wang 2017; Murray et al. 2002; Pang and Jiang 2021; Song et al. 2016; Vamvoudakis 2017; Vamvoudakis and Lewis 2010; Wang et al. 2017; Wang and Qiao 2019; Wang et al. 2021b; Wang and Liu 2018; Wang et al. 2016; Xue et al. 2022, 2021; Yang et al. 2022; Yang and He 2021; Yang et al. 2021a, b, c; Zhang et al. 2018, 2017; Zhao and Liu 2020; Zhao et al. 2018, 2016; Zhu and Zhao 2018). There always exist some monographs and survey papers discussing most of these topics (Lewis and Liu 2013; Lewis et al. 2012; Liu et al. 2013, 2017; Kiumarsi et al. 2018; Liu et al. 2021; Vrabie et al. 2013; Wang et al. 2009; Zhang et al. 2013, 2013). The similar idea and design architectures are contained in these two cases. Actually, they are considered together as an integrated framework of critic intelligence. However, the adaptive critic control for discrete-time systems is different from the continuous-time case. These differences, principally, come from the dynamic programming foundation, the learning mechanism, and the implementation structure. Needless to say, stability and convergence analysis of the two cases are also not the same.

As the end of this section, we present a simple structure of critic-intelligence-based discrete-time advanced nonlinear optimal control design in Fig. 1, which also displays the fundamental idea of this paper. Remarkably, the whole component highlighted in the dotted box of Fig. 1 clearly reflects critic intelligence, which is a combination of dynamic programming, reinforcement learning, and neural networks. The arrows in Fig. 1 indicate that by using the critic intelligence framework with three different components, the control problem of discrete-time dynamical systems can be addressed under nonlinear and unknown environment. What we can construct through this paper is a kind of discrete-time advanced nonlinear optimal control systems with critic intelligence.

Fig. 1
figure 1

Structure of critic-intelligence-based advanced optimal control design

Full size image

2 Discrete-time optimal regulation design

Optimal regulation is an indispensable component of modern control theory and is also useful for feedback control design in engineering practice (Abu-Khalaf and Lewis 2005; Ha et al. 2021b; Lincoln and Rantzer 2006; Liu et al. 2012; Wang et al. 2020, 2012; Wei et al. 2015). Dynamic programming is a basic and important tool to solve such kind of design problems. Consider the general formulation of nonlinear discrete-time systems described by

$$\begin{aligned} x(k+1)=F(x(k),u(k)), \end{aligned}$$
(1)

where the time step \(k=0,1,2,\dotsc \), \(x(k)\in { \mathbb R}^n\) is the state vector, and \(u(k)\in \mathbb R^m\) is the control input . In general, we assume that the function \(F :{\mathbb R}^n \times {\mathbb R}^m \rightarrow {\mathbb R}^n\) is continuous, and without loss of generality, that the origin \(x=0\) is a unique equilibrium point of system (1) under \(u=0\), i.e., \(F(0,0)=0\). Besides, we assume that the system (1) is stabilizable on a prescribed compact set \(\Omega \in \mathbb R^{n}\).

Definition 1

(cf. Al-Tamimi et al. 2008) A nonlinear dynamical system is defined to be stabilizable on a compact set \(\Omega \subset \mathbb R^{n}\) if there exists a control input \(u\in \mathbb R^{m}\) such that, for all initial conditions \(x(0)\in \Omega \), the state \(x(k)\rightarrow 0\) as \(k \rightarrow \infty \).

For the infinite horizon optimal control problem, it is desired to find the control law u(x) which can minimize the cost function given by

$$\begin{aligned} J(x(k),u(k))=\sum _{p=k}^{\infty }U(x(p),u(p)), \end{aligned}$$
(2)

where \(U(\cdot ,\cdot )\) is called the utility function, \(U(0,0)=0\), and \(U(x,u)\ge 0\) for all x and u. Note that the cost function J(x(k), u(k)) can be written as J(x(k)) for short. Particularly, the cost function starting from \(k=0\), i.e., J(x(0)), is often paid more attention.

When considering the discount factor \(\gamma \), where \(0 < \gamma \le 1\), the infinite horizon cost function is described by

$$\begin{aligned} \bar{J}(x(k))=\sum _{p=k}^{\infty }\gamma ^{p-k}U(x(p),u(p)). \end{aligned}$$
(3)

Note that with the discount factor, we can modulate the convergence speed of regulation design and reduce the value of the optimal cost function. In this paper, we mainly discuss the undiscounted optimal control problem.

Generally, the designed feedback control must not only stabilize the system on \(\Omega \) but also guarantee that (2) is finite, i.e., the control law must be admissible.

Definition 2

(cf. Al-Tamimi et al. 2008; Wang et al. 2012; Zhang et al. 2009) A control law u(x) is defined to be admissible with respect to (2) on \(\Omega \), if u(x) is continuous on a compact set \(\Omega _u \subset \mathbb {R}^{m}\), \(u(0)=0\), u(x) stabilizes (1) on \(\Omega \), and \(\forall x(0) \in \Omega \), J(x(0)) is finite.

With this definition, the designed feedback control law \(u(x) \in \Omega _u\), where \( \Omega _u\) is called the admissible control set. Note that admissible control is a basic and important concept of the optimal control field. However, it is often difficult to determine whether a specified control law is admissible or not. Thus, it is meaningful to find advanced methods that do not rely on the requirement of admissible control laws.

The cost function (2) can be written as

$$\begin{aligned} J(x(k))&=U(x(k),u(k))+\sum _{p=k+1}^{\infty }U(x(p),u(p)) \nonumber \\&=U(x(k),u(k))+ J(x(k+1)). \end{aligned}$$
(4)

Denote the control signal as \(u(\infty )\) when the time step approaches to \(\infty \), i.e., \(k \rightarrow \infty \). According to Bellman’s optimality principle, the optimal cost function defined as

$$\begin{aligned} J^{*}(x(k))=\min _{{u(k)},u(k+1),\dotsc ,u(\infty )}\sum _{p=k}^{\infty }U(x(p),u(p)) \end{aligned}$$
(5)

can be rewritten as

$$\begin{aligned} J^{*}(x(k))=\min _{u(k)}\bigg \{U(x(k),u(k))+\min _{u(k+1),u(k+2),\dotsc ,u(\infty )}\sum _{p=k+1}^{\infty }U(x(p),u(p))\bigg \}. \end{aligned}$$
(6)

In other words, \(J^{*}(x(k))\) satisfies the discrete-time HJB equation

$$\begin{aligned} J^{*}(x(k))=\min _{{u(k)}}\big \{U(x(k),u(k))+ J^{*}(x(k+1))\big \}. \end{aligned}$$
(7)

The above expression (7) is called the optimality equation of dynamic programming and is also taken as the basis to implement the dynamic programming technique. The corresponding optimal control law \(u^{*}\) can be derived by

$$\begin{aligned} u^{*}(x(k))=\text{ arg }\min _{{u(k)}}\big \{U(x(k),u(k))+ J^{*}(x(k+1))\big \}. \end{aligned}$$
(8)

Using the optimal control formulation, the discrete-time HJB equation becomes

$$\begin{aligned} J^{*}(x(k))=U(x(k),u^{*}(x(k)))+ J^{*}(x(k+1)), \end{aligned}$$
(9)

which, observing the system dynamics, is specifically

$$\begin{aligned} J^{*}(x(k))=U(x(k),u^{*}(x(k)))+ J^{*}(F(x(k),u^{*}(x(k)))). \end{aligned}$$
(10)

As a special case, we consider a class of discrete-time nonlinear systems with input-affine form

$$\begin{aligned} x(k+1)=f(x(k))+g(x(k))u(k), \end{aligned}$$
(11)

where \(f(\cdot )\) and \(g(\cdot )\) are differentiable in their argument with \(f(0)=0\). Similarly, we assume that \(f+gu\) is Lipschitz continuous on a set \(\Omega \) in \(\mathbb R^{n}\) containing the origin, and that the system (11) is controllable in the sense that there exists a continuous control on \(\Omega \) that asymptotically stabilizes the system.

For this affine nonlinear system, if the utility function is specified as

$$\begin{aligned} U(x(p),u(p))=x^{\mathsf {T}}(p)Qx(p)+u^{\mathsf {T}}(p)Ru(p), \end{aligned}$$
(12)

where Q and R are positive definite matrices with suitable dimensions, then the optimal control law is calculated by

$$\begin{aligned} u^{*}(x(k))=-\frac{1}{2}R^{-1}g^{\mathsf {T}}(x(k)) \frac{\partial {J^{*}(x(k+1))}}{\partial {x(k+1)}}. \end{aligned}$$
(13)

With this special formulation, the discrete-time HJB equation for the affine nonlinear plant (11) is written as

$$\begin{aligned} J^{*}(x(k)) =&\ x^{\mathsf {T}}(k)Qx(k) + \frac{1}{4}\bigg (\frac{\partial {J^{*}(x(k+1))}}{\partial {x(k+1)}}\bigg )^{\mathsf {T}}\nonumber \\&\times g(x(k)) R^{-1} g^{\mathsf {T}}(x(k)) \frac{\partial {J^{*}(x(k+1))}}{\partial {x(k+1)}}+ J^{*}(x(k+1)). \end{aligned}$$
(14)

This is also a special expression of (10), when considering the affine dynamics and the quadratic utility.

When studying the classical linear quadratic regulator problem, the discrete-time HJB equation reduces to the Riccati equation that can be solved efficiently. However, for the general nonlinear problem, it is not the case. Furthermore, we observe from (13) that the optimal control \(u^{*}(x(k))\) is related to \(x(k+1)\) and \(J^{*}(x(k+1))\), which cannot be determined at the present time step k. Hence, it is necessary to employ approximate strategies to address this kind of discrete-time HJB equations and the adaptive critic method is a good choice. In other words, it is helpful to adopt the adaptive critic framework to deal with optimal control design under nonlinear dynamics environment.

As the end of this section, we recall the optimal control basis of continuous-time nonlinear systems (Vamvoudakis and Lewis 2010; Wang et al. 2017, 2016; Zhu and Zhao 2018). Consider a class of affine nonlinear plants given by

$$\begin{aligned} \dot{x}(t)=f(x(t))+g(x(t))u(t), \end{aligned}$$
(15)

where x(t) is the state vector and u(t) is the control vector. Similarly, we introduce the quadratic utility function formed as (12) and define the cost function as

$$\begin{aligned} J(x(t))=\int _{t}^{\infty }U(x(\tau ),u(\tau ))\text {d}\tau . \end{aligned}$$
(16)

Note that in the continuous-time case, the definition of admissible control laws can be found in Abu-Khalaf and Lewis (2005). For an admissible control law u(x), if the related cost function (16) is continuously differentiable, the infinitesimal version is the nonlinear Lyapunov equation

$$\begin{aligned} 0 = U(x,u(x))+(\nabla J(x))^\mathsf {T}[f(x)+g(x)u(x)] \end{aligned}$$
(17)

with \(J(0)=0\). Define the Hamiltonian of system (15) as

$$\begin{aligned} H(x,u(x),\nabla J(x))= U(x,u(x)) +(\nabla J(x))^{\mathsf {T}} [f(x)+g(x)u(x)]. \end{aligned}$$
(18)

Using Bellman’s optimality principle, the optimal cost function defined as

$$\begin{aligned} J^{*}(x)= \min _{u \in \mathscr {A}(\Omega )}\int _{t}^{\infty }U(x(\tau ),u(\tau ))\text {d}\tau \end{aligned}$$
(19)

satisfies the continuous-time HJB equation

$$\begin{aligned} \min _{u \in \mathscr {A}(\Omega )}H(x,u(x),\nabla J^{*}(x))=0. \end{aligned}$$
(20)

The optimal feedback control law is computed by

$$\begin{aligned} u^{*}(x)&= \text{ arg }\min _{u}H(x,u(x),\nabla J^{*}(x))\nonumber \\ {}&=-\frac{1}{2}R^{-1}g^\mathsf {T}(x) \nabla J^{*}(x). \end{aligned}$$
(21)

Using the optimal control expression (21), the continuous-time HJB equation for the affine nonlinear plant (15) turns to be the form

$$\begin{aligned} 0=x^{\mathsf {T}}Qx+(\nabla J^{*}(x))^{\mathsf {T}}f(x)-\frac{1}{4}(\nabla J^{*}(x))^{\mathsf {T}}g(x)R^{-1}g^{\mathsf {T}}(x)\nabla J^{*}(x) \end{aligned}$$
(22)

with \(J^{*}(0)=0\).

Although the general nonaffine dynamics is not discussed, it is clear to observe the differences of continuous-time and discrete-time optimal control formulations from the above affine case. The optimal control laws (13) and (21) are not identical while the HJB equations (14) and (22) are also different. In particular, the optimal control expression of the continuous-time case depends on the state vector and optimal cost function of the same time instant. Hence, if the optimal cost is approximated by function approximators like neural networks, the optimal controller can be calculated directly, which is quite distinctive with the discrete-time case.

3 Discrete-time trajectory tracking design

The tracking control problem is common in many areas, where a dynamical system is forced to track a desired trajectory (Li et al. 2021; Modares and Lewis 2014b; Wang et al. 2021c, d). For the discrete-time system (1), we define the reference trajectory r(k) as

$$\begin{aligned} r(k+1)=\zeta (r(k)). \end{aligned}$$
(23)

The tracking error is defined as

$$\begin{aligned} e(k)=x(k)-r(k). \end{aligned}$$
(24)

In many situations, it is supposed that there exists a steady control \(u_d(k)\) which satisfies the following equation

$$\begin{aligned} r(k+1)=F(r(k),u_d(k)). \end{aligned}$$
(25)

The feedforward or steady-state part of the control input is used to assure perfect tracking. If \(x(k)=r(k)\), i.e., \(e(k)=0\), the steady-state control \(u_d(k)\) corresponding to the reference trajectory can be directly used to make \(x(k+1)\) reach the desired point \(r(k+1)\). If there does not exist a solution of (25), the system state \(x(k+1)\) can not track the desired point \(r(k+1)\).

Here, we assume that the function of \(u_d(k)\) about r(k) is not implicit and \(u_d(k)\) is unique. Then, we define the steady control function as

$$\begin{aligned} u_d(k)=\xi (r(k)). \end{aligned}$$
(26)

By denoting

$$\begin{aligned} \mu (k)=u(k)-u_d(k) \end{aligned}$$
(27)

and using (1), (23), and (24), we derive the following augmented system:

$$\begin{aligned} \left\{ \begin{aligned} e(k+1)&= F(x(k),u(k))-r(k+1),\\ r(k+1)&= \zeta (r(k)). \end{aligned} \right. \end{aligned}$$
(28)

Based on (23), (24), (26), and (27), we can write (28) as

$$\begin{aligned} \left\{ \begin{aligned} e(k+1)&= F(e(k)+r(k),\mu (k)+\xi (r(k)))-\zeta (r(k)),\\ r(k+1)&= \zeta (r(k)). \end{aligned} \right. \end{aligned}$$
(29)

By defining

$$\begin{aligned} \bar{F}(e(k),r(k),\mu (k))=\left[ \begin{array}{c} F(e(k)+r(k),\mu (k)+\xi (r(k)))-\zeta (r(k))\\ \zeta (r(k)) \end{array}\right] \end{aligned}$$
(30)

and \(X(k)=[e^{\mathsf {T}}(k),r^{\mathsf {T}}(k)]^{\mathsf {T}}\), the new augmented system (29) can be written as

$$\begin{aligned} X(k+1)=\bar{F}(X(k),\mu (k)), \end{aligned}$$
(31)

which also takes the nonaffine form. With such a system transformation and a proper definition of the cost function, the trajectory tracking problem can always be formulated as the regulation design of the augmented plant.

Similarly, in the following, we discuss the optimal tracking design of affine nonlinear systems formed as (11), with respect to the reference trajectory (23).

Here, we discuss the case with \(x(k)=r(k)\). For \(x(k+1)=r(k+1)\), we need to find the steady control input \(u_d(k)\) of the desired trajectory to satisfy

$$\begin{aligned} r(k+1)=f(r(k))+g(r(k))u_d(k). \end{aligned}$$
(32)

If the system dynamics and the desired trajectory are known, \(u_d(k)\) can be solved by

$$\begin{aligned} u_d(k)=g^+(r(k))[\zeta (r(k))-f(r(k))], \end{aligned}$$
(33)

where \(g^+(r(k))\) is called the Moore-Penrose pseudoinverse matrix of g(r(k)).

According to (11), (23), (24), (27) and (33), the augmented system dynamics is given as follows:

$$\begin{aligned} \left\{ \begin{aligned} e(k+1) =\;&f(e(k)+r(k))+g(e(k)+r(k))g^+(r(k))\\&\times [\zeta (r(k))-f(r(k))]-\zeta (r(k))+g(e(k)+r(k))\mu (k),\\ r(k+1) =\;&\zeta (r(k)). \end{aligned} \right. \end{aligned}$$
(34)

By denoting

$$\begin{aligned} \mathcal {F}(e(k),r(k))=\;&f(e(k)+r(k))+g(e(k)+r(k))g^+(r(k))\nonumber \\&\times [\zeta (r(k))-f(r(k))]-\zeta (r(k)),\nonumber \\ \mathcal {G}(e(k),r(k))=\;&g(e(k)+r(k)), \end{aligned}$$
(35)

then, the augmented plant (34) can be rewritten as

$$\begin{aligned} \begin{bmatrix} e(k+1) \\ r(k+1) \end{bmatrix}&= \begin{bmatrix} \mathcal {F}(e(k),r(k))\\ \zeta (r(k)) \end{bmatrix} + \begin{bmatrix} \mathcal {G}(e(k),r(k))\\ 0 \end{bmatrix}\mu (k). \end{aligned}$$
(36)

In this case, through observing \(X(k)=[e^{\mathsf {T}}(k),r^{\mathsf {T}}(k)]^{\mathsf {T}}\), the affine augmented system is established by

$$\begin{aligned} X(k+1)=\;&\mathfrak {F}(X(k))+\mathfrak {G}(X(k))\mu (k), \end{aligned}$$
(37)

where the system matrices are

$$\begin{aligned} \mathfrak {F}(X(k))&= \begin{bmatrix} \mathcal {F}(X(k))\\ \zeta (r(k)) \end{bmatrix}=\begin{bmatrix} \mathcal {F}(e(k),r(k))\\ \zeta (r(k)) \end{bmatrix}, \end{aligned}$$
(38a)
$$\begin{aligned} \mathfrak {G}(X(k))&= \begin{bmatrix} \mathcal {G}(X(k))\\ 0 \end{bmatrix}=\begin{bmatrix} \mathcal {G}(e(k),r(k))\\ 0 \end{bmatrix}. \end{aligned}$$
(38b)

For the augmented system (37), we define the cost function as

$$\begin{aligned} \mathcal {J}(X(k),\mu (k))=\sum _{p=k}^{\infty }\mathcal {U}(X(p),\mu (p)), \end{aligned}$$
(39)

where \(\mathcal {U}(X(p),\mu (p)) \ge 0\) is the utility function. Here, considering the quadratic utility formed as (12), it is found that

$$\begin{aligned} \mathcal {U}(X(p),\mu (p))&= \begin{bmatrix} e^{\mathsf {T}}(p), r^{\mathsf {T}}(p) \end{bmatrix} \begin{bmatrix} Q &{} 0 \\ 0 &{} 0 \end{bmatrix} \begin{bmatrix} e(p) \\ r(p) \end{bmatrix}+\mu ^{\mathsf {T}}(p)R\mu (p)\nonumber \\&= e^{\mathsf {T}}(p)Qe(k)+\mu ^{\mathsf {T}}(p)R\mu (p)\nonumber \\&=\mathcal {U}(e(p),\mu (p)). \end{aligned}$$
(40)

Then, we can write the cost function as the following form:

$$\begin{aligned} \mathcal {J}(e(k))=\sum _{p=k}^{\infty }\mathcal {U}(e(p),\mu (p)). \end{aligned}$$
(41)

Note that the controlled plant related to (41) can be regarded as the tracking error dynamics of the augmented system (37) without involving the part of the desired trajectory. For clarity, we express it as follows:

$$\begin{aligned} e(k+1)=\mathcal {F}(e(k),r(k))+\mathcal {G}(e(k),r(k))\mu (k), \end{aligned}$$
(42)

where \(\mathcal {G}(e(k),r(k))=g(e(k)+r(k))\). Since r(k) is not relevant to e(k), the tracking error dynamics (42) can be simply rewritten as

$$\begin{aligned} e(k+1)=\mathcal {F}(e(k))+\mathcal {G}(e(k))\mu (k). \end{aligned}$$
(43)

In this sense, we should study the optimal regulation of error dynamics (43) with respect to the cost function (41). It means that, the trajectory tracking problem has been transformed into the nonlinear regulation design.

Based on Bellman’s optimality principle, the optimal cost function \(\mathcal {J}^*(e(k))\) satisfies the HJB equation

$$\begin{aligned} \mathcal {J}^*(e(k))=\;&\min _{\mu (k)}\{e^\mathsf {T}(k)Qe(k)+\mu ^\mathsf {T}(k)R\mu (k)+\mathcal {J}^*(e(k+1))\}. \end{aligned}$$
(44)

Then, the corresponding optimal control is obtained by

$$\begin{aligned} \mu ^*(e(k))=\;&\text{ arg }\min _{\mu (k)}\{e^\mathsf {T}(k)Qe(k)+\mu ^\mathsf {T}(k)R\mu (k)+\mathcal {J}^*(e(k+1))\}. \end{aligned}$$
(45)

Observing (42), \(\mu ^*(e(k))\) is solved by

$$\begin{aligned} \mu ^*(e(k))=\;&-\frac{1}{2}R^{-1}\left( \frac{\partial {e}(k+1)}{\partial {\mu }(e(k))} \right) ^{\mathsf {T}}\frac{\partial {\mathcal {J}^*(e(k+1))}}{\partial {e(k+1)}}\nonumber \\ =\;&-\frac{1}{2}R^{-1}g^{\mathsf {T}}(e(k)+r(k))\frac{\partial {\mathcal {J}^*(e(k+1))}}{\partial {e(k+1)}}. \end{aligned}$$
(46)

If the optimal control law \(\mu ^*(e(k))\) is derived via adaptive critic, the feedback control \(u^*(k)\) that applies to the original system (11) can be computed by

$$\begin{aligned} u^*(k)=\mu ^*(e(k))+u_d(k). \end{aligned}$$
(47)

By using such a system transformation and the adaptive critic framework, the trajectory tracking problem of general nonlinear plants can be addressed. Overall, the idea of critic intelligence is helpful to cope with both optimal regulation and trajectory tracking problems, where the former is the basis and the latter one is an extension.

4 The construction of critic intelligence

For constructing the critic intelligence framework, it is necessary to provide the bases of reinforcement learning and neural networks. They are introduced to solve nonlinear optimal control problems under the dynamic programming formulation.

4.1 Basis of Reinforcement Learning

The learning ability is an important property and one of the bases of intelligence. In a reinforcement learning system, several typical elements are generally included: the agent, the environment, the policy, the reward signal, the value function, and optionally, the model of the environment (Sutton and Barto 2018; Li et al. 2018). In simple terms, the reinforcement learning problem is meant to learn through interaction to achieve a goal. The interacting process between an agent and the environment consists of the agent selecting actions and the environment responding to those actions as well as presenting new situations to the agent. Besides, the environment gives rise to rewards or penalties, which are special numerical values that the involved agent tries to maximize or minimize over time. Hence, such a process is closely related to the dynamic optimization.

Different from general supervised learning and unsupervised learning, reinforcement learning is inspired by natural learning mechanisms and is considered as a relatively new machine learning paradigm. It is actually a behavioral learning formulation and belongs to the learning category without a teacher. As the core idea of reinforcement learning, the agent-environment interaction is characterized by the agent judges the adopted action through a corresponding numerical reward signal generated by the environment. It is worth mentioning that actions may affect not only the current reward but also the next time step situation and even all subsequent rewards. Within the filed of reinforcement learning, the real-time evaluative information is required to explore the optimal policy. As mentioned in Sutton and Barto (2018), the challenge of reinforcement learning lies in how to reach a compromise between exploration and exploitation, so as to maximize the reward signal. In the learning process, the agent needs to determine which actions yield the largest reward. Therefore, the agent is able to sense and control the states of the environment or the system.

As stated in Haykin (2009); Sutton and Barto (2018), dynamic programming provides the mathematical basis of reinforcement learning and hence lies at the core of reinforcement learning. In many practical situations, the explicit system models are always unavailable, which diminishes the application range of dynamic programming. Reinforcement learning can be considered as an approximate form of dynamic programming and is greatly related to the framework of ADP. One of their common focuses is how to solve the optimality equation effectively. There exist some resultful ways to compute the optimal solution, where policy iteration and value iteration are two basic ones.

When the state and action spaces are small enough, the value functions can be represented as tables to exactly find the optimal value function and the optimal policy, such as for Gridworld and FrozenLake problems. In this case, the policy iteration, value iteration, Monte Carlo, and temporal-difference methods have been developed to address these problems (Sutton and Barto 2018). However, it is difficult to find accurate solutions for other problems with arbitrarily large state spaces. Needless to say, some new techniques are required to effectively solve such complex problems. Therefore, a series of representative approaches have been adopted, including policy gradient and Q-learning (Sutton and Barto 2018). In addition, reinforcement learning with function approximation has been widely applied to various aspects of decision and control system design (Bertsekas 2019). The adaptive critic also belongs to these approximate strategies and serves as the basis of advanced optimal control design in this paper. In particular, for various systems containing large state spaces, the approximate optimal policy can be iteratively obtained by using value iteration and policy iteration with function approximation.

4.2 The Neural Network Approximator

As an obbligato branch of computational intelligence, neural networks are rooted in many disciplines, such as neurosciences, mathematics, statistics, physics, computer science, and engineering (Haykin 2009). Traditionally, the term neural network is used to refer to a network or a circuit of biological neurons. The modern usage of the term often represents artificial neural networks, which are composed of artificial neurons or nodes. Artificial neural networks are composed of interconnecting artificial neurons, or namely, programming constructs that can mimic the properties of biological neurons. They are used either to gain an understanding of biological neural networks, or to solve artificial intelligence problems without necessarily creating authentic models of biological systems.

Neural networks possess the massively parallel distributed structure and the ability to learn and generalize. The generalization denotes the reasonable output production of neural networks, with regard to inputs not encountered during the learning process. Since the real biological nervous systems are highly complex, artificial neural network algorithms attempt to abstract the complexity and focus on what may hypothetically matter most from an information processing point of view. Good performance, including good predictive ability and low generalization error, can be regarded as one source of evidence towards supporting the hypothesis that the abstraction really captures something important from the perspective of brain information processing. Another incentive for these abstractions is to reduce the computation amount when simulating artificial neural networks, so as to allow one to experiment with larger networks and train them on larger data sets (Haykin 2009).

There exist many kinds of neural networks in literature, such as the single-layer neural networks, multilayer neural networks, radial-basis function networks, and recurrent neural networks. Multilayer perceptrons represent a frequently used neural network structure, where a nonlinear differentiable activation function is included in each neuron model and one or more layers hidden from both the input and output modes are contained. Besides, a high degree of connectivity is possessed and the connection extent is determined by synaptic weights of the network. A computationally effective method for training the multilayer perceptrons is the backpropagation algorithm, which is regarded as a landmark during the development of neural networks (Haykin 2009). In recent years, some new structures of neural networks are proposed, where convolutional neural networks provide an efficient method to constrain the complexity of feedforward neural networks by weight sharing and restriction to local connections. Convolutional neural networks are the truly successful deep learning approach where many layers of a hierarchy are successfully trained in a robust manner (LeCun et al. 2015).

Till now, neural networks are still a hot topic, especially under the background of artificial intelligence. Due to the remarkable properties of nonlinearity, adaptivity, self-learning, fault tolerance, and universal approximation of input-output mapping, neural networks can be extensively applied to various research areas of different disciplines, such as dynamic modeling, time series analysis, pattern recognition, signal processing, and system control. In this paper, neural networks are most importantly taken as an implementation tool or a function approximator.

4.3 The Critic Intelligence Framework

The combination of dynamic programming, reinforcement learning, and neural networks is the so-called critic intelligence framework. The advanced optimal control design based on critic intelligence is named as intelligent critic control. It is almost a same concept as the existing adaptive critic method, only note that the intelligence property is highlighted. The basic idea of intelligent critic design is depicted in Fig. 2, where three main components are included, i.e., critic, action, and environment. In line with the general reinforcement learning formulation, the components of critic and action are integrated into an individual agent. When implementing this technique in the sense of feedback control design, three kinds of neural networks are built to approximate the cost function, the control, and the system. They are called the critic network, the action network, and the model network, performing the function of evaluation, decision, and prediction, respectively.

Fig. 2
figure 2

Basic idea of intelligent critic design

Full size image

Before implementing the adaptive critic technique, it is necessary to determine which structure should be adopted. Different advantages are contained in different implementation structures. Heuristic dynamic programming (HDP) (Dong et al. 2017) and dual heuristic dynamic programming (DHP) (Zhang et al. 2009) are two basic, but commonly used structures for adaptive critic design. The globalized dual heuristic dynamic programming (globalized DHP or GDHP) (Liu et al. 2012; Wang et al. 2012) is an advanced structure with an integration of HDP and DHP. Besides, the action-dependent versions of these structures are also used sometimes. It should be pointed out that, neural dynamic programming (NDP) also has been adopted in (Si and Wang 2001), with an emphasis on the new idea for training the action network.

Considering the classical structures with critic, action, and model networks, the primary difference is reflected by the outputs of their critic networks. After the state variable is input to the critic network, only the cost function is approximated as the critic output in HDP while the derivative of the cost function is approximated in DHP. However, for GDHP, both the cost function and its derivative are approximated as the critic output. Therefore, the structure of GDHP is somewhat more complicated than HDP and DHP. Since the derivative of the cost function can be directly used to obtain the control law, the computational efficiency of DHP and GDHP is obviously higher than HDP. However, because of the inclusion of the cost function itself, the convergence process of HDP and GDHP is more intuitive than DHP. Overall, when pursuing simple architecture and low computational amount, the DHP strategy is a good choice. In addition, the HDP and GDHP strategies can be selected to intuitively observe the evolution tendency of the cost function, but HDP is more simple than GDHP in architecture. For clarity, the comparisons of three main structures of adaptive critic are given in Table 1.

Table 1 Comparisons of three main structures of adaptive critic
Full size table

As a summary, the major characteristics of the critic intelligent framework are highlighted as follows.

  • The theoretical foundation of optimization is considered under the formulation of dynamic programming with system, cost function, and control being included.

  • A behavioral interaction between the environment and an agent (critic and action) along with reinforcement learning is embedded as the key learning mechanism.

  • Neural networks are constructed to serve as an implementation tool of main components, i.e., environment (system), critic (cost function), and action (control).

5 The iterative adaptive critic formulation

As two basic iterative frameworks in the field of reinforcement learning, value iteration and policy iteration provide great inspirations to adaptive critic control design. Although the adaptive critic approach has been applied to deal with optimal control problems, the initially stabilizing control policies are often required in the policy iteration process for instance. It is often difficult to obtain such control policies, particulary for complex nonlinear systems. In addition, since much attentions are paid on system stability, the convergence proofs of adaptive critic schemes are quite limited. Hence, it is necessary to develop an effectively iterative framework with respect to adaptive critic. The main focuses include how to construct the iterative process to solve the HJB equation (9) and then prove its convergence (Al-Tamimi et al. 2008; Dierks et al. 2009; Heydari 2014; Jiang and Zhang 2018; Liu et al. 2012; Wang et al. 2012; Zhang et al. 2009).

In fact, the derivation of iterative adaptive critic formulation is inspired by the numerical analysis method. Consider an algebraic equation

$$\begin{aligned} z=\varphi (z), \end{aligned}$$
(48)

which is difficult to solve analytically. By denoting i as the iteration index, where \(i=0,1,2,\dotsc \), we can solve it iteratively from an initial value \(z^{(0)}\). Then, we conduct an iterative process with respect to \(z^{(i)}\) until the iteration index reaches to infinity. Using mathematical expressions, the iterative process is written as follows:

$$\begin{aligned} z^{(i+1)}=\varphi \big (z^{(i)}\big ) \Longrightarrow z^{(\infty )}=\varphi \big (z^{(\infty )}\big ). \end{aligned}$$
(49)

From the above formulation, the convergence result can be obtained.

Employing the similar idea as the above approach, we construct two sequences to iteratively solve the optimal regulation problem in terms of the cost function and the control law. They are called the iterative cost function sequence \(\{J^{(i)}(x(k))\}\) and the iterative control law sequence \(\{u^{(i)}(x(k))\}\), respectively. When using the HDP structure, the successive iteration mode is described as follows:

$$\begin{aligned} J^{(0)}(x(k)) \rightarrow u^{(0)}(x(k)) \rightarrow J^{(1)}(x(k)) \rightarrow \cdots \rightarrow u^{(i)}(x(k)) \rightarrow J^{(i+1)}(x(k)) \rightarrow \cdots \end{aligned}$$
(50)

Note that this is the common value iteration process which begins from a cost function, rather than the policy iteration.

Specifically, for the nonaffine system (1) and the HJB equation (9), the iterative adaptive critic algorithm is performed as follows. First, we start with the initial cost function \(J^{(0)}(\cdot )=0\) and solve

$$\begin{aligned} u^{(0)}(x(k))&=\text{ arg }\min _{u(k)}\big \{U(x(k),u(k))+ J^{(0)}(x(k+1))\big \}\nonumber \\&=\text{ arg }\min _{u(k)}\big \{U(x(k),u(k))+ J^{(0)}(F(x(k),u(k)))\big \}. \end{aligned}$$
(51)

Then, we update the cost function by

$$\begin{aligned} J^{(1)}(x(k))&= \min _{u(k)}\big \{U(x(k),u(k))+ J^{(0)}(x(k+1))\big \}\nonumber \\&=U(x(k),u^{(0)}(x(k)))+ J^{(0)}(F(x(k),u^{(0)}(x(k)))). \end{aligned}$$
(52)

Next, for \(i=1, 2, \dotsc \), the algorithm iterates between

$$\begin{aligned} u^{(i)}(x(k))&=\text{ arg }\min _{u(k)}\big \{U(x(k),u(k))+ J^{(i)}(x(k+1))\big \}\nonumber \\&=\text{ arg }\min _{u(k)}\big \{U(x(k),u(k))+ J^{(i)}(F(x(k),u(k)))\big \} \end{aligned}$$
(53)

and

$$\begin{aligned} J^{(i+1)}(x(k))&= \min _{u(k)}\big \{U(x(k),u(k))+ J^{(i)}(x(k+1))\big \}\nonumber \\&=U(x(k),u^{(i)}(x(k)))+ J^{(i)}(F(x(k),u^{(i)}(x(k)))). \end{aligned}$$
(54)

How to guarantee convergence of the iterative algorithm is an important topic of the adaptive critic field. The convergence proof of the iterative process (51)–(54) has been presented in Abu-Khalaf and Lewis (2005); Wang et al. (2012), where the cost function \(J^{(i)}(x(k))\rightarrow J^{*}(x(k))\) and the control law \(u^{(i)}(x(k))\rightarrow u^{*}(x(k))\) as \(i\rightarrow \infty \).

When implementing the DHP scheme, we often introduce a new costate function sequence to denote the derivative of the cost function (Wang et al. 2020; Zhang et al. 2009). By letting

$$\begin{aligned} \lambda ^{(i+1)}(x(k))=\frac{\partial J^{(i+1)}(x(k))}{\partial x(k)}, \lambda ^{(i)}(x(k+1))=\frac{\partial J^{(i)}(x(k+1))}{\partial x(k+1)}, \end{aligned}$$
(55)

the derivative of the iterative cost function (54), i.e.,

$$\begin{aligned} \frac{\partial J^{(i+1)}(x(k))}{\partial x(k)}= \frac{\partial U\big (x(k),u^{(i)}(x(k))\big )}{\partial x(k)} +\bigg [ \frac{\partial x(k+1)}{\partial x(k)}\bigg ]^{\mathsf {T}}\frac{\partial J^{(i)}(x(k+1))}{\partial x(k+1)}, \end{aligned}$$
(56)

can be concisely written as

$$\begin{aligned} \lambda ^{(i+1)}(x(k))= \frac{\partial U\big (x(k),u^{(i)}(x(k))\big )}{\partial x(k)} +\bigg [ \frac{\partial x(k+1)}{\partial x(k)}\bigg ]^{\mathsf {T}}\lambda ^{(i)}(x(k+1)). \end{aligned}$$
(57)

Using the costate function, the iterative control law can be obtained more directly, since the partial derivative computation of \(J^{(i)}(x(k+1))\) with respect to \(x(k+1)\) is eliminated. Note that (57) is an important expression during implementing the iterative DHP algorithm as the following mode:

$$\begin{aligned} \lambda ^{(0)}(x(k)) \rightarrow u^{(0)}(x(k)) \rightarrow \lambda ^{(1)}(x(k)) \rightarrow \cdots \rightarrow u^{(i)}(x(k)) \rightarrow \lambda ^{(i+1)}(x(k)) \rightarrow \cdots \end{aligned}$$
(58)

After establishing the iterative adaptive critic framework, three kinds of neural networks are built to approximate the iterative cost function, the iterative control law, and the control system. Here, the output of the critic network is denoted as \(\hat{C}^{(i+1)}(x(k))\), which is a uniform expression including the cases of HDP, DHP, and GDHP. It can be specified to represent the approximate cost function \(\hat{J}^{(i+1)}(x(k))\) in HDP, the approximate costate function \(\hat{\lambda }^{(i+1)}(x(k))\) in DHP, or both of them in GDHP. Clearly, the dimension of the critic output in the iterative GDHP algorithm is \(n+1\). Besides, the output of the action network is the approximate iterative control law \(\hat{u}^{(i)}(x(k))\). The controlled plant is approximated by using the model network so that its output is \(\hat{x}(k+1)\). For clarity, the critic outputs of main iterative adaptive critic algorithms are given in Table 2.

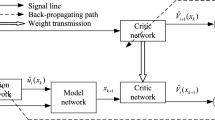
Table 2 The critic outputs of main iterative adaptive critic algorithms
Full size table

As the end of this section, the general structure of discrete-time optimal control via iterative adaptive critic is depicted in Fig. 3. There are two critic networks included in Fig. 3, which outputs cost functions at different iteration steps and time steps. The two critic networks possess same architecture and are connected by the weight transmission. The model network is often trained before carrying out the main iterative process and the final converged weight matrices should be recorded. The critic network and action network are trained according to their error functions, namely the critic error function and the action error function. These error functions can be defined as different formulas in accordance with the design purpose.

Fig. 3
figure 3

General structure of the iterative adaptive critic method

Full size image

Overall, there exist several main features for the above iterative structure, which are listed as follows.

  • The iteration index is always embedded in the expressions of the cost function and the control law function.

  • Different neural network structures can be employed, where the multilayer perceptrons are most commonly used with gradient descent.

  • Error functions of the critic network and action network can be determined with the specific choice of implementation structures, such as HDP, DHP, and GDHP.

  • Three neural networks are built and integrated into a whole formulation, even though their training sequences are different.

  • It is more readily to be implemented in an offline manner, since the final action weight matrices are adopted to construct the available control law.

  • It is also applicable to deal with other control problems that can be transformed to and considered as the regulation design.

The fundamental objective of employing the iterative adaptive critic framework is to solve the HJB equation approximately, which for instance, takes the form of (44) with regard to the proposed tracking control problem. It should be pointed out that, when addressing the trajectory tracking problems, the tracing error e(k) can be regarded as the new state of Fig. 3 and the same iterative formulation can be conducted to the transformed optimal regulation design expediently. That is to say, both the optimal regulation and trajectory tracking problems can be effectively handled under the iterative adaptive critic framework.

6 Significance and prospects

Optimization methods have been widely used in many research areas. As a fundamental element of artificial intelligence techniques, the idea of optimization is also being paid largish attentions at present. When combining with automatic control, it is necessary to establish a series of intelligent methods to address discrete-time optimal regulation and trajectory tracking problems. This is more important because of the increasing complexity of controlled plants, the augmenting of available data resources, and the generalization of unknown dynamics (Wang et al. 2017). In fact, various advanced-control-based applications have been conducted on transportation systems, power systems, chemical processes, and so on. However, they also should be addressed via critic-intelligence-based methods due to the complexity of the practical issues. For example, the complex wastewater treatment problems are needed to be considered under the intelligent environment and more advanced control strategies are required. It is an indispensable part during the process of accomplishing smart environmental protection. In this survey, the wastewater treatment process control is regarded as a typical application of the critic intelligence approach. Developing other application fields with critic intelligence is also an interesting topic of the future research.

In this paper, by involving the critic intelligence formulation, the advanced optimal control methods towards discrete-time nonlinear systems are developed in terms of normal regulation and trajectory tracking. The given strategies are also verified via simulation experiments and wastewater treatment applications. Through providing advanced solutions for nonlinear optimal control problems, we guide the development of intelligent critic learning and control for complex systems, especially the discrete-time case. It is important to note that the given strategies can not only strengthen the theoretical results of adaptive critic control, but also provide new avenues to intelligent learning control design of complex discrete-time systems, so as to effectively address unknown factors, observably enhance control efficiencies, and really improve intelligent optimization performances. Additionally, it will be beneficial for the construction of advanced automation techniques and intelligent systems as well as be of great significance both in theory and application. In particular, it is practically meaningful to enhance the level of wastewater treatment techniques and promote the recycling of water resources, and therefore, to the sustainable development of our economy and society. As described in Alex et al. (2008); Han et al. (2019), the primary control objective of the common wastewater treatment platform, i.e., Benchmark Simulation Model No. 1, is to ensure that the dissolved oxygen concentration in the fifth unit and the nitrate level in the second unit are maintained at their desired values. In this case, such desired values can be regarded as the reference trajectory. Note the control parameters are, respectively, the oxygen transfer coefficient of the fifth unit and the internal recycle flow rate of the fifth-second units. In fact, the control design of the proper dissolved oxygen concentration and nitrate level is actually a trajectory tracking problem. Thus, the intelligent critic framework can be constructed for achieving effective control of wastewater treatment processes. There have been some basic conclusions in Wang et al. (2021a, 2020, 2021c, 2021d) and more results will be reported in the future.

Reinforcement learning is an important branch of machine learning and is being gained rapid development. It is meaningful to introduce more advanced learning approaches to the automatic control field. Particularly, the consideration of reinforcement learning under the deep neural network formulation can result in dual superiorities of perception and decision in high-dimensional state-action space. Moreover, it is also necessary to utilize big data information more sufficiently and establish advanced data-driven schemes for optimal regulation and trajectory tracking. Additionally, since we only consider discrete-time optimal control problems, it is necessary to propose advanced methods for continuous-time nonlinear systems in the future. Using proper system transformations, the advanced optimal control schemes also can be extended to other fields, such as robust stabilization, distributed control, and multi-agent systems. Except the wastewater treatment, the critic intelligence approaches can be applied to more practical systems in engineering and society. With developments in theory, methods, and applications, it is beneficial to constitute a unified framework for intelligent critic learning and control. In summary, more fantastic achievements will be generated through the involvement of critic intelligence.