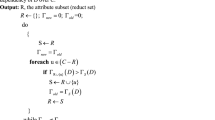Attribute reduction in an incomplete categorical decision information system based on fuzzy rough sets

Abstract

Categorical data is an important class of data in machine learning. Information system based on categorical data is called a categorical information system (CIS), a CIS with missing values is known as an incomplete categorical information system (ICIS) and an ICIS with decision attributes is said to be an incomplete categorical decision information system (ICDIS). Attribute selection is an important subject in rough set theory. This paper investigates attribute reduction in an ICDIS based on fuzzy rough sets. To depict the similarity for incomplete categorical data, fuzzy symmetry relations in an ICDIS are first introduced. Then, some attribute-evaluation functions, such fuzzy positive regions, dependency function and attribute importance functions are given. Next, the fuzzy-rough iterative computation model for an ICDIS is presented, and an attribute reduction algorithm in an ICDIS based on fuzzy rough sets is given. Finally, experiments are carried out as so to evaluate the performance of the proposed algorithm, and Friedman test and Bonferroni-Dunn test in statistics are conducted. The experimental results indicate that the proposed algorithm is more effective than some existing algorithms.

1 Introduction

1.1 Research background

Rough set theory (RST), initiated by Pawlak (1982, 1991), is a significant method to deal with imprecision, fuzziness and uncertainty. Its biggest advantage is that it doesn’t require any prior information other than the data set to process the problem (Cattaneo et al. 2016; Chen et al. 2017; Huang et al. 2017; Li et al. 2016; Lang et al. 2017; Tran et al. 2018; Tan et al. 2018; Yao and Zhang 2017). RST is based on classification mechanism, which regards classification as equivalence relation in a specific space, and equivalence relation constitutes space partition. The main idea of this method is to use the knowledge in the known knowledge base to describe the imprecise or uncertain knowledge. It is widely known that it can effectively deal with the uncertainty of an information system (IS). In recent years, RST has attracted many researchers’ attention, and its application is mostly related to an IS (Li et al. 2020, 2020, 2019; Xie et al. 2019; Yu et al. 2019; Zhang et al. 2017, 2018).

Fuzzy rough set theory is a mathematical theory proposed by Dubois and Prade (1990). Chen et al. (2005) systematically studied fuzzy rough set theory and its related applications. Moresi and Yankout (1998) gave axiomatic definition for fuzzy rough sets. Radzikowska and Kerre (2002) investigated a comparative study of fuzzy rough sets. Wang et al. (2016) proposed a fitting model for attribute reduction with fuzzy rough sets. Chen et al. (2012) a novel attribute reduction algorithm based on fuzzy rough sets. Hu et al. (2011) developed kernelized fuzzy rough sets and their applications.

1.2 The related works

Categorical data is one of the most common types of data in people’s life, and it is an important class of data in machine learning. In order to overcome the deficiency of classical rough sets processing classification data, several improved models are proposed. Ziarko (1993) introduced a variable precision rough set model (VPRSM). Yao (2008) proposed probabilistic rough set approximations. Duntsch and Gediga (1998) studied uncertainty measures of VPRSM. Liang et al. (2014) presented a group incremental approach to attribute reduction applying VPRSM. Liang et al. (2013) came up with an accelerator for attribute reduction based on perspective of objects and attributes in VPRSM. Slezak (2002) brought up approximate entropy reducts of VPRSM.

Attribute reduction aims to remove redundant attributes in the calculation process, solve the complexity of high-dimensional data calculation and boost its accuracy. There is no doubt that attribute reduction is one of the focuses and hotspots of rough set theory from beginning to end. Up to now, there have been many outstanding results. Dai et al. (2013) presented attribute attribute based on conditional entropies for incomplete decision systems. Meng and Shi (2009) proposed a fast approach to attribute reduction in incomplete decision systems with tolerance relation-based rough sets. Yao and Zhang (2017) brought up class-specific attribute reduction in RST. Zhao and Qin (2014) put forward mixed attribute reduction in incomplete decision table. Teng et al. (2010) came up with attribute reduction algorithm based on conditional entropy under incomplete information system. Cornelis et al. (2010) obtained a generalized model of attribute reduction based on fuzzy tolerance relation within the context of fuzzy rough set theory; Wang et al. (2019) constructed fuzzy rough set-based attribute reduction using distance measures; Giang et al. (2020) gave an incremental method for attribute reduction of dynamic decision tables by using fuzzy partition distance and hybrid filter-wrapper, which obtains better classification ability than other methods; Chen et al. (2019) introduced a fuzzy kernel-attribute reduction method for heterogeneous data; Dai et al. (2018) applied maximal-discernibility-pair-based approach to attribute reduction in fuzzy rough sets; Liu et al. (2020) defined the notions of accurate reduction and reduced invariant matrix, which are used to attribute reduction in an IS.

1.3 Motivation and inspiration

In the real world, there are mostly missing data sets. Wang et al. (2020) studied attribute reduction for categorical data and did not consider the case of incomplete categorical data. In order to solve practical problems more effectively, fuzzy symmetry relations in characterizing incomplete categorical data are generalized in this paper. First, fuzzy tolerance relations applicable to both complete and incomplete data are defined. Then a fuzzy rough iterative computing model with stronger generalization ability is established. Finally, this model are applied in some real data sets to test the performance effect of the model. Therefore, it is meaningful to study attribute reduction in an ICDIS based on fuzzy rough sets.

In this paper, a fuzzy rough iterative calculation model is derived theoretically. Then a reduction algorithm FR-IC is designed by using the model. The advantage of this algorithm is that an iterative formula is defined to reduce the attributes of incomplete information systems. By iterating the fuzzy relation matrix continuously, the maximum dependency of attributes is found, and the reduction set is obtained. With the increase of iteration times, the calculation formula of dependency is dynamically adjusted to ensure the convergence of the algorithm. The algorithm is fast and does not occupy too much memory. Through a large number of numerical experiments and comparison with other algorithms, it is found that the proposed algorithm is obviously better than some existing algorithms. The results are shown in the tables and images drawn in this paper.

1.4 Organization

This paper is organized as follows. In Sect. 2, some basic concepts of fuzzy relations and ICDISs are reviewed, and in order to depict the similarity for incomplete categorical data, fuzzy symmetry relations in an ICDIS are introduced. In Sect. 3, some attribute-evaluation functions including fuzzy positive regions, dependency functions and attribute importance functions are given. In Sect. 4, the fuzzy-rough iterative computation model for an ICDIS is presented. In Sect. 5, attribute reduction in an ICDIS based on fuzzy rough sets is studied and the corresponding algorithm is proposed. In Sect. 6, an attribute reduction algorithm in an ICDIS based on fuzzy rough sets is proposed and its complexity is analyzed. In Sect. 7, some experiments are carried out and the performance of the proposed algorithm is evaluated. In Sect. 7, this paper is concluded.

The framework of this paper is revealed in Fig. 1.

Fig. 1

Framework of this paper

2 Preliminaries

In this section, some notions of fuzzy relations and ICDISs are reviewed, and fuzzy symmetry relations in an ICDIS are defined.

Throughout this paper, U and A signify two finite sets.

Put

$$\begin{aligned} U=\{u_1,u_2,\ldots ,u_n\},\,A=\{a_1,a_2,\ldots ,a_m\}. \end{aligned}$$

2.1 Fuzzy relations

Fuzzy sets are extensions of ordinary sets (Zadeh 1965). A fuzzy set P in U is defined as a function assigning to each element u of U a value $P(u)\in I$ and P(u) is called the membership degree of u to the fuzzy set P.

Throughout this paper, I expresses [0, 1], $I^U$ indicates the family of all fuzzy sets in U.

If R is a fuzzy set in $U\times U$, then R is called a fuzzy relation on U. In this paper, $I^{U\times U}$ denotes the set of all fuzzy relations on U.

Let $R\in I^{U\times U}$. Then R may be represented by

$$\begin{aligned}M(R)= \left( \begin{array}{cccc} r_{11} &{} r_{12} &{} ... &{} r_{1n}\\ r_{21} &{} r_{22} &{} ... &{} r_{2n}\\ ... &{} ... &{} ... &{}...\\ r_{n1} &{} r_{n2} &{} ... &{} r_{nn} \end{array}\right) , \end{aligned}$$

where $r_{ij}=R(u_i,u_j)\in I$ means the similarity between two objects $u_i$ and $u_j$.

2.2 Incomplete categorical decision information systems

Definition 2.1

(Pawlak 1991) Suppose that U is a finite object set and A is a finite attribute set. Then the ordered pair (U, A) is referred to as an information system (IS), if for any $a\in C$, a is able to decide a information function  $a: U\rightarrow V_a$, where $V_a=\{a(u): u\in U\}$.

If $A=C\cup D$, where C is a set of conditional attributes and D is a set of decision attributes, then (U, A) is called a decision information system (DIS).

Let (U, A) be an IS. If there is $a\in A$ such that $*\in V_a$, here $*$ means a null or unknown value, then (U, A) is called an incomplete information system (IIS).

Suppose that (U, A) is an IIS. Given $P\subseteq A$. Then a binary relation $T_P$ on U can be defined as

$$\begin{aligned} T_P\,or\,sim(P)=\{(u,v)\in U\times U:\forall \,a\in P,\,a(u)=a(v)\,or\, a(u)=*\,or\,a(v)=*\}. \end{aligned}$$

Clearly, $T_P$ is a tolerance relation on U.

For each $u\in U$, denote

$$\begin{aligned} T_P(u)=\{v\in U:(u,v)\in T_P\}. \end{aligned}$$

Then, $T_P(u)$ is called the tolerance class of x under the tolerance relation $T_P$.

For convenience, $T_{\{a\}}$ and $T_{\{a\}}(u)$ are denoted by $T_a$ and $T_a(u)$, respectively.

Obviously,

$$\begin{aligned} T_P=\bigcap \limits _{a\in P}T_a,\,\,T_P(u)=\bigcap \limits _{a\in P}T_a(u). \end{aligned}$$

Let $(U,C\cup \{d\})$ be an DIS. If there exist $a\in C$ such that $*\in V_a$, but $*\not \in V_d$, then $(U,C\cup \{d\})$ is called an incomplete decision information system (IDIS).

Let $(U,C\cup \{d\})$ be an IDIS. Then

$$\begin{aligned} T_d\,{is\,an\,equivalence\,relation\,on\,U}. \end{aligned}$$

Obviously,

$$\begin{aligned} \forall \,u\in U,\,\,T_d(u)=\{v\in U:d(u)=d(v)\}. \end{aligned}$$

Definition 2.2

Let $(U,C\cup \{d\})$ be an IDIS. Then the pair (U, A) is called an incomplete categorical decision information system (ICDIS), if each attribute is categorical.

If $P\subseteq C$, then $(U,P\cup \{d\})$ is known as the subsystem of $(U,C\cup \{d\})$.

2.3 Fuzzy symmetry relations in an ICDIS

In $T_P$, “ $\forall \,a\in P,\,a(u)=a(v)\,or\, a(u)=*\,or\,a(v)=*$ " is fed back to the object set of an IIS. Naturally, we may consider that “ $\forall \,a\in P,\,a(u)=a(v)\,or\, a(u)=*\,or\,a(v)=*$ " is fed back to the attribute set of an IIS. For this purpose, inspired by the paper Wang et al. (2020), we introduce the following definition.

Definition 2.3

Let $(U, C\cup \{d\})$ be an ICDIS. Given $P\subseteq C$ and $\lambda \in [|P|,|C|]$. Then the fuzzy relation on U can be defined as

$$\begin{aligned} R^\lambda _P(u,v)=\frac{1}{\lambda }|\{a\in P: a(u)=a(v)\, or\,a(u)=*\, or \,a(v)=*\}|, \end{aligned}$$

(2.1)

where $*$ is a missing value.

Moreover,

$$\begin{aligned} T_d=\{(u,v)\in U\times U:d(u)=d(v)\}. \end{aligned}$$

Clearly,

$R^\lambda _P$ is a fuzzy symmetry relation on U, and $T_d$ is an equivalence relation on U. If $\lambda =|P|$, then $R^\lambda _P$ is a fuzzy tolerance relation on U.

In this paper, denote

$$\begin{aligned} U/d=\{T_d(u):u\in U\}=\{D_1,D_2,\ldots ,D_r\}. \end{aligned}$$

For convenience, denote

$$\begin{aligned} P_{uv}=\{a\in P: a(u)=a(v)\, or\,a(u)=*\, or \,a(v)=*\}. \end{aligned}$$

Then

$$\begin{aligned} R^\lambda _P(u,v)=\frac{1}{\lambda }|P_{uv}|. \end{aligned}$$

Proposition 2.4

Let $(U,C\cup \{d\})$ be an ICDIS. If $P_1\subseteq P_2\subseteq C$, then for $\lambda \in [|P_2|,|C|]$, $R^\lambda _{P_1}\subseteq R^\lambda _{P_2}$.

Proof

By Definition 2.3,

$$\begin{aligned} R^\lambda _{P_1}(u,v)=\frac{1}{\lambda }|(P_1)_{uv}|,\,R^\lambda _{P_2}(u,v)=\frac{1}{\lambda }|(P_2)_{uv}|. \end{aligned}$$

Since $P_1\subseteq P_2$, we have $\forall \,u,v\in U$, $(P_1)_{uv}\subseteq (P_2)_{uv}.$

So $\forall \,u,v\in U$, $R^\lambda _{P_1}(u,v)\le R^\lambda _{P_2}(u,v)$.

Thus, $R^\lambda _{P_1}\subseteq R^\lambda _{P_2}$. $\square$

3 Attribute-evaluation functions

In this section, some attribute-evaluation functions, such as fuzzy positive regions, dependency functions and attribute importance functions are presented.

Definition 3.1

Let $(U,C\cup \{d\})$ be an ICDIS. Given $P\subseteq C$ and $\lambda \in [|P|,|C|]$. Suppose that $R^\lambda _P$ is the fuzzy tolerance relation induced by the subsystem $(U,P\cup \{d\})$. Based on the fuzzy approximation space $(U,R^\lambda _P)$, a pair of operations $\underline{R^\lambda _P}$, $\overline{R^\lambda _P}$: $2^U\longrightarrow I^U$ are defined as follows:

$$\begin{aligned} \underline{R^\lambda _P}(X)(u)=\bigwedge _{v\notin X}[1-R^\lambda _P(u,v)],\,\forall \,u\in U;\end{aligned}$$

(3.1)

$$\begin{aligned} \overline{R^\lambda _P}(X)(u)=\bigvee _{v\in X}R^\lambda _P(u,v),\,\forall \,u\in U. \end{aligned}$$

(3.2)

Then $\underline{R^\lambda _P}(X)$ and $\overline{R^\lambda _P}(X)$ are called the lower and upper fuzzy approximations of X, respectively.

Proposition 3.2

Let $(U,C\cup \{d\})$ be an ICDIS. Suppose $P\subseteq C$ and $\lambda \in [|P|,|C|]$. Then the following properties hold.

(1) $\overline{R^\lambda _P}(\emptyset )=\underline{R^\lambda _P}(\emptyset )={\bar{0}}$, $\ \underline{R^\lambda _P}(U)=\overline{R^\lambda _P}(U)={\bar{1}}$.

(2) $\underline{R^\lambda _P}(X)\subseteq X\subseteq \overline{R^\lambda _P}(X)$, where

$$\begin{aligned} X(u)=\left\{ \begin{array}{rcl} 1, &{} &{}u\in X;\\ 0, &{} &{}u\notin X. \end{array} \right. \end{aligned}$$

(3) $X\subseteq Y\Rightarrow \ \underline{R^\lambda _P}(X)\subseteq \ \underline{R^\lambda _P}(Y),\,\overline{R^\lambda _P}(X)\subseteq \ \overline{R^\lambda _P}(Y)$.

(4) $\underline{R^\lambda _P}(X\cap Y)= \underline{R^\lambda _P}(X)\cap \underline{R^\lambda _P}(Y)$, $\overline{R^\lambda _P}(X\cap Y)= \overline{R^\lambda _P}(X)\cup \overline{R^\lambda _P}(Y)$.

(5) $\underline{R^\lambda _P}(U-X)={\bar{1}}-\overline{R^\lambda _P}(X)$,

$\overline{R^\lambda _P}(U-X)={\bar{1}}-\underline{R^\lambda _P}(X)$.

Proof

We only prove (2) and (5).

(2) (i) By Definition 2.3, $\forall \,u,v\in U,$ $0\le R^\lambda _P(u,v)\le 1.$

Then

$$\begin{aligned} 0\le \bigwedge _{v\notin X}[1-R^\lambda _P(u,v)]\le 1. \end{aligned}$$

It can be obtained that $\forall \,u\in U,$

$$\begin{aligned} 0\le \underline{R^\lambda _P}(X)(u)\le 1. \end{aligned}$$

So $\forall \,u\in X$,

$$\begin{aligned} \underline{R^\lambda _P}(X)(u)\le 1=X(u). \end{aligned}$$

Note that $\forall \,u\not \in X$, $\underline{R^\lambda _P}(X)(u)=1-R^\lambda _P(u,u)=0$. Then $\forall \,u\not \in X,$

$$\begin{aligned} \underline{R^\lambda _P}(X)(u)=0\le 0=X(u). \end{aligned}$$

This implies that $\forall \,u\in U,$

$$\begin{aligned} \underline{R^\lambda _P}(X)(u)\le X(u). \end{aligned}$$

Thus

$$\begin{aligned} \underline{R^\lambda _P}(X)\subseteq X. \end{aligned}$$

(ii) Obviously,

$$\begin{aligned} \forall \,u\in U,\,\,0\le \overline{R^\lambda _P}(X)(u)\le 1. \end{aligned}$$

Then $\forall \,u\not \in X$,

$$\begin{aligned} X(u)=0\le \overline{R^\lambda _P}(X)(u) . \end{aligned}$$

Note that $\forall \,u\in X$, $\overline{R^\lambda _P}(X)(u)=R(u,u)=1$. Then $\forall \,u\in U,$

$$\begin{aligned} X(u)=1\le 1=\overline{R^\lambda _P}(X)(u). \end{aligned}$$

Thus

$$\begin{aligned} X\subseteq \overline{R^\lambda _P}(X). \end{aligned}$$

From the above,

$$\begin{aligned} \underline{R^\lambda _P}(X)\subseteq X\subseteq \overline{R^\lambda _P}(X). \end{aligned}$$

(5) (i) By Definition 3.1, we have $\forall \,u\in U,$

$$\begin{aligned} \begin{aligned} \underline{R^\lambda _P}(U-X)(u)&=\bigwedge _{v\notin {U-X}}[1-R^\lambda _P(u,v)]\\&=1-\bigvee _{v\notin {U-X}}R^\lambda _P(u,v)\\&=1-\bigvee _{v\in X}R^\lambda _P(u,v)\\&=1-\overline{R^\lambda _P}(X)(u). \end{aligned} \end{aligned}$$

Thus

$$\begin{aligned} \underline{R^\lambda _P}(U-X)={\bar{1}}-\overline{R^\lambda _P}(X). \end{aligned}$$

(ii) By Definition 3.1, we have $\forall \,u\in U,$

$$\begin{aligned} \begin{aligned} \overline{R^\lambda _P}(U-X)(u)&=\bigvee _{v\in {U-X}}R^\lambda _P(u,v)\\&=1-[1-\bigvee _{v\in {U-X}}R^\lambda _P(u,v)]\\&=1-[1-\bigvee _{v\notin X}R^\lambda _P(u,v)]\\&=1-\bigwedge _{v\notin X}[1-R^\lambda _P(u,v)]\\&=1-\underline{R^\lambda _P}(X)(u). \end{aligned} \end{aligned}$$

Thus

$$\begin{aligned} \overline{R^\lambda _P}(U-X)={\bar{1}}-\underline{R^\lambda _P}(X). \end{aligned}$$

$\square$

Proposition 3.3

Let $(U,C\cup \{d\})$ be an ICDIS. If $P_1\subseteq P_2\subseteq C$, then for $\lambda \in [|P_2|,|C|]$ and $X\in 2^U$,

$$\begin{aligned} \underline{R^\lambda _{P_1}}(X)\subseteq \ \underline{R^\lambda _{P_2}}(X), \,\overline{R^\lambda _{P_2}}(X)\subseteq \,\overline{R^\lambda _{P_1}}(X). \end{aligned}$$

Proof

(1) Since $P_1\subseteq P_2\subseteq C$, by Proposition 2.4, we have $R^\lambda _{P_1}\subseteq R^\lambda _{P_2}$.

Then $\forall \,u\in U, v\notin X,$

$$\begin{aligned} R^\lambda _{P_1}(u,v)\le R^\lambda _{P_2}(u,v). \end{aligned}$$

This implies that $\forall \,u\in U,$

$$\begin{aligned} \bigwedge \limits _{v\notin X}[1-R^\lambda _{P_2}(u,v)]\le \bigwedge \limits _{v\notin X}[1-R^\lambda _{P_1}(u,v)]. \end{aligned}$$

Thus $\forall \,u\in U,$

$$\begin{aligned} \underline{R^\lambda _{P_2}}(X)(u)\le \underline{R^\lambda _{P_1}}(X)(u). \end{aligned}$$

Therefore,

$$\begin{aligned} \underline{R^\lambda _{P_2}}(X)\subseteq \underline{R^\lambda _{P_1}}(X). \end{aligned}$$

(2) Since $P_1\subseteq P_2\subseteq C$, by Proposition 2.4, we have $R^\lambda _{P_1}\subseteq R^\lambda _{P_2}$.

Then $\forall \,u\in U, v\in X,$

$$\begin{aligned} R^\lambda _{P_1}(u,v)\le R^\lambda _{P_2}(u,v). \end{aligned}$$

This implies that $\forall \,u\in U,$

$$\begin{aligned} \bigvee \limits _{v\in X}R^\lambda _{P_1}(u,v)\le \bigvee \limits _{v\in X}R^\lambda _{P_2}(u,v). \end{aligned}$$

Thus $\forall \,u\in U,$

$$\begin{aligned} \overline{R^\lambda _{P_1}}(X)(u)\le \overline{R^\lambda _{P_2}}(X)(u). \end{aligned}$$

Therefore, $\overline{R^\lambda _{P_1}}(X)\subseteq \overline{R^\lambda _{P_2}}(X)$. $\square$

Suppose $D\in U/d$. Then

$$\begin{aligned} \underline{R^\lambda _P}(D),\overline{R^\lambda _P}(D)\in I^U. \end{aligned}$$

$\underline{R^\lambda _P}(D)(u)$ denotes the membership degree of u certainly being included in the equivalence class D . If $u\notin D$, the value of $\underline{R^\lambda _P}(D)(u)$ is the smallest. Otherwise, it is equal to the smallest value of dissimilar degrees between u and the samples not falling into class D.

$\overline{R^\lambda _P}(D)(u)$ represents the membership degree of sample u possibly belonging to equivalence class D. If $u\notin D$, the value of $\overline{R^\lambda _P}(D)(u)$ is the largest. If not, it is equal to the max-value of the fuzzy similarities between u and all the samples in class D.

Definition 3.4

Let $(U,C\cup \{d\})$ be an ICDIS. Suppose $P\subseteq C$ and $\lambda \in [|P|,|C|]$. Then $\lambda$-fuzzy positive region of decision d relative to P can be defined as

$$\begin{aligned} POS^\lambda _P(d)=\bigcup _{D\in U/d}\underline{R^\lambda _P}(X). \end{aligned}$$

(3.3)

Proposition 3.5

Let $(U,C\cup \{d\})$ be an ICDIS. Suppose $P_1\subseteq P_2\subseteq C$. Given $\lambda \in [|P_2|,|C|]$. Then $POS^\lambda _{P_2}(d)\subseteq POS^\lambda _{P_1}(d)$.

Proof

It follows from Proposition 3.2. $\square$

Definition 3.6

Let $(U,C\cup \{d\})$ be an ICDIS. Suppose $P\subseteq C$ and $\lambda \in [|P|,|C|]$. Then $\lambda$-dependency function of d relative to P can be defined as

$$\begin{aligned} \Gamma ^\lambda _P(d)=\frac{|POS^\lambda _P(d)|}{n}. \end{aligned}$$

(3.4)

Proposition 3.7

Let $(U,C\cup \{d\})$ be an ICDIS. Suppose $P_1\subseteq P_2\subseteq C$. Given $\lambda \in [|P_2|,|C|]$. Then $\Gamma ^\lambda _{P_2}(d)\le \Gamma ^\lambda _{P_1}(d)$.

Proof

It follows from Proposition 3.5. $\square$

Definition 3.8

Let $(U,C\cup \{d\})$ be an ICDIS. Suppose $P\subseteq C$ and $a\in C-P$. Given $\lambda \in [|P|,|C|]$. Then $\lambda$-importance of a relative to P about d can be defined as

$$\begin{aligned} sig^\lambda (a,P,d)=\Gamma ^\lambda _P(d)-\Gamma ^\lambda _{P\cup \{a\}}(d). \end{aligned}$$

(3.5)

4 Fuzzy rough computation models

Fuzzy relations introduced above are crucial for defining a fuzzy rough computation model. Noticed that there is a constant parameter $\lambda$. For a dataset with a large number of attributes, the membership degrees of samples to a relation can get very small when a few of the attributes are included in rough computation. That is to say, the lower the number of the included attributes in rough computation, the smaller the discrimination of memberships. To overcome this problem, a fuzzy rough iterative computation model for incomplete categorical data is proposed in this section.

Let $(U, C\cup \{d\})$ be an ICDIS. Given $P\subseteq C$. Suppose $|P|\le \lambda _1<\lambda _2<\cdots \le |C|$. Denote

$$\begin{aligned} R_P^{(i)}(u,v)= & {} R^{\lambda _i}_P(u,v);\end{aligned}$$

(4.1)

$$\begin{aligned} \underline{R_P^{(i)}}(D)(u)&= \bigwedge _{v\notin D}[1-R_P^{(i)}(u,v)]\,(D\in U/d,\,u\in U);\end{aligned}$$

(4.2)

$$\begin{aligned} \overline{R_P^{(i)}}(D)(u)&= \bigvee _{v\in D}R_P^{(i)}(u,v)\,(D\in U/d,\,u\in U);\end{aligned}$$

(4.3)

$$\begin{aligned} POS^{(i)}_P(d)&=\bigcup _{D\in U/d}\underline{R_P^{(i)}}(D);\end{aligned}$$

(4.4)

$$\begin{aligned} \Gamma ^{(i)}_P(d)&=\frac{|POS^{(i)}_P(d)|}{n};\end{aligned}$$

(4.5)

$$\begin{aligned} sig^{(i)}(a,P,d)&= \Gamma ^{(i)}_P(d)-\Gamma ^{(i)}_{P\cup \{a\}}(d)\,(P\subseteq C,\,a\in C-P). \end{aligned}$$

(4.6)

Obviously,

$$\begin{aligned} POS^{(i)}_P(d)&= POS^{\lambda _i}_P(d); \\ \Gamma ^{(i)}_P(d)&=\Gamma ^{\lambda _i}_P(d); \\ sig^{(i)}(a,P,d)&= sig^{\lambda _i}(a,P,d)\,(P\subseteq C,\,a\in C-P). \end{aligned}$$

Theorem 4.1

Let $(U,C\cup \{d\})$ be an ICDIS. Given $P\subseteq C$. Then $\forall \,D\in U/d$, $\forall \,u\in U$, $\forall \,i$,

$$\begin{aligned} \underline{R_P^{(i+1)}}(D)(u)=\frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\frac{\lambda _i}{\lambda _{i+1}}\underline{R_P^{(i)}}(D)(u). \end{aligned}$$

(4.7)

Proof

$$\begin{aligned} \begin{aligned} \underline{R_P^{(i)}}(D)(u)&=\bigwedge _{v\notin D}(1-\frac{1}{\lambda _{i}}|P_{uv}|)\\&=1-\bigvee _{v\notin D}\frac{1}{\lambda _{i}}|P_{uv}|\\&=1-\frac{1}{\lambda _{i}}\bigvee _{v\notin D}|P_{uv}|. \end{aligned} \end{aligned}$$

Similarly,

$$\begin{aligned} \underline{R_P^{(i+1)}}(D)(u)=1-\frac{1}{\lambda _{i+1}}\bigvee _{v\notin D}|P_{uv}|. \end{aligned}$$

Then

$$\begin{aligned} \begin{aligned} \frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\frac{\lambda _i}{\lambda _{i+1}}\underline{R_P^{(i)}}(D)(u)&=\frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\frac{\lambda _i}{\lambda _{i+1}} \left( 1-\frac{1}{\lambda _{i}}\bigvee _{v\notin D}|P_{uv}|\right) \\&=1-\frac{1}{\lambda _{i+1}}\bigvee _{v\notin D}|P_{uv}|. \end{aligned} \end{aligned}$$

Thus

$$\begin{aligned} \underline{R_P^{(i+1)}}(D)(u)=\frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\frac{\lambda _i}{\lambda _{i+1}}\underline{R_P^{(i)}}(D)(u). \end{aligned}$$

$\square$

Corollary 4.2

Let $(U,C\cup \{d\})$ be an ICDIS. Given $P\subseteq C$ and $\lambda \in [|P|,|A|]$. Then $\forall \,D\in U/d$, $\forall \,u\in U$, $\forall \,i\in [|P|,|C|-1]$,

$$\begin{aligned} \underline{R_P^{(i+1)}}(D)(u)=\frac{1}{i+1}+\frac{i}{i+1}\underline{R_P^{(i)}}(D)(u). \end{aligned}$$

(4.8)

Theorem 4.3

Let $(U,C\cup \{d\})$ be an ICDIS. Given $P\subseteq C$ and $\lambda \in [|P|,|A|]$ and $D\in U/d$. Then $\forall \,i$,

$$\begin{aligned} \overline{R_P^{(i+1)}}(D)=\frac{\lambda _i}{\lambda _{i+1}}\overline{R_P^{(i)}}(D). \end{aligned}$$

(4.9)

Proof

Obviously. $\square$

Corollary 4.4

Let $(U,C\cup \{d\})$ be an ICDIS. Given $P\subseteq C$ and $D\in U/d$. Then $\forall \,i\in [|P|,|C|-1]$,

$$\begin{aligned} \overline{R_P^{(i+1)}}(D)=\frac{i}{i+1}\overline{R_P^{(i)}}(D). \end{aligned}$$

(4.10)

Theorem 4.5

Let $(U,C\cup \{d\})$ be an ICDIS. Given $P\subseteq C$. Then $\forall \,u\in U$, $\forall \,i$,

$$\begin{aligned} POS^{(i+1)}_P(d)(u)=\frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\frac{\lambda _i}{\lambda _{i+1}}POS^{(i)}_P(d)(u). \end{aligned}$$

(4.11)

Proof

By Theorem 4.1, we can obtain that $\forall \,u\in U$, $\forall \,i$,

$$\begin{aligned} \begin{aligned} POS^{(i+1)}_P(d)(u)&=\bigvee _{D\in U/d}\underline{R_P}^{(i+1)}(D)(u)\\&=\bigvee _{D\in U/d}\left( \frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\frac{\lambda _i}{\lambda _{i+1}}\underline{R_P}^{(i)}(D)(u)\right) \\&=\frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\bigvee _{D\in U/d}\frac{\lambda _i}{\lambda _{i+1}}\underline{R_P}^{(i)}(D)(u)\\&=\frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\frac{\lambda _i}{\lambda _{i+1}}\bigvee _{D\in U/d}\underline{R_P}^{(i)}(D)(u). \end{aligned} \end{aligned}$$

Thus

$$\begin{aligned} POS^{(i+1)}_P(d)(u)=\frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\frac{\lambda _i}{\lambda _{i+1}}POS^{(i)}_P(d)(u). \end{aligned}$$

$\square$

Corollary 4.6

Let $(U,C\cup \{d\})$ be an ICDIS. Given $P\subseteq C$. Then $\forall \,u\in U$, $\forall \,i\in [|P|,|C|-1]$,

$$\begin{aligned} POS^{(i+1)}_P(d)(u)=\frac{1}{i+1}+\frac{i}{i+1}POS^{(i)}_P(d)(u). \end{aligned}$$

(4.12)

Theorem 4.7

Let $(U,C\cup \{d\})$ be an ICDIS. Given $P\subseteq C$. Then $\forall \,i$,

$$\begin{aligned} \Gamma ^{(i+1)}_P(d)=\frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\frac{\lambda _i}{\lambda _{i+1}}\Gamma ^{(i)}_P(d). \end{aligned}$$

(4.13)

Proof

By Theorem 4.5,

$$\begin{aligned} \begin{aligned} |POS^{(i+1)}_P(d)|&=\sum \limits _{i=1}^nPOS^{(i+1)}_P(d)(u_i)\\&=\sum \limits _{i=1}^n\left( \frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\frac{\lambda _i}{\lambda _{i+1}}POS^{(i)}_P(d)(u_i)\right) \\&=\frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}n+\frac{\lambda _i}{\lambda _{i+1}}\sum \limits _{i=1}^nPOS^{(i)}_P(d)(u_i)\\&=\frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}n+\frac{\lambda _i}{\lambda _{i+1}}|POS^{(i)}_P(u_i)|. \end{aligned} \end{aligned}$$

Then

$$\begin{aligned} \frac{|POS^{(i+1)}_P(d)|}{n}=\frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\frac{\lambda _i}{\lambda _{i+1}}\frac{|POS^{(i)}_P(d)|}{n}. \end{aligned}$$

Thus

$$\begin{aligned} \Gamma ^{(i+1)}_P(d)=\frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\frac{\lambda _i}{\lambda _{i+1}}\Gamma ^{(i)}_P(d). \end{aligned}$$

$\square$

Corollary 4.8

Let $(U,C\cup \{d\})$ be an ICDIS. Given $P\subseteq C$. Then $\forall \,i\in [|P|,|C|-1]$,

$$\begin{aligned} \Gamma ^{(i+1)}_P(d)=\frac{1}{i+1}+\frac{i}{i+1}\Gamma ^{(i)}_P(d). \end{aligned}$$

(4.14)

Theorem 4.9

Let $(U,C\cup \{d\})$ be an ICDIS. Suppose $P\subseteq C$, $a\in C-P$. Then $\forall \,i$, 

$$\begin{aligned} sig^{(i+1)}(a,P,d)=\frac{\lambda _i}{\lambda _{i+1}}sig^{(i)}(a,P,d). \end{aligned}$$

(4.15)

Proof

By Theorem 4.7,

$$\begin{aligned} \begin{aligned} sig^{(i+1)}(a,P,d)&=\Gamma ^{(i+1)}_P(d)-\Gamma ^{(i+1)}_{P\cup \{a\}}(d)\\&=\frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\frac{\lambda _i}{\lambda _{i+1}}\Gamma ^{(i)}_P(d)-( \frac{\lambda _{i+1}-\lambda _i}{\lambda _{i+1}}+\frac{\lambda _i}{\lambda _{i+1}}\Gamma ^{(i)}_{P\cup \{a\}}(d))\\&=\frac{\lambda _i}{\lambda _{i+1}}\Gamma ^{(i)}_P(d)- \frac{\lambda _i}{\lambda _{i+1}}\Gamma ^{(i)}_{P\cup \{a\}}(d)\\&= \frac{\lambda _i}{\lambda _{i+1}}(\Gamma ^{(i)}_P(d)-\Gamma ^{(i)}_{P\cup \{a\}}(d)). \end{aligned} \end{aligned}$$

Thus

$$\begin{aligned} sig^{(i+1)}(a,P,d)=\frac{\lambda _i}{\lambda _{i+1}}sig^{(i)}(a,P,d). \end{aligned}$$

$\square$

Corollary 4.10

Let $(U,C\cup \{d\})$ be an ICDIS. Suppose $P\subseteq C$, $a\in C-P$. Then $\forall \,i\in [|P|,|C|-1]$,

$$\begin{aligned} sig^{(i+1)}(a,P,d)=\frac{i}{i+1}sig^{(i)}(a,P,d). \end{aligned}$$

(4.16)

5 Attribute reduction in an ICDIS

In this section, attribute reduction in an ICDIS based on fuzzy rough sets is studied and the corresponding algorithm is proposed.

Definition 5.1

Let $(U,C\cup \{d\})$ be an ICDIS. Given $P\subseteq C$. Then P is called a coordination subset of C relative to d, if $POS^\lambda _P(d)= POS^\lambda _C(d)$ where $\lambda =|P|$.

Definition 5.2

Suppose that $(U,C\cup \{d\})$ is an ICDIS. Given $a\in P\subseteq C$. Then a is called independent in P, if $POS^\lambda _P(d)\ne POS^\lambda _{P-\{a\}}(d)$ where $\lambda =|P|$.

Definition 5.3

Assume that $(U,C\cup \{d\})$ is an ICDIS. Given $P\subseteq C$. Then P is called independent, if for any $a\in P$, a is independent in P.

Definition 5.4

Let $(U,C\cup \{d\})$ be an ICDIS. Given $P\subseteq C$. Then P is called a reduct of C to d, if P is both coordination and independent.

In this paper, the family of all coordination subsets (resp., all reducts) of C to d is denoted by co(C) (resp., red(C)).

Obviously,

$$\begin{aligned} P\in red(C)\,\,\Longleftrightarrow \,\,P\in co(C)\, and \,\forall \,P'\subset P,P'\not \in co(C). \end{aligned}$$

Theorem 5.5

Suppose that $(U,C\cup \{d\})$ is an ICDIS. Given $P\subseteq C$. Then

$$\begin{aligned} P\in co(C)\,\,\Longleftrightarrow \,\,\Gamma ^\lambda _P(d)=\Gamma ^\lambda _C(d),\,where\,\lambda =|P|. \end{aligned}$$

Based on the discussion above, the following attribute reduction algorithm in an ICDIS based on fuzzy rough sets is proposed.

By using Algorithm 1, the time complexity of attribute reduction in an ICDIS is polynomial. First, Steps 2 to 8 take $O(n^2)$ time complexity and Steps 9 to 20 is $O(mn^2)$. The time complexity of Step 23 to 29 is $O(mn^2)$, and that of Step 30 is O(m). The time complexity of Steps 32 to 37 is $O(n^2)$, so the overall complexity from Step 21 to Step 38 is $O(m(m+1)n^2/2+m^2+mn^2)=O(m^2n^2)$. Thus the time complexity of Algorithm 1 is $O(n^2+mn^2+m^2n^2)=O(m^2n^2)$. Furthermore, its space complexity is $O(mn^2)$.

6 Experimental analysis

In this section, the performance of the proposed attribute reduction algorithm and existing algorithms is evaluated. The frame work chart of experiments is displayed in Fig. 2.

Fig. 2

The frame work chart of experiments

6.1 Datasets

Eight data sets are used in the experimental analysis, which are selected from UCI (Frank and Asuncion 2010) Machine Learning Repository. These data sets containing missing values are described in Table 1.

Table 1 The data sets excerpted from the UCI machine learning repository

6.2 Data preprocessing

Data preprocessing composed of three main steps: Label Transfer and Data Transfer, Missing value processing, Remove duplication, and Data normalization. In label transfer and data transfer, all the symbolic data are transferred to numeric values. It is important to process missing value in the training set to calculate the distance between individuals. For categorical data, we usually use frequency values to deal with missing values. It is important to remove duplicate records in the training set to avoid the classifiers to be biased to most frequent records and prevent it from learning infrequent records. Normalizing the data is an important step to eliminate the biased with the features of larger values from the data set. Data normalization is the process of transforming or scaling the data values of each feature into a proportional range. The used dataset was normalized into the range [0, 1] according to Eq.(6.1).

$$\begin{aligned} X_{normalized}=\frac{X-X_{min}}{X_{max}-X_{min}}. \end{aligned}$$

(6.1)

In this paper, because fuzzy relations are constructed directly and attribute reduction is performed based on fuzzy relations, there is no need to deal with missing values and normalize the data before attribute reduction.

6.3 Classifier training and testing

To evaluate these attribute reduction approaches, three learning mechanisms which can create classifiers are employed. They are frequently-used classifiers which the one is k-nearest nearest rule (KNN,K=3), the others are decision tree induction algorithms (ID3 and C4.5). We use confusion matrix to calculate the accuracy. As shown in Fig. 3.

$$\begin{aligned} accuracy=\frac{\sum _{i=1}^nc_{ii}}{\sum _{i=1}^n\sum _{j=1}^nc_{ij}}. \end{aligned}$$

(6.2)

Fig. 3

Confusion matrix of classifier

The proposed algorithm is compared with the other six algorithms. These are representative forward attribute reduction algorithms based on intuitionistic fuzzy rough (FMIFRFS) Pankhuri et al. (2020), fuzzy similarity-based rough set (FSRS) Singh et al. (2020), dependency (SFFSNTCE) Zhao and Qin (2014), positive regions (PR) Meng and Shi (2009), conditional entropies (IE) Teng et al. (2010) and the heuristic search algorithm of SetCover approach (SetCover) Dai et al. (2013).

The parameter $\delta$ of FR-IC method is introduced to control the variable precision. The $\delta$ is increased from 0.05 to 0.25 with a step of 0.01. Because different values of $\delta$ produce different reductes, the experimental results with the highest classification accuracies are compared. In order to make the calculation more accurate, we did 10 experiments for each result. In each experiment, 20% was randomly selected as the test set and 80% as the training set, and then the classification accuracy calculated was averaged.

The experiments are carried out on a personal computer. All attribute reduction algorithms are run in Matlab 2018b and hardware environment with an Intel(R)Core(TM)i7-9700CPU@3.0GHZ and 8GB RAM.

6.4 Classification results

Table 2 provides the average sizes of attribute reduction with these algorithms. Among these seven algorithms, only algorithm FMIFRFS deals with complete data. For this reason, the frequency mode method is used. The missing values in each column are replaced by the most frequent attribute values in this column. In algorithm FMIFRFS, the $\mu (x)$ function value is obtained by normalizing the data, and then the $\nu (x)$ function value is equal to 1-$\mu (x)$-rand/c, where rand is a random number between (0,1) and c is a constant.

It is easily seen that these attributes of data sets can be reduced effectively. From Table 2, it is easy to find out that the less average number of selected attributes are FR-IC and SETCOVER, which both are approximately equal to 6. The most number of selected attributes was carried out by FMIFRFS method, because its ending condition: The positive field of attribute reduction must be equal to 1, or the two values before and after are equal. Most data sets are difficult to achieve this condition for FMIFRFS, resulting in a large number of reduction. FSRS algorithm also requires that the positive field of the reduction attribute be equal to 1. Therefore, the positive field of all attributes in two datasets (Vote, Mammographic) cannot reach 1. So the reduction sets generated by FSRS algorithms are the original data for the two datasets.

Table 2 Numbers of attribute reduction

The optimal attribute subsets with the highest classification accuracy of the seven algorithms are shown in Table 3. It is obvious to see that most of the attributes selected by these methods are not the same, because they may have more than one reduct. In Table 3, the “-" represents a gradual increase from one number to another.

Table 3 The optimal attribute reduction among FMIFRFS, FSRS,SFFSNTCE, PR, IE, SETCOVER and FR-IC

Tables 4, 5 and 6 present the classification results with KNN (k=3), ID3 and C4.5. The underlined symbol denotes the highest classification accuracy among these attribute reduction algorithms. In Table 4, for Dermatology, FMIFRFS performs better than FR-IC in classifier KNN. The classification accuracy of FR-IC is a little worse than that of FSRS for Mushroom and Mammographic. FSRs algorithm does not complete attribute reduction in Vote and Mammographic, in other words, no attribute has been deleted, so the accuracy used is the original dataset. For the classifier KNN, the classification accuracy of three data is higher than that of the proposed algorithm in this paper.

As can be clearly seen from Table 5, for Dermatology, FR-IC is not good enough for FMIFRFS in classifier ID3. For Large Soybean and Mushroom, the classification accuracy of FSRS do better than other algorithms in ID3. From Table 6, for Mushroom, PR and SETCOVER execute better than FR-IC in classifier C4.5. The FMIFRFS algorithm performs better than other algorithms in Dermatology dataset. On the whole, classification accuracy based on the FR-IC method is higher than the other six methods in most case. We have done 168 numerical experiments, and 13 of them show that other algorithms are better than FR-IC algorithm. That is to say the excellent rate of FR-IC is 92.3% and it reaches a good effect. Therefore, our algorithm is superior to other six algorithms. In a word, the FR-IC method is more effective for attribute reduction in an ICDIS.

Table 4 Comparison of classification accuracies of reduced data with KNN

Table 5 Comparison of classification accuracies of reduced data with ID3

Table 6 Comparison of classification accuracies of reduced data with C4.5

By discussing the influence of parameter $\delta$ on FR-IC algorithm, it is found that a reduct is related to $\delta$, and the relationship between $\delta$ and classification accuracy is closely related. So it is easy to find the $\delta$ value of the optimal reduct. Figures 4, 5, 6, 7, 8, 9 and 10 show that the classification accuracy curve has no obvious change with the number of selected attributes decreasing. This shows that the proposed algorithm is effective. These figures show that the proposed algorithm has achieved good results. Figures 4, 5, 6, 7, 8, 9 and 10 show the relationship between the size of the reduct and the threshold $\delta$, and the relationship between the classification accuracy of different classifiers and $\delta$. The x-axis expresses the threshold $\delta$, that value increases from 0.05 to 0.25 in 0.01 step. The left pink Y-axis indicates number of attributes of the reduct P, and the right blue Y-axis represents classification accuracy. The pink curve represents the relationship between $\delta$ and the size of the reduct P, and the function value of each point on the curve corresponds to the left pink y-axis. The other three curves with different colors reflect the classification accuracy of $\delta$ and three different classifiers, and the function value corresponds to the right blue y-axis. It is obvious that most of data sets can get higher classification accuracy in this experiment. Although classification accuracy curves of KNN and ID3 are gentle, the classification accuracy curve of C4.5 fluctuate obviously. The classification accuracy of C4.5 is lower than KNN and ID3 in most data sets, such as Large Soybean, Dermatology, Breast Cancer, Mammographic and Audiology.standardiz. This may be due to the insufficient number of samples. Because the small number of samples and the large number of total categories in Audiology.standardiz, the classification accuracy of Audiology.standardiz is low. Figure 5 shows that the classification accuracy curves of KNN, ID3 and C4.5 are very close for the Vote dataset.

Figure 11 shows the optimal attribute set size of eight data reduced by seven algorithms. Figures 12, 13 and 14 show the trend of the best classification accuracy of eight data sets under seven algorithms. The x-axis represents eight data sets, and the y-axis expresses the classification accuracy of the classifier. The pink curve, the FR-IC algorithm proposed in this paper, is obviously slightly higher than other curves. This means that the performance of FR-IC algorithm is better than other algorithms in most cases.

Fig. 4

Effective of $\delta$ in attribute reduction (Lung Cancer)

Fig. 5

Effective of $\delta$ in attribute reduction (Large Soybean)

Fig. 6

Effective of $\delta$ in attribute reduction (Dermatology)

Fig. 7

Effective of $\delta$ in attribute reduction (Vote)

Fig. 8

Effective of $\delta$ in attribute reduction (Breast Cancer)

Fig. 9

Effective of $\delta$ in attribute reduction (Mammographic)

Fig. 10

Effective of $\delta$ in attribute reduction (Audiology.standardiz)

Fig. 11

The size of attribute reduction for seven algorithms

Fig. 12

Variation of classification accuracies with KNN for seven algorithms

Fig. 13

Variation of classification accuracies with ID3 for seven algorithms

Fig. 14

Variation of classification accuracies with C4.5 for seven algorithms

6.5 Sensitivity analysis

Next, we discuss sensitivity analysis. The original record may not be the most true because there will be deviation when observing attribute values. Two information systems Dermatology and Large Soybean are selected to generate random small disturbances on their attribute values respectively. Firstly, 0%, 2%, 5%, 8%, 15%, 20%, 25% and 30% attribute values in the information system are selected to generate random interference respectively. The purpose is to observe whether the proposed algorithm can still get a consistent reduction set under different disturbance ratios. Then the proposed algorithm is used to complete multiple attribute reduction. The difference between the reduced sets obtained under different proportions of data disturbance will be calculated. Therefore, we use Jaccard similarity coefficient to measure the similarity between the two sets:

$$\begin{aligned} rate = \frac{{\left| {P_i \cap P_j } \right| }}{{\left| {P_i \cup P_j } \right| }} \end{aligned}$$

where $\left| {P_i \cap P_j} \right|$ represents the same number of statistical sets $P_i$ and $P_j$, $\left| {P_i \cup P_j } \right|$ represents the total number of different elements in two sets. Rate indicates the similarity of two sets.

Figures 15 and 16 show that FR-IC algorithm obtains five different reduction sets when taking different parameters . The horizontal axis represents the disturbance rate, which is 0%, 5%, 8%, 15%, 20%, 25% and 30% respectively. When the disturbance rate is 0%, it indicates the original data set. The vertical axis represents the similarity rate. When there is no disturbance, the similarity rate is 1, and all curves start from point (0,1).

As can be seen from Figures 15 and 16, when the disturbance rate is 2%, the similarity of the reduced set is very high, reaching about 90%. When the disturbance rate increases gradually, the similarity becomes lower and lower, and finally reaches a stable state.

Fig. 15

Attribute sensitivity analysis (Dermatology)

Fig. 16

Attribute sensitivity analysis (Large Soybean)

Through sensitivity analysis, we can know that when the disturbance rate is no more than 2%, the similarity of reduced sets is high and the algorithm model is stable.

6.6 Friedman test and Nemenyi test

To further assess the performance of classification of seven methods, Friedman test and Nemenyi test are given in this section.

Friedman test is a statistical test that uses the rank of algorithms. Friedman statistic is defined as

$$\begin{aligned} \chi _{F}^{2}=\frac{12N}{k(k+1)}\left( \sum _{i=1}^{k}r_{i}^{2}-\frac{k(k+1)^{2}}{4}\right) \end{aligned}$$

where k is the number of algorithms, N is the number of data sets, $r_{i}$ is the average ranking of the i-th algorithm. When k and N are large enough, Friedman statistic follows the chi-square distribution with $k-1$ degrees of freedom. However, such Friedman test is too conservation, and is usually replaced by the next statistic

$$\begin{aligned} F_F=\frac{(N-1)\chi _{F}^{2}}{N(k-1)-\chi _{F}^{2}}. \end{aligned}$$

The statistic $F_F$ follows a Fisher distribution with $k-1$ and $(k-1)(N-1)$ degrees of freedom. If the statistic $F_F$ is greater than the critical value of $F_{\alpha }(k-1, (k-1)(N-1))$, it means the null hypothesis is rejected under Friedman test. Nemenyi test can be used to further explore which algorithm is better in the statistical term. If the average level of distance exceeds the critical distance $CD_{\alpha }$, then the performance of two algorithms will be significantly different. The critical distance $CD_{\alpha }$ is denoted as

$$\begin{aligned} CD_{\alpha }=q_{\alpha }\sqrt{\frac{k(k+1)}{6N}}, \end{aligned}$$

where $q_{\alpha }$ is the critical tabulated value for the test and $\alpha$ is the significance level of the Nemenyi test.

Below, these seven methods are viewed as seven algorithms and the statistical significance is demonstrated by using Friedman test and Nemenyi test.

• (1) The ranking of classification accuracies of the seven methods on eight data sets is given, respectively (From Tables 7, 8, 9).

• (2) Friedman test is conducted to investigate whether the classification ability of the seven methods are significantly different. Under the seven methods and the ranking of classification accuracies with three classifiers, $F_F$ follows the distribution with 6 and 138 degrees of freedom. The critical value of Fisher distribution $F_{0.05}(6, 138)$ is 2.165, and the test statistic of $F_F=9.143$. Obviously, the statistic value $F_F$ is bigger than that of $F_{0.05}(6, 138)$. This means that at the significant level $\alpha =0.05$, it is evidence to reject the null hypothesis, which means that the classification ability of the seven methods are different in the statistical significance.

• (3) To further show the significant difference of the seven methods, Nemenyi test is introduced. For $\alpha =0.05$, it is easy to calculate $q_{\alpha }=2.948$ and $CD_\alpha =2.948\times \sqrt{\frac{7\times (7+1)}{6\times 24}}=1.838$. Figure 17 shows the Nemenyi test results with $\alpha =0.05$ on the seven methods, in which the two algorithms with horizontal line connections have no significant differences on classification accuracy and the line segments in the figure carves out the scope of $CD_{\alpha }$. Figure 18 shows the significance level p-values of each pair of algorithms.

• (4) From Figs. 17 and 18, the following results are obtained:

  • (a) The classification accuracy of FR-IC is statistically higher than that of FMIFRFS, SFFSNTCE, PR, IE and SETCOVER, respectively;

  • (b) The classification accuracy of FSRS is statistically higher than that of FMIFRFS, SFFSNTCE, PR, IE and SETCOVER, respectively;

  • (c) There is no significant difference between the classification accuracy of FR-IC and FSRS;

  • (d) There is no significant difference among the classification accuracy of FMIFRFS, SFFSNTCE, PR, IE and SETCOVER.

Fig. 17

The results of the Nemenyi test

Fig. 18

Thermodynamic chart of the p-values of the Nemenyi test

Table 7 Ranking of classification accuracies of reduced data with KNN

Table 8 Ranking of classification accuracies of reduced data with ID3

Table 9 Ranking of classification accuracies of reduced data with C4.5

7 Conclusion and future work

In this paper, a fuzzy rough set model for an ICDIS has been given. Some attribute-evaluation functions, such as fuzzy positive regions, dependency functions and attribute importance functions have been presented. These attribute-evaluation functions represent the classification ability of attribute reduction. A fuzzy rough computation model for an ICDIS has been established by using the iterative relations of fuzzy positive regions and dependency functions. Attribute reduction in an ICDIS based on fuzzy rough sets has been studied and the corresponding algorithm has been proposed. Experiments have been carried out by using 8 datasets from UCI, and statistical tests have been used to evaluate the performance of the proposed algorithm. Experimental results show that the proposed algorithm can effectively reduce redundant attributes and maintain high classification accuracy. In the future, some applications of the fuzzy rough computation model in data mining and classification learning will be studied.