Improved arithmetic optimization algorithm for design optimization of fuzzy controllers in steel building structures with nonlinear behavior considering near fault ground motion effects

Abstract

In recent decades, near fault ground motions has been of great importance due to the difference in characteristics of earthquake records in the regions near to the active faults. Most of the developed control systems for structural vibration control have difficulties in dealing with these kinds of strong ground motions regarding the deficiencies of the human knowledge-based control systems such as fuzzy logic controllers for this purpose. Hence, the optimization of these controllers has been concerned in recent years. The main aim of this paper is to optimize the fuzzy controllers implemented in steel structures with nonlinear behavior in which the arithmetic optimization algorithm (AOA) is utilized as the main optimization algorithm while an improved version of this algorithm as IAOA is also proposed for performance enhancement of the standard algorithm. In the IAOA, a new parameter identification process is proposed in which the Levy flight as a well-known stochastic process with step length determined by levy distribution is implemented in the main loop of the AOA. The IAOA and AOA are utilized for optimization of the membership functions and the rule base of the fuzzy controllers implemented in a large-scale building structure. The overall performance of the IAOA is compared with the standard AOA and other metaheuristics. The obtained results of the improved method demonstrate the capability of this method in providing very competitive solutions which results in decreasing structural responses and damages of the considered building in dealing with the near-fault strong ground motions.

1 Introduction

Control systems are some sort of intelligent procedures which provide the desired actions for controlling a predefined output of a considered system. In other words, control systems are intelligent systems which are configured as a procedure for maintaining a predefined variable at a desired point in order to achieve a better performance for the system. Active vibration control system are a kind of control procedures in which some sorts of control algorithms and control devices are utilized for conducting the controlling process. One of the well-known control algorithms that is mostly utilized in active systems is Fuzzy Logic Controller (FLC) which is formulated based on the fuzzy logic as a mathematical system that deals with logical variables in a continuous space between 0 and 1 in opposition to the classical systems with discrete variables of either 0 or 1. Zadeh (1965) proposed the fuzzy theory for the first time in his seminal paper while the fuzzy algorithms (Zadeh 1968), decision making with fuzzy (Bellman and Zadeh 1970), and fuzzy ordering (Zadeh 1971) were the first research attempts in this area. Zadeh (1973) proposed the idea of fuzzy control in which the linguistic variables and IF–THEN rules were utilized as the key aspects of this type of controller. The general framework of the fuzzy controllers were developed by Mamdani and Assilian (1975) while the applicability of these controllers in full-scale industrial systems were investigated by Holmblad and Østergaard (1993). Faravelli and Yao (1996) presented the basic guidelines in application of FLC in engineering structures while the first application of FLC in structural vibration control with active mass driver system were investigated by Battaini et al. 1998.

Due to the necessity of keeping the occupants safe in the engineering structures and also considering economic issues, improving the overall performance of the knowledge-based FLCs is very important. However, the optimum design of FLCs with metaheuristic algorithms has been of great importance in recent years. In this paragraph, some of the most recent and important researches in this field are provided. Fu et al. (2018) used the Genetic Algorithm (GA) for optimization of a nonlinear fuzzy controller utilized in the magnetorheological elastomer isolators. Soltani et al. (2018) utilized the Particle Swarm Optimization (PSO) for optimal design of a fuzzy logic-based sliding mode controller implemented in the parallel-distributed compensator in order to overcome the complication of the inappropriate parameter configuration of the sliding surface. Chen et al. (2019) developed a parameter estimation process for sliding mode fuzzy controller utilized in regulating systems of hydraulic turbine by means of the Imperialist Competitive Algorithm (ICA). Olivas et al. (2017) generalized the type-2 fuzzy logic approach for dynamic parameter adaptation with the Ant Colony Optimization (ACO) algorithm in order to optimize the rule base and the membership functions of the fuzzy control systems. Amador-Angulo and Castillo (2018) utilized the Bee Colony Optimization (BCO) method for optimal configuration of the membership functions in the implementation of the fuzzy controllers in complex nonlinear plants. Chamorro et al. (2019) proposed the application of the Differential Evolution (DE) algorithm for optimal tuning of a fuzzy controller in order to improve the synthetic inertia control in power systems. Debnath et al. (2017) discussed the optimal parameter configuration of the fuzzy Proportional–Integral–Derivative (PID) controllers by means of the Firefly Algorithm (FA) with application of the derivative filter for the frequency control with thermal non-reheat type turbine of a unified power system. Chrouta et al. (2018) presented optimal control of an irrigation station process based on the FLC with Takagi–Sugeno (TS) model using the Cuckoo Search Algorithm (COA). Giri and Bera (2018) developed a fuzzy proportional-integral controller for oscillation attenuation of system frequency with damping in the distributed energy generation of wind turbines and optimized the gains of this controller with the Grey Wolf Optimization (GWO) algorithm. Zadeh and Bathaee (2018) discussed load frequency control procedures for interconnected power systems considering uncertainty considerations and nonlinear term based on fuzzy logic controller using Harmony Search (HS) algorithm. Noureldin et al. (2021) investigated the optimum allocations of energy dissipation devices by means of fuzzy logic and artificial neural networks. Mahmoud (2021) utilized efficient fuzzy controllers for increasing the induction motors of the islanded networks in wind turbines. Kumar et al. (2021) proposed a metaheuristic-based parameter tuning process for optimal design of fuzzy controllers by means of the PSO algorithm. Lin et al. (2021) investigated the optimal control of adjacent buildings by means of fuzzy magnetorheological dampers. Tripathy et al. (2021) utilized Jaya Algorithm (JA) as an intelligent technique for optimal design of fuzzy control systems combined with optimum frequency control scheme. Besides, the improved versions of the metaheuristic algorithms alongside the standard methods have also been utilized for optimization of different engineering design problems including the Tribe–Charged System Search (T-CSS) for parameter identification of the nonlinear systems with large search domains (Talatahari et al. 2021d) and global optimization purposes (Talatahari and Azizi 2020a, b, c, d), Quantum‐behaved Developed Swarm Optimizer for optimal design of real-size structural buildings (Talatahari and Azizi 2020a, b, c, d), Chaos Game Optimization (CGO) algorithm for optimum design of engineering design problems (Talatahari and Azizi 2020a, b, c, d) and global optimization (Talatahari and Azizi 2020a, b, c, d), Tribe-Interior Search Algorithm for design optimization of building structures (Talatahari and Azizi 2020a, b, c, d), Atomic Orbital Search (AOS), Material Generation Algorithm (MGA), Crystal Structure Algorithm (CryStAl) and Fuzzy Adaptive Charged System Search for optimization of global and engineering design problems (Azizi 2021; Talatahari et al. 2021a, b, c).

Mostly, the FLC optimization problem was discussed in the situations that the linear behavior of the structural material alongside the inaccurate mathematical models of the structures were utilized for the structural analysis purposes (Abubaker et al. 2016). The main purpose of this paper is to propose an improved metaheuristic algorithm for optimal design of the FLC in dealing with the severe earthquake records in order to intelligently control the seismic vibration of structural buildings. In this regard, the Arithmetic Optimization Algorithm (AOA) is utilized as the main optimization method while an improved version of this algorithms is also proposed as Improved AOA (IAOA) in order to achieve better performance in dealing with the FLC optimum design problem. The AOA proposed by Abualigah et al. (2021), is a metaheuristic algorithm that is formulated based on the arithmetic as one of the important aspects of the number theory in mathematics alongside the other components like the algebra and geometry. In this optimization algorithm, the general operators in arithmetic are determined as the main parts of the algorithm while the exploration and exploitation phases are also considered by utilization of the diversification and intensification as two of the main aspects in arithmetic. The main advantages of this algorithm are the simplicity of this method and the capability of the method in seeking the optimal global best candidate in an organized way in dealing with the engineering optimization problems. Regarding the fact that a nonlinear distribution is utilized in this algorithm for step size determination of the solution candidates during the optimization process, a new methodology is presented in this paper for this purpose by means of the Levy flight as a well-known stochastic process with step length determined by levy distribution. The proposed IAOA is utilized for optimal tuning of the FLC which is implemented in a 20-story steel structure, while the nonlinearity of the structure is taken into account and the mathematical model of the building structure is some kind of accurate model. The seismic inputs for dynamic analysis are considered based on some destructive Near-fault Earthquake (NFE) records. The selected NFE records are utilized as seismic input for the 20-story steel structure and the capability of the IAOA is examined with respect to the destructive effects of the considered ground motions. Also, the capability and performance of the IAOA in FLC optimum design process is compared with the standard AOA and some other advanced and classical optimization algorithms. For the FLC tuning process, the improved and most recent versions of these metaheuristic algorithms are utilized in this study.

It is proved in the literature that applying different modification procedures in the general formulation of standard metaheuristics can lead to a method which can provide proper solutions and demonstrate better performance in dealing with different kinds of problems (Agrawal et al. 2021; Chen et al. 2021). The novelty and main concept of this paper is investigated based on the “metaheuristics”, “fuzzy parameter tuning” and “structural dynamic responses” as the three key points of this paper. From the “metaheuristics” point of view, a new improved metaheuristic algorithm (IAOA) is proposed in order to enhance the overall performance of the standard AOA in dealing with multiple mathematical and real-world optimization problems. The proposed improved approach is developed based on the fact that the Brownian motion with a Gaussian distribution as one of the most utilized random distribution procedures cannot guarantee the optimal performance of the considered system problem so utilizing a method with higher levels of efficiency and capability in dealing with uncertain complex environments can be handful. Hence, this improvement technique is proposed and utilized for the first time in performance improvement of the AOA which can be considered as one of the novel aspects of this paper. Besides, the capability of the IAOA in improving the convergence behavior, exploration rate and exploitation phase of the standard AOA is investigated by means of some simple and complex optimization problems. The results of the improved method are also backed up by conducting some specific analyses such as the computational complexity and cost analysis which provides a complete validation process for the proposed new optimization method. From the “fuzzy parameter tuning” point of view, the previously developed fuzzy systems based on the expert knowledge in both numerical and practical approaches have not provided the expected optimal and reasonable results in dealing with complex system problems such as vibration control of real-size building structures. The fuzzy systems in these approaches which rely on the human intelligence have not efficient performance in dealing with the modern complex system problems. In most cases, the parameter tuning of the fuzzy systems with multiple inputs and outputs leads to a complicated tuning problem in which the human knowledge is incapable of resolving the case. The research of Al-Dawod et al. (2004) and Edrees (2015) can be mentioned in this purpose; however, the results of these research works have been of great importance and interest in recent years due to the limitations of computer-aided tools in practical applications of fuzzy controllers. Based on the provided information, an FLC based on the metaheuristics is developed in this paper which is implemented into a building structure in order to decrease the complexity of the structural and control system by inserting the artificial intelligence into the FLC tuning process. The presented methodology in this paper is capable of dealing with very complex system problems which is amongst the most recent challenges of this research area. From the “structural dynamic responses” point of view, the complexity of the structural systems are of great importance due to the fact that considering different levels of complexity leads to a system with different levels of precision and capability. Most of the previously published research papers (Abubaker et al. 2016; Kaveh et al. 2015), have assumed a linear behavior for the utilized material in the structural elements which leads to some inaccurate structural responses due to the inaccuracy of the linear system models. In this regard, a mathematical model which have an approximately precise levels of complexity for the material behavior of the structural elements is utilized and the nonlinear structural analysis is also conducted based on the provide information. It also should be noted that the nonlinear structural analysis provides some useful structural responses which represents many important aspects of the current design codes and practices. Considering the mentioned results based on the utilized precise mathematical model and conducted nonlinear analysis, the presented methodology will change our point of view in dealing with so many system problems in the research area. Besides, the near fault ground motion effects are considered in this paper while the near fault earthquake records have been considered for the first time in this paper as seismic inputs of the structure in the optimum design process of fuzzy controllers. According to the mentioned key points, the proposed improved metaheuristic alongside the seismic inputs, and complex fuzzy formulations make this paper a unique research work with acceptable levels of novelty.

2 Arithmetic optimization algorithm (AOA)

2.1 The standard AOA

The inspirational concept of the AOA is based on the arithmetic as one of the important aspects of the number theory in mathematics alongside the other components like the algebra and geometry. The general operators in arithmetic including the Multiplication (M), Addition (A), Subtraction (S), and Division (D) are determined as the main aspects of the AOA which are utilized as main operators in providing a solution to an arithmetic problem. In this algorithm, the exploration and exploitation phases are being taken care of by utilization of the diversification and intensification as two of the main principles of arithmetic. The hierarchy of the operators in arithmetic are presented in Fig. 1.

Fig. 1

Hierarchy of the operators in arithmetic

In the AOA, an initialization process is conducted in the first stage of the algorithm in which a predefined number of solution candidates ($X$) are generated randomly while the objective function values for these candidates are also calculated for evaluation purposes. These aspects are mathematically represented in the following:

$$X = \left[ {\begin{array}{*{20}c} {x_{1}^{1} } & {x_{1}^{2} } & \cdots & {x_{1}^{j} } & \cdots & { x_{1}^{n} } \\ {x_{2}^{1} } & {x_{2}^{2} } & \cdots & {x_{2}^{j} } & \cdots & {x_{2}^{n} } \\ \vdots & \vdots & {} & \vdots & \ddots & \vdots \\ {x_{i}^{1} } & {x_{i}^{2} } & \cdots & {x_{i}^{j} } & \cdots & {x_{i}^{n} } \\ \vdots & \vdots & {} & \vdots & \ddots & \vdots \\ {x_{N}^{1} } & {x_{N}^{2} } & \cdots & {x_{N}^{j} } & \cdots & {x_{N}^{n} } \\ \end{array} } \right],\quad \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {i = 1,2, \ldots ,N.} \\ \end{array} } \\ {j = 1,2, \ldots ,n.} \\ \end{array} } \right.$$

(1)

where N is the total number of considered solution candidates in the search and n is the dimension in the considered problem.

In the AOA, the diversification and intensification procedures are utilized for considering the exploration and exploitation phases in the algorithm while the Math Optimizer Accelerated (MOA) is determined as a mathematical function for this purpose as follows after the initialization stage:

$$MOA\left( {C_{Iter} } \right) = Min + C_{Iter} \times \left( {\frac{Max - Min}{{M_{Iter} }}} \right)$$

(2)

where MOA(C_Iter) represents MOA function value at the iteration of t; C_Iter is the current iteration; M_Iter is the maximum number the considered iteration number; Max and Min are the maximum and the minimum amount of the MOA.

In order to consider between the exploration and exploitation phases, a random number (r₁) which is distributed uniformly in the range of [0, 1] is generated for each of the solution candidates in the arch space. If r₁ > MOA, the exploration is in perspective in which the multiplication and diversion from arithmetic are utilized in the mathematical model for position updating of the solution candidates due to the fact that these operators represent higher distributed decisions or values regarding different reigns. In order to decide between these two operators during the optimization process, another random number (r₂) is created which is distributed uniformly in the range of [0, 1]. For r₂ ≥ 0.5, the diversion operator is considered as the main aspects for position updating while for the r₂ < 0.5, the multiplication is determined by considering the fact that a stochastic scaling coefficient (μ) is also implemented in the process for improving the diversification (exploration) of the algorithm. These aspects are mathematically formulated as follows:

$$x_{i}^{j} \left( {C_{Iter + 1} } \right) = \left\{ {\begin{array}{*{20}l} {Best\left( {x^{j} } \right) \div \left( {MOP + \epsilon{}} \right) \times \left( {\left( {UB_{j} - LB_{j} } \right) \times \mu + LB_{j} } \right),} \hfill & {\quad r_{2} < 0.5} \hfill \\ {Best\left( {x^{j} } \right) \times \left( {MOP} \right) \times \left( {\left( {UB_{j} - LB_{j} } \right) \times \mu + LB_{j} } \right),} \hfill & {\quad r_{2} \ge 0.5} \hfill \\ \end{array} } \right.$$

(3)

where $x_{i}^{j} \left( {C_{Iter + 1} } \right)$ is the upcoming jth decision variable in the ith solution candidate; $x_{i}^{j}$ represents the current jth decision variable in the ith solution candidate; Best(x^j) is the jth decision variable in the best solution candidate found so far; LB_j and UB_j are the lower and upper bounds of the jth decision variable; μ represents a controlling parameter which is set to 0.5; $\epsilon$ represents an small integer number; and MOP is the Math Optimizer Probability which is determined as follows:

$$MOP\left( {C_{Iter} } \right) = 1 - \frac{{C_{Iter}^{1/\alpha } }}{{M_{Iter}^{1/\alpha } }}$$

(4)

where C_Iter is the current iteration; M_Iter is the maximum number the considered iteration number; α is a sensitive parameter which is set to 5.

On the other hand, If r₁ ≤ MOA, the exploitation is in perspective in which the subtraction and addition from arithmetic are utilized in the mathematical model for position updating of the solution candidates due to the fact that these operators represent lower dispersion of values considering different reigns which are utilized to deduce the solution candidates during the optimization process. In order to decide between subtraction and addition, a random number (r₃) is created which is distributed uniformly in the range of [0, 1]. For r₃ ≥ 0.5, the addition operator is considered as the main aspects for position updating while for the r₂ < 0.5, the subtraction is determined. Utilization of these two operators helps the algorithm to deeply exploit the entire search space by conducting a thorough search while the mathematical formulation in this purpose are as follows:

$$x_{i}^{j} \left( {C_{Iter + 1} } \right) = \left\{ {\begin{array}{*{20}l} {Best\left( {x^{j} } \right) - \left( {MOP} \right) \times \left( {\left( {UB_{j} - LB_{j} } \right) \times \mu + LB_{j} } \right),} \hfill & {\quad r_{3} < 0.5} \hfill \\ {Best\left( {x^{j} } \right) + \left( {MOP} \right) \times \left( {\left( {UB_{j} - LB_{j} } \right) \times \mu + LB_{j} } \right),} \hfill & {\quad r_{3} \ge 0.5} \hfill \\ \end{array} } \right.$$

(5)

where $x_{i}^{j} \left( {C_{Iter + 1} } \right)$ is the upcoming jth decision variable in the ith solution candidate; $x_{i}^{j}$ represents the current jth decision variable in the ith solution candidate; Best(x^j) is the jth decision variable in the best solution candidate found so far; LB_j and UB_j are the lower and upper bounds of the jth decision variable; μ represents a controlling parameter which is set to 0.5; $\epsilon$ represents an small integer number.

In Fig. 2a, the effects of utilizing different arithmetic operators in mathematics are presented in which the exploitation operators including the addition and subtraction are intended to deduce the near optimum results of the exploration operators including the diversion and multiplication. In addition, the searching process by arithmetic operator is also presented schematically in Fig. 2b while the pseudo code of the AOA is provided in Fig. 3.

Fig. 2

a Mathematical behavior of different operators and b schematic presentation of the positon updating process by different operators (Abualigah et al. 2021)

Fig. 3

Pseudo code of the AOA (Abualigah et al. 2021)

2.2 Improved arithmetic optimization algorithm (IAOA)

In most of the previously developed standard optimization algorithms, the exploration and exploitation of the algorithms have been satisfied by implementing different parameters with random or even linear and nonlinear distributions during the optimization process. In the AOA, the step size of the solution candidates in both of the considered phases of the algorithm is decreased by MOP as the math optimizer probability which is a nonlinear distribution in the range of [0, 1]. Utilizing these kinds of distributions for conducting position updating processes in the optimization algorithms mostly results in poor convergence behavior and entrapment of solutions candidates in the local optimum. In this regard, a new methodology is presented in this paper for updating the MOP during the optimization process which is based on the Levy flight as a stochastic process with step length determined by levy distribution. This distribution is a continuous probability distribution represented for non-negative variables. Levy flight is a specific class of random procedure while the jumping size in each step follows the well-known Levy distribution function which has a mathematical simple power-law formula as presented in Eq. 6 while a simple presentation of this distribution is provide in Eq. 7.

$$Levy\left( s \right) = \left| s \right|^{ - 1 - \beta } \quad 0 < \beta \le 2$$

(6)

$$Levy\left( {s,\gamma ,\mu } \right) = \left\{ {\begin{array}{*{20}l} {\sqrt {\frac{\gamma }{2\pi }} \exp \left[ { - \frac{\gamma }{{2\left( {s - \mu } \right)}}} \right]\frac{1}{{\left( {s - \mu } \right)^{\frac{3}{2}} }}} \hfill & {\quad 0 < \mu < 0} \hfill \\ 0 \hfill & {\quad s \le 0} \hfill \\ \end{array} } \right.$$

(7)

where β is an index for controlling the shape of the Levy distribution; μ is an scale parameter; γ is the position parameter; and s is the sample collection in the distribution.

Regarding the fact that the Brownian motion governed by a Gaussian distribution is one of the most respected random distributing which is utilized in mathematical presentation of the most important natural phenomenon, the Levy flight is also capable of improving the efficiency of the searching methods in uncertain complex environments. In this purpose, the Levy flight is utilized for deliberate detection of MOP in the AOA. In Fig. 4, the Brownian motion and Levy flight are presented for comparative purposes by 1000 steps while the pseudo code of IAOA is provided in Fig. 5.

Fig. 4

Comparison of Brownian motion (a) with Levy flight (b) (Barthelemy et al. 2008)

Fig. 5

Pseudo code of the IAOA

3 Near-fault ground motion

Near-fault region is supposed to be within a range of about 20–60 km from a ruptured fault. In this region, ground motions are affected by the rupture mechanism, rupture direction and the permanent ground displacements in the fault. These factors are denoted in research as “rupture-directivity” and “fling step”. These characteristics should be taken into account when ground motions close to an active fault is considered. When an earthquake happens, a shear rupture begins at a special point on the fault and starts to spread at a velocity mostly larger than the shear wave velocity. The situation in which the rupture propagates toward a site is called “forward-directivity”. In this situation, the direction of slip on the fault is also toward the site and most of the seismic energy arrive in a single large pulse of motion that represents the cumulative effects of the fault rupture. When rupture propagates away from the site, the “backward-directivity” occurs. In this situation, ground motions have relatively long duration and low amplitude (Stewart et al. 2002). These two characteristics are presented in Fig. 6 while in “site 5” the forward-directivity and in “site 0”, the backward directivity is occurred.

Fig. 6

Direction of propagation for fault rupture at different sites (Naeim 2001)

In the near-fault region, the ground motion records have acceleration spikes which result in higher Peak Ground Acceleration (PGA) vales with short-duration pulses. Besides, some of the pulses have lower PGA with longer duration (Bolt 2004). In addition, some of the NFE records include impulsive motions with lower frequency in the velocity time history and lower PGA to Peak Ground Velocity (PGV) ratio (Galal and Ghobarah 2006). In this paper, a set of seven NFE records are selected based on the mentioned characteristics. The special characteristics and principles of the NFE records are provided in Table 1. The selected ground motion records cover a moment magnitude (M_w) range from 6.53 to 7.62 and a distance (R) range from 0.96 to 5.35 km to the fault.

Table 1 Characteristics of the selected earthquake records

Because of the fact that the North–South (N–S) components of the NFE records have higher PGA values and the numerical study is conducted as a 2-Dimentional (2-D) approach, so the N–S components of the selected earthquake records are utilized for the dynamic analysis purposes. In Fig. 7, the acceleration time histories of these records for the NS components are illustrated.

Fig. 7

Acceleration time histories of the selected NFE records

In Fig. 8, the acceleration, velocity and displacement spectra of the selected NFE records for the N–S components alongside the mean spectra for 5% of damping are depicted. In this figure, the severity of pulse-type near-fault ground motions is in perspective.

Fig. 8

Acceleration, velocity and displacement spectra of the selected NFE records

4 Design example

4.1 Structural details

For design purposes, a building structure with 20 story is selected as the numerical design example. The height of this building is 80.77 m while the width of the plan is 36.58 by 30.48 m. There are six bays in the East–West (E–W) direction and five bays in the North–South (N–S) direction in which the width of these bays are all 6.10 m. In Fig. 9, an illustrative view of this building together with one of the perimeter N–S frames are depicted. There are two basement levels in this building including the first basement level which is below the ground level and the second basement level which is below the first basement level. These two basement levels are labeled as B1 and B2 in Fig. 9. The heights of these basement levels are 3.65 m while the height of the ground level is 5.49 m and the heights of the first to twentieth levels are all 3.69 m. The complete description of this building alongside the design sections can be found in Ohtori et al. (2004).

Fig. 9

Twenty-story steel building (left) and the N–S perimeter frame (right)

4.2 Nonlinear model

Based on the fact that when a structural system is confronted with some severe earthquakes or the simulated effects of some strong ground motions, the structural members may experience very large displacements. In these situations, the structural material may yield into the nonlinear phase of their behavior which requires a proper nonlinear model for modeling the utilized material for structural analysis. In most of the cases, a linear approximation is utilized in order to model the material behavior of the structural element which does not provide the real and exact behavior of these material. In order to perform an exact nonlinear analysis, a hysteresis model which is configured as a bilinear model is utilized in this paper for structural analysis purposes. The schematic view of this hysteresis model is illustrated in Fig. 10 while the required parameters of the model are presented in Table 2. It should be noted that the corresponding point of the yield strain (ε_y) and the yield strength (σ_y) demonstrates the point of yielding which represents the plastic hinge in the structural members.

Fig. 10

Bilinear hysteresis model for structural members

Table 2 Parameter summary of the nonlinear hysteresis model

For the structural analysis purposes, the Newmark-β method (Newmark 1959) is utilized which is presented by Subbaraj and Dokainish (1989) in details and is coded by Ohtori and Spencer (1999) in MATLAB.

4.3 Implementation of fuzzy logic controller

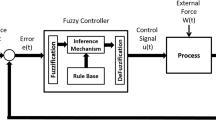
The fuzzy logic theory is one of the hypotheses in which the verbal interpretation and human deduction alongside the proximity of these information can easily and systematically be modeled and utilized in dealing with real-world complex problems. Considering the fact that a fuzzy logic controller is utilized in this paper for control purposes in dealing with building structures, an active control system based on the fuzzy logic controller is implemented into the described 20-story design example in order to arrange a closed-loop control system for seismic response control. Fuzzification, rule base, inference mechanism and defuzzification are the main aspects of a FLC in which the proper determination of these important factors are of great importance in performance evaluation of these control systems. At first, eleven linguistic fuzzy variables are defined for the fuzzy control system which are presented in Table 3.

Table 3 Fuzzy linguistic variables

The accelerations of the adjacent stories in the building is utilized for the feedback control purposes which represents the control system as the acceleration-based feedback controller. The accelerations of the fourth, eighth, twelfth, sixteenth, and twentieth are utilized in this purpose. The implemented active control system is arranged by utilizing the active bracing theory in which the control actuators provide the required control force in the building. These actuators are positioned in different story levels above the ground level of the structure in which the four of them are located in the ground level, two of them are positioned in the first and the second level and one actuator is positioned in each of the third to ninetieth stories. The maximum control force provided by the actuators is 1000 kilo newton. The schematic view of the simulation of structural and control systems are depicted in Fig. 11.

Fig. 11

Simulation of the nonlinear evaluation model for 20-Story building

Based on the presented information about the fuzzy systems and fuzzy controllers in Sect. 4, the maximum accelerations of the selected story levels (fourth, eighth, twelfth, sixteenth, and twentieth) are utilized as the fuzzy inputs and the required control force in multiple stories are utilized as the fuzzy outputs in which the membership functions for the inputs and the output are represented in a linguistic way. It should be noted that based on the obtained results, when the NM is selected for a fuzzy input value, it demonstrates that the maximum acceleration of the story level has a negative and medium value. Besides, when the PS is selected for a fuzzy output value, it shows that the maximum control force of the story level has a positive and small value. In Fig. 12, the precise positions of the control sensors and the utilized control actuators are demonstrated for one of the perimeter frames of the considered building. Besides, the specific details of the active control system including the total number of utilized sensors, actuators and computers are presented in Table 4.

Fig. 12

Precise positions of the control actuators and sensors in building

Table 4 Specific details of the active control system

4.4 Evaluation criteria

In order to evaluate the performance of the structural lateral resisting system and the implemented control system based on the fuzzy logic theory, some Evaluation Criteria (EC) are defined and utilized in which the responses of the Controlled Structure (CS) are compared to the responses of the Uncontrolled Structure (US). The complete description of these EC are presented by Ohtori et al. (2004) while the basic description of these criteria are presented in Table 5.

Table 5 Basic description of the considered evaluation criteria

5 Statement of the optimization problem

Optimization is the process of searching for the best solution of a specific design problem through all of the possible solutions. In order to implement an optimization process for a targeted problem, an optimization problem is supposed to be formulated and the required components of this problem should be determined properly. The general formulation of the optimization problems is presented as follows:

• A function $f:A \to R$ from some set (A) to the real numbers (R).

• An element $x_{0} \in A$ is supposed while the $f\left( {x_{0} } \right) \le f\left( x \right)$ represents a minimization problem and $f\left( {x_{0} } \right) \ge f\left( x \right)$ represents a maximization problem for all $x \in A$.

In this formulation, the set A indicates a subset of the Euclidean space and the domain of this set is named as the optimization search space. Each components of the set A is considered as one of the feasible solutions of the optimization problem. The function f is named as the objective/fitness/cost function and for any components of the set A which minimize or maximize this function, the obtained solution is named as the optimal solution. It should be noted that for optimization of the structural control systems, the optimization problems are commonly formulated based on the minimization process.

Based on the provided information, the optimization problem for the optimal configuration of the fuzzy logic controller is formulated in this section and the presented details for the fuzzy control systems in Sect. 4.3 are utilized accordingly. In this paper, the optimization problem is formulated to perform an optimization process through the important components of the fuzzy systems in order to enhance the overall performance of the control system and improve the seismic behavior of the structure. In this regard, optimization variables are selected by considering the membership functions of the fuzzy inputs and outputs alongside the fuzzy rule base. The FLC in this paper is comprised of two inputs and one output variables. Each of the input variables has eight membership functions while the only output variable has eleven membership functions. The membership functions in the fuzzy system is considered to be triangular shaped while the rule base of the proposed fuzzy system is comprised of 64 fuzzy IF–THEN rules. Regarding the provided details, the decision (design) variables of the fuzzy optimization problem are defined based on the important aspects of fuzzy controllers including the membership functions as representative of fuzzification process, and weigh of the rules as representative of rule base and inference mechanism while for the “Defuzzification” part, the “Centroid” method is utilized in this purpose. In Fig. 13, $a_{1} ,a_{2} , \ldots ,a_{11}$ represents the optimization variables of the fuzzy inputs and $b_{1} ,b_{2} , \ldots ,b_{15}$ represents the optimization variables of the fuzzy output while $c_{1} ,c_{2} , \ldots ,c_{64}$ represents the optimization variables of the fuzzy rule base. It should be noted that the presented variables in Table 6 is related to the weight of each fuzzy rule.

Fig. 13

Optimization variables of membership functions for fuzzy inputs (a) and fuzzy output (b)

Table 6 Optimization variables for the fuzzy rule base

In order to define the objective function as one of the main components of the optimization problem, the seismic responses of the 20-story steel structure are utilized based on the nonlinear behavior of the structure and the conducted structural analysis. In this regard, the optimization problem is formulated as a single-objective problem and the objective function (Obj) is generally formulated as follows:

$$Obj = \frac{{\mathop \sum \nolimits_{i = 1}^{n} P_{i} \frac{{CR_{i} }}{{UR_{i} }}}}{{\mathop \sum \nolimits_{i = 1}^{n} P_{i} }}$$

(8)

where UR_i and CR_i are the controlled and uncontrolled responses of the structure, and P_i is the weighting factor which is required when multiple earthquake records are utilized.

Considering which structural responses should appear in the objective function formulation, is one of the great concerns of the researchers. Based on the fact that the presented evaluation criteria in Sect. 4.4 are formulated as the ratio of the controlled to uncontrolled structural responses, all of these EC can be utilized in this purpose. In this paper, the ductility ratio (EC₄) is utilized in the objective function formulation regarding the fact that this ratio is one of the most important aspects of the recently developed seismic design codes and practices. Meanwhile, one of the main contributions of this paper is the consideration of the nonlinear behavior of the structure and its effects on the overall performance of the control systems and devices so the EC₄ is selected accordingly. The weighting factors are selected to be the PGAs of the utilized earthquake records which have been presented thoroughly in Sect. 3. The more detailed formulation of the objective function is as follows:

$$Obj = \frac{{\begin{array}{*{20}c} {0.854 \times \left( {PC_{4} } \right)_{Tabas } + 0.777 \times \left( {PC_{4} } \right)_{{{\text{Im}} perial Valley}} + 0.654 \times \left( {PC_{4} } \right)_{Loma \Pr ieta} } \\ { + 0.789 \times \left( {PC_{4} } \right)_{Landers} + 0.923 \times \left( {PC_{4} } \right)_{Northridge} + 0.834 \times \left( {PC_{4} } \right)_{Kobe} + 0.760 \times \left( {PC_{4} } \right)_{Chi Chi} } \\ \end{array} }}{{\left( {0.854 + 0.777 + 0.654 + 0.789 + 0.923 + 0.834 + 0.760} \right)}}$$

(9)

where $\left( {PC_{4} } \right)_{Tabas }$ is the ductility factor considering Tabas earthquake, $\left( {PC_{4} } \right)_{Imperial Valley}$ is the ductility factor considering Imperial Valley earthquake, $\left( {PC_{4} } \right)_{Loma Prieta}$ is the ductility factor considering Loma Prieta earthquake, $\left( {PC_{4} } \right)_{Landers}$ is the ductility factor considering Landers earthquake, $\left( {PC_{4} } \right)_{Northridge}$ is the ductility factor considering Northridge earthquake, $\left( {PC_{4} } \right)_{Kobe}$ is the ductility factor considering Kobe earthquake and $\left( {PC_{4} } \right)_{Chi Chi}$ is the ductility factor considering Chi Chi earthquake. The mentioned values alongside the ductility factors for each earthquake are the PGAs of the earthquakes which are derived from Table 1.

In this paper, optimization of the FLC is conducted by means of a parameter tuning process in which the fuzzy inputs, fuzzy outputs and fuzzy rule base are represented through some specific parameters called optimization variables. As the optimization problem is formulated and the optimization process is started, different configurations of these variables are considered. Based on the fuzzy inputs, outputs and rule base which are represented as optimization variables, each configuration of these variables is related to a specific fuzzy system with specific objective function evaluation. In other words, for each configuration of these parameters, a fuzzy system is formulated which provides a specific control strategy for structural motion control. In terms of the selected objective function, the capability of this fuzzy system in structural control is checked through some evaluation criteria while the optimization process is reiterated until the termination criteria is satisfied.

6 Numerical results

In this section, the overall performance of the proposed improved optimization method (IAOA) is evaluated through some simple and complex optimization problems. Regardless of the fact that the main contribution of this paper is to optimize the implemented fuzzy logic controller in building structures, some of the other simple optimization problems are also considered utilizing the IAOA in order to improve the generality of this method and discover more details and capabilities of the proposed new method. These simple optimization problems are consisting of eight mathematical test functions which are represented in order to evaluate the efficiency of the IAOA comparing to the standard AOA. In this regard, the convergence history of the best solutions of these test functions are presented for the IAOA and AOA. The computational complexity and cost of the improved and standard methods are also discussed based on the mentioned mathematical test functions. Besides, the convergence history of the best solutions for the improved and standard algorithms in dealing with the FLC optimization problem is presented based on the formulated objective function. The evaluation criteria in terms of the best solutions of the optimization methods are also calculated and presented accordingly. The convergence history of the optimization variables is also presented for the IAOA in order to perform a valid judgment in performance assessment of this algorithm. Finally, the results of the proposed IAOA in dealing with the FLC optimization problem is also evaluated through some advanced and classical metaheuristic algorithms.

6.1 Mathematical test functions

In this section, the performance of the proposed improved method is evaluated through some mathematical test functions while a comparing study is conducted in order to compare the capability of the proposed IAOA and the standard AOA in dealing with some simple optimization problems. In this purpose, four unimodal and four multimodal test functions are formulated accordingly by considering the fact that unimodal test functions are some kinds of mathematical functions that have single optimum point while the multimodal test functions have multiple optimum points. In this regard, the unimodal functions are capable of evaluating the convergence and the exploitation of the algorithms while the multimodal functions are capable of evaluating the local optima avoidance and the exploration of the algorithms. The mathematical formulations of the utilized unimodal and multimodal functions are described in Table 7.

Table 7 Unimodal and multimodal mathematical test functions

6.1.1 Convergence analysis

For the unimodal and multimodal test functions, the convergence history of the best solutions for the proposed IAOA along with the AOA are presented in Fig. 14. The obtained so far best solutions for the IAOA and the AOA are all presented in Table 8. The minimum values of the best solutions for the improved and standard algorithms are bolded and underlined for a better representation. Based on the obtained results, it is confirmed that the proposed improved method has better performance than the standard AOA in dealing with different kinds of the mathematical test functions.

Fig. 14

Convergence history of the mathematical test functions

Table 8 The best solutions obtained so far the IAOA and AOA

6.1.2 Computational complexity and cost analysis

The computational complexity and cost of the optimization algorithms are two of the most significant aspects of these algorithms which are considered as the effective tools for performance evaluation of the algorithms in dealing with challenging optimization problems. In this paper, the “big O notation” is utilized for the computational complexity analysis of the proposed new improved method and the standard AOA. For the initialization phase, the population size of NP is utilized for both of these algorithms, so the computational complexity for the position initialization of the vibrating particles is O(NP) for both of the algorithms. Besides, the computational complexity for the evaluation of the objective function (F(x)) for both of the algorithms is $O\left( {NP} \right) \times O\left( {F\left( x \right)} \right)$ in this phase. In this regard, the computational complexity of the proposed IAOA and the AOA are equal in the initialization phase. In both of the IAOA and AOA, the main loop of these algorithms begins after the initialization phase and terminates after a specified number of iterations named the Iter_max while the computational complexity of each line in this loop is multiplied by Iter_max. For each of the vibrating particle, the position updates are conducted with complexity of $O\left( {Iter_{max} \times NP} \right)$ while the creation of the new solution candidates are considered based on the dimension (Dim) of these particles. Therefore, the complexity of the position updates of the solution candidates are $O\left( {Iter_{max} \times NP \times Dim} \right)$ accordingly. For the solution candidates with updated positions, the evaluation of the objective function (F(x)) has complexity of $O\left( {Iter_{max} \times NP} \right) \times O\left( {F\left( x \right)} \right)$. Based on the provided information, the computational complexity of the IAOA and the standard AOA for the main loop of these algorithms are equal so the overall computational complexity of these algorithms are equal.

The time and memory cost issues as two of the most important aspects of the metaheuristic algorithms are considered for the computational cost analysis of the IAOA and AOA. Based on the maximum number of iterations, population size, number of function evaluations and the maximum number of internal loops for these algorithms, the computational time and memory cost analysis are conducted accordingly. For both of the improved and the standard algorithms, the maximum number of iterations is taken as 1000, the population size is taken as 30, and the number of function evaluations is taken as 30,000. Dealing with different kinds of mathematical test functions as the unimodal and multimodal functions, the CPU time and memory usage of the IAOA and the AOA are calculated and presented in Table 9. Based on the provided results, the time and memory costs for the IAOA and the AOA have slight differences. Regarding the instrumental deficiencies of the computers such as the CPU saturation issues, these differences are negligible. The minimum values of the CPU time and memory usage for the improved and standard algorithms are bolded and underlined for a better representation.

Table 9 Computational cost analysis results for different methods

Regarding the fact that the big O notation analysis resulted in equal complexity level for both of the IAOA and AOA, there should be mentioned that the proposed improved algorithm has lower computational times and memory usage rates in most of the considered test functions. The main reason for this fact is the capability of the utilized improvement technique for enhancing the performance of the IAOA in spending less effort in generating new solution candidates with better objective function values. In other words, the Levy flight is capable of directing the candidates toward better solution candidates during the search process by reducing the overall computational cost and complexity of the improved algorithm.

6.2 Optimized FLC by IAOA and AOA

In order to formulate the fuzzy optimization process with the IAOA and the standard AOA, 30 solution candidates are selected as the initial population of the optimization process and the maximum demanded number of iterations is selected as 100 iterations which is approachable due to the time cost issues in fuzzy systems. The convergence history for the best solutions of the IAOA and the standard AOA in dealing with the fuzzy optimization problem is presented in Fig. 15. The Obj in this figure is the objective function which is formulated in Eq. 9 for the fuzzy optimization process. Based on the provided information, The IAOA is capable of decreasing the maximum amount of the objective function by up to 0.8857 while this reduction for the standard AOA algorithm is by up to 0.9035.

Fig. 15

The convergence history of Obj for the 20-story building by IAOA and AOA

In order to evaluate the overall performance of the optimization process and the obtained results on the basis of the considered objective function, the evaluation criterial which have been presented in Sect. 6.4 are also calculated regarding the best results of the optimization process. In this purpose, the EC related to the obtained best solutions of the IAOA are all presented in Table 10. Based on the provided information, the maximum inter-story drift ratio (EC₁) is decreased for all of the seven earthquakes in which the maximum reduction for this EC is for Kobe earthquake that is up to 13% and the minimum reduction for this EC is for Chi Chi earthquake that is up to 1%. For the EC₂ which represents the maximum acceleration of the story levels, the responses is decreased for all of the earthquakes in which the maximum and the minimum reduction is for the Tabas (9%) and the Northridge (1%) earthquakes. The response of the EC₃ is decreased for six of the earthquakes in which the maximum reduction for this EC is for Chi Chi earthquake that is up to 21% and the minimum reduction for this EC is for Landers earthquake that is up to 3%. The maximum and the minimum reduction of the EC₄ which is utilized in the objective function is up to 19% (Kobe) and 2% (Landers) respectively. For all of the earthquakes, the energy dissipated ratio (EC₅) is reduced by up to 71%, 55%, 9%, 8%, 6%, 2% and 1% for Imperial Valley, Loma Prieta, Tabas, Kobe, Northridge, Chi Chi and Landers earthquakes respectively. The plastic hinges ratio (EC₆) is reduced by up to 4% (Tabas), 21% (Imperial Valley), 40% (Loma Prieta), 2% (Northridge), and 4% (Chi Chi) while for Kobe and Landers earthquake, this ratio has been unaffected due to the uncontrolled of the structure. 

Table 10 Optimized evaluation criteria for the 20-story building utilizing IAOA

The evaluation criteria for the best solutions of the standard IAOA in dealing with the fuzzy optimization problem are all presented in Table 11. It should be mentioned that for the majority of the calculated EC, the responses of the AOA are higher than the ones related to the IAOA (Table 10). Based on the fact that the improvement technique has a great effect on the reduction of the objective function value, the provided results of the EC demonstrates that the IAOA has the ability of reducing the EC in dealing with the destructive earthquakes for most of the cases. For the EC related to the structural responses and the structural damages, the reduction factors are more than 10% in most of the cases while there are also some slight decrease for the EC in the control system requirements category by mean of the improved method. For the EC₇ which represents the maximum control force of the building, the maximum of the calculated values for the IAOA and the AOA are 0.0071 and 0.0069 respectively. The calculated values of the EC₈ and the EC₉ for the IAOA have much smaller values than the ones related to the AOA which denoted that the improvement technique has the ability of increasing the overall performance of the control system and devices alongside the structural system.

Table 11 Optimized evaluation criteria for the 20-story building utilizing AOA

As one of the important aspects of the nonlinear behavior of building structures, the maximum curvature in both ends of the structural elements are evaluated and the curvature ratio (CR) which calculates the ratio of the maximum curvature in both ends of the structural elements to the yield curvature (ϕ_j/ϕ_yj) for the IAOA- and AOA-based controlled structures alongside the uncontrolled structure is considered (Fig. 16). The maximum difference between the CR values of the controlled structure with the improved method and the uncontrolled structure is for Imperial Valley earthquake which is about 19% while this difference between the controlled structures with the standard AOA and the uncontrolled structure is about 16% which is for the Imperial Valley earthquake. The maximum difference between the CR of the controlled structures with the improved and the standard methods is for Loma Prieta earthquake which is about 6%. Based on the presented details of the CR values, the IAOA-based controlled structure has smaller values of CR which demonstrates the capability of this method in dealing with the severe and destructive earthquakes.

Fig. 16

Comparison of the curvature ratio for different earthquakes

Considering the energy dissipation of the structural members as one of the important aspects of the structural nonlinear behavior, the ratio of the maximum energy dissipation in both ends of the structural elements ($\smallint dE_{j}$) to the yield moment (F_yj) and the yield curvature (ϕ_yj) for the IAOA- and the AOA-based controlled structures alongside the uncontrolled structure is determined for evaluation purposes (Fig. 17). The maximum difference between the EDR values of the controlled structure with the improved method and the uncontrolled structure is for Imperial Valley earthquake (71%) which is up to 57% for the standard method for the same earthquake. The maximum difference between the EDR values of the controlled structures with the improved and the standard methods is for Imperial Valley earthquake which is about 30%.

Fig. 17

Comparison of the energy dissipation ratio for different earthquakes

In the structural engineering, the term “plastic hinges” is utilized to describe the deformation or rotation of a section where plastic bending occurs (ϕ_j > ϕ_yj). In Fig. 18, the maximum number of plastic hinges in both ends of the structural elements (N_d) are presented for the IAOA- and the AOA-based controlled structures alongside the uncontrolled structure. The maximum difference between the calculated numbers of plastic hinges for the IAOA-based controlled structure and the uncontrolled structure is about 40% which is related to the Loma Prieta earthquake. Besides, the maximum difference between the number of plastic hinges for the controlled structures based on the AOA and the IAOA is for Imperial Valley earthquake that is about 12%. Based on the presented details of the EDR and N_d, the proficiency of the improved method is proved.

Fig. 18

Comparison of the number of plastic hinges for different earthquakes

6.3 Variation of design variables

One of the important features of the optimization algorithms is the convergence history of the optimization variables in which the capability of the algorithms in different phases of the optimization process such as the exploration and the exploitation is checked. In this regard, the convergence history for some of the fuzzy optimization variables are depicted in Fig. 19 utilizing the IAOA. It should be mentioned that the big steps in variable modification is changed to some small steps as the optimization process is moving forward which demonstrates the exploration effects in the first iterations and the exploitation effects in the later ones. These aspects indicate that the local and the global search are performed through the optimization process.

Fig. 19

Convergence history for the fuzzy input, output and rule base variables corresponding to the best design obtained by IAOA for the 20-story building

6.4 Comparing to other metaheuristics

In order to evaluate the overall performance of the IAOA in comparison to some different classical and novel optimization algorithms, the Genetic Algorithm (GA) (Holland 1992), Particle Swarm Optimization (PSO) (Eberhart and Kennedy 1995), Ant Colony Optimization (ACO) (Socha and Dorigo 2008) and Imperialist Competitive Algorithm (ICA) (Atashpaz-Gargari and Lucas 2007) are utilized in this purpose. The population size for the selected optimization algorithms is taken as 30 while the maximum number of function evaluations is taken as 3000. The parameter summary for the considered algorithms is provided in Table 12.

Table 12 Parameter summary of the different metaheuristic algorithms

Regarding the best solutions of the utilized algorithms in the comparing study, the convergence history of the objective function (which is formulated in Eq. 9) is presented in Fig. 20. Through the mentioned algorithms, the IAOA can find 0.8846 for objective function which is the best one while the PSO with 0.9004, ICA with 0.9010, GA with 0.9019, AOA with 0.9035 and ACO with 0.9124, have second to sixth places.

Fig. 20

The convergence history of Obj for the 20-story building obtained by different metaheuristics

The maximum values of the evaluation criteria based on the obtained solutions of the selected optimization algorithms are all presented in Table 13. The underlined values represents the smallest EC among the selected algorithms. Based on the presented data, the IAOA has the smallest feasible values among other algorithms while the GA and AOA have some advantages too. In this regard, the performance of the IAOA is better than the other metaheuristics.

Table 13 Maximum EC of seven earthquake records obtained by different metaheuristic

7 Conclusions

Optimization of fuzzy logic controllers implemented in steel building structures was considered in this paper by utilization of metaheuristic algorithms in which the Arithmetic Optimization Algorithm was utilized as the main optimization technique. For performance enhancement of this algorithm, a new methodology is presented for parameter identification of the AOA in which the Levy flight as a well-known stochastic process with step length determined by levy distribution is utilized in this purpose. Based on the obtained results, the proposed IAOA is capable of providing acceptable results in dealing with the mathematical test functions. The IAOA is capable outranking the standard AOA in dealing with three of the unimodal mathematical functions in which the differences between the two algorithms are extremely high in these cases. Besides, the IAOA calculates better results for all of the multimodal functions which demonstrates the ability of the improvement technique in these cases. The computational complexity and cost analysis of the IAOA and AOA proved that the performance of the improved method is much better than the standard method. The maximum difference between these two methods are for Step function (F₄) which is about 20%. The results of the fuzzy optimization problem demonstrate that the objective function for the IAOA converges to 0.8857 which is the best value among different optimization techniques while the PSO with 0.9004, ICA with 0.9010, GA with 0.9019, AOA with 0.9035 and ACO with 0.9124, have second to sixth places. The results of the evaluation criteria for the best solutions of the different metaheuristics revealed that for the EC related to the structural responses (EC₁ ~ EC₃), the IAOA is capable of reducing these criteria by up to 13%, 9% and 21% respectively. The reduction of these criteria for the standard AOA are 11%, 5% and 19% respectively which are larger than the results of the improved method. For EC related to the structural damages (EC₄ ~ EC₆), the maximum reduction of these criteria is by up to 19%, 71% and 40% respectively which are smaller than the related values for the AOA (16%, 57% and 36%). The provided information proves the superiority of the IAOA in response control and damage prevention of the structural system. For the EC related to the requirements of the control system (EC₇ ~ EC₉), the maximum required control force for the structure in the IAOA-based controlled structure is smaller than the standard AOA. The comparison results of the IAOA and the AOA for the CR, EDR and the maximum number of plastic hinges demonstrates that the IAOA-based controlled structure is adequately capable of dealing with the severe NFE records. Based on the results of different metaheuristics in dealing with the fuzzy optimization process, the results of the IAOA are much better and reasonable than the other algorithms. Comparing the responses of the structure with IAOA-based control system with the ones related to different metaheuristics displays that when the selection of ground motions is considered based on the NFE characteristics, an optimization process should be implemented to maintain an efficient control strategy in order to prevent damages in structural members. The main advantage of the proposed IAOA is its capability in optimal tuning of fuzzy controllers in dealing with strong seismic inputs which results in reduced structural responses.