1 Introduction

Given a bounded smooth connected domain \(\Omega \subset M^n\) of a Riemannian manifold, the eigenvalue equation of the Laplacian on \(\Omega\) with Dirichlet boundary condition is

$$\begin{aligned} \Delta \phi = -\lambda \, \phi , \ \ \phi |_{\partial \Omega } =0. \end{aligned}$$
(1.1)

The eigenvalues consist of an infinite sequence going off to infinity. Indeed, the eigenvalues satisfy

$$\begin{aligned} 0< \lambda _1 < \lambda _2 \le \lambda _3 \cdots \rightarrow \infty . \end{aligned}$$

In quantum physics the eigenvalues are possible allowed energy values, and the eigenvectors are the quantum states which correspond to those energy levels.

The fundamental (or mass) gap refers to the difference between the first two eigenvalues

$$\begin{aligned} \Gamma (\Omega ) = \lambda _2 - \lambda _1 >0 \end{aligned}$$
(1.2)

of the Laplacian or more generally for Schrödinger operators. It is a very interesting quantity both in mathematics and physics and has been an active area of research recently.

In 2011, Andrews and Clutterbuck [1] proved the fundamental gap conjecture: for convex domains \(\Omega \subset {\mathbb {R}}^n\) with diameter D,

$$\begin{aligned} \Gamma (\Omega ) \ge 3\pi ^2/D^2. \end{aligned}$$

The result is sharp, with the limiting case being rectangles that collapse to a segment. We refer to their paper for the history and earlier works on this important subject, see also the survey article [5].

Recently, Dai, He, Seto, Wang, and Wei (in various subsets) [4, 8, 10] generalized the estimate to convex domains in \({\mathbb {S}}^n\), showing that the same bound holds: \(\lambda _2 - \lambda _1 \ge 3\pi ^2/D^2\). Very recently, the second author with coauthors [3] showed the surprising result that there is no lower bound on the fundamental gap of convex domains in the hyperbolic space with arbitrary fixed diameter. This is done by estimating the fundamental gap of some suitable convex thin strips.

For specific convex domains, one expects that the lower bound is larger. For triangles in \({\mathbb {R}}^2\) with diameter D, Lu-Rowlett [9] showed that the fundamental gap is \(\ge \frac{64 \pi ^2}{9D^2}\) and equality holds if and only if it is an equilateral triangle. With a few exceptions, eigenvalues may not be written in closed form in terms of known constants. For triangles the eigenvalues of only three types (the equilateral triangle and the two special right triangles) can be computed explicitly.

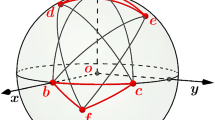
In this paper we study some corresponding questions on the sphere. First we review the eigenvalues and eigenfunctions of the spherical lune \(L_\beta\) with angle \(\beta\) which is the area bounded between two geodesics, see Fig. 1. The statement about the eigenvalues and eigenfunctions are included in Sect. 2. We then use the explicit formula for the first two eigenfunctions on the equilateral triangle to prove the main theorem that a spherical equilateral triangle of diameter \(\frac{\pi }{2}\) is a local minimizer of the fundamental gap.

Theorem 1.1

The equilateral spherical triangle with angle \(\frac{\pi }{2}\) is a strict local minimum for the gap on the space of the spherical triangles with diameter \(\frac{\pi }{2}\). Moreover

$$\begin{aligned} \lambda _2 (T(t)) - \lambda _1(T(t)) \ge \lambda _2 (T(0)) - \lambda _1(T(0)) + \frac{16}{\pi }t + O(t^2), \end{aligned}$$

where T(t) is the triangle with vertices (0, 0), \((\frac{\pi }{2},0)\) and \((\frac{\pi }{2}-bt,\frac{\pi }{2}-at)\) with \(a^2+b^2=1, a \ge 0, \ b\ge 0\) under geodesic polar coordinates centered at the north pole.

This is analogous Lu-Rowlett’s result [9] for the gap of triangles on the plane. On the plane, all equilateral triangles are related by scaling. On the other hand two equilateral triangles on the sphere are not conformal to each other. We are only able to obtain the result for the equilateral triangle with angle \(\frac{\pi }{2}\) as for this one the eigenvalues and eigenfunctions can be computed explicitly.

To get the estimate we compute and estimate the first derivative of the first two eigenvalues at \(t=0\) as in [9]. For this we construct a diffeomorphism \(F_t\) which maps the triangle T(0) to the triangle T(t) to pull back the metric on T(t) to the fixed triangle T(0). Unlike in the plane case, the diffeomorphism \(F_t\) here is nonlinear, which makes the computations quite involved. The proof is given in Sect. 3. To keep the idea clear we put a large part of the computation in the appendix.

2 Eigenvalues of spherical lunes and the equilateral triangle

In this section we review the Dirichlet eigenvalues and eigenfunctions for the spherical lunes and a family of spherical triangles, summarized in Lemma 2.1 and 2.2. These results can be obtained by separation of variables, see [2, 6, 7] for example. The first two eigenvalues and eigenfunctions will be used in the next section for the estimate of the fundamental gap.

Consider a lune of angle \(\beta\) (\(0<\beta <2\pi\)) on a sphere, \(L_\beta\) (see Fig. 1), which is the area between two meridians each connecting the north pole and south pole and forming an angle \(\beta\). Take \((r,\theta )\) to be the geodesic polar coordinates centered at the north pole, then the spherical metric is given by

$$\begin{aligned} g= dr^{2}+\sin ^{2}r d\theta ^{2}, \ 0\le r\le \pi ,\ 0\le \theta \le \beta . \end{aligned}$$
Fig. 1
figure 1

A spherical lune of angle \(\beta\)

Full size image

The Laplacian associated to this metric is given by

$$\begin{aligned} \Delta u(r,\theta )=\partial _{r}^{2}u + \frac{\cos r}{\sin r}\partial _{r}u +\frac{1}{\sin ^{2} r} \partial _{\theta }^{2}u. \end{aligned}$$
(2.1)

Hence the Dirichlet eigenvalue problem \(\Delta u +\lambda u=0\) becomes

$$\begin{aligned} \partial _{r}^{2}u + \frac{\cos r}{\sin r}\partial _{r}u +\frac{1}{\sin ^{2} r} \partial _{\theta }^{2}u +\lambda u=0, \ u(r,0)=u(r,\beta )=0. \end{aligned}$$

Lemma 2.1

[7, Page 112] The eigenvalues of Dirichlet Laplacian of the spherical lunes \(L_\beta\),

without counting multiplicities, are given by the set

$$\begin{aligned} \left\{ \left( \frac{k\pi }{\beta }+j\right) \left( \frac{k\pi }{\beta }+j+1\right) : k\in {\mathbb {N}}^{+}, j\in {\mathbb {N}}\right\} . \end{aligned}$$

Remark 2.1

In particular, the first eigenvalue is \(\frac{\pi }{\beta }(\frac{\pi }{\beta }+1)\), the fundamental gap is given by

$$\begin{aligned} 3 \left( \frac{\pi }{\beta }\right) ^{2}+\frac{\pi }{\beta }, \text { if }\beta >\pi ; \ \ \ 2\frac{\pi }{\beta }+2, \text{ if } \beta \le \pi . \end{aligned}$$

Remark 2.2

One way to prove this result is by doing separation of variables and analyzing the behavior of Legendre associated functions. As pointed out by Luc Hillairet, there is another way which involves less knowledge of special functions, by noticing that for each mode the solution is represented by a triangular infinite matrix in the ‘basis’ \((\sin x)^{k\pi /\beta } (\cos x)^j\), and the spectrum is given by the diagonal elements \(\left( \frac{k\pi }{\beta }+j\right) \left( \frac{k\pi }{\beta }+j+1\right)\). This computation was inspired by [11, 12] in which only the first two eigenvalues of the lunes are exactly computed.

With this one can derive the eigenvalues and eigenfunctions of the isosceles triangle which is bounded by \(\theta =0, \theta =\beta , r=\pi /2\) using the same coordinates as before, i.e. half of the spherical lunes discussed above. Its eigenvalues are a subset of the ones of the lune.

Lemma 2.2

( [7]) For a spherical triangle with angles \(\beta , \pi /2\) and \(\pi /2\), its eigenvalues are given by

$$\begin{aligned} \left\{ \left( \frac{k\pi }{\beta }+2j+1\right) \left( \frac{k\pi }{\beta }+2j+2\right) : k\in {\mathbb {N}}^{+}, j\in {\mathbb {N}}\right\} . \end{aligned}$$

In particular, the first eigenvalue is \((\frac{\pi }{\beta }+1)(\frac{\pi }{\beta }+2)\), and the fundamental gap is given by

$$\begin{aligned} 3 \left( \frac{\pi }{\beta }\right) ^{2}+ 3\frac{\pi }{\beta }, \text { if }\beta >\frac{\pi }{2}; \ \ \ 4\frac{\pi }{\beta }+10, \text{ if } \beta \le \frac{\pi }{2}. \end{aligned}$$
(2.2)

When \(\frac{k\pi }{\beta }\in {\mathbb {N}}\), the eigenfunction corresponding to eigenvalue \(\left( \frac{k\pi }{\beta }+2j+1\right) \left( \frac{k\pi }{\beta }+2j+2\right)\) is given by

$$\begin{aligned} u=P_{\frac{k\pi }{\beta }+2j+1}^{\frac{k\pi }{\beta }}\left( \cos (r)\right) \sin (\tfrac{k\pi }{\beta }\theta ), \end{aligned}$$

where \(P_{\ell }^{\mu }\) is the first kind of general Legendre functions.

For the equilateral triangle, we give the explicit form of the first two eigenvalues and eigenfunctions which will be used in the next section.

Corollary 2.1

For the equilateral triangle with \(\beta =\frac{\pi }{2}\), the first eigenvalue is 12 and the corresponding eigenfunction with normalized \(L^{2}\) norm is given by

$$\begin{aligned} u_{1}={\tilde{C}}_{1}P_{3}^{2}(\cos (r))\sin (2\theta )=\sqrt{\frac{105}{2\pi }} \sin ^{2}(r) \cos (r) \sin (2\theta ). \end{aligned}$$
(2.3)

The second eigenvalue is 30, and there are two corresponding linearly independent normalized eigenfunctions given by

$$\begin{aligned} \begin{aligned}&u_{2}^{(1)}={\tilde{C}}_{2}P_{5}^{2}(\cos (r))\sin (2\theta )=\sqrt{\frac{1155}{8\pi }}(3\cos ^5(r)-4\cos ^3(r)+\cos (r))\sin (2\theta ), \\&u_{2}^{(2)}={\tilde{C}}_{3}P_{5}^{4}(\cos (r))\sin (4\theta )=\sqrt{\frac{3465}{32\pi }}\cos (r)\sin ^4(r)\sin (4\theta ). \end{aligned} \end{aligned}$$
(2.4)

3 Variation of Gap of Spherical triangle with diameter \(\frac{\pi }{2}\)

In this section we consider all spherical triangles with a fixed diameter \(\frac{\pi }{2}\). It is not difficult to show that any such triangle can be moved on the sphere to have vertices (0, 0), \((\frac{\pi }{2},0)\) and (A, B) with \(0<A<\frac{\pi }{2},\ 0<B<\frac{\pi }{2}\).

Denote by T the right triangle with vertices (0, 0), \((\frac{\pi }{2},0)\), \((\frac{\pi }{2},\frac{\pi }{2})\) and T(t) the triangle with vertices (0, 0), \((\frac{\pi }{2},0)\) and \((\frac{\pi }{2}-bt,\frac{\pi }{2}-at)\) with \(a^2+b^2=1, a \ge 0, \ b\ge 0\), see Fig. 2.

Fig. 2
figure 2

The deformed triangle T(t) with three vertices at \((0,0), (\frac{\pi }{2}, 0), (\frac{\pi }{2}-bt, \frac{\pi }{2}-at)\)

Full size image

We first construct a diffeomorphism \(F_t\) which maps the triangle T to T(t), shown in Fig. 2. To construct such a mapping, we compute the function \(l(\alpha ,\theta )\) which gives the geodesic distance from the equator to the edge of the deformed triangle, see Fig. 3.

Fig. 3
figure 3

A spherical triangle with one side of length \(\theta\) and two angles \(\alpha , \pi /2\). The function \(\ell (\alpha , \theta )\) computes the length of the side opposite to \(\alpha\)

Full size image

For the spherical triangle with side lengths \(\theta , l , l_1\), by the spherical cosine law,

$$\begin{aligned} \cos (l_1) = \cos (l)\cos (\theta ), \end{aligned}$$

and spherical law of sines

$$\begin{aligned} \sin (l_1) = \frac{\sin (l)}{\sin (\alpha )} \end{aligned}$$

we get

$$\begin{aligned} \frac{\sin ^2(l)}{\sin ^2(\alpha )} + \cos ^2(\theta )\cos ^2(l) =1. \end{aligned}$$

Re-writing in terms of \(\sin ^2(l)\),

$$\begin{aligned} (1-\sin ^2(\alpha )\cos ^2(\theta ))\sin ^2(l) = \sin ^2(\alpha )\sin ^2(\theta ), \end{aligned}$$

so

$$\begin{aligned} \sin (l) = \pm \frac{\sin (\alpha )\sin (\theta )}{\sqrt{1-\sin ^2(\alpha )\cos ^2(\theta )}}. \end{aligned}$$

Since \(\ell \le \pi /2\),

$$\begin{aligned} l(\alpha ,\theta ) = \arcsin \left( \frac{\sin (\alpha )\sin (\theta )}{\sqrt{1-\sin ^2(\alpha )\cos ^2(\theta )}}\right) . \end{aligned}$$
(3.1)

Now let z(a, b, t) be the distance between the vertex \((\frac{\pi }{2},\frac{\pi }{2})\) to the intersection of the edge of the deformed triangle and the \(x=0\) plane. With the notation given in Fig. 2, we have \(z(a,b,t) = \alpha\).

Since we have

$$\begin{aligned} l\left( z(a,b,t),\tfrac{\pi }{2}-at\right) = bt, \end{aligned}$$

using (3.1) this gives

$$\begin{aligned} \frac{\sin (\alpha )\sin (\theta )}{\sqrt{1-\sin ^2(\alpha )\cos ^2(\theta )}} = \sin (bt). \end{aligned}$$

Solving for \(\sin \alpha\) gives

$$\begin{aligned} \sin (\alpha ) = \frac{\sin (bt)}{\sqrt{\sin ^2(\theta )+\sin ^2(bt)\cos ^2(\theta )}}. \end{aligned}$$

Hence

$$\begin{aligned} z(a,b,t) =\alpha&= \arcsin \left( \frac{\sin (bt)}{\sqrt{\sin ^2(\frac{\pi }{2}-at)+\sin ^2(bt)\cos ^2(\frac{\pi }{2}-at)}} \right) \\&=\arcsin \left( \frac{\sin (bt)}{\sqrt{\cos ^2(at)+\sin ^2(bt)\sin ^2(at)}} \right) . \end{aligned}$$

3.1 Deformation map and the Laplacian

We define the deformation map \(F_t: T \rightarrow T(t)\) by

$$\begin{aligned} F_t(r,\theta ) = \left( r-l\left( z(a,b,t),\theta -\frac{2a}{\pi }\theta t\right) \frac{2r}{\pi },\theta -\frac{2a}{\pi }\theta t\right) . \end{aligned}$$
(3.2)

With the computation above, we have

$$\begin{aligned} F_t(\tfrac{\pi }{2},\tfrac{\pi }{2}) = \left( \frac{\pi }{2}-bt,\frac{\pi }{2}-at\right) . \end{aligned}$$

We also have

$$\begin{aligned} F_{t}(0,0)=(0,0), \ F_{t}(\tfrac{\pi }{2}, 0)=(\tfrac{\pi }{2},0). \end{aligned}$$

We will need the following asymptotics. Since \(z(a,b,0) = 0, \ \frac{\partial }{\partial _{t}}z(a,b,0) = b\), we have

$$\begin{aligned} z(a,b,t) = bt + O(t^2). \end{aligned}$$

By (3.1),

$$\begin{aligned} l(z,(1-A)\theta ) = \arcsin \left( \frac{\sin (z)\sin ((1-A)\theta )}{\sqrt{1-\sin ^2(z)\cos ^2((1-A)\theta )}}\right) \end{aligned}$$

where \(A=\frac{2at}{\pi }\). Then \(l|_{t=0} = 0, \ \frac{\partial l}{\partial t}|_{t=0} =b\sin (\theta ),\) so

$$\begin{aligned} l(z,(1-A)\theta ) = b\sin (\theta ) t + O(t^2). \end{aligned}$$
(3.3)

Define

$$\begin{aligned} L:= \frac{\partial }{\partial \theta }[l(z,(1-A)\theta )]. \end{aligned}$$

Then

$$\begin{aligned} L = b\cos (\theta )t +O(t^2), \ \ \ \partial _\theta L = -b\sin (\theta )t + O(t^2). \end{aligned}$$
(3.4)

To compute the variation of the Laplacian of the triangle T(t), we pullback the round metric

$$\begin{aligned} g_{S} = dr^2 +\sin ^2(r)d\theta \end{aligned}$$

on T(t) with the diffeomorphism \(F_t\) to T. Note that when evaluating the pullback metric at \(p\in T\), we evaluate the round metric at \(F_{t}(p) \in T(t)\) so that

$$\begin{aligned} g_t|_{p} = (F_{t}^*g_S)|_{p} = (dF_t|_p)^Tg_S|_{F_{t}(p)}dF_t|_p, \end{aligned}$$

where

$$\begin{aligned} g_S|_{F_t(p)} = \begin{pmatrix} 1 &{} 0 \\ 0 &{} \sin ^2(r(1-\frac{2l}{\pi })) \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} dF_t = \begin{pmatrix} 1-\frac{2}{\pi }l &{} -\frac{2r}{\pi }L \\ 0 &{} (1-A) \end{pmatrix}. \end{aligned}$$

Then

$$\begin{aligned} g_t = F_{t}^*g_S = \begin{pmatrix} (1-\frac{2}{\pi }l)^2 &{} -\frac{2r}{\pi }(1-\frac{2}{\pi }l)L\\ -\frac{2r}{\pi }(1-\frac{2}{\pi }l)L &{} \frac{4r^2}{\pi ^2}L^2 + (1-A)^2\sin ^2(r(1-\frac{2l}{\pi })) \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} \det (g_t)&= (1-\tfrac{2}{\pi }l)^2(1-A)^2\sin ^2(r(1-\tfrac{2l}{\pi })),\nonumber \\ g_t^{-1}&=\begin{pmatrix} \frac{\frac{4r^2}{\pi ^2}L^2}{(1-\frac{2}{\pi }l)^2(1-A)^2}\csc ^2(r(1-\frac{2l}{\pi })) + \frac{1}{(1-\frac{2}{\pi }l)^2} &{} \frac{\frac{2r}{\pi }L}{(1-\frac{2}{\pi }l)(1-A)^2}\csc ^2(r(1-\frac{2l}{\pi })) \\ \frac{\frac{2r}{\pi }L}{(1-\frac{2}{\pi }l)(1-A)^2}\csc ^2(r(1-\frac{2l}{\pi })) &{} \frac{1}{(1-A)^2}\csc ^2(r(1-\frac{2l}{\pi })) \end{pmatrix}. \end{aligned}$$
(3.5)

From this we can compute the Laplacian \(\Delta _t\) of \(g_t\) using the formula

$$\begin{aligned} \Delta f = \frac{1}{\sqrt{\deg (g)}}\partial _i[g^{ij}\sqrt{g}\partial _j f]. \end{aligned}$$

We compute

$$\begin{aligned} \partial _r(g^{rr}\sqrt{g}\partial _r)&=\partial _r\left[ \left( \frac{4r^2}{\pi ^2}\frac{L^2}{(1-\frac{2}{\pi }l)(1-A)}\csc (r(1-\tfrac{2l}{\pi })) + \frac{(1-A)\sin (r(1-\frac{2l}{\pi }))}{(1-\frac{2}{\pi }l)}\right) \partial _r\right] \\&=\left( \frac{4r^2}{\pi ^2}\frac{L^2}{(1-\frac{2}{\pi }l)(1-A)}\csc (r(1-\tfrac{2l}{\pi })) + \frac{(1-A)\sin (r(1-\frac{2l}{\pi }))}{(1-\frac{2}{\pi }l)}\right) \partial _r^2\\& + \left( (1-A)\cos (r(1-\tfrac{2l}{\pi }))-\frac{4r^2}{\pi ^2}\frac{L^2}{(1-A)}\csc (r(1-\tfrac{2l}{\pi }))\cot (r(1-\tfrac{2l}{\pi }))\right. \\&\left. + \frac{8r}{\pi ^2}\frac{L^2}{(1-\frac{2}{\pi }l)(1-A)}\csc (r(1-\tfrac{2l}{\pi })) \right) \partial _r, \end{aligned}$$

and

$$\begin{aligned} \partial _r(g^{r\theta }\sqrt{\det g}\partial _\theta )&=\partial _r\left[ \frac{\frac{2r}{\pi }L}{(1-A)}\csc \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _\theta \right] \\&=\frac{2r}{\pi }\frac{L}{1-A}\csc \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _r\partial _\theta + \frac{2}{\pi }\frac{L}{(1-A)}\csc \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _\theta \\& - \frac{2r}{\pi }\frac{L(1-\frac{2l}{\pi })}{1-A}\csc \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \cot \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _\theta , \end{aligned}$$

and

$$\begin{aligned} \partial _\theta [g^{\theta r}\sqrt{\deg g}\partial _r]&=\partial _\theta \left[ \frac{\frac{2r}{\pi }L}{(1-A)}\csc \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _r \right] \\&=\frac{2r}{\pi }\frac{L}{(1-A)}\csc \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _\theta \partial _r +\frac{2r}{\pi }\frac{\partial _\theta L}{1-A}\csc \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _r \\& + \frac{4r^2}{\pi ^2}\frac{L^2}{1-A}\csc \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \cot \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _r, \end{aligned}$$

and

$$\begin{aligned} \partial _\theta [g^{\theta \theta }\sqrt{\det g}\partial _\theta ]&=\partial _\theta \left[ \frac{(1-\frac{2}{\pi }l)}{(1-A)}\csc \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _\theta \right] \\&=-\frac{2}{\pi }\frac{L}{(1-A)}\csc \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _\theta + \frac{(1-\frac{2}{\pi }l)}{(1-A)}\csc \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _\theta ^2 \\& + \frac{2rL}{\pi }\frac{(1-\frac{2}{\pi }l)}{(1-A)}\csc \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \cot \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _\theta . \end{aligned}$$

Combining terms and using \(l,L=O(t)\), we have

$$\begin{aligned} \Delta _t&= \frac{1}{(1-\frac{2}{\pi }l)^2}\partial _r^2 + \frac{1}{(1-\frac{2}{\pi }l)}\cot \left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _r+\frac{2r}{\pi }\frac{\partial _\theta L}{(1-\frac{2l}{\pi })(1-A)^2}\csc ^2\left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _r \\& + \frac{4r}{\pi }\frac{L}{(1-\frac{2}{\pi }l)(1-A)^2}\csc ^2\left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _r\partial _\theta + \frac{1}{(1-A)^2}\csc ^2\left( r\left( 1-\tfrac{2l}{\pi }\right) \right) \partial _\theta ^2 + O(t^2) \end{aligned}$$

Using the series expansions

$$\begin{aligned} \cot (r(1-\tfrac{2l}{\pi }))&= \cot (r) + \frac{2rl}{\pi }\csc ^2(r) + O(t^2),\\ \csc ^2(r(1-\tfrac{2l}{\pi }))&= \csc ^2(r)+\frac{4rl}{\pi }\cot (r)\csc ^2(r)+O(t^2), \end{aligned}$$

and

$$\begin{aligned} \frac{1}{(1-\frac{2}{\pi }l)^2} = 1+\frac{4}{\pi }l + O(t^2), \ \ \ \frac{1}{(1-A)^2} = 1+2A + O(t^2), \end{aligned}$$

and plugging in the first-order term for l, L and \(\partial _\theta L\) from (3.3), (3.4), and \(A=\frac{2at}{\pi }\), we obtain the following asymptotic formula.

Lemma 3.1

The first-order asymptotic expansion of the Laplacian of the deformed triangle T(t) is given by

$$\begin{aligned} \Delta _t&=\Delta _S+t L_1 + O(t^2), \end{aligned}$$
(3.6)

where \(\Delta _S\) is the standard sphere Laplacian (2.1) and

$$\begin{aligned} L_1&:= \frac{4}{\pi }b\sin (\theta )\partial _r^2 + \frac{2}{\pi }b\sin (\theta )\cot (r)\partial _r + \frac{4}{\pi }br\cos (\theta )\csc ^2(r)\partial _r\partial _\theta \nonumber \\&+\frac{4}{\pi }br\sin (\theta )\cot (r)\csc ^2(r)\partial _\theta ^2 + \frac{4}{\pi }a\csc ^2(r)\partial _\theta ^2. \end{aligned}$$
(3.7)

3.2 Perturbation of eigenvalues

Let \(u_1\) be the eigenfunction for \(\lambda _1\) on the equilateral triangle T with unit norm (for explicit form see (2.3)). Let \(f_1(t)\) and \(\lambda _1(t)\) be the first eigenfunction and eigenvalue for T(t). By the simplicity of \(\lambda _1(t)\), it is differentiable. Then

$$\begin{aligned} \lambda _1(t)&= \lambda _1+t\dot{\lambda _1}+O(t^2)\\ f_1(t)&= u_1 +t\dot{f_1} + O(t^2). \end{aligned}$$

Denote by \(\langle \ \ \rangle _{T}\) the inner product over the equilateral triangle T (with round metric instead of the pullback metric). For small t we have

$$\begin{aligned} \lambda _1(t)\langle f_1(t),f_1(t)\rangle _{T}&= -\langle \Delta _tf_1(t),f_1(t)\rangle _T\\&= -\langle (\Delta _{S^2}+tL_1)[u_1+t\dot{f_1}],u_1+t\dot{f_1}\rangle _T + O(t^2)\\&= \lambda _1 +2t\lambda _1\langle u_1,\dot{f_1}\rangle _{T} -t\langle L_1u_1,u_1\rangle _T + O(t^2). \end{aligned}$$

On the other hand

$$\begin{aligned} \lambda _1(t)\langle f_1(t),f_1(t)\rangle _T&= (\lambda _1+t\dot{\lambda _1})\langle u_1+t\dot{f_1},u_1+t\dot{f_1}\rangle _T + O(t^2)\\&=\lambda _1+2t\lambda _1\langle u_1,\dot{f_1}\rangle _T+t\dot{\lambda _1} + O(t^2) \end{aligned}$$

so that

$$\begin{aligned} \dot{\lambda _1} = -\langle L_1u_1,u_1\rangle _T. \end{aligned}$$
(3.8)

Under the deformation, the relation between the integral over the deformed triangle T(t) with the round metric and the equilateral triangle T with the pullback metric is

$$\begin{aligned} \int _{T(t)} f \sin (r)drd\theta =\int _{F_t(T)} f \sqrt{\det (g_S)} = \int _T F_t^{*}[f] \sqrt{\det (F^*_t g_S}) = (1-A)(1-\tfrac{2}{\pi }l)\int _T F_t^{*}[f] \sin (r(1-\tfrac{2l}{\pi }))drd\theta \end{aligned}$$

where the second equality comes from (3.5). Therefore, using (3.3) and the definition of A, we have

$$\begin{aligned} \int _{T(t)}f_1f_2\sin (r)drd\theta&= (1-A)(1-\tfrac{2}{\pi }l)\int _T F_{t}^*[f_1f_2] \sin (r(1-\tfrac{2l}{\pi }))drd\theta \\&=(1-A)(1-\tfrac{2}{\pi }l)\int _T F_{t}^*[f_1f_2] (\sin (r)-\tfrac{2rl}{\pi }\cos (r))drd\theta +O(t^2)\\&= \int _T F_{t}^*[f_1f_2]\sin (r)drd\theta -A\int _TF_{t}^*[f_1f_2]\sin (r)drd\theta \\&-\frac{2}{\pi } l \left( \int _TF_{t}^*[f_1f_2]\sin (r)drd\theta +\int _TF_{t}^*[f_1f_2]r\cos (r)drd\theta \right) +O(t^2)\\&:= \int _T F_{t}^*[f_1f_2]\sin (r)drd\theta + tZ+O(t^2). \end{aligned}$$

Here in the second line, we used the series expansion \(\sin (t+a) = \sin (a)+t\cos (a)+O(t^2)\). Recall also that \(l=O(t)\) and \(A=O(t)\).

If \(f_1\) and \(f_2\) are eigenfunctions for the first two Dirichlet eigenvalues on T(t) then by orthogonality we have that

$$\begin{aligned} \int _T F_{t}^*[f_1f_2]\sin (r)drd\theta =-tZ+O(t^2). \end{aligned}$$
(3.9)

Lemma 3.2

Let \(u_{1}, u_{2}\) be eigenfunctions for T with unit \(L^{2}\) norm corresponding to the first two eigenvalues \(\lambda _{1}, \lambda _{2}\). Suppose that for any \(a,b\ge 0\), with respect to the linear order operator \(L_1\) defined in (3.7),

$$\begin{aligned} \int _T u_2L_1 u_2- u_1L_1u_1 < 0. \end{aligned}$$

Then the equilateral triangle T is a strict local minimum for the gap function among all spherical triangles with diameter \(\frac{\pi }{2}\).

Proof

Let \(f_1\) and \(f_2\) be eigenfunctions for the first two Dirichlet eigenvalues of the deformed triangle T(t). Note the integration is over T. Since \(\Delta _tf_2 = -\lambda (t)f_2\) is pointwise, it still satisfies the eigenvalue equation after pullback and up to first order, \(F_{t}^*[f_2] = f_2+O(t)\). By abuse of notation, \(f_i = F_{t}^*[f_i]\). Then define

$$\begin{aligned} \varepsilon (t) := \frac{-\int _{T }u_1 f_2}{\int _{T} u_1f_1}. \end{aligned}$$

Since \(T(0) =T\) and \(F_0 = {{\,\mathrm{id}\,}}\), the expansion \(f_1=u_1+t\frac{d}{dt}|_{t=0}f_1+ O(t^2)\) implies \({\int _{T} u_1f_1}=1+O(t)\). Then by (3.9),

$$\begin{aligned} \varepsilon (t) = \frac{\int _{T}f_2(f_1-u_1)}{\int _{T} u_1f_1} +tZ +O(t^2). \end{aligned}$$

Using the same expansion \(f_1=u_1+t\frac{d}{dt}|_{t=0}f_1+ O(t^2)\) it implies that \(\varepsilon (t) = O(t)\), for small t. By definition of \(\varepsilon (t)\), we have

$$\begin{aligned} \int _{T} (f_2+\varepsilon f_1)u_1 = 0. \end{aligned}$$

So we can use \(f_2 +\varepsilon f_1\) as a test function for \(\lambda _2\),

$$\begin{aligned} \lambda _2 \le \frac{-\int _T (f_2+\varepsilon f_1)\Delta _{S^2}(f_2+\varepsilon f_1)}{\int _T (f_2+\varepsilon f_1)^2}. \end{aligned}$$

Using the asymptotic \(\Delta _{S^2} = \Delta _t -tL_1+O(t^2)\),

$$\begin{aligned} \frac{-\int _T (f_2+\varepsilon f_1)\Delta _{S^2}(f_2+\varepsilon f_1)}{\int _T (f_2+\varepsilon f_1)^2}&= \frac{-\int _T (f_2+\varepsilon f_1)(\Delta _t-tL_1)(f_2+\varepsilon f_1)+O(t^2)}{\int _T (f_2+\varepsilon f_1)^2}\\&=\frac{\lambda _2(t)\int _Tf_2^2 + t\int _T f_2L_1f_2 +O(t^2)}{\int _T (f_2+\varepsilon f_1)^2}. \end{aligned}$$

Since \(\int _T f_1f_2 = O(t)\) and \(\int _T f_2^2 = 1+O(t)\), we have

$$\begin{aligned} \lambda _2 \le \lambda _2(t) +t\int _Tf_2L_1f_2+O(t^2). \end{aligned}$$

Therefore, combining with (3.8) gives

$$\begin{aligned} \lambda _2-\lambda _1 \le \lambda _2(t)-\lambda _1(t) + t\left( \int _T f_2L_1f_2 - \int _T u_1L_1 u_1 \right) +O(t^2). \end{aligned}$$

Using the asymptotics of \(f_2\) once more, we have

$$\begin{aligned} \lambda _2-\lambda _1 \le \lambda _2(t)-\lambda _1(t) + t\left( \int _T u_2L_1 u_2 - \int _Tu_1L_1u_1 \right) + O(t^2). \end{aligned}$$

Hence, with the assumption

$$\begin{aligned} \int _T u_2L_1 u_2- u_1L_1u_1 < 0, \end{aligned}$$

for small t we have \(\lambda _2-\lambda _1 < \lambda _2(t)-\lambda _1(t)\). \(\square\)

3.3 Computation for \(\int _T u_1 L_1 u_1\)

Using the explicit expressions for \(u_1\) (2.3) and \(L_1\) (3.7), we have

$$\begin{aligned} \int _T u_1 L_1 u_1\sqrt{\det g_{S}} =&\frac{4}{\pi }b\int _T u_1 \sin (\theta )\partial _r^2[u_1]\sin (r)drd\theta (\text {I})\\&+\frac{2}{\pi }b\int _T u_1\sin (\theta )\cot (r)\partial _r[u_1]\sin (r)drd\theta (\text {II})\\&+\frac{4}{\pi }b \int _T u_1 r\cos (\theta )\csc ^2(r) \partial _r\partial _\theta [u_1]\sin (r)drd\theta (\text {III}) \\&+\frac{4}{\pi }b\int _T u_1 r\sin (\theta )\cot (r)\csc ^2(r)\partial _\theta ^2[u_1]\sin (r)drd\theta \quad (\text {IV})\\&+\frac{4}{\pi }a\int _T u_1 \csc ^2(r)\partial _\theta ^2[u_1]\sin (r)drd\theta . (\text {V}) \end{aligned}$$

Denote \(C_1 = \frac{105}{2\pi }\). Now calculating each term, we have for term I

$$\begin{aligned} \frac{4}{\pi }bC_1\int _0^{\frac{\pi }{2}}\sin ^2(2\theta )\sin (\theta )d\theta \int _0^{\frac{\pi }{2}}\sin ^3(r)\cos (r)\partial _r^2[\sin ^2(r)\cos (r)]dr&= -bC_1\frac{1408}{1575\pi }. \end{aligned}$$

For term II

$$\begin{aligned} \frac{2}{\pi }bC_1\int _0^{\frac{\pi }{2}}\sin ^2(2\theta )\sin (\theta )d\theta \int _0^{\frac{\pi }{2}}\sin ^2(r)\cos ^2(r)\partial _r[\sin ^2(r)\cos (r)]dr= bC_1 \frac{64}{1575\pi }. \end{aligned}$$

For term III

$$\begin{aligned} \frac{4}{\pi }bC_1\int _0^{\frac{\pi }{2}}\sin (2\theta )\cos (\theta )\partial _\theta [\sin (2\theta )]d\theta \int _0^{\frac{\pi }{2}}r\sin (r)\cos (r)\partial _r[\sin ^2(r)\cos (r)]dr =bC_1\left( \frac{16}{450} - \frac{448}{3375\pi }\right) . \end{aligned}$$

For term IV

$$\begin{aligned} \frac{4b}{\pi }C_1 \int _0^{\frac{\pi }{2}}\sin (2\theta )\sin (\theta )\partial _\theta ^2[\sin (2\theta )]d\theta \int _0^{\frac{\pi }{2}}r\cos ^3(r)\sin ^2(r)dr&= bC_1\left( \frac{3328}{3375\pi }-\frac{128}{225}\right) . \end{aligned}$$

For term V

$$\begin{aligned} \frac{4}{\pi }aC_1\int _0^{\frac{\pi }{2}}\sin (2\theta )\partial _\theta ^2[\sin (2\theta )]d\theta \int _0^{\frac{\pi }{2}}\sin ^3(r)\cos ^2(r)dr = -\frac{8a}{15}C_1. \end{aligned}$$

Combining, we obtain

$$\begin{aligned} \int _Tu_1L_1u_1dA_{S^2}&=bC_1\left( -\frac{1408}{1575\pi }+\frac{64}{1575\pi }-\frac{448}{3375\pi }+\frac{3328}{3375\pi } + \frac{16}{450}-\frac{128}{225}\right) - \frac{8}{15}aC_1 \nonumber \\&=-b\frac{28}{\pi }-a\frac{28}{\pi }. \end{aligned}$$
(3.10)

3.4 Computation for \(\int _T u_2 L_1 u_2\)

By linearity, the second eigenfunction is of the form

$$\begin{aligned} u_2:= pu^{(1)}_2+qu^{(2)}_2 \end{aligned}$$

with \(p^2+q^2=1\) and \(u_{2}^{(1)}, u_{2}^{(2)}\) given in (2.4). Then

$$\begin{aligned} \int _T u_2 L_1 u_2&= p^2\int _T u^{(1)}_2(L_1u^{(1)}_2) + pq\int _T u^{(2)}_2(L_1 u^{(1)}_2) + pq\int _Tu^{(1)}_2(L_1u^{(2)}_2)+q^2\int _T u^{(2)}_2(L_1u^{(2)}_2) \nonumber \\&=-p^2\left( b\frac{77}{\pi }+a\frac{44}{\pi }\right) + pqb\frac{22\sqrt{3}}{\pi } -q^2\left( b\frac{55}{\pi }+a\frac{88}{\pi }\right) . \end{aligned}$$
(3.11)

The details of the computation are shown in the appendix.

Define

$$\begin{aligned} I&:= -\int _T u_2 (L_1 u_2) + \int _T u_1(L_1u_1) \\&=b\left( p^2\frac{77}{\pi }-pq\frac{22\sqrt{3}}{\pi }+q^2\frac{55}{\pi }-\frac{28}{\pi }\right) + a\left( p^2\frac{44}{\pi }+q^2\frac{88}{\pi }-\frac{28}{\pi }\right) . \end{aligned}$$

Using \(p=\cos (z)\), \(q=\sin (z)\) and \(a = \sqrt{1-b^2}\),

$$\begin{aligned} I&= b\left( \frac{27}{\pi }+\cos ^2(z)\frac{22}{\pi }-\cos (z)\sin (z)\frac{22\sqrt{3}}{\pi }\right) +\sqrt{1-b^2}\left( \frac{16}{\pi }+\sin ^2(z)\frac{44}{\pi }\right) . \end{aligned}$$

To find the minimum over \(0\le z \le 2\pi\) and \(0\le b \le 1\), notice that the function \(f(x) = Ax+B\sqrt{1-x^2}\) has \(f''(x) = -\frac{B}{(1-x^2)^{\frac{3}{2}}} <0\) for \(B>0\). Hence for each fixed z, any interior critical point of I will be a maximum so the minimum must occur at the boundary (\(b=0\) or \(b=1\)). The minimum of \(\frac{27}{\pi }+\cos ^2(z)\frac{22}{\pi }-\cos (z)\sin (z)\frac{22\sqrt{3}}{\pi }\) is \(\frac{16}{\pi }\), which is also the minimum of \(\frac{16}{\pi }+\sin ^2(z)\frac{44}{\pi }\), hence the minimum value is \(I=\frac{16}{\pi }\).

Combine with Lemma 3.2 this finishes the proof of Theorem 1.1.

Remark 3.1

Note that when \(a=1, \ b=0\) or \(a=0, b=1\), the variation is along one side of the equilateral spherical triangle. In both cases the minimum is \(\frac{16}{\pi }\). In this case the gap is explicitly given in (2.2). Namely \(\Gamma (T(t)) = \frac{4\pi }{(\frac{\pi }{2}-t)}+10\). Hence \(\frac{d}{dt}\Gamma (T(t))|_{t=0} = \frac{16}{\pi }\). So the above computation matches up with this direct computation.