The classification of flat Riemannian metrics on the plane

Abstract

We classify all smooth flat Riemannian metrics on the two-dimensional plane. In the complete case, it is well known that these metrics are isometric to the Euclidean metric. In the incomplete case, there is an abundance of naturally occurring, non-isometric metrics that are relevant and useful. Remarkably, the study and classification of all flat Riemannian metrics on the plane—as a subject—is new to the literature. Much of our research focuses on conformal metrics of the form $e^{2\varphi }g_0$, where $\varphi : {\mathbb {R}}^2\rightarrow {\mathbb {R}}$ is a harmonic function and $g_0$ is the standard Euclidean metric on ${\mathbb {R}}^2$. We find that all such metrics, which we call “harmonic,” arise from Riemann surfaces.

1 Motivation for incomplete Riemannian metrics

There is a broad consensus among mathematicians that incomplete Riemannian metrics are uninteresting. Reasons include the dominance of completeness as a condition for most of the important results in Riemannian geometry and the ease with which incomplete metrics can be contrived—for example, remove a point from a complete Riemannian manifold. In this paper, we offer a large family of naturally occurring incomplete flat Riemannian metrics on ${\mathbb {R}}^2$ whose underlying geometries are non-trivial. It is noteworthy that the classification of all incomplete flat metrics on ${\mathbb {R}}^2$ fills a gap in the literature. (In Sect. 6, we provide some comments on incomplete, constant curvature $+1$ and $-1$, Riemannian metrics on ${\mathbb {R}}^2$.)

To begin, let $g_0$ be the Euclidean metric on ${\mathbb {R}}^2$ and consider a conformally equivalent metric $g = e^{2\varphi }g_0$, where $e^{2\varphi }$ is the conformal factor and $\varphi : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}$ is harmonic. The Gaussian curvature of g is easily calculated to be $K = -e^{-2\varphi }\Delta _0\varphi$, where $\Delta _0$ is the standard Laplacian for $g_0$. It follows that g is flat precisely when $\varphi$ is harmonic. When $\varphi$ is a non-constant harmonic function, we call $e^{2\varphi }g_0$ a harmonic metric and the resulting flat plane a harmonic plane, written $({\mathbb {R}}^2, e^{2\varphi }g_0 )$.

Here are important facts about harmonic metrics and harmonic planes:

• Every harmonic metric on the plane is incomplete (see Proposition 2.1), and

• No harmonic plane is isometric to a subset of the Euclidean plane (see Proposition 2.2). More generally, no harmonic plane is isometric to a proper subset of another harmonic plane (see Proposition 2.3).

One of the key reasons motivating the study of harmonic metrics is the direct correspondence between harmonic functions and harmonic metrics. Preliminary investigations here reveal unexpected relationships between the analytic behavior of harmonic functions and the geometry of the associated harmonic metrics (see Sect. 5.4 and the examples in Sect. 7). Another reason is that every harmonic plane is a Riemann surface. Of course, this is obvious because the conformal structure of a harmonic plane is the same as the Euclidean plane $({\mathbb {R}}^2, g_0)$, but a harmonic metric provides a distinctive geometry that is lost by Uniformization. For example, in Sect. 5.1 we show that the Riemann surface for $\log {z}$ is isometric to $({\mathbb {R}}^2,e^{2x}g_0)$. This simplest harmonic metric was the initial motivation to explore the geometry of harmonic planes and disks and, more generally, Riemannian flat planes and disks.

The main purpose of this paper is to provide a classification of smooth incomplete flat Riemannian metrics on ${\mathbb {R}}^2$ and the open unit disk D. This classification is in terms of harmonic metrics, but it should be made clear that not all such metrics are harmonic metrics. Sections 5 and 7 provide a diverse collection of examples and applications of harmonic planes and disks.

2 Preliminaries

Conventions We assume that all metrics g are Riemannian and $C^\infty$ smooth unless otherwise noted. Additionally, all surfaces are positively oriented, all mappings are orientation preserving, and a region or domain in the plane is a non-empty, open, connected subset. To ease the exposition, we will use the function F to represent a diffeomorphism and f to represent a biholomorphism.

It is well known that a complete flat plane $({\mathbb {R}}^2, g)$ is isometric to the Euclidean plane $({\mathbb {R}}^2, g_0)$. Specifically, there is a diffeomorphism $F: ({\mathbb {R}}^2,g) \rightarrow ({\mathbb {R}}^2,g_0)$ for which the pull-back $F^*(g_0)$ is g and F becomes an isometry. This follows from the proof of the theorem of Cartan–Hadamard, where the exponential map $\exp : T_p({\mathbb {R}}^2,g) \rightarrow ({\mathbb {R}}^2, g)$ is a diffeomorphism at any point $p\in {\mathbb {R}}^2.$ By another theorem of Cartan on mappings that preserve curvature (see [7], Theorem 2.1, Chapter 8), it follows that this exponential map is an isometry. Using a linear isometry $L: T_p({\mathbb {R}}^2,g) \rightarrow ({\mathbb {R}}^2, g_0)$, we set $F= L \circ \exp ^{-1}$ to conclude that, up to isometry, the $({\mathbb {R}}^2,g_0)$ is the only complete flat plane. If F is also holomorphic, then it must be a complex affine transformation and $g=cg_0$, for some constant c. In the incomplete case, we have the following result (cf. [1], Proposition 2.2).

Proposition 2.1

Every harmonic plane is incomplete.

Proof

Consider the harmonic plane $({\mathbb {R}}^2, g_\varphi )$, with $g_\varphi = e^{2\varphi }g_0$ and $\varphi$ is a non-constant harmonic function. Assume further, for a contradiction, that $({\mathbb {R}}^2, g_\varphi )$ is complete. From the above discussion, there is a diffeomorphic isometry $F: ({\mathbb {R}}^2, g_\varphi )\rightarrow ({\mathbb {R}}^2, g_0)$. Since Euclidean angles are preserved, F is a biholomorphism, hence a complex affine map, and the pull-back metric satisfies $e^{2\varphi }= c$, for some constant c. This is a contradiction. $\square$

We define a subset metric to be a flat metric g on ${\mathbb {R}}^2$ that can be “realized” as a proper subset of $({\mathbb {R}}^2,g_0)$ by an isometric embedding. Specifically, there exists a diffeomorphic isometry $F: ({\mathbb {R}}^2,g) \rightarrow \Omega \subsetneq ({\mathbb {R}}^2,g_o)$.

Proposition 2.2

No harmonic metric on ${\mathbb {R}}^2$ is a subset metric of the Euclidean plane.

Proof

Assume the contrary, so let $F: ({\mathbb {R}}^2,g_\psi ) \rightarrow (S\subsetneq {\mathbb {R}}^2, g_0)$ be a (diffeomorphic) isometric embedding onto S; hence F is entire. Picard’s little theorem states that S is either ${\mathbb {R}}^2$ or ${\mathbb {R}}^2-\{point\}$. It can’t be the former since S is a proper subset. And it can’t be the latter since S is simply connected. $\square$

Subset metrics can be constructed on ${\mathbb {R}}^2$ in two different ways. If F is a diffeomorphism from ${\mathbb {R}}^2$ to a proper open subset of ${\mathbb {R}}^2$, then $F^*(g_0)$ gives ${\mathbb {R}}^2$ a flat metric for which F is an isometry. Alternatively, subset metrics on ${\mathbb {R}}^2$ can be constructed as product metrics on ${\mathbb {R}}\times {\mathbb {R}}$; for example, consider the metric $e^{-2x^2} \mathrm{d}x^2 + e^{-2y^2} \mathrm{d}y^2$. This product metric can be realized as a proper subset of $({\mathbb {R}}^2,g_0)$ by an isometric embedding to an open square with sides of length $\sqrt{\pi }$. However, ${\mathbb {R}}^2$ admits interesting flat metrics which are both natural and incomplete, but which are decidedly not subset or product metrics; the harmonic metrics described in Sect. 1 are examples.

An immediate corollary to Proposition 2.2 is the following.

Proposition 2.3

No harmonic metric on ${\mathbb {R}}^2$ is a subset metric of another harmonic plane.

Proof

The proof of Proposition 2.2 remains valid replacing $g_0$ with any harmonic metric. $\square$

3 The classification theorem

Theorem 3.1

For any incomplete Riemannian flat plane $({\mathbb {R}}^2, \widehat{g} )$, the metric has the form $\widehat{g}=F^*(g)$ for exactly one of the following cases:

Case 1. The map $F: {\mathbb {R}}^2 \rightarrow ({\mathbb {R}}^2, g)$ is a diffeomorphism and g is a harmonic metric, or

Case 2. The map $F: {\mathbb {R}}^2 \rightarrow (D, g)$ is a diffeomorphism and g is a harmonic metric.

In particular, the isometry class of $({\mathbb {R}}^2, \widehat{g})$ contains a harmonic plane or a harmonic disk—but not both. Furthermore, for a harmonic metric g on ${\mathbb {R}}^2$ or D, the isometry class [g] in the space of harmonic metrics on ${\mathbb {R}}^2$ or D is given by:

Case 1 (continued). The isometry class $[g]= \{f^*(g)~ |~f: {\mathbb {R}}^2 \rightarrow ({\mathbb {R}}^2,g)$ is a complex affine mapping $z\rightarrow az+b ,~for~ a,b \in {\mathbb {C}}, ~a\ne 0\}$, or

Case 2 (continued). The isometry class $[g] = \{ f^*(g)~ |~f: D \rightarrow (D,g)$ is a Möbius automorphism $z\rightarrow e^{i\theta } \frac{z-a}{\bar{a}z-1},~for~ |a|<1 ~and~ 0\le \theta <2\pi \}.$ (See Sect. 4.4 for the role of the Euclidean metric in Case 2.)

Remark 3.2

The classification statement for incomplete Riemannian flat metrics on D carries over mutatis mutandis from Theorem 3.1—with the obvious changes to the first sentence of the theorem, namely, replacing “flat plane $({\mathbb {R}}^2, \widehat{g})$” with “flat disk $(D, \widehat{g})$” and replacing the domain ${\mathbb {R}}^2$ for the map F in Cases 1 and 2 with D, and in the second sentence, replacing $({\mathbb {R}}^2, \widehat{g})$ with $(D, \widehat{g})$.

Proof of Theorem 3.1:

It is known (see [13], Theorem 3.11.1) that an oriented surface with a Riemannian metric admits a conformal structure transforming the surface into Riemann surface and the metric into a conformal metric in the holomorphic coordinate system. More specifically, the atlas of isothermal coordinates for a given Riemannian metric has holomorphic transition functions.

For our focus on flat planes, it follows that (${\mathbb {R}}^2, \widehat{g})$, admits a holomorphic atlas, hence becomes a Riemann surface $\mathscr {R}$ satisfying the following properties.

• The metric $\widehat{g}$ is represented in local holomorphic coordinates (u, v) by $g_1=\tau (u,v)(\mathrm{d}u^2+\mathrm{d}v^2)$.

• There is a diffeomorphic isometry $H_1: ({\mathbb {R}}^2,\widehat{g})\rightarrow (\mathscr {R} ,g_1)$.

From Uniformization, there is a biholomorphism $H_2$ from $\mathscr {R}$ to ${\mathbb {C}}$ or D which can be used to push $g_1$ forward to obtain a conformal metric $g=e^{2\varphi }g_0.$ Hence,

$$\begin{aligned} F=H_2\circ H_1:({\mathbb {R}}^2, \widehat{g})\rightarrow ({\mathbb {C}}~ or~ D,g) \end{aligned}$$

is a diffeomorphic isometry and $\widehat{g}=F^*(g)$. Since $\widehat{g}$ is an incomplete flat metric, it follows that g is a harmonic metric.

We have shown that the isometry class of a flat plane $({\mathbb {R}}^2,\widehat{g})$ includes a harmonic plane or harmonic disk. Both cannot occur, for if $F_1$ and $F_2$ are isometries from $({\mathbb {R}}^2,\widehat{g})$ to $({\mathbb {R}}^2, g_{\varphi _1})$ and $(D,g_{\varphi _2})$, respectively, the composition

$$\begin{aligned} F_2 \circ F_1^{-1}: ({\mathbb {R}}^2, g_{\varphi _1}) \rightarrow (D, g_{\varphi _2}) \end{aligned}$$

is an isometry, hence a conformal mapping with respect to Euclidean angles. By complexifying ${\mathbb {R}}^2$ and D, the composition becomes a bounded non-constant holomorphic mapping—a contradiction.

To complete the classification, we characterize the isometry classes of harmonic planes and harmonic disks as follows. Let $f: ({\mathbb {R}}^2, g_\varphi ) \rightarrow ({\mathbb {R}}^2, g_\psi )$ be a diffeomorphic isometry between harmonic planes. Then $g_\varphi = f^*(g_\psi )$ and, by complexifying, f becomes a one-to-one entire function, hence a complex affine transformation. Similarly for harmonic disks, if $f: (D,g_\varphi )\rightarrow (D, g_\psi )$ is a diffeomorphic isometry, then f becomes a Möbius transformation. This completes the proof of the classification theorem.$\square$

Finally, Remark 3.2 describes the classification result for incomplete flat disks by highlighting the notational changes needed to Theorem 3.1. The classification proof for D follows the same analysis as the proof of Theorem 3.1, with similar notational changes.

4 Remarks on the classification theorem

4.1 General remarks

The classification theorem asserts that every (smooth) flat plane is isometrically diffeomorphic to a harmonic plane or disk. Since isometries preserve angles, this might suggest that these diffeomorphisms are biholomorphisms, which is false. To see this, consider the flat plane with the subset product metric given by $({\mathbb {R}}^2, e^{-2x}\mathrm{d}x^2 + e^{-2y}\mathrm{d}y^2)$, as discussed in Sect. 2. This flat plane is isometric to a square in the Euclidean plane and the “classification” isometric diffeomorphism maps this flat plane first to the square, and then to D by a Riemann map. Per Liouville, this diffeomorphism cannot be holomorphic. More specifically, none of the diffeomorphisms in Case 2 are holomorphic.

The conformal property of holomorphic functions relies on Euclidean angles, as evident from the reliance of the Cauchy–Riemann equations on $g_0$. If a Riemannian metric on the plane is not conformally equivalent to $g_0$, then by its very definition, it cannot have the same conformal structure as $g_0$. For instance, the subset product metric in Sect. 2 is not conformal to $g_0$, though locally it is isometric to $({\mathbb {R}}^2,g_0)$. In fact, the proof of the Cartan–Hadamard theorem discussed in Sect. 2 shows that any flat plane is locally isometric to $({\mathbb {R}}^2, g_0)$. In this respect, our classification theorem showcases the global geometry of flat planes, in contrast to the “companion” local result which simply asserts that all flat planes are locally isometric to $({\mathbb {R}}^2, g_0)$. See [5].

4.2 Remarks on Case 1

In Case 1, F is holomorphic if and only if  $\widehat{g}$ is a harmonic metric. In particular, it follows from Liouville’s Theorem that there is no isometry from a harmonic plane to a harmonic disk.

In contrast to Propositions 2.2, every harmonic plane can be isometrically immersed into $({\mathbb {R}}^2,g_0)$. See Sect. 5. For example, consider the “exponential mapping” $F(x,y)=(e^x\cos {y}, e^x\sin {y})$. A straightforward calculation shows that $F^*(g_0)=e^{2x}g_0$, so this mapping is an isometric immersion $F: ({\mathbb {R}}^2, e^{2x}g_0)\rightarrow ({\mathbb {R}}^2,g_0)$ with image ${\mathbb {R}}^2-\{origin\}$.

4.3 Remarks on Case 2

In Case 2, we find that the geometry of a harmonic disk is more nuanced than the geometry of a harmonic plane. The Riemann Mapping Theorem provides a wealth of harmonic disks of the form $(D, f^*(g_0))$, where $f: D \rightarrow \Omega \subsetneq {\mathbb {R}}^2$ is a Riemann map to a simply connected region. Clearly, these are all subset metrics on D and, likewise, any harmonic subset metric on D) is the pull-back of a Riemann map. In Sect. 5.1, we provide an easy example of a harmonic disk that cannot be isometrically embedded in $({\mathbb {R}}^2,g_0)$; however, it does isometrically embed in the harmonic plane $( {\mathbb {R}}^2, e^{2x}g_0 )$.

If a harmonic disk is not a subset metric of any harmonic plane (or the Euclidean plane), nor a subset metric of any harmonic disk (or the Euclidean disk), then we call it exotic. The existence of exotic harmonic disks has not yet been established, but our preliminary research on harmonic metrics derived from the real and imaginary parts of lacunary functions suggests the likelihood of their existence. See Sect. 5.4.

4.4 Additional remarks

The Euclidean disk $(D, g_0)$ requires special attention since $g_0$ is not a harmonic metric, and hence its use is not allowed in Case 2. However, the isometry class of $(D,g_0)$ contains a harmonic metric, as follows. If $\eta : D \rightarrow (D,g_0)$ is a Möbius automorphism that is not a pure rotation, then $\eta ^*(g_0) = e^{2\varphi }g_0 = g_1$ is a harmonic metric on D. Hence, for the isometry classes, we have $[g_0] = [g_1]$ and so $g_1$ and $[g_1]$ are allowed in Case 2 and its continuation.

5 Examples and applications

This section presents examples and applications of the two primary constructions for harmonic metrics. The two constructions are:

• The pull-back harmonic metric $f^*(g_0)$ from a holomorphic function $f:\Omega \rightarrow {\mathbb {C}}=({\mathbb {R}}^2,g_0)$ with non-vanishing derivative, and

• The harmonic metric formed directly from a harmonic function.

On simply connected domains $\Omega \subseteq {\mathbb {R}}^2$, these two constructions are equivalent as follows. Any harmonic metric of the form $e^{2\varphi }g_0$ is the pull-back metric $f^*(g_0)$, where $f:\Omega \rightarrow {\mathbb {C}}=({\mathbb {R}}^2,g_0)$ is defined by

$$\begin{aligned} f(z) = \int _{z_0}^z e^h \mathrm{d}w, \end{aligned}$$

(1)

for any $z_0\in \Omega$ and a holomorphic $h:\Omega \rightarrow {\mathbb {C}}$ with $\text {Re}(h)=\varphi$. A straightforward calculation shows that $f^*(g_0) = |f^\prime (z)|^2g_0 = e^{2\varphi }g_0.$¹ When $\Omega$ is ${\mathbb {R}}^2$ or D, it follows that every harmonic plane and harmonic disk can be isometrically immersed in $({\mathbb {R}}^2,g_0)$.

In Sect. 5.1, we consider the special case $h(z) = z$, and show the equivalence of the Riemann surface $\mathscr {L}$ for $\log {z}$ and the harmonic plane $({\mathbb {R}}^2, e^{2x}g_0)$. In Sect. 5.2, we make direct use of the real and imaginary parts of the powers $z^n$, for $n > 1$. Most of this section focuses on the construction of the Riemann surface identified with the harmonic plane having the harmonic metric derived from $\text {Re}(z^2) = x^2 - y^2$. In Sect. 5.3, we offer a variation of the usual cut-and-paste construction of Riemann surfaces and apply it to $\mathscr {L}$ discussed in Sect. 5.1. In Sect. 5.4, we consider lacunary functions on the D, and leverage the harmonic disks associated with the real and imaginary parts to analyze the flat geometry near the unit circle boundary. We focus on two lacunary functions and determine the length and curvature of selected radial line segments.

5.1 The simplest harmonic metric

Consider the Riemann surface $\mathscr {L}$ for $\log {z}$, consisting of an infinite stack of Euclidean planes, each cut along the positive x-axis with edges of adjacent planes glued together in the usual manner. The surface $\mathscr {L}$ has a global polar coordinate system $(r,\theta )$ along with the extended Euclidean metric $g_0=\mathrm{d}r^2+r^2\mathrm{d}\theta ^2$. (We will use the same notation for a metric and its extension.) We will use the biholomorphism $\log : \mathscr {L}\rightarrow {\mathbb {C}}={\mathbb {R}}^2$ defined by $\log (r,\theta )=(\log {r},\theta )$, where the “log” function is overloaded to represent both the real log and the complex log in polar coordinates.

It is easy to show that the push-forward metric by the log mapping is $e^{2x}g_0$ on ${\mathbb {R}}^2$. This is the simplest harmonic metric on ${\mathbb {R}}^2$ because the function $\varphi (x,y)=x$ is the simplest non-constant harmonic function.

To analyze the underlying geometry, we leverage the Euclidean geometry of $\mathscr {L}$ to construct geometric objects and then push them from $\mathscr {L}$ to $({\mathbb {R}}^2,e^{2x}g_0)$ by the log isometry. For example, the geodesic rays in $\mathscr {L}$, defined by $\theta =$ constant and $0<r<\infty$, are isometrically mapped to geodesics in $({\mathbb {R}}^2,e^{2x}g_0)$ as horizontal lines with finite length in the direction $x\rightarrow -\infty$; see Fig. 1a. In $\mathscr {L}$, the geodesic rays converge as $r\rightarrow 0$, so in $({\mathbb {R}}^2,e^{2x}g_0)$, the horizontal lines also converge as $x\rightarrow -\infty$. Moreover, the constant curvature spirals in $\mathscr {L}$, corresponding to $r=$ constant and $-\infty<\theta <\infty$, isometrically map to the vertical lines in $({\mathbb {R}}^2,e^{2x}g_0)$ and inherit the constant curvature $\frac{1}{r}$ from the corresponding spiral of radius r. For example, the y-axis is distance one from $x=-\infty$ and hence has constant curvature one, which means the y-axis is an infinite-length, non-intersecting “unit circle.” This is an obstruction to $e^{2x}g_0$ being a subset metric on ${\mathbb {R}}^2$.

This metric also supports the construction of a harmonic disk that is not isometric to a subset of the $({\mathbb {R}}^2,g_0)$. Let $\Omega$ be a simply connected proper domain that contains the segment of the y-axis from (0, 0) to $(0, 3\pi )$. From a Riemann map $f: D\rightarrow (\Omega , e^{2x}g_0))$, we construct a harmonic disk $(D,f^*(e^{2x}g_0))$ that contains a non-intersecting curve with constant curvature one and length 3$\pi$. Such a curve cannot exist in the $({\mathbb {R}}^2,g_0)$.

Of course, the metric $e^{2x}g_0$ is sufficiently simple for direct analysis, e.g., in (x, y) coordinates, half of the Christoffel symbols are 0 and the other half are $\pm 1$, so the geodesic equations are simple. A visualization of $({\mathbb {R}}^2, e^{2x}g_0)$ has already been described as the infinitely sheeted Riemann surface for $\log {z}$, but a simpler visualization is an infinitely spiraling cone (see Fig. 1b). Placing the cone’s vertex at the origin in ${\mathbb {R}}^3$, we see that the intersection with the unit sphere is the “unit circle.”

Fig. 1

On the harmonic plane $({\mathbb {R}}^2, e^{2x}g_0$), the behavior of horizontal and vertical lines are labeled in (a). The two U-shaped curves are examples of geodesics corresponding to two parallel lines in a sheet of the log z Riemann surface. The infinite spiraling cone in (b) represents an isometric embedding of $({\mathbb {R}}^2, e^{2x}g_0)$ in ${\mathbb {R}}^3$, where the cone vertex corresponds to the point $x=-\infty$ in Fig. 1a

We end this example with a curious observation. Consider the different locations of $e^{2x}$ in the following three metrics on ${\mathbb {R}}^2$: $e^{2x}(\mathrm{d}x^2+\mathrm{d}y^2)$, $e^{2x}\mathrm{d}x^2 +\mathrm{d}y^2$, $\mathrm{d}x^2+e^{2x}\mathrm{d}y^2$. The first metric is the topic of this section. The second is a product metric and isometric to a Euclidean half-plane. The third is a complete metric with constant curvature $-1$ and isometric to the upper half-plane with the Poincaré metric.

5.2 The second simplest harmonic metric

In the previous section, we had a uniformization map from the Riemann surface for $\log {z}$ to the complex plane, and this map became an isometry when the (extended) Euclidean metric was pushed forward to construct the harmonic metric $e^{2x}g_0$. This allowed the geometry of the harmonic metric to be understood in terms of the (Euclidean) geometry of the Riemann surface and the isometry map. Without an explicit uniformization map or, equivalently, without an explicit solution to the integral (1) for a given harmonic function $\varphi$, the pull-back metric $e^{2\varphi }g_0$ must be analyzed directly.

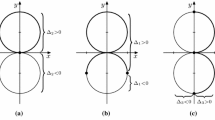
In this section, we consider the harmonic function Re$(z^2)=x^2-y^2$ and show that the geometry of $({\mathbb {R}}^2,e^{2(x^2-y^2)},g_0)$ is surprisingly non-trivial. For simplicity, we only describe the behavior of radial lines $y=cx$ emanating from the origin; see Fig. 2, where we also provide a visualization in ${\mathbb {R}}^3$. Figure 2a shows the first quadrant divided into two $45^\circ$ sectors. The geometry of the diagonal ray separating these two sectors is an Euler spiral in the harmonic metric, i.e., its curvature is proportional to its arclength. The rays corresponding to the positive x and y axes are geodesic rays, one with infinite length and the other with finite length $\frac{1}{2}\sqrt{\pi }$. The geometry of other first-quadrant rays is noted in the figure and this geometry is duplicated in the other three quadrants. Figure 2b represents an isometric embedding of this harmonic plane in ${\mathbb {R}}^3$. An Euler spiral (not shown) winds around each of the four infinite-spiraling cones. All four cones are shown with initial up/down wrapping along the y-axis branch cut. Each of the four Euler spirals converges to the cone vertex points of the form $(0, \pm \frac{1}{2}\sqrt{\pi }).$

Fig. 2

In a, the behavior of rays in the first quadrant is shown for the specified harmonic metric. b shows a portion of the harmonic plane isometrically embedded in ${\mathbb {R}}^3$. The two finite length geodesic rays (comprising the entire y-axis in (a) are correctly represented with finite length in (b), ending at the points $(0, \pm \frac{\sqrt{\pi }}{2})$, which are the start of two branch cuts from which four infinite spiraling cones emerge

Finally, the behavior of the harmonic metrics based on Re$(z^n)$, for $n>2$, is similar. There are n finite-length geodesic rays, uniformly spaced around the origin, with length $\Gamma (1+\frac{1}{n})$, where $\Gamma$ is the Gamma function. Between two adjacent finite-length geodesic rays, there is an infinite length geodesic ray. Between adjacent geodesic rays, there is a generalized Euler spiral; that is, one for which the curvature is directly proportional to a power of the arc length—here the power is n. The spirals between a geodesic ray and the generalized Euler spiral follow the same pattern of behavior as described above for $n=2$. The isometric embedding in ${\mathbb {R}}^3$ has n vertex points, and each of these points is the beginning of a branch cut which is a continuation of the direction of the finite-length geodesic. The harmonic planes derived from Re$(z^n)$ and Im$(z^n)$ are isometric by rotation $\frac{\pi }{2n}$ around the origin.

5.3 Cut-and-paste with harmonic planes

In this section, we re-purpose harmonic planes to be the building blocks—replacing Euclidean planes—in the cut-and-paste construction of Riemann surfaces. Our example begins with $\mathscr {L}$, and replaces $({\mathbb {R}}^2,g_0)$ with $({\mathbb {R}}^2, e^{2x}g_0)$, the latter also representing $\mathscr {L}$. The biholomorphism $\log : \mathscr {L}\rightarrow {\mathbb {R}}^2$ pushes forward the extended metric $e^{2x}g_0$ on $\mathscr {L}$ to ${\mathbb {R}}^2$, and a straight-forward calculation shows that the resulting harmonic metric is $e^{(e^x\cos {y}+x)}g_0$, with associated harmonic function Re($e^z +z$).

From Sect. 5.1 (and Fig. 1a), we know the geometry of the building block $({\mathbb {R}}^2, e^{2x}g_0)$. And since the log function is an explicitly defined isometry, we can push geometric objects in $({\mathbb {R}}^2, e^{2x}g_0)$ to $({\mathbb {R}}^2, e^{2(e^x\cos {y}+x)}g_0)$. This process is simple in concept, but the details are challenging and we cannot offer an isometric embedding in ${\mathbb {R}}^3$.

Furthermore, the process can be iterated, using the resulting harmonic plane at each stage as the building block for the next stage. It is straight-forward to show that the second iteration of this example produces a harmonic metric on ${\mathbb {R}}^2$ with associated harmonic function Re($e^{e^z}+e^z +z)$. The pattern is now apparent.

5.4 Lacunary functions

The existence of analytic functions with natural boundaries—that is, functions that cannot be extended analytically at any point on the circle of convergence—was first discovered by Weierstrass and Kronecker in the 1860s. Research into these lacunary functions flourished through the mid-twentieth century, and continues today as an active area of study, based primarily on methods that are analytic in nature.

In this section, we suggest that harmonic disks may provide a geometric tool for the study of these functions. For example, using the harmonic disks associated with a lacunary function (via the real and imaginary parts), the behavior of various curves in these disks (e.g., radial lines, geodesics) offers insight into the geometry of lacunary functions near the $S^1$ boundary.

Below, we select two lacunary functions $f_1(z)$ and $f_2(z)$, and describe the geometry of certain radial segments in the associated harmonic disks.

$$\begin{aligned} f_1(z)=\sum _1^\infty z^{2^n} \; \text {and } \; f_2(z)=\sum _1^\infty z^{n!} \end{aligned}$$

Consider the two sets of angles A and B:

$$\begin{aligned} A= \left\{ \theta \in [0,2\pi ]~|~\frac{\theta }{2\pi }=\frac{p}{q},~ \text {with}~ p\in {\mathbb {N}}~\text {and}~ q= 2^s, ~\text {for}~ s\in {\mathbb {N}}\right\} , ~\text {and}~ B= \left\{ \theta \in [0,2\pi ]~|~\frac{\theta }{2\pi }\in {\mathbb {Q}}\right\} . \end{aligned}$$

For $f_1(z)$, it is a straightforward calculation (using equation (1.5) in [12]) for the curvature calculations) to establish the following geometry of radial line segments with angle $\theta \in A$ and radial parameter $r\in (0,1)$:

• Harmonic disk derived from Re$(f_1(z))$

  • Length of these radial segments is infinite

  • Curvature of these radial segments approaches zero as $r\rightarrow 1$

• Harmonic disk derived from Im$(f_2(z))$

  • Length of these radial segments is finite

  • Curvature of these radial segments approaches $\infty$ as $r\rightarrow 1$

For $f_2(z)$, it is also a straightforward calculation (again using equation (1.5) in [12]) to establish the following curvature properties of radial line segments with $\theta \in B$:

• Harmonic disk derived from Re($f_2$): The curvature of radial segments approaches zero as $r\rightarrow 1$.

• Harmonic disk derived from Im($f_2$): The curvature of radial segments approaches infinity as $r\rightarrow 1$.

Somewhat less straightforward is the fact that for the harmonic disks derived from Re($f_2$) and Im($f_2$), all radial segments have finite length. This latter fact follows from the curious convergence of the improper integral

$$\begin{aligned} I=\int _0^1\exp \left( \sum _{k=0}^{\infty }r^{k!}\right) \mathrm{d}r. \end{aligned}$$

6 Constant curvature metrics on simply connected surfaces

Although the classification theorem focuses on flat planes—and by intimation, flat disks—some of the proof remains valid for the general constant curvature metrics on a the plane. We consider this next. We will need to extend the definition of a subset metric to be context dependent. For constant curvature $K=\pm 1$, the requisite isometric embedding will be to a proper subset of the standard 2-sphere $(S^2,g_s$) or the Poincaré disk $(D,g_p)$.

6.1 Complete metrics

The classification of complete metrics with nonzero constant curvature K on simply connected surfaces is well known. See [7], Chap. 8, Theorem 4.1.

• For $K = 1$, the surface is isometric to $(S^2,g_s$).

• For $K = -1$, the surface is isometric to the $(D,g_p)$.

6.2 Incomplete metrics

Our classification proof in Sect. 3 remains valid for any metric $\widehat{g}$ on ${\mathbb {R}}^2$ or D, ignoring references to flat planes and harmonic metrics, but retaining the step establishing a conformal metric $g = e^{2\sigma } g_0$ on ${\mathbb {C}}={\mathbb {R}}^2$ or D and the construction of F. If the metric g has constant curvature, then Liouville’s equation² applies to the conformal factor:

$$\begin{aligned} \Delta _0 \sigma = -Ke^{2\sigma }, \end{aligned}$$

(2)

where $\Delta _0$ is the Euclidean Laplacian. Of course for $K = 0$, the solutions are harmonic.

6.2.1 $K=1$ metrics on the plane

On ${\mathbb {R}}^2$, there are many (necessarily) incomplete $K = 1$ metrics. For example, given a diffeomorphism $F: {\mathbb {R}}^2 \rightarrow \Omega \subsetneq (S^2, g_s)$, the pull-back $F^*(g_s)$ is a subset metric on ${\mathbb {R}}^2$. However, these subset metrics are not the only $K = 1$ metrics on ${\mathbb {R}}^2$, as we now describe. Let $M=S^2-\{north ~ pole\}$ and consider the conformal map given by stereographic projection

$$\begin{aligned} Proj: (M,g_s) \rightarrow ({\mathbb {R}}^2,g_0). \end{aligned}$$

The inverse map $Proj^{-1}$ is also conformal and so $({\mathbb {R}}^2, (Proj^{-1})^*(g_s))$ has curvature $K=1$ and the metric is conformal to $g_0$; that is,

$$\begin{aligned} (Proj^{-1})^*(g_s))=e^{2\sigma }g_0=g_\sigma . \end{aligned}$$

We will use $({\mathbb {R}}^2,g_\sigma )$ for the sheets in the cut-and-paste construction of $\mathscr {L}$, similar to that used in Sect. 5.3. Here we denote the resulting Riemann surface by $\mathscr {L}_1$ and continue to use the same notation $g_\sigma$ for the extended metric on $\mathscr {L}_1$. It follows that ($\mathscr {L}_1, g_\sigma )$ has curvature $K=1$. Note that each sheet in this construction is naturally endowed with two conformally equivalent metrics, $g_0$ and $g_\sigma$. Evidently, the extended metrics are likewise conformally equivalent.

From Sect. 5.1, we have a biholomorphism $\log ^{-1}: {\mathbb {C}}={\mathbb {R}}^2 \rightarrow (\mathscr {L}_1,g_\sigma )$. Note that $({\mathbb {R}}^2, (\log ^{-1})^*(g_\sigma ))$ has curvature $K =1$ and the metric is conformal to $g_0$; that is, $(\log ^{-1})^*(g_\sigma )=e^{2\tau }g_0=g_\tau$. The metric $g_\tau$ is incomplete and the conformal terms $\sigma$ and $\tau$ satisfy (2) with $K = 1$. Furthermore, the area of $({\mathbb {R}}^2, g_\tau )$ is infinite, and thus the metric cannot be a subset metric of $(S^2,g_s)$. Alternatively, any great circle on $S^2$ that avoids the north pole is a closed geodesic in $({\mathbb {R}}^2, g_\sigma)$, which then becomes an infinitely long, non-intersecting geodesic in $(\mathscr {L}_1, g_\sigma )$; thus again, the metric cannot be a subset metric of $(S^2, g_S)$. Note that $({\mathbb {R}}^2, g_\tau )$ can be isometrically immersed in $({\mathbb {R}}^3,g_\sigma)$ as M—by infinitely wrapping it around $(S^2,g_s)$—but it seems unlikely that it can be isometrically embedded in ${\mathbb {R}}^3$.

6.2.2 $K=-1$ metrics on the plane

The previous section’s discussion on $K = 1$ metrics is relevant here for $K = -1$ metrics. For example, the pull-back metric from a diffeomorphism of ${\mathbb {R}}^2$ to a proper subset of $(D,g_p)$ yields a subset metric on ${\mathbb {R}}^2$. As before, these subset metrics are not the only $K = -1$ metrics on ${\mathbb {R}}^2$, as we now describe (cf. the observation at the end of Sect. 5.1).

We begin with a brief review of circles in $(D,g_p)$. Every Euclidean circle in $(D,g_p)$—including horocycles tangent to the $S^1$ boundary of $(D,g_p)$—is a hyperbolic circle, though a circle’s radius, center, and geodesic curvature will differ between the Euclidean and hyperbolic metrics. A hyperbolic circle contained entirely within $(D,g_p)$ has finite radius r, constant curvature $(\tanh {r})^{-1}>1$, and finite length. In particular, all of these hyperbolic circles have constant curvature greater than one. By contrast, a horocycle has infinite radius (with center the point of tangency to the boundary of D), constant curvature one, and infinite length; that is, the horocycles are infinite-length, non-intersecting “unit circles” .

The construction of a $K = -1$ non-subset metric leverages the cut-and-paste process discussed above by replacing planes with unit disks. Specifically, the disks are cut along the line segment $(-1, 0]$ and then glued along contiguous edges to form a Riemann surface $\mathscr {L}_{-1}$. We impose the Poincaré metric $g_p$ on each disk sheet, thereby creating an “extended” Poincaré metric on $\mathscr {L}_{-1}$. Before cutting, consider a small circle of radius r, centered at the origin in each sheet. On $\mathscr {L}_{-1}$, these small circles stitch together to become an infinitely long curve with constant curvature $(\tanh {r})^{-1}>1$. The biholomorphism used in Sect. 6.2.1 maps $\mathscr {L}_{-1}$ to a half-plane, which can be mapped to ${\mathbb {R}}^2$ by a diffeomorphism. The $K = -1$ metric on $\mathscr {L}_{-1}$ can now be pushed forward to a $K = -1$ metric on ${\mathbb {R}}^2$.

Note that this metric cannot be conformal to $g_0$ because the diffeomorphism above cannot be holomorphic. If this metric on ${\mathbb {R}}^2$ was a subset metric on $(D,g_p)$, then the Poincaré disk would admit a hyperbolic circle with infinite length and constant curvature greater than one—a contradiction.

As an aside, we could have biholomorphically mapped the half-plane to D and then pushed the metric on $\mathscr {L}_{-1}$ to D. In this case, the resulting metric would be conformal to $g_0$, so our result shows the existence of a $K=-1$ non-subset, conformal metric on the unit disk, and the conformal factor satisfies (2) for $K =-1$. In particular, there are solutions to (2) for $K = -1$ on the D, but not on the plane.

Remark 6.3

Although there is a construction (see [6]) for the most general solutions to (2) for $K = \pm 1$, the construction process offers no insight into the resulting elliptic or hyperbolic geometry. It would be interesting to have criteria that distinguishes the solutions in terms of the Riemannian metric’s behavior, such as being complete or incomplete and, in the latter case, being a subset metric or not.

7 Epilogue

The impetus for this paper was the result of a calculation to determine the geometry of vertical and horizontal lines in the incomplete flat metric $e^{2x}g_0$. As noted in Sect. 5.1, this led to the realization that the harmonic plane $({\mathbb {R}}^2, e^{2x}g_0)$ is isometric to the Riemann surface for $\log {z}$ and that this surface could be isometrically embedded in ${\mathbb {R}}^3$ as a flat infinitely spiraling cone, in contrast to the more common renderings which are visibly non-flat. We were surprised that such a nice observation, based on such a routine calculation, was absent from the literature. Ultimately, we were led to the classification theorem of Sect. 3.

The essential approach of this paper is to view the Riemannian geometry of flat surfaces through the lens of classical complex analysis. It is particularly noteworthy that by avoiding uniformization, the richness of the geometry of incomplete flat metrics can be exposed. For example, in a recent note [4], we show that the well-known four-vertex theorem is true for any flat plane. This is a non-trivial extension of the four-vertex theorem since harmonic planes cannot be isometrically embedded into the $({\mathbb {R}}^2,g_0)$, but this extension is a corollary of a more general result by Ghomi (Theorem 1.1, [9]).

These pleasing results, coupled with the importance of harmonic functions, suggest that the study of the geometry of harmonic metrics should not be ignored. With the classification theorem in place, there are a number of questions which will be of ongoing interest. We list a few.

• 1. The curve-shortening flows [8, 11] start with a smooth Jordan curve and, during the flow, require that the intermediate curves remain smooth and without self-intersections. Using the smooth Riemann Mapping Theorem [2], the initial Jordan curve can be modelled as the $S^1$ boundary of a harmonic disk with harmonic metric that extends smoothly to the boundary. During the flow, the intermediate curves can also be modelled as $S^1$ boundaries of harmonic disks, so the entire curve-shortening flow can be modelled as a flow of harmonic metrics (i.e., a flow of harmonic functions) on the closed unit disk. What are the defining equations for this flow of harmonic functions? The authors were not able to construct the differential equation(s) for a harmonic flow that reproduced the classical curve shortening flow, but instead found and solved another differential equation for a harmonic flow (see Eq. (4) below). Our approach relies on the observation that, for a given flow of harmonic metrics on the closed unit disk $\bar{D}$, the associated flow of harmonic functions on D can be characterized as a flow of Dirichlet initial condition on $S^1$. A harmonic flow on D begins (at time 0) with a harmonic metric on D obtained as the pull-back metric from a Riemann map F of D to the interior of the given smooth Jordan curve. Since the Riemann map extends smoothly to the $S^1$ boundary of D, the pull-back metric and associated harmonic function smoothly extend to $S^1$, thereby establishing the Dirichlet boundary conditions at time 0. Setting $\varphi (1,\theta , t)$ to be the flow of Dirichlet boundary conditions, with time parameter t and $S^1$ parameters $(1,\theta )$, the flow differential equation is

  $$\begin{aligned} \varphi _t(1,\theta , t) = -k(1,\theta , t)e^{\varphi (1,\theta , t)}+ 1, \end{aligned}$$

  (4)

  where $\varphi _t$ is the time derivative and $k(1, \theta , t)$ is the curvature of $S^1$ in the metric $g_{\varphi (r,\theta ,t)}$ defined by the harmonic function $\varphi$, which has the specified boundary conditions. The initial condition at $t = 0$ is written as $\varphi (1, \theta , 0) = \varphi (1, \theta )$ where, by abuse of notation, the second “$\varphi$” is derived from the Riemann map F. We can show that the flow solution to (4) converges to a circle as $t\rightarrow \infty$ and satisfies the condition that once the flow curve becomes convex, it remains convex. Furthermore, our flow solution includes explicit formulas for the length, area, and curvature of the flow curve for any time t > 0.

• 2. From the Nash embedding theorem, it is known that all harmonic planes and harmonic disks can be isometrically embedded into some Euclidean space. What is the relationship between the harmonic functions and the dimension of the Euclidean space? For harmonic disks being isometrically embedded in $({\mathbb {R}}^2,g_0)$ this question is equivalent to asking for a characterization of harmonic metrics that are Euclidean subset metrics, and hence are associated to a Riemann map. A related question asks for a characterization when the harmonic disk is convex.

• 3. Manifolds of Riemannian metrics have been studied by various researchers (e.g., [10]). These infinite-dimensional manifolds have natural metrics with geodesics, Jacobi fields, etc. For the manifold of harmonic metrics on the plane or unit disk, per our classification, what is the behavior of geodesics, Jacobi fields, and other geometric objects in terms of the underlying harmonic functions? For example, given a curve-shortening flow—along with its representation as an arc in the space of harmonic metrics on the disk—what is the geometry of this arc?