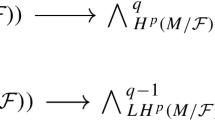The ${\mathcal {L}}_B$-cohomology on compact torsion-free $\mathrm {G}_2$ manifolds and an application to ‘almost’ formality

Abstract

We study a cohomology theory $H^{\bullet }_{\varphi }$, which we call the ${\mathcal {L}}_B$-cohomology, on compact torsion-free $\mathrm {G}_2$ manifolds. We show that $H^k_{\varphi } \cong H^k_{\mathrm {dR}}$ for $k \ne 3, 4$, but that $H^k_{\varphi }$ is infinite-dimensional for $k = 3,4$. Nevertheless, there is a canonical injection $H^k_{\mathrm {dR}} \rightarrow H^k_{\varphi }$. The ${\mathcal {L}}_B$-cohomology also satisfies a Poincaré duality induced by the Hodge star. The establishment of these results requires a delicate analysis of the interplay between the exterior derivative $\mathrm {d}$ and the derivation ${\mathcal {L}}_B$ and uses both Hodge theory and the special properties of $\mathrm {G}_2$-structures in an essential way. As an application of our results, we prove that compact torsion-free $\mathrm {G}_2$ manifolds are ‘almost formal’ in the sense that most of the Massey triple products necessarily must vanish.

1 Introduction

Let $(M, \varphi )$ be a manifold with $\mathrm {G}_2$-structure. Here $\varphi$ is a smooth 3-form on M that is nondegenerate in a certain sense that determines a Riemannian metric g and a volume form $\mathsf {vol}$, hence a dual 4-form $\psi$. We say that $(M, \varphi )$ is a torsion-free$\mathrm {G}_2$ manifold if $\nabla \varphi = 0$. Note that this implies that $\nabla \psi = \mathrm {d}\varphi = \mathrm {d}\psi = 0$ as well. In fact, it is now a classical result [7] that the pair of conditions $\mathrm {d}\varphi = \mathrm {d}\psi = 0$ is actually equivalent to $\nabla \varphi = 0$.

The forms $\varphi$ and $\psi$ can be used to construct a vector-valued 2-form B and a vector-valued 3-form K, respectively, by raising an index using the metric. These vector-valued forms were studied in detail by Kawai–Lê–Schwachhöfer in [16] in the context of the Frölicher–Nijenhuis bracket.

These vector-valued forms B and K induce derivations${\mathcal {L}}_B$ and ${\mathcal {L}}_K$ on the space $\varOmega ^{\bullet }$ of forms on M, of degree 2 and 3, respectively. From these derivations, we can define cohomology theories. We call these the $\mathcal {L}_B$-cohomology, denoted $H^{\bullet }_{\varphi }$, and the $\mathcal {L}_K$-cohomology, denoted $H^{\bullet }_{\psi }$. When M is compact, the ${\mathcal {L}}_K$-cohomology was studied extensively by Kawai–Lê–Schwachhöfer in [17]. In the present paper, we study in detail the ${\mathcal {L}}_B$-cohomology when M is compact. Specifically, we compute $H^k_{\varphi }$ for all k. The results are summarized in Theorem 3.19, which we restate here:

Theorem 3.19. The following relations hold.

• $H^k_{\varphi } \cong H^k_{dR}$ for $k=0,1,2,5,6,7$.

• $H^k_{\varphi }$is infinite-dimensional for$k = 3,4$.

• There is a canonical injection$\mathcal {H}^k \hookrightarrow H^k_{\varphi }$for allk.

• The Hodge star induces isomorphisms$*: H^k_{\varphi } \cong H^{7-k}_{\varphi }$.

The proof involves a very delicate analysis of the interplay between the exterior derivative $\mathrm {d}$ and the derivation induced by B and uses Hodge theory in an essential way.

As an application of our results, we study the question of formality of compact torsion-free $\mathrm {G}_2$ manifolds. This is a long-standing open problem. It has been studied by many authors, including Cavalcanti [3]. In particular, the paper [22] by Verbitsky has very close connections to the present paper. What is called $\mathrm {d}_c$ in [22] is ${\mathcal {L}}_B$ in the present paper. Verbitsky’s paper contains many excellent ideas. Unfortunately, there are some gaps in several of the proofs in [22]. Most important for us, there is a gap in the proof of [22, Proposition 2.19], which is also used to prove [22, Proposition 2.20], among several other results in [22]. We give a different proof of this result, which is our Proposition 4.4. We then use this to prove our Theorem 4.6, which essentially says that a compact torsion-free $\mathrm {G}_2$ manifold is ‘almost formal’ in the sense that its de Rham complex is equivalent to a differential graded algebra with all differentials trivial except one.

A consequence of our Theorem 4.6 is that almost all of the Massey triple products vanish on a compact torsion-free $\mathrm {G}_2$ manifold. This gives a new topological obstruction to the existence of torsion-free $\mathrm {G}_2$-structures on compact manifolds. The precise statement is the following:

Corollary 4.9. LetMbe a compact torsion-free$\mathrm {G}_2$ manifold. Consider cohomology classes$[\alpha ]$, $[\beta ]$, and$[\gamma ] \in H^{\bullet }_{\mathrm {dR}}$. If the Massey triple product$\langle [\alpha ], [\beta ], [\gamma ] \rangle$is defined and we have$|\alpha | + |\beta | \ne 4$and$|\beta | + |\gamma | \ne 4$, then$\langle [\alpha ], [\beta ], [\gamma ] \rangle = 0$.

We also prove the following stronger result in the case of full holonomy $\mathrm {G}_2$ (the ‘irreducible’ case):

Theorem 4.10. LetMbe a compact torsion-free$\mathrm {G}_2$ manifold with full holonomy$\mathrm {G}_2$, and consider cohomology classes$[\alpha ]$, $[\beta ]$, and$[\gamma ] \in H^{\bullet }_{\mathrm {dR}}$. If the Massey triple product$\langle [\alpha ], [\beta ], [\gamma ] \rangle$is defined, then$\langle [\alpha ], [\beta ], [\gamma ] \rangle = 0$except possibly in the case when$|\alpha | = |\beta | = |\gamma | = 2$.

The Massey triple products on a compact torsion-free $\mathrm {G}_2$ manifold are not discussed in [22].

Organization of the paper In the rest of this section, we discuss the domains of validity of the various results in this paper in Remark 1.1; then, we consider notation and conventions and conclude with the statement of a trivial result from linear algebra that we use frequently.

Section 2 is the heart of the paper, where we establish the various relations between the derivations $\mathrm {d}$, $\iota _B$, $\iota _B$, ${\mathcal {L}}_B$, and ${\mathcal {L}}_K$. We begin with a brief summary of known facts about $\mathrm {G}_2$-structures that we will need in Sect. 2.1. In Sect. 2.2, we study the operators $\mathrm {d}$ and $\varDelta$ in detail. Some of the key results are Proposition 2.12, which establishes Fig. 1, and Corollary 2.13 and Proposition 2.16 which establish second-order differential identities. These have appeared before (without proof) in a paper of Bryant [2, Section 5.2]. But see Remark 2.18. A new and crucial result in Sect. 2.2 is Theorem 2.19 which relates the kernels of various operators on $\varOmega ^1$. In Sect. 2.3, we introduce the derivations $\iota _B$, $\iota _K$, ${\mathcal {L}}_B$, and ${\mathcal {L}}_K$ and study their basic properties. One of the highlights is Corollary 2.32, which establishes Figs. 4 and 5.

In Sect. 3, we study and compute the $\mathcal L_B$-cohomology $H^{\bullet }_{\varphi }$ of a compact torsion-free $\mathrm {G}_2$ manifold. We use heavily both the results of Sect. 2 and Hodge theory. This section culminates with the proof of Theorem 3.19. Then in Sect. 4, we apply the results of Sect. 3 to study the Massey triple products of compact torsion-free $\mathrm {G}_2$ manifolds.

Remark 1.1

We summarize here the domains of validity of the various sections of the paper.

• All results of Sect. 2.1 except the last one (Proposition 2.8) are valid for any $\mathrm {G}_2$-structure.

• Proposition 2.8 and the entirety of Sect. 2.2 assume that $(M, \varphi )$ is torsion-free.

• In Sect. 2.3, the results that only involve the algebraic derivations $\iota _B$ and $\iota _K$, up to and including Proposition 2.31, are valid for any $\mathrm {G}_2$-structure.

• The rest of Sect. 2.3, beginning with Corollary 2.32, uses the results of Sect. 2.2 heavily and is only valid in the torsion-free setting.

• The cohomology theories introduced in Sect. 3.1 make sense on any torsion-free $\mathrm {G}_2$ manifold. However, beginning in Sect. 3.2 and for the rest of the paper, we assume that $(M, \varphi )$ is a compact torsion-free $\mathrm {G}_2$ manifold, as we use Hodge theory throughout. $\square$

Notation and conventions We mostly follow the notation and conventions of [12], and we point out explicitly whenever our notation differs significantly. Let (M, g) be an oriented smooth Riemannian 7-manifold. Let $\{ e_1 , \ldots , e_7 \}$ be a local frame for TM with dual coframe $\{ e^1, \ldots , e^7 \}$. It can be a local coordinate frame $\{ \frac{\partial }{\partial x^{1}}, \ldots , \frac{\partial }{\partial x^{7}} \}$ with dual coframe $\{ d x^{1}, \ldots , d x^{7} \}$, but this is not necessary. Note that the metric dual 1-form of $e_i$ is $(e_i)^{\flat } = g_{ij} e^j$.

We employ the Einstein summation convention throughout. We write $\varLambda ^k$ for the bundle $\varLambda ^k (T^* M)$ and $\varOmega ^k$ for its space of smooth sections $\varGamma (\varLambda ^k (T^* M))$. Then $\varLambda ^{\bullet } = \oplus _{k=1}^n \varLambda ^k$ is the exterior algebra of $T^*M$ and $\varOmega ^{\bullet } = \oplus _{k=0}^n \varOmega ^k$ is the space of smooth differential forms on M. Similarly, we use $S^2 (T^* M)$ to denote the second symmetric power of $T^* M$, and $\mathcal {S}= \varGamma (S^2 (T^* M))$ to denote the space of smooth symmetric 2-tensors on M.

The Levi–Civita covariant derivative of g is denoted by $\nabla$. Let $\nabla _p = \nabla _{e_p}$. The exterior derivative $d\alpha$ of a k-form $\alpha$ can be written in terms of $\nabla$ as

$$\begin{aligned} \begin{aligned} \mathrm {d}\alpha&= e^p \wedge \nabla _p \alpha , \\ (\mathrm {d}\alpha )_{i_1 i_1 \cdots i_{k+1}}&= \sum _{j=1}^{k+1} \nabla _{i_j} \alpha _{i_1 \cdots \hat{i_j} \cdots i_k}. \end{aligned} \end{aligned}$$

(1.1)

The adjoint $d^{*}$ of $\mathrm {d}$ with respect to g satisfies ${\mathrm {d}}{}^{\star }= (-1)^k *\mathrm {d}*$ on $\varOmega ^k$. It can be written in terms of $\nabla$ as

$$\begin{aligned} \begin{aligned} {\mathrm {d}}{}^{\star }\alpha&= - g^{pq} e_p \lrcorner \nabla _q \alpha , \\ ({\mathrm {d}}{}^{\star }\alpha )_{i_1 \cdots i_{k-1}}&= - g^{pq} \nabla _p \alpha _{q i_1 \cdots i_{k-1}}. \end{aligned} \end{aligned}$$

(1.2)

An element $h \in \mathcal {S}$ can be decomposed as $h = \tfrac{{\text {Tr}}_g h}{7} g + h^0$, where ${\text {Tr}}_g h = g^{ij} h_{ij}$ is the trace and $h^0$ is the trace-free component of h, which is orthogonal to g. We use $S^2_0 (T^* M)$ to denote the bundle whose sections $\mathcal {S}_0= \varGamma (S^2_0 (T^* M))$ are the trace-free symmetric 2-tensors. Finally, if X is a vector field on M, we denote by $X^{\flat }$ the 1-form metric dual to X with respect to the metric g. Sometimes we abuse notation and write $X^{\flat }$ as simply X when there is no danger of confusion.

We write $H^k_{\mathrm {dR}}$ for the $k{\text {th}}$ de Rham cohomology over ${\mathbb {R}}$ and ${\mathcal {H}}^k$ for the space of harmonic k-forms. If $[\alpha ]$ is a cohomology class, then $|\alpha |$ denotes the degree of any of its representative differential forms. That is, if $[\alpha ] \in H^k_{\mathrm {dR}}$, then $|\alpha | = k$.

We use $C^{\bullet }$ to denote a ${\mathbb {Z}}$-graded complex of real vector spaces. A degree k map P of the complex $C^{\bullet }$ maps $C^i$ into $C^{i+k}$, and we write

$$\begin{aligned} \begin{aligned} (\ker \,P)^i&= \ker (P : C^i \rightarrow C^{i+k}), \\ ({\text {im}}\,P)^i&= {\text {im}}(P : C^{i-k} \rightarrow C^i). \end{aligned} \end{aligned}$$

(1.3)

Lemma 1.2

We state two trivial results from linear algebra that we use several times in Sect. 3.

• (i) Let $V \subseteq U \subseteq (V \oplus W)$ be nested subspaces. Then $U = V \oplus (W \cap U)$.

• (ii) Let $U = A \oplus B \oplus C$ be a direct sum decomposition of a vector space into complementary subspaces A, B, C. Let V, W be subspaces of U such that $V = A' \oplus B' \oplus C'$ and $W = A'' \oplus B'' \oplus C''$ where $A',A''$ are subspaces of A, and $B',B''$ are subspaces of B, and $C',C''$ are subspaces of C. Then $V \cap W = (A' \cap A'') \oplus (B' \cap B'') \oplus (C' \cap C'')$.

2 Natural derivations on torsion-free $\mathrm {G}_2$ manifolds

We first review some facts about torsion-free $\mathrm {G}_2$ manifolds and the decomposition of the exterior derivative $\mathrm {d}$. Then, we define two derivations on $\varOmega ^{\bullet }$ and discuss their properties.

2.1 $\mathrm {G}_2$-Structures and the decomposition of $\varOmega ^{\bullet }$

Let $(M^7, \varphi )$ be a manifold with a $\mathrm {G}_2$-structure. Here $\varphi$ is the positive 3-form associated with the $\mathrm {G}_2$-structure, and we use $\psi$ to denote the dual 4-form $\psi = *\varphi$ with respect to the metric g induced by $\varphi$. We will use the sign/orientation convention for $\mathrm {G}_2$-structures of [12]. In this section we collect some facts about $\mathrm {G}_2$-structures, taken from [12], that we will need. We recall the fundamental relation between $\varphi$ and g, which allows one to extract the metric from the 3-form. This is:

$$\begin{aligned} (X \lrcorner \varphi ) \wedge (Y \lrcorner \varphi ) \wedge \varphi = - 6 g(X, Y) \mathsf {vol}. \end{aligned}$$

(2.1)

Lemma 2.1

The tensors g, $\varphi$, $\psi$ satisfy the following contraction identities in a local frame:

$$\begin{aligned} \varphi _{ijk} \varphi _{abc} g^{kc}&= g_{ia} g_{jb} - g_{ib} g_{ja} - \psi _{ijab}, \\ \varphi _{ijk} \varphi _{abc} g^{jb} g^{kc}&= 6 g_{ia}, \\ \varphi _{ijk} \varphi _{abc} g^{ia} g^{jb} g^{kc}&= 42, \\ \varphi _{ijk} \psi _{abcd} g^{kd}&= g_{ia} \varphi _{jbc} + g_{ib} \varphi _{ajc} + g_{ic} \varphi _{abj} - g_{aj} \varphi _{ibc} - g_{bj} \varphi _{aic} - g_{cj} \varphi _{abi}, \\ \varphi _{ijk} \psi _{abcd} g^{jc} g^{kd}&= - 4 \varphi _{iab}, \\ \varphi _{ijk} \psi _{abcd} g^{ib} g^{jc} g^{kd}&= 0, \\ \psi _{ijkl} \psi _{abcd} g^{ld}&= -\varphi _{ajk} \varphi _{ibc} - \varphi _{iak} \varphi _{jbc} - \varphi _{ija} \varphi _{kbc} \\&\quad + g_{ia} g_{jb} g_{kc} + g_{ib} g_{jc} g_{ka} + g_{ic} g_{ja} g_{kb} - g_{ia} g_{jc} g_{kb} \\&\quad - g_{ib} g_{ja} g_{kc} - g_{ic} g_{jb} g_{ka} \\&\quad -g_{ia} \psi _{jkbc} \\&\quad - g_{ja} \psi _{kibc} - g_{ka} \psi _{ijbc} + g_{ab} \psi _{ijkc} - g_{ac} \psi _{ijkb}, \\ \psi _{ijkl} \psi _{abcd} g^{kc} g^{ld}&= 4 g_{ia} g_{jb} - 4 g_{ib} g_{ja} - 2 \psi _{ijab}, \\ \psi _{ijkl} \psi _{abcd} g^{jb} g^{kc} g^{ld}&= 24 g_{ia}, \\ \psi _{ijkl} \psi _{abcd} g^{ia} g^{jb} g^{kc} g^{ld}&= 168. \end{aligned}$$

Proof

This is proved in Lemmas A.12, A.13, and A.14 of [12]. $\square$

For $k = 0, \ldots , 7,$ the bundle $\varLambda ^k := \varLambda ^k (T^* M)$ decomposes as follows:

$$\begin{aligned} \begin{matrix} \varLambda ^0 &{} = &{} \varLambda ^0_1, \\ \varLambda ^1 &{} = &{} &{} &{} \varLambda ^1_7, \\ \varLambda ^2 &{} = &{} &{} &{} \varLambda ^2_7 &{} \oplus &{} \varLambda ^2_{14}, \\ \varLambda ^3 &{} = &{} \varLambda ^3_1 &{} \oplus &{} \varLambda ^3_7 &{} &{} &{} \oplus &{} \varLambda ^3_{27}, \\ \varLambda ^4 &{} = &{} \varLambda ^4_1 &{} \oplus &{} \varLambda ^4_7 &{} &{} &{} \oplus &{} \varLambda ^4_{27}, \\ \varLambda ^5 &{} = &{} &{} &{} \varLambda ^5_7 &{} \oplus &{} \varLambda ^5_{14}, \\ \varLambda ^6 &{} = &{} &{} &{} \varLambda ^6_7, \\ \varLambda ^7 &{} = &{} \varLambda ^7_1. \end{matrix} \end{aligned}$$

(2.2)

Here $\varLambda ^k_l$ is a rank l subbundle of $\varLambda ^k$, and the decomposition is orthogonal with respect to g. Moreover, we have $\varLambda ^{7-k}_l = *\varLambda ^k_l$. In fact, there are isomorphisms $\varLambda ^k_l \cong \varLambda ^{k'}_l$, so the bundles in the same vertical column of (2.2) are all isomorphic. Moreover, the Hodge star $*$ and the operations of wedge product with $\varphi$ or with $\psi$ all commute with the projections $\pi _l$ for $l = 1, 7, 14, 27$.

We will denote by $\varOmega ^k_l$ the space of smooth sections of $\varLambda ^k_l$. The isomorphisms $\varLambda ^k_l \cong \varLambda ^{k'}_l$ induce isomorphisms $\varOmega ^k_l \cong \varOmega ^{k'}_l$. The descriptions of the $\varOmega ^k_l$ and the particular identifications that we choose to use in this paper are given explicitly as follows:

$$\begin{aligned} \begin{aligned} \varOmega ^0_1&= C^{\infty } (M), \\ \varOmega ^1_7&= \varGamma (T^* M) \cong \varGamma (TM), \\ \varOmega ^2_7&= \{ X \lrcorner \varphi : \, X \in \varGamma (TM) \} \cong \varOmega ^1_7 \\ \varOmega ^2_{14}&= \{ \beta \in \varOmega ^2 : \, \beta \wedge \psi = 0 \} = \{ \beta \in \varOmega ^2 : \, \beta _{pq} g^{pi} q^{qj} \varphi _{ijk} = 0 \}, \\ \varOmega ^3_1&= \{ f \varphi : \, f \in C^{\infty }(M) \} \cong \varOmega ^0_1, \\ \varOmega ^3_7&= \{ X \lrcorner \psi : \, X \in \varGamma (TM) \} \cong \varOmega ^1_7, \\ \varOmega ^3_{27}&= \{ \beta \in \varOmega ^3 : \, \beta \wedge \varphi = 0 \text { and } \beta \wedge \psi = 0 \} = \{ h_{ip} g^{pk} d x^{i} \wedge (\partial _{k} \lrcorner \varphi ) : \, h \in \mathcal {S}_0\} \\ \varOmega ^k_l&= \{ *\beta : \, \beta \in \varOmega ^{7-k}_l \}, \quad \hbox { for}\ k = 4, 5, 6, 7. \end{aligned} \end{aligned}$$

(2.3)

Remark 2.2

We emphasize that the particular identifications we have chosen in (2.3) are not isometric. Making them isometric identifications would require introducing irrational constant factors, but this will not be necessary. See also Remark 2.15. $\square$

We will denote by $\pi ^k_l$ the orthogonal projection $\pi ^k_l : \varOmega ^k \rightarrow \varOmega ^k_l$. We note for future reference that $\beta \in \varOmega ^3_1 \oplus \varOmega ^3_{27}$ if and only if $\beta \perp (X \lrcorner \psi )$ for all X, and $\beta \in \varOmega ^3_7 \oplus \varOmega ^3_{27}$ if and only if $\beta \perp \varphi$. In a local frame, these observations are

$$\begin{aligned} \begin{aligned} \beta \in \varOmega ^3_1 \oplus \varOmega ^3_{27} \,&\longleftrightarrow \, \beta _{ijk} g^{ia} g^{jb} g^{kc} \psi _{abcd} = 0, \\ \beta \in \varOmega ^3_7 \oplus \varOmega ^3_{27} \,&\longleftrightarrow \, \beta _{ijk} g^{ia} g^{jb} g^{kc} \varphi _{abc} = 0. \end{aligned} \end{aligned}$$

(2.4)

Similarly, we have that $\gamma \in \varOmega ^4_1 \oplus \varOmega ^4_{27}$ if and only if $\gamma \perp (\varphi \wedge X)$ for all X, and $\gamma \in \varOmega ^4_7 \oplus \varOmega ^4_{27}$ if and only if $\gamma \perp \psi$. In a local frame, these observations are

$$\begin{aligned} \begin{aligned} \gamma \in \varOmega ^4_1 \oplus \varOmega ^4_{27} \,&\longleftrightarrow \, \gamma _{ijkl} g^{ia} g^{jb} g^{kc} \varphi _{abc} = 0, \\ \gamma \in \varOmega ^4_7 \oplus \varOmega ^4_{27} \,&\longleftrightarrow \, \gamma _{ijkl} g^{ia} g^{jb} g^{kc} g^{ld} \psi _{abcd} = 0. \end{aligned} \end{aligned}$$

(2.5)

Lemma 2.3

The following identities hold:

$$\begin{aligned} *(\varphi \wedge X^{\flat })&= X \lrcorner \psi ,&*( \psi \wedge X^{\flat })&= X \lrcorner \varphi , \\ \psi \wedge *(\varphi \wedge X^{\flat })&= 0,&\varphi \wedge *(\psi \wedge X^{\flat })&= -2 \psi \wedge X^{\flat }, \\ \varphi \wedge ( X \lrcorner \varphi )&= -2 *(X \lrcorner \varphi ),&\psi \wedge (X \lrcorner \varphi )&= 3 *X^{\flat }, \\ \varphi \wedge (X \lrcorner \psi )&= -4 *X^{\flat },&\psi \wedge ( X \lrcorner \psi )&= 0. \end{aligned}$$

Proof

This is part of Proposition A.3 in [12]. $\square$

Lemma 2.4

Identify $\varOmega ^1 \cong \varGamma (TM)$ using the metric. The cross product$\times : \varOmega ^1 \times \varOmega ^1 \rightarrow \varOmega ^1$ is defined by $X \times Y = Y \lrcorner X \lrcorner \varphi = *(X \wedge Y \wedge \psi )$. It satisfies the identity

$$\begin{aligned} X \times (X \times Y) = - g(X, X) Y + g(X, Y) X. \end{aligned}$$

Proof

This is part of Lemma A.1 in [12]. $\square$

In terms of a local frame, we define a map $\ell _{\varphi } : \varGamma (T^* M \otimes T^* M) \rightarrow \varOmega ^3$ by

$$\begin{aligned} \ell _{\varphi } A = A_{ip} g^{pq} e^i \wedge (e_q \lrcorner \varphi ). \end{aligned}$$

(2.6)

In components, we have

$$\begin{aligned} (\ell _{\varphi } A)_{ijk} = A_{ip} g^{pq} \varphi _{qjk} + A_{jp} g^{pq} \varphi _{iqk} + A_{kp} g^{pq} \varphi _{ijq}. \end{aligned}$$

Analogous to (2.6), we define $\ell _{\psi } : \varGamma (T^* M \otimes T^* M) \rightarrow \varOmega ^4$ by

$$\begin{aligned} \ell _{\psi } A = A_{ip} g^{pq} e^i \wedge (e_q \lrcorner \psi ). \end{aligned}$$

(2.7)

In components, we have

$$\begin{aligned} (\ell _{\psi } A)_{ijkl} = A_{ip} g^{pq} \psi _{qjkl} + A_{jp} g^{pq} \psi _{iqkl} + A_{kp} g^{pq} \psi _{ijql} + A_{lp} g^{pq} \psi _{ijkq}. \end{aligned}$$

It is easy to see that when $A = g$ is the metric, then

$$\begin{aligned} \ell _{\varphi } g = 3 \varphi , \quad \ell _{\psi } g = 4 \psi . \end{aligned}$$

(2.8)

In [12, Section 2.2], the map $\ell _{\varphi }$ is written as D, but we use $\ell _{\varphi }$ to avoid confusion with the many instances of ‘D’ throughout the present paper to denote various natural linear first-order differential operators. We can orthogonally decompose sections of $\varGamma (T^* M \otimes T^* M)$ into symmetric and skew-symmetric parts, which then further orthogonally decompose as

$$\begin{aligned} \varGamma (T^* M \otimes T^* M) = \varOmega ^0_1 \oplus \mathcal {S}_0\oplus \varOmega ^2_7 \oplus \varOmega ^2_{14}. \end{aligned}$$

In [12, Section 2.2], it is shown that $\ell _{\varphi }$ has kernel $\varOmega ^2_{14}$ and maps $\varOmega ^0_1$, $\mathcal {S}_0$, and $\varOmega ^2_7$ isomorphically onto $\varOmega ^3_1$, $\varOmega ^3_{27}$, and $\varOmega ^3_7$, respectively. One can similarly show that $\ell _{\psi }$ has kernel $\varOmega ^2_{14}$ and maps $\varOmega ^0_1$, $\mathcal {S}_0$, and $\varOmega ^2_7$ isomorphically onto $\varOmega ^4_1$, $\varOmega ^4_{27}$, and $\varOmega ^4_7$, respectively. (See also [15] for a detailed proof.) In particular, we note for future references that

$$\begin{aligned} \begin{aligned} \beta \in \varOmega ^2_{14}&\iff (\ell _{\varphi } \beta )_{ijk} = \beta _{ip} g^{pq} \varphi _{qjk} + \beta _{jp} g^{pq} \varphi _{iqk} + \beta _{kp} g^{pq} \varphi _{ijq} = 0, \\&\iff (\ell _{\psi } \beta )_{ijkl} = \beta _{ip} g^{pq} \psi _{qjkl} + \beta _{jp} g^{pq} \psi _{iqkl} \\&\quad \quad \quad + \beta _{kp} g^{pq} \psi _{ijql} + \beta _{lp} g^{pq} \psi _{ijkq} = 0. \end{aligned} \end{aligned}$$

(2.9)

When restricted to $\mathcal {S}$, the map $\ell _{\varphi }$ is denoted by i in [12]. We use $\ell _{\varphi }$ rather than i, to avoid confusion with the algebraic derivations $\iota _B$ and $\iota _K$ that we introduce later in Sect. 2.3.

Lemma 2.5

Let $h \in \mathcal {S}_0$. Then $*(\ell _{\varphi } h) = - \ell _{\psi } h$.

Proof

This is part of Proposition 2.14 in [12]. $\square$

The next two propositions will be crucial to establish properties of the algebraic derivations $\iota _B$ and $\iota _K$ in Sect. 2.3.

Proposition 2.6

Let $h = h_{ij} e^i e^j$ be a symmetric 2-tensor. The following identities hold:

$$\begin{aligned} \begin{aligned} h^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner \varphi )&= - 2 ({\text {Tr}}_g h) \psi + 2 \ell _{\psi } h, \\ h^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner \psi )&= 0, \\ h^{pq} (e_p \lrcorner \psi ) \wedge (e_q \lrcorner \psi )&= 0. \end{aligned} \end{aligned}$$

(2.10)

Proof

Let $\alpha \in \varOmega ^k$ and $\beta \in \varOmega ^l$. Then, we have

$$\begin{aligned} (e_p \lrcorner \alpha ) \wedge (e_q \lrcorner \beta ) = e_p \lrcorner \big ( \alpha \wedge (e_q \lrcorner \beta ) \big ) - (-1)^k \alpha \wedge (e_p \lrcorner e_q \lrcorner \beta ). \end{aligned}$$

Since the second term above is skew in p, q, when we contract with the symmetric tensor $h^{pq}$ we obtain

$$\begin{aligned} h^{pq} (e_p \lrcorner \alpha ) \wedge (e_q \lrcorner \beta ) = h^{pq} e_p \lrcorner \big ( \alpha \wedge (e_q \lrcorner \beta ) \big ). \end{aligned}$$

(2.11)

We will repeatedly use the identities from Lemma 2.3. When $\alpha = \beta = \psi$ in (2.11), we have $\psi \wedge (e_q \lrcorner \psi ) = 0$, establishing the third equation in (2.10). When $\alpha = \varphi$ and $\beta = \psi$ in (2.11), we have

$$\begin{aligned} \varphi \wedge (e_q \lrcorner \psi ) = - 4 *(g_{qm} e^m), \end{aligned}$$

and hence using that $X \lrcorner (*\alpha ) = - *(X^{\flat } \wedge \alpha )$ for $\alpha \in \varOmega ^1$, we find

$$\begin{aligned} h^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner \psi )&= h^{pq} e_p \lrcorner ( - 4 *g_{qm} e^m ) = -4 h^{pq} g_{qm} e_p \lrcorner (*e^m) \\&= + 4 h^{pq} g_{qm} *\big ( (e_p)^{\flat } \wedge e^m \big ) = 4 h^{pq} g_{qm} g_{pl} *(e^l \wedge e^m) \\&= 4 h_{lm} *(e^l \wedge e^m) = 0, \end{aligned}$$

establishing the second equation in (2.10). Finally, when $\alpha = \beta = \varphi$ in (2.11), we have

$$\begin{aligned} \varphi \wedge (e_q \lrcorner \varphi ) = - 2 *(e_q \lrcorner \varphi ) = - 2 \big ( \psi \wedge (e_q)^{\flat } \big ) = - 2 g_{qm} e^m \wedge \psi , \end{aligned}$$

and hence, using (2.7), we find

$$\begin{aligned} h^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner \varphi )&= h^{pq} e_p \lrcorner (- 2 g_{qm} e^m \wedge \psi ) = -2 h^{pq} g_{qm} e_p \lrcorner (e^m \wedge \psi ) \\&= - 2 h^{pq} g_{qm} \delta ^m_p \psi + 2 h^{pq} g_{qm} e^m \wedge (e_p \lrcorner \psi ) \\&= - 2 h^{pq} g_{pq} \psi + 2 h_{ml} g^{lp} e^m \wedge (e_p \lrcorner \psi ) = - 2 ({\text {Tr}}_g h) \psi + 2 \ell _{\psi } h, \end{aligned}$$

establishing the first equation in (2.10). $\square$

Proposition 2.7

For any fixed m, the following identities hold:

$$\begin{aligned} \begin{aligned} g^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner e_m \lrcorner \varphi )&= 3 (e_m \lrcorner \psi ), \\ g^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner e_m \lrcorner \psi )&= -3 *(e_m \lrcorner \psi ), \\ g^{pq} (e_p \lrcorner \psi ) \wedge (e_q \lrcorner e_m \lrcorner \varphi )&= -3 *(e_m \lrcorner \psi ), \\ g^{pq} (e_p \lrcorner \psi ) \wedge (e_q \lrcorner e_m \lrcorner \psi )&= 4 *(e_m \lrcorner \varphi ). \end{aligned} \end{aligned}$$

(2.12)

Proof

In this proof, we use $e^{ijk}$ to denote $e^i \wedge e^j \wedge e^k$ and similarly for any number of indices. First, we compute

$$\begin{aligned} g^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner e_m \lrcorner \varphi )&= \tfrac{1}{2} (g^{pq} \varphi _{pij} \varphi _{mqk}) e^{ijk} \\&= \tfrac{1}{2} ( g_{ik} g_{jm} - g_{im} g_{jk} - \psi _{ijkm}) e^{ijk} \\&= 0 - 0 - \tfrac{1}{2} \psi _{ijkm} e^{ijk} = 3 (\tfrac{1}{6} \psi _{mijk} e^{ijk}) = 3 (e_m \lrcorner \psi ), \end{aligned}$$

establishing the first equation in (2.12).

Similarly, we compute

$$\begin{aligned}&g^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner e_m \lrcorner \psi )\\&\quad = \tfrac{1}{4} (g^{pq} \varphi _{pij} \psi _{mqkl}) e^{ijkl} \\&\quad = \tfrac{1}{4} ( g_{ik} \varphi _{jlm} + g_{il} \varphi _{kjm} + g_{im} \varphi _{klj} - g_{jk} \varphi _{ilm} - g_{jl} \varphi _{kim} - g_{jm} \varphi _{kli} ) e^{ijkl} \\&\quad = 0 + 0 + \tfrac{1}{4} g_{im} \varphi _{klj} e^{ijkl} + 0 + 0 - \tfrac{1}{4} g_{jm} \varphi _{kli} e^{ijkl} = \tfrac{1}{2} g_{im} \varphi _{jkl} e^{ijkl} \\&\quad = 3 (g_{mi} e^i) \wedge \left( \tfrac{1}{6} \varphi _{jkl} e^{jkl} \right) = 3 (e_m)^{\flat } \wedge \varphi = - 3 *(e_m \lrcorner \psi ), \end{aligned}$$

establishing the second equation in (2.12). Now let $h = g$ in the second equation of (2.10). Taking the interior product of $g^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner \psi ) = 0$ with $e_m$, we obtain

$$\begin{aligned} g^{pq} (e_m \lrcorner e_p \lrcorner \varphi ) \wedge (e_q \lrcorner \psi ) + g^{pq} (e_p \lrcorner \varphi ) \wedge (e_m \lrcorner e_q \lrcorner \psi ) = 0, \end{aligned}$$

which, after rearrangement and relabeling of indices, becomes

$$\begin{aligned} g^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner e_m \lrcorner \psi ) = g^{pq} (e_p \lrcorner \psi ) \wedge (e_q \lrcorner e_m \lrcorner \varphi ), \end{aligned}$$

establishing the third equation in (2.12).

Finally, we compute

$$\begin{aligned}&g^{pq} (e_p \lrcorner \psi ) \wedge (e_q \lrcorner e_c \lrcorner \psi ) \\&\quad = \tfrac{1}{12} (g^{pq} \psi _{pijk} \psi _{cqab}) e^{ijkab} \\&\quad = -\tfrac{1}{12} (g^{pq} \psi _{ijkp} \psi _{abcq} ) e^{ijkab} \\&\quad = -\tfrac{1}{12} \bigg ( -\varphi _{ajk} \varphi _{ibc} - \varphi _{iak} \varphi _{jbc} - \varphi _{ija} \varphi _{kbc} + g_{ia} g_{jb} g_{kc} + g_{ib} g_{jc} g_{ka} \\&\qquad + g_{ic} g_{ja} g_{kb} - g_{ia} g_{jc} g_{kb} - g_{ib} g_{ja} g_{kc} - g_{ic} g_{jb} g_{ka} -g_{ia} \psi _{jkbc} \\&\qquad - g_{ja} \psi _{kibc} - g_{ka} \psi _{ijbc} + g_{ab} \psi _{ijkc} - g_{ac} \psi _{ijkb} \bigg ) e^{ijkab}. \end{aligned}$$

The first three terms above combine, and all the remaining terms except the last one vanish. Thus using Lemma 2.3, we have

$$\begin{aligned} g^{pq} (e_p \lrcorner \psi ) \wedge (e_q \lrcorner e_c \lrcorner \psi )&= -\tfrac{1}{12} ( -3 \varphi _{ajk} \varphi _{ibc} - g_{ac} \psi _{ijkb} ) e^{ijkab} \\&= -\tfrac{1}{4} (\varphi _{ajk} e^{ajk}) \wedge (\varphi _{cib} e^{ib}) - \tfrac{1}{12} (g_{ac} e^a) \wedge (\psi _{ijkb} e^{ijkb}) \\&= -3 ( \tfrac{1}{6} \varphi _{ajk} e^{ajk} ) \wedge ( \tfrac{1}{2} \varphi _{cib} e^{ib} ) - 2 (g_{ca} a^a) \wedge ( \tfrac{1}{24} \psi _{ijkb} e^{ijkb} ) \\&= -3 \varphi \wedge (e_c \lrcorner \varphi ) - 2 (e_c)^{\flat } \wedge \psi = 6 *(e_c \lrcorner \varphi ) \\&\quad - 2 *(e_c \lrcorner \varphi ) = 4 *(e_c \lrcorner \varphi ), \end{aligned}$$

establishing the fourth equation in (2.12). $\square$

For the rest of this section and all of the next section, we assume $(M, \varphi )$ is torsion-free. See also Remark 1.1.

Proposition 2.8

Suppose $(M, \varphi )$ is a torsion-free $\mathrm {G}_2$ manifold. Then $*(\pi _{27} {\mathcal {L}}_X \varphi ) = - \pi _{27} {\mathcal {L}}_X \psi$ for any vector field X.

Proof

Because $\varphi$ and $\psi$ are both parallel, from [12, equation (1.7)] we have

$$\begin{aligned} ({\mathcal {L}}_X \varphi ) = (\nabla _i X_p) g^{pq} e^i \wedge (e_q \lrcorner \varphi ), \quad ({\mathcal {L}}_X \psi ) = (\nabla _i X_p) g^{pq} e^i \wedge (e_q \lrcorner \psi ). \end{aligned}$$

Applying $\pi _{27}$ to both of the above expressions and using Lemma 2.5 yields the desired result. $\square$

2.2 The exterior derivative $\mathrm {d}$ and the Hodge Laplacian $\varDelta$

In this section, we analyze the exterior derivative $\mathrm {d}$ and the Hodge Laplacian $\varDelta$ on a manifold with torsion-free $\mathrm {G}_2$-structure. Much, but not all, of the results in this section have appeared before, without proof, in [2, Section 5.2]. See Remark 2.18 for details. Theorem 2.19, which relates kernels of various operators on $\varOmega ^1$, is fundamental to the rest of the paper and appears to be new.

We first define three first-order operators on torsion-free $\mathrm {G}_2$ manifolds, which will be used to decompose $\mathrm {d}: \varOmega ^k \rightarrow \varOmega ^{k+1}$ into components. More details can be found in [13, Section 4].

Definition 2.9

Let $(M, \varphi )$ be a torsion-free $\mathrm {G}_2$ manifold. We define the following first-order linear differential operators:

$$\begin{aligned} {\text {grad}}: \varOmega ^0_1&\rightarrow \varOmega ^1_7,&f&\mapsto \mathrm {d}f, \\ {\text {div}}: \varOmega ^1_7&\rightarrow \varOmega ^0_1,&X&\mapsto - {\mathrm {d}}{}^{\star }X, \\ {\text {curl}}: \varOmega ^1_7&\rightarrow \varOmega ^1_7,&X&\mapsto *(\psi \wedge \mathrm {d}X). \end{aligned}$$

In a local frame, these operators have the following form:

$$\begin{aligned} ({\text {grad}}f)_k = \nabla _k f, \quad {\text {div}}X = g^{ij} \nabla _i X_j, \quad ({\text {curl}}X)_k = (\nabla _i X_j) g^{ip} g^{jq} \varphi _{pqk}. \end{aligned}$$

(2.13)

$\square$

Definition 2.10

Denote by $D^{l}_{m}$ the composition

$$\begin{aligned} D^l_m : \varOmega ^k_l \hookrightarrow \varOmega ^k \xrightarrow {\mathrm {d}} \varOmega ^{k+1} \twoheadrightarrow \varOmega ^{k+1}_{m}, \end{aligned}$$

where k is the smallest integer such that this composition makes sense. Here the surjection is the projection $\pi ^{k+1}_m$. That is, $D^l_m = \pi ^{k+1}_m \circ {\left. {\mathrm {d}} \right| }_{\varOmega ^k_l}$. $\square$

Proposition 2.11

The operators $D^1_1$, $D^1_{14}$, $D^{14}_1$, $D^1_{27}$, $D^{27}_1$, and $D^{14}_{14}$ are all zero.

Proof

It is clear from (2.2) that $D^{14}_{14} = 0$. The operators $D^1_1 : \varOmega ^3_1 \rightarrow \varOmega ^4_1$ and $D^1_{27} : \varOmega ^3_1 \rightarrow \varOmega ^4_{27}$ are both zero because $\mathrm {d}(f \varphi ) = (\mathrm {d}f) \wedge \psi \in \varOmega ^4_7$. Similarly, since $\mathrm {d}(f \psi ) = (\mathrm {d}f) \wedge \psi \in \varOmega ^5_7$, we also have $D^1_{14} = 0$. If $\beta \in \varOmega ^2_{14}$, then $\beta \wedge \psi = 0$, so $(\mathrm {d}\beta ) \wedge \psi = 0$, and thus $\pi _1 (\mathrm {d}\beta ) = 0$, hence $D^{14}_1 = 0$. Similarly, if $\beta \in \varOmega ^3_{27}$, then $\beta \wedge \varphi = 0$, so $(\mathrm {d}\beta ) \wedge \varphi = 0$, and thus $\pi _1 (\mathrm {d}\beta ) = 0$, hence $D^{27}_1 = 0$. $\square$

Fig. 1

Decomposition of the exterior derivative $\mathrm {d}$ into components

Proposition 2.12

With respect to the identifications described in (2.3), the components of the exterior derivative $\mathrm {d}$ satisfy the relations given in Fig. 1.

Proof

We will use repeatedly the contraction identities of Lemma 2.1 and descriptions (2.3) of the $\varOmega ^k_l$ spaces.

• (i) We establish the relations for $\pi _7 \mathrm {d}\pi _1 : \varOmega ^k_1 \rightarrow \varOmega ^{k+1}_7$ for $k=0,3,4$. $k=0$: Let $f \in \varOmega ^0_1$. By Definition 2.10, we have $D^1_7 f = \mathrm {d}f$. $k=3$: Let $\beta = f \varphi \in \varOmega ^3_1$. Since $\mathrm {d}\beta = (\mathrm {d}f) \wedge \varphi \in \varOmega ^4_7$, we have $\pi _7 (\mathrm {d}\beta ) = - \varphi \wedge (\mathrm {d}f) = - *( (\mathrm {d}f) \lrcorner \psi )$, so $\pi _7 \mathrm {d}\pi _1 : \varOmega ^3_1 \rightarrow \varOmega ^4_7$ is identified with $-D^1_7$. $k=4$: Let $\gamma = f \psi \in \varOmega ^4_1$. Since $\mathrm {d}\gamma = (\mathrm {d}f) \wedge \psi \in \varOmega ^5_7$, we have $\pi _7 (\mathrm {d}\gamma ) = \psi \wedge (\mathrm {d}f) = *( (\mathrm {d}f) \lrcorner \varphi )$, so $\pi _7 \mathrm {d}\pi _1 : \varOmega ^4_1 \rightarrow \varOmega ^5_7$ is identified with $D^1_7$.

• (ii) We establish the relations for $\pi _1 \mathrm {d}\pi _7 : \varOmega ^k_7 \rightarrow \varOmega ^{k+1}_1$ for $k=2,3,6$. $k=2$: Let $\alpha = X \lrcorner \varphi \in \varOmega ^2_7$. Then $(\pi _1 \mathrm {d}\alpha )_{ijk} = f \varphi _{ijk}$ for some function f. Using (2.4), we compute

  $$\begin{aligned} (\mathrm {d}\alpha )_{ijk} g^{ia} g^{jb} g^{kc} \varphi _{abc}&= (\pi _1 \mathrm {d}\alpha )_{ijk} g^{ia} g^{jb} g^{kc} \varphi _{abc} = f \varphi _{ijk} g^{ia} g^{jb} g^{kc} \varphi _{abc} = 42 f, \\&= ( \nabla _i \alpha _{jk} + \nabla _j \alpha _{ki} + \nabla _k \alpha _{ij} ) g^{ia} g^{jb} g^{kc} \varphi _{abc} \\&= 3 (\nabla _i \alpha _{jk}) g^{ia} g^{jb} g^{kc} \varphi _{abc}, \end{aligned}$$

  and thus $f = \tfrac{3}{42} (\nabla _i \alpha _{jk}) g^{ia} g^{jb} g^{kc} \varphi _{abc}$. Substituting $\alpha _{jk} = X^m \varphi _{mjk}$, we obtain

  $$\begin{aligned} f = \tfrac{3}{42} (\nabla _i X^m) \varphi _{mjk} \varphi _{abc} g^{ia} g^{jb} g^{kc} = \tfrac{18}{42} (\nabla _i X^m) g^{ia} g_{ma} = \tfrac{3}{7} \nabla _i X^i, \end{aligned}$$

  and comparing with Definition 2.9, we find that

  $$\begin{aligned} D^7_1 X = \pi _1 \mathrm {d}(X \lrcorner \varphi ) = f \varphi = (\tfrac{3}{7} {\text {div}}X) \varphi . \end{aligned}$$

  (2.14)

  $k=3$: Let $\beta = X \lrcorner \psi \in \varOmega ^3_7$. Then $(\pi _1 \mathrm {d}\beta )_{ijkl} = f \psi _{ijkl}$ for some function f. Using (2.5), we compute

  $$\begin{aligned} (\mathrm {d}\beta )_{ijkl} g^{ia} g^{jb} g^{kc} g^{ld} \psi _{abcd}&= (\pi _1 \mathrm {d}\beta )_{ijkl} g^{ia} g^{jb} g^{kc} g^{ld} \psi _{abcd} \\&= f \psi _{ijkl} g^{ia} g^{jb} g^{kc} g^{ld} \psi _{abcd} = 168 f, \\&= ( \nabla _i \beta _{jkl} - \nabla _j \beta _{ikl} + \nabla _k \beta _{ijl} - \nabla _l \beta _{ijk} ) g^{ia} g^{jb} g^{kc} g^{ld} \psi _{abcd} \\&= 4 (\nabla _i \beta _{jkl}) g^{ia} g^{jb} g^{kc} g^{ld} \psi _{abcd}, \end{aligned}$$

  and thus $f = \tfrac{4}{168} (\nabla _i \beta _{jkl}) g^{ia} g^{jb} g^{kc} g^{ld} \psi _{abcd}$. Substituting $\beta _{jkl} = X^m \psi _{mjkl}$, we obtain

  $$\begin{aligned} f = \tfrac{4}{168} (\nabla _i X^m) \psi _{mjkl} \psi _{abcd} g^{ia} g^{jb} g^{kc} g^{ld} = \tfrac{4 \cdot 24}{168} (\nabla _i X^m) g^{ia} g_{ma} = \tfrac{4}{7} \nabla _i X^i, \end{aligned}$$

  and comparing with (2.14), we find that $\pi _1 \mathrm {d}\pi _7 : \varOmega ^3_7 \rightarrow \varOmega ^4_1$ is identified with $\tfrac{4}{3} D^7_1$. $k=6$: Let $*X \in \varOmega ^6_7$. Then $\pi _1 \mathrm {d}(*X) = \mathrm {d}*X = *^2 \mathrm {d}*X = - *({\mathrm {d}}{}^{\star }X) = - ({\mathrm {d}}{}^{\star }X) \mathsf {vol}$, where we have used ${\mathrm {d}}{}^{\star }= - *\mathrm {d}*$ on odd forms. Comparing with Definition 2.9 and (2.14), we find that $\pi _1 \mathrm {d}\pi _7 : \varOmega ^6_7 \rightarrow \varOmega ^7_1$ is identified with $\tfrac{7}{3} D^7_1$.

• (iii) We establish the relations for $\pi _7 \mathrm {d}\pi _7 : \varOmega ^k_7 \rightarrow \varOmega ^{k+1}_7$ for $k=1,2,3,4,5$. $k=1$: Let $X \in \varOmega ^1_7$. Then $(\pi _7 \mathrm {d}X)_{ij} = Y^m \varphi _{mij}$ for some vector field Y. We compute

  $$\begin{aligned} (\mathrm {d}X)_{ij} g^{ia} g^{jb} \varphi _{kab}&= (\pi _7 \mathrm {d}X)_{ij} g^{ia} g^{jb} \varphi _{kab} = Y^m \varphi _{mij} g^{ia} g^{jb} \varphi _{kab} = 6 Y_k, \\&= ( \nabla _i X_j - \nabla _j X_i ) g^{ia} g^{jb} \varphi _{kab} = 2 (\nabla _i X_j) g^{ia} g^{jb} \varphi _{abk}, \end{aligned}$$

  from which it follows from Definition 2.10 that

  $$\begin{aligned} D^7_7 X = \pi _7 \mathrm {d}X = Y = \tfrac{1}{3} {\text {curl}}X. \end{aligned}$$

  (2.15)

  $k=2$: Let $\alpha = X \lrcorner \varphi \in \varOmega ^2_7$. Then $(\pi _7 \mathrm {d}\alpha )_{ijk} = Y^m \psi _{mijk}$ for some vector field Y. Using (2.4), we compute

  $$\begin{aligned}&(\mathrm {d}\alpha )_{ijk} g^{ia} g^{jb} g^{kc} \psi _{labc} \\&\quad = (\pi _7 \mathrm {d}\alpha )_{ijk} g^{ia} g^{jb} g^{kc} \psi _{labc} = Y^m \psi _{mijk} g^{ia} g^{jb} g^{kc} \psi _{labc} = 24 Y_l, \\&\quad = ( \nabla _i \alpha _{jk} + \nabla _j \alpha _{ki} + \nabla _k \alpha _{ij} ) g^{ia} g^{jb} g^{kc} \psi _{labc}\\&\quad = 3 (\nabla _i \alpha _{jk}) g^{ia} g^{jb} g^{kc} \psi _{labc}, \end{aligned}$$

  and thus $Y_l = \tfrac{1}{8} (\nabla _i \alpha _{jk}) g^{ia} g^{jb} g^{kc} \psi _{labc}$. Substituting $\alpha _{jk} = X^m \varphi _{mjk}$, we obtain

  $$\begin{aligned} Y_l = \tfrac{1}{8} (\nabla _i X^m) \varphi _{mjk} \psi _{labc} g^{ia} g^{jb} g^{kc} = -\tfrac{4}{8} (\nabla _i X^m) g^{ia} \varphi _{mla} = - \tfrac{1}{2} {\text {curl}}X, \end{aligned}$$

  and comparing with (2.15), we find that $\pi _7 \mathrm {d}\pi _7 : \varOmega ^2_7 \rightarrow \varOmega ^3_7$ is identified with $-\tfrac{3}{2} D^7_7$. $k=3$: Let $\beta = X \lrcorner \psi \in \varOmega ^3_7$. Then $\pi _7 (\mathrm {d}\beta ) = *(Y \lrcorner \psi ) = \varphi \wedge Y$ for some vector field Y. We have $(\pi _7 \mathrm {d}\beta )_{ijkl} = \varphi _{ijk} Y_l - \varphi _{ijl} Y_k + \varphi _{ikl} Y_j - \varphi _{jkl} Y_i$. Using (2.4), we compute

  $$\begin{aligned}&(\mathrm {d}\beta )_{ijkl} g^{ia} g^{jb} g^{kc} \varphi _{abc} \\&\quad = (\pi _7 \mathrm {d}\beta )_{ijkl} g^{ia} g^{jb} g^{kc} \varphi _{abc} \\&\quad = (\varphi _{ijk} Y_l - \varphi _{ijl} Y_k + \varphi _{ikl} Y_j - \varphi _{jkl} Y_i) g^{ia} g^{jb} g^{kc} \varphi _{abc} \\&\quad = 42 Y_l - 3 \varphi _{ijl} Y_k g^{ia} g^{jb} g^{kc} \varphi _{abc} = 42 Y_l - 3(6 Y_k g^{kc} g_{lc}) = 24 Y_l. \end{aligned}$$

  But we also have

  $$\begin{aligned} (\mathrm {d}\beta )_{ijkl} g^{ia} g^{jb} g^{kc} \varphi _{abc}&= ( \nabla _i \beta _{jkl} - \nabla _j \beta _{ikl} + \nabla _k \beta _{ijl} - \nabla _l \beta _{ijk} ) g^{ia} g^{jb} g^{kc} \varphi _{abc} \\&= 3 (\nabla _i \beta _{jkl}) g^{ia} g^{jb} g^{kc} \varphi _{abc} - (\nabla _l \beta _{ijk}) g^{ia} g^{jb} g^{kc} \varphi _{abc}. \end{aligned}$$

  Substituting $\beta _{ijk} = X^m \psi _{mijk}$, we obtain

  $$\begin{aligned} (\mathrm {d}\beta )_{ijkl} g^{ia} g^{jb} g^{kc} \varphi _{cab}&= 3 (\nabla _i X^m) \psi _{mljk} g^{ia} g^{jb} g^{kc} \varphi _{abc} - (\nabla _l X^m) \psi _{mijk} g^{ia} g^{jb} g^{kc} \varphi _{abc} \\&= - 12 (\nabla _i X^m) g^{ia} \varphi _{aml} - 0, \end{aligned}$$

  and thus $Y_l = -\tfrac{12}{24} (\nabla _i X^m) g^{ia} \varphi _{aml} = - \tfrac{1}{2} {\text {curl}}X$. Comparing with (2.15), we find that $\pi _7 \mathrm {d}\pi _7 : \varOmega ^3_7 \rightarrow \varOmega ^4_7$ is identified with $-\tfrac{3}{2} D^7_7$. $k=4$: Let $\gamma = *( X \lrcorner \psi ) = \varphi \wedge X \in \varOmega ^4_7$. Then $\pi _7 (\mathrm {d}\gamma ) = \pi _7 \mathrm {d}(\varphi \wedge X) = -\pi _7 (\varphi \wedge \mathrm {d}X) = *( Y \lrcorner \varphi )$ for some vector field Y. We compute

  $$\begin{aligned} *( Y \lrcorner \varphi ) = -\pi _7 (\varphi \wedge \mathrm {d}X) = - \varphi \wedge (\pi _7 \mathrm {d}X) = 2 *(\pi _7 \mathrm {d}X). \end{aligned}$$

  Comparing with (2.15), we find that $\pi _7 \mathrm {d}\pi _7 : \varOmega ^4_7 \rightarrow \varOmega ^5_7$ is identified with $2 D^7_7$. $k=5$: Let $\eta = *( X \lrcorner \varphi ) = \psi \wedge X \in \varOmega ^5_7$. Then $\pi _7 (\mathrm {d}\eta ) = \mathrm {d}\eta = \mathrm {d}(\psi \wedge X) = \psi \wedge \mathrm {d}X = *Y$ for some vector field Y. Using Definition 2.9, we compute

  $$\begin{aligned} Y = *( \psi \wedge \mathrm {d}X) = {\text {curl}}X. \end{aligned}$$

  Comparing with (2.15) we find that $\pi _7 \mathrm {d}\pi _7 : \varOmega ^5_7 \rightarrow \varOmega ^6_7$ is identified with $3 D^7_7$.

• (iv) We establish the relations for $\pi _{14} \mathrm {d}\pi _7 : \varOmega ^k_7 \rightarrow \varOmega ^{k+1}_{14}$ for $k=1,4$. $k=1$: Let $X \in \varOmega ^1_7$. By definition, we have $\pi _{14} \mathrm {d}X = D^7_{14} X$. $k=4$. Let $\gamma = *(X \lrcorner \psi ) = \varphi \wedge X \in \varOmega ^4_7$. Then $\mathrm {d}\gamma = - \varphi \wedge (\mathrm {d}X)$, so $\pi _{14} \mathrm {d}\gamma = - \pi _{14} (\varphi \wedge \mathrm {d}X) = - \varphi \wedge (\pi _{14} \mathrm {d}X) = - *(\pi _{14} \mathrm {d}X)$. Thus, we find that $\pi _{14} \mathrm {d}\pi _7 : \varOmega ^4_7 \rightarrow \varOmega ^5_{14}$ is identified with $- D^7_{14}$.

• (v) We establish the relations for $\pi _7 \mathrm {d}\pi _{14} : \varOmega ^k_{14} \rightarrow \varOmega ^{k+1}_7$ for $k=2,5$. $k=1$: Let $\alpha \in \varOmega ^2_{14}$. By definition, we have $\pi _7 \mathrm {d}\alpha = D^{14}_7 X$. $k=4$. Let $\eta = *\beta \in \varOmega ^5_{14}$ where $\beta \in \varOmega ^2_{14}$. We have $*\beta = \varphi \wedge \beta$, so $\pi _7 \mathrm {d}(*\beta ) = \mathrm {d}(*\beta ) = - \varphi \wedge \mathrm {d}\beta \in \varOmega ^6_7$. We can write $\pi _7 \mathrm {d}\beta = Y \lrcorner \psi \in \varOmega ^3_7$ for some vector field Y. Then using Lemma 2.3, we find $\pi _7 \mathrm {d}(*\beta ) = - \varphi \wedge \mathrm {d}\beta = - \varphi \wedge (\pi _7 \mathrm {d}\beta ) = - \varphi \wedge (Y \lrcorner \psi ) = 4 *Y$. Thus, we find that $\pi _7 \mathrm {d}\pi _{14} : \varOmega ^5_{14} \rightarrow \varOmega ^6_7$ is identified with $4 D^{14}_7$.

• (vi) We establish the relations for $\pi _{27} \mathrm {d}\pi _7 : \varOmega ^k_7 \rightarrow \varOmega ^{k+1}_{27}$ for $k=2,3$. $k=2$: Let $\alpha \in \varOmega ^2_7$. By definition, we have $\pi _{27} \mathrm {d}\alpha = D^7_{27} \alpha$. $k=3$: Let $\beta = X \lrcorner \psi \in \varOmega ^4_7$. Then $\pi _{27} \mathrm {d}\beta = \pi _{27} \mathrm {d}(X \lrcorner \psi ) = \pi _{27} {\mathcal {L}}_X \psi$. Consider $\alpha = X \lrcorner \varphi$. Then similarly, we have $\pi _{27} \mathrm {d}\alpha = \pi _{27} {\mathcal {L}}_X \varphi$. By Proposition 2.8, we have $\pi _{27} \mathrm {d}(X \lrcorner \psi ) = - *(\pi _{27} \mathrm {d}(X \lrcorner \varphi ))$. Thus, we find that $\pi _{27} \mathrm {d}\pi _7 : \varOmega ^3_{27} \rightarrow \varOmega ^4_7$ is identified with $- D^7_{27}$.

• (vii) We establish the relations for $\pi _7 \mathrm {d}\pi _{27} : \varOmega ^k_{27} \rightarrow \varOmega ^{k+1}_7$ for $k=3,4$. $k=3$: Let $\beta = \ell _{\varphi } h \in \varOmega ^3_{27}$, where $h \in \mathcal {S}_0$. Then $\pi _7 (\mathrm {d}\beta ) = *(Y \lrcorner \psi ) = \varphi \wedge Y$ for some vector field Y. We have $(\pi _7 \mathrm {d}\beta )_{ijkl} = \varphi _{ijk} Y_l - \varphi _{ijl} Y_k + \varphi _{ikl} Y_j - \varphi _{jkl} Y_i$. Using (2.5), we compute

  $$\begin{aligned} (\mathrm {d}\beta )_{ijkl} g^{ia} g^{jb} g^{kc} \varphi _{abc}&= (\pi _7 \mathrm {d}\beta )_{ijkl} g^{ia} g^{jb} g^{kc} \varphi _{abc} \\&= (\varphi _{ijk} Y_l - \varphi _{ijl} Y_k + \varphi _{ikl} Y_j - \varphi _{jkl} Y_i) g^{ia} g^{jb} g^{kc} \varphi _{abc} \\&= 42 Y_l - 3 \varphi _{ijl} Y_k g^{ia} g^{jb} g^{kc} \varphi _{abc} = 42 Y_l - 3(6 Y_k g^{kc} g_{lc}) = 24 Y_l. \end{aligned}$$

  But we also have

  $$\begin{aligned} (\mathrm {d}\beta )_{ijkl} g^{ia} g^{jb} g^{kc} \varphi _{abc}&= ( \nabla _i \beta _{jkl} - \nabla _j \beta _{ikl} + \nabla _k \beta _{ijl} - \nabla _l \beta _{ijk} ) g^{ia} g^{jb} g^{kc} \varphi _{abc} \\&= 3 (\nabla _i \beta _{jkl}) g^{ia} g^{jb} g^{kc} \varphi _{abc} - (\nabla _l \beta _{ijk}) g^{ia} g^{jb} g^{kc} \varphi _{abc}. \end{aligned}$$

  Substituting $\beta _{ijk} = h_{ip} g^{pq} \varphi _{qjk} + h_{jp} g^{pq} \varphi _{qki} + h_{kp} g^{pq} \varphi _{qjk}$, we obtain

  $$\begin{aligned} 24 Y_l&= (\mathrm {d}\beta )_{ijkl} g^{ia} g^{jb} g^{kc} \varphi _{cab} \\&= 3 (\nabla _i (h_{jp} g^{pq} \varphi _{qkl} + h_{kp} g^{pq} \varphi _{qlj} + h_{lp} g^{pq} \varphi _{qjk})) g^{ia} g^{jb} g^{kc} \varphi _{abc} \\&\qquad {} - (\nabla _l (h_{ip} g^{pq} \varphi _{qjk} + h_{jp} g^{pq} \varphi _{qki} + h_{kp} g^{pq} \varphi _{qjk})) g^{ia} g^{jb} g^{kc} \varphi _{abc} \\&= 6 (\nabla _i h_{jp}) g^{pq} g^{ia} g^{jb} (g^{kc} \varphi _{lqk} \varphi _{abc}) + 3 (\nabla _i h_{lp}) g^{pq} g^{ia} (g^{jb} g^{kc} \varphi _{qjk} \varphi _{abc}) \\&\qquad {} - 3 (\nabla _l h_{ip}) g^{pq} g^{ia} (g^{jb} g^{kc} \varphi _{qjk} \varphi _{abc}). \end{aligned}$$

  We further simplify this as

  $$\begin{aligned} 24 Y_l&= 6 (\nabla _i h_{jp}) g^{pq} g^{ia} g^{jb} (g_{la} g_{qb} - g_{lb} g_{qa} - \psi _{lqab}) \\&\quad + 3 (\nabla _i h_{lp}) g^{pq} g^{ia} (6 g_{qa}) - 3 (\nabla _l h_{ip}) g^{pq} g^{ia} (6 g_{qa}) \\&= 6 (\nabla _l h_{jp}) g^{jp} - 6 (\nabla _i h_{lp} )g ^{ip} - 0 + 18 (\nabla _i h_{lp}) g^{ip} - 18 (\nabla _l h_{ip}) g^{ip} \\&= 6 \nabla _l ({\text {Tr}}h) - 6 (\nabla _{i} h_{jl}) g^{ij} + 18 (\nabla _i h_{jl}) g^{ij} - 18 \nabla _l ({\text {Tr}}h) = 12 g^{ij} (\nabla _{i} h_{jl}), \end{aligned}$$

  and thus $Y_l = \tfrac{1}{2} g^{ij} (\nabla _{i} h_{jl})$. It follows from Definition 2.10 that

  $$\begin{aligned} D^{27}_7 h = \pi _7 \mathrm {d}(\ell _{\varphi } h) = *( Y \lrcorner \psi ), \quad \hbox { where}\ Y_l = \tfrac{1}{2} g^{ij} (\nabla _{i} h_{jl}). \end{aligned}$$

  (2.16)

  $k=4$: Let $\gamma = *(\ell _{\varphi } h) \in \varOmega ^4_{27}$, where $h \in \mathcal {S}_0$. Then $\pi _7 (\mathrm {d}\gamma ) = *(Y \lrcorner \varphi )$ for some vector field Y. Taking Hodge star of both sides, we have $Y \lrcorner \varphi = *\pi _7 (\mathrm {d}*\ell _{\varphi } h) = \pi _7 *\mathrm {d}*(\ell _{\varphi } h) = -\pi _7 {\mathrm {d}}{}^{\star }(\ell _{\varphi } h)$. Thus, we have

  $$\begin{aligned} -({\mathrm {d}}{}^{\star }(\ell _{\varphi } h))_{ij} g^{ia} g^{jb} \varphi _{kab}&= -(\pi _7 {\mathrm {d}}{}^{\star }(\ell _{\varphi } h))_{ij} g^{ia} g^{jb} \varphi _{kab} = (Y \lrcorner \varphi )_{ij} g^{ia} g^{jb} \varphi _{kab} \\&= Y^m \varphi _{mij} g^{ia} g^{jb} \varphi _{kab} = 6 Y_k. \end{aligned}$$

  But we also have

  $$\begin{aligned}&-({\mathrm {d}}{}^{\star }(\ell _{\varphi } h))_{ij} g^{ia} g^{jb} \varphi _{kab}\\&\quad = g^{pq} (\nabla _p (\ell _{\varphi } h)_{qij}) g^{ia} g^{jb} \varphi _{kab} \\&\quad = g^{pq} (\nabla _p (h_{ql} g^{lm} \varphi _{mij} + h_{il} g^{lm} \varphi _{mjq} + h_{jl} g^{lm} \varphi _{mqi})) g^{ia} g^{jb} \varphi _{kab} \\&\quad = g^{pq} (\nabla _p h_{ql}) g^{lm} (g^{ia} g^{jb} \varphi _{mij} \varphi _{kab}) + 2 g^{pq} (\nabla _p h_{il}) g^{lm} g^{ia} (g^{jb} \varphi _{qmj} \varphi _{kab}) \\&\quad = g^{pq} (\nabla _p h_{ql}) g^{lm} (6 g_{mk}) + 2 g^{pq} (\nabla _p h_{il}) g^{lm} g^{ia} (g_{qk} g_{ma} - g_{qa} g_{mk} - \psi _{qmka}) \\&\quad = 6 g^{pq} (\nabla _p h_{qk}) + 2 \nabla _k ({\text {Tr}}h) - 2 g^{ip} (\nabla _p h_{ik}) - 0 = 4 g^{ij} (\nabla _{i} h_{jk}) \end{aligned}$$

  Thus, we have $Y_k = \tfrac{2}{3} g^{ij} (\nabla _{i} h_{jk}) = \tfrac{4}{3} (\tfrac{1}{2} g^{ij} (\nabla _{i} h_{jk}))$. Comparing with (2.16), we find that $\pi _7 \mathrm {d}\pi _{27} : \varOmega ^4_{27} \rightarrow \varOmega ^5_7$ is identified with $\tfrac{4}{3} D^{27}_7$.

$\square$

Corollary 2.13

The operators of Definition 2.10 satisfy the following fourteen relations:

$$\begin{aligned} \begin{aligned} D^7_7 D^1_7&= 0, \qquad \qquad&D^7_{14} D^1_7&= 0, \\ D^7_1 D^7_7&= 0, \qquad \qquad&\tfrac{3}{2} D^7_7 D^7_7 - D^{14}_7 D^7_{14}&= 0, \\ - D^1_7 D^7_1 + \tfrac{9}{4} D^7_7 D^7_7 + D^{27}_7 D^7_{27}&= 0, \qquad \qquad&\tfrac{3}{2} D^7_{14} D^7_7 - D^{27}_{14} D^7_{27}&= 0, \\ \tfrac{3}{2} D^7_{27} D^7_7 + D^{27}_{27} D^7_{27}&= 0, \qquad \qquad&D^7_{27} D^7_7 + D^{14}_{27} D^7_{14}&= 0, \\ D^7_1 D^{14}_7&= 0, \qquad \qquad&\tfrac{3}{2} D^7_7 D^{14}_7 - D^{27}_7 D^{14}_{27}&= 0, \\ D^7_{27} D^{14}_7 - D^{27}_{27} D^{14}_{27}&= 0, \qquad \qquad&D^7_7 D^{27}_7 + D^{14}_7 D^{27}_{14}&= 0, \\ \tfrac{3}{2} D^7_7 D^{27}_7 + D^{27}_7 D^{27}_{27}&= 0, \qquad \qquad&D^7_{14} D^{27}_7 - D^{27}_{14} D^{27}_{27}&= 0. \end{aligned} \end{aligned}$$

(2.17)

Proof

These relations all follow from Fig. 1 and the fact that $\mathrm {d}^2 = 0$, by computing $\pi _{l'} \mathrm {d}^2 \pi _{l} : \varOmega ^k_l \rightarrow \varOmega ^{k+2}_{l'}$ for all $l, l' \in \{ 1, 7, 14, 27 \}$ and all $k = 0, \ldots , 5$. Some of the relations arise multiple times this way. Moreover, there are two distinct relations for $(l, l') = (7,7)$, (7, 27), and (27, 7). $\square$

Corollary 2.14

Consider the maps $D^l_m : \varOmega ^k_l \rightarrow \varOmega ^{k+1}_m$ introduced in Definition 2.10. Recall these were only defined for the smallest integer k where the composition makes sense. The formal adjoint is a map $(D^l_m)^* : \varOmega ^{k+1}_m \rightarrow \varOmega ^l_m$. With respect to the identifications described in (2.3), these adjoint maps are given by

$$\begin{aligned} \begin{aligned} (D^1_7)^*&= -\tfrac{7}{3} D^7_1, \qquad&(D^7_7)^*&= 3 D^7_7, \qquad&(D^7_{14})^*&= 4 D^{14}_7, \\ (D^7_1)^*&= - D^1_7, \qquad&(D^7_{27})^*&= - \tfrac{4}{3} D^{27}_7, \qquad&(D^{14}_7)^*&= D^7_{14}, \\ (D^{14}_{27})^*&= - D^{27}_{14}, \qquad&(D^{27}_7)^*&= - D^7_{27}, \qquad&(D^{27}_{27})^*&= D^{27}_{27}, \\ (D^{27}_{14})^*&= - D^{14}_{27}. \end{aligned} \end{aligned}$$

(2.18)

Proof

These follow from Fig. 1 and the facts that ${\mathrm {d}}{}^{\star }= (-1)^k *\mathrm {d}*$ on $\varOmega ^k$ and that $*$ is compatible with the identifications given in (2.3). $\square$

Remark 2.15

One has to be very careful with the ‘equations’ in (2.18). In particular, taking the adjoint of both sides of an equation in (2.18) in general violates $P^{**} = P$. This is because these are not really equalities, but identifications, and recall that unfortunately the identifications in (2.2) are not isometries, as explained in Remark 2.2. However, this will not cause us any problems, because the notation $D^l_m$ will always only refer to the maps introduced in Definition 2.10, and we will never have need to consider the adjoints of any other components of $\mathrm {d}$. $\square$

We can now describe the Hodge Laplacian $\varDelta = \mathrm {d}{\mathrm {d}}{}^{\star }+ {\mathrm {d}}{}^{\star }\mathrm {d}$ on each summand $\varOmega ^k_l$ in terms of the operators of Definition 2.10.

Proposition 2.16

On $\varOmega ^k_l$, the Hodge Laplacian $\varDelta$ can be written as follows:

$$\begin{aligned} \begin{aligned} \left. \varDelta \right| _{\varOmega ^k_1}&= -\tfrac{7}{3} D^7_1 D^1_7&\hbox { for}\ k=0,3,4,7, \\ \left. \varDelta \right| _{\varOmega ^k_7}&= 9 D^7_7 D^7_7 - \tfrac{7}{3} D^1_7 D^7_1&\hbox { for}\ k=1,2,3,4,5,6, \\ \left. \varDelta \right| _{\varOmega ^k_{14}}&= 5 D^7_{14} D^{14}_7 - D^{27}_{14} D^{14}_{27}&\hbox { for}\ k=2,5, \\ \left. \varDelta \right| _{\varOmega ^k_{27}}&= -\tfrac{7}{3} D^7_{27} D^{27}_7 - D^{14}_{27} D^{27}_{14} + (D^{27}_{27})^2&\text { for } k=3,4. \end{aligned} \end{aligned}$$

(2.19)

Proof

Recall that ${\mathrm {d}}{}^{\star }= (-1)^k *\mathrm {d}*$ on $\varOmega ^k$ and that $*$ is compatible with the identifications given in (2.3). The expressions in (2.19) can be checked on a case-by-case basis using these facts, Fig. 1, and the relations in Corollary 2.13. Note that one can show from general principles that $\varDelta _{\mathrm {d}}$ preserves splittings (2.2) when $\varphi$ is parallel, which we always assume. (See [11] for details.) However, the proof of the present proposition gives an explicit verification of this fact, viewing it as a consequence of fundamental relations (2.17). $\square$

Remark 2.17

We emphasize that for Proposition 2.12, Corollary 2.13, and Proposition 2.16, the torsion-free assumption is essential, as the proofs frequently made use of $\nabla \varphi = \nabla \psi = \mathrm {d}\varphi = \mathrm {d}\psi = 0$. For $\mathrm {G}_2$-structures with torsion, there would be many additional terms involving torsion, and in particular the Laplacian $\varDelta$ would not preserve splittings (2.2). See also Remark 1.1. $\square$

Remark 2.18

As mentioned in Introduction, the results of Proposition 2.12, Corollary 2.13, and Proposition 2.16 have appeared before in [2, Section 5.2, Tables 1–3], where Bryant says the results follow by routine computation. We have presented all the details for completeness and for readers to be able to use the computational techniques for possible future applications. Note that one has to be careful to compare our results with [2]. First, we use a different orientation convention, which effectively replaces $*$ by $-*$ and $\psi$ by $-\psi$, although Bryant denotes the 3-form by $\sigma$. Secondly, we use slightly different identifications between the spaces $\varOmega ^k_l$ for different values of k. Finally, Bryant defines the ‘fundamental’ operators differently. For example, Bryant’s $\mathrm {d}^7_7$ is our $3 D^7_7$, and Bryant’s $- \tfrac{3}{7} \mathrm {d}^7_1$ is our $D^7_1$. We did notice at least one typographical error in [2]. The equation $\mathrm {d}(\alpha \wedge *_{\sigma } \sigma ) = - *_{\sigma } \mathrm {d}^7_7 \alpha$ in Table 1 is inconsistent with the definition $\mathrm {d}^7_7 \alpha = *_{\sigma } ( \mathrm {d}(\alpha \wedge *_{\sigma } \sigma ))$ on the previous page, since $(*_{\sigma })^2 = +1$, not $-1$.

$\square$

From now on, we assume M is compact, as we will be using Hodge theory throughout. Moreover, we can integrate by parts, so if P is a linear operator on forms, then $P \alpha = 0 \iff P^* P \alpha = 0$, which we will use often. The next result relates the kernel of the operators in Definition 2.10 with harmonic 1-forms. This result is fundamental and is used often in the rest of the paper.

Theorem 2.19

We have $\ker D^7_7 = \ker D^7_{14}$. Furthermore, let ${\mathcal {H}}^1 = \ker \left. \varDelta \right| _{\varOmega ^1}$ denote the space of harmonic 1-forms. Then, we have

$$\begin{aligned} \begin{aligned} {\mathcal {H}}^1&= \ker D^7_1 \cap \ker D^7_7 \cap \ker D^7_{14} \\&= \ker D^7_1 \cap \ker D^7_7 \\&= \ker D^7_1 \cap \ker D^7_{27} \\&= \ker D^7_7 \cap \ker D^7_{27}. \end{aligned} \end{aligned}$$

(2.20)

In particular, the intersection of any two of the three spaces $\ker D^7_1$, $\ker D^7_7$, $\ker D^7_{27}$ is $\mathcal H^1$.

Proof

From Corollary 2.14, on $\varOmega ^1_7$ we have that ${\mathrm {d}}{}^{\star }= (D^1_7)^* : \varOmega ^1_7 \rightarrow \varOmega ^0_1$ equals $-\tfrac{7}{3} D^7_1$, and thus

$$\begin{aligned} \mathcal {H}^1&= (\ker \mathrm {d})^1 \cap (\ker {\mathrm {d}}{}^{\star })^1 = \ker (D^7_7 +D^7_{14}) \cap \ker \left( -\tfrac{7}{3} D^7_1\right) \\&= \ker D^7_7 \cap \ker D^7_{14} \cap \ker D^7_1, \end{aligned}$$

establishing the first equality in (2.20).

Similarly, from Corollary 2.14, we have $(D^7_7)^* = 3 D^7_7$ and $(D^7_{14})^* = 4 D^{14}_7$. Hence, using $D^{14}_7 D^7_{14} = \tfrac{3}{2} D^7_7 D^7_7$ from (2.17), we have

$$\begin{aligned} D^7_7 \alpha = 0&\iff (D^7_7)^* D^7_7 \alpha = 3 D^7_7 D^7_7 \alpha = 0 \\&\iff D^{14}_7 D^7_{14} \alpha = \tfrac{1}{4} (D^7_{14})^* D^7_{14} \alpha = 0 \\&\iff D^7_{14} \alpha = 0. \end{aligned}$$

Thus, we deduce that $\ker D^7_7 = \ker D^7_{14}$ as claimed, and hence, the second equality in (2.20) follows.

Finally, from Corollary 2.14 we have $(D^7_1)^* = - D^1_7$ and $(D^7_{27})^* = - \tfrac{4}{3} D^{27}_7$ and $(D^7_7)^* = 3 D^7_7$. Thus, the relation $- D^1_7 D^7_1 + \tfrac{9}{4} D^7_7 D^7_7 + D^{27}_7 D^7_{27} = 0$ from (2.17) can be written as

$$\begin{aligned} (D^7_1)^* D^7_1 + \tfrac{3}{4} (D^7_7)^* D^7_7 - \tfrac{3}{4} (D^7_{27})^* D^7_{27} = 0. \end{aligned}$$

From the above relation, we easily deduce again by integration by parts that any two of $D^7_1 \alpha = 0$, $D^7_7 \alpha = 0$, $D^7_{27} \alpha = 0$ implies the third, establishing the remaining equalities in (2.20). $\square$

2.3 The derivations ${\mathcal {L}}_B$ and ${\mathcal {L}}_K$ and their properties

We begin with a brief discussion of derivations on $\varOmega ^{\bullet }$ arising from vector-valued forms on a general n-manifold M. A good reference for this material is [18]. We use notation similar to [4, 6].

Let $\varOmega ^r_{TM} = \varGamma (\varLambda ^r (T^* M) \otimes TM)$ be the space of vector-valued r-forms on M. Given an element $K \in \varOmega ^r_{TM}$, it induces two derivations on $\varOmega ^{\bullet }$. They are the algebraic derivation$\iota _K$, of degree $r-1$, and the Nijenhuis–Lie derivation$\mathcal {L}_K$, of degree r. They are defined as follows. Let $\{ e_1, \ldots , e_n \}$ be a (local) tangent frame with dual coframe $\{ e^1, \ldots , e^n \}$. Then locally $K = K^j e_j$ where each $K^j$ is an r-form. The operation $\iota _K : \varOmega ^k \rightarrow \varOmega ^{k+r-1}$ is defined to be

$$\begin{aligned} \iota _K \alpha = K^j \wedge (e_j \lrcorner \alpha ), \end{aligned}$$

(2.21)

where $e_j \lrcorner \cdot$ is the interior product with $e_j$. The operation $\iota _K$ is well defined and is a derivation on $\varOmega ^{\bullet }$. Moreover, $\iota _K$ vanishes on functions, so $\iota _K (h \alpha ) = h (\iota _K \alpha )$ for any $h \in \varOmega ^0$ and $\alpha \in \varOmega ^k$, which justifies why $\iota _K$ is called algebraic. If $Y \in \varOmega ^1$, then

$$\begin{aligned} (\iota _K Y) (X_1, \ldots , X_r) = Y( K(X_1, \ldots , X_r) ). \end{aligned}$$

(2.22)

The operation $\mathcal {L}_K : \varOmega ^k \rightarrow \varOmega ^{k+r}$ is defined to be

$$\begin{aligned} \mathcal {L}_K \alpha = \iota _K (\mathrm {d}\alpha ) - (-1)^{r-1} \mathrm {d}(\iota _K \alpha ) = [ \iota _K, \mathrm {d}] \alpha . \end{aligned}$$

(2.23)

That is, $\mathcal {L}_K$ is the graded commutator of $\iota _K$ and $\mathrm {d}$. The graded Jacobi identity on the space of graded linear operators on $\varOmega ^{\bullet }$ and $\mathrm {d}^2 = 0$ together implies that

$$\begin{aligned}{}[ \mathrm {d}, \mathcal {L}_K ] = \mathrm {d}\mathcal {L}_K - (-1)^r \mathcal {L}_K \mathrm {d}= 0. \end{aligned}$$

(2.24)

From now on, let g be a Riemannian metric on M.

Lemma 2.20

Let $K \in \varOmega ^r_{TM}$ be obtained from an $(r+1)$-form $\eta$ by raising the last index. That is, $g( K(X_1, \ldots , X_r), X_{r+1}) = \eta (X_1, \ldots , X_{r+1})$. In a local frame, we have $K_{i_1 \cdots i_r}^q = \eta _{i_1 \cdots i_r p} g^{pq}$. The operator $\iota _K$ is of degree $r-1$. For any $\alpha \in \varOmega ^k$, the $(k+r-1)$-form $\iota _K \alpha$ is given by

$$\begin{aligned} \iota _K \alpha = (-1)^r g^{pq} (e_p \lrcorner \eta ) \wedge (e_q \lrcorner \alpha ). \end{aligned}$$

(2.25)

Proof

In a local frame, we have $K = \tfrac{1}{k!} K_{i_1 \cdots i_r}^q e^{i_1} \wedge \cdots \wedge e^{i_r} \otimes e_q$, and thus, from (2.21), we have

$$\begin{aligned} \iota _K \alpha&= \tfrac{1}{k!} K_{i_1 \cdots i_r}^q e^{i_1} \wedge \cdots \wedge e^{i_r} \wedge (e_q \lrcorner \alpha ) \\&= \tfrac{1}{k!} \eta _{i_1 \cdots i_r p} g^{pq} e^{i_1} \wedge \cdots \wedge e^{i_r} \wedge (e_q \lrcorner \alpha ) \\&= (-1)^r g^{pq} \big ( \tfrac{1}{k!} \eta _{p i_1 \cdots i_r} e^{i_1} \wedge \cdots \wedge e^{i_r} \big ) \wedge (e_q \lrcorner \alpha ) \\&= (-1)^r g^{pq} (e_p \lrcorner \eta ) \wedge (e_q \lrcorner \alpha ) \end{aligned}$$

as claimed. $\square$

Corollary 2.21

Let K be as in Lemma 2.20. If $\alpha \in \varOmega ^{n-(r-1)}$, then $\iota _K \alpha = 0$ in $\varOmega ^n$.

Proof

Let $\alpha \in \varOmega ^{n-(r-1)}$. Since $e_p \lrcorner \eta \in \varOmega ^r$, the form $(e_p \lrcorner \eta ) \wedge \alpha$ is of degree $(n+1)$ and hence zero. Taking the interior product with $e_q$, we have

$$\begin{aligned} 0 = e_q \lrcorner \big ( (e_p \lrcorner \eta ) \wedge \alpha \big ) = (e_q \lrcorner e_p \lrcorner \eta ) \wedge \alpha + (-1)^r (e_p \lrcorner \eta ) \wedge (e_q \lrcorner \alpha ). \end{aligned}$$

Thus, by the skew symmetry of $e_q \lrcorner e_p \lrcorner \eta$ in p, q, we find from (2.25) that

$$\begin{aligned} \iota _K \alpha = (-1)^r g^{pq} (e_p \lrcorner \eta ) \wedge (e_q \lrcorner \alpha ) = - g^{pq} (e_q \lrcorner e_p \lrcorner \eta ) \wedge \alpha = 0 \end{aligned}$$

as claimed. $\square$

Corollary 2.22

Let K be as in Lemma 2.20. Then the adjoint $\iota _K^*$ is a degree $-(r-1)$ operator on $\varOmega ^{\bullet }$ and satisfies

$$\begin{aligned} \iota _K^* \beta = (-1)^{nk + rk + nr + n + 1} *\iota _K *\beta \quad \hbox { for}\ \beta \in \varOmega ^k. \end{aligned}$$

(2.26)

Proof

Let $\alpha \in \varOmega ^{k-(r-1)}$ and $\beta \in \varOmega ^k$. Then $\alpha \wedge *\beta \in \varOmega ^{n-(r-1)}$, so by Lemma 2.20 we have $\iota _K (\alpha \wedge *\beta ) = 0$. Since $\iota _K$ is a derivation of degree $r-1$, and $\iota _K *\beta$ is an $(n-k+r-1)$-form, this can be written as

$$\begin{aligned} 0&= (\iota _K \alpha ) \wedge *\beta + (-1)^{(r-1)(k-(r-1))} \alpha \wedge (\iota _K *\beta ) \\&= g(\iota _K \alpha , \beta ) \mathsf {vol}+ (-1)^{rk + k + r + 1} \alpha \wedge (-1)^{(n-k+r-1)(k-r+1)} *(*\iota _K *\beta ) \\&= g(\iota _K \alpha , \beta ) \mathsf {vol}+ (-1)^{rk + k + r + 1} (-1)^{k + r + 1 + nk + nr + n} g(\alpha , *\iota _K *\beta ) \mathsf {vol}\\&= g(\iota _K \alpha , \beta ) \mathsf {vol}+ (-1)^{nk + rk + nr + n} g(\alpha , *\iota _K *\beta ) \mathsf {vol}, \end{aligned}$$

and hence $\iota _K^* \beta = (-1)^{nk + rk + nr + n + 1} *\iota _K *\beta$ as claimed. $\square$

Now let $(M, \varphi )$ be a manifold with $\mathrm {G}_2$-structure. In particular, $n=7$ from now on.

Definition 2.23

From the $\mathrm {G}_2$-structure $\varphi$ on M, we obtain two particular vector-valued forms $B \in \varOmega ^2_{TM}$ and $K \in \varOmega ^3_{TM}$ by raising the last index on the forms $\varphi$ and $\psi$, respectively. That is,

$$\begin{aligned} g( B(X, Y), Z) = \varphi (X, Y, Z), \quad g( K(X, Y, Z), W) = \psi (X, Y, Z, W). \end{aligned}$$

In local coordinates, we have

$$\begin{aligned} B_{ij}^q = \varphi _{ijp} g^{pq}, \quad K_{ijk}^q = \psi _{ijkp} g^{pq}. \end{aligned}$$

The vector-valued 2-form B is also called the cross product induced by $\varphi$, and, up to a factor of $-\tfrac{1}{2}$, the vector-valued 3-form K is called the associator. (See [9, p.116] for details.) Thus, $\iota _B$ and $\iota _K$ are algebraic derivations on $\varOmega ^{\bullet }$ of degrees 1 and 2, respectively. We also have the associated Nijenhuis–Lie derivations ${\mathcal {L}}_B$ and ${\mathcal {L}}_K$. From (2.23), we have

$$\begin{aligned} {\mathcal {L}}_B = \iota _B \mathrm {d}+ \mathrm {d}\iota _B, \quad {\mathcal {L}}_K = \iota _K \mathrm {d}- \mathrm {d}\iota _K. \end{aligned}$$

(2.27)

The operators ${\mathcal {L}}_B$ and ${\mathcal {L}}_K$ are of degree 2 and 3, respectively. $\square$

Remark 2.24

In much of the literature, the associator K is denoted by $\chi$, but we are following the convention of [4, 6] of denoting vector-valued forms by capital Roman letters. $\square$

Proposition 2.25

Let $\iota _B$, $\iota _K$, ${\mathcal {L}}_B$, and ${\mathcal {L}}_K$ be as in Definition 2.23. Then on $\varOmega ^k$, we have

$$\begin{aligned} \begin{aligned} \iota _B^*&= (-1)^k *\iota _B *,&\quad \iota _K^*&= -*\iota _K *, \\ {\mathcal {L}}_B^*&= - *{\mathcal {L}}_B *,&\quad {\mathcal {L}}_K^*&= (-1)^k *{\mathcal {L}}_K *. \end{aligned} \end{aligned}$$

(2.28)

Proof

The first pairs of equations follow from (2.26) with $n=7$ and $r=2,3$, respectively. In odd dimensions, ${\mathrm {d}}{}^{\star }= (-1)^k *\mathrm {d}*$ on k-forms, and $*^2 = 1$. The second pair of equations follows from these facts and taking adjoints of (2.27). $\square$

The operations $\iota _B$ and $\iota _K$ are morphisms of $\mathrm {G}_2$-representations, and in fact, they are constants on $\varOmega ^l_{l'}$ after our identifications (2.3). We will prove this in Propositions 2.30 and 2.31, but first we need to collect several preliminary results.

Lemma 2.26

Let $f \in \varOmega ^0$ and $X \in \varOmega ^1$. The following identities hold:

$$\begin{aligned} \begin{aligned} \iota _B f&= 0,&\quad \iota _K f&= 0, \\ \iota _B X&= X \lrcorner \varphi ,&\quad \iota _K X&= - X \lrcorner \psi . \end{aligned} \end{aligned}$$

(2.29)

Proof

The first pair of equations is immediate since any algebraic derivation vanishes on functions. Letting $\alpha = X$ in (2.25) gives $\iota _K X = (-1)^r g^{pq} (e_p \lrcorner \eta ) \wedge X_q = (-1)^r X^p e_p \lrcorner \eta = (-1)^r X \lrcorner \eta$. The second pair of equations now follows using $r = 2$ for $\eta = \varphi$ and $r = 3$ for $\eta = \psi$. $\square$

Lemma 2.27

The following identities hold:

$$\begin{aligned} \begin{aligned} \iota _B \varphi&= - 6 \psi ,&\quad \iota _K \varphi&= 0, \\ \iota _B \psi&= 0,&\quad \iota _K \psi&= 0. \end{aligned} \end{aligned}$$

(2.30)

Proof

To establish each of these, we use (2.25) and Proposition 2.6 with $h = g$. First, using (2.8) and ${\text {Tr}}_g g = 7$, we have

$$\begin{aligned} \iota _B \varphi = g^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner \varphi ) = - 2 ({\text {Tr}}_g g) \psi + 2 \ell _{\psi } g = - 14 \psi + 8 \psi = -6 \psi . \end{aligned}$$

Similarly, from Proposition 2.6, we find that

$$\begin{aligned} \iota _B \psi = g^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner \psi ) = 0, \end{aligned}$$

and hence also $\iota _K \varphi = - g^{pq} (e_p \lrcorner \psi ) \wedge (e_q \lrcorner \varphi ) = - \iota _B \psi = 0$. Finally, again from Proposition 2.6 we deduce that

$$\begin{aligned} \iota _K \psi = -g^{pq} (e_p \lrcorner \psi ) \wedge (e_q \lrcorner \psi ) = 0 \end{aligned}$$

as well. $\square$

Lemma 2.28

Let $X \in \varOmega ^1$. The following identities hold:

$$\begin{aligned} \begin{aligned} \iota _B (X \lrcorner \varphi )&= 3 (X \lrcorner \psi ),&\quad \iota _K (X \lrcorner \varphi )&= 3 *(X \lrcorner \psi ), \\ \iota _B (X \lrcorner \psi )&= -3 *(X \lrcorner \psi ),&\quad \iota _K (X \lrcorner \psi )&= -4 *(X \lrcorner \varphi ). \end{aligned} \end{aligned}$$

(2.31)

Proof

Let $X = X^m e_m$. By linearity of derivations and (2.25), we have

$$\begin{aligned} \iota _B (X \lrcorner \beta )&= X^m g^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner e_m \lrcorner \beta ), \\ \iota _K (X \lrcorner \beta )&= - X^m g^{pq} (e_p \lrcorner \psi ) \wedge (e_q \lrcorner e_m \lrcorner \beta ). \end{aligned}$$

The equations in (2.31) now follow immediately from Proposition 2.7. $\square$

Lemma 2.29

Let $\beta \in \varOmega ^2_{14}$. The following identities hold:

$$\begin{aligned} \iota _B \beta = 0, \quad \quad \iota _K \beta = 0. \end{aligned}$$

(2.32)

Proof

We use the notation of Proposition 2.7. Let $\beta \in \varOmega ^2_{14}$. Using (2.25) and (2.9), we compute

$$\begin{aligned} \iota _B \beta&= g^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner \beta ) \\&= \tfrac{1}{2} g^{pq} \varphi _{pij} \beta _{qk} e^{ijk} \\&= - \tfrac{1}{6} (\beta _{kq} g^{qp} \varphi _{pij} + \beta _{iq} g^{qp} \varphi _{pjk} + \beta _{jq} g^{qp} \varphi _{pki} ) e^{ijk} = 0. \end{aligned}$$

Similarly, again using (2.25) and (2.9), we compute

$$\begin{aligned} \iota _K \beta&= -g^{pq} (e_p \lrcorner \psi ) \wedge (e_q \lrcorner \beta ) \\&= -\tfrac{1}{6} g^{pq} \psi _{pijk} \beta _{ql} e^{ijkl} \\&= + \tfrac{1}{24} (\beta _{lq} g^{qp} \psi _{pijk} - \beta _{iq} g^{qp} \psi _{pljk} - \beta _{jq} g^{qp} \psi _{pilk} - \beta _{kq} g^{qp} \psi _{pijl} ) e^{ijkl} = 0 \end{aligned}$$

as claimed. $\square$

We are now ready to establish the actions of $\iota _B$ and $\iota _K$ on the summands of $\varOmega ^{\bullet }$ with respect to identifications (2.3).

Fig. 2

Decomposition of the algebraic derivation $\iota _B$ into components

Proposition 2.30

With respect to the identifications described in (2.3), the components of the operator $\iota _B$ satisfy the relations given in Fig. 2.

Proof

The derivation $\iota _B$ is of degree 1, so it vanishes on $\varOmega ^7$. Moreover, by Corollary 2.21 it also vanishes on $\varOmega ^6$. We establish the rest of Fig. 2 by each vertical column.

$\varOmega ^k_1$ column: This follows from (2.29) and (2.30). In particular, the map $\iota _B : \varOmega ^3_1 \rightarrow \varOmega ^4_1$ is identified with multiplication by $-6$.

$\varOmega ^k_7$ column: The map $\iota _B : \varOmega ^1_7 \rightarrow \varOmega ^2_7$ is identified with multiplication by 1 by (2.29). The maps $\iota _B : \varOmega ^2_7 \rightarrow \varOmega ^3_7$ and $\iota _B : \varOmega ^3_7 \rightarrow \varOmega ^4_7$ are identified with multiplication by 3 and $-3$, respectively, by (2.31). Let $*(X \lrcorner \psi ) = \varphi \wedge X \in \varOmega ^4_7$. Then

$$\begin{aligned} \iota _B \big ( *(X \lrcorner \psi ) \big )&= \iota _B (\varphi \wedge X) = (\iota _B \varphi ) \wedge X - \varphi \wedge (\iota _B X) \\&= (-6 \psi ) \wedge X - \varphi \wedge (X \lrcorner \varphi ) = - 6 *(X \lrcorner \varphi ) + 2 *(X \lrcorner \varphi ) \\&= - 4 *(X \lrcorner \varphi ), \end{aligned}$$

and hence, the map $\iota _B : \varOmega ^4_7 \rightarrow \varOmega ^5_7$ is identified with multiplication by $-4$. Finally, let $*(X \lrcorner \varphi ) = \psi \wedge X \in \varOmega ^5_7$. Then

$$\begin{aligned} \iota _B \big ( *(X \lrcorner \varphi ) \big )&= \iota _B (\psi \wedge X) = (\iota _B \psi ) \wedge X + \psi \wedge (\iota _B X) \\&= 0 + \psi \wedge (X \lrcorner \varphi ) = 3 *X, \end{aligned}$$

and hence, the map $\iota _B : \varOmega ^5_7 \rightarrow \varOmega ^6_7$ is identified with multiplication by 3.

$\varOmega ^k_{14}$ column: The map $\iota _B$ on $\varOmega ^2_{14}$ is zero by Lemma 2.29. Let $\mu = *\beta \in \varOmega ^5_{14}$ where $\beta \in \varOmega ^2_{14}$. Then $\mu = *\beta = \varphi \wedge \beta$, so $\iota _B \mu = (\iota _B \varphi ) \wedge \beta - \varphi \wedge (\iota _B \beta ) = - 6 \psi \wedge \beta - 0 = 0$, by the description of $\varOmega ^2_{14}$ in (2.3).

$\varOmega ^k_{27}$ column: Let $\gamma = \ell _{\varphi } h \in \varOmega ^3_{27}$, where $h \in S^2_0 (T^* M)$. By (2.6) we have $\gamma = h_{kl} g^{lm} e^k \wedge (e_m \lrcorner \varphi )$. Since $\iota _B$ is algebraic, we can pull out functions, and using (2.29) and (2.31) we compute

$$\begin{aligned} \iota _B \gamma&= \iota _B \big ( h_{kl} g^{lm} e^k \wedge (e_m \lrcorner \varphi ) \big ) \\&= h_{kl} g^{lm} \big ( (\iota _B e^k) \wedge (e_m \lrcorner \varphi ) - e^k \wedge \iota _B (e_m \lrcorner \varphi ) \big ) \\&= h_{kl} g^{lm} \big ( g^{kp} (e_p \lrcorner \varphi ) \wedge (e_m \lrcorner \varphi ) - e^k \wedge (3 e_m \lrcorner \psi ) \big ) \\&= h^{pm} (e_p \lrcorner \varphi ) \wedge (e_m \lrcorner \varphi ) - 3 h_{kl} g^{lm} e^k \wedge (e_m \lrcorner \psi ). \end{aligned}$$

By (2.10) and (2.7), since ${\text {Tr}}_g h = 0$, the above expression is

$$\begin{aligned} \iota _B \gamma = 2 \ell _{\psi } h - 3 \ell _{\psi } h = - \ell _{\psi } h. \end{aligned}$$

Using Lemma 2.5, we conclude that $\iota _B (\ell _{\varphi } h) = *(\ell _{\varphi } h)$, and thus, the map $\iota _B : \varOmega ^3_{27} \rightarrow \varOmega ^4_{27}$ is identified with multiplication by 1. Finally, let $\eta = \ell _{\psi } h \in \varOmega ^4_{27}$, where $h \in S^2_0 (T^* M)$. By (2.7), we have $\eta = h_{kl} g^{lm} e^k \wedge (e_m \lrcorner \psi )$. Computing as before, we find

$$\begin{aligned} \iota _B \eta&= \iota _B \big ( h_{kl} g^{lm} e^k \wedge (e_m \lrcorner \psi ) \big ) \\&= h_{kl} g^{lm} \big ( (\iota _B e^k) \wedge (e_m \lrcorner \psi ) - e^k \wedge \iota _B (e_m \lrcorner \psi ) \big ) \\&= h_{kl} g^{lm} \big ( g^{kp} (e_p \lrcorner \varphi ) \wedge (e_m \lrcorner \psi ) - e^k \wedge (-3 *( e_m \lrcorner \psi ) ) \big ) \\&= h^{pm} (e_p \lrcorner \varphi ) \wedge (e_m \lrcorner \psi ) + 3 h_{kl} g^{lm} e^k \wedge (\varphi \wedge (e_m)^{\flat }). \end{aligned}$$

Using (2.10), the above expression becomes

$$\begin{aligned} \iota _B \eta = 0 + 3 h_{kl} g^{lm} e^k \wedge \varphi \wedge (g_{mp} e^p) = - 3 h_{kp} e^k \wedge e^p \wedge \varphi = 0, \end{aligned}$$

so the map $\iota _B$ on $\varOmega ^4_{27}$ is zero. $\square$

Proposition 2.31

With respect to the identifications described in (2.3), the components of the operator $\iota _K$ satisfy the relations given in Fig. 3.

Proof

The derivation $\iota _K$ is of degree 2, so it vanishes on $\varOmega ^6$ and $\varOmega ^7$. Moreover, by Corollary 2.21 it also vanishes on $\varOmega ^5$. We establish the rest of Fig. 2 by each vertical column. Note that $\iota _K$ preserves the parity (even/odd) of forms.

Fig. 3

Decomposition of the algebraic derivation $\iota _K$ into components

$\varOmega ^k_1$ column: This follows from (2.29) and (2.30).

$\varOmega ^k_7$ column: The map $\iota _K : \varOmega ^1_7 \rightarrow \varOmega ^3_7$ is identified with multiplication by $-1$ by (2.29). The maps $\iota _K : \varOmega ^2_7 \rightarrow \varOmega ^4_7$ and $\iota _K : \varOmega ^3_7 \rightarrow \varOmega ^5_7$ are identified with multiplication by 3 and $-4$, respectively, by (2.31). Let $*(X \lrcorner \psi ) = \varphi \wedge X \in \varOmega ^4_7$. Then, since $\iota _K$ is an even derivation,

$$\begin{aligned} \iota _K \big ( *(X \lrcorner \psi ) \big )&= \iota _K (\varphi \wedge X) = (\iota _K \varphi ) \wedge X + \varphi \wedge (\iota _K X) \\&= 0 + \varphi \wedge (-X \lrcorner \psi ) = -\varphi \wedge (X \lrcorner \psi ) = 4 *X \end{aligned}$$

and hence, the map $\iota _K : \varOmega ^4_7 \rightarrow \varOmega ^6_7$ is identified with multiplication by 4.

$\varOmega ^k_{14}$ column: The map $\iota _K$ on $\varOmega ^2_{14}$ is zero by Lemma 2.29.

$\varOmega ^k_{27}$ column: Let $\gamma = \ell _{\varphi } h \in \varOmega ^3_{27}$, where $h \in S^2_0 (T^* M)$. By (2.6), we have $\gamma = h_{kl} g^{lm} e^k \wedge (e_m \lrcorner \varphi )$. Computing as in the proof of Proposition 2.31, we find that

$$\begin{aligned} \iota _K \gamma&= \iota _K \big ( h_{kl} g^{lm} e^k \wedge (e_m \lrcorner \varphi ) \big ) \\&= h_{kl} g^{lm} \big ( (\iota _K e^k) \wedge (e_m \lrcorner \varphi ) - e^k \wedge \iota _K (e_m \lrcorner \varphi ) \big ) \\&= h_{kl} g^{lm} \big ( -g^{kp} (e_p \lrcorner \psi ) \wedge (e_m \lrcorner \varphi ) - e^k \wedge (3 *( e_m \lrcorner \psi ) ) \big ) \\&= -h^{pm} (e_p \lrcorner \psi ) \wedge (e_m \lrcorner \varphi ) - 3 h_{kl} g^{lm} e^k \wedge \varphi \wedge (e_m)^{\flat }. \end{aligned}$$

The first term vanishes by (2.10) and the second term vanishes as it is $-3 h_{kl} g^{lm} g_{mp} e^k \wedge \varphi \wedge e^p = 3 h_{kp} e^k \wedge e^p \wedge \varphi = 0$. Thus, the map $\iota _K$ vanishes on $\varOmega ^3_{27}$. Finally, let $\eta = \ell _{\psi } h \in \varOmega ^4_{27}$, where $h \in S^2_0 (T^* M)$. By (2.7), we have $\eta = h_{kl} g^{lm} e^k \wedge (e_m \lrcorner \psi )$. Computing as before, we find

$$\begin{aligned} \iota _K \eta&= \iota _K \big ( h_{kl} g^{lm} e^k \wedge (e_m \lrcorner \psi ) \big ) \\&= h_{kl} g^{lm} \big ( (\iota _K e^k) \wedge (e_m \lrcorner \psi ) - e^k \wedge \iota _K (e_m \lrcorner \psi ) \big ) \\&= h_{kl} g^{lm} \big ( -g^{kp} (e_p \lrcorner \psi ) \wedge (e_m \lrcorner \psi ) - e^k \wedge (-4 *( e_m \lrcorner \varphi ) ) \big ) \\&= -h^{pm} (e_p \lrcorner \psi ) \wedge (e_m \lrcorner \psi ) + 4 h_{kl} g^{lm} e^k \wedge (\psi \wedge (e_m)^{\flat }). \end{aligned}$$

Again, the first term vanishes by (2.10) and the second term vanishes as it is $4 h_{kl} g^{lm} g_{mp} e^k \wedge \psi \wedge e^p = 4 h_{kp} e^k \wedge e^p \wedge \psi = 0$. Thus, the map $\iota _K$ vanishes on $\varOmega ^4_{27}$.

$\square$

Fig. 4

Decomposition of the Nijenhuis–Lie derivation ${\mathcal {L}}_B$ into components

Fig. 5

Decomposition of the Nijenhuis–Lie derivation $\mathcal L_K$ into components

From now on in the paper, we always assume that $(M, \varphi )$ is torsion-free. See also Remark 1.1.

Corollary 2.32

With respect to the identifications described in (2.3), the components of the operators $\mathcal L_B$ and ${\mathcal {L}}_K$ satisfy the relations given in Figs. 4 and 5.

Proof

This is straightforward to verify from Figs. 1, 2, and 3 using the equations in (2.27). $\square$

Next we discuss some properties of ${\mathcal {L}}_B$ and $\mathcal L_K$.

Lemma 2.33

Let $\alpha$ be a form. In a local frame, the actions of $\mathcal L_B$ and ${\mathcal {L}}_K$ are given by

$$\begin{aligned} \begin{aligned} {\mathcal {L}}_B \alpha&= g^{pq} (e_p \lrcorner \varphi ) \wedge (\nabla _q \alpha ), \\ {\mathcal {L}}_K \alpha&= - g^{pq} (e_p \lrcorner \psi ) \wedge (\nabla _q \alpha ). \end{aligned} \end{aligned}$$

(2.33)

Proof

It is clear that both expressions in (2.33) are independent of the choice of frame. To establish these expressions at $x \in M$, we choose a local frame determined by Riemannian normal coordinates centered at x. In particular, at the point x we have $\nabla _p e_j =$ and $\nabla _p e^j = 0$. Recalling that M is torsion-free, so $\nabla \varphi = 0$, using (2.27), (2.25), and (1.1) at the point x we compute

$$\begin{aligned} {\mathcal {L}}_B \alpha&= (\iota _B \mathrm {d}+ \mathrm {d}\iota _B) \alpha \\&= \iota _B (e^m \wedge \nabla _m \alpha ) + e^m \wedge \nabla _m (\iota _B \alpha ) \\&= g^{pq} (e_p \lrcorner \varphi ) \wedge \big ( e_q \lrcorner (e^m \wedge \nabla _m \alpha ) \big ) + e^m \wedge \nabla _m \big ( g^{pq} (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner \alpha ) \big ) \\&= g^{pq} (e_p \lrcorner \varphi ) \wedge \big ( \delta ^m_q \nabla _m \alpha - e^m \wedge (e_q \lrcorner \nabla _m \alpha ) \big ) + g^{pq} e^m \wedge (e_p \lrcorner \varphi ) \wedge (e_q \lrcorner \nabla _m \alpha ) \\&= g^{pq} (e_p \lrcorner \varphi ) \wedge \nabla _q \alpha , \end{aligned}$$

establishing the first equation in (2.33). The other equation is proved similarly using $\nabla \psi = 0$. $\square$

Corollary 2.34

For any for $\alpha$, we have

$$\begin{aligned} \begin{aligned} {\mathcal {L}}_B \alpha&= - {\mathrm {d}}{}^{\star }(\varphi \wedge \alpha ) - \varphi \wedge {\mathrm {d}}{}^{\star }\alpha , \\ {\mathcal {L}}_K \alpha&= {\mathrm {d}}{}^{\star }(\psi \wedge \alpha ) - \psi \wedge {\mathrm {d}}{}^{\star }\alpha . \end{aligned} \end{aligned}$$

(2.34)

Proof

Consider a local frame determined by Riemannian normal coordinates centered at $x \in M$ as in the proof of Lemma 2.33. Using (2.33) and (1.2), we compute

$$\begin{aligned} {\mathcal {L}}_B \alpha&= g^{pq} (e_p \lrcorner \varphi ) \wedge (\nabla _q \alpha ) \\&= g^{pq} \big ( e_p \lrcorner ( \varphi \wedge \nabla _q \alpha ) + \varphi \wedge (e_p \lrcorner \nabla _q \alpha ) \big ) \\&= g^{pq} e_p \lrcorner \nabla _q (\varphi \wedge \alpha ) + \varphi \wedge ( g^{pq} e_p \lrcorner \nabla _q \alpha ) \\&= - {\mathrm {d}}{}^{\star }(\varphi \wedge \alpha ) - \varphi \wedge ({\mathrm {d}}{}^{\star }\alpha ), \end{aligned}$$

establishing the first equation in (2.34). The other equation in proved similarly.

$\square$

Proposition 2.35

The derivations ${\mathcal {L}}_B$ and ${\mathcal {L}}_K$ satisfy the following identities:

$$\begin{aligned} {\mathcal {L}}_B {\mathrm {d}}{}^{\star }&= {\mathrm {d}}{}^{\star }{\mathcal {L}}_B,&{\mathcal {L}}_K {\mathrm {d}}{}^{\star }&= -{\mathrm {d}}{}^{\star }{\mathcal {L}}_K, \end{aligned}$$

(2.35)

$$\begin{aligned} {\mathcal {L}}_B \varDelta&= \varDelta {\mathcal {L}}_B,&{\mathcal {L}}_K \varDelta&= \varDelta {\mathcal {L}}_K, \end{aligned}$$

(2.36)

$$\begin{aligned} {\mathcal {L}}_B {\mathcal {L}}_K = {\mathcal {L}}_K {\mathcal {L}}_B&= 0,&({\mathcal {L}}_K)^2&= 0, \end{aligned}$$

(2.37)

and

$$\begin{aligned} {\mathcal {L}}_B = {\mathcal {L}}_K = 0 \text { on } \mathcal {H}^k \quad \text {if }M \text { is compact}. \end{aligned}$$

(2.38)

Proof

The identities in (2.35)–(2.37) can be verified directly from the Figs. 1, 4, and 5 using ${\mathrm {d}}{}^{\star }= (-1)^k *\mathrm {d}*$ on $\varOmega ^k$ and $\varDelta = \mathrm {d}{\mathrm {d}}{}^{\star }+ {\mathrm {d}}{}^{\star }\mathrm {d}$, the identities in Corollary 2.13, and recalling that our identifications were chosen compatible with $*$.

However, we now give an alternative proof of the first equation in (2.35) that is less tedious and more illuminating. A similar proof establishes the second equation in (2.35). (In fact, this proof can be found in [17]). Using (2.34) and $({\mathrm {d}}{}^{\star })^2 = 0$, we compute

$$\begin{aligned} {\mathcal {L}}_B {\mathrm {d}}{}^{\star }\alpha&= - {\mathrm {d}}{}^{\star }(\varphi \wedge {\mathrm {d}}{}^{\star }\alpha ) - \varphi \wedge \big ( {\mathrm {d}}{}^{\star }({\mathrm {d}}{}^{\star }\alpha ) \big ) \\&= {\mathrm {d}}{}^{\star }\big ( - \varphi \wedge ({\mathrm {d}}{}^{\star }\alpha ) - {\mathrm {d}}{}^{\star }(\varphi \wedge \alpha ) \big ) \\&= {\mathrm {d}}{}^{\star }{\mathcal {L}}_B \alpha . \end{aligned}$$

The equations in (2.36) can also be established from (2.35), (2.24), and $\varDelta = \mathrm {d}{\mathrm {d}}{}^{\star }+ {\mathrm {d}}{}^{\star }\mathrm {d}$.

Equation (2.38) can be similarly verified using Figs. 1, 4, and 5, noting that in the compact case, the space ${\mathcal {H}}^k$ of harmonic k-forms coincides with the space of $\mathrm {d}$-closed and ${\mathrm {d}}{}^{\star }$-closed k-forms. $\square$

Remark 2.36

For a k-form $\gamma$, let $L_{\gamma }$ be the linear operator of degree k on $\varOmega ^{\bullet }$ given by $L_{\gamma } \alpha = \gamma \wedge \alpha$. In terms of graded commutators, in the torsion-free case Corollary 2.34 says that $[ {\mathrm {d}}{}^{\star }, L_{\varphi } ] = - {\mathcal {L}}_B$ and $[ {\mathrm {d}}{}^{\star }, L_{\psi } ] = {\mathcal {L}}_K$, and Proposition 2.35 says that $[ {\mathrm {d}}{}^{\star }, {\mathcal {L}}_B ] = [ {\mathrm {d}}{}^{\star }, {\mathcal {L}}_K ] = 0$, $[ \varDelta , {\mathcal {L}}_B ] = [ \varDelta , {\mathcal {L}}_K ] = 0$, and $[ {\mathcal {L}}_B, {\mathcal {L}}_K ] = [ {\mathcal {L}}_K, {\mathcal {L}}_K ] = 0$. (In fact, the first equation in (2.37) is actually stronger than $[ {\mathcal {L}}_B, {\mathcal {L}}_K ] = 0$.) These graded commutators and others are considered more generally for $\mathrm {G}_2$ manifolds with torsion in [14] using the general framework developed in [6] in the case of ${\mathrm{U}}{m}$-structures. $\square$

3 The ${\mathcal {L}}_B$-cohomology $H^{\bullet }_{\varphi }$ of M and its computation

In this section, we define two cohomologies on a torsion-free $\mathrm {G}_2$ manifold using the derivations ${\mathcal {L}}_B$ and $\mathcal L_K$. The cohomology determined by ${\mathcal {L}}_K$ was studied extensively by Kawai–Lê–Schwachhöfer in [17]. We recall one of the main results of [17] on the $\mathcal L_K$-cohomology, stated here as Theorem 3.2. We then proceed to compute the cohomology determined by ${\mathcal {L}}_B$. This section culminates with the proof of Theorem 3.19, which is our analog of Theorem 3.2 for the $\mathcal L_B$-cohomology. An application to formality of compact torsion-free $\mathrm {G}_2$ manifolds is given in Sect. 4.

3.1 Cohomologies determined by ${\mathcal {L}}_B$ and ${\mathcal {L}}_K$

Recall from (2.37) that $({\mathcal {L}}_K)^2 = 0$. This observation motivates the following definition.

Definition 3.1

For any $0 \le k \le 7$, we define

$$\begin{aligned} H^k_{\psi } : = \frac{\ker ({\mathcal {L}}_K: \varOmega ^k \rightarrow \varOmega ^{k+3})}{{\text {im}}({\mathcal {L}}_K: \varOmega ^{k-3} \rightarrow \varOmega ^k)}. \end{aligned}$$

We call these groups the ${\mathcal {L}}_K$-cohomology groups. $\square$

The ${\mathcal {L}}_K$-cohomology is studied extensively in [17]. Here is one of the main results of [17].

Theorem 3.2

(Kawai–Lê–Schwachhöfer [17]) The following relations hold.

• $H^k_{\psi } \cong H^k_{\mathrm {dR}}$ for $k=0,1,6,7$.

• $H^k_{\psi }$ is infinite-dimensional for $k=2,3,4,5$.

• There is a canonical injection $\mathcal {H}^k \hookrightarrow H^k_{\psi }$ for all k.

• The Hodge star induces isomorphisms $*: H^k_{\psi } \cong H^{7-k}_{\psi }$.

Proof

This is part of [17, Theorem 1.1]. $\square$

From Fig. 4 and (2.17), we see that in general $({\mathcal {L}}_B)^2 \ne 0$. Because of this, we cannot directly copy the definition of $H^k_{\psi }$ to define ${\mathcal {L}}_B$-cohomology groups. However, we can make the following definition.

Definition 3.3

For any $0 \le k \le 7$, we define

$$\begin{aligned} H^k_{\varphi } := \frac{\ker ({\mathcal {L}}_B: \varOmega ^k \rightarrow \varOmega ^{k+2})}{{\text {im}}({\mathcal {L}}_B: \varOmega ^{k-2} \rightarrow \varOmega ^k) \cap \ker ({\mathcal {L}}_B: \varOmega ^k \rightarrow \varOmega ^{k+2})}. \end{aligned}$$

(3.1)

We call these groups the ${\mathcal {L}}_B$-cohomology groups. $\square$

In Sects. 3.2 and 3.3, we compute these ${\mathcal {L}}_B$-cohomology groups, and then in Sect. 3.4, we prove Theorem 3.19, which is the analog to Theorem 3.2.

3.2 Computation of the groups $H^0_{\varphi }$, $H^1_{\varphi }$, $H^2_{\varphi }$, and $H^3_{\varphi }$

From now on, we always assume that $(M, \varphi )$ is a compact torsion-free $\mathrm {G}_2$ manifold as we use Hodge theory frequently. See also Remark 1.1.

Remark 3.4

In particular, we will often use the following observations. (There is no summation over $l, l', l''$ in this remark. The symbols $l, l', l'' \in \{ 1, 7, 14, 27 \}$ are not indices.) By Corollary 2.14, we have $D^{l'}_{l} = c (D^{l}_{l'})^*$ for some $c \ne 0$. Thus, by integration by parts,

$$\begin{aligned} \text {whenever } D^{l'}_l D^l_{l'} \omega = 0\text { for some }\omega , \text { then } D^l_{l'} \omega = 0. \end{aligned}$$

More generally, by Corollary 2.14 an equation of the form $a D^{l'}_l D^l_{l'} \omega + b D^{l''}_l D^l_{l''} \omega = 0$ can be rewritten as ${\tilde{a}} (D^{l}_{l'})^* D^{l}_{l'} \omega + {\tilde{b}} (D^{l}_{l''})^* D^{l}_{l''} \omega = 0$ for some ${\tilde{a}}, {\tilde{b}}$. If ${\tilde{a}}, {\tilde{b}}$have the same sign, then again by integration by parts, we conclude that both $D^l_{l'} \omega = 0$ and $D^l_{l''} \omega = 0$. $\square$

In the first two propositions, we establish that $H^k_{\varphi } \cong H^k_{\mathrm {dR}}$ for $k = 0,1,2$.

Proposition 3.5

We have $H^0_{\varphi } = \mathcal {H}^0$ and $H^1_{\varphi } = \mathcal {H}^1$.

Proof

From Figs. 4 and 1, we observe that

$$\begin{aligned} {\text {im}}({\mathcal {L}}_B: \varOmega ^{-2} \rightarrow \varOmega ^0)&= 0, \\ \ker ({\mathcal {L}}_B: \varOmega ^0 \rightarrow \varOmega ^2)&= \ker (D^1_7) = \mathcal {H}^0, \end{aligned}$$

and thus that $H^0_{\varphi } = \mathcal {H}^0$.

Similarly, using Fig. 4 and Theorem 2.19, we observe that

$$\begin{aligned} {\text {im}}({\mathcal {L}}_B: \varOmega ^{-1} \rightarrow \varOmega ^1)&= 0, \\ \ker ({\mathcal {L}}_B: \varOmega ^1 \rightarrow \varOmega ^3)&= \ker (D^7_1) \cap \ker (D^7_7) \cap \ker (D^7_{27}) = \mathcal {H}^1 \end{aligned}$$

and hence $H^1_{\varphi } = \mathcal {H}^1$. $\square$

In the remainder of this section and the next, we will often use the notation introduced in (1.3).

Proposition 3.6

We have $H^2_{\varphi } \cong \mathcal {H}^2$.

Proof

We first show that the denominator in (3.1) is trivial. Let $\omega \in (\ker {\mathcal {L}}_B)^2 \cap ( {\text {im}}{\mathcal {L}}_B)^2$. Then by Fig. 4, we have

$$\begin{aligned} \omega = {\mathcal {L}}_B f = D^1_7 f \quad \text {for some } f \in \varOmega ^0_1 \end{aligned}$$

and also that

$$\begin{aligned} 0 = {\mathcal {L}}_B \omega = -2 D^7_1 (D^1_7 f) - 2 D^7_{27} (D^1_7 f). \end{aligned}$$

Projecting onto the $\varOmega ^4_1$ component, we find that $D^7_1 D^1_7 f = 0$. By Remark 3.4, we deduce that $\omega = D^1_7 f = 0$. Thus, we have shown that $(\ker {\mathcal {L}}_B)^2 \cap ( {\text {im}}{\mathcal {L}}_B)^2 = 0$. Hence, $H^2_{\varphi } = (\ker {\mathcal {L}}_B)^2$.

Write $\omega = \omega _7 + \omega _{14} \in \varOmega ^2_7 \oplus \varOmega ^2_{14}$. By Fig. 4 we have

$$\begin{aligned} \omega \in (\ker {\mathcal {L}}_B)^2 \iff \left\{ \begin{aligned}&-2 D^7_1 \omega _7 = 0, \\&-3 D^{14}_7 \omega _{14} = 0, \\&-2 D^7_{27} \omega _7 + D^{14}_{27} \omega _{14} = 0. \end{aligned} \right\} \end{aligned}$$

(3.2)

Taking $D^{27}_7$ of the third equation in (3.2), using Corollary 2.13 to write $D^{27}_7 D^{14}_{27} = \tfrac{3}{2} D^7_7 D^{14}_7$, and using the second equation in (3.2), we find that

$$\begin{aligned} 0&= D^{27}_7 (-2 D^7_{27} \omega _7 + D^{14}_{27} \omega _{14}) \\&= -2 D^{27}_7 D^7_{27} \omega _7 + \tfrac{3}{2} D^7_7 D^{14}_7 \omega _{14} = -2 D^{27}_{7} D^7_{27} \omega _7, \end{aligned}$$

implying by Remark 3.4 that $D^7_{27} \omega _7 = 0$. Therefore, we have established that

$$\begin{aligned} \omega \in (\ker {\mathcal {L}}_B)^2 \iff \left\{ \begin{aligned}&D^7_1 \omega _7 = 0, \\&D^{14}_7 \omega _{14} = 0, \\&D^7_{27} \omega _7 = 0, \\&D^{14}_{27} \omega _{14} = 0, \end{aligned} \right\} \iff \left\{ \begin{aligned} \omega _7&\in \mathcal {H}^2_7 \cong \mathcal {H}^1_7 \text { by Theorem}~2.19, \\ \omega _{14}&\in \mathcal {H}^2_{14} \text { by Fig.}~1 \text { and Corollary}~2.14. \end{aligned} \right\} \end{aligned}$$

We conclude that $H^2_{\varphi } = (\ker {\mathcal {L}}_B)^2 = \mathcal {H}^2$. $\square$

Proposition 3.7

We have $H^3_{\varphi } = \mathcal {H}^3 \oplus \big ( ({\text {im}}{\mathrm {d}}{}^{\star })^3 \cap (\ker {\mathcal {L}}_B)^3 \big )$.

Proof

We first show that the denominator in (3.1) is trivial. Let $\omega \in (\ker {\mathcal {L}}_B)^3 \cap ( {\text {im}}{\mathcal {L}}_B)^3$. Then by Fig. 4 we have

$$\begin{aligned} \omega = {\mathcal {L}}_B \alpha = D^7_1 \alpha + \tfrac{3}{2} D^7_7 \alpha + D^7_{27} \alpha \quad \text {for some } \alpha \in \varOmega ^1_7. \end{aligned}$$

Also, using Corollary 2.13 to write $D^{27}_{14} D^{7}_{27} = \tfrac{3}{2} D^7_{14} D^7_7$ and $D^{27}_7 D^7_{27} = D^1_7 D^7_1 - \tfrac{9}{4} D^7_7 D^7_7$, we have that

$$\begin{aligned} 0 = {\mathcal {L}}_B \omega&= -2 D^1_7 (D^7_1 \alpha ) + 3 D^7_{14} \left( \tfrac{3}{2} D^7_7 \alpha \right) + \left( - \tfrac{8}{3} D^{27}_7 + D^{27}_{14}\right) (D^7_{27} \alpha ) \\&= -2 D^1_7 D^7_1 \alpha - \tfrac{8}{3} D^{27}_7 D^7_{27} \alpha + \tfrac{9}{4} D^7_{14} D^7_7 \alpha + D^{27}_{14} D^7_{27} \alpha \\&= - 2 D^1_7 D^7_1 \alpha - \tfrac{8}{3} \left( D^1_7 D^7_1 \alpha - \tfrac{9}{4} D^7_7 D^7_7 \alpha \right) + \tfrac{9}{4} D^7_{14} D^7_7 \alpha + \tfrac{3}{2} D^7_{14} D^7_7 \alpha \\&= \left( -\tfrac{14}{3} D^1_7 D^7_1 \alpha + 6 D^7_7 D^7_7 \alpha \right) + \tfrac{15}{4} D^7_{14} D^7_7 \alpha . \end{aligned}$$

Projecting onto the $\varOmega ^5_7$ component, we find that

$$\begin{aligned} -\tfrac{14}{3} D^1_7 D^7_1 \alpha + 6 D^7_7 D^7_7 \alpha = 0. \end{aligned}$$

Using Corollary 2.14, the above expression becomes

$$\begin{aligned} \tfrac{14}{3} (D^7_1)^* D^7_1 \alpha + 2 (D^7_7)^* D^7_7 \alpha = 0, \end{aligned}$$

and hence, by Remark 3.4 we deduce that $D^7_1 \alpha = 0$ and $D^7_7 \alpha = 0$. By Theorem 2.19, we then have $D^7_{27} \alpha = 0$ automatically. Therefore, we have shown that $(\ker {\mathcal {L}}_B)^3 \cap ( {\text {im}}{\mathcal {L}}_B)^2 = 0$, and so $H^3_{\varphi } = (\ker {\mathcal {L}}_B)^3$.

Write $\omega = \omega _1 + \omega _7 + \omega _{27} \in \varOmega ^3_1 \oplus \varOmega ^3_7 \oplus \varOmega ^3_{27}$. By Fig. 4, we have

$$\begin{aligned} \omega \in (\ker {\mathcal {L}}_B)^3 \iff \left\{ \begin{aligned} -2 D^1_7 \omega _1 - \tfrac{8}{3} D^{27}_7 \omega _{27}&= 0, \\ 3 D^7_{14} \omega _7 + D^{27}_{14} \omega _{27}&= 0. \end{aligned} \right\} \end{aligned}$$

(3.3)

Taking $D^{14}_7$ of the second equation in (3.3), using Corollary 2.13 to write $D^{14}_7 D^{27}_{14} = - D^7_7 D^{27}_7$ and $D^7_7 D^1_7 = 0$, and using $D^{27}_7 \omega _{27} = - \tfrac{3}{4} D^1_7 \omega _1$ from the first equation in (3.3), we find that

$$\begin{aligned} 0&= D^{14}_7 (3 D^7_{14} \omega _7 + D^{27}_{14} \omega _{27}) \\&= 3 D^{14}_7 D^7_{14} \omega _7 - D^7_7 D^{27}_7 \omega _{27} \\&= 3 D^{14}_7 D^7_{14} \omega _7 + \tfrac{3}{4} D^7_7 D^1_7 \omega _1 = 3 D^{14}_7 D^7_{14} \omega _7, \end{aligned}$$

implying by Remark 3.4 that $D^7_{14} \omega _7 = 0$. Therefore, we have established that

$$\begin{aligned} \omega \in (\ker {\mathcal {L}}_B)^3 \iff \left\{ \begin{aligned}&2 D^1_7 \omega _1 + \tfrac{8}{3} D^{27}_7 \omega _{27} = 0, \\&D^7_{14} \omega _7 = 0, \\&D^{27}_{14} \omega _{27} = 0, \end{aligned} \right\} \overset{\text {Theorem}~2.19}{\iff } \left\{ \begin{aligned}&2 D^1_7 \omega _1 + \tfrac{8}{3} D^{27}_7 \omega _{27} = 0, \\&D^7_7 \omega _7 = 0, \\&D^{27}_{14} \omega _{27} = 0. \end{aligned} \right\} \nonumber \\ \end{aligned}$$

(3.4)

From ${\mathrm {d}}{}^{\star }= - *\mathrm {d}*$ on $\varOmega ^3$ and Fig. 1 we find that

$$\begin{aligned} {\mathrm {d}}{}^{\star }\omega = 0 \iff \left\{ \begin{aligned}&D^1_7 \omega _1 + 2 D^7_7 \omega _7 + \tfrac{4}{3} D^{27}_7 \omega _{27} = 0, \\&^-D^7_{14} \omega _7 + D^{27}_{14} \omega _{27} = 0. \end{aligned} \right\} \end{aligned}$$

(3.5)

Now Eqs. (3.4) and (3.5) together imply that $(\ker {\mathcal {L}}_B)^3 \subseteq (\ker {\mathrm {d}}{}^{\star })^3$. By the Hodge theorem,we have $(\ker {\mathrm {d}}{}^{\star })^3 = \mathcal {H}^3 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^3$, and by (2.38) we have $\mathcal {H}^3 \subset (\ker {\mathcal {L}}_B)^3$. Thus,

$$\begin{aligned} \mathcal {H}^3 \subseteq (\ker \mathcal {L}_B)^3 \subseteq \mathcal {H}^3 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^3. \end{aligned}$$

Applying Lemma 1.2(i), we conclude that $H^3_{\varphi } =(\ker \mathcal {L}_B)^3 = \mathcal {H}^3 \oplus \big ( ({\text {im}}{\mathrm {d}}{}^{\star })^3 \cap (\ker {\mathcal {L}}_B)^3 \big )$. $\square$

We have thus far computed half of the ${\mathcal {L}}_B$-cohomology groups $H^k_{\varphi }$, for $k = 0,1,2,3$. The other half, for $k=4,5,6,7$, will be computed rigorously in Sect. 3.3. However, we can predict the duality result that $H^k_{\varphi } \cong H^{7-k}_{\varphi }$ by the following formal manipulation:

$$\begin{aligned} H^k_{\varphi }&= \frac{(\ker {\mathcal {L}}_B)^k}{({\text {im}}{\mathcal {L}}_B)^k \cap (\ker {\mathcal {L}}_B)^k} \cong \frac{(\ker {\mathcal {L}}_B)^k + ({\text {im}}{\mathcal {L}}_B)^k}{({\text {im}}{\mathcal {L}}_B)^k} \text { by the second isomorphism theorem} \\&\cong \frac{(\ker {\mathcal {L}}_B)^{7-k} + ({\text {im}}{\mathcal {L}}_B)^{7-k}}{({\text {im}}{\mathcal {L}}_B)^{7-k}} \text { by applying * and using equation}~(2.28) \\&\overset{\text {{(!)}}}{=} \frac{\big ( ({\text {im}}{\mathcal {L}}_B)^{7-k} \big )^{\perp } + \big ( (\ker {\mathcal {L}}_B)^{7-k} \big )^{\perp }}{\big ( (\ker {\mathcal {L}}_B)^{7-k} \big )^{\perp }} \\&= \frac{\big ( ({\text {im}}{\mathcal {L}}_B)^{7-k} \cap (\ker {\mathcal {L}}_B)^{7-k} \big )^{\perp }}{\big ( (\ker {\mathcal {L}}_B)^{7-k} \big )^{\perp }} \text { by properties of orthogonal complement} \\&\overset{\text {{(!!)}}}{\cong } \frac{(\ker \mathcal L_B)^{7-k}}{({\text {im}}{\mathcal {L}}_B)^{7-k} \cap (\ker \mathcal L_B)^{7-k}}=H^{7-k}_{\varphi }. \end{aligned}$$

Note that the above formal manipulation is not a rigorous proof of duality because at step (!), we do not have ${\text {im}}P^* = (\ker P)^{\perp }$ in general for an arbitrary operator P, and step (!!) is also not justified. Because $\varOmega ^k$ is not complete with respect to the $\mathcal {L}^2$-norm, the usual Hilbert space techniques do not apply. We will use elliptic operator theory to give a rigorous computation of $H^k_{\varphi }$ for $k = 4,5,6,7$, in the next section.

3.3 Computation of the groups $H^4_{\varphi }$, $H^5_{\varphi }$, $H^6_{\varphi }$, and $H^7_{\varphi }$

The material on regular operators in this section is largely based on Kawai–Lê–Schwachhöfer [17].

Definition 3.8

Let P be a linear differential operator of degree r on $\varOmega ^{\bullet }$. Then $P : \varOmega ^{k - r} \rightarrow \varOmega ^k$ is said to be regular if $\varOmega ^k = {\text {im}}P \oplus \ker P^*$, where by $\ker P^*$ we mean the kernel of the formal adjoint $P^* : \varOmega ^k \rightarrow \varOmega ^{k - r}$ with respect to the $L^2$ inner product. The operator P is said to be elliptic, overdetermined elliptic, underdetermined elliptic, if the principal symbol $\sigma _{\xi } (P)$ of P is bijective, injective, surjective, respectively, for all $\xi \ne 0$. $\square$

Remark 3.9

It is a standard result in elliptic operator theory (see [1, p.464; 32 Corollary]) that elliptic, overdetermined elliptic, and underdetermined elliptic operators are all regular. $\square$

Proposition 3.10

The operator ${\mathcal {L}}_B: \varOmega ^{k-2} \rightarrow \varOmega ^k$ is regular for all $k = 0, \ldots , 9$.

Proof

Consider the symbol $P = \sigma _{\xi } ({\mathcal {L}}_B)$. By (2.33), this operator is $P (\omega ) = (\xi \lrcorner \varphi ) \wedge \omega$. Note that this is an algebraic (pointwise) map, and thus, at each point it is a linear map between finite-dimensional vector spaces. We will show that $P : \varOmega ^{k-2} \rightarrow \varOmega ^k$ is injective for $k = 0,1,2,3,4$ and surjective for $k=5,6,7,8,9$. The claim will then follow by Remark 3.9.

First we claim that injectivity of $P : \varOmega ^{k-2} \rightarrow \varOmega ^k$ for $k=0,1,2,3,4$ implies surjectivity of $P : \varOmega ^{k-2} \rightarrow \varOmega ^k$ for $k=5,6,7,8,9$. Suppose $P : \varOmega ^{k-2} \rightarrow \varOmega ^k$ is injective. Then the dual map $P^* : \varOmega ^k \rightarrow \varOmega ^{k-2}$ is surjective. But we have

$$\begin{aligned} P^* = ( \sigma _{\xi } ({\mathcal {L}}_B) )^* = \sigma _{\xi } (\mathcal L_B^*), \end{aligned}$$

and by (2.28), this equals $\sigma _{\xi } (- *{\mathcal {L}}_B *) = - *\sigma _{\xi } ({\mathcal {L}}_B) *= - *P *$. Since $*: \varOmega ^l \rightarrow \varOmega ^{7-l}$ is bijective, and we have that $*P *: \varOmega ^k \rightarrow \varOmega ^{k-2}$ is surjective, we deduce that $P : \varOmega ^{(9-k) - 2} \rightarrow \varOmega ^{9-k}$ is surjective. But $9-k \in \{ 5, 6, 7, 8, 9 \}$ if $k = \{ 0, 1, 2, 3, 4 \}$. Thus, the claim is proved.

It remains to establish injectivity of $P : \varOmega ^{k-2} \rightarrow \varOmega ^k$ for $k = 0, 1, 2, 3, 4$. This is automatic for $k = 0, 1$ since $\varOmega ^{k-2} = 0$ in these cases.

If $k = 2$, then $P : \varOmega ^0 \rightarrow \varOmega ^2$ is given by $Pf = (\xi \lrcorner \varphi ) \wedge f = f (\xi \lrcorner \varphi )$. Suppose $Pf = 0$. Since $\xi \ne 0$, we have $\xi \lrcorner \varphi \ne 0$, and thus, $f = 0$. So P is injective for $k=2$.

If $k=3$, then $P : \varOmega ^1 \rightarrow \varOmega ^3$ is given by $P \alpha = (\xi \lrcorner \varphi ) \wedge \alpha$. Suppose $P \alpha = 0$. Taking the wedge product of $P \alpha = 0$ with $\psi$ and using Lemma 2.3 gives

$$\begin{aligned} 0&= \psi \wedge (\xi \lrcorner \varphi ) \wedge \alpha = 3 (*\xi ) \wedge \alpha \\&= 3 g( \xi , \alpha ) \mathsf {vol}. \end{aligned}$$

Thus, $g(\xi , \alpha ) = 0$. Similarly, taking the wedge product of $P \alpha = 0$ with $\varphi$ and using Lemmas 2.3 and 2.4 gives

$$\begin{aligned} 0&= \varphi \wedge (\xi \lrcorner \varphi ) \wedge \alpha = -2 \big ( *(\xi \lrcorner \varphi ) \big ) \wedge \alpha \\&= -2 \psi \wedge \xi \wedge \alpha = - 2 *( \xi \times \alpha ). \end{aligned}$$

Thus, $\xi \times \alpha = 0$. Taking the cross product of this with $\xi$ and using Lemma 2.4 gives

$$\begin{aligned} - g(\xi , \xi ) \alpha + g(\xi , \alpha ) \xi = 0. \end{aligned}$$

Since $g(\xi , \alpha ) = 0$ and $\xi \ne 0$, we conclude that $\alpha = 0$. So P is injective for $k=3$.

If $k=4$, then $P : \varOmega ^2 \rightarrow \varOmega ^4$ is given by $P \beta = (\xi \lrcorner \varphi ) \wedge \beta$. Suppose $P \beta = 0$. This means

$$\begin{aligned} (\xi \lrcorner \varphi ) \wedge \beta = 0. \end{aligned}$$

(3.6)

Write $\beta = \beta _7 + \beta _{14} \in \varOmega ^2_7 \oplus \varOmega ^2_{14}$, where by (2.3) we can write $\beta _7 = Y \lrcorner \varphi$ for some unique Y. Taking the wedge product of (3.6) with $\varphi$ and using (2.3) and (2.1), we have

$$\begin{aligned} 0&= (\xi \lrcorner \varphi ) \wedge \varphi \wedge \beta = (\xi \lrcorner \varphi ) \wedge (- 2 *\beta _7 + *\beta _{14}) \\&= - 2 (\xi \lrcorner \varphi ) \wedge *\beta _7 + 0 = (\xi \lrcorner \varphi ) \wedge (Y \lrcorner \varphi ) \wedge \varphi = - 6 g(\xi , Y) \mathsf {vol}. \end{aligned}$$

Thus, we have

$$\begin{aligned} g(\xi , Y) = 0. \end{aligned}$$

(3.7)

Now we take the interior product of (3.6) with $\xi$. This gives $(\xi \lrcorner \varphi ) \wedge (\xi \lrcorner \beta ) = 0$. By the injectivity of P for $k=3$, we deduce that

$$\begin{aligned} \xi \lrcorner \beta = 0. \end{aligned}$$

(3.8)

Using (3.8) and (2.3), we can rewrite (3.6) as

$$\begin{aligned} 0 = \xi \lrcorner (\varphi \wedge \beta ) = \xi \lrcorner ( - 2 *\beta _7 + *\beta _{14} ). \end{aligned}$$

Taking $*$ of the above equation and using $*( \xi \lrcorner *\gamma ) = \pm \xi \wedge \gamma$, where in general the sign depends on the dimension of the manifold and the degree of $\gamma$, we find that

$$\begin{aligned} - 2 \xi \wedge \beta _7 + \xi \wedge \beta _{14} = 0. \end{aligned}$$

(3.9)

Equation (3.9) implies that

$$\begin{aligned} \xi \wedge \beta = \xi \wedge \beta _7 + \xi \wedge \beta _{14} = 3 \xi \wedge \beta _7. \end{aligned}$$

(3.10)

Taking the interior product of (3.10) with $\xi$ and using (3.8) yields

$$\begin{aligned} g(\xi , \xi ) \beta = 3 g(\xi , \xi ) \beta _7 - 3 \xi \wedge (\xi \lrcorner \beta _7). \end{aligned}$$

(3.11)

By Lemma 2.4, we have $\xi \lrcorner \beta _7 = \xi \lrcorner Y \lrcorner \varphi = Y \times \xi$. Thus, (3.11) becomes

$$\begin{aligned} g(\xi , \xi ) \beta = 3 g(\xi , \xi ) \beta _7 - 3 \xi \wedge (Y \times \xi ). \end{aligned}$$

(3.12)

Now we take the wedge product of (3.12) with $\psi$, use Lemma 2.4 again, and the fact that $\beta _{14} \wedge \psi = 0$ from (2.3). We obtain

$$\begin{aligned} g(\xi , \xi ) \beta _7 \wedge \psi&= 3 g(\xi , \xi ) \beta _7 \wedge \psi - 3 \xi \wedge (Y \times \xi ) \wedge \psi \\&= 3 g(\xi , \xi ) \beta _7 \wedge \psi - 3 *(\xi \times (Y \times \xi )), \end{aligned}$$

which can be rearranged to give, using Lemma 2.4 and (3.7), that

$$\begin{aligned} - 2 g(\xi , \xi ) \beta _7 \wedge \psi = 3 *(\xi \times (\xi \times Y)) = - 3 *\big ( g(\xi , \xi ) Y \big ). \end{aligned}$$

(3.13)

But from Lemma 2.3 we find $\beta _7 \wedge \psi = (Y \lrcorner \varphi ) \wedge \psi = 3 *Y$. Substituting this into (3.13) and taking $*$, we find that

$$\begin{aligned} - 3 g(\xi , \xi ) Y = -2 g(\xi , \xi ) *\big ( 3 *Y \big ) = - 6 g(\xi , \xi ) Y. \end{aligned}$$

Since $\xi \ne 0$, we deduce that $Y = 0$, and thus, $\beta _7 = 0$. Substituting back into (3.11) then gives $g(\xi , \xi ) \beta _{14} = 0$, and thus, $\beta _{14} = 0$ as well. So P is injective for $k=4$. $\square$

Corollary 3.11

For any $k = 0, \ldots , 7$, we have

$$\begin{aligned} ({\text {im}}{\mathcal {L}}_B)^k = *( (\ker {\mathcal {L}}_B)^{7-k})^{\perp }. \end{aligned}$$

(3.14)

Proof

By (2.28), we have $({\text {im}}\mathcal {L}_B)^k = *({\text {im}}\mathcal {L}^*_B)^{7-k}$, and because ${\mathcal {L}}_B$ is regular by Proposition 3.10, we have $({\text {im}}\mathcal {L}^*_B)^{7-k} = ((\ker \mathcal {L}_B)^{7-k})^{\perp }$. The result follows. $\square$

Proposition 3.12

We have $H^7_\varphi \cong \mathcal {H}^7$ and $H^6_\varphi \cong \mathcal {H}^6$.

Proof

In the proof of Proposition 3.5, we showed that $(\ker \mathcal {L}_B)^0 = \mathcal {H}^0$ and $(\ker \mathcal {L}_B)^1 = \mathcal {H}^1$. Thus, using (3.14) we have

$$\begin{aligned} ({\text {im}}\mathcal {L}_B)^7&= *((\ker \mathcal {L}_B)^0)^\perp = *(\mathcal {H}^0)^{\perp }&\\&= ({\text {im}}\mathrm {d})^7 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^7 \qquad \text {by the Hodge decomposition.} \end{aligned}$$

In exactly the same way we get $({\text {im}}\mathcal {L}_B)^6 = ({\text {im}}\mathrm {d})^6 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^6$.

Moreover, since ${\mathcal {L}}_B$ has degree two, we have $(\ker \mathcal {L}_B)^6 = \varOmega ^6$ and $(\ker \mathcal {L}_B)^7 = \varOmega ^7$. Thus, we conclude that

$$\begin{aligned} H^k_\varphi = \frac{\varOmega ^k}{({\text {im}}\mathrm {d})^k \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^k} \cong \mathcal {H}^k \quad \text { for k = 6,7.} \end{aligned}$$

by the Hodge decomposition. $\square$

Proposition 3.13

We have $H^5_\varphi \cong \mathcal {H}^5$.

Proof

In the proof of Proposition 3.6, we showed that $(\ker {\mathcal {L}}_B)^2 = \mathcal {H}^2$, so using (3.14) just as in the proof of Proposition 3.12 we deduce that

$$\begin{aligned} ({\text {im}}\mathcal {L}_B)^5 = ({\text {im}}\mathrm {d})^5 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^5. \end{aligned}$$

(3.15)

Let $\alpha \in \varOmega ^6$. Then, since ${\mathrm {d}}{}^{\star }= *\mathrm {d}*$ on $\varOmega ^6$, we find from Fig. 1 that up to our usual identifications, ${\mathrm {d}}{}^{\star }\alpha = D^7_7 \alpha + D^7_{14} \alpha \in \varOmega ^5_7 \oplus \varOmega ^5_{14}$. Then, Fig. 4 and (2.17) gives

$$\begin{aligned} {\mathcal {L}}_B {\mathrm {d}}{}^{\star }\alpha = {\mathcal {L}}_B (D^7_7 \alpha + D^7_{14} \alpha ) = 7 D^7_1 D^7_7 \alpha + 0 = 0, \end{aligned}$$

so $({\text {im}}{\mathrm {d}}{}^{\star })^5 \subset (\ker {\mathcal {L}}_B)^5$. We also have $\mathcal {H}^5 \subset (\ker \mathcal {L}_B)^5$ by (2.37). Using the Hodge decomposition of $\varOmega ^5$, we therefore have

$$\begin{aligned} \mathcal {H}^5 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^5 \subseteq (\ker \mathcal {L}_B)^5 \subseteq \varOmega ^5 = \mathcal {H}^5 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^5 \oplus ({\text {im}}\mathrm {d})^5. \end{aligned}$$

Applying Lemma 1.2(i), we deduce that

$$\begin{aligned} (\ker {\mathcal {L}}_B)^5 = \mathcal {H}^5 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^5 \oplus \big ( ({\text {im}}\mathrm {d})^5 \cap (\ker {\mathcal {L}}_B)^5 \big ). \end{aligned}$$

(3.16)

Applying Lemma 1.2(ii) to (3.15), (3.16), as subspaces of $\varOmega ^5 = \mathcal {H}^5 \oplus ({\text {im}}\mathrm {d})^5 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^5$, we obtain

$$\begin{aligned} ({\text {im}}{\mathcal {L}}_B)^5 \cap (\ker {\mathcal {L}}_B)^5 = ({\text {im}}{\mathrm {d}}{}^{\star })^5 \oplus \big ( ({\text {im}}\mathrm {d})^5 \cap (\ker {\mathcal {L}}_B)^5 \big ). \end{aligned}$$

(3.17)

Therefore, we find that

$$\begin{aligned} H^5_\varphi&= \frac{(\ker \mathcal {L}_B)^5}{(\ker \mathcal {L}_B)^5 \cap ({\text {im}}\mathcal {L}_B)^5}&\\&= \frac{\mathcal {H}^5 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^5 \oplus \big ( ({\text {im}}\mathrm {d})^5 \cap (\ker \mathcal {L}_B)^5 \big )}{({\text {im}}{\mathrm {d}}{}^{\star })^5 \oplus ({\text {im}}\mathrm {d})^5 \cap (\ker \mathcal {L}_B)^5}&\text { by}~(3.16) \text { and}~(3.17) \\&\cong \mathcal {H}^5&\end{aligned}$$

as claimed. $\square$

Before we can compute $H^4_{\varphi }$, we need two preliminary results.

Lemma 3.14

We have

$$\begin{aligned} (\ker \mathcal {L}_B)^4 \cap \big ( ({\text {im}}{\mathrm {d}}{}^{\star })^4 \oplus ({\text {im}}\mathrm {d})^4 \big ) = \big ( (\ker \mathcal {L}_B)^4 \cap ({\text {im}}{\mathrm {d}}{}^{\star })^4 \big ) \oplus \big ( (\ker \mathcal {L}_B)^4 \cap ({\text {im}}\mathrm {d})^4 \big ).\nonumber \\ \end{aligned}$$

(3.18)

Proof

Let $\beta = \beta _7 + \beta _{14} \in \varOmega ^5_7 \oplus \varOmega ^5_{14}$, and $\gamma = \gamma _1 + \gamma _7 + \gamma _{27} \in \varOmega ^3_1 \oplus \varOmega ^3_7 \oplus \varOmega ^3_{27}$. We need to prove that

$$\begin{aligned} \begin{aligned}&\mathcal {L}_B {\mathrm {d}}{}^{\star }(\beta _7 + \beta _{14} ) + \mathcal {L}_B \mathrm {d}(\gamma _1 + \gamma _7 + \gamma _{27}) = 0 \\&\quad \iff \mathcal {L}_B {\mathrm {d}}{}^{\star }(\beta _7 + \beta _{14}) = \mathcal {L}_B \mathrm {d}(\gamma _1 + \gamma _7 + \gamma _{27}) = 0. \end{aligned} \end{aligned}$$

(3.19)

From ${\mathrm {d}}{}^{\star }= - *\mathrm {d}*$ on $\varOmega ^5$ and Figs. 1 and 4, we have

$$\begin{aligned} \mathcal {L}_B{\mathrm {d}}{}^{\star }(\beta _7 + \beta _{14})&= \mathcal {L}_B (-D^7_1 \beta _7 + \tfrac{3}{2} D^7_7 \beta _7 - D^7_{27} \beta _7 - D^{14}_7 \beta _{14} - D^{14}_{27} \beta _{14} ) \\&= 3 D^1_7 (-D^7_1 \beta _7) - 6 D^7_7 ( \tfrac{3}{2} D^7_7 \beta _7 - D^{14}_7 \beta _{14} ) + 4 D^{27}_7 ( - D^7_{27} \beta _7 - D^{14}_{27} \beta _{14}) \\&= - 3 D^1_7 D^7_1 \beta _7 - 9 D^7_7 D^7_7 \beta _7 + 6 D^7_7 D^{14}_7 \beta _{14} - 4 D^{27}_7 D^7_{27} \beta _7 - 4 D^{27}_7 D^{14}_{27} \beta _{14}. \end{aligned}$$

Using the relations in (2.17), the above expression simplifies to

$$\begin{aligned} \mathcal {L}_B{\mathrm {d}}{}^{\star }(\beta _7 + \beta _{14}) = -7 D^1_7 D^7_1 \beta _7. \end{aligned}$$

(3.20)

Similarly, from Figs. 1 and 4 and $D^7_7 D^1_7 = 0$, we have

$$\begin{aligned}&\mathcal {L}_B \mathrm {d}(\gamma _1 + \gamma _7 + \gamma _{27}) \\&\quad = \mathcal {L}_B (\tfrac{4}{3} D^7_1 \gamma _7 + ( - D^1_7 \gamma _1 - \tfrac{3}{2} D^7_7 \gamma _7 + D^{27}_7 \gamma _{27} ) + ( - D^7_{27} \gamma _7 + D^{27}_{27} \gamma _{27}) ) \\&\quad = 3 D^1_7 (\tfrac{4}{3} D^7_1 \gamma _7) - 6 D^7_7 ( - D^1_7 \gamma _1 - \tfrac{3}{2} D^7_7 \gamma _7 + D^{27}_7 \gamma _{27} ) + 4 D^{27}_7 ( - D^7_{27} \gamma _7 + D^{27}_{27} \gamma _{27}) ) \\&\quad = 4 D^1_7 D^7_1 \gamma _7 + 9 D^7_7 D^7_7 \gamma _7 - 6 D^7_7 D^{27}_7 \gamma _{27} - 4 D^{27}_7 D^7_{27} \gamma _7 + 4 D^{27}_7 D^{27}_{27} \gamma _{27}. \end{aligned}$$

Using the relations in (2.17), the above expression simplifies to

$$\begin{aligned} \mathcal {L}_B \mathrm {d}(\gamma _1 + \gamma _7 + \gamma _{27}) = 18 D^7_7 D^7_7 \gamma _7 - 12 D^7_7 D^{27}_7 \gamma _{27}. \end{aligned}$$

(3.21)

Combining Eqs. (3.20) and (3.21), if $\mathcal {L}_B {\mathrm {d}}{}^{\star }(\beta _7 + \beta _{14}) + \mathcal {L}_B \mathrm {d}(\gamma _1 + \gamma _7 + \gamma _{27}) = 0$, then we have

$$\begin{aligned} - 7 D^1_7 D^7_1 \beta _7 + 18 D^7_7 D^7_7 \gamma _7 - 12 D^7_7 D^{27}_7 \gamma _{27} = 0, \end{aligned}$$

and thus, applying $D^7_1$ and using $D^7_1 D^7_7 = 0$, we deduce that

$$\begin{aligned} 7 D^7_1 D^1_7 D^7_1 \beta _7 = D^7_1 D^7_7 ( 18 D^7_7 \gamma _7 - 12 D^{27}_7 \gamma _{27} ) = 0. \end{aligned}$$

Thus, we have $D^7_1 D^1_7 D^7_1 \beta _7 = 0$. Applying Remark 3.4, we deduce that $D^1_7 D^7_1 \beta _7 = 0$, and thus, by (3.20) that ${\mathcal {L}}_B {\mathrm {d}}{}^{\star }(\beta _7 + \beta _{14}) = 0$. Thus, we have established (3.19) and consequently

$$\begin{aligned} (\ker \mathcal {L}_B)^4 \cap \big ( ({\text {im}}{\mathrm {d}}{}^{\star })^4 \oplus ({\text {im}}\mathrm {d})^4 \big ) = \big ( (\ker \mathcal {L}_B)^4 \cap ({\text {im}}{\mathrm {d}}{}^{\star })^4 \big ) \oplus \big ( (\ker \mathcal {L}_B)^4 \cap ({\text {im}}\mathrm {d})^4 \big ) \end{aligned}$$

as claimed. $\square$

Lemma 3.15

We have

$$\begin{aligned} ({\text {im}}\mathrm {d})^4 \cap (\ker \mathcal {L}_B)^4 \cap ({\text {im}}\mathcal {L}_B)^4 = 0. \end{aligned}$$

(3.22)

Proof

Let $\omega \in ({\text {im}}\mathrm {d})^4 \cap (\ker \mathcal {L}_B)^4 \cap ({\text {im}}\mathcal {L}_B)^4$. We write $\omega = \mathcal {L}_B (\alpha _7 + \alpha _{14})$ for some $\alpha _7 + \alpha _{14} \in \varOmega ^2_7 \oplus \varOmega ^2_{14}$. Using Fig. 4, we find

$$\begin{aligned} \begin{aligned} \omega = \mathcal {L}_B (\alpha _7 + \alpha _{14})&= (- 2 D^7_1 \alpha _7) + (- 3 D^{14}_7 \alpha _{14}) + (- 2 D^7_{27} \alpha _7 + D^{14}_{27} \alpha _{14}) \\&= \omega _1 + \omega _7 + \omega _{27} \in \varOmega ^4_1 \oplus \varOmega ^4_7 \oplus \varOmega ^4_{27}. \end{aligned} \end{aligned}$$

That is, we have

$$\begin{aligned} \begin{aligned} \omega _1&= - 2 D^7_1 \alpha _7, \\ \omega _7&= - 3 D^{14}_7 \alpha _{14}, \\ \omega _{27}&= - 2 D^7_{27} \alpha _7 + D^{14}_{27} \alpha _{14}. \end{aligned} \end{aligned}$$

(3.23)

Using Fig. 4 again, the equation $\mathcal {L}_B \mathcal {L}_B (\alpha _7 + \alpha _{14}) = \mathcal {L}_B \omega = 0$ gives

$$\begin{aligned} 0&= \mathcal {L}_B \big ( - 2 D^7_1 \alpha _7 - 3 D^{14}_7 \alpha _{14} + (- 2 D^7_{27} \alpha _7 + D^{14}_{27} \alpha _{14} ) \big ) \\&= 3 D^1_7( - 2 D^7_1 \alpha _7) - 6 D^7_7 ( - 3 D^{14}_7 \alpha _{14} ) + 4 D^{27}_7 (- 2 D^7_{27} \alpha _7 + D^{14}_{27} \alpha _{14} ) \\&= -6 D^1_7D^7_1\alpha _7 + 18 D^7_7D^{14}_7 \alpha _{14} - 8 D^{27}_7 D^7_{27} \alpha _7 + 4 D^{27}_7 D^{14}_{27} \alpha _{14}. \end{aligned}$$

Using relations (2.17), we can rewrite the above expression in two different ways, both of which will be useful. These are

$$\begin{aligned} -6 D^1_7 D^7_1 \alpha _7 - 8 D^{27}_7 D^7_{27} \alpha _7 + 24 D^7_7 D^{14}_7 \alpha _{14}&= 0, \end{aligned}$$

(3.24)

$$\begin{aligned} -14 D^1_7 D^7_1 \alpha _7 + 18 D^7_7 D^7_7 \alpha _7 + 24 D^7_7 D^{14}_7 \alpha _{14}&= 0. \end{aligned}$$

(3.25)

Applying $D^7_1$ to (3.25) and using $D^7_1 D^7_7 = 0$, we deduce that

$$\begin{aligned} 14 D^7_1 D^1_7 D^7_1 \alpha _7 = (D^7_1 D^7_7)(18 D^7_7 \alpha _7 + 24 D^{14}_7 \alpha _{14}) = 0. \end{aligned}$$

Thus, we have $D^7_1 D^1_7 D^7_1 \alpha _7 = 0$. Applying Remark 3.4 twice, we deduce first that $D^1_7 D^7_1 \alpha _7 = 0$ and then that

$$\begin{aligned} D^7_1 \alpha _7 = 0. \end{aligned}$$

(3.26)

Comparing (3.26) and (3.23), we find that $\omega _1 = 0$. Since $\omega \in ({\text {im}}\mathrm {d})^4$, it is $\mathrm {d}$-closed. Using Figs. 1 and 4, the conditions $\pi _7 \mathrm {d}\omega = 0$ and $\mathcal {L}_B \omega = 0$ give, respectively,

$$\begin{aligned} 2 D^7_7 \omega _7 + \tfrac{4}{3} D^{27}_7 \omega _{27}&= 0, \\ -6 D^7_7 \omega _7 + 4 D^{27}_7 \omega _{27}&= 0. \end{aligned}$$

These two equations together force

$$\begin{aligned} D^7_7 \omega _7 = 0 \quad \text {and} \quad D^{27}_7 \omega _{27} = 0. \end{aligned}$$

(3.27)

Also, from (3.23) we have $\omega _7 = - 3 D^{14}_7 \alpha _{14}$, and thus, since $D^7_1 D^{14}_7 = 0$, we deduce that

$$\begin{aligned} D^7_1 \omega _7 = 0. \end{aligned}$$

(3.28)

Combining the first equation in (3.27) with (3.28), we find by Theorem 2.19 that, considered as a 1-form, $\omega _7 \in \mathcal {H}^1$ and in particular

$$\begin{aligned} D^7_{14} \omega _7 = 0 \quad \text {and} \quad D^7_{27} \omega _7 = 0. \end{aligned}$$

(3.29)

From Fig. 1, the condition $\pi _{14} \mathrm {d}\omega = 0$ gives $- D^7_{14} \omega _7 + D^{27}_{14} \omega _{27} = 0$, which, by the first equation in (3.29), implies that

$$\begin{aligned} D^{27}_{14} \omega _{27} = 0. \end{aligned}$$

(3.30)

Recalling from (3.23) that $\omega _7 = - 3 D^{14}_7 \alpha _{14}$, substituting (3.26) into (3.24) and using the first equation in (3.27) now gives

$$\begin{aligned} 0 = -8 D^{27}_7 D^7_{27} \alpha _7 - 8 D^7_7 \omega _7 = -8 D^{27}_7 D^7_{27} \alpha _7, \end{aligned}$$

which by Remark 3.4 implies that

$$\begin{aligned} D^7_{27} \alpha _7 = 0. \end{aligned}$$

(3.31)

Combining (3.31) with (3.26) and using Theorem 2.19, we find that $\alpha _7$ is harmonic.

Recalling from (3.23) that $\omega _{27} = - 2 D^7_{27} \alpha _7 + D^{14}_{27} \alpha _{14}$, substituting (3.31) and taking $D^{27}_{27}$, we obtain by the relations in (2.17) that

$$\begin{aligned} D^{27}_{27} \omega _{27} = D^{27}_{27} D^{14}_{27} \alpha _{14} = D^7_{27} D^{14}_7 \alpha _{14}. \end{aligned}$$

Substituting $D^{14}_7 \alpha _{14} = - \tfrac{1}{3} \omega _7$ from (3.23) into the above expression and using the second equation in (3.29), we find that

$$\begin{aligned} D^{27}_{27} \omega _{27} = - \tfrac{1}{3} D^7_{27} \omega _{7} = 0. \end{aligned}$$

(3.32)

Combining the second equation in (3.27), Eq. (3.30), and (3.32), with Eq. (2.19), we deduce that $\omega _{27}$ is a harmonic $\varOmega ^4_{27}$ form. We already showed that $\omega _7$ is a harmonic $\varOmega ^4_7$ form and that $\omega _1 = 0$. Thus, we have $\omega \in \mathcal {H}^4$, and moreover, we assumed that $\omega \in ({\text {im}}\mathrm {d})^4$. By Hodge theory, we conclude that $\omega = 0$ as claimed. $\square$

Proposition 3.16

We have $H^4_{\varphi } \cong \mathcal {H}^4 \oplus \big ( ({\text {im}}\mathrm {d})^4 \cap (\ker \mathcal {L}_B)^4 \big )$.

Proof

In the proof of Proposition 3.7, we showed that

$$\begin{aligned} H^3_{\varphi } = (\ker \mathcal {L}_B)^3 = \mathcal {H}^3 \oplus \big ( ({\text {im}}{\mathrm {d}}{}^{\star })^3 \cap (\ker \mathcal {L}_B)^3 \big ). \end{aligned}$$

We also have $\mathcal {H}^3 \subset (\ker \mathcal {L}_B)^3$ by (2.38). Thus,

$$\begin{aligned} \mathcal {H}^3 \subseteq (\ker \mathcal {L}_B)^3 \subseteq \mathcal {H}^3 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^3. \end{aligned}$$

Taking orthogonal complements of the above chain of nested subspaces and using the Hodge decomposition $\varOmega ^3 = \mathcal {H}^3 \oplus ({\text {im}}\mathrm {d})^3 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^3$, we find

$$\begin{aligned} ({\text {im}}\mathrm {d})^3 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^3 \supseteq ((\ker \mathcal {L}_B)^3)^{\perp } \supseteq ({\text {im}}\mathrm {d})^3. \end{aligned}$$

Taking the Hodge star of the above chain of nested subspaces and using $({\text {im}}\mathcal {L}_B)^4 = *((\ker \mathcal {L}_B)^3)^{\perp }$ from (3.14), we obtain

$$\begin{aligned} ({\text {im}}{\mathrm {d}}{}^{\star })^4 \subseteq ({\text {im}}\mathcal {L}_B)^4 \subseteq ({\text {im}}{\mathrm {d}}{}^{\star })^4 \oplus ({\text {im}}\mathrm {d})^4. \end{aligned}$$

Applying Lemma 1.2(i) to the above yields

$$\begin{aligned} ({\text {im}}\mathcal {L}_B)^4 = ({\text {im}}{\mathrm {d}}{}^{\star })^4 \oplus \big ( ({\text {im}}\mathrm {d})^4 \cap ({\text {im}}\mathcal {L}_B)^4 \big ). \end{aligned}$$

(3.33)

Now recall that $\mathcal {H}^4 \subseteq (\ker \mathcal {L}_B)^4$ by (2.38). Thus, we have

$$\begin{aligned} \mathcal {H}^4 \subseteq (\ker \mathcal {L}_B)^4 \subseteq \varOmega ^4 = \mathcal {H}^4 \oplus ({\text {im}}\mathrm {d})^4 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^4. \end{aligned}$$

Applying Lemma 1.2(i) to the above and using Lemma 3.14 gives

$$\begin{aligned} (\ker \mathcal {L}_B)^4 = \mathcal {H}^4 \oplus \big ( ({\text {im}}{\mathrm {d}}{}^{\star })^4 \cap (\ker \mathcal {L}_B)^4\big ) \oplus \big ( ({\text {im}}\mathrm {d})^4 \cap (\ker \mathcal {L}_B)^4 \big ). \end{aligned}$$

(3.34)

Thus, applying Lemma 1.2(ii) to (3.33), (3.34), as subspaces of $\varOmega ^4 = \mathcal {H}^4 \oplus ({\text {im}}\mathrm {d})^4 \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^4$, we obtain

$$\begin{aligned} (\ker \mathcal {L}_B)^4 \cap ({\text {im}}\mathcal {L}_B)^4 = \big ( ({\text {im}}{\mathrm {d}}{}^{\star })^4 \cap (\ker \mathcal {L}_B)^4 \big ) \oplus \big ( ({\text {im}}\mathrm {d})^4 \cap (\ker \mathcal {L}_B)^4 \cap ({\text {im}}\mathcal {L}_B)^4 \big ). \end{aligned}$$

(3.35)

By Lemma 3.15, Eq. (3.35) simplifies to

$$\begin{aligned} (\ker \mathcal {L}_B)^4 \cap ({\text {im}}\mathcal {L}_B)^4 = ({\text {im}}{\mathrm {d}}{}^{\star })^4 \cap (\ker \mathcal {L}_B)^4. \end{aligned}$$

(3.36)

Hence, by (3.34) and (3.36), we have

$$\begin{aligned} \mathcal {H}^4_{\varphi }&= \frac{(\ker \mathcal {L}_B)^4}{(\ker \mathcal {L}_B)^4 \cap ({\text {im}}\mathcal {L}_B)^4} \\&= \frac{\mathcal {H}^4 \oplus \big ( ({\text {im}}{\mathrm {d}}{}^{\star })^4 \cap (\ker \mathcal {L}_B)^4 \big ) \oplus \big ( ({\text {im}}\mathrm {d})^4 \cap (\ker \mathcal {L}_B)^4 \big )}{({\text {im}}{\mathrm {d}}{}^{\star })^4 \cap (\ker \mathcal {L}_B)^4}\\&\cong \mathcal {H}^4 \oplus ({\text {im}}\mathrm {d})^4 \cap (\ker \mathcal {L}_B)^4 \end{aligned}$$

as claimed. $\square$

Lemma 3.17

We have $({\text {im}}{\mathrm {d}}{}^{\star })^3 \cap (\ker {\mathcal {L}}_B)^3=({\text {im}}{\mathrm {d}}{}^{\star })^3 \cap (\ker \mathcal {L}^*_B)^3$.

Proof

Let $\omega = {\mathrm {d}}{}^{\star }(\gamma _1 + \gamma _7 + \gamma _{27}) \in ({\text {im}}{\mathrm {d}}{}^{\star })^3$ where $\gamma _1 + \gamma _7 + \gamma _{27} \in \varOmega ^4_1 \oplus \varOmega ^4_7 \oplus \varOmega ^4_{27}$. From ${\mathrm {d}}{}^{\star }= *\mathrm {d}*$ on $\varOmega ^5$ and Fig. 1, we find that

$$\begin{aligned} {\mathrm {d}}{}^{\star }(\gamma _1 + \gamma _7 + \gamma _{27}) = \tfrac{4}{3} D^7_1 \gamma _7 + (- D^1_7 \gamma _1 - \tfrac{3}{2} D^7_7 \gamma _7 + D^{27}_7 \gamma _{27}) + (-D^7_{27} \gamma _7 + D^{27}_{27} \gamma _{27}).\nonumber \\ \end{aligned}$$

(3.37)

Using (3.37) and Fig. 4, we have

$$\begin{aligned} {\mathcal {L}}_B {\mathrm {d}}{}^{\star }(\gamma _1 + \gamma _7 + \gamma _{27})&= - 2 D^1_7 \left( \tfrac{4}{3} D^7_1 \gamma _7 \right) + 3 D^7_{14} \left( - D^1_7 \gamma _1 - \tfrac{3}{2} D^7_7 \gamma _7 + D^{27}_7 \gamma _{27}\right) \\&\qquad + \left( -\tfrac{8}{3} D^{27}_7 + D^{27}_{14}\right) \left( -D^7_{27} \gamma _7 + D^{27}_{27} \gamma _{27}\right) \\&\quad = \left( -\tfrac{8}{3} D^1_7 D^7_1 \gamma _7 + \tfrac{8}{3} D^{27}_7 D^7_{27} \gamma _7 - \tfrac{8}{3} D^{27}_7 D^{27}_{27} \gamma _{27}\right) \\&\qquad + \left( -3 D^7_{14} D^1_7 \gamma _1 - \tfrac{9}{2} D^7_{14} D^7_7 \gamma _7 + 3 D^7_{14} D^{27}_7 \gamma _{27} \right. \\&\left. \qquad - D^{27}_{14} D^7_{27} \gamma _7 + D^{27}_{14} D^{27}_{27} \gamma _{27}\right) . \end{aligned}$$

Using the various relations in (2.17), the above expression simplifies to

$$\begin{aligned} \begin{aligned} {\mathcal {L}}_B {\mathrm {d}}{}^{\star }(\gamma _1 + \gamma _7 + \gamma _{27})&= -6 D^7_7 D^7_7 \gamma _7 + 4 D^7_7 D^{27}_7 \gamma _{27} - 6 D^7_{14} D^7_7 \gamma _7 + 4 D^7_{14} D^{27}_7 \gamma _{27} \\&= 2 D^7_7 ( -3 D^7_7 \gamma _7 + 2 D^{27}_7 \gamma _{27}) + 2 D^7_{14} ( -3 D^7_7 \gamma _7 + 2 D^{27}_7 \gamma _{27}). \end{aligned} \end{aligned}$$

(3.38)

Using ${\mathcal {L}}_B^* = - *\mathcal {L}_B *$ from (2.28), Eq. (3.37), and Fig. 4 again, we also have that

$$\begin{aligned} \mathcal {L}^*_B {\mathrm {d}}{}^{\star }(\gamma _1 + \gamma _7 + \gamma _{27})&= - 3 D^1_7 ( \tfrac{4}{3} D^7_1 \gamma _7 ) + 6 D^7_7 ( - D^1_7 \gamma _1 - \tfrac{3}{2} D^7_7 \gamma _7 + D^{27}_7 \gamma _{27}) \\&\qquad {} - 4 D^{27}_7 (-D^7_{27} \gamma _7 + D^{27}_{27} \gamma _{27}) \\ =&-4 D^1_7 D^7_1 \gamma _7 - 6 D^7_7 D^1_7 \gamma _1 - 9 D^7_7 D^7_7 \gamma _7 + 6 D^7_7 D^{27}_7 \gamma _{27} \\&\qquad {} + 4 D^{27}_7 D^7_{27} \gamma _7 - 4 D^{27}_7 D^{27}_{27} \gamma _{27}. \end{aligned}$$

Using the various relations in (2.17), the above expression simplifies to

$$\begin{aligned} \begin{aligned} \mathcal {L}^*_B {\mathrm {d}}{}^{\star }(\gamma _1 + \gamma _7 + \gamma _{27})&= -18 D^7_7 D^7_7 \gamma _7 + 12 D^7_7 D^{27}_7 \gamma _{27}) \\&= 6 D^7_7 (-3 D^7_7 \gamma _7 + 2 D^{27}_7 \gamma _{27}). \end{aligned} \end{aligned}$$

(3.39)

Thus, for $\omega \in ({\text {im}}{\mathrm {d}}{}^{\star })^3$ we conclude that

$$\begin{aligned} \omega \in (\ker {\mathcal {L}}_B)^3&\iff \left\{ \begin{aligned} D^7_7 (-3 D^7_7 \gamma _7 + 2 D^{27}_7 \gamma _{27})&= 0, \\ D^7_{14} (-3 D^7_7 \gamma _7 + 2 D^{27}_7 \gamma _{27})&= 0, \end{aligned} \right\}&\text {by}~(3.38) \\&\iff D^7_7 (- 3 D^7_7 \gamma _7 + 2 D^{27}_7 \gamma _{27} = 0)&\text {by Theorem}~2.19 \\&\iff \omega \in (\ker \mathcal {L}^*_B)^3&\text {by}~(3.39) \end{aligned}$$

which is what we wanted to show. $\square$

Corollary 3.18

We have

$$\begin{aligned} H^3_{\varphi }&= \mathcal {H}^3 \oplus \big ( ({\text {im}}{\mathrm {d}}{}^{\star })^3 \cap (\ker {\mathcal {L}}_B)^3 \cap (\ker \mathcal {L}^*_B)^3 \big ), \\ H^4_{\varphi }&= \mathcal {H}^4 \oplus \big ( ({\text {im}}\mathrm {d})^4 \cap (\ker {\mathcal {L}}_B)^4 \cap (\ker \mathcal {L}^*_B)^4 \big ). \end{aligned}$$

Proof

Lemma 3.17 says that

$$\begin{aligned} ({\text {im}}{\mathrm {d}}{}^{\star })^3 \cap (\ker {\mathcal {L}}_B)^3 =({\text {im}}{\mathrm {d}}{}^{\star })^3 \cap (\ker {\mathcal {L}}_B)^3 \cap (\ker \mathcal {L}^*_B)^3 = ({\text {im}}{\mathrm {d}}{}^{\star })^3 \cap (\ker \mathcal {L}^*_B)^3. \end{aligned}$$

Applying $*$ to the above equation and using (2.28) gives

$$\begin{aligned} ({\text {im}}\mathrm {d})^4 \cap (\ker {\mathcal {L}}_B)^4 = ({\text {im}}\mathrm {d})^4 \cap (\ker {\mathcal {L}}_B)^4 \cap (\ker \mathcal {L}^*_B)^4 = ({\text {im}}\mathrm {d})^4 \cap (\ker \mathcal {L}^*_B)^4. \end{aligned}$$

The claim now follows from Propositions 3.7 and 3.16. $\square$

3.4 The main theorem on ${\mathcal {L}}_B$-cohomology

We summarize the results of Sect. 3 in the following theorem, which is intentionally stated in a way to mirror Theorem 3.2.

Theorem 3.19

The following relations hold.

• $H^k_{\varphi } \cong H^k_{dR}$ for $k=0,1,2,5,6,7$.

• $H^k_{\varphi }$ is infinite-dimensional for $k = 3,4$.

• There is a canonical injection $\mathcal {H}^k \hookrightarrow H^k_{\varphi }$ for all k.

• The Hodge star induces isomorphisms $*: H^k_{\varphi } \cong H^{7-k}_{\varphi }$.

Proof

All that remains to show is that $H^3_{\varphi }$ is indeed infinite-dimensional. But observe by (3.38) that for all $\alpha \in \varOmega ^4_1$, we have ${\mathcal {L}}_B {\mathrm {d}}{}^{\star }\alpha = 0$. Therefore, $\{ {\mathrm {d}}{}^{\star }\alpha : \alpha \in \varOmega ^4_1 \} \cong {\text {im}}D^1_7 \cong ({\text {im}}\mathrm {d})^1$ is an infinite-dimensional subspace of $({\text {im}}{\mathrm {d}}{}^{\star })^3 \cap (\ker {\mathcal {L}}_B)^3 \subseteq H^3_{\varphi }$. $\square$

4 An application to ‘almost’ formality

In this section, we consider an application of our results to the question of formality of compact torsion-free $\mathrm {G}_2$ manifolds. We discover a new topological obstruction to the existence of torsion-free $\mathrm {G}_2$-structures on compact manifolds and discuss an explicit example in detail.

4.1 Formality and Massey triple products

Recall from (2.24) that $\mathrm {d}$ commutes with $\mathcal L_B$. Hence, $\mathrm {d}$ induces a natural map

$$\begin{aligned} \mathrm {d}: H^k_{\varphi } \rightarrow H^{k+1}_{\varphi }. \end{aligned}$$

Also, because ${\mathcal {L}}_B$ is a derivation, it is easy to check that the wedge product on $\varOmega ^{\bullet }$ descends to $H^{\bullet }_{\varphi }$, with the Leibniz rule $\mathrm {d}(\omega \wedge \eta ) = (\mathrm {d}\omega ) \wedge \eta + (-1)^{|\omega |} \omega \wedge (\mathrm {d}\eta )$ still holding on $H^{\bullet }_{\varphi }$. These two facts say that the complex $(H^{\bullet }_{\varphi }, \mathrm {d})$ is a differential graded algebra, henceforth abbreviated dga.

Additionally, because $[ \mathrm {d}, \mathcal {L}_B ] = 0$, we also have that $( (\ker {\mathcal {L}}_B)^{\bullet }, \mathrm {d})$ is a subcomplex of the de Rham complex $( \varOmega ^{\bullet }, \mathrm {d})$. The natural injection and projection give homomorphisms of dga’s

$$\begin{aligned} (\varOmega ^{\bullet }, \mathrm {d}) \hookleftarrow ((\ker {\mathcal {L}}_B)^{\bullet }, \mathrm {d}) \twoheadrightarrow (H^{\bullet }_{\varphi }, \mathrm {d}). \end{aligned}$$

One goal of this section is to show that these two homomorphisms of dga’s are both quasi-isomorphisms. This means that they induce isomorphisms on the cohomologies of the complexes. As mentioned in Introduction, some of the results in this section appeared earlier in work of Verbitsky [22]. For example, our Proposition 4.1 is exactly [22, Proposition 2.21], with the same proof. However, the proof of [22, Proposition 2.19] has several errors. The critical error is the following: first Verbitsky correctly shows that $\alpha - \Pi \alpha$ is an element of both $({\text {im}}\mathrm {d}_c + {\text {im}}{\mathrm {d}}{}^{\star }_c)$ and $({\text {im}}{\mathrm {d}}{}^{\star }_c)^{\perp }$. But then he incorrectly concludes that $\alpha - \Pi \alpha$ must be an element of ${\text {im}}\mathrm {d}_c$. This conclusion is only valid if $(\mathrm {d}_c)^2 = 0$, which is not true in general. We give a correct proof of this result, which is our Proposition 4.4. One consequence is the result about the Massey triple product in our Corollary 4.9, which appears to be new.

Proposition 4.1

(Verbitsky [22]) The inclusion $((\ker {\mathcal {L}}_B)^{\bullet }, \mathrm {d}) \hookrightarrow (\varOmega ^{\bullet }, \mathrm {d})$ is a quasi-isomorphism.

Proof

This is proved in [22, Proposition 2.11]. We reproduce the short proof here for completeness and convenience of the reader. Since the differential for both complexes $\varOmega ^{\bullet }$ and $(\ker {\mathcal {L}}_B)^{\bullet }$ is the same exterior derivative $\mathrm {d}$, we will omit it from the notation for simplicity.

It is well known that the Hodge Laplacian $\varDelta$ determines an eigenspace decomposition $\varOmega ^k = \oplus _{\lambda } \varOmega ^k_{\lambda }$ where the sum is over all eigenvalues $\lambda$ of $\varDelta$, which form a discrete set of nonnegative real numbers, and $\varOmega ^k_{\lambda } = \{ \alpha \in \varOmega ^k : \varDelta \alpha = \lambda \alpha \}$ are the associated eigenspaces. Note that $\varOmega ^k_0 = \mathcal {H}^k$ is the space of harmonic k-forms. It is well known that the cohomology of $\varOmega ^k_{\lambda }$ is trivial for $\lambda > 0$. This is because, if $\alpha \in \varOmega ^k_{\lambda }$ with $\lambda > 0$ and $\mathrm {d}\alpha = 0$, then

$$\begin{aligned} \alpha = \tfrac{1}{\lambda } \varDelta \alpha = \tfrac{1}{\lambda } (\mathrm {d}{\mathrm {d}}{}^{\star }\alpha + {\mathrm {d}}{}^{\star }\mathrm {d}\alpha ) = \mathrm {d}(\tfrac{1}{\lambda } {\mathrm {d}}{}^{\star }\alpha ) \end{aligned}$$

(4.1)

is exact.

By (2.36), the operator ${\mathcal {L}}_B$ commutes with $\varDelta$, and thus, we obtain a decomposition

$$\begin{aligned} (\ker {\mathcal {L}}_B)^k = \oplus _{\lambda } \big ( \varOmega ^k_{\lambda } \cap (\ker {\mathcal {L}}_B)^k \big ). \end{aligned}$$

Note by (2.38) that $\varOmega ^k_0 \cap (\ker \mathcal L_B)^k = \mathcal {H}^k \cap (\ker {\mathcal {L}}_B)^k = \mathcal {H}^k = \varOmega ^k_0$. Thus, it remains to show that the cohomology of $\varOmega ^k_{\lambda } \cap (\ker {\mathcal {L}}_B)^k$ is also trivial for all $\lambda > 0$. But if $\alpha \in \varOmega ^k_{\lambda } \cap (\ker {\mathcal {L}}_B)^k$, we have ${\mathcal {L}}_B \alpha = 0$ and $\alpha = \mathrm {d}(\tfrac{1}{\lambda } {\mathrm {d}}{}^{\star }\alpha )$ by (4.1). Since ${\mathcal {L}}_B$ commutes with ${\mathrm {d}}{}^{\star }$ by (2.35), we have ${\mathcal {L}}_B (\tfrac{1}{\lambda } {\mathrm {d}}{}^{\star }\alpha ) = \tfrac{1}{\lambda } {\mathrm {d}}{}^{\star }{\mathcal {L}}_B \alpha = 0$, so the class of $\alpha$ in the cohomology of $(\ker {\mathcal {L}}_B)^k$ is indeed trivial. $\square$

In Sect. 3, while computing $H^{\bullet }_{\varphi }$, we explicitly computed the complex $((\ker {\mathcal {L}}_B)^{\bullet }, \mathrm {d})$. The results are collected in Fig. 6. The isomorphisms displayed in Fig. 6 are explained in Corollary 4.2.

Fig. 6

The complex $((\ker {\mathcal {L}}_B)^{\bullet }, \mathrm {d})$

Corollary 4.2

For all $0 \le k \le 7$, we have $({\text {im}}\mathrm {d})^k \cap (\ker \mathcal L_B)^k = \mathrm {d}(\ker {\mathcal {L}}_B)^{k-1}$.

Proof

Let $\varOmega ^k = \mathcal {H}^k \oplus ({\text {im}}\mathrm {d})^k \oplus ({\text {im}}{\mathrm {d}}{}^{\star })^k$ denote the Hodge decomposition of $\varOmega ^k$. For simplicity in this proof, we will write $A^k = \mathcal {H}^k$, $B^k = ({\text {im}}\mathrm {d})^k$, and $C^k = ({\text {im}}{\mathrm {d}}{}^{\star })^k$. Thus, $\varOmega ^k = A^k \oplus B^k \oplus C^k$. We can see from Fig. 6 that for all $0 \le k \le 7$, we have $(\ker {\mathcal {L}}_B)^k = A^k \oplus {\tilde{B}}^k \oplus {\tilde{C}}^k$, where ${\tilde{B}}^k$ and ${\tilde{C}}^k$ are subspaces of $B^k$ and $C^k$, respectively. Depending on k, we can have ${\tilde{B}}^k = 0$, ${\tilde{B}}^k = B^k$, or $0 \subsetneq \tilde{B}^k \subsetneq B^k$ and similarly for ${\tilde{C}}^k$. By Hodge theory, $(\ker \mathrm {d})^k = A^k \oplus B^k$, so applying Lemma 1.2(ii) we find that

$$\begin{aligned} (\ker {\mathcal {L}}_B)^k \cap (\ker \mathrm {d})^k = A^k \oplus {\tilde{B}}^k. \end{aligned}$$

(4.2)

Applying $\mathrm {d}$ to $(\ker {\mathcal {L}}_B)^{k-1}$, we have

$$\begin{aligned} \mathrm {d}(\ker {\mathcal {L}}_B)^{k-1} = \mathrm {d}({\tilde{C}}^{k-1}) \subseteq {\tilde{B}}^k. \end{aligned}$$

(4.3)

By Proposition 4.1, the cohomology of $(\varOmega ^k, \mathrm {d})$ equals the cohomology of $( (\ker {\mathcal {L}}_B)^k, \mathrm {d})$. But by Hodge theory, the cohomology of $(\varOmega ^k, \mathrm {d})$ is $\mathcal {H}^k = A^k$, and Eqs. (4.2) and (4.3) say that the cohomology of $( (\ker {\mathcal {L}}_B)^k, \mathrm {d})$ is $A^k \oplus \big ( {\tilde{B}}^k/(\mathrm {d}\tilde{C}^{k-1}) \big )$. Thus, in fact, we have $\mathrm {d}{\tilde{C}}^{k-1} = \tilde{B}^k$, and since $\mathrm {d}$ is injective on $C^k$, we deduce that

$$\begin{aligned} \mathrm {d}\text { maps }{\tilde{C}}^{k-1}\text { isomorphically onto } {\tilde{B}}^k\text { for all } 0 \le k \le 7. \end{aligned}$$

(4.4)

From $({\text {im}}\mathrm {d})^k \cap (\ker {\mathcal {L}}_B)^k = {\tilde{B}}^k$, and $\mathrm {d}(\ker {\mathcal {L}}_B)^{k-1} = \mathrm {d}(A^{k-1} \oplus {\tilde{B}}^{k-1} \oplus {\tilde{C}}^{k-1}) = \mathrm {d}{\tilde{C}}^{k-1}$, we conclude that $({\text {im}}\mathrm {d})^k \cap (\ker {\mathcal {L}}_B)^k = \mathrm {d}(\ker {\mathcal {L}}_B)^{k-1}$ as claimed. $\square$

Remark 4.3

Corollary 4.2 may be related to a $\mathrm {G}_2$-analog of the generalized$\partial {\bar{\partial }}$-lemma, called the $\mathrm {d}\mathcal {L}_J$-lemma, introduced by the authors in [4] in the context of ${\mathrm{U}}{m}$-structures. See [4, Equation (3.27)]. $\square$

Proposition 4.4

The quotient map $((\ker {\mathcal {L}}_B)^{\bullet }, \mathrm {d}) \twoheadrightarrow (H^{\bullet }_{\varphi }, \mathrm {d})$ is a quasi-isomorphism.

Proof

We have a short exact sequence of chain complexes

$$\begin{aligned} 0 \rightarrow ((\ker {\mathcal {L}}_B)^{\bullet } \cap ({\text {im}}{\mathcal {L}}_B)^{\bullet }, \mathrm {d}) \rightarrow ((\ker {\mathcal {L}}_B)^{\bullet }, \mathrm {d}) \twoheadrightarrow (H^{\bullet }_{\varphi }, \mathrm {d}) \rightarrow 0, \end{aligned}$$

so it suffices to show that the cohomology of $((\ker \mathcal L_B)^{\bullet } \cap ({\text {im}}{\mathcal {L}}_B)^{\bullet }, \mathrm {d})$ is trivial. In Sect. 3, while computing $H^{\bullet }_{\varphi }$, we explicitly computed the complex $((\ker {\mathcal {L}}_B)^{\bullet } \cap ({\text {im}}{\mathcal {L}}_B)^{\bullet }, \mathrm {d})$. The results are collected in Fig. 7. The isomorphisms in Fig. 7 are a subset of the isomorphisms from Fig. 6 and are colored in the same way. It is clear from Fig. 7 that the cohomology of $((\ker {\mathcal {L}}_B)^{\bullet } \cap ({\text {im}}{\mathcal {L}}_B)^{\bullet }, \mathrm {d})$ is trivial. $\square$

Fig. 7

The complex $((\ker {\mathcal {L}}_B \cap {\text {im}}\mathcal L_B)^{\bullet }, \mathrm {d})$

The next two definitions are taken from [10, Section 3.A].

Definition 4.5

Let $(A, \mathrm {d}_A)$ and $(B, \mathrm {d}_B)$ be two differential graded algebras (dga’s). We say that A and B are equivalent if there exists a finite sequence of dga quasi-isomorphisms

A dga $(A, \mathrm {d}_A)$ is called formal if it is equivalent to a dga $(B, \mathrm {d}_B)$ with $\mathrm {d}_B = 0$. $\square$

It is well known [10, Section 3.A] that a compact Kähler manifold is formal. That is, the de Rham complex of a compact Kähler manifold is equivalent to a dga with zero differential. It is still an open question whether or not compact torsion-free $\mathrm {G}_2$ manifolds are formal. We show in Theorem 4.6 that compact torsion-free $\mathrm {G}_2$ manifolds are ‘almost formal’ in the sense that the de Rham complex is equivalent to a dga which has only one nonzero differential.

Theorem 4.6

The de Rham complex of a compact torsion-free $\mathrm {G}_2$ manifold $(\varOmega ^{\bullet }, \mathrm {d})$ is equivalent to $(H^{\bullet }_{\varphi }, \mathrm {d})$, which is a dga with all differentials trivial except for $\mathrm {d}: H^3_{\varphi } \rightarrow H^4_{\varphi }$.

Proof

In Sect. 3, we explicitly computed the complex $(H^{\bullet }_{\varphi }, \mathrm {d})$. The results are collected in Fig. 8. The isomorphism in Fig. 8 appeared already in Fig. 6 and is colored in the same way. The zero maps in Fig. 8 are a consequence of $\mathcal {H}^k \subseteq (\ker \mathrm {d})^k$. $\square$

Fig. 8

The complex $(H^{\bullet }_{\varphi }, \mathrm {d})$

One consequence of almost-formality is that most of the Massey triple products of the de Rham complex will vanish. This is established in Corollary 4.9 below.

Definition 4.7

Let $(A,\mathrm {d}_A)$ be a dga, and denote by $H^k (A)$ the degree k cohomology of A with respect to $\mathrm {d}_A$. Let $[\alpha ]\in H^p(A)$, $[\beta ] \in H^q(A)$, $[\gamma ] \in H^r(A)$ be cohomology classes satisfying

$$\begin{aligned}{}[\alpha ] [\beta ] = 0 \in H^{p+q}(A) \quad \text {and} \quad [\beta ] [\gamma ] = 0 \in H^{q+r}(A). \end{aligned}$$

Then $\alpha \beta =\mathrm {d}f$ and $\beta \gamma = \mathrm {d}g$ for some $f \in A^{p+q-1}$ and $g \in A^{q+r-1}$. Consider the class

$$\begin{aligned}{}[f \gamma - (-1)^p \alpha g] \in H^{p+q+r-1}(A). \end{aligned}$$

It can be checked that this class is well defined up to an element of $H^{p+q-1} \cdot H^r + H^p \cdot H^{q+r-1}$. That is, it is well defined as an element of the quotient

$$\begin{aligned} \frac{H^{p+q+r-1}(A)}{H^{p+q-1} \cdot H^r + H^p \cdot H^{q+r-1}}. \end{aligned}$$

We call this element the Massey triple product and write it as $\langle [\alpha ], [\beta ], [\gamma ] \rangle$. It is easy to see that the Massey triple product is linear in each of its three arguments. $\square$

In the following, we only consider the case when $(A,\mathrm {d}_A) = (\varOmega ^*, \mathrm {d})$ is the dga of smooth differential forms. If the dga $(A, \mathrm {d}_A)$ is formal, then all the Massey triple products vanish due to the naturality of the triple product (see [10, Proposition 3.A.33] for details). In fact, the proof of [10, Proposition 3.A.33] actually yields the following more general result.

Corollary 4.8

Let $(A, \mathrm {d}_A)$ be a dga such that the differentials $\mathrm {d}_A$ are all zero except for $\mathrm {d}: A^{k-1} \rightarrow A^k$. Then if the Massey triple product $\langle [\alpha ], [\beta ], [\gamma ] \rangle$ is defined and we have $|\alpha | + |\beta | \ne k$ and $|\beta | + |\gamma | \ne k$, then $\langle [\alpha ], [\beta ], [\gamma ] \rangle = 0$.

Combining Corollary 4.8 and Theorem 4.6 yields the following.

Corollary 4.9

Let M be a compact torsion-free $\mathrm {G}_2$ manifold. Consider cohomology classes $[\alpha ]$, $[\beta ]$, and $[\gamma ] \in H^{\bullet }_{\mathrm {dR}}$. If the Massey triple product $\langle [\alpha ], [\beta ], [\gamma ] \rangle$ is defined and we have $|\alpha | + |\beta | \ne 4$ and $|\beta | + |\gamma | \ne 4$, then $\langle [\alpha ], [\beta ], [\gamma ] \rangle = 0$.

In Theorem 4.10 in the next section, we establish a stronger version of Corollary 4.9 when the holonomy of the metric on M is exactly $\mathrm {G}_2$.

4.2 A new topological obstruction to existence of torsion-free $\mathrm {G}_2$-structures

A key feature of the criterion in Corollary 4.9 is that it is topological. That is, it does not depend on the differentiable structure on M. Therefore, it gives a new topological obstruction to the existence of torsion-free $\mathrm {G}_2$-structures on compact 7-manifolds. There are several previously known topological obstructions to the existence of a torsion-free $\mathrm {G}_2$-structure on a compact 7-manifold. These obstructions are discussed in detail in [11, Chapter 10]. We summarize them here. Let $\varphi$ be a torsion-free $\mathrm {G}_2$-structure on a compact manifold M with induced metric $g_{\varphi }$. Let $b^k_M = \dim H^k_{\mathrm {dR}} (M)$. Then

$$\begin{aligned} \left. \begin{aligned}&b^3_M \ge b^1_M + b^0_M, \\&b^2_M \ge b^1_M, \\&b^1_M \in \{ 0, 1, 3, 7 \}, \\&\text {if }g_{\varphi } \text { is not flat, then }p_1 (M) \ne 0,\text { where }p_1 (M)\text { is the first Pontryagin class of }TM, \phantom {A} \\&\text {if }g_{\varphi } \text { has full holonomy }\mathrm {G}_2, \text {then the fundamental group } \pi _1 (M)\text { is finite}. \end{aligned} \right\} \nonumber \\ \end{aligned}$$

(4.5)

Note that the first three conditions are simply obstructions to the existence of torsion-free $\mathrm {G}_2$-structures. The fourth condition can be used to rule out non-flat torsion-free $\mathrm {G}_2$-structures, and the fifth condition can be used to rule out non-irreducible torsion-free $\mathrm {G}_2$-structures. In fact, the third condition determines the reduced holonomy of $g_{\varphi }$, which is $\{1\}$, $\mathrm {SU}(2)$, $\mathrm {SU}(3)$, or $\mathrm {G}_2$, if $b^1_M = 7$, 3, 1, or 0, respectively.

Theorem 4.10

Let M be a compact torsion-free $\mathrm {G}_2$ manifold with full holonomy $\mathrm {G}_2$, and consider cohomology classes $[\alpha ]$, $[\beta ]$, and $[\gamma ] \in H^{\bullet }_{\mathrm {dR}}$. If the Massey triple product $\langle [\alpha ], [\beta ], [\gamma ] \rangle$ is defined, then $\langle [\alpha ], [\beta ], [\gamma ] \rangle = 0$ except possibly in the case when $|\alpha | = |\beta | = |\gamma | = 2$.

Proof

Recall that the hypothesis of full holonomy $\mathrm {G}_2$ implies that $b^1_M = 0$, so $H^1_{\mathrm {dR}} = \{0\}$. Suppose $|\alpha | = 1$. Then $[\alpha ] \in H^1_{\mathrm {dR}}$, so $[\alpha ] = 0$, and by linearity it follows that $\langle [\alpha ], [\beta ], [\gamma ] \rangle = 0$. The same argument holds if $|\beta | = 1$ or $|\gamma | = 1$. Suppose $|\alpha | = 0$. Then $\alpha$ is a constant function. The condition $[\alpha \beta ] = [\alpha ][\beta ] = 0$ forces the form $\alpha \beta$ to be exact, so either $\alpha = 0$ (in which case the Massey product vanishes), or $\beta$ is exact, so $[\beta ] = 0$ and again the Massey product vanishes. A similar argument holds if $|\beta | = 0$ or $|\gamma | = 0$.

Thus, we must have $|\alpha |, |\beta |, |\gamma | \ge 2$ if the Massey product has any chance of being nontrivial. Moreover, since $\langle [\alpha ], [\beta ], [\gamma ] \rangle$ lies in a quotient of $H^{|\alpha | + |\beta | + |\gamma | - 1}_{\mathrm {dR}}$, we also need $|\alpha | + |\beta | + |\gamma | \le 8$. Finally, Corollary 4.9 tells us that we must have either $|\alpha | + |\beta | = 4$ or $|\beta | + |\gamma | = 4$. Hence, the only possibilities for the triple $(|\alpha |, |\beta |, |\gamma |)$ to obtain a nontrivial Massey product are (2, 2, 2), (2, 2, 3), (2, 2, 4), (3, 2, 2), and (4, 2, 2). For (2, 2, 3) or (3, 2, 2), the Massey product lies in a quotient of $H^6_{\mathrm {dR}}$, which is zero since $b^6_M = b^1_M = 0$. For (2, 2, 4) or (4, 2, 2), the Massey product lies inside $H^7_{\mathrm {dR}}/ (H^2_{\mathrm {dR}} \cdot H^6_{\mathrm {dR}} + H^3_{\mathrm {dR}} \cdot H^4_{\mathrm {dR}})$, but $H^3_{\mathrm {dR}} \cdot H^4_{\mathrm {dR}} = H^7_{\mathrm {dR}}$ since $\varphi \wedge \psi = 7 \mathsf {vol}$ is a generator of $H^7_{\mathrm {dR}}$. Thus, in this case, the quotient space is zero. We conclude that the only possibly nontrivial Massey product corresponds to the case $(|\alpha |, |\beta |, |\gamma |) = (2,2,2)$. $\square$

In the remainder of this section, we will apply our new criterion to a particular nontrivial example. Consider a smooth compact connected oriented 7-manifold M of the form $M = W \times L$, where W and L are smooth compact connected oriented manifolds of dimensions 3 and 4, respectively. In order for M to admit $\mathrm {G}_2$-structures, we must have $w_2 (M) = 0$, where $w_2 (M)$ is the second Stiefel–Whitney class of TM, by [19, pp. 348–349].

Take W to be the real Iwasawa manifold, which is defined to be the quotient of the set

$$\begin{aligned} \left\{ \begin{pmatrix} 1 &{} t_1 &{} t_2 \\ 0 &{} 1 &{} t_3 \\ 0 &{} 0 &{} 1 \end{pmatrix} : t_1, t_2, t_3 \in {\mathbb {R}}\right\} \cong {\mathbb {R}}^3 \end{aligned}$$

by the left multiplication of the group

$$\begin{aligned} \left\{ \begin{pmatrix} 1 &{} a &{} b \\ 0 &{} 1 &{} c \\ 0 &{} 0 &{} 1 \end{pmatrix} : a, b, c \in {\mathbb {Z}}\right\} . \end{aligned}$$

The manifold W is a compact orientable 3-manifold, so it is parallelizable and hence $w_2 (W) = 0$. Moreover, it is shown in [10, Example 3.A.34] that $b^1_W = 2$ and that

$$\begin{aligned} \text { there exist }\alpha , \beta \in H^1_{\mathrm {dR}}(W)\text { such that } \langle \alpha , \beta , \beta \rangle \ne 0. \end{aligned}$$

(4.6)

By the Whitney product formula, we have $w_2 (M) = w_2 (W) + w_2 (L)$. Thus, if we choose L to have vanishing $w_2$, then $w_2 (M)$ will vanish as required, and $M = W \times L$ will admit $\mathrm {G}_2$-structures.

Theorem 4.11

Let L be a smooth compact connected oriented 4-manifold with $w_2 (L) = 0$, and let W be the real Iwasawa manifold described above. Then $M = W \times L$ admits $\mathrm {G}_2$-structures but cannot admit any torsion-free$\mathrm {G}_2$-structures.

Proof

Let $\pi : M \rightarrow W$ be the projection map. Consider the classes $\pi ^* \alpha , \pi ^* \beta \in H^1_{\mathrm {dR}}(M)$. By naturality of the Massey triple product, and since $p=q=r=1$, we have

$$\begin{aligned} \langle \pi ^* \alpha , \pi ^* \beta , \pi ^* \beta \rangle = \pi ^* \langle \alpha , \beta , \beta \rangle \in \frac{H^2 (M)}{H^1 (M) \cdot H^1 (M)}. \end{aligned}$$

Let $s: W \rightarrow W \times L$ be any section of $\pi$. Since $s^* \pi ^* = (\pi \circ s)^* = \mathrm {Id}$, we deduce that

$$\begin{aligned} \pi ^*: \frac{H^2(W)}{H^1(W) \cdot H^1(W)} \rightarrow \frac{H^2(M)}{H^1(M) \cdot H^1(M)} \quad \text { is injective.} \end{aligned}$$

Thus, since $\langle \alpha , \beta , \beta \rangle \ne 0$ we have

$$\begin{aligned} \langle \pi ^* \alpha , \pi ^* \beta , \pi ^* \beta \rangle = \pi ^* \langle \alpha , \beta , \beta \rangle \ne 0. \end{aligned}$$

Since $| \pi ^* \alpha | = | \pi ^* \beta | = 1$ and $1 + 1 \ne 4$, we finally conclude by Corollary 4.9 that Mdoes not admit a torsion-free$\mathrm {G}_2$-structure. $\square$

It remains to find an L with $w_2 (L) = 0$ such that no previously known topological obstructions (4.5) are violated, so that we have indeed established something new. We first collect several preliminary results that we will require.

By Poincaré duality $b^3_L = b^1_L$ and $b^2_W = b^1_W = 2$. The Künneth formula therefore yields

$$\begin{aligned} \left. \begin{aligned} b^1_M&= b^1_W + b^1_L = 2 + b^1_L, \\ b^2_M&= b^2_W + b^1_W b^1_L + b^2_L = 2 + 2 b^1_L + b^2_L, \\ b^3_M&= b^3_W + b^2_W b^1_L + b^1_W b^2_L + b^3_L = 1 + 2 b^1_L + 2 b^2_L + b^1_L = 1 + 3 b^1_L + 2 b^2_L. \phantom {A} \end{aligned} \right\} \end{aligned}$$

(4.7)

Remark 4.12

Let M, N be smooth compact oriented n-manifolds. There is a canonical way to make the connected sum $M \# N$ smooth, by smoothing around the $S^{n-1}$ with which we paste them together. With coefficients in either $R = {\mathbb {Z}}$ or $R = {\mathbb {Z}}/2 {\mathbb {Z}}$, we have $H^k (M \# N, R) \cong H^k (M, R) \oplus H^k (N, R)$ for $k = 1, \ldots ,n-1$. This can be seen using the Mayer–Vietoris sequence. The isomorphism is induced by the map $p : M \# N \rightarrow M$ collapsing N, and the map $q: M \# N \rightarrow N$ collapsing M. For $k = n$, we have $H^k (M \# N) \cong H^n (M, R) \cong H^n (N, R)$ with isomorphisms induced by p and q as before. $\square$

Lemma 4.13

Let L be a simply connected smooth compact oriented 4-manifold, with intersection form

$$\begin{aligned} Q: H_2 (L, {\mathbb {Z}}) \times H_2 (L, {\mathbb {Z}}) \rightarrow {\mathbb {Z}}. \end{aligned}$$

If the signature of Q is (p, q), let $\sigma (L) = p - q$. Then we have

• $w_2 (L) = 0$ if and only if $Q(a, a) \in 2 {\mathbb {Z}}$ for all $a \in H^2 (L, {\mathbb {Z}})$;

• $p_1(L) = 0$ if and only if $\sigma (L)$ is zero.

Proof

The first statement can be found in [19, Corollary 2.12]. The Hirzebruch signature theorem for 4-manifolds, which can be found in [8, Theorem 1.4.12], says that $p_1(L) = 3 \sigma (L)$. This immediately implies the second statement. $\square$

Recall that K3 is the unique connected simply connected smooth manifold underlying any compact complex surface with vanishing first Chern class. One way to define the K3 surface is by

$$\begin{aligned} \text {K3} = \{ [z_0 : z_1 : z_2 : z_3] \in {\mathbb {C}}{\mathbb {P}}^3 : z_0^4 + z_1^4 +z_2^4 + z_3^4 = 0 \}. \end{aligned}$$

It is well known (see [8, Page 75] or [21, Pages 127–133]) that K3 has intersection form $Q_{\text {K3}} = -2 E_8 \oplus 3 H$, where $E_8$ is a certain even positive definite bilinear form, and $H = \begin{bmatrix} 0&1 \\ 1&0 \end{bmatrix}$, which is also even and has signature 0. It follows that $Q_{\text {K3}}$ has signature (3, 19), and thus, $\sigma (\text {K3}) = -16$. We also have that the Betti numbers of K3 are $b^1_{\text {K3}} = b^3_{\text {K3}} = 0$ and $b^2_{\text {K3}} = 22$.

Proposition 4.14

Let $L = \text {K3} \, \# (S^1 \times S^3)$. Then $w_2 (L) = 0$, and for $M = W \times L$ where W is the real Iwasawa manifold, none of the first four topological obstructions (4.5) are violated. Thus, M cannot admit any torsion-free $\mathrm {G}_2$-structure.

Proof

Since $b^1_{S^1 \times S^3} = b^3_{S^1 \times S^3} = 1$ and $b^2_{S^1 \times S^3} = 0$, Remark 4.12 tells us that the Betti numbers of L are $b^1_L = b^3_L = 1$ and $b^2_L = 22$. In [8, Pages 20, 456], it is shown that $Q_{M \# N} = Q_M \oplus Q_N$, and consequently $\sigma (M \# N) = \sigma (M) + \sigma (N)$. Since $Q_{S^1 \times S^3} = 0$, we find that $Q_L$ is even and has nonzero signature. Thus, by Lemma 4.13, we deduce that $p_1(L) \ne 0$ and $w_2 (L) = 0$. Now Eq. (4.7) tell us that the Betti numbers of M are $b^1_M = 3$, $b^2_M = 26$, and $b^3_M = 48$. In particular, the first three conditions in (4.5) are satisfied.

We now claim that $p_1 (M) \ne 0$. To see this, consider the inclusion $\iota : L \rightarrow M = W \times L$ into some vertical fiber $\{ *\} \times L$ of M over W. Then $\iota ^* (TM) = TL \oplus E$ where W is the trivial rank 3 real vector bundle over L. If $p_1 (TM) = 0$, then by naturality we he have $p_1 (TL) = \iota ^* (p_1 (TM)) = 0$, which we showed was not the case. Thus, the fourth condition in (4.5) is satisfied. $\square$

Remark 4.15

Because $b^1_M = 3$, if M had any compact torsion-free $\mathrm {G}_2$-structure, it would have reduced holonomy $\mathrm {SU}(2)$. We have shown in Proposition 4.14 that such a Riemannian metric cannot exist on M. It is not clear whether there is any simpler way to rule out such a Riemannian metric on M. $\square$

Other examples of compact orientable spin 7-manifolds that cannot be given a torsion-free $\mathrm {G}_2$-structure can likely be constructed similarly.

Remark 4.16

The formality of compact 7-manifolds with additional structure has been studied by several authors, in particular recently by Crowley–Nordström [5] and Munoz–Tralle [20]. Two of the results in [5] are: There exist non-formal compact 7-manifolds that have only trivial Massey triple products, and a non-formal compact manifold M with $\mathrm {G}_2$ holonomy must have $b^2 (M) \ge 4$. One of the results in [20] is that a compact simply connected 7-dimensional Sasakian manifold is formal if and only if all its triple Massey products vanish. $\square$

Remark 4.17

A natural question is: Can we actually establish formality by extending our chain of quasi-isomorphisms? One idea is to quotient out the unwanted summands, but such a quotient map is not a dga morphism. One can also try to involve $\mathcal {L}_K$ or other operators that can descend to $H^{\bullet }_{\varphi }$, but the authors have so far had no success in this direction. $\square$