A new approach to analysing the adsorption of non-electrolyte binary liquid solutions by solid adsorbents. Prediction of absolute adsorption from excess adsorption data only

Abstract

This paper presents a new approach for calculating the absolute adsorption values of a binary mixture of liquids, relying only on the experimental adsorption excess isotherm. This approach was tested on precisely measured isotherms of excess adsorption in benzene (1)-cyclohexane (2)-zeolite NaX system at three temperatures: 303.15, 338.15, and 363.15 K. In addition, we had absolute adsorption isotherms measured for the same system and at the same temperatures on a specially designed apparatus. Thus, it was possible to compare the results of theoretically predicted isotherms of absolute adsorption with independent experimental data. The essence of the new approach is that it offers a possibility to find the dependence of the concentration of the adsorption phase on the concentration of the bulk phase in an explicit form, while remaining within the framework of the data on the excess adsorption isotherm. The accuracy of the predicted functions for absolute adsorption is within the accuracy of the original experimental data for excess adsorption isotherms.

1 Introduction

Excess adsorption values, absolute adsorption (or total content), and adsorption volume should undoubtedly be assigned to the most important, deeply rooted concepts in adsorption science. These characteristics of adsorption systems are so pronounced in both theory and practice that their exact interpretation attracts common attention in adsorption science.

It is known that the Gibbs adsorption theory [1] has not been fully developed as applied to fluid–solid interfaces in comparison with fluid–fluid interfaces. The main difference (and the basic difficulty) is the fact that the reversible work consumed for the formation of unit surface area of a fluid–solid interface is not governed by surface tension only; i.e., the work of surface stretching and the work of surface formation are not equal like they are in fluid–fluid interfaces. Gibbs considered an approximation at which the state of a solid remains unchanged, whereas a fluid, having a constant density of the volume energy, ranges not to the Gibbs interface, but rather up to the solid surface posed by its external atoms. This approximation did not take into account the curvature of the interface. Excess adsorption value, which is commonly measured by physical experiments (with allowances for the measurement and calibration methods), is most suited to the Gibbs’ approximation.

On the other hand, in fact, any equation that is based on molecular-kinetic concepts as well as any statistical molecular models of adsorption theory are formulated using the notion of absolute adsorption. Moreover, in any spectroscopic or calorimetric study the measured values are related to all molecules in the region of inhomogeneity.

All three quantities: adsorption volume, absolute and excess adsorption are strictly related to each other, with only the latter being known from experiment. If we find a way to determine (estimate) one of the unknown quantities through the known adsorption excess, we thereby find (estimate) the other unknown. Many attempts to solve the problem by approximating the adsorption volume have been described in the literature [2,3,4,5,6,7].

This paper proposes a more rigorous and reliable approach for finding the absolute adsorption directly.

2 Materials and methods

The system benzene—cyclohexane—zeolite NaX, experimentally studied at three temperatures 303.15, 338.15 and 365.15 K [8] was chosen for testing a new approach predicting absolute adsorption isotherms from the known isotherms of excess adsorption, Fig. 1. This system was chosen due to the fact that for the same system, absolute adsorption isotherms were measured experimentally at the same temperatures [9] using a specially developed technique. The weight method for direct measurement of the total absolute adsorption of a liquid mixture, developed by one of the authors in the mid-80 s [10] and subsequently refined, was an apparatus, the main component of which were coupled McBain balances that allowed the Archimedean upward buoyant force to be taken into account. The average relative error over the concentration range did not exceed 3%. In the concentration range of 0.1–0.8, the accuracy of 0.5—1% was achieved.

Fig. 1

Family of excess adsorption isotherms for the system benzene (1)—cyclohexane (2)—zeolite NaX (●—at 303.15 K, ■—at 338.15 K, ♦—at 363.15 K)

This allowed the predicted isotherms to be compared with those measured experimentally. It is important to emphasise that all experiments were carried out in the same laboratory and therefore the same batch of substances were used. Zeolite NaX was without binder with ratio Si/Al = 1.33. Benzene was spectrally pure, cyclohexane had brand “Pure for analysis”.

3 Results and discussion

The isotherms of excess adsorption of completely miscible binary liquid mixtures by solid adsorbents show different shapes depending on the particular system. According to the classification proposed by Schay [11], there are five basic types of isotherms shown in Fig. 2. The approach developed in this paper applies to types 1, 2, and 3. As for types 4 and 5, this is the subject of our further research.

Fig. 2

Basic types of excess adsorption isotherms according to Schay’s classification [11]

Consider the dependence of the composition of the adsorption phase ${C}_{1}^{s}$ on the composition of the bulk phase ${C}_{1}$, where component 1 is the predominantly adsorbed component. A typical dependence of the function ${C}_{1}^{s}$ = f(${C}_{1}$) has the form shown in Fig. 3. On this curve there is inevitably a point A, where the derivative $d{C}_{1}^{s}/d{C}_{1}$ is equal to one and the slope of tangent is parallel to the diagonal. This means that at point A the rate of change of composition is equal to the mean value, while before point A it is higher and after point A it is lower than the mean value.

Fig. 3

Typical dependence of adsorbed phase mass fraction on bulk phase mass fraction

At first sight it may seem that this point corresponds to the maximum on the isotherm of excess adsorption (see Fig. 1 and Appendix 1), but it can be strictly shown that this is not so and that the point is to the left of the maximum. Let us show that. For this purpose, we will proceed from the rigorous Williams equation [12].

$${w}_{1}^{e}={w}_{1}^{s}{C}_{2}-{w}_{2}^{s}{C}_{1}$$

(1)

Taking into account the obvious relations ${C}_{1}+{C}_{2}=1, { w}_{1}^{s}+{w}_{2}^{s}={w}^{s}$ and ${w}_{i}^{s}/{w}^{s}={C}_{i}^{s}$, Eq. 1 can be reduced to the form

$$\frac{{w}_{1}^{e}}{{w}^{s}}={C}_{1}^{s}-{C}_{1}$$

(2)

By differentiating relation (2) we obtain

$$\frac{\frac{d{w}_{1}^{e}}{d{C}_{1}}{w}^{s}-{w}_{1}^{e}\frac{d{w}^{s}}{d{C}_{1}}}{{\left({w}^{s}\right)}^{2}}=\frac{d{C}_{1}^{s}}{d{C}_{1}}-1$$

(3)

Because in range of definition 0 < C₁ < 1 product ${w}_{1}^{e}{w}^{s}\ne 0$ we can reduce relation (3) to the form

$$\frac{\frac{dln{w}_{1}^{e}}{d{C}_{1}} - \frac{dln{w}^{s}}{d{C}_{1}}}{\frac{{w}^{s}}{{w}_{1}^{e}}}=\frac{d{C}_{1}^{s}}{d{C}_{1}}-1$$

(4)

At point A, where the derivative $d{C}_{1}^{s}/d{C}_{1}$ is equal to one, we have.

$$\frac{\frac{dln{w}_{1}^{e}}{d{C}_{1}} - \frac{dln{w}^{s}}{d{C}_{1}}}{\frac{{w}^{s}}{{w}_{1}^{e}}}=0$$

(5)

From (5) follows

$$\frac{dln{w}_{1}^{e}}{d{C}_{1}}=\frac{dln{w}^{s}}{d{C}_{1}}$$

(6)

Derivative $\frac{dln{w}^{s}}{d{C}_{1}}>0$ in all range of C₁, therefore maximum point of excess isotherm at which $\frac{dln{w}_{1}^{e}}{d{C}_{1}}=0$ is not valid for equality (6). Suitable value of C₁ must be less than C_1m because only at C₁ < C_1m $\frac{dln{w}_{1}^{e}}{d{C}_{1}}>0$. Let us denote this value as C_1*

3.1 Finding a value for C _1*

Since the rate of concentration growth of component 1 reaches its mean value at point (C_1*, w^e_1*), it is reasonable a fortiori to assume that the equation of tangent to the isotherm at point (C_1*, w^e _1*) at concentration C₁ = 1 takes on a value equal to the adsorption limit of pure component 1, that is, m₀₁. It should be noted that the point on the adsorption excess isotherm, the tangent in which passes through point m₀₁, exists without regard to the assumptions we have made.

Correspondingly the equation of the tangent to the excess adsorption isotherm when abscissa is equal to $C_{1**} = 1 - C_{1*} = C_{2*}$, at C₁ = 0 (C₂ = 1) takes on a value which is nearly identical to the limit value of the absolute adsorption of pure component 2 m₀₂.

To find point (C_1*, w^e _1*), we propose the following method of calculation. Searching point on the isotherm of excess adsorption undoubtedly is a turning-point in the process of selective adsorption. To find it we assumed that a straight line passing through the centre of gravity (or centroid for non-symmetrical figures) of the uniform figure bounded by the isotherm curve and the abscissa axis and dividing the area of the figure in half crosses the isotherm curve at the required point.

Consider the limiting case of adsorption of a liquid binary solution when the selectivity of adsorption is equal to unity. In this case in the whole concentration range ${C}_{1}^{s}={C}_{1}$ and this dependence is represented by the diagonal in Fig. 3. In this case the adsorption excess isotherm represents the segment [0,1] on the abscissa axis. Obviously, the centre of gravity of this segment (i.e. degenerate isotherm) is at the point ${C}_{1}=0.5$.

Both assumptions made have been confirmed with high accuracy in independent direct experimental data.

The technique for finding the centre of gravity (or centroid) is described in Appendix 2.

From Eq. (3) two useful relations can be derived which relate the initial and final slopes of the adsorption excess isotherm and function ${C}_{1}^{s}$ = f(${C}_{1}$). At C₁ = 0, from Eq. (3) follows,

$${K}_{H0}^{{C}_{1}^{s}}=1+\frac{{K}_{H0}^{e}}{{m}_{02}}$$

(7)

and at C₁ = 1, respectively

$${K}_{H1}^{{C}_{1}^{s}}=1+\frac{{K}_{H1}^{e}}{{m}_{01}}$$

(8)

3.2 Procedure for finding the analytic form of a function ${{\varvec{C}}}_{1}^{{\varvec{s}}}={\varvec{f}} \left({{\varvec{C}}}_{1}\right)$

Thus, we have the values of the initial and final slope of the curve shown in Fig. 1, as well as the value of derivative at the point C_1*, which equals 1 in the middle part of the desired curve. To describe the ${C}_{1}^{s}$ = f(${C}_{1}$) curve, we used a three-constant empirical equation of the following form

$${C}_{1}^{s}=\frac{\left(1+a+b\right){C}_{1}}{1+a{C}_{1}+b{\left({C}_{1}\right)}^{n}}$$

(9)

and the associated derivative is

$$\frac{d{C}_{1}^{s}}{d{C}_{1}}=\frac{\left(1+a+b\right)\left[1+\left(1-n\right)b{\left({C}_{1}\right)}^{n}\right]}{{\left[1+a{C}_{1}+b{\left({C}_{1}\right)}^{n}\right]}^{2}}$$

(10)

From Eq. (10) follows

$${\left(\frac{d{C}_{1}^{s}}{d{C}_{1}}\right)}_{{C}_{1}=0}={K}_{H0}^{{C}_{1}^{s}}=1+a+b$$

(11)

$${\left(\frac{d{C}_{1}^{s}}{d{C}_{1}}\right)}_{{C}_{1}=1}={K}_{H1}^{{C}_{1}^{s}}=\frac{1+\left(1-n\right)b}{1+a+b}$$

(12)

$${\left(\frac{d{C}_{1}^{s}}{d{C}_{1}}\right)}_{{C}_{1}={C}_{1*}}=\frac{\left(1+a+b\right)\left[1+\left(1-n\right)b{\left({C}_{1*}\right)}^{n}\right]}{{\left[1+a{C}_{1*}+b{\left({C}_{1*}\right)}^{n}\right]}^{2}}=1$$

(13)

the last three relations form a system of equations with respect to the variables a, b and n, by solving which we find the required coefficients.

Substituting the found coefficients into Eq. (9), we obtain the equation predicting the curve ${C}_{1}^{s}$ = f(${C}_{1}$). The results of the calculations are summarized in Table 1.

Table 1 Summary table of calculated parameter values

While this is obvious, it makes sense to stress that since our approach uses derivatives, the accuracy of the original experiment is very important.

It also raises the question of how universal the 3-parametric Eq. 9 is. There are two circumstances that allow Eq. 9 to be considered sufficiently universal for the most common types of isotherms. Firstly, the curve of dependence of ${C}_{1}^{s}$ = f(${C}_{1}$). for isotherms of types 1, 2 and 3 is quite simple and easily described by three known points. Secondly, these three points are not clustered in one area of the curve, but are as far apart as possible, which also contributes to a better description.

3.3 Step-by-step procedure for finding the absolute adsorption isotherms

• 1. Description of the experimental excess adsorption isotherm by the empirical equation (A1). Determination of the slope of the tangent at points C₁ = 0 and C₁ = 1.

• 2. Find the coordinates of the centre of gravity of the plane area bounded by curve ${w}_{1}^{e}=f\left({C}_{1}\right)$ and the abscissa axis. The line passing through the centre of gravity and point C = 0.5 on the abscissa axis intersects the isotherm curve at point (C_1*, w^e_1*). Figure 4.

• 3. The line of the tangent at point (C_1*, w^e_1*) on the excess isotherm curve takes the value m₀₁ at C₁ = 1. Figure 4.

• 4. The line of the tangent at point (C_1**, w^e_1**) on the excess isotherm curve (notice that C_2** numerically equal C_1*) takes the value m₀₂ at C₁ = 0. Figure 4.

• 5. Using the found values of ${K}_{H0}^{e}$, ${K}_{H1}^{e}$(step 1) and, m₀₁, m₀₂ (steps 3 and 4) we calculate ${K}_{H0}^{{C}_{1}^{s}}$ and ${K}_{H1}^{{C}_{1}^{s}}$ by formulas (7) and (8).

• 6. Solving the system of three Eqs. (11), (12) and (13), we find three unknown parameters a, b and n for Eq. (9). The results are shown in Figs. 5, 6, 7.

• 7. Having the dependence ${C}_{1}^{s}$ = f(${C}_{1}$), using Eq. (2) we can find the dependence of the total absolute adsorption on the composition ${w}^{s}=f\left({C}_{1}\right)$ as well as the absolute partial adsorption of the components ${w}_{i}^{s}= {w}^{s}{C}_{1}^{s}$. Figure 8.

Fig. 4

Excess adsorption isotherm for the system benzene (1)—cyclohexane (2)—zeolite NaX at T = 303.15 K. Co-ordinates of centre of gravity (CG) (C₁ = 0.3335, w^e₁ = 0.072); co-ordinates of point A (C_1* = 0.04257, w^e_1* = 0.20354); predicted m₀₁ = 0.23268 g/g. Co-ordinates of point A₁ (C_1** = 1—C_1* = C_2* = 0.95743, w^e_2** = 0.00998); predicted m₀₂ = 0.22086 g/g

Fig. 5

The dependence of adsorbed phase mass fraction on bulk phase mass fraction for 303.15 K. (Curve—predicted by Eq. (9), points—experimental values)

Fig. 6

The dependence of adsorbed phase mass fraction on bulk phase mass fraction for 338.15 K. (Curve—predicted by Eq. (9), points—experimental values)

Fig. 7

The dependence of adsorbed phase mass fraction on bulk phase mass fraction for 363.15 K. (Curve—predicted by Eq. (9), points—experimental values)

Fig. 8

Experimental (curve 1) and predicted (curve 2) total absolute adsorption (maximum deviation is 3%); predicted partial absolute adsorption for benzene (curve 3) and cyclohexane (curve 4)

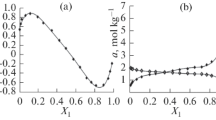
3.4 Evaluation of the adsorption volume of zeolite NaX

First of all, it should be emphasized that the adsorption volume is not identical to the crystallographic void volume of a solid adsorbent. Adsorption volume is a characteristic of the adsorbent-adsorbate system. It is the volume of pore space available to the molecules of a given adsorbate at a given temperature and pressure. This is why the adsorption volume of a given adsorbent, estimated from different adsorbates, turns out to be different [13]. Having the values of m₀₁ and m₀₂, it is easy to estimate the adsorption volume by dividing these values by the corresponding densities of the adsorbate. As a first approximation it can be assumed that the density of the adsorbate is equal to the density of the bulk liquid, then the adsorption volume W₀ calculated for benzene takes the following values: 0.2720 cm³/g (T = 303.15 K), 0.2736 cm³/g (338.15 K), 0.2774 cm³/g (363.15 K).

As shown by direct high pressure pycnometric experiments over a wide temperature range [14], the density of adsorbed benzene in zeolite NaX is equal to the density of bulk benzene only at the reduced temperature τ₀ = T/T_c = 0.85 (T = 477.74 K). At lower τ₀ the density of adsorbed benzene is less, and at higher τ₀ the density of adsorbed benzene is greater than the bulk liquid. If we take the true densities of the adsorbed benzene, which are equal to 0.81353 g/cm³ (at T = 303.15 K), 0.78108 g/cm³ (at T = 338.15 K), and 0.75893 g/cm³ (at T = 363.15 K), then the corresponding adsorption volumes W₀ will be 0.2904 cm³/g, 0.2906 cm³/g, and 0.2910 cm³/g, which is on average 6% higher than the volumes found through the densities of the bulk phase. Unfortunately, cyclohexane is not among the systems studied in [14].

4 Conclusions

Analysis of excess adsorption isotherms made it possible to reveal a number of new regularities, not described in the literature, operating in the binary liquid solution – solid adsorbent adsorption system. As a consequence, it has become possible to predict the isotherms of absolute adsorption solely from the known isotherms of excess adsorption. Following the submission of this paper we generalised our approach on a rigorous theoretical basis, which will allow universal application to all types of isotherms. In addition, we are going to propose an alternative classification of isotherm types based on the new information. We are working on this paper at present.

Appendices

Appendix 1

To approximate the experimental excess adsorption isotherms and perform the calculations.analytically, we used the following empirical equation

$${w}_{1}^{e}=\frac{{k}_{1}{C}_{1}}{{C}_{1}^{3}+{k}_{2}{C}_{1}^{2}+{k}_{3}{C}_{1}+{k}_{4}}-\frac{{k}_{1}{C}_{1}}{1+{k}_{2}+{k}_{3}+{k}_{4}}$$

and the corresponding derivative is

$$\frac{d{w}_{1}^{e}}{d{C}_{1}}=\frac{{k}_{1}{k}_{4}-{k}_{1}{k}_{2}{C}_{1}^{2}-2{k}_{1}{C}_{1}^{3}}{{\left({C}_{1}^{3}+{k}_{2}{C}_{1}^{2}+{k}_{3}{C}_{1}+{k}_{4}\right)}^{2}}-\frac{{k}_{1}}{1+{k}_{2}+{k}_{3}+{k}_{4}}$$

Appendix 2

The coordinates of the centroid of figure D, the area of which equals S are given by.

${x}_{0}=\frac{\iint xdxdy}{\iint dxdy}=\frac{\iint xdxdy}{S} , {y}_{0}=\frac{\iint ydxdy}{\iint dxdy}=\frac{\iint ydxdy}{S}$,

where the double integrals are taken over the whole surface D.

Here x ≡ C₁ and y ≡ w₁^e.

In practice, we can avoid the integration procedure because the line passing through the centre of gravity and point C₁ = 0.5 divides the area in half, we can find the line passing through point C₁ = 0.5 and dividing the area in half by method of successive approximation, without knowing the coordinates of the centre of gravity.