1 Introduction

In this paper we present, a new molecular interpretation of the chemical potential in terms of molecular energetics. The chemical potential is an intensive thermodynamic quantity that plays a central role in describing phase equilibria in physical systems, in both uniform and non-uniform systems it has the same value everywhere at equilibrium and its spatial gradients are the driving force in molecular transport processes (Baierlein 2001; Job and Herrmann 2006; Moore and Wheeler 2012).

From the fundamental thermodynamic equation for the change in internal energy, the chemical potential (µ) can be defined as a partial derivative of the internal energy (U) with respect to the number of molecules at constant entropy, volume and interfacial area, \(\mu ={\left( {\partial U/\partial N} \right)_{S,V,A}}\). Other definitions of chemical potential can be made in terms of the partial derivatives of the enthalpy, the Helmholtz free energy, and the Gibbs free energy; \(\mu ={\left( {\partial H/\partial N} \right)_{S,P,A}}={\left( {\partial F/\partial N} \right)_{T,V,A}}={\left( {\partial G/\partial N} \right)_{T,P,A}}\). At equilibrium, these free energies have reached a minimum in their respective ensembles, and the chemical potential is constant everywhere in a uniform system, irrespective of whether the system is of uniform or non-uniform density or closed or open to the surroundings. Although the interpretation of chemical potential via the thermodynamic route is mathematically exact, it does not provide a clear physical meaning because both the free energies and the entropy are non-mechanical properties and therefore, it is less easy to apprehend intuitively, than quantities such as temperature and pressure.

In a comprehensive review by Baierleen (2001), the author offers descriptions for chemical potential in very broad terms, and in a similar argument, Job and Hermann (2006) describe the chemical potential as the tendency to change of location, or chemical composition or state of aggregation. All examples provided by these authors have a thermodynamic basis relating to the non-mechanical free energy, and do not offer any link to the energetics of molecules forming the system.

In an ideal gas, where there are no intermolecular forces acting between molecules, the chemical potential has a firm foundation in statistical mechanics in terms of the molecular density and thermal de Broglie wavelength, \(\mu ={\mu ^{INTRA}}+{k_B}T\ln \left( {{\Lambda ^3}\rho } \right)\). In non-ideal systems, the chemical potential can be determined by density functional theory or molecular simulation. In a Metropolis Monte Carlo simulation (mMC), the chemical potential is usually determined by the Widom (1963, 1982) method. The accuracy of this method depends on the number of insertions, which needs to be very large in regions of high density, and the method is therefore computationally intensive. Even with a large number of insertions, the computed chemical potential may not be accurate for dense systems. In an attempt to overcome this problem, Shing and Gubbins (1982) proposed a particle extraction method for use in dense phases, which is an inverse of the Widom insertion technique. The correctness of this method has been questioned (Kofke and Cummings 1997; Frenkel 2013), except where it is used in conjunction with umbrella sampling (Bennett 1976) and is clearly not applicable in the limit of hard sphere fluids. Other methods available prior to 1997 (umbrella sampling, Widom insertion, and staged insertion) have been reviewed and applied to hard sphere fluids (Kofke and Cummings 1997).

As an alternative to Metropolis Monte Carlo, kinetic Monte Carlo (kMC), was originally developed (Gillespie 1977; Battaile 2008; Ustinov and Do 2012a, b; Nguyen et al. 2012) to investigate the microscopic kinetic behaviour of a system, and it was later introduced as a method to study equilibrium systems (Ustinov and Do 2012; Fan et al. 2013b; Nguyen et al. 2015) in a canonical (NVT) ensemble. The method was subsequently extended to other ensembles (Tan et al. 2015, 2016a, b, 2017). A major advantage of kMC over mMC is the very accurate determination of the chemical potential, regardless of the density of the system (Nguyen et al. 2015). This stems from the use of the actual molecules in the system, rather than insertions of ghost molecules, which means that the method can take advantage of all configurations in sampling the energy space, rather than just a finite number of frozen configurations, as in mMC (Fan et al. 2013b; Nguyen et al. 2015). The results from kMC simulations have been found to give excellent agreement with experimental data. A comparison between kMC and mMC for hard spheres demonstrates the superior accuracy of the kMC method, especially at high densities (Ustinov 2017).

2 Theory

2.1 Molecular energy and mobility rate

In a canonical ensemble of N molecules, the molecular energy uj, of molecule j, is defined as the energy of interaction between this molecule and all other entities in the system:

$${u_j}=\sum\limits_{\begin{subarray}{l} k=1 \\ k \ne j \end{subarray} }^{N} {{\varphi _{j,k}}+{\varphi _{j,S}}}$$
(1)

The first term is the sum of the pairwise interaction energies, and the second term is the interaction energy of molecule j with all atoms in a solid adsorbent. We define the molecular mobility as \({v_j}=\exp \left( {\beta {u_j}} \right)\), where \(\beta ={\left( {{k_B}T} \right)^{ - 1}}\). The total rate (mobility) of the system is the sum of all molecular mobilities and it defines the system’s energetics:

$$R=\sum\limits_{{j=1}}^{N} {\exp \left( {\beta {u_j}} \right)}$$
(2)

The lifetime of a configuration is proportional to the inverse of the total rate of the system.

2.2 The chemical potential

The chemical potential is calculated from the following equation (Ustinov and Do 2012; Fan et al. 2013a), which is a function of the time average of the total rate:

$$\mu - {\mu ^{Intra}}={k_B}T\ln \left( {{\Lambda ^3}\frac{{\left\langle R \right\rangle }}{V}} \right)={k_B}T\ln \left( {{\Lambda ^3}\frac{N}{V}} \right)+{k_B}T\ln \left( {\frac{{\left\langle R \right\rangle }}{N}} \right)$$
(3)

The weighted time average of the total rate\(\left\langle R \right\rangle\), is defined as:

$$\left\langle R \right\rangle =\frac{{\sum\limits_{{K=1}}^{M} {\Delta {t_K}{R_K}} }}{\tau };\;\tau =\sum\limits_{{K=1}}^{M} {\Delta {t_K}} \quad \Delta {t_K}=\frac{{\ln \left( {{1 \mathord{\left/ {\vphantom {1 {{\xi _K}}}} \right. \kern-0pt} {{\xi _K}}}} \right)}}{{{R_K}}}$$
(4)

where M is the number of configurations, \(\Delta {t_K}\) is the lifetime, and ξk is a random number. Since there are many configurations in a simulation having the same total rate, the lifetime of the configuration K, given in Eq. (4), is taken to follow a Poisson distribution law.

In place of the chemical potential, we define an activity as follows:

$$\lambda =\frac{1}{{{\Lambda ^3}}}\exp \left[ {\beta \left( {\mu - {\mu ^{Intra}}} \right)} \right]=\frac{{\left\langle R \right\rangle }}{V}$$
(4)

in which we have used Eq. (3). Given this linear relationship between the activity and the averaged total rate, it is convenient to study the molecular interpretation of the activity in terms of the average total rate of the system. Since the total rate is the sum of molecular mobilities of all molecules, this allows us to investigate which specific molecular mobilities govern the activity and hence the chemical potential. This is the crux of our theory.

2.2.1 Decomposition of the total rate at the molecular level

For a given configuration K, molecules in the system can be divided into: (1) those having non-positive molecular energies \(\left\{ {{u_{j,K}} \leq 0;\;j=1,2, \cdots ,N} \right\}\), called attracting molecules, and (2) those having positive molecular energies \(\left\{ {{u_{j,K}}>0;\;j=1,2, \cdots ,N} \right\}\), called repelling molecules. This classification allows us to investigate the relative contributions of these two groups to the energetics of the system, and therefore their contributions to the chemical potential, and we are thus able to provide a meaningful interpretation of the chemical potential, that is directly related to intermolecular energy.

For a given configuration K, the total rate can be decomposed into two parts, one contributed by attracting molecules and the other by repelling molecules:

$${R_K}=R_{K}^{+}+R_{K}^{ - }$$
(6)

The term with the superscript “+” is the total rate of molecules having positive molecular energies (i.e. those are under repulsion), and the term with the superscript “−” is the total rate of molecules having non-positive molecular energies (i.e. those are under attraction). The weighted time average of the above equation is \(\left\langle R \right\rangle =\left\langle {{R^+}} \right\rangle +\left\langle {{R^ - }} \right\rangle\).

2.3 Simulation parameters

To illustrate the link between the energetics of molecules and the chemical potential of a system, we chose argon as an example species with the following molecular parameters \({\sigma _{Ar}}=0.3405\,{\text{nm}}\) and \({\varepsilon _{Ar}}/{k_B}=119.8\;{\text{K}}\) (Michels et al. 1949). We chose graphite as the model adsorbent and the solid–fluid potential energy was calculated from the 10-4-3 equation with molecular parameters for a carbon atom: \({\sigma _C}=0.34\,{\text{nm}}\) and \({\varepsilon _C}/{k_B}=28\;{\text{K}}\), and the interlayer spacing of 0.3354 nm (Steele 1973). The cross-parameters were calculated with the Lorentz-Berthelot mixing rule. The dimensions of the simulation box in the x-, y-, and z-directions were 10nm × 10nm × 2 nm with the graphite surface positioned at z = 0. Periodic boundary conditions were imposed at the boundaries in the x and y directions.

3 Results and discussion

3.1 Adsorption of argon on a surface

The simulated adsorption isotherm for argon at 87 K on graphite against the absolute pressure is presented on semi-logarithmic and linear scales in Fig. 1a, b, respectively. Also plotted in Fig. 1b are the contributions to the total rate from the attracting and repelling molecules, \(\left\langle {{R^ - }} \right\rangle\) and \(\left\langle {{R^+}} \right\rangle\), as a function of pressure. Within the adsorbed film, where the density is high, we would expect, that \(\left\langle {{R^+}} \right\rangle\) would be much greater than \(\left\langle {{R^ - }} \right\rangle\). Therefore, to study these properties, we determined the time averages of the rate locally by dividing the distance from the graphite surface into small bins of equal width.

Fig. 1
figure 1

a Adsorption isotherm (semi-log plot) of argon at 87K on graphitic surface, b contribution of rate (top panel) by attractive (circles) and repulsive (triangle) molecules and (bottom panel) adsorption isotherm (linear plot). Error bars are smaller than the circle diameters

Full size image

Since the chemical potential varies with pressure, it is useful to assess the evolution of the total rate \(\left\langle R \right\rangle\) and its components \(\left\langle {{R^{\,+}}} \right\rangle\) and \(\left\langle {{R^{\,\, - }}} \right\rangle\) with respect to pressure. We selected six points of interest, as shown in Fig. 1a: low coverage zone (A & B), transition zone (C & D), the monolayer coverage zone (E) and the onset of the second layer (F). The density distribution and the time-averaged rates are plotted against the reduced distance from the graphite surface in Fig. 2.

Fig. 2
figure 2

Density distribution (symbols), attraction (solid line) and repulsion (dotted line) rate distribution for points corresponding to Fig. 1a

Full size image

At equilibrium, the total rate (proportional to the chemical potential) is constant throughout the simulation box for all points considered, as expected. Although the total rate is constant, its components \(\left\langle {{R^{\,+}}} \right\rangle\) and \(\left\langle {{R^{\,\, - }}} \right\rangle\) vary with the distance from the surface. Within the rarefied region, far away from the surface and the adsorbed layer, \(\left\langle {{R^ - }} \right\rangle\) dominates the total rate. On the other hand, in the adsorbed film, \(\left\langle {{R^+}} \right\rangle\) dominates the total rate, and determines the chemical potential. In the intermediate region between the gas phase, the two components \(\left\langle {{R^{\,+}}} \right\rangle\) and \(\left\langle {{R^{\,\, - }}} \right\rangle\) of the total rate are comparable, and it could be argued that the position where they cross locates the interfacial plane.

To understand the contribution of molecules under attraction and those under repulsion, we take Point C in the sub-monolayer region as an illustration. Even though the repelling molecules dominate the chemical potential in the first layer, since \(\left\langle {{R^{\,+}}} \right\rangle\) >> \(\left\langle {{R^{\,\, - }}} \right\rangle\), most molecules in the first layers are under attraction because the largest contribution to \(\left\langle N \right\rangle\) comes from \(\left\langle {{N^{\, - }}} \right\rangle\) (see Fig. 3).

Fig. 3
figure 3

Distribution of \(\left\langle {{N^+}} \right\rangle\) and \(\left\langle {{N^{\, - }}} \right\rangle\) at transition point towards monolayer coverage

Full size image

3.2 Distribution of rate at the vapour liquid coexisting region

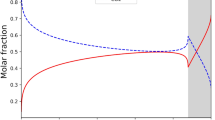
In addition to an adsorbent-adsorbate system, we have also studied the structure of the coexisting phases at a vapour-liquid boundary in a bulk fluid at equilibrium. Here we used an elongated simulation box of length \(10\;{\text{nm}}\) with a cross section of \(4\;{\text{nm}} \times 4\;{\text{nm}}\). Figure 4 shows the local density profile of argon at 87 K along the direction normal to the interface in the coexistence region. It shows two phases: the liquid phase in the middle, surrounded by the gas phase, separated by an interface whose thickness is about three times the collision diameter.

Fig. 4
figure 4

Distribution of attractive (solid) and repulsive (dashed) rates in comparison to the local density distribution (circles) of a slab configuration in a coexisting region. Error bars are smaller than the diameter of the symbols

Full size image

Within the coexistence region, the following condition is true at equilibrium:

$${\left\langle R \right\rangle _{gas}}={\left\langle {{R^ - }} \right\rangle _{coex}}+{\left\langle {{R^+}} \right\rangle _{coex}}={\left\langle R \right\rangle _{liquid}}$$
(7)

This equation is not only true for the whole simulation box, but is also true for any local region within the box by virtue of the constant chemical potential. To show the local chemical potential or local \(\left\langle {{R^ - }} \right\rangle\) and \(\left\langle {{R^+}} \right\rangle\), we divided the box into bins of equal width in the direction normal to the interface and calculated \({R^ - }\) and \({R^+}\) for molecules in each bin for each configuration, and then obtained their averages \(\left\langle {{R^ - }} \right\rangle\) and \(\left\langle {{R^+}} \right\rangle\) at the end of the simulation. The plots of these local variables are shown in the top panel of Fig. 4, which shows how attracting and repelling molecules behave in the gas phase, the liquid phase and the interface region. Within the coexistence region the values of \({\left\langle {{R^ - }} \right\rangle _{coex}}\) and \({\left\langle {{R^+}} \right\rangle _{coex}}\) are not constant, but their sum is a constant.

In the vapour phase, far away from the interface, the average total rate is dominated by the contribution from the attracting molecules, i.e. \(\left\langle {{R^ - }} \right\rangle ={\left\langle R \right\rangle _{gas}}\), but in the bulk liquid phase it is dominated by the contribution from the repelling molecules, i.e. \(\left\langle {{R^+}} \right\rangle ={\left\langle R \right\rangle _{liquid}}\). In the interface region, the rate crosses between the two contributions \(\left\langle {{R^ - }} \right\rangle\) and \(\left\langle {{R^+}} \right\rangle\). It is interesting to note that the crossing point does not coincide with the Gibbs dividing surface. The crossing of \(\left\langle {{R^ - }} \right\rangle\) and \(\left\langle {{R^+}} \right\rangle\) is also observed for argon adsorption at 87K on a graphite surface discussed in Sect. 3.1. We conclude that this is a common feature in systems with a non-uniform distribution of molecules.

4 Conclusion

In this paper we have presented a new interpretation of chemical potential in terms of molecular energetics, analysed according to the rates \(\left\langle R \right\rangle\) derived from kMC simulations. In an adsorbate-adsorbent system, the chemical potential of the adsorbed phase is determined by the contribution of \(\left\langle {{R^{\,+}}} \right\rangle\) from the repelling molecules, even though their number is very small. At densities much lower than the saturated vapour density, where there is very little interaction between the molecules, the chemical potential is ideal and \(\left\langle R \right\rangle\) is determined by \(\left\langle {{R^{\,\, - }}} \right\rangle\). At a bulk liquid interface, where the vapour and liquid phases coexist, contributions from the attracting and the repelling molecules towards the total rate are comparable.