Numerical Analysis of the Thermodynamic Definition of the Surface Tension of a Vapor–Liquid System in the Lattice Gas Model

Abstract

A numerical analysis is performed of Gibbs’ thermodynamic definition of the surface tension (ST) of a vapor–liquid system as excess free energy ΔF of a two-phase system with and without assuming the existence of an interface. Calculations are made using the simplest version of the lattice gas model (LGM) by assuming interaction between nearest neighbors in the quasi-chemical approximation (QCA). Different ways of calculating ST, which is expressed through different partial contributions from $M_{q}^{i}$ to excess energy ΔF (where i = A is molecule А and i = V denotes vacancies, 1 ≤ q ≤ κ, q is the number of monolayers inside a interface, and κ is its width), are compared. The ambiguity of ST values depending on the type of functions $M_{q}^{i}$ is obtained. These differences in ST values are demonstrated through the temperature dependence of ST for a planar boundary and the dependence of ST on the size of drops at a specific temperature. Results from calculating ST thermodynamically are compared to analogous calculations according to the version of the definition of ST that considers the specificity of vacancies in the LGM as a mechanical characteristic of the system.

INTRODUCTION

According to Gibbs, surface tension (ST) is excess free energy ΔF of a two-phase system with and without assuming there is an interface [1–6]. Starting from general thermodynamic definitions for free Helmholtz (F) and Gibbs energy (G), F = G − PV_sys and $G = \sum\nolimits_{i = 1}^{{{s}_{c}}} {{{\mu }_{i}}{{N}_{i}}}$, where P is pressure and V_sys is the volume of system, and μ_i and N_i correspond to chemical potential and the number of molecules of component i of a mixture consisting of s_c types of molecules [7–9]:

$$F = \sum\limits_{i = 1}^{{{s}_{c}}} {{{\mu }_{i}}} {{N}_{i}} - P{{V}_{{{\text{sys}}}}}.$$

(1)

The excess of free energy at an interface is then $\Delta F = F - {{F}_{\alpha }} - {{F}_{\beta }} = \sum\nolimits_{i = 1}^{{{s}_{c}}} {{{\mu }_{i}}\Delta {{N}_{i}}} + \sigma A$, where ${{F}_{\alpha }}$ and ${{F}_{\beta }}$ are free energies of uniform regions of liquid (α) and vapor (β) phases, $\Delta {{N}_{i}}$ is the excess of component i at interface, and σ and А are the ST and area of the interface. Equations for ${{F}_{\alpha }}$ and ${{F}_{\beta }}$ are analogous to Eq. (1), with characteristics associated with the vapor and liquid phases. Condition $\sum\nolimits_{i = 1}^{{{s}_{c}}} {{{\mu }_{i}}} \Delta {{n}_{i}} = 0$ determines the position of the equimolecular separating surface, which is related to the ST:

$$\sigma = \Delta F{\text{/}}A.$$

(2)

Until recently, there were four approaches to calculating ST [1] that were based on Gibbs’ approach [2–6], showing there was no uniform procedure for calculating this parameter. These thermodynamic constructs had different ideas about the form of the distribution of stress for the local pressure tensor inside the transitional region of the interfaces of metastable drops. Even though physical bases of thermodynamics could not use it inside interfaces [10], these approaches were later transformed into corresponding molecular-statistical theories [2, 6, 10].

A strictly equilibrium approach to calculating ST was proposed in [11, 12] on the basis of Gibbs’ definition that excluded the formation of metastable drops. This approach differs fundamentally from conventional thermodynamic definitions of ST [1–10] by the requirement of fulfilling the relationship for the periods of the relaxation of transfer of pulse and mass, which are missing in classical thermodynamics (which uses the Laplace equation for curved boundaries) and statistical thermodynamics (which uses integral equations and MD) is transferred to the transitional region [2, 6, 10]. This feature results in using mean values of local chemical potentials and pressures inside the local domains of a interface rather than their tensor components when calculating ST values.

This approach was formulated on the basis of the so-called lattice gas model (LGM) [13–15]. The LGM is the most widely used model in studies of the phase states of substances, and the most important results for the theory of phase transitions, including the critical ranges of a vapor–liquid system, were obtained with it [13–21]. This model has long been used in studying planar interfaces [15, 22–27]. Approaches that describe curved surfaces (spherical and cylindrical drops) were developed later within the LGM [10, 28–31], and for describing curved vapor–liquid interfaces with complex geometry in three-unit systems [32–34].

In the LGM, equation for free energy (1) in the bulk phase is written as $F = \sum\nolimits_{i = 1}^s {{{\mu }_{i}}{{N}_{i}}}$, where free cells (vacancies) are particles of type i = s (${{\mu }_{s}} = - P{{v}_{0}}$, since V_s = ${{{v}}_{0}}$N, ${{{v}}_{0}}$ is the cell volume) and they represent the volume of a system not blocked by real molecules of type 1 ≤ i ≤ s_c = s – 1; $N = \sum\nolimits_{i = 1}^s {{{N}_{i}}}$. Equation (1) is rewritten in normalized form per node of system:

$$F{\text{/}}N = \sum\limits_{i = 1}^s {{{\mu }_{i}}{{\theta }_{i}}} ,$$

(3)

where ${{\theta }_{i}}$ is the molar fraction of the particles of component i of the lattice system in the uniform phase. In analogy with Eq. (1), Eq. (3) corresponds to the chemical potential of the component of lattice structure where chemical potential of vacancies μ_s was introduced.

An interface is a transitional region between coexisting phases of vapor and liquid with variable density of matter, which is described within the laminar distributions of molecules; i.e., it is a range with a nonuniform distribution of components in space. It was found in [35, 36] that the free energy of the transitional region can be written in the normalized form

$$F{\text{/}}N = \sum\limits_{q = 1}^\kappa {\sum\limits_{i = 1}^s {M_{q}^{i}(k)\theta _{q}^{i}} } ,$$

(4)

where number of nodes N is associated a transitional region consisting of κ monolayers, 1 ≤ q ≤ κ. The values of М_i(k) in Eq. (4) characterize contributions from components i to the free energy of the bulk phase and the same components in locally heterogeneous domains q of the interface, through which ST is calculated.

Depending on how Eq. (4) is constructed, three types of function are possible: $M_{q}^{i}(k)$: k = 1, by rearranging the components of the equation for F with the pair potential; k = 2, by differentiation according to the molar fraction of particles of type i at a specific number of nodes of type q; or k = 3, according to the variable number of nodes of type q [36]. All types of function $M_{q}^{i}(k)$ in Eq. (4) are associated with chemical potentials of the components of the system in Eqs. (1) and (3), and analysis of these relations could reveal the connection between functions $M_{q}^{i}(k)$ and ST based on the thermodynamic definition of ST [11, 12]. To analyze the idea of such a thermodynamic definition of ST, we need only consider a binary mixture of a lattice system in which the components are molecules A and vacancy V, which correspond to a pure fluid.

In this work, we perform a numerical analysis of equations obtained for the ST [11, 12, 35, 36] of planar and spherical boundaries by allowing for the pair interaction potential between particles, in order to determine the effect the type of functions $M_{q}^{i}$ has on values of ST calculated according to Eq. (2), where excess free energy ΔF is defined by the microscopic model as the difference between Eqs. (4) and (3).

MODEL

In calculations, the simplest versions of the LGM are used by assuming there is interaction between closest neighbors in the quasi-chemical approximation (QCA) on a rigid lattice structure with number of neighbors z [13–15]. Let us consider a system consisting of a drop with radius R and a vapor–liquid interface, with surrounding vapor as a counterpart of an equilibrium two-phase system at specific temperature Т (the planar interface is represented by limit case R → ∞). The transitional region is split into monomolecular layers with width λ that have homogeneous characteristics (where λ is the mean distance between molecules in the liquid phase). These layers are denoted by index q, where q is the number of the node associated with the considered monolayer, 1 ≤ q ≤ κ, and κ is the width of a transitional region with one monolayer from each bulk phase (q = 1 corresponds to liquid and q = κ corresponds to vapor).

Let us characterize the structure of a fluid in the bulk phase using a set of $z_{{qp}}^{*}$ values that indicate the numbers of the nearest neighboring layers p around the nodes of layer q; $\sum\nolimits_{p = q - 1}^{q + 1} {z_{{qp}}^{*}}$ = z. The total balance of nodes of the bonds between neighboring molecules is written as $\sum\nolimits_{p = q - 1}^{q + 1} {{{z}_{{qp}}}}$(R) = z. For spherical drops in the thermodynamic version of the model, structural numbers for curved lattice z_qp(R) are expressed through analogous numbers for planar lattice $z_{{qp}}^{*}$ in the form of corrections that depend on the radius of the monolayer in the transitional region [12, 28]:

$$\begin{gathered} {{z}_{{q < p}}}(R) = z_{{qp}}^{*},\quad {{z}_{{q > p}}}(R) = z_{{qp}}^{*}\left[ {1 + {\text{ }}1{\text{/}}(R + q - 1)} \right], \\ {{z}_{{q = p}}}(R) = z - {{z}_{{q < p}}}(R) - {{z}_{{q > p}}}(R). \\ \end{gathered} $$

(5)

At the asymptotic limit of large drops, all values of z_qp(R) reach limits $z_{{qp}}^{*}$ when there is a planar interface.

Molecular distributions of particles of type А (and thus vacancies V $\theta _{q}^{{\text{V}}} = 1 - \theta _{q}^{{\text{A}}}$) are specified by densities $\theta _{q}^{{\text{A}}}$ of particles А in layer q, 1 ≤ q ≤ κ, which are described in the QCA by the system of equations

$$\beta {{v}_{0}}{{a}_{q}}P = \theta _{q}^{{\text{A}}}{\text{/}}(1 - \theta _{q}^{{\text{A}}})\prod\limits_{p = q - 1}^{q + 1} {{{{\left[ {1 + t_{{qp}}^{{{\text{AA}}}}x_{{{\text{AA}}}}^{{}}} \right]}}^{{{{z}_{{qp}}}(R)}}}} ,$$

(6)

where $t_{{qp}}^{{{\text{AA}}}}$ is the conditional probability of a particle of type A being in a cell of layer p near another particle A in a cell of layer q: $t_{{qp}}^{{{\text{AA}}}} = \theta _{{qp}}^{{{\text{AA}}}}{\text{/}}\theta _{q}^{{\text{A}}} = 2\theta _{p}^{{\text{A}}}{\text{/}}[\delta _{{qp}}^{{{\text{AA}}}} + b_{{qp}}^{{{\text{AA}}}}]$, $\delta _{{qp}}^{{{\text{AA}}}} = 1 + x_{{{\text{AA}}}}^{{}}(1 - \theta _{q}^{{\text{A}}} - \theta _{p}^{{\text{A}}})$, $b_{{qp}}^{{{\text{AA}}}}$ = $\{ {{[\delta _{{qp}}^{{{\text{AA}}}}]}^{2}}$ + $4x_{{{\text{AA}}}}^{{}}\theta _{q}^{{\text{A}}}\theta _{p}^{{\text{A}}}{{\} }^{{1{\text{/}}2}}}$, and $\theta _{{qp}}^{{{\text{AA}}}}$ is the probability of there being a pair of particles АА in neighboring cells of monolayers q and p, respectively; P is the pressure in the system; ${{x}_{{{\text{AA}}}}} = \exp \{ - \beta {{\varepsilon }_{{{\text{AA}}}}}\} - 1$, $\beta = {{({{R}_{B}}T)}^{{ - 1}}}$, where ${{R}_{B}}$ is the gas constant, and ${{\varepsilon }_{{{\text{AA}}}}}$ is the energy of interaction between a pair of particles АА, which is described by the Lennard–Jones potential function. Interactions with vacancies correspond to zero: ${{\varepsilon }_{{{\text{AV}}}}} = {{\varepsilon }_{{{\text{VA}}}}} = 0$.

The system of Eq. (6) with respect to local densities $\theta _{q}^{{\text{A}}}$ is obtained from the condition of the equivalence of chemical potential μ_А of particles А in all layers where 1 ≤ q ≤ κ.

One-particle contributions from $\nu _{q}^{i}$ to free energy F of component i at nodes of type q of a nonuniform system with an interface are introduced in the LGM. Difference $\nu _{q}^{{\text{A}}} - \nu _{q}^{{\text{V}}} = {{\beta }^{{ - 1}}}\ln (\beta {{v}_{0}}{{a}_{q}}P)$ between these contributions includes statistical sums of internal motions of components i, the effect of external fields, and chemical potentials [15] where ${{a}_{q}} = {{F}_{q}}{\text{/}}{{F}_{0}}$ is the ratio of statistical sums of a molecule in the lattice structure (F_q) to those in the bulk phase (F₀). With vacancies, we must formally consider that $\nu _{q}^{{\text{V}}} = 0$ or a_qP fixes the chemical potential of the material in different layers q (in Eq. (6)).

Knowing function $\theta _{{qp}}^{{{\text{AA}}}}$, other pair functions $\theta _{{qp}}^{{ij}}$ are determined through normalized relations $\sum\nolimits_{j = 1}^s {\theta _{{qp}}^{{ij}}} = \theta _{q}^{i}$ (s = 2). The dimensionality of the system of Eq. (6) relative to local densities $\theta _{q}^{i}$ corresponds to the number of layers (κ – 2) of the transitional region between vapor and liquid. It is solved via Newton iteration at specified values of the vapor density for q = 1 and liquid for q = κ. The accuracy of the solution to this system is greater than 0.1%. The densities of the coexisting gas and liquid phases in the bulk and equilibrium pressure P in the system were determined in [12–15] using Maxwell’s construction.

Using concentration profile (6), ST is calculated according to three versions of function $M_{q}^{i}(k)$, k = 1–3. According to the equations from [11, 12], thermodynamic definition of ST (2) is expressed through above functions $M_{q}^{i}(k)$:

$$\begin{gathered} A\sigma = \frac{1}{{{{F}_{\rho }}}}\sum\limits_{i = 1}^s {\left( {\sum\limits_{q \leqslant q\text{*}} {{{F}_{q}}(M_{q}^{i}(k) - M_{1}^{i}(k))\theta _{q}^{i}} } \right.} \\ \, + \left. {\sum\limits_{q > q\text{*}} {{{F}_{q}}(M_{q}^{i}(k) - M_{\kappa }^{i}(k))\theta _{q}^{i}} } \right), \\ \end{gathered} $$

(7)

where functions $M_{q}^{i}(k)$ are determined with equations from [35], and А is the surface area of a lattice gas cell:

$$\begin{gathered} M_{q}^{i}(1) = \nu _{q}^{i} + kT\ln \theta _{q}^{i} + \frac{{kT}}{2}\sum\limits_{p = q - 1}^{q + 1} {{{z}_{{qp}}}\ln \frac{{\hat {\theta }_{{qp}}^{{ii}}\hat {\theta }_{{qp}}^{{ik}}}}{{{{{(\theta _{q}^{i})}}^{2}}\theta _{{qp}}^{{ki}}}}} , \\ \hat {\theta }_{{qp}}^{{ij}} = \theta _{{qp}}^{{ij}}\exp ( - \beta {{\varepsilon }_{{AA}}}), \\ \end{gathered} $$

(8)

$$M_{q}^{i}(2) = \nu _{q}^{i} + kT\ln \theta _{q}^{i} + kT\sum\limits_{p = q - 1}^{q + 1} {{{z}_{{qp}}}\ln \frac{{\hat {\theta }_{{qp}}^{{iV}}}}{{\theta _{q}^{i}}}} ,$$

(9)

$$M_{q}^{i}(3) = \nu _{q}^{i} + kT\ln \theta _{q}^{i} + \frac{{kT}}{2}\sum\limits_{p = q - 1}^{q + 1} {{{z}_{{qp}}}\ln \frac{{\hat {\theta }_{{qp}}^{{ii}}}}{{\theta _{q}^{i}\theta _{p}^{i}}}} .$$

(10)

Results from calculating ST according to the thermodynamic definition are also compared to the ST definition given in [10, 28], where it is considered that vacancies reflect mechanical characteristics of the system (i.e., a fourth version of the ST definition is added)

$$A\sigma = \frac{1}{{{{F}_{\rho }}}}\left( {\sum\limits_{q \leqslant q\text{*}} {{{F}_{q}}(\mu _{q}^{{\text{V}}} - \mu _{1}^{{\text{V}}})} + \sum\limits_{q > q\text{*}} {{{F}_{q}}(\mu _{q}^{{\text{V}}} - \mu _{\kappa }^{{\text{V}}})} } \right),$$

(11)

where functions $\mu _{q}^{{\text{V}}} = M_{q}^{{\text{V}}}(3)$ are defined in Eq. (10) using $\nu _{q}^{{\text{V}}} = 0$ at any q.

As a separating surface in the equilibrium system for a planar or curved boundary, we use an equimolecular surface that lies in monolayer q* and is determined as

$$\sum\limits_{q \leqslant q\text{*}} {{{F}_{q}}(\theta _{q}^{{\text{A}}} - \theta _{1}^{{\text{A}}})} + \sum\limits_{q > q\text{*}} {{{F}_{q}}(\theta _{q}^{{\text{A}}} - \theta _{\kappa }^{{\text{A}}})} = 0.$$

(12)

There are layers with increased density when q ≤ q*, and layers with reduced density when q > q*. The contribution from each monolayer is expressed through weight functions F_q = N_q/N, N = $\sum\nolimits_{q = 2}^{k - 1} {{{N}_{q}}}$, 2 ≤ q ≤ κ – 1.

CONDITIONS OF CALCULATIONS

A cubic primitive lattice with number z = 6 of neighbors in the first coordination sphere was used to model the bulk phase of a fluid. Only interactions between nearest neighbors were considered with the Lennard–Jones potential and parameters of interaction that yielded ε_АА = 238 cal/mol.

Isotherms for the bulk characteristics and profiles of surface properties were plotted for temperatures τ = 0.68 and 0.85 (τ = T/T_cr, where T_cr is the critical temperature of a fluid in the bulk phase). To simplify calculations, it was assumed that ${{a}_{q}} = 1$, meaning there was no external potential.

The width of the interface (κ) and the radii of equilibrium drops (R) were measured in units of lattice structure parameter λ (λ = 1.12σ, where σ is the parameter of the Lennard–Jones potential), which is the mean distance between molecules in the dense phase, or in the numbers of monolayers. In other words, κ and R represented dimensionless values.

The values of ST were derived as the product per cell area of lattice gas А in the same units specified for ${{\varepsilon }_{{{\text{AA}}}}}$, cal/mol. Functions $M_{q}^{i}(k)$ were also derived in units of cal/mol.

We considered the temperature dependences of ST on a planar interface in the τ = 0.6 to 1 range of temperatures (up to the critical point), along with the dependences of ST on minimum size R = R₀ of a drop up to R = 800 monolayers at τ = 0.68 and 0.85.

RESULTS AND DISCUSSION

Bulk Phase

Figure 1а shows isothermal dependences of the density of component A, θ_A, and chemical potential ln(a₀P) in the system at (1) τ = 0.68 and (2) 0.85, where a₀ = β${{{v}}_{0}}$. The dashed line indicates the Van der Waals loop.

Fig. 1.

(a) Isothermal dependences of the chemical potential on the density of А; (b) pressure a₀P in phases and temperature dependences of the properties of coexisting phases.

A real isotherm (the bold curves in Fig. 1a) is split into two branches of vapor (on the left at low densities) and liquid (on the right at high densities), separated from each other by a horizontal section that shows the isothermal delayering of the two-phase system at equilibrium chemical potential ln(a₀P). The densities of the liquid and gas are constant and correspond to values $\theta _{{{\text{liq}}}}^{{\text{A}}}$ and $\theta _{{{\text{vap}}}}^{{\text{A}}}$. Densities $\theta _{{{\text{liq}}}}^{{{\text{A(1)}}}}$ and $\theta _{{{\text{vap}}}}^{{{\text{A(1)}}}}$ correspond to curve 1; densities $\theta _{{{\text{liq}}}}^{{{\text{A(2)}}}}$ and $\theta _{{{\text{vap}}}}^{{{\text{A(2)}}}}$, to curve 2. According to Fig. 1a, equilibrium chemical potential ln(a₀P) grows along with temperature, and densities $\theta _{{{\text{liq}}}}^{{\text{A}}}$ and $\theta _{{{\text{vap}}}}^{{\text{A}}}$ of the coexisting phases converge. The part of the loop indicated by the dashed line in Fig. 1a with negative compressibility does not correspond to thermodynamic stability (i.e., the points on these sections correspond to unstable states of matter, and such states cannot be obtained). These sections reflect the concept of Maxwell’s rule [12–15].

Figure 1b shows the temperature dependences of densities (1) $\theta _{{{\text{liq}}}}^{{\text{A}}}$ and (2) $\theta _{{{\text{vap}}}}^{{\text{A}}}$ of coexisting phases, the magnitudes of which are plotted on the left ordinate axis, and equilibrium chemical potential ln(a₀P) (3), the magnitudes of which are plotted on the right ordinate axis. The chemical potential in system (3) grows along with temperature, and the densities of coexisting phases (1 and 2) converge.

Figure 2a shows concentration profiles of component A in monolayers of the transitional region, 1 ≤ q ≤ κ, where q = 1 and κ corresponds to monolayers from the liquid and vapor phases, respectively, at the planar interface (1, 2), and in the case of an equilibrium drop with radius R = 200 (3, 4) at τ = 0.68 (1, 3) and 0.85 (2, 4). Figure 2b shows the temperature dependence of the width of transitional region κ with the planar interface.

Fig. 2.

(a) Concentration dependences of the density of А between coexisting phases (clarification in text) and (b) temperature dependence of the width of transitional region between phases.

The curves in Fig. 2a show that the width of the transitional region of the flat boundary grows along with temperature. Curve 1 transitions to curve 2 and curve 3 transitions to curve 4, while the densities of coexisting phases converge.

The transition from curve 1 to 3 in Fig. 2a (and by analogy, from curve 2 to 4) is associated with a transition from a flat boundary to a spherical equilibrium drop with radius R = 200, and a reduction in the width of the transitional region at constant densities of coexisting phases is observed. The concentration profile transitions to a liquid with a reduction in the radius of an equilibrium drop (i.e., the equimolecular surface shifts from the center of the transitional region, where it is located when there is a flat interface, to the drop).

The temperature dependence of the width of the transitional region between phases is presented in Fig. 2b. Width κ of the of transitional region grows along with temperature. Width κ changes in a discrete manner according to the number of monolayers, reflecting the discrete nature of matter at the molecular level.

Functions М _i(k) in the Bulk Phase

Before calculating ST, let us compare functions (8)–(10) in the bulk phase. In addition to the three versions of functions М_i(k), k = 1–3, we consider М_i(k = 2) [36] indicated as М_i(k = 2*). It is expressed as

$$M_{q}^{i}(2) = \nu _{q}^{i} + kT\ln \theta _{q}^{i} + kT\sum\limits_{p = q - 1}^{q + 1} {{{z}_{{qp}}}\ln \frac{{\hat {\theta }_{{qp}}^{{i{\text{V}}}}}}{{\theta _{q}^{i}\theta _{q}^{{\text{V}}}}}} .$$

(9*)

Its differs from functions М_i(k = 2) because of the division according to the density of vacancies in the logarithmic component (at p = q). The form of this function converges to that of functions М_i(k = 3) (10). When there are vacancies in function М_V(k = 2*), the logarithmic component coincides with the analogous one in Eq. (10), except for coefficient 1/2 before the sign of logarithm.

Figure 3 shows temperature dependences of functions Mⁱ(k) in liquid $M_{{{\text{liq}}}}^{i}$(k) (1–4) and pair $M_{{{\text{vap}}}}^{i}$(k) (5–8) of components i = A (Fig. 3a) and V (Fig. 3b). Version k = 1 is shown by curves 1 and 5; version k = 2, by curves 2 and 6; version k = 2*, by curves 3 and 7; and version k = 3, by curves 4 and 8. The left ordinate axis plots the values on curves 1, 3–5, and 7, 8 for versions k = 1, 2*, and 3, while the right ordinate axis plots those on curves 2 and 6 for version k = 2. The curves associated with different axes differ notably from one another.

Fig. 3.

Temperature dependences of functions Mⁱ(k) of components i = (a) A and (b) V.

In versions k = 1 and 3, the values of functions Mⁱ(k) coincide in liquid and vapor, $M_{{{\text{liq}}}}^{i}$(k) = $M_{{{\text{vap}}}}^{i}$(k). Between these versions, they coincide for i = A (Fig. 3a) and V (Fig. 3b). Curves 1, 4, 5, and 8 coincide on both fields of Fig. 3. In versions k = 2 and 2*, the values of functions Mⁱ(k) differ in liquid and vapor, and their magnitudes converge as the temperature rises. Curves 2 and 6 for k = 2 and curves 3 and 7 for k = 2* converge as the temperature rises.

Chemical Potential

The difference between functions М_i(k) added to Eq. (4) for i = A and V determines the chemical potential in the bulk phase. Using the above relations and conditions of calculation, we obtain

$$\begin{gathered} M_{q}^{{\text{A}}}(k)-M_{q}^{{\text{V}}}(k) = {{M}_{{\text{A}}}}(k)-{{M}_{{\text{V}}}}(k) \\ = {{\beta }^{{ - 1}}}\ln (\beta {{v}_{0}}P) = {{\nu }_{{\text{A}}}} - {{\nu }_{{\text{V}}}}. \\ \end{gathered} $$

(13)

In all four versions of the functions, k = 1 (8), 2 (9), 3 (10), and 2* (9*). In other words, all considered versions of the differences between functions М_i(k) in the bulk phase are equivalent, since they reflect the general state of the bulk phase, which is in no way related to the presence of a phase boundary. This is essential when comparing approaches to calculating ST under identical conditions in the bulk phases.

Equations for concentration profile (6) have these phases as boundary conditions, so the solutions presented in Fig. 2 are identical for all subsequent versions of calculating ST. (However, there are no calculations of ST for version 2* below because all values for it are negative, which contradicts the physical meaning of ST for delayering.) Our consideration of version 2* is due to Eq. (13) being fulfilled for it as with other versions of functions M_i(k). This testifies to the variety of different ways of constructing functions M_i(k) that correspond to the constant value of chemical potential in bulk phases and the constant value of concentration profile.

Functions $M_{q}^{i}$(k) of Interfaces

The values of functions $M_{q}^{i}$(k) for different monolayers q of the transitional regions of interfaces show their relative contributions to local values of free energy. Profile (6) is fixed, while to calculate ST we must know the differences between these functions for components i = A and V. Figure 4 shows the profiles of contributions ($M_{q}^{i}$(k) − M_i(k)) of components i = A (1–3) and V (4–6) to ST in the transitional region on the planar lattice (Figs. 4a, 4b) and for a drop with radius R = 200 (Figs. 4c, 4d) at τ = 0.68 (Figs. 4a, 4c) and 0.85 (Figs. 4b, 4d). Version k = 1 is shown by curves 1 and 4 with squares; version k = 2, curves 2, 5 with dots; and version k = 3, curves 3, 6 with triangles. The left ordinate axis plots the values on curves 1, 3, 4, and 6 for versions k = 1 and 3; the right ordinate axis, on curves 2 and 5 for version k = 2. The dashed line shows the level of zero values ($M_{q}^{i}$(k) − M_i(k)) on the left and right ordinate axes.

Fig. 4.

Profiles of contributions to ST. See designations in the text.

In all fields of Fig. 4, curves 1 and 2 plotted for component A coincide with curves 4 and 5 plotted for V. This is a consequence of fulfilling identity $M_{q}^{i}$(k) − $M_{q}^{j}$(k) = M_i(k) − M_j(k) = β⁻¹ln(a₀P) for versions k = 1 and 2. In version k = 3, this identity is valid only for bulk phases M_i(3) − M_j(3) = β^–1ln(a₀P) and not for transitional zone $M_{q}^{i}$(3) − $M_{q}^{j}$(3) ≠ β^–1ln(a₀P).

Curves 1 and 4 according to version k = 1, curves 2 and 5 according to version k = 2, and curve 6 according to version k = 3 show positive contributions ($M_{q}^{i}$(k) − M_i(k)) from the liquid and negative values from the vapor. Curve 3 according to version k = 3 gives only positive contributions ($M_{q}^{i}$(k) − M_i(k)) from the vapor and negative values from the liquid.

According to version k = 3, curves 3 and 6 on the planar interface (Figs. 4а, 4b) are symmetric relative to θ = 0.5, which is also not greatly distorted for a drop with radius R = 200 (Figs. 4c, 4d). According to versions k = 1 and 2, curves 1, 4 and 2, 5, respectively, do not have the same symmetry of contributions from liquid and vapor. ST values (7) according to definitions 1–3 are calculated as the sum of positive and negative contributions ($M_{q}^{i}$(k) − M_i(k)) from components А (1–3) and V (4–6), which are weighed according to the local densities of A and V component, respectively. It should be noted that due to the identities of $M_{q}^{{\text{A}}}$(k) − $M_{q}^{{\text{V}}}$(k) = M_A(k) − M_V(k) in versions k = 1 and 2, the ST values can also be calculated as the sum of contributions ($M_{q}^{i}$(k) − M_i(k)) according to only one A or V component (without weighing according to density).

The analogous statement for version k = 3 is not valid, due to inequality $M_{q}^{{\text{A}}}$(3) − $M_{q}^{{\text{V}}}$(3) ≠ M_A(3) − M_V(3). The definition of (7) through functions (10) is therefore the weighted mean of the densities of molecules A and vacancies. It differs from ST through functions (11), which contain only contributions from vacancies, and this gives different values of ST.

Planar Boundary

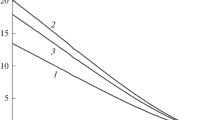
Figure 5 shows temperature dependences of ST according to versions 1–4 (curve numbers correspond to version numbers). The ordinate axis on the left gives the values on curves 1, 3, and 4 for corresponding definitions of ST and the ordinate axis on the right shows those on curve 2 for the second definition of ST.

Fig. 5.

Temperature dependences of ST in the considered versions of ST definitions.

Figure 5 shows a drop in ST upon raising T to zero at the critical point (τ = 1) for all definitions. Curves 1 and 4 have similar values and virtually coincide, according to corresponding definitions of ST.

All curves 1–4 in Fig. 5 have a nearly linear form at temperatures τ of 0.6 to 0.8. Near critical point (τ = 1), definitions 1, 3, and 4 (1, 3, and 4) give a positive value of the second derivative of ST according to temperature T, while curve 2 has a negative band in this region according to definition 2.

Drop Boundary

Figure 6 shows the size dependences σ of ST, normalized according to the value for planar interface σ_bulk according to versions 1–4 (curve numbers correspond to version numbers) at τ = 0.85 (Fig. 6a), 0.68 (Fig. 6b), and 0.54 (Fig. 6c). The dashed line in the plots shows the level of σ/σ_bulk = 1.

Fig. 6.

Dimensional dependences of ST in considered versions of ST definitions for three temperature values: τ = (а) 0.85, (b) 0.68, and (c) 0.54.

In Fig. 6a, there is a monotonous drop in ST with a rise in the radius of an equilibrium drop according to all four versions (curves 1–4) from ST value σ_bulk on a planar interface up to zero at minimum drop radius R₀, which corresponds to its state as the phase. The highest R₀ value is observed for the first definition (curve 1). There is then R₀ according to version 4 (curve 4); and the lowest R₀ value is for versions 2 and 3 (curves 2 and 3, respectively). These relations are the same for all considered temperatures in Figs. 6а–6c.

At reduced temperatures (Figs. 6b, 6c), we observe a gradual change in ST with a reduction in R. This is a consequence of a discrete change in the width of transitional region κ (i.e., a characteristic of matter that is especially clear at small sizes of the phase at low temperatures). The monotonous drop in ST upon a reduction in R is preserved (curves 1, 2, and 4, respectively) in versions of ST according to definitions 1, 2, and 4. Version 3 at low temperatures (curve 3 in Fig. 6b) above R* raises ST with a reduction in R from ST value σ_bulk on a planar interface and above. Below R* on curve 3 in Fig. 6b, ST acquires a value below σ_bulk as a result of a gradual drop. It then falls monotonously with a reduction in R.

The relative arrangement of curves changes at temperatures near the triple point (Fig. 6c), and curve 1 above R* raises the ST upon a reduction in R (its maximum value is higher than line σ/σ_bulk = 1 by ~5%). It is zero below R* on curve 1 in Fig. 6c as a result of a gradual drop in ST. Curves 2–4 show a monotonous drop in ST upon a reduction in R.

CONCLUSIONS

All of the considered ST definitions represent the sum of local excess values of $M_{q}^{i}$(k) in monolayers of the liquid–vapor transitional zone, compared to the values in the phases, which vary from liquid to vapor in a sinusoidal form, creating a minimum in the range of negative contributions to ST and a maximum in the range of positive contributions.

Calculations according to thermodynamic definition of ST (7), which are based on three functions $M_{q}^{i}$(k), k = 1–3, showed different behavior for the planar and curved drop boundaries. This testifies to the ambiguity of the thermodynamic definition of ST (7), since all types of M_i(k) functions in the bulk phase are clearly associated with chemical potential of molecules (13). The temperature and size dependences of ST at τ = const for different versions of the ST definition were compared using the general concentration profile of molecules between phases.

With a planar boundary (Fig. 5), curves 1, 2, and 3 differ considerably from one another, even though a drop in ST was obtained for all definitions upon raising T to zero at the critical point (τ = 1). A comparison of these curves and definition (11) of ST based on additional consideration of the specific character of vacancies in the LGM as a mechanical characteristic of the system shows that curves 1 and 4 virtually coincide, while curves 2 and 3 differ notably from curve 4. Curve 2 differs fundamentally from other versions in its temperature dependence, due to the negative bend (the second derivative according to temperature is less than zero) of the curve of the dependence near the critical point.

Size dependences of the considered definitions of ST (Fig. 6) diverge for all versions, even though a monotonous drop in the normalized value of ST is a general trend from the total bulk value upon reducing drop radius R to the minimum size of phase R₀, except for curve 3 at τ = 0.68 and curve 1 at τ = 0.54. The slight exceeding of line σ(R)/σ_bulk = 1 by ST on these curves (up to several percent) are due to the drastic change in the profile at short drop radii within the LGM. Assuming the lattice structure is soft lowers the maximum values of σ(R)/σ_bulk near line σ(R)/σ_bulk = 1 [37]. A comparison of the dependences for three types of ST calculated according to thermodynamic definition with curve 4 (Eq. (11)) shows the strong dependence of the relative position of curve 4 and dimensional curves σ(R)/σ_bulk with different functions $M_{q}^{i}$(k), k = 1–3, depending on temperature.

Our analysis of different definitions of ST created by using different functions $M_{q}^{i}$(k) in the LGM has shown the ambiguity of definitions of ST (k = 1, 2, 2*, and 3) according to the thermodynamic definition of ST at identical phase states of coexisting vapor and liquid phases and identical concentration profiles between these phases. Identical conditions of the state of a system correspond to different functions $M_{q}^{i}$(k), k = 1, 2, 2*, and 3, which represent local partial contributions from components of lattice system i at nodes of type q in the equation for excess free energy ΔF within the LGM. Equalities $\mu _{q}^{{\text{A}}}$(k) = $M_{q}^{{\text{A}}}$(k) − $M_{q}^{{\text{V}}}$(k) = μ_А are fulfilled for functions $M_{q}^{i}$(k), k = 1, 2, and 2*, but not for functions $M_{q}^{i}$(3). (It was indicated above that all ST values have nonphysical negative values for version 2*, even though $\mu _{q}^{{\text{A}}}$(2*) = $M_{q}^{{\text{A}}}$(2*) − $M_{q}^{{\text{V}}}$(2*) = μ_А).

The ambiguity of definitions of ST means it is not a purely equilibrium thermodynamic function with which fixed external conditions could clearly specify the internal characteristics of the system.